The Future Internet: A World of Secret Shares
Abstract
:1. Introduction
2. Founding Principles around Secure Data Storage
- Keyless encryption method. While the methods employed in modern encryption are often theoretically watertight, it is the actual implementation in real-life systems which are flawed. Most systems still rely on digital certificates holding a key-pair, and these certificates are all too easily stolen or compromised through brute force attacks. The Superfish compromise highlights a weakness introduced by the software developers, where a digital certificate with both the public and private key was distributed with the software, and which also had a default password based on the name of the company who developed the software [2].
- Self-destruct. Some techniques support the concept of a self-destructing data system. With this, all the stored information and their copies, as well as decryption keys, will become unusable after a user-specified time period and without any user involvement. SeDas [3] causes sensitive information, such as account numbers, passwords and notes to irreversibly self-destruct, without any action on the user’s part. This technique is applicable in a multiple server-based system, admittedly incurring an operational overhead.
- Break-glass data recovery. Many systems have strict access control policies for data, but in some circumstances it is important that access to data can be granted in emergency situations. This is typical in life-threatening scenarios, such as in health and social care. The loss of an encryption key can also cause major problems in data recovery, which would hinder a break-glass requirement.
- In-built failover protection. For instance, data which needs redundancy can be replicated and encoded across multiple cloud-based storage systems using an any k-from-n sharing policy. So for example, with a storage system striped across three Cloud storage platforms, a policy of 2-from-3 can support a single Cloud storage systems failure, while still allowing the original data to be recovered.
3. Related Methods
3.1. Basic Data Striping and RAID Storage Systems
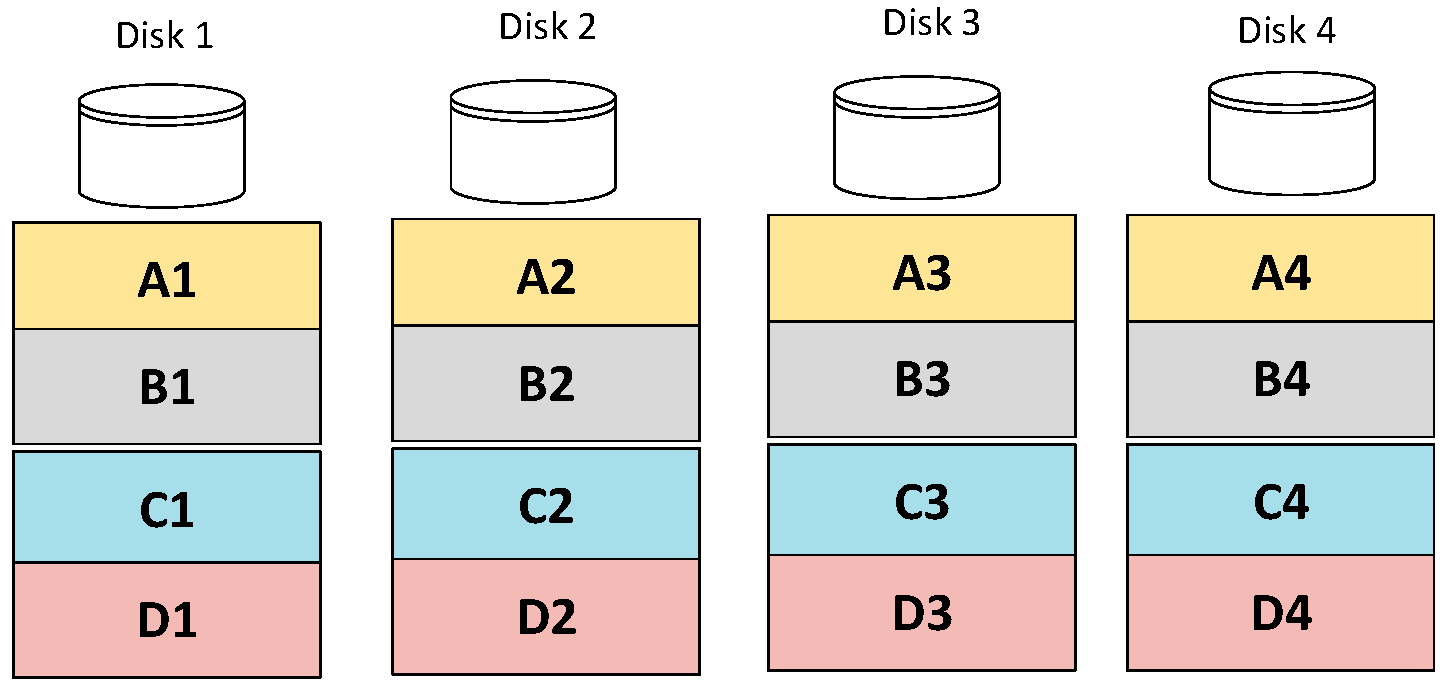
3.2. Reed-Solomon Error Correcting Code
4. Basic Data Striping Schemes in Cloud-Based Systems
- The Sharing Algorithm:Share(M) → (S1, S2, …. Sn, pub). The secrets S1, S2, …. Sn are distributed securely among servers 1 through to n, and pub is a public share.
- The Recovery Algorithm:(Sʹ1, Sʹ2, …. Sʹn, pub) = Mʹ. The correctness property of the algorithm defines that, for any message M, Rec(Share(M)) = M
- tp—the privacy threshold. This describes the maximum number of servers that cannot determine the secret, even when they combine their shares together.
- tf—the fault-tolerance threshold. With this, supposing that every server is honest, this is the minimum number of servers you need to recover the secret (if the other servers are absent).
- tr—the robustness threshold. This is arguably the most important, as this is the minimum number of correct shares you need to recover the secret if all other servers are compromised.
- ts—the soundness threshold. This determines the minimum number of correct shares such that it is not possible to recover the wrong secret.
- ti—the information rate threshold. This describes the amount of information that the server needs to keep on a secret and determines the efficiency and idealness of a secret sharing scheme.
4.1. Sharing Methods
4.1.1. Perfect Secret Sharing Scheme (PSS)
| x | y | |
| 1 | 42 + 1 + 2 × 1 | 45 |
| 2 | 42 + 2 + 2 × 4 | 52 |
| 3 | 42 + 3 + 2 × 9 | 63 |
| 4 | 42 + 4 + 2 × 16 | 78 |
| 5 | 42 + 5 + 2 × 25 | 97 |
| x | p | y | |
| 1 | 61 | (42 + 1 + 2 × 1) % 61 | 45 |
| 2 | 61 | (42 + 2 + 2 × 4) % 61 | 52 |
| 3 | 61 | (42 + 3 + 2 × 9) % 61 | 2 |
| 4 | 61 | (42 + 4 + 2 × 16) % 61 | 17 |
| 5 | 61 | (42 + 5 + 2 × 25) % 61 | 36 |
- Secure—Anyone with fewer than t shares has no extra information about the secret than someone with zero shares.
- Extensible—When n is fixed, new shares can be dynamically added or deleted without affecting the existing shares.
- Dynamic—With this it is possible to modify the polynomial and construct new shares without changing the secret.
- Flexible—In organisations where hierarchy is important, it is possible to supply each participant different number of shares according to their importance.
- Computational overheads—The preparation of the polynomial, the generation of shares, and the reconstruction of the secret may consume significant computational resources.
- Storage and transmission overheads—Given t − 1 shares, no information whatsoever can be determined about the secret. Hence, the final share must contain as much information as the secret itself, which means effectively each share of the secret must be at least as large as the secret itself. The storage and transmission of the shares requires an amount of storage space and network bandwidth equivalent to the size of the secret times the total number of shares.
4.1.2. Share Distribution
4.1.3. Information Dispersal Algorithm (IDA)
4.1.4. Krawczyk’s Computational Secret Sharing (CSS)
4.1.5. Rabin’s and Ben-Or’s Publicly Verifiable Secret Sharing (PVSS)
- (1)
- The dealer creates shares S1, S2, ..., Sn for each participant P1, P2, ..., Pn respectively;
- (2)
- The dealer encrypts the shares for each participant using their public keys and publishes the ciphertexts Ei(Si);
- (3)
- The dealer also publishes a string ProofD to show that each Ei encrypts Si and the reconstruction protocol will result in the same secret S;
- (4)
- Anybody knowing the public keys for the encryption methods Ei, can verify the shares;
- (5)
- If one or more verifications failed, the dealer fails and the protocol is aborted;
- (6)
- Each participant Pi decrypts their shares Si using Ei(Si);
- (7)
- The participant releases Si plus a string ProofPi to show that the released share is correct;
- (8)
- Dishonest participants who failed to decrypt Si or to generate ProofPi will be excluded;
- (9)
- The secret S can be securely reconstructed from the shares of any qualified set of participants.
5. Secret Sharing in a Multi-Cloud Environment
- Application platform. Its function is to: determines the access structure; encodes secrets; sends secrets to the main multi-cloud proxy server for distribution to multi-cloud service providers, as well as keeping the secret shares when recovered.
- Main multi-cloud proxy server with router. This splits and distributes encoded shares to multi-cloud based on pre-determined access structure and manages the fail-over protection of shares.
- Metadata server. This includes the functionality of: User management; Server management; Session management; and File metadata management [3].
- Multi-cloud proxy server. This Gathers shares and reconstruct secret as well manages break-glass data recovery.
- Sub-routers. This creates a path between the Cloud Service Provider (CSP) (considered here as front-end) with other Cloud Service providers (considered here as the Back-ends) thereby creating a quick and alternative recovery path for all the shares. For example: R4 connects with R3 + R2 + R1, so R4 is a path for CSP1 + R3 + R2 + R1 + S1, and so on.
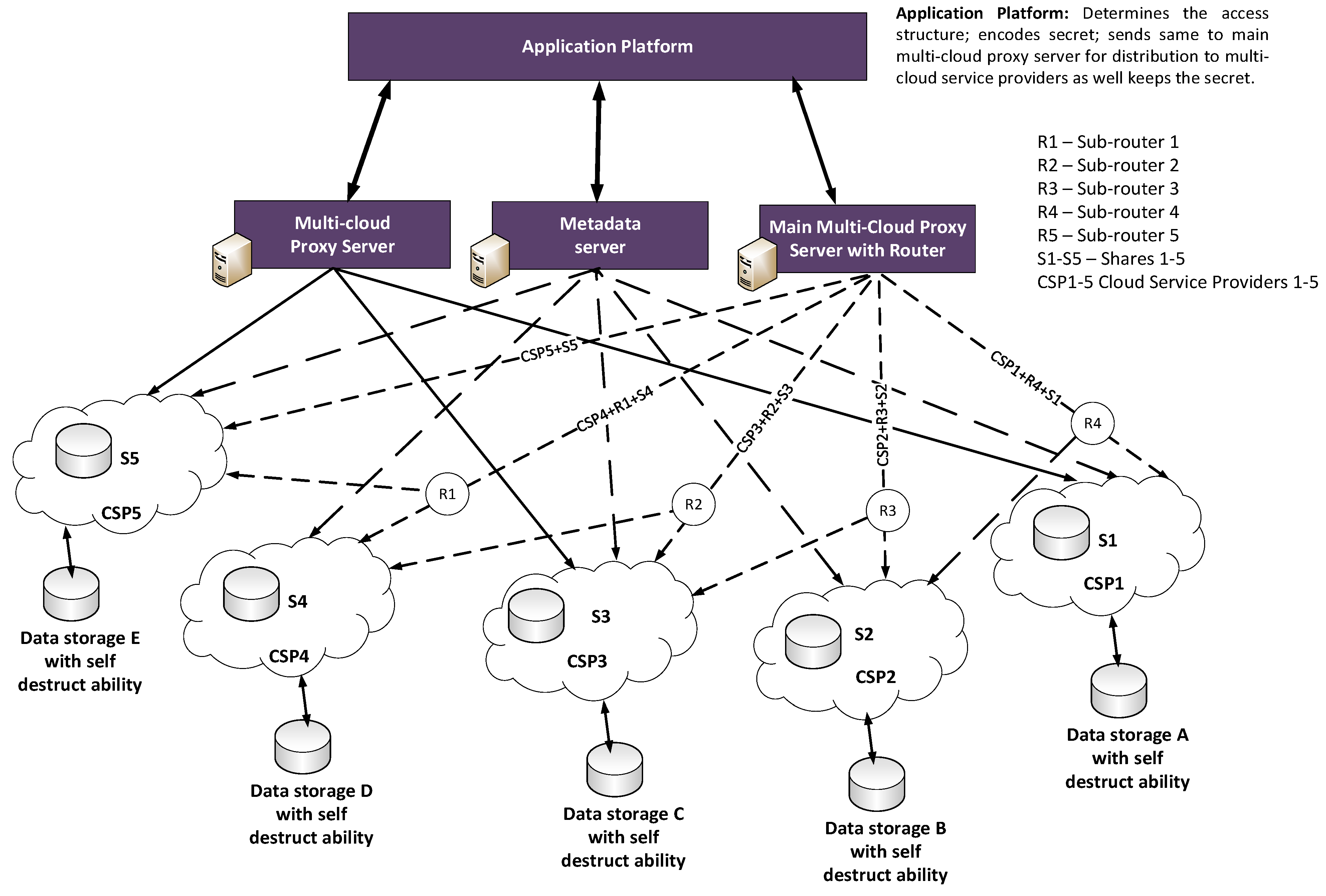
5.1. The SECRET Architecture
5.2. How It Works
- Fast and efficient data/key distribution to multi-cloud service providers.
- Keyless encryption and by extension data security and reduced key management hassles.
- Provide data owner’s privacy by implementing SeDas, as it meets all the privacy-preserving goals [3].
- SeDas supports security erasing files and random storage in drives (Cloud, HDD or SSD) respectively [3].
- Backup operational mode in which the function of 5 CSPs can be assumed by 3 CSPs when 2-out-of-the-5 CSPs become unavailable either through failure or scheduled down time.
- Break-glass data recovery.
6. Evaluation
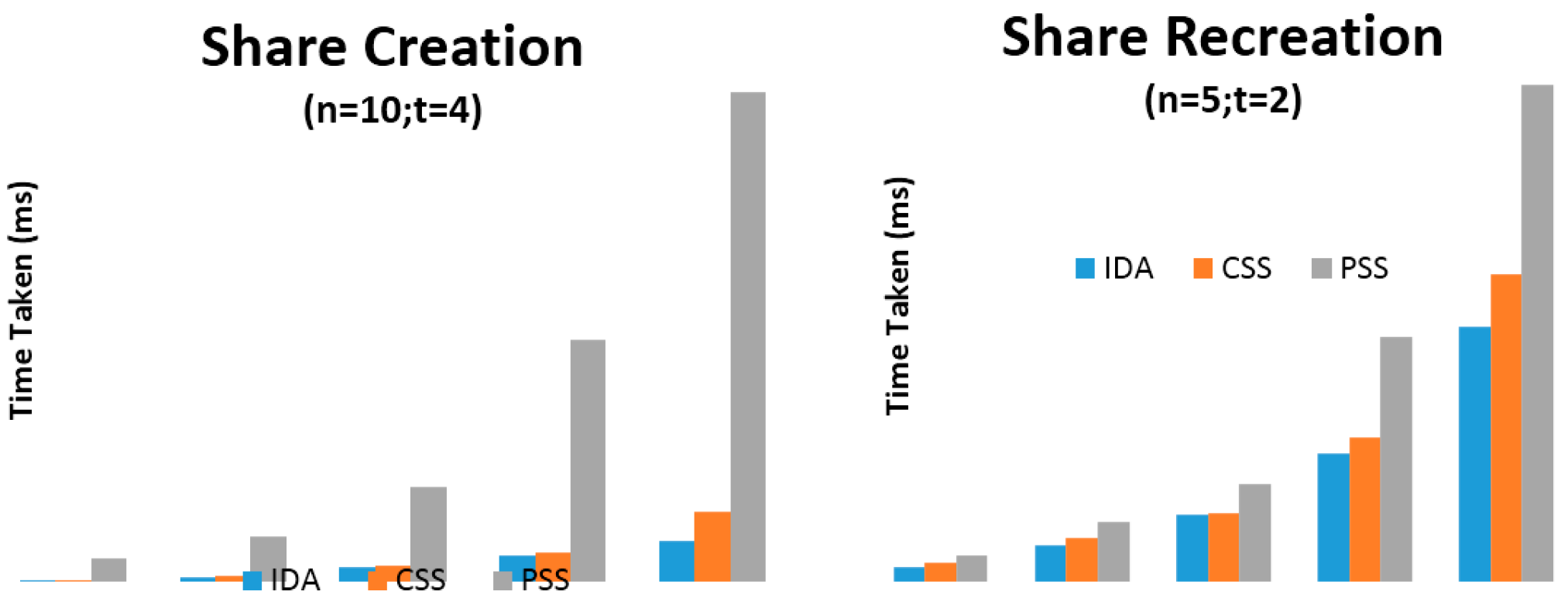
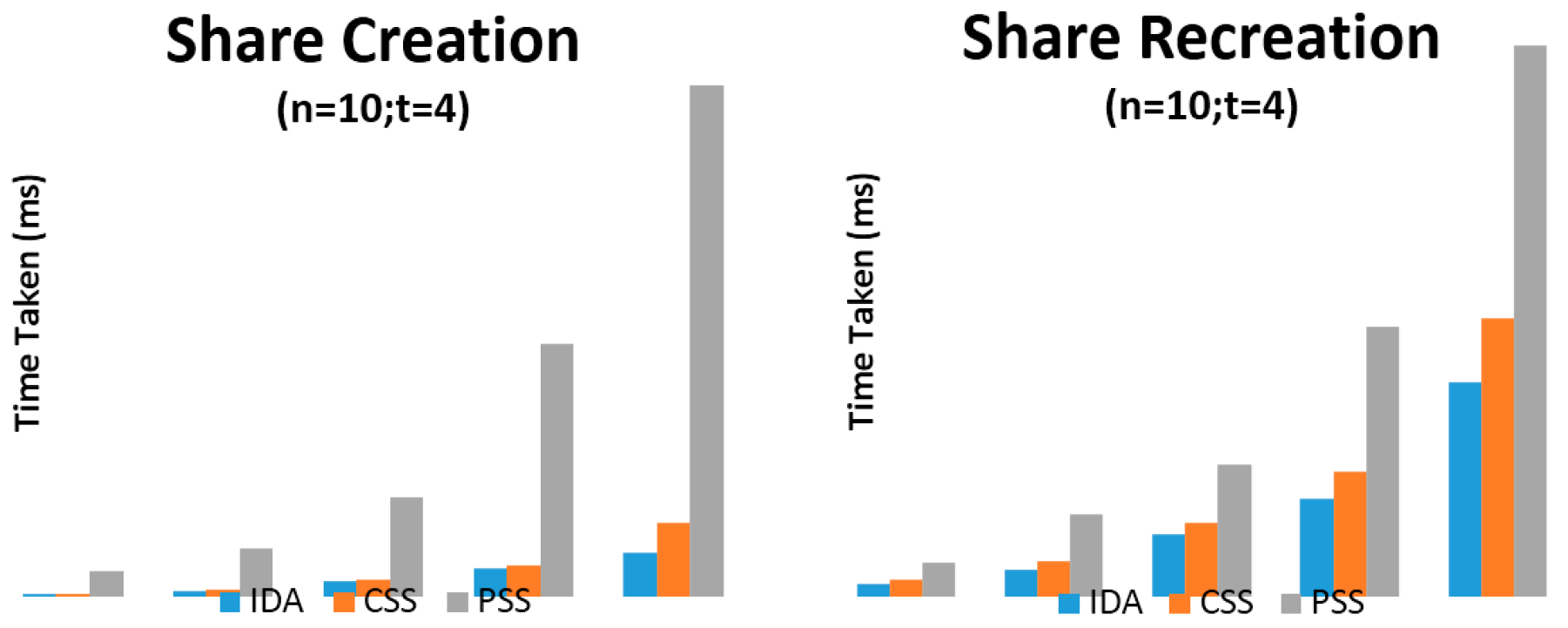
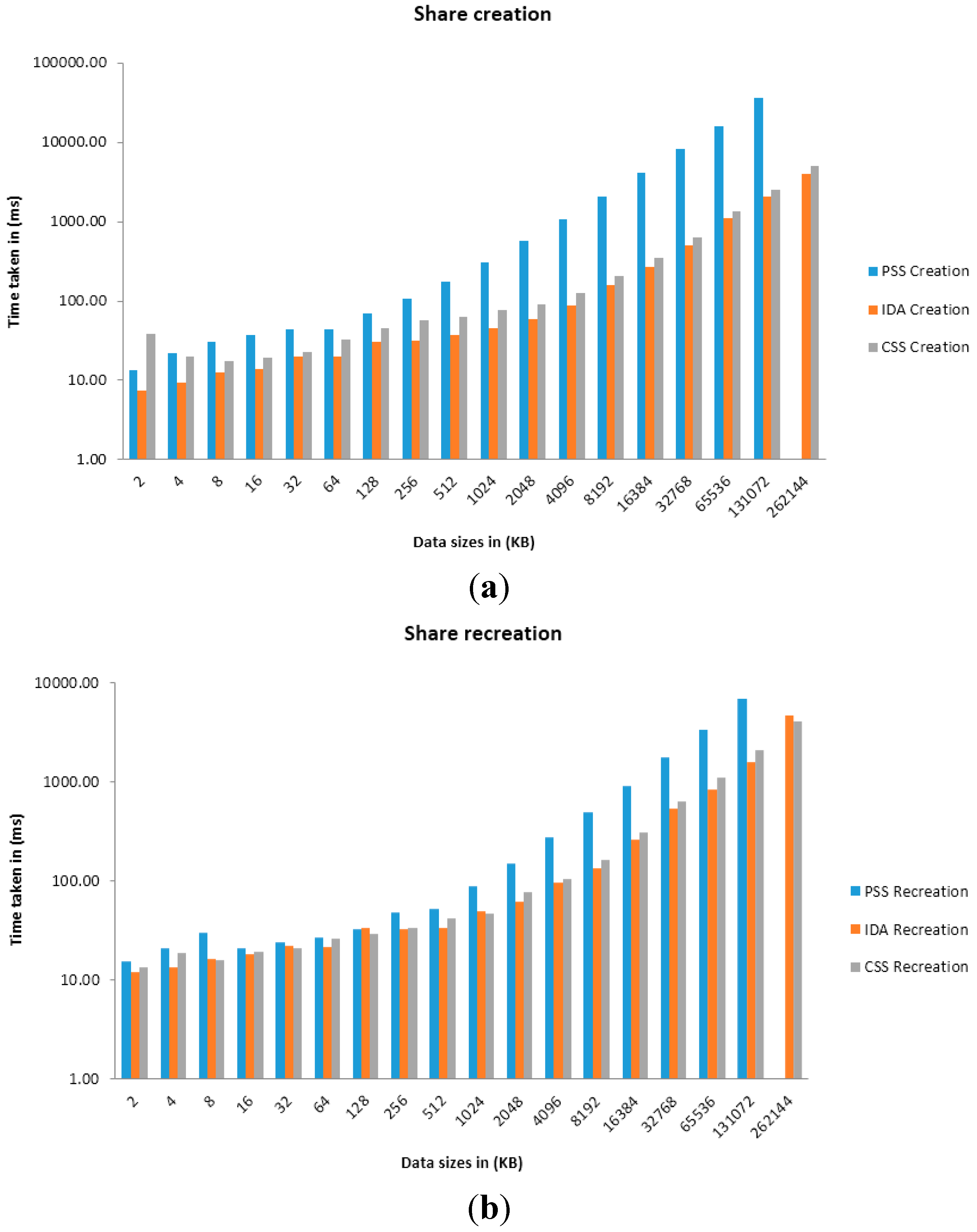
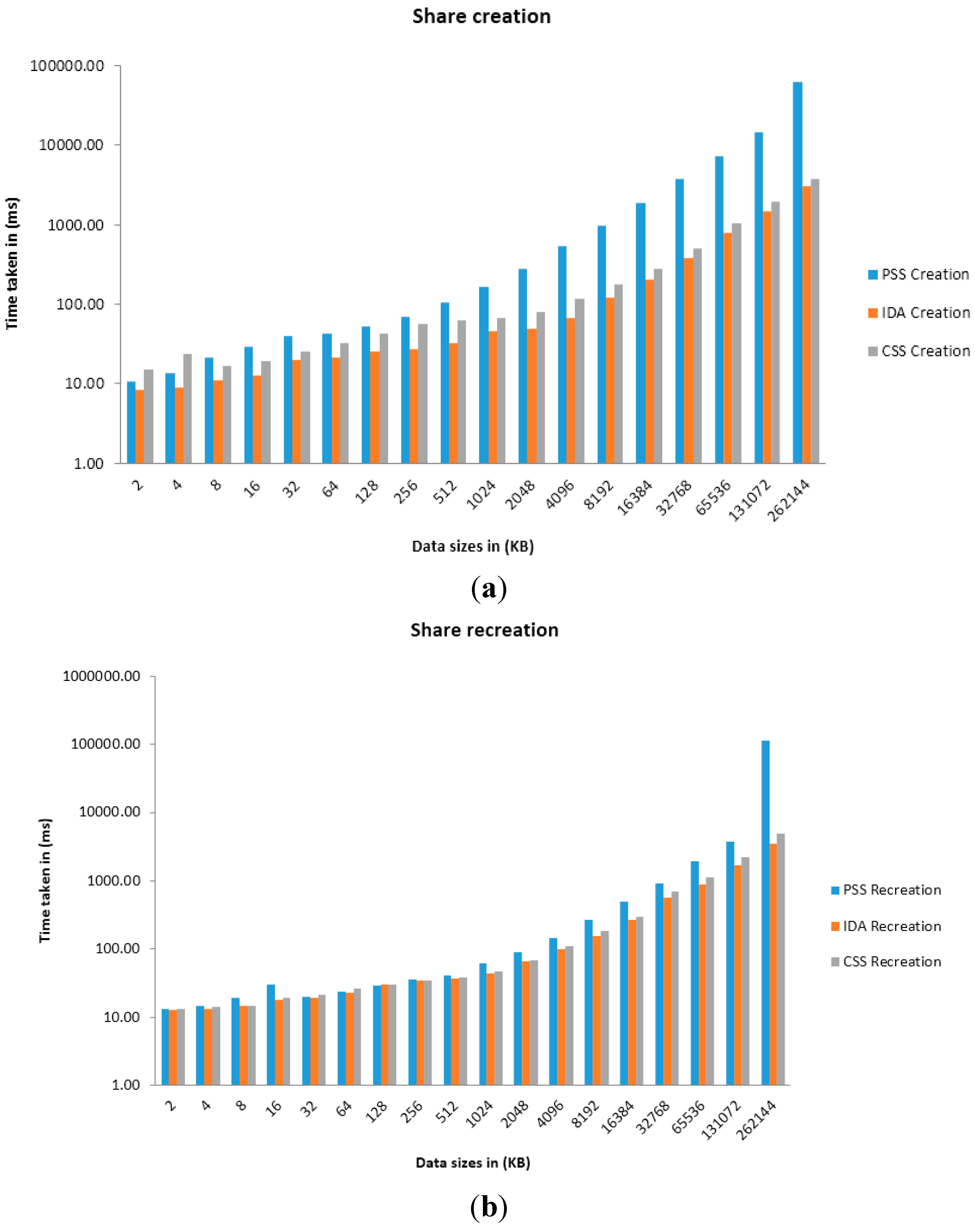
| Algorithm | 1024 (KB) | 2048 (KB) | 4096 (KB) | 8192 (KB) | 16384 (KB) |
|---|---|---|---|---|---|
| IDA | 14.42 | 31.90 | 65.83 | 126.52 | 274.43 |
| CSS | 21.27 | 43.29 | 97.25 | 174.97 | 380.53 |
| PSS | 172.21 | 304.94 | 622.16 | 1065.41 | 2228.30 |
| Algorithm | 1024 (KB) | 2048 (KB) | 4096 (KB) | 8192 (KB) | 16384 (KB) |
|---|---|---|---|---|---|
| IDA | 26.35 | 63.39 | 116.69 | 223.60 | 445.53 |
| CSS | 35.01 | 76.88 | 121.42 | 251.43 | 536.36 |
| PSS | 45.69 | 104.73 | 171.81 | 428.29 | 867.35 |
| Algorithm | 1024 (KB) | 2048 (KB) | 4096 (KB) | 8192 (KB) | 16384 (KB) |
|---|---|---|---|---|---|
| IDA | 19.97 | 58.90 | 185.20 | 333.22 | 518.00 |
| CSS | 26.80 | 70.81 | 192.48 | 367.04 | 871.62 |
| PSS | 298.25 | 567.11 | 1169.94 | 3013.11 | 6091.91 |
| Algorithm | 1024 (KB) | 2048 (KB) | 4096 (KB) | 8192 (KB) | 16384 (KB) |
|---|---|---|---|---|---|
| IDA | 21.04 | 45.11 | 104.75 | 163.78 | 362.32 |
| CSS | 26.83 | 59.10 | 122.94 | 210.51 | 470.08 |
| PSS | 56.79 | 139.10 | 222.47 | 455.58 | 932.91 |
| Algorithm | 2 (KB) | 4 (KB) | 8 (KB) | 16 (KB) | 32 (KB) | 64 (KB) | 128 (KB) | 256 (KB) | 512 (KB) | 1024 (KB) | 2048 (KB) | 4096 (KB) | 8192 (KB) | 16384 (KB) | 32768 (KB) | 65536 (KB) | 131072 (KB) | 262144 (KB) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CSS | 38.21 | 20.26 | 17.21 | 19.31 | 23.07 | 32.86 | 44.94 | 56.65 | 63.39 | 77.71 | 90.95 | 125.22 | 203.46 | 350.05 | 637.28 | 1337.67 | 2492.91 | 5005.75 |
| IDA | 7.31 | 9.47 | 12.43 | 13.78 | 19.98 | 20.21 | 30.82 | 31.14 | 36.97 | 44.93 | 59.78 | 87.37 | 156.65 | 268.90 | 505.48 | 1109.95 | 2042.17 | 4030.90 |
| PSS | 13.44 | 22.21 | 30.40 | 37.04 | 44.05 | 44.65 | 70.71 | 106.58 | 175.70 | 306.61 | 564.58 | 1067.90 | 2078.61 | 4129.68 | 8163.94 | 15999.61 | 36832.71 | - |
| Algorithm | 2 (KB) | 4 (KB) | 8 (KB) | 16 (KB) | 32 (KB) | 64 (KB) | 128 (KB) | 256 (KB) | 512 (KB) | 1024 (KB) | 2048 (KB) | 4096 (KB) | 8192 (KB) | 16384 (KB) | 32768 (KB) | 65536 (KB) | 131072 (KB) | 262144 (KB) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CSS | 13.57 | 18.60 | 16.08 | 19.05 | 21.23 | 26.35 | 29.21 | 33.62 | 41.61 | 46.66 | 77.40 | 104.98 | 162.85 | 305.54 | 639.02 | 1104.15 | 2103.79 | 4050.72 |
| IDA | 12.03 | 13.32 | 16.56 | 18.49 | 21.94 | 21.66 | 33.58 | 32.53 | 34.03 | 48.91 | 62.42 | 96.28 | 135.73 | 263.71 | 535.24 | 832.55 | 1595.89 | 4722.39 |
| PSS | 15.44 | 20.92 | 29.91 | 20.73 | 24.11 | 26.85 | 32.96 | 48.69 | 52.16 | 88.83 | 149.98 | 272.39 | 492.71 | 908.36 | 1779.57 | 3341.85 | 6930.38 | - |
| Algorithm | 2 (KB) | 4 (KB) | 8 (KB) | 16 (KB) | 32 (KB) | 64 (KB) | 128 (KB) | 256 (KB) | 512 (KB) | 1024 (KB) | 2048 (KB) | 4096 (KB) | 8192 (KB) | 16384 (KB) | 32768 (KB) | 65536 (KB) | 131072 (KB) | 262144 (KB) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CSS | 15.08 | 23.72 | 16.70 | 19.45 | 25.03 | 31.80 | 42.57 | 55.58 | 61.69 | 68.02 | 79.97 | 115.65 | 175.01 | 277.30 | 501.91 | 1040.84 | 1943.00 | 3765.50 |
| IDA | 8.34 | 8.97 | 11.05 | 12.82 | 19.59 | 21.19 | 24.93 | 27.22 | 32.88 | 45.00 | 49.39 | 67.36 | 119.23 | 204.49 | 377.09 | 792.22 | 1468.66 | 3034.31 |
| PSS | 10.82 | 13.51 | 21.51 | 28.78 | 40.01 | 42.89 | 52.80 | 68.67 | 106.28 | 166.79 | 277.36 | 529.73 | 971.72 | 1902.44 | 3792.03 | 7311.64 | 14605.74 | 63156.81 |
| Algorithm | 2 (KB) | 4 (KB) | 8 (KB) | 16 (KB) | 32 (KB) | 64 (KB) | 128 (KB) | 256 (KB) | 512 (KB) | 1024 (KB) | 2048 (KB) | 4096 (KB) | 8192 (KB) | 16384 (KB) | 32768 (KB) | 65536 (KB) | 131072 (KB) | 262144 (KB) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CSS | 13.19 | 14.12 | 14.53 | 19.27 | 21.63 | 26.11 | 29.64 | 33.98 | 37.52 | 47.30 | 69.14 | 109.34 | 181.29 | 300.20 | 707.48 | 1106.48 | 2215.46 | 4826.05 |
| IDA | 12.69 | 13.13 | 14.71 | 17.82 | 19.51 | 22.57 | 29.58 | 34.79 | 37.39 | 44.34 | 64.87 | 98.49 | 152.63 | 269.23 | 561.52 | 885.50 | 1711.26 | 3466.03 |
| PSS | 13.18 | 14.87 | 19.02 | 30.01 | 20.00 | 23.89 | 29.25 | 35.07 | 40.46 | 60.76 | 89.60 | 145.85 | 265.34 | 498.64 | 906.07 | 1935.26 | 3692.24 | 113498.21 |
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Abbadi, I.M. Cloud Management and Security; John Wiley & Sons Ltd.: Chichester, UK, 2014; p. 2. [Google Scholar]
- Buchanan, W.J. Storing The Keys to your House Under a Plant Pot. Available online: https://www.linkedin.com/pulse/storing-keys-your-house-under-plant-pot-william-buchanan (accessed on 1 April 2015).
- Zeng, L.; Chen, S.; Wei, Q.; Feng, D. Sedas: A self-destructing data system based on active storage framework. In Proceedings of the 2012 Digest APMRC, Singapore, 31 October–2 November 2012; pp. 1–8.
- Cipra, B.A. The Ubiquitous Reed-Solomon Codes; SIAM: Philadelphia, PA, USA, 1993; Volume 26, (1). [Google Scholar]
- Morozan, I. Multi-Clouds Database: A New Model to Provide Security in Cloud Computing. Available online: https://www.researchgate.net/publication/273136522 (accessed on 1 April 2015).
- Dodis, Y. Exposure-Resilient Cryptography. PhD Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, August 2000. [Google Scholar]
- Patel, A.; Soni, K. Three Major Security Issues in Single Cloud Environment. Int. J. Adv. Res. Comput. Sci. Software Eng. 2014, 4, 268–271. [Google Scholar]
- Padsala, C.; Palav, R.; Shah, P.; Sonawane, S. Survey of Cloud Security Techniques. Int. J. Res. Appl. Sci. Eng. Technol. 2015, 3, 47–50. [Google Scholar]
- Mounica, D.; Rani, M.C.R. Optimized Multi-Clouds using Shamir Shares. Int. J. Dev. Comput. Sci. Technol. 2013, 1, 83–87. [Google Scholar]
- Bharambe, J.V.; Makhijani, R.K. Secured Data Storage and Retrieval in Multi-Cloud using Shamir’s Secret Sharing Algorithm. Int. J. Comput. Sci. Eng. 2013, 2, 15–19. [Google Scholar]
- Mallareddy, A.; Bhargavi, V.; Rani, K.D. A Single to Multi-Cloud Security based on Secret Sharing Algorithm. Int. J. Res. 2014, 1, 910–915. [Google Scholar]
- Padmavathi, M.; Sirisha, D.; Lakshman, R.A. The Security of Cloud Computing System Enabled by Shamir’s Secret Sharing Algorithm. Int. J. Res. Stud. Sci. Eng. Technol. 2014, 1, 103–109. [Google Scholar]
- Makkena, T.; Rao, T.P. A Shamir Secret Based Secure Data sharing between Data owners. Int. J. Eng. Trends Technol. 2014, 16, 362–165. [Google Scholar]
- Beimel, A.; Chee, Y.M.; Guo, Z.; Ling, S.; Shao, F.; Tang, Y.; Wang, H.; Xing, C. (Eds.) Secret-Sharing Schemes: A Survey; Springer: Berlin Heidelberg, Germany, 2011; pp. 11–46.
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Rabin, M.O. Efficient Dispersal of Information for Security, Load Balancing and Fault Tolerance. J. ACM 1989, 36, 335–348. [Google Scholar] [CrossRef]
- Krawczyk, H. Secret Sharing Made Short. In Proceedings of the 13th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, CA, USA, 22–26 August 1993.
- Resch, J.; Plank, J. AONT-RS: Blending Security and Performance in Dispersed Storage Systems. In Proceedings of the 9th USENIX on File and Storage Technologies, San Jose, CA, USA, 15–17 February 2011.
- Rabin, T.; Ben-Or, M. Verifiable secret sharing and multiparty protocols with honest majority. In Proceedings of the Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 14–17 May 1989.
- Peng, K. Critical survey of existing publicly verifiable secret sharing schemes. Inf. Secur. 2012, 6, 249–257. [Google Scholar] [CrossRef]
- Ermakova, T.; Fabian, B. Secret sharing for health data in multi-provider clouds. In Proceedings of the 2013 IEEE 15th Conference on Business Informatics (CBI), Vienna, Austria, 15–18 July 2013; pp. 93–100.
- Fabian, B.; Ermakova, T.; Junghanns, P. Collaborative and secure sharing of healthcare data in multi-clouds. Inf. Syst. 2015, 48, 132–150. [Google Scholar] [CrossRef]
- Srinivasan, S. Building Trust in Cloud Computing: Challenges in the midst of outages. In Proceedings of the Informing Science & IT Education Conference (InSITE), Wollongong, Australia, 30 June–4 July 2014; pp. 305–312.
- Khoshkholghi, M.A.; Abdullah, A.; Latip, R.; Subramaniam, S.; Othman, M. Disaster recovery in cloud computing: A survey. Comput. Inf. Sci. 2014, 7, 39–54. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buchanan, W.J.; Lanc, D.; Ukwandu, E.; Fan, L.; Russell, G.; Lo, O. The Future Internet: A World of Secret Shares. Future Internet 2015, 7, 445-464. https://doi.org/10.3390/fi7040445
Buchanan WJ, Lanc D, Ukwandu E, Fan L, Russell G, Lo O. The Future Internet: A World of Secret Shares. Future Internet. 2015; 7(4):445-464. https://doi.org/10.3390/fi7040445
Chicago/Turabian StyleBuchanan, William J., David Lanc, Elochukwu Ukwandu, Lu Fan, Gordon Russell, and Owen Lo. 2015. "The Future Internet: A World of Secret Shares" Future Internet 7, no. 4: 445-464. https://doi.org/10.3390/fi7040445
APA StyleBuchanan, W. J., Lanc, D., Ukwandu, E., Fan, L., Russell, G., & Lo, O. (2015). The Future Internet: A World of Secret Shares. Future Internet, 7(4), 445-464. https://doi.org/10.3390/fi7040445






