Managing Emergencies Optimally Using a Random Neural Network-Based Algorithm

Abstract

Emergency rescues require that first responders provide support to evacuate injured and other civilians who are obstructed by the hazards. In this case, the emergency personnel can take actions strategically in order to rescue people maximally, efficiently and quickly. The paper studies the effectiveness of a random neural network (RNN)-based task assignment algorithm involving optimally matching emergency personnel and injured civilians, so that the emergency personnel can aid trapped people to move towards evacuation exits in real-time. The evaluations are run on a decision support evacuation system using the Distributed Building Evacuation Simulator (DBES) multi-agent platform in various emergency scenarios. The simulation results indicate that the RNN-based task assignment algorithm provides a near-optimal solution to resource allocation problems, which avoids resource wastage and improves the efficiency of the emergency rescue process.

1. Introduction

In real emergency environments, unprotected evacuees may be seriously injured and even immobilized, due to hazards, or may be trapped in disasters and find that there is no way out [1]. As a result, they need emergency personnel [2] to provide assistance and to take them out of the danger. Rescuers can move to the target locations quickly and protect themselves and evacuees from the danger by wearing special clothes and using protective devices, so that they can make a great contribution toward saving people from hazards [1]. However, the rescuers may run into danger and fail in saving a victim, since they move into hazardous sites, and they may not know which victim has been allocated a rescuer or which rescuer has been assigned a victim if there is no interaction between each assignment. These uncertain factors lead to a waste of resources and the inefficiency of resource allocations. Moreover, during an ongoing hazard, the decision making of how to allocate rescuers to victims requires a fast computational algorithm to provide advice in real-time. Therefore, a fast and efficient assignment approach that considers the possibility of unsuccessful rescue and the influence of other assignments should be addressed.

The paper investigates the problem of how to dispatch rescuers to save people out of danger efficiently when a limited set of rescuers needs to be allocated simultaneously to a set of injured civilians [3]. This is a kind of task assignment problem that aims at optimally matching the elements of two or more sets and reducing the overall cost of associated matchings [4]. Here, only two sets will be considered, which we refer to as “tasks (i.e., injured civilians)” and “resources (i.e., rescuers)”. Previous work [3] proposes that the random neural network (RNN) can be applied to resource allocation problems arising in emergency management to provide a decision quickly and exactly. Thus, we incorporate RNN-based techniques into a practical and realistic model where the evacuees and rescuers are modelled as agents with the help of the Distributed Building Evacuation Simulator (DBES), and the cost for each assignment is considered. Additionally, we test the effectiveness of the RNN-based algorithm for task assignments in an emergency.

In the RNN, every possible assignment is considered to be a neuron, and all neurons in the network are fully connected, that is, each executed assignment can have an effect on other allocations through the links between them. Furthermore, there is a cost objective function that can be formulated considering any uncertain parameters (i.e., RNN parameters) defined as needed, and an optimal assignment will minimize the expected cost. In this case, we can pick out an assignment that can maximally reduce the overall expected cost by updating RNN parameters iteratively until convergence, and then, this assignment will be executed.

The DBES multi-agent environment can capture the position and action of people in the area by using RFIDdevices and audiovisual sensors [5]; thus, if the evacuees are at stake in the building, the sensors will send a message to the rescuers and ask for help. The message received by the rescuers can include detailed information of the injured civilians, such as their ID and position. By applying the RNN-based algorithm, an assignment with the highest active probability will be executed. The duty of rescuers is then to move to the locations of the injured civilians, relying on the information received, and lead or take them to the best evacuation exit or assembly point. The rescuers will wear protective clothes to be less susceptible to injuring themselves, and they will carry protective devices to assist evacuees.

The remainder of the paper is organized as follows. Section 2 summarizes the related work on emergency management and the RNN-based techniques. Section 3 describes the design details of the RNN-based task assignment algorithm. Then, the simulation results are presented in Section 4, in which we show that the RNN-based algorithm can provide a near-optimal solution to resource allocation problems arising in emergency management. Finally, in Section 5, we conclude on the results and discuss the remaining problems of the algorithm and possible directions for future work.

2. Literature Review

In the paper, we investigate the resource allocation problem for emergency management, which covers the areas of evacuation navigation, distributed simulation, analytical performance modelling and the RNN-based algorithms. We discuss the related work in each of these areas below.

A distributed navigation algorithm proposed in [6] is applied in mobile networks to guide people to a exit safely during an emergency with a 2D layout, and the work is extended to a 3D indoor environment in [7]. In [8] is presented a distributed algorithm to find safe paths for evacuees taking into account predictions of the movement of the hazards, but there are some shortcomings addressed in [9]. The distributed building evacuation simulator used in our simulations is firstly proposed in [10] and particularly in [11], and it can reduce the simulation time required for large-scale systems and facilitate the modelling of the agents. In [12,13] is discussed the use of analytical models based on graph and queueing theories, which provide fast estimates for the conditions in frequently changing circumstances. The authors in [2] present a distributed decision support system for building evacuation based on the distributed simulator. Regarding evacuating civilians quickly and safely, [14] illustrates that routing emergency evacuees with a cognitive packet network (CPN) [15,16,17] can alleviate slow convergence time for large and fast-changing networks, and [18] proposes the use of Opportunistic Communications (oppcomms), which can provide emergency support when a stable communication infrastructure is unavailable.

The above work attempts to direct the evacuees to get out of danger quickly and avoid injury; however, people might be seriously injured and obstructed by the hazards in real emergency environments. Thus, a system that can efficiently search for the injured civilians and coordinate rescue is necessary for emergency management. In [19] is designed efficient and intelligent algorithms to search for the mines autonomously in static environments. In [20,21], the authors address a robot-sensor network to identify the locations of possible victims for providing rescue of those trapped people. A distance-sensitive service discovery algorithm is illustrated in [22], which combines the concepts of Voronoi polygons [23] and the quorum-based approaches [24] and guarantees the closest tasks (e.g., victims) being executed with very high probability. By considering the energy issue, [25] explores two algorithms to dispatch mobile resources (e.g., emergency units) to visit task locations in an energy-balanced way. Furthermore, [26] takes into account the situation where people may be trapped with no escape path, due to congestion, and designs a scheme for allocating resources to eliminate key dangerous areas in order to ease congestion and increase the number of rescued people. Furthermore, the authors in [27] consider that a resource may fail in executing a task in dynamic hazard environments and address a task assignment algorithm with a probabilistic successful execution outcome. The algorithm is on the basis of the RNN techniques, so that it is able to solve the resource allocation problems accurately and in real-time. The random neural network is powerful in obtaining desired input-output mappings through learning and has been widely used in solving real world problems. In [28], the research work based on the RNN techniques is surveyed, and the properties and applications of it are described. The author shows that the RNN has been applied into diverse engineering areas, which reflects its prominence as a modelling and learning tool. The theory and applications of the RNN are introduced below.

The excitatory and inhibitory signals concept of the RNN is first introduced in [29], where each neuron has an active potential, which will be affected by the input signals from other neurons and the outside world. The neuron will be excited if its active potential is a positive value, and if a neuron is excited, it will send excitatory or inhibitory signals at an excited rate to other neurons or to the outside world. The RNN has a product form in the Markovian case and leads to a concise representation for its steady-state behaviour. However, the signal flow equations of the model are nonlinear, so that the unique solutions are only obtained in the case of feedforward networks. Thus, [30] establishes the uniqueness of solutions in the networks with feedback and shows that the signal flow equations have a unique solution whenever the solution exists. In [31], the authors illustrate that the RNN with feedforward structures can provide a good approximation to input-output matching problems, while [32] addresses that the feedforward RNN with more constraints also can uniformly approximate a continuous function. In engineering applications, the need to process different classes of information simultaneously is required; hence [33] proposes an extension to the RNN model, which includes multiple classes of signals and preserves the existence and uniqueness of the product form solution of the networks. A learning algorithm used in multiple class random neural networks is introduced in [34], which is capable of learning sets of given input-output examples and, then, making a prediction on input-output mappings under new environments. Another extension of the RNN is discussed in [35], where the network incorporates the usual excitatory and inhibitory information, but also creates the probability that a synchronous interaction between two neurons affects some third neuron. The network also has the product form and preserves the unique solution property.

One kind of application of the RNN is image processing and video compression. In [36] is described a scheme for real-time adaptive compression and decompression of video based on the RNN, and [37] presents a geometric recurrent neural network to solve magnetic resonance imaging (MRI) brain morphometry problems effectively and efficiently. Furthermore, the RNN can discover a new route in a self-aware manner. In [17], a self-aware network (SAN) based on the RNN techniques is introduced, where the nodes are able to discover the network state autonomously without relying on an overall routing table and compute the next hop as needed and on demand. Based on the work in [17,38], a measurement-based admission control algorithm to make sure packet delivery occurs under quality of service (QoS) constraints is presented, and [39] proposes an autonomic approach to defend against denial of service (DoS) attacks. Additionally, the authors in [40] apply a genetic algorithm (GA) on the source nodes, which can modify and select the paths discovered by the SAN on the basis of their own needs. The RNN has also been suggested as a tool to make decisions quickly and accurately for optimization problems. The paper, [41], develops a dynamic random neural network (DRNN) approach to solve the traveling salesman problem optimally, and the results verify that the DRNN can provide substantially better performance compared with other neural networks. Furthermore, the RNN can be equipped to route multicast communications in an efficient manner by constructing a minimum Steiner tree, which is presented in [42]. Moreover, [3] applies the RNN model into optimal resource allocation problems based on the work in [35]. The letter presents that the network can efficiently dispatch a set of emergency personnel to a given set of events (e.g., fire events or injured people) to provide services. In [43], the uncertainty of the outcome of the assignments is considered, and the allocations of the resources to tasks are formulated in order to minimize the cost of the objective function, which is firstly proposed in [27]. Furthermore, the paper presents an approach for obtaining the tight lower bounds of the optimal solutions by using piecewise linear approximation. The authors in [44] discuss the problem of assigning each task in a parallel program to some resources, and the results show that the RNN can be easier to implement on a parallel machine and improve the speed of processing compared with other heuristic approaches.

3. The RNN-Based Algorithm for Resource Allocation

During an ongoing hazard, although the rescuers can identify the location of victims with the help of the DBES platform, reach the injured sites quickly and wear protective devices, it is inappropriate to assume that the rescuers can always succeed in executing a mission [45], and it is uncertain whether the rescuer will reach the hazardous areas and carry the trapped people to the exits. Furthermore, the decision making of the assignment of rescuers to victims should be fast, since long exposure to the hazard means less chance of survival [1]. Therefore, this section introduces an RNN-based algorithm to provide near-optimal advice in real-time in uncertain environments. The mathematical model and the most important properties of the RNN are introduced firstly, and then, we describe a task assignment algorithm based on the RNN techniques.

3.1. The Random Neural Network Model

The RNN can solve the optimization problem of allocating a set of tasks to a limited set of resources simultaneously very quickly and quite accurately [3], and the basic ideas for the RNN model purposed in [29,30] are shown below.

The main symbols used for the RNN model are summarized in Table 1, and an application of one earlier result (Theorem 1) proposed in [46] is being used.

Table 1. List of the random neural network (RNN) training model symbols [3].

Notation	Definition
$f_i$	Firing rate for neuron i
$k_i\left(t\right)$	Internal state of neuron i at time t
$\Lambda \left(i\right)$	Excitatory spike from the outside world to neuron i
$\lambda \left(i\right)$	Inhibitory spike from the outside world to neuron i
$p^{+}(i,j)$	Probability of excitatory spike from neuron i to neuron j
$p^{-}(i,j)$	Probability of inhibitory spike from neuron i to neuron j
$d\left(i\right)$	Probability of departure spike from neuron i to the outside world
$q_i$	Probability of neuron i being excited
$\pi \left(\underline{k}\right)$	Stationary probability distribution

Table 1. List of the random neural network (RNN) training model symbols [3].

Notation	Definition
$f_i$	Firing rate for neuron i
$k_i\left(t\right)$	Internal state of neuron i at time t
$\Lambda \left(i\right)$	Excitatory spike from the outside world to neuron i
$\lambda \left(i\right)$	Inhibitory spike from the outside world to neuron i
$p^{+}(i,j)$	Probability of excitatory spike from neuron i to neuron j
$p^{-}(i,j)$	Probability of inhibitory spike from neuron i to neuron j
$d\left(i\right)$	Probability of departure spike from neuron i to the outside world
$q_i$	Probability of neuron i being excited
$\pi \left(\underline{k}\right)$	Stationary probability distribution

Theorem 1

Let ${\lambda }^{-}\left(i\right)$ and ${\lambda }^{+}\left(i\right)$, $i=1,...,N$ be given by the following system of equations

$${\lambda }^{-}\left(i\right)=\lambda \left(i\right)+\sum _{j=1}^N{f}_j{q}_j{p}^{-}(j,i)$$

(1)

$${\lambda }^{+}\left(i\right)=\Lambda \left(i\right)+\sum _{j=1}^N{f}_j{q}_j{p}^{+}(j,i)$$

(2)

where

$$q_i={\lambda }^{+}\left(i\right)/(f_i+{\lambda }^{-}\left(i\right))$$

(3)

If a unique nonnegative solution, $\{{\lambda }^{-}\left(i\right),{\lambda }^{+}\left(i\right)\}$, exists for the nonlinear system of Equations (1) to Equation (3), such that $q_i<1\forall i$, then

$$\pi \left(\underline{k}\right)=\prod _{i=1}^N(1-q_i)q_i^{k_i}$$

(4)

The network will have a solution if $q_i<1$: this guarantees that the total arrival rate is less than the total departure rate, so that the network will be finally in steady state. According to the definition of $p^{+}(i,j)$, $p^{-}(i,j)$ and $d\left(i\right)$ in Table 1, we have a relationship between three different types of probabilities.

$$d\left(i\right)=1-\sum _{j=1}^N\left[p^{+}(i,j)+p^{-}(i,j)\right]$$

(5)

We now use notation “weight” [47] to represent the rates at which the neurons interact [3], and the weights are defined as a simple product form of the firing rate and its corresponding probability.

$$w^{+}(i,j)=f_i{p}^{+}(i,j)$$

(6)

$$w^{-}(i,j)=f_i{p}^{-}(i,j)$$

(7)

By combining Equations (5) to (7), we can rewrite Equation (5):

$$\begin{array}{ccc}\hfill f_i& =& \frac{f_i{\sum }_{j=1}^N\left[p^{+}(i,j)+p^{-}(i,j)\right]}{1-d\left(i\right)}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill f_i& =& \frac{{\sum }_{j=1}^N\left[w^{+}(i,j)+w^{-}(i,j)\right]}{1-d\left(i\right)}\hfill \end{array}$$

(8)

The denominator of $q_i$ in Equation (3) can then be rewritten by combining Equations (1) and (7):

$$\begin{array}{ccc}\hfill D\left(i\right)& =& f_i+{\lambda }^{-}\left(i\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill D\left(i\right)& =& f_i+\lambda \left(i\right)+\sum _{j=1}^N{f}_j{q}_j{p}^{-}(j,i)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill D\left(i\right)& =& f_i+\lambda \left(i\right)+\sum _{j=1}^N{q}_j{w}^{-}(j,i)\hfill \end{array}$$

(9)

By combining Equations (2) and (6), its numerator becomes:

$$\begin{array}{ccc}\hfill N\left(i\right)& =& {\lambda }^{+}\left(i\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill N\left(i\right)& =& \Lambda \left(i\right)+\sum _{j=1}^N{f}_j{q}_j{p}^{+}(j,i)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill N\left(i\right)& =& \Lambda \left(i\right)+\sum _{j=1}^N{q}_j{w}^{+}(j,i)\hfill \end{array}$$

(10)

$$sothat{q}_i=N\left(i\right)/D\left(i\right)$$

(11)

The results can be used to design an efficient learning algorithm by updating the weights of all neurons and then selecting a neuron that has the largest q.

3.2. Task Assignment Algorithm Based on the RNN Model

Consider a group of rescuers, R, waiting at the building exits and some victims, V, being trapped in hazardous areas, and assume that the initial locations of both rescuers and injured civilians are known with the support of the DBES platform. According to the work in [27], the RNN parameters can be defined as a cost, $C(r,v)$, associated with each possible assignment of rescuer r to victim v, a fail execution probability, $L(r,v)$, representing that rescuer r is unable to rescue victim v, though rescuer r has been dispatched to it, and a penalty, $K\left(v\right)$, for not executing rescue for victim v. In this case, any assignment of rescuers to victims will have an expected cost, and the objective of the algorithm is to minimize the overall expense by selecting the optimal assignments in order to increase the number of injured civilians collected. We represent the decision of dispatching rescuer r to save victim v by the probability, $p(r,v)$, and $p(r,v)=1$ if rescuer r is allocated to victim v and $p(r,v)=0$, if not [27]. Hence:

$$p(r,v)\in \{0,1\},and\sum _{v\in V}p(r,v)=\pi \left(r\right)\in \{0,1\},r\in R,v\in V$$

(12)

where $p(r,v)$ are either zero or one; $\pi \left(r\right)\in \{0,1\}$ represents (a) $\pi \left(r\right)=0$, rescuer r will not be assigned a task if the assignments related to rescuer r increases the overall cost; and (b) $\pi \left(r\right)=1$, a rescuer cannot be re-assigned some other victims if the rescuer already has task (i.e., the rescuers are non-reusable).

The number of victims and rescuers are denoted as $\left|V\right|$ and $\left|R\right|$, respectively. Based on the RNN parameters, $C(r,v)$, $K\left(v\right)$, $L(r,v)$ and $p(r,v)$, the objective function that we try to minimize can be written as [27]:

$$\begin{array}{c}\hfill MinimizeC=\sum _{v\in V}\sum _{r\in R}C(r,v)p(r,v)+\sum _{v\in V}K\left(v\right)\prod _{r\in R}\{1-(1-L(r,v))p(r,v)\}\end{array}$$

(13)

$$\begin{array}{c}\hfill Subjectto:\left(1\right)\sum _{v\in V}p(r,v)=\pi \left(r\right)\in \{0,1\},r\in R,\left(2\right)p(r,v)\in \{0,1\},r\in R,v\in V\end{array}$$

where the first term of Equation (13) is the average cost used by the rescuers, and the second term represents the accumulative average cost of failing in executing rescue for each victim. For each possible task assignment, we assume that there are only two results, success or failure, and Equation (13) takes both the cost of succeeding in rescue and the penalty of failing in the save into account. Thus, the addition of the first term and the second term indicates that the minimization of Equation (13) is to find an optimal balance between the successful execution costs and the fail rescue penalties. The first constraint ensures that we can allocate one particular rescuer to at most one victim, and the total number of allocations can be less than $\left|R\right|$ [27]. The second one assumes that $p(r,v)=1$ if rescuer r is allocated to victim v and $p(r,v)=0$ if not. The expected failure probability $\{1-(1-L(r,v)\left)p\right(r,v\left)\right\}$ [27] can be rewritten in an exponential form:

$$\begin{array}{ccc}\hfill F& =& 1-(1-L(r,v\left)\right)p(r,v)=1-(1-L(r,v\left)\right)\left(p\right(r,v)=0or1)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill F& =& 1,ifp(r,v)=0orL(r,v),ifp(r,v)=1\hfill \end{array}$$

$$\begin{array}{ccc}\hfill Thus,F& =& L{(r,v)}^{p(r,v)}\hfill \end{array}$$

(14)

Substitute Equation (14) into Equation (13); we obtain:

$$MinimizeC=\sum _{v\in V}\sum _{r\in R}C(r,v)p(r,v)+\sum _{v\in V}K\left(v\right)\prod _{r\in R}L{(r,v)}^{p(r,v)}$$

(15)

$$\begin{array}{c}\hfill Subjectto:\left(1\right)\sum _{v\in V}p(r,v)=\pi \left(r\right)\in \{0,1\},r\in R,\left(2\right)p(r,v)\in \{0,1\},r\in R,v\in V\end{array}$$

In order to find the minimum solution of Equation (15), it is possible to enumerate all possible allocations of rescuers to victims and then select the optimal result. Because of the high computational complexity, the RNN algorithm described before is used to solve Equation (15), which can provide a quick and accurate solution. Here, each possible assignment decision $(r,v)$ is represented by a neuron, $N(r,v)$, and a list of symbols used for the approach is summarized in Table 2.

Table 2. List of RNN parameter association approach symbols [27].

Notation	Definition
$K\left(v\right)$	Penalty for not rescuing victim v
$L(r,v)$	Probability rescuer r is unable to rescue victim v
$C(r,v)$	Cost for saving victim v by rescuer r
$\Lambda (r,v)$	External arrival rate of excitatory signals to neuron (r, v)
$\lambda (r,v)$	External arrival rate of inhibitory signals to neuron (r, v)
$w^{+}(r,v;r^{\prime },v^{\prime })$	Rate of excitatory signals to neuron (r, v) from firing neuron (r’, v’)
$w^{-}(r,v;r^{\prime },v^{\prime })$	Rate of inhibitory signals to neuron (r, v) from firing neuron (r’, v’)
$f(r,v)$	Firing rate of neuron (r, v)
$q(r,v)$	Probability neuron (r, v) is excited

Table 2. List of RNN parameter association approach symbols [27].

Notation	Definition
$K\left(v\right)$	Penalty for not rescuing victim v
$L(r,v)$	Probability rescuer r is unable to rescue victim v
$C(r,v)$	Cost for saving victim v by rescuer r
$\Lambda (r,v)$	External arrival rate of excitatory signals to neuron (r, v)
$\lambda (r,v)$	External arrival rate of inhibitory signals to neuron (r, v)
$w^{+}(r,v;r^{\prime },v^{\prime })$	Rate of excitatory signals to neuron (r, v) from firing neuron (r’, v’)
$w^{-}(r,v;r^{\prime },v^{\prime })$	Rate of inhibitory signals to neuron (r, v) from firing neuron (r’, v’)
$f(r,v)$	Firing rate of neuron (r, v)
$q(r,v)$	Probability neuron (r, v) is excited

The excitatory and inhibitory signals’ arrival rates of each neuron, $N(r,v)$, are specified so that the RNN can be used for the heuristic solution to optimization problems [27]. Hence, we represent the external rate of excitation and inhibition as:

$$\Lambda (r,v)=max\{0,b(r,v\left)\right\} \lambda (r,v)=max\{0,-b(r,v\left)\right\}$$

$$\text{where} b(r,v)=K\left(v\right)(1-L(r,v\left)\right)-C(r,v)$$

where $K\left(v\right)(1-L(r,v\left)\right)$ is the expected reduction in the penalty of not rescuing victim v if rescuer r has been dispatched to save it, and $C(r,v)$ is the cost of triggering rescuer r to save victim v. $b(r,v)$ can be viewed as a characteristic of the neuron, $(r,v)$, where $b(r,v)>0$ if this allocation could minimize the overall cost of task assignments and $b(r,v)\le 0$ if not. That is, if the expected reduction in the cost of not saving victim v is larger than the cost of allocating rescuer r to victim v (i.e., $b(r,v)>0$), then we think this assignment is efficient, while if not, then this allocation will not be executed. Moreover, in order to avoid resource wastage [45], we discourage the allocation of more than one rescuer to the same victim; thus, we set the inhibitory weights [27]:

$$w^{-}(r,v;r^{\prime },v)=max\{0,b(r,v)\},ifr\ne r^{\prime }$$

which indicates that if the allocation of rescuer r to victim v is able to minimize the objective function (i.e., $b(r,v)>0$), the allocations of other rescuers to the same victim should be discouraged, otherwise ($b(r,v)\le 0$); this allocation should have no effect on other assignments ($w^{-}(r,v;r^{\prime },v)=0$). Similarly, we wish to avoid assigning more than one victim to the same rescuer:

$$w^{-}(r,v;r,v^{\prime })=max\{0,b(r,v)\},ifv\ne v^{\prime }$$

For the sake of simplicity, we are not reinforcing or impairing the other assignments [27], so that $w^{+}(r,v;r^{\prime },v^{\prime })=0$ and $w^{-}(r,v;r^{\prime },v^{\prime })=0$ for all other r, $r^{\prime }$ and v, $v^{\prime }$. Hence, we rewrite Equation (8):

$$f(r,v)=\frac{{\sum }_{r^{\prime },v^{\prime }}\left[w^{+}(r,v;r^{\prime },v^{\prime })+w^{-}(r,v;r^{\prime },v^{\prime })\right]}{1-d(r,v)}=\sum _{r^{\prime },v^{\prime }}{w}^{-}(r,v;r^{\prime },v^{\prime })$$

(16)

Equation (11) is then rewritten:

$$\begin{array}{ccc}\hfill q(r,v)& =& \Lambda (r,v)/[\lambda (r,v)+f(r,v)+\sum _{r^{\prime },v^{\prime }}q(r^{\prime },v^{\prime })w^{-}(r^{\prime },v^{\prime };r,v)]\hfill \end{array}$$

$$\begin{array}{ccc}\hfill q(r,v)& =& \Lambda (r,v)/[\lambda (r,v)+f(r,v)+\sum _{r^{\prime }\ne r}q(r^{\prime },v)w^{-}(r^{\prime },v;r,v)+\sum _{v^{\prime }\ne v}q(r,v^{\prime })w^{-}(r,v^{\prime };r,v)]\hfill \end{array}$$

(17)

When there are civilians who are trapped in hazardous areas, the rescuers will be notified by the sensor network in the DBES multi-agent environment. Next, Equation (17) is solved iteratively until convergence in the following manner (Algorithm 1) to obtain an optimal assignment of rescuers to victims. In the algorithm, R is the original set of rescuers and $R_{rem}$ is the set of remaining rescuers. S is the solution set where the assigned rescuer-victim pairs are stored [27], and $K_{cur}\left(v\right)$ is the current penalty of victim v, which will be updated if victim v is allocated a rescuer.

Algorithm Description:

• Initialization: initialize (a) $R_{rem}$ to R; (b) S to empty; (c) $K_{cur}\left(v\right),v\in V$; (d) the fail probability $L(r,v)$ for each neuron, $r\in R,v\in V$; (e) the cost $C(r,v)$ for each neuron, $r\in R,v\in V$; (f) $q(r,v)$ for $r\in R,v\in V$ to zero: assume that all possible assignments have no effect on the cost of the objective function at the beginning.
• Compute the RNN parameters, $\Lambda (r,v)$, $\lambda (r,v)$, $w^{-}(r,v;r^{\prime },v)$, $w^{-}(r,v;r,v^{\prime })$ and $f(r,v)$, and construct a neural network for $r\in R_{rem}$ and $v\in V$.
• Iteratively compute $q(r,v)$ for $r\in R_{rem}$ and $v\in V$ based on Equation (17) until $q(r,v)$ converges for all neurons.

Algorithm 1 Task assignment for optimal emergency management.

initialize $R_{rem}=R$; $S=\varnothing$; $K_{cur}\left(v\right)=K\left(v\right)v\in V$; $L(r,v)r\in R,v\in V$; $C(r,v)r\in R,v\in V$; $q_{pre}(r,v)=q(r,v)=0r\in R,v\in V$; for each possible assignment pairs $(r,v)\in \left[neurons\right]$ do $b(r,v)=K\left(v\right)(1-L(r,v\left)\right)-C(r,v)$; $\Lambda (r,v)=max\{0,b(r,v\left)\right\}$; $\lambda (r,v)=max\{0,-b(r,v\left)\right\}$; $w^{-}(r,v;r^{\prime },v)=max\{0,b(r,v)\},ifr\ne r^{\prime }$; $w^{-}(r,v;r,v^{\prime })=max\{0,b(r,v)\},ifv\ne v^{\prime }$; end for for each possible assignment pairs $(r,v)\in \left[neurons\right]$ do $f(r,v)={\sum }_{r^{\prime },v^{\prime }}{w}^{-}(r,v;r^{\prime },v^{\prime })$; end for for each possible assignment pairs $(r,v)\in \left[neurons\right]$ do $q(r,v)=\Lambda (r,v)/[\lambda (r,v)+f(r,v)+{\sum }_{r^{\prime }\ne r}q(r^{\prime },v)w^{-}(r^{\prime },v;r,v)+{\sum }_{v^{\prime }\ne v}q(r,v^{\prime })w^{-}(r,v^{\prime };r,v)]$; end for if $convergenceforallneurons$ then $//$ select the most excited neuron (line 20); else $//$ continue iterating until convergence (line 12); end if initialize maxValue = 0; for each possible assignment pairs $(r^{*},v^{*})\in \left[neurons\right]$ do if $q(r^{*},v^{*})>maxValue$ then $maxValue=q(r^{*},v^{*})$; select rescuer-victim pair $(r^{*},v^{*})$ ; end if end for update $S=S\bigcup (r^{*},v^{*})$, $R_{rem}=R_{rem}\setminus r^{*}$, $K_{cur}\left(v^{*}\right)=K_{cur}\left(v^{*}\right)L(r^{*},v^{*})$; if $R_{rem}$ is not empty then $//$ allocate next rescuer (line 2); else stop; end if

4.

Select a rescuer-victim pair $(r^{*},v^{*})$ that has the highest probability of being active; if all $q(r,v)=0$ for $r\in R_{rem}$ and $v\in V$, then stop: there is no assignment that can reduce the cost of the objective function.

5.

Update the solution set, S, by adding new rescuer-victim pair $(r^{*},v^{*})$ into it.

6.

Update the remaining rescuers set, $R_{rem}$, by removing rescuer $r^{*}$ from $R_{rem}$.

7.

Reduce the penalty of the victim, $v^{*}$, by the expected reduction: $K_{cur}\left(v^{*}\right)=K_{cur}\left(v^{*}\right)-K_{cur}\left(v^{*}\right)(1-L(r^{*},v^{*}))=K_{cur}\left(v^{*}\right)L(r^{*},v^{*})$.

8.

Check the remaining rescuers set $R_{rem}$, and if $R_{rem}$ is not empty, then go to step (2); otherwise, stop: all rescuers have tasks.

Note that using this algorithm, the assignments in solution set S always result in reducing the cost of the objective function [27], since an assignment may be selected if $q(r,v)>0$ or $\Lambda (r,v)>0$ (see Line 22) (i.e., $b(r,v)>0$), otherwise, if $q(r,v)=\Lambda (r,v)=0$ (i.e., $b(r,v)\le 0$), the allocation will not be executed.

For example, a network of four fully connected neurons is modelled in Figure 1a with two rescuers ($r_1$, $r_2$) and two victims ($v_1$, $v_2$). If neuron $(r_1,v_1)$ has the highest active probability, q, it will be selected. Then, the neurons, including rescuer $r_1$, are removed from the network, and the RNN parameters of other neurons are updated by the current penalty of victim $v_1$. An updated neural network will be constructed (Figure 1b). Next, do the calculation again and select the most excited neuron. This is the last step for the example, since if one of the neurons is selected, the rescuer set will be empty, or if no neuron is selected, it means that these two assignments cannot minimize the cost of the objective function. Similarly, an N fully connected neuron network can be solved step by step until the resource set is empty or the remaining possible assignments cannot reduce the cost of the objective function.

Figure 1. Graph representation of the interactions of a four neuron network.

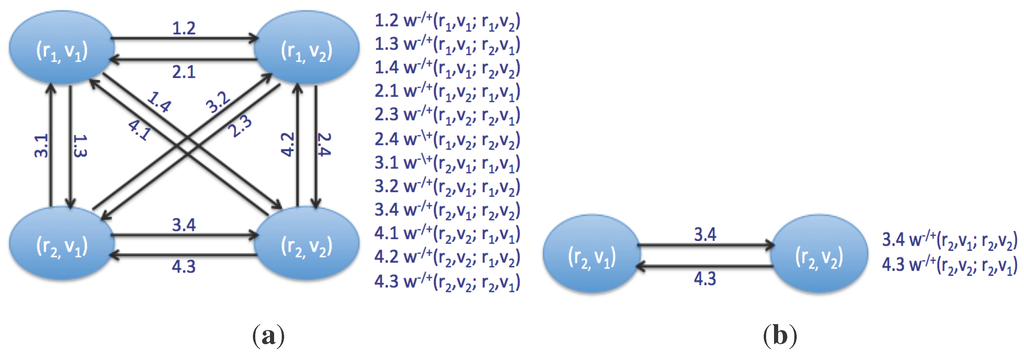
Figure 1. Graph representation of the interactions of a four neuron network.

3.3. Algorithm Complexity

The complexity of the solution of Equations (1) to (3) is $O(I·N^2)$ [48], where I is the number of iterations required for convergence. However, we can reduce the complexity of each iteration by taking advantage of the special structure of the RNN-based algorithm [27].

In Equation (17), there are $N=\left|V\right|\left|R\right|$ neurons; thus, its computational complexity is $O(I·|V{|}^2\left|R{|}^2\right)$. According to the definition of inhibitory weights, Equation (17) can be rewritten as [27]:

$$q(r,v)=\Lambda (r,v)/[\lambda (r,v)+f(r,v)+{\theta }_1\left(v\right)+{\theta }_2\left(r\right)-2q(r,v)max\{0,b(r,v)\}]$$

(18)

where:

$${\theta }_1\left(v\right)=\sum _{r^{\prime }\in R}q(r^{\prime },v)max\{0,b(r^{\prime },v)\},\forall v;{\theta }_2\left(r\right)=\sum _{v^{\prime }\in V}q(r,v^{\prime })max\{0,b(r,v^{\prime })\},\forall r$$

Based on Equation (18), the computation for each neuron requires $O\left(1\right)$ operations; hence, the computational complexity of N neurons where $N=\left|V\right|\left|R\right|$ is $O\left(\right|V|·|R\left|\right)$. Moreover, the computation of the terms ${\theta }_1\left(v\right)$ and ${\theta }_2\left(r\right)$ is also of complexity $O\left(\right|V|·|R\left|\right)$. Therefore, the complexity of solving Equation (18) is $O(I·|V|·|R\left|\right)$. Because there are $\left|R\right|$ rescuers, Equation (18) will be performed at most $\left|R\right|$ times. The complexity of the RNN-based task assignment algorithm is $O(I·|R{|}^2·\left|V\right|)$.

4. Evaluation of the Task Assignment Algorithm

In this section, we begin by presenting the assumptions we made for the simulations, and then, we describe the simulation model. Finally, the results will be illustrated.

4.1. Assumptions

The first assumption is that the initial health status of civilians and rescuers is 100, and the health will be affected by the hazards, i.e., their health level decreases gradually when they are exposed to hazards. If the remaining health of civilians is less than a threshold, they are assumed to be immobilized. These victims are referred to as tasks, and they need to be assigned to the rescuers. Additionally, in real emergencies, the rescuers will wear protective clothes; thus, we assume that the health level of rescuers decreases slower than that of civilians. Another assumption is that the capacity of each rescuer is one, and the maximum capacity of each of them is two. This means that each rescuer will be allocated one trapped civilian each time, but this allows for the possibility that another trapped civilian is assigned to them if the location of the civilian is near the way selected by the rescuer towards the exits. Finally, the rescuers are assumed to be non-usable, so that they will execute tasks only once.

4.2. Description of the Simulation Model

The simulation model is established based on the Distributed Building Evacuation Simulator [11], where all simulated entities, including evacuees, as well as rescuers, are modelled as agents, and these entities are able to communicate with each other. We assume that this is a fire-related emergency evacuation, and the area to evacuate is a building based on the three lower floors of Imperial College London’s EEEbuilding [14]. A coarse graph representation of this building is shown in Figure 2.

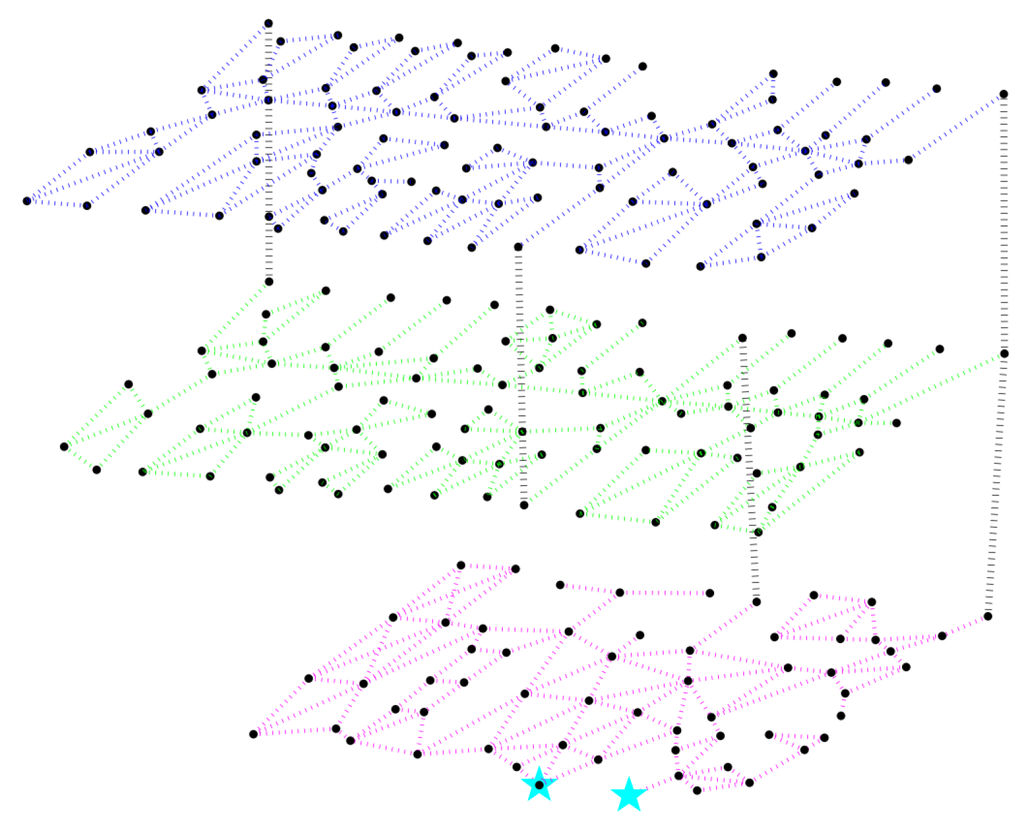
Figure 2. Graph representation of the building model [14]. The two cyan stars on the ground floor mark the position of the building’s exits.

Figure 2. Graph representation of the building model [14]. The two cyan stars on the ground floor mark the position of the building’s exits.

The civilians’ goal is to get out of the hazards along with a safe path to avoid injury, but if they are at stake, they will send a message, including their ID and location, to the rescuers and ask for help, while the rescuers’ aim is to get into the hazardous areas to carry victims to safe sites. When the evacuees need help in the building, the RNN-based algorithm computes an optimum resource allocation scheme to dispatch a limited set of rescuers to the location of victims to provide support. The navigation algorithm used by the rescuers is considered separately for two stages of the rescue process, moving to the injured civilians and carrying them to the exits. In the first stage, the rescuers try to arrive at the emergency sites quickly to assist the injured civilians in real-time, and we assume that they cannot be hurt by fire when they get through the hazards themselves, since they wear protective clothes. Therefore, the dominant factor for the navigation algorithm is the time, i.e., the algorithm should guide the rescuers to the injured persons’ locations as fast as possible. We choose to use Dijkstra’s Shortest Path Algorithm, which can compute the shortest path between two nodes based on the physical length of every link between them, and here, the shortest path is regarded as the fastest path, since the moving speed of rescuers is assumed to be fixed. However, the rescuers take injured people to the exits in the second stage, so that the rescuers should not only go to the exits rapidly, but protect people from further injury. Thus, we still use Dijkstra’s Algorithm, but the length between two nodes is computed based on its physical distance and, also, the hazard intensity on the link [2]. Thus, the path selected by the rescuers can navigate them to the evacuation exits in a quick and safe way.

4.3. Performance Evaluation

The effectiveness of the proposed RNN-based task assignment algorithm is evaluated in terms of three performance metrics: (1) the percentage of evacuees who are saved by rescuers under diverse population densities (30, 60 and 90 evacuees in the building); (2) the number of victims saved by rescuers with the sizes of the set of rescuers and the set of victims given; and (3) the average remaining health of the rescued evacuees. Metrics (1) and (2) denote straightforwardly the efficiency of the RNN-based algorithm; and (3) indicates if the algorithm is fast enough to save people in a timely manner. The results of our experiments are obtained by comparing two different scenarios, without the task assignment algorithm and with the RNN-based algorithm. The “without algorithm” scenario is run with the random assignment, where the rescuers will save the victims in a random way. In the “with the algorithm” scenario, each rescuer holds an RNN and executes the task, relying on the solutions of the RNN computation.

Each result is obtained by executing 10 simulation runs, and for each simulation run, the locations of injured civilians are randomized around the hazards in the building. The purpose of the simulations is to check if the RNN-based algorithm can avoid the waste of resources and reduce the inefficiency of resource allocations. Thus, to keep things as simple as possible, the cost of each assignment, $C(r,v)$, and the failed rescue probability, $L(r,v)$, are taken to be independent from the assigned victim, v [27], and generated randomly. Specifically, $K\left(v\right)$, $C\left(r\right)$ and $L\left(r\right)$ are generated from the uniform distribution in the interval $[0,50]$, $[0,10]$ and $[0.05,0.15]$, respectively, and $q(r,v)$ is initialized to zero for all assignments. All RNN parameters are updated 20 times for each allocation to reach convergence, and the assignment with the highest probability of being active (i.e., $q(r,v)$) will be selected. The simulation results are shown below with a 95% confidence interval.

In Figure 3, it is clear that the percentage of rescued civilians decreases with the increasing number of evacuees in the building. This is due to the fact that it takes a relatively long time to evacuate in high population density environments, because of congestion problems, which then increases the time of exposure to the hazards and reduces the number of survivors. Without the task assignment algorithm, the system with seven rescuers reduces the percentage of rescued civilians compared with the system with five rescuers for each case (30, 60 and 90 evacuees), which is more obvious in high population densities (60 and 90 evacuees). The reason is that when there are people who need help, the rescuers enter the building and move towards the hazardous areas, so that some of them may increase congestion along the road [26]. Hence, the rescuers and the remaining evacuees will probably spend a long time waiting or be obstructed by congestion. Moreover, it is possible that: (1) different rescuers are allocated to the same victim; (2) different victims are assigned to the same rescuer; and (3) a rescuer may be injured during rescue and, then, cannot finish the task. The reason for phenomena (1) and (2) is that there is no relationship and effect between each assignment, that is, the allocation of a rescuer to a victim does not consider the assignments that have already been done. In high population density environments, more evacuees may be at stake at bottleneck points [49], such as stairs and exits, due to pedestrian congestion, and then, more people need to be assigned a rescuer simultaneously. Therefore, it is more likely that the rescuers receive more than one rescue message from the sensor network, and/or the same rescue message is sent to more than one rescuer. In this case, the rescuers select their target randomly, which leads to problems (1) and (2). The result of (3) indicates that the rescuer may not be perfectly suited to save a victim, though the rescuer has been allocated [27]. Because the rescuers may not know the inside situations in uncertain environments, they may be exposed to highly hazardous areas for a long time, since they move into the disasters and may be obstructed by the congestion. Therefore, more rescuers in a “without algorithm” system not only aggravate congestion, but also may not increase the number of rescued people, due to problems (1) to (3). In this case, the performance of the system with more rescuers may be worse.

However, with the RNN-based algorithm, the percentage of rescued civilians has a tendency to increase with more rescuers in the system (Figure 3). Although the rescuers still increase the congestion in the building, the RNN-based algorithm makes the rescuers save victims effectively, which dominates the overall performance of the rescue system. This is because the RNN-based algorithm can alleviate the three problems mentioned above by modelling a network of N fully connected neurons with a cost objective function.

The algorithm treats each rescuer-victim pair as a neuron, such as neuron i means that rescuer r is allocated to victim v, and it can minimize the total cost by solving the objective function. The objective function takes into account the cost of allocating rescuer r to victim v, the probability that rescuer r is unable to save victim v (say, the failed rescue probability of neuron i), and the penalty of not rescuing victim v. Therefore, a rescuer-victim pair will be selected if the allocation can minimize the cost of the objective function. For example, if the failed rescue probability of neuron i is high, the neuron may not be selected, since it might increase the overall cost. Although the fail rescue probability, $L(r,v)$, is initialized randomly in the simulations, we notice that the RNN-based approach can avoid the selection of a neuron with high L. Thus, problem (3) can be solved if we generate the fail rescue probability relying on the situations of the rescuers and victims, which will be discussed in future work. Moreover, the algorithm considers the rate of excitatory and inhibitory signals from firing neuron i to neuron j. If neuron i has been selected, the inhibitory signals from neuron i to other neurons, j, where $j\ne i$, will be updated to discourage the allocations of different rescuers to the same victim and different victims to the same rescuer. Then, problems (1) and (2) can be avoided to some degree. Therefore, more rescuers are able to save more people with the RNN-based algorithm, and the percentage of rescued civilians can be increased.

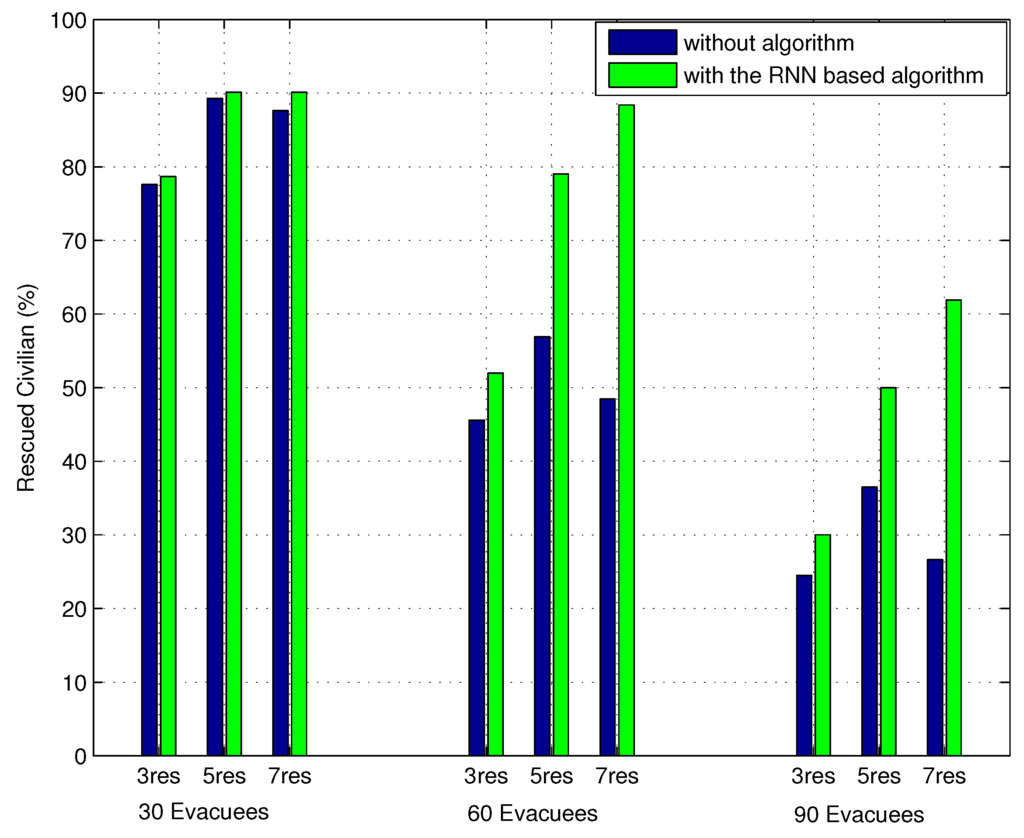
Figure 3. Percentage of evacuees saved by rescuers under diverse population densities.

Figure 3. Percentage of evacuees saved by rescuers under diverse population densities.

Table 3. Number of evacuees saved by rescuers.

No. of rescuers $\left|R\right|$	No. of victims $\left|V\right|$	Without algorithm	With the RNN-based algorithm	Optimal solutions
3	4	3.00	3.80	4
5	4	3.43	4.00	4
7	4	4.00	4.00	4
3	8	4.71	5.75	6
5	8	6.00	7.50	8
7	8	5.89	8.00	8
3	16	4.88	6.00	6
5	16	7.40	9.75	10
7	16	6.67	13.25	14

Table 3. Number of evacuees saved by rescuers.

No. of rescuers $\left|R\right|$	No. of victims $\left|V\right|$	Without algorithm	With the RNN-based algorithm	Optimal solutions
3	4	3.00	3.80	4
5	4	3.43	4.00	4
7	4	4.00	4.00	4
3	8	4.71	5.75	6
5	8	6.00	7.50	8
7	8	5.89	8.00	8
3	16	4.88	6.00	6
5	16	7.40	9.75	10
7	16	6.67	13.25	14

In Table 3, given a set of victims, the increase of the number of rescuers cannot significantly improve the performance on the number of rescued evacuees without the task assignment algorithm, which agrees with the results obtained from Figure 3. However, the system with the RNN-based algorithm can provide a near-optimal performance compared with the optimal solutions, where:

$$\begin{array}{cc}& If\left|V\right|<overallmaximumcapacityofrescuers\hfill \\ & numberofrescuedevacuees\stackrel{approximately}{⟶}\left|V\right|\hfill \\ & else\hfill \\ & numberofrescuedevacuees\stackrel{approximately}{⟶}overallmaximumcapacityofrescuers\hfill \\ & end.\hfill \end{array}$$

Here, the capacity of rescuers is one, and the maximum capacity of rescuers is two. Note that, with the RNN-based algorithm, a rescuer will not be allocated to distinct victims since the assigned rescuer is removed from the rescuer set, and it cannot be re-used. The problem of a victim being assigned to distinct rescuers can be alleviated. However, a victim with a high penalty may be assigned to two rescuers, since the expected reduction on the penalty of not saving the victim may be larger than the cost of the rescue.

Comparing the two scenarios, without and with the task assignment algorithm, Figure 3 shows that the system with the RNN-based algorithm performs better, especially in high population density environments, which accords with the analyses above. The RNN-based algorithm is implemented in Java, and we notice that the simulation time for “with the algorithm” scenarios takes longer, since it needs $O(I·|R{|}^2·\left|V\right|)$ operations to complete all allocations. Here, I is the number of iterations for convergence and is equal to 20 in the simulations. However, the algorithm is fast enough, since the remaining health of the rescued civilians can stay at a good level (Table 4). Furthermore, Table 4 shows that the scenarios with the algorithm can significantly increase the average remaining health of rescued evacuees in more task environments ($\left|V\right|=8$ and 16) compared with the scenarios without the algorithm. Moreover, the RNN-based approach is implemented in Matlab in [27], and the results show that it can solve large problems of up to 200 resources and 200 tasks in one second.

Table 4. Average remaining health of the rescued civilians.

No. of rescuers $\left|R\right|$	No. of victims $\left|V\right|$	Without algorithm	With the RNN-based algorithm
3	4	24.00	25.25
5	4	25.25	24.15
7	4	24.79	24.70
3	8	17.40	20.67
5	8	20.45	22.35
7	8	18.38	23.23
3	16	7.89	11.10
5	16	12.28	15.35
7	16	8.11	18.01

Table 4. Average remaining health of the rescued civilians.

No. of rescuers $\left|R\right|$	No. of victims $\left|V\right|$	Without algorithm	With the RNN-based algorithm
3	4	24.00	25.25
5	4	25.25	24.15
7	4	24.79	24.70
3	8	17.40	20.67
5	8	20.45	22.35
7	8	18.38	23.23
3	16	7.89	11.10
5	16	12.28	15.35
7	16	8.11	18.01

5. Conclusions and Future Work

In the paper, we propose a task assignment algorithm based on the RNN techniques that can efficiently dispatch rescuers to aid victims to decrease the fatalities in emergency situations considering the uncertainty of dynamic hazard environments. The simulations show that the algorithm can provide an approximate real-time allocation of rescuers to victims. Furthermore, the allocation solutions are close to the optimal ones, where if the number of injured civilians is less than the total number of people that the rescuers can save, all injured civilians could be rescued by the rescuers, and if not, the number of saved civilians could reach the overall maximum capacity of the rescuers.

In future work, the task assignment algorithm can be evaluated with more constraints, such as the cost of each assignment, $C(r,v)$, and the fail rescue probability, $L(r,v)$, can be generated, relying on the situations of both the rescuers and victims. Our simulations take these two parameters to be independent from the assigned victim and initialize them randomly, but it may be better if we generate them considering the associated victim. For example, for each rescuer-victim pair, the distance between them can be computed with the help of the DBES platform, and the hazard intensity around the victim also can be estimated. Then, the cost of assignment and the failed execution probability can be evaluated taking these two factors into account. In this way, we can obtain a more precise prediction of the expense of the allocation and make a more optimal assignment. Furthermore, we will explain more details about distributed control and information flows, for instance, how to get information for failed execution and how to re-assign tasks in the case of a failed execution. Additionally, when there are fewer rescuers than injured civilians, an efficient clustering scheme [25] can be applied to group victims according to their locations. Thus, the rescuer can provide support to as many civilians as possible, such as delivering protective devices, though they cannot carry all of them out of the building. What is more, the congestion problem caused by the rescuers should be alleviated. The navigation approach with the CPN can be applied in the rescue process, which is able to provide a faster optimal path finding and cause less congestion compared with Dijkstra’s algorithm [14].