Abstract
In wireless sensor networks, energy efficiency is mainly achieved by making nodes sleep. In this paper, we present the combination of SERENA, a new node activity scheduling algorithm based on node coloring, with TDMA/CA, a collision avoidance MAC protocol. We show that the combination of these two protocols enables substantial bandwidth and energy benefits for both general and data gathering applications. As a first contribution, we prove that the three-hop node coloring problem is NP-complete. As a second contribution, the overhead induced by SERENA during network coloring is reduced, making possible the use of these protocols even in dense networks with limited bandwidth. The third contribution of this paper is to show that applying any slot assignment algorithm with spatial reuse based on node neighborhood without taking into account link quality can lead to poor performances because of collisions. The use of good quality links will prevent this phenomenon. The fourth contribution consists of optimizing end-to-end delays for data gathering applications, by means of cross-layering with the application. However, color conflicts resulting from topology changes, mobility and late node arrivals can give rise to collisions. As a fifth contribution, we show how the MAC layer can detect color conflicts, and cope with them at the cost of a slightly reduced throughput. Then, we discuss the tradeoff between requesting SERENA to solve the color conflicts and dealing with them at the MAC layer, our third contribution. The combination of SERENA and TDMA/CA is evaluated through simulations on realistic topologies.
1. Introduction
Wireless sensor networks (WSNs) are having a very significant growth in segment markets such as industrial, automotive, defence, intelligent transportation and smart homes. However, such networks have resources of limited capacity. For instance, the bandwidth of a ZigBee network is restricted to 250 kbps. Hence, a challenging issue is the design of an efficient medium access protocol. We can distinguish three types of medium access protocols: TDMA, CSMA/CA and hybrid ones. TDMA ensures a deterministic access without collision and exhibits very good performances in case of heavy loads evenly distributed. CSMA/CA is very efficient in case of moderate traffic load and provides spatial reuse of the bandwidth. That is why hybrid solutions tend to combine the advantages of both. For instance, they behave like TDMA in case of heavy load and like CSMA/CA in case of light load. In this paper, we propose an hybrid medium access protocol called TDMA/CA (Time-Division Multiple Access with Collision Avoidance) and evaluate its quantitative performances. TDMA/CA keeps the determinism of TDMA and the spatial reuse of CSMA/CA. TDMA/CA aims at providing an efficient medium access in wireless sensor networks where bandwidth is the first resource that must be efficiently used. The second resource is energy that must be saved to prolong network lifetime. Since the sleep state is the least consuming, the MAC protocol should support sleeping nodes. Furthermore, communication being energy expensive, wasteful transmissions should be avoided. The third resource to consider is time. The delay to reach the sink should be minimized in data gathering applications. In TDMA/CA, node coloring provided by an activity scheduling module called SERENA (SchEdule RoutEr Node Activity) allows several nodes to transmit simultaneously without interfering, whereas the nodes that are not one-hop neighbors of the transmitters save energy by sleeping. Moreover, in data gathering applications, colors are assigned in such a way that data collected from the sensors reach the sink in a single cycle.
This paper is organized as follows. We first give a brief state of the art in Section 2 dealing with MAC protocols in wireless networks and node activity scheduling based on graph coloring. In Section 3, we present our solution consisting of two modules: the node coloring module SERENA and the medium access module TDMA/CA. We show how this solution can be adapted to various application requirements and different environment constraints. We consider two types of applications: general ones and data gathering applications. As a first contribution, we prove that the three-hop coloring problem is NP-complete. As a second contribution, we show in this paper how to reduce the overhead induced by the coloring algorithm. Thus, SERENA can be used even in dense networks with limited bandwidth. The properties met by each module are given in an ideal environment. The performances of SERENA and TDMA/CA are evaluated by simulation in Section 4 for general applications and data gathering ones. Our third contribution shows that if links of poor quality are used, collisions can occur in any slot assignment algorithm providing spatial reuse based on node neighborhood. We give a rule that prevents this phenomenon and quantify the benefits brought by SERENA and TDMA/CA in terms of throughput, delivery rate and response time. We focus on data gathering applications and quantify the optimization of the end-to-end delays, our fourth contribution. In Section 5, we consider a real environment where color conflicts can occur due to the occurrence of new links resulting from the dynamicity of the wireless topology. We evaluate the impact of such conflicts on the throughput, delivery rate and response time. We propose a solution to detect and solve the color conflicts, our fifth contribution and determine when such a solution should be applied. Finally, we conclude in Section 6.
2. State of the Art
A large number of energy-efficient MAC protocols have been proposed for wireless sensor networks to reduce energy consumption by avoiding the essential sources of energy consumption at the MAC level, which are: overhearing that is the reception of unwanted traffic, collisions that is the simultaneous reception of more than one frame, idle listening that is being active without neither receiving nor transmitting, and overhead that is the exchange of non application related data. These MAC protocols can be categorized into three broad families: contention-based protocols using a CSMA/CA (Carrier Sense Multiple Access with Collision Avoidance) algorithm that is based on the IEEE 802.11 CSMA/CA [1], TDMA-based (Time Division Medium Access-based) protocols where time slots are assigned for collision free data communication, and hybrid protocols that try to benefit from the advantages of both. In what follows we present a quick overview of some existing protocols and we focus on the different slot assignment algorithms.
2.1. Contention-based Protocols
One of the first MAC protocols based on contention to reduce energy consumption is PAMAS (Power Aware Multi-Access protocol with Signalling) [2]. Its goal is to eliminate overhearing by using a separate channel to exchange RTS/CTS. S-MAC (Sensor MAC) [3] avoids overhearing, but it uses only one channel. Moreover, S-MAC reduces the idle listening of nodes by allowing them to switch their network interfaces off periodically during predefined time intervals. T-MAC (Timeout MAC) [4] is an improvement of S-MAC. It dynamically modifies the time intervals during which the sensors sleep. D-MAC (Data gathering MAC) [5] has been proposed to reduce the latency: all the nodes along the path from the source to the destination are awaken to forward the packets. All these protocols use the RTS/CTS exchange to allow one-hop neighbors of the sender and the one-hop neighbors of the receiver to sleep for the duration of the communication. IEEE 802.15.4 [6] proposed a slotted CSMA/CA algorithm that is more adapted to the energy constraints of LP-WPAN (Low Power Wireless Personal Area Network) than IEEE 802.11 CSMA/CA algorithm.
2.2. TDMA-based Protocols
In wireless networks, it has been shown in [9] that scheduling packet transmissions taking into account the conflict graph modeling the interferences optimizes the network throughput. However, this omniscient scheduling is unrealistic. In radio networks where medium access is scheduled by TDMA, energy is saved because of the absence of collisions and a deterministic access is guaranteed. However, in order to maximize the efficiency of the MAC protocol, to save energy, bandwidth and delay, the active period during which each node can transmit must be kept small to improve application reactivity. Hence, the schedule should allow several nodes to transmit in the same slot. However, to be valid, this schedule must ensure that all nodes allowed to transmit in the same slot do so without interfering. We can distinguish two types of slot assignment:
- slots are assigned per link. In this case, only the transmitter and the receiver, the two extremities of the link are awake, all other nodes are sleeping. However, if the traffic on this link is light, the slot is not used at 100%. Broadcast transmissions are expensive: they require to copy the same information n times where n is the number of neighbors. Such solutions are also called link scheduling in [10,11]. A genetic solution is proposed in [12]. Two examples of deterministic slot assignment per link are given by TRAMA for general communications and FLAMA for tree-based communications like in data gathering applications. TRAMA [13], consists of 1) a neighborhood discovery protocol, 2) a schedule exchange protocol and 3) an adaptive election algorithm that selects the transmitter and the receiver(s) for each time slot. The node having the highest priority among its one-hop and two-hop neighbors wins the right to transmit in the considered slot. Each node declares in advance the list of its slots and for each slot its receiver(s). TRAMA is adaptive but also complex. To mitigate this complexity, a solution named FLAMA [14] is introduced for data gathering applications. FLAMA is simplified both in terms of message exchange and processing complexity.
- slots are assigned per node. In such a case, the transmitting node can use its slots as it wants: it can broadcast, send a unicast transmission to one of its neighbors then to another one. The advantage is that it can optimize the utilization of its slot. The drawback is that any neighbor of the transmitter must be awake during this slot, because it can be the destination of a message. Such solutions are also called broadcast scheduling as in [15] for instance. Krumke et al. have defined the problem called channel assignment in radio networks and have established complexity results for different types of network configurations [16]. They propose a 2-approximation algorithm for the minimum two-hop coloring on bounded degree planar graphs. With two-hop coloring, two nodes that are one-hop or two-hop neighbors must not have the same color.
More generally, medium access scheduling can also be done according to graph coloring in order to improve bandwidth and energy efficiency. In graph theory, graph coloring is a special case of graph labeling. It is an assignment of colors to either edges or vertices of the graph subject to certain constraints. Edge coloring [17] is an assignment of colors to the graph edges, such that two edges incident on the same vertex receive different colors. Whereas vertex coloring [19,20] is an assignment of colors to nodes such that two adjacent vertices have not the same color. In both cases, the number of colors used to color the graph should be minimized. Both use one-hop coloring. Extensions have been brought to two-hop or three-hop coloring. Vertex or node coloring enables broadcast communications, unlike edge coloring. Broadcast is needed to discover the neighborhood of a node and to advertise topology information to name a few. That is why we choose vertex coloring in SERENA. The one-hop node coloring problem has been proved NP-complete in [18]. That is why heuristics are used. Among them, those based on node degree achieve the best performance as shown in [19,20,21]. SERENA [22] takes advantage of this property by means of node priority computation.
The closest work to our is TDMA-ASAP [23], where this protocol, designed for data gathering applications, can be classified as an adaptive TDMA. It uses node coloring to provide spatial reuse, save energy and decrease the end-to-end delays to collect data at the sink node. Moreover, this protocol can adapt to various traffic conditions by slot stealing: a node can take the unused slot of its brother in the data gathering tree. The solution we propose in this paper differs from TDMA-ASAP because it supports general applications, where the communication is not limited to a tree. Moreover, broadcast transmissions are allowed as well as immediate acknowledgement of unicast transmissions. Furthermore, we show how to detect and solve color conflicts when they occur due to the wireless environment.
2.3. Hybrid Protocols
Hybrid protocols combine the advantages of TDMA and CSMA/CA. Z-MAC [7] is an hybrid protocol that optimizes the bandwidth utilization by selecting CSMA/CA under low contention and TDMA under heavy contention. Z-MAC is based on DRAND [8] which assigns slots to nodes in such a way that any node has a slot different from those assigned to its one-hop and two-hop neighbors. The advantage of Z-MAC is that it does not depend on the number of network nodes but on the cost of an asymptotic convergence.
There are several differences between Z-MAC and our solution combining TDMA/CA and SERENA:
- We can notice that Z-MAC does not allow an immediate acknowledgement of unicast messages, while this acknowledgement is needed in wireless communications to confirm quickly the correct reception of the frame. Z-MAC uses the channel noise level to estimate contention: nodes refrain from sending when the channel noise level is too high. TDMA/CA uses both CCA (Clear Channel Assessment) and acknowledgements.
- Z-MAC allows nodes to transmit a frame during any time-slot, but prioritizes the owners of a slot by setting different backoff ranges for owners and for non-owners. On the other hand, TDMA/CA forbids nodes to send outside of their time-slot, which allows nodes to transmit without any backoff.
- In case of data gathering applications, where all traffic is done according to a tree rooted at the sink, the end-to-end delays can be high with Z-MAC, where slot allocation is totally arbitrary with regard to the parent-child relation. With the combination of TDMA/CA and SERENA, in an upstream cycle, a child always transmits before its parent, allowing it to aggregate data collected from all its children before transmitting them to its own parent. Thus, all collected data can reach the sink in a single cycle. In a downstream cycle, the propagation of information originated at the root to all network nodes is done in a single cycle. Moreover, the frequency of upstream/downstream cycles is determined according to the application constraints.
- From the energy point of view, Z-MAC reduces the activity period duration in the polling cycle enforced by the application. It does not allow nodes to sleep during this activity period because nodes are allowed to send during any time slot. SERENA, on the other hand (see Section 3) aims at maximizing network lifetime by scheduling node activity. SERENA increases the sleep period of nodes without reducing the amount of data transferred.
A performance comparison is done on an example in Section 3.7.
3. Framework
In this section we present the combination of TDMA/CA, a medium access protocol and SERENA, its associated node coloring algorithm. We first define the logical architecture and then detail each module.
3.1. Architecture
Globally, the combination of TDMA/CA and SERENA works as follows:
- SERENA (SchEdule RoutEr Node Activity) is a generic node coloring algorithm able to adapt to various application requirements and different environment/MAC layer constraints (e.g., unicast with/without immediate acknowledgement, broadcast). SERENA assigns colors to nodes in such a way that the number of colors used is small and two nodes having the same color can transmit simultaneously without interfering. More precisely, SERENA builds for any node N the set of nodes that cannot have the same color as N. Such a node would cause a collision making impossible for an intended destination to correctly receive its frame.
- The synchronization module receives a list of colors from SERENA. This synchronization module allocates time slots according to node colors, by means of beacons [24].
- TDMA/CA schedules the medium access according to the colors assigned by SERENA. It assigns one time slot per color. All nodes having the color corresponding to the current time slot are allowed to transmit. Any other node that has a one-hop neighbor of this color must be awake to receive its message. All the other nodes save energy by sleeping. In data gathering applications, we distinguish two types of cycles: those favoring upstream traffic, where colors are scheduled in decreasing order and those favoring downstream traffic, where colors are scheduled in the reverse order. The frequency of each cycle type is determined by the application constraints.
Before detailing the functioning of SERENA and TDMA/CA, we present the requirements that must be met by their combination as well as the assumptions done by SERENA.
3.2. Requirements and Assumptions
In this paper, we focus on two types of applications that must be supported by the combination of TDMA/CA and SERENA. With regard to unicast communications, we distinguish:
- general applications where any node can communicate with any other node in unicast mode. We also call them general communications. This type is the default one. It is used in the absence of knowledge of the application, because it introduces no restriction.
- data gathering applications where all sensor nodes send their data to a sink in unicast mode. Consequently, the only unicast communications that are used are either between a node and its parent, or between a node and its children. We also call them tree communications.
Notice that these two types of application can support broadcast in addition.
3.2.1. Requirements
To build the set , we have to consider all the types of communication provided by the network and identify collisions that should be avoided. In this paper, we consider the following requirements:
- Req1 for general communications: Any node can communicate in unicast mode with any other node.
- Req1’ for tree communications: Any node can communicate in unicast mode only with its parent or its children in the data gathering tree.
- Req2 for immediate acknowledgement of unicast transmissions: since radio transmission is unreliable, the receiver must transmit its acknowledgement immediately after receipt of the MAC frame. In other words, the receiver uses the slot of the sender to transmit its acknowledgement. Thus, the sender can use its slot to retransmit if needed.
- Req3 for broadcasts: Any node can broadcast information to its neighbors.
Consequently, SERENA must meet requirements , and for a general application, while it must meet , and for a data gathering application. In the following, we abusively use the terms general coloring for the first case and tree-based coloring for the second one.
3.2.2. Assumptions
Whatever the application type, whatever the communication requirements, SERENA assumes an ideal environment where:
- A0: Any node has a unique identifier in the network.
- A1: Any node X that is not in transmission range of any node N does not prevent the correct receipt on any link used by N.
- A2: links are stable and symmetric.
Assumption ensures that we can disambiguate node priority by considering node identifier. Assumption means that a node should use for routing and association only links of good quality. We will see in Section 4 the consequences of a violation of this assumption. We will also see how to meet this assumption in a real environment. In Section 5, we will evaluate the impact of color conflicts that can occur when assumption is not met and show how such conflicts can be detected and solved.
3.3. Complexity Analysis
Let be a graph representing the network topology. Each vertex represents a network node and for all vertices u and v in V, the edge if and only if the two nodes u and v are one-hop neighbors. One-hop coloring of G consists in coloring each vertex in V using the smallest number of colors and in such a way that two vertices with the same color have no common edge. The associated decision problem can be defined as follows. Let k be a positive integer strictly smaller than the cardinal of V. Can G be colored with k colors in such a way that two nodes that are one-hop neighbors have not the same color? Clearly, the answer is yes if and only if G can be one-hop colored with k colors. This problem has been proved NP-complete in [18]. We want to generalize this property to three-hop coloring problem.
For simplicity reasons, colors are represented by natural integers, starting with zero.
Theorem 1: The decision problem of three-hop coloring is NP-complete.
Proof: First, we show that this problem is in NP. Given a three-hop coloring of G, we can check in polynomial time (, where n is the number of nodes) that the coloring produced by a given three-hop algorithm does not assign the same color to two nodes that are one, two or three-hop neighbors, and the total number of colors is k. Second, we reduce the k-color one-hop coloring problem that has been shown NP-complete in [18] to the -color three-hop coloring problem, with a positive integer. Let us consider any graph , we can build a graph where:
- assuming a bijective function fwe define the set , where is called the conjunction node and U denotes the set of mapping nodes. Hence, the cardinal of U is equal to n, the number of nodes in G.
- we define the set .
This construction is polynomial in time. An example of graphs G and is illustrated in Figure 1.
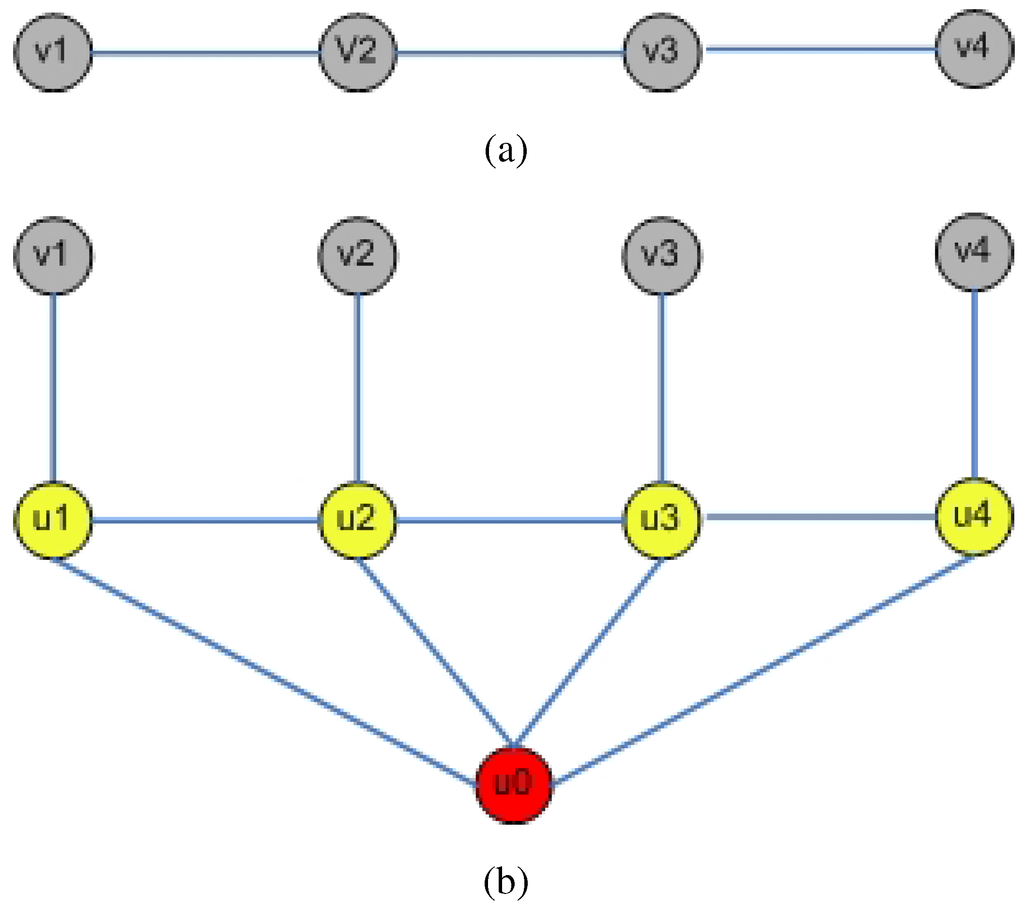
Figure 1.
Example of: (a) Graph G; (b) Transformed graph .
Lemma 1: All nodes in are one-hop or two-hop neighbors.
Proof: By construction of . ■
Lemma 2: The number of colors needed by a three-hop coloring of nodes in in graph is equal to , where n is the number of nodes in G.
Proof: From lemma 1, all nodes in are one-hop or two-hop neighbors. Hence, no color can be reused with three-hop coloring. By construction of , the number of these nodes is equal to . ■
Lemma 3: Any color used for a node in V by a three-hop coloring of cannot be used by any node in .
Proof: Let us consider any node and any node . By construction, the distance between v and u, denoted meets . From Lemma 1, . Hence . Hence, they should use different colors with three-hop coloring.
■
We want to show that has a one-hop coloring with k colors if and only if has a three-hop coloring with colors.
Given a one-hop coloring of G with k colors, we want to show that there exists a three-hop coloring of with colors as follows. This three-hop coloring will use k colors for nodes in V and colors for nodes in according to Lemma 2. From Lemma 3, colors used in V cannot be reused in . It follows that there exists a three-hop coloring of with exactly colors.
Now, let us assume that we have a three-hop coloring of with colors and we want to show that we can find a one-hop coloring of G with k colors. From Lemma 2, colors are needed for three-hop coloring of nodes in . From Lemma 3, colors used in V cannot be reused in . Hence, colors are used to color the nodes in V. Since, any two nodes and in V that are one-hop neighbors in G are three-hop neighbors in , by construction of , we deduce that no two one-hop neighbors in G use the same color. Hence, we can find a valid one-hop coloring of G with colors. ■
3.4. Principles of SERENA Coloring Algorithm
The SERENA coloring algorithm is distributed and localized. Any node N proceeds as follows:
- N builds its set , denoting the set of nodes that cannot have the same color as N. This set is built from the requirements previously expressed. A collision table is built as we will see later, to identify all possible collisions between the frames transmitted in the network. Such collisions should be avoided.In a general application with broadcast and immediate acknowledgement support, SERENA will use a three-hop node coloring. Indeed, from and , no one 1-hop or 2-hop neighbor can have the same color as N, otherwise a collision would occur between the data frames sent by N and the other node. From and , no 3-hop neighbor should have the same color as N, otherwise a collision would occur between an acknowledgement and a data frame as illustrated in Figure 2. Nodes N and Q having the same color, transmit simultaneously to O and P respectively. The acknowledgement of P to Q causes a collision on node O that fails to receive the data frame sent by N. Hence, for a general application, 3-hop coloring is needed: two nodes N and M can share the same color if and only if they are neither 1-hop, nor 2-hop, nor 3-hop neighbors.
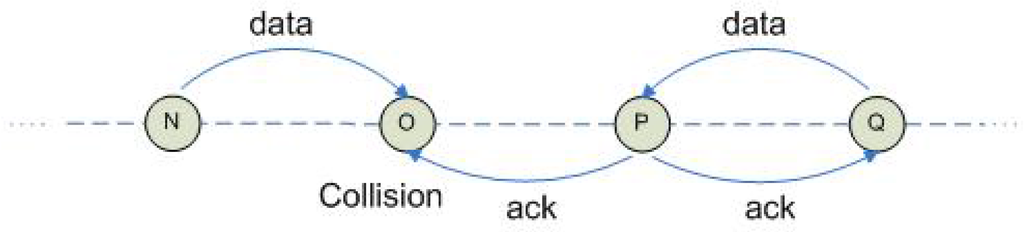 Figure 2. Collision with two-hop coloring and immediate acknowledgement.
Figure 2. Collision with two-hop coloring and immediate acknowledgement.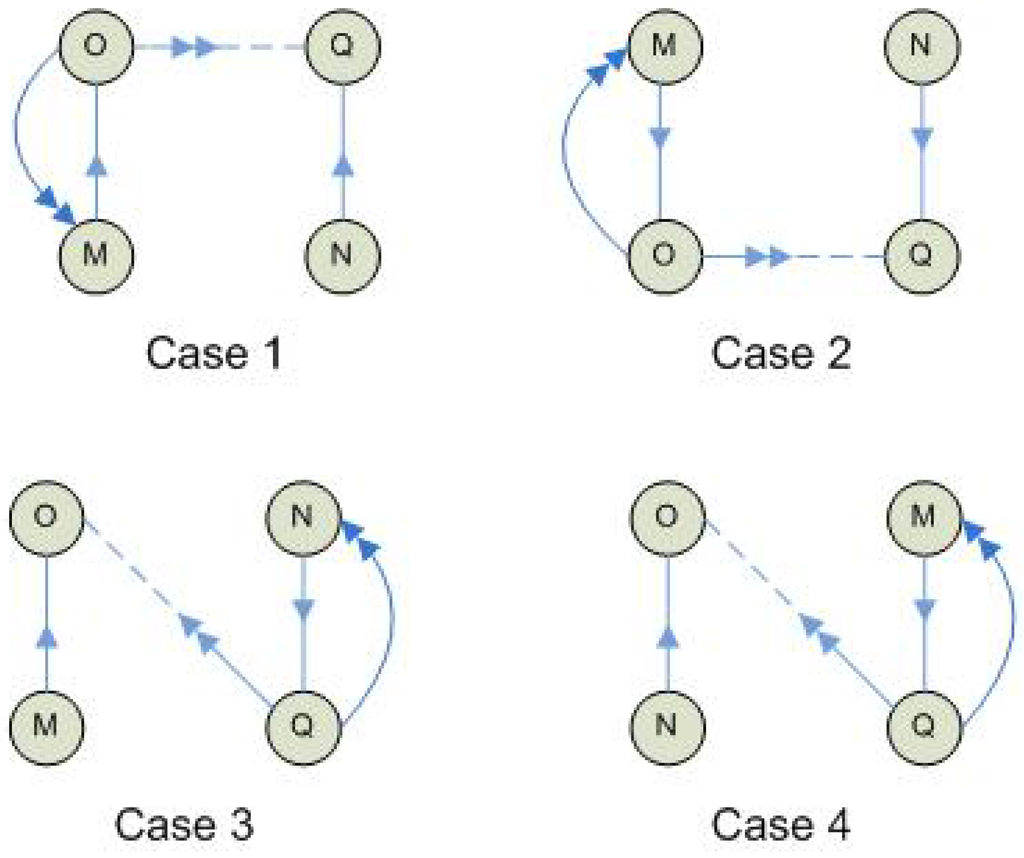 Figure 3. Collision between nodes N and M having the same color with two-hop coloring and immediate acknowledgement in a tree.In a data gathering application with broadcast and immediate acknowledgement support, two-hop coloring is required by : no one-hop or two-hop neighbor of N can have the same color as N. Moreover, adds the following constraints: nodes M and N cannot have the same color, otherwise the conflicts illustrated in Figure 3 would occur. We adopt the following convention: the link between a node and its parent is represented by a vertical plain line, the parent node being represented over its child node. A dotted line represents a one-hop neighbor link that is not a parent link: it is either horizontal or diagonal. A single arrow represents the transmission of a data frame, whereas a double arrow represents the transmission of an acknowledgement. Cases 1 and 2 correspond to a conflict between a unicast transmission by N and the acknowledgement of another unicast transmission originated from M. Cases 3 and 4 correspond to a conflict caused by the acknowledgement of a unicast transmission and a broadcast transmission, originated from M in case 3 and from N in case 4. For data gathering applications, to color itself, N should know:
Figure 3. Collision between nodes N and M having the same color with two-hop coloring and immediate acknowledgement in a tree.In a data gathering application with broadcast and immediate acknowledgement support, two-hop coloring is required by : no one-hop or two-hop neighbor of N can have the same color as N. Moreover, adds the following constraints: nodes M and N cannot have the same color, otherwise the conflicts illustrated in Figure 3 would occur. We adopt the following convention: the link between a node and its parent is represented by a vertical plain line, the parent node being represented over its child node. A dotted line represents a one-hop neighbor link that is not a parent link: it is either horizontal or diagonal. A single arrow represents the transmission of a data frame, whereas a double arrow represents the transmission of an acknowledgement. Cases 1 and 2 correspond to a conflict between a unicast transmission by N and the acknowledgement of another unicast transmission originated from M. Cases 3 and 4 correspond to a conflict caused by the acknowledgement of a unicast transmission and a broadcast transmission, originated from M in case 3 and from N in case 4. For data gathering applications, to color itself, N should know:- its one-hop and two-hop neighbors;
- the children of the one-hop neighbors of its parent: case 1 of Figure 3;
- the parents of the one-hop neighbors of its children: case 2 of Figure 3;
- the children of the one-hop neighbors of its children: case 3 of Figure 3;
- the parents of the one-hop neighbors of its parent: case 4 of Figure 3.
Each case allows node N to add conflicting nodes in its set . - N computes its priority, denoted . To minimize the number of colors needed to color all network nodes, the priority is chosen as the cardinal of:
- in case of general communications;
- in case of tree communications. This choice tends to alleviate the color constraints imposed to the descendants of the node and thus to reduce the number of colors used.
Ties are broken by the smallest node identifier. The priority choice is done according to the simulation results published in [19,20,21]. - N colors itself according to its priority order in . This leads to the two following rules:
- Rule R1: any node N colors itself if and only if all nodes in having a higher priority than N are already colored.
- Rule R2: node N takes:
- –
- the smallest color unused in in case of general communications;
- –
- the smallest color unused in and higher than the color of its parent in case of tree-based communications.
These rules tend to minimize the number of colors needed to color all network nodes. Notice that in the case of tree communication, the rule obliging a node to take a color higher than the color of its parent has been introduced to minimize the delay needed to collect data by the sink. Scheduling medium access according to the decreasing order of colors enables each node to aggregate the information received from its children before transmitting it to its parent. Consequently, information from all nodes can reach the sink in a single cycle. Thus, delays are minimized, as we will see in Section 4.4.
3.5. Overhead Reduction and Properties of SERENA
We now show how to minimize the overhead caused by the messages exchanged during network coloring.
3.5.1. Overhead Reduction
During the coloring algorithm, each node N periodically broadcasts a message to its 1-hop neighbors. In a naive implementation, this message would include the priority and color of (a) the node N itself, (b) its 1-hop neighbors in , as well as (c) its 2-hop neighbors in . Such messages lead to a high overhead, that can be unacceptable in dense networks with a short MAC frame size. That is why we propose in this paper, an optimized message. The content of the message is reduced: it is no longer required to transmit each one-hop and two-hop neighbor with its priority and its color.
More precisely, in a general application with broadcast and immediate acknowledgement of unicast communications, any node N after having built its two-hop neighborhood by means of the messages sends a message containing all its two-hop neighbors. Notice that this message can be fragmented if requested by the MAC layer. New fields are added such as a fragment number and a flag indicating the last fragment. This message is sent once, at the beginning of the coloring in general applications. This message should also be transmitted whenever the one or two-hop neighborhood changes. Hence, any receiving node M can build its set and determine its priority. The priority of node N is equal to its number of neighbors up to three-hop.
The optimized message sent by node N to its one-hop neighbors contains:
- For node N: its address, priority and color.
- The address and priority, denoted , of the uncolored one-hop neighbor having the highest priority. Let denote the set of one-hop neighbors of N. We have: ,
- The bitmap of colors already selected by its one-hop neighbors.
- The address and priority, denoted , of the uncolored node P providing the highest among all nodes .By definition, ,
- The bitmap of colors already selected by its two-hop neighbors.
In a data gathering application with broadcast and immediate acknowledgement of unicast communications, each node first computes its priority. For this, it sends its number of descendants to its parent. This parent computes its priority by summing the number of descendants of each child and sends it to its own parent. In its message, any node uses two specific flags to indicate its parent and children among its one-hop neighbors. Node N sends to its one-hop neighbors its message containing:
- For node N: its address, priority and color.
- The address and priority, denoted , of the uncolored one-hop neighbor having the highest priority. We have ,
- The bitmap of colors already selected by its one-hop neighbors.
- The bitmap of colors already selected by its parent and children.
- The address and priority, denoted , of the uncolored parent or child of one-hop neighbors having the highest priority.By definition, where P is a parent or child of . This is because only a subset of the three-hop neighbors is needed by the receivers.
- The bitmap of colors already selected by the parents or children of one-hop neighbors.
Notice that it is sufficient to know that a node is parent or child of one-hop neighbors of the parent or children node. It does not matter to know which exact role it plays among the two.
In general applications as well as in data gathering ones, node N processes the received messages and applies the principles previously given to color itself. This optimization considerably reduces the overhead induced by the coloring algorithm, making possible its use in dense networks with small MAC frame size.
Property P0: With assumptions to , in three-hop coloring and tree coloring, any node N can color itself if and only if , with: , , in the general case, in the tree case, where where P is a parent or child of .
Proof: With three-hop coloring and tree coloring, any node N can color itself if and only if no uncolored node in has a priority higher than N. We recall that two different nodes never have the same priority insofar as ties are broken by node identifiers that are assumed unique in the considered network.
Let us show that if any node N is coloring itself, then .
If node N is coloring itself, it means that:
- all its uncolored one-hop neighbors have a smaller priority. Hence, for any M uncolored one-hop neighbor of N, we have . Hence, ;
- all its uncolored two-hop neighbors have a smaller priority. is the maximum priority of uncolored nodes P that are one-hop neighbors of M, any one-hop neighbor of N. Consequently, we have the following cases:
- –
- node P is the node N itself and has priority ;
- –
- P is a one-hop or two-hop neighbor of node N. In which case, we have by assumption: .
Hence, . - and all its uncolored three-hop neighbors in have a smaller priority.
- –
- In the general coloring, is the maximum priority of uncolored nodes Q that are one-hop neighbors of P, itself one-hop neighbor of M, one-hop neighbor of N. Consequently, we have the following cases:
- *
- node Q is the node N itself and has priority ;
- *
- Q is a one-hop, two-hop or three-hop neighbor of node N. In which case, we have by assumption: .
Hence, . - –
- In the tree coloring, is the maximum priority of uncolored nodes Q that are parent or child of P, itself one-hop neighbor of M a parent or child of N. We then have the following cases:
- *
- node Q is the node N itself and has priority ;
- *
- Q is a one-hop or two-hop neighbor of node N. In which case, we have by assumption: .
- *
- Q is a three-hop neighbor . In which case, we have by assumption: .
Hence, .
Hence, in both colorings, .
Conversely, let us assume:
. We now show than N can color itself. Since , no uncolored one-hop neighbor has a priority higher than N. Since , no uncolored two-hop neighbor has a priority higher than N, otherwise we would have the contradiction . Since , no uncolored three-hop neighbor in has a priority higher than N, otherwise we would have the contradiction . Hence, node N has the highest priority among the uncolored nodes in . ■
3.5.2. Properties
More generally, we can now give the properties met by SERENA algorithm.
Property P1: With assumptions A0, A1 and A2, ∀ node N if ∃ node then .
Proof: This property is deduced from assumptions , and . ■
Property P2: In an ideal environment, the only types of collision that can occur in a general application with broadcast and immediate acknowledgement are between one-hop, two-hop or three-hop neighbors.
Proof: In a general application with broadcast and immediate acknowledgement, the only collisions that can occur are caused by a unicast data frame, a broadcast data frame or an acknowledgement frame. Table 1 summarizes all possible cases. In case of a collision involving a unicast or broadcast data frame, the color of the data frame sender is conflicting, whereas in the case of a collision involving an acknowledgement frame, the destination of the acknowledgement has a conflicting color. That is why this table is symmetric and lines corresponding to unicast and broadcast data are identical.

Table 1.
Possible collisions in case of general application, broadcast and immediate acknowledgement.
| Unicast Data | Acknowledgement | Broadcast Data | |
| Unicast Data | 1 or 2-hop nodes | 1 or 3-hop nodes | 1 or 2-hop nodes |
| Acknowledgement | 1 or 3 hop nodes | 2-hop nodes | 1 or 3-hop nodes |
| Broadcast Data | 1 or 2-hop nodes | 1 or 3-hop nodes | 1 or 2-hop nodes |
As a consequence, all possible collisions are taken into account by three-hop coloring. ■
Property P3: SERENA three-hop coloring provides a valid coloring for general applications, assuming an ideal environment.
Proof: For three-hop coloring, the set contains by construction all nodes up to 3-hop from N, assuming an ideal environment. SERENA ensures by construction that no node in will color simultaneously with N. Moreover, when N colors itself, it knows all the colors taken by nodes in with a higher priority. Hence, it takes a color that is not already used in . Furthermore, assuming an ideal environment, nodes that do not belong to cannot create a collision with data sent by N or acknowledgement sent to N, as shown by Property P2. Hence, SERENA does not create collision. ■
Property P4: In an ideal environment, the only types of collision that can occur in a data gathering application with broadcast and immediate acknowledgement are between one-hop, two-hop nodes or correspond to cases 1 to 4 in Figure 2.
Proof: In a data gathering application with broadcast and immediate acknowledgement, the only collisions that can occur are caused by a unicast data frame sent to its parent or child, a broadcast data frame sent to its neighbors or an acknowledgement frame sent to its parent or child. Table 2 summarizes all possible cases. This table is symmetric. In case of tree communications where all unicast data transmissions of a cycle are either upstream or downstream, unicast and broadcast data frames do not cause the same collisions, unlike in the general communications case (see for instance the acknowledgement column).

Table 2.
Possible collisions in case of data gathering application, broadcast and immediate acknowledgement.
| Unicast Data | Acknowledgement | Broadcast Data | |
| Unicast Data | same parent | cases 1 to 4 | 1 or 2-hop nodes |
| Acknowledgement | cases 1 to 4 | a child of a 1-hop node of the other | 2-hop node of parent or child |
| Broadcast Data | same parent | 2-hop node of parent or child | 1 or 2-hop nodes |
As a consequence, all possible collisions are taken into account by tree coloring. ■
Property P5: SERENA tree coloring provides a valid coloring for data gathering applications, assuming an ideal environment.
Proof: For SERENA tree coloring, the set contains by construction, all nodes up to 2-hop from N, and all nodes M meeting one of the four cases depicted in Figure 3. Assuming an ideal environment, SERENA ensures that no other node in can take the same color as N. Furthermore, assuming an ideal environment, nodes that do not belong to cannot create a collision with data sent by N or acknowledgement sent to N, as shown by property P4. Hence, SERENA does not create collision. ■
3.6. TDMA/CA MAC Protocol
TDMA/CA (Time-Division Multiple Access with Collision Avoidance) is an hybrid protocol that combines TDMA and CSMA/CA approaches. TDMA/CA uses a synchronization module that divides time into cycles. Each cycle starts with a synchronization period, is followed by a period for each color, and ends with an inactivity period.
During the synchronization period, all the nodes of the network are synchronized, and the color sequence is broadcast to each node. During the colored period of a color c, only nodes of color c are allowed to send frames. Similarly, all the nodes having a one-hop neighbor of color c are listening. The other nodes sleep. During the inactivity period, all the nodes sleep. The cycle organization is represented on Figure 4. On this example, color slots are sequenced according to a decreasing order and they all have the same duration.
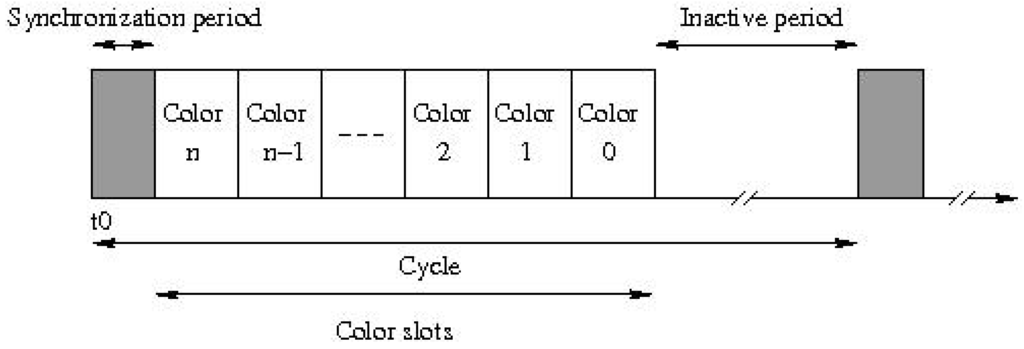
Figure 4.
Cycle with the active period and the inactive one.
The novelty of TDMA/CA resides in the medium access mechanism used during each colored slot. The mechanism is based on the two following facts:
- As SERENA reduces the possibility of color conflicts, the probability of frame collisions is limited. Thus, the nodes should transmit frames immediately, without having to wait for a backoff.
- As SERENA cannot guarantee that there is no color conflict (such conflicts can occur due to propagation condition changes or node mobility), there should be a collision detection mechanism.
The medium access mechanism used by TDMA/CA in each colored slot acts as follows. When a node decides to transmit a frame, it waits for its colored slot. Then, it first attempts to transmit the frame without backoffs. If it receives an acknowledgement, from the receiving node, the transmission was successful (and in this case, the medium is used efficiently as there was no unnecessary backoff). However, if the sender does not receive an acknowledgement from the receiving node, TDMA/CA assumes that there has been a collision due to a color conflict. In this case, the sender attempts to retransmit the frame with a random backoff, similarly to the IEEE 802.15.4 standard. At the end of the backoff, the sender performs two CCAs in order to ensure that there is no other node transmitting. If it detects activity on the channel, the sender draws a backoff in a larger window. For each transmission attempt, the backoffs are randomly chosen within ranges , where i denotes the number of times the channel was detected busy, and . If the channel is detected busy more than five times, or if there has been more than five transmission attempts, the frame is dropped by TDMA/CA.
TDMA/CA has the following properties:
- If there is no color conflict and no frame loss, frames are transmitted immediately (that is, without backoffs).
- If there is no color conflict but frame losses, frames are transmitted with a small backoff, as with CSMA/CA.
- If there is a color conflict, frames can still be received but at the cost of a throughput reduction as backoffs are added.
In this paper, we assumed that the traffic distribution is balanced among all the nodes. Heterogeneous traffic has an impact on the performance of our method. If a node does not have enough time during its time slot to send its data, it has to wait for its next time slot, which introduces significant delays. This issue can be dealt with in the following ways.
- The assignment and duration of time slots is achieved by a centralized entity (which is the coordinator of the PAN). If the traffic production rate is known by this entity, it can allocate longer time slots for colors having high traffic. However, it is not sufficient to increase the duration of the sender time slots, as the traffic is routed to other nodes with other colors. The central entity has to take into account the routes used by the routing protocol in order to optimize the color allocation.
- If the traffic production rate is not known by the central entity, it is possible to insert a CSMA/CA period between the colored period and the inactivity period. All the nodes are active during this period, and they are all able to send. This period can be used as a buffer for the traffic that exceeds the duration of the colored time slots, and it can also be used to accommodate non-colored nodes to join the network. This approach has been studied in [26,27].
- SERENA is based on node coloring. Node coloring has the advantage to allow a node to transmit any type of traffic (unicast or broadcast) in its slots. Hence, a node can optimize its transmissions in the slots associated with its color, unlike link coloring where the slots granted to a link cannot be used for another traffic sent by the same node. If the node has no more traffic to send, it can sleep, as well as its one-hop neighbors after having detected a silent period.
However, taking into account traffic heterogeneity has an impact on the delay of the mechanism. This issue is a perspective of our work. Some simulation results are reported in Section 4.6.
3.7. Comparison with Z-MAC Protocol
We now compare the performances of Z-MAC and SERENA on a small example. The chosen configuration, depicted in Figure 5, is very close to the one used by the authors of Z-MAC in [7]. We first evaluate the number of colors needed to color the nine nodes using DRAND (see [8] for more details) and SERENA. DRAND is the probabilistic two-hop node coloring algorithm used by Z-MAC. For SERENA, we use different variants: two-hop coloring because it supports the same requirements as DRAND, tree-coloring for data gathering applications and three-hop coloring for general applications.
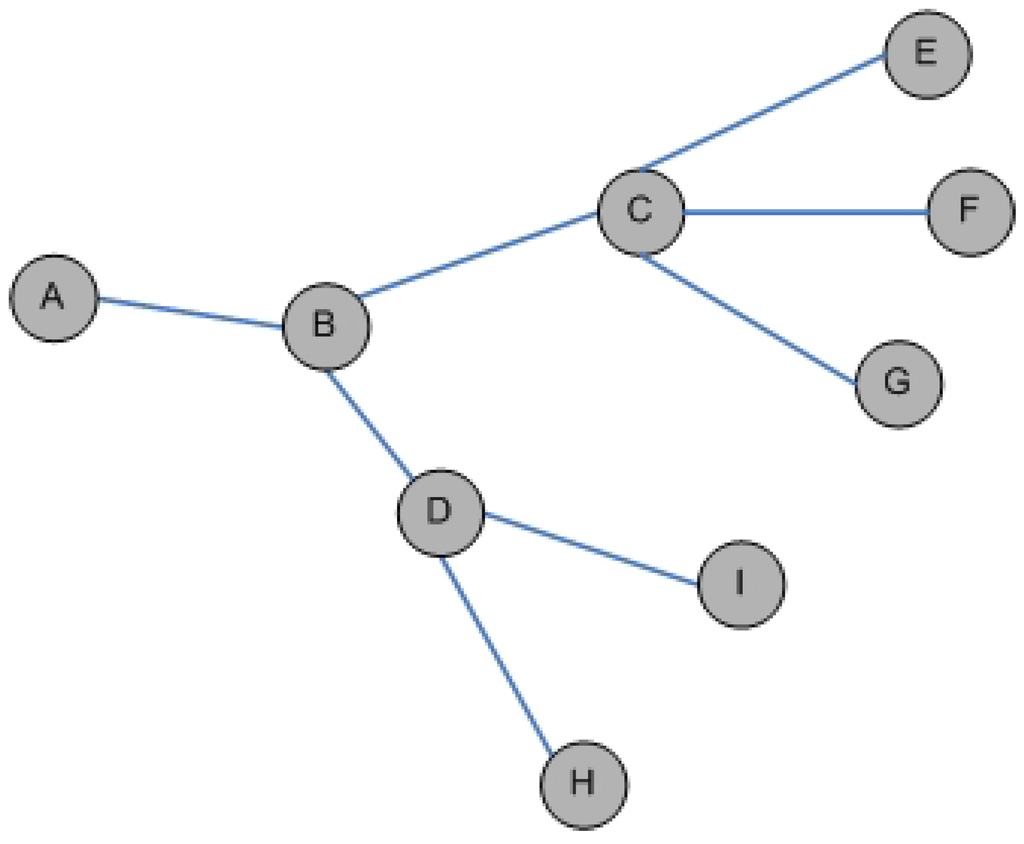
Figure 5.
Configuration used for comparing Z-MAC and SERENA.
With Z-MAC, the nodes with a small number of one-hop neighbors have a higher probability to color themselves before the others and to take the smallest colors. For the configuration considered, six colors are needed. Color 0 is used by three nodes whereas color 1 is used by two nodes. The Z-MAC superframe is illustrated in Table 3. Since the size of the superframe is equal to 1 + the maximum number of (one-hop nodes + two-hop nodes), the superframe contains 9 slots. A node N uses the slot corresponding to its color c as well as all slots corresponding to , with a and k positive integers such that , where is the maximum number of one-hop neighbors of any node M up to two hops from node N. In this configuration, we have =4 for any network node. It follows that only color 0 can use several slots in the same cycle. Notice that color 0 is used by nodes A, G and H having a low number of one-hop neighbors. If we assume that the amount of traffic forwarded by a node depends on its number of neighbors, offering these nodes a bandwidth amount twice the amount of other nodes has a limited interest. We can also observe that slots 6 and 7 are unused at each cycle, leading to about 22% of bandwidth waste at each cycle. Furthermore, two cycles of Z-MAC correspond to three cycles of SERENA with two-hop coloring, giving the opportunity to transmit more frames.
With SERENA two-hop coloring, we get 5 colors, one less than DRAND. With SERENA, the nodes with the highest number of neighbors up to two-hop color themselves first. Color 1 is used twice, as well as color 2, whereas color 3 is used three times. We obtain the cycle illustrated in Table 4.
If the support of immediate acknowledgement is required for this tree whose root is node A, SERENA tree-coloring is applied, leading to seven colors, one more than DRAND but with the support of immediate acknowledgement. Colors 4 and 5 are used twice. The MAC cycle comprising seven color slots, is depicted in Table 5. The main advantage of tree-coloring is that in a single cycle, the data sent by all nodes can reach the sink, assuming data aggregation. We will evaluate the end-to-end delays in more details in Section 4.4. This property is not ensured with Z-MAC, where in the worst case, the maximum end-to-end delay is equal to the superframe size times the hop number toward the sink.

Table 3.
Slot schedule with Z-MAC.
| Node | slot0 | slot1 | slot2 | slot3 | slot4 | slot5 | slot6 | slot7 | slot8 |
| A | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| B | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| D | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| E | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| F | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| G | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| H | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| I | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |

Table 4.
Slot schedule with SERENA two-hop coloring.
| Node | slot0 | slot1 | slot2 | slot3 | slot4 | slot5 |
| A | 0 | 0 | 0 | 1 | 0 | 0 |
| B | 1 | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 1 | 0 | 0 | 0 | 0 |
| D | 0 | 0 | 1 | 0 | 0 | 0 |
| E | 0 | 0 | 0 | 0 | 1 | 0 |
| F | 0 | 0 | 0 | 1 | 0 | 0 |
| G | 0 | 0 | 1 | 0 | 0 | 0 |
| H | 0 | 1 | 0 | 0 | 0 | 0 |
| I | 0 | 0 | 0 | 1 | 0 | 0 |

Table 5.
Slot schedule with SERENA tree or three-hop coloring.
| Node | slot0 | slot1 | slot2 | slot3 | slot4 | slot5 | slot6 |
| A | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| B | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| D | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| E | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| F | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| G | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| H | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| I | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
If now we apply SERENA three-hop coloring, we get exactly the same colors as previously. We conclude that for this configuration, our solution combining SERENA and TDMA/CA is more efficient for both general applications and data gathering ones.
4. Performance of SERENA and TDMA/CA
To evaluate the performance of TDMA/CA with SERENA, we proceed by simulation and consider various network configurations. Each network configuration is characterized by a number of nodes and a density (i.e., the average number of neighbors per node +1). For each configuration, we perform 20 simulation runs and evaluate for each the four following performance criteria:
- the number of colors: The difference between the node number and the color number gives the number of slots saved by our algorithm in each cycle compared with classical TDMA where the slot number is equal to the node number.
- the active period duration: During the active period, each node is able to transmit during a slot. This does not mean that all nodes are active during this period. On the contrary, nodes sleep during the slots that correspond neither to their color, nor to the colors of their one-hop neighbors. The active period duration can be computed from the number of colors and the slot duration. Notice that if the active period is shortened, the application manager has the choice between:
- –
- either increasing the inactive period during which all nodes sleep;
- –
- or reducing the cycle comprising the active period followed by the inactive period.
The active period duration is equal to the number of colors multiplied by the slot duration. - the average number of nodes sharing the same slot. This criterion evaluates the bandwidth spatial reuse. It is equal to the number of nodes divided by the number of colors.
- the error rate. It shows that SERENA ensures the absence of collision, assuming an ideal environment.
- the end-to-end delay. In the simulations reported in this paper, we consider two types of traffic. For general traffic, each node transmits data to a destination randomly chosen. For data gathering traffic, all nodes transmit data to the sink node, which is the PAN coordinator denoted by node 0.
The result for a network configuration that is depicted in Figure 7 and Figure 11 is the average of the 20 simulation runs corresponding to this configuration. In this section, we assume that all links are stable and symmetric. We will see what happens if this is not the case in Section 5. We first point out the necessity of using links of good quality only and then compare the performances of general coloring and tree-based coloring.
4.1. Simulation Setup
We undertook the simulations using NS2, Network Simulator 2. We completely redesigned layers 1 to 3 of the simulator in order to implement the synchronization module detailed in [24], the time segmentation access method and the physical phenomena of wireless networking such as the capture effects, collisions, interferences, etc. In addition, we used a hierarchical routing algorithm based on the hierarchical addresses proposed by ZigBee [25]. Simulation parameters are specified in Table 6. The reception threshold denotes the minimum received signal power needed to decode the received frame. The capture threshold is the minimum ratio power between two signals allowing the receiver to capture the strongest one and lock on it. The capture threshold and the reception threshold are used to assess the quality of links, as shown in the next section.

Table 6.
Simulation parameters.
| Simulation parameter | Value | |
| Configuration | Number of nodes | 25–100 |
| Density | 8–10–12 | |
| PHY | Bandwidth | 250 kbps |
| Transmission range | 11.5 m | |
| Reception threshold | –92 dBm | |
| Sensitivity threshold | –95 dBm | |
| Capture threshold | 5 dBm |
4.2. Necessity of Using Exclusively Links of Good Quality
We first show the necessity of using exclusively links of good quality, both in the association protocol and in the routing protocol. We consider a configuration with 49 nodes and a density of 8. In this configuration, any node received with a power higher than the receiver sensitivity is considered as a one-hop neighbor from the routing point of view and can be used in the association process. We apply SERENA general coloring. Nodes with the same color transmit simultaneously.
By definition, a color conflict occurs between two nodes having the same color when these nodes prevent each other or some neighbor destination to receive correctly the intended message because of a collision.
Contrary to what coloring algorithms generally suppose, conflicts still occur for any number of hops considered for color reuse. This is due to interferences received from nodes that could not be detected as neighbors (having a received signal power ).
For instance, let us consider Figure 6(a) that uses the same notation as Figure 3. Node 2 is one-hop neighbor of nodes 0 and 4. Nodes 3 and 13 have the same color and transmit simultaneously. A collision occurs on node 2 between the acknowledgements sent by node 0 to node 3 and by node 4 to node 13. This does not matter since node 2 is not the destination and any destination correctly receives its frame. This is no longer the case with the next example. Nodes 6 and 27 have the same color and transmit data to their one-hop neighbor, nodes1 and 26 respectively. Node 1 that acknowledges node 6, prevents node 26, a two-hop node, to receive correctly from node 27. This is due to the fact that the link between nodes 26 and 27 is of poor quality (–92 dBm) and the signal from node 1 is received by node 26 at –96 dBm.
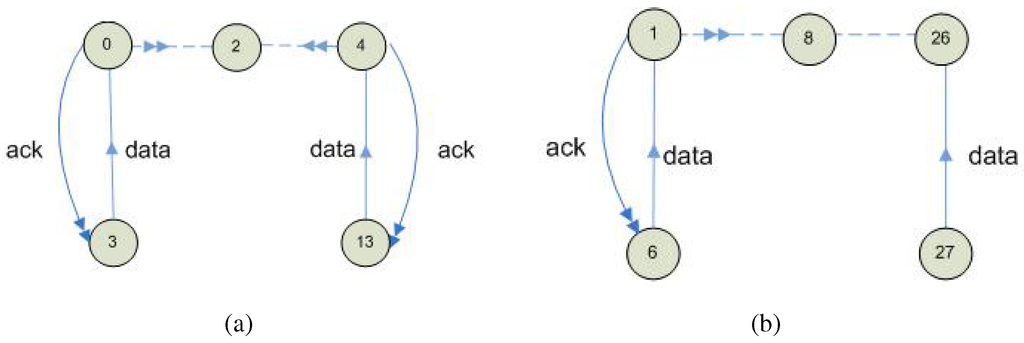
Figure 6.
Example of: (a) No color conflict; (b) Color conflict.
More generally, such conflicts can occur with any slot assignment algorithm providing bandwidth spatial reuse based on node neighborhood and using links of bad quality. The explanation comes from the violation of assumption required by such algorithm and among them SERENA. Indeed, node 1, a two-hop neighbor of node 26, prevents the correct reception from a one-hop neighbor. That is why we recommend the following rule:
Rule R3: Only links of good quality, where each link node receives the other with a power higher than or equal to the receiver sensitivity plus the capture threshold, are used for routing and association.
Notice that SERENA considers as one-hop node any node received with a power higher than or equal to the receiver sensitivity, whereas only nodes with a power higher than or equal to the receiver sensitivity plus the capture threshold are used as parent in the association process and as next hop in the routing protocol. When this rule is met, we get a colored configuration without conflict. This has been checked with all the simulations we did. From now on, is assumed to be met, whatever the application considered.
4.3. Simulations in an Ideal Environment for a General Application
We first consider a general application and apply SERENA with three-hop coloring, as shown in Section 3. Figure 7 depicts the number of colors as a function of the number of nodes for different densities. We notice that the number of colors increases with network density and more slightly with the number of nodes. The increase with network density is expected because the neighborhood up to 3-hop increases with density and neighbors up to three hops do not share the same color. It appears that the impact of density on the number of colors is stronger with a higher number of nodes.
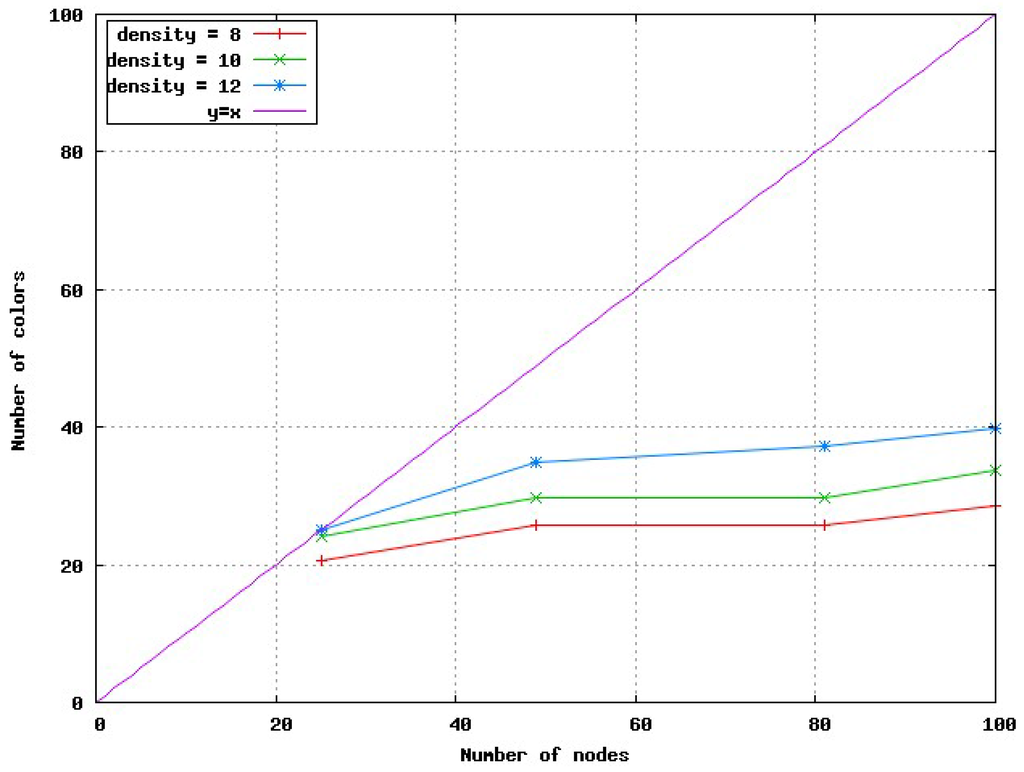
Figure 7.
Number of colors in a general application.
Since TDMA/CA uses a time slot per color, the number of colors obtained with SERENA is equal to the number of time slots required in the active period. Figure 7 shows that except for 25 nodes with a density higher than 9, the number of slots used by TDMA/CA is considerably smaller than with TDMA, materialized by the first bisectrix. The benefit is around 48% for 49 nodes and a density 8 and reaches 71% for 100 nodes and a density of 8. We have also evaluated the average number of nodes sharing the same slot. It is higher than one in all configurations except this with 25 nodes and a density of 12. It reaches 3.5 for 100 nodes and a density of 8.
We now consider the topology depicted in Figure 8 with 49 nodes and a density 8. In what follows, the duration of the cycle is fixed to 4 seconds. In the evaluation we did for the end-to-end delay, we considered the simple case where all color slots are equal. The duration of a color slot is fixed to second. All the nodes of the network generate 1 message every 5 seconds. Each message contains 4 bytes of user data. First, we assume a general traffic, where destinations are randomly chosen. We consider the end-to-end delay as the difference between the time the packet is generated and the time it is received by the final destination. End-to-end delays are illustrated in Figure 9.
In a general traffic scenario, the average end-to-end delay that a packet undergoes is seconds (see Figure 9). It is interesting to notice that we have of packet loss. Indeed, is the expected result since the routing protocol used in these simulation runs uses only the links of good quality (having a received signal power of at least −86 dBm).
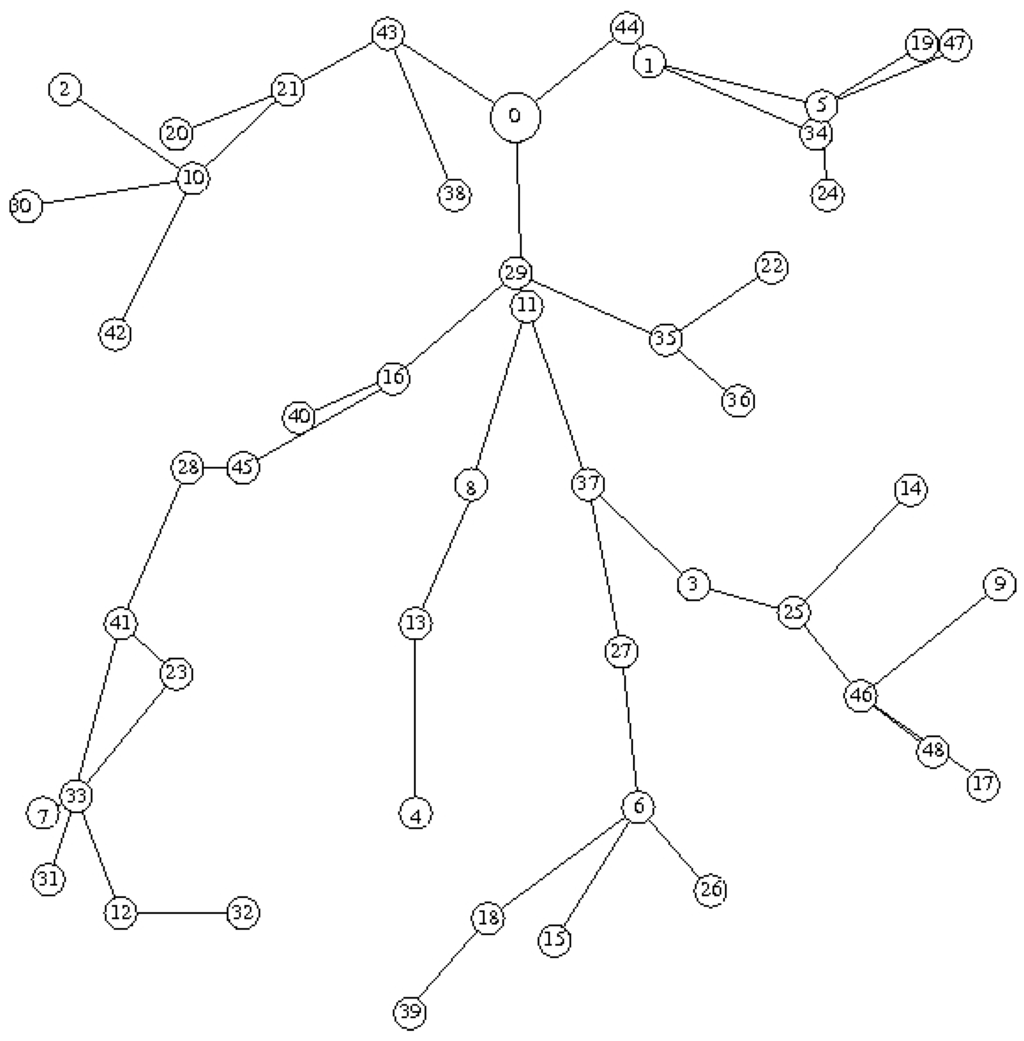
Figure 8.
Topology of 49 nodes and a density 8 selected for delay evaluation.
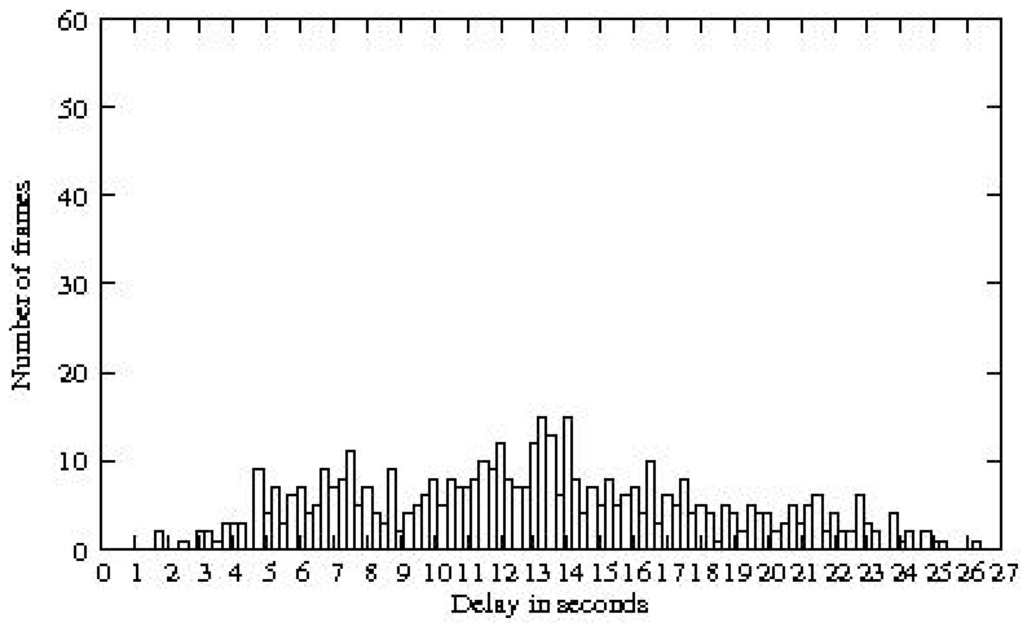
Figure 9.
End-to-end delays for general traffic obtained with a general coloring.
We now consider the case where each node sends traffic to a sink, denoted node 0. End-to-end delays obtained with the general coloring are depicted in Figure 10. In a data-gathering traffic scenario, the average end-to-end delay that a packet undergoes is seconds.
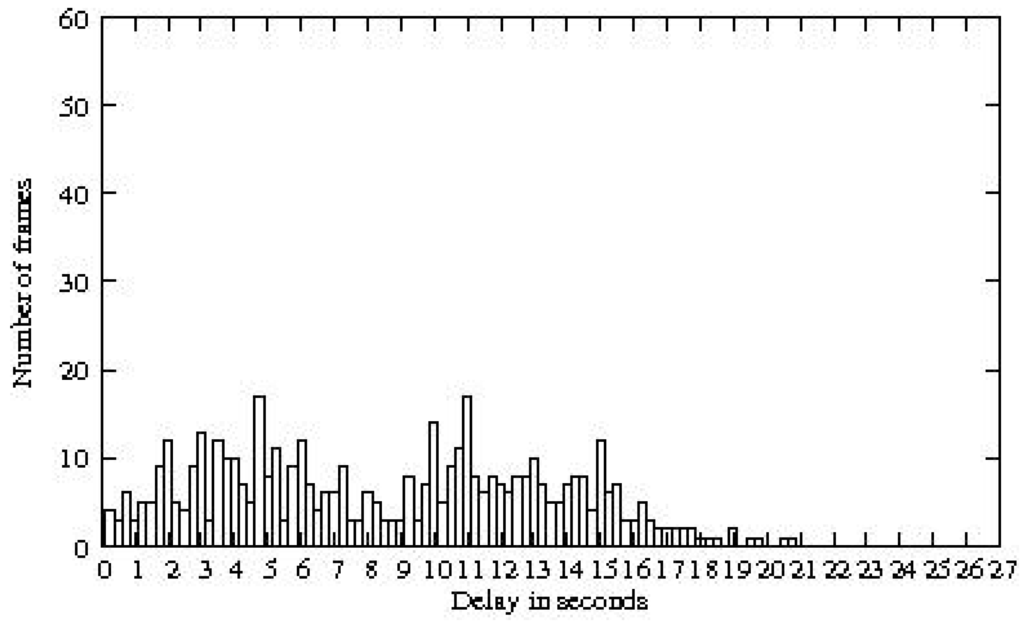
Figure 10.
End-to-end delays for data-gathering traffic obtained with a general coloring.
4.4. Simulations in an Ideal Environment for a Data Gathering Application
We now consider a data gathering application and report the results obtained in the same conditions as the general application, but with a tree-based coloring. All the configurations tested have a maximum tree depth of 8. Node 0 is the sink, the other nodes are at a distance less than or equal to 8 from it in the tree. We observe first that unsurprisingly the coloring of the same configuration is not the same as previously. This result points out the importance of the coloring rules. For instance, in a configuration with 49 nodes and density 8, node 0 that had color 21 in the previous general coloring has now color 0. Its one-hop neighbors, nodes 1, 11, 16, 21, 29, 35, 38, 43 and 44 had colors 17, 5, 2, 25, 6, 11, 13, 24 and 14 respectively have now colors 8, 2, 4, 9, 1, 13, 15, 6 and 7. Figure 11 depicts the number of colors as a function of the number of nodes for different densities. As previously, the number of colors is smaller than the number of nodes, but here in all configurations tested. The benefit is around 57% for 49 nodes and a density 8 and reaches 72% for 100 nodes and a density of 8. The average number of nodes sharing the same slot is higher than in the general case.
Moreover, we notice that the number of colors is smaller than in the general case. The increase with the number of nodes is significantly smaller than in the general case. This can be explained by the fact that the set computed for the tree coloring is smaller than the set of nodes up to three-hop from N. Although the rule requiring the color of a child to be higher than the color of its parent tends to mitigate that, the number of colors is smaller than in a general coloring. To prove that, we have computed for each node, the number of nodes meeting one of the four cases depicted in Figure 3. This number is smaller than the number of three-hop neighbors, explaining the smaller number of colors. For instance, for 49 nodes and a density 8, its average value is 1 whereas the average number of 3-hop neighbor is about 13. More generally, this number is less than 10 as long as the number of nodes is less than or equal to 49.
The average number of nodes sharing the same slot is depicted by Figure 12. It reaches 3.6 for 100 nodes and a density of 8. The spatial reuse of the bandwidth is better than in the general case.
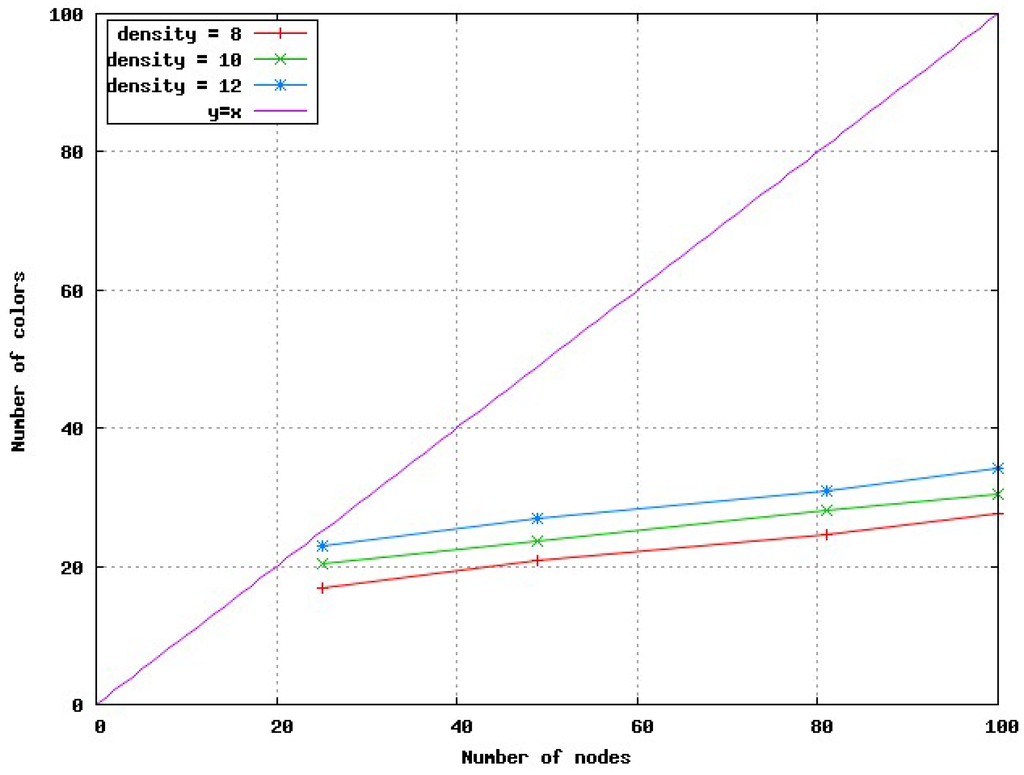
Figure 11.
Number of colors in a data gathering application.
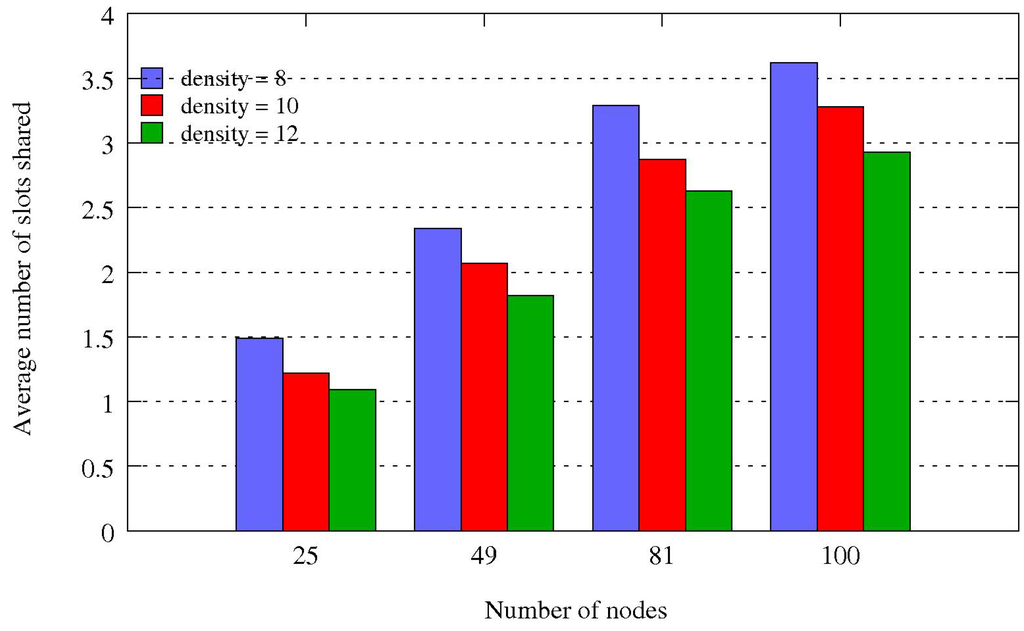
Figure 12.
Average number of nodes sharing the same slot.
We consider again the topology depicted in Figure 8 with 49 nodes and a density 8 and evaluate the end-to-end delays with the tree-based coloring. Figure 13 shows the gain we obtain by using a tree-based coloring. The average end-to-end delay that a packet undergoes is seconds which is less than the duration of a cycle. It is interesting to notice that all the traffic generated is received in less than seconds (the maximum value of end-to-end delay obtained is seconds). Indeed, frames are generated without taking into consideration the start of the color slot. Hence, in the worst case scenario, a frame is generated just after the end of the color slot during which it should have been transmitted. In that case, this packet is kept in queue until the next color slot of the next cycle. Thus, packets may suffer an end-to-end delay higher than one cycle which explains why the delay can exceed 4 seconds with the tree-based coloring. The delivery rate is equal to 100%.
We also evaluate the percentage of time a node is awake in the active period to send its frames and receive the frames from its neighbors. Results are depicted in Figure 14. As expected, this percentage decreases with the number of nodes and increases with the density. These results give an idea of the energy saving that can be done. More energy saving can be achieved by allowing a node to sleep when the sender node has completed its transmissions before the end of the slot. Furthermore, a one-hop neighbor of the sender can quickly detect that it is not the destination of the message, if the sender orders its transmissions according to the increasing order of destination addresses.
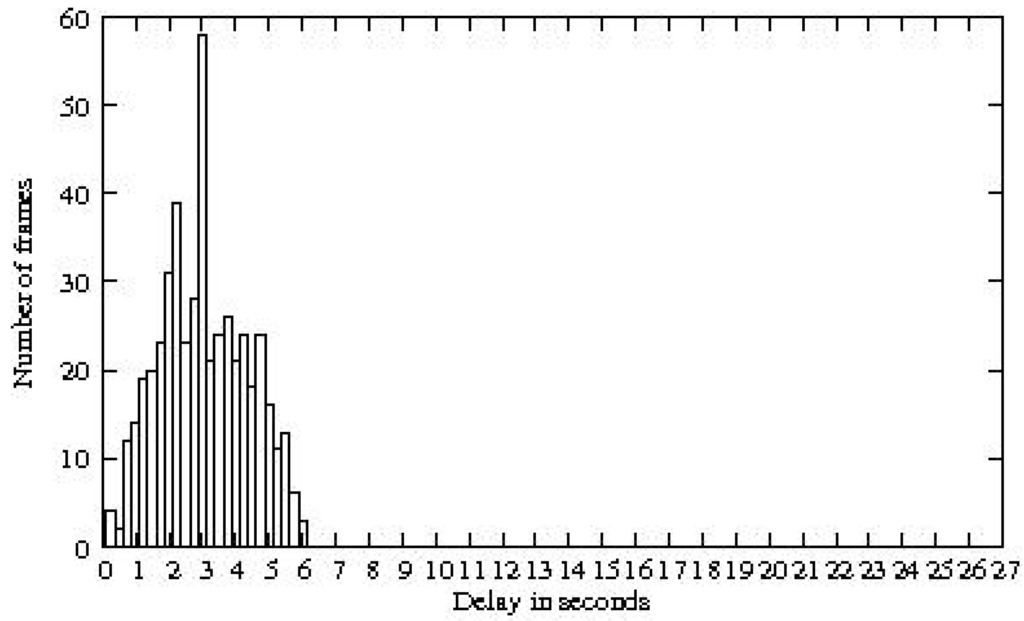
Figure 13.
End-to-end delays obtained with a tree-based coloring.
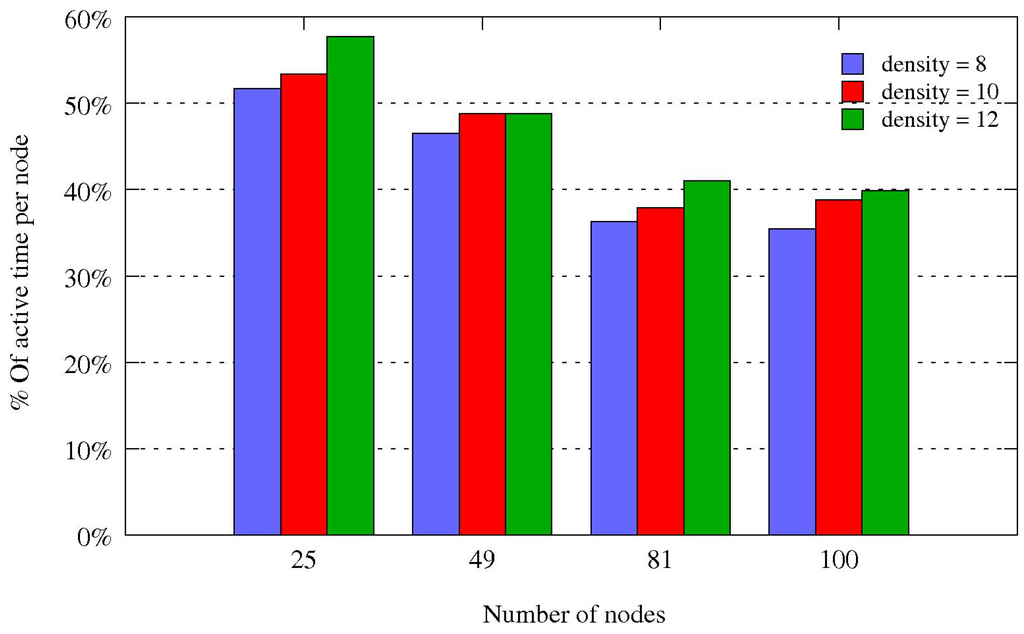
Figure 14.
Percentage of time a node is awake in the active period.
4.5. General Communications versus Tree Communications
We notice that the number of colors needed for a data gathering application is smaller than for a general application for all the configurations tested. Indeed, coloring for a data gathering application ensures a tradeoff between two opposite trends:
- the set contains less nodes in a data gathering application than in a general one. Hence, coloring is less constrained in a data gathering application, leading to a smaller number of colors.
- the choice of the color is more restricted with a data gathering application, where any node is obliged to take a color higher than the color of its parent. This tends to increase the number of colors in a data gathering application.
Figure 15 depicts the benefit in color percentage for all the configurations tested. The benefit is higher than 8% for all configurations except for 81 nodes with densities 8 and 10 and for 100 nodes with a density of 8. This benefit is perceived by the user in terms of smaller end-to-end delays. The benefits brought by data gathering coloring are twice. By restricting the set , SERENA uses a smaller number of colors, leading to a smaller active period. By obliging any node to take a color higher than the color of its parent, SERENA allows TDMA/CA to schedule medium access from any node before its parent. Hence, this node can aggregate the data received from all its children before forwarding it to its parent. Thus, in a single cycle, data collected from the sensors will be aggregated and forwarded to the sink. If this coloring rule was not introduced, the time needed by a data originated from a sensor to reach the sink could be equal to a number of cycles equal to the distance in hop number of this sensor to the sink. That would be unacceptable.
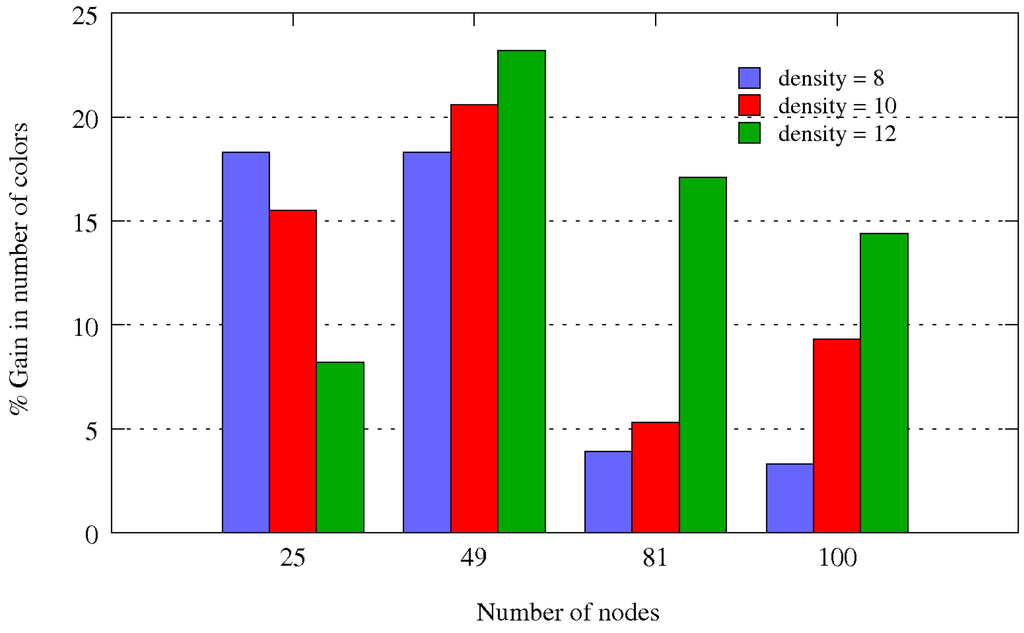
Figure 15.
Benefits brought by tree coloring.
Notice that using a data gathering coloring for a general application would lead to color conflicts, because 3-hop coloring is needed and data gathering coloring is not 3-hop coloring. Hence, tree coloring can only be used when unicast communications are done according to a tree.
4.6. Impact of Heterogeneous Traffic
We now study the impact of heterogeneous traffic on end-to-end delays. We always consider the topology depicted in Figure 8 with 49 nodes and a density 8 and a data gathering application. Instead of considering that each node generates a message every 5 seconds like in Section 4.4, we now assume that one third of nodes, randomly chosen, generate a message every 2 seconds, the second third of nodes, randomly chosen, generate a message every 5 seconds and the last third once every 8 seconds. Globally the same amount of traffic is generated as considered in Section 4.4. We measure the end-to-end delays in the same conditions as previously, a buffer size of 40 messages at each node. Results are depicted in Figure 16.
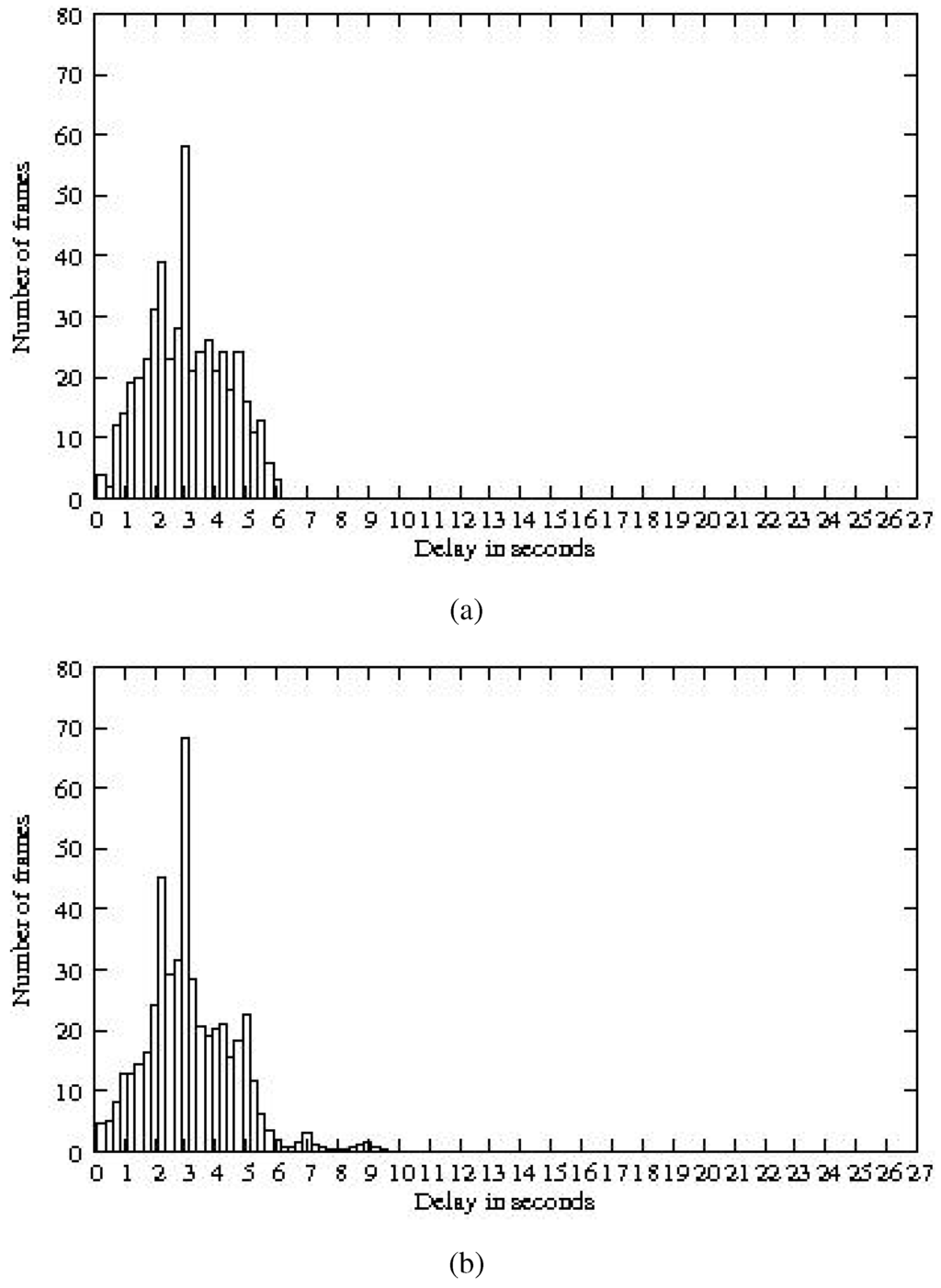
Figure 16.
End-to-end delays with: (a) homogeneous traffic; (b) heterogeneous traffic.
We get an average end-to-end delay of 3.05 seconds instead of 2.93 seconds for the homogeneous case. However, the maximum delay now reaches 10.25 seconds instead of 5.99 seconds. We also observe some losses: in average over 100 simulation runs, four messages are lost because of buffer overflow. Only one node is subject to buffer overflow, it is node 29, which has 32 descendants in the tree (see the topology depicted in Figure 8). Indeed, the paths of 32 nodes toward the sink converge at node 29, explaining the high load submitted by this node.
We now vary the size of the buffer present at each node (20, 40, or 60 messages) and study its impact on message loss. Results are depicted in Figure 17. Notice that the size of 40 messages correspond to the size used in the previous simulations. When the buffer size decreases, case of 20 messages, the number of message loss increases to reach 76 in average. However, messages that are delivered experiment shorter delays. Conversely, there is no message loss for a buffer size of 60 messages.
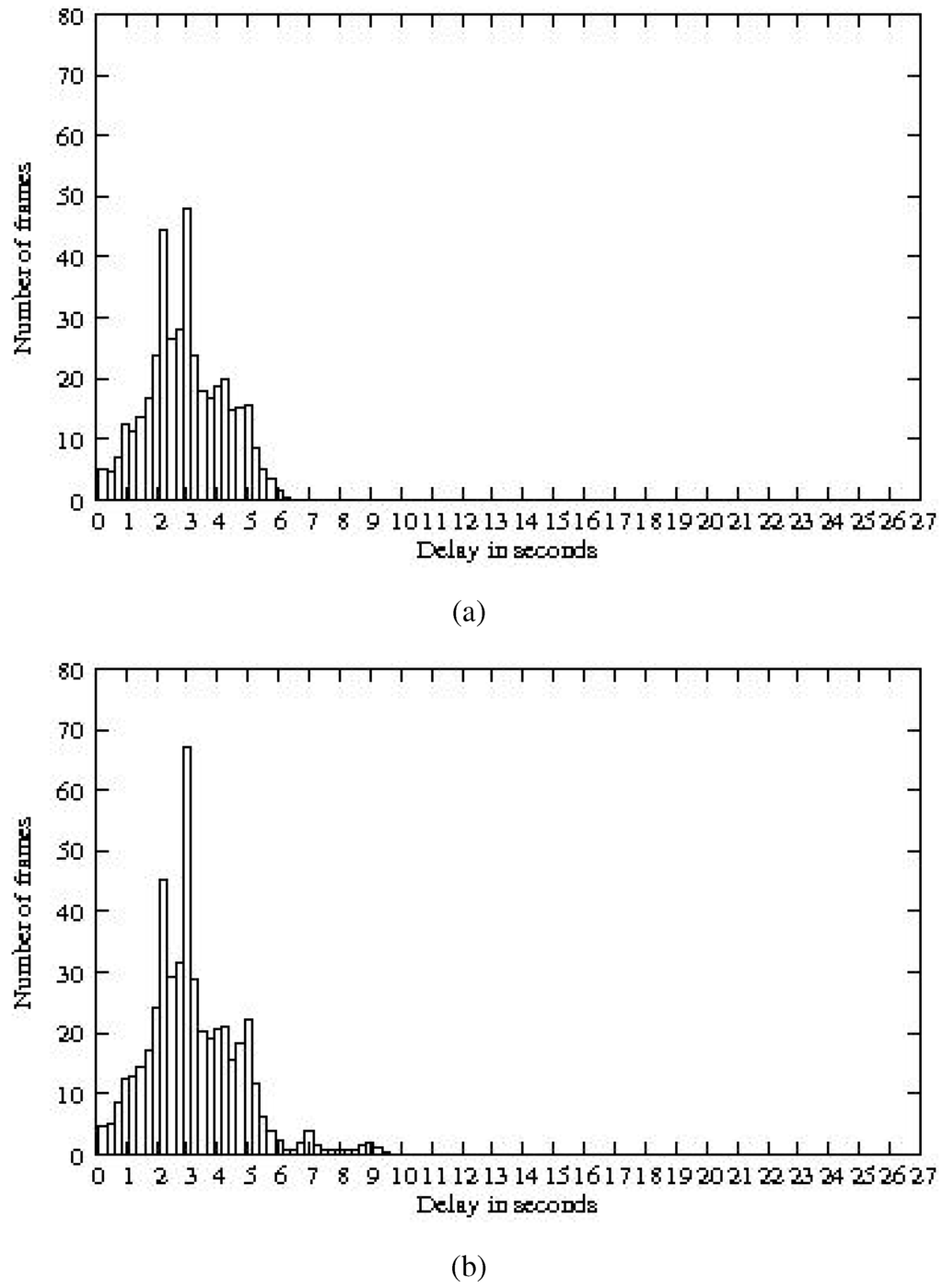
Figure 17.
End-to-end delays with heterogeneous traffic with buffers of: (a) 20 messages; (b) 60 messages.
As expected, packet loss due to buffers overflow and additional delays are observed when nodes sharing the same color generate heterogeneous traffic. In order to avoid packet loss, at least two solutions are possible. First, each parent in the tree should aggregate the data received from its children before transmitting them to its own parent. All the simulations results reported in this paper are obtained without aggregation. Aggregation would decrease message losses. A second solution would be the use of colored slots of different sizes. More precisely, the size of the colored slots should be affected according to the highest traffic amount present in the buffers of nodes sharing the same color. This enhancement will be studied in our future work by adding a new primitive to inform the coordinator of the network of the maximum traffic size for each color. Notice that in a data gathering application where the amount of traffic sent by a node is directly proportional to its number of descendants, it suffices to attribute a larger size to the slots corresponding to small colors. Indeed, nodes with a high number of descendants are colored first and consequently receive a small color. This small color will get a larger slot size. A more precise buffer dimensioning can be done with Network Calculus, as done in [28].
5. Impact of Color Conflicts Caused by Late Arrivals, Node Mobility or Topology Changes
5.1. Ideal Functioning
For a given stable topology, if the coloring process has been done according the assumptions and the rules introduced in Section 3.4, the expected behavior of node is the following:
Let us assume that gets the color k, it has to know the list of its 1-hop neighbors and the color of each of them . has to be awake during all the slots of color k but also during the slots of color of each of its 1-hop neighbors.
When it has to send a data frame, can only transmit it to one of its 1-hop neighbors during the slot of color k. When it receives a data frame, it is a frame sent by one of its 1-hop neighbors having the color . When it receives an acknowledgement, it has been sent by one of its 1-hop neighbors having the color .
5.2. Conflict Causes
In this section, we analyze all possible causes of conflicts.
5.2.1. About the Stability of WSN Topologies
WSNs devices use reception power thresholds that are very low. This choice is beneficial from the energy point of view but leads the radio links to be unstable. Fluctuations in the area of are very numerous for real WSN deployments [6]. Even if the problem of node mobility is not addressed in this study, it is however necessary to consider the fact that a link can appear or disappear because of the evolution of the propagation conditions.
5.2.2. Creation of New Links
A valid coloring can become invalid due to the creation of new links. These new links cause color conflicts because there exist two nodes with the same color that violate the coloring rules. For instance in a general application, two nodes A and B that initially were not 1-hop, 2-hop or 3-hop neighbors become 1-hop, 2-hop or 3-hop neighbors. This happens because of node mobility, late arrival of a node or topology change. Let us assume that C arrives late and becomes 1-hop neighbor of node A and 1-hop or 2-hop neighbor of node B. Because of C, nodes A and B that are now 2-hop or 3-hop neighbors can no longer share the same color. We can notice that the breakage of existing links never causes color conflicts. In other words, link breakage preserves the valid coloring, unlike link creation.
5.2.3. Existence of Asymmetric Links
Another reason for color conflicts is the existence of asymmetric links as shown in [29] where we propose a solution to limit the number of such conflicts. However, this number cannot be nullified. Notice that conflicts created by topology changes, asymmetric links, node mobility or late node arrivals cannot be avoided even by using exclusively links of good quality.
5.3. Dysfunction Detected at the MAC Layer
The non-stability of the propagation conditions induces conflicts in the local medium sharing, these conflicts can be detected either by listening or by deduction. We are going to specify for each case how TDMA/CA tackles the effects of these conflicts and how it informs the higher layers, and in particular SERENA, in order to take into account that conflict.
We assume that the synchronization module that provides color time slots allocation runs perfectly, that is to say it ensures that the borders of each time slot are nearly the same for all the nodes of the WSN.
5.3.1. Detection by Listening
If during the slot of color k, receives a data frame which was not sent by the neighboring node of this color ( having the color equal to k), but was sent by a source , it means that a new link exists and has just been discovered by , SERENA does not know the existence of this link yet. k is the color of the node . Till now, this new link was not taken into account at the local level, but the case does not induce any particular problem. It is mainly a warning pointing out a possible evolution of the network topology. It can affect the performance of the MAC layer when TDMA/CA is in the CA mode because channel sensing (CCA) will return a busy channel state.
The situation is practically identical if during the slot of color k, receives an acknowledgement which was not sent by the neighboring node representing this color, but which was sent by a source , it means that a new link exists. In the protocol implementation of TDMA/CA we use acknowledgements which contain the source and destination addresses. Thus node can deduce the existence of a new link .
5.3.2. By Deduction
At the medium access level a real conflict happens when frames are lost due to collisions. But in the wireless network domain, collisions cannot be easily detected (in the sense of CSMA/CD), however they can possibly be deduced. Due to the conditions of power threshold that have been taken especially concerning of this contribution, our coloring process applied to a stable topology reduces considerably the risk of frame losses due to bad link quality. Hence the following dysfunctions can be deduced:
If a frame sent by is not acknowledged by the target node , it is reasonable to assume that this frame (or its acknowledgement) was subject to a collision. In that case TDMA/CA switches to the CA mode and a backoff value is randomly chosen before retransmitting. Thus TDMA/CA compensates this dysfunction but at the cost of a bandwidth reduction and an increase in medium access delay.
If such a dysfunction persists, it is necessary to signal it to SERENA in order to expect that a solution will be given. In this purpose, the sender node is able to specify the couple (source address and destination address of the frame as well as their respective color of the two conflicting nodes).
An indication to the SERENA is sent when the sliding average of the value of Backoff exceeds a given threshold or when n consecutive collisions occur. It means that dysfunction is persistent.
If has already acknowledged a given data frame from and yet it receives another copy of the same frame, it is possible to deduce that the acknowledgement was corrupted by a collision. In this case, TDMA/CA reacts at the level of . Thus, if for this situation becomes persistent, SERENA will be notified.
If TDMA/CA succeeds in desynchronizing the sending of the two competing frames, and if these two frames in competition can be sent in the same colored slot, any receiver will be able to detect the conflict that can be treated as stated before.
5.4. Resolution of Notified Color Conflicts
Upon detection of a color conflict, the MAC layer locally notifies SERENA indicating the addresses of the two conflicting nodes [29]. When a node N receives such an indication, two cases are possible:
- either N is a conflicting node. If N has the smallest priority or the conflicting node is not a 1, 2 or 3-hop neighbor, then N selects another color. Otherwise N sends a message to the other conflicting node inviting it to change its color.
- or N is not a conflicting node. N sends a message to the conflicting node that is either the only 1, 2 or 3-hop neighbor, or has the smallest priority.
The message can be routed to reach its final destination. When a node must change its color, it selects the smallest color different from the previous one and not used in .
5.5. Should Color Conflicts Always be Solved?
In this section, we summarize our recommendations concerning color conflicts. Color conflicts caused by the use of bad links should always be avoided: only links of good quality should be used for routing and association. For other color conflicts, if they are not detected, no specific action is taken, because no data is lost. If they are detected, nothing is done as long as the packet loss is tolerated by the application. As soon as it is no longer the case, SERENA is able to react in order to solve them.
The benefits brought by this approach are:
- If there is no color conflict, TDMA/CA does not introduce any delay and acts in this sense like any other TDMA approach.
- Even if there is a color conflict, TDMA/CA does not notify SERENA as long as the desired frames can be captured.
- TDMA/CA approach allows collision avoidance: color conflicts can be tolerated as long as the number of collisions does not exceed a threshold.
- TDMA/CA is able to detect locally any color conflict generated by SERENA.
6. Conclusion
In this paper, we have presented a medium access protocol, called TDMA/CA, providing bandwidth spatial reuse and ensuring the absence of conflict when only links of good quality are used, links are stable and symmetric. This protocol schedules medium access according to node colors provided by SERENA. We have pointed out that the use of bad quality links leads to collisions even in case of a stable topology with symmetric links. Such conflicts would also occur in any slot assignment algorithm providing spatial reuse based on node neighborhood. With data gathering applications, the tree-based coloring enables optimization of the number of colors and the end-to-end delays. Concerning energy efficiency, TDMA/CA and SERENA reduces the duration of the active period. Depending on the application requirements, the duration of the inactive period is increased or the reactivity of the application is improved by a more frequent active period. In case of mobility, late node arrival, topology changes, or asymmetric links, color conflicts can occur. TDMA/CA is able to detect the conflicts causing data losses. Such conflicts are tolerated as long as application requirements are met. In the negative, conflicts detected by TDMA/CA are notified to SERENA which is in charge of solving the color conflicts. Currently, we are implementing SERENA and TDMA/CA on a real wireless sensor network.
Acknowledgements
This work has been partly funded by the ANR OCARI project.
References
- IEEE Computer Society. Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications; ANSI/IEEE Standard 802.11; IEEE Computer Society: Washington, DC, USA, 1999. [Google Scholar]
- Singh, S.; Raghavendra, C. PAMAS—Power Aware Multi-access protocol with Signalling for Ad Hoc Networks. ACM SIGCOMM Comput. Commun. Rev. 1998, 28, 5–26. [Google Scholar] [CrossRef]
- Ye, W.; Heidemann, J.; Estrin, D. An Energy-efficient MAC Protocol for Wireless Sensor Networks. In Proceedings of the IEEE Infocom; IEEE: New York, NY, USA, 2002; pp. 1567–1576. [Google Scholar]
- Van Dam, T.; Langendoen, K. An Adaptive Energy-efficient MAC Protocol for Wireless Sensor Networks. In Proceedings of ACM Sensys, Los Angeles, CA, USA, November 2003.
- Lu, G.; Krishnamachari, B.; Raghavendra, C. An adaptive energy-efficient and low-latency MAC for data gathering in sensor networks. In Proceedings of International Parallel and Distributed Processing Symposium, Santa Fe, NM, USA, April 2004.
- IEEE Computer Society. Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks (WPANs); ANSI/IEEE Standard 802.15.4; IEEE Computer Society: Washington, DC, USA, 2006. [Google Scholar]
- Rhee, I.; Warrier, A.; Aia, M.; Min, J. Z-MAC: A hybrid (MAC) for wireless sensor networks. In Proceedings of SenSys’05, San Diego, CA, USA, November 2005.
- Rhee, I.; Warrier, A.; Xu, L. Randomized dining philosophers to TDMA scheduling in wireless sensor networks; Technical Report TR-2005-21; North Carolina State University: Raleigh, NC, USA, April 2005. [Google Scholar]
- Jain, K.; Padhye, J.; Padmanabhan, V.; Qiu, L. Impact of interference on multi-hop wireless network performance. In Proceedings of ACM MobiCom, San Diego, CA, USA, September 2003.
- Gandham, S.; Dawande, M.; Prakash, R. Link scheduling in sensor networks: distributed edge coloring revisited. J. Paral. Distrib. Comput. 2008, 68, 8. [Google Scholar] [CrossRef]
- Ma, J.; Lou, W.; Wu, Y.; Li, X.-Y. Energy efficient TDMA sleep scheduling in wireless sensor networks. In Proceedings of INFOCOM 2009, Rio de Janeiro, Brazil, April 2009.
- Chakraborty, G. Genetic algorithm to solve optimum TDMA transmission schedule in broadcast packet radio networks. IEEE Trans. Commun. 2004, 52, 5. [Google Scholar] [CrossRef]
- Rajendran, V.; Obraczka, K.; Garcia-Luna-Aceves, J.-J. Energy-efficient, collision-free medium access control for wireless sensor networks. In Proceedings of Sensys’03, Los Angeles, CA, USA, November 2003.
- Rajendran, V.; Garcia-Luna-Aceves, J.J.; Obraczka, K. Energy-efficient, application-aware medium access for sensor networks. In Proceedings of IEEE MASS 2005, Washington, DC, USA, November 2005.
- Ramaswami, R.; Parhi, K. Distributed scheduling of broadcasts in a radio network. In Proceedings of INFOCOM 1989, Ottawa, Canada, April 1989.
- Krumke, S.; Marathe, M.; Ravi, S. Models and approximation algorithms for channel assignment in radio networks. Wirel. Netw. 2000, 7, 575–584. [Google Scholar] [CrossRef]
- Gandham, S.; Dawande, M.; Prakash, R. Link scheduling in sensor networks: distributed edge coloring revisited. In Proceedings of INFOCOM 2005, Miami, FL, USA, March 2005.
- Garey, M.; Johnson, D. Computers and Intractability: A Guide to Theory of NP-Completeness; W.H. Freeman and Co.: San Francisco, CA, USA, 1979. [Google Scholar]
- Brelaz, D. New methods to color the vertices of a graph. Commun. ACM 1979, 22, 251–256. [Google Scholar] [CrossRef]
- Hansen, J.; Kubale, M.; Kuszner, L.; Nadolski, A. Distributed largest-first algorithm for graph coloring. In Proceedings of EURO-PAR 2004, Pisa, Italy, August 2004.
- Minet, P.; Mahfoudh, S. SERENA: SchEduling RoutEr Nodes Activity in wireless ad hoc and sensor networks. In Proceedings of IWCMC 2008, IEEE International Wireless Communications and Mobile Computing Conference, Crete Island, Greece, August 2008.
- Mahfoudh, S.; Minet, P. Performance evaluation of the SERENA algorithm to SchEdule Router Nodes Activity. In Proceedings of AINA 2008, Ginowan, Japan, March 2008.
- Gobriel, S.; Mosse, D.; Cleric, R. TDMA-ASAP: sensor network TDMA scheduling with adaptive slot stealing and parallelism. In Proceedings of ICDCS 2009, Montreal, Canada, June 2009.
- Chalhoub, G.; Guitton, A.; Jacquet, F.; Freitas, A.; Misson, M. Medium Access Control for a Tree-Based Wireless Sensor Network: Synchronization Management. In Proceedings of IFIP Wireless Days, Dubai, United Arab Emirates, November 2008.
- Zigbee-Alliance. Zigbee Specification. January 2008. [Google Scholar]
- Dang, T.; Val, T.; Guitton, A.; Al Agha, K.; Minet, P.; Bertin, M.-H.; Viollet, J.-B. Which wireless technology for industrial wireless sensor network? The development of OCARI technology. IEEE Trans. Ind. Electron. 2009, 56, 4266–4278. [Google Scholar]
- Al Agha, K.; Chalhoub, G.; Guitton, A.; Mahfoudh, S.; Minet, P.; Misson, M.; Rahme, J.; Val, T.; Van Den Bossche, A. Cross-layering in an industrial wireless sensor network: Case study of OCARI. J. Netw. 2009, 4, 411–420. [Google Scholar] [CrossRef]
- Minet, P.; Mahfoudh, S. Energy, bandwidth and time efficiency in data gathering applications. In Proceedings of IFIP Wireless Days, Paris, France, December 2009.
- Minet, P.; Mahfoudh, S.; Chalhoub, G.; Guitton, A. Node coloring in a wireless sensor network with unidirectional links and topology changes. In Proceedings of IEEE WCNC 2010, Sidney, Australia, April 2010.
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).