3D Spatial Path Planning Based on Improved Particle Swarm Optimization

Abstract

Three-dimensional path planning is critical for the successful operation of unmanned aerial vehicles (UAVs), automated guided vehicles (AGVs), and robots in industrial Internet of Things (IIoT) applications. In 3D path planning, the standard Particle Swarm Optimization (PSO) algorithm suffers from premature convergence and a tendency to fall into local optima, leading to significant deviations from the optimal path. This paper proposes an improved PSO (IPSO) algorithm that enhances particle diversity and randomness through the introduction of logistic chaotic mapping, while employing dynamic learning factors and nonlinear inertia weights to improve global search capability. Experimental results demonstrate that IPSO outperforms traditional methods in terms of path length and computational efficiency, showing potential for real-time path planning in complex environments.

1. Introduction

Path planning plays a crucial role in Industrial Internet of Things (IIoT) applications, where autonomous systems must navigate complex environments while maintaining high operational efficiency and safety standards [1,2,3].

Typical implementations include: (1) Unmanned Aerial Vehicles (UAVs) performing inspection and monitoring tasks in complex facilities [4,5,6,7], (2) Automated Guided Vehicles (AGVs) navigating structured 3D spaces such as warehouses [8,9,10,11], and (3) Industrial robotic arms executing precision tasks in collaborative workspaces [12,13,14]. The primary challenge lies in dynamically avoiding obstacles while optimizing path quality under multiple constraints, including spatial limitations and real-time computational demands [15,16,17,18].

Beyond these established applications, path planning is increasingly critical in more complex and collaborative autonomous systems. For instance, multi-UGV formation cooperative reconnaissance for defense tasks, where patrol strategies are inspired by human behaviors [19]. UAVs operating under terrain limitations require advanced perception capabilities for visual tracking, geolocation, and inter-platform data transmission [20]. Moreover, recent research proposes novel 3D path planning methods, including enhanced dynamic artificial potential field (ED-APF) techniques, to enable UAV–MGV cooperation and adaptive reconnaissance trajectories [21]. These advanced applications impose even more stringent requirements on path planning algorithms, including scalability to multi-agent systems, resilience to uncertainty, and the ability to generate efficient trajectories in deeply complex environments.

Compared to 2D planning, 3D path planning introduces additional complexity from altitude constraints in aerial navigation, volumetric obstacle avoidance, spatial limitations, and the need for smooth, collision-free trajectories [22,23,24]. While conventional approaches (e.g., A, RRT) are widely used in UAV navigation and robotic systems [25,26,27], they exhibit critical limitations when applied to complex 3D scenarios. Specifically, they often struggle with: (1) exponentially expanded search spaces due to 3D obstacle distributions; and (2) limited adaptability in dynamic or uncertain environments [28,29,30,31].

In addition to computational challenges, recent studies emphasize system-level factors that directly shape UAV path planning requirements. Excessive curvature, torsion, or sudden trajectory changes can violate UAV dynamic stability limits [32], motivating the use of smoothness constraints such as B-splines to ensure controllability. Moreover, damping properties of sustainable UAV materials may influence allowable maneuver accelerations [33], linking material characteristics to safe and reliable trajectory design.

Particle Swarm Optimization (PSO) has been widely studied for path planning; however, standard implementations suffer from issues such as premature convergence and insufficient avoidance of poor local optima [34,35,36]. To address these limitations, we propose an enhanced PSO algorithm featuring three key innovations:

• Logistic chaotic initialization that ensures population diversity.
• Adaptive dynamic learning factors that automatically balance exploration and exploitation.
• Nonlinear inertia weights enabling stage-specific convergence control.

Comparative experimental results demonstrate consistent enhancements across multiple performance dimensions—including path length reduction and computational efficiency—relative to conventional methods.

The proposed method is relevant for Industrial Internet of Things (IIoT) applications that demand real-time responsiveness, with potential extensions to multi-agent systems and edge computing architectures.

2. Related Works

In the field of 3D path planning research, the evolution of various algorithms has consistently focused on addressing the core challenge of achieving efficient and secure pathfinding in complex environments. Traditional approaches like the A* algorithm demonstrate exceptional performance in structured environments through heuristic search [37,38]. At the same time, Rapidly-exploring Random Trees (RRTs)-based methods prove more effective for path exploration in high-dimensional spaces [39,40]. Although these methods perform well in specific scenarios, they often struggle to simultaneously satisfy requirements for path quality, real-time performance, and multiple constraints when confronted with complex 3D terrains.

Recent advances in intelligent optimization algorithms have introduced new approaches to three-dimensional path planning. The integration of neural networks with Particle Swarm Optimization (PSO) in [41] demonstrated improved path planning performance, though its heavy reliance on high-dimensional encoding substantially increased algorithmic complexity and implementation challenges. Hybrid intelligent algorithms combining standard PSO with other swarm intelligence techniques, as proposed in [42,43], enhanced local search capabilities but required significantly more iterations and exhibited slower convergence rates, resulting in increased computational overhead.

Studies employing chaos theory to modify pheromone update mechanisms [44,45] achieved notable improvements in global search capabilities and path smoothness; however, the failure to optimize initial pheromone concentrations led to considerable computational redundancy and reduced convergence speed, ultimately limiting practical applicability. While the modified Ant Colony Optimization (ACO) algorithm in [46,47] showed improved convergence speed and optimization capabilities, it remained prone to local optima in complex 3D environments, adversely affecting path planning outcomes.

The introduction of chasing behavior from the Artificial Fish Swarm algorithm (AFSA) in [48] significantly reduced search time, and the incorporation of crowding distance operators with multi-objective optimization methods in [49] generated diversified Pareto-optimal solution sets. However, both approaches were primarily designed for two-dimensional path optimization and showed limited effectiveness when applied to complex 3D terrains. Although artificial potential field methods [50] successfully enabled UAV path planning with obstacle avoidance, they frequently converged to local optima when targets were proximate to obstacles. Similarly, the terrain-aware PSO variant in [51], which incorporated elevation variations and radar threat modeling, still exhibited insufficient precision and convergence speed for practical applications. Despite demonstrating feasibility in 3D environments, the algorithms in [50,51] consistently faced challenges with local optima convergence and solution accuracy.

Building on these foundations, recent years (2023–2025) have witnessed a series of hybrid PSO-based UAV path planning approaches that integrate swarm intelligence with auxiliary mechanisms such as chaotic mapping, adaptive learning, and hybrid operators. Representative examples are summarized in

Table 1. Comparison of representative PSO-based algorithms for UAV path planning (2023–2025).

Method	Algorithmic Structure	Complexity	Reported Performance
IPSO	Logistic chaotic initialization + adaptive learning factors + nonlinear inertia weights	Low–Moderate	14.4% shorter paths, 65% faster runtime vs. standard PSO
HCPSOA	PSO + coyote optimization + chaotic map and dynamic weight adaptation	Moderate	~10% lower path cost in 2D/3D terrains
PPSwarm	RRT* 1 + PSO + priority planning + randomization for multi-UAV coordination	High	Scalable to 500 UAVs; improved path quality and runtime
Adaptive PSO	PSO with adaptive parameter tuning strategy	Low–Moderate	Improved path quality under dynamic conditions
HSI-HIO	Hybrid swarm intelligence (incl. PSO) + human-inspired operators for decision-making	Moderate–High	Improved path smoothness, energy efficiency, and robustness in urban UAV navigation

Sources: HCPSOA [52], PPSwarm [53], Adaptive PSO [54], HSI-HIO [35]. ¹ The asterisk in RRT* denotes the ‘optimal’ variant of RRT, which asymptotically converges to the optimal path.

, which contrasts IPSO with state-of-the-art PSO-based methods in terms of algorithmic structure, complexity, and reported performance.

In summary, existing 3D path planning algorithms still exhibit significant limitations in complex environments, particularly regarding real-time performance and computational efficiency. The Improved Particle Swarm Optimization algorithm (IPSO) proposed in this work addresses these challenges through three key innovations: (1) Logistic chaotic mapping for enhanced population diversity; (2) Dynamic learning factors enabling adaptive exploration–exploitation balance; and (3) Nonlinear inertia weights optimizing convergence characteristics. Collectively, these enhancements achieve a 14.4% reduction in path length and 65.0% improvement in computational efficiency compared to conventional algorithms, delivering an efficient, reliable solution for real-time path planning in complex 3D environments.

3. Problem Formulation

3.1. Three-Dimensional Path Planning Problem Description

The core objective of 3D path planning is to identify an optimal trajectory while avoiding obstacles in complex environments. To realistically simulate such environments, this study constructs mountainous terrain and benchmark topography [55] as obstacle representations. The benchmark terrain model characterizes fundamental undulations of the landscape through Equation (1):

$$\begin{gathered} Z_1\left(x,y\right)=\mathrm{s}\mathrm{i}\mathrm{n}\left(y+a\right)+b·\mathrm{s}\mathrm{i}\mathrm{n}\left(x\right)+c·\mathrm{c}\mathrm{o}\mathrm{s}\left(d·\sqrt{x^2+y^2}\right)+e·\mathrm{c}\mathrm{o}\mathrm{s}\left(y\right) \\ +f·\mathrm{s}\mathrm{i}\mathrm{n}(g·\sqrt{x^2+y^2}) \end{gathered}$$

(1)

where $x$ and $y$ represent the projected coordinates of the model on the XOY plane; and $Z_1$ denotes the elevation value corresponding to the horizontal plane point. The constant coefficients $a$, $b$, $c$, $d$, $e$, $f$, and $g$ are used to control the undulation characteristics of the benchmark terrain in the digital map.

To more realistically simulate natural environments, this paper employs an exponential function to characterize natural mountain features, with the mathematical model expressed by Equation (2):

$$Z_2(x,y)=\sum _{i=1}^n{h}_i\mathrm{e}\mathrm{x}\mathrm{p}[-{\left({\displaystyle \frac{x-x_i}{x_{si}}}\right)}^2-{\left({\displaystyle \frac{y-y_i}{y_{si}}}\right)}^2]$$

(2)

where the following are expressed:

• $Z_2$ represents the elevation of the mountain terrain;
• $n$ denotes the total number of mountain peaks;
• $(x,y)$ indicates the 2D planar coordinates;
• ${(x}_i,y_i$) specifies the center coordinates of the $i$-th peak;
• $h_i$ serves as the terrain parameter controlling peak height;
• $x_{si}$ and $y_{si}$ are the attenuation coefficients for the $i$-th peak along the x- and y-axes. These coefficients govern the slope steepness.

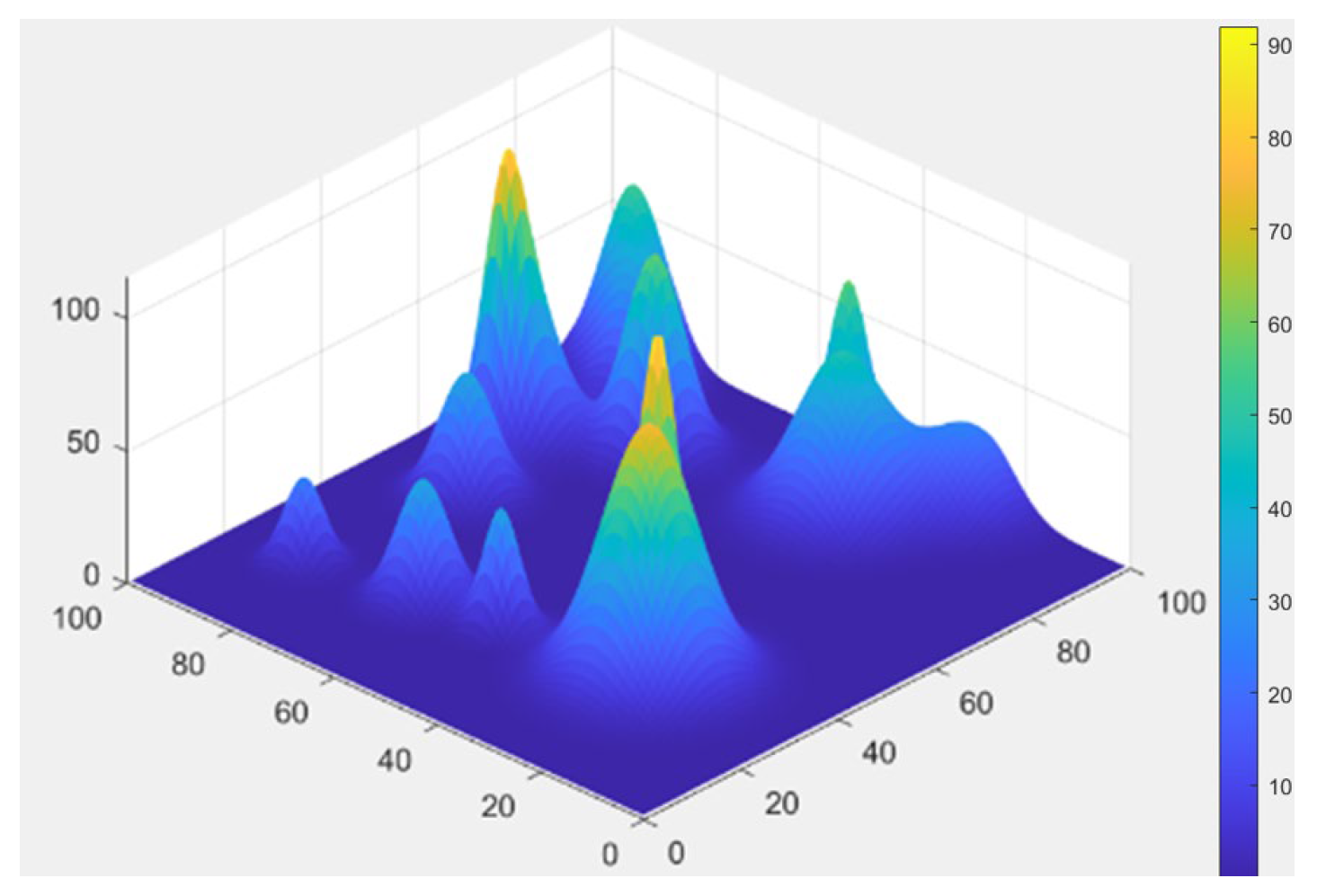
Based on this model, we constructed a 100 m × 100 m × 100 m 3D spatial environment with 15 randomly generated mountain features, as illustrated in Figure 1. This modeling approach effectively simulates complex 3D environments and provides a reliable experimental scenario for validating path planning algorithms.

The model effectively simulates complex three-dimensional environments, providing a reliable experimental scenario for validating path planning algorithms, and suitable for real-time path planning in edge intelligence applications.

3.2. B-Spline Based 3D Path Parameterization Method

When planning 3D paths in complex terrain environments, trajectory smoothness directly impacts stability and energy efficiency. As shown in Figure 1, the 3D terrain model contains multiple mountain obstacles where traditional straight-line connections would cause abrupt curvature changes, failing to meet the kinematic constraints of typical autonomous agents (e.g., UAVs, AGVs).

To address this, we employed parametric cubic uniform B-splines for smooth waypoint interpolation. The method’s local support property (where each curve segment is influenced only by adjacent control points) and C² continuity (ensuring curvature continuity) effectively balance path smoothness with computational efficiency, making it suitable for various 3D path planning requirements [29,30].

3.2.1. Path Smoothness Constraints

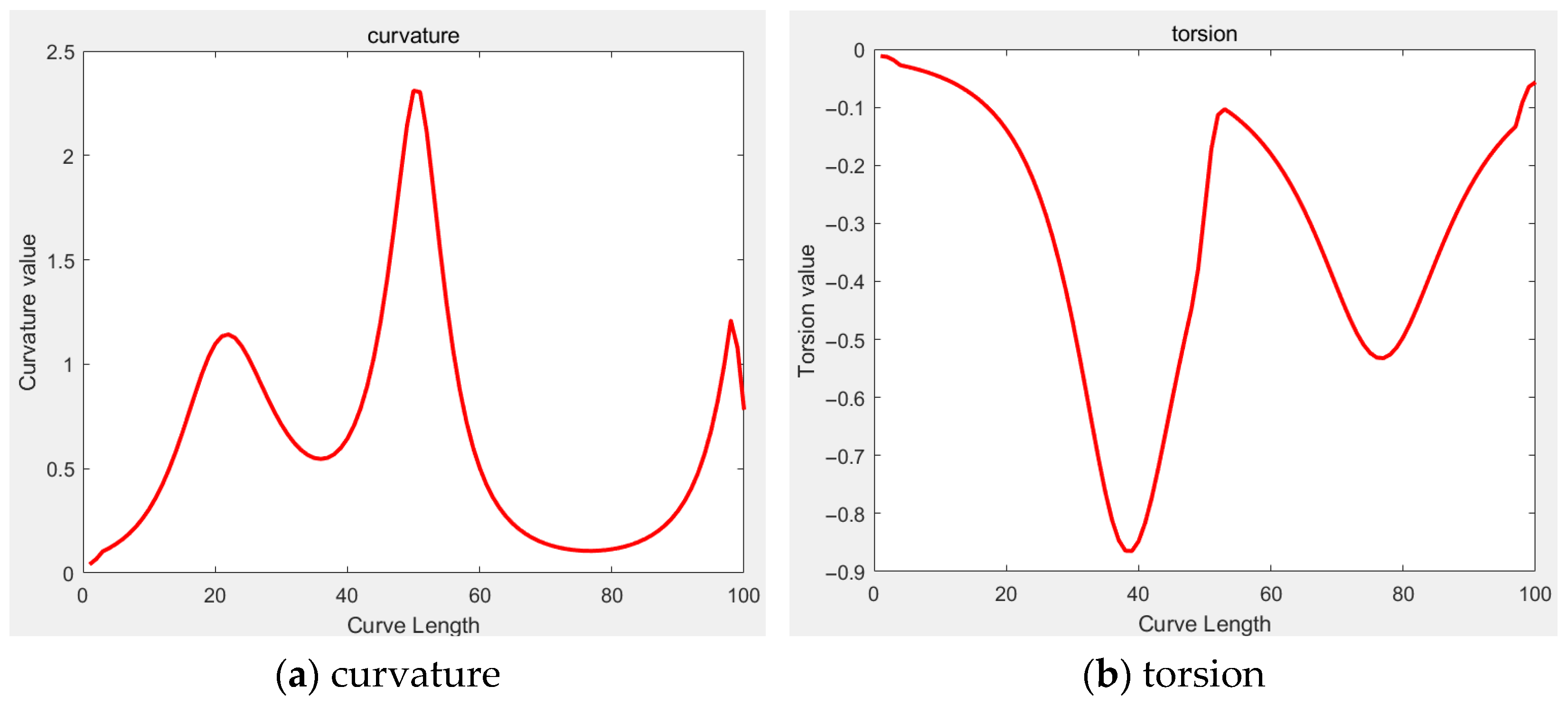
The quality of spatial curves is determined by two differential geometric characteristics: curvature and torsion.

• Curvature (κ)

Quantifies the local bending degree of a curve, defined as the rate of change in the tangent vector angle with respect to arc length, given by Equation (3):

$$k={\displaystyle \frac{‖r^{\prime }\left(t\right)\times r^{″}\left(t\right)‖}{{‖r^{\prime }\left(t\right)‖}^3}}$$

(3)

where $r\left(t\right)=\left(x\left(t\right),y\left(t\right),z\left(t\right)\right)$ represents the parametric equation of the curve. For planar trajectories, the torsion is identically zero (τ ≡ 0).

2.

Torsion (τ)

Torsion quantitatively describes the spatial twisting behavior of 3D curves, defined as the rate of change in the binormal vector angle with respect to arc length, given by Equation (4):

$$\tau ={\displaystyle \frac{\left(r^{\prime }\left(t\right)\times r^{″}\left(t\right)\right)·r^{‴}\left(t\right)}{{‖r^{\prime }\left(t\right)\times r^{″}\left(t\right)‖}^2}}$$

(4)

For strictly 2D trajectories, the torsion remains identically zero.

In three-dimensional space, path smoothness requires both curvature and torsion to remain continuous without abrupt changes. The B-spline formulation inherently ensures continuous variation in curvature and torsion through its control points, effectively eliminating path discontinuities (see Figure 2).

3.2.2. B-Spline Parametric Implementation

• Waypoint Configuration

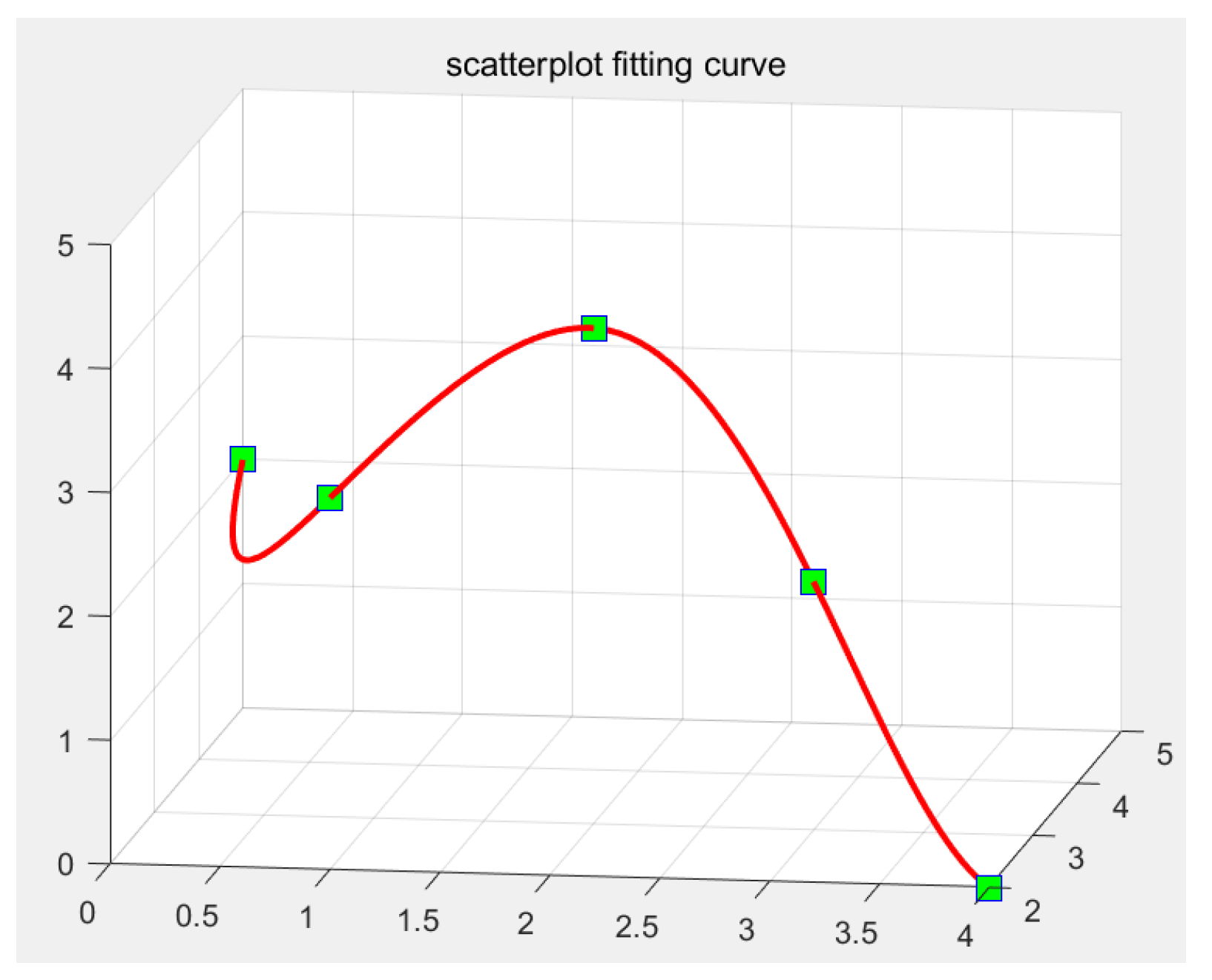
Although increasing the number of waypoints may improve path fitting accuracy, it has a negligible impact on the algorithm’s performance. To streamline the fitting process, this study selects five key waypoints to construct the spatial path: a start point, an end point, and three intermediate waypoints.

2.

Control Point Optimization

The MATLAB (version R2021a) spaps function is then employed to perform smooth fitting, converting the waypoints into B-spline control points. This function automatically balances:

• Path adherence: Mean squared error (MSE) to waypoints < 0.3 m;
• Curvature smoothness: Minimization of overall curvature variation.

3.

Path Generation

The final trajectory is generated as a linear combination of the control points, achieving smooth interpolation between the 3D waypoints (see Figure 3).

3.3. Objective Function Design

In UAV path planning, the design of the objective function requires comprehensive consideration of factors including trajectory cost, flight safety, and boundary constraints.

3.3.1. Trajectory Cost

The trajectory cost refers to the total path distance from the starting node to the destination. Given a path consisting of n nodes, the path distance is calculated using Equation (5):

$$S_c=\sum _{i=1}^{n-1}{L}_i$$

(5)

where

• $S_c$ represents the UAV’s cumulative trajectory cost;
• $n$ specifies the total number of discretized path nodes;
• $L_i$ denotes the Euclidean distance between node $i$ and node $i+1$.

3.3.2. Terrain Cost

To ensure flight safety, the UAV must avoid collisions with obstacles. A collision is considered to occur when the UAV’s flight altitude is lower than the current obstacle height. Accordingly, a collision coefficient with a significantly large value is established to substantially increase the collision penalty. The terrain cost is defined by Equation (6):

$$\left\{\begin{array}{l}{H}_{C_0}=0\hfill \\ H_{C_i}={\displaystyle \sum _{i=1}^n{H}_{C_i}}\hfill \\ H_{C_i}=\left\{\begin{array}{cc}{M}_T\hfill & {\mathrm{z}}_i<{\mathrm{z}}_2\left(x_i,y_i\right)\\ 0\hfill & otherwise\end{array}\right.\hfill \end{array}\right.$$

(6)

where

• $H_C$ denotes the terrain cost;
• $M_T$ represents the collision coefficient;
• $z_i$ indicates the flight altitude at the $i$-th node;
• $z_2(x_i,y_i)$ refers to the obstacle height at the $i$-th node location;
• $z_i<z_2(x_i,y_i)$ represents that the UAV has collided with an obstacle.

3.3.3. Boundary Cost

To ensure the UAV operates within prescribed flight boundaries, a boundary cost coefficient $B_E$ is implemented. When the UAV’s position exceeds the defined operational limits, $B_E$ adopts a significantly large value to enforce spatial constraints. The boundary cost is formulated in Equation (7):

$$R_C=\{\begin{array}{cc}{B}_E& x_i\notin [1,x_{max}] \mathrm{or} y_i\notin [1,y_{max}] \mathrm{o}\mathrm{r} z_i\notin [1,z_{max}]\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}$$

(7)

where

• $R_{\mathrm{c}}$ represents the boundary cost;
• $B_E$ denotes the boundary penalty coefficient;
• $x_i$, $y_i$, $z_i$ indicate the UAV’s 3D positional coordinates at the $i$-th waypoint;
• $x_{max}$, $y_{max}$, $z_{max}$ specify the maximum allowable flight range along each axis.

The objective function is suitable for real-time path planning in edge-intelligent environments, and can effectively balance path length, flight safety, and boundary constraints.

3.3.4. Comprehensive Objective Function

By integrating the aforementioned trajectory cost, terrain cost, and boundary cost, the comprehensive flight cost function for the UAV is defined by Equation (8) [56]:

$$\mathrm{m}\mathrm{i}\mathrm{n}\left(S\right)=\mathrm{m}\mathrm{i}\mathrm{n}(S_{\mathrm{c}}+H_{\mathrm{c}}+R_{\mathrm{c}})$$

(8)

where $S$ represents the UAV’s total flight cost, $S_{\mathrm{c}}$ denotes the trajectory distance cost (Section 3.3.1), $H_{\mathrm{c}}$ indicates the terrain collision penalty (Section 3.3.2), and $R_{\mathrm{c}}$ signifies the boundary constraint cost (Section 3.3.3). Minimization of this composite objective function yields an optimal path that simultaneously satisfies flight safety requirements and operational boundary constraints.

4. Improved Particle Swarm Optimization Algorithm (IPSO)

Owing to its inherent suitability for high-dimensional search spaces and robust environmental adaptability achieved through dynamic parameter adjustment, Particle Swarm Optimization (PSO) has been widely applied in 3D path planning.

4.1. Classical Particle Swarm Optimization Algorithm

PSO is a swarm intelligence-based heuristic algorithm inspired by the social behavior of bird flocks or fish schools. In PSO, the solution space is conceptualized as a particle swarm space, where each particle represents a potential solution. Each particle possesses two primary attributes: position and velocity. The position denotes a candidate solution in the search space, while the velocity determines the particle’s search direction and step size. The algorithm’s core principle involves simulating particles’ exploration and following behaviors to progressively converge toward optimal solutions. Each particle updates its position and velocity based on its personal historical best solution (individual extremum) and the swarm’s global historical best solution (global extremum), thereby discovering improved solutions.

Assume that there are N particles in the D-dimensional search space, each particle representing a potential solution. Where the position $X_i$ and velocity $V_i$ of the $i$-th particle can be expressed by a D-dimensional vector, formally defined by Equations (9) and (10):

$$X_i=(x_{i1},x_{i2},\cdots ,x_{iD}),i=\mathrm{1,2},\dots ,N$$

(9)

$$V_i=(v_{i1},v_{i2},\cdots ,v_{iD}),i=\mathrm{1,2},\dots ,N$$

(10)

During iteration, the optimal position discovered by the $i$-th particle thus far is termed the individual extreme value(pbest), which is represented by Equation (11):

$$P_i=\left(p_{i1},p_{i2},\cdots ,p_{iD}\right),i=\mathrm{1,2},\dots ,N$$

(11)

The optimal position discovered by all particles thus far is termed the global best (gbest) and is formally expressed by Equation (12):

$$P_g=(p_{g1},p_{g2},\cdots ,p_{gD}),g=\mathrm{1,2},\dots ,N$$

(12)

Particles update their positions and velocities based on both personal best (pbest) and global best (gbest) values, with update rules given in Equations (13) and (14), respectively:

$$v_{id}^{k+1}=\omega v_{id}^k+c_1{r}_1(p_{id}^k-x_{id}^k)+c_2{r}_2(p_{gd}^k-x_{id}^k)$$

(13)

$$x_{id}^{k+1}=x_{id}^k+v_{id}^{k+1}t$$

(14)

where

• $v_{id}^k$: Velocity of particle $i$ in dimension $d$ at iteration $k$ ($v_{id}\in [-v_{\mathrm{m}\mathrm{a}\mathrm{x}}{,v}_{\mathrm{m}\mathrm{a}\mathrm{x}}]$), $d=\mathrm{1,2},\dots ,N$.
• $k$: Current number of iterations.
• $\omega$: Inertia weight (typically constant).
• $c_1$, $c_2$: Acceleration coefficients (or learning factors) are non-negative constants that, respectively, control the step-size weights for particles moving toward their personal historical best positions (pbest) and the global historical best position (gbest).
• $r_1$, $r_2$: Uniformly distributed random numbers ∈$[0, 1]$.
• $t$: Time step (usually $t=1$).

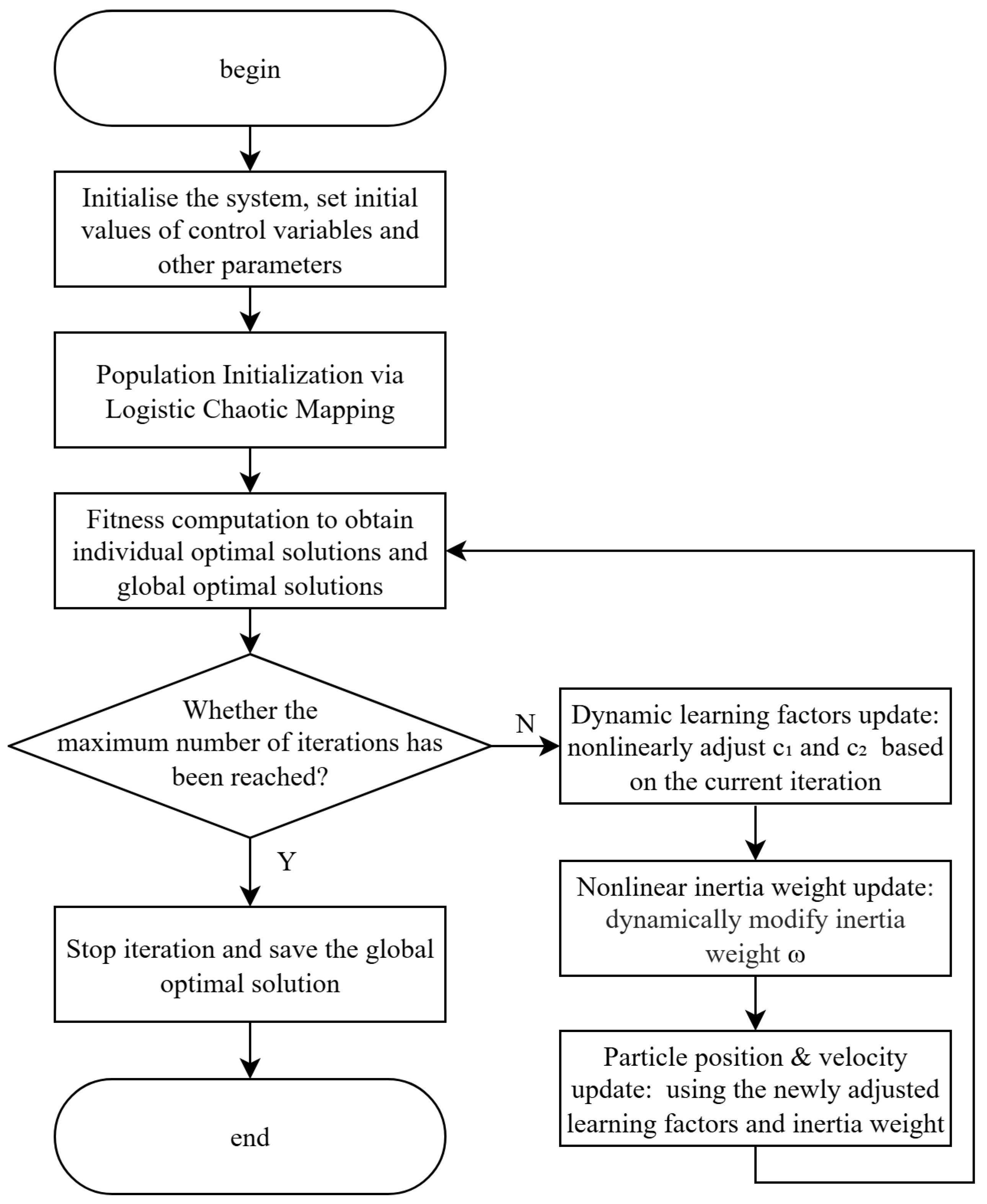
The standard PSO algorithm, constrained by its fixed-parameter mechanism, exhibits three fundamental limitations: progressive convergence degradation, acute parameter dependence, and premature convergence tendencies, which collectively impair its path planning performance in complex scenarios. In order to solve the above problems, this paper introduces logistic chaotic mapping, the dynamic learning factor and nonlinear inertia weights to avoid the particle swarm algorithm falling into the local optimal solution and the defects of too fast convergence speed. The following is the improvement of the particle swarm algorithm. The workflow of IPSO algorithm is shown in Figure 4.

4.2. Population Initialization via Logistic Chaotic Mapping

Conventional PSO initializes particle positions randomly, often inducing clustered distributions in local regions that increase susceptibility to local optima trapping, reduce convergence speed, and constrain global exploration capacity. To address these limitations, we employ logistic chaotic mapping for population initialization. By enhancing particle diversity and stochasticity, this approach significantly improves adaptability in edge intelligence environments through real-time generation of diversified solution distributions. This capability enables a dynamic response to environmental perturbations and effective adaptation to moving obstacles, while edge computing scenarios such as UAV path planning, empowers edge nodes to rapidly generate globally dispersed initial trajectories that intrinsically prevent premature convergence.

The logistic chaotic system is mathematically defined by Equation (15):

$$x_{i+1}=\mu x_i(1-x_i)$$

(15)

where $x_i$ denotes the chaotic variable at iteration $i$, and $\mu$ in (3.57, 4] represents the bifurcation parameter. When $\mu =4$, the system exhibits maximal chaotic behavior. Following prior studies [57,58,59], values of $\mu$ within this range are widely adopted to enhance chaotic dynamics and increase population diversity in path planning algorithms. In this study, we set $\mu =3.8$, which maintains sufficient chaotic characteristics while improving numerical stability during initialization.

4.3. Dynamic Learning Factor Scheme

To enhance global convergence capabilities, we refined the learning factor adaptation mechanism. In conventional PSO, learning factors $c_1$ and $c_2$ typically remain static constants. Oversized $c_1$ values lead to excessive local exploitation through over-reliance on individual experience, while elevated $c_2$ values trigger premature convergence to local optima. Addressing these limitations, we propose a dynamic learning factor scheme that adaptively modulates $c_1$ and $c_2$ values according to iterative progression phases.

During the initial iteration phases of the algorithm, it is essential to strengthen particles’ cognitive learning capabilities to facilitate extensive exploration of the search space. Conversely, in later iteration stages, enhancing particles’ social learning abilities becomes critical to preventing algorithmic entrapment in local optima and to drive asymptotic convergence toward the global optimum. Therefore, we adopt an elevated $c_1$ value and a reduced $c_2$ value during early iterations. This configuration amplifies cognitive learning while diminishing social influence, thereby augmenting population diversity. During later iterations, a diminished $c_1$ value and an elevated $c_2$ value are employed to intensify social learning, promoting convergence toward the globally optimal solution.

Prior research has implemented linear modifications to the learning factors [60], where $c_1$ decreases monotonically and $c_2$ increases monotonically with progressive iterations. These refined linear learning factors are expressed in Equations (16) and (17):

$$c_1=c_1^{start}+(c_1^{end}-c_1^{start})\times {\displaystyle \frac{k}{T}}$$

(16)

$$c_2=c_2^{start}+(c_2^{end}-c_2^{start})\times {\displaystyle \frac{k}{T}}$$

(17)

where $c_1^{start}$, $c_1^{end}$, $c_2^{start}$, $c_2^{end}$, respectively, represent the starting and final values of $c_1$ and the starting and final values of $c_2$, $k$ represents the current iteration number, and $T$ represents the maximum iteration number.

Although linearly modified learning factors achieve accelerated convergence rates, they remain prone to premature convergence to local optima in path planning scenarios. To address this limitation, this paper introduces a nonlinear refinement of the learning factors. The enhanced formulation intensifies global exploration capabilities during initial search phases while amplifying local exploitation efficacy in later stages. These modified learning factors are defined in Equations (18) and (19):

$$c_1=0.8+1.5{\mathrm{c}\mathrm{o}\mathrm{s}}^2\left({\displaystyle \frac{\pi k}{2T}}\right)$$

(18)

$$c_2=2.3-1.5{\mathrm{c}\mathrm{o}\mathrm{s}}^2\left({\displaystyle \frac{\pi k}{2T}}\right)$$

(19)

where $k$ denotes the current iteration count and $T$ represents the maximum iteration count. Let $x={\displaystyle \frac{\pi k}{2T}},x\in [0, \pi ]$. The equality $0.8+1.5{\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(x\right)=2.3-1.5{\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(x\right)$ holds if and only if $x={\displaystyle \frac{\pi }{4}}$, which yields $k={\displaystyle \frac{T}{2}}$. For this study, $T=100$, resulting in $c_1=c_2$ at $k=50$. 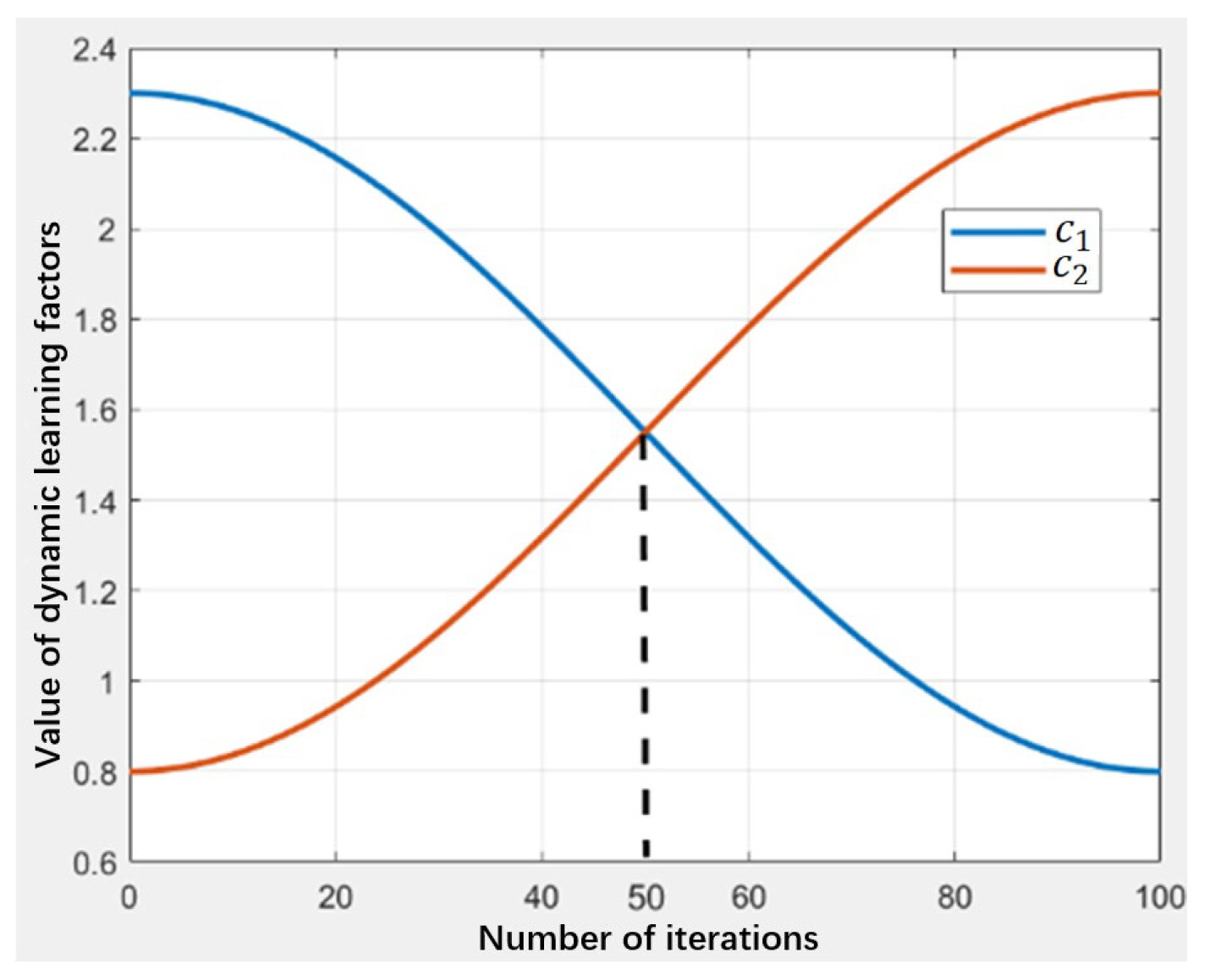The functional profiles of the refined learning factors are illustrated in Figure 5.

As evidenced in Figure 5, the inequality $c_1>c_2$ holds for $1\le k\le T/2,$ whereas $c_1<c_2$ is maintained for $T/2\le k\le T$. Consequently, the refined learning factors achieve the intended behavioral adaptation: elevated $c_1$ with suppressed $c_2$ during initial iterations for enhanced exploration, transitioning to diminished $c_1$ with amplified $c_2$ in later stages to intensify exploitation.

The incorporation of dynamic learning factors enables the algorithm to adaptively modulate its search strategy according to iterative phases, demonstrating particular efficacy for complex task allocation in edge intelligence environments. Within edge-cloud collaborative computing frameworks, these adaptive factors optimally balance global exploration and local exploitation, thereby enhancing both computational efficiency and solution accuracy in path planning.

4.4. Nonlinear Inertia Weight Mechanism

The performance of standard PSO exhibits significant dependence on the configuration of the inertia weight parameter. During initial algorithm iterations, enhancing particles’ global optimization capabilities necessitates assigning a larger inertia weight, enabling rapid exploration of the entire search space. Conversely, in later iterations, strengthening local optimization proficiency requires a reduced inertia weight to prevent premature convergence to local optima. Consequently, a progressively decaying inertia weight strategy effectively mitigates particle entrapment in suboptimal solutions. Prior research has adopted a linear decay strategy for the inertia weight [61], formulated in Equation (20):

$$w_i^k={\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}-k·{\displaystyle \frac{{\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{T}}$$

(20)

where ${\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and ${\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ denote the minimum and maximum inertia weights, respectively, $k$ represents the current iteration count, and $T$ signifies the maximum iteration count.

However, the linear decay inertia weight strategy exhibits critical deficiencies, including premature convergence, suboptimal convergence rates, and limited environmental adaptability. To overcome these limitations, this paper proposes a nonlinear inertia weight strategy. During real-time data processing on edge nodes, this mechanism dynamically adjusts particles’ search velocity according to iterative phases, preventing premature convergence while simultaneously enhancing algorithmic stability and convergence speed. The formulation is presented in Equation (21):

$$w_i^k={\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}}+\left({\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}}\right)\sin \left({\displaystyle \frac{\pi }{2}}{\mathrm{e}}^{-(k/h{)}^2}\right)$$

(21)

In this work, ${\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ = 0.9 and ${\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}}$= 0.4, consistent with widely adopted parameter settings in swarm intelligence research [62,63]. These values provide a practical balance: a larger initial inertia weight encourages global exploration, while a smaller final inertia weight strengthens local exploitation and stabilizes convergence. $k$ denotes the current iteration count, and $h$ is a positive constant that controls the nonlinearity of the inertia weight decay, set to 40 in this study based on preliminary tuning, which we found to be sufficient in preventing premature convergence without compromising computational efficiency. The refined velocity update formulation is given in Equation (22):

$$v_i^k=w_i^k{V}_{id}^{k-1}+c_1{r}_1(P_{id}^k-X_{id}^k)+c_2{r}_2(P_{gd}^k-X_{id}^k)$$

(22)

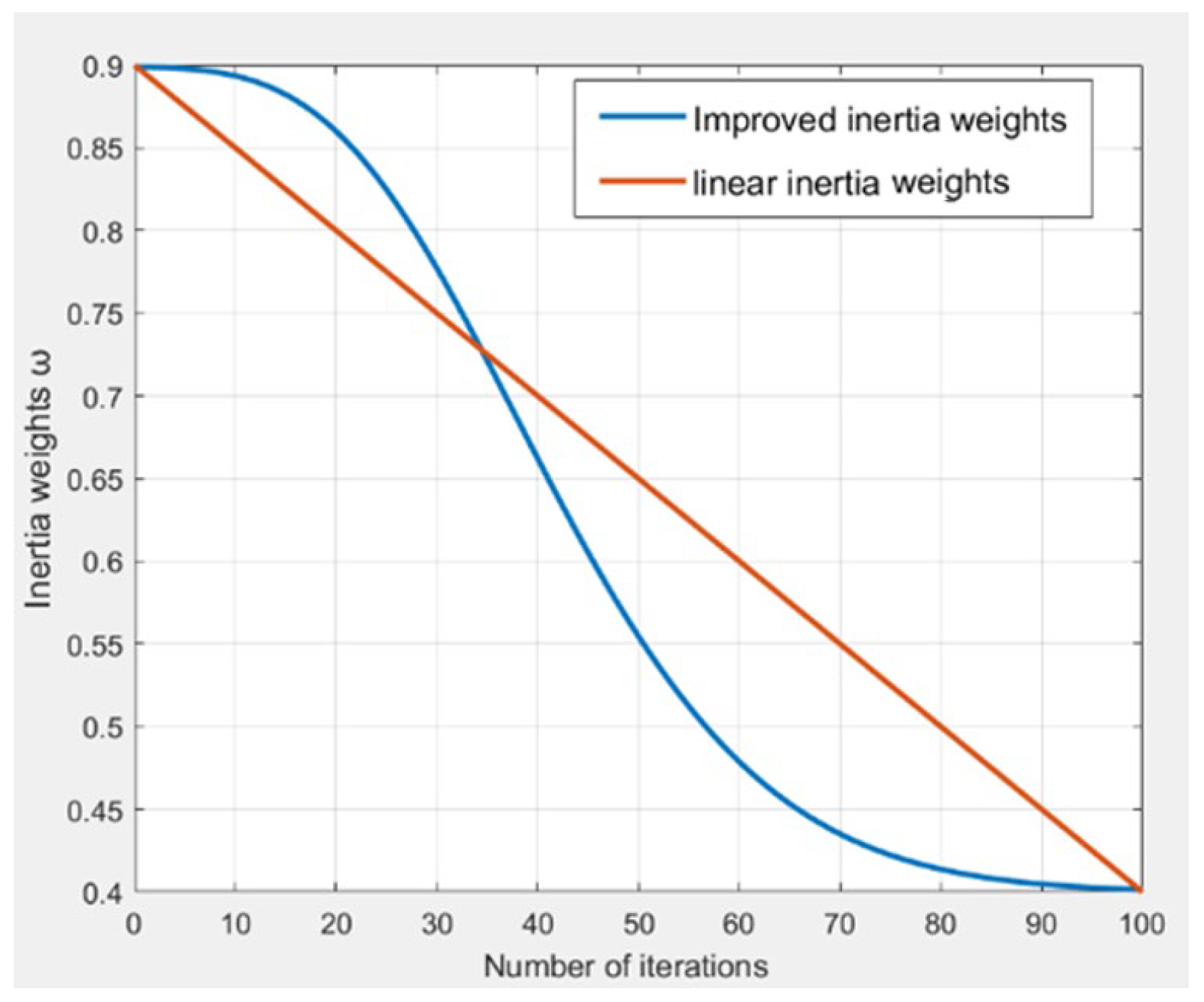
The comparative profiles of the improved nonlinear inertia weight versus its linear counterpart are illustrated in Figure 6.

As evidenced in Figure 6, the refined nonlinear inertia weight exhibits higher magnitudes than its linear counterpart during initial iterations, thereby intensifying particles’ global exploration capabilities. Conversely, in later stages, it maintains lower values than the linear variant, enhancing local exploitation efficacy. Consequently, this adaptive formulation better aligns with the iterative requirements of Particle Swarm Optimization.

The design of this nonlinear inertia weight enables superior adaptation to dynamic computational resources in edge intelligence environments. During real-time data processing on edge nodes, it significantly accelerates convergence rates and improves algorithmic stability, delivering robust support for path planning in complex scenarios.

5. Experimental Simulations and Results Analysis

5.1. Experimental Setup

To validate the efficacy of the Improved Particle Swarm Optimization (IPSO) in path planning, comparative experiments were conducted against six benchmark algorithms: Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), Artificial Fish Swarm Algorithm (AFSA) [64], Grey Wolf Optimizer (GWO) [65], Artificial Bee Colony (ABC) [66], and Genetic Algorithm (GA) [67]. To ensure fairness, all algorithms utilized the B-spline parameterization method from Section 3.2 with five control points and a smoothing factor $\mathrm{\lambda }=0.1$. Simulations employed three distinct terrain maps, with key parameters configured as shown in

Table 2. Experimental parameter configuration.

Parameter Category	Parameter Settings	Symbol	Parameter Value
Map	Experimental space	—	100 m × 100 m × 100 m
	Path starting point	startPos	(1, 1, 1)
	Path endpoint	goalPos	(100, 100, 20)
	Number of peaks	peaks	15
Algorithm	Population size	M	100
	Number of iterations	N	100

.

5.2. Results Analysis

5.2.1. Path Planning Distance Comparison

Firstly, path planning experiments were executed on Map 1. To evaluate optimal path identification capabilities, 100 Monte Carlo trials per algorithm were performed, with path lengths recorded at iterative milestones ($\mathrm{k}=1,20,40,60,80,100$). Results are quantified in

Table 3. Comparative path planning distances of different algorithms (meters).

Algorithm	Iterations 1 Path/m	Iterations 20 Path/m	Iterations 40 Path/m	Iterations 60 Path/m	Iterations 80 Path/m	Iterations 100 Path/m
IPSO	224.8277	159.7685	155.5084	153.3981	152.1034	152.0671
ACO	312.889	249.3382	222.3816	222.0625	222.0625	222.0625
GA	267.032	229.1915	229.1915	229.1915	229.1915	229.1915
ABC	251.0649	166.2471	161.0495	159.7091	158.0548	157.8318
GWO	285.9876	182.2613	163.0806	158.3342	155.9511	154.9267
AFSA	254.9221	184.753	166.6227	156.3458	154.547	154.1106

.

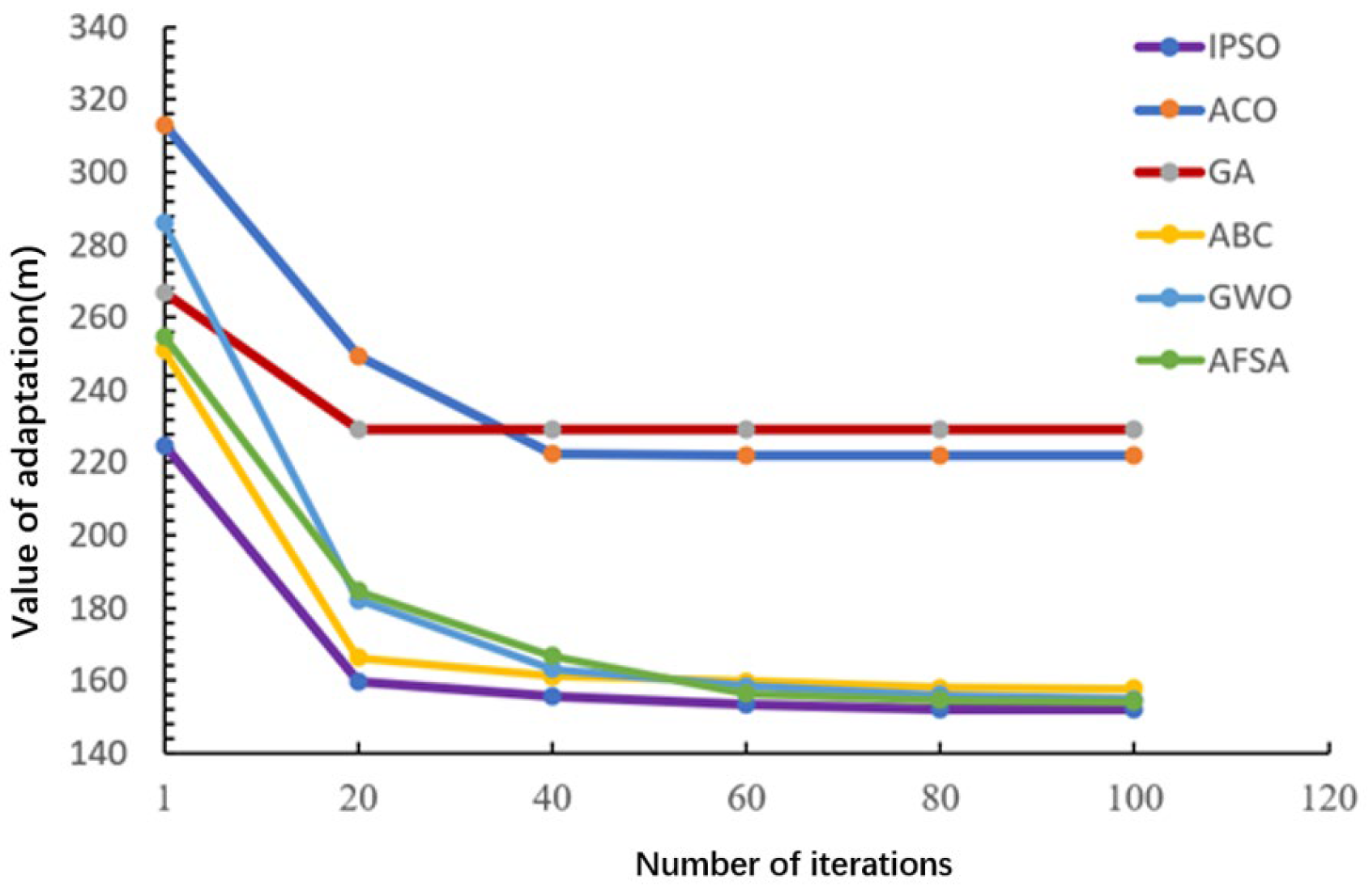
As quantified in Table 3, IPSO generates the shortest planned path at only 152.0671 m, while the Genetic Algorithm (GA) exhibits the poorest performance with a path length of 229.1915 m. Significant divergence exists in the iterations required for algorithms to converge to their respective optimal solutions.

Given the experimental configuration with start point (1, 1, 1) and goal (100, 100, 20), the theoretical global optimum path length is calculated as 141.2905 m. Algorithmic efficacy is evaluated by proximity to this theoretical minimum. As empirically demonstrated in Figure 7, IPSO achieves its algorithmic optimum within 20 iterations, whereas other methods—particularly GA and ACO—yield solutions significantly farther from the theoretical optimum.

5.2.2. Computational Time Analysis

Computational time represents a critical performance metric for path planning algorithms. We conducted 100 experimental trials on Map 1 and recorded the execution time at iterative milestones ($\mathrm{k}=\left\{\mathrm{1,20,40,60,80,100}\right\}$). Quantitative results are presented in

Table 4. Computational time comparison across algorithms (seconds).

Algorithm	Iterations 1 Time Consumed/S	Iterations 20 Time Consumed/S	Iterations 40 Time Consumed/S	Iterations 60 Time Consumed/S	Iterations 80 Time Consumed/S	Iterations 100 Time Consumed/S
IPSO	1.258	7.478	13.569	17.490	23.118	30.039
ACO	2.554	33.176	70.562	116.893	164.811	239.148
GA	1.473	11.659	22.876	33.743	45.937	55.344
ABC	1.535	13.160	26.913	34.074	43.618	58.664
GWO	1.453	18.977	42.278	54.971	118.472	210.493
AFSA	2.027	10.714	19.378	32.354	57.305	70.744

.

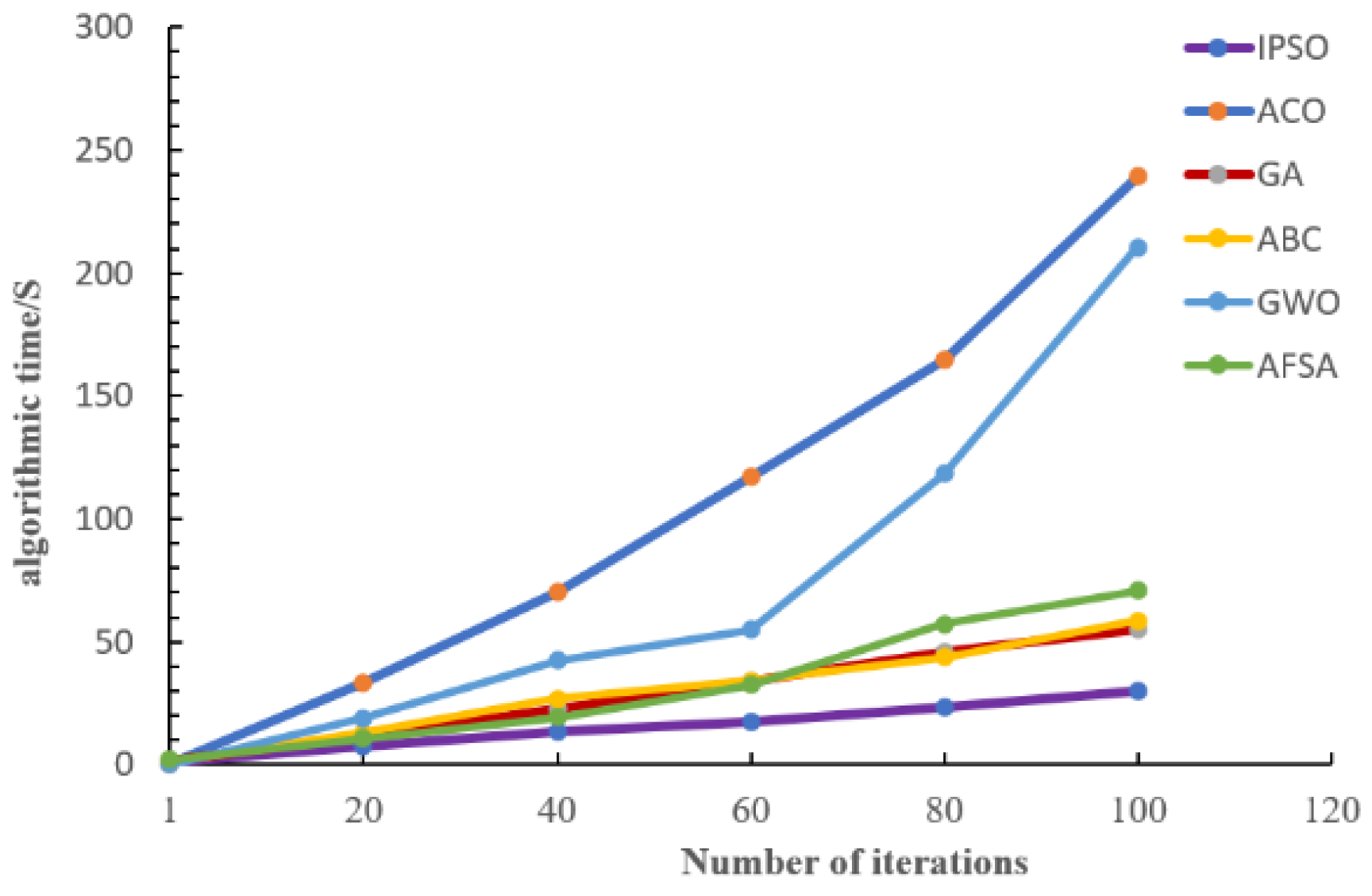
As quantified in Table 4, IPSO exhibits significantly lower computational overhead, while Ant Colony Optimization (ACO) and Grey Wolf Optimizer (GWO) demonstrate prohibitive time consumption—approximately eight times longer than IPSO at final iteration. This substantial disparity stems from the inherently higher computational complexity and iteration constraints of ACO and GWO. The comparative time costs across algorithms at 100 iterations are empirically validated in Figure 8.

As empirically validated in Figure 8, IPSO exhibits a flat computational-time progression with significantly reduced total execution time compared to alternative algorithms. This efficiency advantage fundamentally originates from IPSO’s robust avoidance of local optima entrapment, which prevents redundant recomputation cycles.

5.2.3. Comparison of Path Planning Outcomes

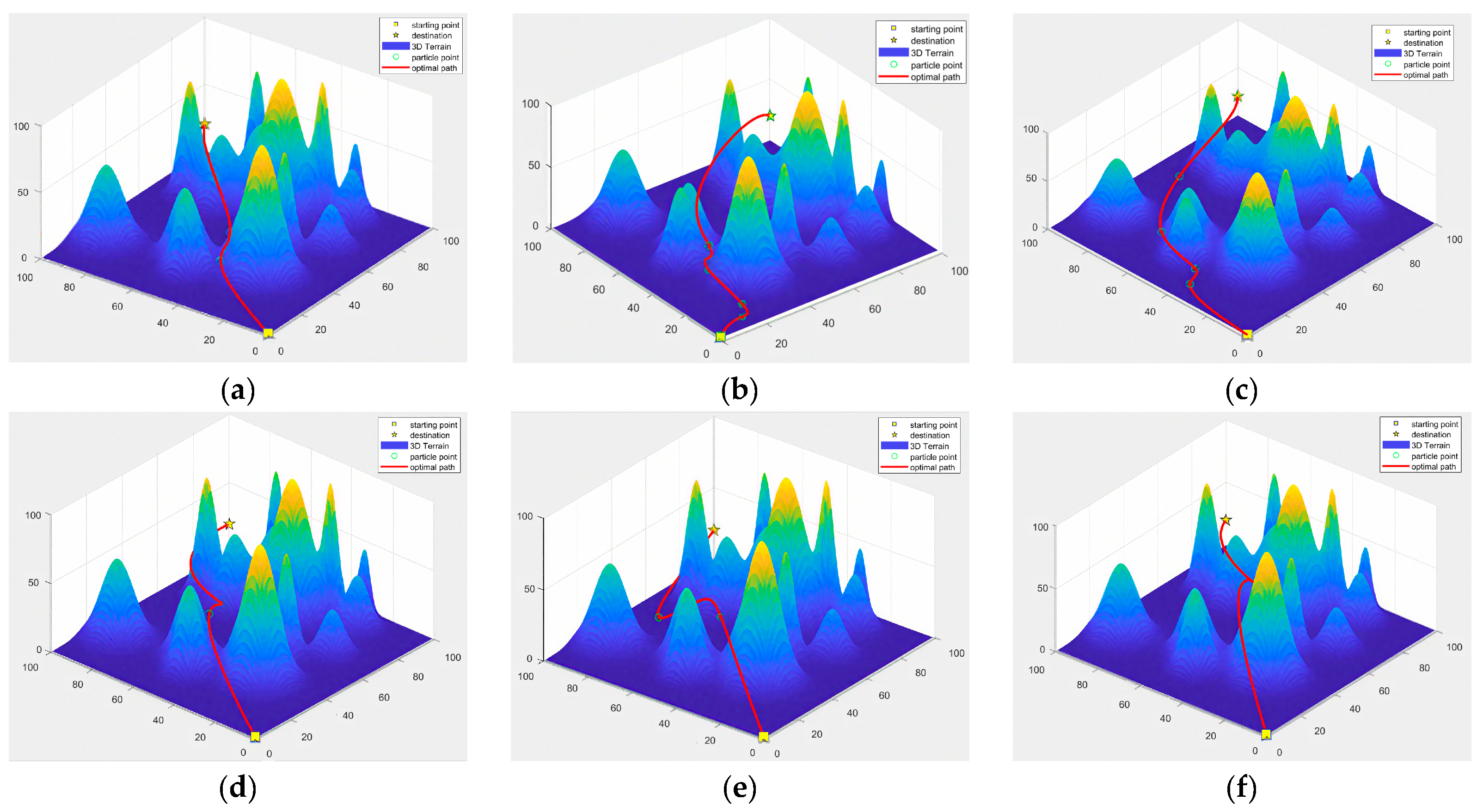
For intuitive evaluation of algorithmic path planning efficacy, the optimal path generated by each algorithm are comparatively visualized in Figure 9.

As shown in Figure 9, the B-spline path planned by IPSO is smoother and shorter, making it particularly suitable for complex task allocation in edge intelligence environments. In practical applications, this path planning effect can significantly enhance the system’s real-time performance and robustness. In contrast, paths planned by other algorithms (such as Ant Colony Optimization and Genetic Algorithm) exhibit significant inflection points. While the Wolf Pack Algorithm does not produce nodes with high curvature, the planned path distance is longer, resulting in greater implementation complexity.

5.2.4. Multi-Map Performance Validation

To validate algorithm adaptability across diverse environments, experiments were conducted on Maps 2 and 3. Combined with Map 1 results, we calculated six metrics per algorithm:

• Longest path;
• Shortest path;
• Average path length;
• Effective path rate (proportion of constraint-satisfying paths);
• Standard deviation;
• Theoretical deviation (difference between average path length and the theoretical shortest path of 141.2905 m).

Experimental results are presented in

Table 5. Performance metrics of algorithms across different maps.

Maps	Arithmetic	Longest Path	Shortest Path	Average Value	Theoretical Deviation	Standard Deviation	Effective Path Rate
Map1	IPSO	149.2662	143.5635	147.2405	2.273	1.52694	100%
	ACO	235.734	211.8496	219.3274	7.4778	7.03185	88%
	GA	211.1669	183.1672	195.5944	12.4272	9.1412	75%
	ABC	157.8412	146.4485	149.8579	3.4094	3.34708	92%
	GWO	158.0708	144.9463	150.9967	6.0504	3.60489	53%
	AFSA	173.7543	144.8027	153.5565	8.7538	8.7084	86%
Map2	IPSO	155.7485	150.646	153.3095	2.66348	1.66057	100%
	ACO	230.1602	209.343	220.0907	10.7477	6.81844	83%
	GA	228.1707	186.4867	197.9158	11.4291	13.0572	70%
	ABC	165.2351	157.2112	160.7375	3.5263	2.10432	88%
	GWO	176.3018	153.1128	161.6341	8.5213	7.60363	58%
	AFSA	186.3142	152.0923	170.6623	18.57	10.2801	90%
Map3	IPSO	154.0234	149.6343	151.9671	1.4328	1.20618	100%
	ACO	223.338	218.3417	222.0625	3.7208	3.07827	85%
	GA	254.8776	204.5876	229.1915	24.6039	14.6745	68%
	ABC	162.4134	153.2028	157.8318	4.629	2.59307	85%
	GWO	164.1629	150.4598	155.9267	5.4669	4.39716	62%
	AFSA	173.4014	150.3702	154.5106	4.1404	6.47081	88%

.

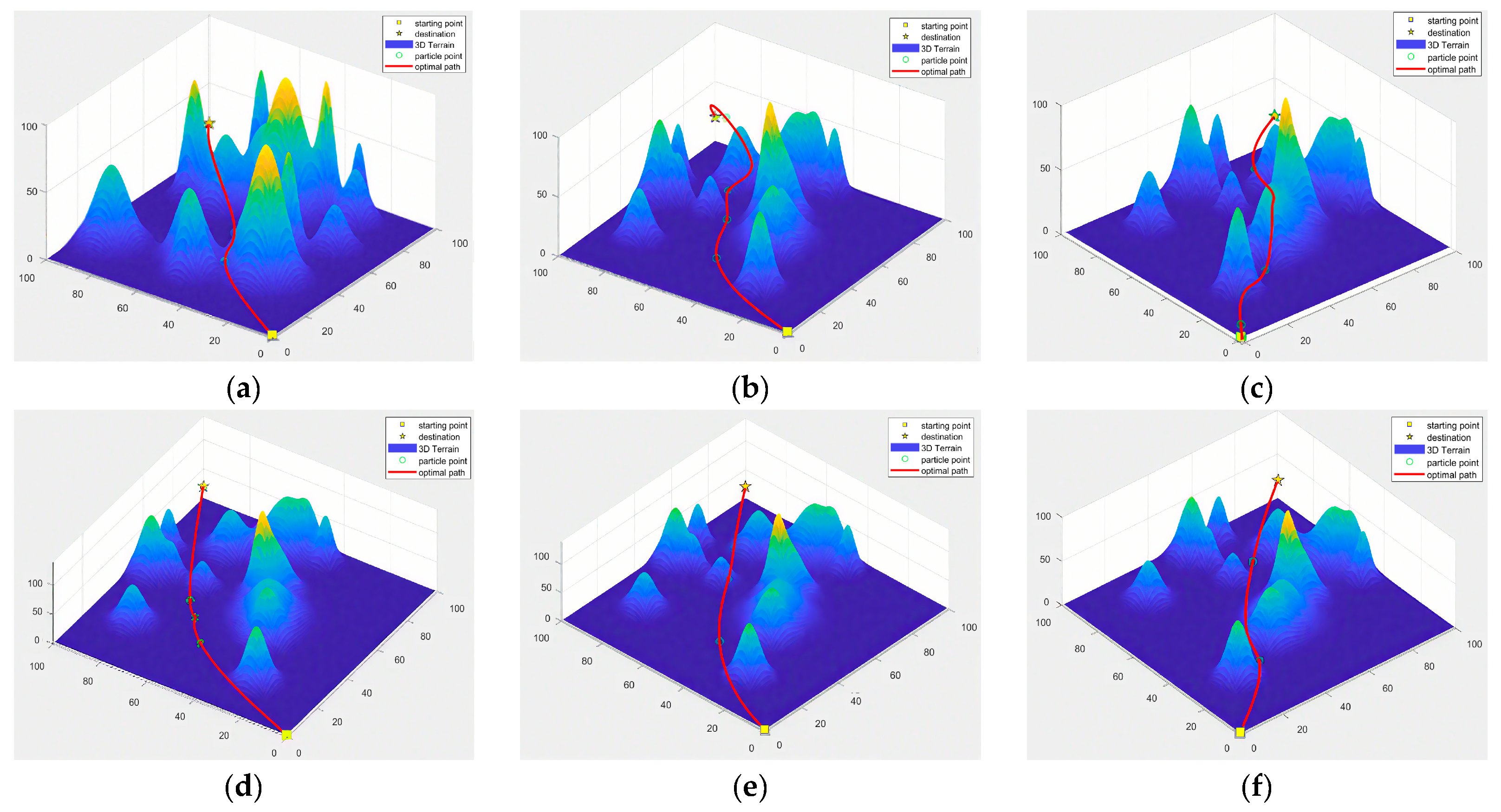
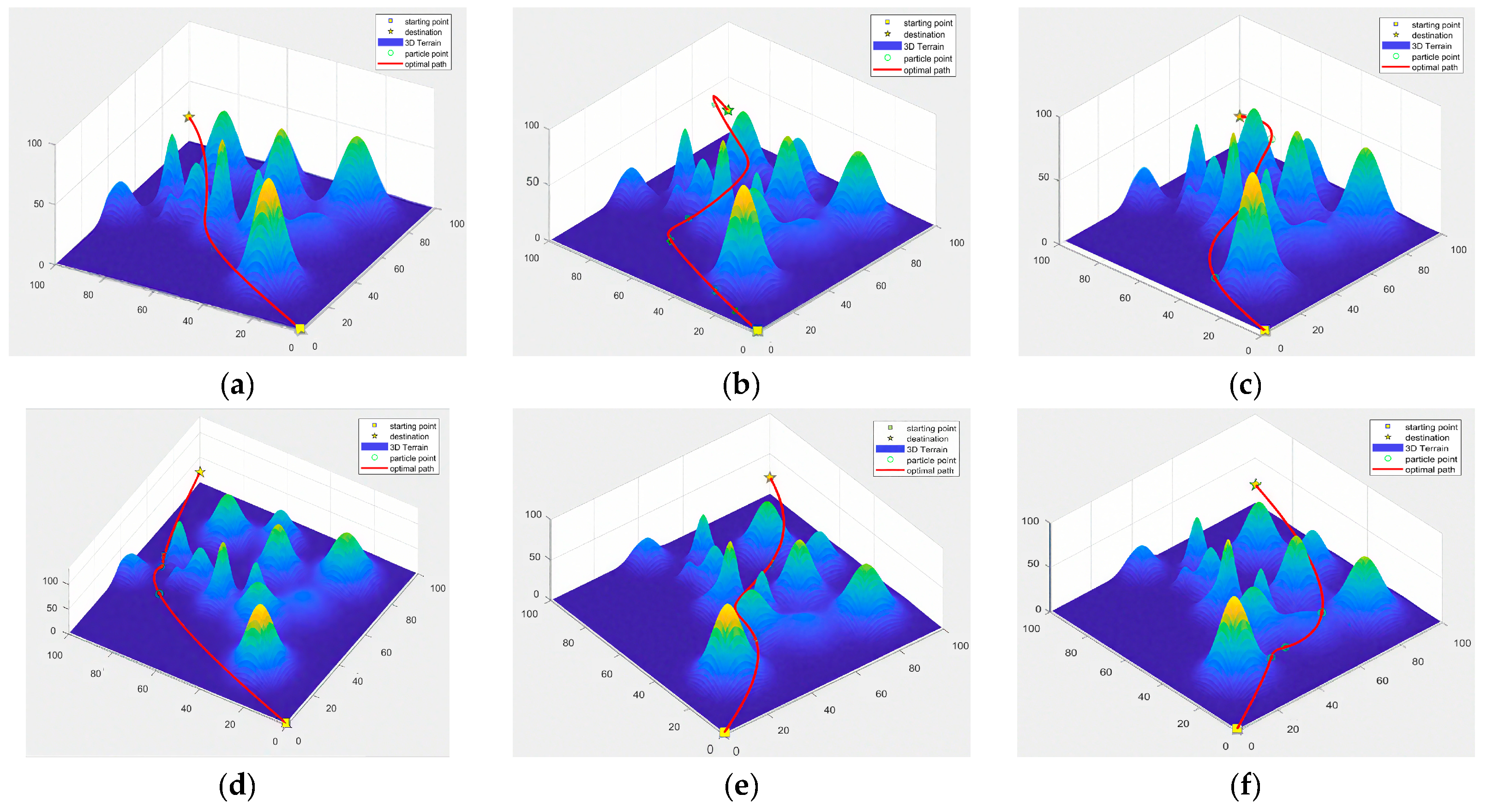
As shown in Table 5, IPSO outperforms other algorithms across all performance metrics on different terrain environments. It achieves optimal path length while exhibiting lower dispersion in path length distribution and a more minor standard deviation, indicating enhanced stability and robust adaptability for edge intelligence environments. The path planning results of all algorithms on Map 2 and Map 3 are illustrated in Figure 10 and Figure 11, respectively.

As visually apparent in Figure 10 and Figure 11, the IPSO algorithm generates significantly smoother and shorter paths while demonstrating superior map adaptability. Conversely, paths planned by other algorithms exhibit pronounced inflection points, resulting in substantially higher implementation complexity.

6. Conclusions and Future Work

Traditional Particle Swarm Optimization (PSO) updates particle velocity through a weighted summation of global and individual optimal solutions. Yet, its fixed learning factors and inertia weights frequently precipitate premature convergence to local optima, accompanied by excessively rapid convergence rates. To mitigate these limitations, this paper proposes an enhanced PSO algorithm (IPSO) incorporating dynamically adjusted learning factors and nonlinear inertia weights, substantially augmenting algorithmic flexibility and adaptability. The dynamic learning factors modulate the relative influence of global versus individual optima across iterative phases, facilitating extensive search space exploration during initial iterations while accelerating convergence toward the global optimum in later stages. Concurrently, nonlinear inertia weights dynamically regulate particle search velocity to prevent premature convergence while enhancing stability and convergence efficiency. Additionally, logistic chaotic mapping is employed for particle population initialization, significantly enhancing randomness and diversity. Through judicious parameter selection and adjustment, the refined algorithm demonstrates superior adaptability to heterogeneous terrains and achieves marked improvements in path planning efficacy. Experimental validation confirms the enhanced PSO’s consistent outperformance of conventional algorithms across critical metrics: path length reduction (average 14.4% shorter paths) and computational efficiency (65.04% faster processing), while exhibiting strengthened adaptability and robustness.

Looking ahead, while IPSO excels in simulation-based path planning, its practical deployment requires further validation on real UAV and robotic platforms, particularly under noisy sensor data, communication latency, and dynamic obstacle environments. Such real-world testing will be crucial for bridging the gap between controlled experiments and operational scenarios. Moreover, extending the current geometric optimization framework to incorporate UAV dynamics, turning radius constraints, and energy consumption models will be essential to ensure that planned trajectories are not only smooth and collision-free but also physically realizable and energy-efficient.

Another important avenue is to broaden the benchmarking of IPSO by including state-of-the-art Deep Reinforcement Learning (DRL) and hybrid heuristic learning approaches, which represent emerging paradigms in autonomous navigation. In parallel, the integration of IPSO with edge intelligence and industrial IoT infrastructures offers promising opportunities for real-time path planning in complex and resource-constrained environments.

Furthermore, future research will explore multi-agent UAV coordination and energy-aware path planning as logical extensions of IPSO. Additionally, integrating onboard sensing feedback for dynamic re-planning in uncertain environments will improve the algorithm’s robustness in real-world applications.

Finally, deeper analyses of the algorithm’s convergence mechanisms, as well as synergistic combinations with complementary optimization strategies, may further enhance its global search ability and adaptability across domains.