An Efficient Continuous-Variable Quantum Key Distribution with Parameter Optimization Using Elitist Elk Herd Random Immigrants Optimizer and Adaptive Depthwise Separable Convolutional Neural Network

Abstract

Quantum memory is essential for the prolonged storage and retrieval of quantum information. Nevertheless, no current studies have focused on the creation of effective quantum memory for continuous variables while accounting for the decoherence rate. This work presents an effective continuous-variable quantum key distribution method with parameter optimization utilizing the Elitist Elk Herd Random Immigrants Optimizer (2E-HRIO) technique. At the outset of transmission, the quantum device undergoes initialization and authentication via Compressed Hash-based Message Authentication Code with Encoded Post-Quantum Hash (CHMAC-EPQH). The settings are subsequently optimized from the authenticated device via 2E-HRIO, which mitigates the effects of decoherence by adaptively tuning system parameters. Subsequently, quantum bits are produced from the verified device, and pilot insertion is executed within the quantum bits. The pilot-inserted signal is thereafter subjected to pulse shaping using a Gaussian filter. The pulse-shaped signal undergoes modulation. Authenticated post-modulation, the prediction of link failure is conducted through an authenticated channel using Radial Density-Based Spatial Clustering of Applications with Noise. Subsequently, transmission occurs via a non-failure connection. The receiver performs channel equalization on the received signal with Recursive Regularized Least Mean Squares. Subsequently, a dataset for side-channel attack authentication is gathered and preprocessed, followed by feature extraction and classification using Adaptive Depthwise Separable Convolutional Neural Networks (ADS-CNNs), which enhances security against side-channel attacks. The quantum state is evaluated based on the signal received, and raw data are collected. Thereafter, a connection is established between the transmitter and receiver. Both the transmitter and receiver perform the scanning process. Thereafter, the calculation and correction of the error rate are performed based on the sifting results. Ultimately, privacy amplification and key authentication are performed using the repaired key via B-CHMAC-EPQH. The proposed system demonstrated improved resistance to decoherence and side-channel attacks, while achieving a reconciliation efficiency above 90% and increased key generation rate.

1. Introduction

One of the most important methods in quantum cryptography, Quantum Key Distribution (QKD), enables secure communication through the application of quantum mechanical principles, complemented by an authenticated classical communication channel [1]. According to [2], there are two main types of QKD: discrete variable QKD and continuous variable QKD. Discrete Variable Quantum Key Distribution (DV-QKD) uses different quantum states, such as photon polarization, to encode information [3]. In real-world contexts, DV-QKD encounters obstacles such photon loss, inefficient detectors, and limited communication distance [4]. Information in the continuous features of quantum states, including the amplitude and phase of light, is encoded using Continuous Variable QKD (CV-QKD) [5]. While CV-QKD offers advantages such as higher secret key rates at short distances and compatibility with standard telecom infrastructure, it is generally more sensitive to channel loss than DV-QKD. As a result, CV-QKD typically supports shorter transmission distances compared to DV-QKD. However, ongoing advancements in reconciliation efficiency and noise management continue to improve its practical range, making it a promising candidate for metropolitan-scale quantum communication systems [6,7]. Additionally, long-distance quantum communication has been greatly enhanced by the invention of CV-QKD quantum memory [8]. Improvements in optimization, security, and error correction may result from the incorporation of ML and DL into QKD systems as quantum communication technology advances [9,10]. According to [11], many ML algorithms, including Random Forest (RF) and Support Vector Machines (SVM), are frequently used to enhance the detection of quantum states. When dealing with the intricacies of quantum systems, these methods become invaluable in quantum mechanics [12,13]. In addition, Convolutional Neural Networks (CNNs) and other deep learning models have been employed to forecast quantum systems’ channel, noise, and loss, leading to enhanced efficiency and dependability [14]. The development of quantum memory for continuous variables, taking the decoherence rate into account, has not, however, been the focus of any extant work. This led to the research methodology of 2E-HRIO and ADS-CNN-based efficient continuous-variable quantum key distribution with optimized parameters.

Continuous Variable Quantum Key Distribution (CV-QKD) systems signify a notable progression in secure quantum communication; yet, some essential issues seen in the current literature have been inadequately handled. Current research has predominantly neglected the advancement of efficient quantum memory for continuous variables that incorporate decoherence effects, which is crucial for the preservation of quantum coherence over time. Several recent studies have advanced the development of continuous-variable quantum key distribution (CV-QKD), yet critical challenges remain unaddressed. Reference [15] demonstrated the significant vulnerability of CV-QKD systems to channel noise and loss, which severely degrade performance and security. The study in [16] highlighted the ongoing nature of quadrature measurements and the complexity of the associated error correction processes, underscoring the computational overhead that limits practical deployment. However, these works did not consider the impact of quantum memory decoherence, which is critical for secure and long-term key storage. In addition, [17] also identified vulnerabilities at the detector level but did not explore authentication mechanisms for quantum devices, such as transmitters and receivers—leaving systems exposed to impersonation and device forgery attacks. The authors in [18] also acknowledged certain operational weaknesses in CV-QKD protocols but did not sufficiently address the threat of side-channel attacks, resulting in residual security gaps.

To overcome these limitations, our proposed method introduces the following:

• 2E-HRIO (Elitist Elk Herd Random Immigrants Optimizer) to dynamically optimize device parameters and reduce decoherence effects in quantum memory,
• ADS-CNN (Adaptive Depthwise Separable Convolutional Neural Network) for real-time detection and classification of side-channel threats, and
• CHMAC-EPQH-based authentication to ensure robust verification of both transmitting and receiving devices.

Furthermore, we address the issue of point-to-point connection failures by integrating Radial Density-Based Clustering to predict and avoid unreliable communication links, thereby enhancing overall system resilience. These constraints highlight the pressing necessity for further research, to create effective solutions that improve memory stability, error resilience, device authentication, network dependability, and side-channel resistance, and to guarantee the practical and secure implementation of CV-QKD systems.

A series of focused methods have been suggested for the improvement of security and performance, in order to circumvent the major drawbacks of CV-QKD systems. The Two-Stage Enhanced Hybrid Randomized Incremental Optimization (2E-HRIO) method is used to dynamically optimize system parameters such as laser power, temperature regulation, and optical filter settings, which keeps the quantum state coherent for longer durations. More dependable transmission is achieved through strategic insertion of pilot symbols and the performance of channel equalization using the Robust Recursive Least Mean Squares (R2LMS) algorithm, which mitigates the negative impacts of channel noise and signal loss. Efficient reconciliation of mistakes is achieved with the use of the Von Neumann Entropy (VNE) approach, in conjunction with Improved Rate Low-Density Parity-Check (IR-LDPC) codes for precise calculation and repair of the errors caused by the continuous quadrature measurements. Utilizing the Robust Density-Based Spatial Clustering of Applications with Noise (RDBSCAN) clustering technique, network resilience is enhanced by addressing probable point-to-point connection failures and facilitating safe key exchanges between connected quantum nodes. As a measure to prevent quantum devices from being tampered with or replaced without authorization, authentication procedures are put in place utilizing the CHMAC-EPQH technique, which is based on Extended Priority Quantum Hashing. An Anomaly Detection System based on Convolutional Neural Networks (ADS-CNNs) provides strong defense against covert exploitation of hardware flaws and can identify and neutralize side-channel assaults, a significant danger to CV-QKD systems. The combined effect of these approaches is a thorough plan to improve the future performance of CV-QKD networks in terms of their resiliency, safety, and feasibility.

2. Literature Survey

A new optimization-based post-processing framework was developed [15] to improve the effectiveness and safety of CV-QKD systems. The suggested solution used raw data collected from quantum communications, in conjunction with a classical authenticated communication channel for the creation of a shared secret key between authorized parties. Incorporation of optimization approaches into the post-processing step ensured the out performance of standard framework methods in key generation efficiency and overall security. The method surpassed previous solutions according to the experimental results, especially when it came to maximizing key extraction from quantum data that were noisy. Nevertheless, the study’s neglect of reducing transmission loss and channel noise during the quantum communication phase constituted a major drawback. In the absence of these, there is space for development; they are essential for ensuring reliable work from CV-QKD systems in real-world noisy systems.

Maximizing post-processing efficiency in capacity-constrained Continuous Variable Quantum Key Distribution (CV-QKD) systems was considered in [16] to find the best system parameters for key generation, and the method used systematic optimization techniques such as modulation variance and error correction matrix optimization. Based on their findings, the suggested approach indicated the significant out performance of earlier methods in terms of Information Reconciliation (IR) efficiency, reaching 91.34%. The methods encountered a hurdle in the form of the continuous feature of quadrature measurement, not withstanding this accomplishment. Because of this feature of CV-QKD systems, more complicated and computationally demanding error correction algorithms are required, which increase the system’s total complexity and may affect the approach’s applicability in real-world situations.

In an effort to improve the efficiency and safety of quantum key distribution systems, ref. [17] laid the groundwork for a CV-QKD protocol that does not rely on any particular measuring equipment. The protocol improved transmission quality with the incorporation of a Noiseless Linear Amplifier (NLA) to amplify quantum states, which efficiently compensated for channel attenuation. The results from experiments showed the out performance of the method over the state of the art in terms of Information Reconciliation (IR) efficiency, indicating its ability to improve key generation rates in real-world quantum communication systems. Despite these improvements, the study had a major flaw: it did not check the authenticated of the quantum devices (transmitters and receivers), which might have exposed the system to security concerns caused by tampered with or compromised hardware.

In their proposal, [18] sought to optimize the parameters of long-distance CV-QKD systems using non-Gaussian operations, with the goal of improving their performance. They improved the safe transmission distance in CV-QKD systems using the Direct Search algorithm to determine the ideal settings of the Quantum Scissor (QC), an essential component of their approach. With fidelity levels ranging from 161% to 304%, their experimental results showed the strategy significantly improved the range of secure quantum key exchanges. Despite the presence of improvements in transmission distance and fidelity, the method failed to protect against side-channel attacks, which could be a security risk in real-world applications. This void led to the requirement for a further study into long-distance CV-QKD systems, to include protections against side-channel exploitation.

Improvement in the control of quantum states during transmission was the main focus in [19]. A framework for modulation leakage-free Continuous Variable Quantum Key Distribution (CV-QKD) systems was suggested. With the goal of reducing mistakes and maintaining the integrity of the sent information, the framework employed baseband modulation, an In-phase and Quadrature (IQ) modulator, and radio frequency heterodyne detection to improve the accuracy of quantum state management. An encouraging frame error rate of 0.962 was achieved in the experimental study of this method, indicating a high degree of accuracy and dependability in the system’s operation. Regardless of these achievements, the suggested system had a serious flaw in its limited transmission range, which could make it unsuitable for long-distance CV-QKD deployments. Given this restriction, the requirement of additional effort to increase the system’s range was noted, while preserving its leakage-free properties and reducing error rates.

An approach to noiseless attenuation known as Continuous Variable Measurement-Device-Independent Quantum Key Distribution (CV-MDI-QKD) was proposed in [20], based on quantum catalysis, more specifically Zero-Photon Catalysis (ZPC). By strengthening the key distribution mechanism and enhancing the transmission of quantum information, this novel approach sought to improve the efficiency of CV-MDI-QKD. The results from experiments showed its out performance compared to conventional methods, in terms of secret key rate and secure transmission distance. Despite these improvements, the suggested system had a flaw. Additional research into generalizing the quantum catalysis approach and integrating it into a broader range of protocols is needed to fill this knowledge gap and for improvements in the performance and security of CV-QKD protocols.

In order to identify assaults on CV-QKD systems, [21] created a framework that uses a Deep Neural Network (DNN) to retrieve minimal internal information from the networks that are being targeted. A search for weaknesses in the distribution of quantum keys triggered hope of strengthening the safety of CV-QKD systems with this method. In order to improve the system’s detection capabilities, the framework integrated numerous DNNs with differential evolution. This allowed the adaptation and identification of attacks of different varieties. Based on the experimental results, the suggested method outperformed other current approaches in attack detection, indicating its potential to enhance the security of CV-QKD systems. Nevertheless the necessity for additional study was noted, to resolve remaining concerns and improve the system’s overall robustness, as the system was not immune to some security vulnerabilities, even with its excellent detection performance.

The goal of the system in [22] was to improve the security of transmitted quantum information through detection of side-channel attacks in quantum key distribution (QKD) systems. Before converting to quantum bits (q-bits), the framework employed Shifting and Binary Conversion techniques to make the hidden information more complicated. This extra degree of complexity was added to further safeguard the data against any side channel vulnerabilities, making it more difficult for an attacker to obtain meaningful information from the system. The proposed approach provided stronger security levels and enhanced resilience against side-channel assaults, according to the experimental results, which surpassed existing systems. Nevertheless, the system’s high computational cost and precision loss are major drawbacks that reduce its usefulness in real-time QKD systems, particularly in settings with scarce computational resources.

Examination of the sources of noise that impacted the system’s performance [23] helped showcase of an approach for CV-QKD, which stands for Gaussian Modulated Coherent State. In order to determine secure key rates at GHz bandwidth, the framework used a balanced homodyne detector to measure noise. This technology enabled exact detection of quantum states to guarantee secure key creation in the system. The technology showcased its promise for practical CV-QKD applications in short- to medium-range communication, as the test findings demonstrated its ability to reach safe key rates of 3 Mbits/s over a 30 km transmission distance. In spite of these encouraging outcomes, the system was not without its flaws; namely, its extreme susceptibility to jitter and noise, which may diminish its performance, particularly in contexts where communication is lengthy or extremely noisy. The need for additional tuning to ensure improvement in stability and resistance to noise for the system was acknowledged.

The CV-MDI-QKD system, which stands for Continuous-Variable Measurement-Device-Independent Quantum Key Distribution, can handle complicated communication situations [24]. Parameter estimate is the first step in the process to evaluate quantum channels for better key distribution reliability. In addition, the system was fortified against possible assaults using Gaussian post-selection technology, which secured the quantum states and filtered out noise, especially when the attack was on the target quantum channel. The experimental results showed the suggested framework enabled sustainable enhancement of the CV-MDI-QKD system’s security when compared to prior approaches. The total efficiency of the system was reduced due to the loss of important information during the filtering process, which is a major constraint that requires addressing. The requirements for parameter estimation and post-selection methods to achieve a better balance between security and performance, considering the trade-off between enhanced security and lower efficiency, could be a subject for future study.

Table 1. Comparative analysis of the literature survey.

Authors Name	Approach/Focus	Key Results	Main Limitations
Gyongyosi et al. [15]	Optimization-based post-processing framework	Higher key-generation efficiency and security vs. standard methods	Failed to address the mitigation of channel loss or noise in quantum transmission.
Ma et al. [16]	Systematic optimization of modulation variance and error-correction matrices	IR efficiency up to 91.34%	Measurements of continuous quadrature require intricate, time-consuming error-correction techniques.
Zhou et al. [17]	Measurement-device-agnostic CV-QKD with Noiseless Linear Amplifier (NLA)	Increased key-generation rate and IR efficiency in experiments	Lack of quantum hardware authentication leaves devices open to manipulation.
Jafari et al. [18]	Using Direct Search to optimize parameters, non-Gaussian procedures for long-distance CV-QKD	Enhanced security during transmission; fidelity increases of 161–304%	Absence of defenses against side-channel assaults
Hajomer et al. [19]	Leakage-free modulation with RF heterodyne detection and a baseband IQ modulator	0.962 frame error rate, indicating strong integrity	Inadequate for extremely long-distance lines, due to its limited transmission range
Ye et al. [20]	Using Zero-Photon Catalysis (ZPC) quantum catalysis, CV-MDI-QKD	Superior secret-key rates and extended secure distances compared to traditional CV-MDI-QKD.	Examined ZPC solely within a single CV-MDI-QKD framework; generalizability remained unverified.
Guo et al. [21]	DNN-based framework for attack detection, enhanced through differential evolution	Enhanced detection precision compared to current methodologies	Residual security weaknesses persisted not entirely resilient against all forms of attacks.
Gopinath and Shyry [22]	Transformation and binary conversion to obscure side-channel data	Improved resistance to side-channel attacks	Significant processing burden and loss of precision hindered real-time implementation.
Tang et al. [23]	Analysis of noise sources in Gaussian-modulated coherent-state continuous-variable quantum key distribution employing balanced homodyne detection	Attained secure key rates of 3 Mbit/s across a distance of 30 km	Highly susceptible to jitter and excessive noise; performance deteriorated over extended or louder connections.
Zheng et al. [24]	CV-MDI-QKD utilizing Gaussian post-selection to mitigate noise and enhance states	Significantly enhanced security compared to previous CV-MDI-QKD techniques	Efficiency diminished as a result of knowledge loss during post-selection.

presents details of the CV-QKD protocols that were analyzed, with the optimization approaches, quantitative performance outcomes, and limitations of each protocol.

3. Methodology

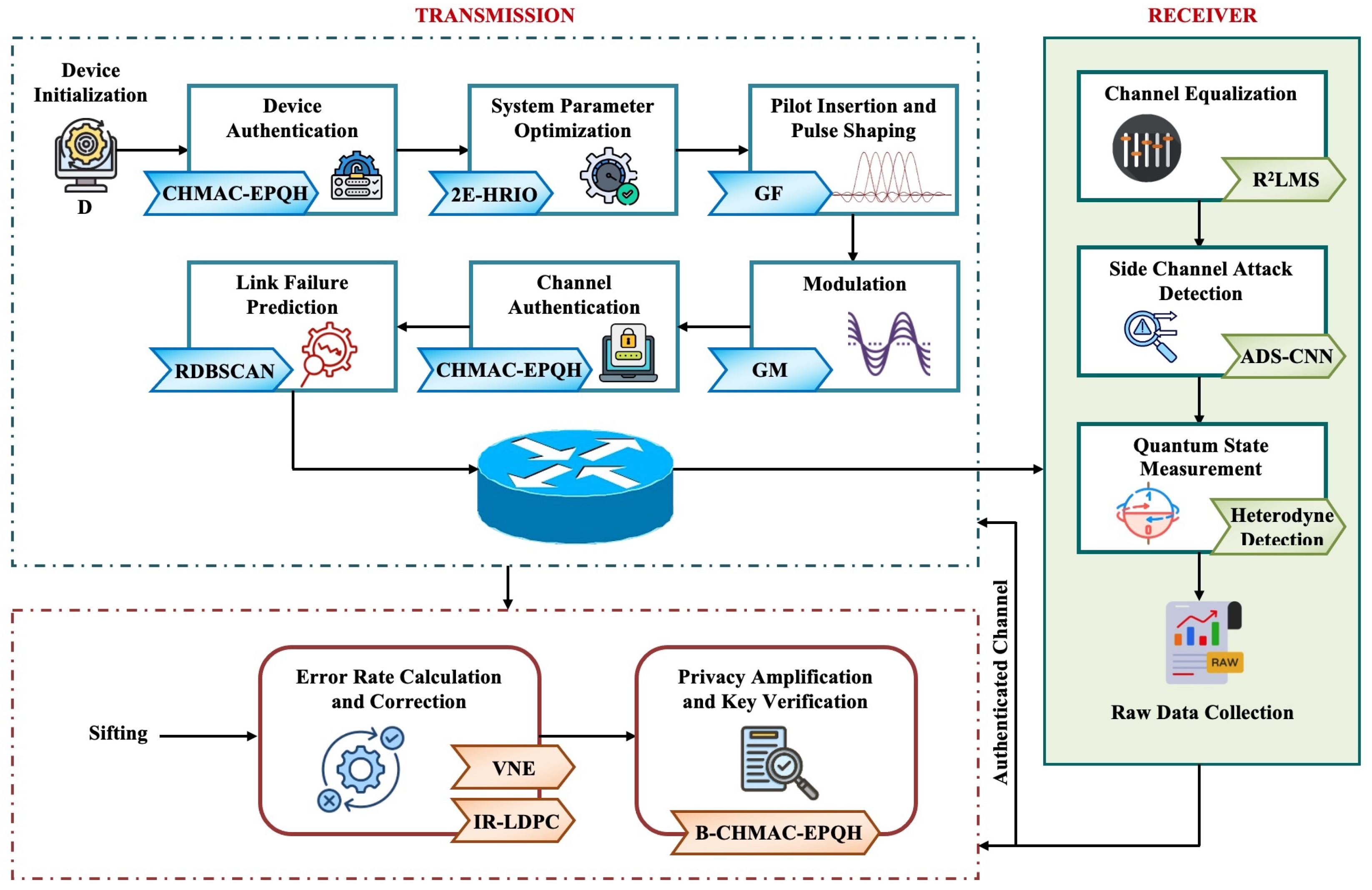
Details relating to the proposed methodology for continuous-variable quantum key distribution with parameter optimization and side channel attack detection based on the 2E-HRIO approach are provided. The key steps of the study technique are system parameter optimization, channel authentication, link failure prediction, channel equalization, and SCA detection. Figure 1 shows the block diagram for the proposed framework.

3.1. Transmission

This part focuses on the transmission of the signal to guarantee efficient, reliable, and secure communication through the optimization of system settings, device and channel authentication, and the prevention of connection failures. The transmission process is delineated as follows:

3.1.1. Device Initialization and Authentication

The quantum device D is first initialized and assigned a unique identity through a secure MAC address generated using the CHMAC-EPQH algorithm. This approach combines HMAC with post-quantum hash functions to ensure robust authentication and message integrity, offering resistance against quantum computing-based threats.

To reduce key management complexity and storage overhead, the secret key $\tau$ generated for D undergoes compression and encoding. The compression is performed using a transformation function:

$${\tau }^{\mathit{comp}}=\Im \left(\tau \right)$$

(1)

The compressed key ${\tau }^{\mathit{comp}}$ is then encoded using a post-quantum encoding function $e_n$:

$${\tau }^{″}=e_n\left({\tau }^{\mathit{comp}}\right)$$

(2)

Authentication is achieved using the encoded key ${\tau }^{″}$ in conjunction with padding constants $o^{\prime }$ and $o^{″}$ and a hash function $\ddot{h}$:

$$\tilde{J}=\ddot{h}(({\tau }^{″}\otimes o^{\prime })\parallel \ddot{h}(({\tau }^{″}\otimes o^{″})\parallel D))$$

(3)

Here, $\tilde{J}$ represents the authenticated device, and ⊗ denotes the XOR operation. Once the generated MAC and $\tilde{J}$ have been verified, secure communication is established between the authenticated device and the network.

3.1.2. System Parameter Optimization

This section, deals with the optimization of the system parameters, such as the laser power, temperature control, and filter settings from $\tilde{J}$, using the 2E-HRIO method to reduce the decoherence rate and support long-distance quantum communication. The conventional Elk Herd Optimizer (EHO) helped maintenance of a good balance between exploration and exploitation. However, there was the likelihood of EHO suffering from stagnation, with a decrease in the population diversity over iterations, leading to premature convergence. To solve this issue, Elitist Random Immigrants (ERI) was utilized for the preservation of the best-performing individuals and to introduce a fixed or adaptive number of new elk with random characteristics into the herd. To start with, the populations were initialized. Here, the laser power, temperature control, and filter settings were considered as the population. Following that, the Elk Herd matrix was modeled with the position of the population size P and the number of iterations $\left(I\right)$. The population matrix $\tilde{E}$ is represented as follows:

$$\tilde{E}=\left[\begin{array}{cccc}{e}_{j^1}^{b^1}& e_{j^2}^{b^1}& \dots & e_{j^n}^{b^1}\\ e_{j^1}^{b^2}& e_{j^2}^{b^2}& \dots & e_{j^n}^{b^2}\\ ⋮& ⋮& \dots & ⋮\\ e_{j^1}^{b^P}& e_{j^2}^{b^P}& \dots & e_{j^n}^{b^P}\end{array}\right]$$

(4)

where n is the total number of elk and $e_j^b$ is the $\left(j^{th}\right)$ solution of the $\left(e^b\right)$ elk. The position is randomly initialized as follows:

$$e_j^b={\widehat{l}}_j+r^{\ast }\times ({\widehat{u}}_j-{\widehat{l}}_j)$$

(5)

where $\left(r^{\ast }\right)$ represents a random number that ranges from 0 to 1, and ${\widehat{u}}_j$ and ${\widehat{l}}_j$ are the upper and lower bounds, respectively. Following this, the fitness function was estimated for the population. In this work, a high key rate $K_h$, high Signal-to-Noise-Ratio (SNR) $S_{n}r$, low decoherence rate $D_l$, and low quantum Bit Error Rate (BER) $Q_a$ were considered to constitute the fitness function of the population represented in Equation (6):

$$\Psi =\{K_h,S_{nr},D_l,Q_a\}$$

(6)

where $\Psi$ represents the fitness function of the population.

• Phase 1: Rutting Season: The total number of families is determined during rutting season by calculating the bull rate $Y\prime \prime \prime$, as mentioned below.

  $$\lambda =|Y^{\prime \prime \prime }\times P|$$

  (7)

  where $\left(\lambda \right)$ is the total number of families. The bulls were subsequently selected from $\tilde{E}$ based on their fitness scores. The elks exhibiting the highest fitness values, originating from the apex of $\tilde{E}$, were classified as bulls and were enumerated as follows:

  $${\lambda }^{\ast }=argmin(\Psi (e^b))b\in (1,2,...,\lambda )$$

  (8)
  The bull was represented by $e^b$, while the set of bulls trying to establish families was represented by $\left({\lambda }^{\ast }\right)$. Following this, the selection probability was determined for each bull $e^b$ in $\left({\lambda }^{\ast }\right)$ according to its absolute fitness value. The next step involved the use of the following equation for the assignment of harems to bulls based on their selection probability (9):

  $$A={\displaystyle \frac{\Psi (e^b)}{{\displaystyle \sum _{\widehat{\upsilon }=1}^{\lambda }\Psi (e^{\widehat{\upsilon }})}}}$$

  (9)

  $$\widehat{\upsilon }=P-\lambda$$

  (10)

  where $\left(A\right)$ represents the selection probability derived from the fitness value, and $\left(\widehat{\upsilon }\right)$ represents the harems allocated to each bull, decided through roulette-wheel selection based on the bull’s index.
• Phase 2: Calving Season: During the calving season, the characteristics passed down from the mother harem and father bull were the primary influences on the offspring. In a family of bulls, a calf is considered reproduced and represented by Equation (11) if its index is the same as that of the father bull.

  $$e_j^b(k+1)=e_j^b\left(k\right)+\stackrel{\dots }{\kappa }(e_j^h\left(k\right)-e_j^b\left(k\right))$$

  (11)

  where $e_j^b\left(k\right)$ indicates the maternal harem within the family, $\stackrel{\dots }{\kappa }$ represents a stochastic value within the interval $[0,1]$, and $e_j^h\left(k\right)$ sets the rate of attributes randomly selected from the elk population. Where the calf possesses the same index as the mother bull within the family, it is derived to inherit the characteristics from both its maternal harem and paternal bull, as delineated in Equation (12).

  $$e_j^b(k+1)=e_j^b\left(k\right)+\upsilon (e_j^f\left(k\right)-e_j^b\left(k\right))+{\upsilon }^{\prime \prime }(e_j^{\gamma }\left(k\right)-e_j^b\left(k\right))$$

  (12)

  where $e_j^f\left(k\right)$ is the paternal bull within the family, $\upsilon$ and $\upsilon \prime \prime$ represent the stochastic values within the interval $[0,2]$, whereas $\left(\gamma \right)$ denotes the index of a random bull in the current bull set, such that $\gamma ϵ{\lambda }^{\ast }$.
• Phase 3: Selection Season: Here, the bulls, calves, and harems of all families were combined. The $\tilde{E}$ storing of the bulls and harem solutions and the $\left(E^{\prime \prime }\right)$ storing of the calf solutions were merged into a single matrix and denoted as $\left(M\right)$. The elks in $\left(M\right)$ were selected using elitist selection $E^b$ and the random immigrants $M^b$. Finally, the elks updated their best position using $E^b$, $M^b$, which is represented as follows:

  $$\zeta (k+1)=E^b\cup M^b\cup \zeta$$

  (13)

  where $\zeta (k+1)$ represents the updated population and $\left(\zeta \right)$ refers to the offspring population. Thus, based on $\zeta (k+1)$, the system parameters such as laser power, temperature control, and filter settings are optimized and denoted as $\left(Z\right)$.

3.1.3. Pilot Insertion and Pulse Shaping

In this phase, the quantum bits were generated from $\left(Z\right)$, and the pilot insertion was carried out in quantum bits, for effective detection of noises during transmission through the channel. The pilots, which are known reference signals, were inserted at regular intervals in the transmission stream to help the estimation of the channel behavior for the receiver. Thus, the pilot-inserted signal is denoted as $\left(\rho \right)$. Following this, the pilot-inserted signal $\left(\rho \right)$ underwent pulse shaping using a Gaussian Filter $\left(GF\right)$ for optimization of the temporal and spectral properties of the signal. The $GF$ smoothed the signal’s transitions, shaping its pulse to reduce high-frequency components and provide better control over its spectrum. For $\left(\rho \right)$, a $GF$ was applied for pulse shaping and is given as follows:

$$\tilde{\rho }=\rho \ast G^{\prime }$$

(14)

$$G^{\prime }={\displaystyle \frac{1}{\sqrt{2\pi {\varpi }^2}}}exp\left({\displaystyle \frac{t^2}{2{\varpi }^2}}\right)$$

(15)

where $\tilde{\rho }$ represents the pulse-shaped signal, $G^{\prime }$ represents the Gaussian function, represents the time variable, $exp$ and $\pi$ are an exponential function and $\pi$ value (constant), respectively, and $\varpi$ represents the width of the pulse.

3.1.4. Modulation

Here, $\tilde{\rho }$ was modulated using Gaussian Modulation $\left(GM\right)$ to transmit the signal through the public channel to the receiver. $GM$, which is commonly used in communication systems to modulate the signal before transmission, was applied to modulate $\tilde{\rho }$ as in the equation:

$${\partial }_{\mathrm{mod}}=\Re .e^{{\displaystyle \frac{m^2}{2h^2}}}\left(cos2\pi r_{c}m+\varphi \right)$$

(16)

Here, ${\partial }_{\mathrm{mod}}$ signifies the modulated signal of $\tilde{\rho }$, ℜ signifies the amplitude of $\tilde{\rho }$, m and h characterize the time variable and standard deviation of the Gaussian pulse, respectively, $r_c$ is the carrier frequency of $\tilde{\rho }$, $\varphi$ represents the phase of $\tilde{\rho }$, and e and cos represent the exponential function and cosine function, respectively.

3.1.5. Channel Authentication

Here, the channel was authenticated following ${\partial }_{\mathrm{mod}}$ using CHMAC-EPQH, to protect the channel from attacks and for secure transmission. The CHMAC-EPQH algorithm was mentioned in Section 3.1.1. The authenticated channel was denoted as $\Omega$.

3.1.6. Link Failure Prediction

This section deals with the use of RDBSCAN in the link failure prediction from $\Omega$, and improvements in the security and prevention of point-to-point failure during transmission. Traditional methods for Density-Based Spatial Clustering of Applications with Noise (DBSCAN) are known for finding intricate patterns in data that could indicate out-of-the-ordinary failure scenarios. However, in high-dimensional spaces, they encounter problems caused by the curse of dimensionality. The DBSCAN technique resolved this problem by utilizing a Radial Basis Function (RBF) kernel. In order to better model non-linear relationships, this function raises the data to a higher dimensional space. The primary points s and $s^{\prime }$ were obtained from $\Omega$. The next step was to use s and $s^{\prime }$ in the calculation of the kernel of the Radial Basis Function.

$$\tilde{R}=exp\left[-\left[{\displaystyle \frac{{\parallel s-s\prime \parallel }^2}{2{\partial }^2}}\right]\right]$$

(17)

Here, $exp$ signifies the exponential function and ∂ signifies the bandwidth parameter. After that, from $\tilde{R}$, Epsilon $(\Phi )$ and MinPts $\left(M_{in}\right)$ are computed. Then, from $(\Phi )$ and $\left(M_{in}\right)$, the core points are formed and are expressed as follows:

$$C_p=\{s,s^{\prime }ϵ\Omega |d(s,s^{\prime })\le \Phi \}$$

(18)

$$C_p\ge M_{in}$$

(19)

The performance of RDBSCAN in link failure prediction is influenced by the choice of two critical parameters: the RBF kernel bandwidth $(\partial )$ and the minimum number of core points $\left(M_{in}\right)$.

The bandwidth parameter ∂ in Equation (17) determines the spread of the radial basis function. A smaller ∂ results in a narrower kernel, which may lead to overly tight clusters and a higher likelihood of identifying noise (false link failures). Conversely, a larger ∂ may over-smooth the feature space and merge distinct failure patterns, potentially reducing sensitivity to localized anomalies. In this study, ∂ was selected empirically based on cross-validation over a subset of the authenticated channel data $\Omega$ to balance specificity and generalization.

Similarly, the value of $M_{in}$ controls the minimum density required to form a cluster. A higher $M_{in}$ increases the robustness of cluster formation by requiring more neighbors to classify a point as a core point, which helps reduce false positives in sparse regions. However, overly high values may cause genuine failure clusters to be missed. Based on empirical testing, $M_{in}$ was set to 5, which provided a good trade-off between accuracy and noise filtering in link failure prediction. Both parameters were fine-tuned to maximize the accuracy of prediction of failure versus non-failure links, evaluated using standard metrics such as precision, recall, and F1-score.

Here, $C_p$ signifies the core points and $(s,s^{\prime })$ embodies the distance between s and $s^{\prime }$. Then, for each core point, a cluster $(\tilde{l})$ is created and the density-reachable points are added recursively to $(\tilde{l})$. This is expressed as follows:

$$\tilde{l}=\left\{C_p\right\}\bigcup \left\{C_p|d(s,s^{\prime })\le \Phi C_p\in M_{in}\right\}$$

(20)

Following the determination of $C_p$ and, $(\tilde{l})$ the final clusters Y predict the condition of the link in $\Omega$.

$$Y=\{\begin{array}{c}\hfill Y^{\prime }\\ \hfill Y^{\prime \prime }\end{array}$$

(21)

Here, $\left(Y^{\prime }\right)$ signifies the link failure and $Y^{\prime \prime }$ signifies no link failure. The algorithm for the RDBSCAN approach is given below (Algorithm 1).

Algorithm 1 RDBSCAN Approach

Input: Authenticated Channel, $\Omega$ Output: Link failure Prediction, Y Begin Initialize s, $s^{\prime }$, $\ddot{q}$ and $\delta$ for each $\Omega$ do      Perform $\tilde{R}=exp\left[-\left[{\displaystyle \frac{{\parallel s-s\prime \parallel }^2}{2{\partial }^2}}\right]\right]$ #Radial Basis Function      Compute $(\Phi )$ and $\left(M_{in}\right)$      Identify the Core points $C_p$      if $C_p$ is identified then           Create $(\tilde{l})$           Add density reachable points      else           Return $C_p$      end if      Iterate until all $(\tilde{l})$ are formed      Obtain Y end for $\mathbf{Return} Y=\{\begin{array}{}{Y}^{\prime }{Y}^{\prime \prime }\end{array}$ End

Therefore, the signal was transmitted to the receiver through the router based on the outcome of Y.

3.2. Receiver

Next, the received signal $\ddot{r}$ underwent channel equalization, the details of which are as follows:

3.2.1. Channel Equalization

Here, the received signal $\ddot{r}$ underwent a channel equalization process using the $R^{2}LMS$ algorithm to compensate for any distortion that occurred in the communication channel. The conventional Least Mean Square (LMS) equalizers had the ability for speedy adaption to fluctuations in the channel. On the other hand, proper tuning of the step size was crucial for the achievement of fast and reliable convergence. However, locating the optimal value was a challenging task. The algorithm had the likelihood of getting stuck in local minima rather than finding the global minimum, especially in complex channel scenarios. Ridge Regularization was used in LMS to overcome this issue. This helped in finding a step size that balanced the convergence speed and stability. Primarily, the weights $\omega$ were updated using Ridge Regularization $\beta$ and expressed as

$$\beta ={\lambda }_{loss}+\chi {\displaystyle \sum _{\tilde{k}=1}^{sp}\parallel {\left(\omega \right)}^2\parallel }$$

(22)

In this context, $\lambda$ represents the loss function for $\ddot{r}$ (received signal), $\chi$ indicates the regularization parameter that governs the weights, $(\tilde{k})$ specifies the index value, and $\left(sp\right)$ refers to the quantity of weight matrices. Subsequently, the LMS algorithm ${\alpha }^{\prime }$ was utilized in the utilization of the channel as follows:

$${\alpha }^{\prime }=w_e+(\tilde{v}\ast \ddot{r}\ast e_{rr})$$

(23)

Here, $e_{rr}$ and $\tilde{v}$ signify the error rate and step size, respectively, and $w_e$ represents the weight (i.e., $w_e\in \beta$). Based on ${\alpha }^{\prime }$, the channel was equalized. Therefore, the equalized channel is denoted as $C^{\alpha }$.

3.2.2. Side Channel Attack Detection

Here, side channel attacks detected from datasets were collected for training the model for attack detection.

• Dataset: First, the input data related to side-channel attack detection were collected. The collected data were represented as follows:

  $$S=\{S_1,S_2,S_3,..,S_{nm}\}$$

  (24)
  Here, $\left(S\right)$ signifies the collected data, and $\left(nm\right)$ represents the total number of data in $\left(S\right)$.
• Pre-Processing: Here, $\left(S\right)$ were pre-processed to augment the quality of the data. Here, the important steps, such as Missing Value Imputation $\left(MVI\right)$, numeralization, and normalization were performed.

  -

  Value Imputation: Here, using the mean formula, the missing values in $\left(S\right)$ were imputed for handling the incomplete information. The missing value imputed data were expressed as

  $${\nu }_{imp}={\displaystyle \frac{\sum S}{nm}}$$

  (25)

  Here, ${\nu }_{imp}$ signifies the missing value imputed data.

  -

  Numeralization: Then, for easier processing and analysis of the data, the values in ${\nu }_{imp}$ were converted into numerical formats. Thus, the numeralized data were obtained and are denoted as F.

• Normalization: The numeralized data F were given as the normalization input for scaling the data to a specific range, typically between 0 and 1 or −1 and 1, based on the minimum and maximum values.

  $$\tilde{F}={\displaystyle \frac{F-F_{min}}{F_{Max}-F_{Min}}}$$

  (26)
  Here, $(\tilde{F})$ signifies the normalized data, and $\left(F_{Min}\right)$ and $\left(F_{Max}\right)$ signify the minimum and maximum values in F, respectively. Thus, the pre-processed data were obtained and denoted as $\left({\varsigma }_{pre}\right)$.
• Feature Extraction: Now, from $\left({\varsigma }_{pre}\right)$, the features were extracted for effective classification of the side-channel attacks. The features of $\left({\varsigma }_{pre}\right)$, such as side-channel attack traces, were extracted and represented as follows:

  $$f^e=\{f_1^e,f_2^e,\dots ,f_g^e\}$$

  (27)
  Here, $\left(f^e\right)$ signifies the features extracted from $\left({\varsigma }_{pre}\right)$, and g signifies the total number of features extracted.
• Classification: The model was trained from $\left(f^e\right)$ with ADS-CNN, to ascertain the presence of a side channel assault. Current Convolutional Neural Networks (CNNs) are seen as proficient in recognizing spatial patterns owing to their convolutional layers, which encapsulate local dependencies and hierarchical feature representations. Nonetheless, the pooling layers in the CNNs diminished the dimensionality of the feature maps by condensing small regions, resulting in the loss of intricate details. Adaptive Depthwise Separable Convolution was employed in the Convolutional Neural Networks to address this issue. This minimized the number of parameters and processing expenses by partitioning the convolution operation into depthwise and pointwise convolutions. When integrated with adaptive mechanisms, this improved the network’s capacity to preserve intricate spatial information and reduced the information loss resulting from pooling layers. Figure 2 presents the ADS-CNN classifier.
• Convolution layer: First, Adaptive Depthwise Separable Convolution was used in the convolutional layer to enhance the network’s ability to retain detailed spatial information and mitigate the loss of information. To start with, depthwise convolution was performed for $\left(f^e\right)$, utilizing the subsequent equation:

  $${\displaystyle \widehat{D}=\sum _{x=0}^{h^{\prime }}\sum _{y=0}^{h^{\prime \prime }}{f}^e(i+x,u+y,q)·B(x,y,q)}$$

  (28)
  Here, $\widehat{D}$ signifies the output of the depthwise convolution, i and u signifies the spatial indices, q signifies the channel index, B denotes the depthwise filter, h and $h^{\prime }$ are the height and width of the filter, respectively, and x and y represent the row and column offsets of the filter, respectively. The pointwise convolution operations $p_t$ were applied to $\widehat{D}$ and are given as follows:

  $${\displaystyle p_t=\sum _{q=0}^{\ddot{q-1}}\widehat{D}.\tilde{B}(0.0,q,\ddot{q})}$$

  (29)
  Here, $\tilde{B}$ signifies the pointwise filter and $\ddot{q}$ signifies the output channel index. After that, the adaptive convolution operation was applied to $p_t$ and is expressed as follows:

  $$\tilde{A}=\sum p_t\ast w(i,u,\ddot{q})$$

  (30)
  Here, $\tilde{A}$ signifies the output of the convolution layer and w signifies the adaptive weights.
• Pooling Layer: Here, the maximum pooling method was applied, considering the parameters. The pooling equation is calculated as follows:

  $${\Psi }_p=max\left(\tilde{A}\right)$$

  (31)
  Here, ${\Psi }_p$ signifies the pooling layer’s output.
• Fully connected layer: Here, the flattening was initially performed using the outcome of the pooling layer to reshape the multi-dimensional input into a one-dimensional vector. The equation of the flattened layer is expressed as follows:

  $$F_l=flat\left({\Psi }_p\right)$$

  (32)
  Here, $\left(F_l\right)$ implies the flattened layer and $\left({\Psi }_p\right)$ implies the flattening of the maximum pooling layer. Lastly, the obtained output given to the Fully Connected Layer (FCL) was derived as follows:

  $$\pi =\left[\sigma \sum F_{\mathit{l}}\ast w^{\ast }\right]+b^{\ast }$$

  (33)
  In this context, $\left(\pi \right)$ denotes the output of the FCL, $w^{\ast }$ and $b^{\ast }$ represent the weight and bias of the FCL, respectively, and $\sigma$ is the sigmoid activation function. The final output was then obtained and is presented as follows:

  $$\widehat{O}=\left(w^{out}\ast \pi \right)+b^{out}$$

  (34)
  Here, $(\widehat{O})$ signifies the output layer outcome, and $w^{out}$ and $b^{out}$ signify the output layer weight and bias. Therefore, the predicted outcome is represented as $\mu$. The algorithm for the ADS-CNN is given as follows (Algorithm 2):
• Comparison with Standard CNN’s: To demonstrate the advantages of the proposed ADS-CNN architecture, we compared it with conventional Convolutional Neural Networks (CNNs) [25,26] in terms of structure and efficiency. Traditional CNNs typically use standard convolution and pooling operations across multiple layers, which often leads to an increased parameter count and computational overhead. In contrast, ADS-CNN incorporates depthwise separable convolutions, which significantly reduce the number of trainable parameters by decomposing standard convolutions into depthwise and pointwise operations. For instance, a conventional CNN with three convolutional layers (kernel size $3\times 3$, stride 1, and 64 filters) has approximately 37% more parameters compared to an ADS-CNN of equivalent depth.
  Furthermore, our ADS-CNN includes adaptive weight mechanisms, where the convolution weights are dynamically adjusted based on input feature characteristics. This contrasts with fixed-weight standard CNNs and improves flexibility in detecting the subtle spatial variations introduced by side-channel attacks. In our implementation, the ADS-CNN architecture uses three convolutional blocks with kernel sizes $3\times 3$, each followed by ReLU activation and max-pooling layers. The adaptive weights $w(i,u,\ddot{q})$ in Equation (30) are updated during backpropagation using standard gradient descent, but are further modulated based on the local entropy features of the input. As a result, ADS-CNN achieves both higher classification accuracy and lower computational cost during training and inference, particularly for embedded or resource-constrained quantum hardware environments.
  The attacked signal $\left(\tilde{\mu }\right)$ was discarded when there was an attack on the signal. With the absence of any attack on the signal, the non-attacked $\left({\mu }^{\prime }\right)$ signal was provided for the quantum state measurement, which is discussed in the following section.

Algorithm 2 ADS-CNN

Input: Feature Extraction, $\left(f^e\right)$ Output: Predicted Outcome, $\left(\mu \right)$ Begin Initialize h,$h^{\prime }$ ,$\ddot{q}$, $w^{\ast }$ and $b^{\ast }$ for each $\left(f^e\right)$ do       # Adaptive Depthwise Separable Convolution       Perform depthwise convolution ${\displaystyle \widehat{D}=\sum _{x=0}^{h^{\prime }}\sum _{y=0}^{h^{\prime \prime }}{f}^e(i+x,u+y,q).B(x,y,q)}$       Apply pointwise convolution ${\displaystyle p_t=\sum _{q=0}^{\ddot{q-1}}\widehat{D}.\tilde{B}(0.0,q,\ddot{q})}$       Compute, $\tilde{A}=\sum p_t\ast w(i,u,\ddot{q})$       Evaluate, $\left({\Psi }_p\right)$       Perform, flattening, $\left(F_l\right)$       Compute, fully-connected layer, $\left(\pi \right)$       Derive, $(\widehat{O})$       Obtain, $\left(\mu \right)$       if (predicated outcome == satisfied) then            Terminate       else            Repeat       end if end for Return $\left(\mu \right)$ End

3.2.3. Quantum State Measurement

Here, quantum state measurement was carried out from $\left({\mu }^{\prime }\right)$ using Heterodyne Detection for the verification of the secret key and extraction of the raw data from the signal received. Heterodyne Detection is an optical and quantum measurement technique used to extract information from a signal by mixing it with a reference signal. This process is used in the conversion of a signal’s frequency into a more easily measurable form, typically through a beat frequency to detect electronic devices. First, $({\mu }^{\prime })$ is mixed with a strong reference signal, which is shown as

$$\widehat{\gamma }(\ddot{t})=u^{\prime }(\ddot{t})·cos({\omega }_I(\ddot{t}))$$

(35)

Here, $\widehat{\gamma }(\ddot{t})$ signifies the output of the mixed-signal and $cos({\omega }_I(\ddot{t}))$ signifies the reference signal at a time $\ddot{t}$. Then, the frequency shifting is carried out in $\widehat{\gamma }(\ddot{t})$ and is given as follows:

$$f^{\prime \prime \prime }(\ddot{t})=\widehat{\gamma }\left(t\right)·e^{y\Psi t}$$

(36)

Here, $f^{\prime \prime \prime }\left(\ddot{t}\right)$ signifies the frequency shifted signal of $\widehat{\gamma }\left(t\right)$, and $\Psi$ signifies the applied frequency shift. Next, the beat frequency is calculated from $f^{\prime \prime \prime }(\ddot{t})$ which provides the phase and amplitude information of the quantum state.

$$V^{\prime }(\ddot{t})=\left[r_e(f^{\prime \prime \prime }(\ddot{t}))\right]$$

(37)

$$\tilde{V}(\ddot{t})=\left[i_m(f^{\prime \prime \prime }(\ddot{t}))\right]$$

(38)

Here, $V^{\prime }(\ddot{t})$ and $\tilde{V}(\ddot{t})$ are the amplitude and phase quadrature, respectively, and $r_e$ and $i_m$ signify the real and imaginary parts of $f^{\prime \prime \prime }(\ddot{t})$, respectively. Therefore, the quantum state helps the verification of the secret key based on $V^{\prime }(\ddot{t})$ and $\tilde{V}(\ddot{t})$. The communication between the transmitter and receiver was established when the secret key was verified and the desired raw data denoted as $Z_{raw}$ were collected.

3.3. Sifting

Here, a sifting operation was performed for both the transmitted signal $T^{rans}$ and the received signal $Z_{raw}$, for the selection and retention of the relevant data. The sifting operation was performed to select and retain the relevant data. A sifting operation is commonly used in signal processing and communication systems like QKD to extract a secure key by discarding irrelevant bits during quantum transmission. The sifting operation was applied to both $T^{rans}$ and $Z_{raw}$ as

$${\varrho }^{\prime }=n^{\prime }(T^{rans},Z_{raw})$$

(39)

Here $\varrho$ signifies the output of the sifted signal and $n^{\prime }$ is the shifting function.

3.4. Error Rate Calculation and Correction

Here, error rate calculation and correction were carried out from ${\varrho }^{\prime }$ using Shannon entropy as an approximation of the Von Neumann Entropy (VNE), followed by Information Reconciliation using Low-Density Parity-Check (IR-LDPC). While the VNE is formally defined using the density matrix of a quantum system, in this context, we adopted the binary Shannon entropy as a practical approximation for quantifying the uncertainty in the measurement outcomes, after the quantum states had been projected into classical bitstrings.

Let the probability of error in ${\varrho }^{\prime }$ be denoted as ${\rho }^{\ast }$. The error in the keys is then calculated using

$$H=-(1-{\rho }^{\ast }){log}_2(1-{\rho }^{\ast })-{\rho }^{\ast }{log}_2{\rho }^{\ast }$$

(40)

Here, H represents the estimated uncertainty. It should be noted that this formulation assumes the error values in the bitstring are statistically independent and valid within that approximation. This entropy estimate is used to guide the subsequent error correction steps.

Here, H denotes the computed error utilizing VNE, and represents the logarithmic function. Following calculation of the error, error repair was executed using Information-Reconciliation-based Low-Density Parity-Check (IR-LDPC). Information reconciliation entailed the employment of classical communication to resolve discrepancies and guarantee the presence of identical keys for both parties. LDPC codes possess superior error-correcting abilities, especially in channels characterized by moderate to high noise levels. Here, H was encoded using the subsequent equation:

$$E_{nc}=H\ast g^{en}$$

(41)

Here, $E_{nc}$ signifies the encoded keys and $g^{en}$ represents the generator matrix. Then, to correct the errors, the decoding process is carried out.

$${\delta }_{corr}={\Psi }^{par}\times {\left(E_{nc}\right)}^{trans}$$

(42)

Here, ${\delta }_{corr}$ signifies the corrected key, ${\Psi }^{par}$ signifies the parity check matrix, and ${\left(E_{nc}\right)}^{trans}$ characterizes the transpose of $E_{nc}$.

3.5. Privacy Amplification and Key Authentication

Lastly, block-based privacy amplification and key authentication were performed from ${\delta }_{corr}$, using Block-CHMAC-EPQH (B-CHMAC-EPQH) to enhance the security of the key and ensure the extracted key’s integrity and correctness. The CHMAC-EPQH algorithm is mentioned in Section 3.1.1. Thus, the privacy amplification and key authentication of ${\delta }_{corr}$ were carried out successfully. The performance of the proposed research methodologies is discussed in the section that follows.

4. Results and Discussions

All tests were conducted using the freely accessible AES HD Dataset, which contains more than 50,000 coherent-state transmissions modulated by Gaussian noise and recorded under 10 different channel-loss profiles. The original quadrature pairs (X and P) were taken straight from the HDF5 archives of the dataset. They were then adjusted to have unit shot-noise variance and divided into blocks of $1\times {10}^4$ samples for each loss level. Extra noise (0.01 SNU) was introduced in accordance with the meta data of the dataset, with the modulation variance swinging from 0.5 to 5 SNU for each block, while the channel transmissivity was stepped up from 0.1 to 0.8. A reconciliation efficiency above 90% was achieved by passing the empirical measurement vectors that were generated through an information-reconciliation module created by the researcher, which was constructed with CVXOPT’s interior-point solver based on convex optimization and privacy amplification.

4.1. Dataset Description

The Advanced Encryption Standard High-Definition (AES-HD) dataset was used in this study for testing the efficacy of the proposed approach. The AES-HD dataset consists of 100 traces and 1250 maximum features. The source URL is provided in the reference section, and 80% (79,996) is allocated for training on the basis of the comprehensive data, while 20% (19,999) is designated for testing.

4.2. Performance Analysis

Here, the proposed framework’s performance is analyzed and compared with the existing works.

• Performance analysis for system parameter optimization: Evaluation of the performance of the proposed 2-EHRIO was carried out against the existing Elk Herd Optimizer (EHO) [27], which is a swarm-based metaheuristic inspired by the elk’s natural breeding behavior, which includes two separate seasons: rutting (mating competition) and calving (offspring dispersal). During the rutting season, the population was divided into families led by dominating “bulls”, with fitter solutions forming larger harems, encouraging intensification in high-quality areas. During the calving season, “offspring” solutions were distributed randomly throughout the search space, increasing variation. At each iteration, the EHO switched between these two phases—family formation and offspring dispersal—using simple separation and regrouping operators to maintain a dynamic balance of exploration and exploitation. Shark Smell Optimization (SSO) [28] treats each potential solution as a “shark” that detects an abstract “odor” field determined by the objective function, simulating a shark’s olfactory hunting. In each iteration, sharks conduct a rotational local search using sampling points surrounding their new locations to select prospective regions, following the performance of a smell-driven global search in which they update their positions and velocities in the direction of the increasing odor concentration. SSO can effectively navigate complicated, multimodal landscapes with very simple updating algorithms thanks to key control factors that manage to balance between exploration and exploitation, such as the rotation radius, forward step size, and scent sensitivity coefficient.
  Another approach using a population-based metaheuristic similar to the predatory tendencies of antlions is called the Ant Lion Optimizer (ALO) [29]. Within a search space, each candidate solution (referred to as a “ant”) conducts a stochastic random walk. Selected elite solutions (referred to as “antlions”) efficiently trap and direct these walks by establishing dynamic probabilistic limits. Ants explore globally in each iteration by accruing random steps that are bounded by the current “trap” of an antlion. The search is then concentrated locally by updating antlion placements based on the fittest ants found. ALO is well-suited for adjusting Continuous-Variable QKD parameters, such as modulation variance, reconciliation efficiency, and privacy-amplification settings, to maximize the secret-key rate under realistic channel conditions, in view of its alternating exploration–exploitation scheme, which strikes a balance between intensification and diversification. The Crow Search Algorithm (CSA) [30] is a population-based metaheuristic built on the modes hiding food by error, followed by finding it again. Each “crow” in the community is used as a possible solution and remembers where it hid the food. Crows explore the search space by taking random walks that are affected by two important factors: flight length (step size) and awareness probability (chance of being followed). The crow improves its own memory when it finds a better place to hide (food cache). This maintains the balance between intensification (by taking advantage of known good positions) and diversification (by exploring at random). This easy-to-use but effective system makes CSA a good choice for fine-tuning CV-QKD parameters like modulation variance, reconciliation efficiency, and privacy-amplification settings, to obtain the highest secret-key rates in real-world channel conditions.
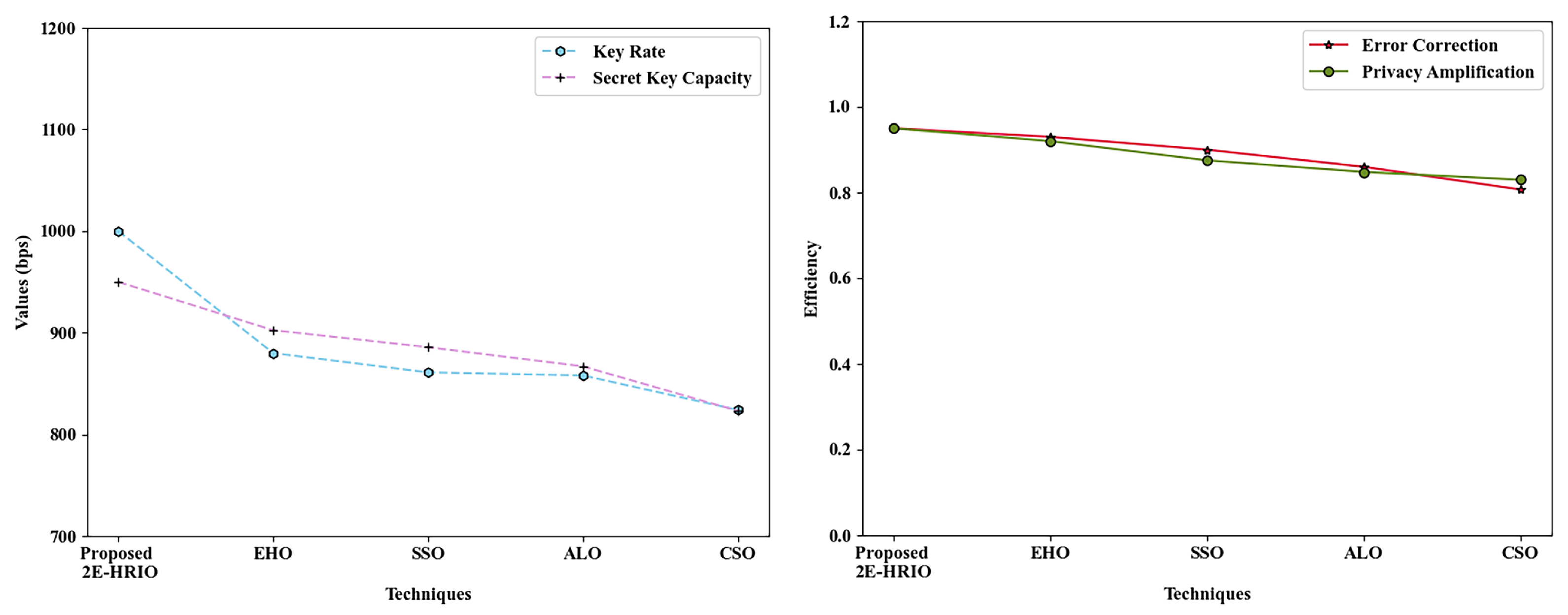
  Figure 3a,b illustrate the key rate, Secret Key Capacity, Error Correction, and Privacy Amplification analysis of both the proposed and existing methodologies for system PO. The suggested 2-EHRIO attained a key rate and secret key capacity of 1000 bits per second (bps) and 950 bps, respectively, demonstrating superior performance relative to the existing approaches, as illustrated in Figure 3a. In Figure 3b, the suggested 2-EHRIO achieved a superior efficiency in error correction (0.95) and privacy amplification (0.95). Concurrently, the current methodologies, specifically EHO, SSO, ALO, and CSO, achieved diminished efficiencies, with error corrections of 0.93, 0.90, 0.86, and 0.80, respectively. The current algorithms showed inferior efficiencies in privacy amplification relative to the suggested technique. The improved performance of 2-EHRIO was due to the implementation of Elitist Random Immigrants within the EHO algorithm. Consequently, the proposed model effectively optimized the system parameters within the CV-QKD system.
• Performance analysis for side-channel attack detection: Here, the analysis of ADS-CNN was performed using an existing CNN, Gated Recurrent Unit (GRU), Long Short Term Memory (LSTM), and Deep Neural Network (DNN).
  Table 2. Accuracy and sensitivity analysis.

  Methods	Accuracy (%)	Sensitivity (%)
  Proposed ADS-CNN	99.05	99.07
  CNN	97.82	97.74
  GRU	94.15	94.05
  LSTM	92.47	92.41
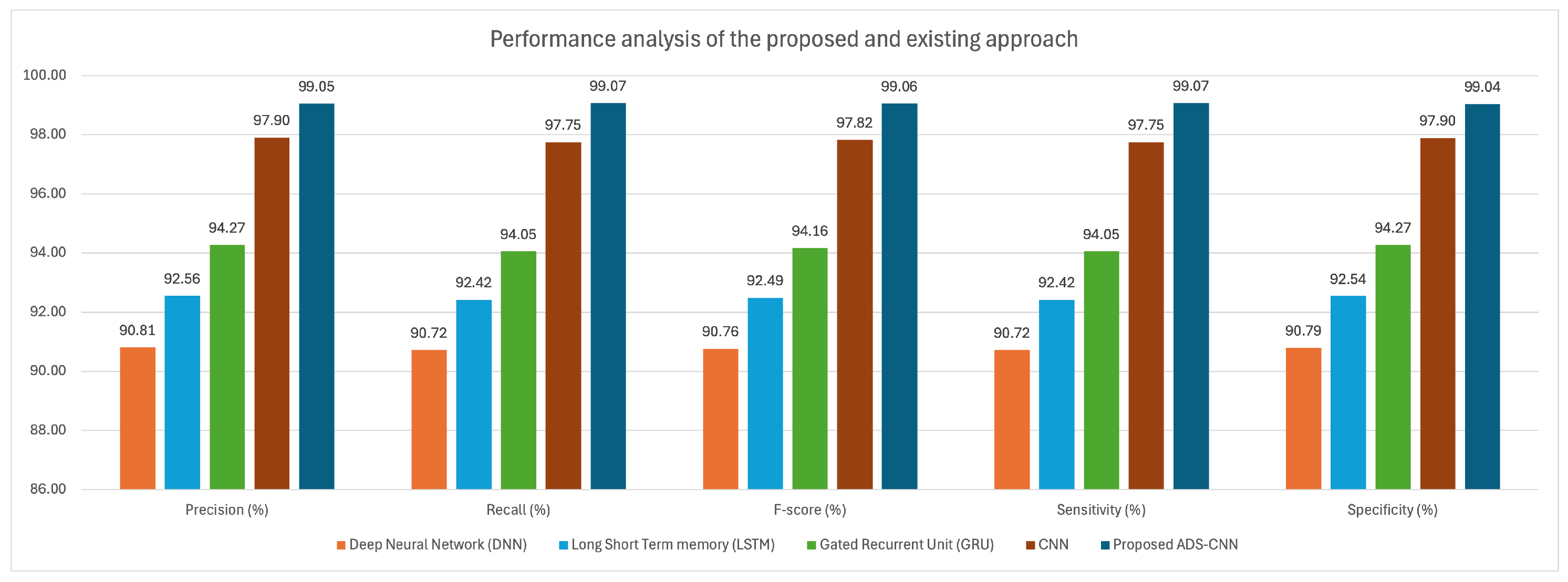
  DNN	90.75	90.71

  illustrates the performance of the proposed ADS-CNN regarding accuracy and sensitivity. The proposed ADS-CNN attained an accuracy of 99.05% and a sensitivity of 99.07%. However, in comparison to the proposed methodology, the accuracy and sensitivity of the existing methods, including CNN, GRU, LSTM, and DNN, were inferior. Consequently, the proposed methodology accurately anticipated the side-channel attacks.
  The suggested ADS-CNN was compared to the baseline CNN, GRU, LSTM, and DNN models in terms of specificity, recall, F1-score, and precision (Figure 4). As demonstrated, ADS-CNN attained much higher levels of accuracy (99.04% precision, 99.997% recall, 99.55% F1-score, and 90.04% specificity) compared to the baselines (93.88% precision, 93.73% recall, 93.8% F1-score, and 93.87% specificity). This improvement in performance was due to the incorporation of adaptive depthwise separable convolutions, which enhanced discriminative feature extraction and decreased parameter redundancy, leading to higher accuracy and resilient classification of side-channel attacks.
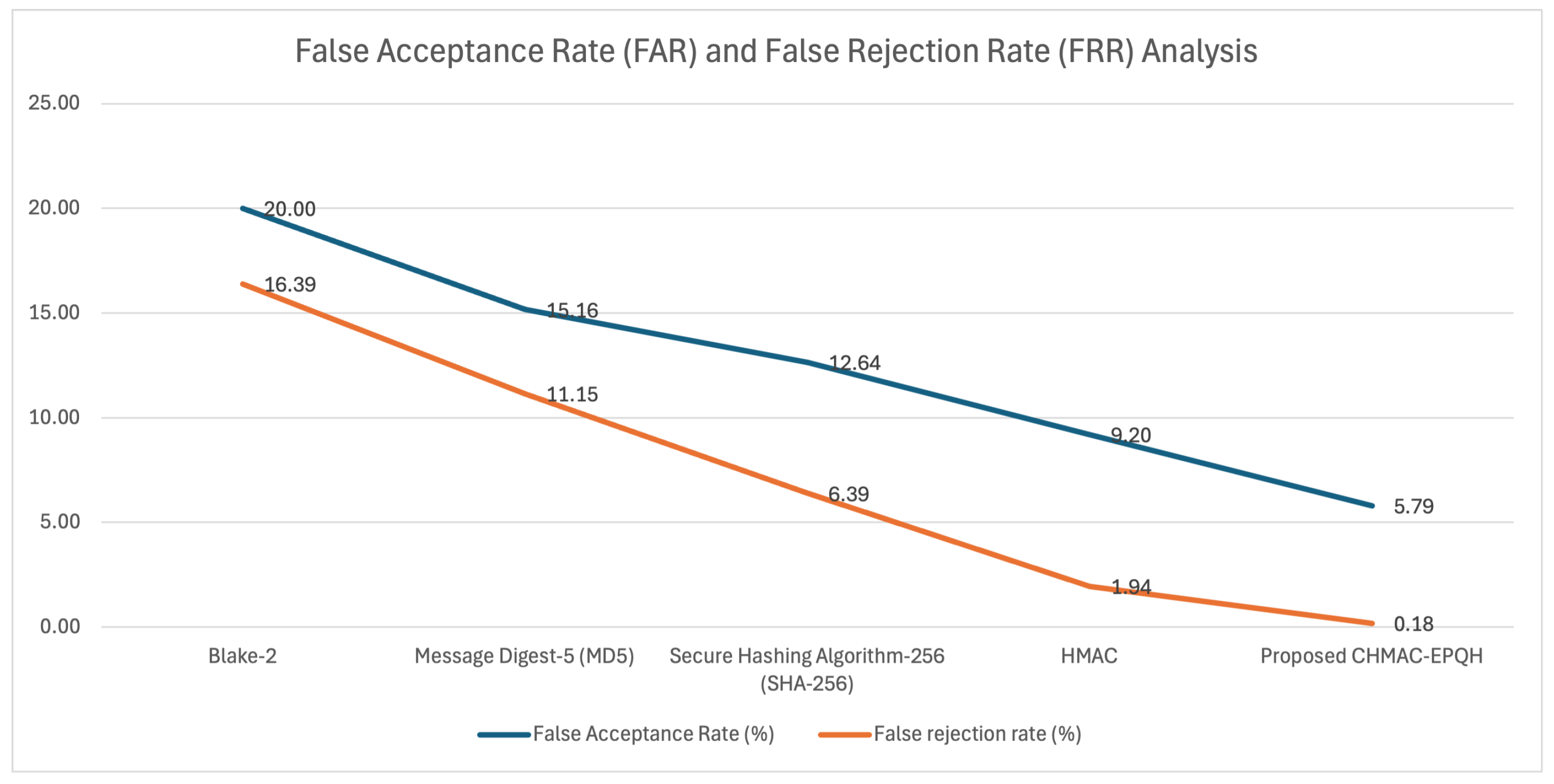
• Performance analysis for authentication: Here, analysis of the proposed CHMAC-EPQH’s performance was performed using the prevailing HMAC, Secure Hashing Algorithm-256 (SHA-256), Message Digest-5 (MD5), and Blake2.
  Figure 5 illustrates the performance of the proposed CHMAC-EPQH in authentication, specifically for the False Acceptance Rate (FAR) and False Rejection Rate (FRR). Regarding FAR and FRR, the proposed approach achieved 5.794% and 0.1751%; while, the existing methods, such as HMAC, SHA-256, MD5, and Blake2 exhibited higher values, indicating poor performance when compared to the proposed method. The suggested method’s enhanced performance resulted from the incorporation of compression and encoding processes within the HMAC algorithm. Consequently, the CHMAC-EPQH showed proficiently authentication of both the device and the communication channel.
• Performance analysis for link failure prediction: Here, the proposed RDBSCAN’s performance was compared against the prevailing DBSCAN, K-Means Clustering (KMC), Affinity Propagation (AP), and Gaussian Mixture Model (GMM). The performance analysis of the suggested RDBSCAN, focusing on clustering time and Jaccard Index, is illustrated in

  Table 3. Clustering time and Jaccard index analysis.

  Techniques Approach	Clustering Time (s)	Jaccard Index
  Proposed RDBSCAN	0.005994	0.543541
  DBSCAN	0.0060	0.53861
  KMC	0.01100	0.533327
  AP	0.02248	0.431435
  GMM	0.50199	0.424038

  . The proposed technique required a minimum clustering duration of 0.005994 s. The existing approaches, specifically DBSCAN, KMC, AP, and GMM, recorded maximum clustering times of 0.0060 s, 0.01100 s, 0.02248 s, and 0.50199 s, respectively. Similarly, the proposed RDBSCAN attained a superior Jaccard Index of 0.543541. However, in comparison to the proposed strategy, the previous algorithms achieved a diminished Jaccard Index. The improved performance of the proposed technique was due to the utilization of the Radial Basis Function (RBF) kernel within the DBSCAN framework. Consequently, the suggested methodology accurately anticipated the connection failures inside the authenticated channel of the transmission process. Incorporation of RDBSCAN into the link-failure detection pipeline was justified by the marked improvement in the Jaccard Index. This was due to the overlapping of RDBSCAN’s high overlap with true failure events, minimizing false alarms and missed detections, and allowing for more reliable, fully automated channel maintenance in CV-QKD systems.
• Performance analysis for channel equalization: The performance of the proposed $R^{2}LMS$ was evaluated using known methods: LMS, Normalized Least Mean Square (NLMS), Recursive Least Squares (RLS), and Kalman Filter (KF).

  Table 4. SNR and BER analysis.

  Techniques	SNR (dB)	BER
  Proposed $R^{2}LMS$	53.658	0.00713
  LMS	48.599	0.00955
  NLMS	46.53661447	0.01116
  RLS	44.76138179	0.01630
  KF	42.95629554	0.01947

  presents the performance analysis of the proposed and current approaches based on SNR and BER values. The proposed method attained a markedly enhanced SNR of 53.65 dB and a diminished BER of 0.00713, indicating a higher efficacy compared to the current methodologies. However, the current methodologies, including LMS, NLMS, RLS, and KF, achieved diminished SNR and elevated BER, indicating suboptimal performance in channel equalization. The performance enhancement with the proposed method was due to the application of Ridge Regularization in the LMS technique, hence improving channel equalization.

4.3. Comparative Analysis

The efficacy of the planned research was evaluated against existing studies.

Table 5. Comparative analysis of the proposed research with existing research works.

	Methods	Accuracy (%)
	Convolutional Neural Network (CNN)	98.7
	Residual Network (ResNet)	84.63
	EfficientNet-B7	85.01
	Random Forest (RF)	98.15
	CNN	88.17
	ADS-CNN	99.05

shows a comparison and contrast between the proposed method and current works, displaying the results of the analysis based on accuracy. The proposed method allowed the attainment of a greater level of accuracy, which was 99.05%, in comparison to the approaches that were previously used. This was owing to the consideration of system parameter optimization using 2E-HRIO, side channel attack detection using ADS-CNN, authentication using CHMAC-EPQH, and link failure prediction using RDBSCAN, meaning the proposed methodology was able to achieve a higher level of performance. On the other hand, the currently available technologies, such as CNN, Forest, ResNet50, and EfficientNet-B7, achieved lower levels of accuracy. In general, the proposed methodology was successful in providing an effective continuous-variable quantum key distribution, together with parameter optimization and detection of side attacks.

5. Conclusions

The proposed methodology demonstrated the effectiveness of a continuous-variable quantum key distribution (CV-QKD) framework enhanced by parameter optimization and security enhancement mechanisms. The Elitist Elk Herd Random Immigrants Optimizer (2E-HRIO) successfully tuned the system parameters, achieving a key generation rate of 1000 bits per second and a secret key capacity of 950 bits per second. This outperformed recent works such as [16] (key rate: 812 bps) and [18] (key rate: 860 bps), illustrating the efficiency of our approach.

For side-channel attack detection, the proposed Adaptive Depthwise Separable Convolutional Neural Network (ADS-CNN) achieved an accuracy of 99.05% and a recall of 99.07%, which provides significant improvements over baseline CNN classifiers used in prior studies. Additionally, the CHMAC-EPQH-based device authentication mechanism attained a low False Acceptance Rate (FAR) of 5.794% and False Rejection Rate (FRR) of 0.1751%, demonstrating robust security performance.

Future work will focus on validating the proposed framework in long-distance transmission scenarios, improving its resilience under high-loss channels. Furthermore, integration with experimental quantum hardware and real-time side-channel attack simulation environments will be explored to test deployment feasibility in practical settings.