A UAV Trajectory Optimization and Task Offloading Strategy Based on Hybrid Metaheuristic Algorithm in Mobile Edge Computing

Abstract

In the UAV-assisted mobile edge computing (MEC) communication system, the UAV receives the data offloaded by multiple ground user devices as an aerial base station. Among them, due to the limited battery storage of a UAV, energy saving is a key issue in a UAV-assisted MEC system. However, for a low-altitude flying UAV, successful obstacle avoidance is also very necessary. This paper aims to maximize the system energy efficiency (defined as the ratio of the total amount of offloaded data to the energy consumption of the UAV) to meet the maneuverability and three-dimensional obstacle avoidance constraints of a UAV. A joint optimization strategy with maximized energy efficiency for the UAV flight trajectory and user device task offloading rate is proposed. In order to solve this problem, hybrid alternating metaheuristics for energy optimization are given. Due to the non-convexity and fractional structure of the optimization problem, it can be transformed into an equivalent parameter optimization problem using the Dinkelbach method and then divided into two sub-optimization problems that are alternately optimized using metaheuristic algorithms. The experimental results show that the strategy proposed in this paper can enable a UAV to avoid obstacles during flight by detouring or crossing, and the trajectory does not overlap with obstacles, effectively achieving two-dimensional and three-dimensional obstacle avoidance. In addition, compared with related solving methods, the solving method in this paper has significantly higher success than traditional algorithms. In comparison with related optimization strategies, the strategy proposed in this paper can effectively reduce the overall energy consumption of UAV.

1. Introduction

As mobile edge computing (MEC) resources are integrated into a unified resource pool and different edge facilities work together, MEC, as an important complement to edge computing, is gradually being more widely used [1]. Unlike traditional fixed edge nodes, MEC provides flexible computing support through mobile devices or nodes, suitable for environments with dynamic network conditions or imperfect infrastructure, especially for future 6G network integrated communication, computing, and caching (3C) [2], such as intelligent transportation, augmented reality, and unmanned aerial vehicle (UAV) communication [3,4].

UAVs have the characteristics of flexible deployment, strong maneuverability, and efficient line-of-sight communication. By integrating computing resources on UAVs, they can achieve efficient computing task assistance processing for terminal devices, reduce system latency, and improve overall energy efficiency [5]. They are an ideal solution for dealing with environments with limited or missing infrastructure, such as military, rescue, and emergency response. At present, UAVs mainly act as air data relays, mobile access points and temporary base stations in MEC network systems. Due to the limited battery storage of a UAV, energy saving is a key issue in a UAV-assisted MEC system. However, for a low-altitude flying UAV, successful obstacle avoidance is also very necessary. Regardless of its form, its flight trajectory is related to the energy consumption and latency of the network and directly affects computing efficiency and the quality of service. In this context, ways to optimize the flight trajectory of UAVs and offload computing tasks reasonably have gradually become a hot topic in academia and industry research.

This paper focuses on a UAV-assisted MEC network system, which provides flexible communication services for multiple ground user devices at different heights in a complex three-dimensional (3D) obstacle environment by carrying caching and computing resources on the UAV as an aerial base station.

The main contributions of this paper are summarized as follows:

(1)

We study the MEC model for receiving data offloaded from multiple ground mobile devices in a single UAV multi-user scenario in 3D space, satisfying the constraints of UAV maneuverability and obstacle avoidance. We propose a joint optimization strategy with maximized energy efficiency (OPMEE) for the UAV flight trajectory and user device task offloading rate.

(2)

To solve this problem, hybrid alternating metaheuristics for energy optimization (HAMEO) are given. Firstly, the Dinkelbach method is used to transform the nonlinear fractional programming problem into a corresponding parameter optimization problem. Then, it is divided into two sub-optimization problems, which are alternately optimized using an improved genetic algorithm and the Arctic puffin algorithm.

(3)

The experimental results show that the strategy proposed in this paper can enable a UAV to avoid obstacles during flight by detouring or crossing, and the trajectory does not overlap with obstacles, effectively achieving two-dimensional and three-dimensional obstacle avoidance. In addition, compared with related solving methods, the solving method in this paper has significantly higher success than traditional algorithms. In comparison with related optimization strategies, the strategy proposed in this paper can effectively reduce the overall energy consumption of a UAV.

The organizational structure of this paper is as follows: Section 2 reviews related works. Section 3 gives the system model and problem description. Section 4 solves optimization problems. Section 5 presents the experimental results and analysis. Finally, we summarize the paper and provide prospects for further work in Section 6.

2. Related Works

In recent years, the application of UAV technology in the field of MEC has become increasingly widespread. More research works focus on key issues such as UAV trajectory optimization, resource scheduling, and computation offloading:

(1)

UAV trajectory optimization. The authors in [6] proposed a reinforcement learning (RL) solution acceleration framework based on an incomplete information communication model and quadcopter UAV energy consumption model, and they designed two responsive UAV trajectory planning algorithms to achieve energy consumption optimization. In [7], the authors proposed a three-layer integrated vehicle networking-based UAV-assisted MEC architecture, which optimizes the trajectory of the UAV, while satisfying the constraints of the evolution law of the vehicle energy consumption state, and maximizes the total system utility. In [8], Lu W. et al. proposed a secure communication scheme for a dual UAV MEC system based on successive convex approximation and block coordinate descent, effectively planning the UAV flight trajectory to maximize the user’s minimum secure computing capability. In [9], Abdel-Basset M. et al. proposed multiple multi-objective trajectory planning algorithms based on metaheuristic algorithms and Pareto optimality theory, which accurately plan the trajectory of UAVs to minimize the energy consumption of data transmission and UAV flight in IoT devices. In [10], the authors considered the deadline for completing tasks for ground users and proposed an offline optimal trajectory design algorithm and an online approximation algorithm suitable for multiple flight scenarios. By optimizing the number of flights and flight trajectories, the energy consumption of UAVs is minimized to the greatest extent possible. A low-complexity UAV trajectory prediction and vehicle selection method is proposed using federated learning, which exploits related information from past trajectories in [11]. In [12], the authors proposed an energy-aware grid-based solution for obstacle avoidance.

(2)

Resource scheduling and computation offloading. The authors aimed to minimize the total power and adopted centralized multi-agent algorithms and federated multi-agent RL algorithms to handle resource allocation and power control problems in the system in [13]. In [14], Ren Y. et al. proposed two offloading schemes based on game theory with the objectives of minimizing computation time and energy consumption, and they successfully determined the optimal offloading ratio. Li J. et al. [15] considered the energy limitation of UAVs and proposed a hybrid approach based on semi-Markov decision processes and deep reinforcement learning (DRL) with the goal of maximizing user task transfer throughput. Tian X. Z. et al. [16] aimed to reduce system energy consumption under latency constraints, and they designed a two-layer iterative algorithm based on a genetic algorithm framework to maximize system energy efficiency by optimizing service caching mechanisms, computation offloading strategies, and resource allocation methods. Wang S. et al. [17] proposed a collaborative multi-agent DRL framework that uses Markov decision processes to optimize the computation offloading strategy of UAVs, and they achieved system latency minimization and fairness between ground terminals. Liu Z. R. et al. [18] applied the idea of cooperative transmission to improve channel conditions and maximized computing efficiency (CE) by using reconfigurable intelligent surfaces (RISs) in MEC.

(3)

In addition to the research on specific issues mentioned above, there are also many studies that jointly optimize UAV trajectories, resource scheduling, and computation offloading. Hu J. et al. [19] proposed an offloading scheme based on near-end strategy optimization to minimize task processing latency, which synergistically optimizes the flight trajectory, task offloading rate, and communication resource allocation of UAVs. Li W. T. et al. [20] considered delay-sensitive tasks and proposed a solution scheme based on the block coordinate descent method to jointly optimize the UAV trajectory, resource allocation, and offloading decisions, which minimized the total energy consumption of the equipment. In [21], UAVs were used as air data relays, and a heuristic algorithm based on particle swarm optimization was proposed to minimize the execution time of user offloading tasks by jointly optimizing the UAV’s task scheduling and flight trajectory. Yang Z. et al. [22] proposed a UAV-assisted edge computing framework based on artificial intelligence and non-orthogonal multiple access, which minimized transmission delay and power consumption by jointly optimizing UAV deployment and resource allocation. Zhang Y. et al. [23] proposed a joint dynamic programming and bidding algorithm with the goal of maximizing the minimum secure computing capability of dynamic end users, through joint optimization of UAV offloading decisions, resource allocation, and trajectory planning. Zeng Y. P. et al. [24] proposed a two-stage dynamic optimization method based on Lyapunov optimization theory, which minimized the comprehensive energy consumption of the system by jointly optimizing task offloading, communication resource allocation, and the UAV 3D trajectory. Chen Y. et al. [25] propose a solution based on deep reinforcement learning for the optimization of UAV trajectories and resource allocation problems, which minimizes the energy consumption of mobile users under the constraints of system performance and UAV energy. Pervez F. et al. [26] proposed an alternating iterative method based on block descent in a multi-UAV-assisted network, which minimized the cost function based on energy and delay by jointly optimizing task offloading and MEC server selection decisions, transmission power, flight trajectory, and CPU frequency allocation.

Based on the analysis of the existing literature, the following problems still exist in the research on UAV-assisted MEC:

(1)

Most of the above studies are based on the premise that user devices are in the same plane, UAVs are flying at a fixed altitude, and the scene environment is naturally open. However, in the practical application of UAV-assisted edge computing, especially in complex scenes such as emergency rescue, the environmental conditions are complex and changeable, and key factors such as obstacles and user positions in 3D space need to be further considered.

(2)

The current research on performance indicators mainly focuses on latency, throughput, power, flight time, and energy consumption, and most of them are single or simply weighted. To improve system performance, the intrinsic correlation between multiple performance indicators in the MEC model can be comprehensively considered and jointly optimized.

(3)

Although traditional convex optimization methods are effective in simplifying models, the number of system variables increases and the complexity of the problem significantly increases in large-scale application scenarios. At this point, traditional convex optimization methods will no longer be applicable, and more advantageous metaheuristic algorithms can be considered for the solution.

3. System Model and Problem Description

The UAV-assisted MEC system model studied in this paper is shown in Figure 1. The system architecture $U(u=\mathrm{1,2},\dots ,U)$ consists of a UAV equipped with high-performance edge servers and user devices distributed at different height levels, with $K(k=\mathrm{1,2},\dots ,K)$ high-threat obstacles present in the scene. The UAV takes off from its initial position to perform communication service tasks. During the flight, it needs to dynamically avoid obstacles and provide stable communication service support for user devices. After completing the service period, the UAV returns to its initial position for energy supply. The user device adopts a partial offloading strategy, offloading some tasks to the UAV edge server for processing, while the remaining tasks are retained for local execution.

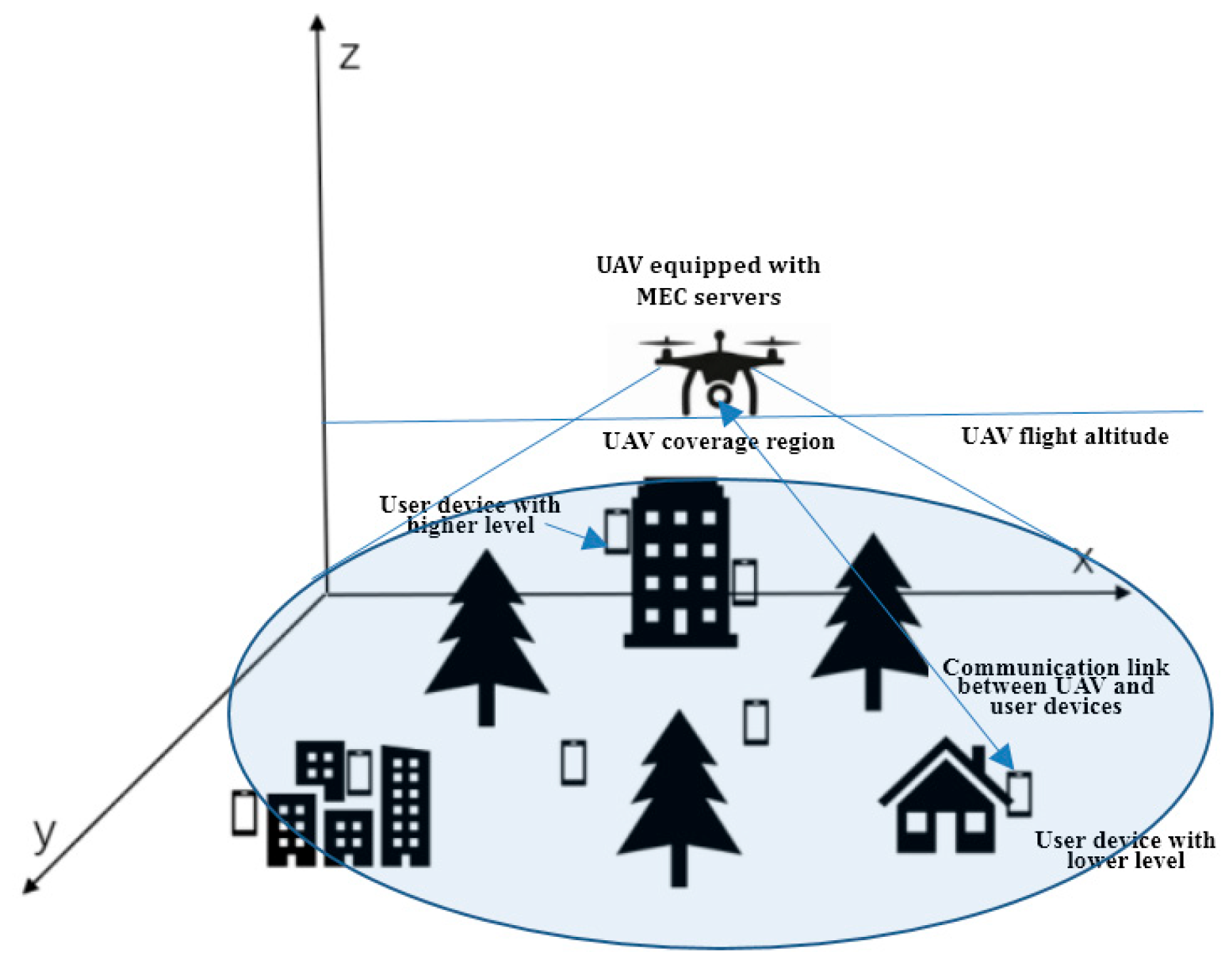
3.1. Network Model

To achieve discretization of continuous UAV trajectories, the UAV flight service period is $T_f$ divided into N equally long time slots, with each slot being longer ${\delta }_t={\displaystyle \frac{T_f}{N}}$.

In the 3D Cartesian coordinate system, the flight altitude of the UAV is denoted as $h_{\left(t\right)}$ in a time slot $t\in \{\mathrm{1,2},\dots ,N\}$, and its projection coordinates $q_{\left(t\right)}$ in the horizontal plane are represented as $\left[x_{\left(t\right)},y_{\left(t\right)}\right]$, while its position coordinates $c_{\left(t\right)}$ in 3D space are represented as $\left[q_{\left(t\right)},h_{\left(t\right)}\right]$.

Due to the need for the UAV to return to the starting point after the service period ends, its trajectory must meet periodic constraints:

$$c_{\left(1\right)}=c_{\left(n\right)}$$

(1)

In addition, during the flight of a UAV, the flight altitude $h_{\left(t\right)}$, flight speed $v_{\left(t\right)},$ and flight acceleration $a_{\left(t\right)}$ are, respectively, constrained by its maximum flight altitude $h_{max}$, maximum flight speed $v_{max},$ and maximum flight acceleration $a_{max}$.

$$h_{\left(t\right)}\le h_{max}$$

(2)

$$v_{\left(t\right)}={\displaystyle \frac{\left|c\left(t+1\right)-c\left(t\right)\right|}{{\delta }_t}}\le v_{max}$$

(3)

$$a_{\left(t\right)}={\displaystyle \frac{\left|v\left(t+1\right)-v\left(t\right)\right|}{{\delta }_t}}\le a_{max}$$

(4)

If the 3D coordinates $w_u$ of user device u are $\left[x_u,y_u,z_u\right]$, then the distance between the UAV and the u-th device is $d_u\left(t\right),$ represented as ${‖w_u-c_{\left(t\right)}‖}_2$.

To simplify the analysis, this paper models obstacles using a cylinder. The center coordinates $o_k$ of the k-th obstacle are $\left[x_k,y_k\right]$, the radius is $r_k$, and the height is $l_k$. To ensure the safety of UAV flight, obstacle avoidance constraints can be decomposed into horizontal and vertical constraints:

$${|q}_{\left(t\right)}-o_k|\ge r_k+d_{safe}$$

(5)

$$h\left(t\right)\ge l_k+d_{safe}$$

(6)

where $d_{safe}$ is the preset safety margin. In a 3D environment, UAVs only need to choose between vertical crossing and horizontal circling to smoothly avoid obstacles. Therefore, combining the above two constraints produces

$$\left[{|q}_{\left(t\right)}-o_k|\ge r_k+d_{safe}\right]\left|\right|\left[h\left(t\right)\ge l_k+d_{safe}\right]$$

(7)

3.2. Communication Model

For complex communication environments with obstacles, we use the Rayleigh fading channel model to characterize the wireless channel characteristics between UAVs and user devices, while considering the large-scale path loss determined by the propagation distance and the small-scale signal fading caused by multipath effects (including reflection, refraction, and scattering phenomena caused by obstacles). The channel gain between user devices and UAVs is expressed as

$$h_u\left(t\right)=\sqrt{{\beta }_{u\left(t\right)}}{g}_u\left(t\right)=\sqrt{{{\beta }_0{d}_{u\left(t\right)}}^{-\alpha }}{g}_u\left(t\right)=\sqrt{{{\beta }_0|w_u-c_{\left(t\right)}|}^{-\alpha }}{g}_u\left(t\right)$$

(8)

where ${\beta }_{u\left(t\right)}$ is the large-scale average channel power gain, ${\beta }_0$ is the reference channel gain when the distance between the sender and receiver is 1 m, and α is the path loss index. The small-scale fading coefficient $g_u\left(t\right)$ is represented as follows:

$$g_u\left(t\right)=\sqrt{{\displaystyle \frac{k_u\left(t\right)}{k_u\left(t\right)+1}}}g+\sqrt{{\displaystyle \frac{1}{k_u\left(t\right)+1}}}\tilde{g}$$

(9)

where $g$ is the line-of-sight component and |$g$|=1, $\tilde{g}$ is a Gaussian random variable, and $k_u\left(t\right)$ is the Rayleigh factor:

$$k_u\left(t\right)=K_1{e}^{K_2{\theta }_u\left(t\right)}$$

(10)

In (10), K₁ and K₂ are environmental coefficients, and ${\theta }_u\left(t\right)$ are the elevation angles between the user equipment u and the UAV in time slot t, expressed as

$${\theta }_u\left(t\right)=\mathit{arcsin}[\left(h\left(t\right)-z_u\right)/d_u\left(t\right)]$$

(11)

As can be seen from the above, the achievable rate between user equipment u and the UAV in time slot t can be expressed as

$$R_u\left(t\right)=B_u(t){1\mathrm{o}\mathrm{g}}_2[1+{\displaystyle \frac{{\left|h_u\left(t\right)\right|}^2{p}_u(t)}{{\sigma }^2\Gamma }}]$$

(12)

where $B_u\left(t\right)$ and $p_u\left(t\right),$ respectively, represent the bandwidth between the u-th user device and the UAV in time slot t, as well as the transmission power when the user device offloads tasks to the UAV. ${\sigma }^2$ is the noise power, and $\Gamma >1$ represents the signal-to-noise ratio (SNR) difference between the theoretical Gaussian signal and the actual modulation and coding scheme.

3.3. Offloading Model

Due to the relatively small amount of data offloading from the UAV to user devices, the delay can be ignored. We consider offloading transmission delay in the UAV-assisted MEC system. We adopt the TDMA protocol for the data offloading of the active user devices. Each user device can transmit data in its own time slot, and thus the interference among different devices can be ignored. The UAV flight service period is $T_f$ divided into N equally long time slots, with each slot being longer ${\delta }_t$. For simplicity, suppose N = k, and the t-th time slot is allocated to the u-th user device for data offloading.

The amount of data that the user device u needs to process in time slot t is defined as $l_u\left(t\right)$. Due to local computing limitations, user devices need to offload some tasks to the UAV for processing. The task offloading rate is denoted as ${\eta }_u\left(t\right)$ and ${\eta }_u\left(t\right)\in \left(\mathrm{0,1}\right)$. The amount of task data requested for processing by user device u in time slot t is

$$I_u\left(t\right)=l_u\left(t\right){\eta }_u\left(t\right)$$

(13)

The offloading bandwidths obtained by the user device u at time slot t is denoted as $b_u\left(t\right)$. Let $B_u\left(t\right)$ denote the total offloading bandwidth capacity in the system. The allocation of bandwidth needs to meet the constraints denoted by (14):

$${\sum }_{t=1}^N{b}_u\left(t\right)\le B_u\left(t\right)$$

(14)

3.4. Energy Consumption Model

System energy consumption includes user device energy consumption and UAV energy consumption, among which UAV energy consumption consists of four parts: flight energy consumption, task receiving energy consumption, computing and processing energy consumption, and communication energy consumption. Due to the magnitude difference between user device energy consumption and UAV energy consumption, this paper only considers the top three types of energy consumption components in UAV energy consumption that are most affected by flight trajectory and offloading data.

The amount of data that the user device needs to process in time slot t is defined as $l_u\left(t\right)$, where the number of CPU cycles required for processing each bit of data is $C_u$. Due to local computing limitations, user devices need to offload some tasks to the UAV for processing. $f$ represents the computing capability of the UAV.

The energy consumption of UAVs receiving pending tasks sent by user devices is

$$E_u^{rec}(t)={\displaystyle \frac{p_u\left(t\right)l_u\left(t\right){\eta }_u\left(t\right)}{R_u\left(t\right)}}$$

(15)

UAVs calculate the energy consumption of the tasks they receive:

$$E_u^{comp}\left(t\right)=l_u\left(t\right){\eta }_u\left(t\right)C_u{f}^2\psi$$

(16)

where ψ depends on the capacitance coefficient of the UAV chip.

The energy consumption of UAV flight is mainly related to its flight trajectory and quality:

$$E^{fly}(t)=\xi {({\displaystyle \frac{\left|\right|c_{\left(t+1\right)}-c_{\left(t\right)}\left|\right|}{{\delta }_t}})}^2$$

(17)

where $\xi =0.5M$, with $M$ the payload of the UAV.

Finally, we get the total energy consumption $E_{total}\left(t\right),\mathrm{w}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{h}$ is

$$E_{total}\left(t\right)=E_u^{rec}\left(t\right)+E_u^{comp}\left(t\right)+E^{fly}\left(t\right).$$

(18)

3.5. Problem Definition

In the UAV-assisted MEC system, the limited airborne energy makes the balance between UAV energy consumption and computing task allocation a key issue. We aim to maximize the energy efficiency of UAVs by jointly optimizing their 3D flight trajectories and user device task offloading rates while meeting UAV maneuverability constraints and other communication resource limitations. The energy efficiency γ is defined as the ratio of the total number of data bits successfully processed by the UAV to the total energy consumed. The expression for γ is as follows:

$$\mathsf{\gamma }={\displaystyle \frac{{\sum }_{t=1}^N{\sum }_{u=1}^U{I}_u\left(t\right)}{{\sum }_{t=1}^N\sum _{u=1}^U\left(E_u^{rec}\left(t\right)+E_u^{comp}\left(t\right)\right)+\sum _{t=1}^N{E}^{fly}\left(t\right)}}$$

(19)

where $I_u\left(t\right)$ is the number of task bits offloaded from user device u to the UAV in time slot t, and the total energy consumption of the UAV $E_u^{comp}\left(t\right)$ includes three parts: flight energy consumption $E^{fly}\left(t\right)$, task receiving energy consumption $E_u^{rec}\left(t\right),$ and computation and processing energy consumption. Formula (19) quantifies the relationship between task processing volume and total energy consumption, directly reflecting the energy efficiency performance of UAVs through γ. Therefore, a joint optimization strategy with maximized energy efficiency (OPMEE) for the UAV flight trajectory and user device task offloading rate problem can be modeled as

$$\begin{array}{cc}\hfill \mathrm{P}1:& {\displaystyle \genfrac{}{}{0pt}{}{max}{c\left(t\right),{\eta }_u\left(t\right)}}{\gamma }_{CSE}\hfill \\ & \hspace{1em}s.t. C1:\left[{|q}_{\left(t\right)}-o_k|\ge r_k+d_{safe}\right]\left|\right|\left[h\left(t\right)\ge l_k+d_{safe}\right]\hfill \\ & \hspace{1em}C2:c_{\left(1\right)}=c_{\left(n\right)}\hfill \\ & \hspace{1em}C3:h_{\left(t\right)}\le h_{max}\hfill \\ & \hspace{1em}C4:v_{\left(t\right)}\le v_{max}\hfill \\ & \hspace{1em}C5:a_{\left(t\right)}\le a_{max}\hfill \\ & \hspace{1em}C6:0<{\eta }_u\left(t\right)<1\hfill \\ & \hspace{1em}C7: {\sum }_{t=1}^N{b}_u\left(t\right)\le B_u\left(t\right)\hfill \end{array}$$

(20)

In problem P1, C1 represents the obstacle avoidance constraint of the UAV, C2 is the periodic constraint of UAV service, C3 to C5, respectively, limit the flight altitude, speed, and acceleration of the UAV, C6 specifies the feasible range of user task offloading rate in each time slot, and C7 limits the amount of migrated data in terms of bandwidth. The optimization of energy efficiency γ needs to be achieved through joint control of UAV trajectory $c\left(t\right)$ and the task offloading rate. Trajectory optimization directly affects flight energy consumption and communication quality, while offloading rate allocation determines the utilization efficiency of computing resources. Constraints C1 to C7 jointly ensure the safety and service stability of UAVs in complex environments, providing clear boundary conditions for subsequent algorithm design.

4. Optimization Problem Solving

There are two main difficulties in solving problem P1: Firstly, the objective function has non-convex characteristics and a fractional structure. Secondly, there is a complex nonlinear coupling relationship between the optimization variables $c\left(t\right)$ and ${\eta }_u\left(t\right)$.

Regarding the first difficulty, we first use the Dinkelbach method to perform convex transformation on the fractional structure of the objective function, transforming the original non-convex problem into an equivalent solvable form. According to Dinkelbach’s method, the optimal solution of the original problem can only be obtained when formula (21) holds $\gamma *$. The proof process is detailed in references [27,28].

$${\displaystyle \genfrac{}{}{0pt}{}{max}{c\left(t\right),{\eta }_u\left(t\right)}}\left\{{\sum }_{t=1}^N{\sum }_{u=1}^U{I}_u\left(t\right)-\gamma \mathrm{*}\left[{\sum }_{t=1}^N{\sum }_{u=1}^U\left(E_u^{rec}\left(t\right)+E_u^{comp}\left(t\right)\right)+{\sum }_{t=1}^N{E}^{fly}\left(t\right)\right]\right\}=0$$

(21)

Thus, P1 can be equivalently transformed into a parameter optimization problem regarding γ:

$$\begin{array}{c}\mathrm{P}2:{\displaystyle \genfrac{}{}{0pt}{}{max}{c\left(t\right),{\eta }_u\left(t\right)}}\left\{{\sum }_{t=1}^N{\sum }_{u=1}^U{I}_u\left(t\right)-\gamma \left[{\sum }_{t=1}^N{\sum }_{u=1}^U\left(E_u^{rec}\left(t\right)+E_u^{comp}\left(t\right)\right)+{\sum }_{t=1}^N{E}^{fly}\left(t\right)\right]\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.25em}\hspace{0.25em}s.t. C1~C6\hfill \end{array}$$

(22)

where γ is a non-negative parameter. When solving P2, we first fix a value of γ, then optimize the variables and ${\eta }_u\left(t\right)$ update γ based on the current solution, and iterate until the algorithm converges to obtain the optimal solution $\gamma \mathrm{*}$.

For the second difficulty, an alternating optimization strategy can be adopted to decouple and block the optimization variables, decomposing the original problem into two more easily solvable sub-problems: (1) Optimizing the user offloading rate under a fixed UAV trajectory. (2) Optimizing the UAV trajectory under a given offloading rate. The definitions and solutions for these two sub-problems are given below.

4.1. Task Offloading Optimization for User Device

Firstly, we discuss the ${\eta }_u\left(t\right)$ optimization problem P3 of the task offloading rate of user equipment u in time slot t under the condition of a fixed UAV trajectory. This sub-problem corresponds to the constraint condition C6 in P1, and its expression is as follows:

$$\begin{gathered} \mathrm{P}3:{\displaystyle \genfrac{}{}{0pt}{}{max}{{\eta }_u\left(t\right)}}{f}_1\left(\gamma \right) \\ s.t. C6 \end{gathered}$$

(23)

where $f_1$($\gamma )$ is related to $\gamma$.

$$f_1(\gamma )={\sum }_{t=1}^N{\sum }_{u=1}^U{I}_u\left(t\right)-\gamma {\sum }_{t=1}^N{\sum }_{u=1}^U\left(E_u^{rec}\left(t\right)+E_u^{comp}\left(t\right)\right)$$

(24)

P3 is essentially a complex combinatorial optimization problem, and traditional mathematical programming methods are difficult to effectively solve. This paper proposes an optimization scheme based on the genetic algorithm (GA), which dynamically adjusts the offloading rate through a biomimetic evolution mechanism. The specific improvements are as follows:

(1)

Design of fitness function

Maximizing $f_1$($\gamma )$ requires balancing data processing and energy consumption costs, and when the UAV trajectory is fixed, the flight energy consumption $E^{fly}\left(t\right)$ is pre-calculated by trajectory planning and treated as a constant term, so $f_1$($\gamma )$ can be directly used as the fitness function.

(2)

Encoding and population initialization

Using a real number encoding strategy, chromosome individuals are represented by U*N-dimensional vectors, corresponding to the offloading rates of U user devices in N time slots. By using a balanced initialization strategy based on preset initial values ${\eta }_u\left(t\right)\in \left(\mathrm{0,1}\right)$ to generate an initial population, ensuring population diversity, the size of population $N_{p1}$ needs to balance search efficiency and computational costs.

(3)

Genetic manipulation design

Selection operation: Adopting a tournament selection strategy, randomly selecting k individuals from the population and retaining the one with the highest fitness to enter the next generation. This strategy can maintain selection pressure while avoiding excessive dependence on extreme fitness values in roulette wheel selection.

Cross operation: Using arithmetic crossover to generate offspring individuals based on the characteristics of continuous variables. Let the individual parents be ${\eta }_1$ and ${\eta }_2$, the individual child be $\eta \prime$, generated by $\eta \prime ={\alpha }_1{\eta }_1+(1-{\alpha }_1){\eta }_2$, where ${\alpha }_1\in [0,1]$ is a random weight, to enhance global exploration ability.

Mutation operation: Non-uniform Gaussian mutation is used. To the gene ${\eta }_u\left(t\right)$, perturbation ${{\eta }_u\left(t\right)}^{\prime }={\eta }_u\left(t\right)$ + N(0,${\sigma }_t^2$) is applied, where ${\sigma }_t$ is the mutation intensity parameter, followed by boundary repair (truncation when exceeded). The mutation rate $P_m$ decreases adaptively with the number of iterations, encouraging diversity in the initial stage and strengthening the local search in the later stage.

(4)

Constraint handling and computation acceleration

Constraint C6 is guaranteed through a dual mechanism of direct restriction and post-mutation repair during the encoding stage. To reduce computational complexity, duplicate terms in the objective function can be precomputed and cached, and parallelized for fitness evaluation.

4.2. UAV Trajectory Optimization Problem

The corresponding solving variables for the UAV flight trajectory optimization problem under the condition of a known user device offloading rate are $c_{\left(t\right)}=\left[q_{\left(t\right)},h_{\left(t\right)}\right]=[x_{\left(t\right)},y_{\left(t\right)},z_t]$, and this sub-problem corresponds to the constraint conditions C1~C5 in P1. The expression for question P4 is

$$\begin{gathered} P4:{\displaystyle \genfrac{}{}{0pt}{}{max}{c_{\left(t\right)}}}{f}_2\left(\gamma \right) \\ \hspace{1em}\hspace{1em}\hspace{1em}s.t. C1~C5 \end{gathered}$$

(25)

where $f_2$($\gamma )$ is related to $\gamma$.

$${ f}_2(\gamma )=-\gamma \left[{\sum }_{t=1}^N{\sum }_{u=1}^U\left(E_u^{rec}\left(t\right)+E_u^{comp}\left(t\right)\right)+{\sum }_{t=1}^N{E}^{fly}\left(t\right)\right]$$

(26)

It is obvious that problem P4 is nonlinear and complicated. In order to balance computational efficiency and solution quality, this paper uses the Arctic puffin optimization (APO) algorithm to solve this problem. The APO algorithm is a metaheuristic optimization algorithm proposed by Wang et al. [29], inspired by the survival and predation behavior of Arctic puffins. Due to its unique algorithm structure and novel iterative method, it has strong adaptive optimization capabilities.

The algorithm mainly consists of three stages: population initialization, aerial flight (global exploration), and underwater foraging (local development). The aerial flight stage utilizes the Levy flight and velocity factor mechanism to improve the global search ability, while the underwater foraging stage enhances the local development ability through synergistic effects and adaptive change factors. The following provides the biological mechanism and key description of using the APO algorithm to solve problem P4.

(1)

Design of fitness function

Based on the objective function $f_2$($\gamma )$ and corresponding constraint conditions, a penalty function is designed to jointly construct the fitness evaluation criteria ${f_2\left(\gamma \right)}^{\prime }$. For solutions that violate the constraint conditions, the penalty term $P\left(\gamma \right)$ is defined as

$$P(\gamma )={\sum }_{k=1}^5{C}_k\ast {max\left(0,g_k\left(\gamma \right)\right)}^2$$

(27)

where $C_k(k=\mathrm{1,2},\mathrm{3,4},5)$ is the dynamic penalty coefficient used to adjust the punishment intensity, which increases with the number of iterations, and $g_k\left(\gamma \right)$ is the standard form of the constraint function corresponding to the k-th constraint condition. The final fitness function can be expressed as

$${f_2\left(\gamma \right)}^{\prime }=f_2\left(\gamma \right)+P\left(\gamma \right)$$

(28)

By balancing the value of the objective function with the degree of constraint violation, ${f_2\left(\gamma \right)}^{\prime }$ selects high-quality populations and eliminates inefficient solutions.

(2)

Population initialization

The initialization population of the APO algorithm is an ${N_{p2}\ast D}_2$ matrix $X={[X_1,X_2,{\dots ,X}_{{Np}_2}]}^T$, where $N_{p2}$ is the population size, $D_2$ is the variable dimension, and $X_i$ is a $D_2$ dimensional variable, where $X_i=[X_i^1,X_i^2,\dots ,X_i^{D_2}]$ corresponds to the discrete coordinates of the 3D trajectory of the UAV in N time slots. In the classical APO algorithm, the initial individual’s position is usually randomly generated within a pre-determined range. To improve algorithm efficiency, the search direction is guided by initial values to avoid complete randomness and accelerate algorithm convergence. Among them, the initial value is obtained based on prior knowledge of the problem (corresponding to the coordinates of the UAV trajectory in the previous iteration when the inner loop alternately optimizes the UAV trajectory and offloading rate in Algorithm 1), and then Gaussian random perturbations are applied to the initial value to guide the search direction, balancing diversity and convergence.

(3)

Aerial flight phase

There are two main strategies used during the aerial flight phase. The first strategy is the aerial search, which simulates the low-altitude collaborative reconnaissance behavior of Arctic puffin populations to search for areas with abundant prey and fewer natural enemies. The dynamic adjustment mechanism of this strategy is as follows:

$$Y_i^{j+1}=X_i^j+(X_i^j-X_r^j) \ast L(D_2)+R$$

(29)

$$R=\mathrm{round}(0.5 \ast (0.05+\mathit{rand}\left)\right)\ast {\alpha }_2$$

(30)

where $X_i^j$ represents the current position of the i-th Arctic puffin, $X_r^j$ represents $X_i^j$ excluding randomly selected Arctic puffins from the current population, and L($D_2$) is a random number generated by Levy’s flight, ${\alpha }_2~Normal\left(\mathrm{0,1}\right)$.

The second strategy is diving predation. When prey is found in the air, Arctic puffins quickly change direction through high-speed diving to hunt. The position update mechanism during this stage is as follows:

$$Z_i^{j+1}=Y_i^{j+1}\ast S$$

(31)

S = tan((rand-0.5) ∗ π)

(32)

where S is used as the velocity coefficient to simulate subduction behavior.

(4)

Underwater foraging stage

After diving into the water to forage, Arctic puffins will dynamically adjust their strategies according to different environments. The first step is to gather and forage, using a collective cooperative foraging strategy to gather and surround fish schools and observe peer behavior to determine the optimal diving point. The location update mechanism is as follows:

$$W_i^{j+1}=\left\{\begin{array}{c}{X}_{r1}^j+F\ast L\left(D_2\right)\ast \left(X_{r2}^j-X_{r3}^j\right),rand\ge 0.5\\ X_{r1}^j+F\ast \left(X_{r2}^j-X_{r3}^j\right) , rand<0.5\end{array}\right.$$

(33)

where $X_{r1}^j$, $X_{r2}^j$, and $X_{r3}^j$ represent three randomly selected candidate solutions in the current population, except for $X_i^j$, and F represents the cooperative factor used to regulate foraging behavior.

After gathering to forage, when Arctic puffins perceive that the current foraging area is depleted of resources, they will adopt an enhanced search strategy, actively adjust their diving position, and explore new areas to maintain food supply. The location update mechanism during this process is as follows:

$$Y_i^{j+1}=W_i^{j+1}\ast \left(1+f_2\right)$$

(34)

$$f_2=0.1\ast \left(rand-1\right)\ast {\displaystyle \frac{ J-j}{J}}$$

(35)

where J represents the total number of iterations, and j represents the current iteration round.

Arctic puffins may encounter other predators underwater, and in this case, they will use their predator avoidance strategy to trigger group avoidance behavior and cooperate to respond to predator threats. The specific location update mechanism is as follows:

$$Z_i^{j+1}=\left\{\begin{array}{c}{X}_i^j+F\ast L\left(D_2\right)\ast \left(X_{r1}^j-X_{r2}^j\right),rand\ge 0.5\\ X_i^j+{\beta }_2\ast \left(X_{r2}^j-X_{r3}^j\right), rand<0.5\end{array}\right.$$

(36)

where ${\beta }_2$ is a random number uniformly distributed between 0 and 1.

Finally, to obtain the optimal solution, the solutions generated by gathering for foraging, enhancing search, and avoiding predation are merged, and the top N individuals are selected as the new population after sorting by fitness.

4.3. Joint Optimization Algorithm Design

(1)

Algorithm design

The energy efficiency maximization algorithm for joint optimization of the UAV flight trajectory and user device task offloading rate proposed in this paper is summarized as follows in Algorithm 1.

Algorithm 1: Hybrid Alternating Metaheuristics for Energy Optimization (HAMEO)

(2)

Complexity analysis

The computational complexity of this algorithm is determined by two layers of iterations: the number iteration of the outer layer is $k_{max}$, they alternately execute the GA algorithm and APO algorithm each time, and the total number of iterations is $n_{max}$.

The single-run complexity of the GA algorithm is $O(T_{ga}\ast N_{p1}\ast U\ast N)$, and the single-run complexity of the APO algorithm is $O(T_{apo}\ast N_{p2}\ast 3\ast N)$, where $T_{\mathrm{g}\mathrm{a}}$ and $T_{\mathrm{a}\mathrm{p}\mathrm{o}}$ are the number of internal iterations of the GA and APO algorithms.

Therefore, the computational complexity of the algorithm can be expressed as $O(k_{max}\ast n_{max}\ast (T_{ga}\ast N_{p1}\ast U\ast N+T_{apo}\ast N_{p2}\ast 3\ast N\left)\right)$, ignoring the constant and further simplifying it $O(k_{max}\ast n_{max}\ast (U\ast N)$, indicating that it mainly depends on the number of user devices U and the number of time slots N.

(3)

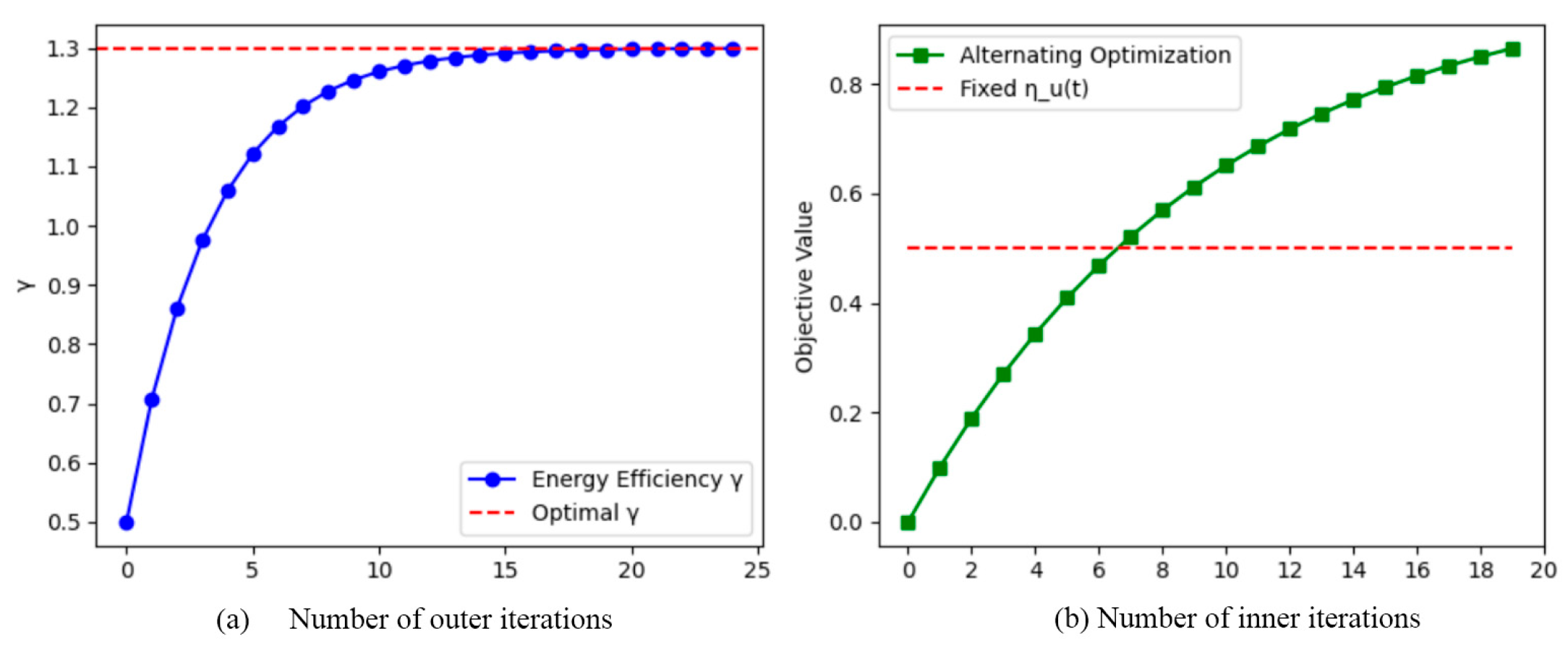
Convergence analysis

Algorithm 1 belongs to a two-layer alternating optimization framework, and its convergence depends on the following mathematical properties:

Outer loop: Based on the Dinkelbach method, the fractional programming problem is transformed into an iterative subtraction problem. In each iteration, the update of $\gamma$ strictly monotonically increases, and the objective function has an upper bound. When $\left|\right|{\mathsf{\gamma }}^{\mathrm{k}+1}-{\mathsf{\gamma }}^{\mathrm{k}}\left|\right|\le \mathsf{ϵ}$, the $\mathsf{ϵ}$- global optimal solution is reached.

Inner loop: Alternate optimization of ${\eta }_u\left(t\right)$ and $c\left(t\right)$, where, in problem P3 (genetic algorithm GA), the global search feature of GA ensures that the optimal ${\eta }_u\left(t\right)$ is approximated with a probability of 1 within a finite generation, but it needs to satisfy the elite retention strategy and appropriate mutation rate. In problem P4 (APO algorithm), APO ensures convergence to the local optimal trajectory $c\left(t\right)$ under the constraint set convexity.

We set the maximum number of outer iterations to 50, convergence threshold to 0.3, optimal energy efficiency value to 1.3, and initial energy efficiency to 0.5. The results are showed in Figure 2.

We can observe that the sequence of the objective function is non-decreasing after each alternating optimization in (b). When the number of iteration is 17, the energy efficiency of outer iteration is converged and bounded in (a). According to the monotonic bounded theorem, Algorithm 1 must converge.

5. Experimental Results and Analysis

Consider a simulation network environment of UAV-assisted MEC, including a single UAV and U randomly distributed user equipment. The UAV starts from the origin (0,0,0) and returns to the origin after completing a task period. The experiment was conducted in the WIN10 environment based on the MATLAB R2020a platform, with a hardware configuration of an Intel Core i5-12400 processor and 16 GB of memory. Firstly, according to the simulation parameters in

Table 1. Simulation parameters.

Parameter	Description	Value
D	Range	1000 m × 1000 m × 50 m
$T_f$	Period duration	70 s
N	Number of time slots	40
${\beta }_0$	Average channel gain at 1 m	−50 dB
${\sigma }^2$	Noise	−100 dBm
$\Gamma$	Signal-to-noise ratio difference	8.2 dB
α	Path loss parameter	2
$B_u\left(t\right)$	Bandwidth	1 MHz
$p_u\left(t\right)$	Device transmission power	30 dBm
$l_u\left(t\right)$	Amount of data offloading by the device	[1, 10] Mbit
$C_u$	CPU cycle required for unit bit data	${10}^3$ cycles/bit
M	UAV payload	5 kg
$v_{max}$	Maximum speed of UAV	20 m/s
$a_{max}$	Maximum acceleration of UAV	5 m/${\mathrm{s}}^2$
$f$	UAV computing capability	1 GHz
ψ	UAV capacitance coefficient	${10}^{-27}$

(the settings of these parameters are from the relevant literature), variables were defined in the MATLAB script and the environment was initialized, including the random distribution of obstacles and user devices, channel models, and configuration of computing tasks. Then, the core module of the HAMEO algorithm in this paper is programmed and compared with the current mainstream algorithms in terms of performance. Finally, the MATLAB Graphics toolbox is used to visualize the experimental data.

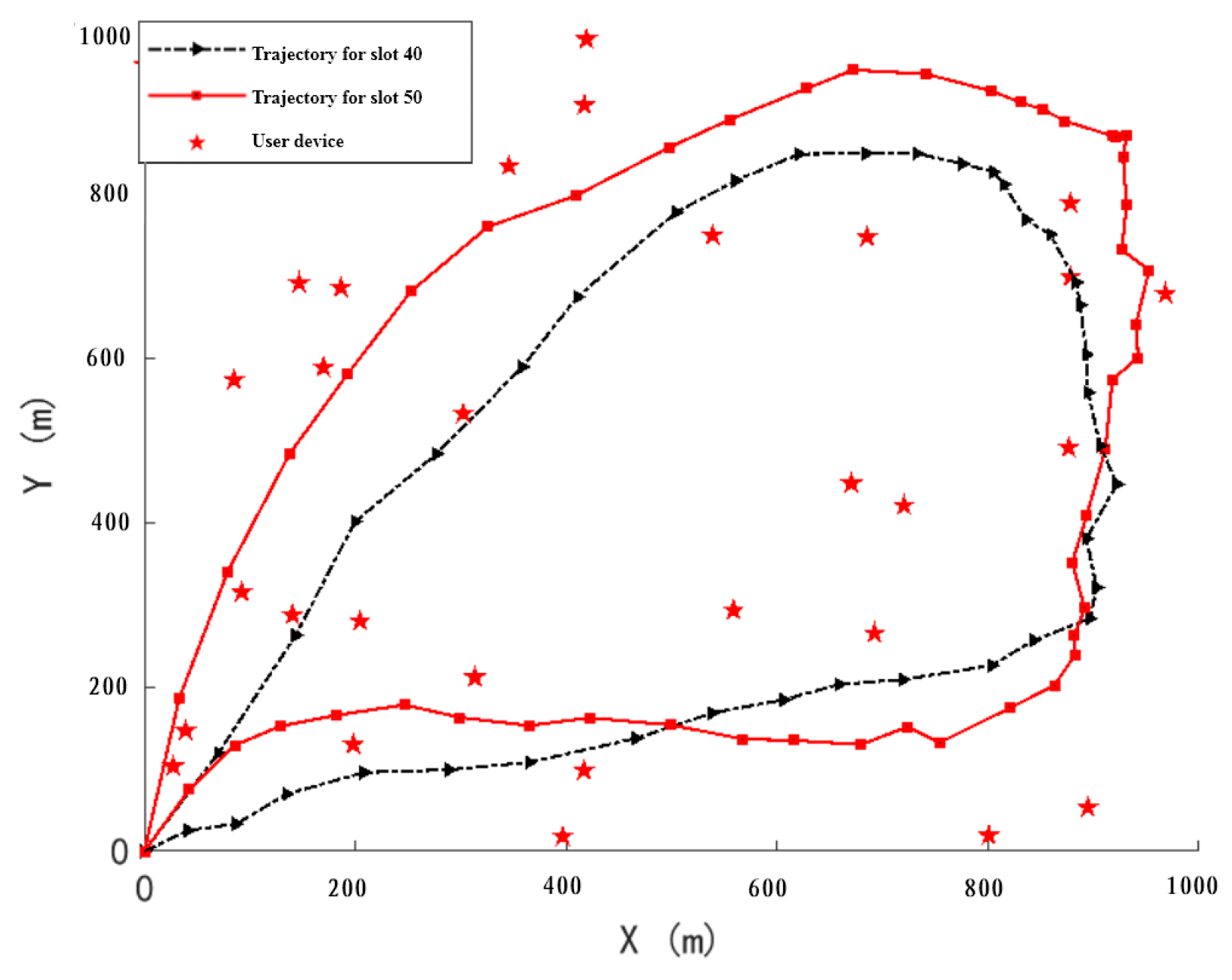
5.1. UAV Trajectory Analysis

By conducting comparative experiments with different flight time slots, the $U=30$ motion of the UAV in 3D space (Figure 3) and its 2D projection (Figure 4) were plotted for the number of user devices.

The experimental results show that the algorithm proposed in this paper can effectively achieve 3D obstacle avoidance. The UAV can avoid obstacles by circling or crossing during flight, and the trajectory does not overlap with the obstacles. Combining 2D trajectory analysis provides a more intuitive display. As the number of time slots increases, the spatial matching degree between the UAV trajectory and the user device position further improves, allowing it to move closer to the user side and effectively improving the quality of communication services.

To verify the performance advantage of the APO algorithm in solving problem P4, we compare it with three UAV trajectory planning algorithms: the GA [30], Ant Colony Optimization (ACO) [31], and Whale Optimization Algorithm (WOA) [32].

Figure 5 shows the running time required for each algorithm to achieve a stable UAV trajectory for the first time at different time slots. When the number of time slots was small, there was not much difference in the time consumption of each algorithm. As the number of slots increased, the time consumption of the GA and WOA increased rapidly, while the ACO algorithm grew slowly, and the overall time consumption of the APO algorithm remained relatively low.

It needs further explanation that as the number of time slots increases, the reason for the increase in the running time of each algorithm is mainly related to the expansion of the problem scale and the search mechanism of the algorithm itself. The number of time slots directly determines the number of discrete time steps in drone trajectory planning. The more time slots there are, the more trajectory points (position, velocity, direction, etc.) need to be optimized, resulting in linear or even polynomial growth in the dimensions of decision variables. For heuristic algorithms such as GA, WOA, ACO, and APO, the size of the solution space exponentially increases with the variable dimension. For example, GA (genetic algorithm): The cost of population evolution is high: as time slots increase, individual encoding lengths become longer, and the time required for crossover and mutation operations increases. The WOA relies on random concatenation and spiral update mechanisms. As the number of time slots increases, adjusting parameters (such as search radius) becomes more difficult and the convergence speed slows down. ACO needs to gradually construct the trajectory for each time slot, and increasing the number of time slots directly extends the iteration time. In this paper, APO utilizes problem decomposability to maintain a low time complexity.

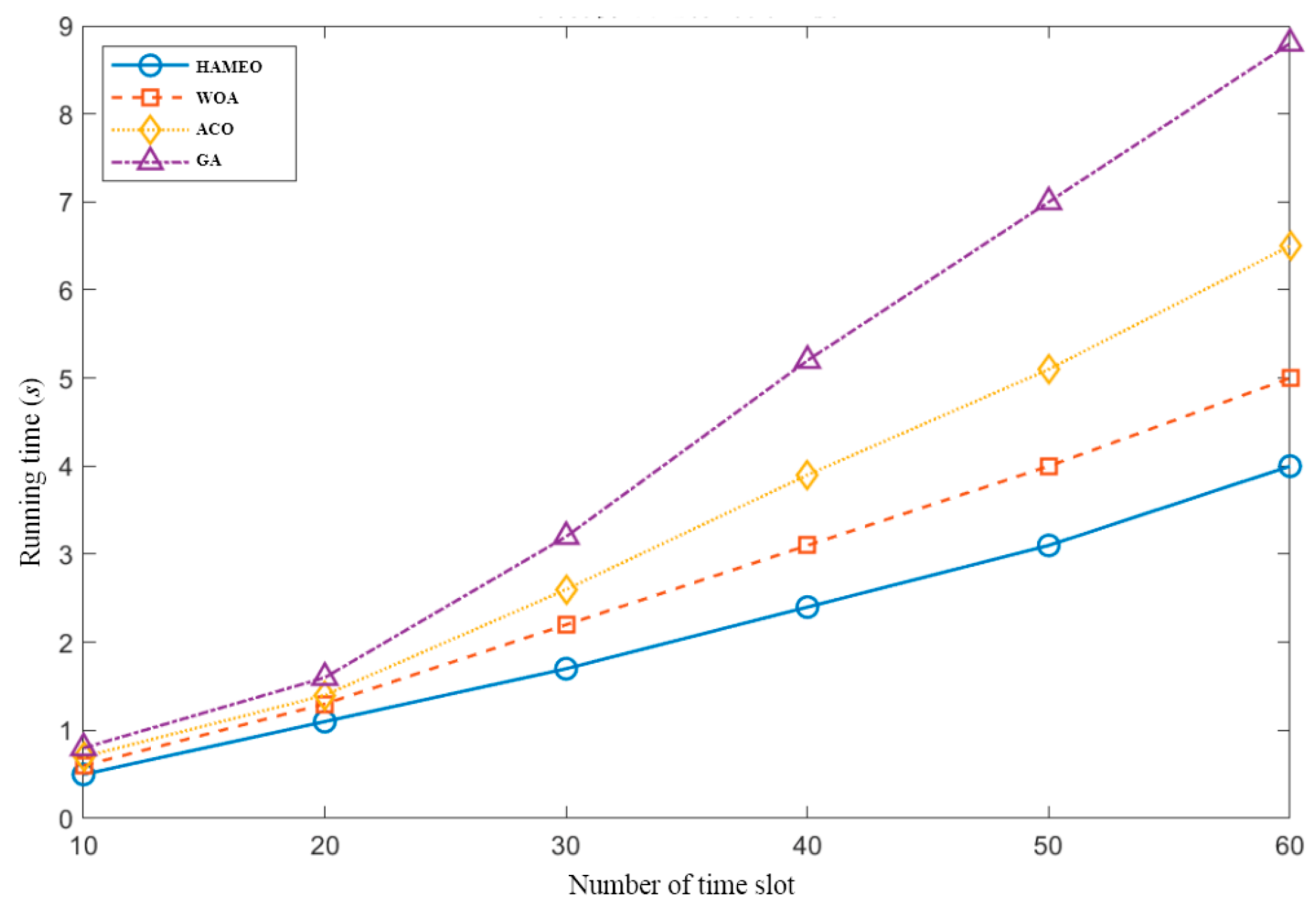
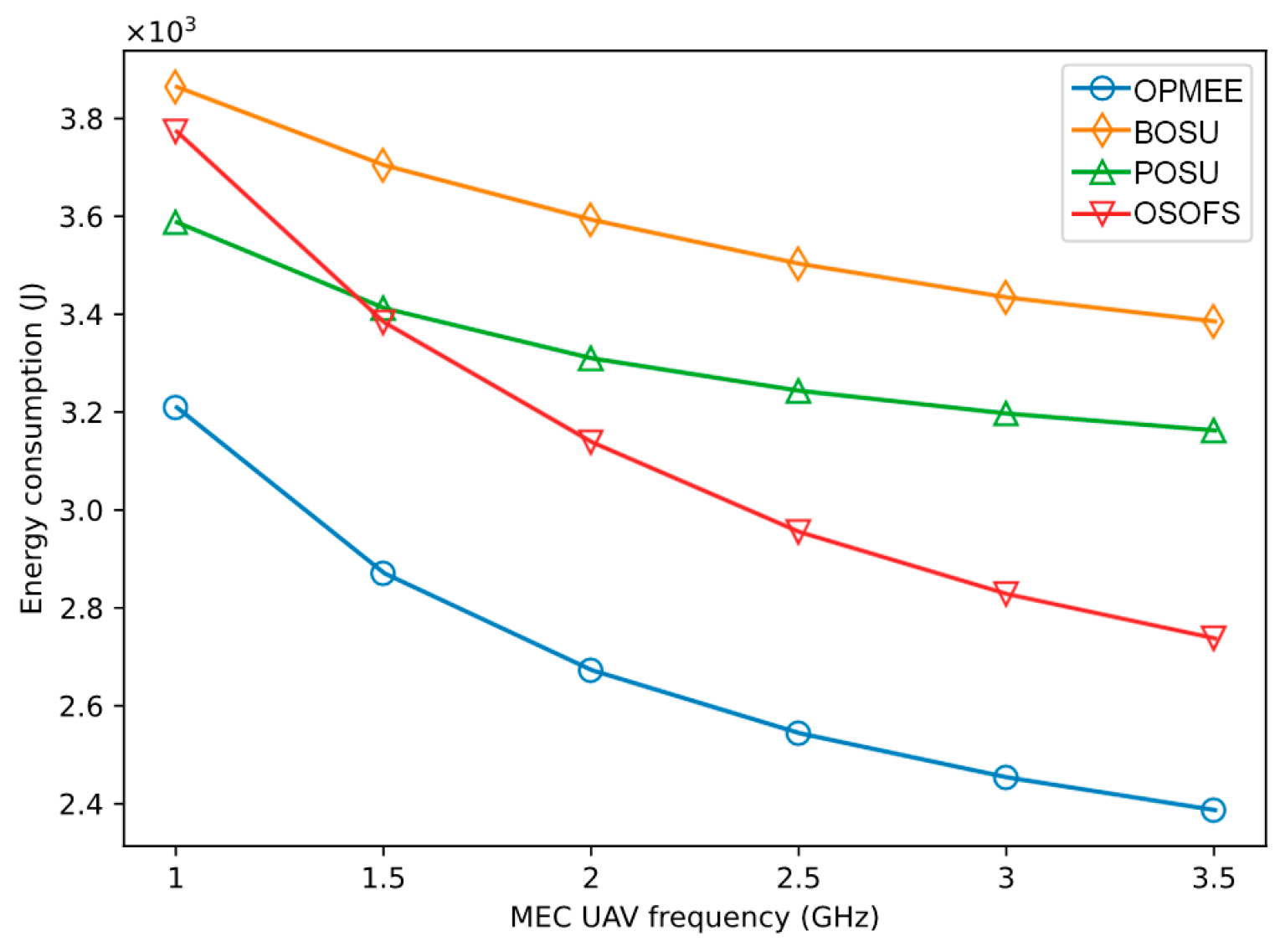
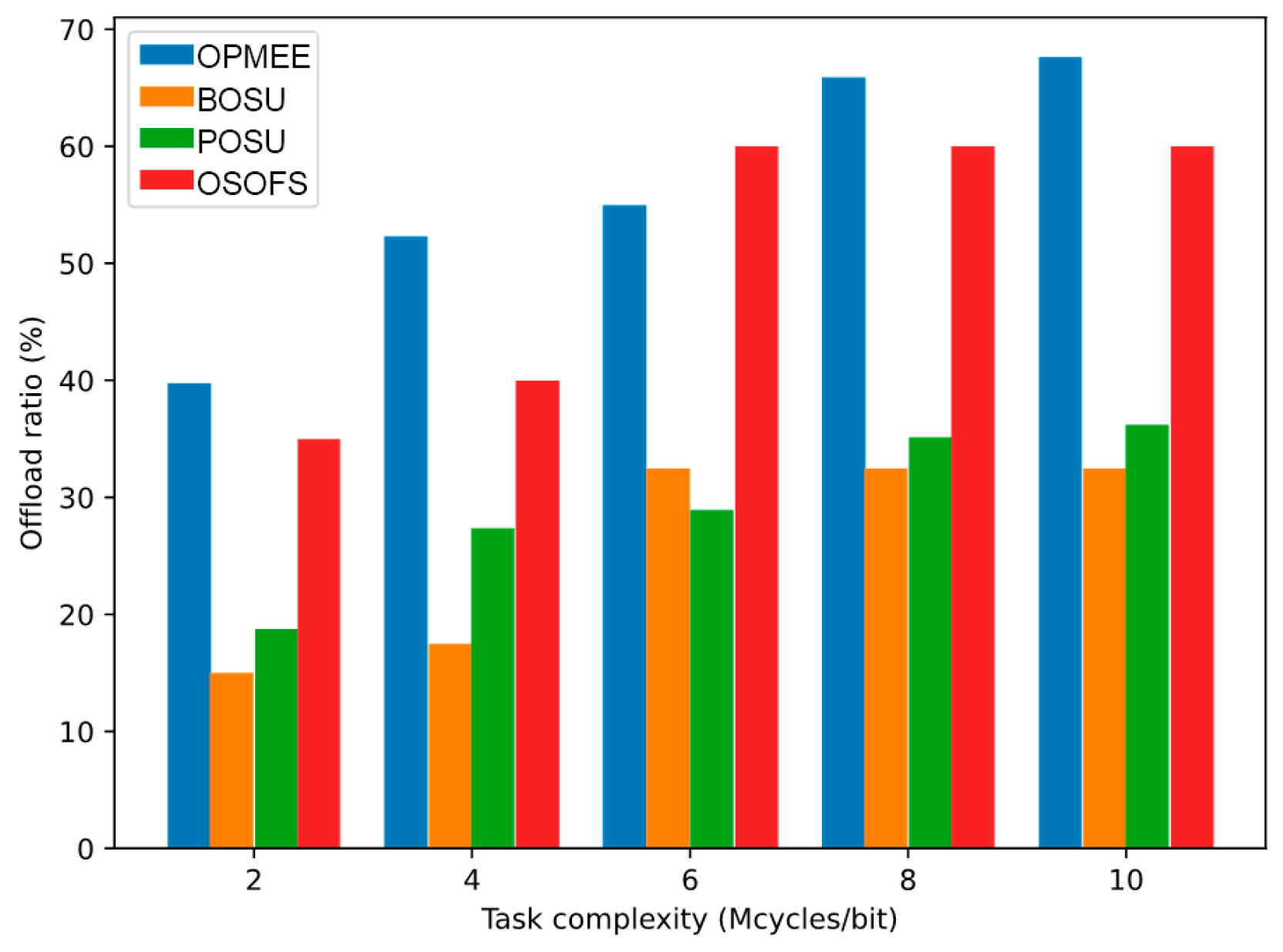
5.2. Performance Analysis

To verify the energy efficiency advantages of the joint optimization strategy with maximized energy efficiency (OPMEE) for the UAV flight trajectory and user device task offloading rate strategy proposed in this paper, several different offloading strategies were compared.

(1)

Optimal Service Order and Flight Speed (OSOFS) [10]: A two-stage optimization algorithm is proposed to minimize the energy consumption of a single UAV-assisted MEC system during each flight.

(2)

Binary Offloading with Single UAV MEC (BOSU) [33]: A single UAV-assisted MEC is used to provide computing resources, where all user tasks are either executed on the user device or offloaded to the UAV MEC for execution, and the UAV flies according to the designed UAV trajectory.

(3)

Partial Offloading with Single UAV MEC (POSU) [34]: The user’s task can be divided into two parts, using the user device and UAV-assisted MEC to complete the computation with a given UAV trajectory.

As shown in Figure 6, the energy consumption of the UAV-assisted MEC system changes with the enhancement of UAV performance. Among them, the BOSU and POSU schemes have higher energy consumption, while the OSOFS and OPMEE schemes have lower energy consumption. With the enhancement of UAV-assisted MEC system performance, the energy consumption reduction of the OPMEE scheme proposed in this paper is more significant. The performance of UAV-assisted MEC systems can affect the trajectory and hovering time of UAVs, thereby affecting the total energy consumption, by affecting the computation delay of tasks. In BOSU and POSU schemes, due to the lack of trajectory optimization capability, UAVs have more wasteful trajectories, thereby increasing energy consumption. In addition, due to their excellent trajectory optimization capabilities and the ability to partition time slots and tasks more finely, the OSOFS and OPMEE schemes make more efficient use of edge network resources, resulting in lower energy consumption.

Figure 7 shows the trend of task offloading ratio as task complexity increases. The offloading ratio of the four task offloading schemes increases with the increase in task complexity, but the offloading ratio of BOSU and POSU schemes is significantly lower than that of OSOFS and OPMEE schemes. Therefore, whether the scheme has trajectory optimization is very important. When the complexity of tasks increases, in order to reduce energy consumption, user devices tend to migrate more tasks to UAV-assisted MEC. In the OSOFS and OPMEE schemes, UAV-assisted MEC performs task offloading and computation along optimized trajectories, thus increasing the task offloading ratio. The task offloading cost in BOSU and POSU schemes is relatively high, so the offloading ratio is lower than that in OSOFS and OPMEE schemes. Note that when task complexity increases 6, the offloading rate of OSOFS is bigger than OPMEE. We point out that OPMEE offloads as many tasks as possible to save energy consumption in the initial stage for saving energy consumption. When the task complexity reaches a certain level, such as 6, in order to balance energy consumption and optimize flight trajectories, the number of offloading tasks may be reduced. After that, a higher offloading ratio is recovered. That is to say, the algorithm will choose a balancing strategy between energy consumption and trajectory optimization.

6. Conclusions and Further Work

Due to the limited battery storage of a UAV, energy saving is a key issue in a UAV-assisted MEC system. However, for a low-altitude flying UAV, successful obstacle avoidance is also very necessary. This paper aims to maximize the system energy efficiency (defined as the ratio of the total amount of offloaded data to the energy consumption of the UAV) to meet the maneuverability and three-dimensional obstacle avoidance constraints of a UAV. A joint optimization strategy with maximized energy efficiency for the UAV flight trajectory and user device task offloading rate is proposed. In order to solve this problem, hybrid alternating metaheuristics for energy optimization are given. Due to the non-convexity and fractional structure of the optimization problem, it can be transformed into an equivalent parameter optimization problem using the Dinkelbach method, and then divided into two sub-optimization problems that are alternately optimized using metaheuristic algorithms. The experimental results show that the strategy proposed in this paper can enable the UAV to avoid obstacles during flight by detouring or crossing, and the trajectory does not overlap with obstacles, effectively achieving two-dimensional and three-dimensional obstacle avoidance. In addition, compared with related solving methods, the solving method in this paper is significantly higher than traditional algorithms. In comparison with related optimization strategies, the strategy proposed in this paper can effectively reduce the overall energy consumption of a UAV. Future research work can further expand to multi-UAV collaboration scenarios, exploring the task offloading relationship between multiple UAVs and user devices.