ERA-MADDPG: An Elastic Routing Algorithm Based on Multi-Agent Deep Deterministic Policy Gradient in SDN
Abstract
1. Introduction
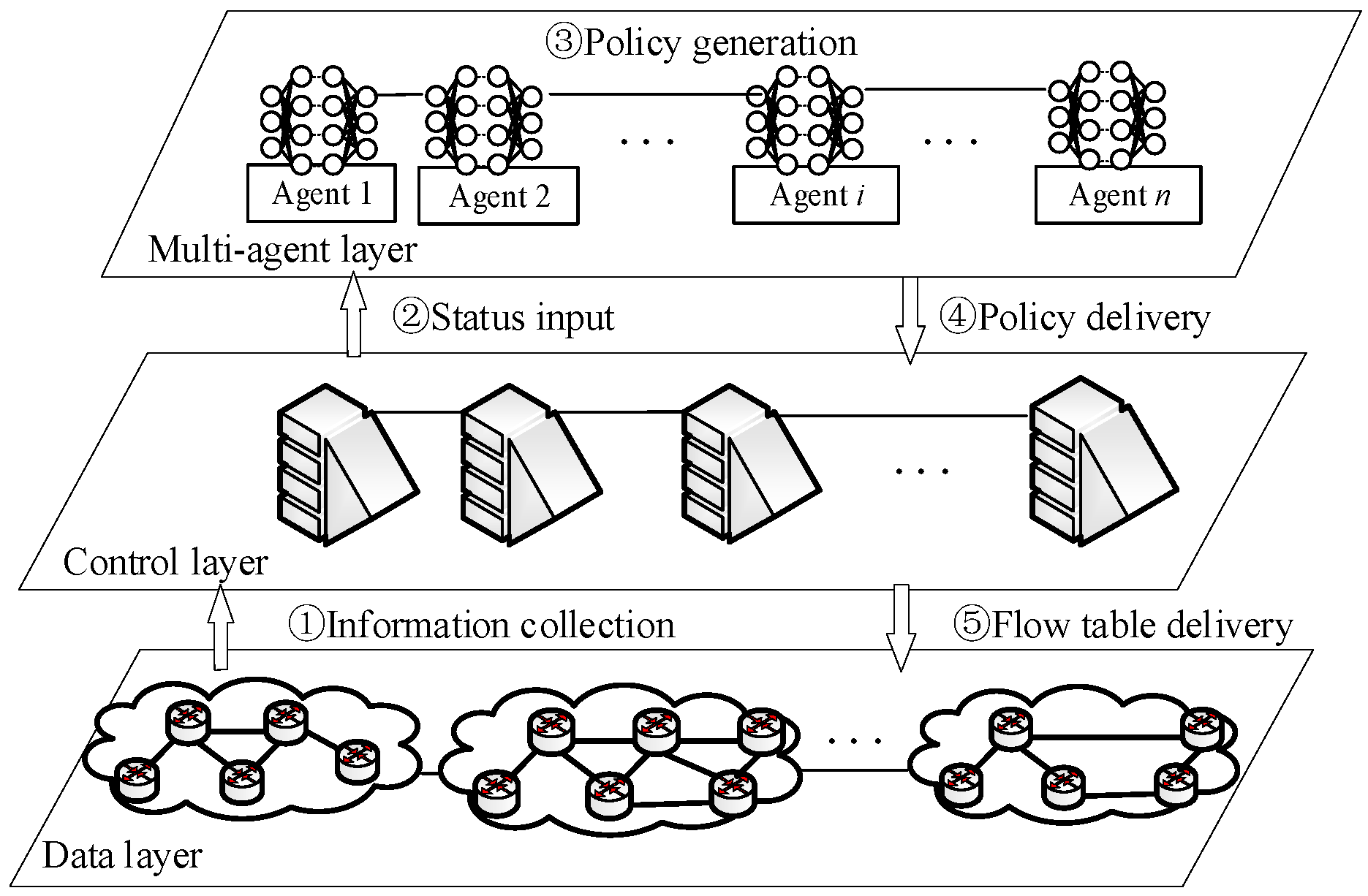
- Proposes a novel SDN-based three-layer architecture for resilient routing, comprising a multi-agent layer, a controller layer, and a data layer. The architecture enables dynamic collaboration among agents to process topology changes through a streamlined workflow (information collection → state input → policy generation → delivery), addressing the limitation of single-agent models in distributed network environments.
- Develops the ERA-MADDPG algorithm by integrating the actor-critic framework with CNN networks. This innovation enhances training efficiency by 20.9–39.1% compared to traditional methods (MADQN, SR-DRL) through centralized training of multi-agent experiences and CNN-based high-dimensional feature extraction, while stabilizing learning through policy gradient optimization in continuous action spaces.
- Demonstrates superior adaptability to topology dynamics: Through simulation experiments, the algorithm achieves re-convergence speeds over 25% faster than baselines under 5–15% node/link changes, validating its robustness in dynamic networks. The multi-agent collaborative mechanism reduces reliance on centralized retraining, providing a scalable solution for real-time routing optimization.
2. System Architecture
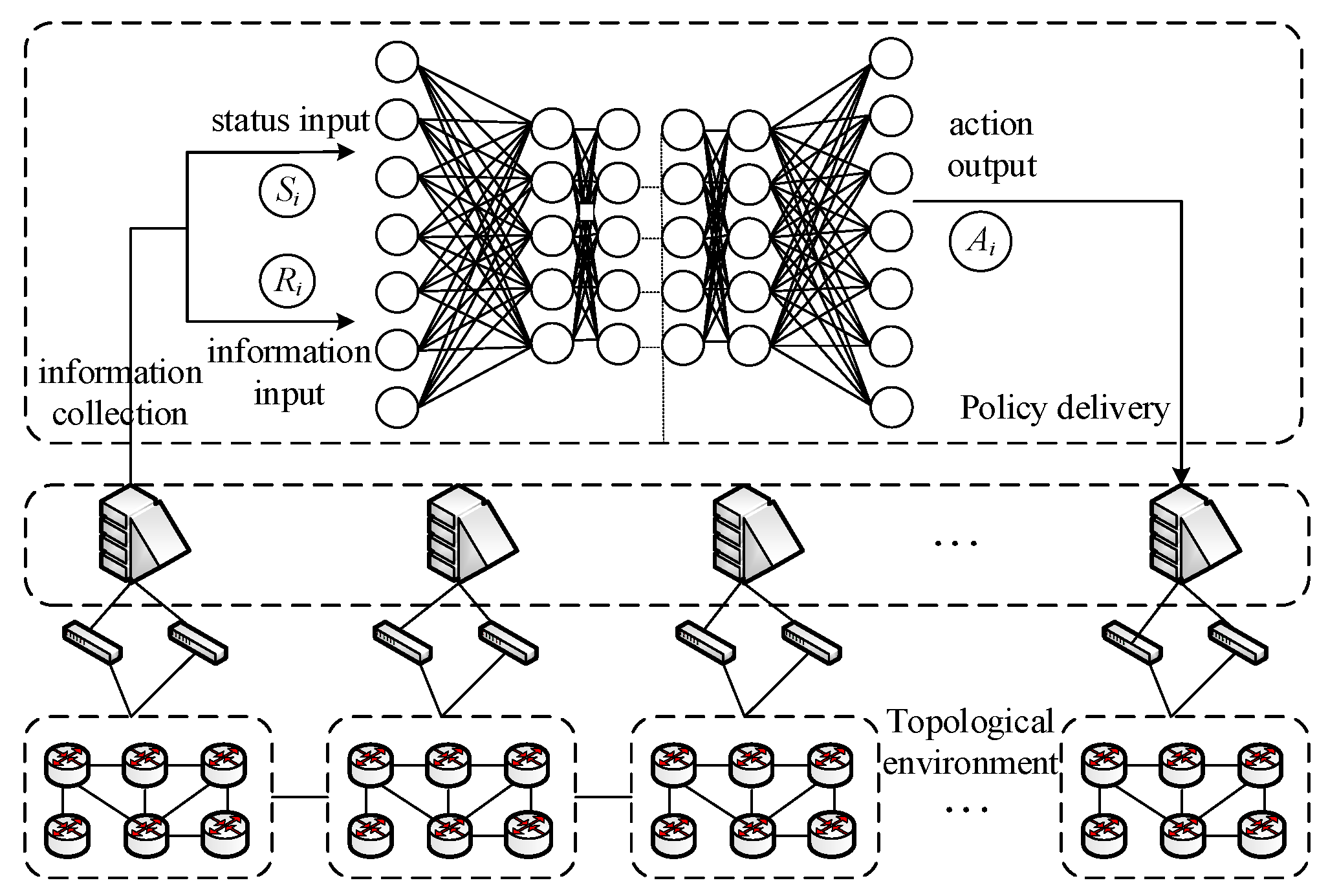
3. ERA-MADDPG Intelligent Routing Solution
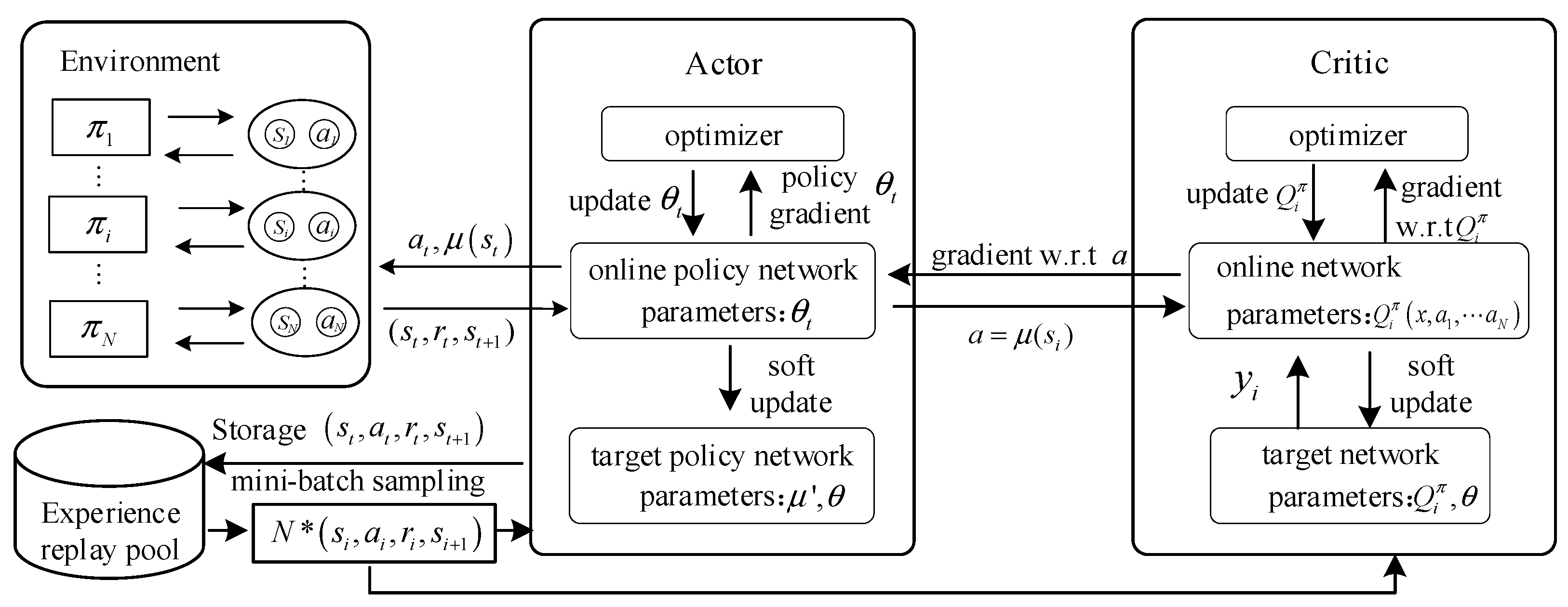
3.1. ERA-MADDPG Intelligent Routing Algorithm
| Algorithm 1 ERA-MADDPG Algorithm Process |
| Input: Network status information bandwidth, latency, and topology information collection, agent actions. |
| Output: Link Weight for routing decisions. |
| (1) for episode = 1 to do; (2) Initialize a random process for action exploration; (3) Receive initial state ; (4) for to max-episode-length do; (5) for each agent do; (6) Select action ; (7) end for (8) Execute joint action and observe the reward new state ; (9) Store in replay buffer ; (10) ; (11) Sample a random minibatch of samples from ; (12) for each sample in minibatch do; (13) Randomly select sub-policy index ~ uniform ; (14) Compute target value ; (15) end for (16) Update critic by minimizing the loss: ; (17) Update actor using the sampled policy gradient: ; (18) end for (19) Update target network parameters: ; (20) end for |
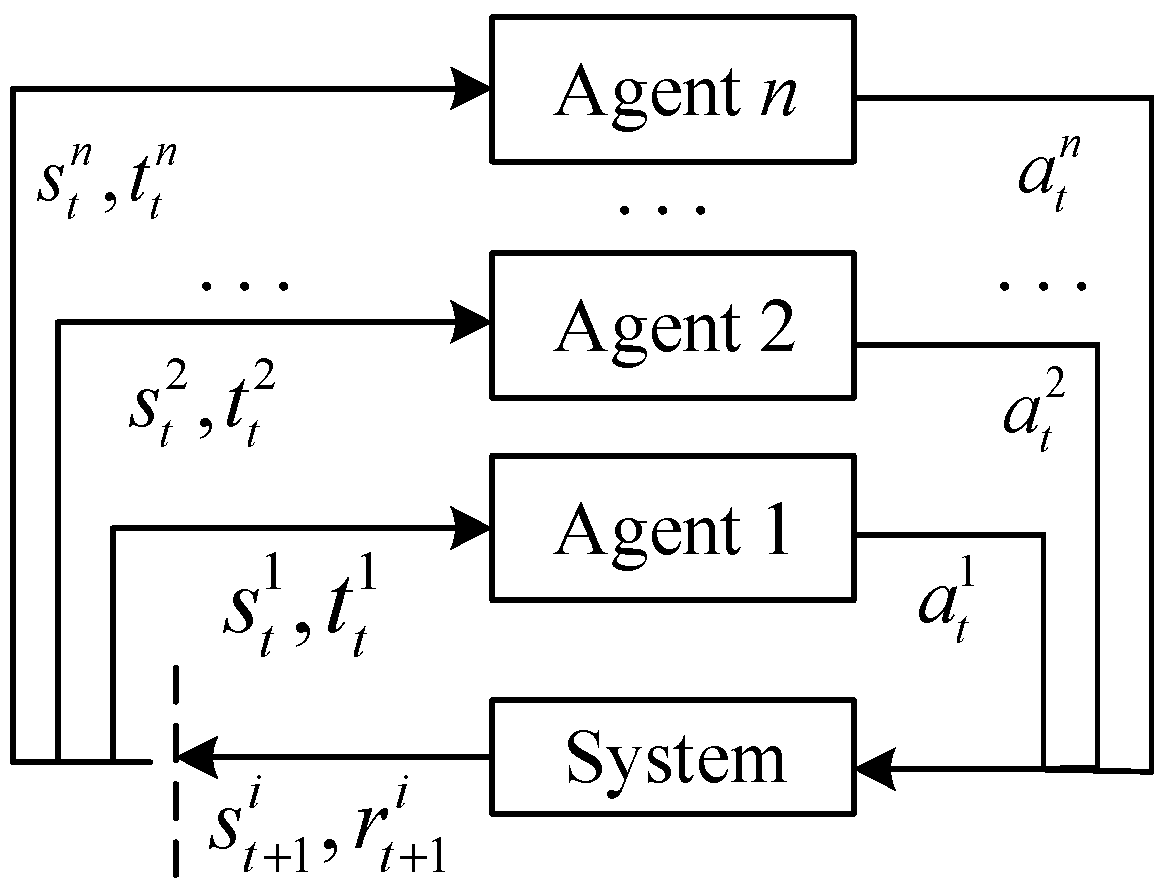
3.2. ERA-MADDPG Intelligent Routing Interacts with the Environment
4. Experimental Evaluation
4.1. Experimental Environment and Parameter Configuration
4.2. Performance Evaluation
- (1)
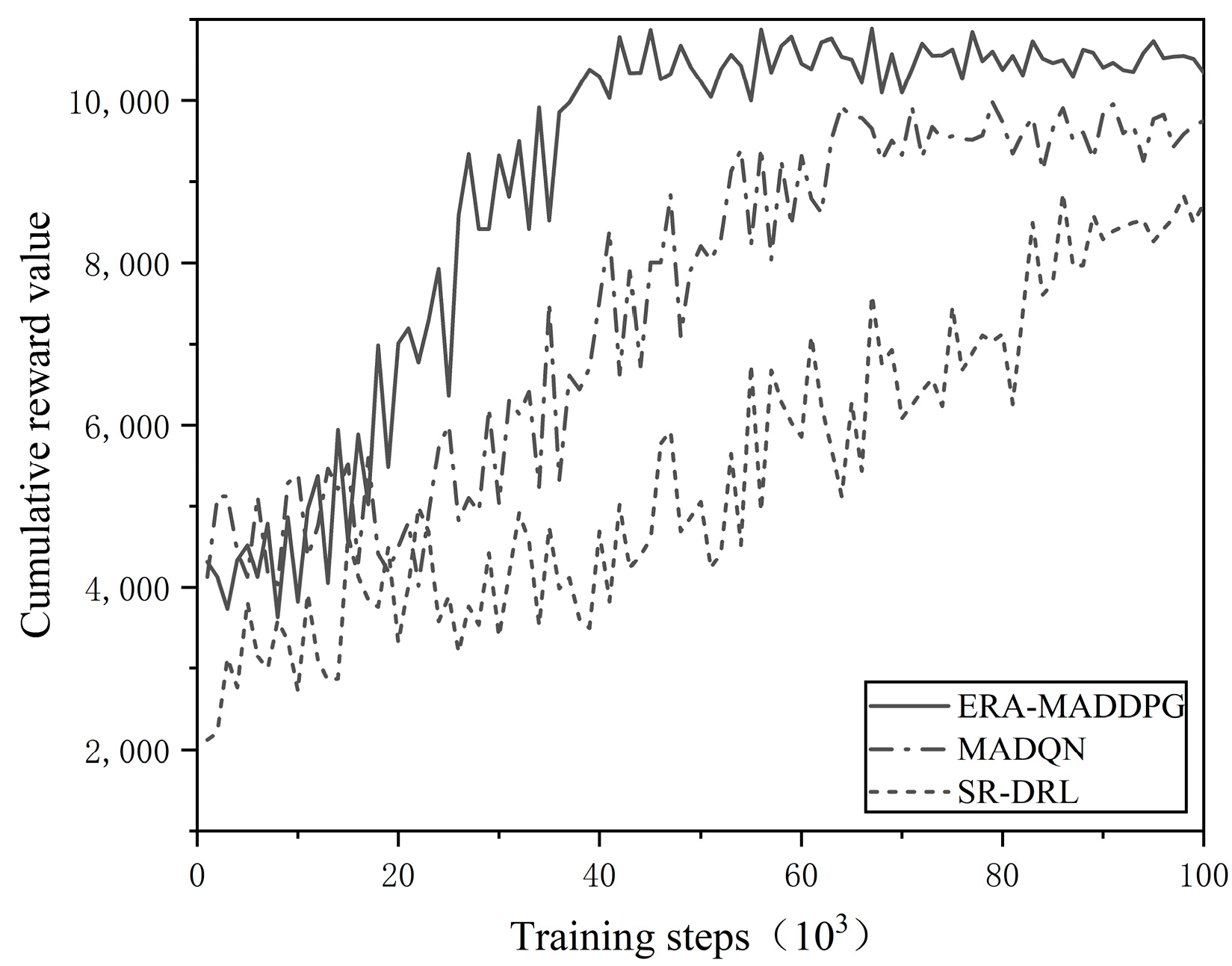
- Convergence comparison of the ERA-MADDPG algorithm, MADQN algorithm, and SR-DRL algorithm
- (2)
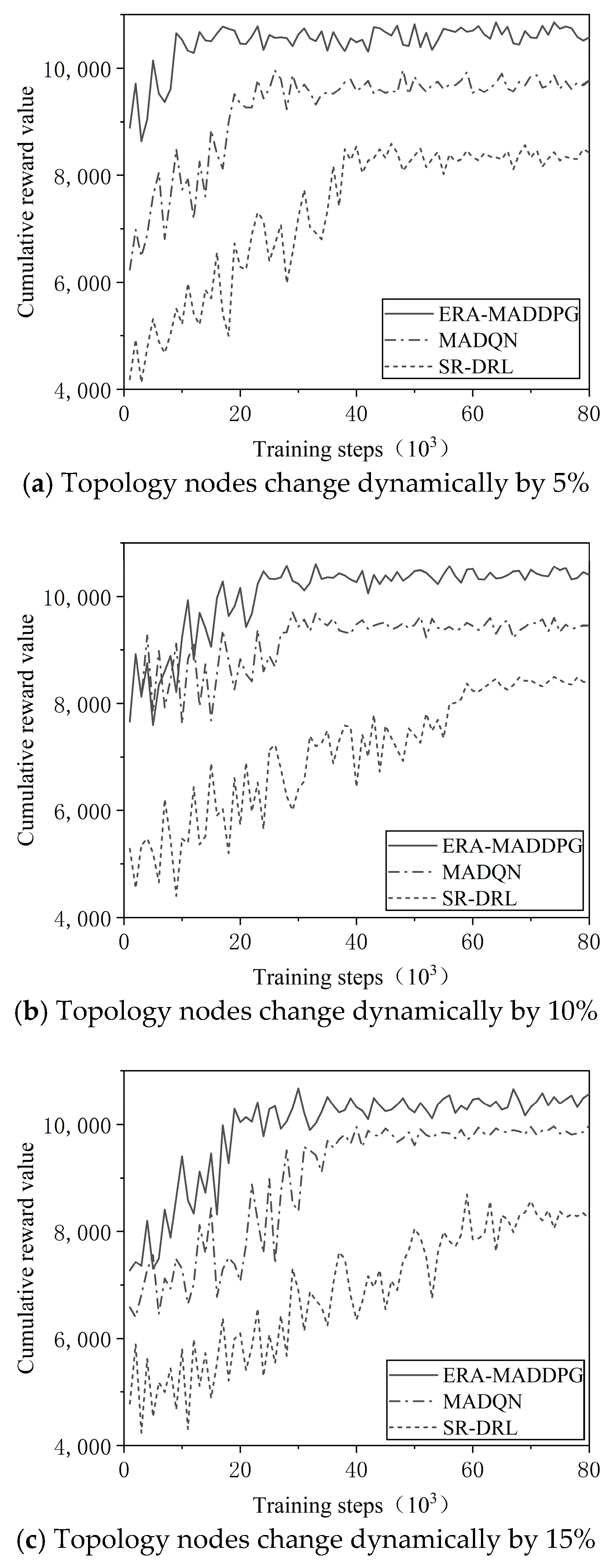
- Comparison of recovery training with topology node changes of 5%, 10%, and 15%
- (3)
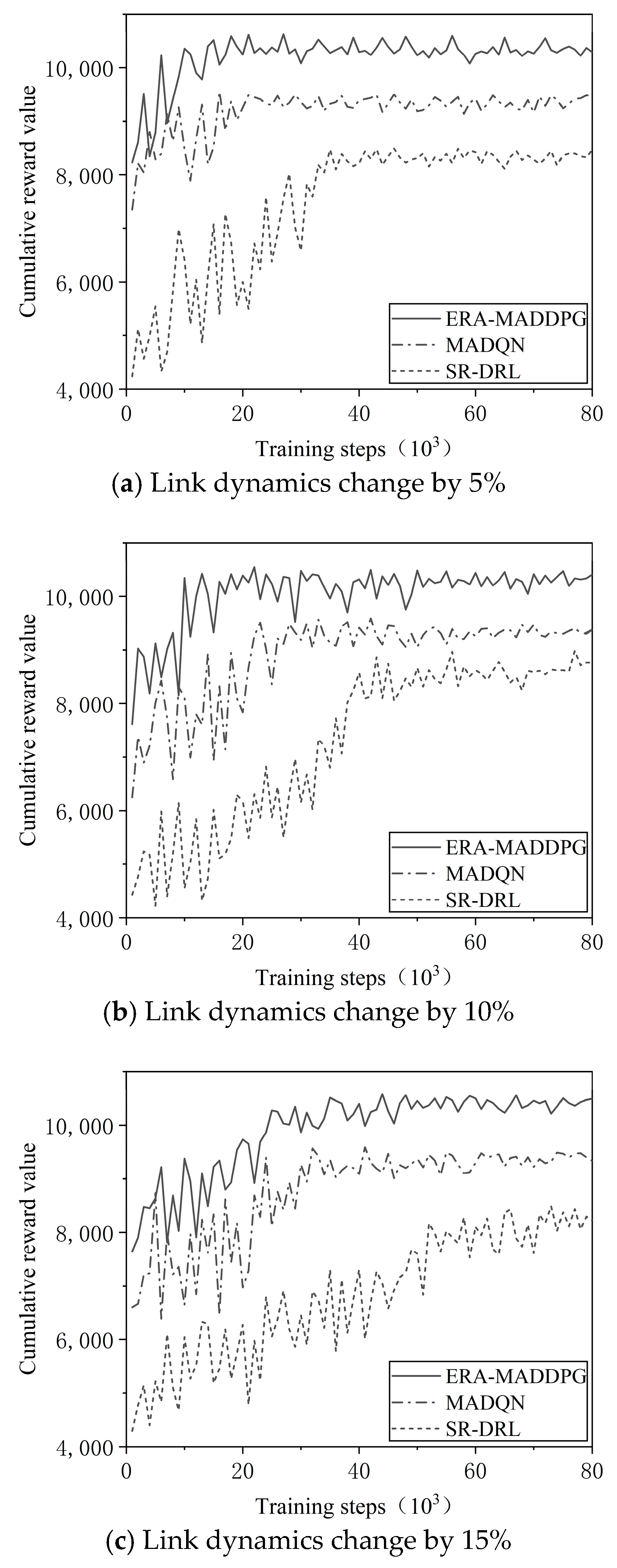
- Comparison of recovery training for link changes of 5%, 10%, and 15%
- (4)
- Comparison of the performance of the ERA-MADDPG algorithm in terms of delay, throughput, and packet loss rate
4.3. Performance Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jain, J.K.; Waoo, A.A.; Chauhan, D. A literature review on machine learning for cyber security issues. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2022, 8, 374–385. [Google Scholar] [CrossRef]
- Fawaz, A.; Mougharbel, I.; Al-Haddad, K.; Kanaan, H.Y. Energy routing protocols for Energy Internet: A review on multi-agent systems, metaheuristics, and Artificial Intelligence approaches. IEEE Access 2025, 13, 41625–41643. [Google Scholar] [CrossRef]
- Prabhu, D.; Alageswaran, R.; Miruna Joe Amali, S. Multiple agent based reinforcement learning for energy efficient routing in WSN. Wirel. Netw. 2023, 29, 1787–1797. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, D.; Strbac, G. Multi-agent deep reinforcement learning for resilience-driven routing and scheduling of mobile energy storage systems. Appl. Energy 2022, 310, 118575. [Google Scholar] [CrossRef]
- Perry, Y.; Frujeri, F.V.; Hoch, C.; Kandula, S.; Menache, I.; Schapira, M.; Tamar, A. A Deep Learning Perspective on Network Routing. arXiv 2023, arXiv:2303.00735. [Google Scholar]
- Bhavanasi, S.S.; Pappone, L.; Esposito, F. Dealing with changes: Resilient routing via graph neural networks and multi-agent deep reinforcement learning. IEEE Trans. Netw. Serv. Manag. 2023, 20, 2283–2294. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, C.; Le, F. Improving inter-domain routing through multi-agent reinforcement learning. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 6–9 July 2020; pp. 1129–1134. [Google Scholar]
- Liu, C.; Wu, P.; Xu, M.; Yang, Y.; Geng, N. Scalable deep reinforcement learning-based online routing for multi-type service requirements. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 2337–2351. [Google Scholar] [CrossRef]
- Kaviani, S.; Ryu, B.; Ahmed, E.; Larson, K.; Le, A.; Yahja, A.; Kim, J.H. DeepCQ+: Robust and scalable routing with multi-agent deep reinforcement learning for highly dynamic networks. In Proceedings of the MILCOM 2021-2021 IEEE Military Communications Conference (MILCOM), San Diego, CA, USA, 29 November–2 December 2021; pp. 31–36. [Google Scholar]
- You, X.; Li, X.; Xu, Y.; Feng, H.; Zhao, J.; Yan, H. Toward packet routing with fully distributed multiagent deep reinforcement learning. IEEE Trans. Syst. Man Cybern. Syst. 2020, 52, 855–868. [Google Scholar] [CrossRef]
- Ding, R.; Xu, Y.; Gao, F.; Shen, X.S.; Wu, W. Deep reinforcement learning for router selection in network with heavy traffic. IEEE Access 2019, 7, 37109–37120. [Google Scholar] [CrossRef]
- He, Q.; Wang, Y.; Wang, X.; Xu, W.; Li, F.; Yang, K.; Ma, L. Routing optimization with deep reinforcement learning in knowledge defined networking. IEEE Trans. Mob. Comput. 2023, 23, 1444–1455. [Google Scholar] [CrossRef]
- Sun, P.; Lan, J.; Guo, Z.; Xu, Y.; Hu, Y. Improving the scalability of deep reinforcement learning-based routing with control on partial nodes. In Proceedings of the ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3557–3561. [Google Scholar]
- Chen, B.; Sun, P.H.; Lan, J.L.; Wang, Y.W.; Cui, P.S.; Shen, J. Inter-Domain Multi-Link Routing Optimization Based on Multi-agent Reinforcement Learning. J. Inf. Eng. Univ. 2022, 23, 641–647. [Google Scholar]
- Gupta, N.; Maashi, M.S.; Tanwar, S.; Badotra, S.; Aljebreen, M.; Bharany, S. A comparative study of software defined networking controllers using mininet. Electronics 2022, 11, 2715. [Google Scholar] [CrossRef]
- Xiang, X.; Foo, S. Recent advances in deep reinforcement learning applications for solving partially observable markov decision processes (pomdp) problems: Part 1—Fundamentals and applications in games, robotics and natural language processing. Mach. Learn. Knowl. Extr. 2021, 3, 554–581. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, Y.; Meng, L.; Qiu, X.; Yu, P. DDPG-Based Energy-Efficient Flow Scheduling Algorithm in Software-Defined Data Centers. Wirel. Commun. Mob. Comput. 2021, 2021, 6629852. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.Z.; Zhang, Y.J.; Wei, W. Deep deterministic policy gradient algorithm based on mean of multiple estimators. J. Zhengzhou Univ. (Eng. Sci.) 2022, 43, 15–21. [Google Scholar]
- Chen, B.; Sun, P.; Zhang, P.; Lan, J.; Bu, Y.; Shen, J. Traffic engineering based on deep reinforcement learning in hybrid IP/SR network. China Commun. 2021, 18, 204–213. [Google Scholar] [CrossRef]
- Wang, B.C.; Si, H.W.; Tan, G.Z. Research on autopilot control algorithm based on deep reinforcement learning. J. Zhengzhou Univ. (Eng. Sci.) 2020, 41, 41–45,80. [Google Scholar]
- Xi, L.; Wu, J.; Xu, Y.; Sun, H. Automatic generation control based on multiple neural networks with actor-critic strategy. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2483–2493. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, S.; Panda, S.N. Performance evaluation using RYU SDN controller in software-defined networking environment. Wirel. Pers. Commun. 2022, 122, 701–723. [Google Scholar] [CrossRef]
- Le, D.H.; Tran, H.A.; Souihi, S.; Mellouk, A. An AI-based traffic matrix prediction solution for software-defined network. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Chen, L.; Lingys, J.; Chen, K.; Liu, F. Auto: Scaling deep reinforcement learning for datacenter-scale automatic traffic optimization. In Proceedings of the 2018 Conference of the ACM Special Interest Group on Data Communication, Budapest Hungary, 20–25 August 2018; pp. 191–205. [Google Scholar]
- Fausto, A.; Gaggero, G.; Patrone, F.; Marchese, M. Reduction of the delays within an intrusion detection system (ids) based on software defined networking (sdn). IEEE Access 2022, 10, 109850–109862. [Google Scholar] [CrossRef]

| Experimental Parameters | Parameter Value |
|---|---|
| Training steps T of the algorithm | 100,000 |
| Actor-Critic learning rate | 0.0001 |
| Reward value discount factor | 0.9 |
| Experience replay pool size | 5000 |
| Traffic load intensity | 80% |
| Reward value weighting parameters ,, and | 0~1 |
| Experience replay unit update iteration steps | 200 |
| Training batch size | 128 |
| Algorithm | First Stabilization Cycle (95% CI) | Corresponding Training Steps (×103, 95% CI) | Delay Cycles Compared to ERA-MADDPG |
|---|---|---|---|
| ERA-MADDPG | 53 ± 2.1 | 53,000 ± 1800 | - |
| MADQN | 67 ± 3.5 | 67,000 ± 2300 | +14 |
| SR-DRL | 87 ± 4.8 | 87,000 ± 3100 | +34 |
| Change Magnitude | Algorithm | Re-Convergence Cycle (Training Cycles) | Delay Cycles Compared to ERA-MADDPG |
|---|---|---|---|
| 5% node change | ERA-MADDPG | 10 ± 0.8 | - |
| MADQN | 22 ± 1.5 | +12 | |
| SR-DRL | 38 ± 2.3 | +28 | |
| 10% node change | ERA-MADDPG | 22 ± 1.2 | - |
| MADQN | 33 ± 2.1 | +11 | |
| SR-DRL | 59 ± 3.7 | +37 | |
| 15% node change | ERA-MADDPG | 21 ± 1.3 | - |
| MADQN | 35 ± 2.4 | +14 | |
| SR-DRL | 60 ± 4.2 | +39 |
| Change Magnitude | Algorithm | Re-Convergence Cycle (Training Cycles) | Delay Cycles Compared to ERA-MADDPG |
|---|---|---|---|
| 5% link change | ERA-MADDPG | 12 ± 0.9 | - |
| MADQN | 15 ± 1.3 | +3 | |
| SR-DRL | 35 ± 2.7 | +23 | |
| 10% link change | ERA-MADDPG | 13 ± 1.1 | - |
| MADQN | 23 ± 1.8 | +10 | |
| SR-DRL | 42 ± 3.2 | +29 | |
| 15% link change | ERA-MADDPG | 22 ± 1.6 | - |
| MADQN | 32 ± 2.5 | +10 | |
| SR-DRL | 54 ± 4.1 | +32 |
| Algorithm | Average Throughput (Mbps) ± SD | Average Delay (ms) ± SD | Average Packet Loss Rate (%) ± SD |
|---|---|---|---|
| ERA-MADDPG | 76 ± 2.1 | 136 ± 4.3 | 4.0 ± 0.8 |
| MADQN | 73 ± 3.5 | 141 ± 5.2 | 5.0 ± 1.1 |
| SR-DRL | 67 ± 4.8 | 163 ± 6.7 | 7.0 ± 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Liu, H.; Li, Y.; Ma, L. ERA-MADDPG: An Elastic Routing Algorithm Based on Multi-Agent Deep Deterministic Policy Gradient in SDN. Future Internet 2025, 17, 291. https://doi.org/10.3390/fi17070291
Huang W, Liu H, Li Y, Ma L. ERA-MADDPG: An Elastic Routing Algorithm Based on Multi-Agent Deep Deterministic Policy Gradient in SDN. Future Internet. 2025; 17(7):291. https://doi.org/10.3390/fi17070291
Chicago/Turabian StyleHuang, Wanwei, Hongchang Liu, Yingying Li, and Linlin Ma. 2025. "ERA-MADDPG: An Elastic Routing Algorithm Based on Multi-Agent Deep Deterministic Policy Gradient in SDN" Future Internet 17, no. 7: 291. https://doi.org/10.3390/fi17070291
APA StyleHuang, W., Liu, H., Li, Y., & Ma, L. (2025). ERA-MADDPG: An Elastic Routing Algorithm Based on Multi-Agent Deep Deterministic Policy Gradient in SDN. Future Internet, 17(7), 291. https://doi.org/10.3390/fi17070291






