A Tale of Many Networks: Splitting and Merging of Chord-like Overlays in Partitioned Networks
Abstract
1. Introduction
- During the Arab Spring in Egypt (2011), from 27 January 2011 until 2 February 2011, approximately 93% of Egyptian networks were unreachable (http://www.nytimes.com/2011/01/29/technology/internet/29cutoff.html, accessed on 26 May 2025), and most parts of the Internet in Egypt had been cut off by the Egyptian government (http://www.circleid.com/posts/egyptian_government_shuts_down_most_internet_and_cell_services/, accessed on 26 May 2025).
- Nepal cut off Internet access entirely in 2005, as did Myanmar two years later in 2007.
- A new report [5] lists further cases in Gabon (https://pulse.internetsociety.org/shutdowns/internet-shutdown-amidst-gabon-elections, accessed on 26 May 2025) (27 August and 14 September 2016, and starting from 26 to 30 August 2023), coinciding with the closure of polling stations after an election.
- In Iran, the Internet was shut down from 15 November to 24 November 2019 to “suppress the widespread aban-e-khoonin” movement. The report states that this was the most severe disconnection tracked by NetBlocks in terms of its technical complexity and scale (https://netblocks.org/reports/internet-disrupted-in-iran-amid-fuel-protests-in-multiple-cities-pA25L18b, accessed on 26 May 2025). In 2023, the initiative “Women, Life, Freedom” led to only a partial Internet shutdown.
- In Cuba, similar events were observed on 11 July 2021 (https://www.yucabyte.org/2023/01/25/cloudflare-radar-cuba-internet/, accessed on 26 May 2025) related to large protests against local COVID-19 regulations.
- Earthquakes, such as in Taiwan in December 2006 (http://news.bbc.co.uk/2/hi/asia-pacific/6211451.stm, accessed on 26 May 2025), might lead to Internet shutdowns due to link damages.
- A Shurfshark report on ongoing Internet limitations (https://surfshark.com/research/internet-censorship, accessed on 26 May 2025) shows that, in general, “protests were the primary trigger for Internet shutdowns”, as [5] points out. A further useful tool to monitor ongoing shutdowns is listed by the Internet Society (https://pulse.internetsociety.org/shutdowns, accessed on 26 May 2025).
- We elaborate on the problem of network partitioning in ring-based peer-to-peer overlay networks in Section 1.1 and discuss related work in Section 2.
- We present our distributed merging approach, named Ring Reunion, in Section 3; this Ring Reunion encompasses steps for identifying new overlays, coordinates the initialization of the merging process in the subnetwork, merges two disjoint rings from that elected starting point (in parallel), and terminates reliably.
- In Section 4, we evaluate our Ring Reunion approach in both simple mode and parallel mode (– instances) in comparison to Chord–Zip [6] and two versions of Shafaat et al’s Ring-Unification [7] approach (Simple and Gossip). We show that only our approach, Ring Reunion, is capable of merging the various Chord rings in demanding scenarios, such as merging multiple rings or having only very few contact points with other rings.
- Finally, we perform a parameter study with Ring Reunion and show the impact of parallelism (i.e., to parallel merging instances) and the impact of , a parameter that specifies how many nodes in a subnetwork (of size ) should be in charge of initiating the merging.
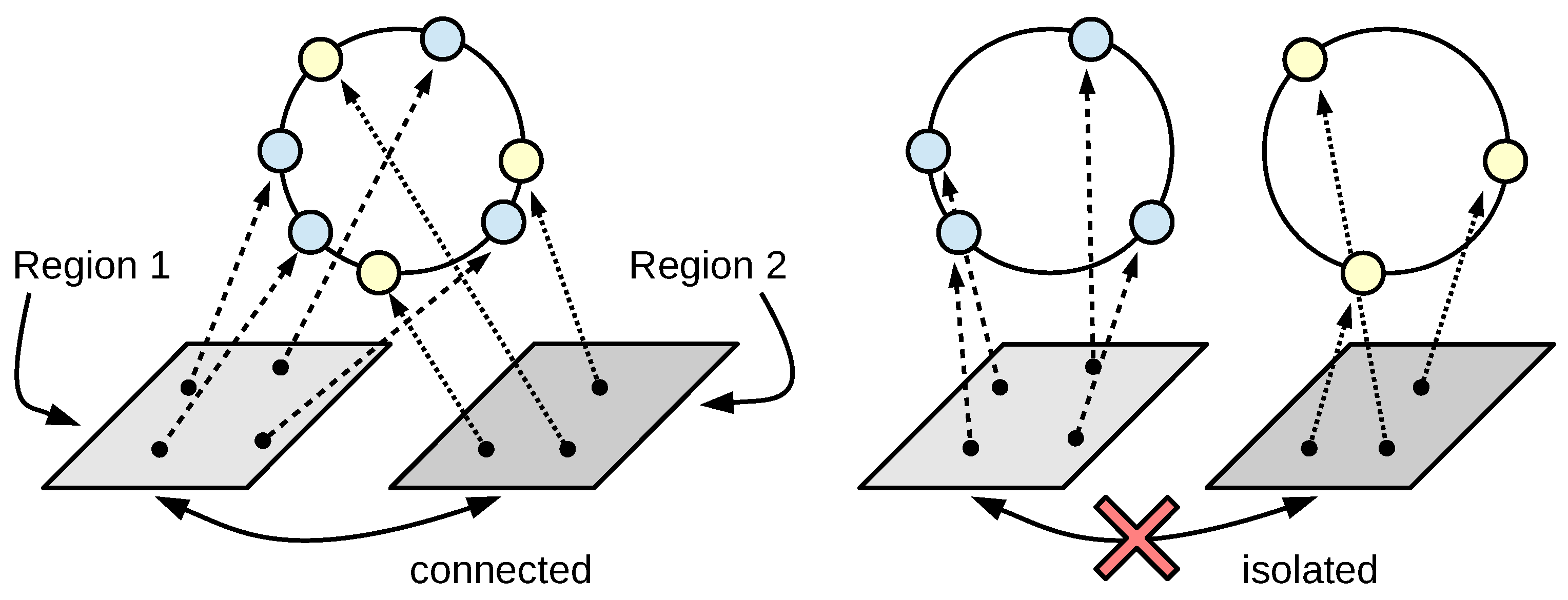
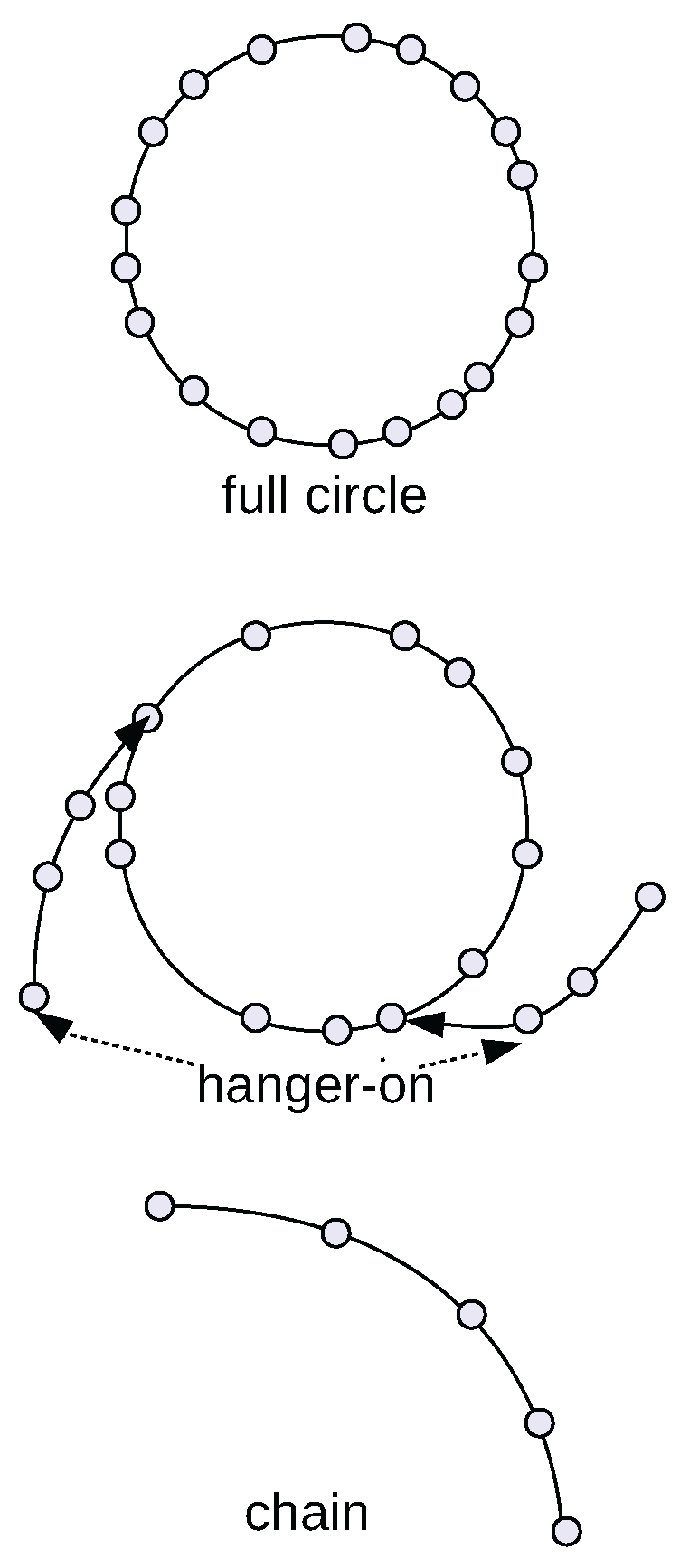
1.1. Characteristics of Network Partitioning
1.2. Outline
2. Related Work
2.1. Re-Chord and Ca-Re-Chord—Self Stabilizing Chord Overlay Network
2.2. Datta et al.—Tale of Two Networks
2.3. Chord–Zip
2.4. Shafaat et al.—Ring-Unification Algorithm (Simple and Gossip-Based)
2.4.1. Simple Ring-Unification Algorithm
2.4.2. Gossip-Based Ring-Unification Algorithm
2.5. Further Surveys on Overlay Network Management
2.6. Specific Overlay Types
2.7. Conclusions on Related Work
3. Our Merging Approach: Ring Reunion Algorithm
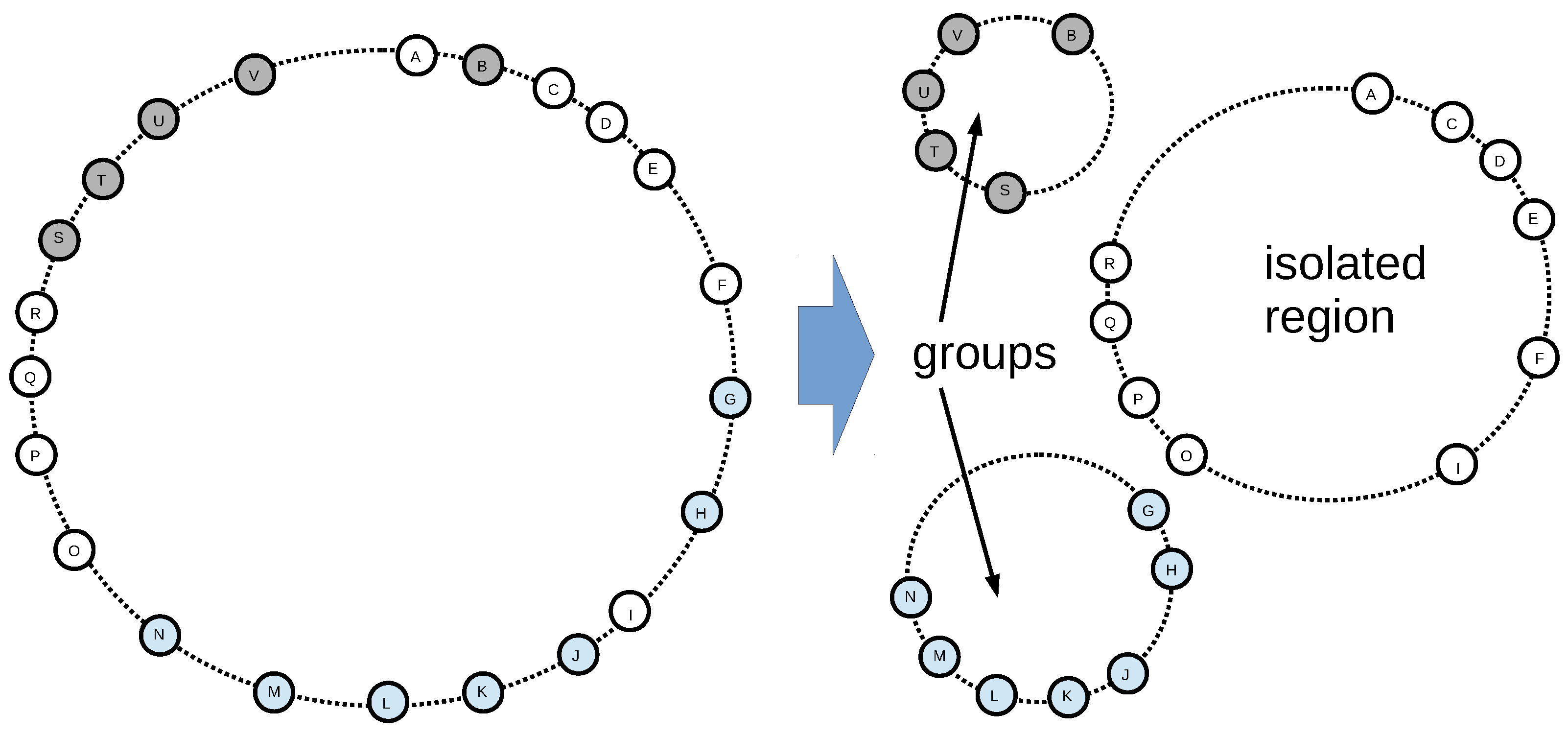
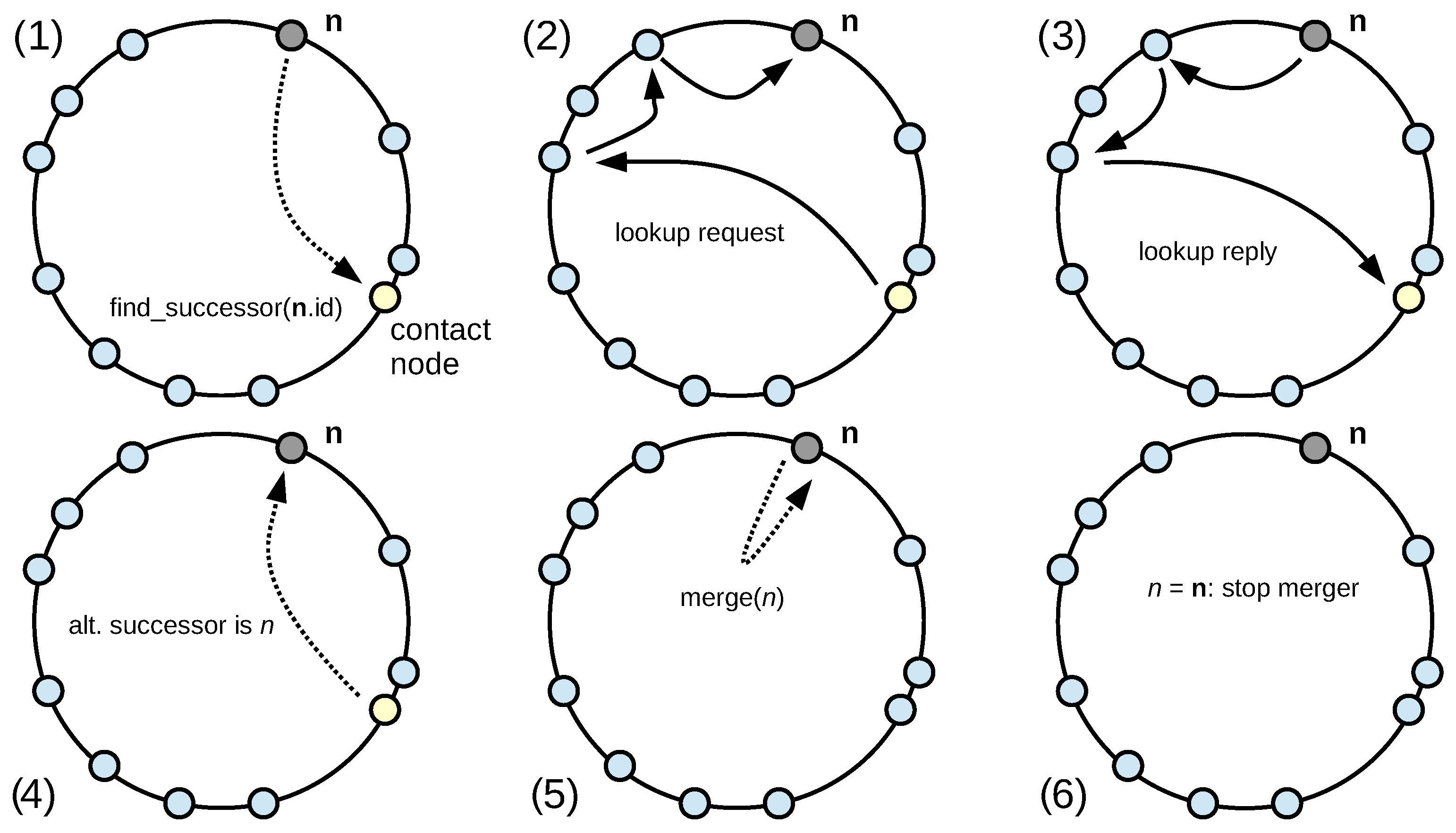
3.1. Identification of New Overlays
3.2. Coordinating the Merging Attempts in a Construct Through a Merging Probability
3.3. Merging Algorithm
3.4. Termination
3.5. Parallelization
3.6. Example of Merging of Several Rings
4. Evaluation
4.1. Evaluation Goals—Metrics
- Number of Constructs:
- Correct Pointers:
- Traffic Overhead:
4.2. Simulation Setup
5. Evaluation Results
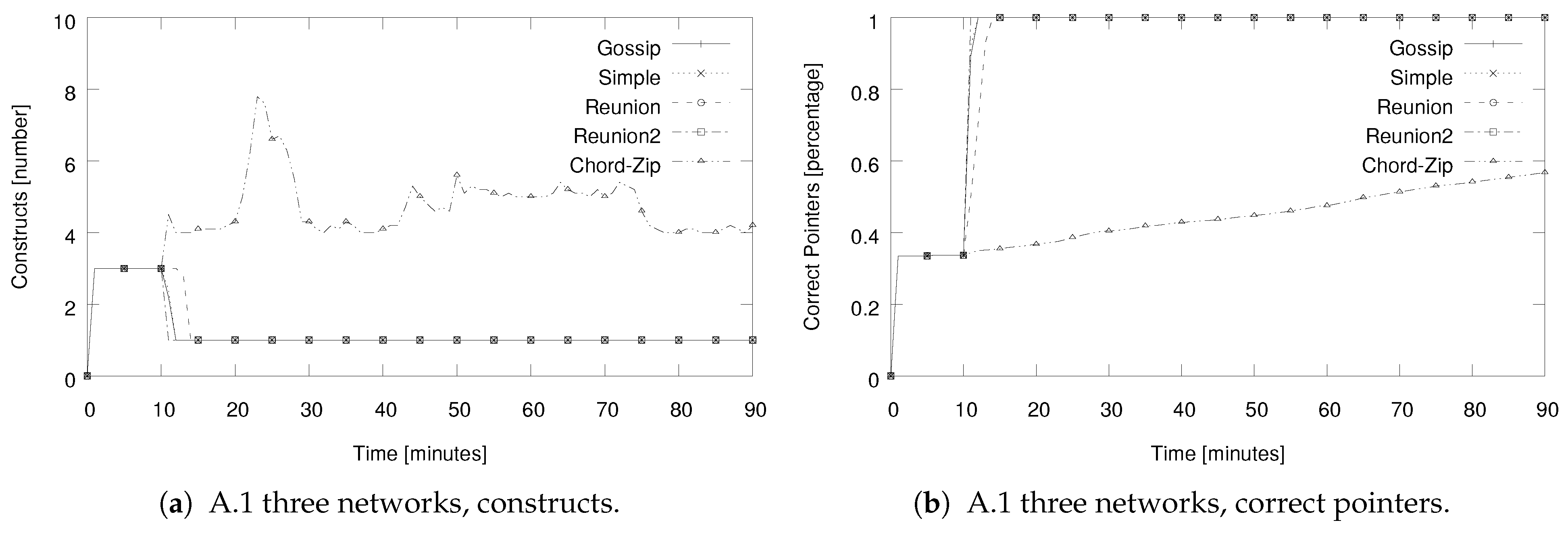
5.1. Evaluation Results for Setup A.1: Simultaneous Merging of Three Networks
5.2. Evaluation Results for Setup B.1: Comparison of Gossip-Based Ring-Unification Algorithm and Ring Reunion Algorithm
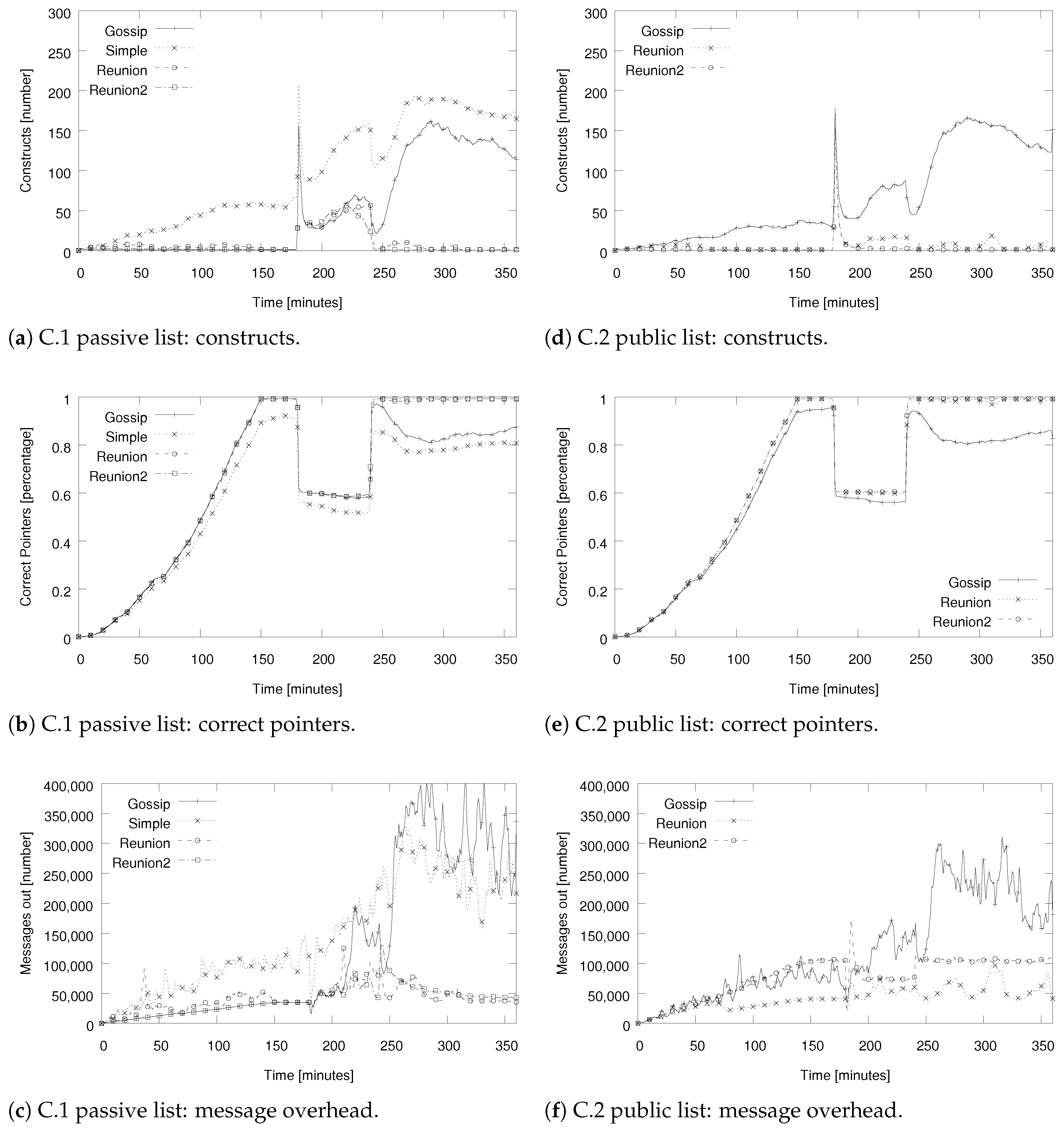
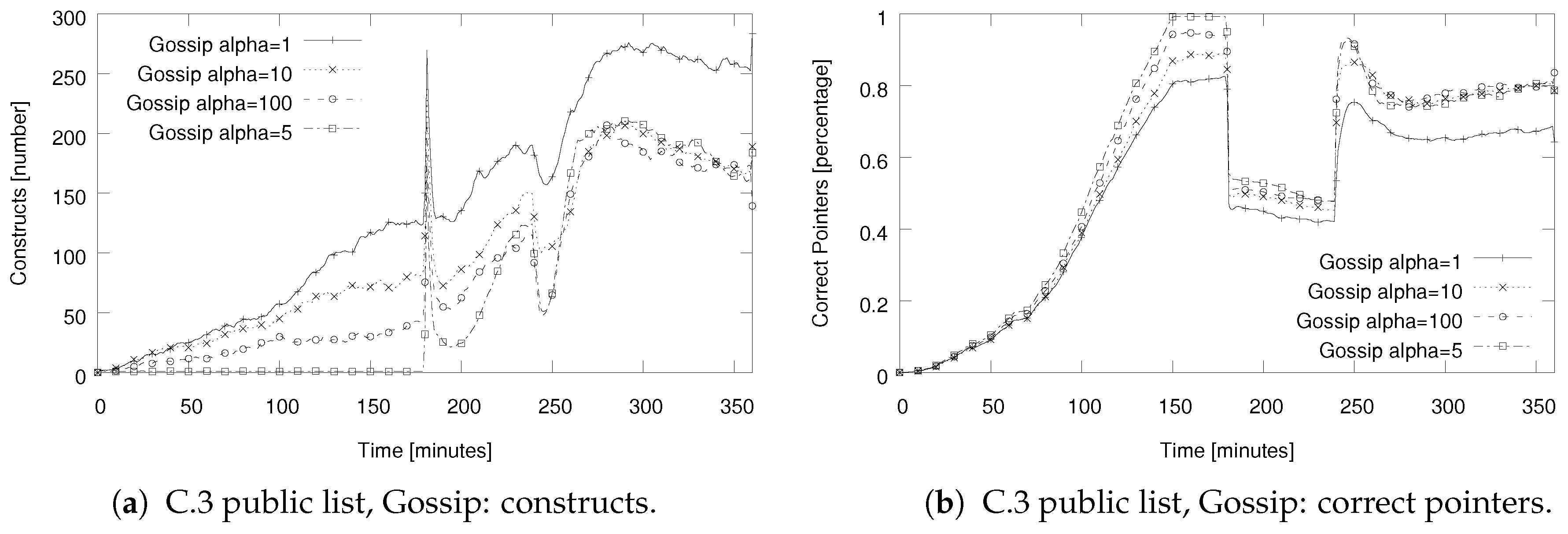
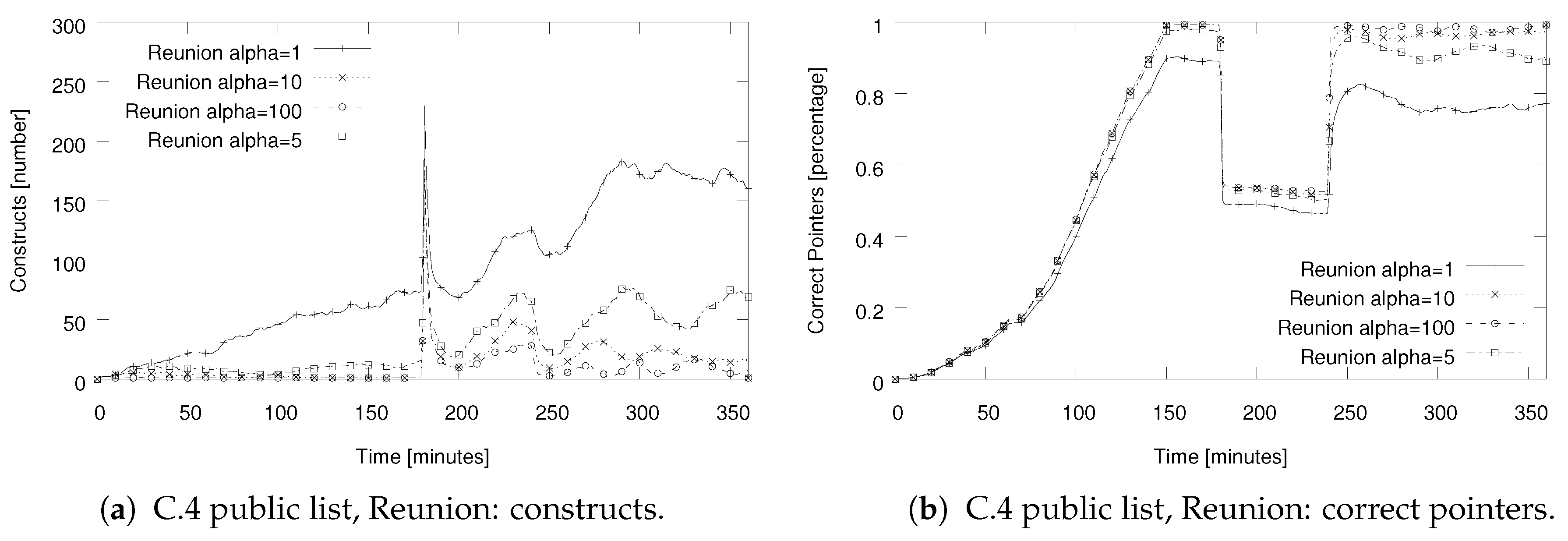
5.3. Evaluation Results for Setups C.1–5: Testing Various Approaches to Start Merging Instances
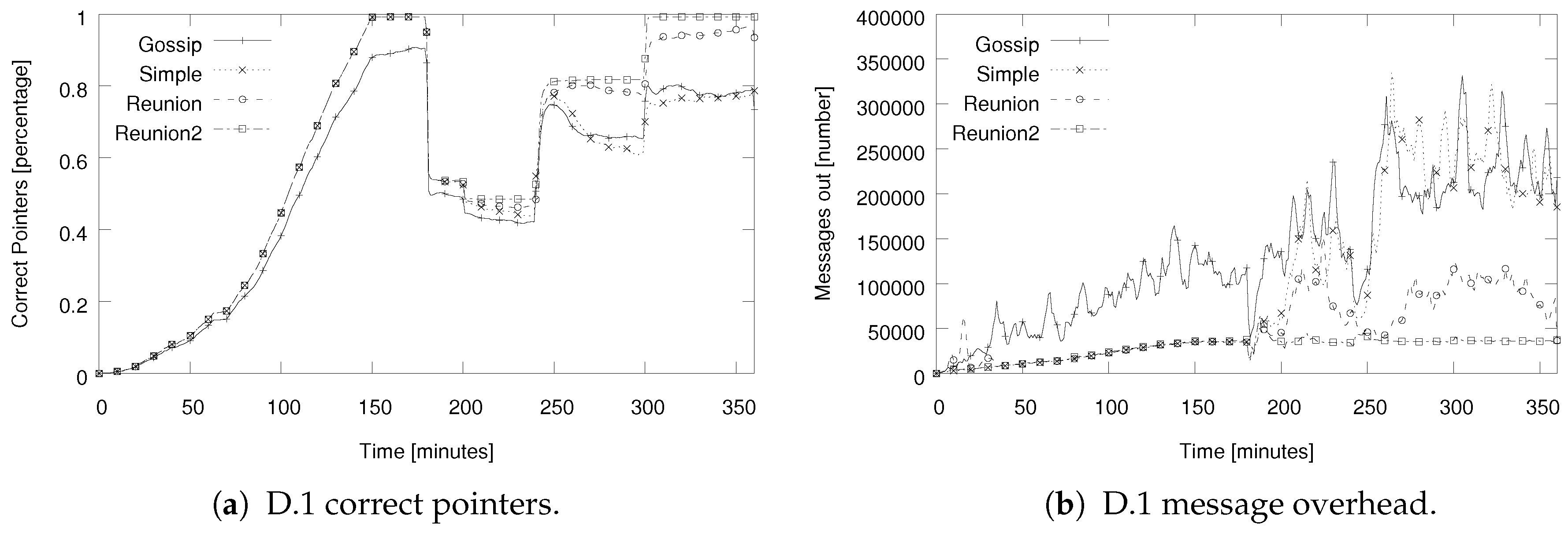
5.4. Evaluation Results for Setup D.1: A Complex Scenario
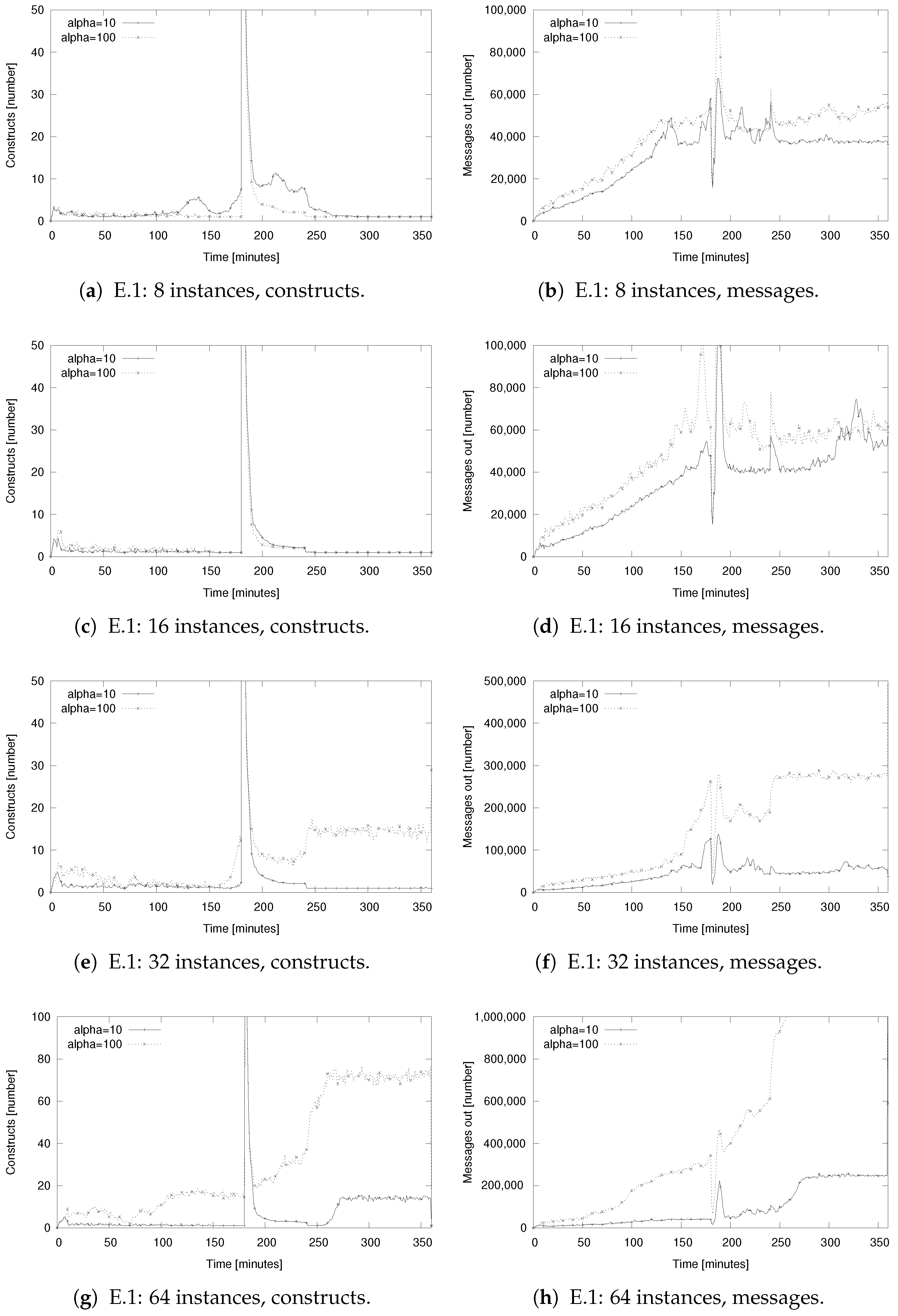
5.5. Evaluation Results for Setups E.1–2: Parameter Studies and Churn
5.6. Discussion on Real-World Deployment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dabek, F.; Zhao, B.; Druschel, P.; Kubiatowicz, J.; Stoica, I. Towards a Common API for Structured Peer-to-Peer Overlays. In Proceedings of the International Workshop on Peer-To-Peer Systems, Berkeley, CA, USA, 21–22 February 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 33–44. [Google Scholar]
- Stoica, I.; Morris, R.; Karger, D.; Kaashoek, M.F.; Balakrishnan, H. Chord: A Scalable Peer-to-Peer Lookup Service for Internet Applications. In Proceedings of the SIGCOMM ’01: Proceedings of the International Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, San Diego, CA, USA, 27–31 August 2001; ACM: New York, NY, USA, 2001; pp. 149–160. [Google Scholar] [CrossRef]
- Rowstron, A.I.T.; Druschel, P. Pastry: Scalable, Decentralized Object Location, and Routing for Large-Scale Peer-to-Peer Systems. In Proceedings of the Middleware 2001, IFIP/ACM International Conference on Distributed Systems Platforms, Heidelberg, Germany, 12–16 November 2001; Guerraoui, R., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2001; Volume 2218, pp. 329–350. [Google Scholar] [CrossRef]
- Graffi, K.; Masinde, N. LibreSocial: A Peer-To-Peer Framework for Online Social Networks. Wiley Concurr. Comput. Pract. Exp. 2021, 33, e6150. [Google Scholar] [CrossRef]
- Aki, H.M.; Alberro, H.; Firoozi, E.; Qiang, X. Internet Shutdowns—Assessing Their Impact and Effective Countermeasures. Available online: https://www.freiheit.org/publikation/internet-shutdowns (accessed on 26 May 2025).
- Kis, Z.L.; Szabó, R. Chord-Zip: A Chord-ring Merger Algorithm. Commun. Lett. 2008, 12, 605–607. [Google Scholar] [CrossRef]
- Shafaat, T.M.; Ghodsi, A.; Haridi, S. Dealing with Network Partitions in Structured Overlay Networks. Peer- Netw. Appl. 2009, 2, 334–347. [Google Scholar] [CrossRef]
- Liebau, N.; Pussep, K.; Graffi, K.; Kaune, S.; Beyer, A.; Jahn, E.; Steinmetz, R. The Impact of the P2P Paradigm on the New Media Industries. In Proceedings of the AMCIS 2007: 13th Americas Conference on Information Systems, Keystone, CO, USA, 9–12 August 2007; Association for Information Systems: Atlanta, GA, USA, 2007; p. 255. [Google Scholar]
- Kniesburges, S.; Koutsopoulos, A.; Scheideler, C. Re-Chord: A Self-Stabilizing Chord Overlay Network. In Proceedings of the Twenty-Third Annual ACM SPAA: Symposium on Parallelism in Algorithms and Architectures (SPAA’11), New York, NY, USA, 4–6 June 2011; pp. 235–244. [Google Scholar] [CrossRef]
- Benter, M.; Soorati, M.D.; Kniesburges, S.; Koutsopoulos, A.; Graffi, K. Ca-Re-Chord: A Churn Resistant Self-Stabilizing Chord Overlay Network. In Proceedings of the 2013 Conference on Networked Systems, NetSys 2013, Stuttgart, Germany, 11–15 March 2013; IEEE Computer Society: Washington, DC, USA, 2013; pp. 27–34. [Google Scholar] [CrossRef]
- Datta, A.; Aberer, K. The Challenges of Merging two similar Structured Overlays: A Tale of Two Networks. In Self-Organizing Systems, First International Workshop, IWSOS 2006, and Third International Workshop on New Trends in Network Architectures and Services, EuroNGI 2006, Passau, Germany, 18–20 September 2006; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4124, pp. 7–22. [Google Scholar] [CrossRef]
- Datta, A. Merging ring-structured overlay indices: Toward network-data transparency. Computing 2012, 94, 783–809. [Google Scholar] [CrossRef]
- Aberer, K.; Cudré-Mauroux, P.; Datta, A.; Despotovic, Z.; Hauswirth, M.; Punceva, M.; Schmidt, R. P-Grid: A Self-organizing Structured P2P System. ACM SIGMOD Rec. 2003, 32, 29–33. [Google Scholar] [CrossRef]
- Kis, Z.L.; Szabó, R. Interconnected Chord-rings. Netw. Protoc. Algorithms 2010, 2, 132–146. [Google Scholar] [CrossRef][Green Version]
- Wu, S.; Raghavan, K.; Di, S.; Chen, Z.; Cappello, F. DGRO: Diameter-Guided Ring Optimization for Integrated Research Infrastructure Membership. arXiv 2024, arXiv:2410.11142. [Google Scholar]
- Nguyen, D.; Hoang, N.; Nguyen, B.M.; Tran, V. PSPChord—A Novel Fault Tolerance Approach for P2P Overlay Network. In Proceedings of the Smart Computing and Communication, Tokyo, Japan, 10–12 December 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 386–396. [Google Scholar] [CrossRef]
- Kaur, R.; Gabrijelčič, D.; Klobučar, T. Churn Handling Strategies to Support Dependable and Survivable Structured Overlay Networks. IETE Tech. Rev. 2022, 39, 179–195. [Google Scholar] [CrossRef]
- Kaur, R.; Sangal, A.L.; Kumar, K. Churn handling strategies for structured overlay networks: A survey. Multiagent Grid Syst. 2017, 13, 331–351. [Google Scholar] [CrossRef]
- Naik, A.R.; Keshavamurthy, B.N. Next level Peer-to-Peer Overlay Networks under high Churns: A Survey. Peer-Netw. Appl. 2020, 13, 905–931. [Google Scholar] [CrossRef]
- Hussain, A.; Keshavamurthy, B.N. A multi-dimensional routing based approach for efficient communication inside partitioned social networks. Peer-Netw. Appl. 2019, 12, 830–849. [Google Scholar] [CrossRef]
- Amft, T.; Guidi, B.; Graffi, K.; Ricci, L. FRoDO: Friendly Routing over Dunbar-based Overlays. In Proceedings of the IEEE 40th Conference on Local Computer Networks (LCN), Clearwater Beach, FL, USA, 26–29 October 2015; pp. 356–364. [Google Scholar]
- Gross, C.; Richerzhagen, B.; Stingl, D.; Münker, C.; Hausheer, D.; Steinmetz, R. Geodemlia: Persistent storage and reliable search for peer-to-peer location-based services. In Proceedings of the 13th IEEE International Conference on Peer-to-Peer Computing, IEEE P2P 2013, Trento, Italy, 9–11 September 2013; IEEE: New York, NY, USA, 2013; pp. 1–2. [Google Scholar] [CrossRef]
- Qiu, H.; Ji, T.; Zhao, S.; Chen, X.; Qi, J.; Cui, H.; Wang, S. A Geography-Based P2P Overlay Network for Fast and Robust Blockchain Systems. IEEE Trans. Serv. Comput. 2023, 16, 1572–1588. [Google Scholar] [CrossRef]
- Aquib, M.; Prashanth, P. GeoConnect: Efficient Peer to Peer Network Connectivity for Blockchain Systems. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Fang, J.; Habibi, F.; Bruhwiler, K.; Alshammari, F.; Singh, A.A.; Zhou, Y.; Nawab, F. PeloPartition: Improving Blockchain Resilience to Network Partitioning. In Proceedings of the IEEE International Conference on Blockchain, Blockchain 2022, Espoo, Finland, 22–25 August 2022; IEEE: New York, NY, USA, 2022; pp. 274–281. [Google Scholar] [CrossRef]
- Paphitis, A.; Kourtellis, N.; Sirivianos, M. Resilience of Blockchain Overlay Networks. In Proceedings of the Network and System Security—17th International Conference, NSS 2023, Canterbury, UK, 14–16 August 2023; Li, S., Manulis, M., Miyaji, A., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2023; Volume 13983, pp. 93–113. [Google Scholar] [CrossRef]
- Marcus, Y.; Heilman, E.; Goldberg, S. Low-Resource Eclipse Attacks on Ethereum’s Peer-to-Peer Network. IACR Cryptol. ePrint Arch. 2018, 236. [Google Scholar]
- Saad, M.; Cook, V.; Nguyen, L.N.; Thai, M.T.; Mohaisen, D. Exploring Partitioning Attacks on the Bitcoin Network. IEEE/ACM Trans. Netw. 2022, 30, 202–214. [Google Scholar] [CrossRef]
- Masinde, N.; Graffi, K. Peer-to-Peer-Based Social Networks: A Comprehensive Survey. SN Comput. Sci. 2020, 1, 299. [Google Scholar] [CrossRef]
- Cutillo, L.A.; Molva, R.; Önen, M. Safebook: A distributed privacy preserving Online Social Network. In Proceedings of the 12th IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks, WOWMOM 2011, Lucca, Italy, 20–24 June 2011; IEEE Computer Society: Washington, DC, USA, 2011; pp. 1–3. [Google Scholar] [CrossRef]
- Guidi, B.; Amft, T.; Salve, A.D.; Graffi, K.; Ricci, L. DiDuSoNet: A P2P architecture for distributed Dunbar-based social networks. Peer-Netw. Appl. 2016, 9, 1177–1194. [Google Scholar] [CrossRef]
- Shafaat, T.M.; Ghodsi, A.; Haridi, S. Managing Network Partitions in Structured P2P Networks. In Handbook of Peer-to-Peer Networking; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1127–1147. [Google Scholar]
- Graffi, K.; Disterhöft, A. SkyEye: A Tree-Based Peer-To-Peer Monitoring Approach. Elsevier Pervasive Mob. Comput. 2017, 40, 593–610. [Google Scholar] [CrossRef]
- Rapp, V.; Graffi, K. Continuous Gossip-Based Aggregation through Dynamic Information Aging. In Proceedings of the 22nd International Conference on Computer Communication and Networks, ICCCN 2013, Nassau, Bahamas, 30 July–2 August 2013; IEEE: New York, NY, USA, 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Binzenhöfer, A.; Staehle, D.; Henjes, R. Estimating the Size of a Chord Ring; Technical Report; University of Würzburg: Würzburg, Germany, 2004. [Google Scholar]
- Feldotto, M.; Graffi, K. Systematic evaluation of peer-to-peer systems using PeerfactSim. KOM. Concurr. Comput. Pract. Exp. 2016, 28, 1655–1677. [Google Scholar] [CrossRef]
- Feldotto, M.; Graffi, K. Comparative evaluation of peer-to-peer systems using PeerfactSim. KOM. In Proceedings of the International Conference on High Performance Computing & Simulation, HPCS 2013, Helsinki, Finland, 1–5 July 2013; IEEE: New York, NY, USA, 2013; pp. 99–106. [Google Scholar] [CrossRef]
- Graffi, K. PeerfactSim.KOM: A P2P System Simulator – Experiences and Lessons Learned. In Proceedings of the IEEE P2P’11: Proceedings of the International Conference on Peer-to-Peer Computing, Kyoto, Japan, 31 August–2 September 2011; IEEE: New York, NY, USA, 2011; pp. 154–155. [Google Scholar] [CrossRef]
- Ng, T.S.E.; Zhang, H. Global Network Positioning: A New Approach to Network Distance Prediction. ACM SIGCOMM Comput. Commun. Rev. 2002, 32, 61. [Google Scholar] [CrossRef]
- Matthews, W.; Cottrell, L. The PingER Project: Active Internet performance Monitoring for the HENP Community. Commun. Mag. 2000, 38, 130–136. [Google Scholar] [CrossRef]
- Masinde, N.; Khitman, L.; Dlikman, I.; Graffi, K. Systematic Evaluation of LibreSocial—A Peer-to-Peer Framework for Online Social Networks. Future Internet 2020, 12, 140. [Google Scholar] [CrossRef]
- Wette, P.; Graffi, K. Adding Capacity-Aware Storage Indirection to Homogeneous Distributed Hash Tables. In Proceedings of the 2013 Conference on Networked Systems, NetSys 2013, Stuttgart, Germany, 11–15 March 2013; IEEE Computer Society: Washington, DC, USA, 2013; pp. 35–42. [Google Scholar] [CrossRef]
- Disterhöft, A.; Graffi, K. Minicamp: Middleware for Incomplete Participation in Structured Peer-to-Peer Monitoring Protocols. In Proceedings of the 32nd IEEE International Conference on Advanced Information Networking and Applications, AINA 2018, Krakow, Poland, 16–18 May 2018; Barolli, L., Takizawa, M., Enokido, T., Ogiela, M.R., Ogiela, L., Javaid, N., Eds.; IEEE Computer Society: Washington, DC, USA, 2018; pp. 1034–1042. [Google Scholar] [CrossRef]
- Ippisch, A.; Sati, S.; Graffi, K. Device to device communication in mobile Delay Tolerant networks. In Proceedings of the 21st IEEE/ACM International Symposium on Distributed Simulation and Real Time Applications, DS-RT 2017, Rome, Italy, 18–20 October 2017; D’Ambrogio, A., Grande, R.E.D., Garro, A., Tundis, A., Eds.; IEEE Computer Society: Washington, DC, USA, 2017; pp. 91–98. [Google Scholar] [CrossRef]
- Ippisch, A.; Graffi, K. Infrastructure Mode Based Opportunistic Networks on Android Devices. In Proceedings of the 31st IEEE International Conference on Advanced Information Networking and Applications, AINA 2017, Taipei, Taiwan, 27–29 March 2017; Barolli, L., Takizawa, M., Enokido, T., Hsu, H., Lin, C., Eds.; IEEE Computer Society: Washington, DC, USA, 2017; pp. 454–461. [Google Scholar] [CrossRef]








| General Settings | |
|---|---|
| Simulator details | PeerfactSim.KOM [36,37,38], 10 seeds per setup |
| Network model | GNP [39], jitter based on [40], no packet loss |
| (A) Simultaneous Merging of Three Networks | |
| Algorithms | Chord–Zip [6], Simple Ring Unification [7], Gossip-based Ring Unification [7], Ring Reunion (1 and 4 instances), no churn |
| A.1 Three rings | 0 min: setup of 1024 nodes in three Chord rings (A: 341, B: 341, and C: 342 nodes). From 10 min: merge algorithm started by passing random nodes from A and B to one node in C. 180 min: simulation end. |
| (B) Direct Comparison of Gossip-based Ring Unification [7] and Ring Reunion with Various Instances | |
| Algorithms | Gossip-based Ring Unification (4 + 4 instances), Ring Reunion (4, 8 and 16 instances), no churn |
| B.1 Two large rings | 0–150 min: setup of 10,242 nodes in two Chord rings (each with 5121 nodes). From 10 min: merge algorithm started by adding one connecting link. 180 min: simulation end. |
| (C) Testing of Various Approaches to Identify Contacts in Other Overlays and to Start the Merging Process | |
| Algorithms | Chord–Zip [6], Simple Ring Unification [7], Gossip-based Ring Unification [7], Ring Reunion (1 and 4 instances), no churn |
| Scenario | 0–150 min: 1024 nodes join two different Chord rings (each with 512 nodes). From 180 min: 310 nodes (in one country) are isolated. 240 min: isolation is canceled, all nodes are reachable. 360 min: simulation end. |
| C.1 Passive list | Maintaining a list of previously online nodes, which is checked every 3 min. If active node is found, start merging process. |
| C.2 Public list | Publicly known 160 contacts are tested every 4 min in iteration. Once an active contact is found, the merging process is started with probability 1. |
| C.3–5 Public list, dynamic probability: Gossip, Reunion, Reunion2 | Nodes maintain a list of 160 nodes which is obtained from bootstrap node during join process. Checking online presence of a random node in this list every 4 min. Start merging process with probability of , where is the estimated number of nodes in the current construct. |
| (D) Complex Scenario Using the Public List Approach | |
| Algorithms | Gossip-based Ring-Unification Algorithm [7] and the Ring Reunion Algorithm (1 and 4 instances), public list with , no churn |
| D.1 Complex rings | 0–150 min: setup of 1024 nodes in one Chord ring. Group of 400 nodes is isolated in 180–240 min. Group of 50 nodes is isolated in 200–240 min. Group of 100 nodes is isolated in 240–300 min. 360 min: simulation end. |
| (E) Parameter Studies and Churn | |
| Algorithms | Ring Reunion (8, 16, 32, 64 instances), public list, churn enabled |
| Scenario | 0–150 min: 1024 nodes join Chord ring. From 180 min: 400 nodes become isolated. 240 min: isolation is stopped, all nodes are reachable. 360 min: simulation end. |
| E.1 Changing and Instances | Algorithm is combined with . The interval with which the public list selects a merging candidate is set to 5 min. |
| E.2 Changing frequency of merge attempts | Algorithm combined with intervals of 5, 10, 15, and 20 min in which merger instances are started, to find compromise between operation time and bandwidth consumption. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amft, T.; Graffi, K. A Tale of Many Networks: Splitting and Merging of Chord-like Overlays in Partitioned Networks. Future Internet 2025, 17, 248. https://doi.org/10.3390/fi17060248
Amft T, Graffi K. A Tale of Many Networks: Splitting and Merging of Chord-like Overlays in Partitioned Networks. Future Internet. 2025; 17(6):248. https://doi.org/10.3390/fi17060248
Chicago/Turabian StyleAmft, Tobias, and Kalman Graffi. 2025. "A Tale of Many Networks: Splitting and Merging of Chord-like Overlays in Partitioned Networks" Future Internet 17, no. 6: 248. https://doi.org/10.3390/fi17060248
APA StyleAmft, T., & Graffi, K. (2025). A Tale of Many Networks: Splitting and Merging of Chord-like Overlays in Partitioned Networks. Future Internet, 17(6), 248. https://doi.org/10.3390/fi17060248







