Grouping-Based Dynamic Routing, Core, and Spectrum Allocation Method for Avoiding Spectrum Fragmentation and Inter-Core Crosstalk in Multi-Core Fiber Networks

Abstract

In this paper, we propose a grouping-based dynamic routing, core, and spectrum allocation (RCSA) method for preventing spectrum fragmentation and inter-core crosstalk in elastic optical path networks based on multi-core fiber environments. Multi-core fibers enable us to considerably enhance the transmission capacity of optical links; however, this induces inter-core crosstalk, which degrades the quality of optical signals. We should thus avoid using the same frequency bands in adjacent cores in order to ensure high-quality communications. However, this simple strategy leads to inefficient use of frequency-spectrum resources, resulting in spectrum fragmentation and a high blocking probability for lightpath establishment. The proposed method allows one to overcome this difficulty by grouping lightpath-setup requests according to their required number of frequency slots. By assigning lightpath-setup requests belonging to the same group to cores according to their priority, the proposed method aims to suppress inter-core crosstalk. Furthermore, the proposed method is designed to mitigate spectrum fragmentation by determining the prioritized frequency bandwidth for lightpath-setup requests according to their required number of frequency slots. We show that the proposed method reduces the blocking of lightpath establishment while suppressing inter-core crosstalk through simulation experiments.

1. Introduction

Elastic optical path networks represent a promising communication infrastructure that can accommodate the rapidly increasing traffic in a future networked society [1,2]. In elastic optical path networks, frequency-spectrum resources are divided into small segments (typically 12.5 GHz) called frequency slots (FSs). Therefore, they can be allocated to communication channels more flexibly than conventional wavelength-division-multiplexing-based optical path networks. Furthermore, with the application of multilevel modulation, such as Quadrature Amplitude Modulation (QAM), elastic optical path networks enable us to enhance the utilization of frequency-spectrum resources [3,4].

Multi-core fibers, which are expected to be used as network links in future optical networks [5,6], consist of multiple cores, where optical signals with the same FSs using different cores can be simultaneously transmitted, considerably enhancing the transmission capacity of optical fibers. However, the use of multi-core fibers induces inter-core crosstalk [7,8] among the optical signals that pass through adjacent cores, which degrades the quality of the optical signals. In order to ensure high communication quality, the optical signal-to-noise ratio (OSNR) should exceed a certain threshold at the receiver nodes [9]. Because the accumulation of the inter-core crosstalk leads to the violation of this criterion, it is essential to maintain inter-core crosstalk at a low level.

In this paper, we propose a dynamic routing, core, and spectrum allocation (RCSA) method to address this problem. RCSA is one of the most important technical issues in elastic optical networks, where data are transmitted via routes assigned FSs named lightpaths [10,11]. RCSA methods determine routes, cores in multi-core fibers, and FSs to establish lightpaths, assuming static or dynamic scenarios [12,13]. In the static scenario, the traffic matrix, i.e., the traffic demand of all senders and receivers in an elastic optical path network, is provided in advance. We can determine routes, cores, and FSs for lightpaths to be established by adopting optimization methods such as meta-heuristic algorithms and mathematical programming. On the other hand, in the dynamic scenario, the traffic matrix is not provided. Instead, we dynamically establish lightpaths in response to lightpath-setup requests generated stochastically over time while satisfying two constraints: spectrum continuity and spectrum contiguity. The spectrum continuity constraint establishes that common FSs in all links along the route must be used for the establishment of each lightpath. The spectrum contiguity constraint establishes that each lightpath must use successive FSs. Lightpath establishment is blocked in the case where there are no candidates satisfying these constraints. Therefore, when designing elastic optical path networks in the dynamic scenario, we should consider the blocking of lightpath establishment in addition to the impact of inter-core crosstalk.

One simple strategy to mitigate the impact of inter-core crosstalk is to avoid the use of the same FSs in adjacent cores. However, this strategy wastes frequency-spectrum resources. As a result, it increases the blocking probability of lightpath establishment, which is an important performance metric of optical networks assuming dynamic RCSA. Furthermore, for the efficient use of frequency-spectrum resources, we should consider situations where the number of available cores is limited compared with the number of FSs required by newly established lightpaths. In such situations, it becomes challenging to simultaneously prevent the blocking of lightpath establishment and suppress inter-core crosstalk. The proposed method allows one to overcome this difficulty by grouping lightpath-setup requests according to their required number of FSs. By assigning lightpath-setup requests belonging to the same group to cores according to their priority, the proposed method aims to suppress inter-core crosstalk. Furthermore, the proposed method mitigates spectrum fragmentation by determining the prioritized frequency bandwidth for lightpath-setup requests based on the number of FSs required by the group to which they belong. Through simulation experiments, we show that the proposed method allows for the suppression of inter-core crosstalk while keeping the blocking probability of lightpath establishment low.

The contributions of this paper are as follows:

• We propose a dynamic RCSA method that prevents the blocking of newly established lightpaths while maintaining inter-core crosstalk at a low level, even in cases where the number of available cores is limited.
• The proposed RCSA method efficiently accommodates lightpath-setup requests with various numbers of required FSs through a grouping-based core allocation approach.
• Furthermore, our proposed RCSA method can utilize frequency-spectrum resources by allocating the preferred frequency bandwidth to lightpath-setup requests in each group.

The rest of this paper is organized as follows. In Section 2, we discuss related works. Section 3 explains the system model, assuming elastic optical path networks with multi-core fiber environments. Our proposed RCSA method is discussed in Section 4. We evaluate the performance of our proposed RCSA method through simulation experiments in Section 5. Finally, we conclude this paper in Section 6.

2. Related Works

In the past, RCSA methods, including both static and dynamic approaches, have been proposed to prevent the blocking of lightpath establishment while suppressing inter-core crosstalk.

In [14], the authors proposed a static RCSA method with multi-input multi-output (MIMO)-based crosstalk suppression. The authors provided an Integer Linear Programming (ILP) model to show the effect of MIMO-based crosstalk suppression. The authors of [15] introduced a static RCSA method using the ILP formulation. It aims to minimize the maximum number of FSs on any core while ensuring a low level of inter-core crosstalk. The authors of [16] considered the asymmetric assignment of fiber cores in a counter-propagating manner to reduce inter-core crosstalk. They proposed a static RCSA method by formulating an ILP problem and developing a heuristic algorithm to optimize the utilization of network-spectrum resources. In [17], the authors addressed the scheduling of simultaneous lightpaths to reduce inter-core crosstalk. A new metric was introduced to estimate crosstalk by jointly considering spatial, spectral, and temporal dimensions, and an ILP model and a heuristic algorithm were developed to address the routing, spectrum, core, and time assignment problem. In [18], the authors introduced the design of multi-core fiber networks using shared-backup path protection, aiming to enhance both survivability and signal quality. They formulated a crosstalk-aware RCSA problem as an ILP model, minimizing spectrum usage and inter-core crosstalk. Furthermore, they proposed an auxiliary graph-based heuristic algorithm.

The authors of [19] introduced a dynamic RCSA method based on the Connected Component Labeling (CCL) algorithm, which is commonly used in image processing. In this method, the spectrum of multi-core fibers is represented as a matrix, and the CCL algorithm efficiently identifies available spectrum regions for lightpath-setup requests with low computational complexity. In [20], the authors proposed a dynamic RCSA method that combines single- and multi-path routing with adaptive modulation and spectrum mapping. The method reduces the blocking probability and improves energy efficiency in dynamic scenarios while maintaining acceptable crosstalk and fragmentation levels. In [21], the authors proposed a dynamic RCSA method using a self-organizing feature mapping model to handle multi-dimensional constraints. By mapping core-level features to transmission quality, the method selects the optimal cores and identifies low-crosstalk spectrum blocks through a two-step classification. The authors of [22] introduced a 3D fragmentation metric, considering frequency, time, and space dimensions. Based on this metric, a dynamic RCSA scheme was developed to minimize future fragmentation and maximize core resource availability. The authors of [23] proposed an energy-efficient grooming and hybrid crosstalk solution algorithm to reduce both energy consumption and inter-core crosstalk. The algorithm selects candidate paths based on path length and load, applying grooming when energy efficiency conditions are met. For other requests, new paths are established using core prioritization and crosstalk-aware strategies. The authors of [24] introduced a dynamic RCSA method that aims to reduce the blocking probability of lightpath establishment by avoiding the use of cores where many FSs are already used while mitigating inter-core crosstalk by avoiding the use of the same FSs in adjacent cores. In [25], the authors proposed an on-demand spectrum and core allocation method based on two policies: core prioritization, which avoids adjacent core usage to reduce inter-core crosstalk, and core classification, which assigns uniform bandwidth connections to minimize fragmentation. They showed improved crosstalk performance and reduced blocking probability under various network conditions through simulation experiments.

3. System Model

3.1. Elastic Optical Path Networks with Multi-Core Fibers

Figure 1 illustrates the system model of elastic optical path networks assumed in this paper. Let $\mathcal{G}=(\mathcal{V},\mathcal{E})$ denote an elastic optical path network represented by a directed graph, where $\mathcal{V}$ represents a set of nodes and $\mathcal{E}$ represents a set of links. Each node has input links and output links, each of which consists of a multi-core fiber. All multi-core fibers have the same number of cores. Let $\mathcal{C}=\{c_1,c_2,\dots ,c_{\left|\mathcal{C}\right|}\}$ denote a set of cores in each fiber. In each core, frequency-spectrum resources are divided into FSs, the unit of which is 12.5 [GHz]. Let $\mathcal{F}=\{f_1,f_2,\dots ,f_{\left|\mathcal{F}\right|}\}$ represent a set of available FSs. In this paper, we assume that the FSs are numbered in ascending order. Multiple optical signals of different FSs can simultaneously pass through each core.

As shown in Figure 1, lightpaths are established to transmit data requested by senders with the use of successive FSs. Note that there is a gap called a guard band between successive lightpaths on the FSs to avoid interference. In this paper, the guard band length is assumed to be 1 FS. The required number $R_p$ of FSs for lightpath-setup request p is calculated based on the traffic demand and the modulation level, which is given by

$$R_p=\lceil {\displaystyle \frac{D}{T{M}_p}}\rceil ,$$

(1)

where D represents the traffic demand [bps] and T represents the transmission capacity [bps] per FS for 1 bit/symbol transmission. $M_p$ denotes the modulation level of lightpath p, which is determined according to the transmission distance of the lightpath. Due to the restriction of the OSNR, simple modulation schemes such as Binary Phase-Shift Keying (BPSK) ($M_p=1$) and Quadrature PSK (QPSK) ($M_p=2$) are used for long-distance lightpaths. On the other hand, for short-distance lightpaths with high OSNRs, modulation schemes such as 8-QAM ($M_p=3$) and 16-QAM ($M_p=4$), which have high frequency utilization efficiency, can be used.

3.2. Lightpath Establishment in Dynamic RCSA Scenario

In the dynamic RCSA scenario, according to the lightpath-setup requests generated by the senders, lightpaths to the receivers are established by selecting routes, cores, and FSs, as shown in Figure 1. The blocking probability of lightpath establishment is generally used as the performance metric in the dynamic scenario. Lightpath establishment is blocked when there are no candidate FSs satisfying the spectrum continuity and contiguity constraints in any core along any route. Spectrum fragmentation is one of the major factors that increase the blocking probability.

Figure 2a shows an example of spectrum fragmentation where the available FSs are divided into many small segments. When spectrum fragmentation occurs, it is difficult to establish lightpaths requiring a large number of FSs. This is because there tends not to be sufficient available FSs along the routing path. On the other hand, in the case shown in Figure 2b, where spectrum fragmentation does not occur, we can easily establish lightpaths requiring a large number of FSs. As a result, the blocking probability can be reduced. Therefore, it is very important to prevent spectrum fragmentation in the dynamic RCSA scenario.

3.3. Inter-Core Crosstalk

Besides the blocking of lightpath establishment, the impact of inter-core crosstalk must also be considered in multi-core fiber environments. We can simultaneously establish lightpaths using the same FSs with different cores within the same fiber. Therefore, using multi-core fiber environments enhances the transmission capacity of elastic optical path networks. However, at the same time, inter-core crosstalk becomes a severe issue for lightpaths using the same FSs in different cores. Inter-core crosstalk impairs the optical signal quality by accumulating at each link along established lightpaths and introducing noise at the receiver nodes. If the crosstalk level at the receiver nodes exceeds a certain threshold, data transmission could fail, even if the lightpaths are correctly established.

Here, we consider the case where there are two cores, $c_i$ and $c_j$, in a homogeneous multi-core fiber with length L, and an optical signal is transmitted through core $c_i$. In this case, a portion of this signal leaks into core $c_j$. Let $P_i\left(L\right)$ and $P_j\left(L\right)$ denote the transmitted power in cores $c_i$ and $c_j$, respectively, at the output of the multi-core fiber. In this case, the crosstalk ${\mathrm{XT}}_{i,j}$ from core $c_i$ to $c_j$ at the output of the multi-core fiber with length L is defined as

$${\mathrm{XT}}_{i,j}={\displaystyle \frac{P_j\left(L\right)}{P_i\left(L\right)}}=tanh\left(h_{i,j}L\right),$$

(2)

where $h_{i,j}$ denotes the power coupling coefficient [26]. When the value of ${\mathrm{XT}}_{i,j}$ is sufficiently small, it can be approximated as $h_{i,j}L$. The power coupling coefficient $h_{i,j}$ is given by

$$h_{i,j}={\displaystyle \frac{2{\kappa }^2{b}_r}{\alpha {\Lambda }_{i,j}}},$$

(3)

where $\kappa$ denotes the mode coupling coefficient, $b_r$ denotes the bending radius, $\alpha$ denotes the propagation constant, and ${\Lambda }_{i,j}$ denotes the core pitch between cores $c_i$ and $c_j$. According to [27], the mode coupling coefficient $\kappa$ is calculated as

$$\kappa ={\displaystyle \frac{\sqrt{\Delta }}{o_r}}{\displaystyle \frac{X^2}{V^3}}{\displaystyle \frac{K_0\left(\frac{{\Lambda }_{i,j}}{c_r}W\right)}{K_1^2\left(W\right)}},$$

(4)

where $o_r$ denotes the core radius and $\Delta$ denotes the relative refractive index difference. V denotes the normalized frequency, and X and W denote the normalized transverse wave number in the core and cladding, respectively. The functions $K_0\left(x\right)$ and $K_1\left(x\right)$ can be approximately defined as

$$K_0\left(x\right)\approx \sqrt{{\displaystyle \frac{\pi }{2x}}}exp(-x),$$

(5)

$$K_1\left(x\right)\approx \sqrt{{\displaystyle \frac{3.3}{x}}}exp(-1.1x),$$

(6)

respectively.

We can calculate the crosstalk level with these equations. For example, in [16], the relationship between the core pitch ${\Lambda }_{i,j}$ and the crosstalk ${\mathrm{XT}}_{i,j}$ was calculated using the parameters listed in

Table 1. Example of parameters.

Parameter	Value
$b_r$	10 [cm]
$\alpha$	$4\times {10}^6$ [m−1]
$\Delta$	0.35 [%]
$o_r$	3.8 [µm]
V	2.2
W	$1.1428V-0.996$
X	$\sqrt{V^2-W^2}$

. The authors showed that the power of inter-core crosstalk decreases exponentially as the core pitch increases. Thus, in this paper, we consider the impact of inter-core crosstalk between adjacent cores, but we do not take inter-core crosstalk between non-adjacent cores into account, as shown in Figure 3.

4. Proposed RCSA Method

4.1. Overview

Our proposed RCSA method aims to reduce the blocking probability of lightpath establishment by preventing the occurrence of spectrum fragmentation while suppressing the impact of inter-core crosstalk in multi-core fiber environments. Whenever a new lightpath-setup request is generated, the proposed method selects a routing path, cores, and FSs for the lightpath establishment based on the following three policies:

(a)

We expect to prevent the blocking of lightpath establishment by balancing the usage of FSs in each routing path. In the case where lightpaths are established intensively on a certain routing path and no available FSs remain in any cores of the routing path, the establishment of new lightpaths is blocked. Therefore, the proposed method selects a routing path so as not to use cores where many FSs are already assigned to existing lightpaths.

(b)

In order to further reduce the blocking probability, the proposed method prevents spectrum fragmentation by assigning lightpath-setup requests to prioritized cores according to their required number of FSs. Establishing lightpaths with the same number of FSs on the same core can prevent the generation of many small fragmented bandwidth gaps, i.e., spectrum fragmentation, because the utilization of FSs is smoothed [25]. However, the required number of FSs takes various values depending on the traffic demand and the modulation level given by (1), while the number of cores is limited, e.g., 3 or 7. Therefore, the proposed method groups lightpath-setup requests based on their required number of FSs and assigns the request groups to cores according to their priority. Furthermore, it utilizes frequency-spectrum resources by allocating preferred frequency bandwidths to lightpath-setup requests in each group, thereby reducing both the blocking probability and inter-core crosstalk.

(c)

As mentioned earlier, using the same FSs in adjacent cores degrades the quality of established lightpaths due to inter-core crosstalk. Therefore, to avoid such a situation, for a newly established lightpath, our proposed RCSA method utilizes FSs so as not to use the same FSs in adjacent cores.

4.2. Detailed Procedure for Proposed RCSA Method

In the following, we describe the procedure for our proposed RCSA method for a newly established lightpath.

4.2.1. Construction of Candidate Routing Paths

We first construct a set ${\mathcal{P}}_{i,j}=\{p_1^{[i,j]},p_2^{[i,j]},\dots ,p_K^{[i,j]}\}$ of candidate routing paths for each pair of sender node $i\in \mathcal{V}$ and receiver node $j\in \mathcal{V}$ on the target graph $\mathcal{G}$ in advance. Our proposed RCSA method chooses a routing path from the constructed candidate paths when a new lightpath-setup request arrives. In this paper, we construct the candidate paths based on the K-shortest-path algorithm [28]. The modulation level $M_p$ for each candidate path $p\in {\mathcal{P}}_{i,j}$ is pre-determined according to the path length. The procedure of the K-shortest-path algorithm is described below.

K-shortest-path algorithm:

1.

${\mathcal{P}}_{i,j}\leftarrow \varnothing$ and $k\leftarrow 1$.

2.

The shortest path $p_k^{[i,j]}$ from node i to node j is computed using a standard shortest-path algorithm, e.g., Dijkstra’s algorithm, assuming that the cost of each link on $\mathcal{G}$ is set to 1.

3.

The path is selected as a candidate routing path, i.e., ${\mathcal{P}}_{i,j}\leftarrow {\mathcal{P}}_{i,j}\cup \left\{p_k^{[i,j]}\right\}$; then, the cost of each link along this routing path is doubled.

4.

If $k=K$, the algorithm terminates; otherwise, $k\leftarrow k+1$, and the algorithm returns to Step 2.

4.2.2. Lightpath Establishment in Proposed Method

For the establishment of each new lightpath, the proposed method uses the establishment cost $U_{p,f}$ for each FS f of each routing path p to select a combination of routing path, FSs, and cores. We assume that the establishment cost becomes small in the case where the three above-mentioned policies are satisfied. The proposed method selects a combination with the smallest establishment cost. To do so, we define the establishment cost $U_{p,f}$ for a lightpath requiring $R_p$ FSs as

$$U_{p,f}=\sum _{e\in p}\left\{\underset{c\in \mathcal{C}}{min}\sum _{f^{\prime }=f}^{f+R_p-1}{S}_{e,c,f^{\prime }}^{\left[R_p\right]}\right\},$$

(7)

where $S_{e,c,f}^{\left[R_p\right]}$ represents the sub-cost of FS f in core c of link e, which is defined later. In (7), ${\sum }_{f^{\prime }=f}^{f+R_p-1}{S}_{e.c,f^{\prime }}^{\left[R_p\right]}$ assumes the case where the successive FSs f to $f+R_p-1$ are allocated to the lightpath. Note that, as defined in (1), the required number $R_p$ of FSs is calculated based on the traffic demand and modulation level. The establishment cost $U_{p,f}$ is calculated, assuming that the core with the minimum sub-cost is selected in each link. Specifically, the proposed method uses core $c_{\left[\min \right]}$ at the link, given by

$$c_{\left[\min \right]}=\underset{c\in \mathcal{C}}{min}\sum _{f^{\prime }=f}^{f+R_p-1}{S}_{e,c,f^{\prime }}^{\left[R_p\right]},$$

(8)

when the link is included in the selected routing path.

The sub-cost $S_{e,c,f}^{\left[R_p\right]}$ is defined as follows so as to include the three above-mentioned policies. Let $s_{e,c,f}$ be 1 if FS f in core c of link e is already used by existing lightpaths; otherwise (i.e., it is available), it is 0. The sub-cost of FS f of core c in link e is defined as

$$S_{e,c,f}^{\left[R_p\right]}=\left\{\begin{array}{cc}{\displaystyle W\left(R_p\right)\times (1+\sum _{f^{\prime }\in \mathcal{F}:f\ne f^{\prime }}{s}_{e,c,f^{\prime }})+\gamma \times \sum _{c^{\prime }\in \mathcal{C}:c\ne c^{\prime }}{u}_{c,c^{\prime }}{s}_{e,c^{\prime },f},}\hfill & \mathrm{if}{s}_{e,c,f}=0\hfill \\ \infty \hfill & \mathrm{if}{s}_{e,c,f}=1,\hfill \end{array}\right.$$

(9)

where $\gamma$ is a constant parameter. $W\left(R_p\right)$ is a weight parameter for lightpaths requiring $R_p$ FSs, the value of which is defined in Section 4.3. $u_{c,c^{\prime }}$ is an indicator function that is equal to 1 if core $c^{\prime }$ is an adjacent core of core c; otherwise, it is 0. In (9), the first term reflects policies (a) and (b) discussed in Section 4.1. Specifically, the sub-cost $S_{e,c,f}^{\left[R_p\right]}$ grows as the number of FSs already used by existing lightpaths in the same core increases. Furthermore, by appropriately selecting $W\left(R_p\right)$, the proposed method reduces the cost $S_{e,c,f}^{\left[R_p\right]}$ of specific cores for each value of $R_p$. Additionally, the second term corresponds to policy (c), where $S_{e,c,f}^{\left[R_p\right]}$ increases in proportion to the number of occupied FSs in adjacent cores. The influence of these policies can be tuned via the parameter $\gamma$. In (9), if $s_{e,c,f}=1$, i.e., the FS is unavailable, the cost is set to infinity because the lightpath cannot be established using this FS in the core.

When a new lightpath-setup request with traffic demand D arrives from sender i to receiver j, the proposed method establishes a lightpath using the procedure described below.

Lightpath establishment procedure:

1.

The required number $R_p$ of FSs for each routing path $p\in {\mathcal{P}}_{i,j}$ is calculated using (1).

2.

The establishment cost $U_{p,f}$ for each FS $f\in \mathcal{F}$ of each routing path $p\in {\mathcal{P}}_{i,j}$ is calculated using (7).

3.

If there are no available combinations of a routing path p and FSs f to $f+R_p-1$, the lightpath-setup request is blocked, and the procedure terminates.

4.

An available combination of a routing path p and FSs f to $f+R_p-1$ with the smallest $U_{p,f}$ is selected according to the following:

(a)

If there exist multiple combinations with the smallest value of $U_{p,f}$, the combination with shorter hops is selected.

(b)

A random one is selected if the number of hops is the same.

5.

A core with the minimum sub-cost obtained using (8) in each link along the selected routing path p is selected.

6.

The lightpath with the selected routing path, FSs, and cores is established. Then, the procedure terminates.

4.3. Definition of Weight Parameters

To efficiently reduce the blocking probability of lightpath establishment, it is important to appropriately determine the weight parameter $W\left(R_p\right)$ for lightpaths requiring $R_p$ FSs, which is utilized in (9). We expect to reduce the blocking probability of lightpath establishment by allocating lightpaths that require the same number of FSs to the same core, as discussed in policy (b). However, the number of FSs required by lightpaths takes various values depending on the traffic demand and path length, while the number of available cores is limited. Therefore, it is difficult to exclusively allocate lightpaths requiring the same number of FSs to dedicated cores.

In order to solve this problem, the proposed method groups lightpath-setup requests based on their required number of FSs. Specifically, in this paper, we form three groups according to the procedure outlined below.

Grouping procedure:

1.

Requests that require a number of FSs divisible by 3 (i.e., $R_p=3,6,9,\dots$) are assigned to Group $g_1$.

2.

Requests, other than those in Group 1, that require a number of FSs divisible by 2 (i.e., $R_p=2,4,8,\dots$) are assigned to Group $g_2$.

3.

The remaining requests (i.e., $R_p=1,5,7,\dots$) are assigned to Group $g_3$.

The proposed method determines the weight parameter $W\left(R_p\right)$ based on these groups. As illustrated in Figure 4, the proposed method aims to allocate lightpaths belonging to the same group to the same core. Furthermore, in each core, the proposed method assigns FS indices with priority to lightpaths based on their required number of FSs. By doing so, we expect to prevent spectrum fragmentation. In order to achieve this, the weight parameter $W\left(R_p\right)$ is given by the sum of the parameters derived from these two strategies, i.e., $W\left(R_p\right)=W_c\left(R_p\right)+W_f\left(R_p\right)$.

In the first strategy, we allocate these groups to specific cores. Here, we assume 3-, 7-, and 13-core fibers, as illustrated in Figure 5. For lightpath-setup requests in the same group, the preferential use of the allocated cores is expected to reduce spectrum fragmentation. This is because by grouping requests whose required number of FSs is divisible by a specific number, frequency allocation can be performed more efficiently. Furthermore, in order to suppress inter-core crosstalk, it is necessary to avoid the simultaneous use of adjacent cores. Therefore, we assign usage priorities to the cores for each group. Specifically, we define a weight parameter $W_c\left(R_p\right)$ for each group, as shown in

Table 2. The value of $W_c\left(R_p\right)$ for each group ($\left|\mathcal{C}\right|=3$).

Core	Group ${\mathit{g}}_1$	Group ${\mathit{g}}_2$	Group ${\mathit{g}}_3$
$c_1$	0.0	1.0	1.0
$c_2$	1.0	0.0	1.0
$c_3$	1.0	1.0	0.0

,

Table 3. The value of $W_c\left(R_p\right)$ for each group ($\left|\mathcal{C}\right|=7$).

Core	Group ${\mathit{g}}_1$	Group ${\mathit{g}}_2$	Group ${\mathit{g}}_3$
$c_1$	0.0	1.0	1.0
$c_2$	0.5	1.0	1.0
$c_3$	1.0	0.0	1.0
$c_4$	1.0	0.5	1.0
$c_5$	1.0	1.0	0.0
$c_6$	1.0	1.0	0.5
$c_7$	1.0	1.0	1.0

and

Table 4. The value of $W_c\left(R_p\right)$ for each group ($|\mathcal{C}=13|$).

Core	Group ${\mathit{g}}_1$	Group ${\mathit{g}}_2$	Group ${\mathit{g}}_3$	Core	Group ${\mathit{g}}_1$	Group ${\mathit{g}}_2$	Group ${\mathit{g}}_3$
$c_1$	0.0	1.0	1.0	$c_8$	0.75	1.0	1.0
$c_2$	0.25	1.0	1.0	$c_9$	1.0	0.5	1.0
$c_3$	1.0	0.0	1.0	$c_{10}$	1.0	0.75	1.0
$c_4$	1.0	0.25	1.0	$c_{11}$	1.0	1.0	0.5
$c_5$	1.0	1.0	0.0	$c_{12}$	1.0	1.0	0.75
$c_6$	1.0	1.0	0.25	$c_{13}$	1.0	1.0	1.0
$c_7$	0.5	1.0	1.0

, to preferentially allocate it to the corresponding cores. For example, in a seven-core fiber, Group $g_1$ uses core $c_1$ with the highest priority because setting the first term results in a low value in (9). Similarly, Group $g_1$ tends to use core $c_2$, which is assigned the second-highest priority. By doing so, we aim to mitigate inter-core crosstalk and reduce the blocking probability of lightpath establishment.

The second strategy introduces a weight parameter $W_f\left(R_p\right)$ based on the FSs used for lightpath establishment to further reduce the blocking probability of lightpath establishment.

This strategy aims to exclusively assign the prioritized FS range to lightpath-setup requests according to their required number $R_p$ of FSs in each group. Specifically, for each $R_p$, we set $W_f\left(R_p\right)=0.0$ for FS f within the prioritized FS range and $W_f\left(R_p\right)=1.0$ for all other FSs. The width of the prioritized FS range is approximately adjusted in proportion to the product of the value of $R_p$ and the intended number of lightpaths requiring $R_P$ FSs to be established. As an example, we assume the case where we intend to preferentially establish 20 lightpaths with $R_p=3$ belonging to Group $g_1$. In this case, the assigned FS width is $3\times 20=60$. Note that we ignore the guard band in this example. Accordingly, we set $W_f\left(3\right)=0.0$ for FSs $f_1\le f\le f_{60}$ as the prioritized FS range, while we set $W_f\left(3\right)=1.0$ for all other FSs. Additionally, we assume the case where we intend to preferentially establish five lightpaths with $R_p=6$, also belonging to Group $g_1$. In this case, the assigned FS width is $6\times 5=30$, so we set $W_f\left(6\right)=0.0$ for FSs $f_{61}\le f\le f_{90}$, while we set $W_f\left(6\right)=1.0$ for all other FSs.

In this way, the proposed method can mitigate spectrum fragmentation by exclusively assigning the prioritized FSs to requests with different $R_p$ in each group. In (9), $W\left(R_p\right)=W_c\left(R_p\right)+W_f\left(R_p\right)$ becomes 0 when both $W_c\left(R_p\right)$ and $W_f\left(R_p\right)$ are 0. Consequently, lightpaths are expected to be established efficiently by preferentially using both prioritized cores and FSs, as shown in Figure 4, thereby reducing inter-core crosstalk and the blocking probability. Note that in this paper, we define the specific values of this weight parameter $W_f\left(R_p\right)$ according to network models in the simulation experiments, which are discussed in Section 5.

5. Performance Evaluation

5.1. Model

Through simulation experiments, we evaluate the performance of our proposed RCSA method. In this paper, we use two network models, as shown in Figure 6. The first network, named NSFNET, has 14 nodes and 21 bidirectional links. The second network, named the USA network, has 24 nodes and 43 bidirectional links. We assume that each node fills the roles of an intermediate switch, a sender node, and a receiver node. In the experiments, we use three types of multi-core fibers, i.e., $\left|\mathcal{C}\right|=3$-, 7-, and 13-core fibers, as shown in Figure 5, for each link. The number $\left|\mathcal{F}\right|$ of available FSs in each fiber is set to 320. We construct $K=3$ candidate routing paths using the K-shortest-path algorithm.

Each sender node generates lightpath-setup requests according to a Poisson process with a rate of $\lambda$ [1/sec]. The receiver node of each lightpath-setup request is independently selected with equal probability from all possible receiver nodes. The holding time of each lightpath is exponentially distributed with an average of H [sec], and the lightpath is released after the holding time. The traffic demand D [Gbps] of each lightpath-setup request is randomly selected from the range [1–10]. The transmission capacity T [Gbps] per FS for 1 bit/symbol transmission is set to 1.

In this paper, to simplify the model, we assume that the length of each link is identical, with the objective of clarifying the potential effectiveness of the proposed method. In this case, the lightpath length is proportional to the number of hops. Thus, as shown in

Table 5. Modulation level $M_p$.

Number of Hops	Modulation Level ${\mathit{M}}_{\mathit{p}}$
≤2	4
3	3
4	2
5≥	1

, we define the modulation level $M_p$ in both networks based on the number of hops instead of the lightpath length.

The required number $R_p$ of FSs is determined by (1) with these values. We define the offered load $\rho$ per FS in a core as

$$\rho ={\displaystyle \frac{\lambda H}{\left|\mathcal{F}\right|\left|\mathcal{C}\right|}}.$$

(10)

From each simulation experiment, we obtain 20 independent samples to show the average performance. In each result, 95 % confidence intervals are shown (even though most of them are invisible).

For comparison, we use the following three methods, whose concepts are related to our proposed method:

1.

First-Fit (FF) Method: The FF method is known to be highly effective in terms of the blocking probability of lightpath establishment, as it can prevent the occurrence of spectrum fragmentation. In the FF method, K candidate paths are prepared, as in our proposed method. It prioritizes the selection of the shortest path based on the number of hops and allocates available FSs along the selected path using a first-fit strategy.

2.

Core-Prioritized (CP) Method: The CP method was proposed in [25] and is known to be effective in reducing both the blocking probability and inter-core crosstalk. In this method, cores are classified into groups based on priority. Then, lightpaths requiring the same number of FSs are allocated to the same core according to priority, similar to the proposed method. However, in [25], the authors assumed that there are only three types of the required number of FSs, i.e., $R_p=3$, 4, and 5. This method cannot be directly applied in the experiments because the required number $R_p$ of FSs is determined by (1), which means that $R_p$ ranges from 1 to 10. Therefore, we slightly modify it in such a way that we apply the same grouping procedure in our proposed RCSA method and then allocate the groups to their prioritized cores.

3.

Load-Balancing (LB) Method: The LB method was proposed in [24]. This method aims to reduce the blocking probability by establishing lightpaths so as not to use cores where many FSs are already used. Moreover, it mitigates inter-core crosstalk by avoiding the use of the same FSs in adjacent cores. This method balances the blocking of lightpath establishment and inter-core crosstalk with a weight parameter $\beta$, similar to the parameter $\gamma$ in the proposed method. Specifically, a larger $\beta$ reduces inter-core crosstalk, while a smaller $\beta$ lowers the blocking probability. In this paper, we use the LB method with $\beta =1.0$, which balances this trade-off, as the comparison baseline.

5.2. Simulation Results

5.2.1. Results for NSFNET

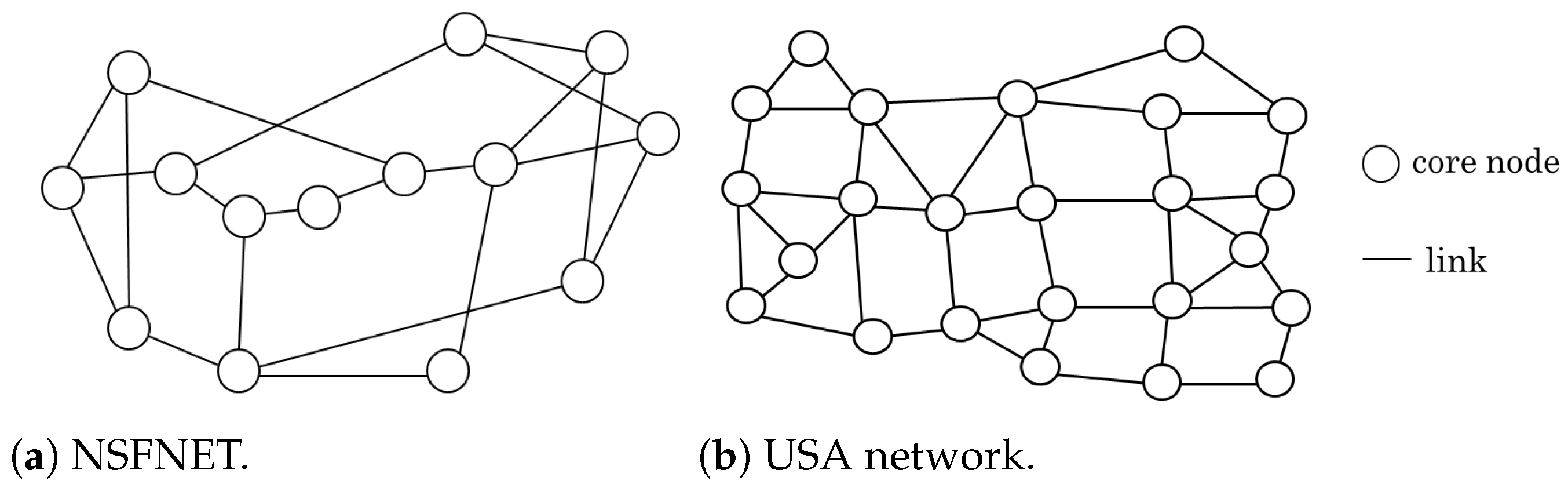
We first evaluated the performance of our proposed method in the NSFNET, as shown in Figure 6a. The constant parameter $\gamma$ in the proposed method was set to 0 or $1.0$, unless stated otherwise. We defined the weight parameter $W_f\left(R_p\right)$ in the proposed method, as shown in

Table 6. Assigned widths for $W_f\left(R_p\right)$ (NSFNET).

${\mathit{R}}_{\mathit{p}}$ (Group)	Assigned Width	${\mathit{R}}_{\mathit{p}}$ (Group)	Assigned Width
1 ($g_3$)	$f_1\le f\le f_{224}$	6 ($g_1$)	$f_{303}\le f\le f_{310}$
2 ($g_2$)	$f_1\le f\le f_{256}$	7 ($g_3$)	$f_{303}\le f\le f_{320}$
3 ($g_1$)	$f_1\le f\le f_{302}$	8 ($g_2$)	$f_{303}\le f\le f_{310}$
4 ($g_2$)	$f_{257}\le f\le f_{302}$	9 ($g_1$)	$f_{311}\le f\le f_{320}$
5 ($g_3$)	$f_{225}\le f\le f_{302}$	10 ($g_2$)	$f_{311}\le f\le f_{320}$

, which was obtained from a preliminary experiment. Note that the table indicates that $W_f\left(1\right)=0.0$ if $f_1\le f\le f_{224}$; otherwise, $W_f\left(1\right)=1.0$. A similar logic was followed for other values of $R_p$.

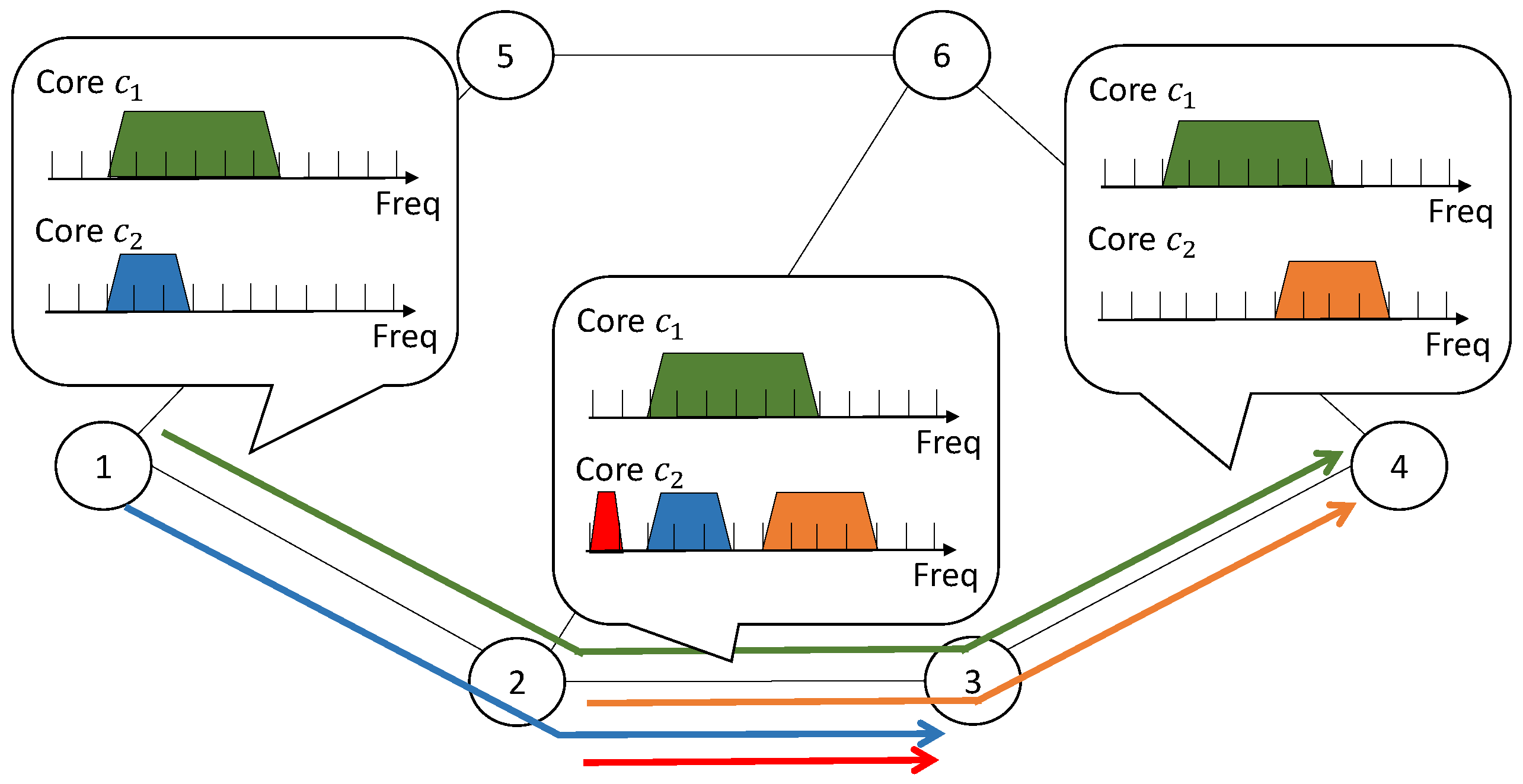
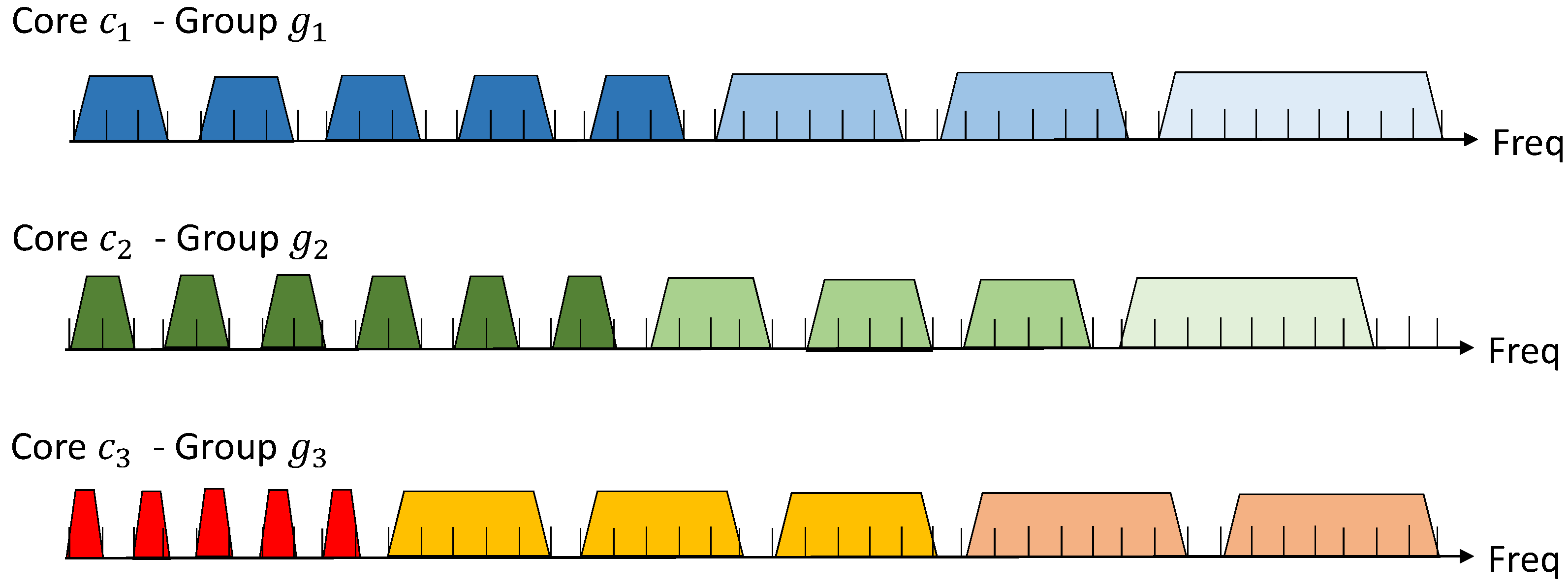
In the preliminary experiments, we obtained the number $n\left(R_p\right)$ of successfully established lightpaths for each required number $R_p$ of FSs when using only the shortest paths. We determined the FS range based on this value by treating it as the intended number of lightpaths requiring $R_p$ FSs to be established, as mentioned in Section 4.3. To achieve this, we calculated $R_p\times n\left(R_p\right)$, which represents the total number of frequency slots used for each $R_p$. Then, the calculated value was normalized by the sum of the values of $R_p\times n\left(R_p\right)$ in the same group in such a way that the total became equal to the total number $\left|\mathcal{F}\right|$ of available FSs. The normalized result was used as the FS width to be assigned to each $R_p$. Accordingly, the prioritized FS range was determined, as discussed in Section 4.3. By doing so, we expected to perform resource allocation that reflected both the required number of frequency slots and the number of lightpath requests generated, as illustrated in Figure 4.

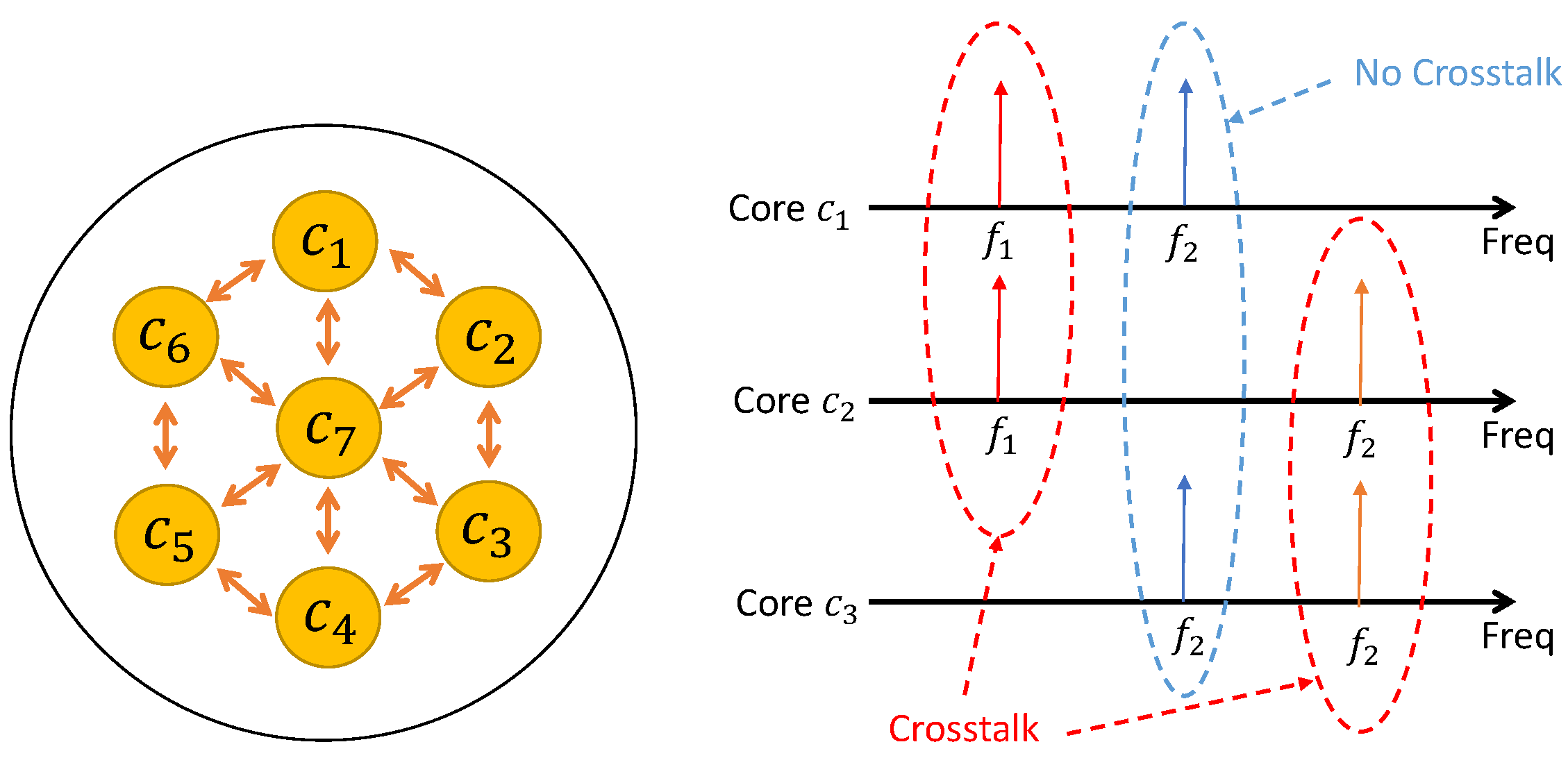
In the experiments, we used two performance metrics: the blocking probability of lightpath establishment and the average number of inter-core crosstalk occurrences between established lightpaths. We define the blocking probability of lightpath establishment as

$$\text{blocking} \text{probability} \text{of} \text{lightpath} \text{establishment}=\frac{\text{number} \text{of} \text{blocked} \text{lightpath-setup} \text{requests}}{\text{total} \text{number} \text{of} \text{lightpath-setup} \text{requests}}.$$

(11)

Additionally, we define the average number of inter-core crosstalk occurrences between established lightpaths as

$$\text{average} \text{number} \text{of} \text{inter-core} \text{crosstalk} \text{occurrences}=\frac{\text{total} \text{number} \text{of} \text{crosstalk} \text{occurrences}}{\text{number} \text{of} \text{successfully} \text{established} \text{lightpaths}}.$$

(12)

In this paper, we define the occurrence of inter-core crosstalk between established lightpaths as the case where identical FSs are used in adjacent cores by the lightpaths. In the experiments, we counted the number of inter-core crosstalk occurrences at each FS whenever a new lightpath was established, and we used their total sum as the denominator in (12). The crosstalk level affecting the established lightpaths strongly depends on the number of inter-core crosstalk occurrences between the lightpaths. Note that we can calculate the crosstalk level using (2), but it depends on specific parameters that vary with assumed environments. In this paper, to conduct the performance evaluation independent of the assumed environments, instead of calculating the crosstalk level using (2), we employed the average number of inter-core crosstalk occurrences, defined in (12), as the performance metric. This performance metric corresponds to the evaluation criteria used in related works, such as the CP method [25] and other existing studies [19,20,24].

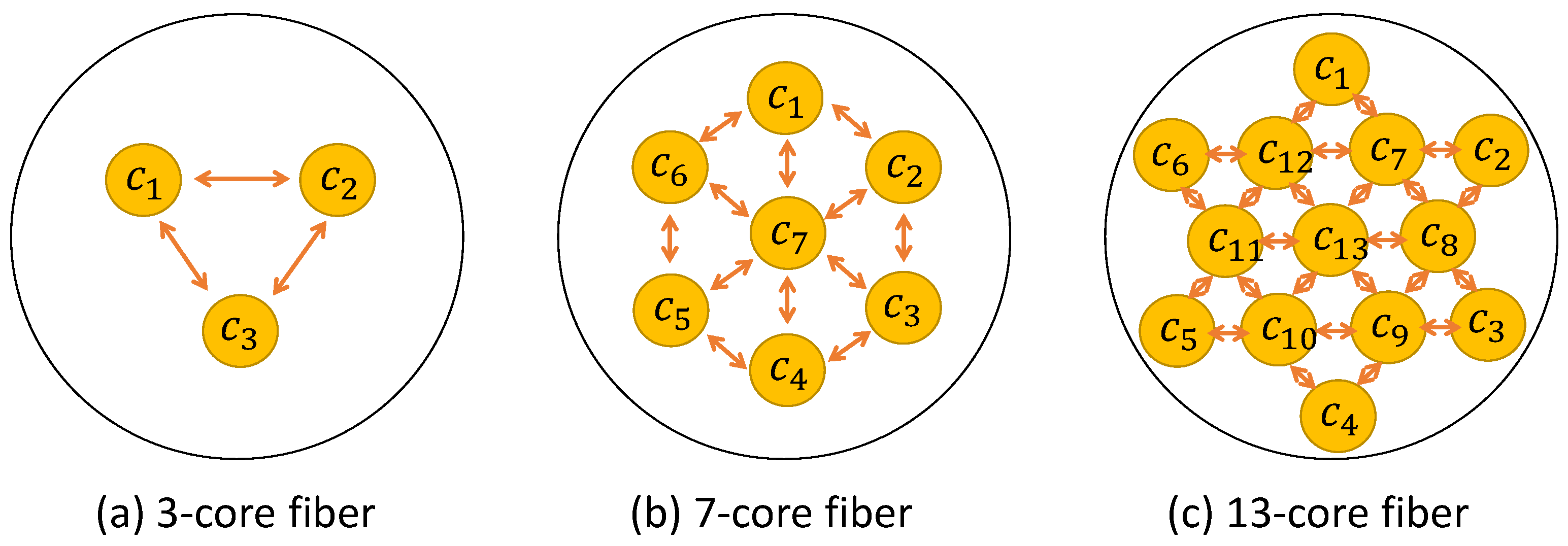
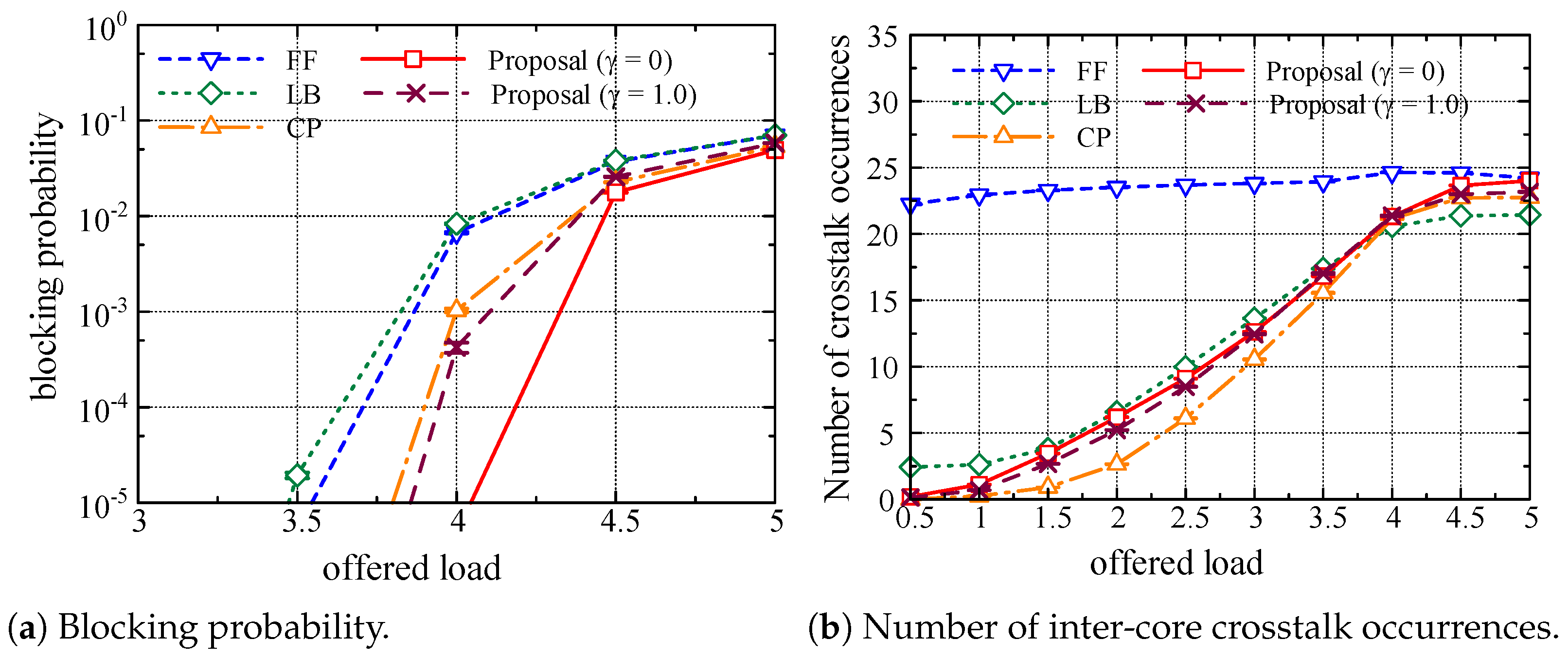
We examined the performance of the proposed method in the scenario where the number $\left|\mathcal{C}\right|$ of cores in each fiber was small, i.e., $\left|\mathcal{C}\right|=3$. Figure 7a shows the blocking probability of lightpath establishment as a function of the offered load $\rho$ in NSFNET with $\left|\mathcal{C}\right|=3$ cores. Additionally, Figure 7b shows the average number of inter-core crosstalk occurrences per lightpath establishment as a function of the offered load $\rho$ in NSFNET with $\left|\mathcal{C}\right|=3$ cores. In Figure 7a, we can observe that the blocking probability of the LB method was the highest. On the other hand, as shown in Figure 7b, the average number of inter-core crosstalk occurrences in the LB method was the lowest. This is because the LB method avoids the use of the same FSs in adjacent cores. However, this strategy also leads to an increase in the blocking probability. The FF method decreases the blocking probability in contrast to the LB method. Meanwhile, the FF method increases the number of inter-core crosstalk occurrences because it does not take into account inter-core crosstalk occurrences during the FS allocation process.

In Figure 7a, we can also observe that the blocking probabilities of the CP method and the proposed method with $\gamma =1.0$ were almost the same as that of the FF method. Furthermore, the proposed method with $\gamma =0$ exhibited the best performance in terms of the blocking probability. On the other hand, as shown in Figure 7b, the number of inter-core crosstalk occurrences in the CP method and the proposed method with $\gamma =0$ was higher than that in the LB method. This result indicates that assigning priority to cores is ineffective in reducing crosstalk when all cores are adjacent to each other. The proposed method with $\gamma =1.0$ avoids the use of the same FSs in adjacent cores, similar to the LB method. Therefore, the number of inter-core crosstalk occurrences in the proposed method with $\gamma =1.0$ was close to that in the LB method, even though the number $\left|\mathcal{C}\right|$ of cores was small.

We then evaluated the performance of our proposed RCSA method when the number $\left|\mathcal{C}\right|$ of cores was increased, i.e., $\left|\mathcal{C}\right|=7$ or 13. Figure 8a,b show the blocking probability of lightpath establishment and the average number of inter-core crosstalk occurrences, respectively, as a function of the offered load $\rho$ in NSFNET with $\left|\mathcal{C}\right|=7$ cores. As shown in Figure 8a, the blocking probability of the LB method was the highest, similar to the result in Figure 7a. In contrast, the CP method and the proposed method with $\gamma =1.0$ exhibited lower blocking probabilities than the FF method. The reason is that these methods suppress spectrum fragmentation by efficiently utilizing prioritized cores. We can also observe that the proposed method with $\gamma =0$ exhibited the best performance in terms of the blocking probability.

In Figure 8b, we can observe that the FF method generated excessive inter-core crosstalk. On the other hand, the other methods efficiently reduced the number of inter-core crosstalk occurrences. The proposed method worked especially well when the offered load was small. This is because it selects cores so as to prevent inter-core crosstalk by appropriately setting the weight parameter $W_c\left(R_p\right)$ according to the required number $R_p$ of FSs. We can also observe that the number of inter-core crosstalk occurrences was almost independent of the value of $\gamma$ in the proposed method. This result means that the impact of the weight parameter $W_c\left(R_p\right)$ becomes more significant as the number of cores increases.

Figure 9a,b show the blocking probability of lightpath establishment and the average number of inter-core crosstalk occurrences, respectively, as a function of the offered load $\rho$ in NSFNET with $\left|\mathcal{C}\right|=13$ cores. In these figures, we can observe that the proposed method with $\gamma =0$ achieved the best performance in terms of the blocking probability, similar to the previous results. On the other hand, the number of inter-core crosstalk occurrences in the proposed method was slightly larger than that in the CP method. The CP method tended to use cores with assigned priorities in order, preventing inter-core crosstalk. Therefore, as the number of cores increased, the crosstalk reduction effect became more significant. On the other hand, the proposed method focused on reducing the blocking probability by flexibly determining the cores to be used based on the weight parameters, even though some inter-core crosstalk occurred. However, the amount of inter-core crosstalk can be considered sufficiently small in this case. Note that with an appropriate choice of the weight parameters, the proposed method is expected to achieve performance comparable to that of the CP method.

Figure 10a,b show the blocking probability of lightpath establishment and the average number of inter-core crosstalk occurrences, respectively, as a function of the value of $\gamma$ in the proposed method in NSFNET. As shown in Figure 10a, the blocking probability increased with the value of $\gamma$, regardless of the number $\left|\mathcal{C}\right|$ of cores. In contrast, the number of inter-core crosstalk occurrences decreased with the increase in the value of $\gamma$.

There exists a trade-off between the blocking probability and the number of inter-core crosstalk occurrences with respect to the value of $\gamma$. Therefore, it is important to decrease the value of $\gamma$ to ensure that any arbitrary crosstalk threshold can be satisfied, taking this trade-off into account. If the crosstalk level is sufficiently low, selecting $\gamma =0$ yields the best performance, as it minimizes the blocking probability of lightpath establishment. The acceptable crosstalk level depends on the assumed environments; thus, we need to select the appropriate value of $\gamma$ accordingly. A detailed discussion on the relationship between the value of $\gamma$ and the crosstalk threshold is left for future work.

5.2.2. Results for USA Network

We then examined the performance of our proposed RCSA method in the USA network shown in Figure 6b. Here, we defined the weight parameter $W_f\left(R_p\right)$ in the proposed method, as shown in

Table 7. Assigned widths for $W_f\left(R_p\right)$ (USA network).

${\mathit{R}}_{\mathit{p}}$ (Group)	Assigned Width	${\mathit{R}}_{\mathit{p}}$ (Group)	Assigned Width
1 ($g_3$)	$f_1\le f\le f_{128}$	6 ($g_1$)	$f_{225}\le f\le f_{272}$
2 ($g_2$)	$f_1\le f\le f_{160}$	7 ($g_3$)	$f_{257}\le f\le f_{320}$
3 ($g_1$)	$f_1\le f\le f_{224}$	8 ($g_2$)	$f_{257}\le f\le f_{288}$
4 ($g_2$)	$f_{161}\le f\le f_{256}$	9 ($g_1$)	$f_{273}\le f\le f_{320}$
5 ($g_3$)	$f_{129}\le f\le f_{256}$	10 ($g_2$)	$f_{289}\le f\le f_{320}$

.

Figure 11a,b show the blocking probability of lightpath establishment and the average number of inter-core crosstalk occurrences, respectively, as a function of the offered load $\rho$ in the USA network with $\left|\mathcal{C}\right|=3$ cores. In these figures, we can observe characteristics similar to the results for NSFNET with $\left|\mathcal{C}\right|=3$ cores, as shown in Figure 7. Specifically, the proposed method with $\gamma =0$ achieved the lowest blocking probability, and the proposed method with $\gamma =1.0$ reduced the number of inter-core crosstalk occurrences more efficiently than the proposed method with $\gamma =0$ when the number of cores $\left|\mathcal{C}\right|$ was small.

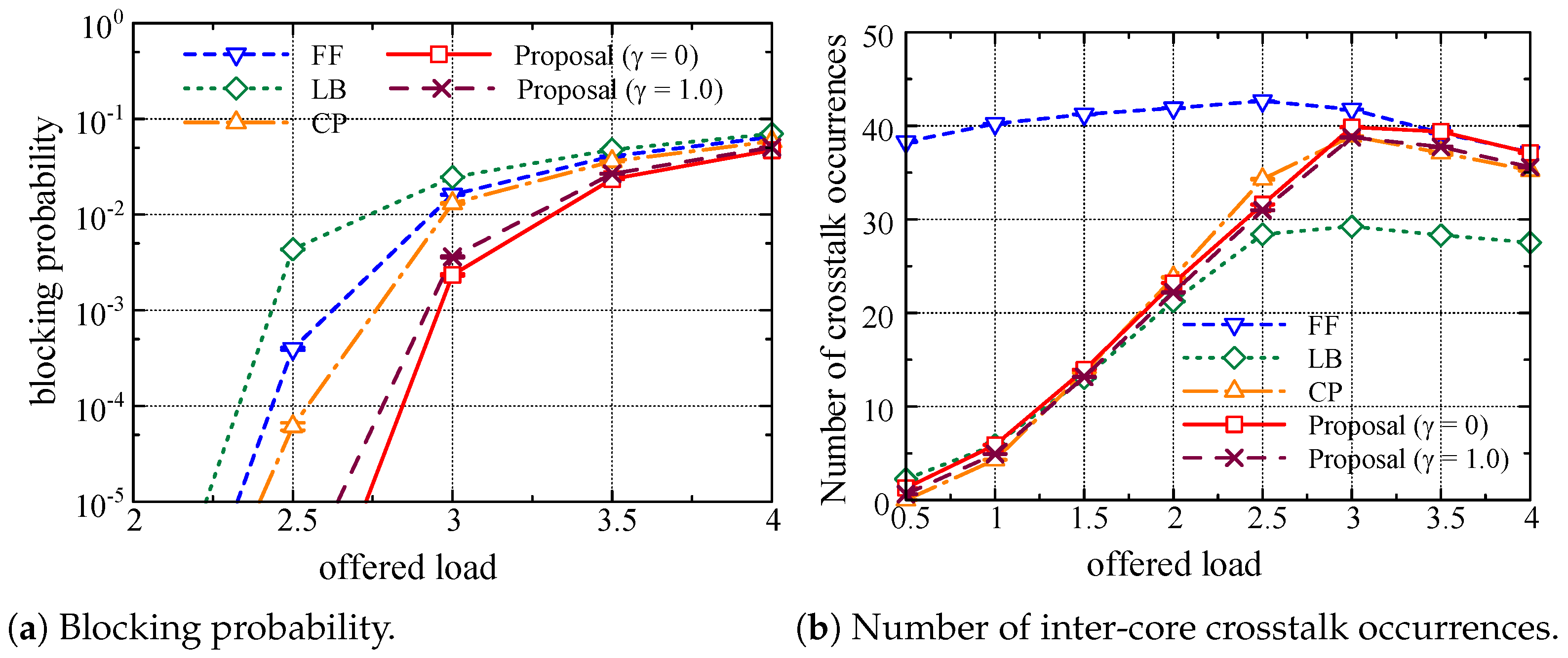
Figure 12a,b show the blocking probability of lightpath establishment and the average number of inter-core crosstalk occurrences, respectively, as a function of the offered load $\rho$ in the USA network with $\left|\mathcal{C}\right|=7$ cores. As we can see in these figures, when the offered load $\rho$ was larger than 2.5, the number of inter-core crosstalk occurrences in the LB method was the lowest, but the blocking probability was too high, which is not acceptable. On the other hand, the blocking probabilities of the proposed method with $\gamma =0$ and $\gamma =1.0$ were too low. Furthermore, our proposed method efficiently reduced the number of inter-core crosstalk occurrences when the offered load $\rho$ was small.

Figure 13a,b show the blocking probability of lightpath establishment and the average number of inter-core crosstalk occurrences, respectively, as a function of the offered load $\rho$ in the USA network with $\left|\mathcal{C}\right|=13$ cores. As shown in these figures, the proposed method with $\gamma =0$ and $\gamma =1.0$ efficiently reduced the blocking probability of lightpath establishment, similar to the result shown in Figure 12a. Moreover, we can also observe that it maintained a low level of inter-core crosstalk. Since the OSNR can be ensured by keeping the inter-core crosstalk below a certain threshold, the proposed method, which minimizes the blocking probability of lightpath establishment while keeping the number of inter-core crosstalk occurrences low, can be considered the most effective approach.

5.3. Discussion

Here, we discuss the scalability and computational complexity of the proposed method.

5.3.1. Scalability

In this paper, we focus on the scenario where the number of available cores is limited compared with the number of FSs required by newly established lightpaths. The proposed method is expected to be effective with the current procedure even as the number of cores increases. On the other hand, more appropriate grouping and core-priority assignment strategies could lead to further performance improvement. In addition, since more diverse traffic patterns could affect the FS range related to the weight parameter $W_f\left(R_p\right)$, it is necessary to implement a new mechanism, e.g., periodically collecting traffic patterns and adjusting the FS range accordingly. We leave the implementation of these mechanisms for future work.

5.3.2. Computational Complexity

Our proposed method performs the lightpath establishment procedure every time a new lightpath-setup request arrives, as described in Section 4.2.2. Here, we discuss the computational complexity of the lightpath establishment procedure. In the procedure, it is necessary to examine all possible combinations of routing paths, cores in the links of those paths, and FSs of the cores in order to establish a new lightpath. Let N denote the maximum number of hops of the routing paths. Because the number of candidate routing paths is K, the number of cores in each link is $\left|\mathcal{C}\right|$, and the number of available FSs is $\left|\mathcal{F}\right|$, the computational complexity is estimated to be $O\left(KN\right|\mathcal{C}\left|\right|\mathcal{F}\left|\right)$.

This complexity may pose challenges for real-time decision-making in optical control planes or hardware implementations. To reduce complexity, a restricted application of the proposed method, e.g., limiting the number of candidate routes, could be considered. In addition, we expect that the use of Software-Defined Networking (SDN) environments is effective. SDN enables flexible network management through centralized control of the control plane. Recently, SDN-based optical network architectures [29] have been introduced. Applying SDN-based optical network architectures is expected to facilitate a more flexible implementation of the proposed method.

6. Conclusions

In this paper, we introduced a dynamic RCSA method that efficiently reduces the blocking probability of lightpath establishment while keeping the amount of inter-core crosstalk low in elastic optical path networks with multi-core fiber environments. Our proposed RCSA method includes a routing, core, and spectrum allocation strategy, which groups lightpath-setup requests according to their required number of FSs to prevent spectrum fragmentation and inter-core crosstalk. Through simulation experiments, we showed the effectiveness of our proposed RCSA method.