Previous Article in Journal
Explainable AI Assisted IoMT Security in Future 6G Networks
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Future Internet
Volume 17
Issue 5
10.3390/fi17050227
futureinternet-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Heuristic Fuzzy Approach to Traffic Flow Modelling and Control on Urban Networks

by
Alexander Gegov
1,2,*,
Boriana Vatchova
3,
Yordanka Boneva
3 and
Alexandar Ichtev
4
1
School of Computing, University of Portsmouth, Portsmouth P01 3HE, UK
2
English Faculty of Engineering, Technical University of Sofia, 1000 Sofia, Bulgaria
3
Institute of Information and Communication Technologies, Bulgarian Academy of Sciences, 1113 Sofia, Bulgaria
4
Department of Systems and Control, Technical University of Sofia, 1000 Sofia, Bulgaria
*
Author to whom correspondence should be addressed.
Future Internet 2025, 17(5), 227; https://doi.org/10.3390/fi17050227
Submission received: 1 March 2025 / Revised: 13 May 2025 / Accepted: 15 May 2025 / Published: 20 May 2025
Browse Figures
Versions Notes

Abstract

:
Computer-aided transport modelling is essential for testing different control strategies for traffic lights. One approach to modelling traffic control is by heuristically defining fuzzy rules for the control of traffic light systems and applying them to a network of hierarchically dependent crossroads. In this paper, such a network is investigated through modelling the geometry of the network in the simulation environment Aimsun. This environment is based on real-world traffic data and is used in this paper with the MATLAB R2019a-Fuzzy toolbox. It focuses on the development of a network of intersections, as well as four fuzzy models and the behaviour of these models on the investigated intersections. The transport network consists of four intersections. The novelty of the proposed approach is in the application of heuristic fuzzy rules to the modelling and control of traffic flow through these intersections. The motivation behind the use of this approach is to address inherent uncertainties using a fuzzy method and analyse its main findings in relation to a classical deterministic approach.

1. Introduction

The problem with congested traffic in urban areas is current in many cities worldwide. The fact is that pedestrians need to cross streets safely and for this reason, traffic light control is needed. The other reason for the need for traffic light control is that conflicting traffic flows need to be distributed in time so they can use the common infrastructure of intersections. There is another option, namely to distribute the conflicting traffic in space by creating infrastructure on different levels, but this approach is out of the scope of this paper.
The goal of this research is design of a network of intersections represented as a hierarchical system of traffic light-regulated intersections managed by fuzzy controllers. These fuzzy controllers are designed and simulated separately in the hierarchical network. The novelty of this paper is that it investigates separately the behaviour of these four different fuzzy models on the hierarchical system and compares them with a classical controller, which is used as a benchmark.
A large amount of scientific research is available on the topic of traffic light control and traffic control and management in general in urban areas. Traffic as a human-made phenomenon is a subject of interdisciplinary interest; e.g., the theory of fluid dynamics is used to describe and compare traffic with the laws of nature.
A variety of approaches, methods, models and experiments are explored worldwide and locally to solve the problems of traffic congestion and improve the utilisation of the infrastructure or to justify the need for new infrastructure [1]. There are different models related to traffic control of intersections based on queuing models [2,3]. There are some well-written sources of information about road control strategies and traffic signal control methods [4,5]. As far as the use of information technologies for traffic is concerned, micro-simulation scenarios are used in conjunction with big data [6]. Even most contemporary research relies on the principles established in the middle of the 20th century by Wardrop, which is to say that even though the traffic is significantly different in terms of intensity nowadays, many discoveries and principles from the past are valid [7,8,9]. On a local level, scientists also investigate traffic flow in networks [10,11].
Computer-aided transport modelling is essential for testing different control strategies for traffic lights [12,13,14,15,16,17]. One approach to modelling traffic control is by defining fuzzy rules for the control of traffic light systems and applying them to a network of hierarchically dependent crossroads [18,19,20,21]. In this paper, a network of four hierarchically dependent crossroads is investigated through modelling the geometry of the network in the simulation environment Aimsun, then by applying the MATLAB Fuzzy toolbox and fuzzy logic theory [22,23,24,25]. Traffic indicators for assessing the performance of the fuzzy approach are mean queues, the throughput of the network, total travel time and delay, traffic indicators which are calculated in the simulation environment and are based on the fuzzy controller inputs and outputs.
Fuzzy logic has been utilised by various researchers in the field of road traffic, including in combination with deep learning techniques for short-term traffic prediction [26,27]. It enables dynamic modelling of traffic conditions in urban environments and is commonly used in traffic management systems through fuzzy logic controllers [28,29]. However, there is a research gap in terms of using suitable heuristics based on expert knowledge, which is the focus of this paper.
The proposed approach utilises the hierarchical dependency between the intersections that allows the same fuzzy rules to be applied to each and every intersection without an increase in the number of inputs and rules in the fuzzy system. Fuzzy rules are determined by the expression R = ki, where R is the set of fuzzy rules, k is the n-valued logic system and i is number of inputs. For example, for a three-valued logic system with two inputs, the fuzzy rules are presented as all possible permutations between the number of values in the logic system and the number of the inputs, i.e., 32 = 9. More details on this are presented in Section 2, where the fuzzy rules for each junction are derived [30].
Another study related to traffic light control systems using fuzzy logic is presented in [31]. Other studies investigating intelligent traffic light control strategies and transport modelling using reinforcement learning techniques and different types of heuristics are presented in [32,33,34,35]. However, most of these works do not include a systematic investigation of the subject and have a fairly narrow scope.
Recent related experiments by the authors have included a three-input fuzzy controller with three linguistic values per input, hence 33 = 27 fuzzy rules. However, this fairly large number of fuzzy rules is difficult to define using expert knowledge. For this reason, a two-input fuzzy controller has been chosen and systematically investigated in a heuristic setting in this study. The latter can still be easily applied not only to an isolated intersection but also to a group of intersections as part of a hierarchical multi-stage network.
The remaining paper is divided into the following sections. Section 2 describes the problem and the investigated network. Section 3 describes the fuzzy controller design by using MATLAB Fuzzy toolbox. Section 4 presents the classical controller design. Section 5 presents a discussion about the results of the experiments. Section 6 is a conclusion that summarises the experiment, its novelty, the results and future work.

2. Problem Description

The paper presents the modelling of a traffic light control system with feedback, as shown in Figure 1, which is taken with some modifications from [19]. The inputs to the controller are the differences between the actual traffic flows and the reference ones. The system is considered as a separate design of four different models of fuzzy controllers and one model of a classical controller in order to compare their behaviour. The system is considered as a network of four junctions in urban area located in Sofia, Bulgaria. The topology of the network consists of three input flows (one on the main road and two for each incoming direction on the secondary crossroads) and two outputs (duration of the green light for the flows on the main road and on the secondary roads); see Figure 2. The simulation environment for modelling of the network has been carried out on the Aimsun platform for the simulation of transportation tasks.
In Figure 1, r1, r2 and r3 are the reference numbers of cars on the urban network. In this case, they are assumed to be 0 in order to reflect the ideal case without any cars; x1, x2 and x3 are the initial numbers of cars (the difference between the initial and the reference numbers) in the Aimsun environment, which are inputs to the controller; u1 and u2 are the outputs from the controller (duration of the green light in seconds); and y1, y2 and y3 are the resulting numbers of cars on the network in the Aimsun environment [19].
Figure 2 presents a typical scenario of the investigated traffic network of four signalised intersections along Shipchenski prohod Blvd.
There are four proposed models for the fuzzy controllers’ design for the transport system. The results have been compared with the results of the classical controller, which is used as a benchmark for optimisation of the traffic light system according to several transportation criteria described in the paper below.

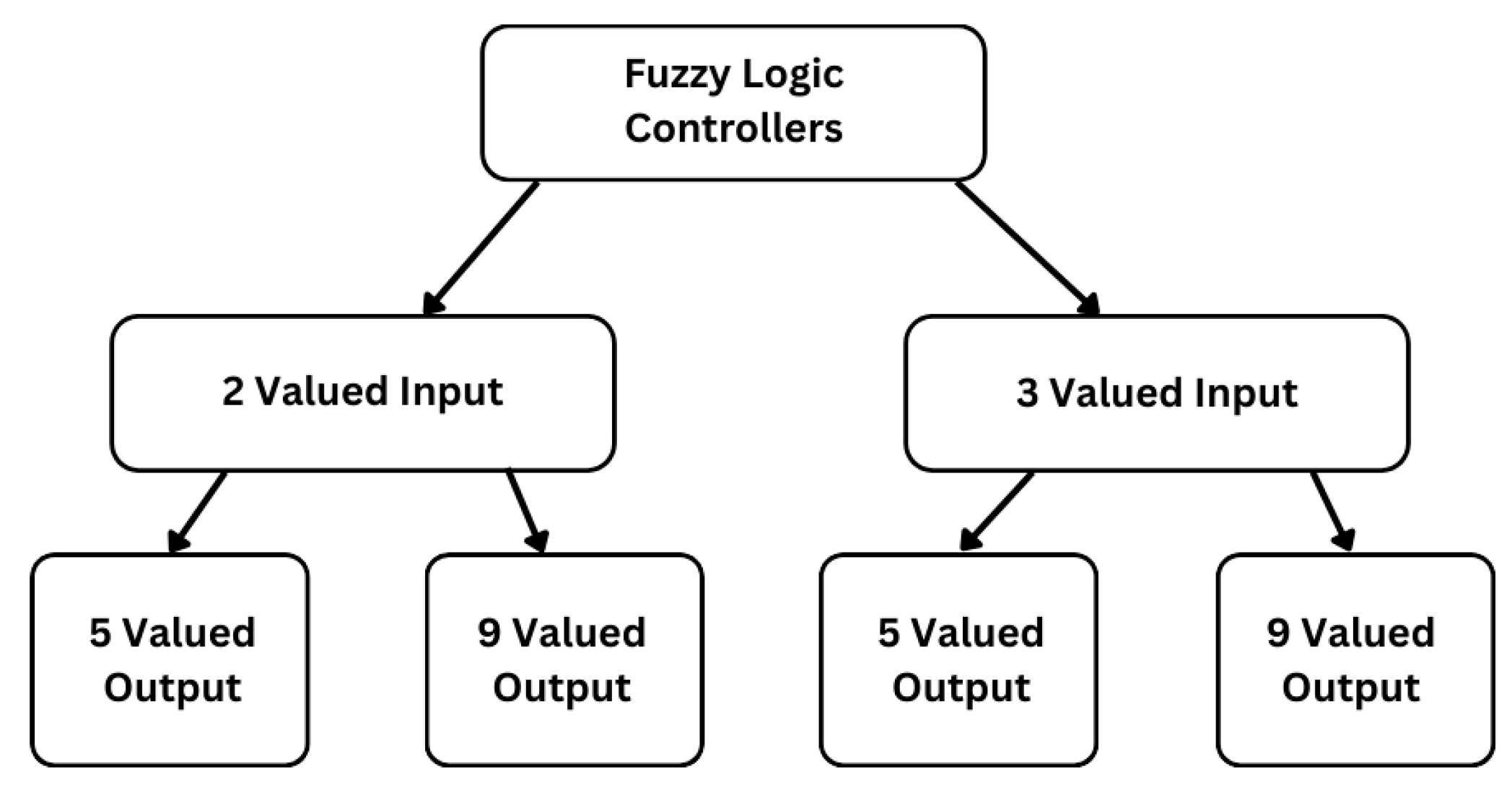
3. Fuzzy Controller Design

Four fuzzy controllers were designed as Fuzzy Mamdani Systems using MATLAB fuzzy toolbox [19,22]. Each system consists of three inputs and one output. The second output u2 for Section 2 is calculated as the difference between the fixed duration of the full cycle of the green light and the duration of the first output u1. In this case, the fixed duration of the full cycle of the green light is 100 s and the following equation holds:
u1 + u2 = 100
The fuzzy controllers are designed as follows.
3.1.
Two-valued logic for the inputs and five-valued logic for the output;
3.2.
Two-valued logic for the inputs and nine-valued logic for the output;
3.3.
Three-valued logic for the inputs and five-valued logic for the output;
3.4.
Three-valued logic for the inputs and nine-valued logic for the output.
Figure 3 presents a flow chart of the fuzzy controllers with regard to their inputs and outputs. The values for the inputs and the inputs of the controllers have been chosen with the purpose of finding a compromise between modelling accuracy and computational efficiency. These values are actually triangular membership functions with three parameters that describe, in a linguistic context, the length of traffic queues on the network and the duration of the green light for the junctions.

3.1. Fuzzy Controller Design Using Two-Valued Logic for the Inputs and Five-Valued Logic for the Output

The number of fuzzy rules for the first fuzzy model is eight for the first, second and third junctions, because there are three inputs using two-valued logic.
The number of fuzzy rules for two-valued logic for the inputs and five-valued logic for the outputs is eight for Junction 1, Junction 2 and Junction 3.
The following heuristic fuzzy rules, which are based on expert knowledge can be also described as if–then rules below.
  • If (numbercars1 is short) and (numbercars2 is short) and (numbercars3 is short), then (greenlight1) is average.
  • If (numbercars1 is short) and (numbercars2 is short) and (numbercars3 is long), then (greenlight1 is short).
  • If (numbercars1 is short) and (numbercars2 is long) and (numbercars3 is short), then (greenlight1 is very short).
  • If (numbercars1 is short), (numbercars2 is long) and (numbercars3 is long), then (greenlight1 is very short).
  • If (numbercars1 is long) and (numbercars2 is short) and (numbercars3 is short), then (greenlight1 is very long).
  • If (numbercars1 is long) and (numbercars2 is short) and (numbercars3 is long) then (the greenlight1 is long).
  • If (numbercars1 is long) and (numbercars2 is long) and (numbercars3 is short), then (greenlight1 is long).
  • If (numbercars1 is long) and (numbercars2 is long) and (numbercars3 is long), then (greenlight1 is average).
The number of membership functions for the output with five-valued logic is presented below, where ‘trimf’ means the triangular membership function from the MATLAB script.
MF1 = ‘very short’: ‘trimf’, [0 0 25]
MF2 = ‘short’: ‘trimf’, [0 25 50]
MF3 = ‘average’: ‘trimf’, [25 50 75]
MF4 = ‘long’: ‘trimf’, [50 75 100]
MF5 = ‘very long’: ‘trimf’, [75 100 100]
The value 100 is measured in seconds, and it is the full cycle of the green light for the two outputs.
The results for the fuzzy controller computations and the simulation of the Aimsun platform are given in Table 1, Table 2, Table 3 and Table 4.
The number of fuzzy rules for the fourth junction with two inputs and one output is 4, according to fuzzy logic description for the number of rules and topology of Junction 4.
The following heuristic fuzzy rules, which are based on expert knowledge, can be also described as if–then rules below.
  • If (numbercars1 is short) and (numbercars2 is short), then (greenlight1) is long.
  • If (numbercars1 is short) and (numbercars2 is long), then (greenlight1 is medium).
  • If (numbercars1 is long) and (numbercars2 is short), then (greenlight1 is very short).
  • If (numbercars1 is long) and (numbercars2 is long), then (greenlight1 is short).

3.2. Fuzzy Controller Using Two-Valued Logic for the Inputs and Nine-Valued Logic for the Output

The heuristic fuzzy rules, which are based on expert knowledge can also be described analogically with if–then rules, as previously (Section 3.1).
Membership functions for the nine-valued logic output are presented below, where ‘trimf’ is triangular membership function from MATLAB script.
MF1 = ‘extremely short’: ‘trimf’, [0 0 12.5]
MF2 = ‘very short’: ‘trimf’, [0 12.5 25]
MF3 = ‘short’: ‘trimf’, [12.5 25 37.5]
MF4 = ‘almost medium’: ‘trimf’, [25 37.5 50]
MF5 = ‘medium’: ‘trimf’, [37.5 50 62.5]
MF6 = ‘after medium’: ‘trimf’, [50 62.5 75]
MF7 = ‘long’: ‘trimf’, [62.5 75 87.5]
MF8 = ‘very long’: ‘trimf’, [75 87.5 100]
MF9 = ‘extremely long’: ‘trimf’, [87.5 100 100]
The results for the fuzzy controller computations and the simulation of the Aimsun platform are given in Table 5, Table 6, Table 7 and Table 8.

3.3. Design of the Fuzzy Controller Using Three-Valued Logic for the Inputs and Five-Valued Logic for the Outputs

Membership functions from the MATLAB script for the five-valued logic output are presented below, where ‘trimf’ is triangular fuzzy membership function.
MF1 = ‘very short’: ‘trimf’, [0 0 25]
MF2 = ‘short’: ‘trimf’, [0 25 50]
MF3 = ‘average’: ‘trimf’, [25 50 75]
MF4 = ‘long’: ‘trimf’, [50 75 100]
MF5 = ‘very long’: ‘trimf’, [75 100 100]
The results for the fuzzy controller computations and the simulation of the Aimsun platform are given in Table 9, Table 10, Table 11 and Table 12.
Membership functions from the MATLAB script for the five-valued output are presented below, where ‘trimf’ is triangular fuzzy membership function.
MF1 = ‘very short’: ‘trimf’, [0 0 25]
MF2 = ‘short’: ‘trimf’, [0 25 50]
MF3 = ‘average’: ‘trimf’, [25 50 75]
MF4 = ‘long’: ‘trimf’, [50 75 100]
MF5 = ‘very long’: ‘trimf’, [75 100 100]

3.4. Design of the Fuzzy Controller Using Three-Valued Logic for the Inputs and Nine-Valued Logic for the Outputs

Membership functions for the nine-valued logic for the output are presented below, where ‘trimf’ is triangular membership function from MATLAB script.
MF1 = ‘extremely short’: ‘trimf’, [0 0 12.5]
MF2 = ‘very short’: ‘trimf’, [0 12.5 25]
MF3 = ‘short’: ‘trimf’, [12.5 25 37.5]
MF4 = ‘almost medium’: ‘trimf’, [25 37.5 50]
MF5 = ‘medium’: ‘trimf’, [37.5 50 62.5]
MF6 = ‘after medium’: ‘trimf’, [50 62.5 75]
MF7 = ‘long’: ‘trimf’, [62.5 75 87.5]
MF8 = ‘very long’: ‘trimf’, [75 87.5 100]
MF9 = ‘extremely long’: ‘trimf’, [87.5 100 100]
The results for the fuzzy controller computations and the simulation of the Aimsun platform are given in Table 13, Table 14, Table 15 and Table 16.
Membership functions for the nine-valued logic output are presented below, where ‘trimf’ is the triangular membership function from the MATLAB script.
MF1 = ‘extremely short’: ‘trimf’, [0 0 12.5]
MF2 = ‘very short’: ‘trimf’, [0 12.5 25]
MF3 = ‘short’: ‘trimf’, [12.5 25 37.5]
MF4 = ‘almost medium’: ‘trimf’, [25 37.5 50]
MF5 = ‘medium’: ‘trimf’, [37.5 50 62.5]
MF6 = ‘after medium’: ‘trimf’, [50 62.5 75]
MF7 = ‘long’: ‘trimf’, [62.5 75 87.5]
MF8 = ‘very long’: ‘trimf’, [75 87.5 100]
MF9 = ‘extremely long’: ‘trimf’, [87.5 100 100]

4. Classical Controller Design

The classical controller is designed using distance and green lights for the two sections.
The classical controller is designed analytically under the assumption that the ratio between the green lights’ durations for the two sections are u1 for Section 1 and u2 for Section 2. However, the presentation format used in this section shows the way in which the system of algebraic equations could be solved, i.e., by replacing u2 in the following equation (Equation (3))
x1/(x2 + x3) = u1/u2
u1 + u2 = 100
where x1, x2 and x3 are the inputs measured as the number of cars for the analytical controller, and u1 and u2 are the outputs measured as the green light in seconds for the analytical controller.
The results for the classical controller computations and the simulation of the Aimsun platform are given in Table 17, Table 18, Table 19 and Table 20.

5. Simulation Results

In this section, the results of the experiments are presented in graphical form. Four indicators are considered for evaluation of the traffic and the performance of different rules with fuzzy logic and the classical controller. The indicators are as follows: flow, total travel time, delay and travel time. The flow and the total travel time represent the behaviour of the whole transport system, and the classical controller is better in terms of these indicators. On the other hand, the delay and travel time represent the behaviour per car unit. In the case of this indicators, the fuzzy controller with three-valued logic for the inputs and five-valued logic for the outputs performs better. Considering the laws of Wardrop for the user and for system equilibrium, it can be concluded that, depending on the desired outcome, the abovementioned fuzzy controller or the classical controller should be used.
Figure 4, Figure 5, Figure 6 and Figure 7 present the results for Fuzzy Controllers 1–4 and the classical controller. For better illustration of the graphical results, a description of the fuzzy controllers is given as follows:
  • Fuzzy Controller 1: two-valued logic input with five-valued logic output;
  • Fuzzy Controller 2: two-valued logic input with nine-valued logic output;
  • Fuzzy Controller 3: three-valued logic input with five-valued logic output;
  • Fuzzy Controller 4: three-valued logic input with nine-valued logic output.
  • Classical Controller
Figure 4 shows the flow measured in vehicles per hour (veh/h) for the five controllers (four fuzzy controllers and one classical controller). As is obvious from the Figure 3, the classical controller has the highest traffic flow with about 3125 veh/h; hence this is the best results of all five experiments presented in the figure below. Among the fuzzy controllers, the best result of 3121 veh/h is obtained with the controller with the two-valued logic inputs with five-valued logic output and the controller with three-valued logic inputs with five-valued logic output.
Figure 5 presents the total travel time measured in hours for the whole traffic system and for the whole duration of the experiment. The classical controller shows the lowest total travel time of 59 h, which is the best result for the total travel time indicator. Hence, again, the advantage is for the classical controller over the other experiments concerning the fuzzy controllers. Among the fuzzy controllers, the best result of 61 h of total travel time is obtained for the controller with three-valued logic inputs and five-valued logic output.
Figure 6 presents the delay time measured in seconds per kilometre. For this traffic indicator, the best result of 59 s/km is obtained for the fuzzy controller with three-valued logic inputs and five-valued logic output. The classical controller gives the second-best result with 61 s/km.
Figure 7 presents travel time by car measured in seconds per kilometre. Here again, the best result of 126 s/km is obtained for the controller with three-valued logic inputs with five-valued logic output. The classical controller gives the second-best result with 127 s/km.
A conclusion can be drawn from the presented traffic indicators that in terms of the overall traffic system performance, the classical controller provides better results. Whereas, when it comes down to behaviour per car unit, Fuzzy Controller 3 (three-valued logic for the inputs and five-valued logic for the output) gives the best results.
The novelty of the study is that it examines, in a heuristic setting, the performance of the four different fuzzy controllers with the hierarchical system and compares them with a classical controller that is used as a benchmark. The practical implications of this study are that the research results can be replicated using a different simulation environment by following the details presented for the design of the fuzzy controllers.
Table 21 presents the graphical results in a tabular form, where the change in the traffic indicators (flow, total travel time, delay and travel time) is shown, based on the experiment with each controller. It can be seen that Fuzzy Controller 3 and the classical controller are the best performing ones with each of them producing the best results for two of the four indicators while being second-best for the remaining two indicators. However, Fuzzy Controller 3 is easier to interpret than the classical controller due to the fact that its linguistic rules are easy to understand even by non-expert users.

6. Conclusions

Depending on the desired outcome, the fuzzy or the classical controller should be used. If the goal is to minimise total travel time and maximise the flow, the classical controller would be a better choice. However, if the delay in travel time per car unit is considered, the choice of preference should be the fuzzy controller with Fuzzy Controller 3 (three-valued logic for inputs and five-valued logic for outputs). Overall, Fuzzy Controllers 1 and 2 (two-valued logic for inputs) show the worst results compared with Fuzzy Controllers 3 and 4 (three-valued logic of inputs) and compared with the classical controller.
For this study, the benchmark was the classical controller. The goal of the research was to design a network of intersections represented as a hierarchical system of traffic light-regulated intersections managed by fuzzy controllers. These fuzzy controllers were designed and simulated separately in the hierarchical network according to traffic indicators such as flow, delay, travel time and total travel time. Overall, the fuzzy controllers lead to better results for the individual units of vehicles, while the classical controller leads to better results in terms of system-wide behaviour.
The main contribution of this study is the development of a hierarchical transport network for an urban environment with interconnected junctions and the use of a traffic light control system for this network by using four different fuzzy controllers and one classical controller.
The main novelty of the study is that it examines, in a heuristic setting, the performance of the four different fuzzy controllers on the hierarchical system and compares them with a classical controller that is used as a benchmark.
The main relevance and significance of this study in relation to previous works is its systematic approach that guarantees the good capability of the associated expert based heuristics and makes it potentially useful for policy decisions in the chosen application area.
Future research will focus on the generalizability and scalability of the experiment so that larger or more complex urban networks can be simulated and tested with this method. It will also consider data-driven optimisation techniques for the fuzzy controllers in the context of scenarios that are different from the one investigated in this paper, as well as more robust statistical analysis of the data. It will also focus on a more advanced implementation of the current fairly basic heuristic fuzzy approach that will be complemented with an associated learning process based on machine learning techniques.

Author Contributions

Conceptualisation, A.G., B.V., Y.B. and A.I.; methodology, A.G., B.V. and A.I.; software, B.V. and Y.B.; validation, B.V. and Y.B.; formal analysis, A.G.; investigation, B.V. and Y.B.; resources, Y.B.; data curation, B.V. and Y.B.; writing—original draft preparation, B.V. and Y.B.; writing—review and editing, A.G. and B.V.; visualisation, B.V. and Y.B.; supervision, A.G.; project administration, A.G.; funding acquisition, not applicable. All authors have read and agreed to the published version of the manuscript.

Funding

This work has been realised with financial support from the European Regional Development Fund within the Operational Programme “Bulgarian national recovery and resilience plan”, the procedure for direct provision of grants “Establishing of a network of research higher education institutions in Bulgaria and, under the Project BG-RRP-2.004-0005 “Improving the research capacity and quality to achieve international recognition and resilience of TU-Sofia”.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Guo, Y.; Zhang, K.; Chen, X.; Li, M. Proactive Coordination of Traffic Guidance and Signal Control for a Divergent Network. Mathematics 2023, 11, 4262. [Google Scholar] [CrossRef]
  2. Elbaum, Y.; Novoselsky, A.; Kagan, E. A Queueing Model for Traffic Flow Control in the Road Intersection. Mathematics 2022, 10, 3997. [Google Scholar] [CrossRef]
  3. Stoilova, K.; Stoilov, T. Optimizing Traffic Light Green Duration Under Stochastic Considerations. Mathematics 2023, 11, 496. [Google Scholar] [CrossRef]
  4. Papageorgiou, M.; Diakaki, C.; Dinopoulou, V.; Kotsialos, A.; Wang, Y. Review of road traffic control strategies. Proc. IEEE 2003, 91, 2043–2067. [Google Scholar] [CrossRef]
  5. Qadri, S.S.S.M.; Gökçe, M.A.; Öner, E. State-of-art review of traffic signal control methods: Challenges and opportunities. Eur. Transp. Res. Rev. 2020, 12, 55. [Google Scholar] [CrossRef]
  6. Schweizer, J.; Poliziani, C.; Rupi, F.; Morgano, D.; Magi, M. Building a large-scale micro-simulation transport scenario using big data. ISPRS Int. J. Geo-Inf. 2021, 10, 165. [Google Scholar] [CrossRef]
  7. Huang, R.; Han, L.D.; Huang, Z. A new network equilibrium flow model: User-equilibrium with quantity adjustment. Transp. Res. Part E Logist. Transp. Rev. 2022, 163, 102719. [Google Scholar] [CrossRef]
  8. Ameli, M.; Lebacque, J.P.; Leclercq, L. Improving traffic network performance with road banning strategy: A simulation approach comparing user equilibrium and system optimum. Simul. Model. Pract. Theory 2020, 99, 101995. [Google Scholar] [CrossRef]
  9. Wardrop, J.G. Some Theoretical Aspects of Road Traffic Research. Proc. Inst. Civ. Eng. 1952, 1, 325–362. [Google Scholar] [CrossRef]
  10. Pavlova, K.; Stoilov, T.; Stoilova, K. Bi-level model for public rail transportation under incomplete data. J. Cybern. Inf. Technol. 2017, 17, 75–91. [Google Scholar] [CrossRef]
  11. Trichkova-Kashamova, E. Modeling and optimization of traffic flows in a network. In Proceedings of the International Conference Automatics and Informatics—ICAI, Varna, Bulgaria, 1–3 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
  12. Lu, J.; Chen, F.; Ma, V. Signal Timing for an Isolated Intersection Based on the Two-Stage Fuzzy Logic Controller. Adv. Eng. Res. 2018, 127, 111–114. [Google Scholar] [CrossRef]
  13. Murat, S.Y.; Gedizlioglu, E. A fuzzy logic multi-phased signal control model for isolated junctions. Transp. Res. Part C Emerg. Technol. 2005, 13, 19–36. [Google Scholar] [CrossRef]
  14. Rahmani, A.M.; Naqvi, R.A.; Yousefpoor, E.; Yousefpoor, M.S.; Ahmed, O.H.; Hosseinzadeh, M.; Siddique, K. A Q-Learning and Fuzzy Logic-Based Hierarchical Routing Scheme in the Intelligent Transportation System for Smart Cities. Mathematics 2022, 10, 4192. [Google Scholar] [CrossRef]
  15. Lee, J.-H.; Lee, K.M.; Lee-Kwang, H. Fuzzy controller for intersection group. In Proceedings of the IEEE Conference on Industrial Automation and Control Emerging Technology Applications, Taipei, Taiwan, 22–27 May 1995; IEEE: Piscataway, NJ, USA, 2002; pp. 376–382. [Google Scholar] [CrossRef]
  16. Yulianto, B. Application of fuzzy logic to traffic signal control under mixed traffic conditions. Traffic Eng. Control 2003, 44, 332–336. Available online: https://www.researchgate.net/publication/293358870_Application_of_fuzzy_logic_to_traffic_signal_control_under_mixed_traffic_conditions (accessed on 1 March 2025).
  17. Almadi, A.I.M.; Mamlook, R.E.; Almarhabi, Y.; Ullah, I.; Jamal, A.; Bandara, N. A fuzzy-logic approach based on driver decision-making behavior modeling and simulation. Sustainability 2022, 14, 8874. [Google Scholar] [CrossRef]
  18. Vatchova, B.; Boneva, Y. Design of Fuzzy and Conventional Controllers for Modeling and Simulation of Urban Traffic Light System with Feedback Control. Mathematics 2023, 11, 373. [Google Scholar] [CrossRef]
  19. Vatchova, B.; Boneva, Y.; Gegov, A. Modelling and Simulation of Traffic Light Control. J. Cybern. Inf. Technol. 2023, 2, 179–191. [Google Scholar] [CrossRef]
  20. Gegov, A. Distributes Fuzzy Control of Multivariable Systems. In International Series in Intelligent Technologies (ISIT); Springer: Berlin/Heidelberg, Germany, 1996; Volume 6, pp. 1–186. ISBN 978-94-015-8640-5. [Google Scholar]
  21. Gegov, A. Complexity Management in Fuzzy Systems. In Studies in Fuzziness and Soft Computing (STUDFUZZ); Springer: Berlin/Heidelberg, Germany, 2007; Volume 211, pp. 1–349. ISBN 978-3-540-38885-2. [Google Scholar]
  22. Fuzzy Logic Toolbox-MATLAB. Available online: https://www.mathworks.com/products/fuzzy-logic.html (accessed on 25 September 2024).
  23. Popchev, I.; Peneva, V. An Algorithm for Comparison of Fuzzy Sets. Fuzzy Sets Syst. 1993, 60, 59–65. [Google Scholar] [CrossRef]
  24. Peneva, V.; Popchev, I. Multicriteria Decision Making Based on Fuzzy Relations. J. Cybern. Inf. Technol. 2008, 8, 3–12. Available online: https://cit.iict.bas.bg/CIT_08/v8-4/3-12.pdf (accessed on 1 March 2025).
  25. Peneva, V.; Popchev, I. Fuzzy Criteria Importance with Weighting Functions. Compt. Rendus Acad. Bulg. Sci. 2008, 61, 293–300. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=b70ac1cba0a2c291a68c4a733bc257923a459357 (accessed on 1 March 2025).
  26. Zhang, D.; Zhang, Z.; Jiao, X.; Zhang, Y. Hybrid fuzzy grammar dynamic graph diffusing attention network for traffic flow prediction. Future Gener. Comput. Syst. 2025, 167, 107725. [Google Scholar] [CrossRef]
  27. Liu, Y.; Wang, X.; Hou, W.; Liu, H.; Wang, J. A novel hybrid model combining a fuzzy inference system and a deep learning method for short-term traffic flow prediction. Knowl. Based Syst. 2022, 255, 109760. [Google Scholar] [CrossRef]
  28. Jamshidnejad, A.; Schutter, B. A combined probabilistic-fuzzy approach for dynamic modeling of traffic in smart cities: Handling imprecise and uncertain traffic data. Comput. Electr. Eng. 2024, 119 Pt A, 109552. [Google Scholar] [CrossRef]
  29. Liu, X.; Jiang, X.; Luo, X.; Zhang, Z.; Ji, P. Exact and heuristic algorithms for team orienteering problem with fuzzy travel times. Expert Syst. Appl. 2025, 278, 127369. [Google Scholar] [CrossRef]
  30. Aliskan, I. The optimization-based fuzzy logic controllers for autonomous ground vehicle path tracking. Eng. Appl. Artif. Intell. 2025, 151, 110642. [Google Scholar] [CrossRef]
  31. Tunc, I.; Yesilyurt, A.Y.; Soylemez, M.T. Different Fuzzy Logic Control Strategies for Traffic Signal Timing Control with State Inputs. IFAC-PapersOnLine 2021, 54, 265–270. [Google Scholar] [CrossRef]
  32. Wiering, M.A.; Van Veenen, J.; Vreeken, J.; Koopman, A. Intelligent Traffic Light Control; Technical Report UU-CS-2004-029; 2004; pp. 1–30. Available online: https://research-portal.uu.nl/en/publications/intelligent-traffic-light-control (accessed on 1 March 2025).
  33. Shi, Y.; Wang, Z.; LaClair, T.J.; Wang, C.; Shao, Y.; Yuan, J. A Novel Deep Reinforcement Learning Approach to Traffic Signal Control with Connected Vehicles. Appl. Sci. 2023, 13, 2750. [Google Scholar] [CrossRef]
  34. Du, Y.; ShangGuan, W.; Rong, D.; Chai, L. RA-TSC: Learning Adaptive Traffic Signal Control Strategy via Deep Reinforcement Learning. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 3275–3280. [Google Scholar]
  35. Guo, Q.; Li, L.; Ban, X.J. Urban traffic signal control with connected and automated vehicles: A survey. Transp. Res. Part C Emerg. Technol. 2019, 101, 313–334. [Google Scholar] [CrossRef]
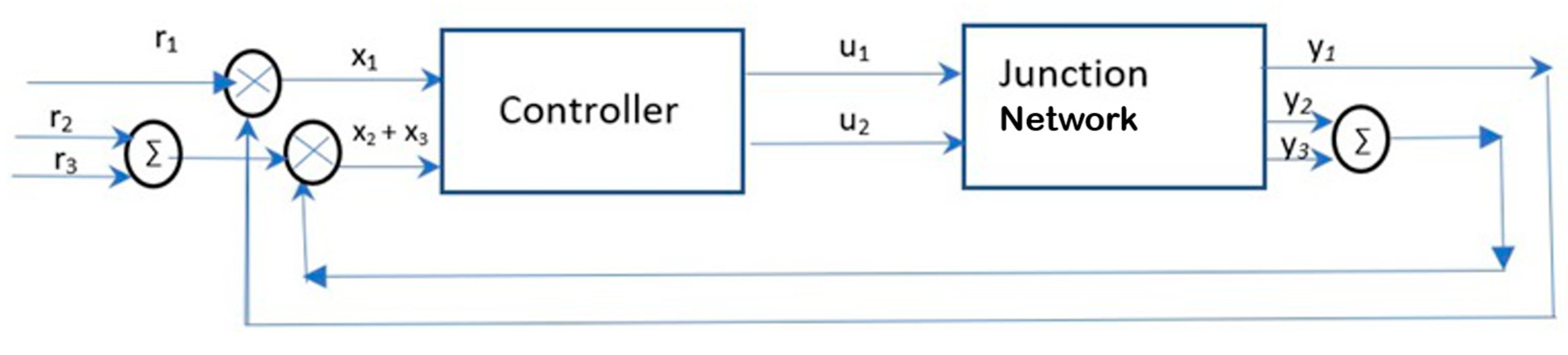
Futureinternet 17 00227 g001
Figure 1. Traffic light system with feedback control.
Figure 1. Traffic light system with feedback control.
Futureinternet 17 00227 g001
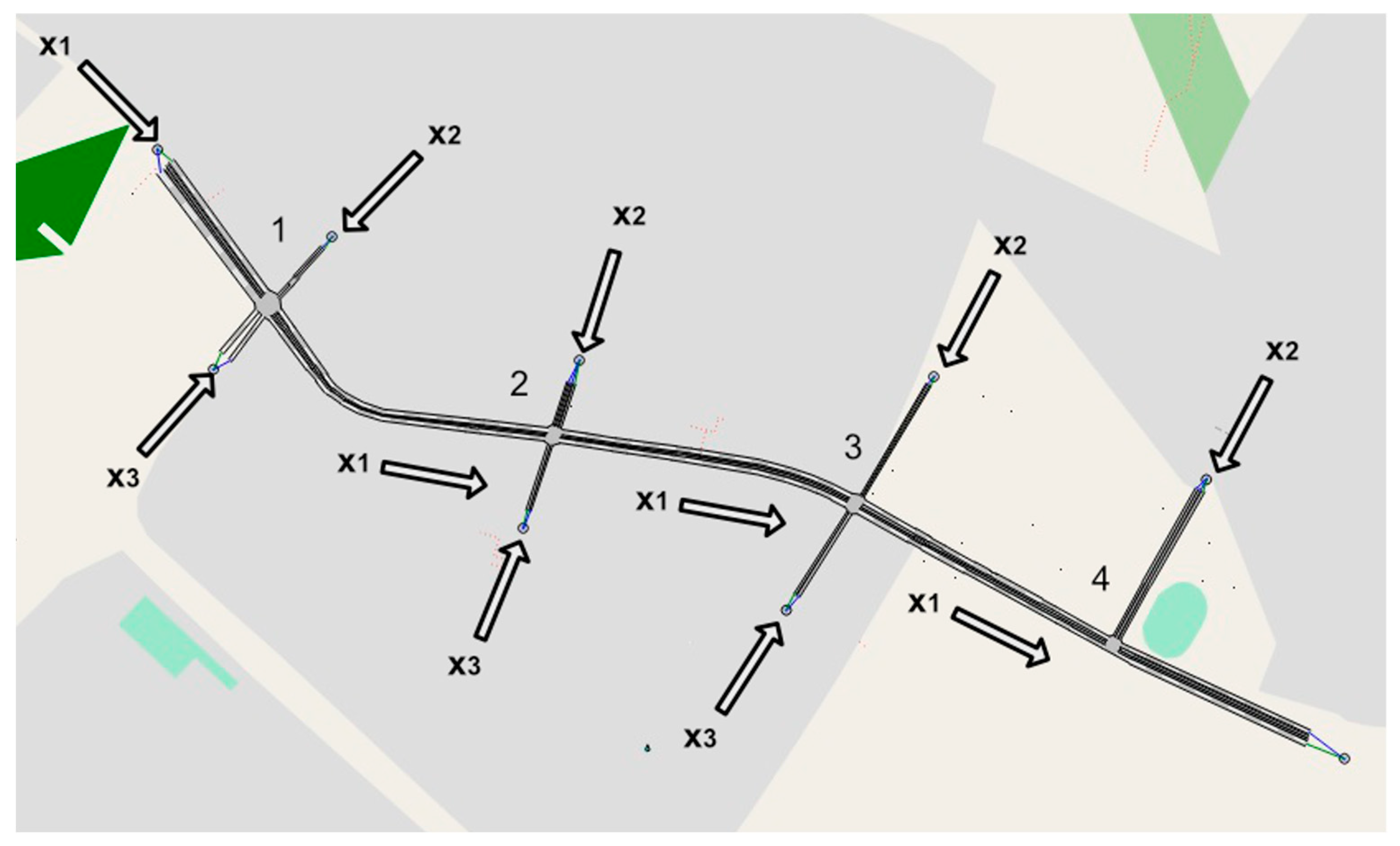
Futureinternet 17 00227 g002
Figure 2. Network of four junctions.
Figure 2. Network of four junctions.
Futureinternet 17 00227 g002
Futureinternet 17 00227 g003
Figure 3. Flow chart of the fuzzy logic controllers.
Figure 3. Flow chart of the fuzzy logic controllers.
Futureinternet 17 00227 g003
Futureinternet 17 00227 g004
Figure 4. Flow for the whole network of crossroads measured in vehicles per hour.
Figure 4. Flow for the whole network of crossroads measured in vehicles per hour.
Futureinternet 17 00227 g004
Futureinternet 17 00227 g005
Figure 5. Total travel time for the whole network measured in hours.
Figure 5. Total travel time for the whole network measured in hours.
Futureinternet 17 00227 g005
Futureinternet 17 00227 g006
Figure 6. Delay time per car measured in seconds per kilometre.
Figure 6. Delay time per car measured in seconds per kilometre.
Futureinternet 17 00227 g006
Futureinternet 17 00227 g007
Figure 7. Travel time per car measured in seconds per kilometre.
Figure 7. Travel time per car measured in seconds per kilometre.
Futureinternet 17 00227 g007
Table 1. Results for Junction 1 for two-valued logic for the inputs and five-valued logic for the output.
Table 1. Results for Junction 1 for two-valued logic for the inputs and five-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection[0 2700][0 900][0 1800]
1 iteration9608722504951
2 iteration9038882565050
3 iteration9038882565050
Table 2. Results for Junction 2 for two-valued logic for the inputs and five-valued logic for the output.
Table 2. Results for Junction 2 for two-valued logic for the inputs and five-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection[0 1800][0 900][0 1800]
1 iteration932841507327
2 iteration9448015773 27
3 iteration9448015773 27
Table 3. Results for Junction 3 for two-valued logic for the inputs and five-valued logic for the output.
Table 3. Results for Junction 3 for two-valued logic for the inputs and five-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900][0 1800]
1 iteration3981001275347
2 iteration4031001275347
3 iteration4031001275347
Table 4. Results for Junction 4 for two-valued logic for the inputs and five-valued logic for the output.
Table 4. Results for Junction 4 for two-valued logic for the inputs and five-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900]
1 iteration4543075248
2 iteration4523075248
3 iteration4523075248
Table 5. Results for Junction 1 for two-valued logic for the inputs and nine-valued logic for the output.
Table 5. Results for Junction 1 for two-valued logic for the inputs and nine-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 2700][0 900][0 800]
1 iteration9608722505050
2 iteration9038882565050
3 iteration9038882565050
Table 6. Results for Junction 2 for two-valued logic for the inputs and nine-valued logic for the output.
Table 6. Results for Junction 2 for two-valued logic for the inputs and nine-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 2700][0 900][0 1800]
1 iteration944801575050
2 iteration932801575050
3 iteration932801575050
Table 7. Results for Junction 3 for two-valued logic for the inputs and nine-vaued logic for the output.
Table 7. Results for Junction 3 for two-valued logic for the inputs and nine-vaued logic for the output.
x1
Number of Cars for the Main Road		 x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 2700][0 900][0 1800]
1 iteration3981001275050
2 iteration3981001275050
3 iteration3981001275050
Table 8. Results for Junction 4 for two-valued logic for the inputs and nine-valued logic for the output.
Table 8. Results for Junction 4 for two-valued logic for the inputs and nine-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900]
1 iteration4523075050
2 iteration4543075050
3 iteration4543075050
Table 9. Results for Junction 1 for three-valued logic for the inputs and five-valued logic for the output.
Table 9. Results for Junction 1 for three-valued logic for the inputs and five-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 2700][0 900][0 1800]
1 iteration9608722504357
2 iteration9038882564159
3 iteration9028882564159
Table 10. Results for Junction 2 for three-valued logic for the inputs and five-valued logic for the output.
Table 10. Results for Junction 2 for three-valued logic for the inputs and five-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900][0 1800]
1 iteration931801576931
2 iteration943801576931
3 iteration943801576931
Table 11. Results for Junction 3 for three-valued logic for the inputs and five-valued logic for the output.
Table 11. Results for Junction 3 for three-valued logic for the inputs and five-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900][0 900]
1 iteration3971001275446
2 iteration3971001275446
3 iteration3971001275446
Table 12. Results for Junction 4 for three-valued logic for the inputs and five-valued logic for the output.
Table 12. Results for Junction 4 for three-valued logic for the inputs and five-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900]
1 iteration4553074753
2 iteration4553074753
3 iteration4553074753
Table 13. Results for Junction 1 for three-valued logic for the inputs and nine-valued logic for the output.
Table 13. Results for Junction 1 for three-valued logic for the inputs and nine-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 2700][0 900][0 1800]
1 iteration9608722503763
2 iteration8988882563664
3 iteration8988882563664
Table 14. Results for Junction 2 for three-valued logic for the inputs and nine-valued logic for the output.
Table 14. Results for Junction 2 for three-valued logic for the inputs and nine-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900][0 1800]
1 iteration942801576832
2 iteration942801576832
3 iteration942801576832
Table 15. Results for Junction 3 for three-valued logic for the inputs and nine-valued logic for the output.
Table 15. Results for Junction 3 for three-valued logic for the inputs and nine-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900][0 900]
1 iteration3971001275347
2 iteration3971001275347
3 iteration3971001275347
Table 16. Results for Junction 4 for three-valued logic for the inputs and nine-valued logic for the output.
Table 16. Results for Junction 4 for three-valued logic for the inputs and nine-valued logic for the output.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900]
1 iteration4543073169
2 iteration4513073169
3 iteration4513073169
Table 17. Results for Junction 1 for the classical controller.
Table 17. Results for Junction 1 for the classical controller.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 2700][0 900][0 1800]
1 iteration9608722504753
2 iteration9038882564456
3 iteration9038882564456
Table 18. Results for Junction 2 for the classical controller.
Table 18. Results for Junction 2 for the classical controller.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900][0 1800]
1 iteration931801578020
2 iteration948801578020
3 iteration948801578020
Table 19. Results for Junction 3 for the classical controller.
Table 19. Results for Junction 3 for the classical controller.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		x3
Number of Cars for the Third Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900][0 1800]
1 iteration3971001276436
2 iteration3991001276436
3 iteration3971001276436
Table 20. Results for Junction 4 for the classical controller.
Table 20. Results for Junction 4 for the classical controller.
x1
Number of Cars for the Main Road		x2
Number of Cars for the Second Road		u1
Green Light for the Main Road/s		u2
Green Light for the Other Two Roads
Range (capacity)/number of cars for the whole intersection [0 1800][0 900]
1 iteration4553076040
2 iteration4553076040
3 iteration4553076040
Table 21. Traffic indicators for the five controllers.
Table 21. Traffic indicators for the five controllers.
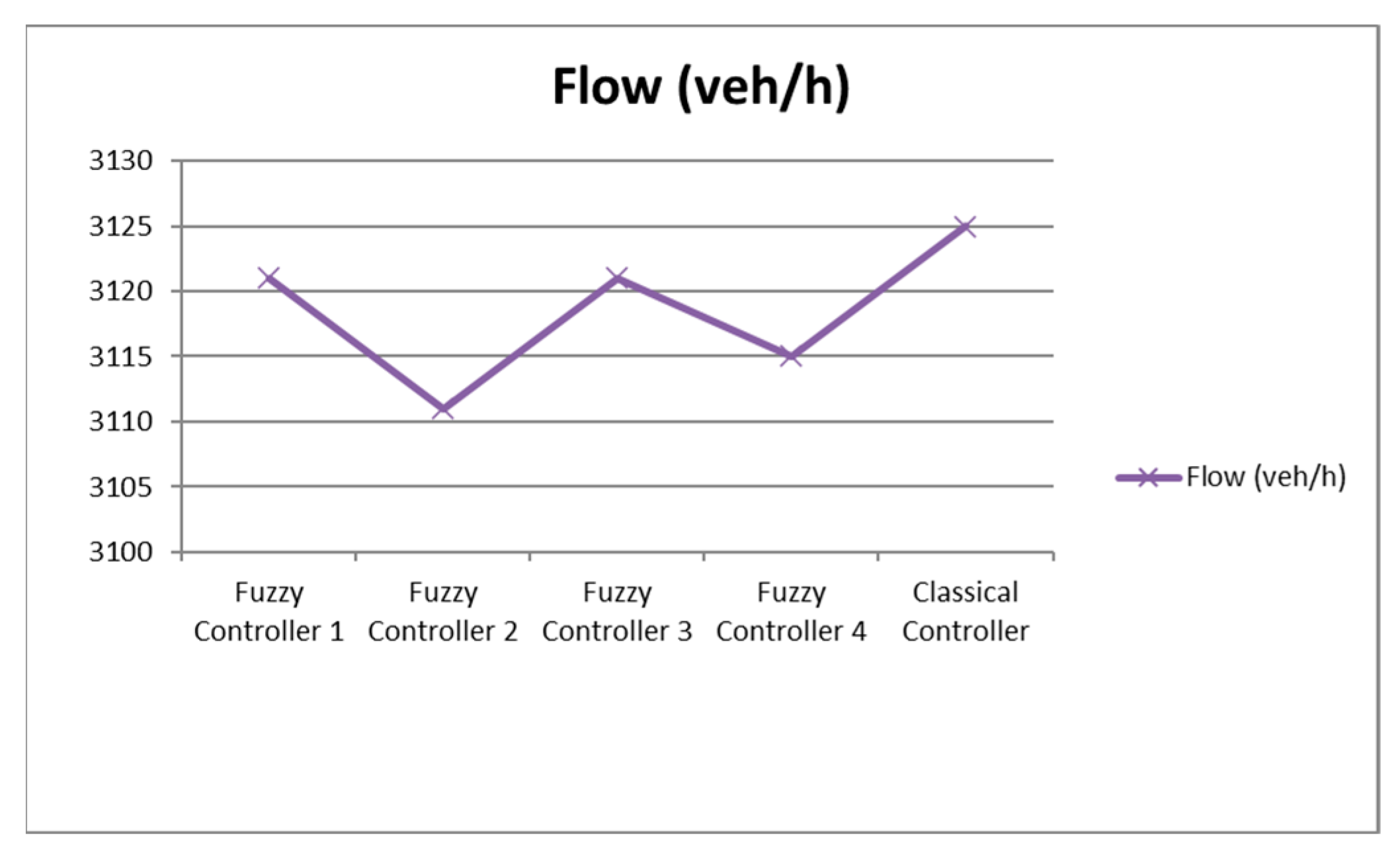
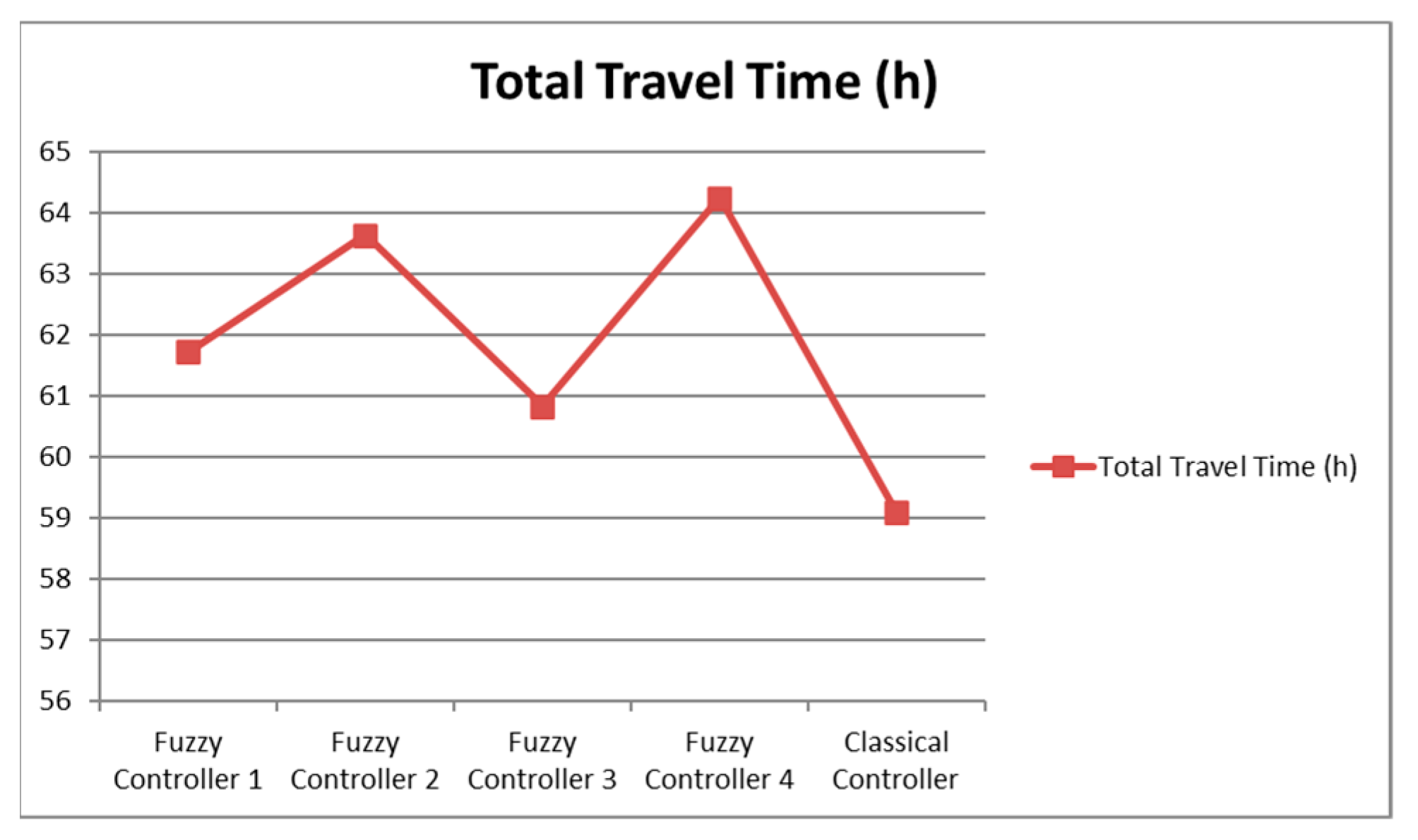
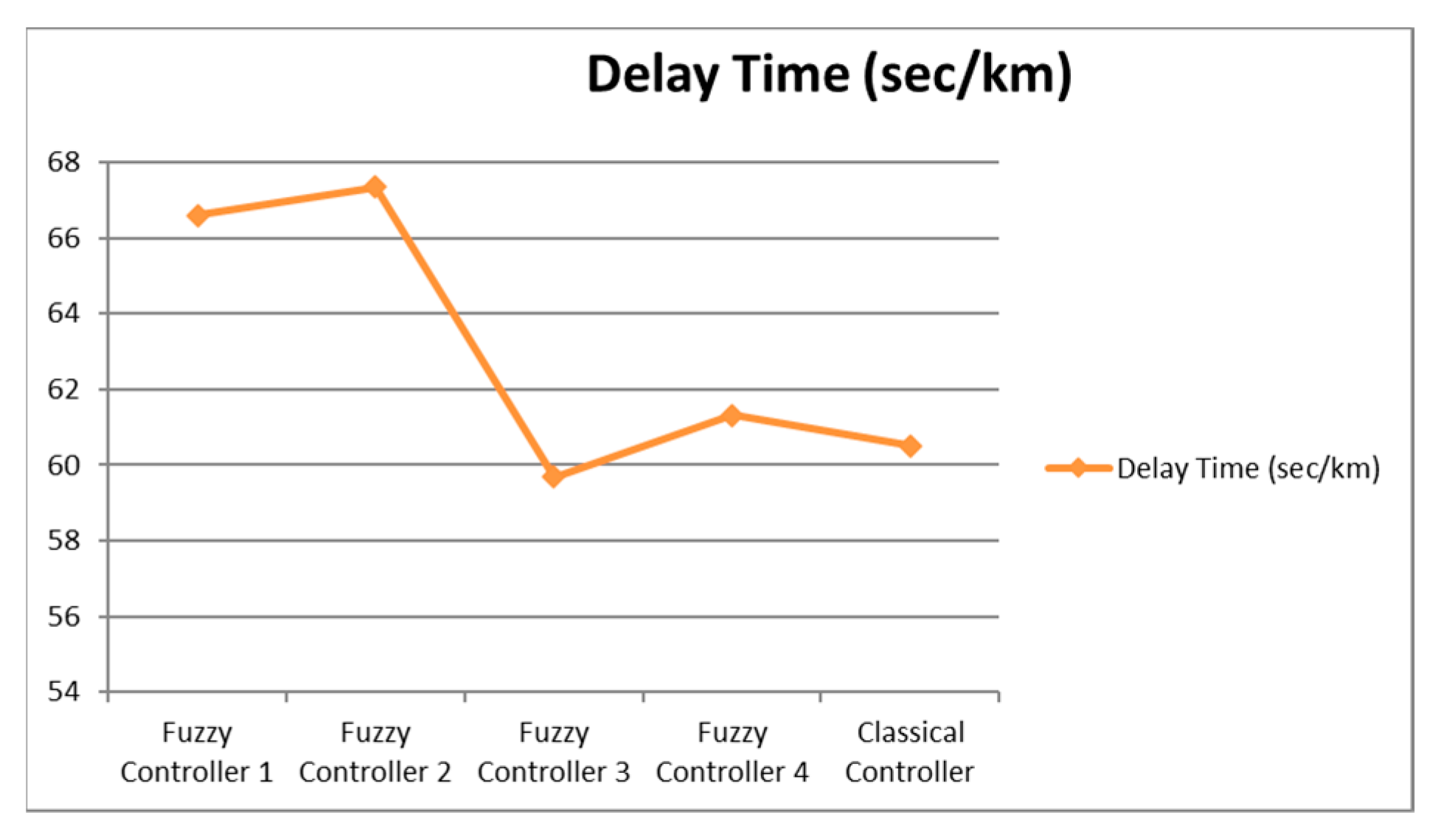
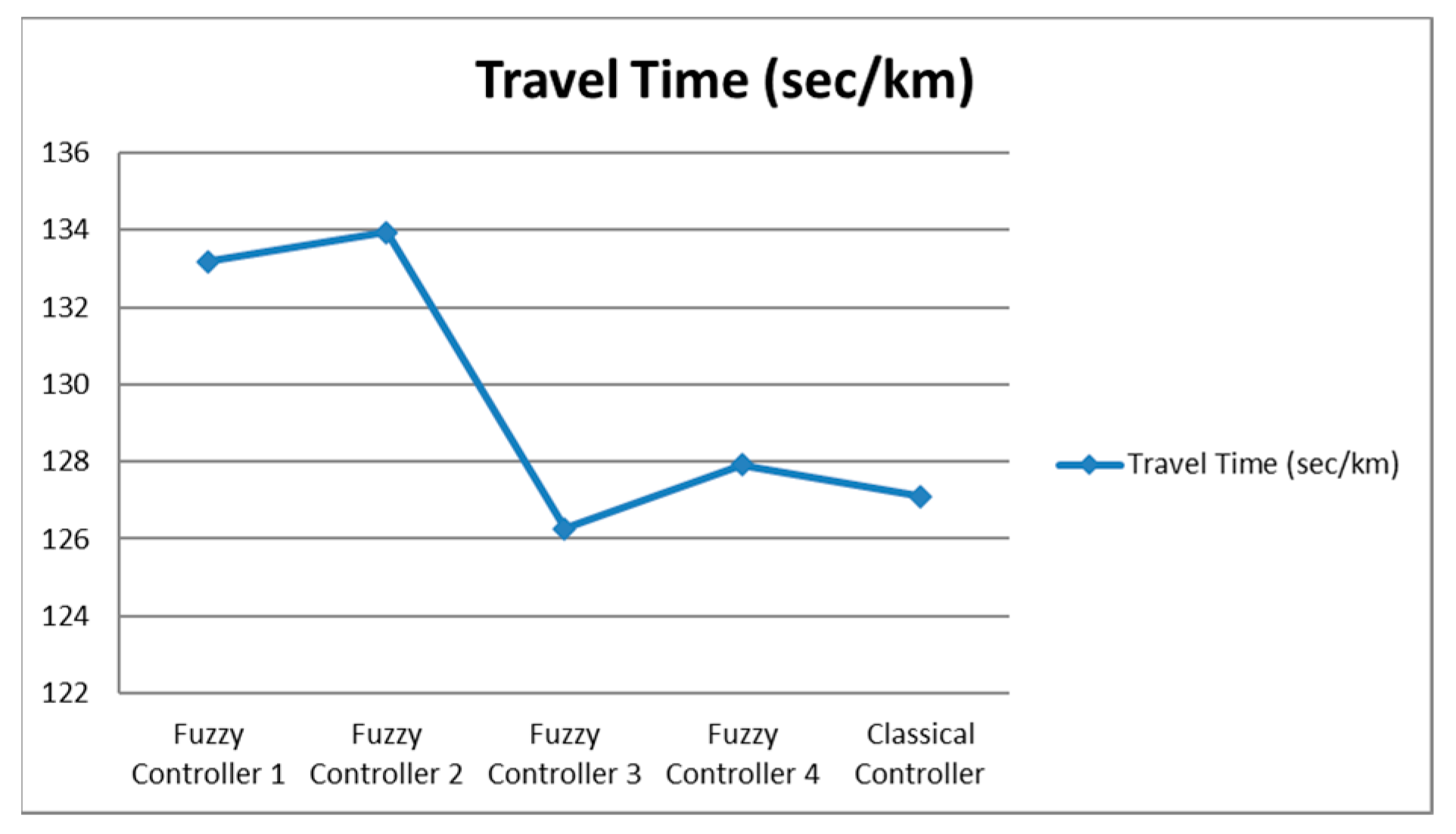
Fuzzy Controller 1Fuzzy Controller 2Fuzzy Controller 3Fuzzy Controller 4Classical Controller
Flow (veh/h)31213111312131153125
Total travel time (h)61.7363.6460.8464.2559.1
Delay (s/km)66.667.3559.6861.3260.51
Travel time (s/km)133.19133.95126.27127.91127.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gegov, A.; Vatchova, B.; Boneva, Y.; Ichtev, A. Heuristic Fuzzy Approach to Traffic Flow Modelling and Control on Urban Networks. Future Internet 2025, 17, 227. https://doi.org/10.3390/fi17050227

AMA Style

Gegov A, Vatchova B, Boneva Y, Ichtev A. Heuristic Fuzzy Approach to Traffic Flow Modelling and Control on Urban Networks. Future Internet. 2025; 17(5):227. https://doi.org/10.3390/fi17050227

Chicago/Turabian Style

Gegov, Alexander, Boriana Vatchova, Yordanka Boneva, and Alexandar Ichtev. 2025. "Heuristic Fuzzy Approach to Traffic Flow Modelling and Control on Urban Networks" Future Internet 17, no. 5: 227. https://doi.org/10.3390/fi17050227

APA Style

Gegov, A., Vatchova, B., Boneva, Y., & Ichtev, A. (2025). Heuristic Fuzzy Approach to Traffic Flow Modelling and Control on Urban Networks. Future Internet, 17(5), 227. https://doi.org/10.3390/fi17050227

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop