Abstract
The federated recommender system (FRS) employs federated learning methodologies to create a recommendation model in a distributed environment, where clients share locally updated data with the server without exposing raw data and achieving privacy preservation. However, varying communication capabilities among devices restrict the participation of only a subset of clients in each round of federated training, resulting in slower convergence and requiring additional training rounds. In this work, we propose a novel federated recommendation framework, called FedRecI2C, which integrates communication and computation resources in the system. This framework accelerates convergence by utilizing not only communication-capable clients for federated training but also communication-constrained clients to leverage their computation and limited communication resources for further local training. This framework offers simplicity and flexibility, providing a plug-and-play architecture that effectively enhances the convergence speed in FRSs. It has demonstrated remarkable effectiveness in a wide range of FRSs when operating under diverse communication conditions. Extensive experiments are conducted to validate the effectiveness of FedRecI2C. Moreover, we provide in-depth analyses of the FedRecI2C framework, offering novel insights into the training patterns of FRSs.
1. Introduction
Recommender systems, which are crucial applications of machine learning algorithms [1], are utilized across various domains such as e-commerce, advertising and other online services. These systems typically rely on historical interaction data between users and items for training. However, frequent access to users’ raw data during training raises privacy concerns [2]. Consequently, due to the federated learning (FL) paradigm’s capability of privacy protection, the adoption of FL in recommendation algorithms has gained significant attention.
Federated recommender systems (FRSs) allow users to keep their personal data locally and share only model parameters with low privacy sensitivity for global model training [3]. This strategy not only significantly strengthens the privacy protection capabilities of the system but also enables the training process to take place directly on end devices, effectively utilizing decentralized computation resources. Additionally, participants can collaborate with other data platforms to boost the recommendation performance while adhering to regulatory and privacy requirements. However, due to the high-frequency exchange of model data between clients and the server, the process is severely restricted by communication conditions such as limited channel bandwidth and network instabilities [4].
In FRSs, users’ participation in training is often limited by their communication capabilities, which prolongs the model training cycle. Despite significant advancements in accelerating convergence for many existing FL algorithms, not all of them can be directly applied to FRSs. This is primarily due to the following reasons:
- Limitation 1: Insufficient training of partial clients. FRSs require modeling both items and clients, with client models remaining local and updated using the latest item models from the server. Existing FL acceleration algorithms, such as [5,6], select a subset of clients based on their computation and communication resources for federated training. However, these algorithms often neglect the training of user models for resource-constrained clients, which negatively affects their recommendation performance.
- Limitation 2: Invalid assumption of always-open communication channels. Some existing FL acceleration algorithms [7,8] require all clients to obtain the global model for local training and upload the correlation between their local updates and the global model to the server. The server makes decisions based on these correlations and notifies partial clients that need to upload their updated data. This process requires that the communication channels always maintain effectiveness, which contradicts the inherent randomness of communication channels.
- Limitation 3: Complexity in modeling relationships among clients. The algorithms proposed in [9,10] need the server to model the relationships among clients based on their updated data. In typical FL scenarios, clients upload data that have the same structure. However, in FRSs, the interactions between clients and items are highly complex, resulting in significant variations in the types of item models uploaded by different clients. This poses a challenge for modeling relationships between clients.
To avoid these issues, we introduce a simple and flexible framework, Federated Recommendation Framework Integrating Communication and Computation (FedRecI2C), aimed at accelerating model convergence in FRSs. Given that only a subset of clients participates in federated training due to communication constraints, we hypothesize that a client with communication constraints can enhance its model by leveraging local idle computation resources and limited communication capabilities. Specifically, motivated by the communication channels involving downloading and uploading in FRSs, we consider two scenarios of communication constraints. See Figure 1 for an illustration.
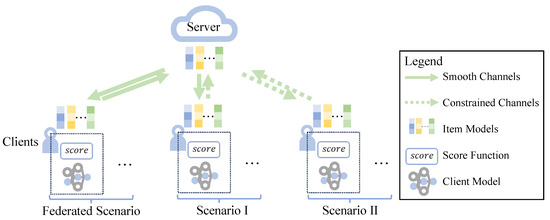
Figure 1.
Communication-constrained scenarios in FRSs.
- Scenario I. Some clients are unable to timely upload their model updates to the server after performing local updates due to fluctuating communication conditions.
- Scenario II. Some clients occasionally face limited communication bandwidth, preventing them from timely downloading and uploading item models.
Furthermore, the storage configuration, wherein global item model parameters are hosted on the server while updated item model parameters are retained locally on client devices, enables the utilization of local item models for FedRecI2C training. See Section 3 for further elaboration.
Compared to other convergence-acceleration methods in FL, FedRecI2C exhibits better compatibility. It can be directly applied to many existing FRSs without the need to modify the client/item models, aggregation method or the network topology, which is different from those methods facing Limitation 3. Moreover, FedRecI2C allows for more severe communication conditions (such as some clients being barely able to upload data) and more complex communication scenarios (see Section 4.2.2 for reference). Therefore, our method, to a certain extent, circumvents the unreasonable assumptions about communication conditions described in Limitation 2. Our effective utilization of communication-constrained clients enables those clients that are typically excluded from training in other FL settings to be fully trained. This addresses the issue described in Limitation 1. The main contributions of this paper are outlined as follows:
- Introducing FedRecI2C that integrates communication and computation resources of both communication-capable and communication-constrained clients to expedite model convergence.
- Demonstrating the broad applicability of FedRecI2C, making it applicable across various FRSs.
- Demonstrating the effectiveness of FedRecI2C under various communication scenarios through experiments.
This paper is structured as follows: Section 2 provides an overview of previous research related to FRS and accelerating convergence in FL. Section 3 describes the general framework of implicit feedback FRSs and the workflow of FedRecI2C. Section 4 presents and discusses the results obtained from our experiments. Section 5 discusses some practical application issues. Finally, Section 6 summarizes the main conclusions and highlights future research directions.
2. Related Work
2.1. Federated Recommender System
The proliferation of privacy protection laws and regulations, coupled with heightened awareness regarding privacy [2], has spurred further research into the application of FL in recommender systems. As a result, numerous FRSs have emerged.
FCF [11] is the pioneering work that introduced the first FRS utilizing FL with collaborative filtering models. FedMF [12] introduces the first federated matrix factorization (MF) [13] algorithm based on non-negative matrix factorization [14], though with limitations in terms of privacy and heterogeneity. Several studies endeavor to address the performance gap between FRSs and centralized recommender systems. FedGNN [15] is a GNN-based FRS that trains locally, aggregates gradients applying differential privacy, and expands user–item graphs for high-order interactions. As a federated contrastive learning method, FedCL [16] aims for privacy-preserving recommendation, exploiting high-quality negatives via local differential privacy and clustering for effective model training.
Some FRSs prioritize safeguarding users’ item interaction history. FedRec [17] introduces a hybrid filling strategy, wherein each client randomly samples uninteractive items and assigns virtual ratings, augmenting true ratings in the calculation of item feature gradients, preventing the server from discerning specific interactions between clients and items. DFedRec [18] is a decentralized recommendation model using a privacy-aware graph, employing fake entries for privacy and reducing communication by sharing parameters with neighbors, ensuring accuracy and privacy.
Focused on reducing the training costs associated with FRSs, FedFast [19] accelerates the training process by diverse client sampling and an active aggregation method that propagates the updated model to other clients, thereby reducing communication costs and ensuring rapid convergence. Zhang et al. [20] proposed a federated discrete optimization model to learn the binary codes of item embeddings, achieving the dual objectives of efficiency and privacy. HFCCD [21] employs the Count Sketch technique to compress item feature vectors to reduce the communication overhead and offer a privacy protection capability. PrivFR [22] uses shared hash embedding to efficiently represent items, conserving resources, addressing the out-of-vocabulary issue, and reducing storage and communication overheads in FRSs. The FedMAvg algorithm [23], which integrates FedAvg [24] with the alternating minimization approach, focuses on MF models and facilitates partial client communication to reduce communication costs. Cali3F [25] is a calibrated fast and fair FRS. By integrating neural networks, adopting a clustering-based method and new sampling and update strategies, it balances fairness and convergence speed.
2.2. Accelerating Convergence in Federated Learning
In FL, the downloading of the global model and the uploading of updated data introduce an additional communication overhead [26]. Consequently, accelerating convergence to mitigate this overhead has become a significant challenge. Various techniques have been proposed to address this [27,28], including selective client sampling, client clustering, upload dropout and network topology optimization.
FLOB [8] evaluates the contributions of clients to the global model using local update information, and determines the optimal probability distribution for client selection to confirm a near-optimal subset of clients that minimizes global loss. The Eiffel [29] algorithm dynamically selects clients for global model aggregation and adjusts the frequency of local and global model updates adaptively, which enables the server to schedule clients considering resource efficiency and model fairness. OCEAN [5] considers clients’ computation and communication resource status, and selects a subset for FL uploads based on both current resource availability and historical energy state tracking. FedMCCS [30] is a multi-criterion method for selecting FL clients. It evaluates CPU, memory, energy and time resources to predict client capacity and maximize participation in FL. The limitation of these FL methods with selective client sampling is that they overlook the training requirements of clients with limited resources in the system. In FRSs that require non-global training of sub-models (i.e., client models), such negligence can slow down the training process of these clients, thus impairing the convergence speed of the entire system.
Wang et al. [9] introduce a cluster aggregation approach in FL, where clients synchronously transmit their local updates to cluster headers and the headers then asynchronously conduct global aggregation. They propose a cluster-based FL to optimize the cluster structure under resource constraints and apply it to dynamic networks. FedCor [10] addresses inter-client correlation using Gaussian processes to model loss correlations. By selectively sampling clients, it aims to reduce global loss per round and accelerate model convergence. These client clustering methods have only been validated on relatively small-scale models. In FRSs, as the number of items in the system increases, so does the number of item models uploaded by each client. Moreover, due to the variations in users’ item interaction histories, the types of item models they upload vary significantly. Conversely, in the studies of [9,10], the data uploaded by each client have the same dimension. These issues pose challenges to the application of client clustering methods in FRSs.
Chen et al. [31] propose an asynchronous model update approach, contending that general features are learned in the shallower layers of neural networks and, consequently, exert a greater influence on convergence. This method mitigates the frequency of uploading parameters from deeper layers to the server and incorporates a time-weighted aggregation strategy on the server. FedKD [32] reduces communicated parameter size via knowledge distillation. It trains a large teacher and a small student model locally. Only the student model is sent to the server. Aggregated gradients are sent back, and knowledge is transferred from student to teacher. However, in FRSs, the relatively small model size and the large number of equally important item models suggest that these dropout methods may not be applicable.
Wang et al. [33] introduce a ring-based decentralized FL framework for deep generative models, utilizing a unique ring topology and map-reduce synchronization to enhance efficiency and bandwidth utilization. Marfoq et al. [6] propose a novel topology design optimizing a minimal cycle time for higher throughput in cross-silo scenarios with high-speed links. The methods proposed in [6,33] are applicable to deep generative models and cross-silo settings, respectively. Introducing the methods proposed in [6,33] into FRSs would disrupt the original client–server architecture, thus raising compatibility concerns.
2.3. Summary of the Surveyed Works
In Table 1, we compare the above related works pertaining to convergence acceleration. Our main focus lies on the following aspects: whether they are designed for FRSs, their plug-and-play nature, their utilization of nodes with limited resources and the comprehensiveness of client-side training (i.e., no omission of any client in training). “Plug-and-play” implies that it has strong compatibility with existing FRSs and that there is no alteration to the structures of client/item models, network topology and aggregation method.

Table 1.
Comparison of the surveyed works.
3. Methodology
In this section, we initially describe the general framework of implicit feedback FRSs and take FedMF and FedNCF as examples for easier understanding. Subsequently, in the following part, we introduce I2CG and I2CL, which integrate communication and computation resources to accelerate the convergence of FRSs under communication constraints in Scenario I and Scenario II, respectively. We put some commonly used notations in Table 2.

Table 2.
Notations.
3.1. Problem Formulation
In implicit feedback recommendation (a common approach in recommendation systems where user actions like clicks or views, rather than explicit ratings, are used as feedback), we solely consider whether the user has interacted with an item, where 1 denotes previous interaction and 0 denotes no interaction [26]. A set of interaction records of the user u with items is , where I is the set of items in the FRS and represents the interaction case. FRSs aim to predict future interactions of user u with an item i that has not been interacted with.
In FRSs, each user is treated as a client who utilizes his local data to model himself and the items for prediction. Typically, models are developed individually for clients and items. At the beginning of FL, the server selects FL clients and distributes initialized model parameters to participants for parallel local updates. On client u’s device, the client’s user model parameter and the model parameter of item i, , are input into the client u’ score function to obtain the predicted value of client u to item i, as Equation (1) shows.
In FedMF, and are user and item embeddings, respectively, and means calculating the inner product of them. The loss function of client u is defined as the binary cross-entropy loss for implicit feedback recommendation, shown as Equation (2).
where is the set of items that ever interacted with client u and is the negative instances set of client u. On the client side, client and item model parameters are alternately updated by Equation (3).
where is the learning rate. is item i’s local model parameters trained by client u. If the parameters of the score function also require updating, perform Equation (3) together with Equation (4).
In the FedMF model, the function is defined as a fixed inner-product calculation operation. In contrast, in FedNCF, the consists of a Hadamard product operation and two shallow neural networks. The neural networks require the execution of Equation (4) for parameter updates. Once the local update is complete, the client model parameters are stored locally and not uploaded to the server. The updated item model parameters are then sent to the server for aggregation. On the server side, the aggregation can be performed by FedAvg, given by Equation (5).
where is the set of clients participating in federated training in communication round t. Specifically, in FedMF, the item embedding parameters uploaded by participants are averaged on the server. The server then distributes the aggregated model parameters to newly selected participants. The process above is repeated until convergence.
3.2. Integration of Communication and Computation Utilizing Global Item Models
In FRSs, considering communication constraints of some clients, only a subset of clients is chosen to participate in the current communication round for federated training [24]. Clients in Scenario I, represented by in communication round t, despite being capable of downloading item models from the server, are unable to upload data due to communication fluctuations.
Evidently, clients in are unable to participate in normal federated training. However, they may retain unaffected local computation resources that are available for utilization. Additionally, their capabilities of downloading item models should not be wasted. We enable clients in to perform normal local updates utilizing global item models downloaded from the server, while clients in concurrently conduct federated training. Afterward, considering communication fluctuations during upload, the clients in refrain from uploading updated item model parameters to the server, opting instead to store them locally. This approach leverages computation resources and download capabilities of communication-constrained clients in Scenario I for local training based on the global item models downloaded from the server. This integration of communication and computation utilizing global item models is abbreviated as I2CG. The workflow of I2CG clients is illustrated by the “I2CG clients” in Figure 2.
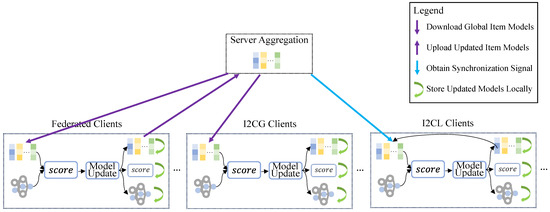
Figure 2.
The framework of FedRecI2C.
3.3. Integration of Communication and Computation Utilizing Local Item Models
In another scenario, i.e., Scenario II, some clients may encounter limited communication bandwidth from time to time, which prevents them from efficiently downloading and uploading large volumes of item models. In this situation, clients with bandwidth limitation are also represented by .
While clients in are unable to engage in standard federated training, they can leverage locally stored item models for local update if they have idle computation resources. In this scenario, clients in require only minimal communication resources to complete synchronization with the server. We enable clients having idle computation resources in under Scenario II to conduct local updates utilizing locally stored item models. Moreover, these clients acquire synchronization signals from the server to coordinate the training process. We refer to this strategy as the integration of communication and computation with local item models (I2CL). The workflow of I2CL clients is illustrated by the “I2CL clients” in Figure 2.
3.4. A Summary of I2CG and I2CL
We collectively refer to I2CG and I2CL as the integration of communication and computation (I2C) strategy. The differences between I2CG and I2CL are as follows. I2CG and I2CL are, respectively, applicable to two communication-constrained scenarios: Scenario I and Scenario II. As stated previously, the communication conditions in Scenario II, where I2CL clients are located, are more stringent. Second, while both methods utilize the local computing resources of communication-constrained clients for local updates, the sources of item model parameters for local updates vary. The item model of I2CG is a global item model sourced from the server, whereas the item model of I2CL is the one saved locally on the client after its previous training.
Algorithms 1 and 2 delineate the comprehensive training procedure on the server and client sides, respectively. As illustrated in Algorithm 1, the server’s objective is to select clients for participation in the ClientUpdate process and to aggregate the item model parameters obtained from these clients. Meanwhile, clients executing Algorithm 2 update their model parameters locally, and manage the downloading, uploading and saving of these parameters based on their client and strategy types. In this paper, we do not consider the combined use of I2CG and I2CL.
FedRecI2C is capable of mitigating the limitations associated with other FL acceleration algorithms as introduced in the Introduction section. In I2CG and I2CL, the client upload channels are nearly entirely severed. This effectively circumvents the unreasonable presumption in Limitation 2, which posits that communication channels remain perpetually open. Owing to its more lenient communication requirements, FedRecI2C overcomes Limitation 1. Moreover, it enables the inclusion of clients that would otherwise be excluded by typical FL approaches in the training process. By ensuring the full engagement of these clients in training, FedRecI2C accelerates the rate of system convergence. Furthermore, our proposed method obviates the need to model client-to-client relationships. It preserves the original structures of client/item models, network topologies and parameter aggregation methods within existing FRSs. As a result, FedRecI2C exhibits enhanced compatibility with existing FRSs and is designed to be plug-and-play.
| Algorithm 1 ServerUpdate |
|
| Algorithm 2 ClientUpdate |
|
4. Experiments
We conduct experiments on four public datasets and seven baselines, and evaluate the Hit Ratio (HR) and Normalized Discounted Cumulative Gain (NDCG) performance and convergence rate of FRSs with or without FedRecI2C. The experiments aim to address the following three main research questions:
- RQ1:What impacts does the FedRecI2C framework have on convergence speed and recommendation performance?
- RQ2: Is FedRecI2C applicable across various communication conditions and FRSs?
- RQ3: What is the impact of the early-stop strategy on FedRecI2C?
4.1. Experimental Setup
4.1.1. Baselines
We apply FedRecI2C to FRSs below to validate its effectiveness on various FRSs.
- FedMF [12] adapts MF for FRS by updating user embeddings locally and aggregating item gradients globally.
- PFedRec [34] is a recently proposed personalized FR with fine-tuned item embeddings based on FedMF.
- FedRECON [35] is a personalized FL framework in the MF scenario, where user embeddings are retrained from scratch between each iteration.
- FedMAvg [23] combines the alternating minimization technique and model averaging to investigate the federated MF problem.
- FedNCF [36] is a federated variant of neural collaborative filtering (NCF) [37] that allows users to update local embeddings and transmit item embeddings and score functions to a server for global aggregation.
- FedGMF [36] is a federated version of generalized MF introduced by NCF.
- FedMLP [36] is a variant of FedNCF based on multilayer perceptrons.
These baselines include two categories of recommender systems: MF and NCF. MF is widely adopted in recommendation systems because of its low number of parameters and fast training speed. It is particularly useful in cold-start phases and resource-constrained environments (e.g., for edge device deployment), where it serves as an initialization benchmark for complex models. Meanwhile, NCF has become a core module in mainstream deep learning-based recommendation frameworks (e.g., those of YouTube and Amazon). It shows irreplaceable advantages in processing multimodal data and enabling real-time personalized recommendations. Therefore, it is of great practical significance to explore the effectiveness of FedRecI2C for them and their variants in the context of FL.
Note that PFedRec utilizes a Dual Personalization Mechanism (DPM) that fine-tunes global item embeddings before prediction, which can apply to the FRSs above. We highlight that the I2CL and I2CG outlined in this article will yield distinct outcomes contingent upon whether the FRS employs DPM before prediction. We will demonstrate this in experimental results.
4.1.2. Datasets
MovieLens-100K, MovieLens-1M [38], Lastfm-2K [39] and Foursquare [40] are frequently employed datasets in recommender systems. The two MovieLens datasets contain user ratings of movies from one to five from the MovieLens website, with each user rating at least 20 movies. The Lastfm-2k dataset, sourced from Last.fm, one of the largest music platforms globally, records user interactions with artists’ works. The Foursquare dataset is retrieved from the Foursquare application’s public API, encompassing numerous user check-ins, social connections and venue ratings. These four are real-world datasets that better align with the data distribution in real-world FRSs. They exhibit diverse properties, such as size, domain and sparsity. Moreover, they are all widely used datasets in the evaluation of recommendation models.
Focused on implicit feedback recommendation scenarios, we convert the ratings in each dataset into implicit data, where a rating of 1 indicates user interaction with an item. We filter out users with fewer than five historic interactions following [34] to simplify dataset partitioning, and the characteristics of the four datasets are detailed in Table 3.

Table 3.
Dataset statistics.
For the dataset split, we employ the leave-one-out method which is widely used in the literature of recommendation [37]. For each user, we assign their most recent interaction as the test set and allocate all other interactions to the training set. Additionally, we designate the latest interaction within the training set as the validation set to identify optimal hyperparameters. For the final evaluation, we follow the established strategy outlined by [37,41], which involves randomly selecting 99 unobserved items for each user and ranking the test item among these 100 items. Additionally, we adopt the experimental setup of He et al. [37], where we randomly sample four negative samples for each positive sample in training set.
4.1.3. Performance Metrics
We evaluate the model performance with HR and NDCG. HR is a straightforward metric used to measure the recall of a recommender system. It evaluates the system’s ability to retrieve relevant items from the test set within the top-K recommendations. NDCG considers both the relevance of recommended items and their position in the recommendation list. NDCG aims to assess the quality of the ranking, ensuring that the most relevant items are ranked at the top, thereby enhancing user satisfaction and engagement. HR and NDCG effectively evaluate the system’s recall and ranking abilities. Together, these metrics provide a comprehensive view of the system’s performance, guiding improvements and ensuring better user experiences. HR and NDCG could be formulated as Equations (6) and (7).
where n is the number of users and indicates that the test item of the user u is in the top-K recommendation list, otherwise . denotes the position of user u’s test item in the top-K recommendation list and when the test item is not in the list. Here, we set for all experiments.
4.1.4. Implementation Details
All methods are implemented in PyTorch 2.3.0. Set the client sample ratio () in FL to 10%, which means randomly selecting 10% of clients to participate in FL in each communication round and selecting clients from the remaining 90% to simulate communication-constrained ones. We will provide experimental results for = 20% and 50% if necessary. Except for partial experiments in Section 4.2.2, we always make all the remaining 90% of clients participate in I2C training. To ensure a fair comparison, we set the size of user–item embeddings as 32, the batchsize as 256 and local epoch E as 1. The total number of communication rounds is set to 300 for the MovieLens-1M dataset and 250 for other datasets, as these values have been experimentally determined to ensure convergence for all training methods. The learning rate is optimized within the range of [0.001, 0.005, 0.01, 0.05, 0.1, 0.2, 0.5], with the detailed configurations for each of the four datasets outlined in Table A1. Adjust other model specifications based on their respective original papers.
4.2. Experimental Results
We analyze the learning curves and focus on HR@10, NDCG@10 and the associated communication rounds required to achieve the performance. PFedGMF denotes FedGMF utilizing DPM, and the same applies to PFedNCF and PFedRECON. For consistency in notation, we denote PFedRec as PFedMF. FedMF-I2CG represents FedMF employing I2CG, with similar notations applying to others. For brevity, we only present the learning curves of PFedMF/FedMF.
4.2.1. RQ1: Impacts on Convergence Speed and Recommendation Performance
We first focus on the relevant results of I2CG. Figure 3 and Table 4 show the impact of I2CG on FRSs with or without DPM. From the results, we observe that, whether FRSs adopt DPM or not, in most cases, the I2CG approach can effectively accelerate the convergence of HR and NDCG. For example, on Foursquare, when PFedMF employs I2CG, it only requires 84 communication rounds to reach convergence, which represents a 64.71% reduction in the number of communication rounds required compared to when I2CG is not employed, which necessitates 238 communication rounds. In a few instances, such as FedRECON on Lastfm-2K, the introduction of I2CG does not reduce the communication rounds needed for convergence (104 → 110). Introducing the I2CG strategy enables the utilization of local computation resources from communication-constrained clients, facilitating the comprehensive training of these clients, thereby accelerating overall model convergence rate.
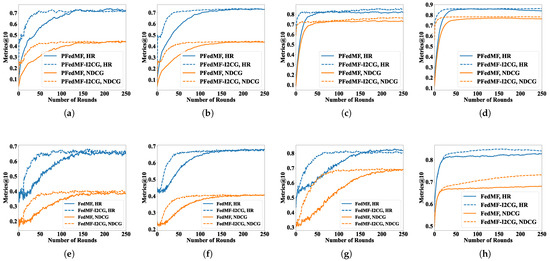
Figure 3.
Learning curves of PFedMF/FedMF with or without I2CG. (a–d) PFedMF-I2CG: (a) MovieLens-100K. (b) MovieLens-1M. (c) Lastfm-2K. (d) Foursquare. (e–h) FedMF-I2CG: (e) MovieLens-100K. (f) MovieLens-1M. (g) Lastfm-2K. (h) Foursquare.

Table 4.
Performance of FRSs with or without I2CG.
The impact of I2CG on the model performance demonstrates variability across diverse FRSs, datasets and evaluation metrics. Specifically, on Lastfm-2K, the introduction of I2CG in PFedMF enhances HR from 0.8196 to 0.8540, representing a 5.2% increase. However, on MovieLens-100K, the introduction of I2CG in PFedMF results in a minor decrease in HR, from 0.7243 to 0.7211, a decline of 0.44%. Fortunately, the introduction of I2CG in experiments has never led to a significant decline in the recommendation performance. The reduction can be alleviated through the early-stop strategy which means removing I2CG from the system after proper rounds. Additionally, early-stop aids in minimizing the extra computation burden imposed by the I2CG approach. Further elaboration on this matter will be provided in Section 4.2.3.
On one hand, I2CG can be seen as semi-federated learning whose clients do not upload the updated item models to the server for aggregation, resulting in a slight “drift” of the global item models compared to the global item models in federated learning incorporating both federated and I2CG clients. On the other hand, abstaining from uploading item models for aggregation could lead to a “delay” in global item models’ updating process compared to client models. During the next round of training, the “drift” and “delay” may have regularizing or negative effects on model performance. The direction of the impact may vary depending on the FRSs, datasets and evaluation metrics.
Now, we turn our attention to I2CL. Figure 4a–d and Table 5 show the impact of I2CL on FRSs with DPM. As Figure 4a–d and Table 5 show, the I2CL strategy markedly boosts the convergence speed of FRSs with DPM. For instance, on Lastfm-2K, the incorporation of I2CL significantly reduces the training rounds required for PFedRECON to reach convergence, decreasing from 198 to 47 rounds (−76.26%). In exceptional cases, such as on Foursquare, the training rounds needed of PFedMF remain unchanged.
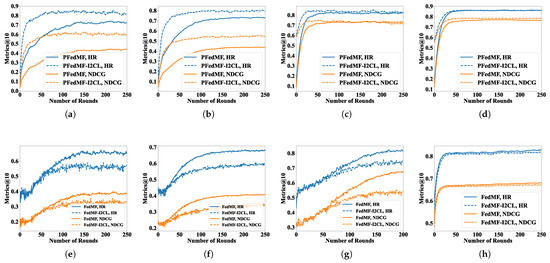
Figure 4.
Learning curves of PFedMF/FedMF with or without I2CL. (a–d) PFedMF-I2CL: (a) MovieLens-100K. (b) MovieLens-1M. (c) Lastfm-2K. (d) Foursquare. (e–h) FedMF-I2CL: (e) MovieLens-100K. (f) MovieLens-1M. (g) Lastfm-2K. (h) Foursquare.

Table 5.
Performance of FRSs with or without I2CL.
Evidently, as dataset sparsity increases, the impact of I2CL in enhancing the model performance decreases. Considering PFedMF, for datasets with sparsity levels of 93.70% (MovieLens-100K), 95.53% (MovieLens-1M), 99.07% (Lastfm-2K), and 99.86% (Foursquare), the improvement rates of I2CL on HR are 16.10%, 8.15%, 1.66%, and 0.21%, respectively.
To explain the above observations, we consider pure local training, which does not leverage the FL paradigm and instead involves each client independently training using only its local data. In this scenario, client communication is absent, and the model is susceptible to overfitting to the local data. In FRS, an appropriate degree of pure local training can enhance the client model’s understanding of local data [34], ultimately the improving model performance. In FRS, an appropriate degree of pure local training can enhance the client model’s understanding of local data [34], ultimately improving the model performance. The introduction of I2CL essentially combines federated training with pure local training, where clients alternately engage in both types of training. For denser datasets, the local data contains more information, and the features extracted by the pure local training introduced by I2CL are more accurate, thereby enhancing the model performance. In contrast, I2CL in sparse datasets may have a minimal effect on improving the model performance, but it still advances the training process for communication-constrained clients, thereby accelerating the convergence of the entire system.
It should be noted that I2CL will damage the convergence speed and model performance on FRSs without DPM, as Figure 4e–h shows. As FRSs without DPM rely on global item embeddings for prediction, I2CL results in a mismatch between purely locally trained client models and global item embeddings, thereby compromising the model performance. Consequently, I2CL not only fails to expedite the FRSs’ convergence but also diminishes their performance.
4.2.2. RQ2: Generality Across Various Communication Conditions and FRSs
In Section 4.2.1, we have demonstrated the applicability of FedRecI2C for multiple FRSs. In practice, it is impractical to include all communication-constrained clients in I2C training during every communication round due to the complexities of real-world conditions. Consequently, we introduce the period parameter p and client participation ratio r for I2C, which not only align more closely with real-world communication conditions but also aim to achieve a balance between the convergence speed and additional computation costs. Taking FedMF/PFedMF on MovieLens-1M as an example, we investigate the impact of p and r on both the convergence speed and model performance. Figure 5 and Figure 6 depict a scenario where 10% of clients undergo federated training, while the remainder can participate in I2C. In Figure 5, I2C is configured with different p. Specifically, indicates that I2C runs in every communication round and so forth. In Figure 6, we set different values of r for clients, selecting r = (100%, 50%, 25%) communication-constrained clients to perform I2C training.
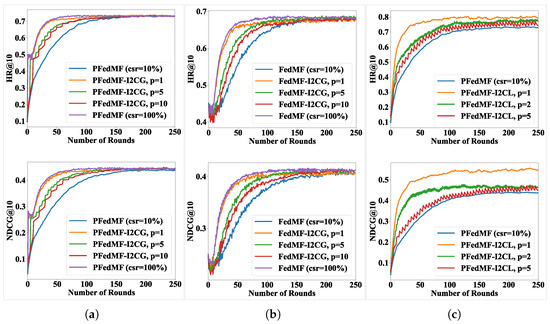
Figure 5.
Learning curves of FedRecI2C with different I2C period p. (a) PFedMF-I2CG. (b) FedMF-I2CG. (c) PFedMF-I2CL.
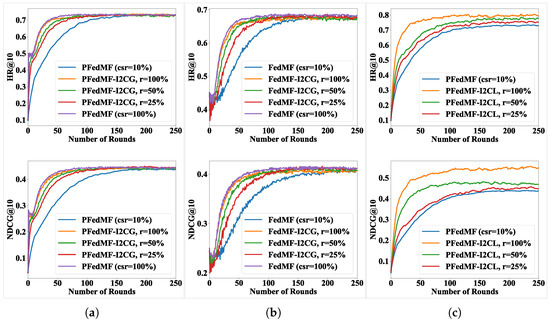
Figure 6.
Learning curves of FedRecI2C with different I2C ratio r. (a) PFedMF-I2CG. (b) FedMF-I2CG. (c) PFedMF-I2CL.
As Figure 5 and Figure 6 show, when the frequency of I2C is higher, and with a larger proportion of clients under communication constraint participating in I2C training, faster convergence is achieved. But the influence of p and r on the model’s final performance is minimal for FRSs with I2CG.
In contrast to the FRSs (10% clients for FL), the introduction of I2CG (p = 1) in FRSs leads to the remaining 90% of uploading-constrained clients implementing local training after obtaining item models from the server. This accelerates the training process of these clients. Compared with FRSs (100% clients for FL), implementing I2CG (p = 1) reduces significant communication costs by sparing the 90% of clients from uploading item models while maintaining a comparable convergence speed, as evidenced by the purple and yellow curves in Figure 5a,b.
Convergence acceleration still happens even with meaning implementing I2CG every ten rounds or % meaning only 25% communication-constrained clients executing I2CG training, while significantly reducing the associated computation overhead. Adjusting p or r can mitigate the additional computation cost associated with I2CG, which facilitates a tradeoff between additional computation overhead and convergence speed, tailored to specific requirements.
FRSs introducing I2CL essentially combine elements of federated training and pure local training. All clients alternate between federated training and pure local training, resulting in a dynamic equilibrium between the two. Federated training contributes to the generalization of item models, whereas pure local training enhances the fit of item models to clients’ local data. Over time, as federated training and pure local training achieve dynamic equilibrium, the entire system converges. As in Figure 5c and Figure 6c, the larger the p or r, the higher the proportion of pure local training in the total number of client training rounds. Higher p or r favor pure local training, facilitating rapid convergence and achieving superior performance. In contrast, lower p or r favor federated training, resulting in slower convergence but improved generalization capabilities.
As shown by the red curves in Figure 5c, when , communication-constrained clients undergo I2CL every five rounds, and in the following four rounds they may participate in federated training or rest. Each time I2CL is performed, the system’s performance will experience a surge, indicating a shift towards pure local training balance; in training rounds without I2CL, the learning curves will fall downwards to the balance of federated learning (blue curve); the system finally reaches a dynamic balance between the two.
4.2.3. RQ3: Impact of the Early-Stop Strategy on FedRecI2C
In FedRecI2C, the early-stop strategy refers to removing the I2C training for communication-constrained clients from the system after a suitable number of communication rounds, whereas the federated training for communication-capable clients persists.
According to Figure 7, early-stop slightly affects the final performance of FRSs with I2CG and the direction of this impact depends on the FRS and the dataset. Specifically, regardless of whether it is PFedMF-I2CG or FedMF-I2CG, early-stop moderately inhibits the performance decline on the MovieLens-100K dataset, with earlier cessation yielding a more pronounced effect. Premature early-stop may compromise the performance of PFedMF-I2CG (on Lastfm-2K) and FedMF-I2CG (Foursquare), which otherwise benefit from I2CG. Furthermore, choosing the right timing for early-stop and halting I2CG promptly can effectively minimize the extra computational burden imposed by I2CG. For example, consider the case in Figure 7e. Here, we focus on FedMF-I2CG on the MovieLens-100K dataset. When we remove I2CG after the 50th communication round (es = 50), two main results occur. Firstly, the final model performance is superior compared to the scenario without early-stop. Secondly, there is a conservation of resources. Specifically, communication resources for downloading the global item models from the server are saved. Also, the computation resources required for local updates during the subsequent 200 communication rounds for communication-constrained clients are conserved.
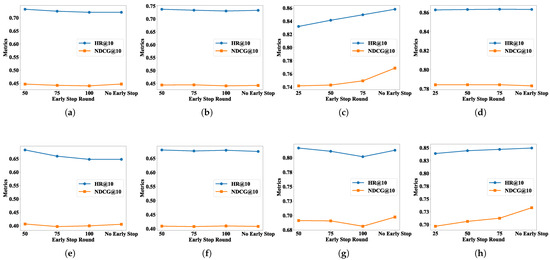
Figure 7.
Impact of early-stop on recommendation performance of PFedMF/FedMF with I2CG. (a–d) PFedMF-I2CG: (a) MovieLens-100K. (b) MovieLens-1M. (c) Lastfm-2K. (d) Foursquare. (e–h) FedMF-I2CG: (e) MovieLens-100K. (f) MovieLens-1M. (g) Lastfm-2K. (h) Foursquare.
As discussed in Section 4.2.2, PFedMF-I2CL integrates both federated training and pure local training, ultimately achieving a dynamic equilibrium between the two. If pure local training is halted before the convergence of the system, the model’s performance will degrade to that of FL ( = 10%), as shown in Figure 8a–c. However, as Figure 8d shows, the removal of I2CL at the communication round of 10 does not diminish the performance of PFedMF-I2CL, which demonstrates the uniqueness of the Foursquare dataset. This observation may be attributed to the unique distribution characteristics of the Foursquare dataset, which motivates us to investigate the impact of early-stop on the performance of I2CL across more datasets in our future work.
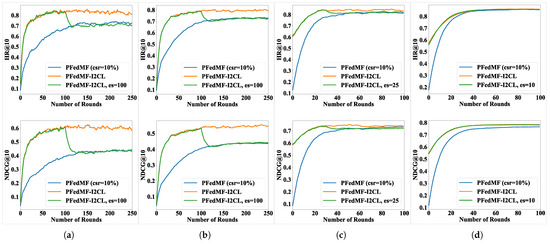
Figure 8.
Impact of early-stop on PFedMF-I2CL. (a) MovieLens-100K. (b) MovieLens-1M. (c) Lastfm-2K. (d) Foursquare. “es = 100” means early-stop I2CL when communication round = 100 and so forth.
5. Discussion
The experimental results demonstrate that clients operating under communication-constrained scenarios (Scenario I and Scenario II) can effectively utilize idle computational resources and limited communication bandwidth to contribute to the system’s training process, thereby accelerating the model convergence. Specifically, under varying FRS environments and complex communication conditions (simulated through parameters p and r), FedRecI2C exhibits a robust convergence acceleration performance without compromising the model recommendation accuracy. Furthermore, its plug-and-play capability highlights significant practical value in accelerating the convergence for FRS implementations. The subsequent discussion addresses practical application considerations of FedRecI2C through three key aspects: client selection criteria, scalability analysis for large-scale deployment and efficiency analysis.
5.1. Client Selection Criteria
In the context of FedRecI2C, client selection in practical application scenarios should be grounded in factors such as the client’s CPU capacity, network bandwidth and historical activity records [30]. In distributed settings, it is feasible to integrate methods from the relevant literature, e.g., [5,30], with FedRecI2C. For a client to partake in an FL training round, specific conditions must be met. First, it must lie within the server’s reachable range. Second, during the training period, it is ideal for the client to be idle, connected to a power source, and have access to an available wireless network [42]. Given these requirements, available or communication-constrained clients are randomly and uniformly distributed within the system [43]. Hence, the client selection process should not only consider the client’s resource status but also incorporate an element of randomness.
5.2. Scalability Analysis for Large-Scale Deployment
Client-side. Unlike general FL, FRSs have distinct requirements. For each client, a user model must be constructed, and this user model does not participate in the federated aggregation. Each client is obligated to partake in the federated training at least a few times to build its own user model. Clients cannot remain entirely idle while anticipating obtaining a user model trained by other clients. As a result, on the client side, the local computational overhead of all clients in FRSs is inevitable. As the number of clients increases, new clients directly utilize the computational resources of local devices for training. Put differently, the computational overhead is dispersed by the distributed architecture. In FedRecI2C, for clients with communication constraints, the I2C period parameter provides them with more time to fetch model parameters from the server and perform local updates. The I2C client ratio parameter r allows for the existence of clients that are entirely unable to communicate. These further demonstrate the scalability of FedRecI2C.
Server-side. With the increase in the number of clients and items, the server may encounter challenges in meeting the communication bandwidth requirements for both downloading and uploading, as well as the computational resources necessary for parameter aggregation. In such circumstances, FedRecI2C opts to select a subset of clients for FL and omits the model parameter upload step for I2CG and I2CL clients. This approach can effectively alleviate the burden on the server’s communication and computational resources.
5.3. Efficiency Analysis
In addition to the communication rounds necessary for convergence, which were discussed previously, we analyze the model’s efficiency, considering factors such as the number of parameters and computational overhead. Since FedRecI2C does not modify the structures of client/item models, the aggregation method or the network topology, it does not introduce additional storage space overhead to the original FRSs. FedRecI2C incorporates communication-constrained clients, which are typically overlooked in other FRSs, into the training process. This incorporation leads to additional computational overhead. However, the learning process is decomposed into multiple small-scale learning processes. These processes are executed on numerous distributed devices that directly utilize local computational resources. This approach ensures the utilization of distributed computational and energy resources and enables parallel and efficient computing. As a result, the additional computational overhead imposed by FedRecI2C is mitigated. Additionally, as mentioned before, the I2C period parameter offers resource-constrained clients more time to retrieve model parameters from the server and perform local updates, which implies reduced-frequency resource usage. Finally, the application of the early-stop strategy in I2CG also helps to reduce the additional computational overhead.
6. Conclusions and Future Work
In this paper, we propose a novel FRS framework, FedRecI2C, which aims to accelerate the convergence of FRSs. To achieve this, we integrate communication and computation resources in the system to utilize not only those communication-capable clients to perform federated training, but also those communication-constrained clients to contribute computation and limited communication resources for further local training. Experiments conducted on four public datasets, seven FRSs and various communication scenarios validate the effectiveness of our FedRecI2C framework. Specifically, our works yield several conclusions:
Firstly, I2CG can significantly expedite the convergence of FRSs, with the direction of its impact on the model performance dependent on the specific dataset. When paired with the DPM mechanism, I2CL not only accelerates the convergence of FRSs but also enhances their performance, with the degree of improvement inversely correlated with the dataset’s sparsity. And then, I2C demonstrates robustness under varying communication conditions, including differing I2C periods and ratios of I2C clients. Finally, integrating the early-stop strategy with I2CG reduces the additional computation overhead and can mitigate potential performance degradation. Conversely, incorporating the early-stop strategy into I2CL leads to a decline in the model performance, comparable to FRSs without I2CL.
FedRecI2C provides simplicity and flexibility, furnishing a plug-and-play architecture that enhances convergence in various FRSs under diverse communication conditions, while also inspiring novel insights into FRSs’ training patterns.
In future work, we aim to investigate the combined use of I2CG and I2CL to assess the effectiveness of FedRecI2C under more complex communication conditions. Specifically, the FRS will include clients with reliable communication channels and those in the communication-constrained scenarios Scenario I and Scenario II. Additionally, we plan to replace random client sampling with client selection methods that consider network bandwidth, computational resources or historical activity to improve realism.
Author Contributions
Conceptualization, Q.Z.; methodology, Q.Z.; software, Q.Z.; validation, Q.Z.; formal analysis, Q.Z.; investigation, Q.Z.; resources, Q.Z. and X.H.; data curation, Q.Z.; writing—original draft preparation, Q.Z.; writing—review and editing, Q.Z. and X.H.; visualization, Q.Z.; supervision, X.H.; project administration, X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Teaching Reform Research Projects of Jinan University (JG2024060).
Data Availability Statement
All models, or code, that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Learning Rate Configuration
For the learning rate, we optimize it in the range of [0.001, 0.005, 0.01, 0.05, 0.1, 0.2, 0.5] and the specific settings for different methods and datasets are summarized below.

Table A1.
Learning rate configuration for all methods on four datasets.
Table A1.
Learning rate configuration for all methods on four datasets.
| Method | ML-100K | ML-1M | Lastfm-2K | Foursquare |
|---|---|---|---|---|
| PFedMF | 0.1 | 0.1 | 0.01 | 0.01 |
| PFedMF-I2CG | 0.1 | 0.1 | 0.01 | 0.01 |
| PFedMF-I2CL | 0.1 | 0.1 | 0.01 | 0.01 |
| FedMF | 0.1 | 0.1 | 0.05 | 0.01 |
| FedMF-I2CG | 0.1 | 0.1 | 0.05 | 0.01 |
| PFedGMF | 0.1 | 0.1 | 0.01 | 0.01 |
| PFedGMF-I2CG | 0.1 | 0.1 | 0.01 | 0.01 |
| PFedGMF-I2CL | 0.1 | 0.1 | 0.01 | 0.01 |
| FedGMF | 0.1 | 0.1 | 0.05 | 0.01 |
| FedGMF-I2CG | 0.1 | 0.1 | 0.05 | 0.01 |
| PFedRECON | 0.1 | 0.1 | 0.1 | 0.1 |
| PFedRECON-I2CG | 0.1 | 0.1 | 0.1 | 0.1 |
| PFedRECON-I2CL | 0.1 | 0.1 | 0.1 | 0.1 |
| FedRECON | 0.1 | 0.1 | 0.1 | 0.1 |
| FedRECON-I2CG | 0.1 | 0.1 | 0.1 | 0.1 |
| PFedNCF | 0.5 | 0.5 | 0.1 | 0.1 |
| PFedNCF-I2CG | 0.5 | 0.5 | 0.1 | 0.1 |
| PFedNCF-I2CL | 0.5 | 0.5 | 0.1 | 0.1 |
| FedNCF | 0.2 | 0.2 | 0.1 | 0.1 |
| FedNCF-I2CG | 0.2 | 0.2 | 0.1 | 0.1 |
References
- Roy, D.; Dutta, M. A systematic review and research perspective on recommender systems. J. Big Data 2022, 9, 59. [Google Scholar] [CrossRef]
- Javeed, D.; Saeed, M.S.; Kumar, P.; Jolfaei, A.; Islam, S.; Islam, A.N. Federated learning-based personalized recommendation systems: An overview on security and privacy challenges. IEEE Trans. Consum. Electron. 2023, 70, 2618–2627. [Google Scholar] [CrossRef]
- Wang, S.; Tao, H.; Li, J.; Ji, X.; Gao, Y.; Gong, M. Towards fair and personalized federated recommendation. Pattern Recognit. 2024, 149, 110234. [Google Scholar] [CrossRef]
- Shahid, O.; Pouriyeh, S.; Parizi, R.; Sheng, Q.; Srivastava, G.; Zhao, L. Communication Efficiency in Federated Learning: Achievements and Challenges. arXiv 2021, arXiv:2107.10996. [Google Scholar]
- Xu, J.; Wang, H. Client selection and bandwidth allocation in wireless federated learning networks: A long-term perspective. IEEE Trans. Wirel. Commun. 2020, 20, 1188–1200. [Google Scholar] [CrossRef]
- Marfoq, O.; Xu, C.; Neglia, G.; Vidal, R. Throughput-optimal topology design for cross-silo federated learning. Adv. Neural Inf. Process. Syst. 2020, 33, 19478–19487. [Google Scholar]
- Chen, W.; Horvath, S.; Richtarik, P. Optimal client sampling for federated learning. arXiv 2020, arXiv:2010.13723. [Google Scholar]
- Nguyen, H.T.; Sehwag, V.; Hosseinalipour, S.; Brinton, C.G.; Chiang, M.; Poor, H.V. Fast-convergent federated learning. IEEE J. Sel. Areas Commun. 2020, 39, 201–218. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, H.; Liu, J.; Huang, H.; Qiao, C.; Zhao, Y. Resource-efficient federated learning with hierarchical aggregation in edge computing. In Proceedings of the IEEE INFOCOM 2021—IEEE Conference on Computer Communications, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Tang, M.; Ning, X.; Wang, Y.; Sun, J.; Wang, Y.; Li, H.; Chen, Y. FedCor: Correlation-based active client selection strategy for heterogeneous federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10102–10111. [Google Scholar] [CrossRef]
- Ammad-Ud-Din, M.; Ivannikova, E.; Khan, S.A.; Oyomno, W.; Fu, Q.; Tan, K.E.; Flanagan, A. Federated collaborative filtering for privacy-preserving personalized recommendation system. arXiv 2019, arXiv:1901.09888. [Google Scholar]
- Chai, D.; Wang, L.; Chen, K.; Yang, Q. Secure federated matrix factorization. IEEE Intell. Syst. 2020, 36, 11–20. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Lee, D.; Seung, H.S. Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst. 2000, 13, 535–541. [Google Scholar]
- Wu, C.; Wu, F.; Cao, Y.; Huang, Y.; Xie, X. Fedgnn: Federated graph neural network for privacy-preserving recommendation. arXiv 2021, arXiv:2102.04925. [Google Scholar]
- Wu, C.; Wu, F.; Qi, T.; Huang, Y.; Xie, X. Fedcl: Federated contrastive learning for privacy-preserving recommendation. arXiv 2022, arXiv:2204.09850. [Google Scholar]
- Lin, G.; Liang, F.; Pan, W.; Ming, Z. Fedrec: Federated recommendation with explicit feedback. IEEE Intell. Syst. 2020, 36, 21–30. [Google Scholar] [CrossRef]
- Li, Z.; Lin, Z.; Liang, F.; Pan, W.; Yang, Q.; Ming, Z. Decentralized federated recommendation with privacy-aware structured client-level graph. ACM Trans. Intell. Syst. Technol. 2024, 15, 1–23. [Google Scholar] [CrossRef]
- Muhammad, K.; Wang, Q.; O’Reilly-Morgan, D.; Tragos, E.; Smyth, B.; Hurley, N.; Geraci, J.; Lawlor, A. Fedfast: Going beyond average for faster training of federated recommender systems. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 1234–1242. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, F.; Wu, J.; He, X.; Li, Y. LightFR: Lightweight federated recommendation with privacy-preserving matrix factorization. ACM Trans. Inf. Syst. 2023, 41, 1–28. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, C.; Feng, D. Privacy-preserving hierarchical federated recommendation systems. IEEE Commun. Lett. 2023, 27, 1312–1316. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, X.; Shen, Z.; Li, Y. PrivFR: Privacy-Enhanced Federated Recommendation With Shared Hash Embedding. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 32–46. [Google Scholar] [CrossRef]
- Wang, S.; Suwandi, R.C.; Chang, T.H. Demystifying model averaging for communication-efficient federated matrix factorization. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 3680–3684. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Zhu, Z.; Si, S.; Wang, J.; Xiao, J. Cali3f: Calibrated fast fair federated recommendation system. In Proceedings of the 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, Y.; Liu, Y.; He, W.; Kong, L.; Wu, F.; Jiang, Y.; Cui, L. A survey on federated recommendation systems. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 6–20. [Google Scholar] [CrossRef]
- Almanifi, O.R.A.; Chow, C.O.; Tham, M.L.; Chuah, J.H.; Kanesan, J. Communication and computation efficiency in federated learning: A survey. Internet Things 2023, 22, 100742. [Google Scholar] [CrossRef]
- Zhao, Z.; Mao, Y.; Liu, Y.; Song, L.; Ouyang, Y.; Chen, X.; Ding, W. Towards efficient communications in federated learning: A contemporary survey. J. Frankl. Inst. 2023, 360, 8669–8703. [Google Scholar] [CrossRef]
- Sultana, A.; Haque, M.M.; Chen, L.; Xu, F.; Yuan, X. Eiffel: Efficient and fair scheduling in adaptive federated learning. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 4282–4294. [Google Scholar] [CrossRef]
- AbdulRahman, S.; Tout, H.; Mourad, A.; Talhi, C. FedMCCS: Multicriteria client selection model for optimal IoT federated learning. IEEE Internet Things J. 2020, 8, 4723–4735. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, X.; Jin, Y. Communication-efficient federated deep learning with layerwise asynchronous model update and temporally weighted aggregation. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 4229–4238. [Google Scholar] [CrossRef]
- Wu, C.; Wu, F.; Liu, R.; Lyu, L.; Huang, Y.; Xie, X. FedKD: Communication Efficient Federated Learning via Knowledge Distillation. arXiv 2021, arXiv:2108.13323. [Google Scholar]
- Wang, Z.; Hu, Y.; Yan, S.; Wang, Z.; Hou, R.; Wu, C. Efficient ring-topology decentralized federated learning with deep generative models for medical data in ehealthcare systems. Electronics 2022, 11, 1548. [Google Scholar] [CrossRef]
- Zhang, C.; Long, G.; Zhou, T.; Yan, P.; Zhang, Z.; Zhang, C.; Yang, B. Dual personalization on federated recommendation. arXiv 2023, arXiv:2301.08143. [Google Scholar] [CrossRef]
- Singhal, K.; Sidahmed, H.; Garrett, Z.; Wu, S.; Rush, J.; Prakash, S. Federated reconstruction: Partially local federated learning. Adv. Neural Inf. Process. Syst. 2021, 34, 11220–11232. [Google Scholar]
- Perifanis, V.; Efraimidis, P.S. Federated neural collaborative filtering. Knowl.-Based Syst. 2022, 242, 108441. [Google Scholar] [CrossRef]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T.S. Neural collaborative filtering. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 173–182. [Google Scholar]
- Harper, F.M.; Konstan, J.A. The movielens datasets: History and context. ACM Trans. Interact. Intell. Syst. 2015, 5, 1–19. [Google Scholar] [CrossRef]
- Cantador, I.; Brusilovsky, P.; Kuflik, T. Second workshop on information heterogeneity and fusion in recommender systems (HetRec2011). In Proceedings of the Fifth ACM Conference on Recommender Systems, Chicago, IL, USA, 23–27 October 2011; pp. 387–388. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, D.; Zheng, V.W.; Yu, Z. Modeling user activity preference by leveraging user spatial temporal characteristics in LBSNs. IEEE Trans. Syst. Man Cybern. Syst. 2014, 45, 129–142. [Google Scholar] [CrossRef]
- Koren, Y. Factorization meets the neighborhood: A multifaceted collaborative filtering model. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 426–434. [Google Scholar] [CrossRef]
- AbhishekV, A.; Binny, S.; JohanT, R.; Raj, N.; Thomas, V. Federated Learning: Collaborative Machine Learning without Centralized Training Data. Int. J. Eng. Technol. Manag. Sci. 2022, 6, 355–359. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Sanjabi, M.; Zaheer, M.; Talwalkar, A.; Smith, V. On the convergence of federated optimization in heterogeneous networks. arXiv 2018, arXiv:1812.06127. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).