GHEFL: Grouping Based on Homomorphic Encryption Validates Federated Learning

Abstract

Federated learning is a powerful tool for securing participants’ private data due to its ability to make data “available but not visible”. In recent years, federated learning has been enhanced by the emergence of multi-weight aggregation protocols, which minimize the impact of erroneous parameters, and verifiable protocols, which prevent server misbehavior. However, it still faces significant security and performance challenges. Malicious participants may infer the private data of others or carry out poisoning attacks to compromise the model’s correctness. Similarly, malicious servers may return incorrect aggregation results, undermining the model’s convergence. Furthermore, substantial communication overhead caused by interactions between participants or between participants and servers hinders the development of federated learning. In response to this, this paper proposes GHEFL, a group-based, verifiable, federated learning method based on homomorphic encryption that aims to prevent servers from maliciously stealing participant privacy data or performing malicious aggregation. While ensuring the usability of the aggregated model, it strives to minimize the workload on the server as much as possible. Finally, we experimentally evaluate the performance of GHEFL.

1. Introduction

In the era of big data, an increasing number of people are benefiting from technological advancements. The digitization of information facilitates daily life; however, it also introduces significant risks of privacy leakage [1]. Data security issues frequently arise [2,3], and users are often concerned that their private information [4] might be exposed. As a result, they are reluctant to share their personal information, a behavior that undoubtedly hinders the flourishing development of industries reliant on massive datasets to enhance model accuracy [5,6,7,8,9]. Balancing the need to collect extensive user information while ensuring its protection has become a pressing challenge for both academia and industry.

Since the introduction of federated learning [10], it has gained significant attention as an effective data protection measure. Figure 1 illustrates the working process of federated learning. In federated learning, multiple nodes collaborate in model training. By utilizing distributed computing and encryption technologies, each node can participate in the training process without exposing its data, thereby achieving the “availability without visibility” of users’ data. In its early stages, federated learning was primarily applied in scenarios with, for example, mobile devices [11,12] and the Internet of Things (IoT) [13], aiming to enable model training and prediction while protecting user privacy [14]. With technological advancements, the application of federated learning has expanded to various fields. For instance, in the financial sector, federated learning is used for risk assessment [15,16], fraud detection, and more. In the medical field [7], it facilitates disease prediction and drug development. In image recognition, federated learning supports tasks such as image classification [17] and object detection [18].

The FedSGD [10] and FedAvg [10] algorithms, proposed alongside the concept of federated learning, are the most fundamental and widely adopted in this field. FedSGD avoids uploading clients’ raw data to servers by iteratively updating model parameters through gradient descent, thereby reducing the risk of data leakage. In contrast, FedAvg adopts a method of uploading model weights after local training to ensure client data security and reduce communication overhead. Since their introduction, numerous algorithms and frameworks for federated learning have been proposed. For example, Xie et al. [19] proposed FedAsync, which enables asynchronous training updates without waiting for other clients’ updates. Melis et al. [20] introduced encryption mechanisms into federated learning by proposing SFL, allowing client model updates or gradients to remain encrypted during global aggregation. Deng et al. proposed FedMA [21], which allows clients to generate local parameters using different models. The server then performs similarity matching on the parameters uploaded by the clients, thereby reducing the impact of noise and abnormal parameters on the global model parameters. In the FedProx algorithm [22], a proximal term is innovatively added to the local training function of the clients to limit the deviation between local and global parameters, accelerating model convergence. Acar proposed FedDyn [23], which introduces a regularization coefficient and a Lagrange multiplier dynamically adjusted by the server into the local training function of the clients, enabling the local models to approximate the global model state and significantly improving the model training performance. To address the issues of client heterogeneity and data imbalance, Karimi et al. introduced the Layer-wise Adaptive Momentum Optimization (LAMB) algorithm into federated learning and proposed FedLamb [24]. By replacing traditional weighted averaging with layer-wise adaptive weighting, FedLamb ensures the stable and rapid convergence of the model even during large-batch training. These algorithms and frameworks have laid a solid foundation for the development and application of federated learning.

However, numerous studies have shown that although federated learning can protect users’ private information to a certain extent, it still poses security risks. Le et al. [25] highlighted the threat of inversion attacks, where an attacker exploits the confidence information from a client’s model updates to reconstruct the private data used during training. Shokri et al. [26] experimentally demonstrated the gradient leakage attack, wherein the gradients uploaded by participants may leak user data or private information related to the learning process. Chen et al. [27] showed that federated learning is vulnerable to Byzantine attacks during the data collection phase, where malicious participants disrupt the learning process, preventing the model from converging properly. In addition to security risks, federated learning is constrained by communication and computational resource limitations. Chen et al. [28] found that the frequent exchange of model updates between participants or with cloud servers introduces significant communication overhead, which can substantially impair the learning performance and convergence speed of federated learning.

From the above analysis, it is evident that federated learning faces two primary challenges: security and efficiency. In federated learning, servers play a crucial role, and a malicious server that does not adhere to protocols can not only compromise the model’s usability but also pose significant privacy threats to participants. During the data reception phase, a malicious server can act as an attacker, launching gradient leakage attacks on participants to infer sensitive information about their local data or learning process [29]. In the parameter aggregation phase, a malicious server may maliciously substitute a participant’s model parameters with its own inputs without following the protocol [30] or selectively aggregate participant model parameters, resulting in incorrect global model aggregation parameters. This, in turn, causes participants to receive unreliable models [29]. Moreover, federated learning also faces performance-related issues. As the number of participants and model parameters increases, the communication cost grows correspondingly [31], which may lead to server overload in terms of computation and storage. This not only imposes an economic burden on participants but may also degrade server performance or even cause system crashes, ultimately impacting global model training. To address these challenges, various solutions have been proposed. Xu et al. [32] introduced VerifyNet, the first privacy-preserving and verifiable federated learning framework. Using a double-masking protocol, VerifyNet ensures that participants’ local gradients remain confidential while enabling the cloud server to verify the correctness of aggregation results. However, the verification process is computationally intensive. Gao et al. [33] employed BLS signatures and secure multi-party computation to verify the correctness of server aggregation results. Fu et al. [34] proposed verifying aggregated gradients through Lagrangian interpolation points and optimized computational overhead using the Chinese Remainder Theorem (CRT). These schemes only partially address either security or performance issues individually. For example, while VerifyNet ensures the correctness of aggregation, its verification process requires substantial computational resources. In the scheme proposed by Gao et al., the BLS signature and verification involve complex bilinear pairing operations, resulting in significant computational overhead and multiple interactions among participants, which adversely affect the efficiency of model training. Although the scheme proposed by Fu et al. optimizes computational costs, it is vulnerable to malicious participants submitting erroneous information to disrupt the aggregation process, potentially enabling the inference of other participants’ private information.

To address the aforementioned problems, we propose a verifiable grouping federated learning scheme, referred to as GHEFL. This scheme is designed to prevent malicious servers from attempting to exploit participants’ local data or performing incorrect aggregation operations that compromise model training. While ensuring the correctness of the aggregation results, the introduction of grouping guarantees the security of participant data and minimizes the workload on the server as much as possible. The main contributions are as follows:

• We propose GHEFL, a verifiable federated learning scheme. This scheme allows each participant to verify the correctness of the aggregation process, preventing malicious servers from tampering with parameters uploaded by participants. Additionally, it prevents servers from returning incorrect aggregated results.
• We adopt a dual-server architecture to replace the single-server architecture commonly used in traditional federated learning. This approach reduces the risk of performance degradation caused by the computational and storage overload of a single server, while also preventing malicious attempts by a single server to extract participants’ private information.
• In our scheme, we introduce a grouping mechanism by dividing participants into groups according to specific rules. Local parameter aggregation is first performed within each group and then the aggregated parameters are uploaded to the server on a group-by-group basis for global aggregation. This approach ensures the security of participant data and minimizes the information exchange between participants and the server compared to traditional federated learning.

This article is organized as follows: Section 2 describes the system architecture and design goals. Section 3 describes the preliminary work. Section 4 describes the proposed scheme in detail. Section 5 performs the experimental and comparative analysis. Section 6 concludes this paper.

2. Scheme Statement

In this section, we outline the general framework of our scheme, define the threat model, and clarify the design goals.

2.1. System Architecture

The system architecture of the proposed scheme is illustrated in Figure 2. The overall system consists of two entities: participants and cloud servers.

• Participants: Participants receive the initial model parameters, train the local model on their local datasets at a specified learning rate, and then upload the local model parameters along with auxiliary computation information to the cloud server for aggregation. During this process, participants may choose to apply masking techniques to safeguard local model parameters and related private information.
• Servers: The cloud servers are responsible for receiving the local model parameters and auxiliary information uploaded by participants and aggregating them based on the proposed aggregation rules. Subsequently, the global aggregation results are returned to each participant for iterative training until model convergence.

2.2. Threat Model

In our proposed scheme, both the participants and the cloud server are required to adhere to the regulations of model consistency and parameter consistency. This means that the server and the participants must maintain synchronization to ensure that all participants utilize the same global model parameters during the same round of training. Additionally, parameters such as the learning rate, which are employed during model training by both the server and the participants, must remain consistent. This uniformity is crucial to guarantee that the direction of model training is aligned across all entities involved. Furthermore, each participant is assumed to be honest and trustworthy, neither curious about the model parameter information of other participants nor maliciously uploading incorrect parameters to disrupt model aggregation, such as uploading parameter label values that do not match the parameter values. Additionally, the cloud servers are classified as one honest and one potentially malicious, which may lead to the following threats.

• The malicious server attempts to extract user data or privacy information from the learning process by analyzing the model parameters uploaded by participants, thereby compromising the security of the protocol [26];
• The malicious server attempts to return incorrect aggregated results, thereby affecting the training of the global model [29];
• The malicious server attempts to falsify the aggregation results to bypass participant verification, causing participants to accept incorrect aggregation results and thereby disrupting model training [31].

2.3. Design Goals

One objective of this scheme is to protect the data privacy of participants, ensuring that the server cannot access the gradients and related information of individual participants, thereby preventing malicious servers from attempting to extract participants’ local data. Simultaneously, it guarantees that participants cannot access the private information of other participants. Another objective is to ensure that participants obtain correct global aggregation results, allowing participants to verify the correctness of the aggregation results. This aims to prevent malicious servers from performing incorrect aggregation operations, which could disrupt the model training process.

3. Preliminaries

This section will cover the fundamentals of the proposed scheme, including party grouping, secret sharing, and homomorphic encryption.

3.1. Party Grouping

Participant grouping involves organizing participants based on certain rules. Participants within each group first perform local model training and aggregate their local model parameters to form the group’s model parameters. Then, a representative party is selected, and the group’s model parameters are uploaded to the cloud server for global aggregation. After the cloud server completes the global aggregation, the aggregation results are returned to each party, and each participant updates their local model based on the global model parameters. The selection of specific grouping strategies can be based on the similarity of data among participants, thereby reducing data heterogeneity within the same group and minimizing the introduction of noise, which is particularly suitable for the medical field. Alternatively, grouping can be conducted according to computational resources such as CPU to rationally utilize the resources of each participant and enhance computational efficiency. Another approach is to group participants based on their varying requirements for data privacy, with different groups adopting distinct privacy protection strategies, which is applicable to scenarios such as banking data. In this scheme, the server determines the grouping rules and plans to simulate the grouping of participants based on their computational resources.

3.2. Secret Sharing

Common secret sharing [35] methods include additive secret sharing, multiplicative secret sharing, and threshold secret sharing. Additive secret sharing was chosen for this scheme, so multiplication and threshold secret sharing methods do not need to be described here.

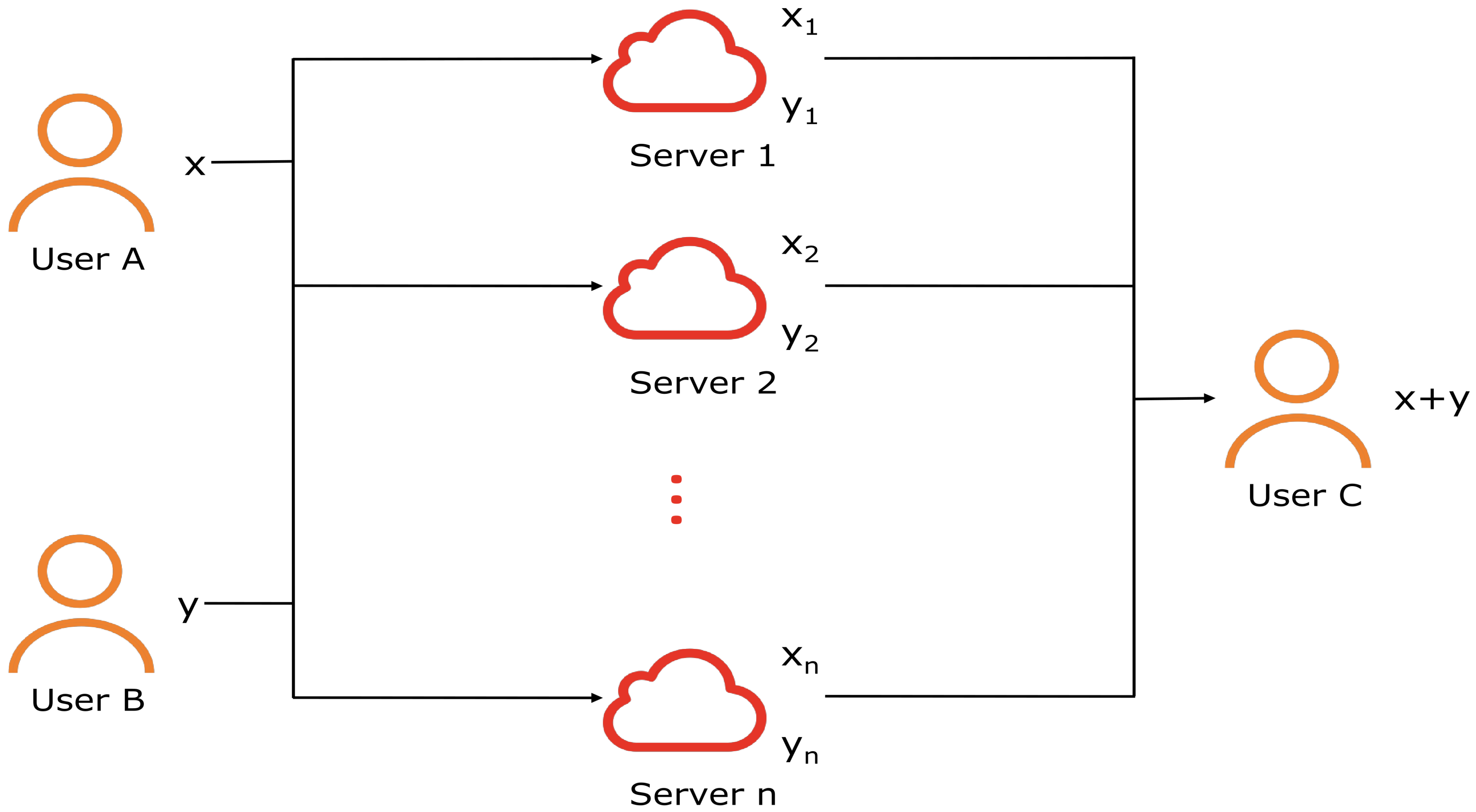
• Additive secret sharing: Suppose there are three users A, B, and C, at this point. Additive secret sharing can make C obtain the value of $x+y$ without knowing the local data x of user A or the local data y of user B. Initially, N cloud servers are selected and denoted as $S_1,S_2,\dots ,S_n$. Subsequently, users A and B randomly partition their local data x and y into n segments, respectively, such that $x=x_1+x_2+\dots +x_n$ and $y=y_1+y_2+\dots +y_n$. The corresponding segments $x_i$ and $y_i$ are then assigned to the ith server, where $i\in \{1,2,...,n\}$. User C sends computation requests to each cloud server, and the cloud server $S_i$ computes $z_i=x_i+y_i$, subsequently transmitting the result back to user C. After receiving it, user C calculates the sum locally: $z=z_1+z_2+\dots +z_n=x_1+y_1+x_2+y_2+\dots +x_n+y_n=x+y$. The specific process is shown in Figure 3.
• Multiplicative secret sharing: This primarily utilizes the multiplication triple $\left(a,b,ab\right)$, which consists of two random numbers, a and b, to achieve secure computation.
• Threshold secret sharing: Threshold secret sharing based on polynomials randomly splits a secret s into n parts, such that $s=s_1+s_2+\dots +s_n$, and distributes these parts to n users. A threshold $t(1<t<n)$ is set, meaning that as long as any t users are selected from the n users, the original secret s can be reconstructed using the shares $s_i$ they hold: $i\in \{1,2,...,n\}$.

3.3. Homomorphic Encryption

Homomorphic encryption [36] refers to an encryption algorithm that satisfies the homomorphic property of ciphertext operations. In this process, the original data are first encrypted homomorphically and then subjected to preset calculations to obtain a ciphertext result. Afterward, the ciphertext result is homomorphically decrypted, producing a plaintext result that is equivalent to the result obtained by directly performing the same calculations on the original plaintext data. Since the receiver cannot access the sender’s original data during the process, homomorphic encryption is commonly used for private data interactions between two or more parties.

According to the type of computations performed on ciphertext, homomorphic encryption can be categorized into semi-homomorphic encryption and fully homomorphic encryption.

• Semi-homomorphic encryption: Also known as partially homomorphic encryption, this supports only specific types of computations on ciphertexts, such as addition only, multiplication only, or a finite number of addition and multiplication operations. Taking additive homomorphism as an example, plaintexts a and b are encrypted using the encryption algorithm $Enc$ to obtain their corresponding ciphertexts $Enc\left(a\right)$ and $Enc\left(b\right)$. Performing an addition operation on these ciphertexts yields $Enc\left(a\right)+Enc\left(b\right)$, which is equal to the result of encrypting the sum of the two plaintexts, $Enc(a+b)$. That is, additive homomorphism satisfies $Enc\left(a\right)+Enc\left(b\right)=Enc(a+b)$. Common semi-homomorphic encryption schemes include the RSA algorithm, ElGamal algorithm, and Paillier algorithm.
• Fully homomorphic encryption: Unlike semi-homomorphic encryption algorithms that support only partial computations, this enables arbitrary computations on ciphertext data. Common fully homomorphic encryption schemes include the BGV scheme, BFV scheme, CKKS scheme, and others.

4. The Proposed Scheme

This section presents the overall framework diagram of GHEFL, as illustrated in Algorithm 1, and elaborates on the technical details of the proposed scheme. In the system initialization phase, the primary tasks include initializing public parameters, generating keys, and grouping participants. The second phase involves local model training by participants, intra-group parameter aggregation, and uploading aggregated parameters. In the third phase, the server receives the parameters, computes the global aggregation, and returns the results. Finally, in the fourth phase, participants verify the correctness of the obtained aggregation results. The detailed steps are as follows:

Algorithm 1 The detailed procedures of GHEFL.

Input: learning rate $\eta$, number of iterations T, loss function $\mathcal{L}(W,D)$, users $\mathcal{U}$, data sets $\mathcal{D}$. Output: a secure global model W.   1: Setup Phase   2: TA generates a pair of key $(pk,sk)$ of Paillier cryptosystem for users, The servers send the global model $w_0$ to each user $U_i$, and group users into group $\mathcal{G}$, server $S_1$ picks up a random seed $seed$.   3: Local Training Phase   4: for each group $G_i$∈$\mathcal{G}$  do   5:       for each user $U_j$∈$G_i$  do   6:           $w_{ij}\leftarrow w_0-\eta *\mathcal{L}(w_0,D_i)$   7:       end for   8: end for   9: Group Aggregation And Upload Phase 10: for each group $G_i$∈$\mathcal{G}$  do 11:       $S_0$ sends $seed$ to the first user in each group $G_i$. 12:       for each first user $G_{i1}$∈$G_i$  do 13:           $r_i\leftarrow PRG\left(seed\right)$, $w_{i1}^{*}=w_{i1}-r_i$, $H\left(r_i\right)\leftarrow Enc(sk,r_i)$ 14:           Computes $H\left(r_i\right)=H_i^0+H_i^1$, then respectively sends to the server $S_1$ and $S_2$. 15:       end for 16:       $G_{i1}$ sends $w_{i1}^{*}$ to the next user, until the last one. 17:       for each last user $G_{ik}$∈$G_i$  do 18:           //Group Aggregation 19:           $W_i$ = ${\sum }_{j=1}^k{w}_{ij}-r_i$ 20:           //Verification tag 21:           ${\sigma }_i\leftarrow Enc(sk,W_i)$ 22:           Computes $W_i=W_i^0+W_i^1$, ${\sigma }_i={\sigma }_i^0+{\sigma }_i^1$, then respectively sends to the server $S_1$ and $S_2$. 23:       end for 24: end for 25: Server Aggregation Phase 26: for server $S_1$  do 27:       constructs $r_i\leftarrow PRG\left(seed\right)$ 28:       // Global Aggregation 29:       $W^0=\sum W_i^0+\sum r_i$ 30:       // Verification tag Aggregation 31:       ${\sigma }^0=\prod {\sigma }_i^0$ 32: end for 33: for server $S_2$  do 34:       $W^1=\sum W_i^1$, ${\sigma }^1=\prod {\sigma }_i^1$ 35: end for 36: Send $W^0,W^1$ and ${\sigma }^0,{\sigma }^1$ to the users. 37: Verification Phase 38: for each users $u_i$  do 39:       $W=W^0+W^1$, $\sigma ={\sigma }^0\ast {\sigma }^1$ 40:       if  $Enc(sk,W)=\sigma$  then 41:           The users accept the aggregated result and start the next round of training. 42:       else 43:           The users reject the aggregated result. 44:       end if 45: end for 46: return W

4.1. System Initialization

Suppose there are n participants in the system, denoted as $U_i$, each with a local dataset $D_i$, where $i\in N$ and $N=\{1,2,\dots ,n\}$.

The server initializes the global model parameters to $w_0$, thus providing a unified model structure to each participant and ensuring that all participants work under the same model framework during subsequent local training and model updates. The participants are then grouped into k groups (this paper proposes simulating the grouping of participants based on their computational resources), denoted as $G_j$, where $j\in K$ and $K=\{1,2,\dots ,k\}$. The essence of grouping is to organize the participants in a group into a participant chain, so the aggregation server should send the neighbor node information of the participants to each participant, thereby facilitating the transfer of training parameters within the group. It is assumed that the neighbor node information of each participant is established before the start of local training. A random $seed$ is generated by $S_1$ and sent to the first participant of each group to assist in the generation of masks by the participants.

In addition, we select a trusted third party to generate a pair of shared Paillier cryptosystem key pairs $(pk,sk)$ for all users and distribute them to each participant. The trusted third party also initializes the necessary parameters for global model training, including the participant learning rate $\eta$, the maximum number of times the training dataset can be entirely traversed T, the loss function $\mathcal{L}(W,D)$, and the global iteration number R.

4.2. Local Model Training and Parameter Uploading

• Local model training phase
  Each participant $U_i$ begins local training using the initial model parameters $w_0$ on its local dataset $D_i$ based on the stochastic gradient descent (SGD) algorithm to obtain its local model parameters $w_i$, as shown below:

  $$w_i=w_0-\eta \ast \mathcal{L}(w_0,D_i)$$

  (1)

  where $i\in \{1,2,\dots ,n\}$.
• Parameter upload stage
  The first participant in each group utilizes a pseudo-random generator to produce a random number $r_i$, which serves as a mask for the local model parameters to obtain the obfuscated local model parameters

  $$w_1^{*}=w_1-r_i,$$

  (2)

  and sends $w_i^{*}$ to the next participant for aggregation $w_{i+1}^{*}$

  $$w_{i+1}^{*}=w_{i+1}+w_i^{*}.$$

  (3)
  The process is repeated until the last participant’s local model parameter in the group also participates in the aggregation, resulting in the local model parameter $W_i$ for the current group.

  $$W_i^{*}=w_k+w_{k-1}+\cdots +w_1-r_i,$$

  (4)
  k denotes the total number of participants in the current subgroup.
  The first participant in each group homomorphically encrypts $r_i$ to obtain $H\left(r_i\right)$, which is then sent to the dual servers in a secret sharing manner, with each server receiving a share as $H{\left(r_i\right)}^x$ and $H{\left(r_i\right)}^y$, where $i\in 1,2,\dots ,m$; the last participant in each group homomorphically encrypts $W_i$ using $sk$ to obtain the validation label

  $${\delta }_i=H\left(W_i\right)$$

  (5)
  The local model parameters $W_i$ and the validation label ${\delta }_i$ are sent to the dual servers in a secret sharing manner, with the servers receiving their respective shares as $W_i^x$, $W_i^y$, ${\delta }_i^x$, and ${\delta }_i^y$, where $i\in 1,2,\dots ,m$. After receiving their respective shares, the servers proceed to the next step. In this step, the operation of adding masks is performed exclusively by the first participant of each group and the operation of homomorphic encryption is performed only by the first and last participants within each group.

4.3. The Servers Compute and Return the Aggregated Results

$S_1$ uses a pseudo-random generator to restore the mask $r_i$ for each group and performs an addition operation with the share $W_i^x$ of the resulting local aggregation result for each group, calculating

$$W^x=\sum _1^m{W}_i^x+\sum _1^m{r}_i,$$

(6)

and also performs a multiplication operation on the validation labels, calculating

$${\delta }^x=\prod _1^m{\delta }_i^x.$$

(7)

Similarly, $S2$ performs an addition operation with the share $W_i^y$ of the resulting local aggregation results of each grouping, calculating

$$W^y=\sum _1^m{W}_i^y,$$

(8)

and also performs a multiplication operation, computing

$${\delta }^y=\prod _1^m{\delta }_i^y.$$

(9)

After the computation, the result is returned to each participant for validation. In this process, the secret shares received by the dual servers represent the data of each grouping. The servers only need to perform addition or multiplication operations on the data as required. After the calculation, the results are returned to the participants for final verification.

4.4. Correctness Verification of Aggregation Results

After receiving the results returned from the server, the participants perform the final aggregation locally by computing the global aggregation result

$$W=W^x+W^y,$$

(10)

encrypt the global aggregation result W with the key $sk$ to obtain $H\left(W\right)$, and compute the labeled value

$$\delta ={\delta }^x+{\delta }^y.$$

(11)

If equation

$$H\left(W\right)=\delta$$

(12)

holds, the verification is successful, and each participant accepts the aggregation result as its own local model parameter to start a new round of iteration; otherwise, it proves that the server has tampered with the participant’s data or maliciously returned incorrect aggregation results to undermine the convergence of the model, and each participant rejects the aggregation result.

5. Evaluation

In this section, we experimentally evaluate the performance of GHEFL and compare its efficiency and accuracy with those of SASH and FedAvg. Both the GHEFL and SASH protocols perform secure aggregation using a dual-server architecture. Meanwhile, the FedAvg protocol, as a generalized protocol for basic federated learning scenarios, is simple, efficient, and easy to implement. Both the FedAvg and GHEFL protocols perform unweighted aggregation.

5.1. Basic Configurations

The computer configuration was Intel Core i9-12900 CPU @ 5.00 GHz with 16 GB of RAM. The code environment was primarily based on the Python programming language version 3.9, with cryptographic algorithms implemented using the SecretFlow framework. The backend was implemented using PyTorch version 2.0 and federated learning aggregation was carried out using FedSGD. In our experiments, we mainly used the LeNet model, which consists of three convolutional layers, two pooling layers, one fully connected layer, and one output layer. The convolution kernel for all convolutional layers was 5 × 5 with a stride of 1. The pooling method used was average pooling and the activation function was the ReLU function, which is commonly used today.

5.2. Datasets

We evaluated the performance of GHEFL using the MNIST dataset, which is commonly used in machine learning. The dataset consists of a total of 70,000 handwritten images, divided into 60,000 training samples and 10,000 test samples.

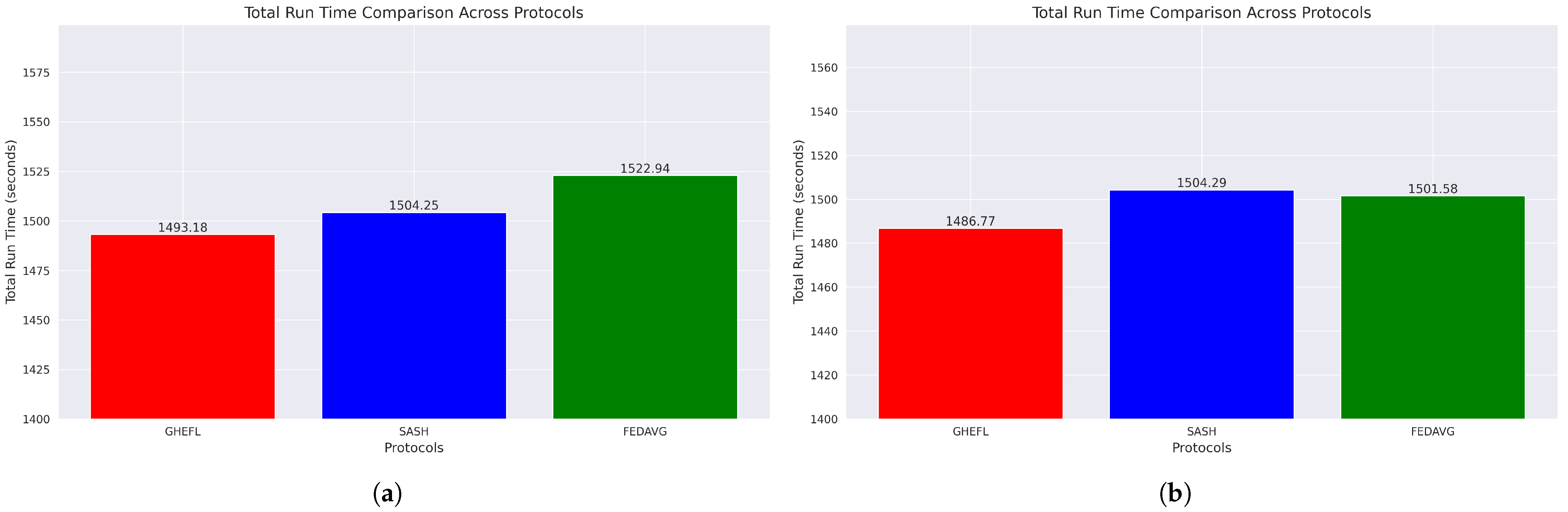
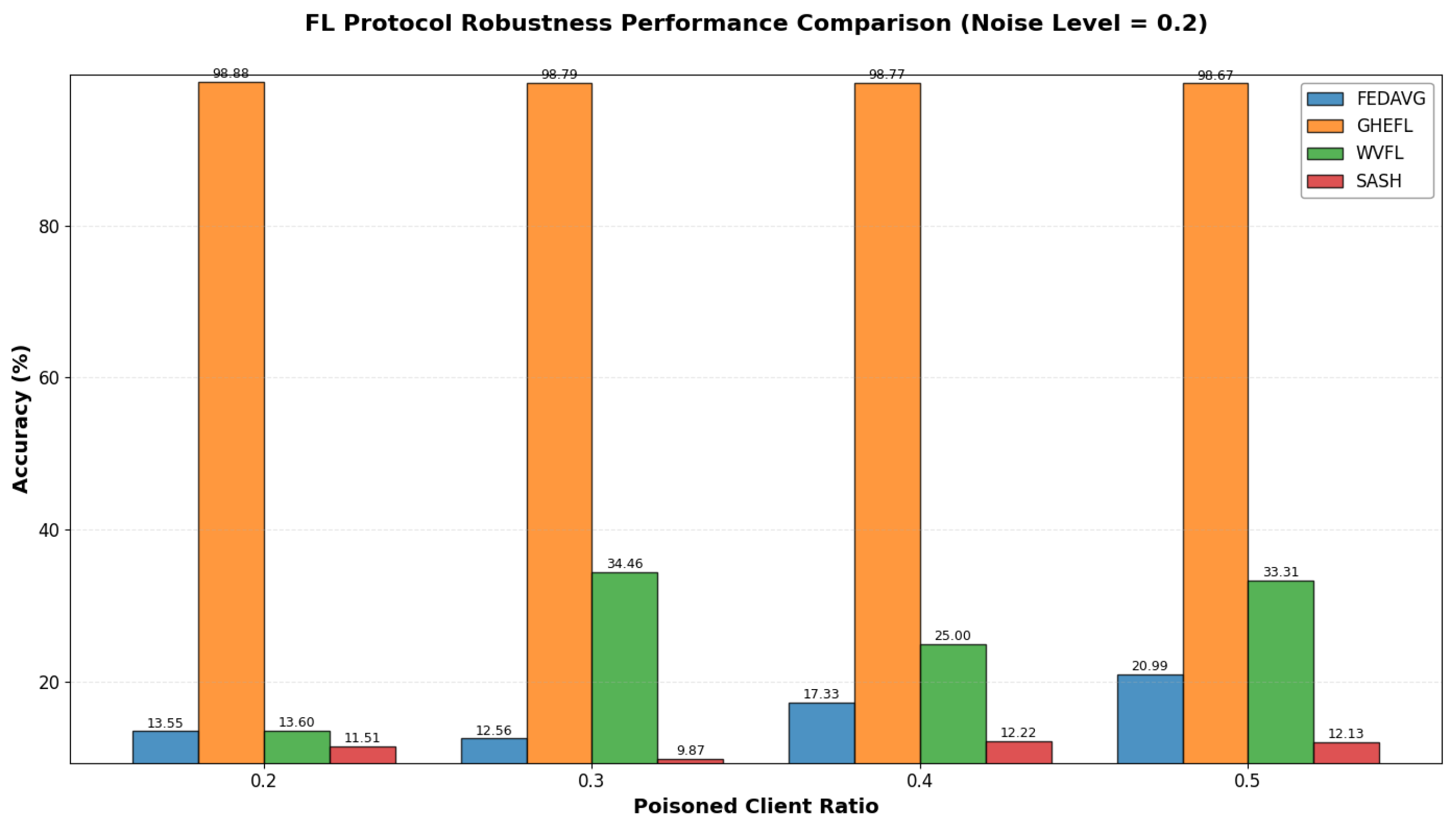
5.3. Experimental Results

We experimentally compared GHEFL with its similar schemes, SASH and FedAvg, on the MNIST dataset. The evaluation primarily focused on two aspects: the difference in model accuracy under the same number of training rounds and the time required to achieve model convergence during the training process. Subsequently, WVFL was introduced, and the resilience to attacks of these four schemes was compared.

When evaluating model accuracy, since communication noise may be introduced during parameter transmission in practical scenarios, noise was added to the parameter transfer process on the client side and its intensity was adjusted to simulate real-world conditions as closely as possible. This approach was adopted to investigate the performance of different schemes under the influence of communication noise. As can be seen from Figure 4a,b, in the iterative training under the preset number of rounds, when the noise scale was small, the model accuracy convergence of GHEFL and the other two protocols was nearly identical; however, when the noise scale was large, the model accuracy convergence of GHEFL was significantly better than that of the other two protocols. In other words, the data protection technology adopted by GHEFL has no negative impact on its accuracy and meets the practical requirements.

The original dataset was divided into a training set and a test set. The training set was used for local training on the client side, while the test set was employed to measure the accuracy of the global model. FedAvg and SASH were selected as comparative schemes for this study. After each round of federated learning training, the test set was used to evaluate the model performance, and curves depicting the accuracy of different schemes as a function of communication rounds were plotted to observe the model accuracy of the different schemes. Figure 5a and Figure 5b respectively show the total execution time required for each scheme’s model to converge under noise levels of 0.2 and 0.5. It can be observed from the figures that as the noise scale increased, the execution time required by the GHEFL scheme rose to a certain extent, but it remained lower than that of the other two protocols. Therefore, GHEFL has better operational efficiency.

Figure 6 presents an evaluation of the resistance to attacks for four federated learning schemes, including GHEFL. A server model tampering attack was employed, where Gaussian noise with a variance of 0.2 was added to the parameters when the server returned the globally aggregated parameters. Attacks were conducted on 20% to 50% of the participants. From the figure, it can be observed that GHEFL consistently maintains superior model accuracy under varying proportions of model tampering attacks, demonstrating high resistance to attacks.

5.4. Functionality

In order to evaluate the performance of GHEFL as comprehensively as possible, we compared GHEFL with state-of-the-art privacy-preserving federated learning solutions. The results are shown in

Table 1. Comparison with federated learning works.

Solution	Techniques	Multi-Servers	Verifiable	Data Privacy	Security	Support for Participants Dropout
FedAvg	-
G-VCFL	-
VeriFL	Secret Sharing + Homomorphic Hash
VerifyNet	Secret Sharing + Homomorphic Hash
VERSA	Secret Sharing
SASH	Secret Sharing
GHEFL(This work)	Secret Sharing + Homomorphic Encryption

. As the most basic and common federated learning framework, FedAvg ensures the efficiency of model training but lacks data protection measures, making it susceptible to attacks and unable to address the security issues raised in this scheme. Although G-VCFL supports participant dropout and meets the requirements for verifiability, it allows participants within the same group to obtain locally aggregated parameters, which may potentially lead to the acquisition of data from other participants. Furthermore, the server must send pseudo-random numbers to the first and last participants in each subgroup, leading to significant communication overhead and difficulty in managing a large number of stored random numbers. VerifyNet, VeriFL, and VERSA meet participants’ needs to verify aggregation results, but their verification processes involve extensive user interactions, resulting in high communication overhead. Additionally, their single-server architectures are prone to network latency issues when the number of participants increases. SASH adopts a dual-server architecture, ensuring global model accuracy while protecting participants’ data privacy. However, it does not support participant dropout and lacks verifiability, preventing participants from confirming the correctness of the training model. Since GHEFL is a verifiable secure aggregation scheme, its design focus is on ensuring data privacy. As a result, it does not support participant dropout. However, GHEFL also addresses some limitations of existing schemes to a certain extent. While protecting user data privacy, it strives to reduce reliance on high bandwidth and improve the efficiency of model training.

5.5. Theoretical Evaluation

• Security: The security mechanism of the verification protocol in this scheme relies on the dual-server architecture and the security guarantees provided by cryptographic techniques, specifically secret sharing and homomorphic encryption. The dual-server architecture, combined with the security of secret sharing, ensures that even if both servers act maliciously and collude, they cannot obtain or tamper with the local model parameters and related information of any participant. Furthermore, the homomorphic and one-way properties of homomorphic encryption ensure that each participant can successfully complete the final verification without gaining access to the information of other participants.
• Low Interaction: In federated learning, it is common for the server to send masks to two participants, allowing one to obfuscate parameters for privacy protection using the mask while the other removes the mask’s influence. This process incurs significant communication overhead, and when the number of participants is large, network bottlenecks become unavoidable. Additionally, the server must manage a large number of random values, resulting in a heavy workload. In this scheme, the server selects a random seed and transmits it only to the first user in each group, significantly reducing the information exchange between the server and participants and decreasing the server’s workload in managing random values. Moreover, using the same random seed ensures consistency in random value generation across participants. Furthermore, having the last participant in each group secretly share the aggregated parameters with the dual servers also reduces communication interactions between participants and servers.

6. Conclusions

In this paper, we proposed a verifiable, group, and homomorphic encryption-based federated learning algorithm (GHEFL) that introduces a grouping mechanism, reducing the information exchange between participants and the server of traditional federated learning, and employs a dual-server architecture with homomorphic authentication to ensure user data privacy while guaranteeing the correctness and usability of model training. Additionally, the performance of GHEFL was evaluated on the MNIST dataset, and the experimental results demonstrate that this scheme improves both model accuracy and execution time compared to common privacy-preserving federated learning schemes. In future work, we will extend GHEFL to scenarios involving users with active attack capabilities or noise introduced during intermediate channel transmission to further optimize algorithm performance. In practical applications, different grouping strategies can be selected based on various scenarios, enabling GHEFL to be applied across multiple domains. When participant data exhibit strong heterogeneity, similar participants can be grouped together. For example, in the medical field, hospitals treating a specific disease can be grouped together, while in the financial sector, banking institutions with similar customer ratings can form a group. When participants have uneven computational resources, they can be grouped according to resource utilization. For instance, in the Internet of Things (IoT) domain, high-resource devices can be grouped together to undertake more computational tasks, thereby fully leveraging available resources.

Considering real-world scenarios where participants may experience dropouts, high data heterogeneity, or varying requirements for privacy protection, as well as the potential for malicious participants to launch data poisoning attacks or model tampering attacks that disrupt model convergence, in future work, we will extend GHEFL to scenarios where participants can individually select models for local training or where users possess active attack capabilities. We will assign different weights to different participants to further optimize algorithm performance and accelerate model convergence. Additionally, we will conduct more detailed and intuitive evaluations of the algorithm’s performance using datasets from various fields, including healthcare and finance.