RIS-Assisted Joint Communication, Sensing, and Multi-Tier Computing Systems

Abstract

This paper investigates the application of Reconfigurable Intelligent Surfaces (RIS) in Joint Communication, Sensing, and Multi-tier Computing (JCSMC). An RIS-assisted JCSMC framework is proposed, wherein a full-duplex multi-antenna Base Station (BS) is employed to sense targets and provide edge computation services to User Equipment (UE). To enhance computational efficiency, a Multi-Tier Computing (MTC) architecture is adopted, enabling joint processing of computing tasks through the deployment of both the BS and the Cloud Servers (CS). Meanwhile, this paper studies the potential advantages of RIS in the proposed framework. It can assist in enhancing the efficiency of resource sharing between sensing and computing functions and then maximize the ability of computing the offload. This study aims to maximize the computation rate by jointly optimizing the BS transmission beamformer, RIS reflection coefficients, and computational resource allocation. The ensuing non-convex optimization problems are addressed using an alternating optimization algorithm based on Block Coordinate Ascent (BCA) for partial offloading mode, which ensures convergence to a local optimum, then extending the proposed joint design algorithms to the scenario with imperfect Self-Interference Cancellation. The effectiveness of the proposed algorithm was confirmed by analyzing and contrasting the simulation results with the benchmark scheme. The simulation results show that, when the BS resources are limited, utilizing MTC architecture can significantly improve the computation rate. In addition, the proposed RIS-assisted JSCMC framework is superior to other benchmark schemes in dealing with resource utilization between different functions, achieving superior computing power while maintaining sensing quality.

1. Introduction

Recently, as technologies like smart cities, intelligent transportation, and intelligent industrial production become more widespread, issues such as spectrum resource shortages and limited computing power have become more prominent, demanding higher performance and efficiency from future wireless networks. Therefore, the Sixth Generation (6G) wireless network is envisioned as an integrated architecture that combines multiple functions. It can integrate multiple functions, such as sensing and computing, while supporting traditional communication functions [1,2]. Integrated Sensing and Communication (ISAC) technology greatly enhances spectrum efficiency by sharing wireless infrastructure and spectrum resources, creating a mutually beneficial environment for both communication and sensing [3,4]. As a result, it has garnered widespread interest from researchers. For a long time, Mobile Edge Computing (MEC) has been one of the solutions to achieve cloud-like computing in the wireless communication field [5]. Nevertheless, with increasing computing demands, Multi-Tier Computing (MTC) structures have the potential to become a new solution for future cloud-like services. MTC can efficiently allocate computing resources between the cloud and mobile devices based on their functional characteristics and offer flexible services through cross-tier collaboration mechanisms [6]. In this context, how to effectively integrate the communication, sensing, and computing functions will become the key issue of the future 6G wireless network. At the same time, the complex resource sharing among these functions will also become a new challenge that must be solved.

Facing the increasingly complex wireless communication environment in urban areas, the performance decline of communication, sensing, and computing functions is inevitable. Consequently, Reconfigurable Intelligent Surface (RIS) technology has been proposed as a novel potential solution. RIS consists of a reflective array composed of numerous passive reflective elements that can efficiently and intelligently shape communication environments [7]. Moreover, given the power limitations of Base Stations (BS), RIS can amplify and reflect signals without relying on transmitting antennas or power amplifiers, thereby significantly reducing the energy consumption associated with signal transmission [8]. Therefore, the advantages of RIS in improving resource utilization efficiency and reducing interference between functions have been widely studied in a variety of emerging fields, such as the Internet of Vehicles [9], unmanned aerial vehicles [10], and autonomous aerial vehicles [11]. Obviously, the research on RIS may help to solve the above challenges faced by joint communication, sensing, and computing functions. Therefore, it is very important to discuss the potential advantages of RIS in future multifunctional wireless networks.

1.1. Related Work

1.1.1. Research on ISAC

The design of the ISAC system primarily encompasses three directions: sensing-centered design [12,13], communication-centered design [14,15], and joint design. However, sensing-centered and communication-centered designs fail to achieve a balance between different functions. Therefore, joint design is deemed a promising approach, aiming to devise a new unified ISAC waveform [16,17]. Recent studies have evaluated the benefits of RIS in ISAC systems. Initially, RIS was utilized solely to enhance communication capabilities without considering adding virtual links for sensing. The authors of [18] studied an RIS-assisted ISAC system in millimeter-wave scenarios, addressing the challenge of maximizing communication rates by jointly optimizing the radar cross-sectional area matrix, beamforming vector, and RIS phase shifts. The authors of [19] discussed traditional optimization methods for managing RIS constraints and introduced artificial intelligence-based optimization techniques to tackle the complex problems arising from the unique phase shift constraints and the high number of reflection units and users within the network. Currently, an increasing number of studies are focusing on using RIS to create virtual links between the BS and the targets, thereby improving radar sensing performance. The authors of [20] proposed a method to maximize radar detection performance by jointly optimizing the radar-to-base station transmission precoding matrix and the RIS’s passive reflection matrix. The authors of [21] presented a multi-user ISAC framework that supports RIS, leading to the development of a location-aware algorithm that enables perception and localization without requiring dedicated location reference signals. The authors of [22] considered an active RIS-assisted ISAC system, which aims to maximize the radar Signal-to-Interference plus Noise Ratio (SINR) by jointly optimizing the beamforming matrix of the Base Station and the reflection coefficients of the active RIS.

1.1.2. Research on MEC and MTC

MEC technology, with its advantages of low latency and high computational efficiency, has been widely discussed in terms of minimizing energy consumption [23], reducing latency [24,25], and maximizing computation efficiency [26]. However, these studies primarily focus on single-tier computation architectures composed solely of edge nodes, which may be insufficient to meet substantial computing demands. To effectively utilize MTC resources such as cloud–edge collaboration, various collaborative edge computing architectures have been proposed in [27,28,29,30]. For instance, by investigating wireless communication technologies and resource allocation methods, an MTC architecture and its optimization approach were introduced in [29] to achieve lower latency services. Additionally, by examining the caching problem of edge nodes, a large-scale Multiple-Input Multiple-Output (MIMO) relay-assisted MTC architecture was proposed in [30] to enhance task computing capabilities. In addition, the application of RIS in edge computing has garnered significant attention, given the impact of complex electromagnetic environments on mobile computing performance. In [31], the authors proposed a method to reduce weighting and delay in MEC systems by jointly optimizing offload data size, computing resource allocation, and active and passive beamforming, with the assistance of RIS. In [32,33], the authors respectively aimed to minimize the energy consumption of IoT devices for computation offloading in RIS-assisted MEC systems and the overall energy consumption of the system.

1.2. Motivation and Contributions

Through the above research, it can be found that both RIS-assisted ISAC systems and RIS-assisted MEC/MTC systems have been extensively studied. However, there is still a relative scarcity of research on systems that integrate communication, sensing, and MTC functions with RIS assistance. It is obvious that, in future wireless networks, BS must not only provide traditional communication functions but also offer computing services for nearby users while being capable of target sensing. This demand will also drive research into integrating communication, sensing, and computing functions. At present, the main challenge is how to integrate computing and sensing functions directly into the BS. These functions usually depend on different hardware components in the BS, such as computing servers and transceivers. This leads to inefficient resource sharing between the two functions. To solve the above issues, we propose an RIS-assisted Joint Communication, Sensing, and Multi-tier Computing (JCSMC) framework, which can effectively integrate multiple functions on the BS and significantly improves the system’s computational rate. In this framework, the multi-antenna BS (directly and with the assistance of RIS) receives computation offloading signals from the uplink of the UE and performs target sensing. Firstly, by utilizing the MTC structure, the sensing signal transmitted by the BS can employ ISAC waveform design to carry information and further offload computation tasks to the Cloud Servers (CS). Therefore, the MTC structure enables the sensing signal to achieve dual advantages in both sensing and computation, thereby enhancing resource utilization efficiency. Secondly, by adjusting the reflection coefficient of RIS and utilizing its ability to reduce energy consumption during signal transmission, RIS can bring dual advantages in both sensing and computation. This ensures sensing performance while improving computing rate. The main contributions of this paper are summarized as follows:

• We propose an innovative RIS-assisted JCSMC framework. In this framework, MTC architecture and RIS technology are used to enhance the integration of multiple functions on the BS. A partial computation offloading mode is selected to coordinate BS and CS computing resources. We formulate a computation rate maximization problem for the joint optimization of the BS transmit beamformer, the RIS reflection coefficients, and the computing resource allocation, subject to constraints on communication–computation causality, sensing quality, the BS transmission power budget, and the unit modulus of the RIS reflection coefficient.
• To effectively solve the non-convex problem of maximizing the computation rate caused by the strong coupling between variables, we adopt a Block Coordinate Ascent (BCA) optimization algorithm. This transforms the problem into two manageable subproblems, which are solved iteratively by deriving new approximate functions. Additionally, we provide theoretical proof that the proposed algorithm can reach a local optimal solution.
• We compare the proposed scheme with three benchmark schemes: a single-tier computing architecture scheme, a scheme without RIS, and the Maximum Ratio Transmission (MRT) scheme. Simulation results demonstrate that the introduction of MTC and RIS significantly enhances the performance of the RIS-assisted JCSMC framework, thereby expanding the trade-off region between computation and sensing. Compared to traditional MRT schemes, the proposed scheme demonstrates a substantial performance boost.

The rest of this paper is organized as follows. In Section 2, we present the system model of the proposed framework, which includes models for signal, channel, communication, sensing, and computing. In Section 3, we formulate the problem of maximizing the computation rate in the RIS-assisted JCSMC system and propose a BCA-based alternating optimization algorithm to solve it. In Section 4, we extend the proposed Algorithm 1 to the scenario with imperfect Self-Interference Cancellation. Section 5 presents simulation results that demonstrate the effectiveness of the proposed optimization algorithm. Finally, conclusions are drawn in Section 6.

The acronyms adopted in this paper are summarized in

Table 1. List of acronyms.

Acronym	Definition
JCSMC	Joint Communication, Sensing, and Multi-tier Computing
RIS	Reconfigurable Intelligent Surfaces
BS	Base Station
UE	User Equipment
CS	Cloud Servers
BCA	Block Coordinate Ascent
6G	Sixth Generation
ISAC	Integrated Sensing and Communication
SI	Self-Interference
MEC	Mobile Edge Computing
MTC	Multi-tier Computing
FD	Full-Duplex
AWGN	Additive White Gaussian Noise
IA	Inner Approximation
MRT	Maximum Ratio Transmission
ULA	Uniform Linear Array
SINR	Signal to Interference plus Noise Ratio
MIMO	Multiple-Input Multiple-Output
RCG	Riemannian Conjugate Gradient
SIC	Self-Interference Cancellation
SDR	semidefinite relaxation
RCS	radar cross-section
KKT	Karush–Kuhn–Tucker

.

The following notation is adopted throughout this paper. Lowercase letters represent scalars, bold lowercase letters represent vectors, and bold uppercase letters represent matrices. (·)^T and (·)^H represent transposition and transposition conjugation, respectively. $a^{\ast }$ represent the conjugate complex of $a$. $\mathbb{C}$ and $\mathbb{R}$ represent sets of complex and real numbers, respectively. |$a$| and ||$\mathit{a}$|| are the magnitude of scalar a and the norm of vector $a$, respectively. $\mathfrak{R}\left\{·\right\}$ represents the real parts of a complex number. $\mathbb{E}\left\{·\right\}$ represents statistical expectation.

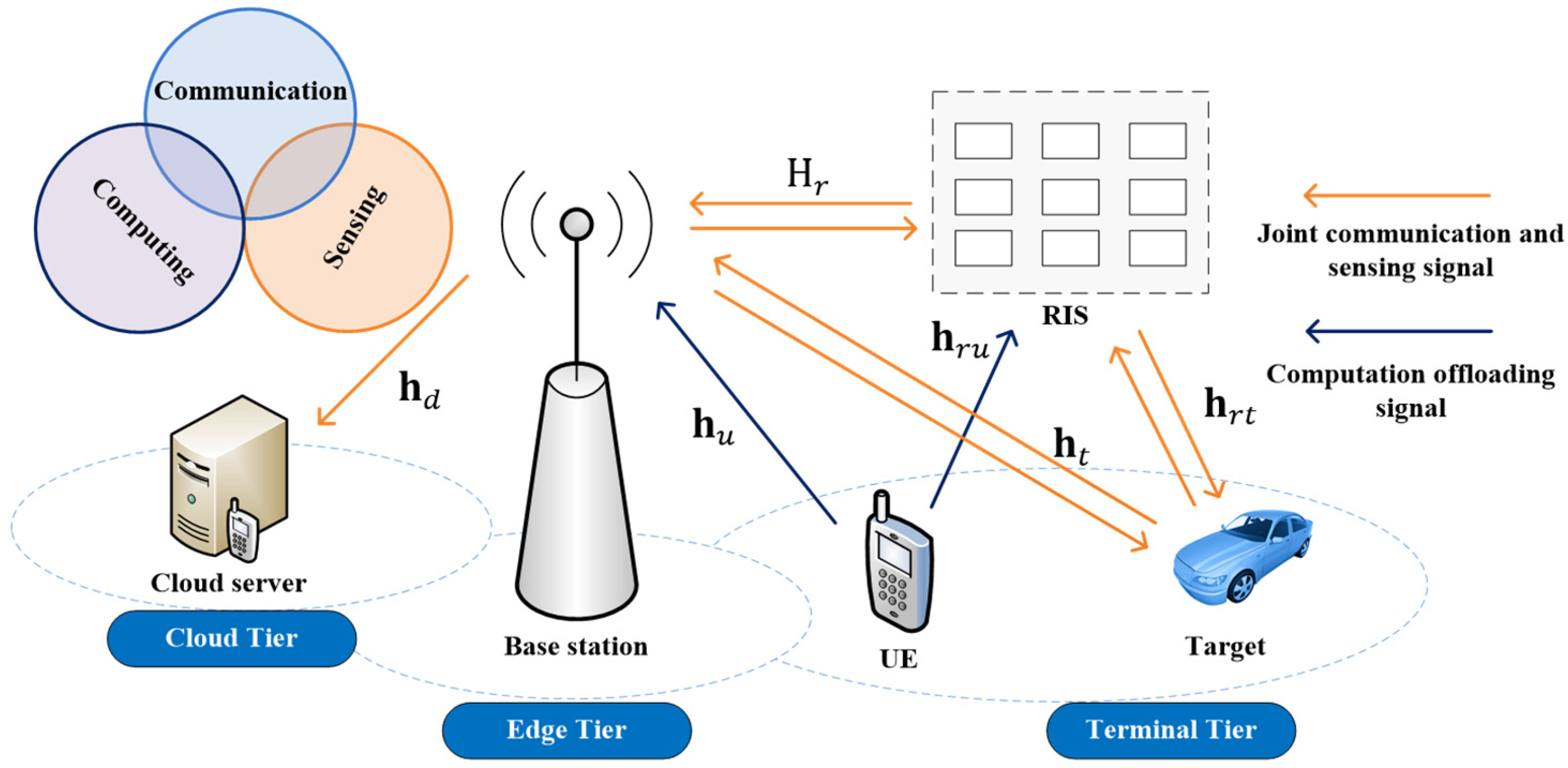
2. System Model

We propose an RIS-assisted JCSMC framework, as depicted in Figure 1. It includes a full-duplex (FD) BS equipped with $N$ transmit antennas and $N$ receive antennas, a single-antenna UE, a RIS composed of the set $\mathcal{K}\triangleq \left\{\mathrm{1,2},\dots ,K\right\}$ of $K$ reflection elements, and a sensing target. We assume that the location of RIS is known. Meanwhile, the location of the UE can be estimated using uplink signals [34]. Additionally, with the application of joint ISAC signals, the computing tasks at the BS can be transferred to a single-antenna CS for execution, demonstrating MTC advantages. Considering the UE’s limited computing power, it is assumed that its tasks are always offloaded either directly or through RIS reflection to the BS, with no direct channel between the UE and the CS [35].

2.1. Signal and Channel Model

In the proposed framework, the received signal at the multifunctional BS consists of four parts. They are the computation offloading signals from the UE, the computation offloading signals reflected by the RIS, the sensing echo signals from the target, and the sensing echo signals reflected by the RIS. In this paper, we assume that BS and RIS can obtain the position of the sensing target by using classical localization methods [36] or maximum likelihood estimation algorithms based on prior knowledge [37]. Assume that ${\phi }_t$ and ${\phi }_{rt}$ represent the angles of the sensing target relative to BS and RIS, respectively. Denote by ${\mathbf{h}}_u \in {\mathbb{C}}^{N\times 1},$ ${\mathbf{h}}_{ru} \in {\mathbb{C}}^{K\times 1}$, ${\mathbf{h}}_{rt} \in {\mathbb{C}}^{K\times 1}$, ${\mathbf{h}}_t \in {\mathbb{C}}^{N\times 1}$, ${\mathbf{h}}_d \in {\mathbb{C}}^{N\times 1}$, and ${\mathbf{H}}_r \in {\mathbb{C}}^{K\times N}$ the channels (matrix/vector) from UE to the BS, from UE to RIS, from RIS to target, from BS to target, from BS to CS, and from BS to RIS, respectively. Denote by $p_u \in {\mathbb{R}}^{+}$ and $\mathbf{p} \in {\mathbb{C}}^{N\times 1}$ the transmit power of UE and the transmit beamformer of BS. Moreover, the reflection matrix of the RIS is represent by $\mathbf{\Phi } \in {\mathbb{C}}^{K\times K}$. The computation offloading signals received by the BS from the UE and reflected by RIS can be given by

$${\mathbf{y}}_c={(\mathbf{h}}_u+{\mathbf{H}}_r^H\mathbf{\Phi }{\mathbf{h}}_{ru})\sqrt{p_u}{s}_c,$$

(1)

where $s_c$ denotes the information stream from computation UE to the BS.

As typically completed in radar sensing, we have ${\mathbf{h}}_t={\alpha }_1{\mathbf{a}}_N({\phi }_t)$ and ${\mathbf{h}}_{rt}={\alpha }_2{\mathbf{a}}_K({\phi }_{rt})$, where ${\alpha }_1$ and ${\alpha }_2$ represent the path loss coefficients of the sensing target for BS and RIS, respectively.${\mathbf{a}}_N\left(\phi \right)$ and ${\mathbf{a}}_K\left(\phi \right)$ represent the steering vectors of the antenna array at the BS and the RIS in the angle of $\phi$, respectively. Assuming the planar waves and the Uniform Linear Array (ULA) at the BS, the steering vector of the transmit antenna array can be given by

$${\mathbf{a}}_N(\phi )=[1,e^{\mathrm{j}{\displaystyle \frac{2\pi }{\lambda }}d\sin \left(\phi \right)}, \dots ,e^{\mathrm{j}{\displaystyle \frac{2\pi }{\lambda }}d\left(N-1\right)\sin \left(\phi \right)} {]}^T,$$

(2)

where $\lambda$ and $d$ denote the signal wavelength and the antenna spacing, respectively. Similarly, it can be concluded that ${\mathbf{a}}_K(\phi )$ has a similar form.

In addition, we define $\mathbf{x}$ as the transmission signal used for target sensing at the BS. The transmitted signal will reach the target via both the direct and reflected links and then also be reflected back to the BS through these two links. Therefore, the sensing echo signal received at the BS can be given by

$${\mathbf{y}}_s={{\alpha }_t(\mathbf{h}}_t+{\mathbf{H}}_r^H\mathbf{\Phi }{\mathbf{h}}_{rt})({\mathbf{h}}_t^H+{\mathbf{h}}_{rt}^H\mathbf{\Phi }{\mathbf{H}}_r)\mathbf{x},$$

(3)

where ${ \alpha }_t$ represents the radar cross-section (RCS) with $\mathbb{E}\left\{{\left|{\alpha }_t\right|}^2\right\}={\sigma }_t^2$.

Therefore, the total received signal at the BS can be given by

$$\begin{array}{cc}{\mathbf{y}}_u& ={\mathbf{y}}_c+{\mathbf{y}}_s+{\mathbf{n}}_u\\ & ={(\mathbf{h}}_u+{\mathbf{H}}_r^H\mathbf{\Phi }{\mathbf{h}}_{ru})\sqrt{p_u}{s}_c+{{ \alpha }_t(\mathbf{h}}_t+{\mathbf{H}}_r^H\mathbf{\Phi }{\mathbf{h}}_{rt})({\mathbf{h}}_t^H+{\mathbf{h}}_{rt}^H\mathbf{\Phi }{\mathbf{H}}_r)\mathbf{x}+{\mathbf{n}}_u\\ & ={(\mathbf{h}}_u+{\mathbf{H}}_r^H\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\mathbf{h}}_{ru})\mathbf{\theta })\sqrt{p_u}{s}_c+{{ \alpha }_t(\mathbf{h}}_t+{\mathbf{H}}_r^H\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\mathbf{h}}_{rt})\mathbf{\theta })({\mathbf{h}}_t^H{\mathbf{\theta }}^T\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathbf{h}}_{rt}\right){\mathbf{H}}_r)\mathbf{x}+{\mathbf{n}}_u,\end{array}$$

(4)

where ${\mathbf{n}}_u~\mathcal{C}\mathcal{N}(0,{\sigma }_u^2{\mathrm{I}}_N)$. $n_u$ represents the Additive White Gaussian Noise (AWGN) with zero mean and variance of ${\sigma }^2$.

In order to effectively offload computing tasks from the BS to the CS, it is necessary to utilize the transmission signal $\mathbf{x}$ at the BS. By embedding the information stream into the signal, the transmission signal $\mathbf{x}$ can be rewritten as

$$\mathbf{x}=\mathbf{p}{s}_d,$$

(5)

where $s_d \in \mathbb{C}$ represents the information stream from the BS to the CS. In order to obtain the simplified mathematical symbols, we denote $\mathbf{\Phi }\triangleq \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\mathbf{\theta }\right),$ where $\mathbf{\theta }=[{\theta }_1,{\theta }_2,\dots ,{\theta }_K{]}^T$ represents the vector of reflection coefficients satisfying $\left|{\theta }_K\right|=1$, $\forall K$. $\widehat{\mathbf{h}}\left(\mathbf{\theta }\right) ={\mathbf{h}}_u+{\mathbf{H}}_r^H\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\mathbf{h}}_{ru})\mathbf{\theta }$, and ${\widehat{\mathbf{H}}}_s(\mathbf{\theta }) = {(\mathbf{h}}_t+{\mathbf{H}}_r^H\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\mathbf{h}}_{rt})\mathbf{\theta })({\mathbf{h}}_t^H+{\mathbf{\theta }}^T\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\mathbf{h}}_{rt}){\mathbf{H}}_r)$. As a result, we can rewrite Equation (4) as ${\mathbf{y}}_u= \widehat{\mathbf{h}}\left(\mathbf{\theta }\right)\sqrt{p_u}{s}_c+{{ \alpha }_t\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right)\mathbf{p}{s}_d+{\mathbf{n}}_u$.

Furthermore, the signal received at CS can be given by

$${\mathrm{y}}_d={\mathbf{h}}_d^H\mathbf{p}{s}_d+n_d,$$

(6)

where $n_d~\mathcal{C}\mathcal{N}(0,{\sigma }_d^2)$ is the AWGN with zero mean and variance of ${\sigma }^2$. We also assume that $s_c$ and $s_d$ are independent random variables with zero means. It should be noted that, although the sensing signal carries information, as long as the BS can fully grasp the relevant knowledge of the transmission waveform, it can still perform sensing functions [38].

2.2. Communication Model

In the RIS-assisted JCSMC framework proposed in this paper, the performance of task offloading is determined by the spectrum efficiency. At the BS receiver, the computation offloading signal from the UE is first decoded, and the influence of the decoding stream in the received signal is eliminated. The available spectrum efficiency from the UE to the BS can be given by

$$R_u={\log }_2\left(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2{p}_u}{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right)\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right).$$

(7)

Furthermore, the available spectrum efficiency from the BS to the CS can be given by

$$R_u={\log }_2\left(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2{p}_u}{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right)\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right).$$

(8)

2.3. Sensing Model

Due to the priority decoding of computation offloading signals, interference with target sensing signals can be effectively eliminated. Thus, the signal ${\mathbf{y}}_c$ can be removed from ${\mathbf{y}}_u$. Therefore, the effective target sensing signal can be represented as ${\mathbf{y}}_s+{\mathbf{n}}_u$. The sensing SINR can be given by

$${\gamma }_s={\displaystyle \frac{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right)\mathbf{p}‖}^2}{{\sigma }_u^2{\mathrm{I}}_N}}.$$

(9)

The detection and localization capabilities of target sensing depend on the sensing SINR ${\gamma }_s$ [39]. Therefore, the sensing performance can only be guaranteed when the sensing SINR ${\gamma }_s$ satisfies the minimum sensing SINR constraint:

$${\gamma }_{s,min}{\le \gamma }_s,$$

(10)

Due to the interference between the computation offloading signal and the sensing signals received at the BS, selecting an appropriate decoding order is particularly important. Notably, we prioritize decoding the computation offloading signal ${\mathbf{y}}_c$ that is subject to sensing signal interference, ensuring that the sensing signal ${\mathbf{y}}_s$ is not affected by interference from the computation offloading signal. This decoding order is chosen because computation offloading signals do not experience the round trip path loss that sensing signals do. Therefore, the power of ${\mathbf{y}}_c$ will be much greater than ${\mathbf{y}}_s$. By encoding the uplink signal of the UE and utilizing interference cancellation techniques at the BS receiver, the influence on the sensing signal can be eliminated by prioritizing decoding of the computation offloading signal [38].

2.4. Computation Model

In this section, the computational model of the proposed framework is introduced. Due to the excellent computational power of the server and the small amount of data in the computation results, the delay in downloading the computation results can be omitted [38]. Denote ${\mathcal{X}}_{BS} \subseteq \mathcal{X}$ and ${\mathcal{X}}_{CS} \subseteq \mathcal{X}$ as the sets that execute their computation tasks at the BS and the CS, respectively. We considered a partial computation offloading mode as the computation model for the proposed framework. For the partial offloading mode, the computation tasks transmitted by the UE can be arbitrarily divided into two sections, which are processed at the BS and the CS, respectively. In this case, it holds that ${\mathcal{X}}_{BS}={\mathcal{X}}_{CS}=\mathcal{X}.$

Define $\varphi$ as the number of computation cycles needed by the BS or the CS to process one bit of data from the UE, which varies based on the nature of the computation tasks. $f_b$ denotes the CPU cycle frequency (cycles/s) allocated by the BS to the UE. The computation rate for data at the BS, which indicates the number of bits that can be processed per second, can be given by

$$r_b={\displaystyle \frac{f_b}{\varphi }},\in \mathcal{X}$$

(11)

In the same way, the computation rate for data at the CS can be given by

$$r_c={\displaystyle \frac{f_c}{\varphi }},\in \mathcal{X}$$

(12)

where $f_c$ denotes the CPU cycle frequency (cycles/s) allocated by the CS to the UE.

Since the BS is normally power constrained, the power consumption for computing at the BS should be considered, which is given by [5]

$$p_b=\mathcal{m}{f}_b^3=\mathcal{m}{(\varphi r_b)}^3$$

(13)

where $\mathcal{m}$ is the power factor related to the CPU architecture of the computation server at the BS.

Furthermore, there are some constraints between computation and task offloading. Thus, the computation rates $r_b$ and $r_c$ need to satisfy

$$r_b+B{R}_{ud }\le B{R}_u,$$

(14)

$${ R}_{ud }\le R_d,$$

(15)

$$r_c\le B{R}_{ud },$$

(16)

where $B$ and $R_{ud }$ denote the channel bandwidth and the offloading spectrum efficiency from the BS to the CS, respectively.

Specifically, Equation (14) represents the sum of the computation rate $r_b$ of the UE at the BS and the offloading rate from the BS to the CS, which is physically constrained by the maximum communication rate available to the UE at the BS. Equation (15) ensures that the offloading spectrum efficiency of the UE from the BS to the CS is limited by the maximum available spectrum efficiency between the BS and the CS. Equation (16) guarantees that the computation rate $r_c$ does not exceed the computation offloading rate from the BS to the CS. Since the CS typically has sufficient capacity to support high-performance computing, Equation (16) can be readily satisfied. Therefore, Equations (14)–(16) can be simplified as a causal constraint between communication and computation, as follows:

$$r_b+r_c\le B{R}_{u },$$

(17)

$$r_c\le B{R}_d,$$

(18)

The total computation rate can be given by

$$\tilde{R}=r_b+r_c.$$

(19)

Remark 1. 

(Computing sensing trade-off) It is worth noting that, in the JCSMC framework, there are trade-offs between computational power and sensing performance. Firstly, allocating more power to the beamformer of the BS can achieve higher sensing SINR, but this will result in a decrease in the power available for computation by the BS, thereby affecting its computation rate. Secondly, to achieve superior sensing performance, it is essential to concentrate the BS’s power in the direction of the sensing target. This will result in the BS having less power available to transmit computation offloading signals to the CS, leading to a diminished offloading rate and ultimately reducing the total computation rate.

Remark 2. 

(Benefits of RIS) In the RIS-assisted JCSMC framework proposed in this paper, RIS can effectively improve the communication environment through passive beamforming. Meanwhile, RIS can reduce energy consumption in signal transmission, and BS transmitters do not need to concentrate a large amount of power on the target angle for sensing. This can further enable more power to be used for offloading tasks to the CS, improving the computation rate. Based on the above advantages and the analysis in Remark 1, the introduction of RIS can bring dual advantages in both sensing and computation, thereby ensuring sensing performance and increasing the computation rate.

3. Problem Formulation and Solution

In this section, we combine the characteristics of partial computation offloading mode and joint optimization of the BS transmit beamformer $\mathbf{p}$, the RIS reflection coefficients $\mathbf{\theta }$, and the computing resource allocations ${ r}_b$ and ${ r}_c$. The maximum computation rate $\tilde{R}$ is obtained while satisfying the causal constraints between communication and computation, sensing quality, and the unit model of RIS reflection coefficients constraint.

3.1. Problem Formulation

In partial computation offloading mode, the problem of maximizing the computation rate can be expressed as follows:

$$\underset{\mathbf{p},\mathbf{\theta },r_b,r_c}{\max } \tilde{R}=r_b+r_c$$

(20a)

$$\mathrm{s}.\mathrm{t}. r_b+r_c\le B{R}_u, \in \mathcal{X}$$

(20b)

$$r_c\le B{R}_d,$$

(20c)

$${\gamma }_{s,min}\le {\gamma }_s,$$

(20d)

$$\left|{\theta }_K\right|=1, \forall K,$$

(20e)

$${‖\mathbf{p}‖}^2+\mathcal{m}{(\varphi r_b)}^3\le P_b,$$

(20f)

$$r_b\ge 0,r_c\ge 0, \in \mathcal{X},$$

(20g)

where Equations (20b) and (20c) represent the causal constraints between communication and computation functions. Equation (20d) represents the constraint on the target sensing SINR. Equation (20e) provides RIS reflection coefficient constraints.$P_b$ in Equation (20f) represents the available total power budget at the BS. However, due to constraints (20b) and constraints (20d) leading to a highly coupled non-convex problem, this often makes it difficult to obtain a global optimal solution.

3.2. Proposed Solution

On the one hand, it is necessary to solve the non-convex problem of high coupling between the transmission beamformer $\mathbf{p}$ and the RIS reflection coefficients $\mathbf{\theta }$ in constraints (20b) and constraints (20d). On the other hand, it is necessary to achieve a faster computation rate while adhering to the constraints of (20e) and constraints (20f).

To solve the above problem, we choose $R_u$ in Equation (20b) as the intermediate optimization objective and Equations (20d)–(20f) as constraints. Using the BCA optimization method to decouple $R_u$ into two coordinate blocks corresponding to $\mathbf{p}$ and $\mathbf{\theta }$, we then adopt the Inner Approximation (IA) method [40] for alternating optimization. Substitute the optimized $\mathbf{p}$ and $\mathbf{\theta }$ into problem (20), process the problem, and obtain the optimization result $\tilde{R}$ for this round. Finally, the local optimal solution ${\tilde{R}}^{\star }$ is obtained through the optimal solutions ${\mathbf{p}}^{\star }$ and ${\mathbf{\theta }}^{\star }$.

Therefore, the intermediate optimization objective can be represented as

$$\underset{\mathbf{p},\mathbf{\theta }}{\max }{R}_u={\log }_2\left(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2{p}_u}{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right)\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right)$$

(21a)

$$\mathrm{s}.\mathrm{t}. {\gamma }_{s,min}\le {\gamma }_s,$$

(21b)

$$\left|{\theta }_K\right|=1,\forall K,$$

(21c)

$${‖\mathbf{p}‖}^2+\mathcal{m}{(\varphi r_b)}^3\le P_b,$$

(21d)

Assume that (${\mathbf{p}}^{(\eta )}$, ${\mathbf{\theta }}^{(\eta )}$) is the feasible point obtained from the ($\eta -1$)-th iteration. Solve problem (21), obtain the optimization result ${\mathbf{p}}^{\star }$ for the given ${\mathbf{\theta }}^{\eta }$ condition, and then update the values (${\mathbf{p}}^{(\eta +1)}:={\mathbf{p}}^{\star })$ to obtain ${\mathbf{\theta }}^{\star }$ by the next iteration.

3.3. Beamformer Iteration

Firstly, we iteratively update the transmit beamformer $\mathbf{p}$ of the BS. For a given ${\mathbf{\theta }}^{(\eta )}$, the $\left(\eta +1\right)$-th iteration in problem (21) can be rewritten as

$$\underset{\mathbf{p}}{\max } R_u(\mathbf{p},{\mathbf{\theta }}^{(\eta )})={\log }_2\left(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right)\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right)$$

(22a)

$$\mathrm{s}.\mathrm{t}. {\gamma }_{s,min}\le {\displaystyle \frac{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right)\mathbf{p}‖}^2}{{\sigma }_u^2{\mathrm{I}}_N}},$$

(22b)

$${‖\mathbf{p}‖}^2+\mathcal{m}{(\varphi r_b)}^3\le P_b,$$

(22c)

where the Equation (22a) is non-concave. To effectively solve problem (22), it can be transformed into an approximate convex program. The concave lower limit of the Equation (22a) can be obtained from [41]:

$$\begin{gathered} {\log }_2(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right)\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}})\ge {\log }_2(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right){\mathbf{p}}^{\left(\eta \right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N})} \\ +{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u+{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right){\mathbf{p}}^{\left(\eta \right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}} \\ \times \left(1-{\displaystyle \frac{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right)\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right){\mathbf{p}}^{\left(\eta \right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right) :={R_u}^{\left(\eta \right)}\left(\mathbf{p}|{\mathbf{\theta }}^{\left(\eta \right)}\right). \end{gathered}$$

(23)

Since Equation (22b) is a non-convex constraint, the right-hand side of its function can be internally approximated as [42]

$${\gamma }_{s,min}\le {\displaystyle \frac{2{\sigma }_t^2\mathfrak{R}\left\{{{(\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta \right)})}^H{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right)\mathbf{p}\right\}-{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta \right)}‖}^2}{{\sigma }_u^2{\mathrm{I}}_N}}\mathbf{.}$$

(24)

In summary, the approximate convex program used for solving problem (22) at the $\left(\eta +1\right)$-th iteration can be represented as

$$\underset{\mathbf{p}}{\mathrm{m}\mathrm{a}\mathrm{x}} {R_u}^{\left(\eta \right)}(\mathbf{p}|{\mathbf{\theta }}^{(\eta )})$$

(25a)

$$\mathrm{s}.\mathrm{t}. {‖\mathbf{p}‖}^2+\mathcal{m}{(\varphi r_b)}^3\le P_b,$$

(25b)

$${\gamma }_{s,min}\le {\displaystyle \frac{2{\sigma }_t^2\mathfrak{R}\left\{{{(\widehat{\mathbf{H}}}_s({\mathbf{\theta }}^{(\eta )}){\mathbf{p}}^{(\eta )})}^H{\widehat{\mathbf{H}}}_s({\mathbf{\theta }}^{(\eta )})\mathbf{p}\right\}-{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s({\mathbf{\theta }}^{(\eta )}){\mathbf{p}}^{(\eta )}‖}^2}{{\sigma }_u^2{\mathrm{I}}_N}},$$

(25c)

3.4. RIS Reflection Coefficients Iteration

Then, we iteratively update the reflection coefficient $\mathbf{\theta }$ of RIS. For a given ${\mathbf{p}}^{(\eta +1)}$, the $\left(\eta +1\right)$-th iteration in problem (21) can be rewritten as

$$\underset{\mathbf{\theta }}{\max } R_u({\mathbf{p}}^{\left(\eta +1\right)},\mathbf{\theta })={\log }_2\left(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2{p}_u}{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right)$$

(26a)

$$\mathrm{s}.\mathrm{t}. {\gamma }_{s,min}\le {\displaystyle \frac{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2}{{\sigma }_u^2{\mathrm{I}}_N}},$$

(26b)

$$\left|{\theta }_K\right|=1, \forall K,$$

(26c)

where Equation (26a) is non-concave. Equations (26b) and (26c) are the non-convex constraints.

To effectively solve problem (26), it can be transformed into an approximate convex program. According to the Cauchy–Schwarz inequality, the first term in the denominator of Equation (26a) can be upper limited as

$$\begin{gathered} {‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2={‖{\widehat{\mathbf{H}}}_{s1}\left(\mathbf{\theta }\right){{\widehat{\mathbf{H}}}_{s1}}^H\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2 \\ \le {{‖{\widehat{\mathbf{H}}}_{s1}\left(\mathbf{\theta }\right)‖}^2‖{{\widehat{\mathbf{H}}}_{s1}}^H\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2 \\ \le \upsilon \zeta . \end{gathered}$$

(27)

where ${\widehat{\mathbf{H}}}_{s1}\left(\mathbf{\theta }\right)={\mathbf{h}}_t+{\mathbf{H}}_r^H\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathbf{h}}_{rt}\right)\mathbf{\theta }$. $\upsilon \in {\mathbb{R}}^{+}$ and $\zeta \in {\mathbb{R}}^{+}$ are newly introduced optimization variables, satisfying ${‖{\widehat{\mathbf{H}}}_{s1}\left(\mathbf{\theta }\right)‖}^2\le \upsilon$ and ${‖{{\widehat{\mathbf{H}}}_{s1}}^H\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2\le \zeta$. The product $\upsilon \zeta$ is convexified as $\upsilon \zeta \le {\displaystyle \frac{{\upsilon }^{\left(\eta \right)}{\zeta }^2}{2{\zeta }^{\left(\eta \right)}}}+{\displaystyle \frac{{\zeta }^{\left(\eta \right)}{\upsilon }^2}{2{\upsilon }^{\left(\eta \right)}}}$.

Thus, the concave lower limit of Equation (26a) can be expressed as

$$\begin{gathered} {\log }_2(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2{p}_u}{{\sigma }_t^2\upsilon \zeta +{\sigma }_u^2{\mathrm{I}}_N}})\ge {\log }_2(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{{\sigma }_t^2\upsilon }^{(\eta )}{\zeta }^{(\eta )}+{\sigma }_u^2{\mathrm{I}}_N}}) \\ +{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{\left(\eta \right)}\right)‖}^2{p}_u}{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{\left(\eta \right)}\right)‖}^2{p}_u+{\sigma }_t^2{\upsilon }^{\left(\eta \right)}{\zeta }^{\left(\eta \right)}+{\sigma }_u^2{\mathrm{I}}_N}} \\ \times \left(2-{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{\left(\eta \right)}\right)‖}^2}{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2}}-{\displaystyle \frac{{\sigma }_t^2(\frac{{\upsilon }^{\left(\eta \right)}{\zeta }^2}{2{\zeta }^{\left(\eta \right)}}+\frac{{\zeta }^{\left(\eta \right)}{\upsilon }^2}{2{\upsilon }^{\left(\eta \right)}})+{\sigma }_u^2{\mathrm{I}}_N}{{\sigma }_t^2{\upsilon }^{\left(\eta \right)}{\zeta }^{\left(\eta \right)}+{\sigma }_u^2{\mathrm{I}}_N}}\right) \\ :={R_u}^{\left(\eta \right)}\left(\mathbf{\theta }|{\mathbf{p}}^{\left(\eta +1\right)}\right). \end{gathered}$$

(28)

Next, to convexify Equation (26b), its right-hand molecule can be innerly approximated as

$$\begin{gathered} {‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2\ge 2\mathfrak{R}\left\{{{(\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta +1\right)})}^H{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}\right\} \\ -{‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2. \end{gathered}$$

(29)

To further simplify the constraint conditions, the first term of the right-hand side of Equation (29) can be rewritten as [42]

$$\begin{gathered} 2\mathfrak{R}\left\{{{(\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta +1\right)})}^H{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}\right\} \\ =2\mathfrak{R}\left\{{{(\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta +1\right)})}^H{\mathbf{h}}_t{\mathbf{h}}_t^H{\mathbf{p}}^{\left(\eta +1\right)}\right\} \\ +2\mathfrak{R}\left\{{{(\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta +1\right)})}^H{\mathbf{h}}_t{\mathbf{\theta }}^T\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\mathbf{h}}_{rt}){\mathbf{H}}_r{\mathbf{p}}^{\left(\eta +1\right)}\right\} \\ +2\mathfrak{R}\left\{{{(\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta +1\right)})}^H{\mathbf{H}}_r^H\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\mathbf{h}}_{rt})\mathbf{\theta }{\mathbf{h}}_t^H{\mathbf{p}}^{\left(\eta +1\right)}\right\} \\ +2\mathfrak{R}\left\{{{(\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta +1\right)})}^H{\mathbf{H}}_r^H\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\mathbf{h}}_{rt})\mathbf{\theta }{\mathbf{\theta }}^T\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\mathbf{h}}_{rt}){\mathbf{H}}_r{\mathbf{p}}^{\left(\eta +1\right)}\right\} \\ ={\mathcal{P}}^{\left(\eta \right)}\left(\mathbf{\theta }|{\mathbf{p}}^{\left(\eta +1\right)}\right)+2\mathfrak{R}\left\{{\mathbf{\theta }}^T\Psi \mathbf{\theta }\right\}. \end{gathered}$$

(30)

where $\Psi \triangleq {{(\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta +1\right)})}^H{\mathbf{H}}_r^H\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathbf{h}}_{rt}\right)\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathbf{h}}_{rt}\right){\mathbf{H}}_r{\mathbf{p}}^{\left(\eta +1\right)}$.

Due to the high coupling of the last term in Equation (30), to solve this problem, it can be convexified as

$$2\mathfrak{R}\left\{{\mathbf{\theta }}^T\Psi \mathbf{\theta }\right\}\ge 2\mathfrak{R}\left\{{\left({\mathbf{\theta }}^{\left(\eta \right)}\right)}^T\Psi \mathbf{\theta }+{\mathbf{\theta }}^T\Psi {\mathbf{\theta }}^{\left(\eta \right)}-{\left({\mathbf{\theta }}^{\left(\eta \right)}\right)}^T\Psi {\mathbf{\theta }}^{\left(\eta \right)}\right\}.$$

(31)

Combining the simplification and analysis of Equations (29)–(31), constraint (26b) can be innerly approximated as

$${ \gamma }_{s,min}\le {\displaystyle \frac{{\sigma }_t^2{\mathcal{P}}^{\left(\eta \right)}\left(\mathbf{\theta }|{\mathbf{p}}^{\left(\eta +1\right)}\right)-{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right){\mathbf{p}}^{(\eta +1)}‖}^2+2{\sigma }_t^2\mathfrak{R}\left\{{\left({\mathbf{\theta }}^{\left(\eta \right)}\right)}^T\Psi \mathbf{\theta }+{\mathbf{\theta }}^T\Psi {\mathbf{\theta }}^{\left(\eta \right)}-{\left({\mathbf{\theta }}^{\left(\eta \right)}\right)}^T\Psi {\mathbf{\theta }}^{\left(\eta \right)}\right\}}{{\sigma }_u^2{\mathrm{I}}_N}},$$

(32)

In addition, the unit modulus constraint (26c) of the RIS reflection coefficient is non-convex. To solve this problem, it can be relaxed by a convex constraint:

$${\left|{\theta }_K\right|}^2\le 1,\forall K.$$

(33)

Further elaboration on Equation (33) can be expressed as

$$\sum {\left|{\theta }_K\right|}^2-K\le 0,$$

(34)

In order to satisfy the constraint (26c) in the optimal state, the penalty optimization problem is introduced, and problem (26) can be rewritten as

$$\underset{\mathbf{\theta }}{\max } R_u\left({\mathbf{p}}^{\left(\eta +1\right)},\mathbf{\theta }\right)+\varrho (\sum {\left|{\theta }_K\right|}^2-K)$$

(35a)

$$\mathrm{s}.\mathrm{t}. {\gamma }_{s,min}\le {\displaystyle \frac{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2}{{\sigma }_u^2{\mathrm{I}}_N}},$$

(35b)

$${\left|{\theta }_K\right|}^2\le 1,\forall K ,$$

(35c)

where $\varrho >0$ represents the penalty parameter. Its function is to make the objective and penalty clauses comparable.

Due to constraint (34) always being negative, the positive value ϱ ensures that the uncertainty of Equation (26c) is penalized, ensuring that $\left|{\theta }_K\right|=1$ is in the optimal state. When $\varrho$ is set large enough, problem (26) and problem (35) can obtain consistent optimal solutions. Similar proof steps can be found in [43], Appendix C.

In summary, the approximate convex program used for solving problem (26) at the $\left(\eta +1\right)$-th iteration can be represented as

$$\underset{\mathbf{\theta },\upsilon ,\zeta }{\mathrm{m}\mathrm{a}\mathrm{x}} {R_u}^{\left(\eta \right)}\left({\mathbf{p}}^{\left(\eta +1\right)},\mathbf{\theta }\right)\triangleq {R_u}^{\left(\eta \right)}\left(\mathbf{\theta }|{\mathbf{p}}^{\left(\eta +1\right)}\right)+\varrho ({\mathcal{Q}}^{\eta }\left(\mathbf{\theta }\right)-K)$$

(36a)

$$\mathrm{s}.\mathrm{t}. {‖{\widehat{\mathbf{H}}}_{s1}\left(\mathbf{\theta }\right)‖}^2\le \upsilon ,$$

(36b)

$${‖{{\widehat{\mathbf{H}}}_{s1}}^H\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2\le \zeta ,$$

(36c)

$${\left|{\theta }_K\right|}^2\le 1, \forall K,$$

(36d)

$${ \gamma }_{s,min}\le {\displaystyle \frac{{\sigma }_t^2{\mathcal{P}}^{\left(\eta \right)}\left(\mathbf{\theta }|{\mathbf{p}}^{\left(\eta +1\right)}\right)-{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right){\mathbf{p}}^{(\eta +1)}‖}^2+2{\sigma }_t^2\mathfrak{R}\left\{{\left({\mathbf{\theta }}^{\left(\eta \right)}\right)}^T\Psi \mathbf{\theta }+{\mathbf{\theta }}^T\Psi {\mathbf{\theta }}^{\left(\eta \right)}-{\left({\mathbf{\theta }}^{\left(\eta \right)}\right)}^T\Psi {\mathbf{\theta }}^{\left(\eta \right)}\right\}}{{\sigma }_u^2{\mathrm{I}}_N}},$$

(36e)

where ${\mathcal{Q}}^{\eta }\left(\mathbf{\theta }\right)\triangleq \sum (2\mathfrak{R}[{({\theta }_K^{(\eta )})}^{\ast }{\theta }_K]-{\left|{\theta }_K^{(\eta )}\right|}^2$).

3.5. Sum Computation Rate Iteration

Finally, after optimizing through problem (25) and problem (36), the result of the $\eta$-th iteration $\left({\mathbf{p}}^{\left(\eta +1\right)},{\mathbf{\theta }}^{\left(\eta +1\right)}\right)$ can be obtained. Substitute them into Equations (20b)–(20e) to further solve for the total computation rate. Therefore, problem (20) can be rewritten as

$$\underset{r_b,r_c}{\max } \tilde{R}=r_b+r_c$$

(37a)

$$\mathrm{s}.\mathrm{t}. r_b+r_c\le B{R}_u\left({\mathbf{p}}^{\left(\eta +1\right)},{\mathbf{\theta }}^{\left(\eta +1\right)}\right), \in \mathcal{X}$$

(37b)

$${ r}_c\le B{R}_d\left({\mathbf{p}}^{\left(\eta +1\right)}\right),$$

(37c)

$${\gamma }_{s,min}\le {\gamma }_s\left({\mathbf{p}}^{\left(\eta +1\right)},{\mathbf{\theta }}^{\left(\eta +1\right)}\right),$$

(37d)

$$r_b\ge 0,r_c\ge 0, \in \mathcal{X}$$

(37e)

The BCA algorithm is described in detail in Algorithm 1. The proof of its optimality can be found in Appendix A.

Algorithm 1. BCA-Based Iterative Algorithm

Input: Convergence criteria and ${\mathbf{p}}^{\left[0\right]}{,\mathbf{\theta }}^{\left[0\right]}$, ${\upsilon }^{\left[0\right]}$, ${\zeta }^{\left[0\right]}$. Output: $r_b^{\star },{ r}_c^{\star }, {\mathbf{p}}^{\star },{\mathbf{\theta }}^{\star }.$ 1: $\eta ≔0$. 2: while $\tilde{R}$ not converged do 3: Given ${\mathbf{\theta }}^{(\eta )}$, solve (25) to obtain ${\mathbf{p}}^{\star }$ and update ${\mathbf{p}}^{(\eta +1)} := {\mathbf{p}}^{\star }$. 4: Given ${\mathbf{p}}^{(\eta +1)}$, solve (36) to obtain ${\mathbf{\theta }}^{\star }$ and update ${\mathbf{\theta }}^{(\eta +1)}:={\mathbf{\theta }}^{\star }$. 5: Given (${\mathbf{p}}^{(\eta +1)}$, ${\mathbf{\theta }}^{(\eta +1)}$), solve (37) to obtain ($r_b^{(\eta +1)},r_c^{(\eta +1)}$). 6: $\eta ≔\eta +1.$ 7: end while 8: return $r_b^{\star } = r_b^{(\eta )},r_c^{\star }=r_c^{(\eta )}, {\mathbf{p}}^{\star }={\mathbf{p}}^{(\eta )},{\mathbf{\theta }}^{\star }={\mathbf{\theta }}^{(\eta )}$.

Based on the above derivation, we can obtain the local optimal solution of problem (20) through Algorithm 1. In addition, the choice of iteration starting point will have a significant impact on the effectiveness of optimization algorithms. We have studied some common initialization methods to select appropriate $\mathbf{\theta }$ and $\mathbf{p}$. One of the purposes of deploying RIS is to minimize the impact of adverse environments on the communication and sensing quality. Meanwhile, channel gain is typically regarded as a measure of channel quality. Therefore, we can cite a classic problem from the RIS literature, which initializes $\mathbf{\theta }$ by maximizing the channel gain of the target and UE, and solve this problem using the Riemannian Conjugate Gradient (RCG) algorithm [44]. Since the RCG algorithm typically finds the corresponding local optimal solution, starting with initial values close to the optimal can improve performance and speed up convergence. After completing the initialization of $\mathbf{\theta }$, further use the available transmission power of BS to initialize $\mathbf{p}$.

Next, we will analyze the complexity of Algorithm 1. The complexity to obtain the initialization of $\mathbf{\theta }$ is, at most, $\mathcal{O}(K^{1.5})$ using the RCG algorithm [44,45], and the complexity to obtain the initialization of $\mathbf{p}$ is, at most, $\mathcal{O}(N^{1.5})$ using the RCG algorithm. The complexity of solving problem (25) and problem (36) is $\mathcal{O}(N^2{2}^{2.5})$ and $\mathcal{O}({\left(K+1\right)}^2\left(K+{2)}^{2.5}\right)$ for each iteration, respectively, where $\mathcal{O}(·)$ is the big O notation. Then, we assume that the popular interior point method [46] is utilized to solve problem (37), and the complexity of solving problem (37) is $\mathcal{O}({(N+K)(N+2K)}^2)$. Thus, the total complexity of Algorithm 1 is $\mathcal{O}(I_{ite}(N^2{2}^{2.5} +{\left(K+1\right)}^2\left(K+{2)}^{2.5}+{(N+K)\left(N+2K\right)}^2\right))$, where $I_{ite}$ denotes the number of iterations. This is much lower than the complexity based on the semidefinite relaxation (SDR) algorithm, which is about $\mathcal{O}(I_{ite}({(N^2+1)}^{3.5}{2}^{3.5} +{\left(K+1\right)}^{3.5}(K+{2)}^{3.5}+{{(N+K)}^{3.5}\left(N+2K\right)}^{3.5})$ [47].

4. Extensions to Imperfect Self-Interference Cancellation Scenario

In this section, we extend the proposed Algorithm 1 to scenarios with incomplete Self-Interference Cancellation (SIC). Specifically, despite the use of advanced SIC technology [48], there are still some residual SI that can interfere with the processing of echo signals by the BS receiving antenna array. Define ${\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}s}_d$ as the residual SI signal, where ${\mathbf{H}}_{\mathrm{S}\mathrm{I}} \in {\mathbb{C}}^{N\times N}$ represents the residual SI channel between the BS transmitting and receiving antenna arrays.

Therefore, the received signal at the BS, including both the sensing echo signal and SI plus noise, can be reformulated as

$${\mathbf{y}}_s={{\alpha }_t(\mathbf{h}}_t+{\mathbf{H}}_r^H\mathbf{\Phi }{\mathbf{h}}_{rt})({\mathbf{h}}_t^H+{\mathbf{h}}_{rt}^H\mathbf{\Phi }{\mathbf{H}}_r){\mathbf{p}s}_d+{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}s}_d,$$

(38)

For the communication model, the available spectrum efficiency from the UE to the BS can be reformulated as

$$R_u={\log }_2\left(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2{p}_u}{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right)\mathbf{p}‖}^2+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right).$$

(39)

Similarly, the sensing SINR can be reformulated as

$${\gamma }_s={\displaystyle \frac{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right)\mathbf{p}‖}^2}{{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}.$$

(40)

It is obvious that this sensing SINR requirement is more complex, since the SI term is associated with the available spectrum efficiency and the minimum sensing SINR constraint. Thus, some modifications to Algorithm 1 are required.

Firstly, for the iteration of the beamformer, problem (22) will be reformulated as

$$\underset{\mathbf{p}}{\max } R_u(\mathbf{p},{\mathbf{\theta }}^{(\eta )})={\log }_2\left(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right)\mathbf{p}‖}^2+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right)$$

(41a)

$$\mathrm{s}.\mathrm{t}. {\gamma }_{s,min}\le {\displaystyle \frac{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right)\mathbf{p}‖}^2}{{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}},$$

(41b)

$${‖\mathbf{p}‖}^2+\mathcal{m}{(\varphi r_b)}^3\le P_b,$$

(41c)

By following the same method as in (23), the concave lower limit of Equation (41a) can be obtained from [41]

$$\begin{gathered} {\log }_2(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right)\mathbf{p}‖}^2+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}})\ge {\log }_2(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right){\mathbf{p}}^{\left(\eta \right)}‖}^2+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta \right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}) \\ +{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u+{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right){\mathbf{p}}^{\left(\eta \right)}‖}^2+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta \right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}} \\ \times \left(1-{\displaystyle \frac{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right)\mathbf{p}‖}^2+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}\mathbf{p}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{(\eta )}\right){\mathbf{p}}^{\left(\eta \right)}‖}^2+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta \right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right) :={R_u}^{\left(\eta \right)}\left(\mathbf{p}|{\mathbf{\theta }}^{\left(\eta \right)}\right). \end{gathered}$$

(42)

By following the same method as in Equation (24), the concave lower limit of Equation (41b) can be internally approximated as [42]

$${\gamma }_{s,min}\le {\displaystyle \frac{2{\sigma }_t^2\mathfrak{R}\left\{{{(\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta \right)})}^H{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right)\mathbf{p}\right\}-{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left({\mathbf{\theta }}^{\left(\eta \right)}\right){\mathbf{p}}^{\left(\eta \right)}‖}^2}{2\mathfrak{R}\left\{{({\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta \right)})}^H{\mathbf{H}}_{\mathrm{S}\mathrm{I}}\mathbf{p}\right\}-{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta \right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}.$$

(43)

In addition, for RIS reflection coefficient iteration, problem (26) will be reformulated as

$$\underset{\mathbf{\theta }}{\max } R_u({\mathbf{p}}^{\left(\eta +1\right)},\mathbf{\theta })={\log }_2\left(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2{p}_u}{{{\sigma }_t^2‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta +1\right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right)$$

(44a)

$$\mathrm{s}.\mathrm{t}. {\gamma }_{s,min}\le {\displaystyle \frac{{\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right){\mathbf{p}}^{\left(\eta +1\right)}‖}^2}{{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta +1\right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}},$$

(44b)

$$\left|{\theta }_K\right|=1, \forall K,$$

(44c)

By following the same method as in Equations (27) and (28), the concave lower limit of Equation (44a) can be obtained from [41]

$$\begin{gathered} {\log }_2(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2{p}_u}{{\sigma }_t^2\upsilon \zeta +{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta +1\right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}})\ge {\log }_2(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{(\eta )}\right)‖}^2{p}_u}{{\sigma }_t^2{\upsilon }^{(\eta )}{\zeta }^{(\eta )}+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta +1\right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}) \\ +{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{\left(\eta \right)}\right)‖}^2{p}_u}{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{\left(\eta \right)}\right)‖}^2{p}_u+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta +1\right)}‖}^2+{\sigma }_t^2{\upsilon }^{\left(\eta \right)}{\zeta }^{\left(\eta \right)}+{\sigma }_u^2{\mathrm{I}}_N}} \\ \times \left(2-{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left({\mathbf{\theta }}^{\left(\eta \right)}\right)‖}^2}{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2}}-{\displaystyle \frac{{\sigma }_t^2(\frac{{\upsilon }^{\left(\eta \right)}{\zeta }^2}{2{\zeta }^{\left(\eta \right)}}+\frac{{\zeta }^{\left(\eta \right)}{\upsilon }^2}{2{\upsilon }^{\left(\eta \right)}})+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta +1\right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}{{\sigma }_t^2{\upsilon }^{\left(\eta \right)}{\zeta }^{\left(\eta \right)}+{‖{\mathbf{H}}_{\mathrm{S}\mathrm{I}}{\mathbf{p}}^{\left(\eta +1\right)}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right) \\ :={R_u}^{\left(\eta \right)}\left(\mathbf{\theta }|{\mathbf{p}}^{\left(\eta +1\right)}\right). \end{gathered}$$

(45)

Given the other variables, the updates of $r_b$ and $r_c$ still maintain a similar form as in problem (37). Therefore, Algorithm 1 can be used to solve the problem of imperfect SIC scenarios.

5. Results and Discussion

In this section, the advantages of the proposed RIS-assisted JCSMC framework are validated by presenting the simulation results. The communication bandwidth is set to $B=30$ MHz. We assume that the BS is equipped with $N=8$ antennas, and the number of RIS elements is $K=20$. Assuming there is an expected target at the $-45°$ angle of BS, RIS is located at the $-30°$ angle of BS, and UE is located at the $-90°$ angle of BS. We use distance-dependent path loss models [49] and set the path loss exponents for the BS–RIS, RIS–target, RIS–UE, BS–target, BS–CS, and BS–UE links as 2.2, 2.1, 2.4, 2.5, 3.5, and 2.7, respectively [50]. The parameter settings in the simulation are as follows: $d_{BU}=60 \mathrm{m}, { d}_{BT}=50 \mathrm{m}, \mathrm{a}\mathrm{n}\mathrm{d} d_{BR}=40 \mathrm{m},$ where $d_{BU}, d_{BT},$ and $d_{BR}$ represent the distances of the BS–UE, BS–target, and BS–RIS, respectively. The noise power at the BS and the CS receivers is set to be ${\sigma }_u^2 ={\sigma }_d^2=-80$ dBm and the RCS as ${\sigma }_t^2=1$. For the computation task, we set $\varphi =3 \times {10}^3$ cycle/bit and $\mathcal{m}={10}^{-26}$ [51]. The residual SI channel is modeled as ${\mathbf{H}}_{\mathrm{S}\mathrm{I}}\left(i,j\right)=\sqrt{p_{\mathrm{S}\mathrm{I}}}{e}^{-\mathrm{j}{\displaystyle \frac{2\pi }{\lambda }}{d}_{i,j}}$, where $p_{\mathrm{S}\mathrm{I}}$ and $d_{i,j}$ denote the power of the residual SI and the distance between the $i$-th transmit antenna and the $j$-th receive antenna, respectively. For simplicity, we set $p_{\mathrm{S}\mathrm{I}}=-110 \mathrm{d}\mathrm{B}$ and let $e^{-\mathrm{j}{\displaystyle \frac{2\pi }{\lambda }}{d}_{i,j}}$ be a unit modulus variable with a random phase [48].

To validate the effectiveness and advantages of the proposed RIS-assisted JCSMC framework (referred to as “proposed”), we have selected the following benchmark schemes for analysis and comparison.

• No RIS-assisted scheme: This benchmark scheme is designed as a JCSMC framework without RIS assistance. By comparing with the proposed framework, the effect of introducing RIS can be demonstrated.
• BS-only/CS-only computing scheme (single-tier computation): This scheme considers a single-tier computation structure, where computation tasks from the UE are only processed on the BS or CS.
• Comm-only scheme: This benchmark scheme does not consider target sensing. Using the proposed framework for multi-tier computational optimization of BS and CS, consider only the UE communication function.
• The MRT scheme: MRT technology is a classic maximum ratio algorithm for multiple transmitting antennas and multiple receiving antennas [52,53], often used in the transmit beamforming model of ISAC. In the MRT scheme, the complexity of active beamforming is reduced, which can be represented as

$${\mathbf{p}}^{MRT}={\displaystyle \frac{\sqrt{\beta }{\mathbf{h}}_t}{‖{\mathbf{h}}_t‖}},$$

(46)

where $\beta$ is the power level.

Thus, the available spectrum efficiency from the UE to the BS can be represented by

$${R_u}^{MRT}={\log }_2\left(1+{\displaystyle \frac{{‖\widehat{\mathbf{h}}\left(\mathbf{\theta }\right)‖}^2{p}_u}{\beta {\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right)\frac{{\mathbf{h}}_t}{‖{\mathbf{h}}_t‖}‖}^2+{\sigma }_u^2{\mathrm{I}}_N}}\right) ,$$

(47)

Furthermore, the available spectrum efficiency from the BS to the CS can be represented by

$${R_d}^{MRT}={\log }_2\left(1+{\displaystyle \frac{{\beta ‖{\mathbf{h}}_d^H\frac{{\mathbf{h}}_t}{‖{\mathbf{h}}_t‖}‖}^2}{{\sigma }_u^2{\mathrm{I}}_N}}\right),$$

(48)

Then, the sensing SINR constraints can be represented by

$${{\gamma }_s}^{MRT}={\displaystyle \frac{\beta {\sigma }_t^2{‖{\widehat{\mathbf{H}}}_s\left(\mathbf{\theta }\right)\frac{{\mathbf{h}}_t}{‖{\mathbf{h}}_t‖}‖}^2}{{\sigma }_u^2{\mathrm{I}}_N}},$$

(49)

The related optimization problems can be solved by using Algorithm 1.

• Imperfect SIC scheme: This benchmark scheme considers the RIS-assisted JCSMC framework in imperfect SIC scenarios. To distinguish imperfect SIC scenarios, we label them with “proposed/SI”.

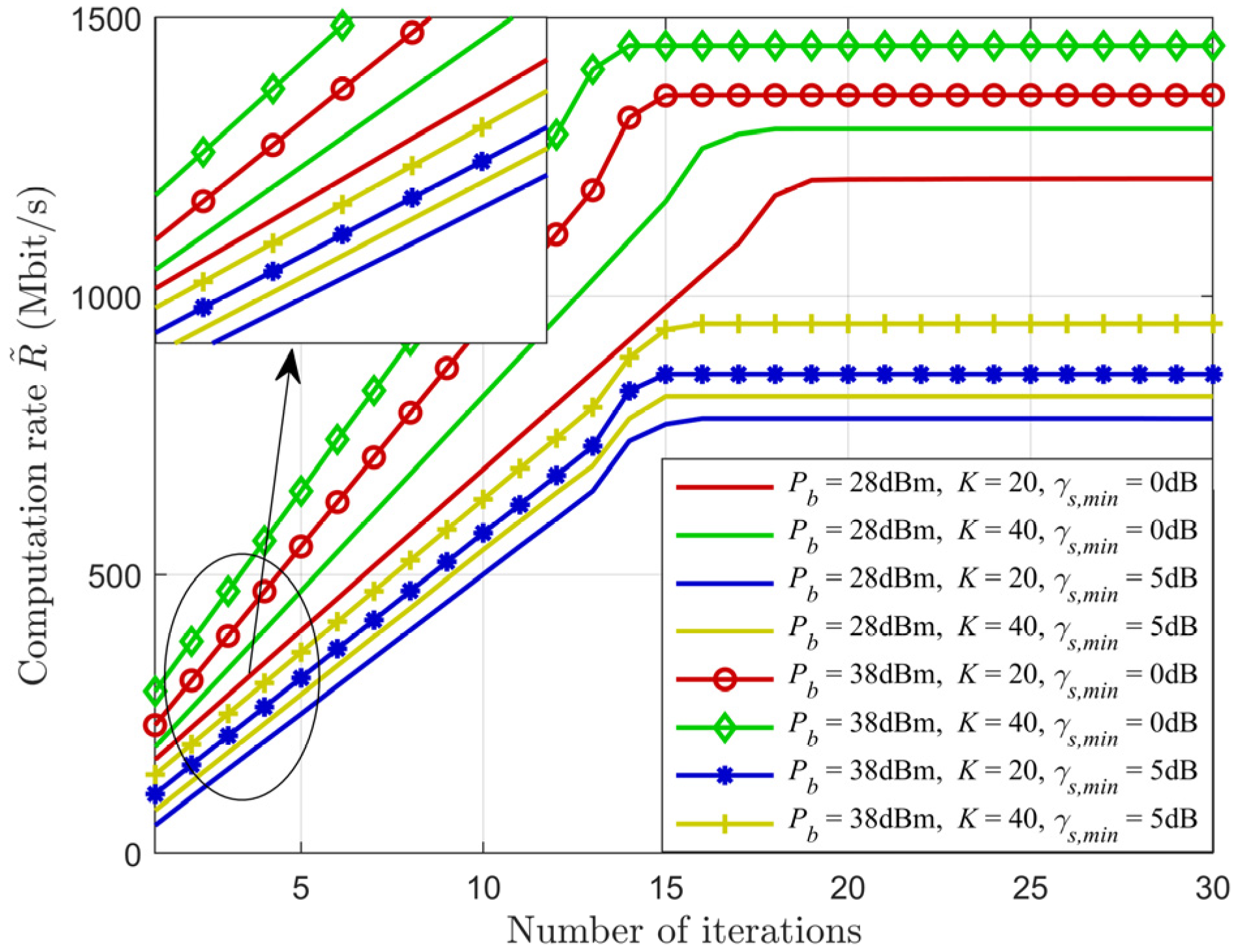
5.1. Convergence Performance of the Proposed Algorithm

In Figure 2, the convergence performance of Algorithm 1 is shown. It can be observed that Algorithm 1 converges within 20 iterations, and the computation rate $\tilde{R}$ obtained from subsequent iterations does not increase, which verifies the fast convergence and effectiveness of the proposed algorithm. By comparing different settings, it can be observed that increasing the RIS reflection elements $K$ under the same conditions can improve the total computation rate $\tilde{R}$. This confirms the benefits of RIS mentioned in Remark 2, where more reflective elements in RIS provide greater passive beamforming gain, allowing them to manipulate the propagation environment with greater degrees of freedom, thereby improving the system’s computation rate. Meanwhile, it can be observed that changes in the sensing SINR constraints ${\gamma }_{s,min}$ and the BS transmission power budget $P_b$ both affect the total computation rate $\tilde{R}$.

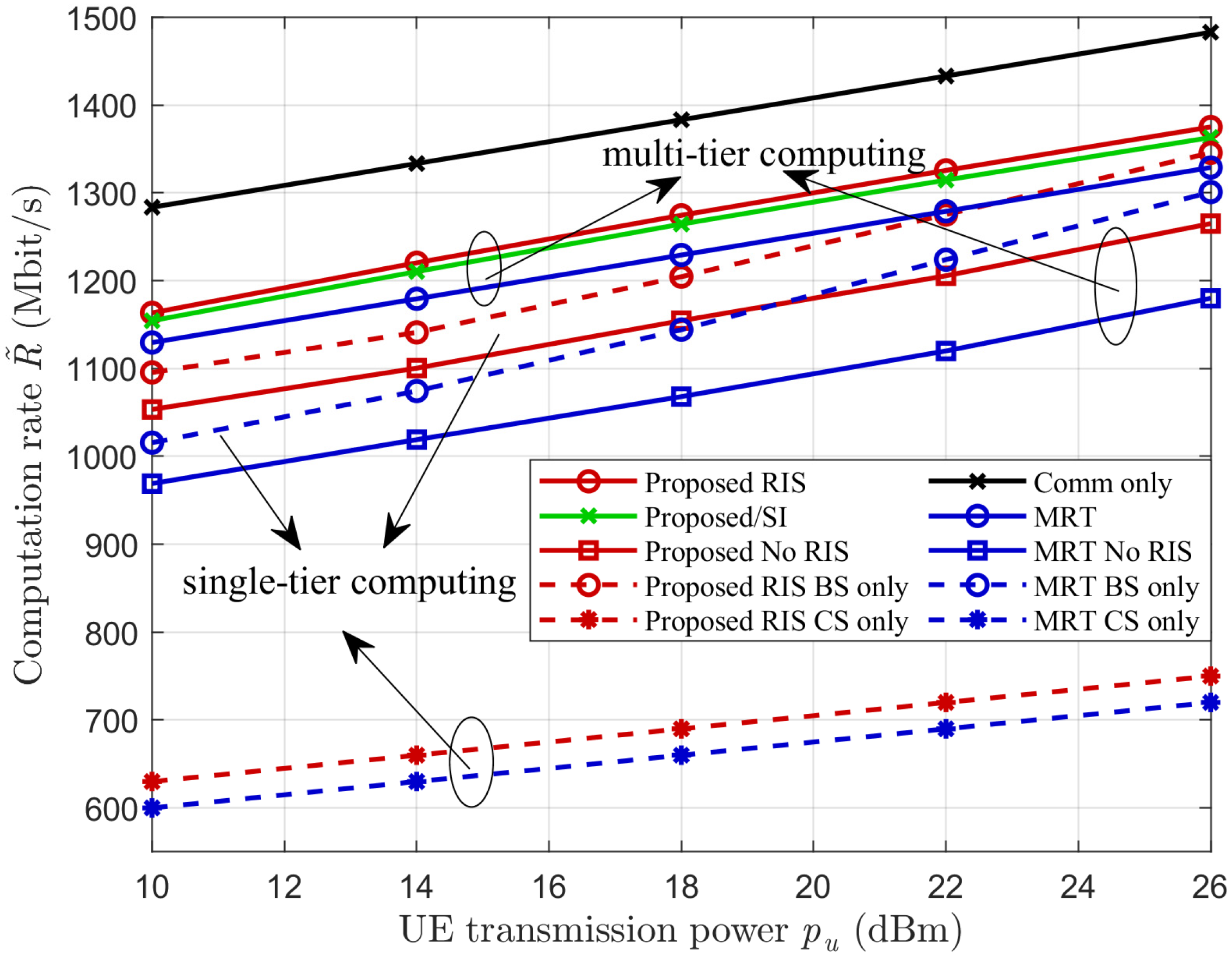
5.2. Computation Rate Versus the UE Transmission Power

In Figure 3, the relationship between computation rate $\tilde{R}$ and UE transmission power ${ p}_u$ under the different schemes is shown. It can be observed that the computation rate increases with the increase in the UE transmission power. This is because increasing the transmission power of the UE results in a higher received signal strength at the BS, thereby improving computational performance. As analyzed in Remark 1, without considering target sensing, the BS can use all power for computing. Therefore, the “Comm-only” scheme can achieve the best computation rate. Meanwhile, regardless of whether RIS is used or not, the proposed scheme is much better than the MRT scheme, reflecting the advantages of the proposed scheme. It is clear that residual SI causes certain performance losses to the proposed scheme. Additionally, it can be observed that the proposed MTC framework achieves significant performance improvements compared to the single-tier “BS-only/CS-only” framework. Taking $p_u=18$ (dBm) as an example, the computation rate $\tilde{R}$ of the proposed MTC framework is approximately 16% higher than that of the “BS-only” framework and about 95% higher than that of the “CS-only” framework. It reflects the important role of the MTC framework in improving computational efficiency.

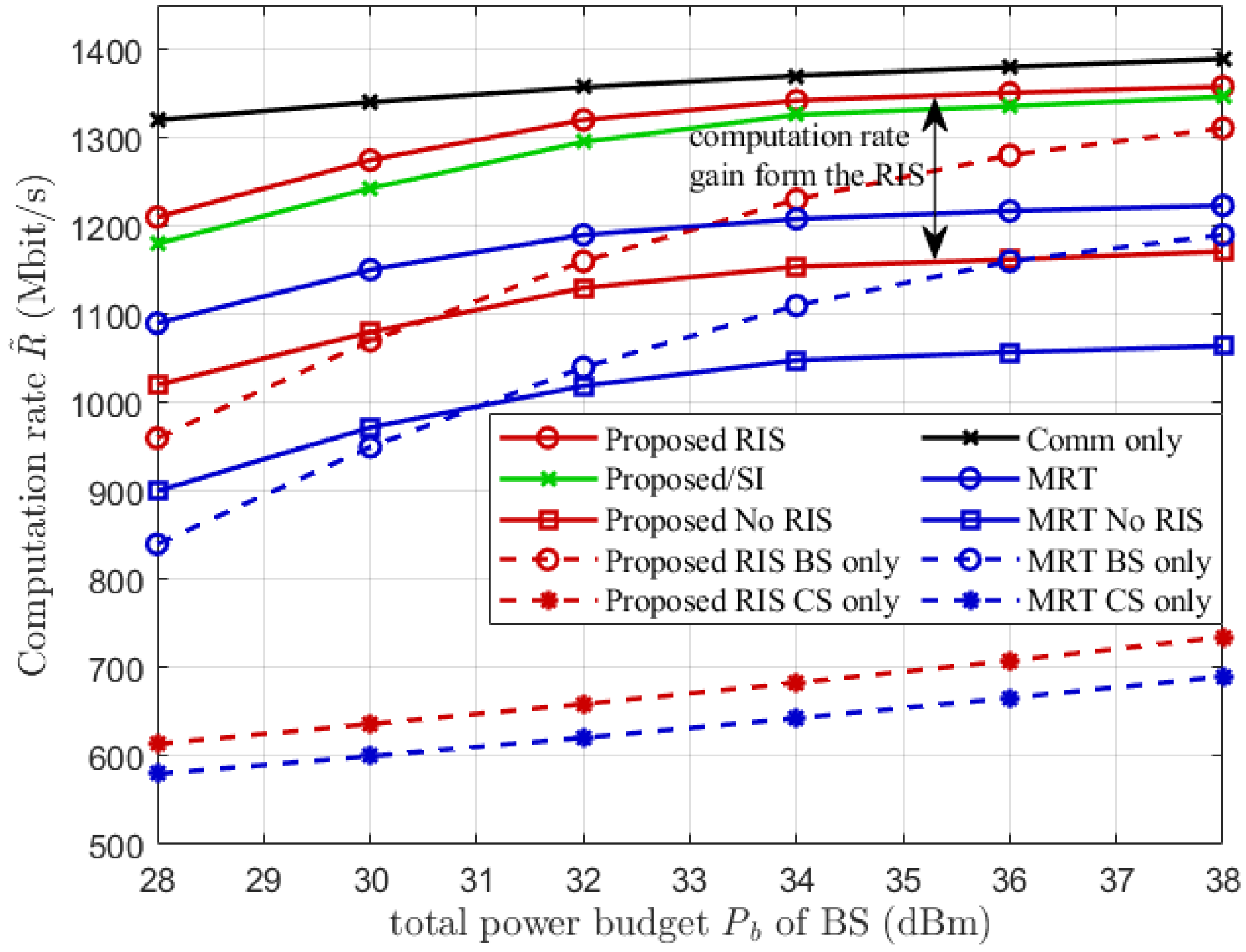
5.3. Computation Rate Versus the Total Power Budget of BS

In Figure 4, the relationship between the computation rate $\tilde{R}$ and the BS available total power budget $P_b$ under the different schemes is shown. The experimental results indicate that, with the increase in $P_b$, the proposed scheme and all the benchmark schemes can achieve higher computation rates. This is because the BS has more resources available for computation and offloading, based on satisfying sensing SINR constraints. Meanwhile, due to the introduction of RIS, the upper limit of the proposed scheme’s computation rate is higher than that of the other benchmark schemes, which is consistent with the analysis in Remark 2. Taking $P_b=34$ (dBm) as an example, the computational rate of the proposed scheme is approximately 18% higher than that of the “No RIS-assisted” scheme. However, as $P_b$ increases, the growth of the computation rate will slow down, because it is limited by the spectrum efficiency $R_u$ from the UE to the BS. Additionally, when $P_b$ is large enough, the BS has sufficient power to support computation and sensing functions, so the “BS-only” scheme gradually approaches the proposed scheme.

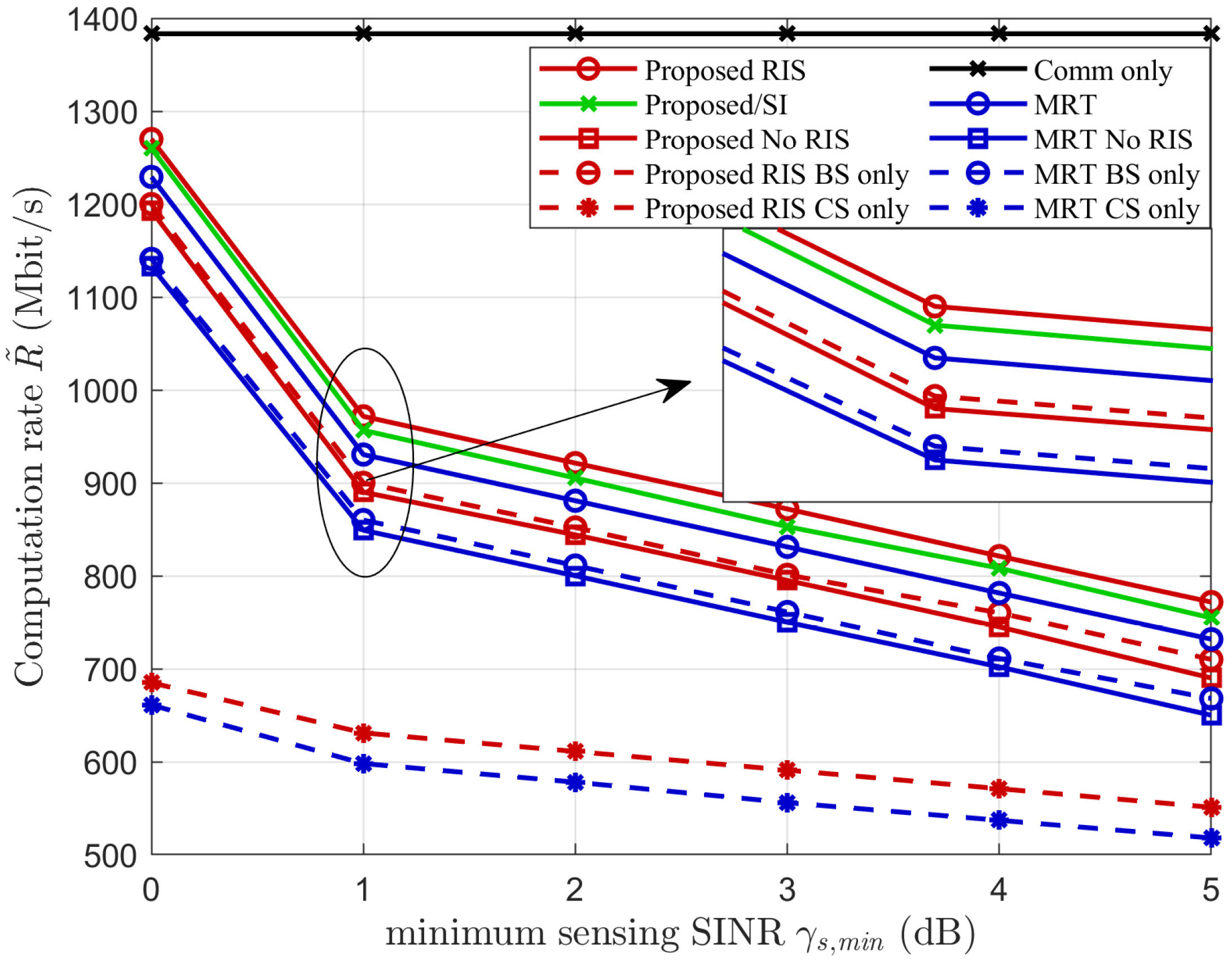
5.4. Computation Rate Versus Minimum Sensing SINR Constraint

In Figure 5, the relationship between the computation rate $\tilde{R}$ and the minimum sensing SINR constraints ${\gamma }_{s,min}$ under the different schemes is shown. It can be observed that the computation rate of all the schemes decreases with the increase of ${\gamma }_{s,min}$. This fully confirms the trade-off between computational power and sensing performance, as analyzed in Remark 1. It can also be observed that, although constrained by sensing SINR, the proposed scheme fully utilizes the computing resources of the BS and the CS, thus achieving the best performance. Meanwhile, the proposed scheme significantly outperforms the “CS-only/BS-only” schemes. This intuitively demonstrates the advantages of MTC structures when the single-tier computing power is insufficient. Furthermore, the introduction of RIS enables the proposed scheme to achieve a much higher computation rate than the “No RIS-assisted” scheme. As analyzed in Remark 2, this result validates the benefits of RIS in the JCSMC framework.

6. Conclusions

In this paper, a RIS-assisted Joint Communication, Sensing, and Multi-tier Computing framework was considered. By adapting to real-world scenarios, partial offloading modes were selected while modeling the problem of maximizing the computation rate based on causal relationships between communication and computation, sensing SINR, and other constraints. This problem was solved through algorithms such as IA and BCA, and simulation results verified the advantages of the proposed algorithm. The simulation results indicated that the introduction of RIS is crucial in ensuring the computing power and sensing performance of the system, demonstrating its advantages. Meanwhile, in cases where BS resources are limited, compared to single-tier computing, MTC structures can significantly improve the system’s computing rate, proving the advantages of the proposed framework. In the future, we will consider studying more complex practical application scenarios, such as multiple communication UEs or multiple sensing targets (including interference targets), and further discuss potential issues such as the computational overhead, real-time implementation challenges, and practical deployment.