Performance Modeling of Cloud Systems by an Infinite-Server Queue Operating in Rarely Changing Random Environment

Abstract

This paper considers a heterogeneous queuing system with an unlimited number of servers, where the parameters are determined by a random environment. A distinctive feature is that the parameters of the exponential distribution of the request processing time do not change their values until the end of service. Thus, the devices in the system under consideration are heterogeneous. For the study, a method of asymptotic analysis is proposed under the condition of extremely rare changes in the states of the random environment. We consider the following problem. Cloud node accepts requests of one type that have a similar intensity of arrival and duration of processing. Sometimes an input scheduler switches to accept requests of another type with other intensity and duration of processing. We model the system as an infinite-server queue in a random environment, which influences the arrival intensity and service time of new requests. The random environment is modeled by a Markov chain with a finite number of states. Arrivals are modeled as a Poisson process with intensity dependent on the state of the random environment. Service times are exponentially distributed with rates also dependent on the state of the random environment at the time moment when the request arrived. When the environment changes its state, requests that are already in the system do not change their service times. So, we have requests of different types (serviced with different rates) present in the system at the same time. For the study, we consider a situation where changes of the random environment are made rarely. The method of asymptotic analysis is used for the study. The asymptotic condition of a rarely changing random environment (entries of the generator of the corresponding Markov chain tend to zero) is used. A multi-dimensional joint steady-state probability distribution of the number of requests of different types present in the system is obtained. Several numerical examples illustrate the comparisons of asymptotic results to simulations.

1. Introduction

To study real data transmission systems, cellular networks, and cloud computing systems, the mathematical apparatus of queuing theory is used. It includes models of the process of request arrivals, operation of service devices, as well as other features such as changes in parameters of the system over time, and so on. Queueing systems with variable service and arrival rates arise naturally in practice, and therefore, one can find many classical works. Such systems in queuing theory are called queuing systems operating in a random environment [1,2,3,4]. These models more accurately reflect real processes compared to classical systems, taking into account the change in the external random environment over time and the system’s response to these changes [5,6].

One of the first works devoted to the study of queuing systems in a random environment is the 1963 publication by M. Eisen and M. Taineter [7], where a single-server system was considered under the assumption that the external environment can be in only two states. Later, in the works of Naor and U. Yechiali [8], the results were generalized to the case of an arbitrary finite number of states of the external environment.

In 1981, M. F. Newts proposed a fundamental method for analyzing queuing systems in a random Markov environment [9]. He reduced the problem of determining the characteristics of the system to solving a matrix equation, which made it possible to study the parameters of systems with dependence on the state of a Markov chain with a finite number of states.

Further development was the expansion of the class of queuing systems in a changing external environment: single- and multi-channel queuing systems [10,11], retrial queues [12], resource queues [13,14], and inventory management systems [15,16,17].

Various works consider various options for the reaction of requests to the transition of the environment to a new state. For example, in [18], a case is presented in which at the moment of the environment state changed, all requests immediately leave the system. In papers [19,20] an option is considered in which, at the moment of the environment transition to a new state, the requests existing in the system switch to the corresponding new service mode. Infinite-server queues are one of the most common models in the queueing theory and are often used to model systems with instant start of the service, such as satellite communication lines or long communication cables, or to approximate the behavior of multi-server systems. There are many works devoted to the study of infinite-server systems in both Markov [1,19,21,22,23] and semi-Markov [2,3,20,24,25] random environments.

Let us present several significant results on the methods of studying infinite-server queues operating in a random environment. In [21], the authors consider queue M/M/∞, where only the service rates are regulated by an external process, which is a Markov chain with continuous time and two states. It is shown that the number of requests in the system in the stationary mode can be written as the sum of two independent random variables, where one of these variables is Poisson. Further, B. D’Auria [24,25], using the stochastic decomposition method, showed that using the basic properties of Poisson processes, it is possible to obtain similar results for the number of requests in a similar system in the case of a non-Markov random environment. In the work of Falin G. [2], a model is considered in which a random environment affects both the rate of arrival and the service rate, which are influenced by a semi-Markov environment. To find the average number of requests in the system in the steady state, the method of supplementary variables is used. Namely, a three-dimensional Markov process is considered, the components of which are the number of customers in the system, the state of the environment, and the residual time until the next transition of the environment. This allows us to obtain an expression for the generating function of the number of customers in the system, and it can be used to calculate numerical characteristics in the steady state. In those cases when the study cannot be found by classical methods of the queueing system, asymptotic methods [19,20] are used. As a rule, these papers consider cases where the mode of servicing requests is not changed until they leave the system.

Cloud systems provide different services for users. Interaction with cloud servers is usually hidden from users under a specific user interface, so, actually, cloud servers receive only requests from this interface. There are many approaches for the mathematical modeling of cloud server operations. One of the most promising and productive approaches is using the queueing theory. In [26,27,28,29] and many other papers, different queueing models of cloud systems were considered, and various methods were provided for their study. A good and actual analysis of the queueing theory application in modeling cloud systems was done in [30].

In this paper, we consider a specific case of the models where there are several types of requests incoming to a cloud server and some input device coordinates their arrivals. We propose to model such system in the form of a heterogeneous queueing system with an unlimited number of servers operating in a random environment, allowing one to take into account the dependence of the service time on the type of the request. For the study, the method of asymptotic analysis [31] is used under the condition of extremely rare changes in the random environment. We rely on the method of asymptotic analysis but extend it to the class of heterogeneous systems operating in a random environment. The main difference from the previous work is the different services provided to different types of clients.

The rest of the paper is organized as follows. System and mathematical models are introduced in Section 2. In Section 3 we derive the main system of equations for analysis of the model. In Section 4 expressions for the evaluation of exact moments of the target distribution are obtained and analyzed. In Section 5, we apply the method of the asymptotic analysis to solve the main system of equations under the asymptotic condition of rare changes in the random environment. Finally, we perform numerical analysis of the precision of the solution to find its error and applicability area in Section 6.

2. Mathematical Model of M/M/∞ in Markov Random Environment

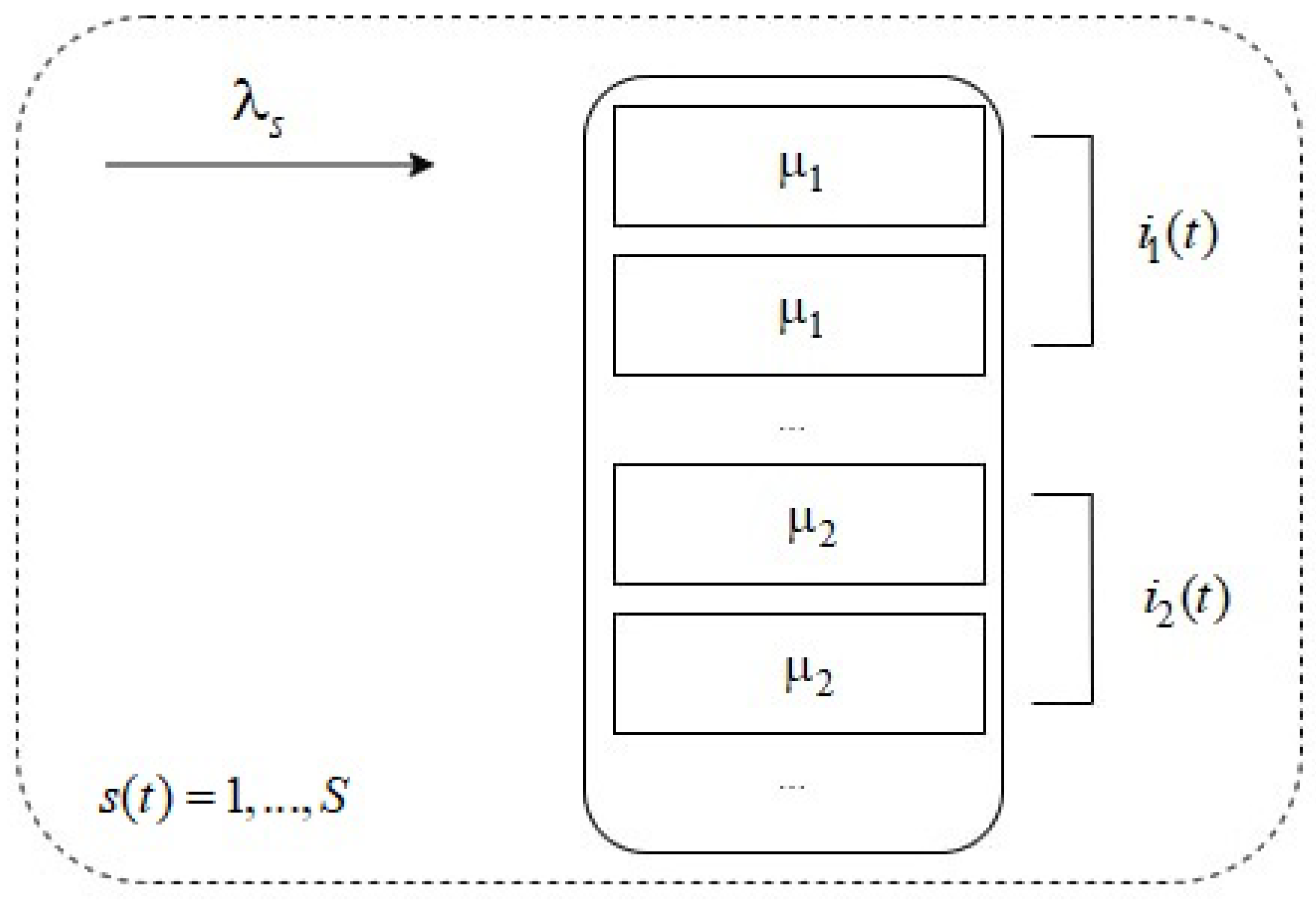
Consider a cloud server that performs some operations according to incoming requests. The execution of these requests and further operations take some time and occupy some hardware resources of the server. In this paper, we consider only computational resources—CPU cores that are used for the execution of requests. We consider a situation where the server executes one type of request for a long time. The ‘type’ can be referred to as the main characteristics of the requests execution: average intensity of their arrivals, average execution time, and so on. Sometimes, an input device (e.g., balancer) switches the server to accept requests of another type. The problem is to find the distribution characteristics of the requests of different types present in the system. Such analysis can give some helpful information for the server owner, for example, how many cores can be required simultaneously for the execution of requests, how many other types of resources (like RAM, disk space, etc.) should be provided for the normal operation of the server if requirements for resources depend on the types of requests, and so on. We propose to use a heterogeneous infinite-server queue operating in a random environment for modeling the described system.

So, let us consider the following heterogeneous queueing system M/M/∞ operating in a Markov random environment (Figure 1).

The process of changing the states of the external environment is a continuous Markov process $s\left(t\right)$ with finite number of states $s=1,\dots ,S$, which is determined by a generator matrix $\mathbf{Q}=\left[q_{ij}\right],i,j=1,\dots ,S.$ The state of the environment determines the intensity of the arrival process, the values of which take the values ${\lambda }_s\ge 0$.

The discipline of servicing the incoming requests is also determined by the state of the environment at the time of the request arrival. If the environment is in the state $s\left(t\right)=s$, then the request is serviced during a random time distributed according to the exponential law with parameter ${\mu }_s:$$F_n\left(x\right)=1-e^{-{\mu }_{s}x}$. The service time is not changed while the request is serviced, even if the random environment changes its state. Thus, the system simultaneously services requests with different service parameters, which is why such systems are called heterogeneous [32,33]. Such systems more adequately describe the processes of information transfer, but their study is significantly complicated due to the multi-dimensionality of the process being studied. Let us denote the number of requests of type s (serviced with parameter ${\mu }_s$) at time moment t by $i_s\left(t\right)$.

The problem is to study multi-dimensional Markov random process $\{i_1\left(t\right),i_2\left(t\right),\dots ,$$i_S\left(t\right),s\left(t\right)\}$, namely, to find its multi-dimensional joint probability distribution.

3. Kolmogorov Equations

Let us introduce the notation.

$$P(\mathbf{i},s,t)=P(i_1,i_2,\dots ,i_S,s,t)=Pr\{i_1\left(t\right)=i_1,i_2\left(t\right)=i_2,\dots ,i_S\left(t\right)=i_S,s\left(t\right)=s\},$$

and the notations for the row vectors

$${\mathbf{e}}_1=[1,0,\dots ,0],{\mathbf{e}}_2=[0,1,\dots ,0],\dots ,{\mathbf{e}}_s=[0,0,\dots ,1],s=1,\dots ,S.$$

Let us use the total probability formula and compose a system of equations for all $i\ge 0$ and $s=1,\dots ,S$:

$$P(\mathbf{i},s,t+\mathsf{\Delta }t)=P(\mathbf{i},s,t)(1-{\lambda }_s\mathsf{\Delta }t)(1+q_{ss}\mathsf{\Delta }t)(1-i_1{\mu }_1\mathsf{\Delta }t)\dots (1-i_S{\mu }_S\mathsf{\Delta }t)+$$

$$P(\mathbf{i}-{\mathbf{e}}_s,s,t){\lambda }_s\mathsf{\Delta }t+\sum _{\nu =1}^{S}P(\mathbf{i}+{\mathbf{e}}_{\nu },s,t)(i_{\nu }+1){\mu }_{\nu }\mathsf{\Delta }t+\sum _{v\ne s}P(\mathbf{i},v,t)q_{vs}\mathsf{\Delta }t+o\left(\mathsf{\Delta }t\right),$$

where

• $q_{vs}\mathsf{\Delta }t$ is the probability that the environment changes its state from v to s during time interval $\mathsf{\Delta }t$;
• ${\lambda }_s\mathsf{\Delta }t$ is the probability of a new request arrival during time interval $\mathsf{\Delta }t$ when the environment is in state s;
• $i_s{\mu }_s\mathsf{\Delta }t$ is the probability that one of the $i_s$ requests of type s finishes its service;
• $(1-{\lambda }_s\mathsf{\Delta }t)(1+q_{ss}\mathsf{\Delta }t)(1-i_1{\mu }_1\mathsf{\Delta }t)\dots (1-i_S{\mu }_S\mathsf{\Delta }t)$ is the probability that nothing happens in the system during time interval $\mathsf{\Delta }t$ when the environment is in state s and the number of requests of the corresponding types present in the system are the components of vector $\mathbf{i}$.

Let us divide each equation by $\mathsf{\Delta }t$ and make limit transition $\mathsf{\Delta }t\to 0$; then the system takes the form

$${\displaystyle \frac{\partial P(\mathbf{i},s,t)}{\partial t}}=-P(\mathbf{i},s,t)({\lambda }_s+\sum _{\nu =1}^S{\mu }_{\nu }{i}_{\nu })+{\lambda }_{s}P(\mathbf{i}-{\mathbf{e}}_s,s,t)+$$

$$+\sum _{\nu =1}^S{\mu }_{\nu }(i_{\nu }+1)P(\mathbf{i}+{\mathbf{e}}_{\nu },s,t)+\sum _{v\ne s}{q}_{vs}P(\mathbf{i},s,t)$$

with initial conditions

$$P(s,i_1,\dots ,i_S,t_0)=\left\{\begin{array}{c}{r}_s,\mathrm{i}\mathrm{f}{i}_1=\dots =i_S=0,\hfill \\ 0,\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\hfill \end{array}\right.$$

(1)

where $\mathbf{r}=[r_1,r_2,\dots ,r_S]$ is a row vector of the stationary probability distribution of the Markov chain $s\left(t\right)$, which can be evaluated from the system of linear equations

$$\{\begin{array}{c}\mathbf{rQ}=\mathbf{0},\\ \mathbf{re}=1.\end{array}$$

(2)

Here and below $\mathbf{e}$ is a column vector which consists of ones.

Suppose that the system has a stationary regime, then we can write the system of linear equations for the stationary probabilities:

$$0=-P(\mathbf{i},s)({\lambda }_s+\sum _{\nu =1}^S{\mu }_{\nu }{i}_{\nu })+{\lambda }_{s}P(\mathbf{i}-{\mathbf{e}}_s,s)+\sum _{\nu =1}^S{\mu }_{\nu }(i_{\nu }+1)P(\mathbf{i}+{\mathbf{e}}_{\nu },s)+\sum _{v\ne s}{q}_{vs}P(\mathbf{i},v),$$

(3)

where $P(\mathbf{i},s)$ is the stationary probability distribution of the random process under consideration.

For further study, we use the method of characteristic functions. Let us denote

$$H(u_1,u_2,\dots ,u_s,s)=H(\mathbf{u},s)=\sum _{i_1}{e}^{j{u}_1{i}_1}\sum _{i_2}{e}^{j{u}_2{i}_2}\dots \sum _{i_S}{e}^{j{u}_S{i}_S}P(\mathbf{i},s).$$

$H(u_1,u_2,\dots ,u_s,s)$ are the partial characteristic functions of the stationary probability distribution of the number of requests in the system. Using matrix notations

$$\mathbf{h}\left(\mathbf{u}\right)=\left[H(\mathbf{u},1),\dots ,H(\mathbf{u},S)\right],$$

$$\mathbf{m}\left(\mathbf{u}\right)=\left[{\mu }_1(e^{-j{u}_1}-1),\dots ,{\mu }_S(e^{-j{u}_S}-1)\right],$$

$${\displaystyle \frac{\partial \mathbf{h}\left(\mathbf{u}\right)}{\partial \mathbf{u}}}=\left[\begin{array}{ccc}\frac{\partial H(\mathbf{u},1)}{\partial u_1}& \dots & \frac{\partial H(\mathbf{u},S)}{\partial u_1}\\ \dots & \dots & \dots \\ \frac{\partial H(\mathbf{u},1)}{\partial u_S}& \dots & \frac{\partial H(\mathbf{u},S)}{\partial u_S}\end{array}\right]$$

$$\mathsf{\Lambda }\left(\mathbf{u}\right)=\left[\begin{array}{cccc}{\lambda }_1(e^{j{u}_1}-1)& 0& \dots & 0\\ 0& {\lambda }_2(e^{j{u}_2}-1)& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & {\lambda }_S(e^{j{u}_S}-1)\end{array}\right].$$

Finally, we can write the system of Kolmogorov Equation (3) in the matrix form for characteristic functions:

$${\displaystyle j\mathbf{m}\left(\mathbf{u}\right)\frac{\partial \mathbf{h}\left(\mathbf{u}\right)}{\partial \mathbf{u}}=\mathbf{h}\left(\mathbf{u}\right)\left[\mathsf{\Lambda }\left(\mathbf{u}\right)+\mathbf{Q}\right].}$$

(4)

4. Evaluating Exact Moments of the Distribution

Using the properties of characteristic functions, we can determine the exact values of moments of the probability distribution of the number of requests of different types present in the system, including correlation coefficients.

To find the mathematical expectation of the number of requests of each type, we differentiate each equation of system (4) with respect to all variables $u_s,s=1,2,\dots ,K$. We obtain a system of differential equations, which we write in matrix form

$$j{\displaystyle \frac{\partial \mathbf{m}\left(\mathbf{u}\right)}{\partial \mathbf{u}}}{\displaystyle \frac{\partial \mathbf{h}\left(\mathbf{u}\right)}{\partial \mathbf{u}}}+j\mathbf{m}\left(\mathbf{u}\right){\displaystyle \frac{{\partial }^2\mathbf{h}\left(\mathbf{u}\right)}{\partial {\mathbf{u}}^2}}=\left[\mathsf{\Lambda }\left(\mathbf{u}\right)+\mathbf{Q}\right]{\displaystyle \frac{\partial \mathbf{h}\left(\mathbf{u}\right)}{\partial \mathbf{u}}}+{\displaystyle \frac{\partial \mathsf{\Lambda }\left(\mathbf{u}\right)}{\partial \mathbf{u}}}\mathbf{h}\left(\mathbf{u}\right),$$

(5)

where

$${\displaystyle \frac{\partial \mathbf{m}\left(\mathbf{u}\right)}{\partial \mathbf{u}}}=-j\left[\begin{array}{cccc}{\mu }_1{e}^{-j{u}_1}& 0& \dots & 0\\ 0& {\mu }_2{e}^{-j{u}_2}& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & {\mu }_S{e}^{-j{u}_S}\end{array}\right],$$

$${\displaystyle \frac{\partial \mathsf{\Lambda }\left(\mathbf{u}\right)}{\partial \mathbf{u}}}=j\left[\begin{array}{cccc}{\lambda }_1{e}^{j{u}_1}& 0& \dots & 0\\ 0& {\lambda }_2{e}^{j{u}_2}& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & {\lambda }_S{e}^{j{u}_S}\end{array}\right].$$

Let us substitute $u_s=0,s=1,2,\dots ,S$ and introduce the notations

$${\displaystyle \frac{\partial H(\mathbf{0},s)}{\partial u_k}}={\left.{\displaystyle \frac{\partial H(\mathbf{u},s)}{\partial u_k}}\right|}_{u_1,\dots ,u_S=0}=\sum _{i_1}\dots \sum _{i_S}{i}_{k}P(\mathbf{i},s)=j{m}_1^k\left(s\right),k=1,2,\dots ,S.$$

Here $m_1^k\left(s\right)$ are partial moments of the first order, i.e., the average number of requests of the k-th type when the random environment is in state s.

$${\displaystyle \frac{\partial \mathbf{h}\left(\mathbf{0}\right)}{\partial \mathbf{u}}}=j{\mathbf{M}}_{\mathbf{1}}=j\left[\begin{array}{ccc}{m}_1^1\left(1\right)& m_1^1\left(2\right)\dots & m_1^1\left(S\right)\\ m_1^2\left(1\right)& m_1^2\left(2\right)\dots & m_1^1\left(S\right)\\ \dots & \dots & \dots \\ m_1^S\left(1\right)& m_1^S\left(2\right)\dots & m_1^S\left(S\right)\end{array}\right],$$

$$\mathbf{A}={\displaystyle \frac{\partial \mathbf{m}\left(\mathbf{0}\right)}{\partial \mathbf{u}}}=\left[\begin{array}{cccc}{\mu }_1& 0& \dots & 0\\ 0& {\mu }_2& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & {\mu }_S\end{array}\right],$$

$$\mathsf{\Lambda }={\displaystyle \frac{\partial \mathsf{\Lambda }\left(\mathbf{0}\right)}{\partial \mathbf{u}}}=\left[\begin{array}{cccc}{\lambda }_1& 0& \dots & 0\\ 0& {\lambda }_2& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & {\lambda }_S\end{array}\right],$$

$$\mathbf{R}=\left[\begin{array}{cccc}{r}_1& 0& \dots & 0\\ 0& r_2& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & r_S\end{array}\right].$$

Entries of matrix $\mathbf{R}$ are determined from the stationary probabilities of the states of the Markov chain (2).

As a result, we derive the following matrix equation for evaluating the first raw moments:

$$\mathbf{A}{\mathbf{M}}_1-{\mathbf{M}}_1\mathbf{Q}=\mathbf{R}\mathsf{\Lambda }.$$

Let us multiply both parts of the equation by vector $\mathbf{e}$; we obtain

$${\mathbf{M}}_1\mathbf{e}={\mathbf{A}}^{-1}\mathbf{R}\mathsf{\Lambda }\mathbf{e}.$$

It follows that the mathematical expectation of the number of requests of the k-th type is calculated by the expression

$$\mathrm{E}\left\{i_k\right\}=m_1^{\left(k\right)}={\displaystyle \frac{{\lambda }_k{r}_k}{{\mu }_k}}.$$

In a similar way, we can find raw moments of the second order. They are determined by expressions.

$$\mathrm{E}\left\{i_k^2\right\}=m_2^{\left(k\right)}={\displaystyle \frac{(2{\lambda }_k+{\mu }_k)m_1^{\left(k\right)}\left(k\right)+{\lambda }_k{r}_k}{2{\mu }_k}}$$

for all $k=1,\dots ,S.$

It is easy to obtain that the raw correlation moment for values of $i_k$ and $i_s$ is determined by the expression.

$$\mathrm{E}\left\{i_k{i}_s\right\}=m_2^{ks}={\displaystyle \frac{{\lambda }_k{m}_1^s\left(k\right)+{\lambda }_s{m}_1^k\left(s\right)}{{\mu }_s+{\mu }_k}}.$$

A detailed description of the derivation of this formula for the special case of $S=2$ can be found in [33].

Thus, the obtained formulas allow us to find exact values of the first- and second-order moments for the stationary distribution of the multi-dimensional random process of the number of requests of different types present in the system.

Obviously, the components of this multi-dimensional random process are dependent random variables. Let us consider how the system parameters affect the values of the correlation coefficient.

$$r^{\left(ks\right)}={\displaystyle \frac{m_2^{\left(ks\right)}-m_1^{\left(k\right)}{m}_1^{\left(s\right)}}{\sqrt{{\mathrm{Var}}^{\left(k\right)}{\mathrm{Var}}^{\left(s\right)}}}},$$

(6)

where

$${\mathrm{Var}}^{\left(l\right)}=m_2^{\left(l\right)}-{\left(m_1^{\left(l\right)}\right)}^2$$

(7)

is a variation of component l.

Consider the following numerical example. Let the random environment have three possible states, which are determined by the generator matrix

$$\mathbf{Q}=\epsilon ·\left[\begin{array}{ccc}-3& 2& 1\\ 1.& -2& 1\\ 4& 2& -6\end{array}\right],$$

(8)

where $\epsilon >0$ takes small values which reflect rare changes in the ransom environment (see Section 5 and Section 6 for details). Let the intensities of arrivals be the following:

$${\lambda }_1=1·N,{\lambda }_2=2·N,{\lambda }_3=10·N,$$

(9)

where $N>0$ takes growing values which correspond to the case of growing intensity of arrivals. Let service rates for all types of requests be equal to ${\mu }_1={\mu }_2={\mu }_3=1$.

Numerical calculations show that the absolute value of the correlation coefficient (6) increases with an increase in the intensity of the arrival process (growing of N) and rarity of changes of states of the random environment (decreasing of $\epsilon$). Values of the correlation coefficient $r^{\left(12\right)}$ of the number of requests of the first and second types present in the system are presented in

Table 1. Dependence of values of correlation coefficient $r^{\left(12\right)}$ on the parameters of intensity of the arrival process N and rarity of the random environment changing $\epsilon$.

N	$\mathit{\epsilon }$	10	1	0.1	0.01
1		−0.005	−0.044	−0.188	−0.304
10		−0.007	−0.063	−0.305	−0.582
100		−0.008	−0.066	−0.325	−0.641

.

5. Asymptotic Analysis Under Extremely Rare Changes of the Environment

The goal of this paper is to find the probability distribution $P(\mathbf{i},s)$ of the random process under consideration in the steady-state regime. To do this, we need to solve the system of Equation (4). Unfortunately, it seems impossible to solve it in a direct way. So, we apply the method of asymptotic analysis similar to [31] to find its solution. In this paper, we will find the solution under the asymptotic condition of extremely rare changes in the states of the random environment. The difference from [31] is that here we have different service rates for customers of different types in the model, which leads us to the multi-dimensional model and multidimensionality of the system of equations in several components. So, we should try to find the solution taking into account this fact. To do this, we will expand (4) by components and solve the system as a series of equations with less multidimensionality.

The average duration of the Markov chain of stay in the k-th state is determined as $T_k=-1/q_{kk}.$ So, a decrease of values $q_{kk}$ leads us to rare changes of the states of the random environment. To perform asymptotic analysis, we represent the generator of the Markov chain in the form ${\mathbf{Q}}^{\prime }=\epsilon \mathbf{Q},$ where $\mathbf{Q}$ is some infinitesimal generator matrix with finite entries and parameter $\epsilon >0$ takes small values and tends to zero in theoretical derivations. Let us substitute ${\mathbf{Q}}^{\prime }$ instead of $\mathbf{Q}$ in (4); we obtain the equation

$$j\mathbf{m}\left(\mathbf{u}\right){\displaystyle \frac{\partial \mathbf{h}\left(\mathbf{u}\right)}{\partial \mathbf{u}}}=\mathbf{h}\left(\mathbf{u}\right)\left(\mathsf{\Lambda }\left(\mathbf{u}\right)+\epsilon \mathbf{Q}\right).$$

Let $\epsilon \to 0$ here; then we obtain

$$j\mathbf{m}\left(\mathbf{u}\right){\displaystyle \frac{\partial \mathbf{h}\left(\mathbf{u}\right)}{\partial \mathbf{u}}}=\mathbf{h}\left(\mathbf{u}\right)\mathsf{\Lambda }\left(\mathbf{u}\right),$$

or in the expanded form:

$$j\left[\begin{array}{c}{\displaystyle \sum _{k=0}^S{\mu }_k(e^{-j{u}_k}-1)\frac{\partial H(\mathbf{u},1)}{\partial u_k}}\\ {\displaystyle \sum _{k=0}^S{\mu }_k(e^{-j{u}_k}-1)\frac{\partial H(\mathbf{u},2)}{\partial u_k}}\\ \dots \\ {\displaystyle \sum _{k=0}^S{\mu }_k(e^{-j{u}_k}-1)\frac{\partial H(\mathbf{u},S)}{\partial u_k}}\end{array}\right]=\left[\begin{array}{c}{\lambda }_1(e^{j{u}_1}-1)H(\mathbf{u},1)\\ {\lambda }_2(e^{j{u}_2}-1)H(\mathbf{u},2)\\ \dots \\ {\lambda }_S(e^{j{u}_S}-1)H(\mathbf{u},S)\end{array}\right].$$

Consider the first equation of the system:

$$j\sum _{k=0}^S{\mu }_k(e^{-j{u}_k}-1){\displaystyle \frac{\partial H(\mathbf{u},1)}{\partial u_k}}={\lambda }_1(e^{j{u}_1}-1)H(\mathbf{u},1).$$

(10)

We can solve this partial differential equation by the method of characteristics:

$${\displaystyle \frac{d{u}_1}{j{\mu }_1(e^{-j{u}_1}-1)}}=\dots ={\displaystyle \frac{d{u}_S}{j{\mu }_S(e^{-j{u}_S}-1)}}={\displaystyle \frac{dH(\mathbf{u},1)}{{\lambda }_1(e^{j{u}_1}-1)H(\mathbf{u},1)}}.$$

(11)

Consider the equations

$${\displaystyle \frac{d{u}_1}{{\mu }_1(e^{-j{u}_1}-1)}}={\displaystyle \frac{d{u}_s}{{\mu }_s(e^{-j{u}_s}-1)}}$$

for $s=2,\dots ,S.$ From each of them, we derive

$${\left({\displaystyle \frac{e^{j{u}_1}-1}{C_s}}\right)}^{\frac{1}{{\mu }_1}}={(e^{j{u}_s}-1)}^{\frac{1}{{\mu }_s}},$$

$$(e^{j{u}_s}-1)={\displaystyle \frac{1}{C_s}}{(e^{j{u}_1}-1)}^{\frac{{\mu }_s}{{\mu }_1}},s=2,\dots ,S.$$

Then we consider the last equation from (11):

$${\displaystyle \frac{d{u}_1}{j{\mu }_1(e^{-j{u}_1}-1)}}={\displaystyle \frac{dH(\mathbf{u},1)}{{\lambda }_1(e^{j{u}_1}-1)H(\mathbf{u},1)}}.$$

Performing the following derivations:

$${\displaystyle \frac{e^{j{u}_1}d{u}_1}{j{\mu }_1(1-e^{j{u}_1})}}={\displaystyle \frac{dH(\mathbf{u},1)}{{\lambda }_1(e^{j{u}_1}-1)H(\mathbf{u},1)}},$$

$${\displaystyle \frac{d\left(e^{j{u}_1}\right)}{j^2{\mu }_1(1-e^{j{u}_1})}}={\displaystyle \frac{dH(\mathbf{u},1)}{{\lambda }_1(e^{j{u}_1}-1)H(\mathbf{u},1)}},$$

$${\displaystyle \frac{d\left(e^{j{u}_1}\right)}{{\mu }_1}}={\displaystyle \frac{dH(\mathbf{u},1)}{{\lambda }_{1}H(\mathbf{u},1)}},$$

we obtain its solution in the form

$$H(\mathbf{u},1)={\mathsf{\Phi }}_1(C_1,\dots ,C_S)exp\left({\displaystyle \frac{{\lambda }_1}{{\mu }_1}}(e^{j{u}_1}-1)\right),$$

where ${\mathsf{\Phi }}_1(C_1,\dots ,C_S)$ is some function which can be found from the initial condition:

$${\mathsf{\Phi }}_1(C_1,\dots ,C_S)=H(\mathbf{0},1)=r_1.$$

So, we obtain the following solution of (10):

$$H(\mathbf{u},1)=r_{1}exp\left({\displaystyle \frac{{\lambda }_1}{{\mu }_1}}(e^{j{u}_1}-1)\right).$$

In a similar way, we obtain

$$H(\mathbf{u},s)=r_{s}exp\left({\displaystyle \frac{{\lambda }_s}{{\mu }_s}}(e^{j{u}_s}-1)\right)$$

for each $s=2,\dots ,S.$ Summing up all these expressions, we find the characteristic function of the joint probability distribution of the number of requests of each type:

$$h\left(\mathbf{u}\right)=h(u_1,u_2,\dots ,u_S)=\sum _{s=1}^S{r}_{s}exp\left({\displaystyle \frac{{\lambda }_s}{{\mu }_s}}(e^{j{u}_s}-1)\right).$$

(12)

One-dimensional characteristic functions of the stationary probability distribution of the number of requests of type $s,s\in \{1,\dots ,S\}$ have the form

$$h\left(u_s\right)=1-r_s+r_{s}exp\left({\displaystyle \frac{{\lambda }_s}{{\mu }_s}}(e^{{ju}_s}-1)\right).$$

(13)

Therefore, the generating function has the form

$$F_s\left(z\right)=\mathrm{E}\left\{z^{i_s}\right\}=1-r_s+r_{s}exp\left({\displaystyle \frac{{\lambda }_s}{{\mu }_s}}(z-1)\right).$$

It follows that the probability of the absence of requests of the s-th type is determined as

$${\pi }_0^{\left(s\right)}=F_s\left(0\right)=1-r_s+r_{s}exp\left(-{\displaystyle \frac{{\lambda }_s}{{\mu }_s}}\right).$$

6. Numerical Analysis

Because the result (12) is obtained under the asymptotic condition of extremely rare changes of the random environment ($\epsilon \to 0$), it is necessary to check the accuracy and find the area of applicability of this result. To do this, we can compare distributions (12) and (13) with exact (not limiting) results.

First of all, we can notice that asymptotic and exact expressions (see Section 4) for the mathematical expectation coincide. Let us compare variations of these distributions. We can do this numerically, for example from Section 4.

For comparison, let us calculate relative errors of theoretical ${\mathrm{Var}}^{\left(s\right)}$ and asymptotical ${\mathrm{Var}}_{\mathrm{as}}^{\left(s\right)}$ variances of one-dimensional distributions of $i_s,$$s\in \{1,2,3\}$:

$${\mathsf{\Delta }}^{\left(s\right)}={\displaystyle \frac{\left|{\mathrm{Var}}^{\left(s\right)}-{\mathrm{Var}}_{\mathrm{as}}^{\left(s\right)}\right|}{{\mathrm{Var}}^{\left(s\right)}}}.$$

The results of the evaluations for various values $\epsilon$ and $N=1$ are presented in

Table 2. Relative errors of asymptotic variances of the number of requests of s-th type ${\mathsf{\Delta }}^{\left(s\right)}$ for various values of asymptotic parameter $\epsilon$.

$\mathit{\epsilon }$	1	0.1	0.01	0.001
${\mathsf{\Delta }}^{\left(1\right)}$	0.481	0.293	0.059	0.007
${\mathsf{\Delta }}^{\left(2\right)}$	0.256	0.162	0.031	0.003
${\mathsf{\Delta }}^{\left(3\right)}$	1.967	0.464	0.053	0.005

. So, we can draw a conclusion that the second moments of the asymptotic distribution become more precise with the decrease of $\epsilon$ and they have enough good accuracy (about 5% and less) for $\epsilon \le 0.01$.

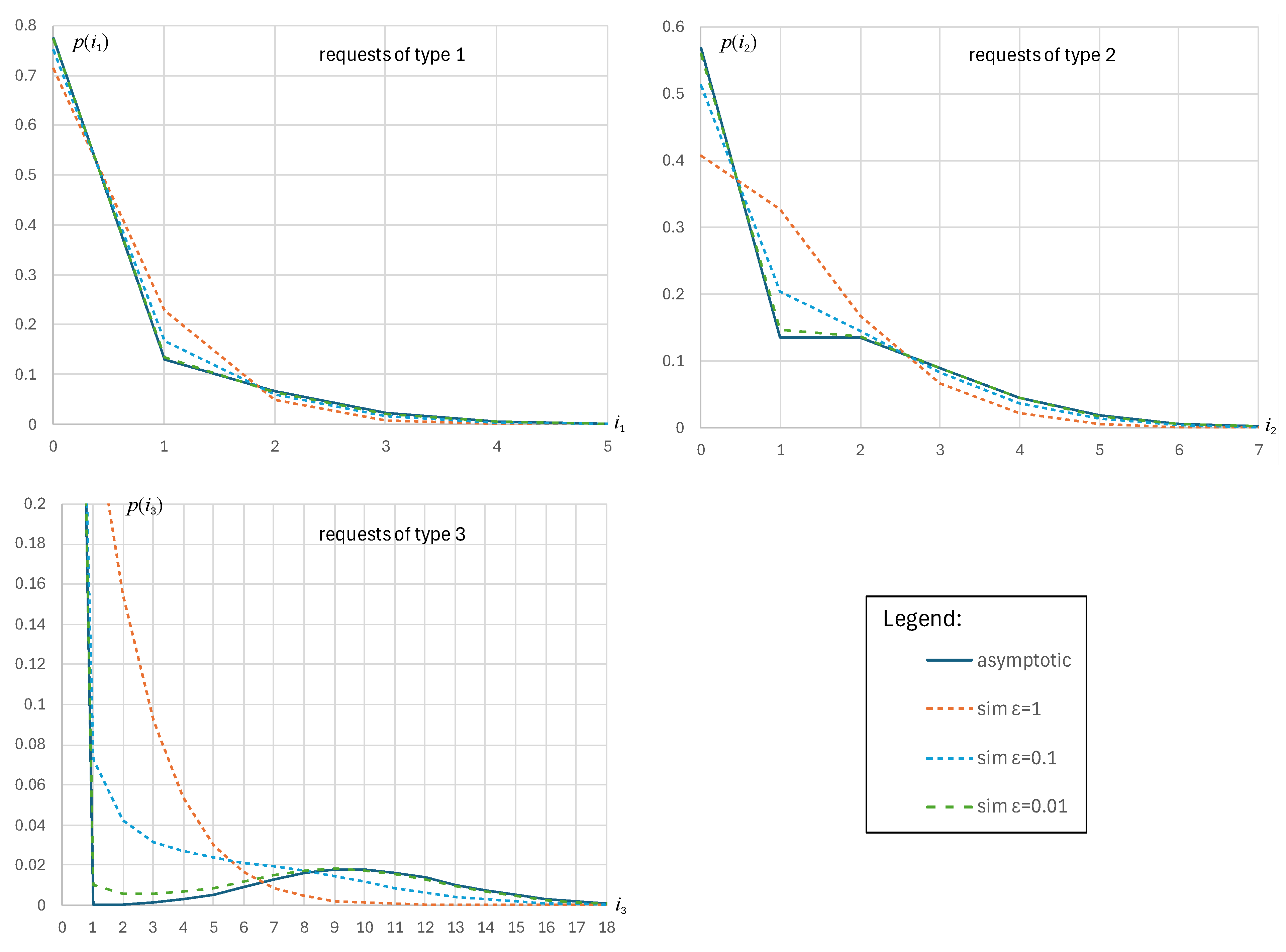
Let us study why the error of the second moments of the asymptotic distribution is so big for greater values of $\epsilon$. This follows from the probability distribution law (12) and (13): it has a jump in point $i=0$ (see solid line in Figure 2). This jump can be big enough in relation to the nearest points, and the distribution has the second mode far from 0. For example, for requests of the third type ${\pi }_0^{\left(3\right)}\approx 0.857$ while ${\pi }_1^{\left(3\right)}\approx 6.5·{10}^{-5}$, and the distribution has the second mode in points 9, 10.

For the analysis of the accuracy of the entire distribution, we performed experiments using simulation modeling. In Figure 2, you can see a graphical comparison of asymptotic distribution (it is not changed when $\epsilon$ changes its values) and probability distributions obtained from simulation results for various values of $\epsilon$.

For numerical analysis of the accuracy of asymptotic distributions (13), we use Kolmogorov distances.

$${\mathsf{\Delta }}_{\epsilon }^{\left(s\right)}=\underset{i\ge 0}{max}\left|F_{\mathrm{as}}^{\left(s\right)}\left(i\right)-F_{\epsilon }^{\left(s\right)}\left(i\right)\right|,$$

where $F_{\mathrm{as}}^{\left(s\right)}\left(i\right)$ is asymptotical one-dimensional cumulative distribution function of the number of requests of type s ($s\in \{1,2,3\}$), $F_{\epsilon }^{\left(s\right)}\left(i\right)$ is cumulative distribution function of the number of requests of type s obtained from simulation for chosen value of $\epsilon$. Values of the Kolmogorov distances evaluated for various values of $\epsilon$ are presented in

Table 3. Values of Kolmogorov distances ${\mathsf{\Delta }}_{\epsilon }^{\left(s\right)}$ for various values of asymptotic parameter $\epsilon$ for the distributions of the number of requests of different types s.

$\mathit{\epsilon }$	1	0.5	0.1	0.05	0.01
${\mathsf{\Delta }}_{\epsilon }^{\left(1\right)}$	0.061	0.050	0.024	0.014	0.003
${\mathsf{\Delta }}_{\epsilon }^{\left(2\right)}$	0.161	0.140	0.056	0.033	0.009
${\mathsf{\Delta }}_{\epsilon }^{\left(3\right)}$	0.469	0.379	0.163	0.093	0.027

.

The number of iterations in the simulation experiments is chosen from a criterion that an estimated error of the simulation result should not be greater 0.001. Such an error does not influence the evaluation of the asymptotic result accuracy. We estimate the error of the simulation by comparing the results of several runs of the simulation and evaluating the maximum difference between them in terms of the Kolmogorov distance. So, we discover that the number of iterations greater than 2 million is enough to reach such accuracy.

Let us assume that the accuracy of the asymptotic distribution is good enough if its value of the Kolmogorov distance is equal to or less than 0.05. So, from the table, we see that such values of accuracy are achieved when $\epsilon \le 0.5$ for requests of the first type, $\epsilon \le 0.05$ for requests of the second type, and $\epsilon \le 0.01$ for requests of the third type.

So, we can draw a conclusion that asymptotic result (12) provides good accuracy for the cases when the average number of requests in the system is not too big (there are no two modes in the distribution) and intensities of changing states of the random environment are small enough. To be more precise, based on the comparative analysis conducted, it can be concluded that the asymptotic Formulas (12) and (13) can be applied when values of the average intensity of changes in the state of random environment do not exceed 0.03.

Let us consider practical usage of the obtained results. First, let us discuss what “rare changes of the states of random environment” mean. Consider the example with parameters (8) and (9), evaluated distributions presented in Figure 2 and estimations of their error presented in Table 3. The average intensity of arrivals in this model is about 2.7. Because we have found that the average intensity of the state changes should be 0.03 or less to the precision of approximation (12) and (13) be acceptable, then we can draw a conclusion that the frequency of the random environment state changes should be less than the intensity of arrivals by 100 times or greater. In practice, this means that the changes should occur after 100 requests or more on average. Such a picture is typical enough for real computing systems—in real systems, we usually encounter situations where thousands or millions of requests of one type arrive before the balancer swithces to receiving another type of request.

Let us discuss the implications of a probability distribution (12) and (13) for real-world problems. When we have a probability distribution represented analytically, we can use it to solve more complex problems of analyzing and improving system performance. In particular, such problems may be related to system optimization. Let us say, in the given example, requests of the second and third types are very demanding on computing resources, but their execution is cost-effective. We can formulate an optimality criterion that depends on the number of requests of these types simultaneously present in the system (a negative factor) and the number of requests of these types processed (a positive factor). The criterion can have the form

$$\mathsf{\Theta }(\mathbf{Q},\mathsf{\Lambda })=-F^{-}\left(h(u_1,u_2,u_3)\right)+F^{+}\left(g(n_2,n_3)\right),$$

(14)

where $F^{-}(·)$ is a cost function of the resources consumed by requests of types 2 and 3 during their execution, $F^{+}(·)$ is a profit function of the number of the requests of the second and third types ($n_2$ and $n_3$ respectively) processed by the system during fixed time interval, $\mathbf{Q}$ and $\mathsf{\Lambda }$ are parameters of the system (intensities of the state changes and arrivals) which we can vary to reach maximum value of the criterion. By adjusting these parameters, for example, the time of the random environment being in states 2 and 3 (the average time when the balancer receives requests of these types), we can find conditions where criterion (14) reaches its maximum value. Unfortunately, a specific solution to problems of this type is beyond the scope of this article.

7. Conclusions

In the paper, we consider the mathematical model of request processing in the cloud system in the form of an infinite-server queue with several types of customers and a random environment. The multi-dimensional probability distribution of the number of requests of different types present in the system is obtained under the condition of rare changes in the random environment. The numerical results and simulation modeling approve the result obtained. Some interesting properties of the distribution are considered.

The result obtained can be helpful in the analysis of real cloud systems and for understanding the processes of requests processing. It can help to answer questions, for example, why we have too many requests of one type in comparison to requests of other types, how many resources should be provided by the server for normal operations (if the resource requirements depend on the types of requests), solving optimization problems, and so on.