Abstract
Workflows orchestrate a collection of computing tasks to form a complex workflow logic. Different from the traditional monolithic workflow management systems, modern workflow systems often manifest high throughput, concurrency and scalability. As service-based systems, execution time monitoring is an important part of maintaining the performance for those systems. We developed a trace profiling approach that leverages quantitative verification (also known as probabilistic model checking) to analyse complex time metrics for workflow traces. The strength of probabilistic model checking lies in the ability of expressing various temporal properties for a stochastic system model and performing automated quantitative verification. We employ semi-Makrov chains (SMCs) as the formal model and consider the first passage times (FPT) measures in the SMCs. Our approach maintains simple mergeable data summaries of the workflow executions and computes the moment parameters for FPT efficiently. We describe an application of our approach to AWS Step Functions, a notable workflow web service. An empirical evaluation shows that our approach is efficient for computer high-order FPT moments for sizeable workflows in practice. It can compute up to the fourth moment for a large workflow model with 10,000 states within 70 s.
1. Introduction
Software-as-a-Service (SaaS) systems are deployed in an increasingly modularised and distributed pattern. The architecture of those systems benefits from a separation between a collection of computing tasks and a workflow that orchestrates those tasks. Traditionally, workflow management systems (WMSs) are (usually monolithic) software tools that are driven by workflow models and automate business processes [1]. In modern service-based workflow-centric systems (called workflow systems hereafter), the workflow and task applications are implemented by software developers and deployed in containers or run by serverless functions. Moreover, those workflow systems often manifest high throughput and high concurrency and consist of scalable computing tasks. One notable example is the web service AWS Step Functions [2].
In order to conform with the quality of service deliveries, workflow systems usually provide an access to a wide range of monitoring metrics. One important kind of performance metric is the execution time. We can easily measure the end-to-end time (i.e., makespan) of any workflow and the task time for individual tasks in the workflows. For complex workflows, it is also useful to consider complex time metrics in the level of execution traces. For example, we may want to know the execution time of traces traversing specific branches and iterating in some loop at most i times (where i is a positive integer). We use the term “trace component” to refer to a subset of traces that can be described by a temporal pattern. The time metrics for trace components can provide more pertinent information to establish a monitoring plan for workflow systems.
In general, there are two approaches used to analyse execution traces. Event stream processing [3,4] is a technique of continuously querying timestamped event logs, which contain low-level and precise footprints of the traces. However, ingesting the telemetry (probably after a cleaning step) from a high-throughput system to a processing platform is not cost-effective. Sampling can alleviate the cost by randomly selecting a portion of data to process, but it comes with the price of lowered accuracy. In contrast, trace profiling is a model-based technique used to build and maintain a statistical profile of the traces. Compared with the set of concrete traces, a profile model is compact and contains rich trace information to be analysed further. In particular, temporal (or behavioural) profiling, which employs models preserving the temporal orders of events, is adopted in various problem domains (e.g., clickstream analysis [5], intrusion detection [6] and process mining [7]).
Following the trace profiling approach, we leverage probabilistic model checking [8] to analyse time metrics for trace components in workflows. Probabilistic model checking, which is a formal technique of quantitative verification, has been applied to address different problems in software engineering, including Quality-of-Service (QoS) management [9], self-adaptive systems [10,11], event-streaming systems [12] and business workflows [13]. One main strength of this technique is the ability of expressing a wide range of temporal properties for a system model in the Markovian model family [14] and performing verification in an automated way. As our focus is on time analysis, the Markovian model of workflow profiles should encode not only the state transition probabilities but also the state holding times. Moreover, because of the uncertain workload and environment of the workflow system, it is more reasonable to consider the state holding times as random variables rather than fixed values.
If we assume that the state holding times are exponentially distributed, we obtain a continuous-time Markov chain (CTMC), which is a widely-adopted model in performance analysis [15]. Based on the memoryless properties of exponential distributions, we can perform automated verification on CTMC using the well-established methods of numerical computation [16]. But the aforementioned assumption is usually too restricted to interpret the empirical trace data and thus results in inaccurate analysis output. Therefore, we consider an extension to CTMC, namely, semi-Markov chain (SMC), in which the state holding times are determined by general distributions. The execution time of a trace component is naturally formalised by a fundamental measure in SMC, called first passage times (FPTs). It is noteworthy that in some existing work [17,18] that aggregate workflow makespans from randomised task times, the workflow is represented as a directed acyclic graph (DAG). But loops, which are allowed in SMC (and other models in the Markovian family), are an essential structure used to build workflow models.
However, the generality of an SMC results in a serious challenge for its quantitative verification. First, it is impractical to estimate the exact distribution functions of state holding times from empirical trace data. Second, even if those distributions are given, it is extremely hard to compute the probability that FPT falls in an interval for SMC [19]. In view of these difficulties, we maintain a simple mergeable summary of workflow executions (which comprises frequency values and power sum values only), and compute a group of generic statistical parameters, namely moments, for FPT. Our core computational method, which is underpinned by a well-established property of SMC [20], resorts to solving a sequence of linear systems in a reasonable size (i.e., the same size as the SMC). We can either use the FPT moments directly as time metrics for trace components or further infer other statistical parameters, such as quantiles, from the FPT moments using the method of moments ([21], Chapter 10.2).
In real-world applications, our approach is suitable for performance monitoring in workflow systems such as AWS Step Functions. In particular, our approach can build compact workflow trace profiles from historical data and recent data in a sliding or decaying time window, and produces a broad range of complex time metrics to define a performance baseline and the current performance for monitoring. We also included an empirical evaluation of the computation time for our approach.
The main contributions of this paper are summarised as follows:
- We leverage probabilistic model checking as a trace profiling approach to formally analyse the complex time metrics for workflow systems.
- We present an efficient method to compute the FPT moments in SMC, which complements the existing quantitative verification technique for SMC.
- We describe an application of our approach to a notable workflow Web service, namely, AWS Step Functions.
The remainder of the paper is organised as follows: Section 2 presents the background of our problem in the time analysis of workflow trace components. Section 3 presents an overview of our approach. Section 4 and Section 5 present the technical details, namely, the model building process and the core time analysis method, respectively. Section 6 describes an application of our approach to a real-world workflow system. Section 7 discusses the related work. Finally, Section 8 concludes the paper.
2. Background and Problem
In this section, we explain the background and problem of workflow execution time analysis using a simple running example.
2.1. Execution Trace Components
A workflow orchestrates a set of computing tasks to form a complex workflow logic. Typically, besides a “start” state and an “end” state, a workflow comprises two kinds of steps, namely tasks (where the main computing functions are performed) and control stages (such as “choice”, “fork”, “join” and “loop”). For illustration purposes, Figure 1 presents the diagram of a simple workflow, called SimpleFlow, which includes two tasks (Task 1 and Task 2). The workflow logic of SimpleFlow is as follows: After the workflow starts, two parallel threads are spawned at the “fork” stage. In the first thread, Task 1 is executed once. In the second thread, Task 2 is executed iteratively, depending on the output of the “ok?” stage. After both threads enter the “join” stage, the workflow terminates.
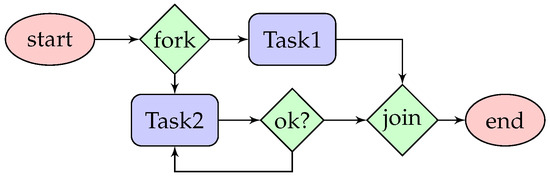
Figure 1.
Specification of SimpleFlow.
In real-world workflow engines (such as AWS Step Functions), workflows are usually defined in a domain-specific specification language (such as a JSON-style language). The execution traces of a workflow can be identified at different levels of abstraction. For example, we can consider each task as a single execution stage of SimpleFlow or a combination of the lower-level execution stages (e.g., scheduling, queuing and processing). For simplicity, we adopt the former (i.e., more abstract) level of execution traces. A trace component can be viewed as a part of the workflow, which can be described by some temporal pattern. Informally speaking, a trace component represents a subset of possible execution traces in a workflow. Consider the following two examples of trace components for SimpleFlow:
- TC-A
- Task 2 is executed only once.
- TC-B
- Task 2 is executed at least twice.
The formalisation of trace components and their relationship with workflows is provided in Section 4.
2.2. Execution Time Metric
Suppose that SimpleFlow is a long-running workflow service, where multiple executions can run simultaneously. Also suppose that the resources allocated to the two tasks in SimpleFlow are scalable at runtime (which is often the case in real-world SaaS systems). To manage the resource allocation, the workflow system needs to have access to a wide range of performance metrics, including the time metrics. Basic time metrics include the end-to-end time of the workflow and the task time (i.e., the time to run an individual task) in the workflow. But in order to provide more pertinent information about the workflow performance, it is also important to consider time metrics for trace components.
Time metrics of those trace components can provide performance information to determine whether more computing resources should be allocated to the two tasks. Unlike the end-to-end time and task time, the time metrics for trace components cannot be measured directly. One generic technique is event stream processing, in which we can route the trace logs to a stream processing platform, filter the traces belonging to an interesting trace component and aggregate the time for those traces. But this technique is resource-consuming especially for high-throughput streams, because the telemetry needs to be streamed into a processing platform from (possibly) multiple sources (e.g., multiple service units), and because fragments of the streams need to remain in main memory for aggregation. In practice, the overhead of performance monitoring atop the operation cost of the applications should be minimised. Therefore, a light-weight trace profiling method, which can produce reasonably accurate time metrics for a variety of trace components, is desirable.
3. Approach Overview
In this section, we present an overview of our approach to workflow execution time analysis, and illustrate its several key aspects.
Because of the uncertain workload and environment for the workflow system, workflow executions manifest stochastic characteristics. Therefore, the execution time of any part of the workflow should be viewed as a random variable. The workflow execution traces, which are collected according to some pre-determined time window function (e.g., a sliding or decaying function), can be considered as some kind of random samples. We assume that those random samples (i.e., traces) are generated by a stochastic process, in which the probabilities and elapsed times of jumping to the next states are dependent on the current states only. This assumption or some equivalent statements are adopted in many QoS composition studies (e.g., [17,22,23,24]). Under this mild assumption, we developed a quantitative verification technique to compute the time metrics for trace components efficiently, just by constructing a fixed workflow model and maintaining an execution summary.
An overview of our approach is illustrated in Figure 2, whilst the technical details are presented later in Section 4 and Section 5. Our approach requires three inputs: (i) a workflow model, which is a transition system, (ii) a simple mergeable summary of workflow executions, and (iii) one or more to-be-analysed trace components, which are formalised by finite-state automata (DFA). The key idea is to build an SMC model for each trace component based on the aforementioned three input and analyse its FPT measure formally. The direct quantitative verification of FPT in SMC is impractical because (i) the probability distribution functions of state holding times in SMC can be arbitrary and difficult to determined precisely from data and (ii) even if those probability distribution functions are given, the probability that FPT falls within some interval is extremely hard to compute [19]. However, we can calculate a data summary, which comprises frequency values and power sum values, and compute a group of important statistical parameters (i.e., moments) for the FPT efficiently [20]. Besides the mean (which is the first moment), some other common statistical parameters (such as variance, skewness and kurtosis) are derivable from moments directly. We can use those statistical parameters for the FPT as time metrics of the trace components. From the FPT moments, we can also infer (approximate) quantiles of the FPT as other time metrics.
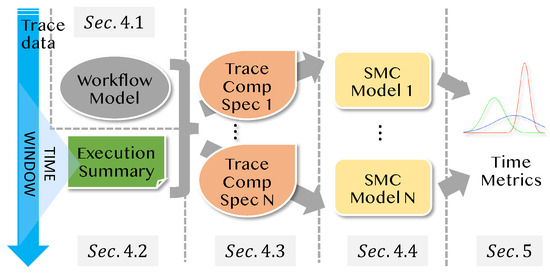
Figure 2.
Overview of the approach.
We highlight the following advantages of our approach. First, our approach early-aggregates simple statistical summaries from the workflow execution data, thus alleviating the cost of transferring and persisting the raw telemetry. Second, owning to the expressive power of DFA (which is equivalent to the regular language), a very broad range of trace components for a given workflow can be defined and analysed. Third, the computation of the FPT moments is very efficient, as it resorts to solving a sequence of linear systems, whose size is not larger than the size of the SMC state space.
4. Model Building
In this section, we focus on the model building stage of our approach, namely the building of the SMC model from a transition system, an execution summary and DFA.
4.1. Transition System for Workflow
Defintion 1
(Transition system). A transition system is the tuple where
- W is a set of states;
- is an initial state;
- is a transition relation;
- is a set of atomic properties;
- is a labelling function that assigns a subset of atomic propositions to each event.
A trace in is a finite sequence such that for all . We present a transition system in Figure 3 as the model of SimpleFlow. In general, to model a workflow as a transition system , the following rules are applied:
- –
- The set includes the names of some stages in the workflow. The excluded stages (such as the control stages “fork”, “join” and “ok?” in SimpleFlow) have almost instant elapsed times, which are negligible.
- –
- The labelling function L assigns to and to a state without outgoing transitions, respectively.
- –
- The parallel threads in the workflow are represented by branches in . For example, the two “fork–join” threads in SimpleFlow are represented by the two branches of and from .
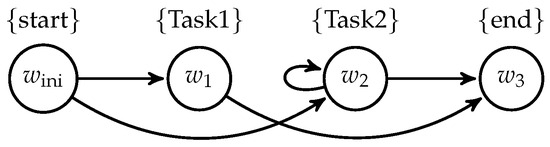
Figure 3.
Transition system for SimpleFlow .
The last rule is worthy of further explanation. Because some threads are temporarily blocked before entering a “join” stage in a workflow execution, only the last-completed thread determines the execution time. As our focus is on time analysis, we can resolve the parallel structures in the workflow by the branching structures in . Thus, the traces in model the traces of last-completed threads in the workflow only. In , the path (for any positive number of ) models an execution trace of SimpleFlow where the thread of Task2 is the last one completed. This can avoid the exponential growth in the size of the transition system as the number of threads in the workflow increases. For convenience, we also use to denote the workflow that it models from now on.
4.2. Workflow Execution Summary
An execution trace of a workflow is a list of events with the following fields: (eventType, timestamp), where eventType is an event type, such as entering a stage in the workflow, and timestamp is the event timestamp. The list may also contain a unique ID to identify the execution instance. Execution traces include all the information to create a workflow execution (data) summary.
Assume that we have collected a set of execution traces falling into a prescribed time window. We remove the events that do not belong to last-completed threads. With the execution trace data, we can replay the executions and calculate two kinds of statistical values. The first kind of statistical values are the frequencies of transitions, denoted Freq , where is a transition in . The frequencies can be calculated by counting the pairs of consecutive events. The second kind of statistical values are power sums of transition time intervals, denoted PSum , where j is a power, and is a transition in . Let t and be the timestamps of two consecutive events that correspond to w and , respectively, and let . Thus, we have a set of time intervals for , where . Then, we calculate , where . An alternative way of interpreting time intervals of transitions is the holding time at state w if the next state is . For example, when the execution of SimpleFlow is located in in , the transition time from to means the task time for Task1.
The pair is an execution summary of the workflow. It is noteworthy that one important property of is mergeability [25,26]: Given and (resp., and ), we can simply merge them, namely, let ). This property enables the parallel calculation of in practice. Moreover, we can calculate the summary with sliding or decaying windows [4]. Assume that we calculate with historical data (e.g., data from the past week) and with recent data (e.g., data from the past hour). In the case of (exponential) decaying windows, we can let , where is a decaying factor. Thus, we represent the entire execution history with a compact summary .
We use a (statistical) workflow profile to refer to the combination of a workflow model and its execution summary , where is fixed, and is updated by the aforementioned method as more recent execution trace data are collected.
4.3. Specification of Trace Component
We present the definition of DFA, which we employ to define trace components of the workflow .
Defintion 2
(Deterministic finite automata). A DFA is a tuple , where
- Q is a set of locations;
- Σ is an alphabet;
- is a transaction function;
- is a set of initial locations;
- is a set of accept locations.
Throughout the paper, we let the alphabet of be the power set of atomic propositions in a workflow , namely . Based on a transition system and a DFA , we can define a product transition system that models the behaviour of a trace component.
Defintion 3
(Product transition system). Given a workflow and a DFA , a product transition system is the tuple where the transition relation is the smallest relation defined by the following rules:
Clearly, traces of are also traces of . This justifies as a trace component of . The DFA is a very expressive formalism used to specify temporal patterns for traces. Figure 4a,b presents two DFA examples and . The production transition systems of and model the two trace components of SimpleFlow in Section 2.1.
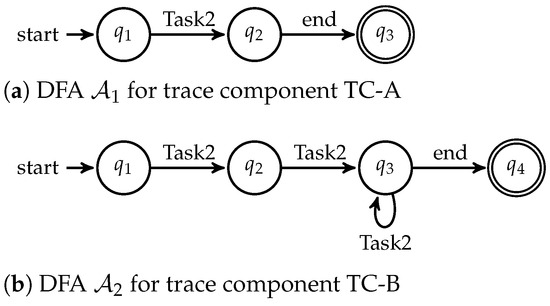
Figure 4.
DFA examples.
Note that Definition 3 is slightly different from the standard definition of production transition systems. For technical purposes, we encode absorbing states in the production transition system with the second rule of transition relations.
4.4. SMC Model
With the workflow profile and DFA, we can define an SMC model. Our presentation of an SMC follows the probabilistic model checking literature [19] but also specifies the absorbing states explicitly.
Defintion 4
(Semi-Markov chain). An SMC (with absorbing states) is the tuple where
- S is a state space of ;
- α is an initial (probability) distribution on S;
- is a transition (probability) matrix on S;
- is an matrix of continuous probability distribution functions (i.e., Cumulative Distribution Functions (CDFs)) whose supports belong to ;
- is a set of absorbing states (i.e., if ).
Let be the set of successor states of s, namely, . A path in is given by an infinite alternating sequence of states and time values, namely with and , such that for all i. For convenience, let , which is the holding time of the path before the i-th jump. We use to denote the set of paths in and to denote the set of those paths in originating from state s. Following the literature [19], we define a probability measure on an SMC as follows: Let , where is a non-empty interval in , and denote a cylinder set consisting of all paths in such that , for all . Then, a probability measure is defined by induction on i: If , ; for all ,
where is the closure of . Based on the probability measure , we can formally analyse a variety of stochastic and timed properties of an SMC .
For convenience, let contain the corresponding Probability Density Functions (PDFs) for the CDFs in . Let and . The k-th moment of a random variable X is the expected value of the k-th power of X, usually denoted as (where E is the “expectation” operator). Formally, let F and f be the CDF and PDF of X, respectively; the k-th moment of X is the following quantity (if it exists):
The first moment of X is just its expected value . The variance of X is derived from the first and second moments of X, namely . We can also mention the moments of a CDF (or PDF) without referring to a random variable.
4.4.1. Building the SMC Structure
We build an SMC based on a product transition system . For convenience, if , let and . We first prune the such that each state in reaches at least one absorbing state and is reachable from at least one initial state. Then, the state space S of is just in the (pruned) , and the set G of absorbing states is the set . Also, is “qualitatively determined” in the sense that if , then .
4.4.2. Estimating the SMC Quantitative Parameters
The initial distribution is a distribution over the states in the intersection of S and . If this intersection is not a singleton, we usually let be a uniform distribution. But in general, can be any discrete distribution over the state space.
Recall that the statistics of execution traces is given as , where includes the frequencies of transitions, and includes the power sums of state holding times. We use to estimate the transition matrix of the SMC. For each , let
Clearly, if , then .
It is very difficult to determine continuous probability distribution functions from data. We use and to estimate the moments of the CDFs in . For each and , let
We briefly summarise the model building stage in our approach. The fixed workflow model and an updatable execution summary form a workflow profile. One or more DFAs are defined to formalise the trace components of . The workflow profile and the DFA are used together to build an SMC model for time analysis (which is detailed in the next section).
5. Time Analysis
In the section, we formalise the time metrics for trace components in the SMC and present our core computational method of time analysis.
5.1. First Passage Time
Time metrics of trace components can be formalised as a group of fundamental measures in SMC, namely, first passage times (FPTs) [14], which informally express “the randomised time until the trace traverses a goal (i.e., absorbing) state for the first time”.
To define an FPT, we first introduce a real-valued function, which is defined almost everywhere on for some state s in (with respect to the probability measure ):
Intuitively, is the total time duration along with the path until an absorbing state is reached. Note that if the first state in is a goal state, by definition. This is slightly different from the standard FPT definition in the literature, where the FPT at an goal state is the time of leaving that state. Also note that, although is not defined on paths that do not reach any absorbing states, the set of those paths has a probability measure of zero (with respect to ), and thus is defined almost everywhere on . Therefore, we can define a random variable
such that , where . Intuitively, means the FPT for the absorbing states from state s. Thus, the FPT of (to the absorbing states) is a linear combination of with a weight given by for all :
Therefore, our objective is to compute the moments , where for some k.
5.2. Linear Systems of Moments
In the following, we present an efficient quantitative verification method to compute for . Although our main result (i.e., Theorem 1) can be proved directly (c.f., Lemma 4.1 in [20]), we relate it to a well-known property of convolution. We first present a basic property of mixture distributions.
Proposition 1.
With the above proposition, it suffices to consider the moments of for all . We recall the following property about the probability distribution of .
Lemma 1
([14]). It holds that
or, equivalently,
where and are the PDFs of and , respectively, and ∗ denotes the convolution.
In the following, we show that the moments of for all can be alternatively characterised by a sequence of linear systems and thus can be computed efficiently in practice. We define an equation system as follows: (i) first,
(ii) second, for ,
Based on Lemma 1, the following theorem holds as a result of a well-known property of convolution [27].
In the first instance, Equations (5) and (6) form a linear system with variables (where S is the state space of SMC ). However, because for each order , only unknowns up to the order j are included in the equations; the whole linear system can be reduced to k smaller linear systems, each of which has at most unknowns. Solving the linear systems can involve inverting a matrix with size . Recall that matrix inversion can be carried out in the time complexity . Therefore, based on the standard time complexity of solving linear systems, we have the following result.
Proposition 2.
The time complexity of computing up to the k-order FPT moments in an SMC is , where S is the state space of the SMC.
We note that Equation (5) is just the standard characterisation of expected accumulated rewards for Markov Reward Models (MRMs) (c.f., ([28], Chapter 10)). If , we have the following equations to compute the second moments:
Our approach can be improved slighly by separating the offline computation and the online computation. The linear systems that produce the FPT moments (Equations (5) and (6)) are entirely based on the SMC model, which is in turn determined by the workflow transition system, the execution summary and DFA. The fixed transition system and the given DFA determine the structures of the linear systems, while the execution summary provides the coefficients of the linear systems. In view of this, we can pre-compute a sequence of abstract linear systems, whose coefficients are instantiated online. In this way, the online computation only includes the necessary part of computation, namely, solving the linear systems of moments.
5.3. Moments to Quantiles
Moments are important statistical parameters for probability distributions. We can report the moments of FPT Y as the final time metrics of the trace components. In particular, the first FPT moment is the mean execution time. The variance of Y, which measures the deviation of the execution time from its mean, equals . Moreover, skewness (a measure of the asymmetry of the probability distribution) and kurtosis (a measure of the “tailedness” of the probability distribution) are also defined by moments.
It is also possible to infer more intuitive metrics, such as quantiles, from moments. If the probability distribution of Y has a specific form, say, a PDF where the parameters are unknown, by the method of moments ([21], Chapter 10.2), we can usually construct an equation system, whose coefficients are moments of Y (up to some order) and whose variables are . By solving this equation system, we can obtain the values of and thus infer the quantiles of . For example, if Y has a normal distribution , we have and immediately; if Y has a Gamma distribution , where is the shape parameter and is the rate parameter, we can derive the following two equations: and . This method can be applied to almost all common forms of probability distributions.
In practice, we can use the historical data to estimate the form of the distribution function for Y. However, if the form of the probability distribution of Y is unknown, there are other existing methods to estimate or approximate the quantiles of Y. For example, one method is to estimate the PDF of Y with the maximum-entropy distribution (i.e., a distribution with “least information” according to information theory) [25]. Another method is to use semidefinite programming to compute the bounds of the quantiles of Y [29]. Hence, it is possible to extend our approach to include those methods in future work.
5.4. Untimed Probabilistic Analysis
It is often useful to combine the untimed probabilistic analysis and our FPT moment analysis in the SMC. Typically, we can analyse the probability of traversing a trace component in the workflow and then analyse the randomised traversing time. For example, before estimating the time metrics for the trace component described in Figure 2, we may want to know how likely an arbitrary execution trace of SimpleFlow traverses that trace component. The untimed probabilistic analysis can employ the standard technique in probabilistic model checking for discrete-time Markov chains (DTMCs) ([28], Chapter 10) and are briefly summarised as follows in the context of our approach. First, we build a DTMC based on the workflow model and its execution summary (in particular, the frequency values in of ). The state space of is the same as that of . The estimation of transition probabilities in uses the same method for the SMC as described in Section 4.4. Second, we build a product model of and DFA in a similar way to Definition 3. The product model is essentially a sub-DTMC in the sense that the transition probability matrix of is sub-stochastic (namely, the sum of outgoing probabilities from states may be smaller than 1). Finally, we can compute the reachability probability to the target states in using the standard probabilistic model checking technique.
6. Application and Evaluation
In this section, to demonstrate the practicality of our time analysis approach, we present a detailed description of applying our approach to establish a monitoring plan for AWS Step Functions, which also includes an empirical evaluation of the computational efficiency.
6.1. AWS Step Functions
AWS Step Functions (https://aws.amazon.com/step-functions/ accessed on 1 June 2024) is a web service that provides a flexible way to coordinate tasks running on other AWS services, such as AWS Lambda (https://aws.amazon.com/lambda/ accessed on 1 June 2024) (a serverless computing service) and AWS ECS (https://aws.amazon.com/ecs/ accessed on 1 June 2024) (a container-based computing service). It is well suited for running high-throughput workflows and processing massive parallel jobs. Workflows in AWS Step Functions are defined with a domain-specific JSON-style language called the Amazon States Language (https://states-language.net/spec.html accessed on 1 June 2024), which employs finite state machines (FSMs) as the semantics.
6.2. Example: JobDeciderWorkflow
We envisage a workflow called JobDeciderWorkflow as an example to explain the applicability of our approach to AWS Step Functions. For readability, we do not present its JSON-style specification directly but instead illustrate the specification in Figure 5. The main purpose of this workflow is to run a job in a cost-effective way, either with Lambda (if the job is small to medium-sized) or ECS (if the job is large). Assume that each job of this workflow can be decomposed into multiple parts. All main stages (except “start” and “end”) are implemented as Lambda functions and play the following different roles: the workflow controllers (i.e., “Job Decider” and “Job Complete?”), job runners (i.e., “Run Job in Parallel”), job submitter (i.e., “Submit Job to ECS”), time keeper (i.e., “Wait X Second’), status checker (e.g., “Get Status”) and event emitter (i.e., “Emit ‘Successful’” and “Emit ‘Failed’”). If the “Job Decider” decides that the job should be run in Lambda, by exploiting the easy parallelisation of this service, a set of parallel threads are spawned to handle different parts of the job. If the “Job Decider” decides that the job should be submitted to ECS and run by it, two loops are used to guarantee the quality of job completion: The inner loop monitors the status of the job, and the outer loop resubmits the job if it has failed. This workflow example manifests many common characteristics of AWS Step Function workflows.
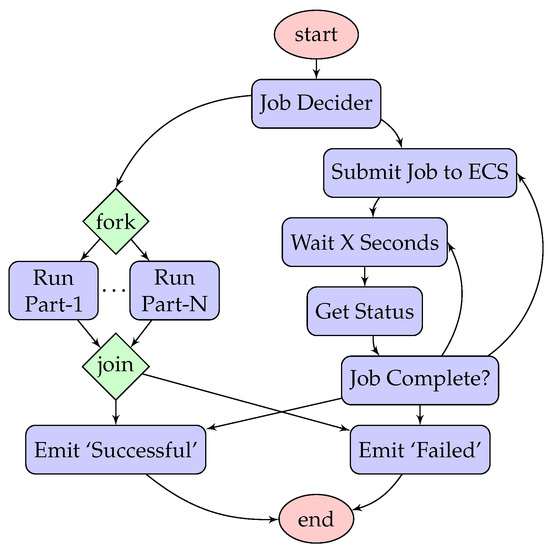
Figure 5.
JobDeciderWorkflow in AWS Step Functions.
6.3. Execution Time Monitoring
Execution time monitoring is an important part of maintaining the performance in service-based systems, such as AWS Step Functions. The historical monitoring data provide a baseline, against which the workflow administrator can compare the current performance of the workflow system. A monitoring plan includes a set of baseline metrics and current performance metrics, which are determined by historical and current data, respectively. If the current performance falls below the baseline, the administrator can undertake various countermeasures, ranging from simply reconfiguring some workflow parameters to purchasing more cloud resources to run the tasks. In JobDeciderWorkflow, parameter reconfiguration can involve updating the criterion of running the job with Lambda or ECS and reseting the maximum number of job resubmissions to ECS.
In this case study, we focus on the metrics of execution times. AWS Step Functions supports the monitoring of the task execution time and the end-to-end workflow execution time. However, it does not provide the time metrics in the level of traces. Consider the following trace component for JobDeciderWorkflow:
The “Submit Job to ECS” stage is traversed up to i times, where i is a parameter, until the“Emit ‘Successful’” stage is reached.
The time metrics of trace components similar to the above one can help to define a performance baseline and the current performance, and to create a thorough monitoring plan.
6.4. Model Building
In the following, we explain how to apply our time analysis approach (as depicted Figure 2) to define the performance baseline and current performance based on the JobDeciderWorkflow example in detail. Recall that there are three inputs to our approach, namely (Input I) a transition system as the workflow model, (Input II) a workflow execution summary and (Input III) one or more DFA, which specify the to-be-analysed trace components.
For Input I, the transition system (denoted ) for JobDeciderWorkflow is built from its specification in the Amazon States Language. There are seven types of states in the FSM of AWS Step Functions, namely Task, Choice, Fail, Succeed, Pass, Wait and Parallel. In the model building, we need to decide the level of abstraction. In AWS Step Functions, when a Lambda Task state (i.e., a Task state that runs a Lambda function) is traversed, the following five low-level events are created (in order): “TaskStateEntered”, “LambdaFunctionScheduled”, “LambdaFunctionStarted”, “LambdaFunctionSucceeded” and “TaskStateExited”. Thus, includes five low-level states for each Lambda Task state in the “Run Job in Parallel” step. Alternatively, we can consider all steps in JobDeciderWorkflow (including the Task states) as single abstract states in . Another problem is the parallel states in the FSM, which if directly translated to a transition system, result in a state explosion: The composition of N parallel Lambda Task states results in lower-level states. However, since our objective is time analysis, we can model the parallel threads with non-deterministic last-completed threads (c.f., Section 4.1). When an execution trace traverses the step “Run Job in Parallel”, the traverse time is determined by the thread that takes the longest time to complete the part of job. Thus, the step “Run Job in Parallel” can be modelled with no more than states in .
For Input II, the statistical values in the execution summary are the frequencies of transitions and the power sums of time intervals (as specified in Section 4.2), which are calculated from the execution traces. The log data of execution traces is available in AWS Step Functions. In particular, the getExecutionHistory API (https://docs.aws.amazon.com/step-functions/latest/apireference/API_Operations.html accessed on 1 June 2024) of AWS Step Functions returns a list of (raw) timestamped trace events for a specific workflow execution. We filter the execution traces where the timestamps of the last events fall into a prescribed time window and then remove the unnecessary events in the following two steps: First, we remove the events that do not belong to the last-completed threads. For example, if “Run Part-1” takes the longest time to complete in a trace, we remove all the events related to “Run Part-2”, “Run Part-3”, …, and “Run Part-N” in the same trace. Second, based on the modelling abstraction level, we may also need to remove the unnecessary low-level events. For example, if we adopt the high-level modelling for , among the aforementioned five low-level events for each Lambda Task state, we retain “TaskStateEntered” only and remove the other four. After removing the unnecessary events, we can replay the traverses of paths in and calculate the values of frequencies and power sums, where the detailed method of calculation is presented in Section 4.2. Moreover, by setting two suitable time windows, we can create two versions of summaries, namely the baseline summary and the current performance summary . For example, we can calculate from data in the past week and from data in the past hour. The detailed method of calculation is given in Section 4.2. Note that the baseline summary can be updated with sliding or decaying windows, and that the mergeability of frequencies and power sums can facilitate the parallel calculation of both summaries in practice.
For Input III, the DFA for specifying trace components are user-defined. The expressive power of DFA allows a broad range of complex trace components to be defined and analysed. The trace component for JobDeciderWorkflow informally described in Section 6.3 can be formalised with DFA in Figure 6, which has states. Note that is parametric on i; in particular, if , just includes the traces traversing the “Run Job in Parallel” step but not the “Submit Job to ECS” step. As DFAs are independent of the two execution summaries and , the set of user-defined DFAs can be updated dynamically.
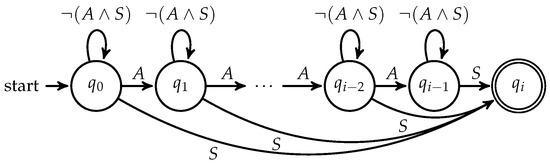
Figure 6.
Trace component DFA for (where , , and refers to all other steps except A and S).
6.5. Evaluation of Computation Time
Provided with the three outputs (i.e., the workflow transition system, an execution summary and DFA, Table 1), the computation includes building the SMC model, and generating and solving the linear systems of FPT moments. In the empirical evaluation, we parametrised the value of i in the DFA in Figure 6 for JobDeciderWorkflow and created SMC models in different sizes. The experimental data, as summarised in Table and depicted in Figure 7, were collected in a Linux system with a 2.8 GHz Intel Core i7 CPU and 32 GB memory. As shown in the figure, the computation time is relevant to the size (i.e., the number of states) of the SMC models, which is also the size of the linear systems. Within 16 s, we can compute the first four moments for SMC models with up to 5000 states, and within 70 s, we can compute the same moments for models with up to 10,000 states. The superlinear increment in computation time with respect to model size is mainly due to the need of solving linear systems (c.f., Proposition 2). However, we believe that the meaningful time analysis of most real-world workflows in our approach results in SMC models with no more than 10,000 states. In Figure 7, the largest SMC model is built from the production of the JobDeciderWorkflow transition system with 13 states and a DFA with 2400 locations. Another observation from Figure 7 is the linear increment in computation time as the order of the FPT moment increases (Note that the computation of the first FPT moment also includes the model building time). This conforms with the fact that the linear systems for FTP moments are of the same size regardless of the moment orders.

Table 1.
Computing time of FPT moments.
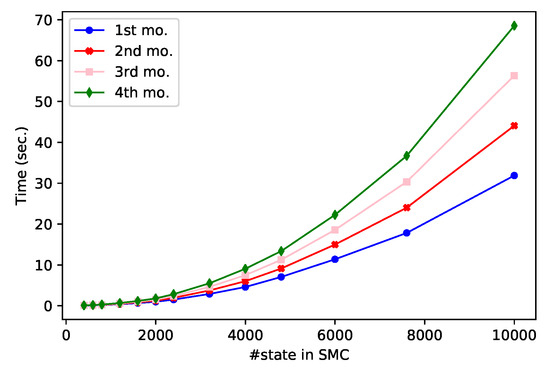
Figure 7.
Plot of computing time of FPT moments.
6.6. Summary and Discussion
To apply our approach to performance monitoring in AWS Step Functions, we translate the JSON-style specification of a workflow into a fixed transition system in a suitable level of abstraction, maintain two sets of execution summaries, which are created from the historical and recent workflow execution traces, respectively, and employ DFA to specify trace components, whose time metrics are interesting to monitor. With these three inputs, the building of the SMC models and the computation of the FPT moments in those models are automated and efficient. We can use the FPT moments as time metrics to define the baseline and current performance. Alternatively, we can further infer the FPT quantiles from the FPT moments using the method of moments. Therefore, our approach is a useful monitoring technique for AWS Step Functions, and the evaluation of computation time also demonstrates its efficiency in general.
It is noteworthy that, although this case study focuses on AWS Step Functions, our approach can be applied to other realistic workflow systems. The process follows the same steps, which is the preparation of the three inputs for model building (c.f., Section 6.4). However, the translation of workflow specifications into transition systems and the collection of execution statistics are platform-dependent. In AWS Step Functions, workflows are specified in the JSON format, and execution statistics can be retrieved by a specific API.
7. Related Work
Workflow execution time analysis is heavily investigated in the existing works, most of which belong to a specific problem domain, such as the makespan estimation for workflow scheduling and the QoS aggregation in service composition (i.e., how to aggregate QoS metrics, such as execution times, for composite services from those of atomic services). Many works in those two domains represent makespans and QoS metrics as constant values (e.g., [30,31,32,33,34]). We discuss only those works in which the makespans and QoS metrics are modelled as stochastic values, as those analytic methods are more related to our approach.
In the framework proposed by Hwang et al. [22], the QoS metrics of atomic services are modelled as independent discrete random variables. Their algorithm works recursively to derive the Probability Mass Functions (PMFs) for the service QoS metrics through five common composition structures (i.e., sequential, conditional, loop, synchronised parallel and unsynchronised parallel) until the PMF of the end-to-end QoS is computed. Although the PMF composition is straightforward, in order to represent the empirical QoS values accurately, the support of the PMF must consist of a high number of small discretised value ranges. The complexity of their algorithm grows exponentially as the support size of the PMF increases. Zheng et al. [24] presented an approach to aggregate the continuously distributed QoS metrics of service components in the same aforementioned five composition patterns. In order to compute the composite QoS, they assumed that the distributions of all QoS metrics must have the same form, and that the histograms must have the same start point and width of intervals. This assumption may be over restricted in application.
Zheng et al. [23] employed an SMC to formally model composite services. They derived basic statistical parameters (i.e., means and variances) of QoS metrics (i.e., the response time and availability probability) for composite services in the closed form of the basic statistical parameters for atomic services. Although we also use an SMC as the formal model, our method computes not only the first and second moments but also high-order moments numerically, which are not so convenient to express in a closed form. Our approach is also equipped with an expressive formalism (i.e., DFA) to specify trace components for quantitative verification.
In the task scheduling framework of workflows proposed by Chirkin et al. [18], an essential component is a method to infer the execution time of workflows from generally (and independently) distributed times of basic tasks. Their method estimates both the CDFs and characteristic functions (CFs) of task times. By representing the workflow as a directed acyclic graph (DAG) (without loops), they can employ the former to aggregate the parallel structure and later to aggregate the sequential structure and branching structure. During the aggregation process, their method uses Fourier transforms between CDFs and CFs at the cost of some approximation error. In contrast, by considering the last-completed parallel threads for execution time analysis purposes, our approach reduces to the parallel structure into the branching structure and works on the computation of moments with loops. Moreover, the moment estimation of task times from workflow execution data is much easier than the estimation of CDFs and CFs.
Glatard et al. [17] proposed a probabilistic model to estimate the workflow makespans for scientific grid applications. In their model, they separated the task time and the grid latency for executing a task, where the former is a constant value and the later is a random variable. In practice, the randomised grid latency represents the time variations caused by factors such as new-resource provision, system failures or network interruptions. They considered the parallel composition (called “data parallel”) and the sequential parallel composition (called “data and service parallel”) only. As with Chirkin et al. [18], their probabilistic model assumes a DAG workflow topology. The aggregation of the makespan means and variances in those two kinds of compositions can be viewed as a special case of Zheng et al’s approach [23] and our approach. Rogge-Solti and Weske [7] presented a method based on the Generalised Stochastic Petri Net (GSPN) [35] (which is a more expressive stochastic model than an SMC in that the independence assumption for the general distributions of state holding times is relaxed) to predict the remaining time to workflow completion and the likelihood of breaching workflow deadlines. However, in order to solve the GSPN, one can only resort to discrete-event simulation, which is suitable for offline analysis but too time-consuming for online monitoring. Meyer et al. [36] proposed Timed Probabilistic Workflow Net (TPMN), which is underpinned by the Markov Decision Process (MDP) semantics, and analysed the expected execution time of TPMN. However, task times are modelled as fixed costs in TPMN rather than random variables. Carnevali et al. [37] employed Stochastic Time Petri Nets to analyse complex workflows that are constructed through sequence, choice/merge, and balanced/unbalanced split/join operators. They provided an efficient and accurate compositional approach to provide an upper bound on the response time distribution. Belgacem and Beghdad-Bey [38] investigated the makespan and cost of virtual machine usage in cloud-computing workflows. They used a multi-objective optimisation method to optimise the trade-off between the two factors. Wang et al. [39] presented a probabilistic modelling and evolutionary optimisation approach to analyse the performance and cost of serverless workflows as well as the tradeoff of the two metrics. Similarly, Zhang et al. [40] considered the effective workflow scheduling strategy for cloud computing services while ensuring the service executing reliability. They proposed a formal approach that includes a reliability checkpoint mechanism to meet the workflow deadline and the energy consumption constraints.
In general, our execution time analysis is different from the aforementioned works in that we adopt a quantitative verification approach. In particular, we use DFA to specify trace components whose time metrics are interesting to analyse in a workflow. Su et al. [12] employed model checking to analyse cloud-native event-streaming systems. Due to the empirical estimation of event stream statistics, they considered how the empirical estimation influences the model checking output. A DTMC was used as the formal model, and thus, their approach does not aim to address continuous-time metrics such as first pass time (FPT), which is the focus of the current work. However, in this work, we do not employ the standard technique of probabilistic model checking directly. The well-established quantitative verification technique for CTMCs (based on uniformisation) [16] cannot be generalised to SMCs, which allow state holding times to be determined by general distributions. We report several recent advancements in probabilistic model checking for SMCs and the related models as follows.
López et al. [19] formalised a quantitative verification framework for an SMC, in which the verification of the SMC against the expressive logic Continuous Stochastic Logic (CSL) is reduced to FPT analysis. They further demonstrated that the FPT analysis for an SMC requires solving a set of Volterra integral equations, which limits its scalability seriously. Paolieri et al. [41] proposed another model called Stochastic Time Petri Net (STPN), whose expressive power is between that of an SMC and GSPN, and demonstrated that the verification of STPN can also resort to (a variant of) the Volterra equation system. Despite an extension to the previous work, no efficiency benefit is gained with their technique. Bryans et al. [42] verified stochastic automata with underlying SMCs against “non-nested until” formulas in CSL by unfolding the model into a region tree, where regions are defined by relations between randomised clocks. And a direct computation of probabilities to reach individual regions includes the number of integration operations, which grows exponentially as the number of regions increases.
Compared with the above model-based and quantitative analysis literature, our work adopts a very different approach. We exploited the history-independence property of SMCs (that is, the moment property of convolution) and developed a sequence of linear systems to compute the moments of the FPT, which contains the moments of state holding times as the coefficients. In addition to the computational efficiency, an advantage of working with moments is the easy estimation of moments from empirical data, especially for probability distributions whose forms are unknown.
It is also noteworthy that, beyond the context of model-based and quantitative analysis, our approach is related to the literature that utilises mergeable summaries of moments to describe data streams and that inverts the quantiles of the streams from the moments [25].
8. Conclusions
We presented a formal approach to analyse time metrics for workflow systems at the level of traces. Our objective is to compute the randomised time metrics of trace components, which represent subsets of workflow traces that satisfy specific temporal patterns. In the model building of our approach, we create compact trace profiles from the workflow specification and the workflow execution data summaries, define trace components using DFA, and build SMC models from the profiles and DFA. Our core computation method is an efficient quantitative verification technique that produces the moments of FPT in an SMC. We demonstrated the applicability of our approach to create a monitoring plan in real-world workflow systems such as AWS Step Functions. The computation time evaluation shows the efficiency of our approach to compute high-order FPT moments for large-workflow instances. In particular, our approach can compute up to the fourth moment for a workflow model with 10,000 states within 70 s.
In future work, we plan to apply our approach to other real-world workflow systems. We also plan to establish an extension to the current approach to analyse not only time metrics but also other commons QoS metrics, such as reliability and availability. Also, despite its expressive power, encoding temporal properties in DFA is at a very low level. To improve the usability of our approach, we can introduce a high-level expressive notation (such as a notation based on the Linear Temporal Logic) to specify trace components. Finally, as mentioned in Section 5.3, in practice, we usually do not know the exact forms of the probability distributions for time metrics. In order to infer quantiles from moments in the absence of distribution functions with known forms, we plan to develop more advanced means of statistical inference than the standard method of moments for our approach.
Author Contributions
Conceptualization, G.S. and L.L.; methodology, G.S.; software, G.S.; validation, G.S. and L.L.; formal analysis, G.S.; writing—original draft preparation, G.S.; writing—review and editing G.S. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Experiment data and implementation is available by contacting the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- van Der Aalst, W.; Van Hee, K.M.; van Hee, K. Workflow Management: Models, Methods, and Systems; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- AWS Step Functions. AWS Step Functions Developer Guide. 2019. Available online: https://docs.aws.amazon.com/step-functions/latest/dg/welcome.html (accessed on 24 August 2019).
- Andrade, H.C.M.; Gedik, B.; Turaga, D.S. Fundamentals of Stream Processing: Application Design, Systems, and Analytics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Cohen, E.; Strauss, M. Maintaining time-decaying stream aggregates. In Proceedings of the 22nd ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, Philadelphia, PA, USA, 12–17 June 2003; ACM: New York, NY, USA, 2003; pp. 223–233. [Google Scholar]
- Wang, G.; Zhang, X.; Tang, S.; Wilson, C.; Zheng, H.; Zhao, B.Y. Clickstream user behavior models. ACM Trans. Web 2017, 11, 21. [Google Scholar] [CrossRef]
- Ye, N.; Zhang, Y.; Borror, C.M. Robustness of the Markov-chain model for cyber-attack detection. IEEE Trans. Reliab. 2004, 53, 116–123. [Google Scholar] [CrossRef]
- Rogge-Solti, A.; Weske, M. Prediction of business process durations using non-Markovian stochastic Petri nets. Inf. Syst. 2015, 54, 1–14. [Google Scholar] [CrossRef]
- Katoen, J.P. The Probabilistic Model Checking Landscape. In Proceedings of the 31th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS’16, New York, NY, USA, 5–8 July 2016. [Google Scholar]
- Calinescu, R.; Grunske, L.; Kwiatkowska, M.; Mirandola, R.; Tamburrelli, G. Dynamic QoS management and optimization in service-based systems. IEEE Trans. Softw. Eng. 2011, 37, 387–409. [Google Scholar] [CrossRef]
- Cámara, J.; Moreno, G.A.; Garlan, D.; Schmerl, B. Analyzing latency-aware self-adaptation using stochastic games and simulations. ACM Trans. Auton. Adapt. Syst. 2016, 10, 23. [Google Scholar] [CrossRef]
- Filieri, A.; Tamburrelli, G.; Ghezzi, C. Supporting self-adaptation via quantitative verification and sensitivity analysis at run time. IEEE Trans. Softw. Eng. 2016, 42, 75–99. [Google Scholar] [CrossRef]
- Su, G.; Liu, L.; Zhang, M.; Rosenblum, D.S. Quantitative Verification for Monitoring Event-Streaming Systems. IEEE Trans. Softw. Eng. 2022, 48, 538–550. [Google Scholar] [CrossRef]
- Mangi, F.A.; Su, G.; Zhang, M. Statistical Model Checking in Process Mining: A Comprehensive Approach to Analyse Stochastic Processes. Future Internet 2023, 15, 378. [Google Scholar] [CrossRef]
- Kulkarni, V.G. Modeling and Analysis of Stochastic Systems; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Su, G.; Chen, T.; Feng, Y.; Rosenblum, D.S. ProEva: Runtime Proactive Performance Evaluation Based on Continuous-time Markov Chains. In Proceedings of the 39th International Conference on Software Engineering, ICSE’ 17, Piscataway, NJ, USA, 20–28 May 2017; pp. 484–495. [Google Scholar]
- Baier, C.; Haverkort, B.; Hermanns, H.; Katoen, J.P. Model-checking algorithms for continuous-time Markov chains. IEEE Trans. Softw. Eng. 2003, 29, 524–541. [Google Scholar] [CrossRef]
- Glatard, T.; Montagnat, J.; Pennec, X. A probabilistic model to analyse workflow performance on production grids. In Proceedings of the 8th IEEE International Symposium on Cluster Computing and the Grid, Lyon, France, 19–22 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 510–517. [Google Scholar]
- Chirkin, A.M.; Belloum, A.S.; Kovalchuk, S.V.; Makkes, M.X.; Melnik, M.A.; Visheratin, A.A.; Nasonov, D.A. Execution time estimation for workflow scheduling. Future Gener. Comput. Syst. 2017, 75, 376–387. [Google Scholar] [CrossRef]
- López, G.G.I.; Hermanns, H.; Katoen, J.P. Beyond memoryless distributions: Model checking semi-Markov chains. In Proceedings of the Joint International Workshop von Process Algebra and Probabilistic Methods, Performance Modeling and Verification, Aachen, Germany, 12–14 September 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 57–70. [Google Scholar]
- Zhang, X.; Hou, Z. The first-passage times of phase semi-Markov processes. Stat. Probab. Lett. 2012, 82, 40–48. [Google Scholar] [CrossRef]
- Wasserman, L. All of Statistics: A Concise Course in Statistical Inference; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hwang, S.Y.; Wang, H.; Tang, J.; Srivastava, J. A probabilistic approach to modeling and estimating the QoS of web-services-based workflows. Inf. Sci. 2007, 177, 5484–5503. [Google Scholar] [CrossRef]
- Zheng, Z.; Trivedi, K.S.; Qiu, K.; Xia, R. Semi-Markov models of composite web services for their performance, reliability and bottlenecks. IEEE Trans. Serv. Comput. 2015, 10, 448–460. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, J.; Zhao, W. Probabilistic QoS aggregations for service composition. ACM Trans. Web 2016, 10, 12. [Google Scholar] [CrossRef]
- Gan, E.; Ding, J.; Tai, K.S.; Sharan, V.; Bailis, P. Moment-based quantile sketches for efficient high cardinality aggregation queries. Proc. VLDB Endow. 2018, 11, 1647–1660. [Google Scholar] [CrossRef]
- Agarwal, P.K.; Cormode, G.; Huang, Z.; Phillips, J.M.; Wei, Z.; Yi, K. Mergeable summaries. ACM Trans. Database Syst. 2013, 38, 26. [Google Scholar] [CrossRef]
- Laury-Micoulaut, C.A. The n-th centered moment of a multiple convolution and its applications to an intercloud gas model. Astron. Astrophys. 1976, 51, 343–346. [Google Scholar]
- Baier, C.; Katoen, J.P. Principles of Model Checking; The MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Bertsimas, D.; Popescu, I. Optimal inequalities in probability theory: A convex optimization approach. SIAM J. Optim. 2005, 15, 780–804. [Google Scholar] [CrossRef]
- Amalarethinam, D.G.; Selvi, F.K.M. A minimum makespan grid workflow scheduling algorithm. In Proceedings of the 2012 International Conference on Computer Communication and Informatics, Coimbatore, India, 10–12 January 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Alrifai, M.; Risse, T.; Nejdl, W. A hybrid approach for efficient Web service composition with end-to-end QoS constraints. ACM Trans. Web 2012, 6, 7. [Google Scholar] [CrossRef]
- Pietri, I.; Juve, G.; Deelman, E.; Sakellariou, R. A performance model to estimate execution time of scientific workflows on the cloud. In Proceedings of the 9th Workshop on Workflows in Support of Large-Scale Science, New Orleans, LA, USA, 16–21 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 11–19. [Google Scholar]
- Zou, G.; Lu, Q.; Chen, Y.; Huang, R.; Xu, Y.; Xiang, Y. QoS-aware dynamic composition of web services using numerical temporal planning. IEEE Trans. Serv. Comput. 2012, 7, 18–31. [Google Scholar] [CrossRef]
- Asghari Alaie, Y.; Hosseini Shirvani, M.; Rahmani, A.M. A hybrid bi-objective scheduling algorithm for execution of scientific workflows on cloud platforms with execution time and reliability approach. J. Supercomput. 2023, 79, 1451–1503. [Google Scholar] [CrossRef]
- Ciardo, G.; German, R.; Lindemann, C. A characterization of the stochastic process underlying a stochastic Petri net. IEEE Trans. Softw. Eng. 1994, 20, 506–515. [Google Scholar] [CrossRef]
- Meyer, P.J.; Esparza, J.; Offtermatt, P. Computing the expected execution time of probabilistic workflow nets. In Proceedings of the International Conference on Tools and Algorithms for the Construction and Analysis of Systems, Prague, Czech Republic, 6–11 April 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 154–171. [Google Scholar]
- Carnevali, L.; Paolieri, M.; Reali, R.; Vicario, E. Compositional Safe Approximation of Response Time Probability Density Function of Complex Workflows. ACM Trans. Model. Comput. Simul. 2023, 33, 1–26. [Google Scholar] [CrossRef]
- Belgacem, A.; Beghdad-Bey, K. Multi-objective workflow scheduling in cloud computing: Trade-Off between makespan and cost. Cluster Comput. 2022, 25, 579–595. [Google Scholar] [CrossRef]
- Wang, W.; Wu, Q.; Zhang, Z.; Zeng, J.; Zhang, X.; Zhou, M. A probabilistic modeling and evolutionary optimization approach for serverless workflow configuration. Softw. Pract. Exp. 2023, 54, 1697–1713. [Google Scholar] [CrossRef]
- Zhang, L.; Ai, M.; Liu, K.; Chen, J.; Li, K. Reliability enhancement strategies for workflow scheduling under energy consumption constraints in clouds. IEEE Trans. Sustain. Comput. 2024, 9, 155–169. [Google Scholar] [CrossRef]
- Paolieri, M.; Horváth, A.; Vicario, E. Probabilistic model checking of regenerative concurrent systems. IEEE Trans. Softw. Eng. 2016, 42, 153–169. [Google Scholar] [CrossRef][Green Version]
- Bryans, J.; Bowman, H.; Derrick, J. Model checking stochastic automata. ACM Trans. Comput. Log. 2003, 4, 452–492. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).