An Innovative Recompression Scheme for VQ Index Tables
Abstract
1. Introduction
2. Related Work
2.1. Vector Quantization Algorithm
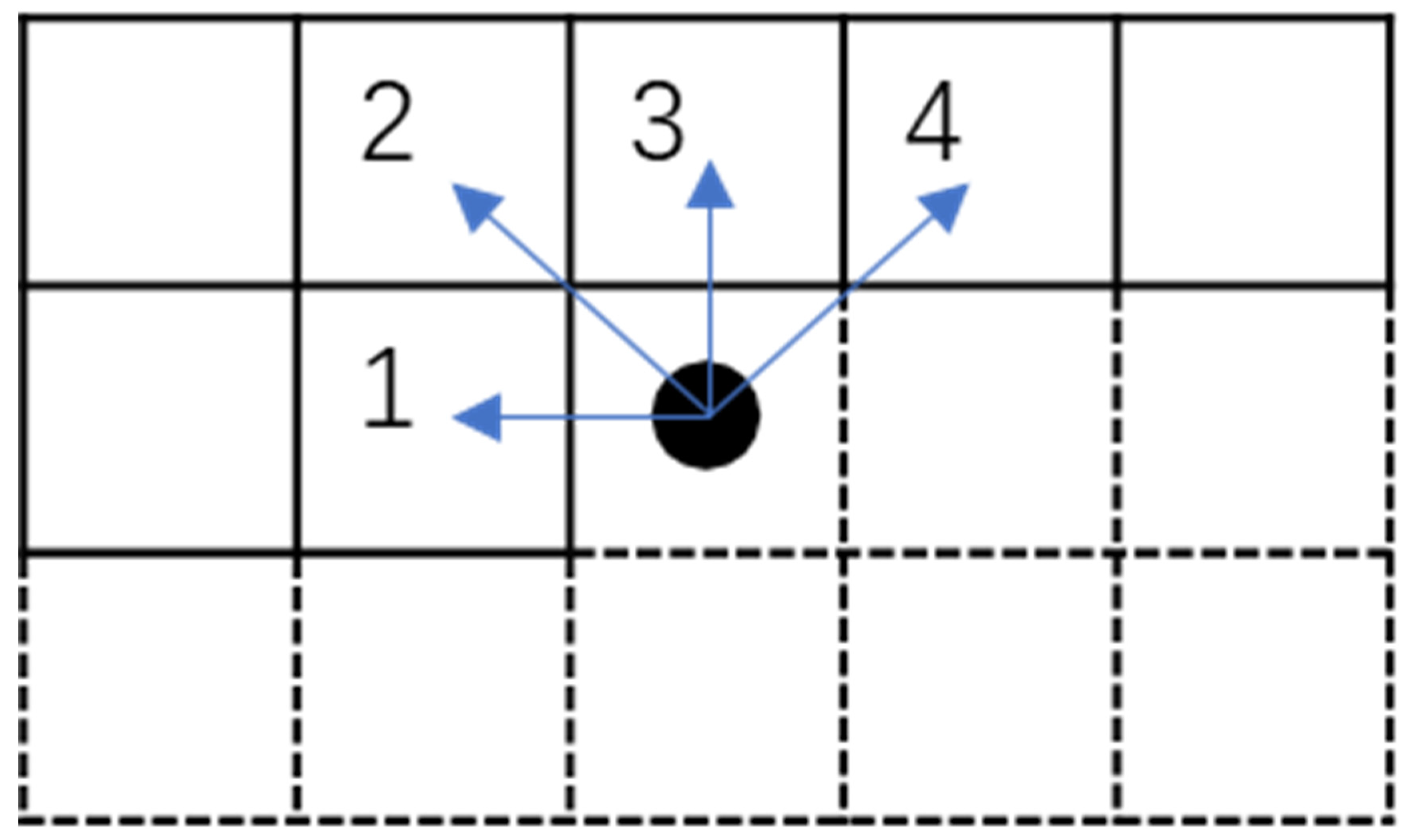
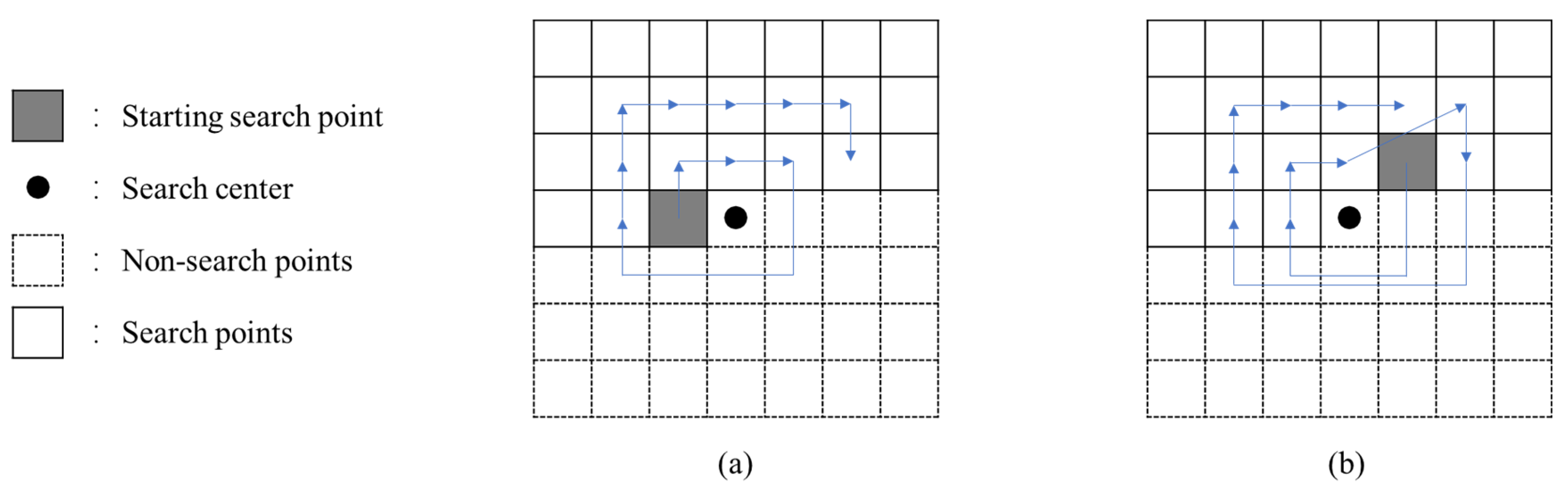
2.2. Search-Order Coding Algorithm
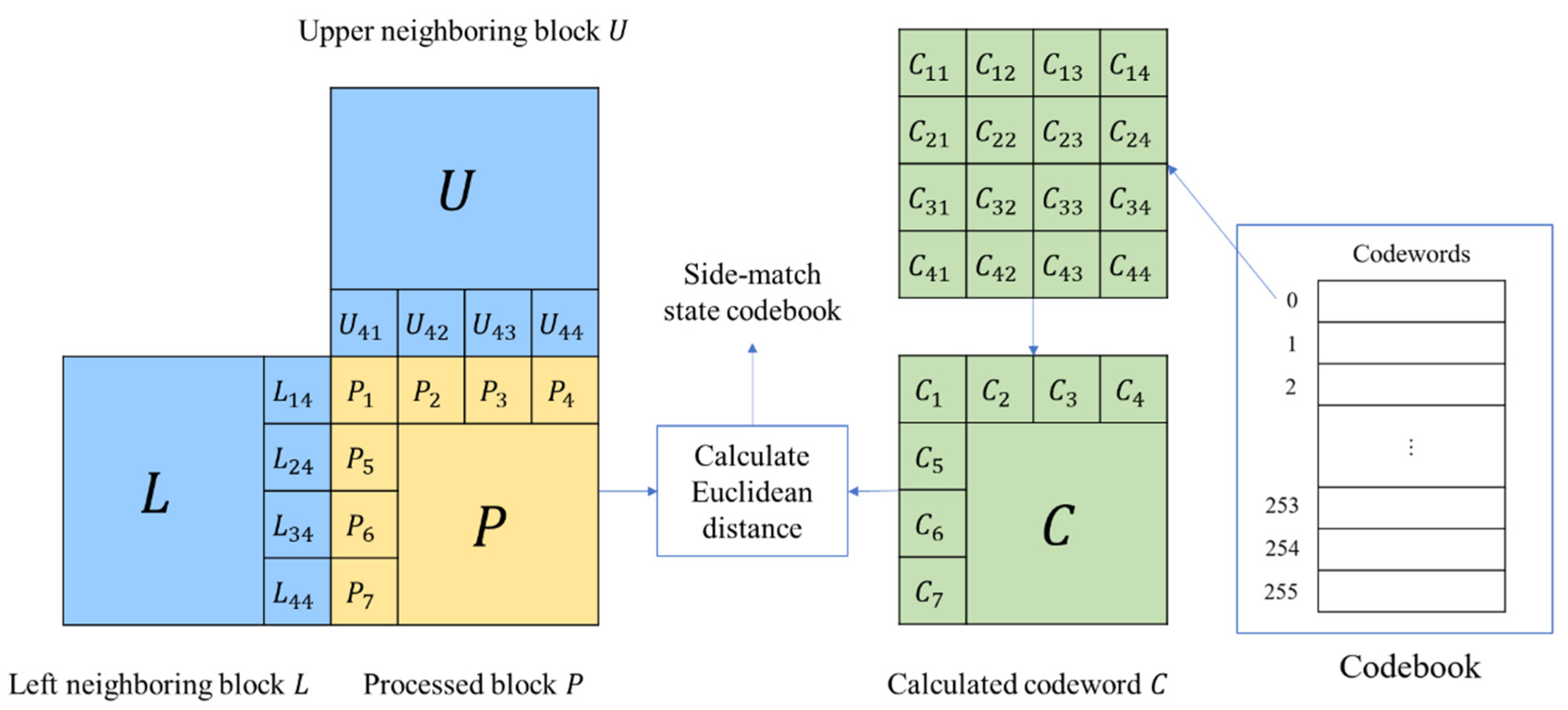
2.3. Side Match Vector Quantization Algorithm
2.4. State Codebook Scheme
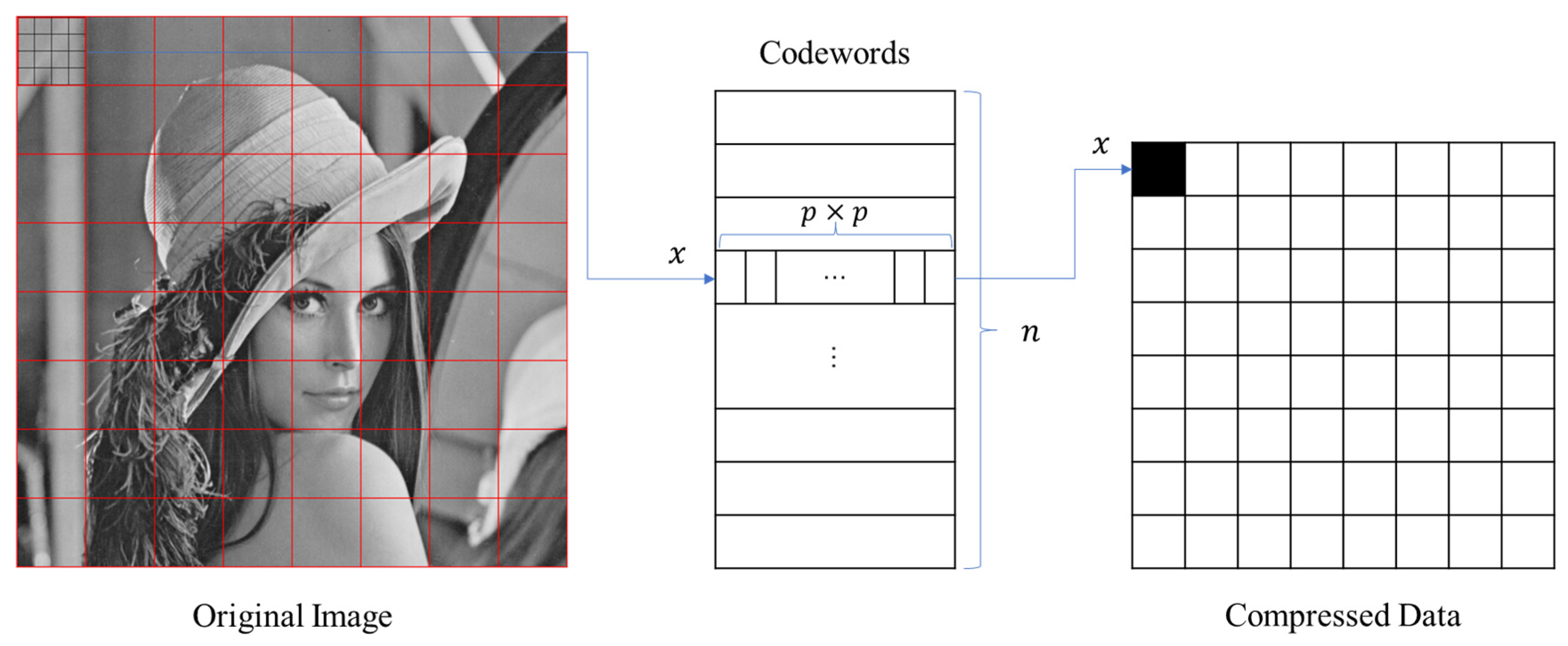
3. Proposed Scheme
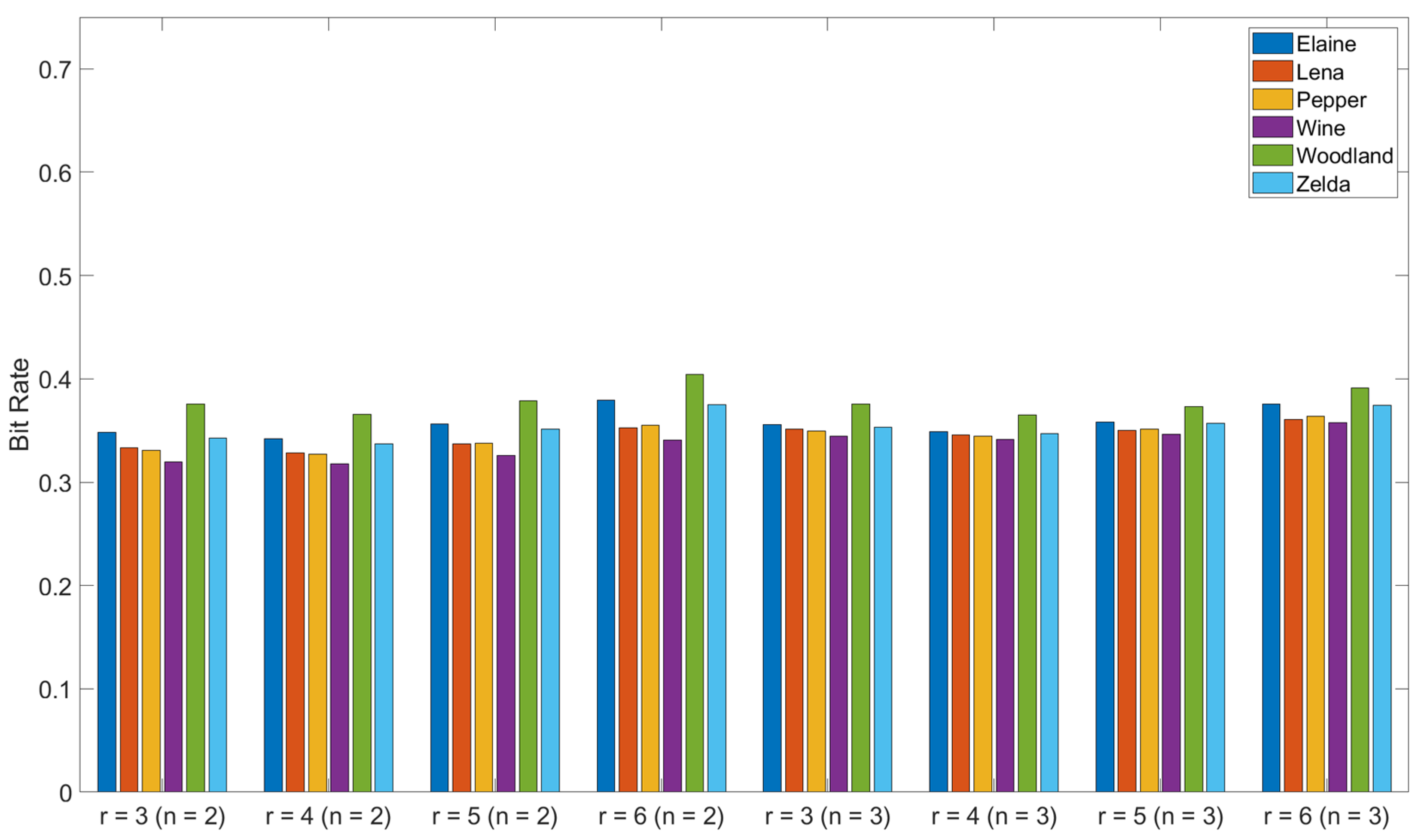
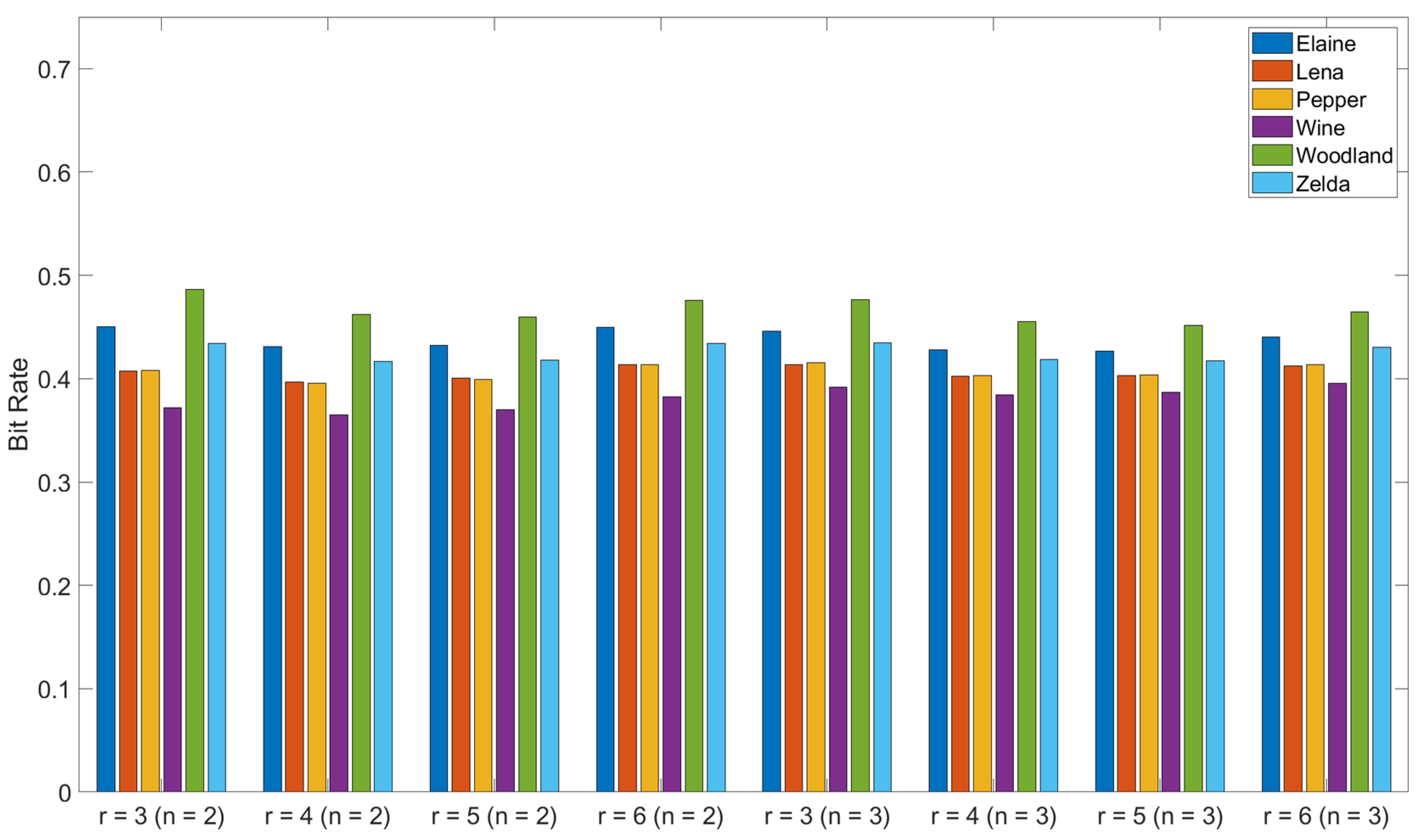
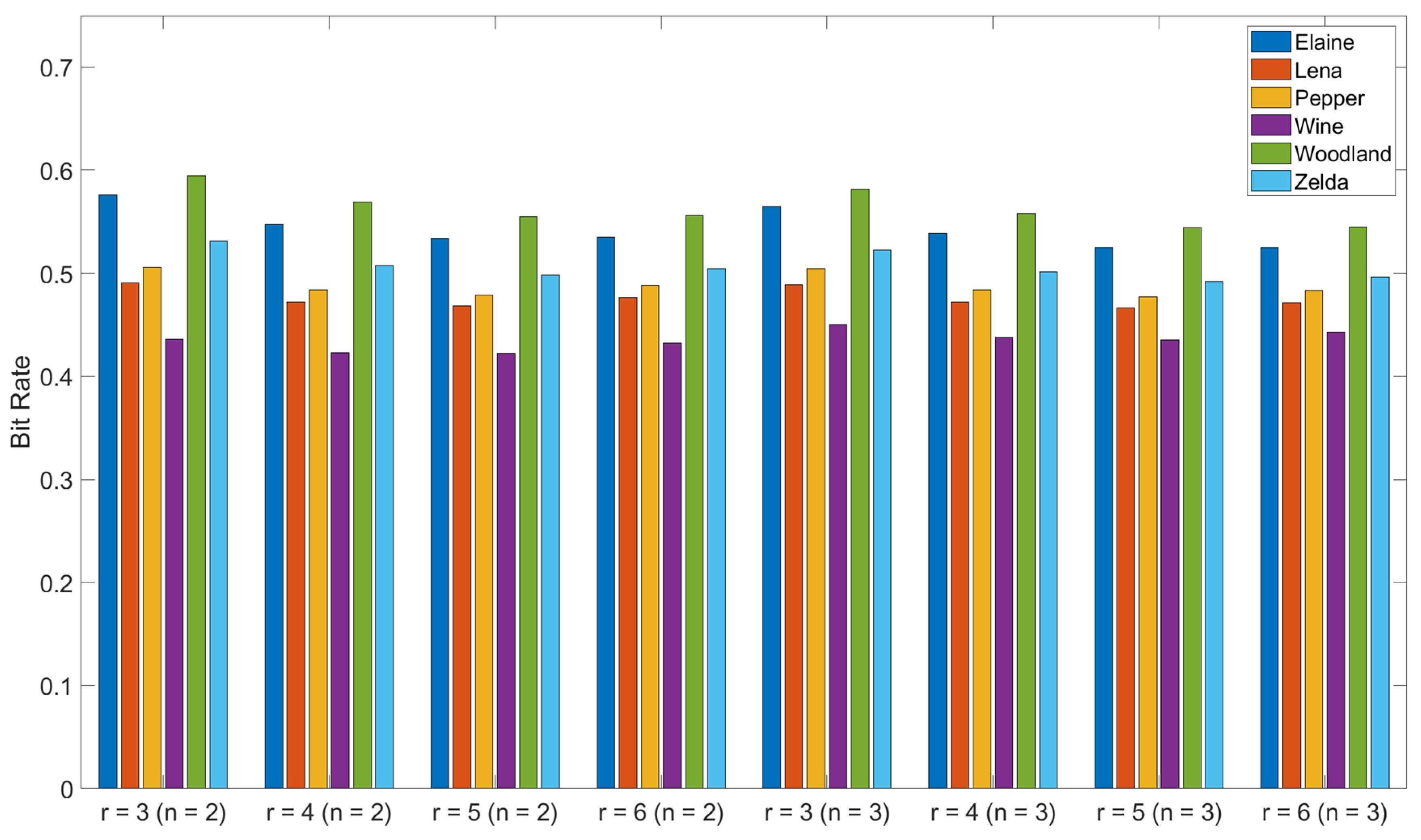
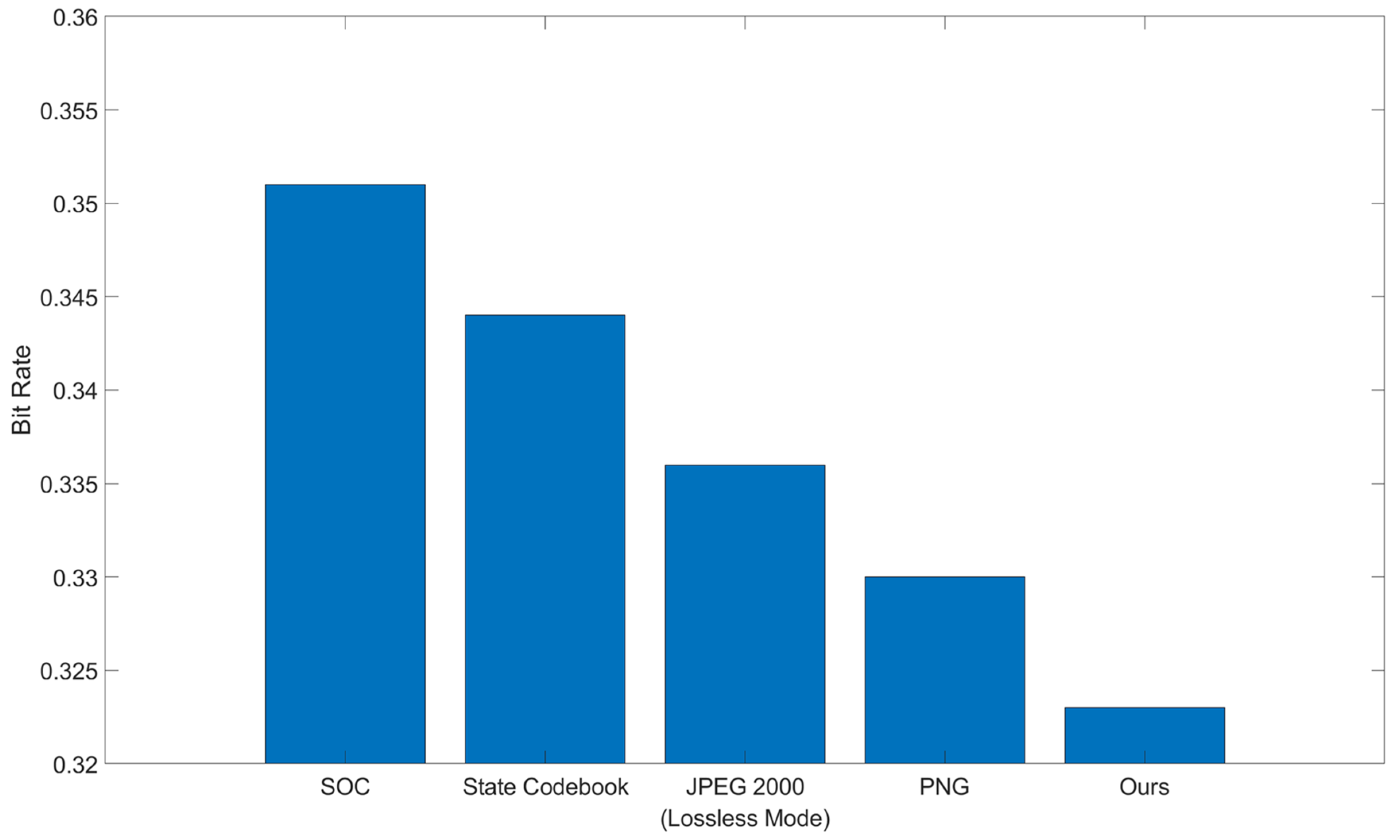
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, L.; Xie, Z.; Yang, C. A novel iterative thresholding algorithm based on plug-and-play priors for compressive sampling. Future Internet 2017, 9, 24. [Google Scholar] [CrossRef]
- Ma, H.; Liu, D.; Yan, N.; Li, H.; Wu, F. End-to-end optimized versatile image compression with wavelet-like transform. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1247–1263. [Google Scholar] [CrossRef] [PubMed]
- Mentzer, F.; Gool, L.V.; Tschannen, M. Learning better lossless compression using lossy compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 6638–6647. [Google Scholar] [CrossRef]
- Chang, C.C.; Chang, J.F.; Kao, W.J.; Horng, J.H. Two-Layer Reversible Data Hiding for VQ-Compressed Images Based on De-Clustering and Indicator-Free Search-Order Coding. Future Internet 2021, 13, 215. [Google Scholar] [CrossRef]
- Razavi, A.; Van den Oord, A.; Vinyals, O. Generating diverse high-fidelity images with vq-vae-2. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Kwon, J.; Lee, S. Improving the robustness of model compression by on-manifold adversarial training. Future Internet 2021, 13, 300. [Google Scholar] [CrossRef]
- Kang, N.; Qiu, S.; Zhang, S.; Li, Z.; Xia, S.T. Pilc: Practical image lossless compression with an end-to-end gpu oriented neural framework. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 14–19 June 2022; pp. 3739–3748. [Google Scholar]
- Duan, Z.; Lu, M.; Ma, J.; Huang, Y.; Ma, Z.; Zhu, F. Qarv: Quantization-aware resnet vae for lossy image compression. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 46, 436–450. [Google Scholar] [CrossRef] [PubMed]
- Gray, R. Vector quantization. IEEE Assp Mag. 1984, 1, 4–29. [Google Scholar] [CrossRef]
- Nasrabadi, N.M.; King, R.A. Image coding using vector quantization: A review. IEEE Trans. Commun. 1988, 36, 957–971. [Google Scholar] [CrossRef]
- Linde, Y.; Buzo, A.; Gray, R. An algorithm for vector quantizer design. IEEE Trans. Commun. 1980, 28, 84–95. [Google Scholar] [CrossRef]
- Dunham, M.; Gray, R. An algorithm for the design of labeled-transition finite-state vector quantizers. IEEE Trans. Commun. 1985, 33, 83–89. [Google Scholar] [CrossRef]
- Kim, T. Side match and overlap match vector quantizers for images. IEEE Trans. Image Process. 1992, 1, 170–185. [Google Scholar] [CrossRef] [PubMed]
- Chang, R.F.; Chen, W.T. Image coding using variable-rate side-match finite-state vector quantization. IEEE Trans. Image Process. 1993, 2, 104–108. [Google Scholar] [CrossRef] [PubMed]
- Chang, R.F.; Chen, W.M. Adaptive edge-based side-match finite-state classified vector quantization with quadtree map. IEEE Trans. Image Process. 1996, 5, 378–383. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.S.; Chang, C.C. A new image coding algorithm using variable-rate side-match finite-state vector quantization. IEEE Trans. Image Process. 1997, 6, 1185–1187. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.C.; Tsai, P.C.; Wang, J.S. Three-sided side match finite-state vector quantization. IEEE Trans. Circuits Syst. Video Technol. 2000, 10, 51–58. [Google Scholar] [CrossRef]
- Chang, C.C.; Liao, C.T. An image coding scheme using SMVQ and support vector machines. Neurocomputing 2006, 69, 2327–2335. [Google Scholar] [CrossRef]
- Gray, R.; Linde, Y. Vector quantizers and predictive quantizers for Gauss-Markov sources. IEEE Trans. Commun. 1982, 30, 381–389. [Google Scholar] [CrossRef]
- Hang, H.M.; Woods, J. Predictive vector quantization of images. IEEE Trans. Commun. 1985, 33, 1208–1219. [Google Scholar] [CrossRef]
- Nasrabadi, N.M.; Feng, Y. Image compression using address-vector quantization. IEEE Trans. Commun. 1990, 38, 2166–2173. [Google Scholar] [CrossRef]
- Lo, K.T.; Feng, J. Predictive mean search algorithms for fast VQ encoding of images. IEEE Trans. Consum. Electron. 1995, 41, 327–331. [Google Scholar] [CrossRef]
- Shanbehzadeh, J.; Ogunbona, P.O. Index-compressed vector quantisation based on index mapping. IEE Proc. Vis. Image Signal Process. 1997, 144, 31–38. [Google Scholar] [CrossRef][Green Version]
- Hsieh, C.H.; Tsai, J.C. Lossless compression of VQ index with search-order coding. IEEE Trans. Image Process. 1996, 5, 1579–1582. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.M.; Ku, B.H.; Wu, C.C.; Lin, T.Y. Improvement of VQ index compression with relative index tables. In Proceedings of the 2008 International Conference on Computer Science and Information Technology, Singapore, 29 August–2 September 2008; pp. 492–496. [Google Scholar]
- Chang, C.C.; Chen, G.M.; Lin, C.C. Lossless Compression Schemes of Vector Quantization Indices Using State Codebook. J. Softw. 2009, 4, 274–282. [Google Scholar] [CrossRef]
- Lee, R.C.T.; Chin, Y.H.; Chang, S.C. Application of principal component analysis to multikey searching. IEEE Trans. Softw. Eng. 1976, SE-2, 185–193. [Google Scholar] [CrossRef]
- Skodras, A.; Christopoulos, C.; Ebrahimi, T. The JPEG 2000 still image compression standard. IEEE Signal Process. Mag. 2001, 18, 36–58. [Google Scholar] [CrossRef]
- Roelofs, G. PNG: The Definitive Guide; O’Reilly & Associates, Inc.: Sebastopol, CA, USA, 1999. [Google Scholar]
- Bas, P.; Furon, T. Image Database of BOWS-2. Volume 20. Available online: https://bows2.ec-lille.fr/ (accessed on 20 June 2017).


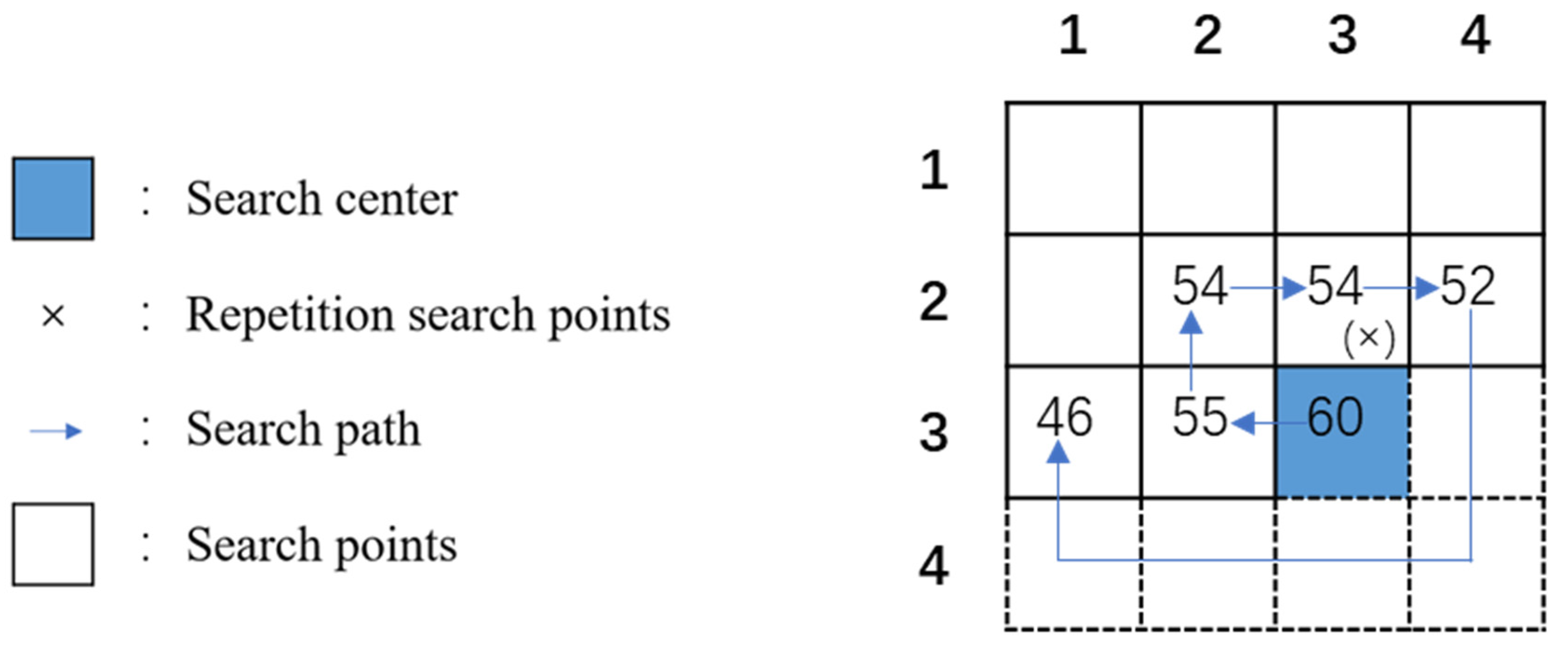
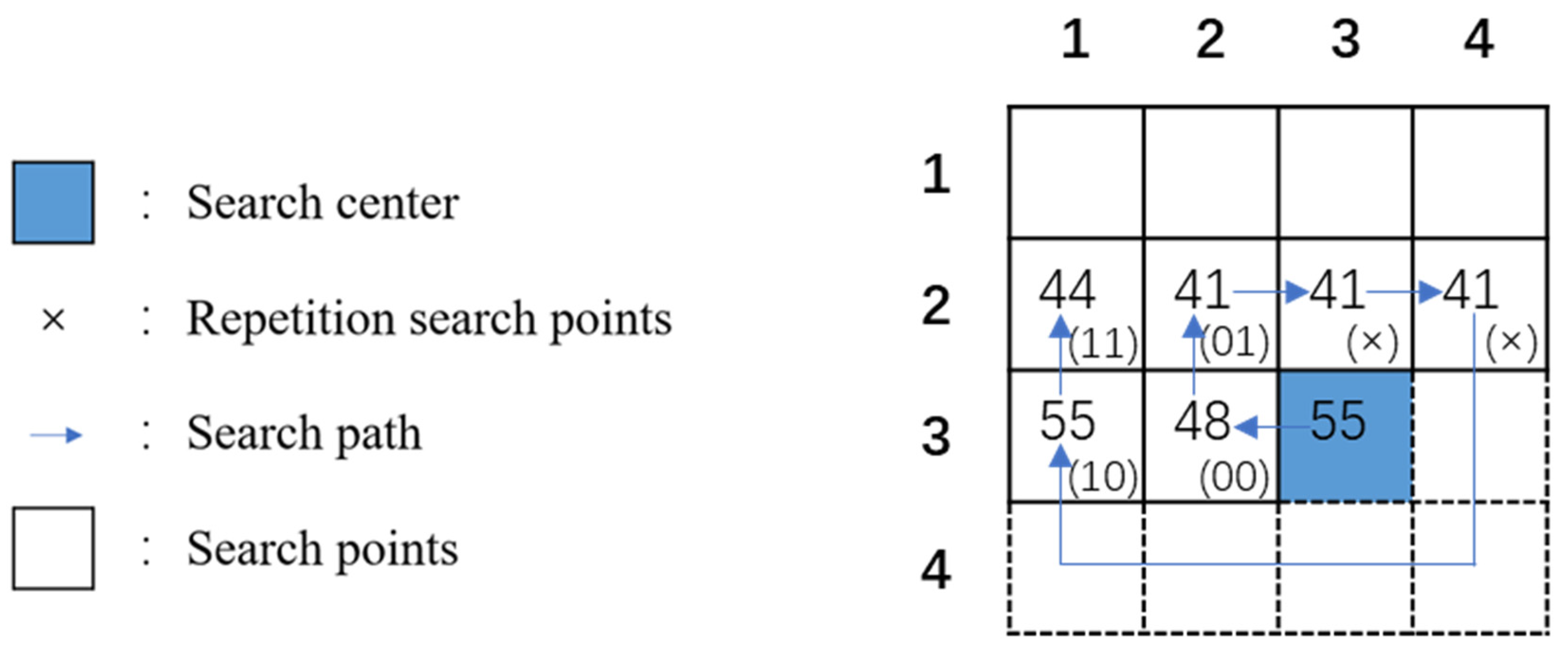
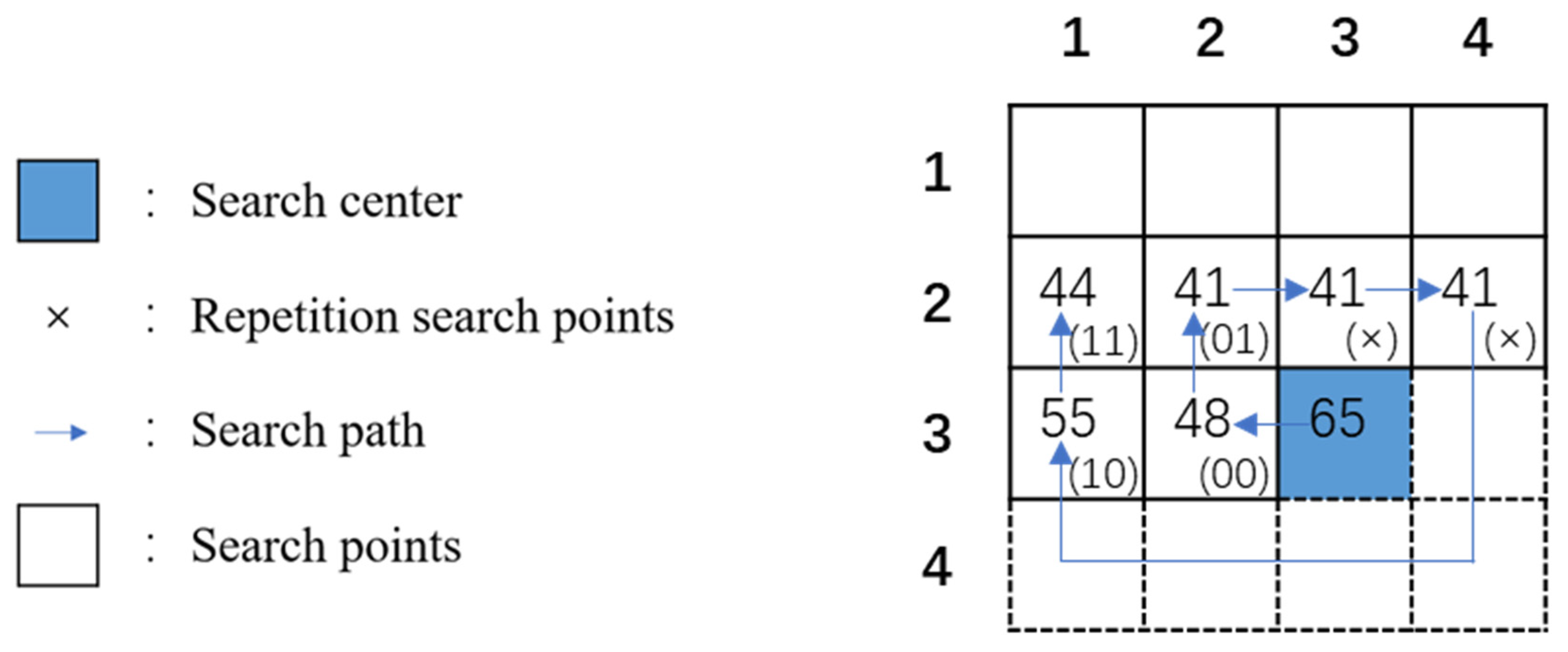


| The similar neighboring (3, 2), which equals “55” | |
| The index of the state codebook | The indices of the closest codewords of “55” in the codebook |
| 0000 | 51 |
| ---- | 52 |
| 0001 | 53 |
| ---- | 54 |
| 0010 | 56 |
| 0011 | 57 |
| The similar neighboring (2, 2), which equals “54” | |
| The index of the state codebook | The indices of the closest codewords of “54” in the codebook |
| 0100 | 49 |
| 0101 | 50 |
| 0110 | 58 |
| 0111 | 89 |
| The similar neighboring (2, 4), which equals “52” | |
| The index of the state codebook | The indices of the closest codewords of “52” in the codebook |
| 1000 | 47 |
| 1001 | 48 |
| 1010 | 60 |
| 1011 | 61 |
| The similar neighboring (3, 1), which equals “46” | |
| The index of the state codebook | The indices of the closest codewords of “46” in the codebook |
| 1100 | 44 |
| 1101 | 45 |
| 1110 | 62 |
| 1111 | 63 |
| Side Match Index | Codeword Index | Euclidean Distance |
|---|---|---|
| 0000 | 44 | 5.62 |
| 0001 | 86 | 7.12 |
| 0010 | 55 | 26.84 |
| 0011 | 77 | 72.23 |
| 0100 | 48 | 72.77 |
| 0101 | 41 | 108.08 |
| 0110 | 89 | 118.02 |
| 0111 | 73 | 191.51 |
| 1000 | 96 | 211.50 |
| 1001 | 83 | 219.61 |
| 1010 | 79 | 226.16 |
| 1011 | 75 | 259.82 |
| 1100 | 65 | 272.74 |
| 1101 | 108 | 290.89 |
| 1110 | 99 | 360.81 |
| 1111 | 85 | 364.79 |
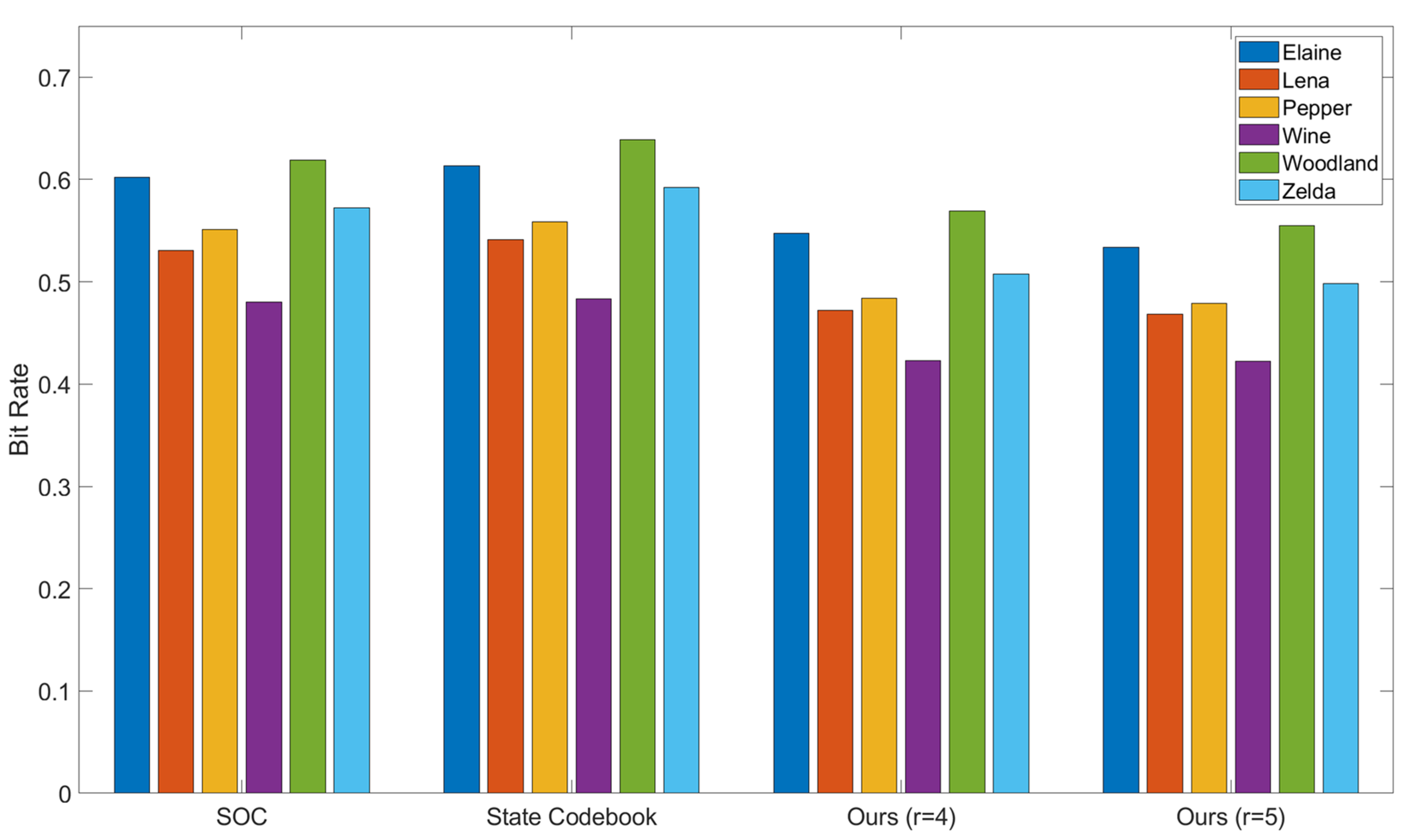
| Images | SOC [24] | Improvement Rate | State Codebook [26] | Improvement Rate | Ours |
| Elaine | 0.4043 | 15.35% | 0.3880 | 11.78% | 0.3423 |
| Lena | 0.3662 | 10.28% | 0.3538 | 7.13% | 0.3286 |
| Pepper | 0.3726 | 12.27% | 0.3602 | 9.25% | 0.3269 |
| Wine | 0.3545 | 10.44% | 0.3393 | 6.43% | 0.3175 |
| Woodland | 0.4322 | 15.41% | 0.4088 | 10.56% | 0.3656 |
| Zelda | 0.4007 | 15.86% | 0.3901 | 13.58% | 0.3371 |
| Average | 0.3884 | 13.41% | 0.3733 | 9.92% | 0.3363 |
| Images | SOC [24] | Improvement Rate | State Codebook [26] | Improvement Rate | Ours |
| Elaine | 0.3940 | 11.39% | 0.3858 | 9.51% | 0.3491 |
| Lena | 0.3697 | 6.52% | 0.3644 | 5.16% | 0.3456 |
| Pepper | 0.3760 | 8.43% | 0.3704 | 7.04% | 0.3443 |
| Wine | 0.3678 | 7.27% | 0.3597 | 5.18% | 0.3411 |
| Woodland | 0.4113 | 11.18% | 0.3988 | 8.40% | 0.3653 |
| Zelda | 0.3939 | 11.88% | 0.3887 | 10.70% | 0.3471 |
| Average | 0.3854 | 9.52% | 0.3780 | 7.73% | 0.3487 |
| best | |||||
| Images | SOC [24] | Improvement Rate | State Codebook [26] | Improvement Rate | Ours |
| Elaine | 0.3940 | 13.12% | 0.3858 | 11.28% | 0.3423 |
| Lena | 0.3662 | 10.28% | 0.3538 | 7.13% | 0.3286 |
| Pepper | 0.3726 | 12.27% | 0.3602 | 9.25% | 0.3269 |
| Wine | 0.3545 | 10.44% | 0.3393 | 6.43% | 0.3175 |
| Woodland | 0.4113 | 11.18% | 0.3988 | 8.40% | 0.3653 |
| Zelda | 0.3939 | 14.41% | 0.3887 | 13.26% | 0.3371 |
| Average | 0.3821 | 11.99% | 0.3711 | 9.38% | 0.3363 |
| Images | SOC [24] | Improvement Rate | State Codebook [26] | Improvement Rate | Ours |
| Elaine | 0.5064 | 14.87% | 0.5011 | 13.97% | 0.4311 |
| Lena | 0.4501 | 11.89% | 0.4441 | 10.71% | 0.3965 |
| Pepper | 0.4558 | 13.27% | 0.4499 | 12.14% | 0.3953 |
| Wine | 0.4127 | 11.49% | 0.4055 | 9.91% | 0.3653 |
| Woodland | 0.5322 | 13.16% | 0.5270 | 12.29% | 0.4622 |
| Zelda | 0.4869 | 14.42% | 0.4902 | 14.99% | 0.4167 |
| Average | 0.4740 | 13.26% | 0.4696 | 12.44% | 0.4112 |
| Images | SOC [24] | Improvement Rate | State Codebook [26] | Improvement Rate | Ours |
| Elaine | 0.4878 | 12.27% | 0.4881 | 12.33% | 0.4279 |
| Lena | 0.4378 | 8.04% | 0.4378 | 8.03% | 0.4026 |
| Pepper | 0.4462 | 9.70% | 0.4457 | 9.60% | 0.4029 |
| Wine | 0.4196 | 8.46% | 0.4177 | 8.05% | 0.3841 |
| Woodland | 0.5112 | 10.96% | 0.5093 | 10.63% | 0.4552 |
| Zelda | 0.4743 | 11.82% | 0.4809 | 13.03% | 0.4183 |
| Average | 0.4628 | 10.30% | 0.4633 | 10.38% | 0.4152 |
| best | |||||
| Images | SOC [24] | Improvement Rate | State Codebook [26] | Improvement Rate | Ours |
| Elaine | 0.4878 | 12.27% | 0.4881 | 12.33% | 0.4279 |
| Lena | 0.4378 | 9.43% | 0.4378 | 9.41% | 0.3965 |
| Pepper | 0.4462 | 11.40% | 0.4457 | 11.30% | 0.3953 |
| Wine | 0.4127 | 11.49% | 0.4055 | 9.91% | 0.3653 |
| Woodland | 0.5112 | 10.96% | 0.5093 | 10.63% | 0.4552 |
| Zelda | 0.4743 | 12.15% | 0.4809 | 13.36% | 0.4167 |
| Average | 0.4617 | 11.30% | 0.4612 | 11.22% | 0.4095 |
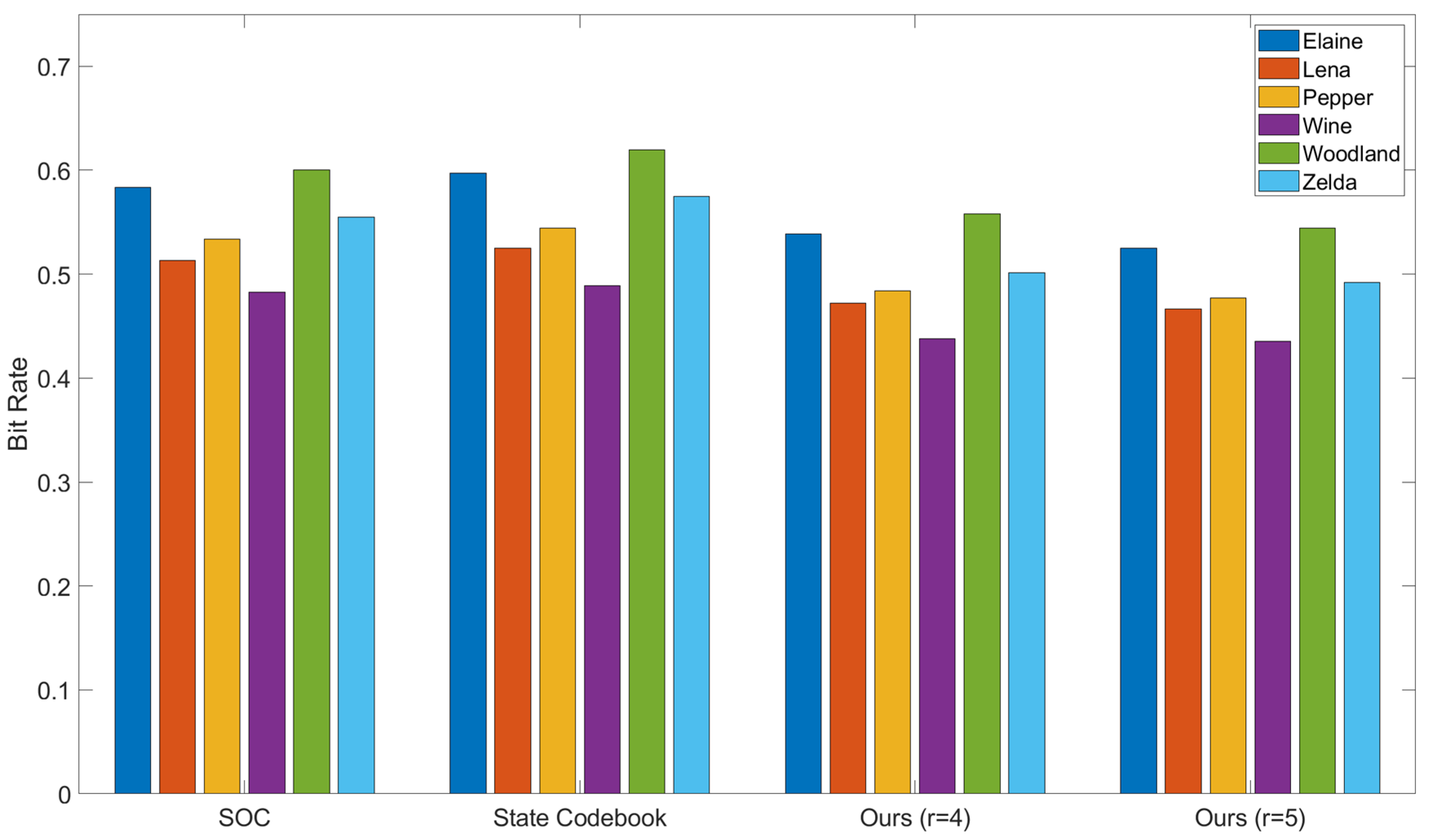
| Images | SOC [24] | Improvement Rate | State Codebook [26] | Improvement Rate | Ours |
| Elaine | 0.6024 | 9.12% | 0.6131 | 10.70% | 0.5475 |
| Lena | 0.5305 | 11.00% | 0.5412 | 12.76% | 0.4721 |
| Pepper | 0.5510 | 12.16% | 0.5583 | 13.31% | 0.4840 |
| Wine | 0.4804 | 11.92% | 0.4834 | 12.47% | 0.4231 |
| Woodland | 0.6190 | 8.09% | 0.6390 | 10.97% | 0.5689 |
| Zelda | 0.5725 | 11.35% | 0.5924 | 14.32% | 0.5076 |
| Average | 0.5593 | 10.51% | 0.5712 | 12.38% | 0.5005 |
| Images | SOC [24] | Improvement Rate | State Codebook [26] | Improvement Rate | Ours |
| Elaine | 0.5838 | 7.74% | 0.5974 | 9.83% | 0.5386 |
| Lena | 0.5130 | 8.00% | 0.5248 | 10.07% | 0.4719 |
| Pepper | 0.5339 | 9.39% | 0.5442 | 11.11% | 0.4837 |
| Wine | 0.4826 | 9.26% | 0.4887 | 10.40% | 0.4379 |
| Woodland | 0.6001 | 7.03% | 0.6199 | 10.00% | 0.5579 |
| Zelda | 0.5550 | 9.71% | 0.5747 | 12.81% | 0.5011 |
| Average | 0.5447 | 8.48% | 0.5583 | 10.70% | 0.4985 |
| best | |||||
| Images | SOC [24] | Improvement Rate | State Codebook [26] | Improvement Rate | Ours |
| Elaine | 0.5838 | 7.74% | 0.5974 | 9.83% | 0.5386 |
| Lena | 0.5130 | 8.00% | 0.5248 | 10.07% | 0.4719 |
| Pepper | 0.5339 | 9.39% | 0.5442 | 11.11% | 0.4837 |
| Wine | 0.4804 | 11.92% | 0.4834 | 12.47% | 0.4231 |
| Woodland | 0.6001 | 7.03% | 0.6199 | 10.00% | 0.5579 |
| Zelda | 0.5550 | 9.71% | 0.5747 | 12.81% | 0.5011 |
| Average | 0.5444 | 8.87% | 0.5574 | 11.00% | 0.4961 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Liu, J.-C.; Chang, C.-C.; Chang, C.-C. An Innovative Recompression Scheme for VQ Index Tables. Future Internet 2024, 16, 297. https://doi.org/10.3390/fi16080297
Lin Y, Liu J-C, Chang C-C, Chang C-C. An Innovative Recompression Scheme for VQ Index Tables. Future Internet. 2024; 16(8):297. https://doi.org/10.3390/fi16080297
Chicago/Turabian StyleLin, Yijie, Jui-Chuan Liu, Ching-Chun Chang, and Chin-Chen Chang. 2024. "An Innovative Recompression Scheme for VQ Index Tables" Future Internet 16, no. 8: 297. https://doi.org/10.3390/fi16080297
APA StyleLin, Y., Liu, J.-C., Chang, C.-C., & Chang, C.-C. (2024). An Innovative Recompression Scheme for VQ Index Tables. Future Internet, 16(8), 297. https://doi.org/10.3390/fi16080297







