A Low-Complexity Solution for Optimizing Binary Intelligent Reflecting Surfaces towards Wireless Communication
Abstract
1. Introduction
| Sl. No. | Paper Title | Pros | Cons | Discussion |
|---|---|---|---|---|
| 1. | Secrecy Rate Maximization for IRS-Assisted Multi-Antenna Communications (2019) [21] |
|
| This paper demonstrates that IRS can significantly boost secrecy rates by careful phase shift optimization, addressing security in wireless networks. |
| 2. | Secure Wireless Communication via IRS (2019) [22] |
|
| This study highlights the potential of IRS in secure communication by optimizing reflect beamforming to enhance desired signals and suppress eavesdropping. |
| 3. | Configuring an IRS for Wireless Communications (2021) [23] |
|
| This paper showcases the practical applications of IRS, underlining its feasibility and effectiveness in enhancing wireless communication systems in controlled environments. |
| 4. | Intelligent Reflecting Surface Enhanced Wireless Network: Joint Active and Passive Beamforming Design(2018) [24] |
|
| This paper proposes a centralized algorithm using semidefinite relaxation (SDR) for the joint optimization of transmit and reflect beamforming, and a distributed algorithm to reduce overheads. The IRS significantly improves link quality and coverage. |
| 5. | SChannel Estimation for Reconfigurable Intelligent Surface Assisted High-Mobility Wireless Systems (2022) [15] |
|
| This research addresses the challenges of channel estimation in high-mobility environments, proposing a novel algorithm that enhances estimation accuracy by leveraging the IRS’s ability to adjust phase shifts dynamically. |
| 6. | Stacked Intelligent Metasurface-Aided MIMO Transceiver Design (2024) [14] |
|
| This recent work proposes a novel SIM concept for MIMO systems, offering significant improvements in processing speed and energy efficiency but requiring further research to address existing challenges. |
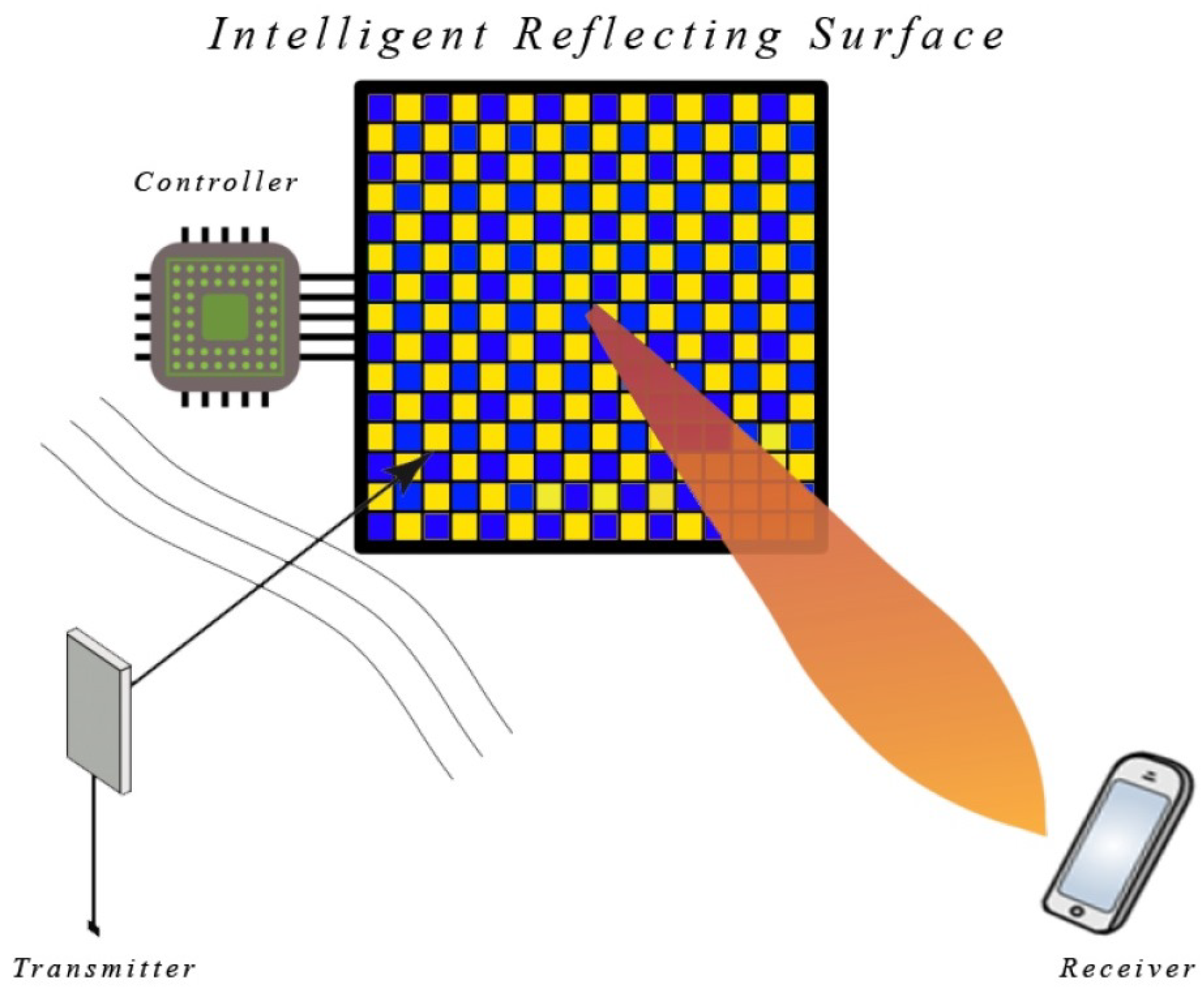
2. System Model
3. Channel Estimation
3.1. Noise Estimation
3.2. Finding and
4. Rate Optimization
4.1. Initialization
| Algorithm 1: Initialization algorithm |
 |
4.2. Further Optimization
| Algorithm 2: Further optimization |
 |
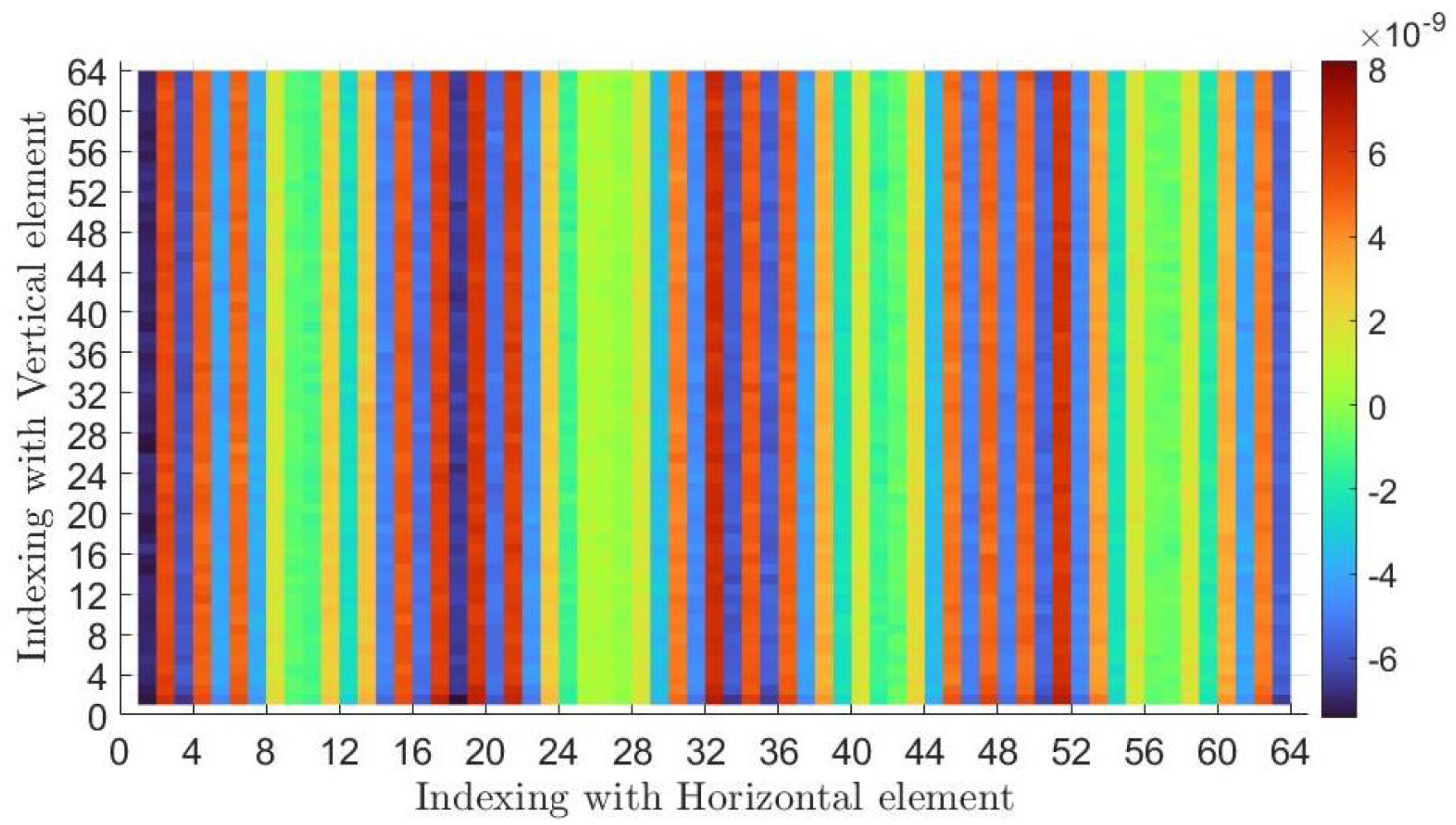
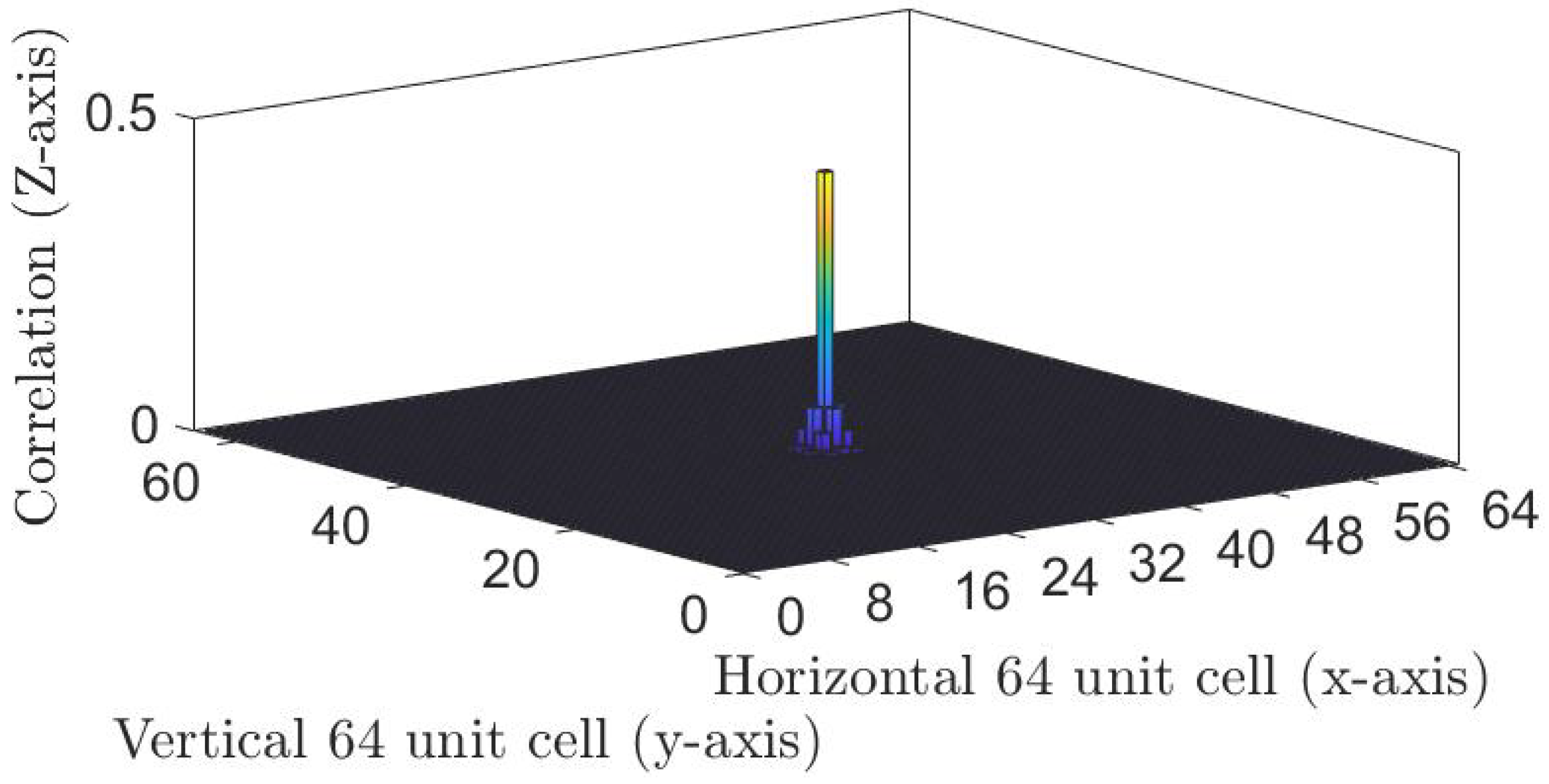
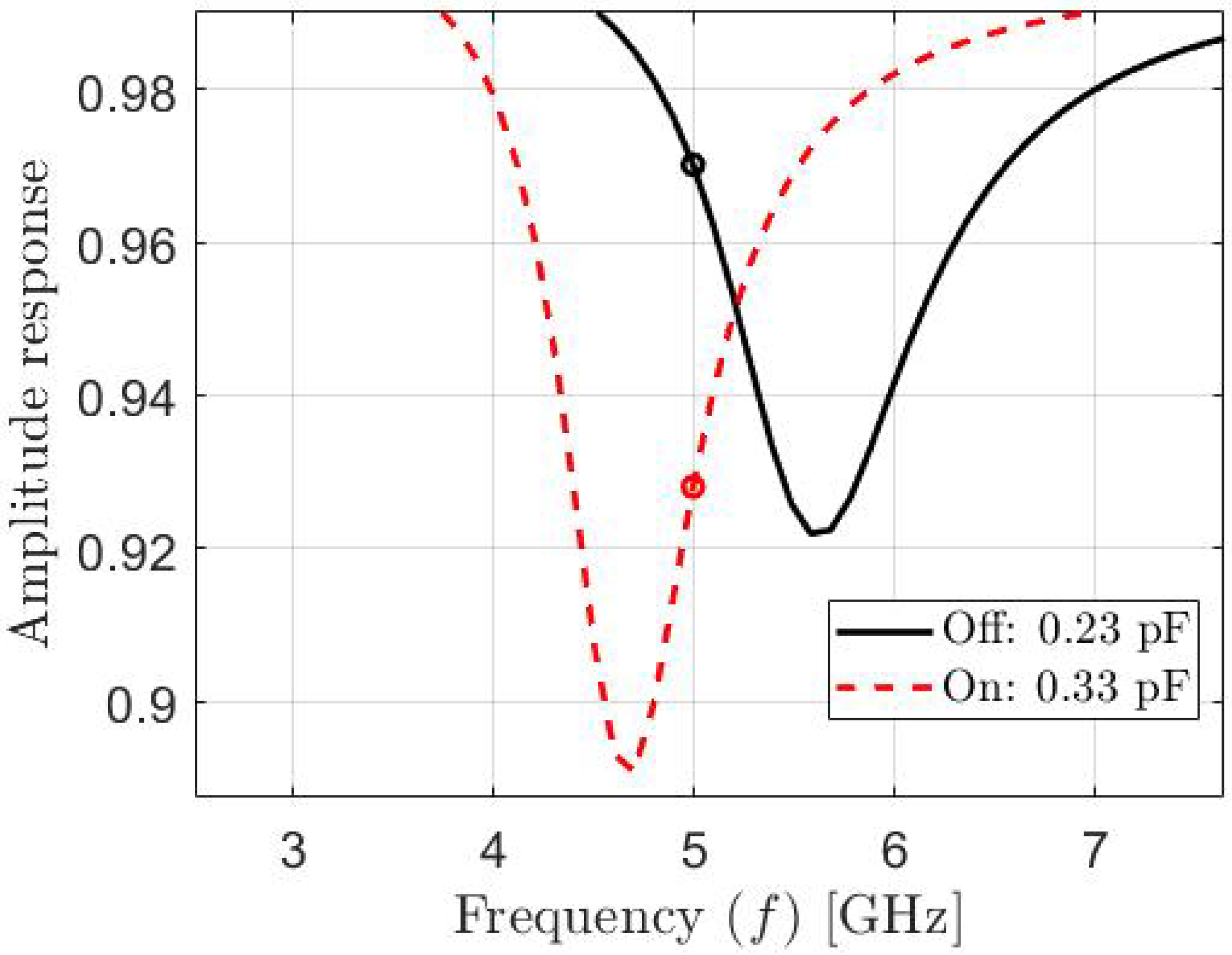
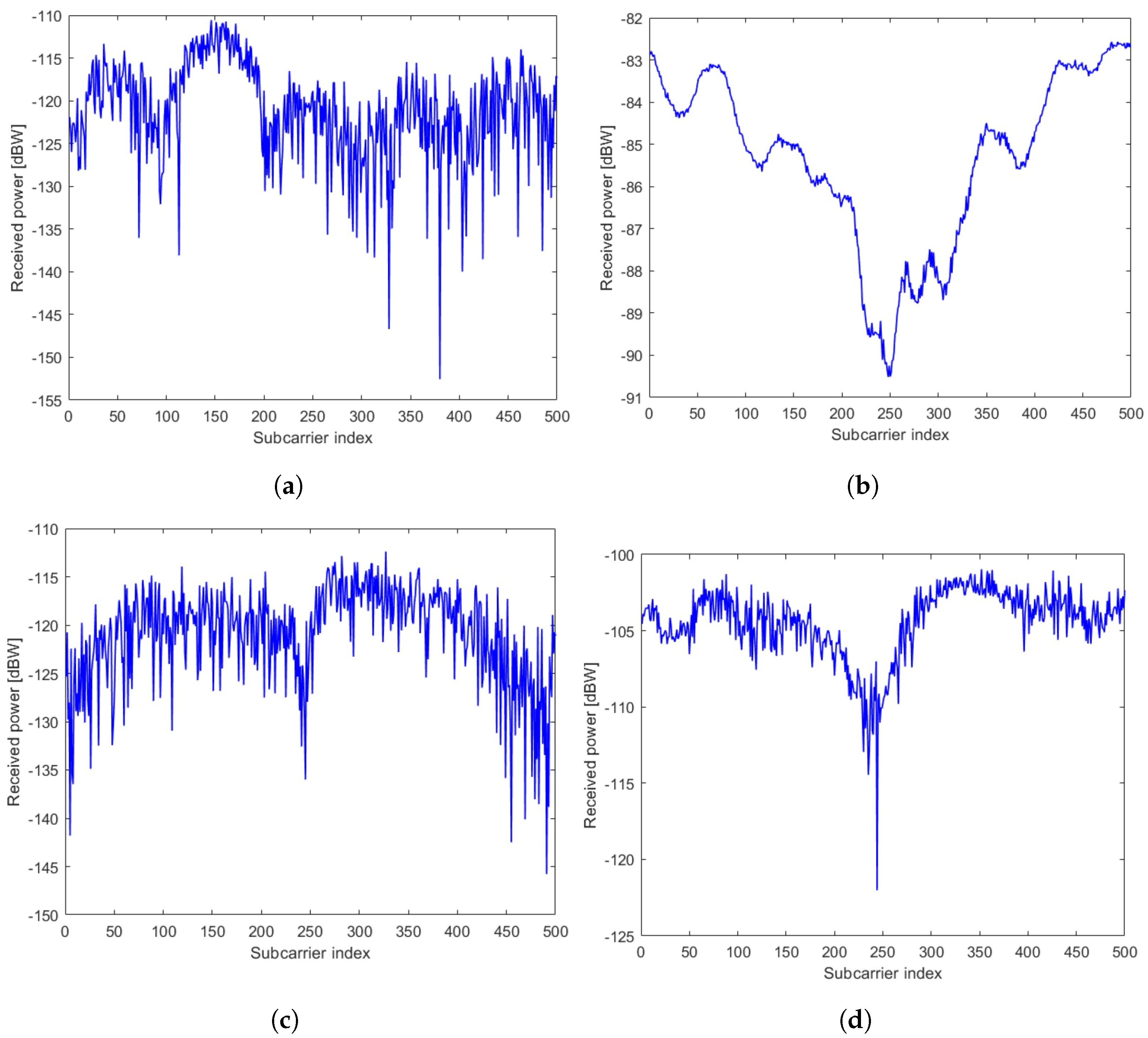
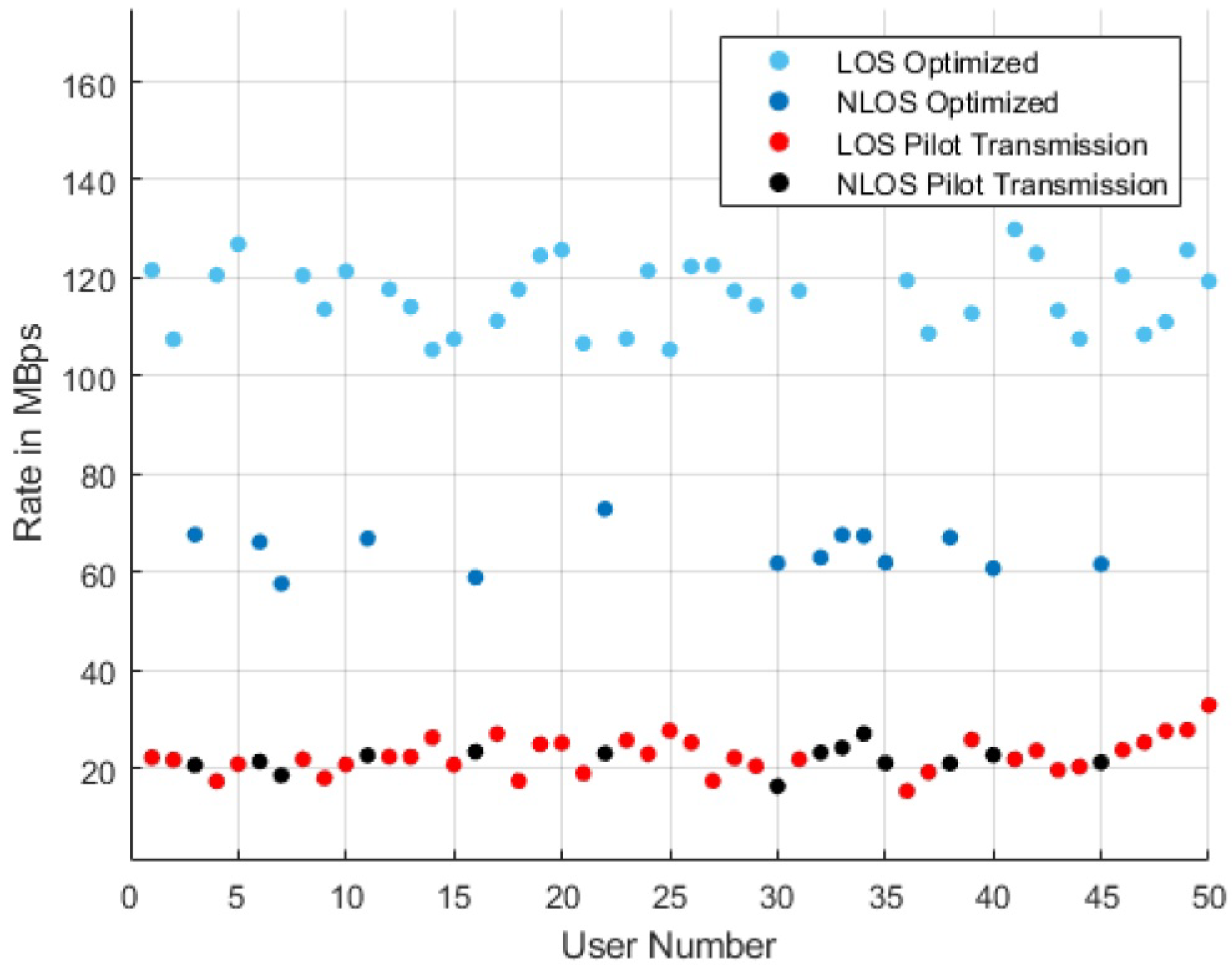
5. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kadir, E.A.; Shubair, R.; Rahim, S.K.A.; Himdi, M.; Kamarudin, M.R.; Rosa, S.L. B5G and 6G: Next Generation Wireless Communications Technologies, Demand and Challenges. In Proceedings of the 2021 International Congress of Advanced Technology and Engineering (ICOTEN), Taiz, Yemen, 4–5 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Feng, Y.; Hu, Q.; Qu, K.; Yang, W.; Zheng, Y.; Chen, K. Reconfigurable Intelligent Surfaces: Design, Implementation, and Practical Demonstration. Electromagn. Sci. 2023, 1, 0020111. [Google Scholar] [CrossRef]
- Pitilakis, A.; Tsilipakos, O.; Liu, F.; Kossifos, K.M.; Tasolamprou, A.C.; Kwon, D.-H.; Mirmoosa, M.S.; Manessis, D.; Kantartzis, N.V.; Liaskos, C.; et al. A Multi-Functional Reconfigurable Metasurface: Electromagnetic Design Accounting for Fabrication Aspects. IEEE Trans. Antennas Propag. 2020, 69, 1440–1454. [Google Scholar] [CrossRef]
- Huang, C.; Zappone, A.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Reconfigurable Intelligent Surfaces for Energy Efficiency in Wireless Communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
- Sultana, A.; Fernando, X. Intelligent reflecting surface-aided device-to-device communication: A deep reinforcement learning approach. Future Internet 2022, 14, 256. [Google Scholar] [CrossRef]
- Okogbaa, F.C.; Ahmed, Q.Z.; Khan, F.A.; Abbas, W.B.; Che, F.; Zaidi, S.A.R.; Alade, T. Design and application of intelligent reflecting surface (IRS) for beyond 5G wireless networks: A review. Sensors 2022, 22, 2436. [Google Scholar] [CrossRef] [PubMed]
- Janawade, S.A.; Prabu, K.; Krishnamoorthy, K. Switchable Wideband phase Gradient Beam Steering Reflector/Absorber for Applications such as Intelligent Reflecting Surfaces. In Proceedings of the 2023 3rd International Conference on Intelligent Technologies (CONIT), Hubli, India, 23–25 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L.; Wymeersch, H.; Hoydis, J.; Marzetta, T.L. Massive MIMO is a reality—What is next? Digit. Signal Process. 2019, 94, 3–20. [Google Scholar] [CrossRef]
- Abeywickrama, S.; Zhang, R.; Wu, Q.; Yuen, C. Intelligent Reflecting Surface: Practical Phase Shift Model and Beamforming Optimization. IEEE Trans. Commun. 2020, 68, 5849–5863. [Google Scholar] [CrossRef]
- Björnson, E.; Eldar, Y.C.; Larsson, E.G.; Lozano, A.; Poor, H.V. Twenty-Five Years of Signal Processing Advances for Multiantenna Communications: From theory to mainstream technology. IEEE Signal Process. Mag. 2023, 40, 107–117. [Google Scholar] [CrossRef]
- An, J.; Xu, C.; Gan, L.; Hanzo, L. Low-complexity channel estimation and passive beamforming for RIS-assisted MIMO systems relying on discrete phase shifts. IEEE Trans. Commun. 2021, 70, 1245–1260. [Google Scholar] [CrossRef]
- An, J.; Xu, C.; Wu, Q.; Ng, D.W.K.; Renzo, M.D.; Yuen, C.; Hanzo, L. Codebook-based solutions for reconfigurable intelligent surfaces and their open challenges. IEEE Wirel. Commun. 2022, 31, 134–141. [Google Scholar] [CrossRef]
- An, J.; Xu, C.; Ng, D.W.K.; Alexandropoulos, G.C.; Huang, C.; Yuen, C.; Hanzo, L. Stacked intelligent metasurfaces for efficient holographic MIMO communications in 6G. IEEE J. Sel. Areas Commun. 2023, 41, 2380–2396. [Google Scholar] [CrossRef]
- An, J.; Yuen, C.; Xu, C.; Li, H.; Ng, D.W.K.; Renzo, M.D.; Debbah, M.; Hanzo, L. Stacked intelligent metasurface-aided MIMO transceiver design. IEEE Wirel. Commun. 2024, 1–9. [Google Scholar] [CrossRef]
- Xu, C.; An, J.; Bai, T.; Sugiura, S.; Maunder, R.G.; Wang, Z.; Yang, L.; Hanzo, L. Channel estimation for reconfigurable intelligent surface assisted high-mobility wireless systems. IEEE Trans. Veh. Technol. 2022, 72, 718–734. [Google Scholar] [CrossRef]
- Xu, C.; An, J.; Bai, T.; Xiang, L.; Sugiura, S.; Maunder, R.G.; Yang, L.; Hanzo, L. Reconfigurable intelligent surface assisted multi-carrier wireless systems for doubly selective high-mobility Ricean channels. IEEE Trans. Veh. Technol. 2022, 71, 4023–4041. [Google Scholar] [CrossRef]
- An, J.; Wu, Q.; Yuen, C. Scalable channel estimation and reflection optimization for reconfigurable intelligent surface-enhanced OFDM systems. IEEE Wirel. Commun. Lett. 2022, 11, 796–800. [Google Scholar] [CrossRef]
- An, J.; Xu, C.; Ng, D.W.K.; Yuen, C.; Hanzo, L. Adjustable-delay RIS is capable of improving OFDM systems. IEEE Trans. Veh. Technol. 2024, 73, 9927–9942. [Google Scholar] [CrossRef]
- Özdogan, Ö.; Björnson, E.; Larsson, E.G. Intelligent Reflecting Surfaces: Physics, Propagation, and Pathloss Modeling. IEEE Wirel. Commun. Lett. 2020, 9, 581–585. [Google Scholar] [CrossRef]
- Pei, X.; Yin, H.; Tan, L.; Cao, L.; Li, Z.; Wang, K.; Zhang, K.; Bjornson, E. RIS-Aided Wireless Communications: Prototyping, Adaptive Beamforming, and Indoor/Outdoor Field Trials. IEEE Trans. Commun. 2021, 69, 8627–8640. [Google Scholar] [CrossRef]
- Shen, H.; Xu, W.; Gong, S.; He, Z.; Zhao, C. Secrecy Rate Maximization for Intelligent Reflecting Surface Assisted Multi-Antenna Communications. IEEE Commun. Lett. 2019, 23, 1488–1492. [Google Scholar] [CrossRef]
- Cui, M.; Zhang, G.; Zhang, R. Secure Wireless Communication via Intelligent Reflecting Surface. IEEE Wirel. Commun. Lett. 2019, 8, 1410–1414. [Google Scholar] [CrossRef]
- Björnson, E.; Marcenaro, L. Configuring an Intelligent Reflecting Surface for Wireless Communications: Highlights from the 2021 IEEE Signal Processing Cup student competition [SP Competitions]. IEEE Signal Process. Mag. 2022, 39, 126–131. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent reflecting surface enhanced wireless network: Joint active and passive beamforming design. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Ma, D.; Li, L.; Ren, H.; Wang, D.; Li, X.; Han, Z. Distributed Rate Optimization for Intelligent Reflecting Surface with Federated Learning. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, H.; Liang, Y.-C.; Chen, J.; Larsson, E.G. Weighted Sum-Rate Maximization for Intelligent Reflecting Surface Enhanced Wireless Networks. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Zheng, B.; Wu, Q.; Zhang, R. Intelligent Reflecting Surface-Assisted Multiple Access with User Pairing: NOMA or OMA? IEEE Commun. Lett. 2020, 24, 753–757. [Google Scholar] [CrossRef]
- Björnson, E.; Wymeersch, H.; Matthiesen, B.; Popovski, P.; Sanguinetti, L.; de Carvalho, E. Reconfigurable Intelligent Surfaces: A signal processing perspective with wireless applications. IEEE Signal Process. Mag. 2022, 39, 135–158. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, B.; Zhang, S.; Zhang, R. Intelligent Reflecting Surface Meets OFDM: Protocol Design and Rate Maximization. IEEE Trans. Commun. 2020, 68, 4522–4535. [Google Scholar] [CrossRef]
- Popovski, P. Wireless Connectivity: An Intuitive and Fundamental Guide; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Goldsmith, A. Wireless Communications; Cambridge Univ. Press: Cambridge, UK, 2005. [Google Scholar]
- Bjoernson, E. Optimizing a Binary Intelligent Reflecting Surface for OFDM Communications under Mutual Coupling. In Proceedings of the WSA 2021; 25th International ITG Workshop on Smart Antennas, French Riviera, France, 10–12 November 2021; pp. 1–6. [Google Scholar]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic algorithms: Concepts and applications [in engineering design]. IEEE Trans. Ind. Electron. 1996, 43, 519–534. [Google Scholar] [CrossRef]
- Tiwari, R.; Venkateswaran, K. Configuring an Intelligent Reflecting Surface using Strongest Tap Maximization Heuristic Technique. In Proceedings of the 2022 International Conference on Signal and Information Processing (IConSIP), Pune, India, 26–27 August 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Cht, K.T.Y.; Tiwari, R.; Venkateswaran, K. Power Allocation of Multiple subcarriers using Water Filling algorithm for RIS Aided Communication Sytsems. In Proceedings of the 2021 Third International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 2–4 September 2021; pp. 308–311. [Google Scholar] [CrossRef]


| BS-user (direct) channel | |
| The n-th IRS element’s BS-IRS channel | |
| The n-th IRS element’s IRS-user channel | |
| IRS reflection coefficients | |
| Reflection coefficient of the IRS | |
| Propagation Loss | |
| Propagation Loss | |
| Dirac delta function | |
| Carrier Frequency | |
| Received Signal | |
| Fourier Transformation on signal | |
| Signal Wavelength | |
| Overall impulse response of the channel | |
| Frequency response of BS-User (direct) channel | |
| Frequency response of the BS-IRS-User channel | |
| Circularly Symmetric Gaussian Noise (CSGN) | |
| F.T. of with variance |
| Sl. No. | Algorithm | LOS | NLOS |
|---|---|---|---|
| 1 | Pilot Transmission [23] | 21.255 | 21.469 |
| 2 | Gradient Descent | 111.683 | 51.389 |
| 3 | Genetic Algorithm | 117.384 | 55.521 |
| 4 | Heuristic Technique [35] | 100 | 50 |
| 5 | Water-filling Algorithm [36] | 119.178 (26th configuration) | Author not verified |
| 6 | Proposed Approach | 126.890 | 66.093 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janawade , S.A.; Krishnan , P.; Kandasamy , K.; Holla , S.S.; Rao , K.; Chandrasekar , A. A Low-Complexity Solution for Optimizing Binary Intelligent Reflecting Surfaces towards Wireless Communication. Future Internet 2024, 16, 272. https://doi.org/10.3390/fi16080272
Janawade SA, Krishnan P, Kandasamy K, Holla SS, Rao K, Chandrasekar A. A Low-Complexity Solution for Optimizing Binary Intelligent Reflecting Surfaces towards Wireless Communication. Future Internet. 2024; 16(8):272. https://doi.org/10.3390/fi16080272
Chicago/Turabian StyleJanawade , Santosh A., Prabu Krishnan , Krishnamoorthy Kandasamy , Shashank S. Holla , Karthik Rao , and Aditya Chandrasekar . 2024. "A Low-Complexity Solution for Optimizing Binary Intelligent Reflecting Surfaces towards Wireless Communication" Future Internet 16, no. 8: 272. https://doi.org/10.3390/fi16080272
APA StyleJanawade , S. A., Krishnan , P., Kandasamy , K., Holla , S. S., Rao , K., & Chandrasekar , A. (2024). A Low-Complexity Solution for Optimizing Binary Intelligent Reflecting Surfaces towards Wireless Communication. Future Internet, 16(8), 272. https://doi.org/10.3390/fi16080272






