INFLUTRUST: Trust-Based Influencer Marketing Campaigns in Online Social Networks

Abstract

This paper introduces the INFLUTRUST framework that is designed to address challenges in trust-based influencer marketing campaigns on Online Social Networks (OSNs). The INFLUTRUST framework enables the influencers to autonomously select products across the OSN platforms for advertisement by employing a reinforcement learning algorithm. The Stochastic Learning Automata reinforcement algorithm considers the OSN platforms’ provided monetary rewards, the influencers’ advertising profit, and the influencers’ trust levels towards the OSN platforms to enable the influencers to autonomously select an OSN platform. The trust model for the influencers incorporates direct and indirect trust, which are derived from past interactions and social ties among the influencers and the OSN platforms, respectively. The OSN platforms allocate rewards through a multilateral bargaining model that supports competition among the influencers. Simulation-based results validate the INFLUTRUST framework’s effectiveness across diverse scenarios, with the scalability analysis demonstrating its robustness. Comparative evaluations highlight the INFLUTRUST framework’s superiority in considering trust levels and reward allocation fairness, benefiting both the influencers and the OSN platforms.

1. Introduction

In recent years, there has been a remarkable increase in the utilization of Online Social Networks (OSNs). OSN platforms have evolved into socializing arenas for dialogue, exchange of opinions among OSN users, dissemination of information, product advertisement, just to name a few applications. Thus, OSNs have become deeply integrated across various sectors including commerce, education, healthcare, finance, governance, and more. The very large number of users utilizing and interacting through the OSNs presents lucrative prospects for the marketers aiming to connect with their customers. Also, certain individuals, named influencers, within these networks wield substantial influence and enjoy widespread popularity. These influencers have the ability to guide the beliefs and attitudes of their followers, making them highly coveted by brands seeking endorsement for their products within these digital communities [1]. The impact exerted by these influencers on social media significantly shapes the effectiveness of advertising and promotional efforts [2,3]. This phenomenon, known as influencer marketing, is recognized for its dominant role in contemporary marketing strategies and the design of online advertisement marketing campaigns [4].

1.1. Related Work

Influencer marketing exploits several concepts tied with the OSNs, such as viral marketing and influence maximization, crowdsourcing in order to collect information from the influencers, and online advertisement campaigns.

1.1.1. Viral Marketing

As OSNs, like Instagram, Facebook, Twitter, and TikTok, gain increasing popularity, viral marketing emerges as a supremely efficient strategy for promoting products and services to customers by leveraging the power of word-of-mouth reputation [5]. A multiobjective optimization-based framework for maximizing the influence spread and minimizing the promotion costs in geo-social networks is presented in [6]. The authors in [7] focus their study on the multiple benefit thresholds problem, in terms of determining the threshold number of influencers that should be recruited in order to successfully advertise a product following the principles of viral marketing. This work has been extended in [8] by introducing an efficient sampling method for selecting multiple influencer seed sets to deal with cases of fluctuating markets. The problem of influence diffusion is studied in [9] by proposing a solution for quantifying the weakening of benefits in influence diffusion caused by competing information in viral marketing and offering efficient approximation methods validated through numerical experiments on real datasets.

1.1.2. Influence Maximization

The problem of influence maximization in viral markets has recently attracted the interest of the research community aiming at maximizing the influence spread into the OSNs by strategically selecting a set of influencers [10,11]. The problem of scalability posed by the massive user base of OSNs is studied in [12] by designing distributed algorithms for influence maximization in viral marketing. The authors in [13] study the problem of influence maximization based on the dynamic personal perception, and they utilize the knowledge graphs to capture the evolving user preferences and social influence. The proposed approach achieves at least six times greater influence spread in large datasets compared to the existing state of the art. The problem of multi-item influence maximization under continuous settings is studied in [14], considering scenarios where different influencers receive varying incentives on multiple products in order to be recruited in the viral marketing process. The cluster greedy algorithm is discussed in [15], aiming at optimizing the influence maximization problem by partitioning the social network into clusters and efficiently selecting seed influencers through a combination of the simple greedy algorithm and an exploration of the diffusion function’s submodularity property. A quantum computing approach for influence maximization is analyzed in [16], aiming to achieve near-optimal solutions by converting the influence maximization problem into a max-cover instance problem and employing efficient quadratic unconstrained binary optimization formulations on quantum annealers.

The maximization of influence in OSNs focusing on the superior impact of negative opinions in societal psychology is analyzed in [17], and a solution based on the label propagation algorithm is proposed for selecting influencers. Blockchain technology is adopted in [18] to design a linear threshold model sensitive to word-of-mouth effects in OSNs and an algorithm based on community segmentation and ranking in order to optimize the efficiency of influence maximization. A novel approach to solve the budgeted influence maximization problem is proposed in [19] by utilizing a local–global influence indicator and employing a constrained evolutionary algorithm with innovative strategies for population evolution. The problem of influence maximization for two products in OSNs is studied in [20], aiming at addressing the complexity of user adoption decisions and proposing adapted greedy and heuristic algorithms to effectively solve the NP-hard problem. A visual analytics system designed to assist the influencers in analyzing, evaluating, and comparing information diffusion processes facilitated by different influence maximization algorithms on OSNs is presented in [21], aiming to provide valuable insights for improving the seed set selection and enhancing the influence spread. The targeted activation probability maximization problem is studied in [22], aiming to identify intermediate users to increase the likelihood of influencing a specific target user.

1.1.3. Crowdsourcing

Crowdsourcing plays a critical role in influencer marketing, as the influencers can provide different types of content, e.g., video, audio, images, text, etc., to guide the customers’ opinions regarding a product that they advertise. The authors in [23] explore how OSN platforms employ crowdsourcing and incentivize the influencers with varying solution accuracies to complete tasks and report their solutions truthfully through an output agreement mechanism. A comprehensive examination of incentive mechanisms in socially aware crowdsourcing is presented in [24] by introducing a multi-leader and multi-follower Stackelberg game approach to model the strategic interactions among the OSN platforms and the influencers and integrating the social influence and strategic interconnections among the influencers and the OSN users. A crowdsourcing method utilizing text-mining techniques and user behavior analysis is proposed in [25] to identify influencers in OSNs.

1.1.4. Online Advertisement

By identifying influencers who can maximize the influence spread within the OSNs, strategic online advertisement campaigns can be designed [26]. An agent-based model to simulate influencer advertising campaigns in various scenarios is analyzed in [27], considering factors like customer interest, behavior, and product nature, towards identifying the most effective influencer marketing strategies based on real-world dynamics. Machine learning models are utilized in [28] to enhance the effectiveness of online advertisement campaigns in OSNs by predicting potential customers. A game model for optimizing referral incentive strategies using customers’ social networks is analyzed in [29] to optimize the successful customer penetration of the online advertisement. A novel continuous formulation of the budgeted influencer marketing problem as a convex program is presented in [30] and solved based on an efficient iterative algorithm exploiting the Frank–Wolfe method to find the optimal set of influencers for maximizing different impact metrics across various OSN platforms. The authors in [31] propose a framework to identify domain-based social influencers by utilizing semantic analysis and machine learning techniques to optimize an online advertisement’s penetration in the customers’ market.

Several recent research works have focused on studying the trust aspects of the recruited influencers and/or the OSN platforms. The authors in [32] introduce and interpret trust in OSNs by analyzing its significance in predicting the impact of these networks on news dissemination and the online advertisement of products. A novel matrix-factorization-based trust prediction model is presented in [33] to address issues related to the sparse social interaction and low trust utilization in OSNs via integrating the social trust graph and recommendation system data to improve the predictive performance of OSN users. A crisis-assessment-oriented and topic-based influence maximization framework is proposed in [34] to address the risk of negative and untrusted information in OSNs [35]. A qualitative model of swift trust formation in global virtual teams is presented in [36] offering insights into how these teams develop trust behaviors among each other for effective virtual collaboration and international management. The trust development in semi-virtual collaboration teams of multicultural and unicultural backgrounds is analyzed in [37], finding that, while trust levels initially show no significant difference between groups, multicultural teams experience unstable trust development influenced by language, values, and habitual behaviors, contrasting with more stable dynamics in unicultural teams. Also, the authors in [38] explore how trust forms and impacts collaboration in virtual teams by identifying key dimensions of interpersonal trustworthiness and system factors influencing virtual interactions. Moreover, the authors in [39] propose a method for predicting trust levels in OSNs by mapping the users onto trustor and trustee profiles and incorporating biases, thus achieving a superior accuracy and scalability compared to existing methods. A novel trust-based matrix factorization technique for recommender systems is designed in [40] by integrating social network data to improve accuracy and address issues of data sparsity and the cold start problem. Also, a novel dictionary learning technique integrating trust information from social networks to enhance collaborative-filtering-based recommender systems is analyzed in [41] to also address issues of cold start and data sparsity.

1.2. Contributions

Though significant research efforts have been devoted to the problem of recruiting influencers to perform online advertisement in OSNs, the problem of enabling the influencers to autonomously choose products from different OSNs to advertise to the corresponding customers (i.e., current and potential future followers) has received little attention in the existing literature. Furthermore, this problem becomes even more complicated when considering the trust levels of the companies and the OSN platforms that request the online advertisement of different products.

In this paper, aiming at addressing those research challenges, we introduce the INFLUTRUST framework to support trust-based influencer marketing campaigns in OSNs. Specifically, the INFLUTRUST framework enables the influencers to autonomously choose a product from different OSN platforms to advertise to their customers based on a reinforcement learning algorithm that considers the reward provided by the corresponding OSN platform, their achieved profit from advertising the product, and the influencers’ trust to the corresponding OSN platform. The influencers’ trust consists of their direct and indirect trust, where the first one is built based on the influencers’ past interactions with the OSN platforms, while the latter one is formed based on the influencers’ interactions among each other and the sharing of their experiences by selecting different OSN platforms. Furthermore, the influencers receive rewards by the OSN platforms based on a multilateral bargaining model, where the influencers compete among each other for the corresponding monetary rewards to advertise the same product. The main contributions of this research work are summarized as follows.

• Initially, the INFLUTRUST framework is presented considering multiple influencers and multiple OSN platforms that request the advertisement of different products. The concept of product quality, as it is evaluated by the influencers, is presented, and the influencers’ profit by contributing to the online advertisement product campaign is quantified.
• A novel trust model for the influencers is introduced quantifying the influencers’ trust in the OSN platforms and the corresponding products that they advertise. The influencers’ trust model consists of direct and indirect trust. Direct trust is quantified based on the influencers’ direct interactions with the OSN platforms, while indirect trust is shaped based on the influencers’ interactions with each other, their social ties, and their past experience from different OSN platforms.
• A Stochastic Learning Automata reinforcement learning algorithm is introduced to enable the influencers to autonomously select an OSN platform and a corresponding product to advertise, considering the monetary reward received by the OSN platform, their achieved profit by advertising the product, and the OSN platforms’ trust levels.
• Focusing on the OSN platforms, the monetary rewards are allocated to the influencers, who choose to advertise a product through the corresponding OSN platform, by following a multilateral bargaining model. Specifically, the influencers compete with each other for the OSN platforms’ monetary rewards while advertising the same product through the same OSN platform.
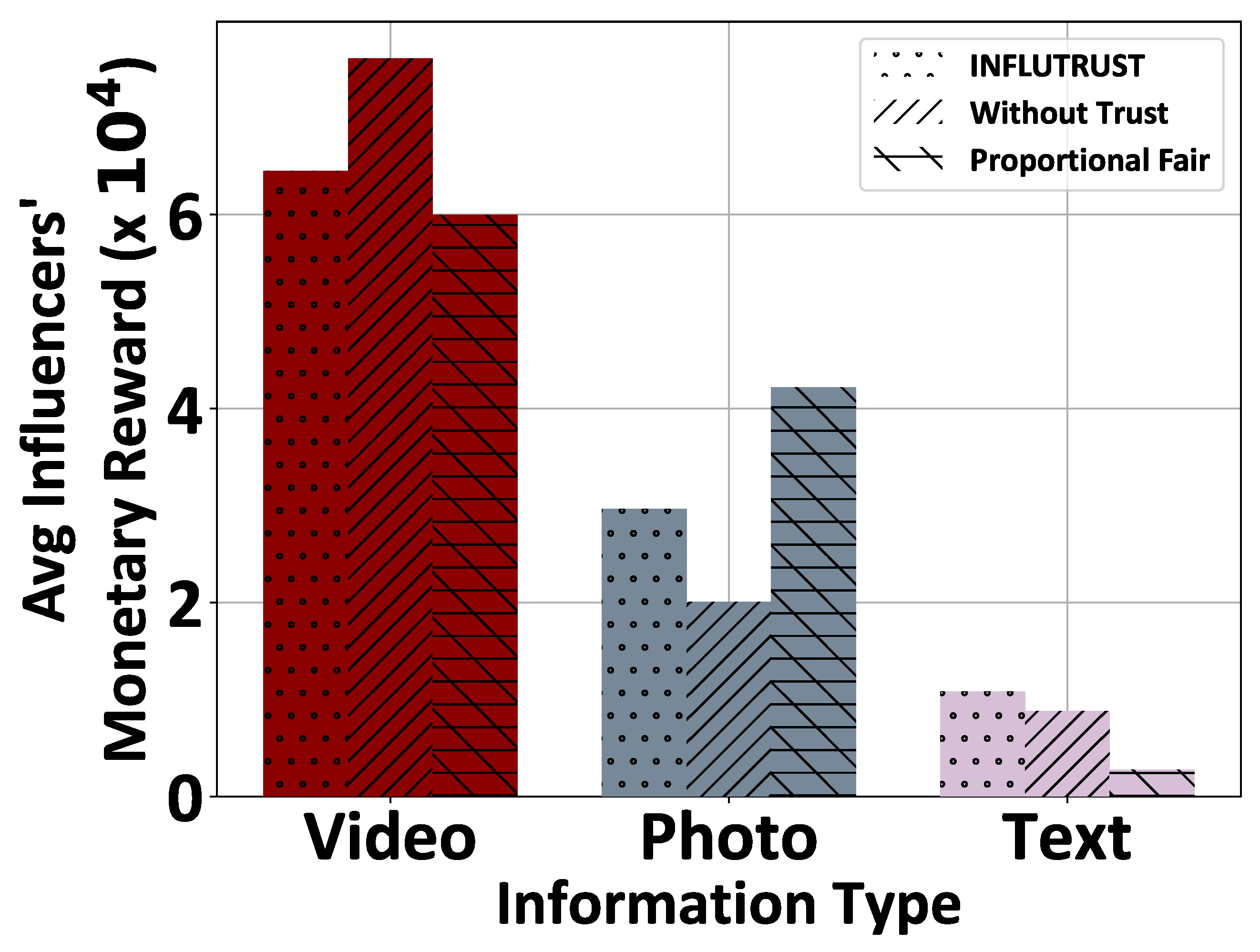
• A detailed set of simulation-based results are provided based on real datasets in order to demonstrate the operation and efficiency of the INFLUTRUST framework under different realistic scenarios. Also, a scalability analysis is performed to highlight the efficiency and robustness of the INFLUTRUST framework under large-scale setups. A thorough comparative evaluation of the INFLUTRUST framework, compared to models that ignore the OSN platforms’ trust levels during the product selection for advertisement by the influencers and/or allocate the OSN platforms’ rewards to the influencers following the principles of proportional fairness, is presented to quantify the benefits of the INFLUTRUST framework both from the influencers’ and the OSN platforms’ perspectives.

1.3. Outline

The remainder of this paper is organized as follows. Section 2 presents the INFLUTRUST model, while the trust-based influencer dynamics are analyzed in Section 3. The design of the INFLUTRUST-based product marketing campaigns, including the reinforcement-learning-based OSN platform selection and the multilateral bargaining-based rewards allocation, is presented in Section 4. Detailed simulation-based results are discussed in Section 5, and Section 6 concludes the paper.

2. INFLUTRUST Model

An influencer marketing campaign environment is considered, consisting of multiple influencers and multiple OSN platforms. The set of influencers is denoted as $\mathcal{I}=\{1,\cdots ,i,\cdots ,I\}$ and the set of OSN platforms as $\mathcal{S}=\{1,\cdots ,s,\cdots ,S\}$. Each OSN platform can advertise several types of products, e.g., fashion and apparel, technology and gadgets, fitness and wellness, personal care and hygiene, and many more. Each influencer, considering their personal interests and the characteristics of their followers, can select a product from an OSN platform to advertise it by providing its information $I_i$, which can range from images to stories to video to carousel or reels type of content. In the rest of our analysis, for simplicity in the notation and without loss of generality, we consider that each OSN platform is associated with one corresponding product, and both of them are denoted as s. Towards recruiting the influencers, the OSN platforms provide a total monetary reward, denoted as ${\mathfrak{R}}_s$, which is allocated among the influencers, considering their contribution to the successful product marketing campaign.

Each influencer contributes to enhancing the perceived quality of a product among their followers through their promotional efforts. The product’s quality, denoted as ${\mathbb{Q}}_s^{\mathbb{T}}$, reflects the cumulative improvement in its word-of-mouth reputation among customers influenced by all selected influencers up to time $\mathbb{T}$. In essence, this metric quantifies the effectiveness of influencer marketing campaigns in shaping customer perceptions.

$${\mathbb{Q}}_s^{\mathbb{T}}=\frac{arctan[\lambda ·({\displaystyle \sum _{\forall t\in {\mathcal{T}}_{\mathbb{T}}}}{\displaystyle \sum _{\forall i^{\prime }\in {\mathcal{I}}_s}}{I}_{i^{\prime }}^t+I_i^{\mathbb{T}})]}{\frac{\pi }{2}}$$

(1)

where $\lambda \in {\mathbb{R}}^{+}$, $\mathbb{T}$ is the current time, ${\mathcal{T}}_{\mathbb{T}}=\{1,\cdots ,t,\cdots ,\mathbb{T}-1\}$ is the set of passed times that the influencers have interacted with the OSN platforms, and ${\mathcal{I}}_s$ denotes the set of influencers that have selected to contribute to advertise a product through the OSN platform s. It is noted that an increasing function of sigmoid form can be used instead of the arctan function, and the latter one is selected for presentation purposes, without limiting the derivations of the rest of the theoretical analysis.

The influencers experience a profit based on the reward provided by the selected OSN platform ${\mathfrak{r}}_{s,i}^t$ in order to advertise the corresponding product, while also accounting for their personal cost ${\mathfrak{c}}_i^t$ to gather the information for the advertisement and distribute it among their followers. This cost can include the video preparation cost, the influencers’ personal time investment, the commuting cost for photo shooting, etc. Thus, each influencer experiences a profit, which is given as follows:

$$U_{s,i}^{\mathbb{T}}=\sum _{\forall t\in {\mathcal{T}}_{\mathbb{T}}\cup \mathbb{T}}({\mathfrak{r}}_{s,i}^t·\Delta {\mathbb{Q}}_{s,i}^t-{\mathfrak{c}}_i^t·I_i^t)$$

(2)

where $\Delta {\mathbb{Q}}_{s,i}^t$ denotes the influencer’s i contribution to the product’s quality.

3. Trust-Based Influencer Dynamics

An open research question in the existing literature is how the influencers select the products that they will advertise among their followers. The goal of the influencers is to increase the population of their followers while, at the same time, make a high profit by participating in the product marketing campaigns. Thus, the influencers need an efficient mechanism to enable them to choose which products to advertise through the OSN platforms. Each product is advertised through an OSN platform and sponsored by the corresponding company that produces the product or delivers a service. Each OSN platform advertising a product is characterized by a trust level ${\mathbb{TR}}_{s,i}^{\mathbb{T}}$ that stems from the rewards provided to the influencers in order to advertise the product and the corresponding profit that the influencers can make by participating in the product marketing campaigns. Specifically, the influencers trust to the OSN platforms consists of the direct and indirect trust as analyzed below.

3.1. Influencers’ Direct Trust

Each influencer is characterized by the direct trust ${\mathbb{DT}}_{s,i}^{\mathbb{T}}$ to an OSN platform considering their potential to make profit during the product marketing campaign by disseminating information related to the product among their followers. Thus, the influencer’s direct trust in an OSN platform that is responsible for a specific product marketing campaign is defined as follows.

$${\widehat{\mathbb{DTR}}}_{s,i}^{\mathbb{T}}=\frac{U_{s,i}^{\mathbb{T}}-U_{s,i}^{\mathbb{T}-1}}{U_{s,i}^{\mathbb{T}-1}}$$

(3)

In the case that the influencer’s profit increases over time, the direct trust ${\widehat{\mathbb{DTR}}}_{s,i}^{\mathbb{T}}$ is positive. Thus, the influencer creates a direct trust ${\widehat{\mathbb{DTR}}}_{s,i}^{\mathbb{T}}\in (0,1]$ related to the OSN platform, where smaller values indicate the relatively limited satisfaction of the influencer with the experienced profit, and the exact opposite holds true for direct trust values close to one. However, the influencer’s profit can decrease over time if the cost to advertise the product is increased due to the excessive effort that the influencer invests in the product marketing campaign or if the acceptance of the product by the followers is very limited; thus, the quality of the product in terms of its word-of-mouth reputation increases slowly. In that case, the direct trust is negative, i.e., ${\widehat{\mathbb{DTR}}}_{s,i}^{\mathbb{T}}\in [-1,0)$. Thus, by combining both cases, the influencer’s direct trust is formulated as follows.

$${\widetilde{\mathbb{DTR}}}_{s,i}^{\mathbb{T}}=\left\{\begin{array}{cc}{\widehat{\mathbb{DTR}}}_{s,i}^{\mathbb{T}}\hfill & ,\mathrm{if}{U}_{s,i}^{\mathbb{T}}\ge U_{s,i}^{\mathbb{T}-1}\hfill \\ \frac{U_{s,i}^{\mathbb{T}}-U_{s,i}^{\mathbb{T}-1}}{U_{s,i}^{\mathbb{T}-1}}\hfill & ,\mathrm{if}{U}_{s,i}^{\mathbb{T}}<U_{s,i}^{\mathbb{T}-1}\hfill \end{array}\right.$$

(4)

Towards holistically representing the influencer’s direct trust in the interval $[0,1]$, we adopt the min–max normalization method as follows.

$${\mathbb{DTR}}_{s,i}^{\mathbb{T}}=\frac{{\widetilde{\mathbb{DTR}}}_{s,i}^{\mathbb{T}}-\underset{\forall j\in {\mathcal{I}}_{i,s}}{min}\left\{{\widetilde{\mathbb{DTR}}}_{s,i}^j\right\}}{\underset{\forall j\in {\mathcal{I}}_{i,s}}{max}\left\{{\widetilde{\mathbb{DTR}}}_{s,i}^j\right\}-\underset{\forall j\in {\mathcal{I}}_{i,s}}{min}\left\{{\widetilde{\mathbb{DTR}}}_{s,i}^j\right\}}=\frac{{\widetilde{\mathbb{DTR}}}_{s,i}^{\mathbb{T}}+1}{2}$$

(5)

where ${\mathcal{I}}_{i,s}$ represents the set of times that the influencer i contributed their information to advertise a product s through the corresponding OSN platform. The influencer’s direct trust ${\mathbb{DTR}}_{s,i}^{\mathbb{T}}$, as summarized in Equation (5), changes over time, by considering the interaction of the influencer with the corresponding OSN platform. Specifically, the influencers tend to give more weight to the most recent evaluation of the direct trust to an OSN platform, while they give a lower weight to their past experience. Therefore, a time decay function is defined to capture the fading of the influencers’ direct trust to a platform over time, as follows.

$$f\left(t_j\right)=exp(-\mu (\mathbb{T}-t_j))$$

(6)

where $\mu \in {\mathbb{R}}^{+}$ denotes a positive real number indicating the rate of decay, $\mathbb{T}$ captures the current time that the influencer interacts with an OSN platform, and $t_j,j\in {\mathcal{I}}_{i,s}$ denotes the historical time that the influencer i interacted with the OSN platform s.

Based on the above analysis, the influencer’s i direct trust ${\mathbb{DT}}_{s,i}^{\mathbb{T}}$ to an OSN platform s is defined as follows.

$${\mathbb{DT}}_{s,i}^{\mathbb{T}}=\frac{{\displaystyle \sum _{\forall j\in {\mathcal{I}}_{i,s}}}{\mathbb{DTR}}_{s,i}^{\mathbb{T}}·f\left(t_j\right)}{{\displaystyle \sum _{\forall j\in {\mathcal{I}}_{i,s}}}f\left(t_j\right)}$$

(7)

3.2. Influencers’ Indirect Trust

The influencers can share their experience among each other regarding their trust levels to the OSN platforms considering the corresponding product marketing campaigns. The influencers can be socially connected among each other through the OSN platforms, where $\mathcal{L}=\{1,\cdots ,l,\cdots ,L\}$ denotes the set of social links among the influencers. Also, the degree of social connection among the influencers i and $i^{\prime }$ is denoted as $d_{i,i^{\prime },l}\in [0,1]$. Specifically, large values of the social connection degree $d_{i,i^{\prime },l}$ capture a strong social connection among the influencers, while the exact opposite holds true for small values of $d_{i,i^{\prime },l}$. The influencers tend to rely more on other influencers with whom they have a strong social connection, and their reliability factor is captured as follows:

$${\mathbb{RL}}_{i,i^{\prime }}^{\mathbb{T}}=\frac{d_{i,i^{\prime },l}·{\mathbb{SIM}}_{i,i^{\prime }}^{\mathbb{T}}}{\underset{l\in \mathcal{L}}{max}{d}_{i,i^{\prime },l}}$$

(8)

where ${\mathbb{SIM}}_{i,i^{\prime }}^{\mathbb{T}}$ captures the similarity among the influencers i and $i^{\prime }$. The similarity among the influencers can be represented by the Pearson correlation coefficient considering that influencers who have closer direct trust among each others for the OSN platforms that they have interacted with exhibit greater similarity score. Therefore, the similarity score is defined as follows.

$${\mathbb{SIM}}_{i,i^{\prime }}^{\mathbb{T}}=\frac{{\displaystyle \sum _{s\in {\mathcal{S}}_{i,i^{\prime }}^{\mathbb{T}}}}({\mathbb{DTR}}_{s,i}^{\mathbb{T}}-{\overline{\mathbb{DTR}}}_i^{\mathbb{T}})({\mathbb{DTR}}_{s,i^{\prime }}^{\mathbb{T}}-{\overline{\mathbb{DTR}}}_{i^{\prime }}^{\mathbb{T}})}{\sqrt{{\displaystyle \sum _{s\in {\mathcal{S}}_{i,i^{\prime }}^{\mathbb{T}}}}{({\mathbb{DTR}}_{s,i^{\prime }}^{\mathbb{T}}-{\overline{\mathbb{DTR}}}_i^{\mathbb{T}})}^2}\sqrt{{\displaystyle \sum _{s\in {\mathcal{S}}_{i,i^{\prime }}^{\mathbb{T}}}}{({\mathbb{DTR}}_{s,i^{\prime }}^{\mathbb{T}}-{\overline{\mathbb{DTR}}}_{i^{\prime }}^{\mathbb{T}})}^2}}$$

(9)

where ${\overline{\mathbb{DTR}}}_i^{\mathbb{T}}$ and ${\overline{\mathbb{DTR}}}_{i^{\prime }}^{\mathbb{T}}$ capture the average direct trust (Equation (5)) of the influencers i and $i^{\prime }$ up to time $\mathbb{T}$, and ${\mathcal{S}}_{i,i^{\prime }}^{\mathbb{T}}$ denotes the set of OSN platforms that the influencers i and $i^{\prime }$ have been engaged with to advertise products up to time $\mathbb{T}$.

Considering the influencers’ reliability (Equation (8)) among each other and their similarity scores (Equation (9)), their overall indirect trust can be formulated as follows.

$${\mathbb{IT}}_{s,i}^{\mathbb{T}}=\frac{{\displaystyle \sum _{i,i^{\prime }\in {\mathcal{I}}_s,i\ne i^{\prime }}}{\mathbb{RL}}_{i,i^{\prime }}^{\mathbb{T}}·{\mathbb{DT}}_{s,i}^{\mathbb{T}}}{{\displaystyle \sum _{i,i^{\prime }\in {\mathcal{I}}_s,i\ne i^{\prime }}}{\mathbb{RL}}_{i,i^{\prime }}^{\mathbb{T}}}$$

(10)

3.3. Influencers’ Overall Trust

The influencers account for their direct ${\mathbb{DT}}_{s,i}^{\mathbb{T}}$ and indirect trust ${\mathbb{IT}}_{s,i}^{\mathbb{T}}$ in order to build their overall trust ${\mathbb{TR}}_{s,i}^{\mathbb{T}}$ for each OSN platform. The influencers’ overall trust by combining Equations (7) and (10) is given as follows:

$${\mathbb{TR}}_{s,i}^{\mathbb{T}}=\left\{\begin{array}{cc}\nu ·{\mathbb{DT}}_{s,i}^{\mathbb{T}}+(1-\nu ){\mathbb{IT}}_{s,i}^{\mathbb{T}}\hfill & ,\mathrm{if}{\mathcal{I}}_s\ne \varnothing \hfill \\ 0.5\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(11)

where the term $\nu$ captures a weight factor considering the times $|{\mathcal{I}}_{i,s}|$ an influencer has contributed their information to advertise a product s through the corresponding OSN platform, defined as follows.

$$\nu =\frac{1-exp(-|{\mathcal{I}}_{i,s}\left|\right)}{1+exp(-|{\mathcal{I}}_{i,s}\left|\right)}$$

(12)

4. INFLUTRUST-Based Product Marketing Campaigns

The influencers consider their trust in the corresponding OSN platforms in order to choose to participate in a product marketing campaign. Additionally, the influencers consider the monetary rewards provided by the OSN platforms for their efforts (in terms of advertising a product), as well as the profit that they make out of this process. Thus, in this section, a novel reinforcement-learning-based approach is introduced aiming at enabling the influencers to select the products that they will advertise in the corresponding OSN platform in order to improve their benefits by participating in the product marketing campaigns. Furthermore, considering the influencers’ choices of OSN platforms and the corresponding products to advertise, a multilateral bargaining model based on the principles of Game Theory is introduced to enable the OSN platforms to fairly distribute the monetary rewards to the participating influencers in the product marketing campaigns.

4.1. Influencers’ Autonomous Selection of Product Marketing Campaign

The Stochastic Learning Automata (SLA) reinforcement learning algorithm is introduced in order to enable the influencers to autonomously select an OSN platform. Specifically, each influencer is represented as a reinforcement learning agent who is able to select among a set of actions $\mathcal{S}=\{1,\cdots ,s,\cdots ,S\}$, which represent the choices of OSN platforms. The influencers tend to explore their actions by considering the received reinforcement learning reward ${\mathcal{R}}_{s,i}^{\mathbb{T}}$ from their interactions with the OSN platforms, which depends on the monetary reward ${\mathfrak{r}}_{s,i}^{\mathbb{T}}$ provided by the OSN platform considering the influencers’ contribution to the product marketing campaign, the profit $U_{s,i}^{\mathbb{T}}$ that the influencer experiences by participating in the campaign, and the trust ${\mathbb{TR}}_{s,i}^{\mathbb{T}}$ that the influencer has in the OSN platforms. Thus, the reinforcement learning reward for an influencer i that chooses to participate in the product market campaign of the OSN platform s is defined as follows:

$${\mathcal{R}}_{s,i}^{\mathbb{T}}=w_1·{\mathfrak{r}}_{s,i}^{\mathbb{T}}+w_2·{\mathbb{TR}}_{s,i}^{\mathbb{T}}+w_3·U_{s,i}^{\mathbb{T}}$$

(13)

where $w_1,w_2,w_3\in {\mathbb{R}}^{+}$ are the weight factors. The reinforcement learning reward is normalized as ${\widehat{\mathcal{R}}}_{s,i}^{\mathbb{T}}=\frac{{\mathcal{R}}_{s,i}^{\mathbb{T}}}{\underset{\forall s,i}{max}{\mathcal{R}}_{s,i}^{\mathbb{T}}}$, and each influencer updates their expected reinforcement learning reward $Q_{s,i}^{\mathbb{T}}$ through the interactions with the OSN platforms following the stochastic learning update rules which are defined as follows:

$$Q_{s,i}^{\mathbb{T}}=Q_{s,i}^{\mathbb{T}-1}+\gamma {\widehat{\mathcal{R}}}_{s,i}^{\mathbb{T}}(1-Q_{s,i}^{\mathbb{T}-1}),s^{\mathbb{T}}=s^{\mathbb{T}-1}$$

(14)

$$Q_{s,i}^{\mathbb{T}}=Q_{s,i}^{\mathbb{T}-1}-\gamma {\widehat{\mathcal{R}}}_{s,i}^{\mathbb{T}}{Q}_{s,i}^{\mathbb{T}-1},s^{\mathbb{T}}\ne s^{\mathbb{T}-1}$$

(15)

where $\gamma \in (0,1)$ denotes the learning rate of the influencer in terms of exploring the best choices among the available OSN platforms and the corresponding marketing campaigns. Larger values of the learning rate capture a more thorough exploration by the influencers, which can result in a longer convergence time for the SLA algorithm to converge to a stable choice of an OSN platform for each influencer. Considering the expected reinforcement learning reward, the influencer selects an OSN platform based on the expected reinforcement learning rewards update rules (14) and (15). The SLA algorithm converges when the expected reinforcement learning reward $Q_{s,i}^{\mathbb{T}}\ge \delta ,\delta =95\%$ converges for one OSN platform, which is the one that the influencer finally selects.

4.2. Monetary Rewards Allocation to the Influencers

In the context where the influencers choose OSN platforms for product marketing campaigns, the OSN platforms must allocate their available monetary rewards ${\mathfrak{R}}_i,\forall i\in \mathcal{I}$ to the influencers who participate in the product marketing campaigns. The allocation considers the influencers’ activity in posting advertising material and their role in initiating the campaigns that attract initial customers/followers, thus influencing their reward levels ${\mathfrak{r}}_{s,i}^{\mathbb{T}}$. This allocation process involves a multilateral bargaining game-theoretic framework, which properly reflects the influencers’ competition for monetary rewards from OSN platforms.

In accordance with the SLA algorithm, each OSN platform has enlisted a group of influencers to participate in their product marketing campaigns. For each influencer contributing to the campaign, the OSN platform assigns a monetary reward ${\mathfrak{r}}_{s,i}^{\mathbb{T}}$ by taking into account an incentive factor ${\delta }_i$ that reflects the influencer’s effort and ensures fairness among them. To distribute these rewards, the influencers involved in the product marketing campaign on OSN platform s engage in a multilateral bargaining game among themselves. Specifically, each influencer is characterized by an individual bargaining operator, defined as follows.

$${\mathcal{B}}_i=\left[\begin{array}{ccccccc}{\delta }_1& \cdots & 0& 0& 0& \cdots & 0\\ 0& \cdots & 0& 0& 0& \cdots & 0\\ ⋮& \cdots & ⋮& ⋮& ⋮& \cdots & ⋮\\ 1-{\delta }_1& \cdots & 1-{\delta }_{i-1}& 1& 1-{\delta }_{i+1}& \cdots & 1-{\delta }_{|{\mathcal{I}}_s|}\\ ⋮& \cdots & ⋮& ⋮& ⋮& \cdots & ⋮\\ 0& \cdots & 0& 0& 0& \cdots & {\delta }_{|{\mathcal{I}}_s|}\end{array}\right]$$

(16)

In the context of the multilateral bargaining game involving influencers on platform s, ${\mathcal{I}}_s$ denotes the set of influencers selecting platform s. For each influencer $i\in {\mathcal{I}}_s$, matrix ${\mathcal{B}}_i$ is defined such that ${\mathcal{B}}_i$ is a matrix where $b_{i^{\prime }{i}^{\prime }}={\delta }_{i^{\prime }}$ for all $i^{\prime }\ne i$, and the i-th row $b_{i{i}^{\prime }}=1-{\delta }_{i^{\prime }}$ for all $i^{\prime }\ne i$, with $b_{ii}=1$. The bargaining operator for this game, $\mathcal{B}$, is composed as $\mathcal{B}={\mathcal{B}}_1{\mathcal{B}}_2\cdots {\mathcal{B}}_{|{\mathcal{I}}_s|}$. The characteristic polynomial of $\mathcal{B}$ is derived accordingly.

$$c\left(\xi \right)=det(\lambda I-\mathcal{B})$$

(17)

The bargaining operator $\mathcal{B}$ can be partitioned as follows:

$$\mathcal{B}={\left(b_{i{i}^{\prime }}\right)}_{|{\mathcal{I}}_s|\times |{\mathcal{I}}_s|}=\left[\begin{array}{cc}{\mathcal{B}}_{11}& {\mathcal{B}}_{12}\\ {\mathcal{B}}_{21}& {\mathcal{B}}_{22}\end{array}\right]$$

(18)

where ${\mathcal{B}}_{11}$ is a scalar, and ${\mathcal{B}}_{22}$ is a square matrix of size $\left(\right|{\mathcal{I}}_s|-1)$. Each influencer is characterized by the monetary incentive share function, which is defined as follows:

$$\begin{array}{cc}\hfill & {\mathbb{S}}_i({\delta }_{i+1},\cdots ,{\delta }_{|{\mathcal{I}}_s|},{\delta }_1,\cdots ,{\delta }_{|{\mathcal{I}}_s|-1})=det(I-{\mathcal{B}}_{22})\hfill \\ \hfill & \hspace{1em}=det(I-{\mathcal{B}}_{22}^{\left(i\right)}{\mathcal{B}}_{22}^{(i+1)}\cdots {\mathcal{B}}_{22}^{\left(\right|{\mathcal{I}}_s\left|\right)}{\mathcal{B}}_{22}^{\left(1\right)}\cdots {\mathcal{B}}_{22}^{\left(\right|{\mathcal{I}}_s|-1)})\hfill \end{array}$$

(19)

where ${\mathcal{B}}_{22}^{\left(i\right)},\forall i\in {\mathcal{I}}_s$ is a square matrix of size $\left(\right|{\mathcal{I}}_s|-1)$ derived from the partition of the worker’s individual bargaining operator ${\mathcal{B}}_i$, following a similar process as in Equation (18).

Based on Rubinstein’s analysis of the multilateral bargaining games [42,43], the optimal share of the monetary incentives is allocated among the influencers, who contribute to the product marketing campaign of the OSN platform s, as follows.

$${\mathfrak{r}}_{s,i}^{\mathbb{T}}=\frac{{\delta }_i^{i-1}·{\mathbb{S}}_i({\delta }_{i+1},\cdots ,{\delta }_{|{\mathcal{I}}_s|},{\delta }_1,\cdots ,{\delta }_{|{\mathcal{I}}_s|-1})}{\frac{\partial c\left(\lambda \right)}{\partial \lambda }{|}_{\lambda =1}}·{\mathfrak{R}}_s$$

(20)

Based on the influencers’ monetary incentive share function (Equation (19)) and the corresponding monetary reward (Equation (20)) that is allocated to each influencer, it is observed that the earlier an influencer is engaged in the product marketing campaign and the more information they contribute to it, the more monetary reward is received from the OSN platform. Considering those two characteristics, the OSN platforms also aim to treat the influencers in a fair manner in terms of allocating their available monetary rewards. Therefore, the OSN platforms can control the incentive factor ${\delta }_i$ based on their strategic planning for the product marketing campaign, as follows:

$${\delta }_i={\delta }_{min}+(I_i-\underset{\forall i\in {\mathcal{I}}_s}{min}\left\{I_i\right\})\frac{({\delta }_{max}-{\delta }_{min})}{(\underset{\forall i\in {\mathcal{I}}_s}{max}\left\{I_i\right\}-\underset{\forall i\in {\mathcal{I}}_s}{min}\left\{I_i\right\})}$$

(21)

where ${\delta }_{max}$ and ${\delta }_{min}$ are controlled by the OSN platform. The multilateral bargaining is performed at each platform s separately for each product marketing campaign to determine the optimal monetary rewards that will be provided to the influencers that select each platform at each time that they interact for a product’s advertisement.

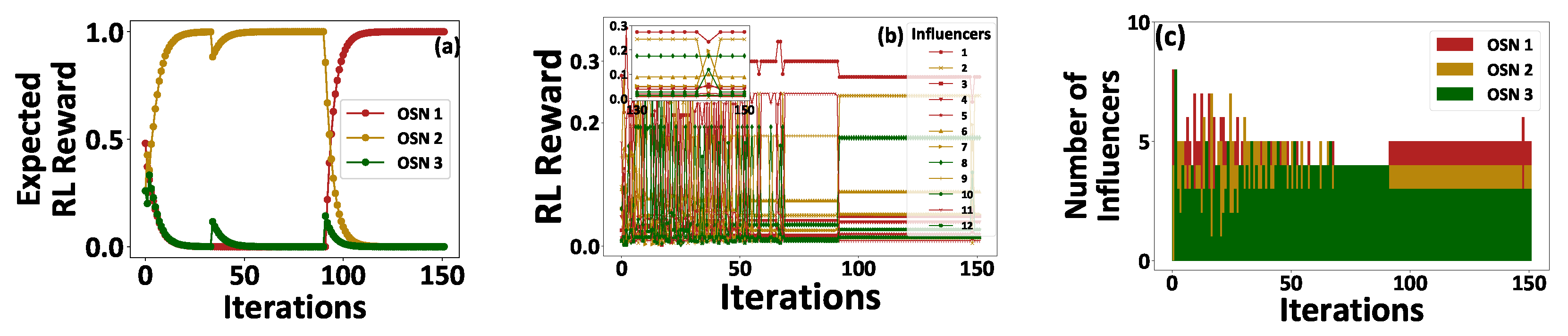
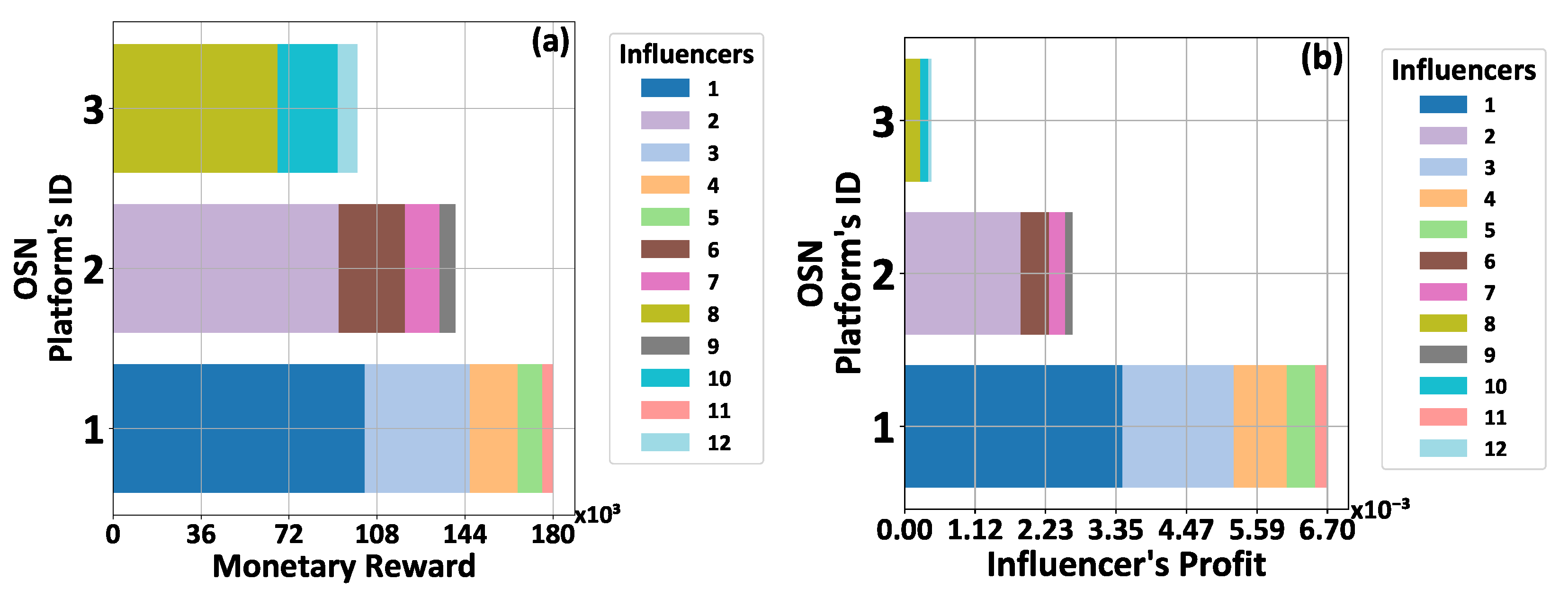
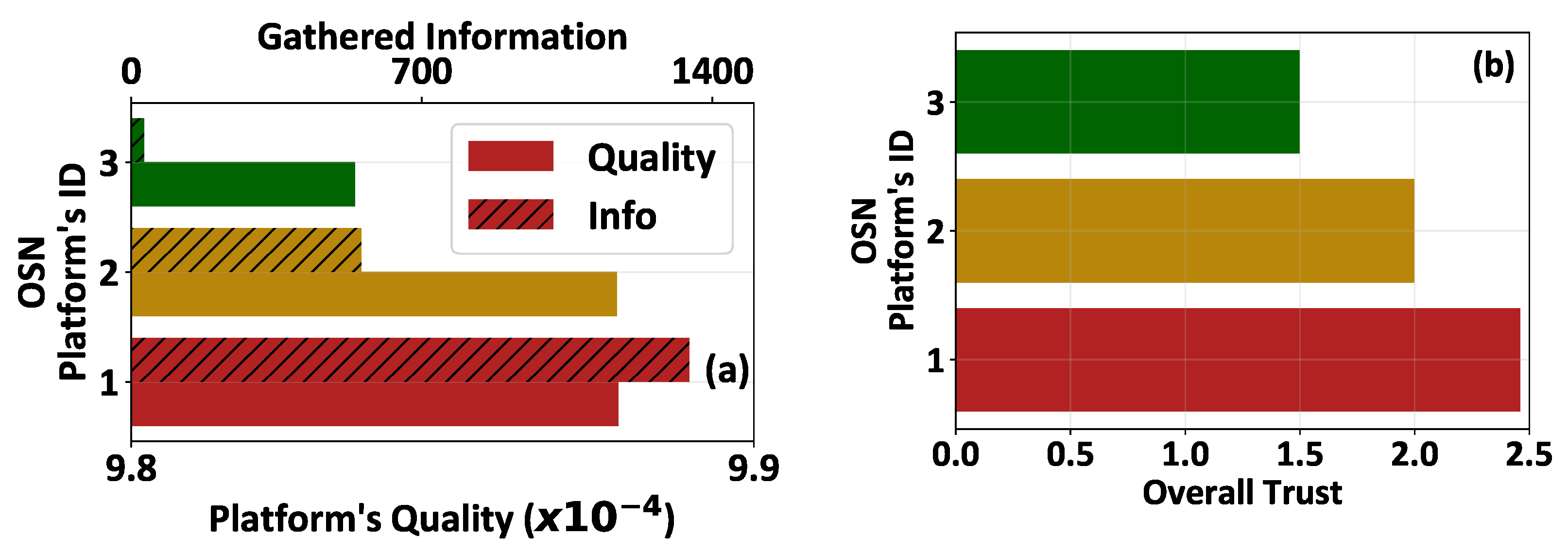
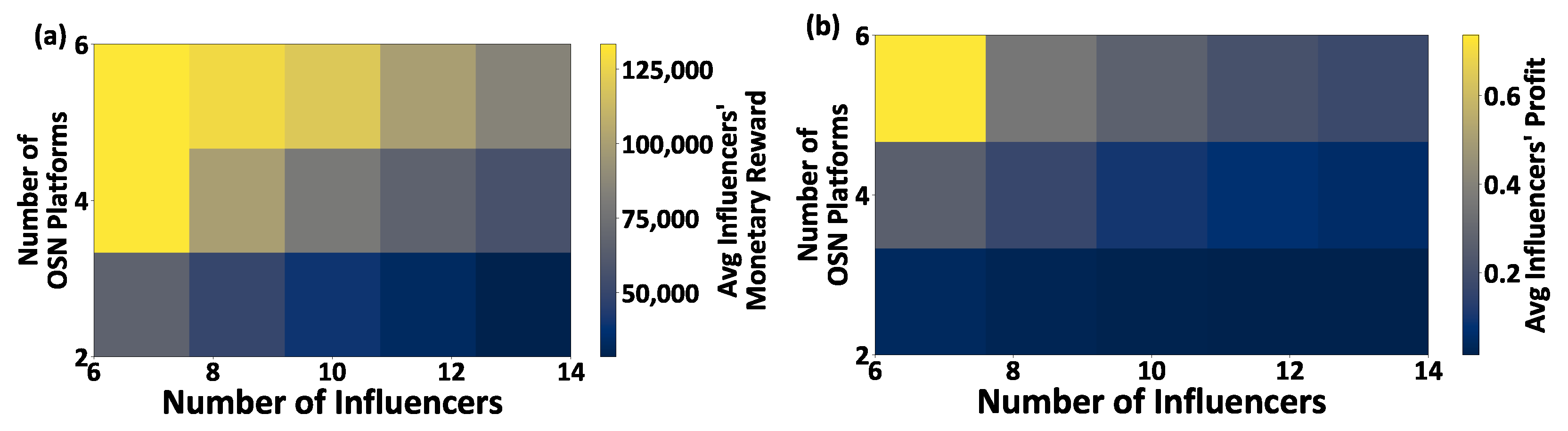
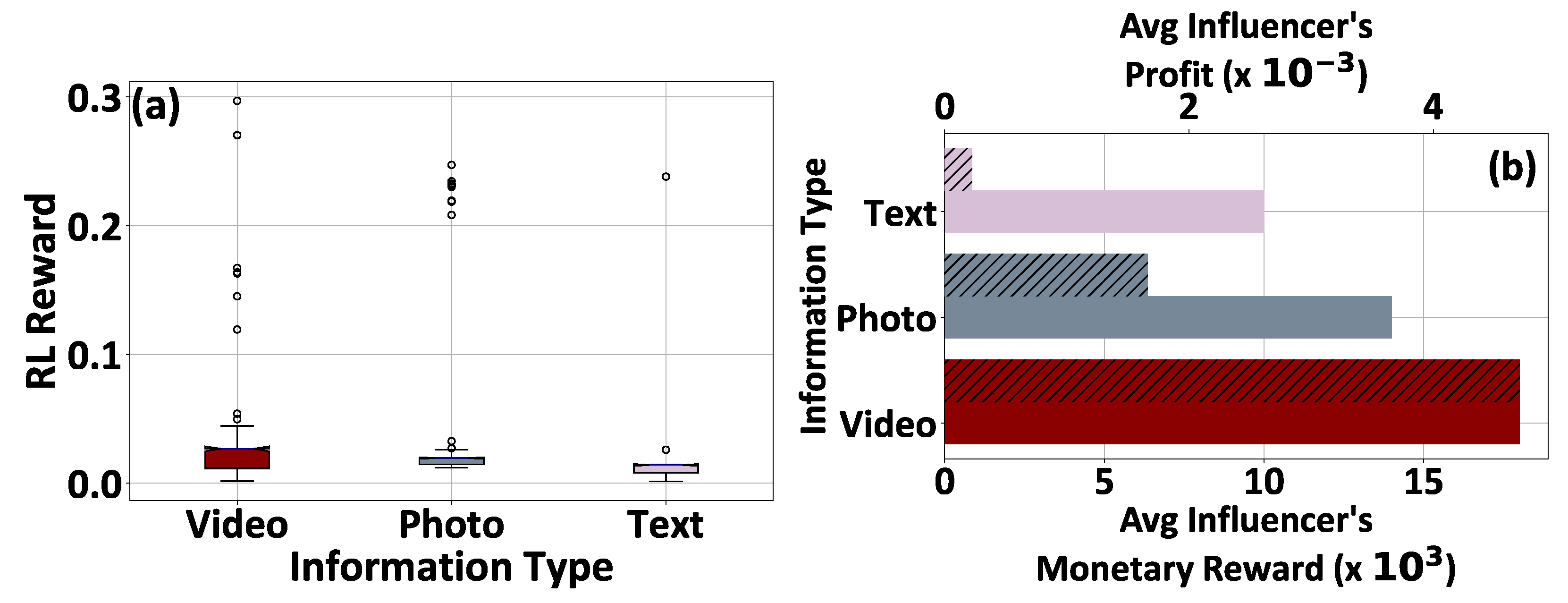
5. Numerical Evaluation

In this section, a detailed simulation-based evaluation is presented to demonstrate the operation and efficiency of the proposed INFLUTRUST framework. Specifically, Section 5.1 presents the pure operation and performance of the proposed INFLUTRUST framework from the influencers and the OSN platforms’ perspectives. Section 5.2 presents a thorough scalability analysis to demonstrate the robustness and efficiency of INFLUTRUST. A realistic application scenario of the INFLUTRUST framework is presented in Section 5.3. Finally, Section 5.4 provides a thorough comparative evaluation of the approaches that allow the influencers to select an OSN platform without considering their trust levels and/or allocate the monetary rewards to the influencers based on the principles of the proportional fairness considering their contribution to the product marketing campaign. In the rest of the analysis, the following simulation-based parameters have been adopted, $I=12$, $S=3$, $\lambda =1$, $\mu =2$, $\gamma =0.8$, $w_1=0.1$, $w_2=0.8$, $w_3=0.1$, $\mathbf{I}=[900,450,300,75,60,50,42.85,12.5,11.1,10,9.1,8.3]$ [Mbits], $c_{s,i}=\frac{{10}^{-6}}{(s+1)(i+1)}$$\left[\frac{¢}{bits}\right]\forall s\in \mathcal{S},i\in \mathcal{I}$, ${\mathfrak{R}}_i=\left[180,000,140,000,100,000\right][$¢$],{\delta }_{min}=0.55,{\delta }_{max}=0.9$, unless explicitly stated otherwise. Please note that in the rest of the analysis, the presented influencer’s profit is presented for each time instance the influencer contributes information to the product marketing campaign. An influencer will ultimately contribute information to the product marketing campaign multiple times in order to cumulatively accumulate their profit.

5.1. Pure Operation and Performance

In this section, the pure operation and performance of the INFLUTRUST framework are presented. Figure 1a–c present the convergence of the expected reinforcement learning reward $Q_{s,i}^{\mathbb{T}}$ for one indicative influencer and the corresponding three available choices, i.e., OSN platforms, the convergence of the normalized reinforcement learning reward for all the influencers for the optimal selected OSN platform, respectively, and the number of influencers per OSN platform, as a function of the SLA algorithm’s iterations, respectively. The results demonstrate that the SLA algorithm converges fast to the selection of an OSN platform by the influencers (Figure 1a). Also, for the selected OSN platforms by each influencer, the results reveal that the influencers with a lower ID who enter the product marketing campaign early and contribute a large amount of information to advertise the products achieve a higher SLA reward (Figure 1b), primarily due to the larger amount of received monetary rewards by their selected OSN platforms. Also, the results show that the OSN platforms which are characterized by a higher budget to recruit influencers for the product marketing campaigns attract a larger number of influencers to advertise their products (Figure 1c).

Figure 2a,b illustrate the influencers’ received monetary reward and profit for each of their selected OSN platforms. The results indicate that more influencers are attracted to advertise products for the OSN platforms that provide higher monetary rewards (Figure 2a), i.e., lower ID OSN platforms, thus achieving a higher profit (Figure 2b). Also, the results confirm that the influencers who contribute more information to the product marketing campaign, i.e., lower ID influencers, achieve a higher monetary reward through the multilateral bargaining process.

Figure 3a,b present the products’ quality, gathered information, and overall trust per OSN platform, respectively. The results reveal that the OSN platforms that are more competitive in the product marketing campaigns by investing more budget for monetary rewards to the influencers achieve an improvement in the products’ quality among their customers, in terms of word-of-mouth reputation, by attracting a higher advertisement effort by the influencers, i.e., contribution of information to the product marketing campaign (Figure 3a). Also, the corresponding OSN platforms achieve a higher trust level among the influencers (Figure 3b) who experience higher monetary rewards.

5.2. Scalability Analysis

In this section, a detailed scalability analysis is performed for an increasing number of influencers and OSN platforms to demonstrate the robustness and efficiency of the INFLUTRUST framework. Figure 4a,b present the average influencers’ achieved monetary reward and profit for an increasing number of influencers and OSN platforms. The results demonstrate that for a small number of influencers and a large number of available product marketing campaigns, the influencers experience high monetary rewards and corresponding profit by participating in the product marketing campaigns, given that the competition with each other is relatively small. The exact opposite phenomenon is observed for a large number of influencers and a large number of OSN platforms, while the influencers experience very limited monetary rewards when many of them compete for a small number of product marketing campaigns.

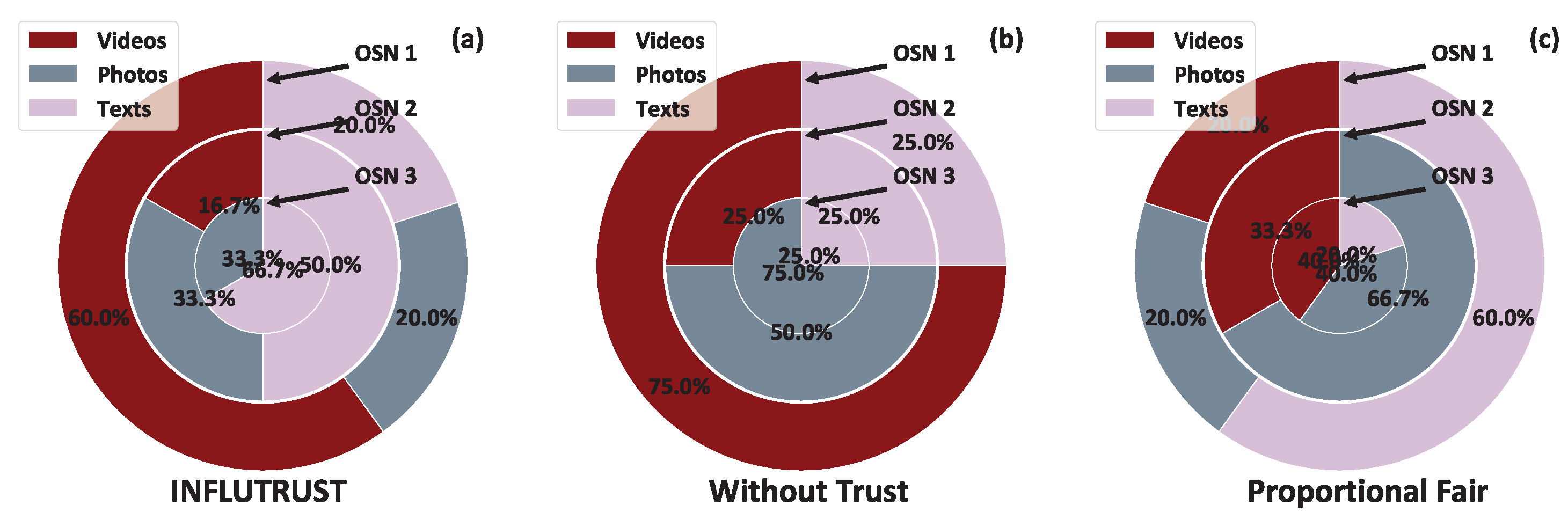
5.3. A Realistic Application Scenario Analysis

In this section, a realistic application scenario of the INFLUTRUST framework is demonstrated to capture its real-life applicability. Specifically, three groups of influencers are considered, each one of them consisting of four influencers, where each group contributes different types of content to support the product marketing campaign, i.e., video, photos, and text, respectively. Figure 5a,b present the RL reward, the average influencers’ monetary reward, and profit for the three groups of influencers, which are differentiated based on the type of content that they provide for the product marketing campaign. The results demonstrate that the influencers who provide enriched content to advertise the products achieve a higher RL reward (Figure 5a), given that they contribute a larger amount of information (Figure 5b). Thus, they also experience higher profit from participating in the product marketing campaign (Figure 5b).

5.4. Comparative Evaluation

In this section, a thorough comparative evaluation of the INFLUTRUST framework is performed against two comparative evaluation scenarios: (i) the influencers choose to participate in a product marketing campaign of an OSN platform based on the SLA algorithm, ignoring the OSN platforms’ trust levels; and (ii) the monetary rewards are allocated to the influencers considering the principles of proportional fairness with respect to the contributed amount of information in the product marketing campaign, while the OSN platform is selected based on the SLA algorithm. Figure 6 presents the average influencers’ monetary reward for the three groups of influencers providing video, photo, and text content for the product marketing campaign under all the comparative scenarios. Furthermore, Figure 7a–c present the percentage allocation of influencers per OSN platform for all the comparative scenarios.

The results reveal that under all the comparative scenarios, the influencers that provide more enriched content achieve a higher monetary reward (Figure 6). Focusing on the comparison among the three scenarios, the results indicate that under the scenario where the influencers select an OSN platform without considering its trust levels, the competitive influencers tend to choose the platform that provides the highest reward (Figure 7b); thus, they experience a higher average monetary reward compared to the INFLUTRUST framework (Figure 6). This observation drives the influencers that provide photos and text as advertisement content for the product marketing campaign to experience a substantially lower monetary reward (Figure 6). In the scenario where the monetary rewards are distributed proportionally based on the content contributed to the product marketing campaign, the results indicate that influencers capable of producing high-quality content tend to receive equitable allocations across the OSN platforms (Figure 7c). This ensures adherence to the principles of proportional fairness in terms of the monetary reward distribution. Consequently, significant disparities emerge in the average monetary rewards obtained by influencers generating video-, photo-, and text-based content (Figure 6) under the proportional fairness scenario. Finally, the INFLUTRUST framework achieves a fair distribution of the monetary rewards among the influencers (Figure 6) considering their contribution to the product marketing campaign and enables the influencers who can provide enriched content to select the OSN platform that provides the highest monetary rewards (Figure 7a).

6. Conclusions

In conclusion, while considerable attention has been given to recruiting influencers for online advertisement in Online Social Networks (OSNs), there is an existing research gap in addressing the influencers’ autonomy in choosing to advertise products across different OSN platforms, particularly in relation to trust dynamics between influencers, companies, and OSN platforms. This paper introduces the INFLUTRUST framework, which enables influencers to autonomously select products across different OSN platforms based on a reinforcement learning algorithm. The Stochastic Learning Automata reinforcement algorithm considers the monetary rewards offered by the OSN platforms to the influencers, the influencers’ profits, and their trust levels towards the OSN platforms in order to enable them to autonomously select an OSN platform. Additionally, a novel trust model is proposed consisting of direct and indirect trust to quantify influencers’ trust in both the OSN platforms and their corresponding advertised products. The INFLUTRUST framework also incorporates a multilateral bargaining model for allocating the monetary rewards among influencers. Simulation-based results demonstrate the effectiveness and scalability of the INFLUTRUST framework across diverse real-life scenarios, while a detailed set of comparative results quantify its superiority over existing models in terms of both the influencers’ and the OSN platforms’ perspectives.

Part of our current and future work focuses on the extension of the INFLUTRUST framework by incorporating more sophisticated trust models that dynamically adapt to evolving relationships and feedback from influencers and OSN platforms in order to improve the accuracy of trust assessments. Furthermore, our goal is to extend the INFLUTRUST framework in order to consider additional factors such as geographical location, cultural differences, and product relevance, aiming at making it more accurate and efficient to support both the influencers, as well as the OSN platforms.