AI-Empowered Multimodal Hierarchical Graph-Based Learning for Situation Awareness on Enhancing Disaster Responses

Abstract

Situational awareness (SA) is crucial in disaster response, enhancing the understanding of the environment. Social media, with its extensive user base, offers valuable real-time information for such scenarios. Although SA systems excel in extracting disaster-related details from user-generated content, a common limitation in prior approaches is their emphasis on single-modal extraction rather than embracing multi-modalities. This paper proposed a multimodal hierarchical graph-based situational awareness (MHGSA) system for comprehensive disaster event classification. Specifically, the proposed multimodal hierarchical graph contains nodes representing different disaster events and the features of the event nodes are extracted from the corresponding images and acoustic features. The proposed feature extraction modules with multi-branches for vision and audio features provide hierarchical node features for disaster events of different granularities, aiming to build a coarse-granularity classification task to constrain the model and enhance fine-granularity classification. The relationships between different disaster events in multi-modalities are learned by graph convolutional neural networks to enhance the system’s ability to recognize disaster events, thus enabling the system to fuse complex features of vision and audio. Experimental results illustrate the effectiveness of the proposed visual and audio feature extraction modules in single-modal scenarios. Furthermore, the MHGSA successfully fuses visual and audio features, yielding promising results in disaster event classification tasks.

1. Introduction

Rapidly sensing and understanding the data generated during a disaster can help in disaster response. On social media, data generated by users in the near future of a disaster are likely to express the situation they are facing as well as disaster-related information, such as the category of the disaster event. Situational awareness (SA) systems are particularly important in this area as they can automate the sensing and understanding of user-generated information to help people perform rapid disaster response [1,2]. However, user-generated information is usually multimodal and typically contains visual, audio, and textual information. Appropriate integration of multimodal features has also been shown in several works to improve the accuracy of data analysis [3,4] and it becomes a challenge to deal with the multimodal information in these messages [5].

The introduction of artificial intelligence has greatly enabled disaster response and situational awareness systems. In disaster response, the application of convolutional neural networks (CNNs) provides a powerful tool to analyze visual information quickly and accurately [6,7,8]. By performing feature extraction and pattern recognition on images of a disaster site, CNNs can help determine the type, scale, and impact of a disaster. However, in the practical application of disaster response, the integration of multimodal data needs to be considered in addition to visual information [9]. The synergistic analysis of multi-source information such as speech data might provide a more comprehensive understanding of the disaster scene.

In previous work, much research has focused on the processing of single-modal information, such as processing only image [6] or text [10] data. Such approaches have been successful in some contexts but they potentially fall short in fully leveraging the correlations between different modal information, limiting the system’s ability to fully understand the overall environment.

In recent years, with the rise of graph learning, multimodal information fusion has become more flexible and efficient. By abstracting information from different modalities into nodes of a graph and using graph convolutional networks (GCNs) for information transfer and fusion, the GCNs can automatically learn the relationships between modalities, enabling the whole system to better understand the association between multimodal information [11]. It is worth noting that the introduction of graph learning does not mean abandoning the deeper mining of each modality. On the contrary, combining graph learning with traditional CNNs allows for a more comprehensive exploitation of the characteristics of each modality, resulting in a more information-rich and robust multimodal feature representation. The introduction of graph learning for modality data [11] can be divided into reconstructing modalities into graph structure [12,13,14] and identifying graph nodes from modalities [15,16,17]. We utilize the latter approach to extract nodes representing different disaster events from multimodal data (visual and audio) and construct a graph using the relationships of the disaster events. This suggests the two following challenges:

• Providing an effective discriminative representation of multimodal data;
• Placing demands on the construction of the graph structure to ensure that the network can learn the relationships between the different modalities.

Therefore, in the light of the challenges outlined above, we focus on extracting disaster-related information from paired visual and audio data (usually represented as video) in this work. Our proposed multimodal hierarchical graph-based SA system can classify disaster events at coarse- and fine-grained for primary and advanced sensing based on visual and audio, referring to the multi-level sensing introduced by the three-layer model of SA [18]. The main contributions of this paper are as follows:

• We propose a multi-branching feature extraction framework that consists of shared convolutional layers and branching convolutional layers for events of specific granularity to provide independent trainable parameters for different granularities during end-to-end joint optimization;
• We construct an event-relational multimodal hierarchical graph to represent disaster events at different granularities to improve the performance of the system in advanced perception by multilayering the perception of the SA system;
• We propose a method for multimodal fusion using hierarchical graph representation learning, which enhances relational learning of multimodal data;
• The proposed MHGSA system is evaluated on datasets and consists of a significant improvement over the unimodal baseline approach.

2. Proposed Methodology

This paper presents the proposed multimodal hierarchical graph-based situational awareness (MHGSA) system for disaster response. It consists of a visual feature extraction module, an audio feature extraction module, and the multimodal hierarchical graph. Figure 1 shows the architecture of the proposed system. This section will first introduce the two multi-branch feature extraction modules for vision and audio and their implementation setups and the subsequent sections will present the proposed methodology for hierarchical graphs, including graph construction, gated graph convolutional neural network, and classification of graph nodes.

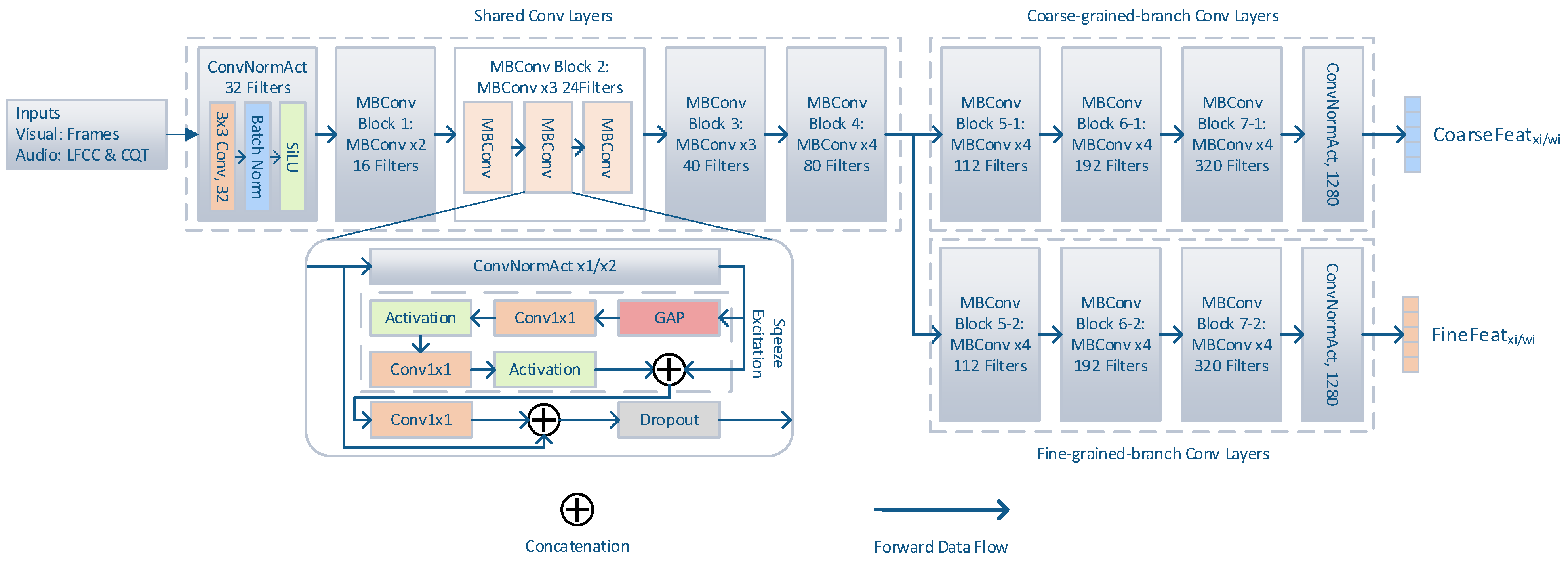
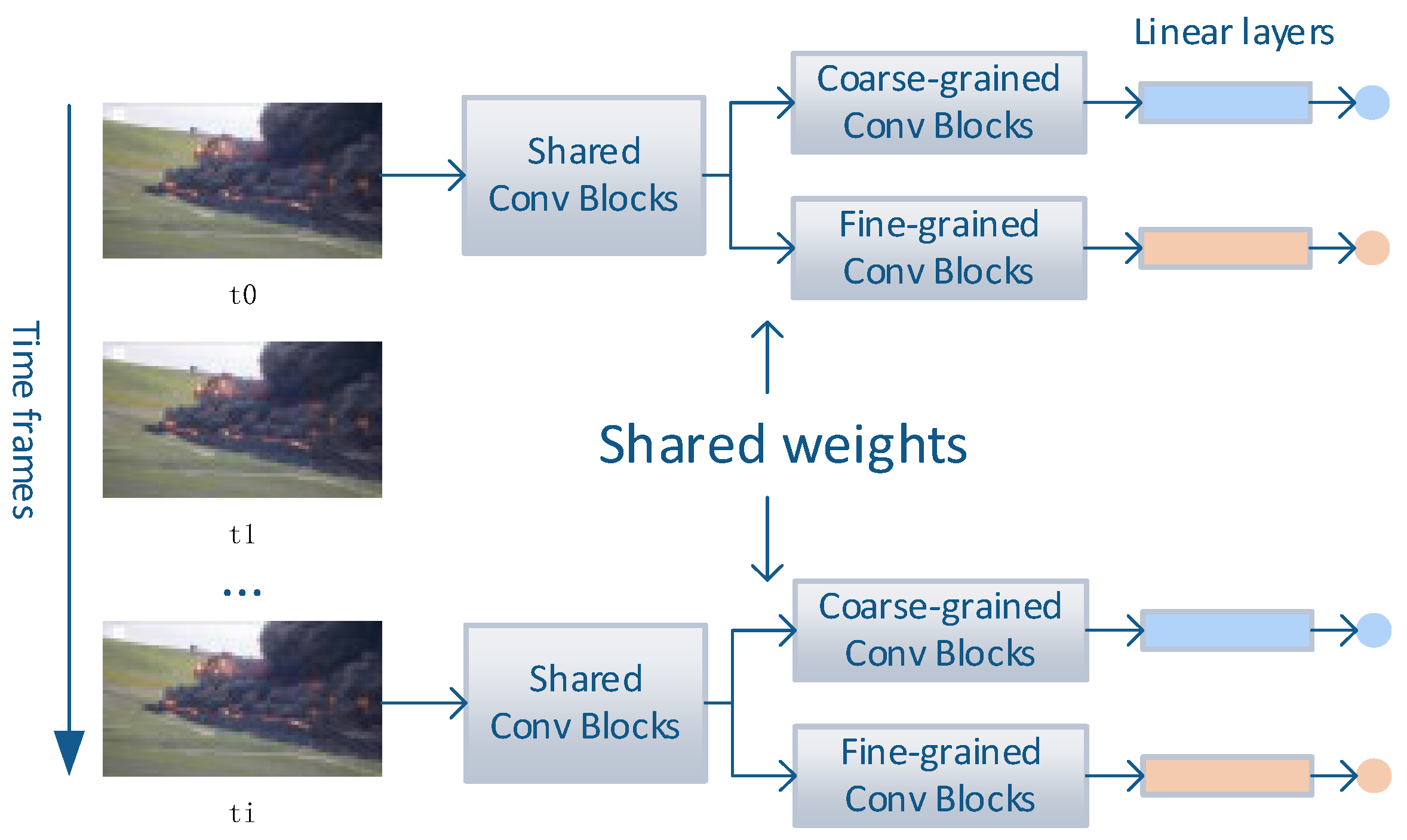
2.1. Multi-Branch Featrue Extraction Module

This section describes two feature extraction modules that provide nodes features for hierarchical graphs. Their role is to extract a representation from a given piece of image and its accompanying audio clip suitable for the task of classifying disaster events. We first define a set of fine-grained disaster events and corresponding coarse-grained disaster events, denoted as $E_f$ and $E_c$, and the number of events they contain are $N$ and $M$, respectively.

$$E_c=\left\{E_{c1}, E_{c2},\dots ,E_{cN}\right\},$$

(1)

$$E_f=\left\{E_{f1},E_{f2},\dots ,E_{fM}\right\},$$

(2)

and any fine-grained event $E_{fn}$ has only one corresponding coarse-grained event $E_{cm}$, as follows:

$$\forall E_{fn}\in E_f,\exists E_{cm}\in E_c such that f\left(E_{fn}\right)=E_{cm}.$$

(3)

$$f:E_f\to E_c,$$

(4)

The multi-branch structure aims to provide separate model parameters for $E_f$ and $E_c$ to cope with end-to-end joint training. This structure has been applied in some work to provide hierarchical (i.e., multi-granularity) image classification [19,20,21,22]. In contrast to the independent branching structure, the multi-branching structure employs a shared convolutional network to extract common visual features in the image, which solves part of the parameter redundancy problem. Using this multi-branch structure, we propose a model derived from EfficientNet [23] for generating nodes feature for the visual and audio outputs, which is designed to work with the event-relational hierarchical graph to model image and acoustic features to features that correspond to different disaster events. As shown in Figure 2, linear layers corresponding to the number of $E_f$ and $E_c$ provided by the nodes with features of the specified dimensions.

2.1.1. Visual Feature Extraction for Multigranularity

Visual signals, an important part of human perception, are understood by computers in the form of pixels that are intuitive and easy to understand. In social media, visual signals usually appear as images or videos (images with multiple frames), which are usually single-channel (monochrome) or three-channel (RGB). Thanks to convolutional neural networks, RGB images represented as three-dimensional arrays are converted into one-dimensional vector representations through multiple layers of convolution and pooling. A common approach is to use one or more layers of fully connected networks defining appropriate input–output dimensions as classifiers for convolutional neural networks to achieve downstream tasks. In this subsection, we only discuss the feature extraction module before the fully connected layers.

Based on the optimization of depth, width, and resolution, EfficientNet, as a CNN model, provides better classification accuracy with a smaller number of parameters by virtue of efficient parameter settings. Seven such models are proposed in [23], from EfficientNet-b0 to EfficientNet-b7, and their number of parameters gradually increases from 5.3 M to 66 M. In the ImageNet [24] dataset, EfficientNet has a much smaller number of parameters compared to other models with similar accuracy. For example, the classic ResNet50 [25] has about 26M parameters but its performance is lower than EfficientNet-b1, which has no more than 8M parameters. In this paper, we utilize the mobile inverted bottleneck convolution (MBConv) block of EfficientNet as the basis to build the feature extraction module. A single MBConv block contains a classical convolutional block (i.e., a stack of convolutional, batch normalization, and activation layers), a squeeze-and-excitation module [26] to provide a channel attention mechanism, and a 1 × 1 convolutional layer paired with residual connections. As shown in Figure 3, our proposed multi-branch visual feature extraction module employs a stack of convolutional layers in a multi-branching pattern, which is divided into a front segment and a back segment. When the model uses only shared convolutional blocks and one branch convolutional block, the model will converge to the same as EfficienNet-b1.

The convolutional blocks in the front segment will be used as a shared set of convolutional layers $VisualCon{v}_{shared}$ and subsequently, two sets of identical convolutional layers, $VisualCon{v}_{paralle{l}_c}$ and $VisualCon{v}_{paralle{l}_f}$, in the back segment are constructed for coarse- and fine-grained event classification.

Given a set of videos $X=\left\{x_1,x_2,\dots ,x_T\right\}$ from dataset $D$ with its corresponding multi-granularity labels $Y=\{y_{f1},y_{c1},y_{f2},y_{c2},\dots ,y_{fT},y_{cT}\}$, frames $F_i=\{f_1,f_2,\dots ,f_K\}$ are extracted from $i^{th}$ video $x_i$. The visual feature extraction module uses shared parameters to process multiple frames in a single video; the feed-forward process of the network can be represented as

$$VisualSharedFea{t}_{f_k}=Con{v}_{shared}\left(f_k\right),$$

(5)

$$VisualCoarseFea{t}_{x_i}=\left\{Con{v}_{paralle{l}_c}\left(VisualSharedFea{t}_{f_k}\right)\right\}, k\in [1,K]$$

(6)

$$VisualFineFea{t}_{x_i}=\left\{Con{v}_{paralle{l}_f}\left(VisualSharedFea{t}_{f_k}\right)\right\}, k\in [1,K]$$

(7)

In this work, we extracted 10 frames $(K=10)$ to represent a video. The multi-branching feature extraction module allows each frame to obtain two feature vectors representing coarse and fine granularity for representing the disaster event. Thus, a single video will obtain $2K$ feature vectors in order to construct a hierarchical graph for visual features. We assign a linear layer to each convolutional branch to obtain a node representation for each image frame, i.e., $F{C}_f$ and $F{C}_c$, which is shown in Figure 3. In this way, the node features of a single video in the hierarchical graph can be represented as

$$NodeFea{t}_{c xi}^{Visual}=\sigma \left(W_c\cdot VisualCoarseFea{t}_{xi}\right),$$

(8)

$$NodeFea{t}_{f xi}^{Visual}=\sigma \left(W_f\cdot VisualFineFea{t}_{xi}\right).$$

(9)

where $W_c$ and $W_f$ are the learnable weights of $F{C}_c$ and $F{C}_f$. $\sigma$ is an activation function, where the rectified linear unit (ReLU) is employed.

When using the module alone for vision-only disaster event classification, we add the corresponding pooling and fully connected layers at the end of the two convolutional branches to normalize the output categories.

$${\widehat{y}}_c=\sigma \left(W_c\cdot VisualCoarseFea{t}_{xi}\right),$$

(10)

$${\widehat{y}}_f=\sigma \left(W_f\cdot VisualFineFea{t}_{xi}\right).$$

(11)

2.1.2. Audio Feature Extraction for Multigranularity

Audio data are typically represented as a sequence of waveforms in the time domain. Our original idea to learn their representation and make them assist visual features for downstream tasks lies in the fact that the occurrence of a disaster event is usually accompanied by a corresponding sound. For example, a fire is usually accompanied by the crackling sound of burning objects or a storm is usually accompanied by the sound of rain or wind. We designed an audio preprocessing algorithm to convert one-dimensional waveforms into two-dimensional audio features. LFCC and CQT as acoustic features are extracted after performing voice active detection (VAD) on the audio.

A Voice Activity Detection (VAD) module was implemented [27] for data preprocessing. This module filters activated speech by calculating the short-time energy and short-time zero-crossing counter of the audio. Suppose there is a segment of audio $w_i$ that is paired with $x_i$, as mentioned before, thus:

$$W=\left\{w_1,w_2,\dots ,w_T\right\}.$$

(12)

The energy and zero crossing counter of $w_i$ can be calculated as follows:

$$Energ{y}_i=w_i^2,$$

(13)

$$ZC{C}_i=\left|sign\left(w_i\right)-sign\left(w_{i-1}\right)\right|$$

(14)

By averaging the $T$-length audio into $F$ segments, the short-time energy and short-time zero-crossing counter can be expressed as follows:

$$Energ{y_{short-time}}_f={\sum }_{f\in F}Energ{y}_f$$

(15)

$$ZC{C_{short-time}}_f={\sum }_{f\in F}ZC{C}_f$$

(16)

Suitable audio clips are filtered through a set threshold with the filtering rule:

$$\left(Energ{y}_f>Threshol{d}_{Energy}\right) \wedge \left(ZC{C}_f<Threshol{d}_{ZCC}\right)$$

(17)

LFCC and CQT are extracted on the activated audio clips

$$LFC{C}_{active}=DCT\left({\log }_{10}LinearFreqFilterBank\left(STFT\left(w_{t=ActiveFrames}\right)\right)\right),$$

(18)

$$CQ{T}_{active}=abs\left(ConstantQFilterBank\left(STFT\left(w_{t=ActiveFrames}\right)\right)\right),$$

(19)

where $LFC{C}_{active}$ and $CQ{T}_{active}$ are both matrices. They are concatenated to form an image-like 2-channel acoustic feature vector for the subsequent audio feature extraction

$$AudioSharedFea{t}_{w_i}=Concat(LFC{C}_{active},CQ{T}_{active})$$

(20)

Multiple audio events may be included in a single audio clip. Inspired by [17], we modified the originally shared single linear layer to linear layers containing only one neuron corresponding to the number of events, i.e., $F{C}_{fi}$ and $F{C}_{ci}$, to obtain a node representation of the corresponding events. Therefore, a single audio can provide feature vectors for all events, i.e., $E_f$ and $E_c$, and the process can be briefly expressed as follows:

$$NodeFea{t}_{c_i}^{Audio}=\sigma \left(W_{ci}\cdot W_{Audio}\cdot \left(AudioSharedFea{t}_{wi}\right)\right)$$

(21)

$$NodeFea{t}_{fj}^{Audio}=\sigma \left(W_{fj}\cdot W_{Audio}\cdot \left(AudioSharedFea{t}_{wi}\right)\right)$$

(22)

where $W_{ci}$ and $W_{fj}$ is the learnable weights of $F{C}_{ci}$ and $F{C}_{fj}$ for the $i^{th}$ and $j^{th}$ event in $E_c$ and $E_f$. $W_{Audio}$ denotes the learnable parameters of the audio feature extraction module. Figure 4 illustrates the structure of the audio feature extraction module.

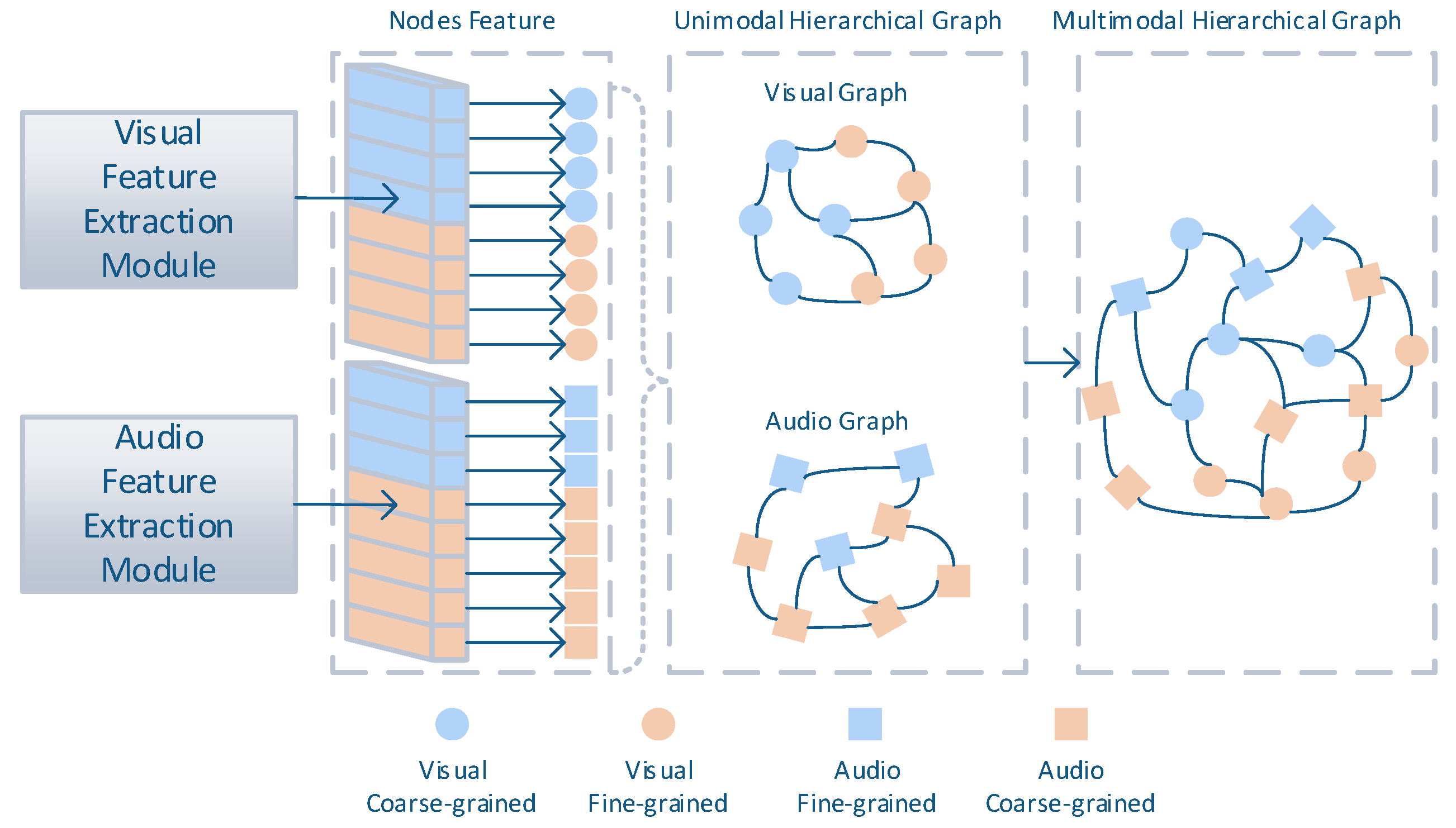
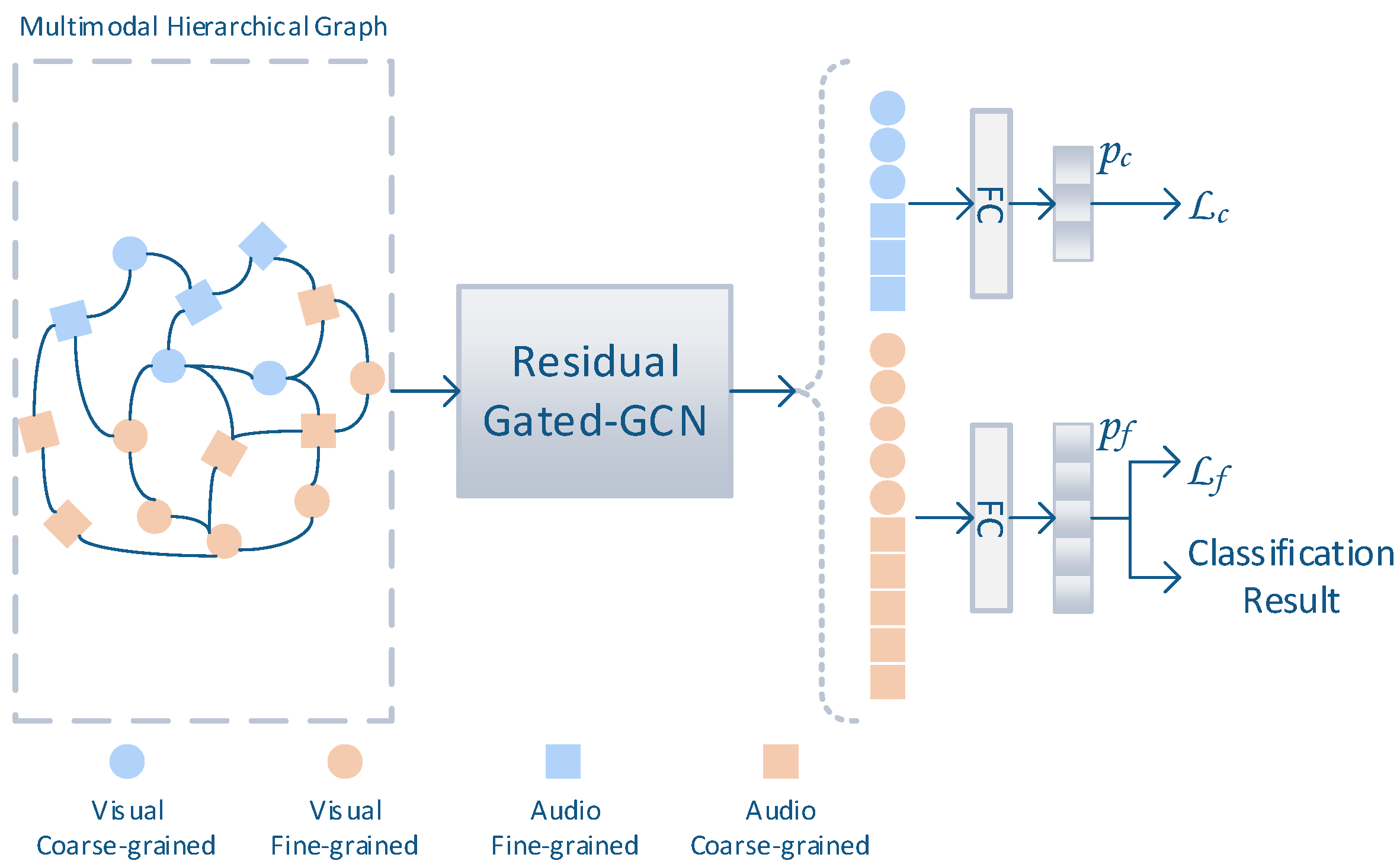
2.2. Hierarchical Graph for Disaster Event Classification

2.2.1. Hierarchical Graph Construction

A multimodal hierarchical graph consisting of events is built after having all the node features of the fine-grained disaster event$E_f$ and the coarse-grained disaster event $E_c$ in visual and audio features. It aims to learn the relationships between different event nodes and update the node features employing the subsequent graph convolutional learning. Inspired by [17], we define a hierarchical graph containing multimodal multi-granularity event nodes. They are all constructed in a fully connected manner. There is a graph $G=(V,E)$, where $V$ and $E$ denote the nodes and edges, respectively. The initial connection of nodes can be represented as follows:

$$A_{i,j}=1, i\in N, j\in N$$

(23)

where $A$ is the adjacency matrix of the graph and $N$ denotes the number of nodes in the graph. This type of connection requires each node to be self-connected, so the number of edges contained in a single graph is indicated below:

$$\left|E\right|=\frac{N\left(N+1\right)}{2},$$

(24)

where $\left|\cdot \right|$ denotes the base of a set, i.e., the number of elements in the set.

The hierarchical graph construction is visually portrayed in Figure 5, where blue nodes correspond to coarse-grained event categories, and yellow nodes signify fine-grained ones. Visual features are represented by circular nodes, whereas audio features are denoted by square nodes. The visual and audio features are output by their corresponding feature extraction module and are concatenated outside the module to form node features for the graph construction.

Based on the proposed visual and audio feature extraction modules, we construct a node for each disaster event and assign a node feature for it. In order to independently learn the node features for each type of event, node features are constructed from the corresponding granularity branches using linear layers, as described in Equations (8) and (9) for visual features and Equations (21) and (22) for audio features.

For single-modal hierarchical graphs, i.e., $G_{Single}^{Visual}$ (visual only) or $G_{Single}^{Audio}$ (audio only), their node features are obtained from the proposed multi-branch feature extraction module for corresponding modality. A single modality hierarchical graph $G_{single}$ can be represented as

$$G_{Single}^m=\left(V_{Coarse}^m\cup V_{Fine}^m,E_{Single}^m\right),m\in \left[Visual, Audio\right],$$

(25)

where $N_i^m$ denotes the node features. This allows subsequent GCN to learn the subordination relationship of coarse-grained and fine-grained events.

The proposed multimodal hierarchical graph $G_{Multi}$, composed using all the event nodes of different modalities, makes it have twice as many nodes as event categories.

$$G_{Multi}=\left(V^{Visual}\cup V^{Audio}, E_{Single}^{Visual}\cup E_{Single}^{Audio}\cup E_{Multi}^{Visual\leftrightarrow Audio}\right),$$

(26)

where $V_{Visual}$ and $V_{Audio}$ denote the nodes from $G_{Single}^{Visual}$ and $G_{Single}^{Audio}$, respectively. Regarding them as subgraphs, $E_{Multi}^{Visual\leftrightarrow Audio}$ contains edges connecting them. Employing the gated graph convolutional network, $E_{Single}^{Visual}$ and $E_{Single}^{Audio}$ can be learned by the previous layers and be passed to the layer for $G_{Global}$ by adding initialed edges connecting $V_{Visual}$ and $V_{Audio}$.

2.2.2. Graph Convolutional Network for Classification

To learn the relationship between coarse granularity events and fine granularity events, we use the residual gated graph convolutional network (RG-GCN) proposed by Bresson and Laurent [28]. It is known that the vanilla GCN can define the feature vector $h_i$ as [29]:

$$h_i^{l+1}=GCN\left(h_i^l, \{h_j^l:j\to i\}\right)=ReLU\left(U^l{h}_i^l+\sum _{j\to i}{V^{l}h}_j^l\right),$$

(27)

where $l$ denotes the layer level, $h_j$ is a set of unordered feature vectors of all neighboring nodes, and $U,V$ are learnable parameters for the message passing on current node and neighboring nodes. After adding a gating mechanism to the edge [30]:

$$h_i^{l+1}=G\text{-}GCN\left(h_i^l, \{h_j^l:j\to i\}\right)=ReLU\left(U^l{h}_i^l+\sum _{j\to i}{\phi }_{ij}⨂V^l{h}_j^l\right),$$

(28)

$${\phi }_{ij}=\sigma \left(\overline{U}{h}_i^l+\overline{V}{h}_j^l\right),$$

(29)

where ${\phi }_{ij}$ denotes the edge gates it brings two sets of weight parameters $\overline{U}$ and $\overline{V}$ to learn on edges. $\sigma$ is the sigmoid activation function and $\otimes$ is the point-wise multiplication operator. Adding the residual mechanism, the RG-GCN is simply denoted as [25]:

$$h_i^{l+1}=RG-GCN\left(h_i^l, {\{h}_j^l:j\to i\}\right)=G-GCN\left(h_i^l, {\{h}_j^l:j\to i\}\right)+h_i^l,$$

(30)

With the depth of graph convolution, each event node can aggregate the features of neighboring event nodes to achieve the update to obtain new own features and the weighting of edges in RG-GCN can model the correlation between different disaster events. For all nodes $I_i^{l+1}$ in $h_i^{l+1}$, as described in Equations (27)–(30), the node features at the $l+1^{th}$ layer will take into account both the features of its own node $I_i^l$, the neighboring node $I_j^l$, and of the edge $e_{ij}^l$ between $I_i^l$ and $I_j^l$ at the $l^{th}$ layer. $e_{ij}^l$ is the edge feature weighted by the edge gates ${\phi }_{ij}$ and its unweighted initial value can be obtained in the adjacency matrix $A_{ij}$ described in Equation (23).

We used a three-layer RG-GCN for learning nodes and edges in the hierarchical graph. We classify the learned event node features for classification. In the multimodal graph, we fused event nodes of the same granularity, as follows:

$$\begin{gathered} {\widehat{y}}_i=\sigma \left(W_{fc}\cdot \left\{I_{ij}^l\right\}\right) \\ i\in \left[Coarse,Fine\right], j\in \left[Visual,Audio\right],l=3 \end{gathered}$$

(31)

2.2.3. Loss Function

The loss function of MHGSA is based on the cross-entropy loss function weighted summation of coarse and fine granularity. It can be expressed as:

$${\mathcal{L}}_c=-log(\frac{e^{p_{{\widehat{y}}_i}^{coarse}}}{{\sum }_j{e}^{p_j^{coarse}}})$$

(32)

$${\mathcal{L}}_f=-log(\frac{e^{p_{{\widehat{y}}_i}^{fine}}}{{\sum }_j{e}^{p_j^{fine}}})$$

(33)

$${\mathcal{L}}_{final}=A_c{\mathcal{L}}_c+A_f{\mathcal{L}}_f$$

(34)

where ${\mathcal{L}}_c$ and ${\mathcal{L}}_f$ denote cross-entropy loss calculated for coarse- and fine- granularity and ${\mathcal{L}}_{final}$ denotes the final loss. $p_{{\widehat{y}}_i}$ represents the $i^{th}$ output logits and $p_j$ represents the $j^{th}$ element of the logits. The value $A$ denotes the loss weight of contributing to the loss function.

As shown in Figure 6, two linear layers are employed to classify the coarse- and fine-grained events from the event nodes of the multimodal hierarchical graph. The logits $\widehat{y}$ output from the linear layers is then used to calculate the error between the true label $y$ utilizing the Equations (32)–(34). Fine-grained classification with more event categories will be used as the final classification result.

The weights assigned to the losses of different granularity classification tasks determine how much a branch contributes to the final loss function. When training with the employment of Adam [31] as the optimizer, the network of branches involved in that classification will not be updated when the weight of a classification task is equal to 0; on the contrary, when the weight is equal to 1, the weights in the network will be involved in training. This allows controlling their relative values to influence how well different branches are trained as well as how fast they are optimized. Our original intention was to add coarse granularity classification as an auxiliary task to the original classification task to better train the shared convolutional blocks. Therefore, the weight of the coarse granularity is the same as that of the fine granularity in the early stage of training, e.g., [0.5, 0.5]. In the later stages of training, the weight of fine granularity is gradually increased and the weight of coarse granularity is decreased until the weight of coarse granularity is decreased to 0, to improve the model’s ability to classify fine granularity.

3. Experiments and Results

In this section, we analyze the performance of the MHGSA system through two main research questions: (1) whether the proposed multibranch structural feature extraction modules for vision and audio lead to better model performance in the unimodal case; and (2) whether the multimodal hierarchical maps lead to effective feature fusion and provide additional performance in the multimodal case. In the following subsections, we provide a detailed description of the experimental datasets and experimental setup and present our experimental results and analysis.

3.1. Experiment Datasets

In order to evaluate each module in the MHGSA system in a more comprehensive way, we introduced VGGSound [32] datasets in the experimental part to evaluate different modules. It is worth mentioning that the datasets typically have only one granularity of event labeling. In order to fit the multi-branching structure, we classified the labels of the dataset with coarse granularity. VGGSound [32], an audio–visual dataset containing more than 300 classes, consists of more than 200 k ten-second video clips, totaling about 560 h of memory. We extracted 12 disaster-related classes from the dataset and categorized them into three coarse-grained categories. The extracted dataset contains a total of 9289 video clips, with 50 video clips in each class for testing.

3.2. Details of Implementation

We built the MHGSA system using the PyTorch (Menlo Park, CA, USA) framework with hardware specifications of Intel (Santa Clara, CA, USA) Core i9 CPU and Nvidia (Santa Clara, CA, USA) GTX 4090 GPU. To minimize losses, an Adam optimizer with 64 batches and an initial learning rate of $1\times {10}^{-3}$ was used. To dynamically adjust the learning rate, we defined a decay rate of 0.1, which was activated when the validation set metrics did not improve within 5 epochs. We performed several training and testing sessions using different random seeds to obtain more balanced results, which made the experiment more credible.

3.3. Experiments on the MHGSA System

The MHGSA system, based on the two previously mentioned multi-branch feature extraction modules for different modalities, uses a residual gated graph convolutional neural network based on hierarchical graphs as multimodal feature fusion. We extracted 12 categories from the original VGGSound dataset and categorized them into three categories as coarse granularity labels (Figure 7). We referred the extracted dataset as VGGSound for Disaster Response (VGGSound-DR).

We conducted three experiments to compare the vision-only, audio-only, and multimodal cases. ResNet50 [25], EfficientNet-b1 [23] ResNet3D [33], and PANNs [34] are used as baselines to explore the performance of our models. It is worth mentioning that the proposed models are constructed differently in terms of classifiers due to the use of a multi-branch structure. We refer to the proposed feature extractor without graph learning as MHSA and to the model that uses the proposed graph-based approach as MHGSA. In addition, the comparison of MHSA and MHGSA demonstrates the effectiveness of the graph-based approach in the multimodal case. The average accuracy and its standard deviation, the best accuracy, the total number of trainable parameters, and the average inference time for one video clip are shown to reveal the performance of models.

As indicated in

Table 1. Experiment on VGGSound-DR in visual-only mode.

Mode	Model	Avg. Acc. (S.D.)	Best Acc.	Avg. Time (ms/Video)	Params
Visual-Only	ResNet-50	54.1 (±0.5)%	54.8%	13.1	26M
	Eff.Net-b1	57.2 (±0.6)%	58.0%	18.2	8M
	R3D-18 *	58.2 (±0.2)%	58.5%	10.4	33M
	MHSA-VO	59.4 (±0.5)%	60.0%	18.8	15M
	MHSA-VO *	64.9 (±0.4)%	65.3%	37.8	15M
	MHGSA-VO *	66.2 (±0.4)%	66.7%	46.1	17M

* Model using multiple frames.

, in the visual-only mode (VO), the best classification accuracy of the MHSA-VO using 10 frames as input and fully connected layers as classifiers is higher than that of EfficientNet-b1 (57.2%), ResNet-50 (54.8%), and R3D-18 (58.5%), at 65.3%, and the number of parameters is much lower than that of ResNet-50 and R3D-18. This suggests that the multi-branch structure is effectively utilized to the coarse-grained classification task to improve the model’s performance on the fine-grained classification task. Multi-frame input significantly improves the performance of the model. MHSA-VO improves accuracy by more than 5% when using multiple frames as input over the single-frame case. To reduce the computational cost, we first trained MHSA-VO using single-frame inputs and froze the trained parameters for multi-frame training. Thus, the multi-frame input does not affect the number of parameters but only the inference time. The MHGSA-VO adds hierarchical graph construction and three layers of RG-GCN for classification compared to MHSA-VO, which provides a slight improvement in accuracy, at 66.7%. This indicates that introducing a single-modal event relational hierarchical graph in the visual-only mode contributes to the model’s performance in disaster event classification. It is worth mentioning that MHSA-VO serves as a subset of MHGSA-VO; the training process of MHGSA-VO introduces and freezes the pre-training parameters of MHSA-VO, i.e., it only trains the graph-related parameters.

In audio-only mode (AO), as shown in

Table 2. Experiment on VGGSound-DR in audio-only mode.

Mode	Model	Avg. Acc. (S.D.)	Best Acc.	Avg. Time (ms/Video)	Params
Audio-Only	ResNet-50	64.8 (±0.2)%	65.1%	49.2	26M
	Eff.Net-b1	65.3 (±0.3)%	65.8%	52.6	8M
	PANNs	51.9 (±0.5)%	52.6%	42.6	75M
	MHSA-AO	66.7 (±0.4)%	67.2%	52.8	15M
	MHGSA-AO	67.3 (±0.4)%	67.8%	74.7	17M

, MHGSA-AO achieved the highest accuracy of 67.8%. It improved 0.6% over MHSA-AO without graph learning and 2.7%, 2.0%, and 15.2% over ResNet-50, EfficientNet-b1, and PANNs, respectively. This indicates that hierarchical graph construction and learning play a positive role when applied to concepts with multiple granularities.

In multimodal mode, we assign a baseline model to vision and audio features and concatenate their feature vectors as the input of the fully connected layer classifier. We used this approach to construct ResNet-50-MM and EfficienNet-b1-MM as baseline models. On the other hand, we used both visual and audio feature extraction modules and compared fully connected layers (MHSA) and RG-GCN (MHGSA) as classifiers. As shown in

Table 3. Experiment on VGGSound-DR in multimodal mode.

Mode	Model	Avg. Acc. (S.D.)	Best Acc.	Avg. Time (ms/Video)	Params
Multi-Modal	ResNet-50-MM	69.1 (±0.4)%	69.7%	61.4	52M
	Eff.Net-b1-MM	71.3 (±0.5)%	71.9%	74.3	17M
	MHSA *	75.9 (±0.5)%	76.5%	91.1	30M
	MHGSA *	77.3 (±0.3)%	77.6%	149.3	34M

* Model using multiple frames on a visual path.

, the highest results were achieved by the MHGSA, obtaining 77.6% accuracy with 34M parameters. The graph-based model outperforms the traditional fully connected layer by about 4M higher number of parameters in the multimodal mode, proving the effectiveness of multimodal hierarchical graph learning. Different from the visual-only and audio-only cases, the introduction of a graph-based approach improves more significantly in the multimodal case. This also confirms our idea of constructing a multimodal hierarchical graph, i.e., modeling the relationship between events across modalities using a graph learning approach, in order to improve the model’s ability to discriminate between different events. We can see the improved performance of the model when using multimodal information. Compared to VO and AO, all models show a substantial increase in accuracy with a doubled number of parameters in the multimodal mode, with the highest increases being in MHGSA at 10.9% and 9.8%.

From the perspective of situation awareness, more comprehensive perception and deeper understanding are important goals. In contrast to baseline models, the proposed MHGSA uses audio–visual modalities to obtain a more comprehensive perception, whereas multi-granularity classification allows the model to have a richer understanding of the environment. The classification results of the events with different granularities provide a richer understanding of the environment, enabling disaster response.

Table 4. Classification precision of MHGSA for coarse-grained and fine-grained categories in visual-only, audio-only, and multimodal cases.

Coarse-Grained	VO	AO	MM	Fine-Grained	VO	AO	MM
Natural Disasters	94.4	86.1	97.4	Hail	91.7	84.2	92.3
				Thunder	56.7	81.2	87.1
				Tornado Roaring	95.0	53.7	72.1
				Volcano explosion	71.2	57.4	80.4
Conflicts	77.2	79.6	91.1	Cap gun shooting	50.7	74.1	75.4
				Machine gun shooting	72.3	80.0	87.0
				Missile launch	73.4	65.1	92.5
Disaster Alerts	90.3	96.2	98.8	Ambulance siren	33.3	48.7	44.2
				Civil defense siren	55.7	89.6	91.7
				Fire truck siren	67.4	49.1	65.9
				Police car (siren)	49.2	44.0	51.0
				Smoke detector beeping	86.0	91.7	97.8
Overall	88.4	88.7	96.4	Overall	67.0	68.3	78.2

Highest results are highlighted in bold.

illustrates the precision metrics for every coarse- and fine-grained category evaluated from the MHGSA in different cases. The results from the coarse-grained categories intuitively show that the visual and audio modalities have different representational capabilities in different categories. For example, visual-only models are much more precise in the ‘Nature Disasters’ category than audio-only models, which is the opposite in the ‘Disaster Alerts’ category. For the fine-grained categories, the multimodal model obtained the highest accuracy in the vast majority of the categories, especially the ‘rocket launch’ category, which obtained 92.5% with less than 75% precision for both VO and AO. This indicates the rationality of building a multimodal situational awareness system, i.e., using different modalities for complementary information.

For inference time, the introduction of multi-branching structure and graph learning implies more computational consumption, so MHGSA-VO, MHGSA-AO, and MHGSA take about 46.1 ms, 74.7 ms, and 149.3 ms, respectively, in recognizing the disaster category of a single video clip, which is higher than the baseline model. However, it could be negligible in comparison to the length of the video clip (10 s). The inference time may vary with the size of the number of frame samples $K$. In addition, as mentioned previously, the training process of MHGSA involves multiple stages. The feature extractors of the corresponding modalities need to be trained in advance to obtain a reasonable representation of the multimodal data. This may imply a more tedious training process when more modalities are introduced. A potential challenge is to introduce textual information, including plain text and text that appears in visual and audio, to obtain more comprehensive information for disaster event recognition. In addition, graph learning approaches may help to introduce modal information with multiple views and features.

4. Conclusions

In this work, we present a multimodal hierarchical graph-based situational awareness system (MHGSA) for rapid disaster response. The multimodal feature extraction module in this system employs a multi-branching architecture that allows it to provide independent parameters for coarse and fine granularity branches to improve model performance in end-to-end joint optimization. In addition, a multimodal hierarchical graph construction method is used for visual and audio feature fusion. The proposed MHGSA has been validated against several disaster-related datasets and has achieved promising results by outperforming the baseline model in both unimodal and multimodal scenarios.