Machine Learning Based Localization of LoRa Mobile Wireless Nodes Using a Novel Sectorization Method
Abstract
1. Introduction
- (1)
- A method for data collection using a mobile LoRa node is proposed, accounting for the dynamics of its movement.
- (2)
- A method for partitioning the experimental area into sectors is introduced, which minimizes the impact of noise and the nonlinearity of signal propagation in areas with significant deviations within the room.
- (3)
- Entirely new routes, distinct from the training data, are utilized as a test sample, allowing for an objective evaluation of the models’ performance at previously unknown locations.
2. Related Work
3. Methodology
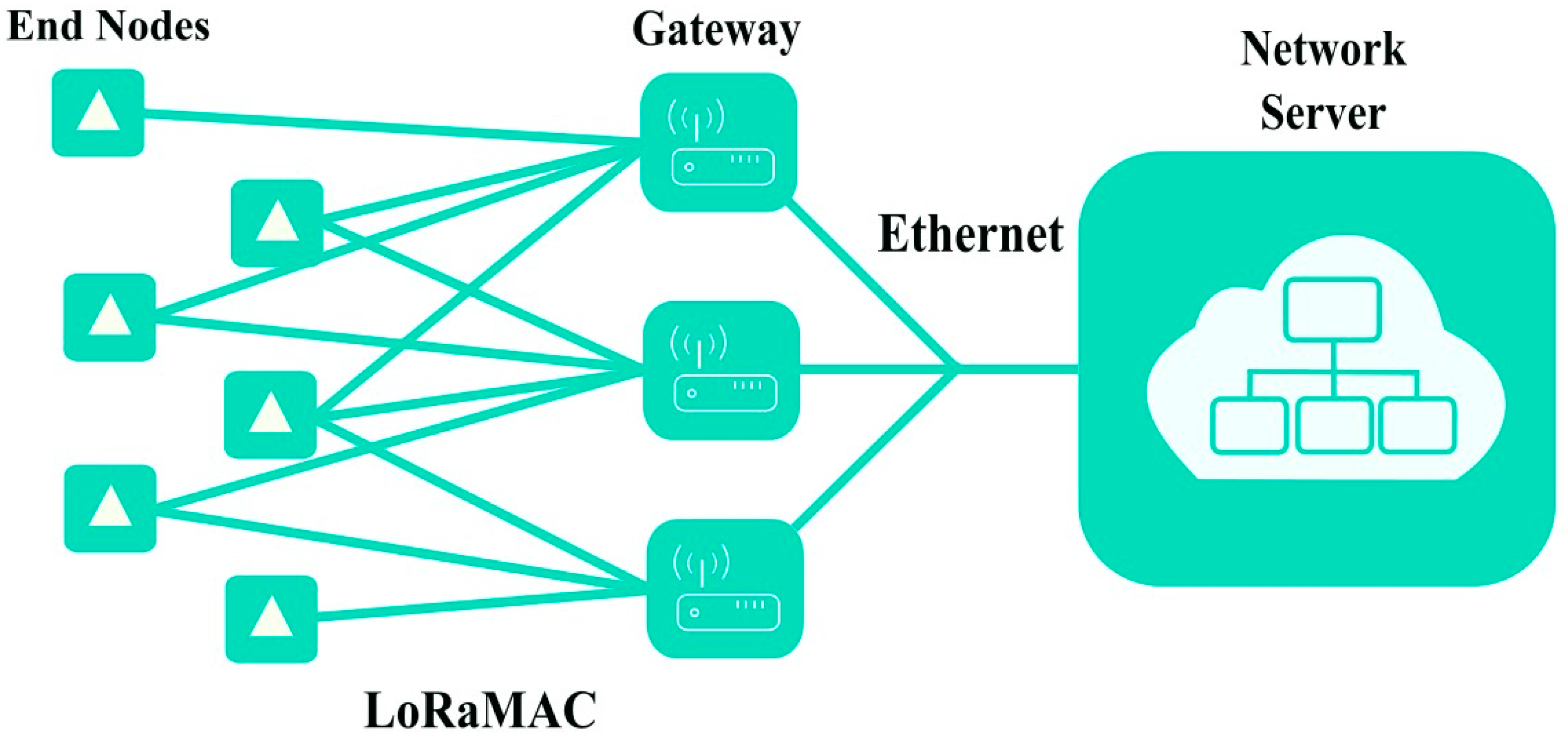
3.1. Overview of LoRaWAN and LoRa Technology
- end devices or nodes, which operate in a star topology and gather data that are subsequently transmitted to the network;
- gateways, which serve as coordinators among the nodes, receiving data from end devices and forwarding to the network server;
- LoRaWAN network server, responsible for managing and processing the data.
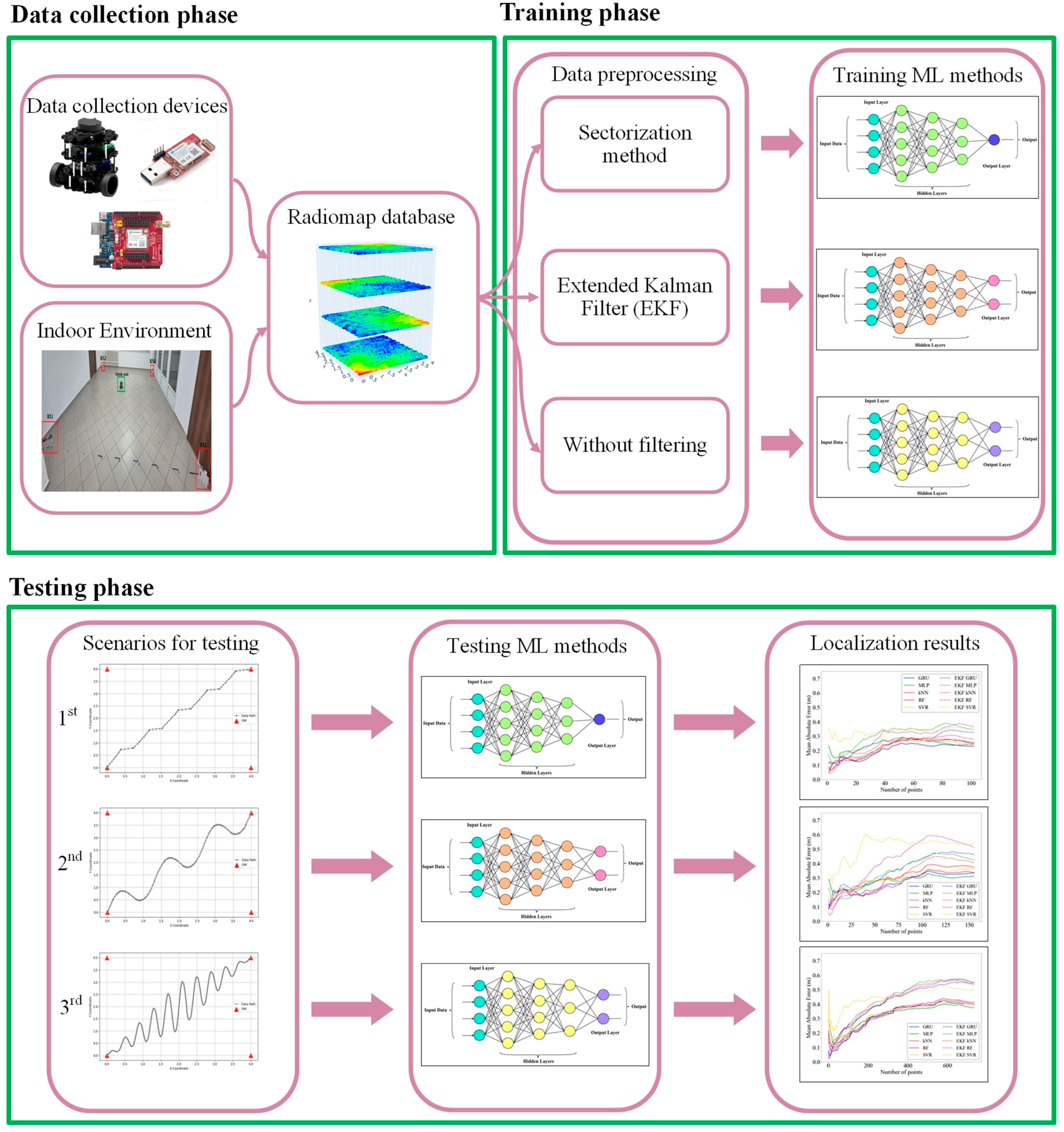
3.2. Research Map
3.3. Data Preprocessing
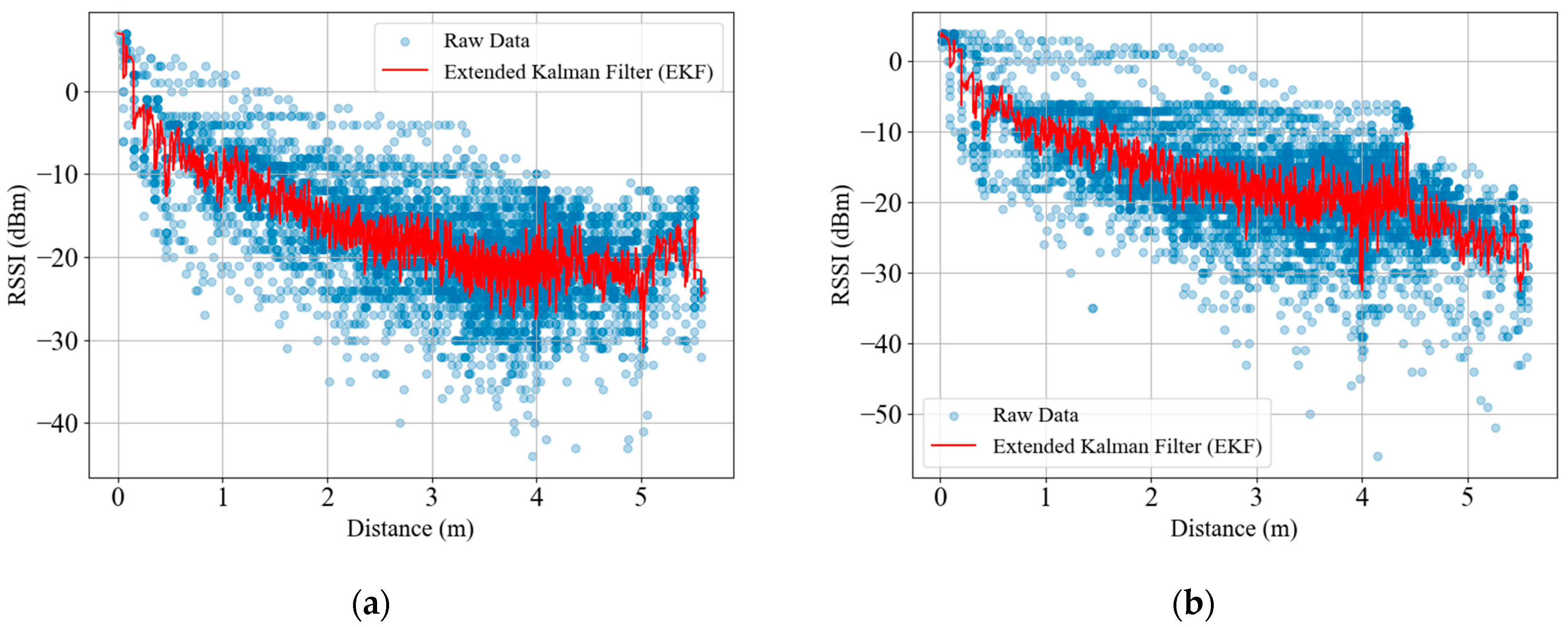
3.3.1. Extended Kalman Filter (EKF)
3.3.2. Sectorization Method
3.4. Machine Learning Methods
3.4.1. Support Vector Regression (SVR)
- Number of neighbors (n_neighbors): {1, 3, 5, 7, 9, 11};
- Weighting scheme (weights): {‘uniform’, ‘distance’};
- Search algorithm (algorithm): {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’};
- Distance metric (p): {1, 2} (1 for Manhattan distance, 2 for Euclidean distance).
3.4.2. k-Nearest Neighbors
- Regularization parameter (C): {0.1, 1, 10, 100};
- Epsilon (epsilon): {0.01, 0.1, 0.2, 0.5};
- Kernel type (kernel): {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’};
- Kernel parameter (gamma): {‘scale’, ‘auto’}.
3.4.3. Random Forest
- Number of trees (n_estimators): {10, 50, 100, 200};
- Maximum tree depth (max_depth): {None, 10, 20, 30, 40, 50};
- Minimum number of samples required to split a node (min_samples_split): {2, 5, 10};
- Minimum number of samples required in a leaf (min_samples_leaf): {1, 2, 4};
- Bootstrap sampling (bootstrap): {True, False}.
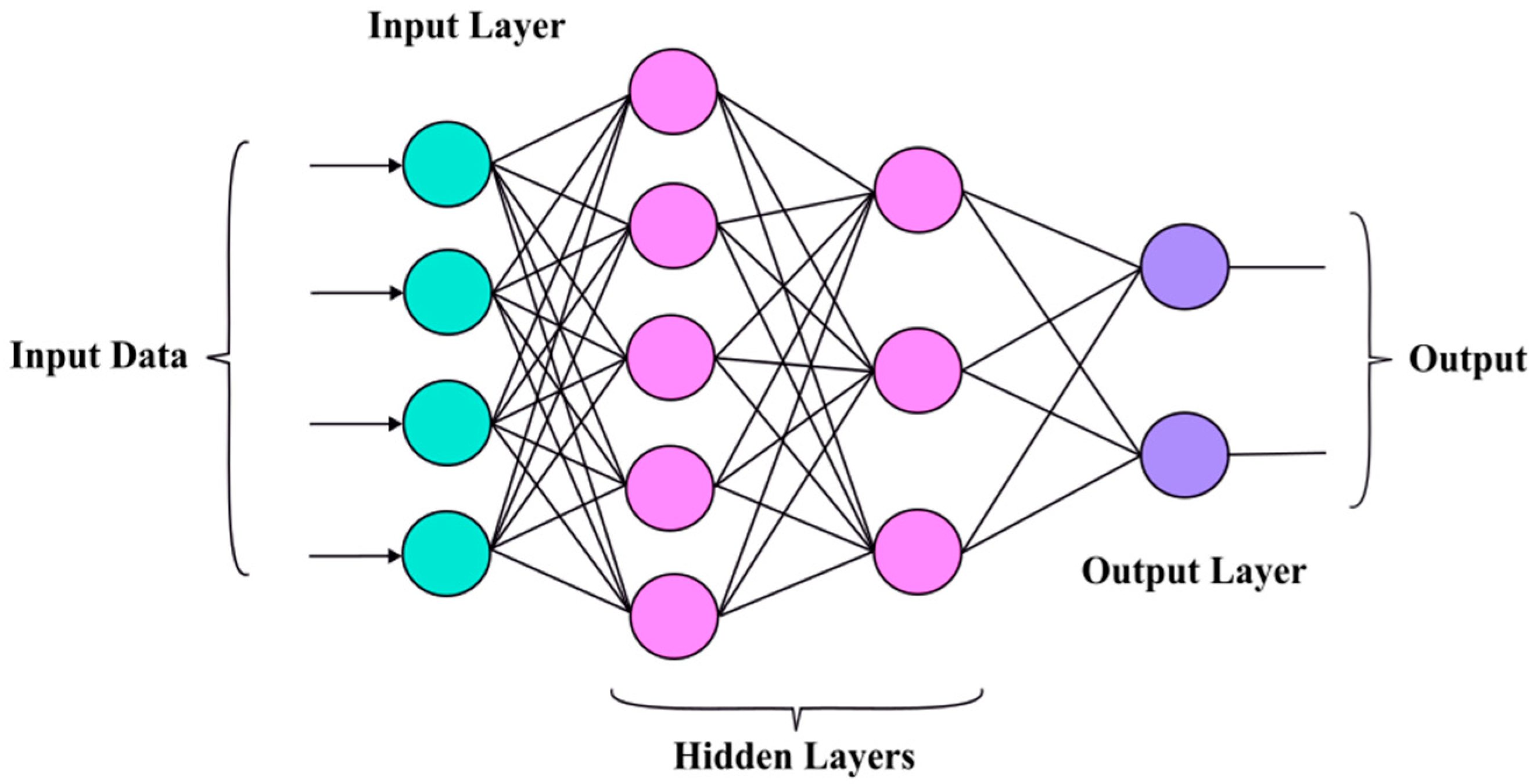
3.4.4. Multilayer Perceptron
- Number of neurons (units): {16, 32, 64, 128};
- Activation function (activation): {‘tanh’, ‘relu’};
- Dropout rate (dropout): {0.0, 0.2, 0.5};
- Recurrent layer dropout rate (recurrent_dropout): {0.0, 0.2, 0.5};
- Optimizer (optimizer): {‘adam’, ‘sgd’};
- Learning rate (learning_rate): {0.001, 0.01, 0.1}.
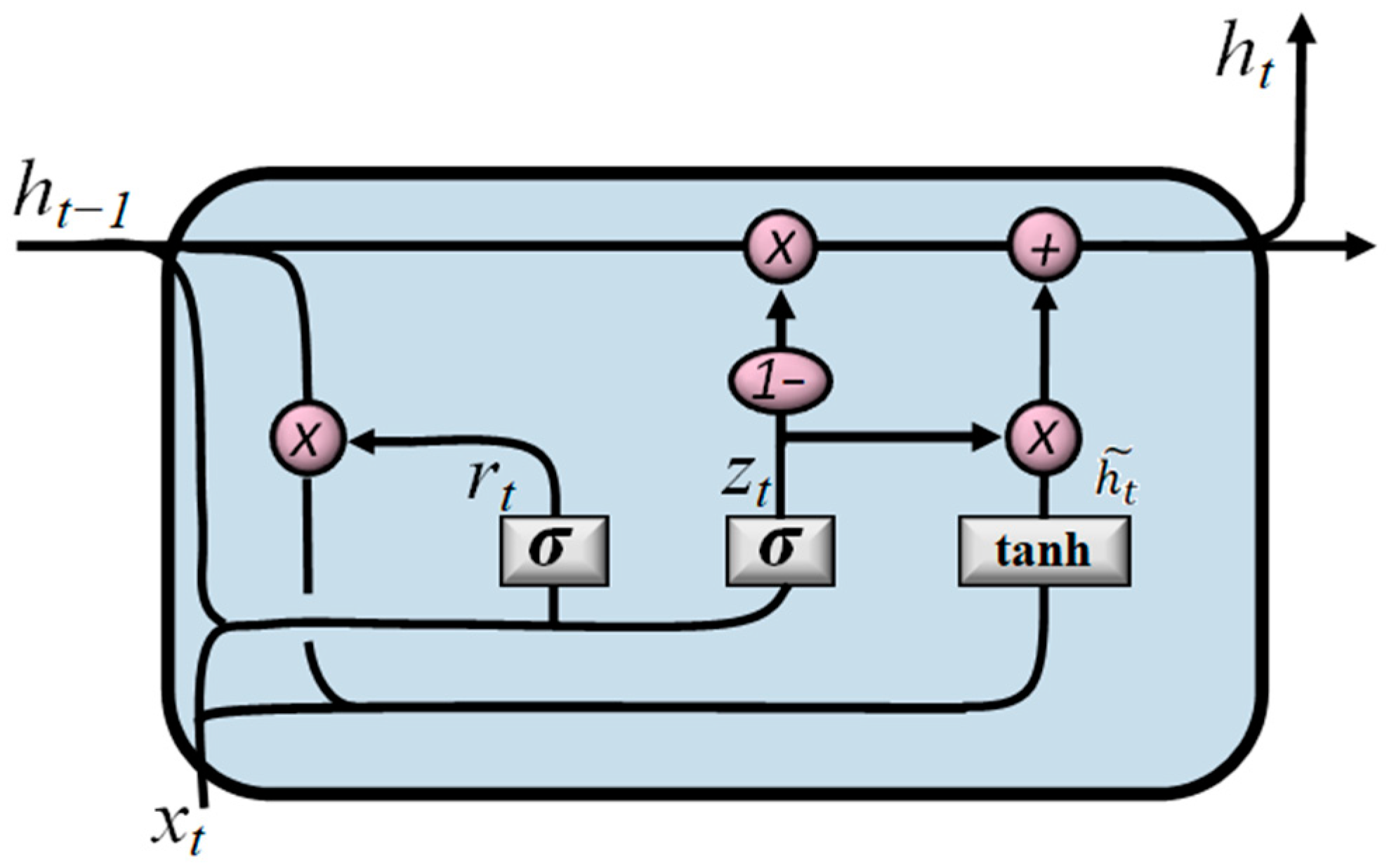
3.4.5. Gated Recurrent Unit
- Hidden layer size (hidden_layer_sizes): {(50,), (100,), (50, 50), (100, 100)};
- Activation function (activation): {‘identity’, ‘logistic’, ‘tanh’, ‘relu’};
- Optimization method (solver): {‘lbfgs’, ‘sgd’, ‘adam’};
- Regularization parameter (alpha): {0.0001, 0.001, 0.01, 0.1};
- Learning rate change schedule (learning_rate): {‘constant’, ‘invscaling’, ‘adaptive’}.
3.4.6. BPNN
- Number of neurons (units): {16, 32, 64, 128};
- Number of Hidden Layers (hidden_neurons): {1,2,3}
- Activation function (activation): {‘tanh’, ‘relu’, ‘sigmoid’};
- Dropout rate (dropout): {0.1, 0.2, 0.5};
- Optimizer (optimizer): {‘adam’, ‘sgd’};
- Learning rate (learning_rate): {0.001, 0.01, 0.1}.
- Number of epochs (epochs): {10, 50, 100, 200};
- Momentum: {0.8, 0.9, 0.99}
3.4.7. RNN
- Number of neurons in the hidden layer: [10, 50, 100, 200]
- Number of hidden layers: [1, 2, 3]
- Excitation rate (λ_in): [0.01, 0.1, 1, 10]
- Inhibition rate (λ_out): [0.01, 0.1, 1, 10]
- Connection weights: [−1, −0.5, 0, 0.5, 1])
- Learning rate: [0.001, 0.01, 0.1, 0.5]
- Batch size: [16, 32, 64, 128]
- Activation function: [‘sigmoid’, ‘tanh’, ‘relu’, ‘linear’]
- Dropout rate: [0.0, 0.2, 0.5]
- Number of epochs: [10, 50, 100, 200]
3.5. Performance Metrics
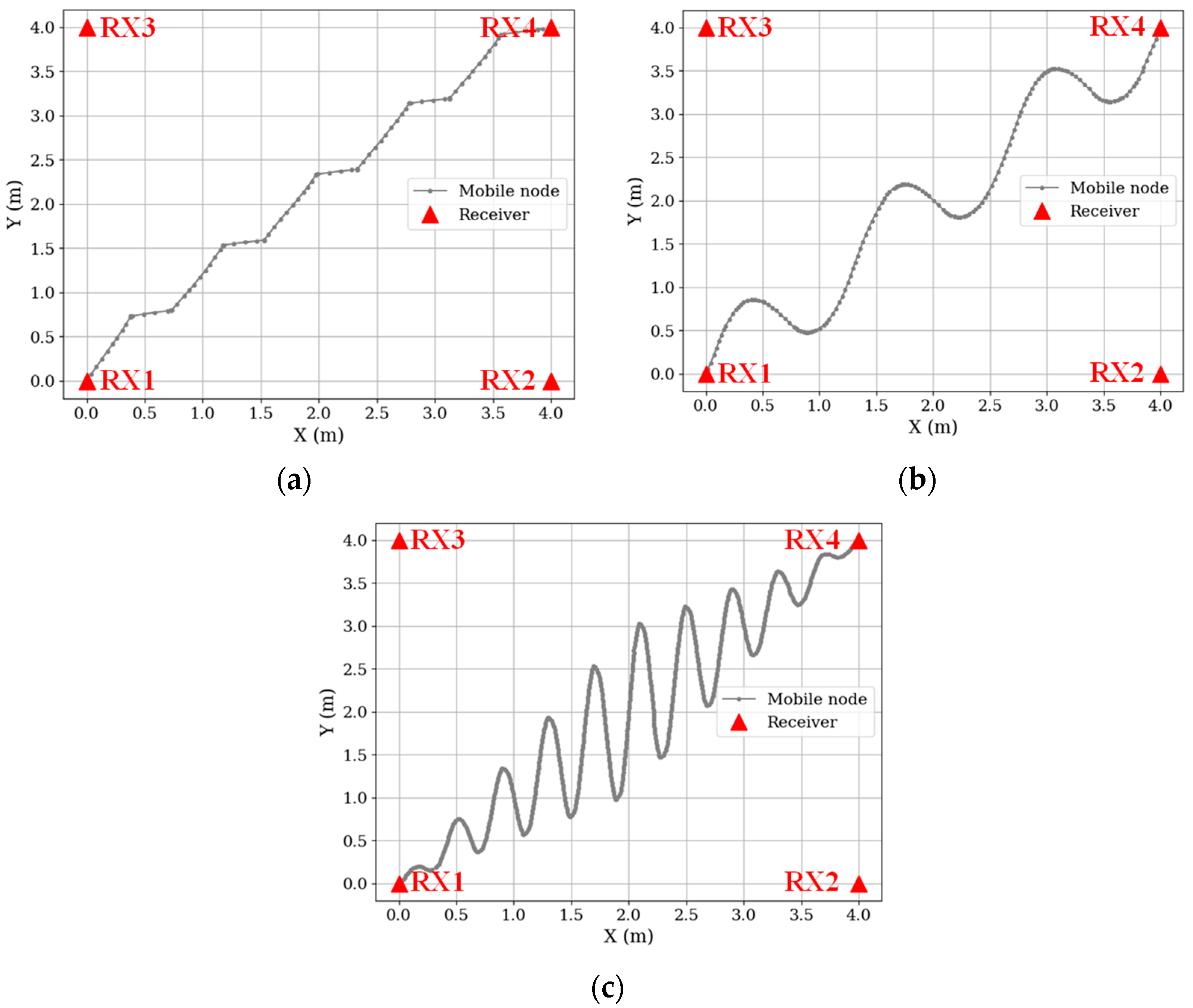
4. Experimental Setup
- (a)
- The first scenario—movements along a step trajectory;
- (b)
- The second scenario—movements along a sinusoidal trajectory;
- (c)
- The third scenario—movements along a sinusoidal trajectory with high amplitude and frequency.
5. Results
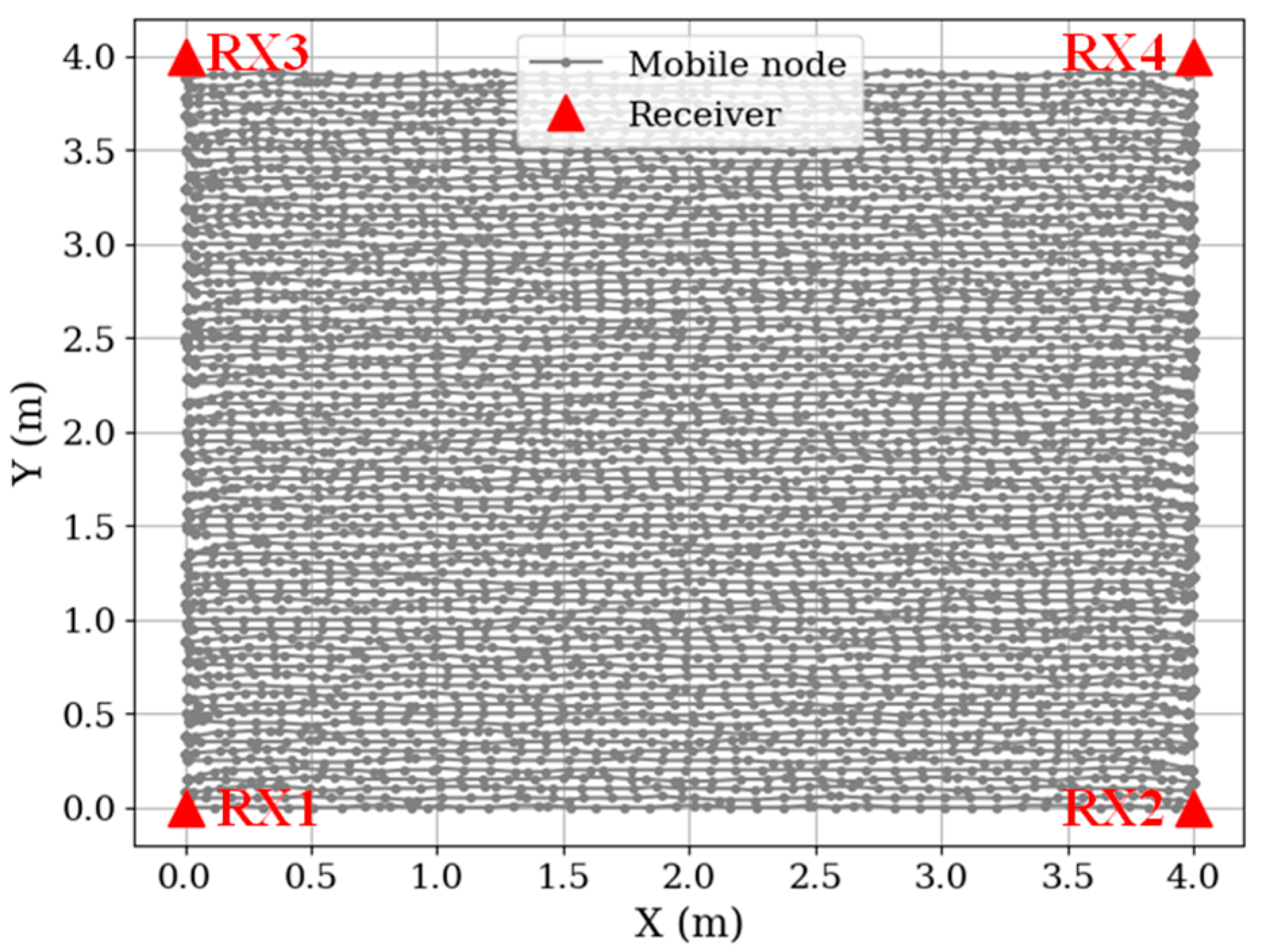
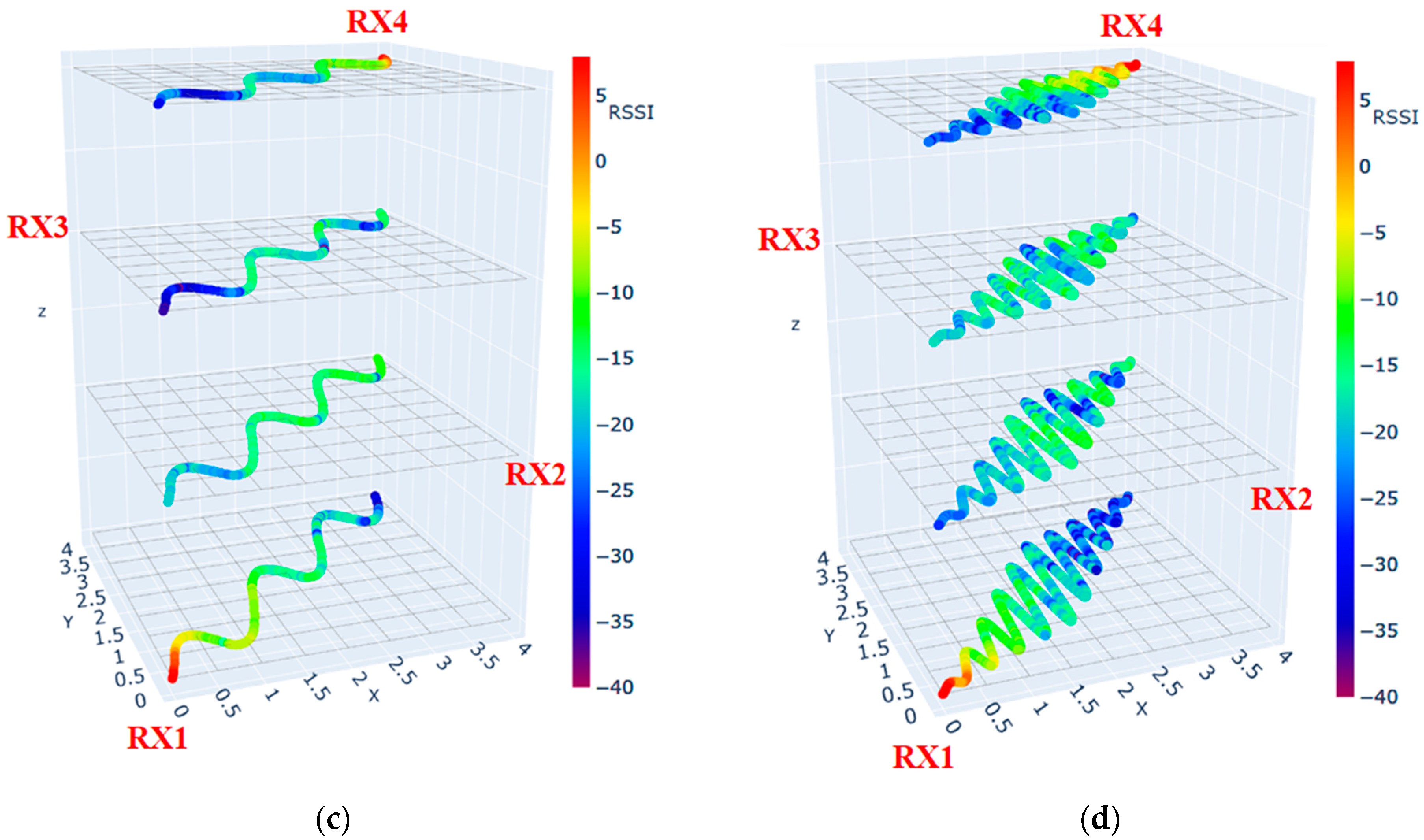
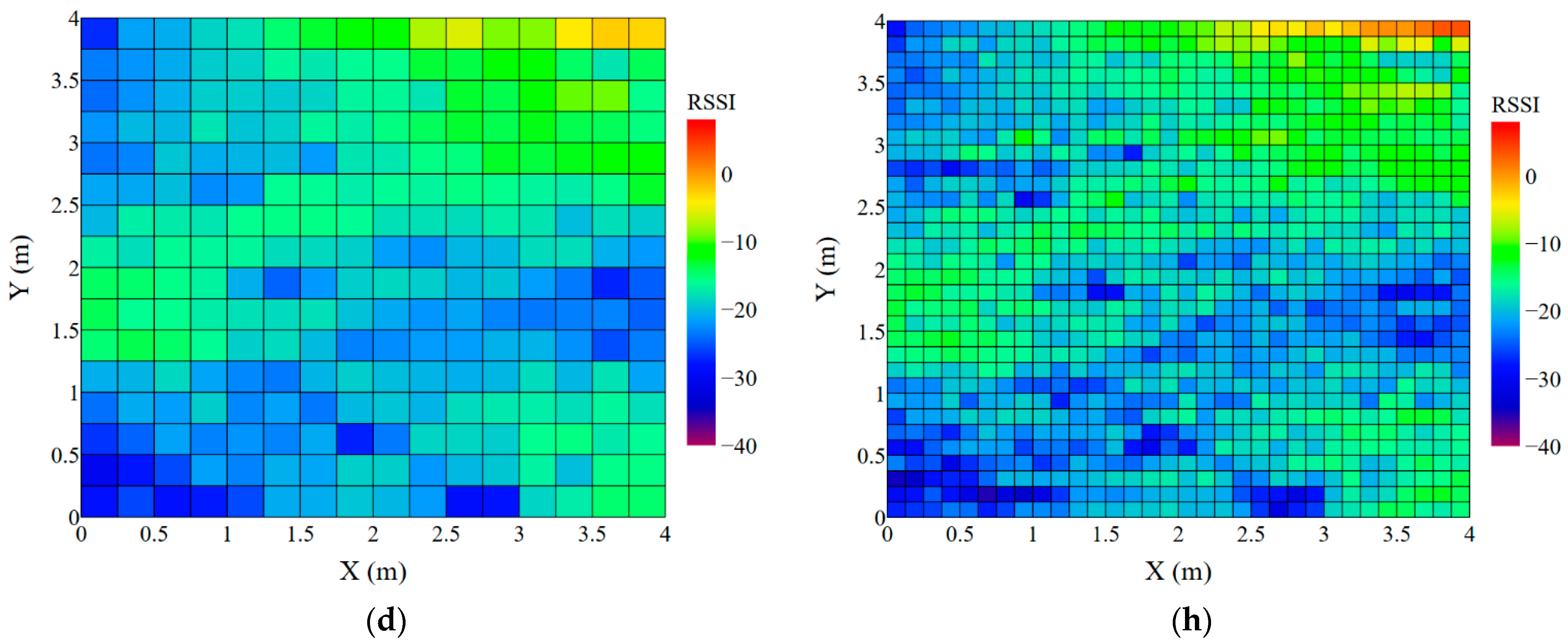
5.1. Radio Map of the Area
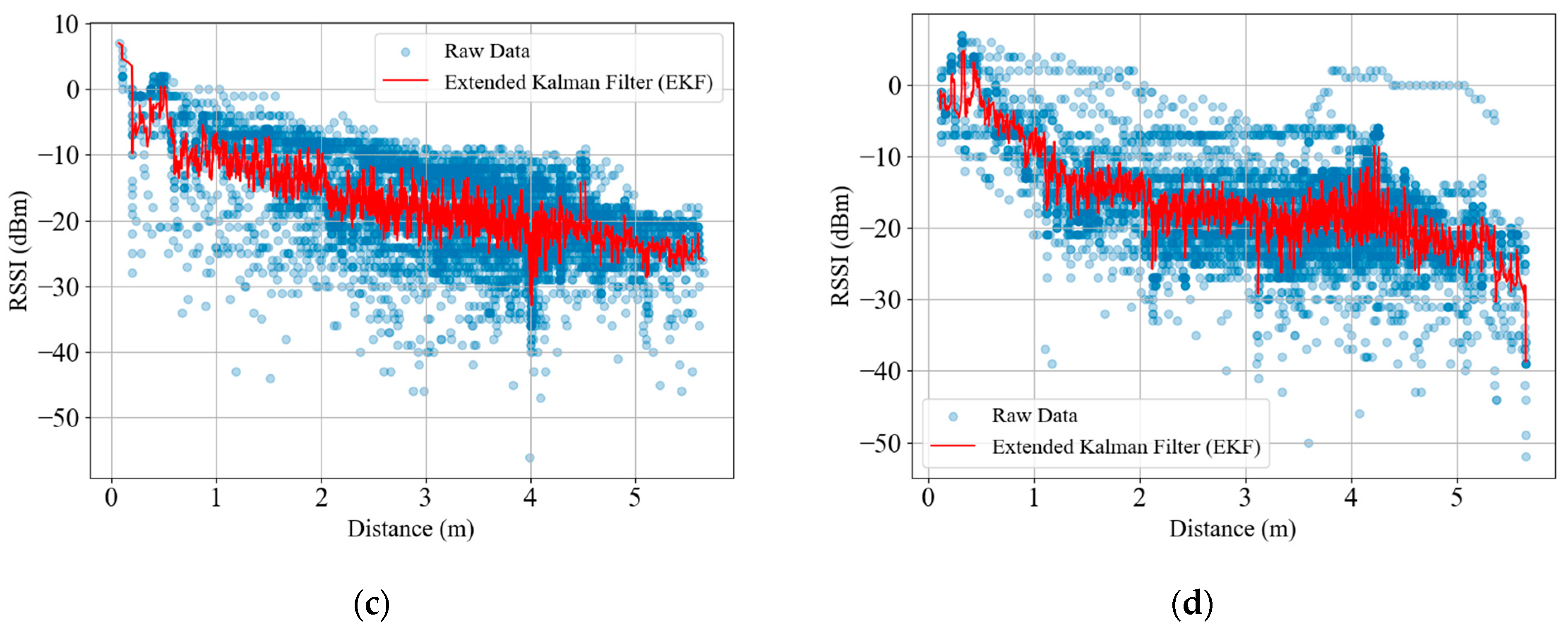
5.2. Data Preprocessing Results
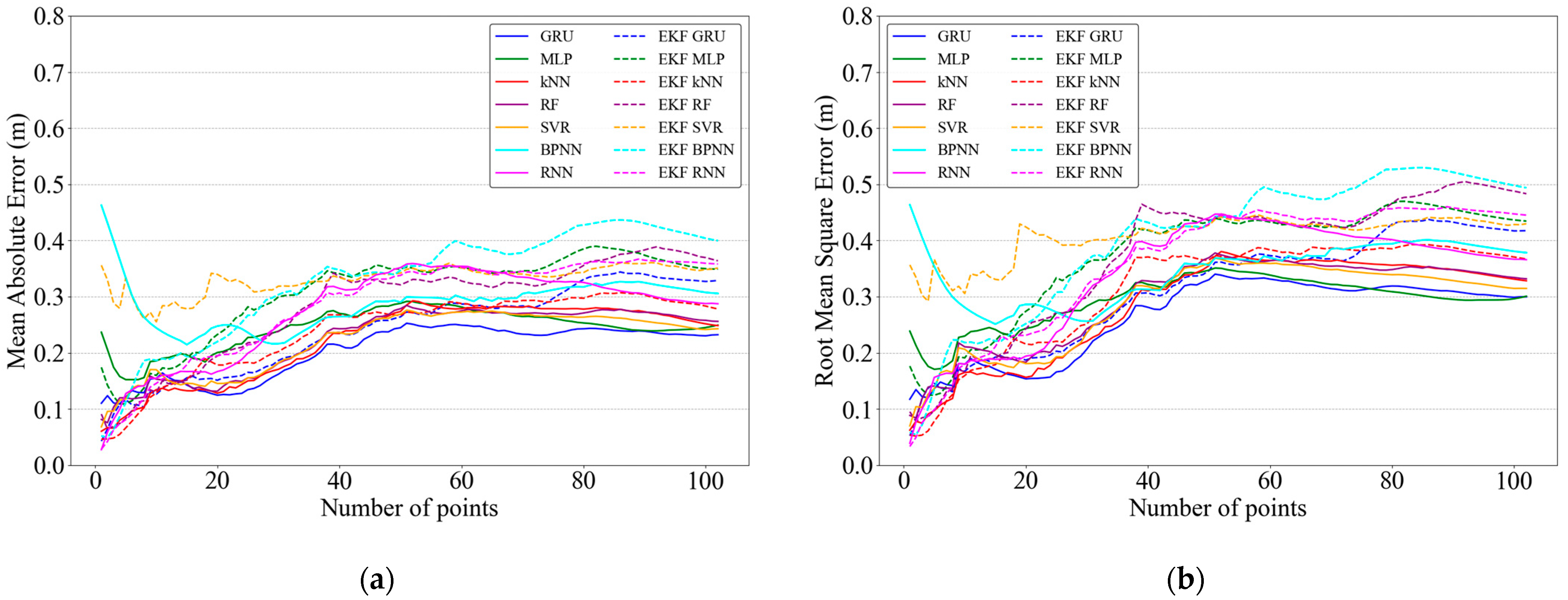
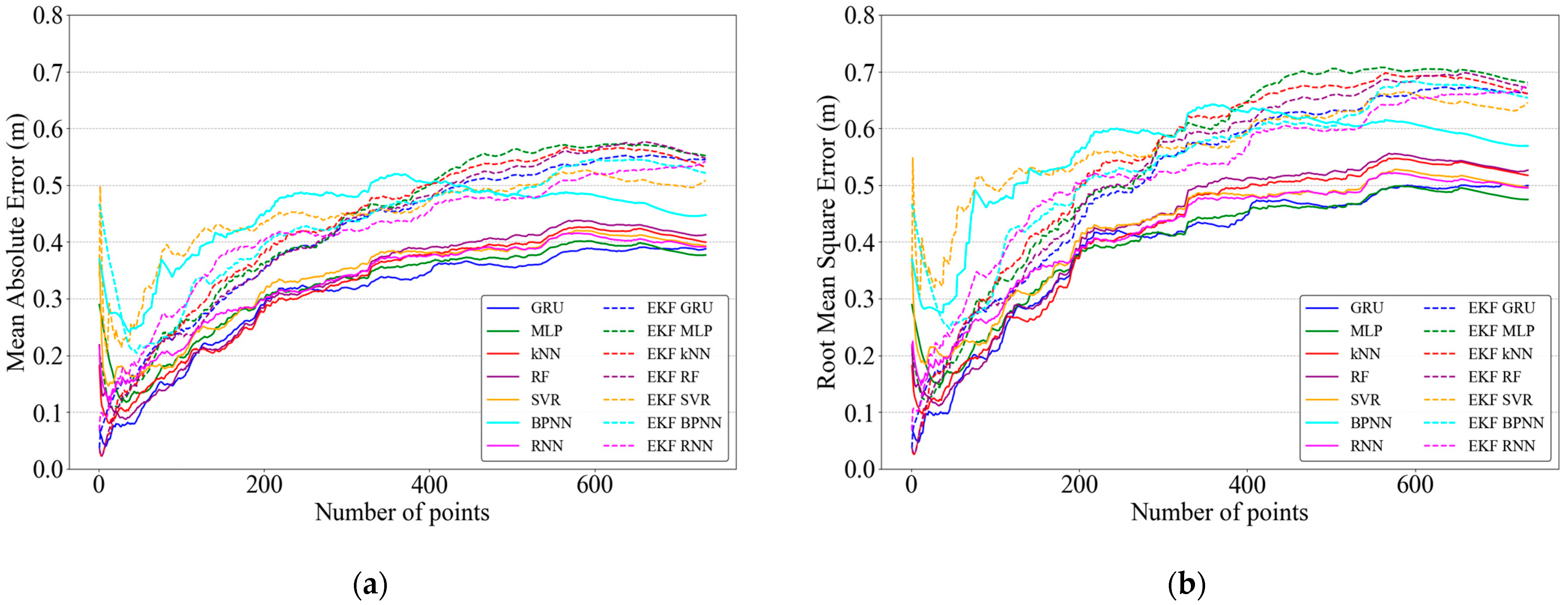
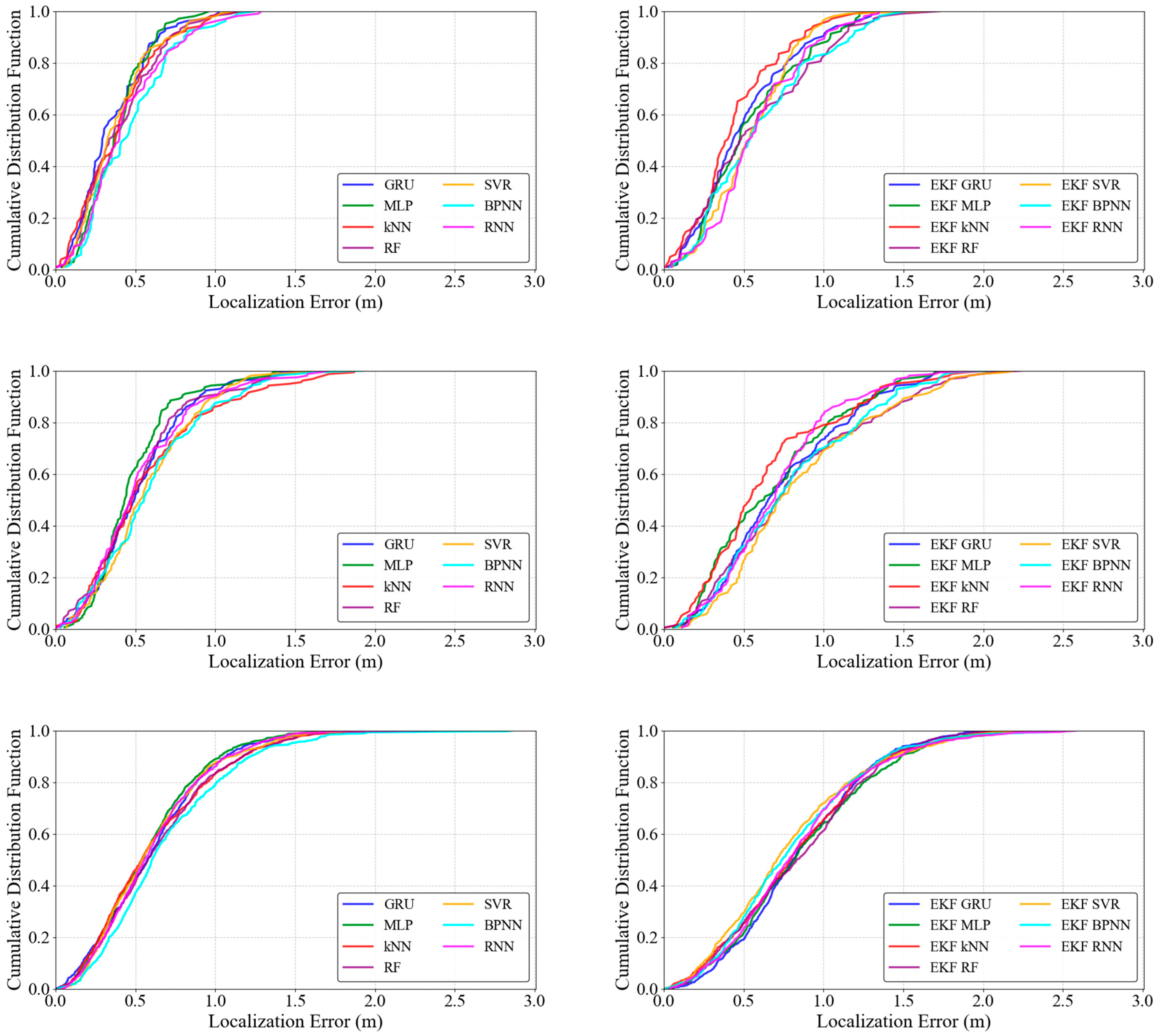
5.3. Accuracy Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dritsas, E.; Trigka, M. Machine Learning for Blockchain and IoT Systems in Smart Cities: A Survey. Future Internet 2024, 16, 324. [Google Scholar] [CrossRef]
- Umetani, T.; Kondo, Y.; Tokuda, T. Rapid Development of a Mobile Robot for the Nakanoshima Challenge Using a Robot for Intelligent Environments. J. Robot. Mechatron. 2020, 32, 1211–1218. [Google Scholar] [CrossRef]
- Fath, A.; Hanna, N.; Liu, Y.; Tanch, S.; Xia, T.; Huston, D. Indoor Infrastructure Maintenance Framework Using Networked Sensors, Robots, and Augmented Reality Human Interface. Future Internet 2024, 16, 170. [Google Scholar] [CrossRef]
- Shit, R.C.; Sharma, S.; Puthal, D.; Zomaya, A.Y. Location of Things (LoT): A Review and Taxonomy of Sensors Localization in IoT Infrastructure. IEEE Commun. Surv. Tutor. 2018, 20, 2028–2061. [Google Scholar] [CrossRef]
- Kang, J.M.; Yoon, T.S.; Kim, E.; Park, J.B. Lane-Level Map-Matching Method for Vehicle Localization Using GPS and Camera on a High-Definition Map. Sensors 2020, 20, 2166. [Google Scholar] [CrossRef]
- Janssen, T.; Koppert, A.; Berkvens, R.; Weyn, M. A survey on IoT positioning leveraging LPWAN, GNSS, and LEO-PNT. IEEE Internet Things J. 2023, 10, 11135–11159. [Google Scholar] [CrossRef]
- Florio, A.; Bnilam, N.; Talarico, C.; Crosta, P.; Avitabile, G.; Coviello, G. LEO-Based Coarse Positioning Through Angle-of-Arrival Estimation of Signals of Opportunity. IEEE Access 2024, 12, 17446–17459. [Google Scholar] [CrossRef]
- Pascacio, P.; Casteleyn, S.; Torres-Sospedra, J.; Lohan, E.S.; Nurmi, J. Collaborative Indoor Positioning Systems: A Systematic Review. Sensors 2021, 21, 1002. [Google Scholar] [CrossRef] [PubMed]
- Ngamakeur, K.; Yongchareon, S.; Yu, J.; Islam, S. Passive infrared sensor dataset and deep learning models for device-free indoor localization and tracking. Pervasive Mob. Comput. 2023, 88, 101721. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Lin, C.-T. Indoor Localization Method for a Mobile Robot Using LiDAR and a Dual AprilTag. Electronics 2023, 12, 1023. [Google Scholar] [CrossRef]
- Do, T.-H.; Yoo, M. An in-Depth Survey of Visible Light Communication Based Positioning Systems. Sensors 2016, 16, 678. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Niu, G.; Cao, Q.; Chen, C.S.; Ho, S.-W. A Survey of Visible-Light-Communication-Based Indoor Positioning Systems. Sensors 2024, 24, 5197. [Google Scholar] [CrossRef]
- Wu, J.; Yang, T.; Zhang, Z. Research on Wi-Fi Fingerprint Database Construction Method Based on Environmental Feature Awareness. Appl. Syst. Innov. 2024, 7, 99. [Google Scholar] [CrossRef]
- Fontaine, J.; Van Herbruggen, B.; Shahid, A.; Kram, S.; Stahlke, M.; De Poorter, E. Ultra Wideband (UWB) Localization Using Active CIR-Based Fingerprinting. IEEE Commun. Lett. 2023, 27, 1322–1326. [Google Scholar] [CrossRef]
- Ahmed, H.M.; Rashid, A.N. Rfid indoor localization based received signal strength. In Proceedings of the 2021 14th International Conference on Developments in eSystems Engineering (DeSE), Sharjah, United Arab Emirates, 7–10 December 2021; pp. 590–593. [Google Scholar] [CrossRef]
- Al Mojamed, M. On the Use of LoRaWAN for Mobile Internet of Things: The Impact of Mobility. Appl. Syst. Innov. 2022, 5, 5. [Google Scholar] [CrossRef]
- Fahama, H.; Ansari-Asl, K.; Kavian, Y.S.; Soorki, M.N. An Experimental Comparison of RSSI-Based Indoor Localization Techniques Using ZigBee Technology. IEEE Access 2023, 11, 87985–87996. [Google Scholar] [CrossRef]
- Asaad, S.M.; Maghdid, H.S. A comprehensive review of indoor/outdoor localization solutions in IoT era: Research challenges and future perspectives. Comput. Netw. 2022, 212, 109041. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A survey of indoor localization systems and technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Islam, B.; Islam, M.T.; Kaur, J.; Nirjon, S. Lorain: Making a case for lora in indoor localization. In Proceedings of the 2019 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Kyoto, Japan, 11–15 March 2019. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R. RSS-AoA-Based Target Localization and Tracking in Wireless Sensor Networks; River Publishers: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Yuan, W.; Wu, N.; Guo, Q.; Huang, X.; Li, Y.; Hanzo, L. TOA-based passive localization constructed over factor graphs: A unified framework. IEEE Trans. Commun. 2019, 67, 6952–6965. [Google Scholar] [CrossRef]
- Antonello, F.; Avitabile, G.; Coviello, G. Digital phase estimation through an I/Q approach for angle of arrival full-hardware localization. In Proceedings of the 2020 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Ha Long, Vietnam, 8–10 December 2020. [Google Scholar] [CrossRef]
- Florio, A.; Avitabile, G.; Coviello, G. A Linear Technique for Artifacts Correction and Compensation in Phase Interferometric Angle of Arrival Estimation. Sensors 2022, 22, 1427. [Google Scholar] [CrossRef] [PubMed]
- Yiu, S.; Dashti, M.; Claussen, H.; Perez-Cruz, F. Wireless RSSI Fingerprinting Localization. Signal Process. 2017, 131, 235–244. [Google Scholar] [CrossRef]
- Nessa, A.; Adhikari, B.; Hussain, F.; Fernando, X. A Survey of Machine Learning for Indoor Positioning. IEEE Access 2020, 8, 214945–214965. [Google Scholar] [CrossRef]
- Khan, I.M.; Thompson, A.; Al-Hourani, A.; Sithamparanathan, K.; Rowe, W.S.T. RSSI and Device Pose Fusion for Fingerprinting-Based Indoor Smartphone Localization Systems. Future Internet 2023, 15, 220. [Google Scholar] [CrossRef]
- Kumar, P.; Reddy, L.; Varma, S. Distance measurement and error estimation scheme for RSSI based localization in wireless sensor networks. In Proceedings of the 2009 Fifth International Conference on Wireless Communication and Sensor Networks (WCSN), Allahabad, India, 15–19 December 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, B.; Jia, X.; Yang, F. Variational Bayesian Adaptive Unscented Kalman Filter for RSSI-Based Indoor Localization. Int. J. Control Autom. Syst. 2021, 19, 1183–1193. [Google Scholar] [CrossRef]
- Potortì, F.; Park, S.; Jiménez Ruiz, A.R.; Barsocchi, P.; Girolami, M.; Crivello, A.; Lee, S.Y.; Lim, J.H.; Torres-Sospedra, J.; Seco, F.; et al. Comparing the Performance of Indoor Localization Systems through the EvAAL Framework. Sensors 2017, 17, 2327. [Google Scholar] [CrossRef] [PubMed]
- Mangalvedhe, N.; Ratasuk, R.; Ghosh, A. NB-IoT deployment study for low power wide area cellular IoT. In Proceedings of the 2016 IEEE 27th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Valencia, Spain, 4–8 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Kim, K.; Li, S.; Heydariaan, M.; Smaoui, N.; Gnawali, O.; Suh, W.; Suh, M.J.; Kim, J.I. Feasibility of LoRa for Smart Home Indoor Localization. Appl. Sci. 2021, 11, 415. [Google Scholar] [CrossRef]
- Chen, H.; Yang, J.; Hao, Z.; Qi, T.; Liu, T. Research on indoor multi-floor positioning method based on LoRa. Comput. Netw. 2024, 254, 110838. [Google Scholar] [CrossRef]
- Anjum, M.; Khan, M.A.; Hassan, S.A.; Mahmood, A.; Qureshi, H.K.; Gidlund, M. RSSI fingerprinting-based localization using machine learning in LoRa networks. IEEE Internet Things Mag. 2020, 3, 53–59. [Google Scholar] [CrossRef]
- Chen, H.; Yang, J.; Hao, Z.; Ga, M.; Han, X.; Zhang, X.; Chen, Z. Research on indoor positioning method based on LoRa-improved fingerprint localization algorithm. Sci. Rep. 2023, 13, 13981. [Google Scholar] [CrossRef]
- Lu, K.; Yue, Y.; Ma, J. Enhanced LoRaWAN RSSI indoor localization based on BP neural network. In Proceedings of the 2021 IEEE 4th International Conference on Information Systems and Computer Aided Education (ICISCAE), Dalian, China, 24–26 September 2021; pp. 190–195. [Google Scholar] [CrossRef]
- Ingabire, W.; Larijani, H.; Gibson, R.M.; Qureshi, A.-U.-H. LoRaWAN Based Indoor Localization Using Random Neural Networks. Information 2022, 13, 303. [Google Scholar] [CrossRef]
- Purohit, J.; Wang, X.; Mao, S.; Sun, X.; Yang, C. Fingerprinting-based indoor and outdoor localization with LoRa and deep learning. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Suroso, D.J.; Rudianto, A.S.; Arifin, M.; Hawibowo, S. Random forest and interpolation techniques for fingerprint-based indoor positioning system in un-ideal Environment. Int. J. Comput. Digit. Syst. 2021, 10, 701–713. [Google Scholar] [CrossRef] [PubMed]
- Perković, T.; Dujić Rodić, L.; Šabić, J.; Šolić, P. Machine Learning Approach towards LoRaWAN Indoor Localization. Electronics 2023, 12, 457. [Google Scholar] [CrossRef]
- Ali, I.T.; Muis, A.; Sari, R.F. A deep learning model implementation based on rssi fingerprinting for lora-based indoor localization. EUREKA Phys. Eng. 2021, 1, 40–59. [Google Scholar] [CrossRef]
- Zhu, H.; Tsang, K.F.; Liu, Y.; Wei, Y.; Wang, H.; Wu, C.K.; Chi, H.R. Extreme RSS based indoor localization for LoRaWAN with boundary autocorrelation. IEEE Trans. Ind. Inform. 2020, 17, 4458–4468. [Google Scholar] [CrossRef]
- Seller, O.B.; Sornin, N. Low Power Long Range Transmitter. U.S. Patent No. 9,252,834, 2 February 2016. [Google Scholar]
- de Carvalho Silva, J.; Rodrigues, J.J.; Alberti, A.M.; Solic, P.; Aquino, A.L. LoRaWAN—A low power WAN protocol for Internet of Things: A review and opportunities. In Proceedings of the 2017 2nd International Multidisciplinary Conference on Computer and Energy Science (SpliTech), Split, Croatia, 12–14 July 2017; pp. 1–6. [Google Scholar]
- Coutinho, M.; Afonso, J.A.; Lopes, S.F. An Efficient Adaptive Data-Link-Layer Architecture for LoRa Networks. Future Internet 2023, 15, 273. [Google Scholar] [CrossRef]
- Ayele, E.D.; Hakkenberg, C.; Meijers, J.P.; Zhang, K.; Meratnia, N.; Havinga, P.J. Performance analysis of LoRa radio for an indoor IoT applications. In Proceedings of the 2017 International Conference on Internet of Things for the Global Community (IoTGC), Funchal, Portugal, 10–13 July 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Anjum, M.; Khan, M.A.; Hassan, S.A.; Mahmood, A.; Gidlund, M. Analysis of RSSI fingerprinting in LoRa networks. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 1178–1183. [Google Scholar] [CrossRef]
- Raghav, R.S.; Thirugnanasambandam, K.; Varadarajan, V.; Vairavasundaram, S.; Ravi, L. Artificial Bee Colony reinforced extended Kalman filter localization algorithm in internet of things with big data blending technique for finding the accurate position of reference nodes. Big Data 2022, 10, 186–203. [Google Scholar] [CrossRef] [PubMed]
- Venkatesh, R.; Mittal, V.; Tammana, H. Indoor localization in BLE using mean and median filtered RSSI values. In Proceedings of the 2021 5th International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 3–5 June 2021; pp. 227–234. [Google Scholar] [CrossRef]
- Aydin, H.M.; Ali, M.A.; Soyak, E.G. The analysis of feature selection with machine learning for indoor positioning. In Proceedings of the 2021 29th Signal Processing and Communications Applications Conference (SIU), Istanbul, Turkey, 9–11 June 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Pak, J.M. Switching Extended Kalman Filter Bank for Indoor Localization Using Wireless Sensor Networks. Electronics 2021, 10, 718. [Google Scholar] [CrossRef]
- Schölkopf, B. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Song, Y.; Liang, J.; Lu, J.; Zhao, X. An efficient instance selection algorithm for k nearest neighbor regression. Neurocomputing 2017, 251, 26–34. [Google Scholar] [CrossRef]
- Devroye, L. The uniform convergence of nearest neighbor regression function estimators and their application in optimization. IEEE Trans. Inf. Theory 1978, 24, 142–151. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pinkus, A. Approximation theory of the MLP model in neural networks. Acta Numer. 1999, 8, 143–195. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Gelenbe, E. Random neural networks with negative and positive signals and product form solution. Neural Comput. 1989, 1, 502–510. [Google Scholar] [CrossRef]
- Available online: https://emanual.robotis.com/docs/en/platform/turtlebot3/overview/ (accessed on 25 November 2024).
- Available online: https://www.dragino.com/products/lora/item/231-la66-lorawan-shield.html (accessed on 25 November 2024).
- Sadowski, S.; Spachos, P. Rssi-based indoor localization with the internet of things. IEEE Access 2018, 6, 30149–30161. [Google Scholar] [CrossRef]
- Abbas, H.A.; Boskany, N.W.; Ghafoor, K.Z.; Rawat, D.B. Wi-Fi based accurate indoor localization system using SVM and LSTM algorithms. In Proceedings of the 2021 IEEE 22nd International Conference on Information Reuse and Integration for Data Science (IRI), Las Vegas, NV, USA, 10–12 August 2021; pp. 416–422. [Google Scholar] [CrossRef]
- Luo, R.C.; Hsiao, T.J. Dynamic wireless indoor localization incorporating with an autonomous mobile robot based on an adaptive signal model fingerprinting approach. IEEE Trans. Ind. Electron. 2018, 66, 1940–1951. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Frequency | 868 MHz |
| Spreading factor (SF) | 7 |
| Transmission power (TP) | 10 dBm |
| Bandwidth (BW) | 125 kHz |
| Coding rate (CR) | 4/5 |
| Sensitivity | −130 dBm |
| ML | Scenario | EKF | No Filter | Sector_256 | Sector_1024 |
|---|---|---|---|---|---|
| GRU | First | 0.8598 | 0.9298 | 0.9454 | 0.9354 |
| Second | 0.7324 | 0.8595 | 0.9102 | 0.8902 | |
| Third | 0.4799 | 0.7152 | 0.8512 | 0.8412 | |
| MLP | First | 0.8440 | 0.9282 | 0.9010 | 0.8810 |
| Second | 0.7593 | 0.8848 | 0.8920 | 0.8720 | |
| Third | 0.4301 | 0.7418 | 0.8413 | 0.8213 | |
| KNN | First | 0.8899 | 0.9151 | 0.8708 | 0.8608 |
| Second | 0.7694 | 0.8093 | 0.8491 | 0.8321 | |
| Third | 0.4773 | 0.6893 | 0.8012 | 0.8129 | |
| RF | First | 0.8125 | 0.9134 | 0.8394 | 0.8235 |
| Second | 0.6611 | 0.8560 | 0.8723 | 0.8456 | |
| Third | 0.4692 | 0.6805 | 0.7984 | 0.7754 | |
| SVR | First | 0.8529 | 0.9218 | 0.9032 | 0.8976 |
| Second | 0.6484 | 0.8382 | 0.8566 | 0.8487 | |
| Third | 0.5247 | 0.7167 | 0.7712 | 0.7885 | |
| BPNN | First | 0.8068 | 0.8330 | 0.8983 | 0.8912 |
| Second | 0.6940 | 0.8195 | 0.8117 | 0.7862 | |
| Third | 0.5462 | 0.5318 | 0.7641 | 0.7510 | |
| RNN | First | 0.8310 | 0.8957 | 0.9200 | 0.9230 |
| Second | 0.7620 | 0.8497 | 0.8579 | 0.8283 | |
| Third | 0.4946 | 0.7212 | 0.7639 | 0. 8165 |
| Paper | Method | Machine Learning | Localization Error | WSN |
|---|---|---|---|---|
| [38] | Fingerprint | ANN, LSTM, CNN | 1.27 m | LoRa |
| [36] | Fingerprint | BPNN (Back-Propagation Neural Network) | 0.5971 m | LoRa |
| [35] | Fingerprint | RF | 0.82 m | LoRa |
| [36] | Fingerprint | RNN | 0.12 m | LoRa |
| [32] | Trilateration | N/A | 1.6 m | LoRa |
| [62] | Trilateration | N/A | 0.846 m and 1.534 m | LoRa |
| [63] | Fingerprint | LSTM, SVM | 0.9 m and 1.1 m | Wi-Fi |
| [64] | Adaptive signal model fingerprinting (ASMF) | kNN | 0.712 m and 0.939 m | Zigbee |
| Proposed research | Fingerprint | GRU, MLP, kNN, RF, SVR, BPNN and RNN | 0.384 m | LoRa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nurgaliyev, M.; Bolatbek, A.; Zholamanov, B.; Saymbetov, A.; Kopbay, K.; Yershov, E.; Orynbassar, S.; Dosymbetova, G.; Kapparova, A.; Kuttybay, N.; et al. Machine Learning Based Localization of LoRa Mobile Wireless Nodes Using a Novel Sectorization Method. Future Internet 2024, 16, 450. https://doi.org/10.3390/fi16120450
Nurgaliyev M, Bolatbek A, Zholamanov B, Saymbetov A, Kopbay K, Yershov E, Orynbassar S, Dosymbetova G, Kapparova A, Kuttybay N, et al. Machine Learning Based Localization of LoRa Mobile Wireless Nodes Using a Novel Sectorization Method. Future Internet. 2024; 16(12):450. https://doi.org/10.3390/fi16120450
Chicago/Turabian StyleNurgaliyev, Madiyar, Askhat Bolatbek, Batyrbek Zholamanov, Ahmet Saymbetov, Kymbat Kopbay, Evan Yershov, Sayat Orynbassar, Gulbakhar Dosymbetova, Ainur Kapparova, Nurzhigit Kuttybay, and et al. 2024. "Machine Learning Based Localization of LoRa Mobile Wireless Nodes Using a Novel Sectorization Method" Future Internet 16, no. 12: 450. https://doi.org/10.3390/fi16120450
APA StyleNurgaliyev, M., Bolatbek, A., Zholamanov, B., Saymbetov, A., Kopbay, K., Yershov, E., Orynbassar, S., Dosymbetova, G., Kapparova, A., Kuttybay, N., & Koshkarbay, N. (2024). Machine Learning Based Localization of LoRa Mobile Wireless Nodes Using a Novel Sectorization Method. Future Internet, 16(12), 450. https://doi.org/10.3390/fi16120450






