Advanced Optimization Techniques for Federated Learning on Non-IID Data
Abstract
1. Introduction
- We identify the negative impact of non-IID data on federated learning performance, demonstrating that the effectiveness of federated learning is particularly inferior when applied to non-IID data compared to IID data.
- We propose an optimization strategy using a cyclical learning rate to adjust the learning rate dynamically during the federated training process, with the goal of increasing accuracy and achieving faster model convergence.
- We introduce a novel approach for data sharing and pre-training on augmented data further to improve the performance of FL under non-IID data conditions.
- We validate our proposed methods through extensive experiments, showing significant improvements in accuracy and convergence speed compared to the baseline FedAvg approach with a fixed learning rate.
- This research attempts to contribute to the field by providing new methods for applying federated learning to real-world scenarios, enhancing the efficiency of federated learning applications.
2. Background
2.1. Federated Learning
2.2. FedAvg Algorithm
| Algorithm 1 Federated Averaging (FedAvg) |
|
1: Server executes: 2: Initialize 3: for each round do 4: 5: (random set of m clients) 6: for each client in parallel do 7: ClientUpdate() 8: end for 9: 10: 11: end for 12: ClientUpdate(): {Run on client k} 13: (split into batches of size B) 14: for each local epoch i from 1 to E do 15: for each batch do 16: 17: end for 18: end for 19: return w to server |
2.3. Learning Rate Policies
- Fixed Learning Rate (Fixed LR): This is the simplest learning rate policy, where a fixed value is used throughout the entire training process. While easy to implement, this approach often proves less effective in more complex models, where the demands for weight adjustments change as the network learns.
- Decaying Learning Rate (Decaying LR): This popular strategy involves gradually decreasing the learning rate as training progresses. The gradual reduction helps better approximate the minimum of the loss function by avoiding drastic weight changes that could lead to instability. Depending on the predefined method for adjusting the learning rate, common decaying strategies include time-based decay, step decay, and exponential decay.
- Cyclic Learning Rate (Cyclic LR): This is an innovative approach where the learning rate oscillates between a minimum and a maximum threshold on a cyclic basis. This method allows the network to explore the parameter space more effectively and avoid local minima, improving the overall performance and stability of the learning process [4].
2.4. Data Augmentation
2.5. Pre-Training
2.6. Adaptive Optimizers
3. Methodology
3.1. Tools and Datasets
- Google Colab: A cloud-based development environment provided by Google, designed for machine learning and data science research. It is based on Jupyter Notebook and provides free access to CPU and GPU resources, allowing users to write and execute Python code through their browser [45].
- TensorFlow: An open-source software library developed by Google for numerical computation and machine learning. It facilitates the creation and training of neural networks, offering a wide array of libraries and tools, making it a leading tool in artificial intelligence and scientific research.
- TensorFlow Federated (TFF): An open-source framework that extends TensorFlow, specifically designed for federated learning. TFF allows machine learning models to be trained on decentralized data while ensuring data privacy and security. It includes two main APIs: the Federated Core (FC) API for low-level distributed computation and the Federated Learning (FL) API for high-level federated training and evaluation [46,47].
- Apache Spark (PySpark): Apache Spark is an open-source framework that serves as a powerful tool for processing and analyzing large datasets in distributed environments. Spark supports multiple programming models and APIs, including the Resilient Distributed Dataset (RDD) and DataFrame API, allowing users to perform data processing and analysis tasks in a simple and optimized manner. PySpark is the Python API for Spark, enabling users to leverage all the capabilities of Spark through the Python programming language [48].
- MNIST: The MNIST (Modified National Institute of Standards and Technology) dataset is a comprehensive collection of handwritten digits, consisting of a training set of 60,000 examples and a test set of 10,000 examples. The dataset includes grayscale images of handwritten digits, each of size 28 × 28 pixels, normalized and centered in a 28 × 28 grid. MNIST is widely used for training and testing machine learning algorithms, particularly for image classification tasks using Convolutional Neural Networks (CNNs), Support Vector Machines (SVMs), and other machine learning algorithms. Its simple and well-organized structure makes MNIST a foundational tool for researchers in machine learning and computer vision [49].
- Fashion MNIST: The Fashion MNIST dataset is a modern and more challenging alternative to the traditional MNIST, consisting of images representing various clothing items. It contains 70,000 grayscale images, each 28 × 28 pixels, categorized into 10 classes, with 60,000 for training and 10,000 for testing. Similar to MNIST, the dataset includes fields for the image and corresponding label. The diversity of clothing items, coupled with their similarities, introduces a greater level of complexity, testing the generalization capabilities of machine learning models [50].
- CIFAR-10: The CIFAR-10 dataset, developed by the Canadian Institute For Advanced Research (CIFAR), contains 60,000 color images, each of size 32 × 32 pixels, divided into 10 categories, with 6000 images per category. These categories include airplanes, automobiles, birds, cats, deer, dogs, frogs, horses, ships, and trucks. The training set consists of 50,000 images, while the test set includes 10,000 images. CIFAR-10 offers higher-resolution and more complex images compared to MNIST and Fashion MNIST, providing a basis for evaluating the performance of more sophisticated and deeper neural networks [51].
3.2. CNN Models
- MNIST: The CNN model for the MNIST dataset starts with a reshape layer to convert images from 1D vectors of 784 elements into 28 × 28 × 1 tensors. It includes two convolutional layers with 5 × 5 filters (10 and 20 filters, respectively), each followed by a 2 × 2 max-pooling layer. A flattened layer then converts the features into a 1D vector, which connects to a dense layer with 50 neurons. The model ends with an output layer of 10 neurons, representing the 10 classes of digits (0–9) in MNIST. The softmax activation function is used to produce a probability distribution across the classes.
- Fashion MNIST: The CNN model for the Fashion MNIST dataset follows a similar approach to that of MNIST but with increased depth, reflecting the added complexity of the images. This model uses three convolutional layers with 16, 32, and 64 filters of size 5 × 5. Max-pooling layers with 2 × 2 windows are applied after the first two convolutional layers, and another pooling layer follows the last convolutional layer. This arrangement enhances the model’s ability to identify the more intricate features in Fashion MNIST images. After flattening the output, the model includes a dense layer with 64 neurons, followed by a softmax output layer with 10 neurons, corresponding to the 10 different clothing categories.
- CIFAR-10: The CNN model for the CIFAR-10 dataset is designed to address the challenge of processing higher-resolution color images (32 × 32 pixels). It begins with a reshape layer that converts the 1D vectors of 3072 elements into 32 × 32 × 3 tensors. This is followed by three convolutional layers with 32, 64, and 64 filters of size 3 × 3. Two 2 × 2 max-pooling layers are included after the first and second convolutional layers to reduce complexity. The features are then flattened into a 1D vector, which feeds into a fully connected layer with 64 neurons. The model concludes with a softmax output layer of 10 neurons, representing the 10 CIFAR-10 classes.
3.3. Pre-Processing
- The first step involves loading the data from CSV files into Spark DataFrames using the spark.read.csv function. The data consist of multiple columns representing the pixel values of the images and one column representing the label of the image.
- The next phase is to convert the pixel columns into a single feature vector for each image. This is done using the VectorAssembler tool in PySpark, which consolidates the pixel values into a unified vector for easier processing and analysis by machine learning models.
- Following this, the pixel values are normalized to a range between 0 and 1 using the MinMaxScaler. This normalization improves the model’s convergence during training.
- The final stage of pre-processing involves transforming sparse vectors (SparseVectors) into dense vectors (DenseVectors). This transformation is necessary because working with sparse tensors in TensorFlow Federated (TFF) is more complex than using dense tensors.
3.4. Data Partitioning
4. Proposed Approach
4.1. Federated Learning with Fixed Learning Rate
- Client Selection: At the beginning of each training round, the server randomly selects a subset of the available clients based on specific criteria such as availability and Wi-Fi connection stability. These selected clients participate in the current training round.
- Model Broadcast: The selected clients receive the current global model weights from the server, distributed via the tff.federated_broadcast function.
- Local Training: Each selected client trains the model locally using its own data. Clients use the tff.learning.Model and tf.GradientTape to compute gradients on their batches of data and update the model weights through the client optimizer, which, in this case, is SGD with a fixed learning rate.
- Aggregation of Updates: After local training, the clients send their model updates, which include the changes in weights calculated during local training, back to the server. This aggregation is handled by the tff.federated_aggregate function, which combines the client updates on the server.
- Global Model Update: Once the server receives all the client updates, it computes a federated average by weighing each client’s contribution based on the number of images used in the training. The server then updates the global model by averaging the client weights, ensuring that each client’s contribution is proportional to the size of their dataset.
- Repeat: This process is repeated for a predetermined number of training rounds.
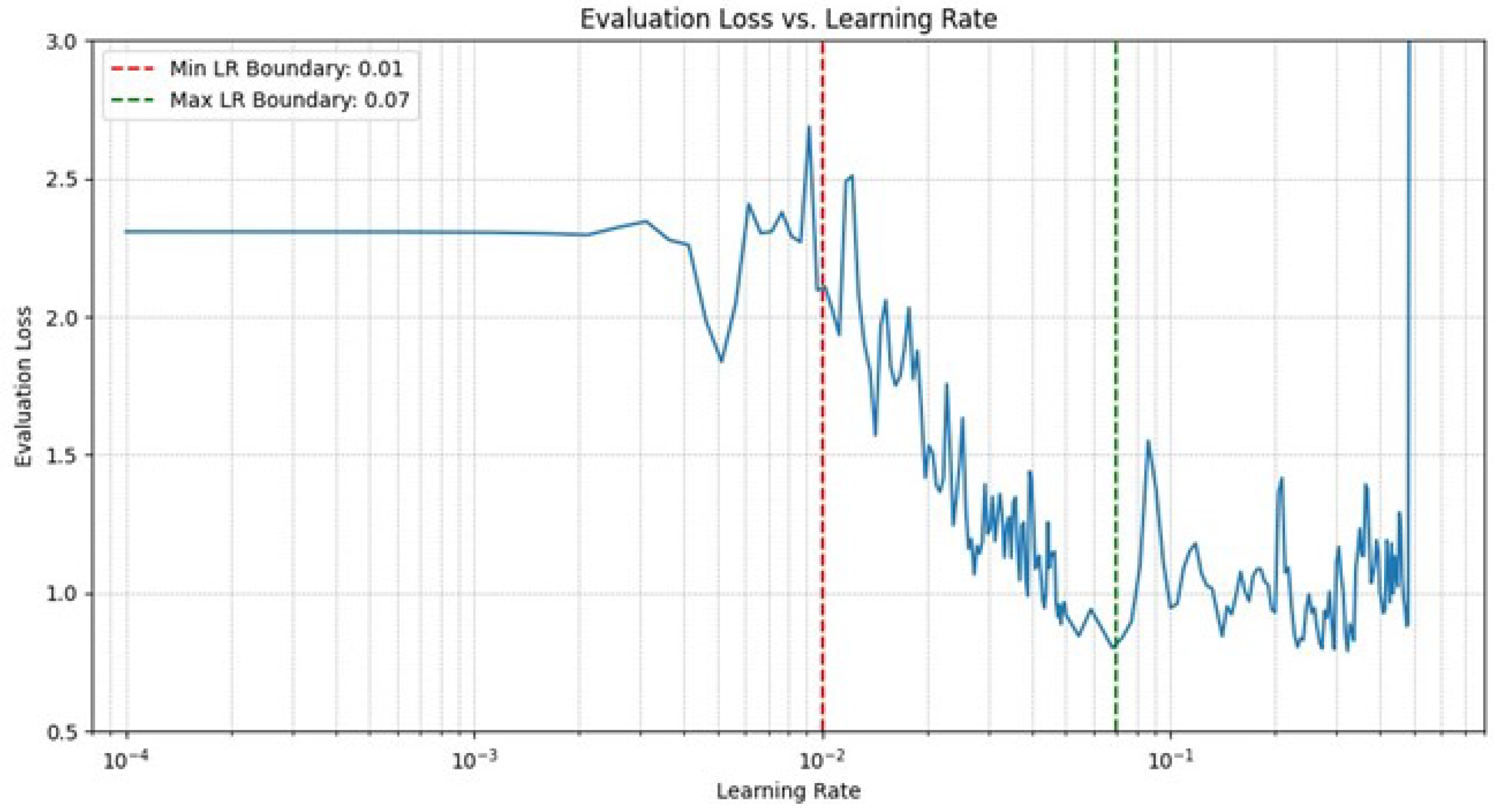
4.2. Federated Learning with Cyclical Learning Rate
- In federated learning (FL), non-IID data can critically degrade performance and converge [53]. The non-IID case means that the data of each client’s datasets may highlight different patterns, so the gradients in local training will be divergent. Experiments with highly skewed data performed with neural networks show that this divergence can lower the accuracy of the global model by up to 55% in some cases [6].
- It also increases communication overhead and has non-IID data that will yield an imbalance in class distributions, which could further impact the convergence and performance of FL. Non-IID data can not only introduce bias but also slow down convergence, regardless of whether batch normalization is used, because the local and global statistical parameters do not align [54].
- More importantly, non-IID data cause fluctuations in historical gradient information, which then results in inconsistent convergence. This is why techniques such as federated gradient scheduling have been suggested for dealing with these challenges by creating IID gradient sets for more stable updates [55].
- Local Overfitting: Clients with other distributions of data are likely to overfit their local models, which, when assembled form the global model, will perform poorly. For example, the simple task of evaluating the performance of multi-modal models concerning uni-modal models showed that the former may be more harmful as a result of this overfitting [56].
- Skewed Contributions: When the clients hold different distributions of data, some of the clients contribute to the global model than others, thus distorting the learning process. Consequently, this can intensify the problems associated with the convergence and, in general, the entire model’s efficiency [57].
- These challenges are addressed by proposing strategies of data sharing, optimal node selection, and new aggregation schemes to reduce accuracy and convergence time [58].
- Triangular: the learning rate increases linearly during the first half of the cycle and decreases linearly during the second half.
- Triangular2: similar to triangular, but the difference in the learning rate is halved at the end of each cycle.
- Exp_range: the learning rate oscillates between the minimum and maximum values, with each boundary value decaying by an exponential factor.
- cycle = tf.floor(1 + (current_round) / (2 ∗ step_size))
- x = tf.abs((current_round) / (step_size - 2 ∗ cycle + 1))
- clr = min_lr + (max_lr - min_lr) ∗ tf.maximum(0.0, (1.0 - x))
- where:
- : represents the current training round in the federated learning process.
- : The minimum learning rate determined from the learning rate range test, below which the learning rate does not drop.
- : The maximum learning rate determined from the learning rate range test, above which the learning rate does not rise.
- : Defines half the length of a cycle in terms of the number of rounds. The learning rate increases from to during the first rounds, then decreases back to during the next rounds, completing a full cycle.
4.3. Federated Learning with Data Sharing and Pre-Training on Augmented Data
- Creation of a Balanced Data Subset: The strategy begins by selecting a balanced subset of the CIFAR-10 dataset. Specifically for this implementation, 10,000 images are selected to uniformly represent all 10 classes of CIFAR-10 (1000 images per class). The remaining 40,000 images are distributed in a non-IID manner among 500 clients, with each client receiving 80 images from two distinct classes (40 from each class).
- Distribution of the Balanced Subset Among Clients: Next, a portion of the balanced subset is randomly distributed to individual clients. Each client is provided with 0.2% of the balanced subset of 10,000 images (20 random images), thus increasing each client’s dataset to 100 images. These 20 images are randomly distributed to each client without adherence to IID or non-IID partitioning methods.
- Data Augmentation: Then, multiple data augmentation techniques are applied to this balanced subset. These techniques aim to increase the diversity of the training data and include:
- Random Crop with Padding: Adds padding to the original images with a random margin between 3 and 7 pixels followed by random cropping to a 32 × 32 pixel area. This method introduces spatial variation in the dataset, helping the model recognize objects despite positional changes.
- Horizontal Flip: Reflects the image along its vertical axis, effectively increasing the dataset size and improving the model’s ability to recognize objects regardless of horizontal orientation.
- Brightness and Contrast Adjustment: Randomly adjusts pixel values within a predefined range (0.8 to 1.2) to simulate different lighting conditions, enhancing the model’s robustness to variations in lighting.
- Random Rotation and Scaling: Applies random rotations between −15 and 15 degrees and scaling images within a range of 0.8 to 1.2. This prepares the model to handle objects at various angles and sizes.
- Random Noise: Adds random pixel values ranging from 8 to 15 to simulate lower-quality images, increasing the robustness of the model in real-world scenarios where perfect image conditions are not always guaranteed.
Through the application of these augmentation techniques, as illustrated in Figure 1, an augmented dataset is created, enriched with a broad range of variations of the images from the balanced subset of CIFAR-10. This increased diversity in the training data is critical for developing a robust model capable of generalizing to unseen data, which is particularly crucial in federated learning environments with non-IID data across clients. - Pre-Training of the Global Model: After augmentation, the global model is pre-trained on the set of 50,000 augmented images. The global model is the CNN model defined for the CIFAR-10 dataset in Section 3.2, which achieves an evaluation accuracy of approximately 70% and an evaluation loss of 0.92 upon completion of pre-training. This pre-training aims to establish a strong basis for performance and accelerate the process of model convergence during federal learning.
- Federated Learning: Finally, after pre-training, the global model is now ready to proceed to federated training with the important difference that it is no longer initialized with random weights. Instead, it loads weights from pre-training, providing a stable starting point based on previous training with the augmented dataset. This approach ensures that the model has already developed a strong understanding of the various features and patterns presented in the augmented images, increasing the chances of more efficient and faster convergence during federated learning. The federated training follows the steps of the FedAvg algorithm described in Section 4.1, while also incorporating the Cyclical Learning Rate (CLR) policy detailed in Section 4.2.
5. Experimental Results
5.1. Impact of Non-IID Data on FedAvg Performance
5.1.1. Results on MNIST Dataset
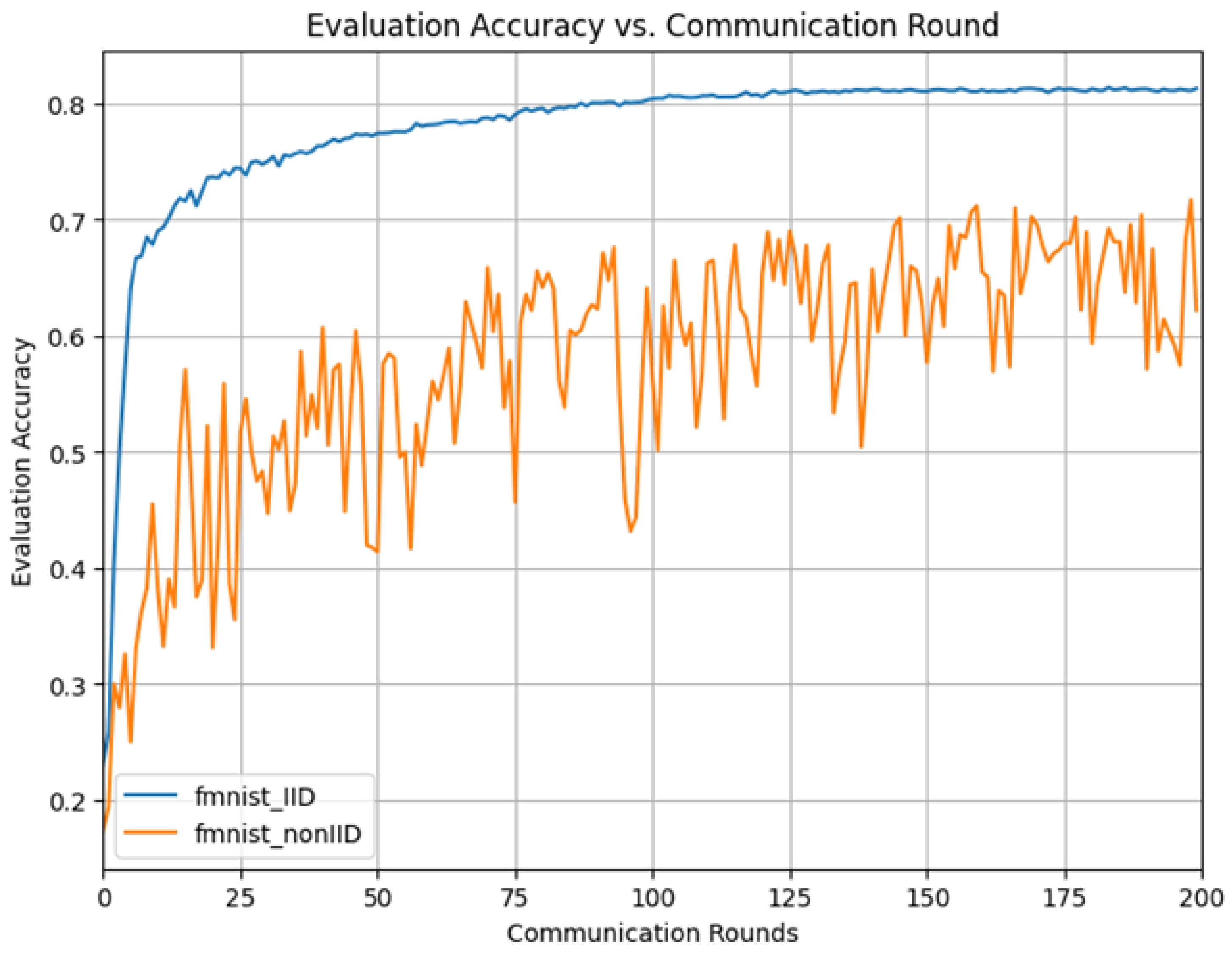
5.1.2. Results on Fashion MNIST Dataset
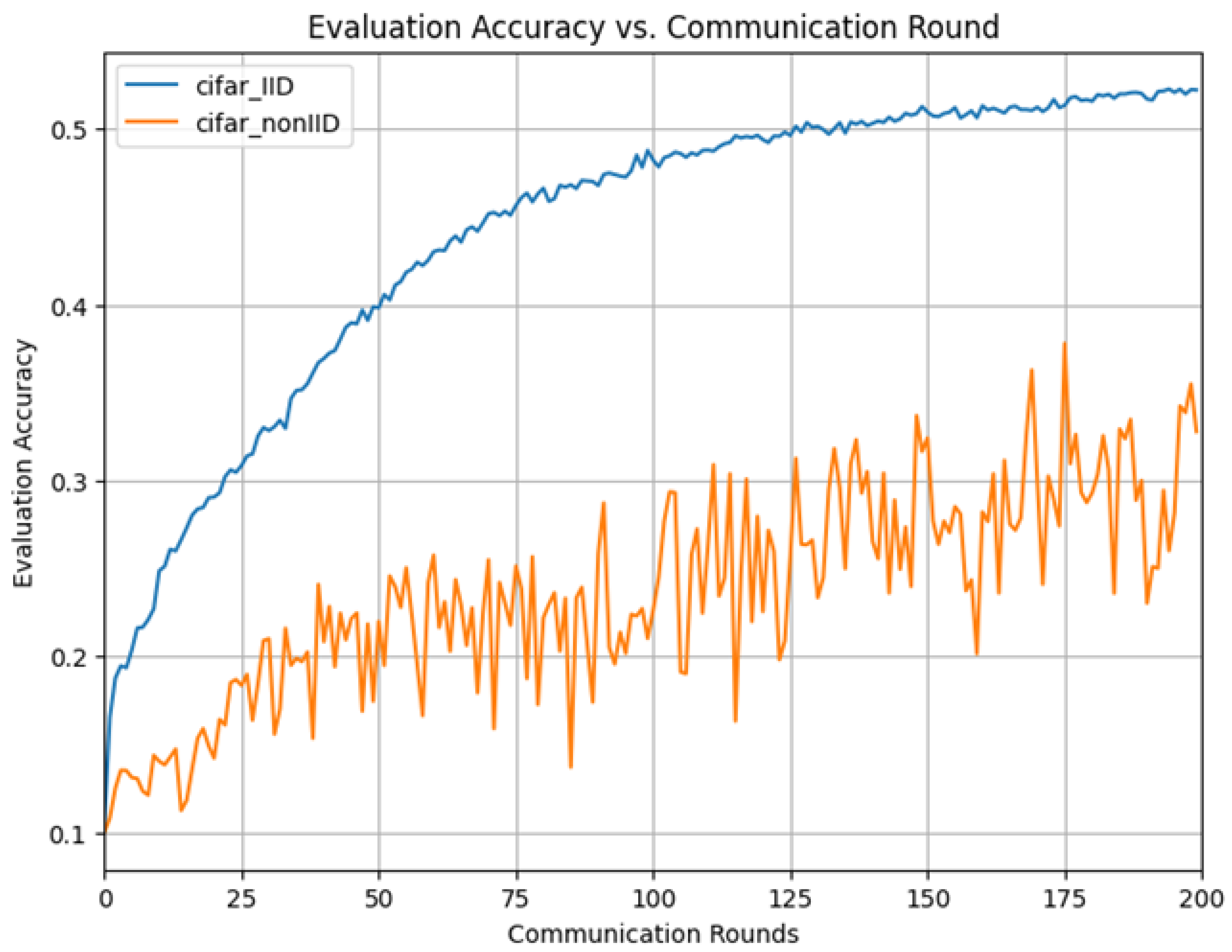
5.1.3. Results on CIFAR-10 Dataset
5.2. Results of Federated Learning with Cyclical Learning Rate
5.2.1. CLR Results on MNIST
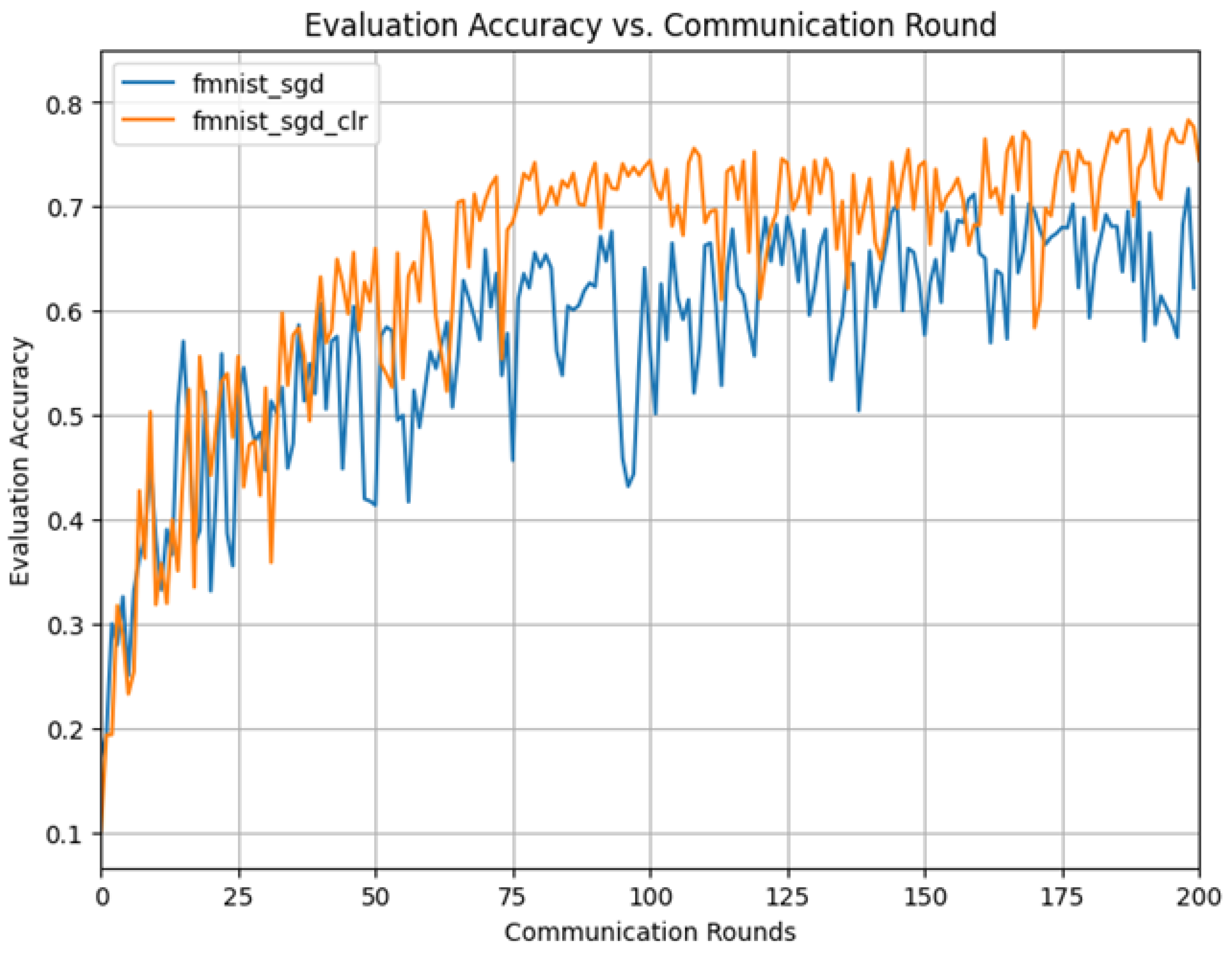
5.2.2. CLR Results on Fashion MNIST
5.2.3. CLR Results on CIFAR-10
5.3. Results of Federated Learning with Data Sharing and Pre-Training on Augmented Data
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNNs | Convolutional Neural Networks |
| CLR | Cyclical Learning Rate |
| Decaying LR | Decaying Learning Rate |
| FedAvg | Federated Averaging |
| FC | Federated Core |
| FedSGD | Federated Stochastic Gradient Descent |
| Fixed LR | Fixed Learning Rate |
| FL | Federated Learning |
| LRRT | Learning Rate Range Test |
| MNIST | Modified National Institute of Standards and Technology |
| RDD | Resilient Distributed Dataset |
| SGD | Stochastic Gradient Descent |
| SVMs | Support Vector Machines |
| TFF | TensorFlow Federated |
References
- Rydning, D.R.J.; Reinsel, J.; Gantz, J. The digitization of the world from edge to core. Fram. Int. Data Corp. 2018, 16, 1–28. [Google Scholar]
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.y. Communication-Efficient Learning of Deep Networks from Decentralized Data. arXiv 2023, arXiv:1602.05629. [Google Scholar]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Smith, L.N. Cyclical Learning Rates for Training Neural Networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar] [CrossRef]
- Chen, H.Y.; Tu, C.H.; Li, Z.; Shen, H.W.; Chao, W.L. On the Importance and Applicability of Pre-Training for Federated Learning. arXiv 2023, arXiv:2206.11488. [Google Scholar]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated Learning with Non-IID Data. arXiv 2018, arXiv:1806.00582. [Google Scholar] [CrossRef]
- Asad, M.; Moustafa, A.; Ito, T. Federated Learning Versus Classical Machine Learning: A Convergence Comparison. arXiv 2021, arXiv:2107.10976. [Google Scholar]
- Giannaros, A.; Karras, A.; Theodorakopoulos, L.; Karras, C.; Kranias, P.; Schizas, N.; Kalogeratos, G.; Tsolis, D. Autonomous vehicles: Sophisticated attacks, safety issues, challenges, open topics, blockchain, and future directions. J. Cybersecur. Priv. 2023, 3, 493–543. [Google Scholar] [CrossRef]
- Kaur, G.; Grewal, S.K.; Jain, A. Federated Learning based Spatio-Temporal framework for real-time traffic prediction. Wirel. Pers. Commun. 2024, 136, 849–865. [Google Scholar] [CrossRef]
- Raghunath, K.K.; Bhat, C.R.; Kumar, V.V.; Velmurugan, A.; Mahesh, T.; Manikandan, K.; Krishnamoorthy, N. Redefining Urban Traffic Dynamics with TCN-FL Driven Traffic Prediction and Control Strategies. IEEE Access 2024, 12, 115386–115399. [Google Scholar] [CrossRef]
- Xu, J.; Glicksberg, B.S.; Su, C.; Walker, P.; Bian, J.; Wang, F. Federated learning for healthcare informatics. J. Healthc. Inform. Res. 2021, 5, 1–19. [Google Scholar] [CrossRef]
- Lakhan, A.; Hamouda, H.; Abdulkareem, K.H.; Alyahya, S.; Mohammed, M.A. Digital healthcare framework for patients with disabilities based on deep federated learning schemes. Comput. Biol. Med. 2024, 169, 107845. [Google Scholar] [CrossRef] [PubMed]
- Sachin, D.; Annappa, B.; Hegde, S.; Abhijit, C.S.; Ambesange, S. Fedcure: A heterogeneity-aware personalized federated learning framework for intelligent healthcare applications in iomt environments. IEEE Access 2024, 12, 15867–15883. [Google Scholar]
- Lee, J.; Solat, F.; Kim, T.Y.; Poor, H.V. Federated learning-empowered mobile network management for 5G and beyond networks: From access to core. IEEE Commun. Surv. Tutor. 2024, 26, 2176–2212. [Google Scholar] [CrossRef]
- Hasan, M.K.; Habib, A.A.; Islam, S.; Safie, N.; Ghazal, T.M.; Khan, M.A.; Alzahrani, A.I.; Alalwan, N.; Kadry, S.; Masood, A. Federated learning enables 6 G communication technology: Requirements, applications, and integrated with intelligence framework. Alex. Eng. J. 2024, 91, 658–668. [Google Scholar] [CrossRef]
- Li, Z.; Hou, Z.; Liu, H.; Li, T.; Yang, C.; Wang, Y.; Shi, C.; Xie, L.; Zhang, W.; Xu, L.; et al. Federated Learning in Large Model Era: Vision-Language Model for Smart City Safety Operation Management. In Proceedings of the Companion Proceedings of the ACM on Web Conference, Singapore, 13–17 May 2024; pp. 1578–1585. [Google Scholar]
- Xu, H.; Seng, K.P.; Smith, J.; Ang, L.M. Multi-Level Split Federated Learning for Large-Scale AIoT System Based on Smart Cities. Future Internet 2024, 16, 82. [Google Scholar] [CrossRef]
- Munawar, A.; Piantanakulchai, M. A collaborative privacy-preserving approach for passenger demand forecasting of autonomous taxis empowered by federated learning in smart cities. Sci. Rep. 2024, 14, 2046. [Google Scholar] [CrossRef]
- Friha, O.; Ferrag, M.A.; Benbouzid, M.; Berghout, T.; Kantarci, B.; Choo, K.K.R. 2DF-IDS: Decentralized and differentially private federated learning-based intrusion detection system for industrial IoT. Comput. Secur. 2023, 127, 103097. [Google Scholar] [CrossRef]
- Farahani, B.; Monsefi, A.K. Smart and collaborative industrial IoT: A federated learning and data space approach. Digit. Commun. Netw. 2023, 9, 436–447. [Google Scholar] [CrossRef]
- Rashid, M.M.; Khan, S.U.; Eusufzai, F.; Redwan, M.A.; Sabuj, S.R.; Elsharief, M. A federated learning-based approach for improving intrusion detection in industrial internet of things networks. Network 2023, 3, 158–179. [Google Scholar] [CrossRef]
- Qin, Z.; Yan, X.; Zhou, M.; Deng, S. BlockDFL: A Blockchain-based Fully Decentralized Peer-to-Peer Federated Learning Framework. In Proceedings of the ACM on Web Conference 2024, Singapore, 13–17 May 2024; pp. 2914–2925. [Google Scholar]
- Wu, X.; Liu, Y.; Tian, J.; Li, Y. Privacy-preserving trust management method based on blockchain for cross-domain industrial IoT. Knowl.-Based Syst. 2024, 283, 111166. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Z.; Srivastava, G.; Alghamdi, T.A.; Khan, F.; Kumari, S.; Xiong, H. Industrial blockchain threshold signatures in federated learning for unified space-air-ground-sea model training. J. Ind. Inf. Integr. 2024, 39, 100593. [Google Scholar] [CrossRef]
- Shaheen, M.; Farooq, M.S.; Umer, T.; Kim, B.S. Applications of federated learning; Taxonomy, challenges, and research trends. Electronics 2022, 11, 670. [Google Scholar] [CrossRef]
- Karras, A.; Karras, C.; Giotopoulos, K.C.; Tsolis, D.; Oikonomou, K.; Sioutas, S. Peer to Peer Federated Learning: Towards Decentralized Machine Learning on Edge Devices. In Proceedings of the 2022 7th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Ioannina, Greece, 23–25 September 2022; pp. 1–9. [Google Scholar] [CrossRef]
- Liu, R.; Cao, Y.; Yoshikawa, M.; Chen, H. FedSel: Federated SGD under Local Differential Privacy with Top-k Dimension Selection. arXiv 2020, arXiv:2003.10637. [Google Scholar] [CrossRef]
- Nilsson, A.; Smith, S.; Ulm, G.; Gustavsson, E.; Jirstrand, M. A Performance Evaluation of Federated Learning Algorithms. In Proceedings of the Second Workshop on Distributed Infrastructures for Deep Learning, Rennes, France, 10 December 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Fallah, A.; Mokhtari, A.; Ozdaglar, A. Personalized Federated Learning: A Meta-Learning Approach. arXiv 2020, arXiv:2002.07948. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Wu, Y.; Liu, L. Selecting and Composing Learning Rate Policies for Deep Neural Networks. ACM Trans. Intell. Syst. Technol. (TIST) 2023, 14, 1–25. [Google Scholar] [CrossRef]
- Yang, S.; Xiao, W.; Zhang, M.; Guo, S.; Zhao, J.; Shen, F. Image Data Augmentation for Deep Learning: A Survey. arXiv 2023, arXiv:2204.08610. [Google Scholar]
- Jeong, E.; Oh, S.; Kim, H.; Park, J.; Bennis, M.; Kim, S.L. Communication-efficient on-device machine learning: Federated distillation and augmentation under non-iid private data. arXiv 2018, arXiv:1811.11479. [Google Scholar]
- Rasouli, M.; Sun, T.; Rajagopal, R. Fedgan: Federated generative adversarial networks for distributed data. arXiv 2020, arXiv:2006.07228. [Google Scholar]
- Yoon, T.; Shin, S.; Hwang, S.J.; Yang, E. Fedmix: Approximation of mixup under mean augmented federated learning. arXiv 2021, arXiv:2107.00233. [Google Scholar]
- Lin, T.; Kong, L.; Stich, S.U.; Jaggi, M. Ensemble distillation for robust model fusion in federated learning. Adv. Neural Inf. Process. Syst. 2020, 33, 2351–2363. [Google Scholar]
- Zhang, L.; Shen, L.; Ding, L.; Tao, D.; Duan, L.Y. Fine-tuning global model via data-free knowledge distillation for non-iid federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10174–10183. [Google Scholar]
- Shen, X.; Liu, Y.; Zhang, Z. Performance-enhanced federated learning with differential privacy for internet of things. IEEE Internet Things J. 2022, 9, 24079–24094. [Google Scholar] [CrossRef]
- Erhan, D.; Courville, A.; Bengio, Y.; Vincent, P. Why does unsupervised pre-training help deep learning? In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Sardinia, Italy, 13–15 May 2010; pp. 201–208. [Google Scholar]
- Hendrycks, D.; Lee, K.; Mazeika, M. Using pre-training can improve model robustness and uncertainty. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 2712–2721. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 17–19 June 2013; pp. 1139–1147. [Google Scholar]
- Ju, L.; Zhang, T.; Toor, S.; Hellander, A. Accelerating fair federated learning: Adaptive federated adam. IEEE Trans. Mach. Learn. Commun. Netw. 2024, 2, 1017–1032. [Google Scholar] [CrossRef]
- Sharma, A. A Comprehensive Guide to Google Colab: Features, Usage, and Best Practices. Available online: https://www.analyticsvidhya.com/blog/2020/03/google-colab-machine-learning-deep-learning/ (accessed on 10 October 2024).
- TensorFlow. Federated Core|TensorFlow. Available online: https://www.tensorflow.org/federated/federated_core (accessed on 10 October 2024).
- TensorFlow. Federated Learning|TensorFlow. Available online: https://www.tensorflow.org/federated/federated_learning (accessed on 10 October 2024).
- Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J.; et al. Apache Spark: A unified engine for big data processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
- Chen, F.; Chen, N.; Mao, H.; Hu, H. Assessing four Neural Networks on Handwritten Digit Recognition Dataset (MNIST). arXiv 2019, arXiv:1811.08278. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, USA, 2009. [Google Scholar]
- Zhang, X.; Sun, W.; Chen, Y. Tackling the non-iid issue in heterogeneous federated learning by gradient harmonization. IEEE Signal Process. Lett. 2024, 31, 2595–2599. [Google Scholar] [CrossRef]
- Tenison, I.; Sreeramadas, S.A.; Mugunthan, V.; Oyallon, E.; Rish, I.; Belilovsky, E. Gradient masked averaging for federated learning. arXiv 2022, arXiv:2201.11986. [Google Scholar]
- Lu, Z.; Pan, H.; Dai, Y.; Si, X.; Zhang, Y. Federated learning with non-iid data: A survey. IEEE Internet Things J. 2024, 11, 19188–19209. [Google Scholar] [CrossRef]
- You, X.; Liu, X.; Jiang, N.; Cai, J.; Ying, Z. Reschedule Gradients: Temporal Non-IID Resilient Federated Learning. IEEE Internet Things J. 2023, 10, 747–762. [Google Scholar] [CrossRef]
- Chen, S.; Li, B. Towards Optimal Multi-Modal Federated Learning on Non-IID Data with Hierarchical Gradient Blending. In Proceedings of the IEEE INFOCOM 2022—IEEE Conference on Computer Communications, London, UK, 2–5 May 2022; pp. 1469–1478. [Google Scholar] [CrossRef]
- Arisdakessian, S.; Wahab, O.A.; Mourad, A.; Otrok, H. Coalitional Federated Learning: Improving Communication and Training on Non-IID Data With Selfish Clients. IEEE Trans. Serv. Comput. 2023, 16, 2462–2476. [Google Scholar] [CrossRef]
- Bansal, S.; Bansal, M.; Verma, R.; Shorey, R.; Saran, H. FedNSE: Optimal node selection for federated learning with non-IID data. In Proceedings of the 2023 15th International Conference on COMmunication Systems & NETworkS (COMSNETS), Bangalore, India, 3–8 January 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 713–721. [Google Scholar]
- Karras, A.; Giannaros, A.; Theodorakopoulos, L.; Krimpas, G.A.; Kalogeratos, G.; Karras, C.; Sioutas, S. FLIBD: A federated learning-based IoT big data management approach for privacy-preserving over Apache Spark with FATE. Electronics 2023, 12, 4633. [Google Scholar] [CrossRef]
- Karras, A.; Giannaros, A.; Karras, C.; Theodorakopoulos, L.; Mammassis, C.S.; Krimpas, G.A.; Sioutas, S. TinyML algorithms for Big Data Management in large-scale IoT systems. Future Internet 2024, 16, 42. [Google Scholar] [CrossRef]
- Vlachou, E.; Karras, A.; Karras, C.; Theodorakopoulos, L.; Halkiopoulos, C.; Sioutas, S. Distributed Bayesian Inference for Large-Scale IoT Systems. Big Data Cogn. Comput. 2023, 8, 1. [Google Scholar] [CrossRef]
- Karras, A.; Karras, C.; Giotopoulos, K.C.; Tsolis, D.; Oikonomou, K.; Sioutas, S. Federated edge intelligence and edge caching mechanisms. Information 2023, 14, 414. [Google Scholar] [CrossRef]
- Malekijoo, A.; Fadaeieslam, M.J.; Malekijou, H.; Homayounfar, M.; Alizadeh-Shabdiz, F.; Rawassizadeh, R. FEDZIP: A Compression Framework for Communication-Efficient Federated Learning. arXiv 2021, arXiv:2102.01593. [Google Scholar] [CrossRef]
- Geyer, R.C.; Klein, T.; Nabi, M. Differentially Private Federated Learning: A Client Level Perspective. arXiv 2018, arXiv:1712.07557. [Google Scholar] [CrossRef]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical Secure Aggregation for Privacy-Preserving Machine Learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1175–1191. [Google Scholar] [CrossRef]
- Dablain, D.; Krawczyk, B.; Chawla, N.V. DeepSMOTE: Fusing deep learning and SMOTE for imbalanced data. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 6390–6404. [Google Scholar] [CrossRef]







| Data Distribution | Maximum Accuracy (%) | Rounds to 94% |
|---|---|---|
| MNIST IID | 96.83 | 55 |
| MNIST Non-IID | 94.04 | 195 |
| Data Distribution | Maximum Accuracy (%) | Rounds to 71% |
|---|---|---|
| FMNIST IID | 81.8 | 15 |
| FMNIST Non-IID | 71.2 | 160 |
| Data Distribution | Maximum Accuracy (%) | Rounds to 37% |
|---|---|---|
| CIFAR-10 IID | 52.2 | 43 |
| CIFAR-10 Non-IID | 37.8 | 176 |
| Communication Rounds | SGD with Fixed Lr | SGD with Cyclical Lr |
|---|---|---|
| 1 | 0.13520 | 0.11860 |
| 10 | 0.30460 | 0.48240 |
| 20 | 0.59600 | 0.76400 |
| 30 | 0.75100 | 0.87330 |
| 40 | 0.77560 | 0.90590 |
| 50 | 0.78870 | 0.91790 |
| 60 | 0.85590 | 0.93350 |
| 70 | 0.86870 | 0.93110 |
| 80 | 0.86620 | 0.93290 |
| 90 | 0.89580 | 0.94440 |
| 100 | 0.89050 | 0.95460 |
| 110 | 0.89560 | 0.95220 |
| 120 | 0.90540 | 0.95310 |
| 130 | 0.91890 | 0.95120 |
| 140 | 0.91720 | 0.95670 |
| 150 | 0.92600 | 0.96390 |
| 160 | 0.90330 | 0.96340 |
| 170 | 0.91490 | 0.94760 |
| 180 | 0.92680 | 0.95770 |
| 190 | 0.93930 | 0.96460 |
| 200 | 0.91890 | 0.96820 |
| Max Accuracy (%) | Rounds to 94% | Speedup (Rounds) | |
|---|---|---|---|
| mnist_sgd_fixed | 94.04 | 195 | x1 |
| mnist_sgd_clr | 97.01 | 64 | x3.04 |
| Communication Rounds | SGD with Fixed Lr | SGD with Cyclical Lr |
|---|---|---|
| 1 | 0.17280 | 0.10160 |
| 10 | 0.45500 | 0.50340 |
| 20 | 0.52260 | 0.50360 |
| 30 | 0.48340 | 0.42310 |
| 40 | 0.52060 | 0.57900 |
| 50 | 0.41760 | 0.60920 |
| 60 | 0.52520 | 0.69540 |
| 70 | 0.57230 | 0.68690 |
| 80 | 0.65590 | 0.74240 |
| 90 | 0.62690 | 0.72660 |
| 100 | 0.64120 | 0.73820 |
| 110 | 0.56650 | 0.74840 |
| 120 | 0.55690 | 0.75260 |
| 130 | 0.59590 | 0.69330 |
| 140 | 0.56990 | 0.70070 |
| 150 | 0.62820 | 0.73910 |
| 160 | 0.71200 | 0.68270 |
| 170 | 0.70300 | 0.76290 |
| 180 | 0.68950 | 0.74180 |
| 190 | 0.70440 | 0.73720 |
| 200 | 0.62200 | 0.77640 |
| Max Accuracy (%) | Rounds to 71% | Speedup (Rounds) | |
|---|---|---|---|
| fmnist_sgd_fixed | 71.2 | 160 | x1 |
| fmnist_sgd_clr | 78.3 | 69 | x2.3 |
| Communication Rounds | SGD with Fixed Lr | SGD with Cyclical Lr |
|---|---|---|
| 1 | 0.09980 | 0.09620 |
| 10 | 0.14370 | 0.15940 |
| 20 | 0.14920 | 0.10310 |
| 30 | 0.20900 | 0.20790 |
| 40 | 0.24100 | 0.23200 |
| 50 | 0.17450 | 0.30710 |
| 60 | 0.24200 | 0.31320 |
| 70 | 0.22480 | 0.26330 |
| 80 | 0.17260 | 0.27600 |
| 90 | 0.17400 | 0.37130 |
| 100 | 0.21020 | 0.42310 |
| 110 | 0.22460 | 0.33850 |
| 120 | 0.27970 | 0.40440 |
| 130 | 0.26620 | 0.42730 |
| 140 | 0.30510 | 0.43270 |
| 150 | 0.31660 | 0.37720 |
| 160 | 0.20150 | 0.42310 |
| 170 | 0.36300 | 0.46350 |
| 180 | 0.28750 | 0.40060 |
| 190 | 0.30010 | 0.41100 |
| 200 | 0.32790 | 0.47660 |
| Max Accuracy (%) | Rounds to 37% | Speedup (Rounds) | |
|---|---|---|---|
| cifar_sgd_fixed | 37.8 | 176 | x1 |
| cifar_sgd_clr | 48.8 | 90 | x1.95 |
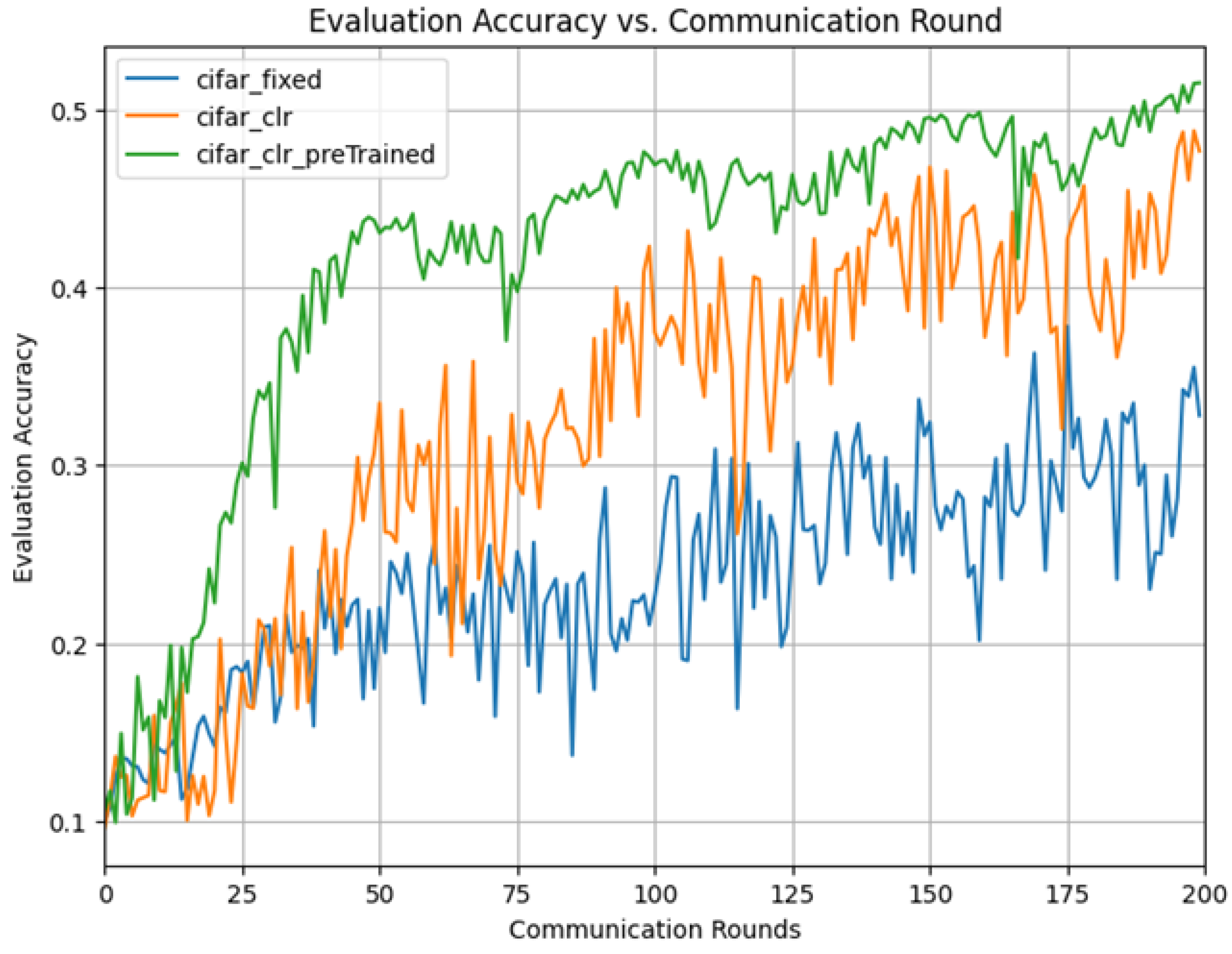
| Training Rounds | SGD Fixed Lr | SGD Cyclical LR (CLR) | SGD CLR + PreTrain |
|---|---|---|---|
| 1 | 0.09980 | 0.09620 | 0.10580 |
| 10 | 0.14370 | 0.15940 | 0.11180 |
| 20 | 0.14920 | 0.10310 | 0.24180 |
| 30 | 0.20900 | 0.20790 | 0.33730 |
| 40 | 0.24100 | 0.23200 | 0.40870 |
| 50 | 0.17450 | 0.30710 | 0.43760 |
| 60 | 0.24200 | 0.31320 | 0.42070 |
| 70 | 0.22480 | 0.26330 | 0.41440 |
| 80 | 0.17260 | 0.27600 | 0.41900 |
| 90 | 0.17400 | 0.37130 | 0.45390 |
| 100 | 0.21020 | 0.42310 | 0.47330 |
| 110 | 0.22460 | 0.33850 | 0.46050 |
| 120 | 0.27970 | 0.40440 | 0.46350 |
| 130 | 0.26620 | 0.42730 | 0.46390 |
| 140 | 0.30510 | 0.43270 | 0.44680 |
| 150 | 0.31660 | 0.37720 | 0.49480 |
| 160 | 0.20150 | 0.42310 | 0.49830 |
| 170 | 0.36300 | 0.46350 | 0.48170 |
| 180 | 0.28750 | 0.40060 | 0.47940 |
| 190 | 0.30010 | 0.41100 | 0.50470 |
| 200 | 0.32790 | 0.47660 | 0.51490 |
| Metric | Fixed LR | CLR | CLR + PreTrain | % Improv. (CLR over Fixed) | % Improv. (CLR+PreTrain over Fixed) | % Improv. (CLR+PreTrain over CLR) |
|---|---|---|---|---|---|---|
| Max Accuracy (%) | 37.8 | 48.8 | 51.4 | 29.1% | 36% | 5.3% |
| Rounds to 37% | 176 | 90 | 33 | 1.95x | 5.33x | 2.72x |
| Speedup (rounds) | x1 | x1.95 | x5.33 | 95% | 433% | 173% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Efthymiadis, F.; Karras, A.; Karras, C.; Sioutas, S. Advanced Optimization Techniques for Federated Learning on Non-IID Data. Future Internet 2024, 16, 370. https://doi.org/10.3390/fi16100370
Efthymiadis F, Karras A, Karras C, Sioutas S. Advanced Optimization Techniques for Federated Learning on Non-IID Data. Future Internet. 2024; 16(10):370. https://doi.org/10.3390/fi16100370
Chicago/Turabian StyleEfthymiadis, Filippos, Aristeidis Karras, Christos Karras, and Spyros Sioutas. 2024. "Advanced Optimization Techniques for Federated Learning on Non-IID Data" Future Internet 16, no. 10: 370. https://doi.org/10.3390/fi16100370
APA StyleEfthymiadis, F., Karras, A., Karras, C., & Sioutas, S. (2024). Advanced Optimization Techniques for Federated Learning on Non-IID Data. Future Internet, 16(10), 370. https://doi.org/10.3390/fi16100370











