Optimizing Task Execution: The Impact of Dynamic Time Quantum and Priorities on Round Robin Scheduling

Abstract

Task scheduling algorithms are crucial for optimizing the utilization of computing resources. This work proposes a unique approach for improving task execution in real-time systems using an enhanced Round Robin scheduling algorithm variant incorporating dynamic time quantum and priority. The proposed algorithm adjusts the time slice allocated to each task based on execution time and priority, resulting in more efficient resource utilization. We also prioritize higher-priority tasks and execute them as soon as they arrive in the ready queue, ensuring the timely completion of critical tasks. We evaluate the performance of our algorithm using a set of real-world tasks and compare it with traditional Round Robin scheduling. The results show that our proposed approach significantly improves task execution time and resource utilization compared to conventional Round Robin scheduling. Our approach offers a promising solution for optimizing task execution in real-time systems. The combination of dynamic time quantum and priorities adds a unique element to the existing literature in this field.

1. Introduction

Scheduling is a critical aspect of computer systems, as it dictates how the computer executes different tasks or processes. A process refers to an instance of a program that can be performed by one or more threads containing the program code and its current activity. Each process has its own memory space, system resources such as open files and network connections, and its state, which includes information about the program counter, register values, and memory management information. When a program is executed, the operating system creates a new process. The process goes through several states during its lifetime, such as “new”, “ready”, “running”, “waiting”, “suspended”, and “terminated”. The process is then allocated memory and system resources and added to the scheduler’s queue. The scheduler decides which method to execute next based on the scheduling algorithm [1,2,3,4]. Therefore, various scheduling algorithms are proposed to address this problem, each with its trade-offs and advantages. The algorithm presented in this article is a scheduling algorithm that combines two popular approaches: dynamic time quantum (TQ) and priority scheduling.

Dynamic time quantum scheduling is a variation of Round Robin (RR) scheduling in which each process is allocated a fixed timespan to complete execution. However, in dynamic time quantum scheduling, the time quantum is not fixed and can vary depending on the behavior of the process [5,6]. For example, if a process uses up its entire time quantum without completing, it is considered CPU-bound and is assigned a more significant time quantum in the next Round. Conversely, if a process completes before its time quantum expires, it is considered I/O-bound and is given a smaller time quantum in the next Round. This approach aims to balance the needs of CPU-bound and I/O-bound processes by ensuring that each process receives a fair share of CPU time. On the other hand, priority scheduling assigns a priority value to each process, and the scheduler selects the process with the highest priority to execute. This approach allows the system to prioritize specific processes over others based on their importance or urgency. For instance, a real-time data-handling process may be prioritized more than a batch-processing process. By combining these two approaches, the scheduler can adapt to the behavior of the process and ensure that essential tasks are executed first while ensuring that all processes receive a fair share of CPU time.

In our proposed algorithm, we combined the concepts of dynamic time quantum and priority to resolve the scheduling problem in computer systems. The operating system sets the priorities of processes, and a dynamic time quantum scheduling approach is implemented to determine the sequence in which the processes are carried out. The time quantum for each process is based on its priority, with higher-priority processes being given a more significant time quantum. This approach balances fairness and efficiency, allowing the system to prioritize critical processes while ensuring all processes get a fair share of CPU time. Dynamic time quantum scheduling is an adaptation of the traditional Round Robin scheduling algorithm that enables the system to modify the time allotted to each process based on requirements and the present workload. By using dynamic time quantum, the scheduler can respond to changing conditions and maintain high levels of efficiency; this is especially important in cases where the system’s workload is dynamic and unpredictable. Moreover, the algorithm considers each process’s priority, enabling the system to prioritize specific tasks based on their importance. This allows the system to focus on time-sensitive or critical tasks and ensure they are executed quickly and efficiently. This algorithm can be used in a wide range of computer systems and can help improve system performance, responsiveness, and overall efficiency. The main contributions of our work are as follows:

• dynamic adjustment of time quantum based on execution time and priority;
• prioritizing higher-priority tasks and executing them first;
• decreasing priority of high-priority processes if not finished;
• combining dynamic time quantum, priorities, and decreasing priority for the first time.

The rest of this paper is organized as follows: Section 2 reviews the literature related to scheduling algorithms. Section 3 outlines the proposed solution and its approach to addressing the problem, and Section 4 discusses the results and analysis of our algorithm implementation. Section 5 concludes the paper with a summary and future directions.

2. Related Work

In this section, we will review the relevant literature on scheduling algorithms, explicitly focusing on the approaches of dynamic time quantum and priority scheduling. For example, the authors in [1] proposed the design of four versions of the Round Robin scheduling algorithm that allows for the dynamic determination of the time quantum based on the candidate process’s overall execution time. The main goal of these variations was to achieve a fair distribution of time quantum among the processes to increase the system’s overall performance. The initial variation was a fixed algorithm that allotted the time quantum to each process based on its execution time. The subsequent variation was a dynamic algorithm, which adapted the time quantum in real time based on the process’s execution time. The third variation was a hybrid algorithm that combined static and dynamic algorithms to balance fairness and efficiency. The fourth variation was an enhanced version of the third variation by adding a process-aging technique. A novel scheduling algorithm, “Intuitionistic Fuzzy-based Round-Robin”, has been created to improve efficiency and handle imprecise parameters. This approach employed an intuitionistic fuzzy inference system and a hybrid Round Robin strategy to adjust the time slice dynamically for inaccurate burst time. On the other hand, the hybrid Round Robin approach determines the task selection process [2].

The authors in [3] designed a Round Robin technique using a mean average and two registers for burst time storage. Upon completing a time slice by a process, the registers and ready queue undergo reformation, whereas adding new processes to the ready queue entails updating the registers. The authors in [4] described an algorithm called Median Average Round Robin (MARR) that calculated time quantum as (a) the average of all processes taken (avg), (b) the median of burst time (MedBt), (c) time quantum (Tq) = (avg + MedBg)/2. Using this process, the time quantum is allotted to the ready process in the queue. This process is repeated when the new process arrives or leaves the ready queue, and a new time quantum is generated for the ready process. The authors in [5] presented a new variant of the RR technique. The author described the algorithm in steps, as follows: (a) In ascending order, sort the burst times of all processes; (b) calculate the differences between consecutive processes; (c) identify the highest difference among these calculated differences; (d) calculate the median value among the sorted processes; (e) calculate the time quantum as the sum of the maximum difference and the median burst time; (f) if the difference between the process burst time and the time quantum is equal to zero, the process will be terminated; (g) if the difference between the process burst time and the time quantum is not equal to zero, the process will be moved to the end of the ready queue, and steps 6 and 7 will be repeated until the process finishes executing; (h) calculate average turnaround and waiting time. A new RR algorithm is presented in [6] to minimize the average waiting time, turnaround time, and NCS by combining the benefits of favoring short processes and the low scheduling overhead of RR. The novel technique classifies processes based on CPU characteristics, such as service period, weights, and allocation count. Each process within a group is allocated the same time quantum, calculated based on the group’s weight and the process’s CPU service period.

In a previous study [7], the authors introduced a novel CPU scheduling algorithm that is a modified version of the preemptive priority scheduling algorithm, a popular technique used in real-time systems. The performance of the traditional priority scheduling algorithm was enhanced by the proposed algorithm, which introduced an aging mechanism to prevent low-priority processes from being indefinitely postponed. Several variations of RR scheduling algorithms, such as shortest job first, preemptive, non-preemptive, and First Come, First Served algorithms, are analyzed in [8,9,10,11] to improve performance, CPU utilization, throughput, and context switching. The Dynamic Time Slice (DTS) algorithm, designed by the authors in [12], aims to minimize time costs by prioritizing short processes and minimizing scheduling overhead. They use clustering to similar group processes and assign the average time slice of the cluster for each process. The DTS was compared with six popular scheduling algorithms using nine groups of processes, measuring waiting and turnaround times and NCS.

Moreover, the RR algorithm and its variants are comprehensively reviewed in [13,14,15,16]. The authors in [17] designed an MMRR (Median Mean Round Robin) method for process scheduling. This used the median and mean of the remaining burst time of the processes in each cluster to calculate an optimal dynamic time quantum. It resulted in significant enhancements in CPU overhead and utilization. A novel method presented in [18] calculates the time quantum for each cycle using the arithmetic average. The algorithm has demonstrated decreased process turnaround and waiting times through analysis and experimentation, regardless of whether the process arrival time is zero or non-zero. This algorithm is well-suited for CPU scheduling and has been shown to outperform traditional Round Robin techniques. In [19], the Dynamic Round Robin Heuristic Algorithm (DRRHA) is introduced. This algorithm dynamically adapts the time slice by considering the task’s average time quantum and the remaining burst time. Experimental results gathered using the CloudSim Plus tool demonstrate that the DRRHA algorithm outperforms other algorithms in terms of average waiting time, turnaround time, and average response time.

A new method for job scheduling in cloud computing was introduced in the research article [20], offering a comprehensive framework for optimizing performance and resource management. The proposed priority-based technique addresses the challenge of fair job scheduling, ensuring equal distribution of resources and opportunities. To provide valuable insights for academics and decision makers, this research demonstrates the benefits of an efficiently optimized cloud computing ecosystem. Equitable task scheduling is critical in cloud computing, and our priority-focused method guarantees equitable resource distribution and task completion. The writer presented an online algorithm that enhances task scheduling in cloud computing systems using dynamic load management [21]. The proposed algorithm incorporates a Gaussian distribution of relevant parameters in its state space, ensuring consistency in input dimensions. Its reward function is designed to accomplish multiple objectives while adapting to varying task workloads for maximum efficiency.

The work in [22] evaluates the performance of task scheduling policies in heterogeneous computing environments through simulation-based experiments. The author considered the realistic capacities of edge and cloud data centers and evaluated RR, Shortest Job First, Min-Min, and Max-Min scheduling schemes. Results showed significant performance degradation of traditional task scheduling algorithms in heterogeneous edge–cloud environments. A new task scheduling approach, multi-queue priority (MQP), is proposed to balance task allocation for latency-sensitive and delay-tolerant applications in fog computing environments. Tasks are categorized as short and long, separate queues are maintained, and the preemption time slot is dynamically updated to reduce response time and address the starvation problem [23]. A new Optimized Round Robin (ORR) CPU Scheduling Algorithm is introduced to minimize the average waiting time, average turnaround time, and number of context switch and maximize the system throughput [24]. This algorithm results from training a learning model to predict the optimum TQ value. The ORR has been experimentally compared to RRSA and five other improved versions of RRSA. The results show that ORR outperforms in terms of performance optimization in time-sharing operating systems. The proposed ORR algorithm gives a new research direction for fair job scheduling in computer systems. The authors in [25] introduced a novel CPU scheduling algorithm called Adjustable Time Slice (ATS) based on RR scheduling. ATS improves performance and reduces time costs by clustering processes according to their execution time, weight, quantum, and context switches. Unlike traditional RR scheduling that uses a fixed time slice, ATS uses a dynamic approach to allocate time quantum by evaluating the resemblances among the processes within each group, where preference is given to shorter processes over longer ones.

The works above analyzed various Round Robin scheduling algorithms for improving system performance compared to traditional algorithms. Therefore, more efforts are required to improve performance in specific scenarios and develop new variants. This work proposes a unique approach for improving task execution in real-time systems by incorporating dynamic time quantum and priorities into the Round Robin scheduling algorithm. The key novelty of our approach lies in the dynamic adjustment of time slices based on the execution time and priority of each task. This results in more efficient resource utilization and ensures that critical tasks are completed on time. Additionally, we prioritize higher-priority tasks and execute them as soon as they arrive in the ready queue, which is also a unique feature in this field. Another unique feature of our approach is that when a high-priority process is executed and does not finish, its priority is decreased by one to prevent low-priority processes from starvation. To the best of our knowledge, no previous research has combined these elements of dynamic time quantum, priorities, and decreasing priority in the Round Robin scheduling algorithm. Our proposed approach offers a promising solution for optimizing task execution in real-time systems and provides an original contribution to the existing literature in this field.

3. Methodology

The proposed approach in this paper addresses the time quantum problem by enabling the operating system to dynamically adapt the TQ based on the burst times and priorities of the processes in the ready queue. The time quantum is determined by computing all the processes’ average burst times. The operating system determines the priority of a process. The operating system evaluates whether a process is critical and assigns it an appropriate priority. If a process is deemed critical, the operating system will prioritize it. On the other hand, if the process is not critical, it will be assigned a low priority. This prioritization helps the operating system efficiently allocate resources and ensure that critical processes are executed promptly.

3.1. Proposed Algorithm

In our proposed algorithm, Round Robin with Adaptive Priority Scheduling (RRAPS), once the new process enters the ready queue (RQ), the CPU loads the high-priority process for execution. If the ready queue is empty, the TQ is set to the burst time and assigned to the process for execution. However, if the ready queue is not empty, the time quantum is set as the average of the burst times of all the processes in the ready queue. The CPU then executes the process for the assigned time quantum. If the process terminates, it is marked as completed. Otherwise, if the process is not terminated and its priority is greater than 1, its priority is decreased by one and returned to the ready queue with its updated burst time. This allows lower-priority processes to have a chance to execute while ensuring that higher-priority processes still receive priority. However, if the process’s priority is already at the lowest level (i.e., 1), it is returned to the ready queue without priority changes. The process flow then repeats until all the processes in the ready queue are completed.

By combining priorities and dynamic time quantum, our algorithm aims to balance fairness and efficiency, allowing the system to prioritize critical processes while ensuring that all processes receive a fair share of CPU time. Lowering the priority of a process ensures that low-priority processes are given a fair share of the CPU and prevents high-priority processes from hogging the CPU and causing starvation. The RRAPS algorithm has several strong points, which are as follows:

• It allocates more CPU time to high-priority processes.
• It helps prevent starvation by periodically boosting the priority of low-priority processes.
• It fairly distributes the CPU time between processes.
• It is easy to implement and requires minimal changes to the existing Round Robin scheduling algorithm.

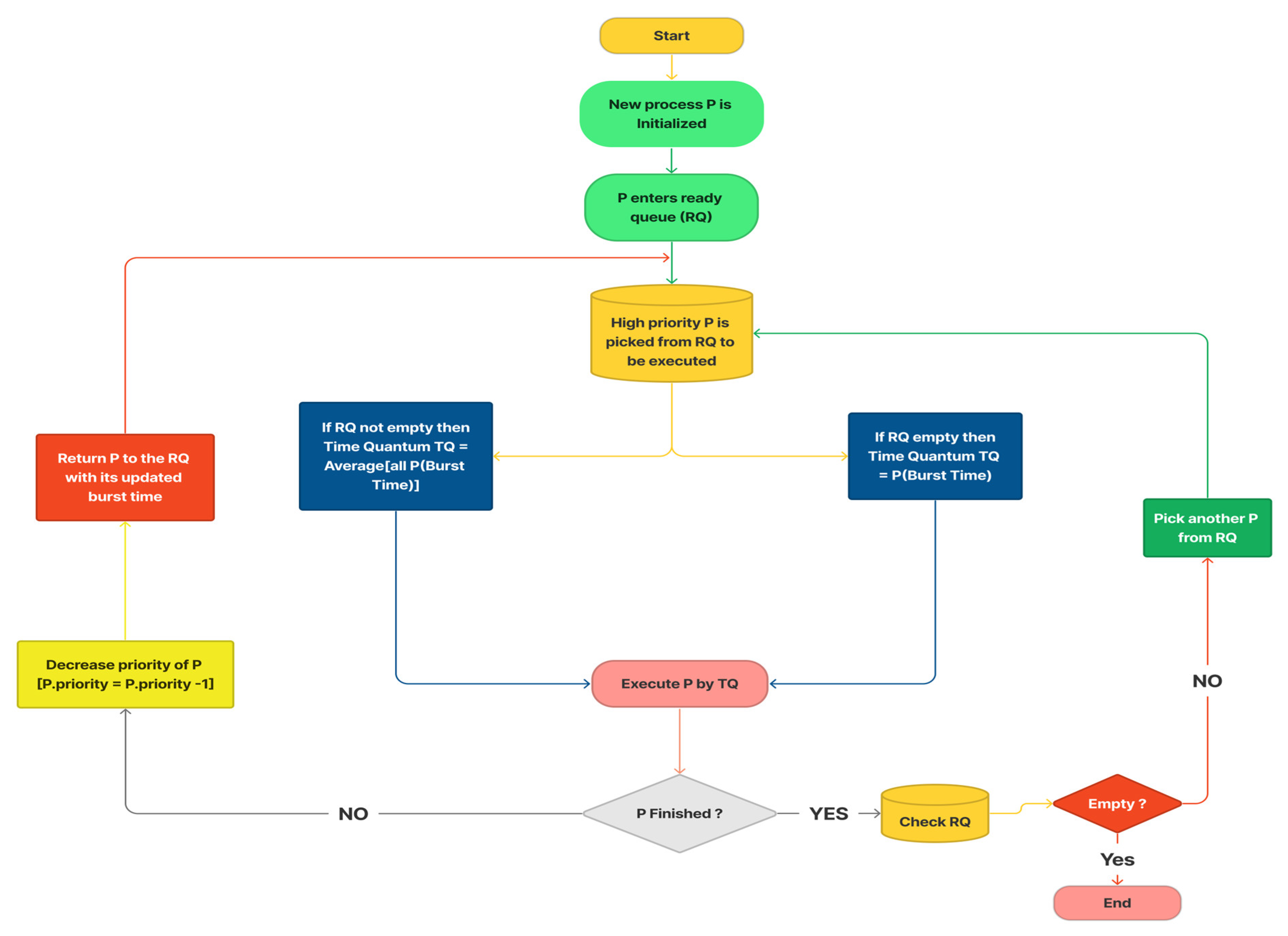
3.2. Pseudocode and Flow Chart

The methodology outlined previously can be precisely articulated through pseudocode in Algorithm 1 and a flow chart in Figure 1.

Algorithm 1 Round Robin with Adaptive Priority Scheduling (RRAPS)

1: New process P Initialized 2: Process P arrives in ready queue (RQ) 3: Load high-priority Process P from the RQ into the CPU to be executed 4: IF (RQ is empty)   Time_Quantum (TQ) = Process_Burst_Time (p_BT) End if 5: IF (RQ is not empty)   TQ = Average (burst_times_of_all_processes_in_ready_queue) End if 6: CPU executes P by TQ time 7: IF (P is terminated)   Marked as completed End if 8: IF (P is not terminated)   IF (p.priority is greater than 1) // 1 is the lowest priority. Priority cannot be less than 1.     p.priority = p.priority − 1     Return p to the RQ with its updated burst time   Else     Return p to the RQ with its updated burst time 9: IF (RQ is empty)   End algorithm Else   Load the next high-priority Process P from RQ into the CPU to be executed 10: Repeat steps 3 to 9

The operational flow of the RRAPS algorithm is shown in Figure 1. The RRAPS functioning is as follows. When a new process enters the ready queue, the CPU loads a high-priority process for execution. If the ready queue is empty, the time quantum will equal process burst time. If multiple processes exist in the queue, the time quantum is determined by averaging their burst times. If a process completes within this time, its priority is decreased and added back to the ready queue with an updated burst time. When a process finishes executing, it is marked as completed. The scheduler examines the available processes in the ready queue and picks the one with the highest priority for execution. This process repeats until all the processes in the ready queue have been executed.

4. Performance Validation

The proposed algorithm is validated on a Core i5 8th generation processor with 16 GB RAM. We developed a simulation tool for evaluating the effectiveness of our RRAPS algorithm in comparison to the conventional Round Robin algorithm in terms of performance. MATLAB 2022b was selected as the programming language for building the simulator due to its graphical representation capabilities. The simulation model receives a quadrant (N, AT, BT, P) as input, where N represents the number of processes, AT is an array that contains the arrival times of each process, BT is an array that contains the burst times of each process, and P is an array that includes the priorities of each process. In our implementation, we introduced a parameter called “decrease_priority”, which determines how much a process’s priority is decreased when it does not complete its execution. Specifically, we set the value of decrease_priority to −1, subtracting it from the process’s priority each time it completes its assigned time quantum without terminating. The RRAPS algorithm computes the waiting and turnaround time of the system with N processes.

To assess the efficacy of our proposed RRAPS algorithm, we will take a sample group of four processes with random burst times for four distinct cases, as used in [3]. The number of processes does not impact the algorithm’s outcome as it performs efficiently even when dealing with many processes. We will compare the results obtained from our RRAPS algorithm for each scenario with the traditional RR approach.

The findings demonstrated that the proposed algorithm was effective in the system by achieving a high utilization rate of the multi-core processor and decreasing the average waiting time of the processes. The simulation begins by creating an instance of the list class, which contains functions for inserting and deleting nodes in the list and calculating the processes’ waiting times and turnaround times. The program then generates a list of methods with random burst times, priorities, and arrival times and inserts them into the list using the insertNode() function.

Next, the program enters a loop until all processes have completed execution. Within the loop, the program uses the select_process_from_ready_queue() function to pick a process from the RQ and the determine_time_quantum() function to determine the time quantum for the selected process based on its priority. The program then uses the execute_process() function to execute the selected process for the determined time quantum. It adjusts the time quantum in the RQ based on the current workload using the adjust_time_quantum() function. If the selected process has completed execution, the program calculates its waiting and turnaround times using the returnWaiting() and returnTurnAround() functions. It removes the process from the list using the deleteNode() function. If the selected process has not completed execution, it is placed back in the ready queue using the insertNode() function, decreasing the process’s priority by one point. Finally, the program calculates the average waiting and turnaround times for all processes and outputs the simulation results.

4.1. Performance Metrics of Scheduling Algorithm

Scheduling algorithms optimize the use of resources by managing their allocation and are widely employed in various systems. One of the critical aspects of scheduling is the ability to measure the algorithm’s performance. This section will discuss three standard performance measures used in scheduling: turnaround time, waiting time, and context switching [10,15].

4.1.1. Turnaround Time

Turnaround time refers to the duration taken for a process to finish, starting from the moment it was submitted to the point of completion. It measures how long it takes for a method to complete and can determine the efficiency of a scheduling algorithm. Turnaround time is calculated by subtracting the submission time from the completion time of a process.

4.1.2. Waiting Time

Waiting time is defined as the time a process spends waiting in a queue before it is executed. It measures how long a process must wait before it can be executed and can determine the fairness of a scheduling algorithm. Waiting time is calculated by subtracting the submission time from the execution time of a process.

4.1.3. Context Switching

Context switching is defined as switching from one process to another. It measures how often the scheduler must switch between processes and can determine the overhead of a scheduling algorithm. Context switching can be costly in terms of both time and resources and can impact the overall performance of a system.

To sum up, evaluating the performance of scheduling algorithms requires assessing three key performance measures: waiting time, turnaround time, and context switching [8,9,10]. They can determine a scheduling algorithm’s efficiency, fairness, responsiveness, and overhead. In the next section, we will compare and contrast the results of various scheduling algorithms based on these performance measures.

4.2. Results and Discussion

In our simulation, we tested our RRAPS algorithm and its performance against traditional scheduling algorithms such as Round Robin with fixed time quantum and Round Robin with dynamic time quantum. In the simulation, we considered a scenario where the ready queue is filled with many processes, all with different burst times and priorities. The RRAPS algorithm uses a priority-based approach, where higher-priority processes are executed first, and lower-priority processes are executed later. In this way, important processes are prioritized and processed efficiently. For processes with the same priority, a decision is made on a first-come-first-served basis to decide which process is executed next. This ensures that processes that have been waiting for longer get executed first. To assess the algorithm’s effectiveness, we computed the processes’ mean turnaround time (in milliseconds) and mean waiting time (in milliseconds). We also counted the number of context switches that transpired while executing the processes. We then compared the results of the RRAPS algorithm to those of traditional Round Robin algorithms, such as Round Robin with fixed time quantum with no priorities and Round Robin with dynamic time quantum with no priorities.

Additionally, we conducted a comparative analysis of RRAPS and the AN algorithm, which utilizes dynamic time quantum [3]. The experiment aimed to assess the efficiency of two scheduling algorithms in a scenario with several processes in the ready queue. The findings demonstrated that the RRAPS algorithm outperformed other approaches, as evidenced by its lower average turnaround and waiting times. Note that we have priorities also associated with processes. We have defined the priority scale from 1 to 5, with 5 being the highest priority level and 1 being the lowest. So, the structure of the process will be a tuple containing two values; the first value is the burst time, and the second value is the priority (Process P = [burst time, priority]).

4.2.1. Case 1

Let us assume four processes arrived at time t = 0. P1 = [20, 5], P2 = [40, 2], P3 = [60, 4], P4 = [80, 5]. The comparison of the traditional Round Robin scheduling algorithm with RRAPS is shown in

Table 1. Analysis of Case 1 between different algorithms.

Algorithms	Turnaround Time (ms)	Waiting Time (ms)	Context Switching
RR with fixed time quantum without priority	111	65	9
RR with dynamic time slice without priority	97.3	52.6	5
AN Algorithm [3]	100	50	5
RRAPS	85.1	44.7	4

.

Table 1 compares our simulation results in MATLAB 2022b, comparing the performance of the RRAPS algorithm with other scheduling algorithms, including RR with fixed time quantum without priority, RR with dynamic time slice without priority, and the AN algorithm [3]. The performance is evaluated based on turnaround time (ms), waiting time (ms), and context switching. As shown in Table 1, RRAPS outperforms the other algorithms in terms of turnaround, waiting times, and context switching, achieving a turnaround time of 85.1 ms, a waiting time of 44.7 ms, and only four instances of context switching.

4.2.2. Case 2

Let us assume four processes arrived at time t = 0. P1 = [20, 5], P2 = [40, 5], P3 = [60, 5], P4 = [80, 5]. All the processes have the same priority. Results are provided in

Table 2. Comparison of Case 2 between different algorithm methodologies.

Algorithms	Turnaround Time (ms)	Waiting Time (ms)	Context Switching
RR with fixed time quantum without priority	111	65	9
RR with dynamic time slice without priority	97.3	52.6	5
AN Algorithm [3]	100	50	5
RRAPS	97.3	52.6	5

.

In the second case, all four processes have the same priority. The results of the Round Robin with a fixed time slice are the same as the results as the algorithm that does not consider the process’s priority, but simply assigns a specified time slice to each process, regardless of priority. This results in nine context switches, a total turnaround time of 111, and a waiting time of 65. In this case, the performance of the Round Robin with dynamic time slice and RRAPS algorithms is the same, as all the processes have the same priority and will be executed in a first-come-first-served manner. The main difference between the two algorithms is that RRAPS uses adaptive priority scheduling.

In contrast, in Round Robin with a dynamic time slice, RRAPS and the AN algorithm adjust the time slice dynamically based on the process’s burst time. In this scenario, the order of process execution is not impacted by the time slice. As a result, the frequency of context switches and turnaround time remain constant. However, the AN algorithm [3] outperforms other algorithms in terms of waiting time.

4.2.3. Case 3

Let us assume five processes arrived at different times. P1 = [22, 4] and arrived at time = 0, P2 = [35, 1] and arrived at time = 2, P3 = [61, 2] and arrived at time = 4, P4 = [75, 5] and arrived at time = 6, and P5 = [96, 3] and arrived at time = 8. The results of Case 3 are provided in

Table 3. The outcome of Case 3 among alternative algorithm techniques.

Algorithms	Turnaround Time (ms)	Waiting Time (ms)	Context Switching
RR with fixed time quantum without priority	119.1	72.7	13
RR with dynamic time slice without priority	100.4	59.1	7
AN Algorithm [3]	103	55	6
RRAPS	83.3	47	5

.

Table 3 compares the performance of four scheduling algorithms: Round Robin with fixed time quantum without priority (RR with fixed time quantum), Round Robin with dynamic time slice without priority (RR with dynamic time slice), the AN algorithm [3], and RRAPS when applied to five processes that arrived at different times. The experimental results demonstrate that the RRAPS algorithm performed better than the other algorithms, achieving the lowest average turnaround time of 83.3, the lowest average waiting time of 47, and only five context switches. The Round Robin scheduling algorithm with dynamic time slice but without priority had the second best performance, with an average turnaround time of 100.5, an average waiting time of 59.1, and seven context switches. In contrast, the AN algorithm has a turnaround time of 103 and a waiting time of 55, with six context switches. The Round Robin with a fixed time quantum without a priority algorithm performs worst, with the highest average turnaround time of 119.1, the highest average waiting time of 72.7, and 13 context switches.

4.2.4. Case 4

Let us assume ten processes arrived at different times. P1 = [22, 4] and arrived at time = 0, P2 = [35, 1] and arrived at time = 2, P3 = [61, 2] and arrived at time = 4, P4 = [75, 5] and arrived at time = 6, P5 = [96, 3] and arrived at time = 8, P6 = [18, 4] and arrived at time = 10, P7 = [30, 1] and arrived at time = 12, P8 = [65, 2] and arrived at time = 14, P9 = [10, 5] and arrived at time = 9, and P10 = [56, 4] and arrived at time = 13.

Table 4. Assessment of Case 4 results for different algorithm strategies.

Algorithms	Turnaround Time (ms)	Waiting Time (ms)	Context Switching
RR with fixed time quantum without priority	170.1	112.7	18
RR with dynamic time slice without priority	145.5	97.1	13
AN Algorithm [3]	120	75	11
RRAPS	105	79.8	10

provides the assessment of Case 4 for various algorithms.

In Case 4, the simulation scenario increases the number of processes to ten, arriving at different times. Table 4 presents the performance data of four scheduling algorithms: Round Robin with fixed time quantum without priority (RR with fixed time quantum), Round Robin with dynamic time slice without priority (RR with dynamic time slice), the AN algorithm [3], and RRAPS when applied to ten processes. The RRAPS algorithm combines the principles of Round Robin scheduling with priority scheduling. Each process is assigned a priority value, and the scheduler selects the process with the highest priority to execute. The RRAPS algorithm achieves the best performance among the three scheduling algorithms presented, with the lowest turnaround time of 105 but a waiting time of 79.8, slightly larger than the waiting time of the AN algorithm, and ten context switches.

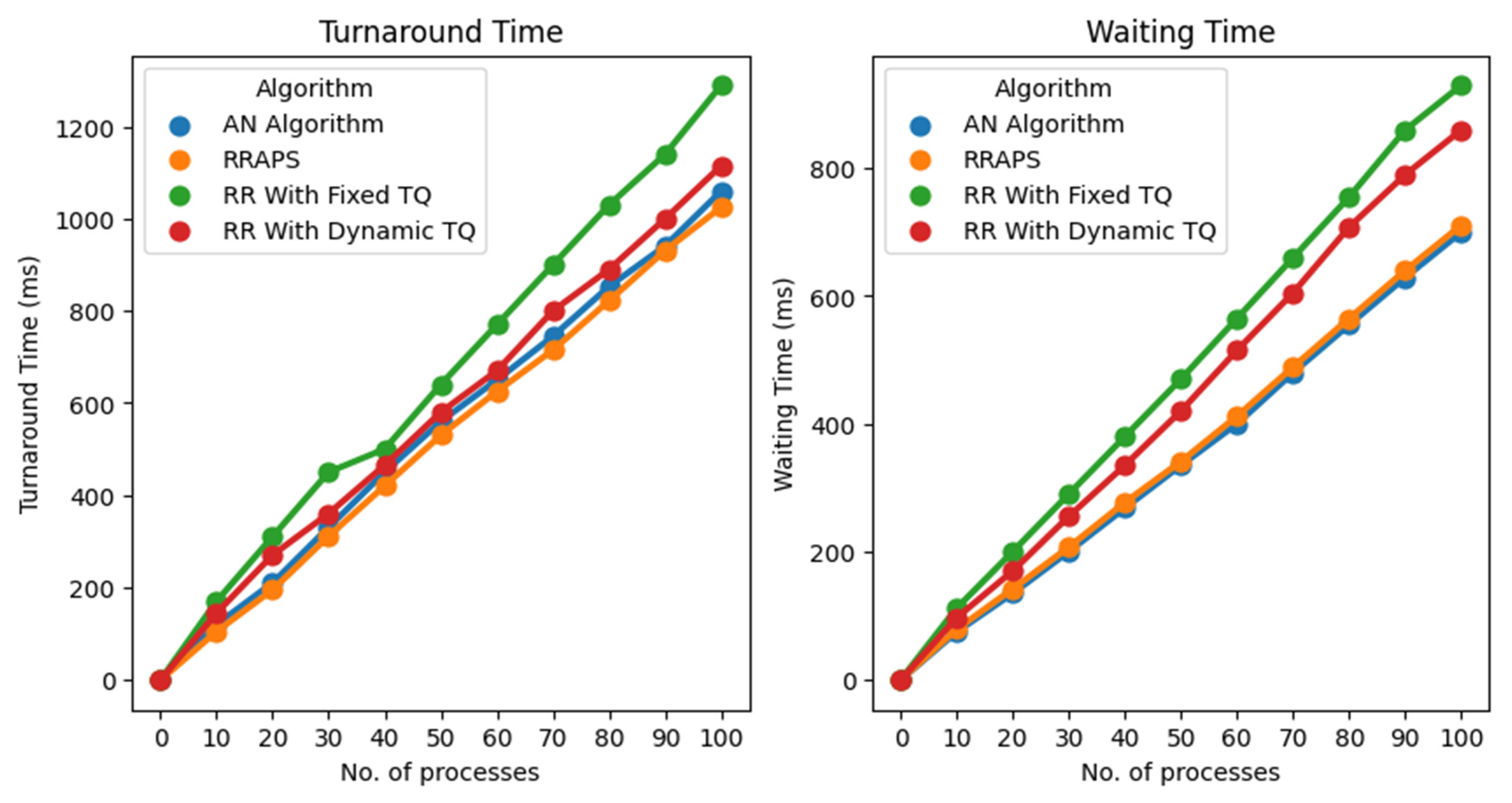
The RRAPS algorithm outperforms traditional RR methods, significantly improving turnaround and waiting times as shown in Figure 2. Turnaround time measures how long it takes for a process to complete execution, from the time of its submission to completion. Waiting time measures how long a process has to wait before it can start execution, from the time of its submission to its execution. The proposed RRAPS algorithm results in shorter turnaround times and waiting times than traditional Round Robin techniques and the AN algorithm [3]. However, the AN algorithm [3] exhibited superior waiting times. This could be attributed to its equitable treatment of all processes, without any distinction between critical and non-critical ones. The RRAPS algorithm, however, considers priorities in its scheduling decisions. Its primary goal is to prevent high-priority and critical processes from experiencing wait times in the ready queue.

The performance of RRAPS using a diverse set of 100 processes, including high-priority and high-burst-time processes and low-priority and low-burst-time processes, is provided in Figure 3. Our findings showed that RRAPS outperformed other algorithms in terms of turnaround time, highlighting its effectiveness in real-world scenarios. However, it was also noted that the AN algorithm [3] exhibited slightly better performance in terms of waiting time. This can be attributed to the AN algorithm’s equal treatment of all processes, without differentiating between critical and non-critical ones. In RRAPS, low-priority processes must wait longer for high-priority processes to finish execution, leading to longer waiting times. Overall, our results demonstrate the advantages and limitations of these different algorithms and suggest that RRAPS can be a valuable tool for optimizing process scheduling in complex systems.

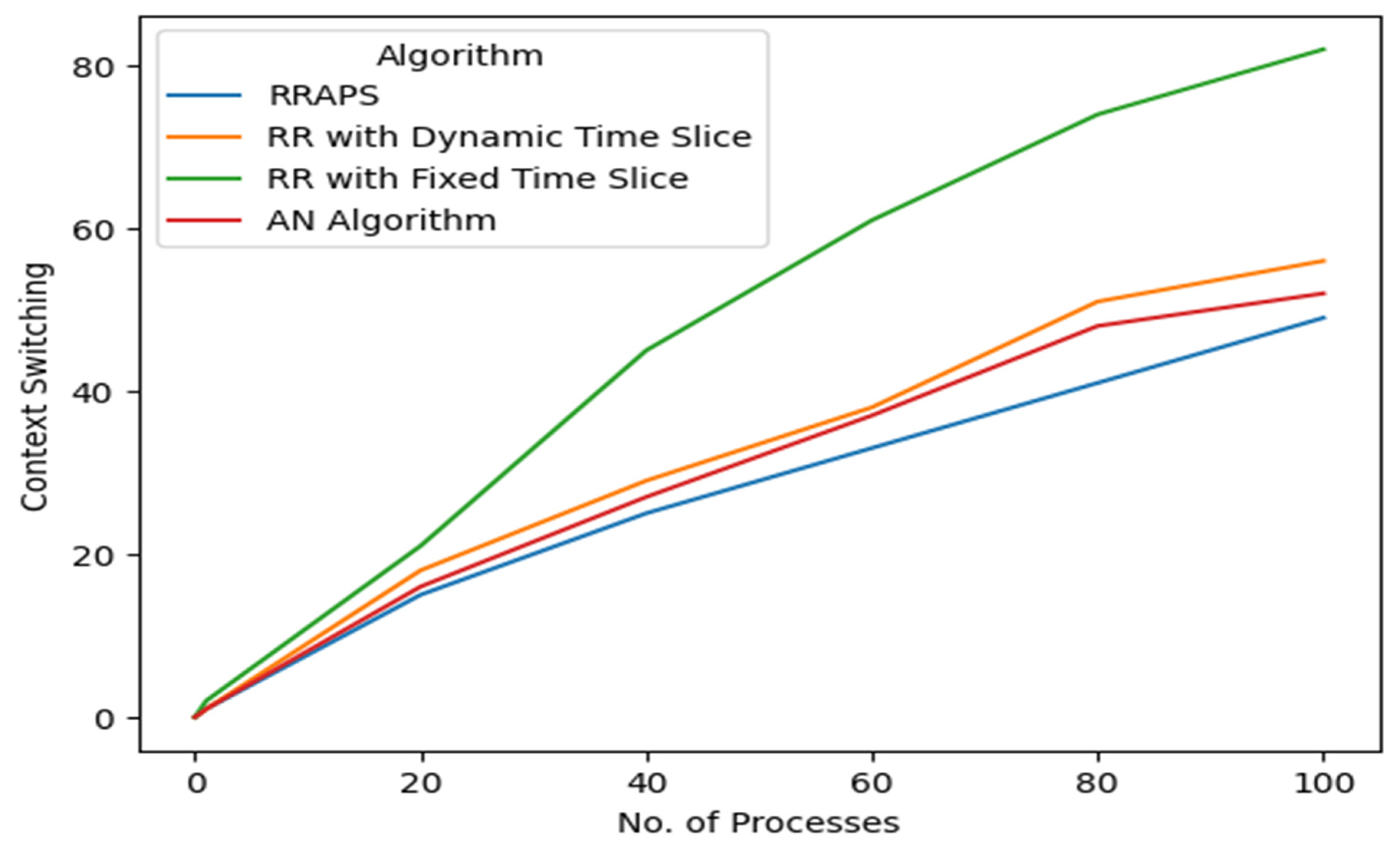
4.3. Comparative Analysis of Context Switching

Context switching saves a process’s current state and restores another process’s saved state. It is a costly operation that incurs a significant overhead on the operating system, as it involves saving and restoring the processor’s state, memory, and other resources. When the number of processes is high, the number of context switches increases, leading to a higher overhead on the operating system. In this case, the operating system’s performance can be affected as the scheduler spends more time between processes and less time executing them. However, as the number of processes decreases, the number of context switches will also decrease significantly. This leads to less overhead on the operating system and, therefore, to better performance. However, it is important to note that it also has its downsides, as a low number of processes running simultaneously could lead to less efficient use of system resources.

The operating system will have less CPU and memory utilization, potentially leading to less efficient use of the system’s resources and a slower response time for the user. Traditional variants of Round Robin scheduling algorithms interrupt and reassign processes, even when only one process is in the ready queue. The operating system allocates a fixed TQ to process. After the quantum expires, the process is interrupted and assigned the same TQ to continue and complete its execution. This can lead to additional unnecessary context switches, as shown in Figure 4, which can add significant overhead to the operating system.

On the other hand, our newly proposed RRAPS algorithm solves this problem by equating the time quantum with the remaining burst time of the process. This means that when there is only a single process in the ready queue, the time quantum will equal the time the process needs to complete its execution, thus avoiding any additional unnecessary context switches. This eliminates the over-scheduling problem and reduces the operating system’s overhead. The new algorithm can be considered more efficient than the traditional variants of the Round Robin scheduling algorithm, as it adjusts the time quantum based on the process’s requirements and eliminates unnecessary context switches.

5. Conclusions and Future Directions

The proposed Round Robin with Adaptive Priority Scheduling (RRAPS) algorithm combines two well-established scheduling techniques: priority scheduling and Round Robin scheduling. The algorithm prioritizes the execution of processes by assigning a priority to each one. When a higher-priority process arrives in the ready queue, it is placed at the front of the queue to be executed as soon as possible. This ensures that essential tasks are completed promptly and meet necessary deadlines. The algorithm also uses dynamic time quantum scheduling to determine the sequence of process execution and to adjust the amount of time allocated to each process based on their needs and the current workload. The mean burst time of all processes in the ready queue is used to calculate the dynamic time quantum. This allows the system to respond to changing conditions and maintain high levels of efficiency. This approach is essential because it adapts to different scenarios and RRPAS workloads, giving a chance to the process that requires more time to finish while ensuring fair access to the CPU by all processes in the RQ. The RRAPS method combines a dynamic time quantum and priorities to balance fairness and efficiency. It prioritizes critical processes while also ensuring that all processes receive equal CPU time, making it an improved scheduling method. The major drawback of the RRAPS algorithm is the potential for starvation, where a process with a low priority may continue to run for an extended duration, causing the starvation of processes with a higher priority.

In the near future, the RRAPS algorithm has potential for further developments, such as integration with other scheduling algorithms, such as Multi-Level Feedback Queue (MLFQ) or Earliest Deadline First (EDF), to enhance performance and adaptability to handle scheduling in multi-core or distributed systems, where processes can execute simultaneously on different nodes. This will involve developing a mechanism for coordinating the scheduling of processes across other cores or nodes. The RRAPS can be applied in real-time embedded and multimedia systems to ensure fast response time and predictability.