Using Metaheuristics (SA-MCSDN) Optimized for Multi-Controller Placement in Software-Defined Networking
Abstract
1. Introduction
- Annealing: Refers to heating a solid to a sufficiently high temperature so that its molecules are arranged randomly. Then, the temperature is gradually reduced, so once cooled, the molecules of the solid are arranged in a lower-energy stable state.
- Heating processing: Whereby the thermal movement of particles is enhanced, eliminating any non-uniform state that may exist in the system.
- Thermal processing: In closed systems that exchange heat with the environment without a change in temperature, the state of the system is altered without constraint as free energy diminishes. When free energy reaches a minimum value, the system achieves a state of harmony.
- Cooling processing: The thermal movement and arrangement of particles are gradually debilitated, and the vitality of the system is gradually reduced, resulting in a low-energy crystal structure. SA is based on the principles of statistical mechanics.
2. Related Work
3. Problem Statement
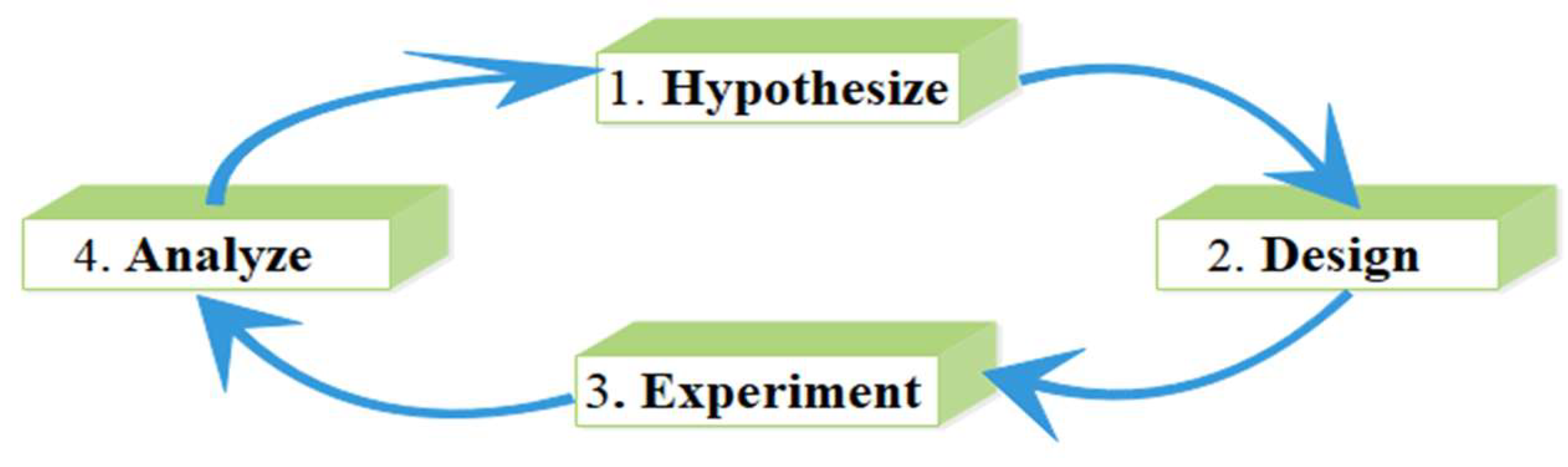
4. The Proposed Work
4.1. Network Construction
4.2. Optimal Controller Selection
| Algorithm 1 Pseudocode FA for Optimal Controller Selection |
| Initialize: |
| Formulate objective function using: |
| Formulate controller absorption coefficient using: ; |
| Initialize absorption coefficient using: |
| While all do |
| Compute controller feature distance using: |
| For to n (all n controllers) |
| For to n (all n controllers) |
| If (), select over |
| End if |
| Update the |
| End for |
| End for |
| Rank the controller and find the current best controller |
| End while |
4.3. Multi-Controller Placement Using Simulated Annealing Algorithm
| Algorithm 2 Pseudocode of the proposed SA-MCSDN algorithm |
| Initialized the objective function, (). |
| Initialize parameters, L, T, T0, and α, ; |
| Set T = T0, V = 3 × D |
| Generate initial, S, ; |
| Calculate objective function, (); |
| S = (); |
| itr = 0; |
| While (itr < ) |
 |
5. Experimental Results
5.1. Simulation Setup
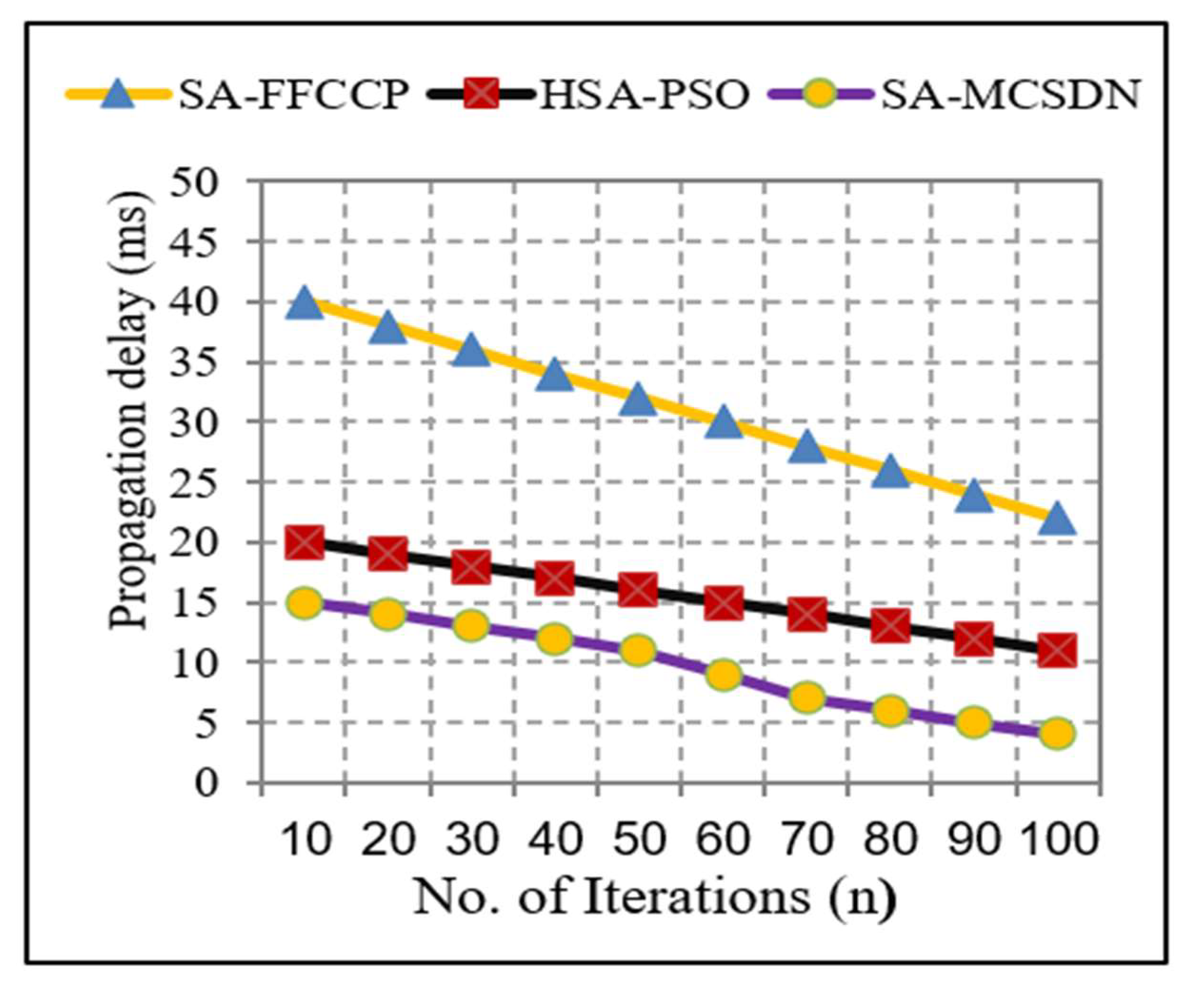
5.2. Comparative Analysis between HAS-PSO and SA-MCSDN Algorithms
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aravind, P.; Varma, G.S.; Reddy, P.P. Simulated annealing based optimal controller placement in software defined networks with capacity constraint and failure awareness. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 5721–5733. [Google Scholar] [CrossRef]
- Sahoo, K.S.; Sahoo, B.; Dash, R.; Jena, N. Optimal controller selection in software defined network using a greedy-SA algorithm. In Proceedings of the 2016 3rd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 16–18 March 2016. [Google Scholar]
- Guo, W.G.; Luo, J.; Han, S.; Zhang, Z.Y.; Ge, Y. Research on Feedback-Sensitive Resource Mapping Algorithm Based On Simulated Annealing in SDN. Procedia Comput. Sci. 2019, 154, 96–101. [Google Scholar] [CrossRef]
- Guo, A.; Yuan, C. Network Intelligent Control and Traffic Optimization Based on SDN and Artificial Intelligence. Electronics 2021, 10, 700. [Google Scholar] [CrossRef]
- He, M.; Varasteh, A.; Kellerer, W. Toward a Flexible Design of SDN Dynamic Control Plane: An Online Optimization Approach. IEEE Trans. Netw. Serv. Manag. 2019, 16, 1694–1708. [Google Scholar] [CrossRef]
- Tahmasebi, S.; Rasouli, N.; Kashefi, A.H.; Rezabeyk, E.; Faragardi, H.R. SYNCOP: An evolutionary multi-objective placement of SDN controllers for optimizing cost and network performance in WSNs. Comput. Netw. 2021, 185, 107727. [Google Scholar] [CrossRef]
- Liao, Z.; Chen, C.; Ju, Y.; He, C.; Jiang, J.; Pei, Q. Multi-Controller Deployment in SDN-Enabled 6G Space–Air–Ground Integrated Network. Remote Sens. 2022, 14, 1076. [Google Scholar] [CrossRef]
- Zilberman, A.; Haddad, Y.; Erlich, S.; Peretz, Y.; Dvir, A. SDN Wireless Controller Placement Problem-The 4G LTE-U Case. IEEE Access 2021, 9, 16225–16238. [Google Scholar] [CrossRef]
- Tahmasebi, S.; Safi, M.; Zolfi, S.; Maghsoudi, M.R.; Faragardi, H.R.; Fotouhi, H. Cuckoo-PC: An Evolutionary Synchronization-Aware Placement of SDN Controllers for Optimizing the Network Performance in WSNs. Sensors 2020, 20, 3231. [Google Scholar] [CrossRef]
- Luong, D.K.; Ali, M.; Hu, Y.F.; Li, J.P.; Asif, R.; Abdo, K. Simulated Annealing-Based Multilink Selection Algorithm in SDN-Enabled Avionic Networks. IEEE Access 2021, 9, 145301–145316. [Google Scholar] [CrossRef]
- Li, C.; Jiang, K.; Luo, Y. Dynamic placement of multiple controllers based on SDN and allocation of computational resources based on heuristic ant colony algorithm. Knowl.-Based Syst. 2022, 241, 108330. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, W.; Liu, J. Joint Placement of Gateways and Controllers in SDN-Enabled Space-Ground Integration Network. In Proceedings of the Asia Conference on Electrical, Power and Computer Engineering, Shanghai, China, 22–24 April 2022. [Google Scholar]
- Yan, B.; Liu, Q.; Shen, J.; Liang, D. BatchUp: Achieve fast TCAM update with batch processing optimization in SDN. Futur. Gener. Comput. Syst. 2022, 134, 93–106. [Google Scholar] [CrossRef]
- Luong, D.K.; Hu, Y.-F.; Li, J.-P.; Ali, M. Metaheuristic Approaches to the Joint Controller and Gateway Placement in 5G-Satellite SDN Networks. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020. [Google Scholar]
- Yong, B.; Muqing, W.; Jing, S.; Min, Z. Optimization Strategy of SDN Control Deployment Based on Simulated Annealing-Genetic Hybrid Algorithm. In Proceedings of the 2018 IEEE 4th International Conference on Computer and Communications (ICCC), Chengdu, China, 7–10 December 2018. [Google Scholar]
- Dvir, A.; Haddad, Y.; Zilberman, A. The controller placement problem for wireless SDN. Wirel. Netw. 2019, 25, 4963–4978. [Google Scholar] [CrossRef]
- Kanodia, K.; Mohanty, S.; Sahoo, B.; Kurroliya, K. HPSOSA: A hybrid approach in resilient controller placement in SDN. In Proceedings of the 2020 International Conference on Emerging Trends in Information Technology and Engineering (ic-ETITE), Vellore, India, 24–25 February 2020. [Google Scholar]
- Misni, F.; Lee, L.S.; Jaini, N.I. Multi-objective hybrid harmony search-simulated annealing for location-inventory-routing problem in supply chain network design of reverse logistics with CO2 emission. J. Phys. Conf. Ser. 2021, 1988, 012054. [Google Scholar] [CrossRef]
- Misni, F.; Lee, L.S.; Seow, H.-V. Hybrid Harmony Search-Simulated Annealing Algorithm for Location-Inventory-Routing Problem in Supply Chain Network Design with Defect and Non-Defect Items. Appl. Sci. 2020, 10, 6625. [Google Scholar] [CrossRef]
- Shaikh, T.A.; Ali, R. An intelligent healthcare system for optimized breast cancer diagnosis using harmony search and simulated annealing (HS-SA) algorithm. Inform. Med. Unlocked 2020, 21, 100408. [Google Scholar] [CrossRef]
- Rego, A.; Garcia, L.; Sendra, S.; Lloret, J. Software Defined Network-based control system for an efficient traffic management for emergency situations in smart cities. Futur. Gener. Comput. Syst. 2018, 88, 243–253. [Google Scholar] [CrossRef]
- Elbasheer, M.O.; Aldegheishem, A.; Lloret, J.; Alrajeh, N. A QoS-Based routing algorithm over software defined networks. J. Netw. Comput. Appl. 2021, 194, 103215. [Google Scholar] [CrossRef]
- Radam, N.S.; Al-Janabi, S.; Jasim, K.S. Using metaheuristics to improve the placement of multi-controllers in software-defined networking enabled clouds. Period. Eng. Nat. Sci. 2022, 10, 79–93. [Google Scholar] [CrossRef]
- Radam, N.S.; Al-Janabi, S.T.F.; Jasim, K.S. Multi-Controllers Placement Optimization in SDN by the Hybrid HSA-PSO Algorithm. Computers 2022, 11, 111. [Google Scholar] [CrossRef]
- Seyedkolaei, A.A.; Seno, S.A.H.; Budiarto, R. Kernel Search-Framework for Dynamic Controller Placement in Software-Defined Network. Comput. Mater. Contin. 2021, 68, 3391–3410. [Google Scholar] [CrossRef]
- Rout, S.; Sahoo, K.S.; Patra, S.S.; Sahoo, B.; Puthal, D. Energy Efficiency in Software Defined Networking: A Survey. SN Comput. Sci. 2021, 2, 308. [Google Scholar] [CrossRef]
- Haque, M.R.; Tan, S.C.; Yusoff, Z.; Nisar, K.; Kwang, L.C.; Kaspin, R.; Chowdhry, B.S.; Buyya, R.; Majumder, S.P.; Gupta, M.; et al. Automated Controller Placement for Software-Defined Networks to Resist DDoS Attacks. Comput. Mater. Contin. 2021, 68, 3147–3165. [Google Scholar]
- Vestin, J. SDN-Enabled Resiliency, Monitoring and Control in Computer Networks. Ph.D. Dissertation, Karlstads Universitet, Karlstad, Sweden, 2020. [Google Scholar]
- Xu, H.; Chai, X.; Chen, H. A Collaborative Approach based on Competitive Game for Multi-Controller Placement in SDN. In Proceedings of the 2022 IEEE 25th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Hangzhou, China, 4–6 May 2022. [Google Scholar]
- Lu, J.; Zhang, Z.; Hu, T.; Yi, P.; Lan, J. A Survey of Controller Placement Problem in Software-Defined Networking. IEEE Access 2019, 7, 24290–24307. [Google Scholar] [CrossRef]
- Lysko, A.; Mwangama, J.; Mamushiane, L. Controller placement optimization for Software Defined Wide Area Networks (SDWAN). ITU J. Futur. Evol. Technol. 2021, 2, 45–66. [Google Scholar] [CrossRef]
- Lavacca, F.G.; Salvo, P.; Ferranti, L.; Speranza, A.; Costantini, L. Performance Evaluation of 5G Access Technologies and SDN Transport Network on an NS3 Simulator. Computers 2020, 9, 43. [Google Scholar] [CrossRef]
- Obaida, T.H.; Salman, H.A. A novel method to find the best path in SDN using firefly algorithm. J. Intell. Syst. 2022, 31, 902–914. [Google Scholar] [CrossRef]




| Study Ref./No | Drawbacks and Weaknesses of Literature Review | Objective(s) | SA-MCSDN Approach |
|---|---|---|---|
| [1] | Focus only on latency, reducing worst-case latency between S2C, and reducing the execution time for large networks; failures and limitations on control capabilities are expected, and this model produces a near-perfect solution. The futuristic view of the researcher is that this work can be expanded by making the position of the controllers and the task of switching energetic. Moreover, controller latency can be included within the objective function and considered as a load-balancing aspect. | SA-FFCCPP-based optimized solution for CPP in SDN. | The MCPP was resolved for distribution simulation, and execution time between S2C and C2C was solved for all metrics. See Table 2. |
| [2] | Handles a limited number of resources within the network, and digital controllers require that all network elements within the network be covered in an optimal manner. The primary criterion was to reduce the distance between all nodes and selected controllers by a greedy SA algorithm. | Implement a greedy SA algorithm to solve the CPP; the goal was to reduce the distance between all selected nodes and controllers. | The primary criterion was to reduce the distance between all nodes and selected controllers and to reduce the execution time by verifying all metrics. |
| [3] | Focused on the resource mapping model. | Feedback-sensitive resource mapping based on an SA algorithm in an SDN. | SA-MCSDN was used to solve the MCPP. |
| [4] | Used machine learning and focused only on network traffic analysis, traffic prediction, and fault diagnosis. | SA algorithm used for path optimization for network control. | SA-MCSDN was used to solve the MCPP. |
| [5] | Focused only on the flexibility dynamic control plane (DCPP) to reduce the total cost without using metrics for measure scalability. | Flexible design of DCPP in an SDN by an online SA algorithm. | SA-MCSDN was used to solve the MCPP. |
| [6] | SA and QA performance is significantly more scalable with higher synchronization cost. | Multi-objective placement evolution of SDN controllers to improve cost and network performance in WSN. | The SA-MCSDN method was used to solve the MCPP in terms of metrics, performance, and cost. |
| [7] | One approximate comparison method was used (n-k-means vs. n times k-means) running a time clustering algorithm, which increased performance by 17.7%, whereas the controller optimized load dynamic strategy (COLDS) increased performance by approximately 7.71%. | Multi-controller deployment of 6G SAGIN in an SDN by an SA algorithm. | The running time of the algorithm (SA-MCSDN) increased by 3.33%. |
| [8] | Fourth-generation long-term evolution (4G LTE-Unlicensed) was implemented with LTE-U-CPP-RS ray-shooting heuristic; the simulation results revealed better and more accurate results than the LTE-U-CPP-SA heuristic. | The use of LTE-U-CPP-SA and LTE-U-CPP-RS algorithms to solve WCPP based on a 4G LTE network with SBI. | SA-MCSDN was used to solve the MCPP. |
| [9] | Experiments showed that Cuckoo-PC surpasses both SA and QA in terms of a range of performance indicators. Cuckoo-PC accomplishes less than 1% deviation in a discernibly shorter time than SA. | Cuckoo placement of controllers (Cuckoo-PC algorithm) in an SDN, employing SA and QA to optimize the network performance in WSNs. | SA-MCSDN was used to solve the MCPP. |
| [10] | By learning with AHP-SA and SA-SWNO, the execution time can be reduced to optimize the weights of factors. | SA-based multilink choice calculation algorithm in SDN-enabled avionic networks. | Without learning, SA-MCSDN can decrease the execution time and encourage optimization of the components. |
| [11] | Focused on delay, C2C, and S2C from where link failure originated, as well as reliability for CPP. Used two algorithms (spectral clustering and ant colony) to generate an adaptive allocation scheme for computing resources. | Dynamic placement of MCSDN and allocation of computational resources based on a heuristic ant colony algorithm. | According to the results of the SA-MCSDN optimized algorithm, it achieved the best performance solving the problem of delay and reliability. |
| [12] | Used DBSAA to achieve nearly optimum performance in a shorter runtime for the joint placement problem of gateways and controllers. | Joint placement of gateways and controllers in an SDN-enabled space–ground integration network. | The SA-MCSDN algorithm processes the appropriate positioning of the controllers of C2C and S2C position and handles the delay time and reliability, i.e., to extend the network efficiency and performance. |
| [13] | Used HRIA based on SA and a greedy algorithm to search for the approximate optimal solution and to alleviate the high time cost of the rule-update process. | To achieve fast ternary content, addressable memory (TCAM) update with BatchUp processing optimization in an SDN for two stages. | The SA-MCSDN algorithm was used to search for the optimal performance with a shorter runtime time of the update process and a shorter distance between S2C and C2C. |
| [14] | Used a combination of GA and SA with a clustering hybrid algorithm. Used double SA to quickly search for a better solution and quickly find the optimal path to achieve improved flexibility, scalability, reliability, and latency with a minimal tradeoff in terms of runtime. | SA of joint controller and gateway placement in 5G-satellite SDN networks. | The SA-MCSDN single optimized algorithm was used to search for the optimal performance with less runtime. |
| [15] | The SA-GA hybrid algorithm solves the CPP by locating wireless controllers in an SDN. It can reduce the cost of cost controller deployment by guaranteeing the delay between S2Cs reduces deployment time. | Optimization of SDN controller deployment based on an SA-GA hybrid algorithm. | The SA-MCSDN single algorithm achieved a short delay time guarantee for communication between S2C and C2C with deployment based on FA. |
| [16] | Used SA and GA to locate wireless controllers and solve the CPP in an SDN using metrics of latency, potential link failure, and transparency in the case of an SBI wireless interface S2C. | CPP for a wireless software-defined network (WSDN). | The SA-MCSDN algorithm was optimized to solve the MCPP between S2C and C2C. |
| [17] | Used the HPSOSA algorithm to solve CPP-SDN flex mode and minimize the average latency to address the issue of node failure or link failure. | HPSOSA hybrid approach to solve CP-SDN. | The SA-MCSDN single algorithm was optimized to solve the MCPP between S2C and C2C. |
| [18] | MOHS-SA algorithm was used to find the optimally Pareto-distributed solutions, for example, to reduce the total cost of operating facilities, improve vehicle mileage, and reduce the cost of CO2 emissions. | Multi-objective hybrid algorithm (MOHS-SA) to solve a location-inventory-routing issue in the supply chain arrangement plan of inverted coordinates with CO2 emissions. | The SA-MCSDN algorithm was optimized to solve the MCPP between S2C and C2C. |
| [19] | Used a hybrid (HS-SA) algorithm that considers dynamic values of HMCR and PMR with local optimization techniques for hybridization and probability based on SA. | Hybrid algorithm(HS-SA) to solve a location-inventory-routing issue in a supply chain network plan (SCN) with deformity and non-defect objects. | The SA-MCSDN single algorithm was optimized for probability Pr (∆F). |
| [20] | Used the HS-SA algorithm for precise and accurate breast cancer detection in an intelligent healthcare system for optimized diagnosis. | An intelligent healthcare framework to optimize breast cancer screening using an HS-SA algorithm. | The SA-MCSDN algorithm was optimized to solve the MCPP between S2C and C2C. |
| [21] | Focused on energy-consuming traffic management in emergency situations. | SDN-based control system for efficient traffic management for emergency situations in smart cities. | SA-MCSDN was used to solve the MCPP. |
| [22] | Used a flow-based routing strategy for video service routing with a focus on addressing two constraints: packet loss and bandwidth. | A QoS-based routing algorithm in an SDN for video surveillance. | SA-MCSDN was used to solve the MCPP. |
| Performance Metrics | SA-FFCCPP | HSA-PSO | SA-MCSDN |
|---|---|---|---|
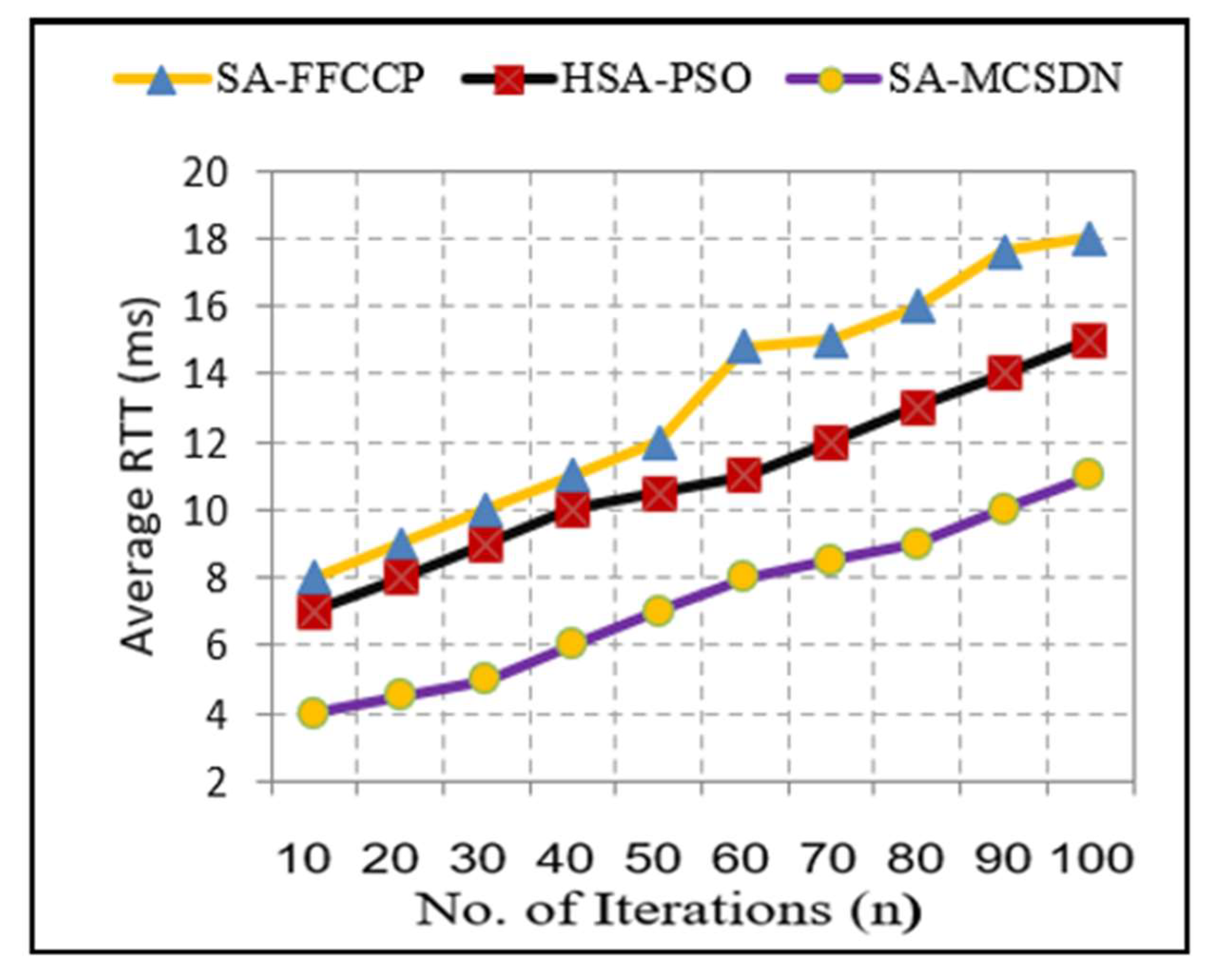
| Propagation delay | 31.3 | 15.6 | 4.80 ms |
| Average RTT | 10.95 | 7.5 | 6.05 ms |
| Matrix of time session | 246.5 | 203.5 | 113.13 |
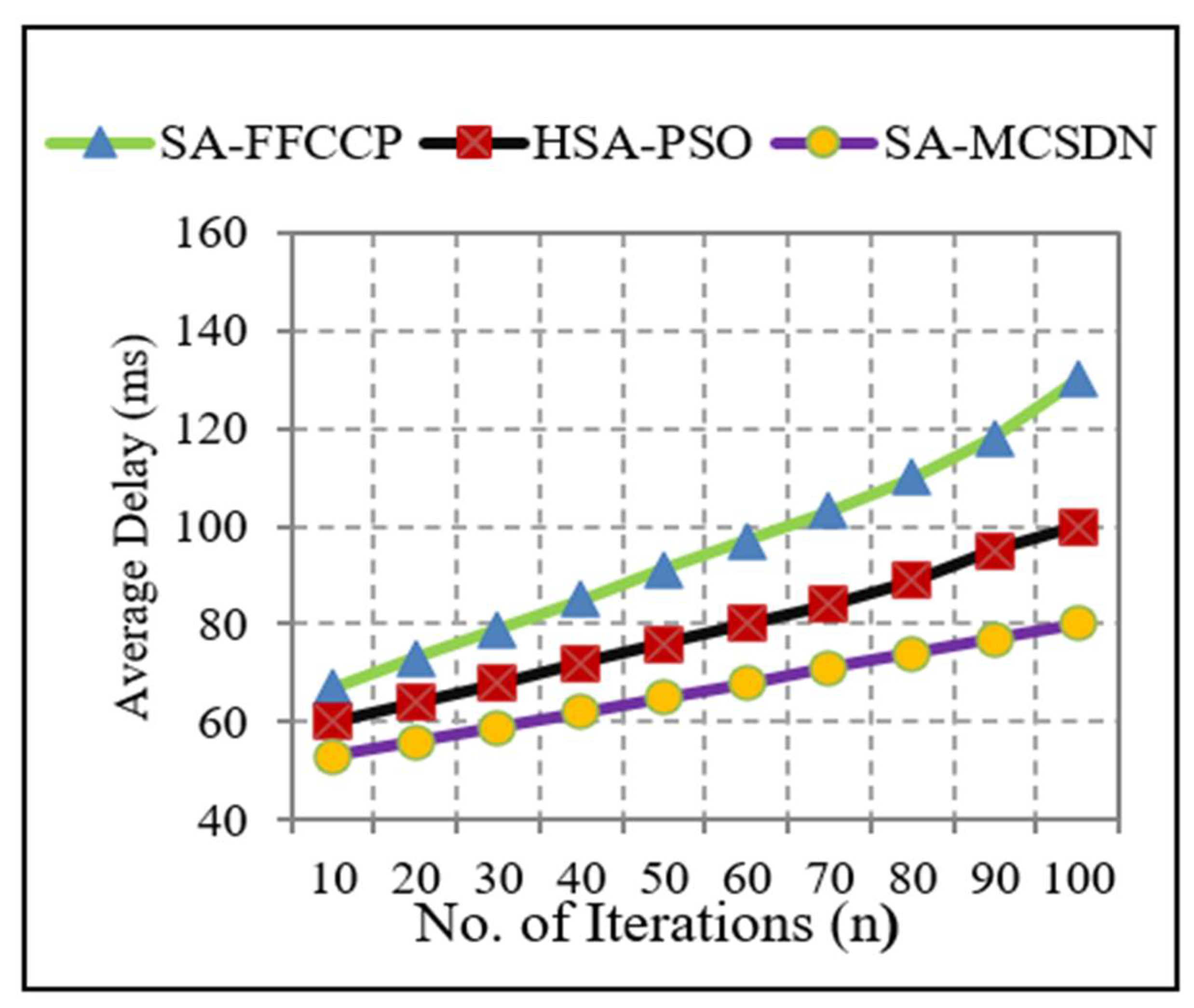
| Average delay | 95.3 | 78.8 | 42.57 ms |
| Reliability | 79% | 87% | 99% |
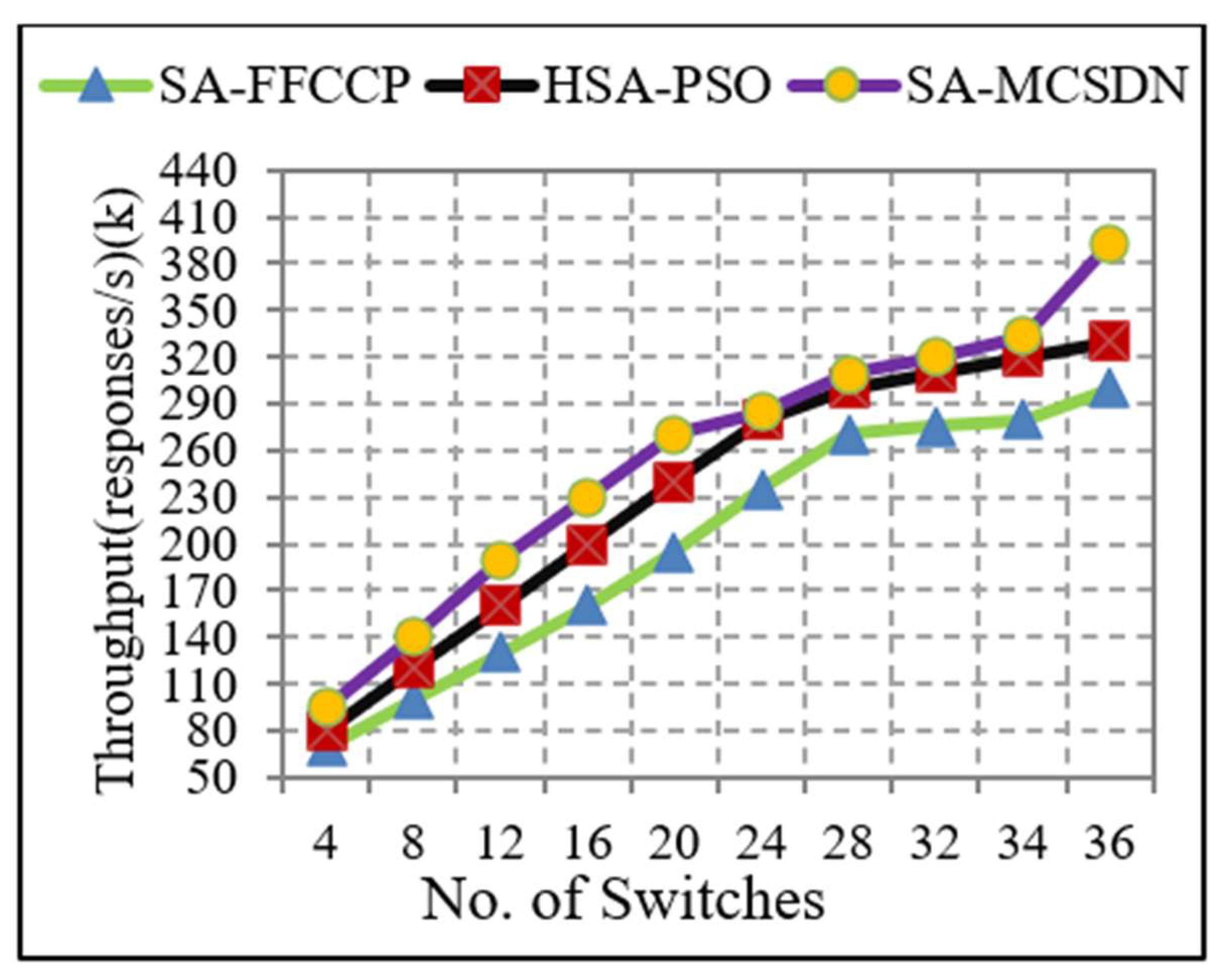
| Throughput (response/s) | 165.71 | 197.14 | 395.57 Kbps |
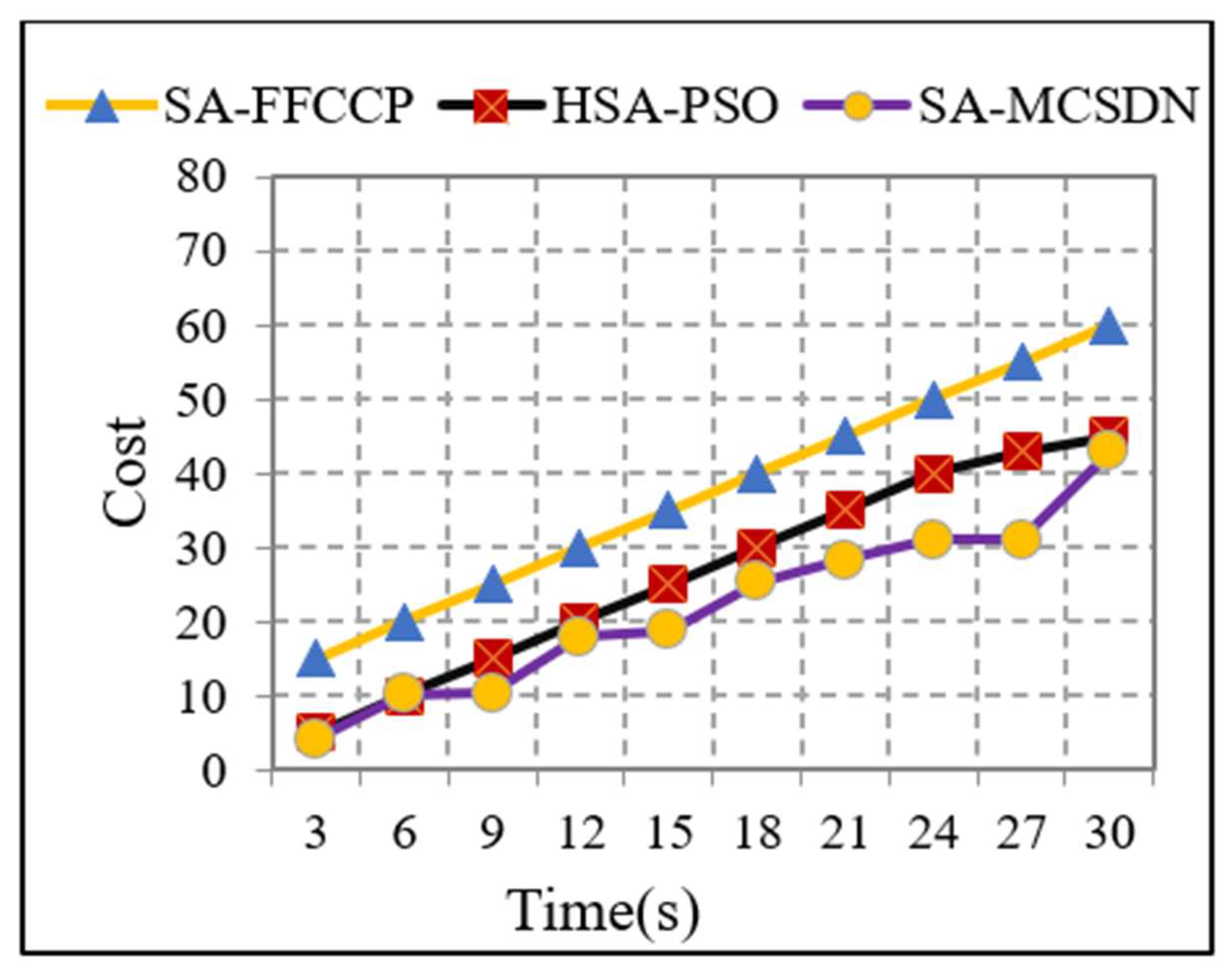
| Cost | 37.5 | 27.4 | 31.27 |
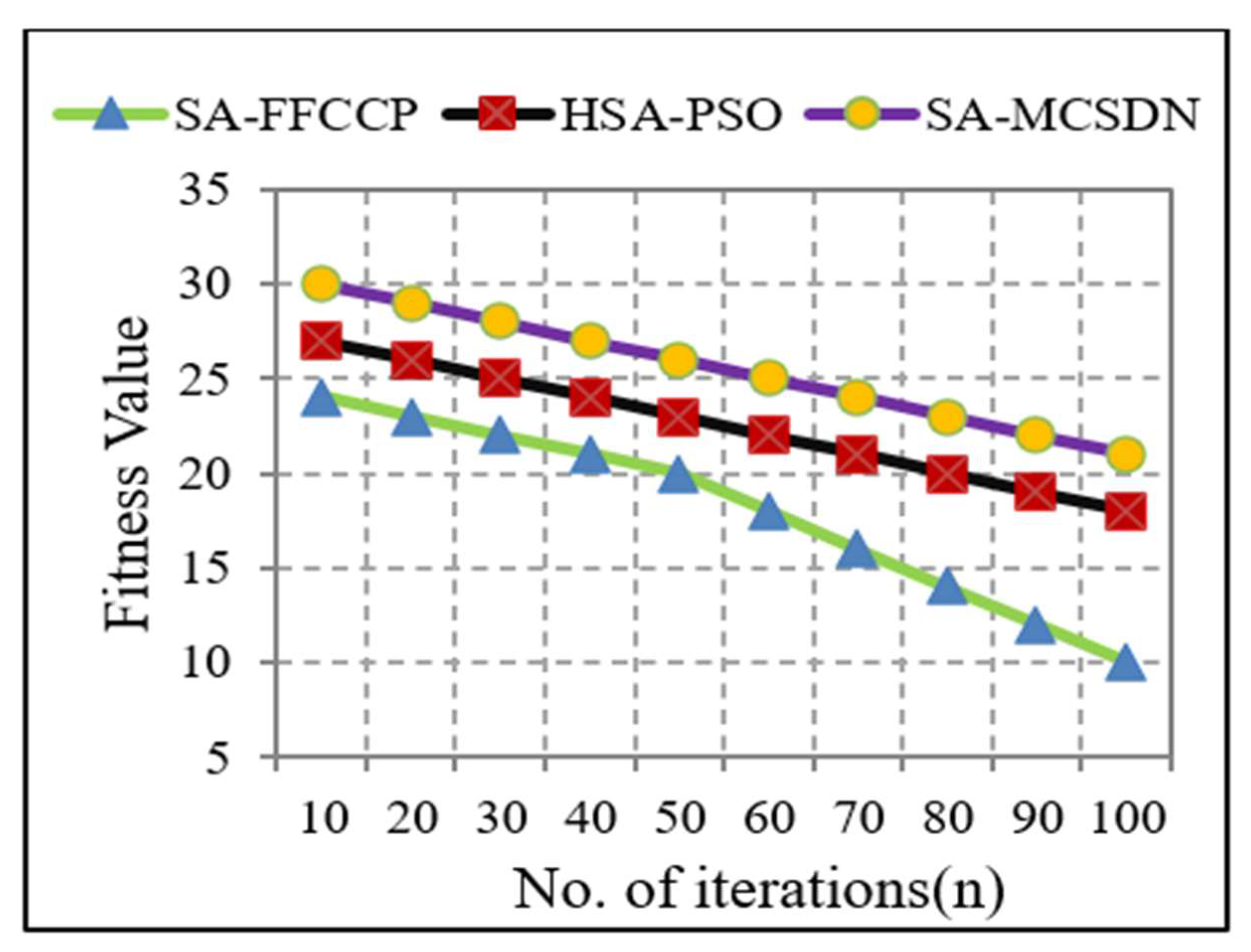
| Fitness value | 18.2 | 22.5 | 19.16 |
| Symbol | Description |
|---|---|
| G = (V, E, U) | Physical network topology graph |
| V | The node set in the network topology set of n switches: data-plane nodes |
| E | Set of physical links between switches (edges) |
| U | Set of k controllers, where k = U |
| C | Set of controllers, where C ⊂ V |
| (i, j) | The link between node i and node j |
| d (S, C) | The distance between switch S V and controller C V |
| n | Total number of switches or nodes in the network elements, where n = V |
| k | Total number of controller clusters to be installed in the network, where k ≤ n |
| Pc | Set of all possible placements for k controllers (probability): the probability of network component failure including nodes and links |
| xi;k | Indicates whether switch i is associated with controller k (= 1) or not (= 0) |
| X | Geographic locations of nodes |
| Sec | Seconds |
| M | Meters |
| ms | Milliseconds |
| j | Latitude of a node |
| Firefly controller of n | |
| Controller features | |
| D | Distance |
| Distance between controllers | |
| Maximum light intensity for firefly | |
| FT(D) | Fault tolerance of distance |
| ℵ(D) | Controller absorption coefficient based on FA |
| γ | Absorption coefficient |
| ℵ | Optimal controller |
| Number of all possible placements of () elements |
| Parameter Name | Parameter Symbol | Value |
|---|---|---|
| Initial temperature | T0 | 10 |
| Final temperature | 0.00001 | |
| No. of iterations at each temperature | 5000 | |
| Iteration | itr | 100 |
| Temperature decrementing factor (cooling rate) | Alpha (α) | 0.8 to 0.99 |
| solution | S | ? |
| Golden ratio (set empty) | ? | |
| Temperature | T | ? |
| Probability | ? | |
| Temperature decline factor (random) | ||
| Original reception rate | 0.95 | |
| Polynomial kernel | d | 2 and 3 |
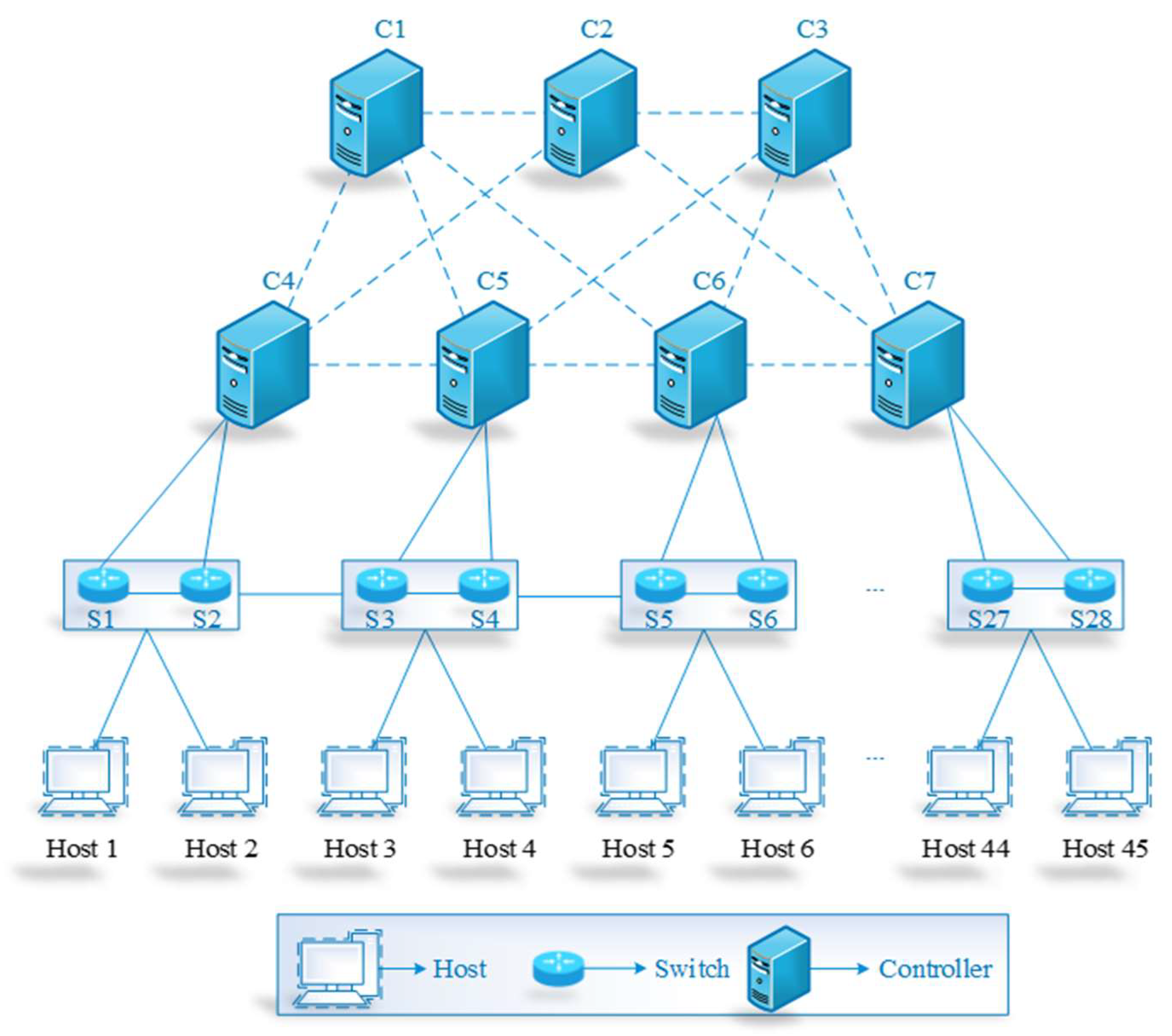
| No. of nodes in the network | N | 3 topology (7, 28, 45) |
| [N N] matrix consisting of shortest paths between every pair of nodes | D | 3 × 3 |
| Boltzmann constant | L | 1.380694 × 10−23 J/K |
| No. of controllers to be deployed | k | 21 |
| Array of size k consisting of capacities of controllers | U | 3 × 3 |
| Array of size N consisting of demands of switches | V | 3 × 3 |
| Array of size k consisting of the current positions of controllers | Pc | ? |
| Software Specifications | Operating System | Windows 10 Pro (64 Bits) |
|---|---|---|
| Type of topology | Undirected graph structure | |
| No. of Topologies | 3 | |
| Hardware Specifications | Hard Disk | 1 T |
| CPU | Intel(R) Core(TM) i7-10510U CPU @ 1.80 GHz 2.30 GHz | |
| RAM | 8.00 GB |
| VM Software and Hardware | Operating System | Linux Ubuntu-16.04 LTS -Desktop-Amd64 |
|---|---|---|
| Integrated development environment (IDE) | VMware Workstation 16 Player | |
| Network simulator | NS3 | |
| Language | C++ | |
| Bandwidth | 100,000 downlink and uplink | |
| Hard disk | 20 GB | |
| RAM | 2048 MB | |
| Delay | 900 ms | |
| MIPS | 44,800 | |
| Devices | Delay | 1 ms |
| MIPS | 1500 | |
| RAM | 4 GB | |
| SDN-CONTROLLER | No. of controllers | 7 |
| No. of switches | 28 | |
| Switch delay | 5 | |
| Bandwidth | Variable | |
| Controller delay | 0.5 | |
| No. of hosts or users | 45 | |
| Packet size | 500 | |
| Static Const Unit SIM_DURATION | 200 | |
| speed | 299,792,458 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radam, N.S.; Al-Janabi, S.T.F.; Jasim, K.S. Using Metaheuristics (SA-MCSDN) Optimized for Multi-Controller Placement in Software-Defined Networking. Future Internet 2023, 15, 39. https://doi.org/10.3390/fi15010039
Radam NS, Al-Janabi STF, Jasim KS. Using Metaheuristics (SA-MCSDN) Optimized for Multi-Controller Placement in Software-Defined Networking. Future Internet. 2023; 15(1):39. https://doi.org/10.3390/fi15010039
Chicago/Turabian StyleRadam, Neamah S., Sufyan T. Faraj Al-Janabi, and Khalid Sh. Jasim. 2023. "Using Metaheuristics (SA-MCSDN) Optimized for Multi-Controller Placement in Software-Defined Networking" Future Internet 15, no. 1: 39. https://doi.org/10.3390/fi15010039
APA StyleRadam, N. S., Al-Janabi, S. T. F., & Jasim, K. S. (2023). Using Metaheuristics (SA-MCSDN) Optimized for Multi-Controller Placement in Software-Defined Networking. Future Internet, 15(1), 39. https://doi.org/10.3390/fi15010039






