Abstract
Information-centric networking (ICN) is an emerging network architecture that has the potential to address low-transmission latency and high-reliability requirements in the fifth generation and beyond communication networks (5G/B5G). In the ICN architectures that use the identifier–locator separation mode, a name resolution system (NRS) is an important infrastructure for managing and maintaining the mappings between identifiers and locators. To meet the demands of time-sensitive applications, researchers have developed a distributed local NRS that can provide name resolution service within deterministic latency, which means it can respond to a name resolution request within a latency upper bound. However, processing name resolution requests only locally cannot take full advantage of the potential of the distributed local NRS. In this paper, we propose a name resolution approach, called adjacency-information-entropy-based cooperative name resolution (ACNR). In ACNR, when a name resolution node receives a name resolution request from a user, it can use neighboring name resolution nodes to respond to this request in a parallel processing manner. For this purpose, ACNR uses the information entropy that takes into account the adjacency and latency between name resolution nodes to describe the local structure of nodes efficiently. The proposed approach is extensively validated on simulated networks. Compared with several other approaches, the experiment results show that ACNR can discover more cooperative neighbors in a reasonable communication overhead, and achieve a higher name resolution success rate.
1. Introduction
In recent years, with the rapid development of emerging network applications, such as industrial Internet of Things (IoT), intelligent transportation, and telemedicine [1,2], higher demands have been placed on the quality of services (QoS) provided by the network. The demands include higher data transmission rates, lower response latency, and better reliability. The fifth generation (5G) and beyond 5G (B5G) communication networks technologies aim to address these performance requirements [3,4,5].
However, the currently widely used internet protocol (IP) network architecture was designed for a host-to-host communication model using a best-effort transmission model. Its data transmission function mainly relies on the endpoint hosts with limited performance, which fails to take full use of the network’s ability. Therefore, it is difficult for IP architecture to meet the forwarding demands of ultra-low latency and ultra-high reliability [6]. Moreover, IP architecture uses IP address both as an identifier for the host and as a locator for routing and forwarding data. The coupling of identifier and locator is the main reason that severely limits the breakthrough of IP architecture in terms of transmission performance, scalability, security, and mobility support [7,8].
Therefore, using the existing IP architecture directly for 5G/B5G will bring bottlenecks to performance breakthroughs. Information-centric networking (ICN) [9,10,11] has emerged as a new network architecture dedicated to improving the performance of the network. Compared with IP architecture, ICN uses an information-centric communication model that enables the separation of content from its server location. ICN can take full advantage of the potential capabilities of the network. The ICN network devices have storage capabilities that can cache content replicas and effectively decouple the interaction between content senders and receivers. ICN also brings up several characteristics such as mobility support, built-in multicast delivery, and inherent security [12], allowing users to obtain content simply, efficiently, and safely. These new characteristics mean that ICN has the potential to provide better network service quality in 5G/B5G networks and bring ICN to widespread attention.
According to the mode of routing and forwarding, ICN architectures can be mainly classified into two categories. One is the identifier-based routing mode, which uses hierarchical content identifiers and aggregates routing information and packet forwarding are according to the hierarchical characteristic, such as content-centric network (CCN) [13] and named data networking (NDN) [14]. The other is the identifier–locator separation mode, in which the identifier and locator are separated into two different namespaces. Users first obtain the locator corresponding to the identifier in the network and then route the data according to the locator. Such ICN architectures include data-oriented network architecture (DONA) [15], MobilityFirst (MF) [16], publish–subscribe internet routing paradigm (PSIRP) [17], network of information (NetInf) [18], and on-site, elastic, autonomous network (SEANet) [11]. The identifier–locator separation mode has gained wide acceptance due to its better scalability and better compatibility with existing IP architecture.
Name resolution system (NRS) is an important infrastructure that provides storage and name resolution services for identifier and locator mapping pair in the identifier–locator separation mode. Content delivery cannot be achieved unless the name resolution process is completed. Every ICN architecture provides its implementation of NRS. DONA and MobilityFirst both manage the mappings of identifiers and locators through global NRSs. PSIRP manages information naming, route addressing, and mapping through a hierarchical distributed hash table (DHT). NetInf uses a nested NRS, based on multi-layer DHT to query name mapping records through a combination of global NRS and local NRS. The global NRS is more concerned with the availability and full searchability of name resolution. To support the name resolution requirements of latency-sensitive applications in 5G/B5G scenarios, such as ultra-reliable and low-latency communications (URLLC), it is necessary to provide the deterministic response latency of name resolution. It is the key to the QoS of NRS, and the related research is very challenging.
SEANet [11] is a novel ICN architecture based on the identifier–locator separation mode. It uses a combination of a global naming and mapping system (GNMRS) and a local naming and mapping system (LNMRS). GNMRS is a general global information service system, which mainly guarantees the full storage of identifier–locator mapping records of the whole network and also ensures the searchability of name resolution. LNMRS is a distributed autonomous system deployed at the edge of the network near users and provides immediate name resolution service. It divides the resolution region into multiple levels according to the communication latency constraint between name resolution nodes and between the nodes and users, and its hierarchical nested structure can provide users with name resolution service with the upper bound of response latency at different levels.
The main principle of the local NRS is to make use of the local characteristics of name resolution requests in the network to provide immediate name resolution responses to nearby users [19]. However, unlike the full searchability service provided by the global NRS, the local NRS cannot guarantee that there will be available addresses in the response messages returned to users, since the name mapping may not be stored in this local name resolution node. A name resolution request in LNMRS [11] is restricted to a corresponding name resolution node to ensure deterministic response latency. This method needs to be improved because the constraint is strict, and the name resolution success rate is not ideal. Once local name resolution fails, users have to access the global NRS, and the QoS will inevitably degrade.
In LNMRS, each service level is divided into several name resolution regions according to the latency upper bound. The name resolution node in each region provides name resolution services only for users in this region. In this paper, we explore the benefits of the proximity between name resolution nodes and propose Adjacency-information-entropy-based cooperative name resolution (ACNR) approach. In ACNR, name resolution nodes can use their neighboring name resolution nodes to respond to users’ name resolution requests in a parallel processing manner. It expands the name mapping search range within the limit of latency constraint and improves the name resolution success rate. In existing neighbor cooperation approaches, there is a trade-off between neighbor discovery efficiency and the search message overhead. Additionally, the name resolution node cannot know the neighbors’ structures well, so it is easy to cause extra cooperation burden for the neighbor, but the overall name resolution benefit is low. ACNR leads into the information entropy of adjacency in neighborhood management, which helps to quantify the system structure more accurately and optimize the discovery and usage strategy of neighborhoods. The main contributions of this paper are as follows:
- We designed a neighbor cooperative name resolution approach for NRS in ICN, including discovery, usage, and maintenance of nodes’ neighbor relationships, which can fully exploit the potential of name resolution nodes while reserving the deterministic latency characteristic.
- We extended the concept of adjacency information entropy in networks with transmission latency constraint and applied it to the neighbor discovery and the name resolution cooperation in ACNR, to quantify and use the system structure more accurately.
- We conducted experiments on simulated networks to measure the performance of the proposed approach. We compared it with several other neighbor cooperation approaches, and the experimental results show that ACNR can discover more neighbors and achieve a better name resolution success rate.
The rest of this paper is organized as follows. We review related work on NRS architecture and neighbor cooperation approaches in distributed systems in Section 2. Section 3 describes the model of LNMRS, and the fundamental theory used in this paper. In Section 4, the ACNR approach is described in detail; then, we evaluate and discuss the performance of the proposed approach through comparative experiments in Section 5. Finally, Section 6 concludes our work.
2. Related Work
2.1. Name Resolution System
In this paper, we focus on the NRS of the ICN architectures which use identifier–locator separation mode, where name resolution and routing are decoupled into two steps. The user first sends a name resolution request to an NRS to find a locator mapped by the identifier and then uses this locator for routing and forwarding.
The NRS is the core infrastructure in ICN, and its structure is crucial and directly affects the capabilities and efficiency of name resolution in ICN. Distributed hash table (DHT) is a widely applied, distributed storage algorithm due to its logarithmic scalability, robustness, and resilience. In studies [20,21], the authors applied DHT to their structures design of NRS and the selection of locations for name mapping records storing, based on chord [22] and content-addressable network [23], respectively. In MobilityFirst [16], the authors designed a global NRS with a one-hop DHT scheme to achieve the dynamic binding of identifiers and locators. An inherent problem of DHT is the non-location-aware characteristic. The path of name resolution queries is relatively long and the upper bound of the resolution latency is difficult to guarantee [24]. As improvements, some researchers have proposed hierarchical NRS architectures to overcome this deficiency. NetInf proposes a multi-level DHT (MDHT) [25], which constructs a hierarchical DHT based on different name resolution domains, using a traditional DHT within a domain and a hierarchical structure to aggregate individual DHTs among domains. Name mappings are published to the local resolution domain and the corresponding upper-level domain, and the query is performed in the direction from low to high. The hierarchical NRS architecture is also used in PSIRP, DHT-NRS [26], and scalable multi-level virtual distributed hash table (SMVDHT) [27]. In addition, some researchers use a tree as the structure of NRS. Sun et al. proposed a flat name-based ICN NRS called Griffin [28], where the name resolution is mapped to a tree-based T-space derived from the network topology, providing efficient name resolution with a more explicit query path compared with DHT schemes. Louati et al. proposed Ftree [29], which tries to avoid accessing the root node and only stores name records in its leaf nodes to achieve fast and proximal name resolution. The tree structure considers proximity among name resolution nodes and reduces query path length. The tree-based NRS architecture is also used in data-oriented networking architecture (DONA) [15], B-NRS [30] in ID-based networking architecture [31], and the dynamic name resolution mechanism (DNRM), proposed by Hassan et al. in [32].
The above-mentioned architectures are primarily concerned with scalability issues. There is little discussion on how to use an NRS to provide name resolution service within a deterministic transmission latency. However, this problem is a key requirement and is a challenge for ICN to effectively support new scenarios of 5G/B5G, such as industrial control and IoT.
2.2. NRS in SEANet
SEANet uses a combination of GNMRS and LNMRS. GNMRS is a general global information service system, which is usually deployed in the cloud and can also be realized in the network. It mainly guarantees the full storage of identifier–locator mapping records of the whole network, and ensures the searchability of name resolution. LNMRS is a distributed autonomous system for on-site name resolution services. It is usually deployed at the edge of the network. Each name resolution node stores the mapping records of identifiers and locators in the local area and provides name resolution services of different service levels. Service levels are defined as differentiated services based on measurements. In this paper, we use the communication latency between network nodes as a measure of the service level. LNMRS and GNMRS complement each other to provide multifaceted name resolution performance guarantees for users with different requirements.
As far as we know, LNMRS introduces multi-level deterministic latencies into NRS for the first time. LNMRS constructs a hierarchical structure based on the underlying network topology, it uses a nested tree structure to give a feasible name resolution scheme for deterministic latency requirements in 5G/B5G scenarios while ensuring scalability, showing better flexibility, and supporting dynamic post-address binding in mobile scenarios.
The structure of LNMRS is key to providing its efficient service assurance. As shown in Figure 1, LNMRS constructs the name resolution nodes into a single-level or a multi-level structure according to the service levels corresponding to the scenario requirements. Among them, name resolution nodes at the same level have the same service level, and name resolution nodes at different levels have different service levels. The higher levels of the structure correspond to the higher service levels, which means larger response latency upper bounds. A name resolution node that can provide a guaranteed name resolution latency upper bound for a user at a service level is called a serviceable node for this user. At each service level, a user may have one or more serviceable nodes, but only one of them is referred to as a master name resolution node, denoted as MN. Each name resolution node records users who take this node as their MN as the set of users of this node. To provide deterministic latency resolution services for each user, the LNMRS restricts the MNs of every user at each level to conform to a nesting relationship. In other words, the user set of the MN at a particular level must be a subset of the user set of this user’s MN at a higher level [11]. From the perspective of LNMRS structure management, the nested relationships between MNs in LNMRS can be represented using a tree structure. The MNs of adjacency service levels can be represented by directly connected parent–child relationships in the tree. All MNs and the nested relationships between them constitute a forest structure.
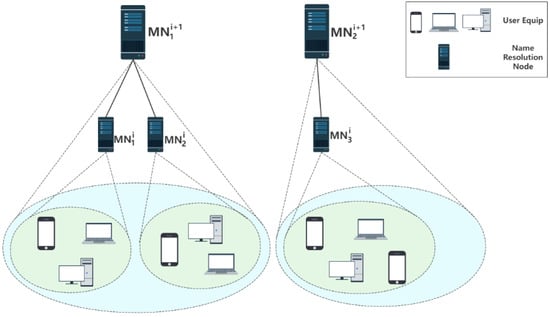
Figure 1.
The nested tree structure in the local name mapping and resolution system. Users select their own master name resolution node (MN) at each service level to provide name resolution service with deterministic response latency. The user set of the MN of the same user at different levels has nesting relationships, which forms a nested tree structure.
To ensure the deterministic latency of name resolution services, LNMRS uses MNs and their nested relationships to provide name resolution services for users, as well as to constrain the system structure. However, there is a limitation for a user to use only its MN as a responder to its name resolution request. For a name resolution request initiated by a user to its MN, it is possible that this MN does not store the required mapping entries locally, or this MN is overload, so there are no available locators in the name resolution response message, which can affect the user’s service experience. The above problems have the opportunity to be solved by other serviceable nodes of this user. Therefore, new structures are required to make full use of these neighboring serviceable nodes as a complement to the name resolution methods, to expand the search range of name resolution, and to share the request load of overloaded nodes, thereby improving the name resolution success rate.
2.3. Neighbor Cooperation
A neighbor relationship is an important concept in distributed systems. In most distributed systems, for the sake of scalability, a variety of functions and algorithms are performed autonomously by nodes deployed in a distributed manner, and the system composed of these distributed nodes forms a whole that unites to provide some service together [33]. Distributed nodes do not have the structure information of the whole system, but they can exchange information with other nodes in close proximity to discover the structure of the local area. Then, they can make better decisions and complete their tasks more efficiently, and these nodes nearby are called neighbor nodes.
The discovery and usage of a neighborhood are key concerns for distributed node cooperation, and researchers have proposed different algorithms. The simplest way to discover and use neighbors is the flooding algorithm; a width-first search is used in Gnutella [34], which forwards query requests to all direct adjacency nodes of the current node. It has a high discovery rate, but the drawback is that it is costly, request messages grow exponentially with the number of hops, and when the requested target is far, the message overhead can impose a significant burden. As an improvement, the literature [35] proposes the SOADP algorithm, which limits the scope of flooding without reducing the query success rate and uses the forwarding state information of the nodes to decide whether to perform the duplication of the discovery message. The DS [36] algorithm is an improved random walker cooperative search algorithm, where the requesting node sends several walker messages to the adjacency nodes based on one-hop flooding messages and forwards a query message based on each node’s neighbor structure index table and node storage capacity, until that walker message finds its target or reaches the maximum hop limit and is discarded. In addition to node storage capacity, node processing capacity, network bandwidth, physical latency, and local network topology information are also references for optimizing the efficiency of neighbor cooperation in distributed systems [37]. The literature [38] proposes an overlay network model where nodes in a close physical location are formed into a group by measuring the communication latency of nodes and establishing neighbor relationships between nodes in the group for inter-node cooperation. However, the neighbor relationships are maintained through a central server and the maintenance overhead increases dramatically when the network size is large. Some other researchers apply heuristic algorithms to neighbor cooperation. One study, [39], introduced theories such as particle swarm and self-organizing networks to describe the selection of neighbors and the process of overlay network evolution; OQF [40] uses a genetic algorithm and maintains historical statistics of neighbors, such as the average number of successful lookup hops, and based on this information the best neighbor node was intelligently selected for message forwarding. Li proposes an improved DBSCAN algorithm in [41] that uses covering trees to retrieve node neighbors in parallel and uses triangular inequalities to filter unnecessary distance computation to improve efficient clustering and neighbor cooperation.
Most of the neighbor cooperation methods mentioned above use topology degree or the direct connection relationship of network nodes to discover and use neighbor nodes. Many studies take the degree as the indicator to quantify the structure characteristics of nodes. These methods cannot well reflect the connection between nodes and their indirect neighbor nodes, and thus they cannot quantify the NRS structure accurately. Therefore, this paper proposes to use information entropy as a metric, to rationally utilize the connection relationship and the structure information of an NRS.
3. Model and Theory Fundamental
In the previous section, we introduced some typical NRS architectures and several neighbor cooperation approaches in distributed systems. In this paper, we focus on LNMRS, which has the novel characteristic of deterministic latency name resolution and can meet the capability requirements of NRS under 5G/B5G scenarios. Considering that the current LNMRS cannot fully exploit the advantages of local NRS, we will design a neighbor structure approach of name resolution nodes based on LNMRS, including the discovery, usage, and maintenance of nodes’ neighbor relationship, expecting that higher name resolution success rates can be achieved while preserving the deterministic latency characteristics.
Before presenting our proposed approach in the next section, the related knowledge is presented in this section. We first model the LNMRS architecture, describe its structural characteristics, and then introduce the concepts related to adjacency information entropy, used in our proposed method. For brevity of presentation, Table 1 summarizes the meanings of the symbolic identifiers used in this paper.

Table 1.
Summary of notation.
3.1. Local Name Mapping and Resolution System
We use an undirected graph, , to model the structure of LNMRS. is the set of nodes in the physical network, representing the network entities with the potential to place name resolution servers. is the total number of network entities. is the set of edges, and means that and can communicate with each other without going through any other nodes in . is the weight set of , and is the transmission latency between and . We used a matrix, , to denote the distances for all pairs of nodes in , where represents the shortest path latency between and . The set of users in the network is denoted as . In our model, users are each connected to the network through one of the nodes in , which can be a router, a base station, etc.; the access node of user is denoted as , and the transmission latency between them is denoted as . is a set that consists of the upper bounds of each layer’s constraint latencies, and is the number of scenarios with different latency requirements. For all , holds, which means that the name resolution service provided by a higher-level MN has a higher latency upper bound. is usually determined by application scenarios in the network.
Based on this model, we can accurately describe the structure using exact formulas. At a layer with latency upper bound of , we assume that is divided into several name resolution regions. The nodes and the edges in each region can form a subgraph of , the set of these subgraphs is donated as and represents the MN corresponding to . The user set of is donated as . In summary, the structural characteristics of LNMRS can be formulated as follows:
Equation (1) means that all the nodes are divided into a subgraph at each level. The constraint of Equation (2) ensures that there is no overlap between name resolution regions in the same level, so the tree structure can be formed. Nested relationships between name resolution regions from different levels are indicated in Expression (3). In Expression (4), the upper bounds of name resolution response latencies at each level are guaranteed. Expression (5) ensures that users can obtain deterministic name resolution latency from its MN.
3.2. Adjacency Information Entropy
Information entropy was proposed by Shannon in 1948 [42]. The advantage of information entropy is that it can characterize the degree of a system disorder embodied in the sample space from the uncertainty of the system sample points, using probabilistic and statistical methods, and quantify the local structure of the network nodes and the neighborhood information well. In recent years, information entropy has been widely used in complex systems and complexity theory, and it has become an effective method to solve problems in complex networks, especially in identifying key nodes and quantifying node adjacency structures [43,44,45,46]. The approach proposed in this paper is based on information entropy and involves the following definition of concepts:
Definition 1.
Neighbor node.
Neighbor nodes refer to the nodes that are directly adjacency to a node in the network topology, neighbor node set of node is defined as Equation (6):
Definition 2.
Adjacency degree.
Several researchers use the degree of a node as an important indicator to quantify its structural characteristics. However, the degree of a node can only reflect the connection of a node with its direct neighbors, and cannot reflect well the connection of a node with other indirect neighbor nodes. In order to more accurately reflect the local structural characteristics of a node, the adjacency degree is proposed. The adjacency of node is defined as Equation (7):
where denotes the degree value of node .
Definition 3.
Neighbor probability function.
The neighbor probability function describes the probability that each node will be selected among its neighbor nodes for operations such as communication. The neighbor probability function of the node is defined as Equation (8):
where the adjacency degree here cannot equal to zero—otherwise, the relative is meaningless.
Definition 4.
Adjacency information entropy.
In the literature [45], the neighbor probability function is considered to describe the influence of neighbor nodes of different nodes on themselves based on the traditional information entropy, thus proposing the adjacency information entropy, defined as Equation (9):
Adjacency information entropy mainly reflects the magnitude of a node’s influence on its direct and indirect neighbor nodes. A higher adjacency information entropy of a node indicates that this node has a higher probability of being selected by the node’ neighbors for communication or cooperation compared with other indirect neighbor nodes. This means that this node’s position in the network is more critical, and the probability that this node contains a large amount of information is higher. Adjacency information entropy takes into account the node’s properties as well as the impact it has on its neighbors, and it has a low computational overhead since only the local properties of the node are utilized. Guo et al. also used the adjacency information entropy as a metric for identifying vital nodes in the network and showed good performances [46].
Based on the above reasons, we believe that the adjacency information entropy has a good fit with the scenario of name resolution neighbor cooperation in this paper. It can help us discover the latency neighbors in complex networks efficiently and can preferentially select nodes with critical location as well as high information content to improve the success rate of name resolution services.
4. Proposed Approach
4.1. Overview of ACNR
In this section, we describe the proposed ACNR approach, which is an enhancement of the functionality of deterministic latency name resolution in LNMRS. The general adjacency information entropy focuses on the connectivity characteristics of the network itself, without considering the latency between neighbor nodes. To exploit the neighbor relationship of LNMRS and to satisfy the need for deterministic latency neighbors, ACNR uses the concept of latency neighbor cooperation to adapt adjacency information entropy.
Definition 5.
Latency neighbor.
The neighbor is a concept often involved in distributed systems to achieve functions such as route forwarding and cooperative processing by building connections between neighbor nodes. Latency neighbor is a structural relationship between name resolution nodes used in this paper and the latency neighbor of a name resolution node, , is defined as follows:
where represents the latency of a name resolution node processing a name resolution request on it. From Equation (10), latency neighbors are specifically the set of other name resolution nodes that have the same service latency level as , and the communication latency with that node is less than the upper bound specified by that level minus the processing time.
Based on the concept of latency neighbor, a distributed discovery method is designed, which makes full use of the structural relationship of the resolution domain division in LNMRS to initialization. Based on adjacency information entropy, we give the measure of the importance of the latency neighbor and then perform periodic discovery and maintenance of latency neighbors based on the neighbor transitivity characteristic [47]. The usage of latency neighbor is designed. The name resolution nodes will also perform cooperative name resolution based on this metric when providing services to users. Finally, the handling of the exit of the name resolution nodes is also presented. The proposed approach utilizes latency neighbor to fully exploit the service capacity of a larger range of name resolution nodes and to balance the request load, thus improving the overall name resolution success rate of the system.
4.2. Latency Neighbor Discovery
To perform cooperative name resolution, each name resolution node must first discover its latency neighbors accurately. Since the centralized management structure of the distributed system has limitations in scalability, the nested tree structure in LNMRS is constructed through the autonomy of nodes, and ACNR uses the same distributed conception for the discovery of latency neighbors. At each name resolution node, the node is responsible for providing services such as name mapping registration, resolution, and deregistration. In addition, each node also maintains a structure management module that has the functionality to perform latency measurements and structure construction algorithms. The discovery function of latency neighbor is also carried through this structure management module, where latency neighbors are maintained in the form of a list. After each name resolution node completes the construction of the main structure of the nested tree, it will perform the following initialization process and discovery process in order.
4.2.1. Initialization Process
When a name resolution node is first started, there is not much information about other name resolution nodes, so it is necessary to initialize its latency neighbors. An important feature that distinguishes LNMRS from other NRS architecture is that the latency constraint of the nested tree structure of LNMRS guarantees a deterministic latency upper bound. We notice that after the process of dividing the resolution domain, name resolution nodes in the same resolution domain already imply a certain degree of proximity property in terms of latency. We take full advantage of this property by relying on the nested tree structure of the system for initialization: each name resolution node obtains its list of latency neighbors from its parent node in the LNMRS nested tree structure, and then communicates to the parent node and all nodes in this list to obtain their children to join the set of latency neighbor candidates, which has the same name resolution service level as the current name resolution node. The current name resolution node measures the latency of each node in the latency neighbor candidate set, adds the nodes satisfying Equation (10) to the latency neighbor list, and records the corresponding communication latency values.
This latency neighbor discovery algorithm is a distributed operation. If the parent node of a name resolution node has not yet completed its discovery of latency neighbors, the current name resolution node needs to retry the communication after waiting. In addition, if a name resolution node performing the initialization process is located at the highest level of the LNMRS nested tree, the node is a root node, and the node needs to query the other root nodes in the system through a root index server. In LNMRS, the root index server only provides a query service to provide information about the root nodes, including—but not limited to—the node identifier and network address. However, to avoid overloading, the root index server is not responsible for complex topology computation and an indication of latency neighbor structure. The above algorithm is described in detail in Algorithm 1.
| Algorithm 1: Initialization Process. |
| Input: |
| Output:neighbors |
| 1: initialization: neighbors ← null |
| 2: if l == L then |
| 3: roots ← query roots from the root index server |
| 4: for r in roots do |
| 5: if then |
| 6: add r to neighbors |
| 7: else |
| 8: candidates ←.siblings |
| 9: for mn in .parent.neighbors do |
| 10: add mn.children with a number up to m to candidates |
| 11: for c in candidates do |
| 12: if then |
| 13: add c to neighbors |
| 14: return neighbors |
4.2.2. Discovery Process
Neighbor relationships in distributed systems tend to be transitive, i.e., if is a neighbor of and is a neighbor of , then there is a high probability that is also a neighbor of . This characteristic is more significant when the network nodes are densely distributed. ACNR also exploits this characteristic for latency neighbor discovery. For more efficient discovery, we found that the practical significance of adjacency information entropy to discover important nodes through comprehensive consideration of direct and indirect neighbors was relatively consistent with the scene of latency neighbor discovery in LNMRS. Forwarding discovery messages to nodes with higher adjacency information entropy is beneficial to discover more latency neighbors, so ACNR adapts the concept related to the adjacency information entropy based on transmission latency. For a name resolution node , the importance of latency neighbor (ILN) can be represented as Equations (11)–(13):
The above equations show that the importance of a node is not only related to itself but also the importance of its neighbor nodes, and the ILN can quantitatively represent the importance of a node in the network. With this metric, the neighbor discovery message can be forwarded to the node with higher influence, and the limitation of considering the node’s low degree but neglecting its high influence neighbors in some degree-greedy methods will not exist. After initialization, each name resolution node communicates with the nodes in its latency neighbor list periodically and obtains others’ latency neighbor lists to join its latency neighbor candidate set. The nodes in this set have the same name resolution service level as the current name resolution node. The current name resolution node also measures the latency of each node in the latency neighbor candidate set, and then adds the nodes satisfying Equation (10) to its latency neighbor set. With the periodic execution of this process, latency neighbor information will also continuously spread among nodes. In this paper, variable n is used to represent the execution rounds of the neighbor discovery process, and this variable also reflects the maximum hops of latency neighbor information spread among nodes. The specific algorithm is given in Algorithm 2.
| Algorithm 2: Discovery Process. |
| Input: |
| Output:neighbors |
| 1: initialization: neighbors←. neighbors |
| 2: candidates ← null |
| 3: for mn in neighbors do |
| 4: calculate ILN of mn.neighbors by formula (13) |
| 5: sort mn.neighbors with ILN in descending order |
| 6: add the first m mn.neighbors to candidates |
| 7: for c in candidates do |
| 8: if then |
| 9: add c to neighbors |
| 10: return neighbors |
4.3. Neighbor Cooperative Name Resolution
Through the aforementioned latency neighbor discovery method, each name resolution node can maintain several latency neighbors with cooperative name resolution capabilities. The ACNR approach also uses ILN as the basic metric for selecting the latency neighbor nodes for cooperative name resolution when receiving a name resolution request. The choice of cooperation neighbor using ILN is also reasonable because the larger the value of ILN means that the node is more important, indicating that the value of the information implied by the node is relatively higher, which means that the username’s name resolution request has a higher probability to be successfully responded at this name resolution node. The specific algorithm of cooperative name resolution is as follows: when a name resolution node receives a name resolution request from a user, if this node is overloaded or if the locator mapped by the identifier is not stored at local storage, it first calculates the remaining response time based on the timestamp carried by the request, then filters out the name resolution nodes from its latency neighbors whose communication latency are less than the remaining response time. Then, it selects several name resolution nodes from which the ILN is maximum to forward this name resolution request. The earliest successful resolution response will be returned to the user as the final name resolution result, thus completing the cooperative process of this name resolution request. The specific algorithm is described in Algorithm 3.
4.4. Latency Neighbor Maintenance
In addition to the latency neighbor discovery and cooperative name resolution methods described above, the dynamic structure maintenance mechanism in the ACNR approach is also designed to cope with the dynamics caused by changes in network topology and network latency. Throughout the lifetime of each name resolution node, it needs to perform latency measurements and heartbeat detection with its latency neighbor nodes periodically. When a name resolution node finds that a latency neighbor failed to respond or the communication latency between them is no longer satisfying the constraints in the definition of latency neighbor, it needs to remove that name resolution node from its latency neighbor list. When the latency neighbor list of a name resolution node becomes empty, the discovery process of latency neighbors needs to be re-executed. The maintenance mechanism here ensures the validity of the latency neighbors and makes ACNR work better in the NRS. The dynamic maintenance mechanism of the tree structure is not the focus of this paper and will not be discussed here.
| Algorithm 3: Cooperative Resolution. |
| Input:Request |
| Output:Response |
| 1: initialization: locators ← . neighbors |
| 2: if . currentLoad < . LoadLimit then |
| 3: locators ← local name resolution by |
| 4: if locators is empty then |
| 5: validNeighbors ← null |
| 6: for mn in . neighbors do |
| 7: if then |
| 8: add mn to validNeighbors |
| 9: sort validNeighbors with ILN in descending order |
| 10: for mn in the first k validNeighbors do |
| 11: send a cooperative name resolution request to mn |
| 12: while do |
| 13: resp ← cooperative name resolution response from . neighbors |
| 14: if resp.locators is not empty then |
| 15: Response.locators ← resp.locators |
| 16: break |
| 17: return Response |
5. Evaluation and Discussion
In this chapter, we conducted extensive simulation experiments on the discovery and cooperative name resolution process of latency neighbors in NRS. Compared with several other approaches, we evaluated the performance of the proposed ACNR approach in terms of recall rate and packet cost of latency neighbors, name resolution success rate, and name resolution load distribution among name resolution nodes.
5.1. Experimental Setup
To evaluate our approach, we performed the implementation of the ACNR approach and several comparison algorithms based on Simpy [48]. Simpy is an efficient and powerful discrete event simulator that allows researchers to easily test customized algorithms and strategies. We generated random topologies following the Barabasi–Albert scale-free model [49]. It is a typical power law degree-distributed network that is widely used to simulate real-world network topologies. According to [50], the current end-to-end latency of the internet is in the order of 10 milliseconds, and we randomly set the latency of each edge from 2 ms to 10 ms. Considering the different requirements of latency for the main application scenarios in 5G/B5G, we choose as upper bounds for the one-way transmission latency [51].
We distribute 104 contents evenly across network nodes in the network and set up 5 × 104 name resolution requests as workloads for the experiment. These workloads are initiated by the network nodes in a stable distribution, where the content of the requests follows a Zipf [52] distribution with parameter , and the request event happens following a Poisson distribution, with a default rate of 1000 requests per second. We assume that the network is responsible for route forwarding with cache-supporting ICN routers, each ICN router sets the same size of cache space and enforces a cache replacement policy of least recently used (LRU) [53]. To address the cold-start problems of network states, such as caching and NRS registration, we treat 104 requests of the workload as warm-up traffic and do not record these request events; the remaining 104 requests are recorded to obtain statistics for analyzing neighbor cooperative name resolution. The basic parameters of our experiments are given in Table 2.

Table 2.
Simulation configuration.
The experimental environment was created and run in Python 3.8 on a computer with an Intel Core (TM) i7-9750H CPU and 16 GB RAM. In each round of simulated experiments, the methods used for comparison applied the same topology and the same LNMRS structure, as well as the same random number generator seed. Additionally, the workload is set at the same to ensure fairness of the comparison. For each set of experiments, we ran 20 times independently and analyzed the results.
5.2. Latency Neighbor Discovery
As the size of the network increases, the communication message overhead caused by the discovery of latency neighbor will be non-negligible traffic. How the name resolution nodes can discover as many nodes that can be their latency neighbors with as little communication overhead as possible is a key indicator of how good the latency neighbor discovery algorithm is. We replicate several existing algorithms or ideas and apply them to the problem of latency neighbor discovery in LNMRS. The comparative algorithms are as follows:
- Global Measurement (GM) [54]: This algorithm uses a centralized server to index all name resolution nodes, and a name resolution node can perform latency measurements on all other name resolution nodes to comprehensively discover all name resolution nodes that are eligible to be latency neighbors. In our experiments, the latency neighbors of each name resolution node given by the GM algorithm are used as a comparison benchmark for other algorithms.
- Promoted Flooding (PF) [35]: The flooding approach is typical in distributed systems where each name resolution node sends latency neighbor discovery messages with hop limits to other network nodes connected in the network, and these messages are diffused recursively. When a name resolution node receives this message, it responds to the message and then the node that initiated the discovery determines the neighbor relationship between the two according to latency measurement. Here, we use a promoted flooding approach where the network node discards duplicate latency neighbor discovery messages received.
- Random Walker (RW) [36]: This algorithm generates m search messages at each name resolution node, and each searches message randomly selects m neighbor nodes per step for latency neighbor discovery message forwarding, which achieves message spreading while attenuating the flood range of messages in the network.
- Latency Greedy (LG) [55]: This algorithm is similar to the RW algorithm, but chooses m neighbor nodes with the shortest latency at each step for search message forwarding.
The parameter m used in the ACNR strategy is set as 4, and the parameter m used in the RW and the LG strategies are set as 6. These parameter values were fine-tuned through multiple rounds of testing different strategies under our experimental setup, based on the balance of experimental results and overhead, etc.
5.2.1. Recall Ratio
To measure the performance of different latency neighborhood discovery algorithms, the average recall ratio is used as an evaluation criterion. The recall ratio of latency neighbor represents the ratio of available latency neighbors of a name resolution node obtained by a discovery algorithm to the number of truly all latency neighbors of that node in the network. Let the set of all name resolution nodes in an NRS be , and for one of the , the latency neighbors obtained by an algorithm are denoted as the set , the set of its true full latency neighbors is denoted as , then the overall average latency neighbor recall ratio is defined in Equation (14):
As shown in Figure 2, we used different algorithms to discover latency neighbors for the nodes and computed their respective average latency neighbor recall ratios. The experiments first use the GM algorithm to compute all the latency neighbors for each name resolution node, using this latency neighbor set of each name resolution node as a benchmark, so the average latency neighbor recall of the GM algorithm is always 100%.
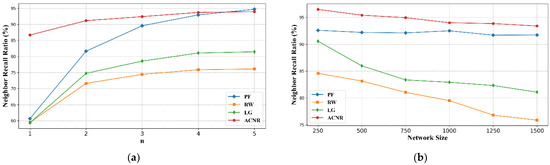
Figure 2.
Latency neighbor recall ratio comparison for each algorithm. (a) Latency neighbor recall ratio with different discovery rounds at network size of 1500; (b) latency neighbor recall ratio with different network sizes at discovery round of 4.
Figure 2a shows the experimental results of the latency neighbor recall ratio of each algorithm for different neighbor finding rounds at a network size of 1500. It can be seen that the latency neighbor recall ratio of each algorithm increases as the number of neighbor discovery rounds increases, and the degree of improvement becomes less pronounced when the number of rounds increases to a certain level, indicating that there is marginal utility in the number of neighbor discovery rounds. The PF algorithm, due to sending discovery requests for neighbors at each network node to all directly connected nodes, finds the latency neighbors most complete when the number of neighbor discovery rounds is large enough. The RW algorithm has blindness in finding latency neighbors and has the worst performance. The LG algorithm chooses the nearest node to forward the latency neighbor discovery message, which is thought to increase the neighbor discovery probability, and the results show that it can be useful compared with RW. However, it is not comprehensive to judge the local structure information only based on the node’s degree. Greedy methods often limit the discovery information to local parts and fail to spread the neighbor discovery information through a key node with a low degree in the structure. Unlike the other algorithms, ACNR achieves a high recall rate with fewer neighbor discovery rounds and consistently achieves better performance, which is attributed to the initialization work performed by taking full advantage of the latency constraint structure of LNMRS itself.
We also investigate the trend of the performance of each algorithm under different size networks. As shown in Figure 2b, where the network size has almost no effect on the PF algorithm, and the LG and RW methods have a significant decreasing trend in performance as the network size increases, probably because the difference in node degrees in the BA scale-free network model becomes large as the network size increases, and the RW and LG methods are closely related to node degrees lead to the decrease. In contrast, the ILN value is not limited to node degrees, and it quantifies the structural characteristic of the nodes relatively more accurately while taking into account the latency, so the latency neighbor recall ratio decreases slowly.
The number of MNs varies across the levels, with the lower levels having the largest number of MNs and occupying the largest proportion of the overall latency neighbor recall ratio. Figure 3 illustrates the average latency neighbor recall ratio for the LNMRS at level 2. It can be seen that in the higher levels, the resolution domain ranges are larger, the average distances between MNs are relatively farther, latency neighbor discovery becomes difficult, and more discovery rounds are required for each algorithm to achieve a stable latency neighbor recall ratio. In comparison, ACNR is more obvious at higher levels in terms of the advantage of discovery effectiveness.
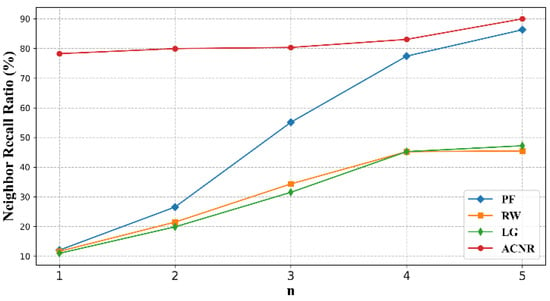
Figure 3.
Neighbor recall ratio comparison for each algorithm with different discovery rounds at the middle level.
5.2.2. Overhead
Pursuing only latency neighbor recall ratio is more one-sided because different latency neighbor discovery algorithms are accompanied by different overheads during execution, and it is not economical or reasonable to spend a large amount of overhead to improve a small amount of latency neighbor recall ratio. We focus on the communication overhead, which specifically includes the communication overhead of querying the index and structural relationships of a name resolution node to other nodes during the execution of an algorithm and the communication overhead of latency measurements among name resolution nodes.
Figure 4 shows the total number of neighbor discovery messages in the network at different discovery rounds for a network size of 1500. The GM algorithm requires measuring the latency between every two nodes in the network, and although it can discover all latency neighbors in a global perspective, its measurement overhead is O(n2) to the network size, and the scalability becomes extremely poor at larger network sizes. The PF algorithm has an exponentially increasing overhead as the diffusion range increases and has exponentially increasing overhead, again with poor scalability. LG and RW make the overhead relatively small due to limiting the number of branches per hop diffusion. The ACNR approach has worse overhead than LG and RW, but it does not have a significant increase with the number of discovery rounds, indicating that ACNR has a smaller overhead share in the periodic latency neighbor discovery process and can support dynamic latency neighbor discovery compared with other algorithms.
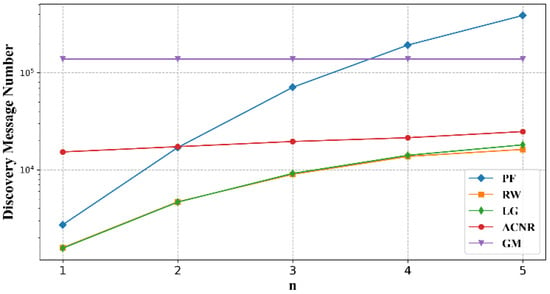
Figure 4.
Discovery message number comparison for each algorithm with different discovery rounds at a network size of 1500.
It is important for name resolution nodes to keep dynamic latency neighbor discovery in the process of providing services to users. Discovering new latency neighbors and stopping using invalid latency neighbors are the guarantee of efficient neighbor cooperation. ACNR does not bring too many discovery messages in the multiple round latency neighbor discovery processes. The controllable discovery round and the limitation of discovery information in local areas also make the maintenance of neighborhood structure in ACNR not bring too much pressure to the packet transmission and processing of name resolution nodes. Taking all these considerations into consideration, ACNR can discover more latency neighbors with reasonable overhead, which is an efficient discovery algorithm.
5.3. Neighbor Cooperative Name Resolution
After obtaining the latency neighbors, a name resolution node has the ability to use these latency neighbors for cooperative name resolution. The usage strategy is closely related to the overall service capability of the NRS. We replicate several existing algorithms or ideas and apply them to the strategy of using latency neighbor to find the best performance strategy. The comparative algorithms are as follows:
- Local Resolution (LR) [24]: This strategy does not use latency neighbors for cooperative name resolution, and each name resolution node only resolves the user’s name resolution request locally.
- All Neighbor (AN): In this strategy, to maximize the range of name resolution requests and thus increase the success rate of name resolution, each name resolution node forwards a name resolution request to all latency neighbors when it does not resolve the requested name mapped address locally.
- Degree Priority (DP): This strategy considers the node with a larger degree and sends the request to the latency neighbors with the k largest degrees when selecting cooperative latency neighbors, and it is a basic baseline strategy.
- Random Neighbor (RN): This strategy randomly selects k latency neighbors for forwarding during cooperative name resolution and is the easiest method to implement.
The parameter k used in the DP, the RN, and the ACNR strategies is default, set as 4, and Section 5.3.3 further describes the tuning for this parameter.
5.3.1. Name Resolution Success Rate
To measure the performance of different latency neighbor cooperative name resolution strategies, the average name resolution success rate is used as an evaluation criterion. The overall name resolution success rate is one of the core metrics of an NRS. It represents the ratio of the number of name resolution requests successfully resolved in an NRS over a period of time to the total number of name resolution requests received by the system directly from users. The successfully resolved means that a name resolution node successfully queries the name mapping corresponding to a name resolution request, either locally or through latency neighbor successfully responds to the user. Denote the set of all name resolution requests received by the NRS in a period as , then the name resolution success rate is defined as in Equation (15):
where I(r) is an indicator function that indicates whether the name resolution request, r, was successfully responded to, as shown in Equation (16):
As shown in Figure 5, we initiate name resolution requests to NRS at different user request rates and count the name resolution success rates of different latency neighbor cooperative name resolution strategies. First, it can be seen that the resolution success rate of the LR strategy, which only resolves the user’s name resolution request locally, is consistently the worst. Thus, using latency neighbors for cooperative resolution is effective in improving the success rate, and it illustrates the necessity of the maintenance of the neighbor structure.
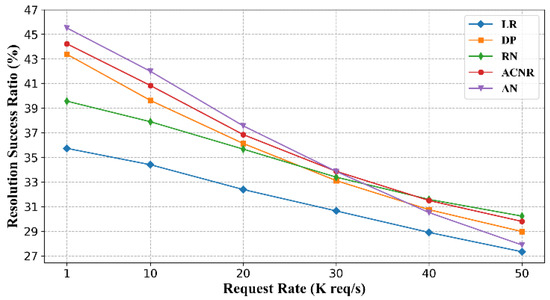
Figure 5.
Name resolution success rate comparison for each algorithm with different name resolution request rates.
Next, we focus on the four strategies that use latency neighbors. When the request rate of name resolution is low, the AN strategy has the highest success rate, ACNR and DP have the next highest success rate, while the RN strategy has the lowest success rate among the strategies using cooperative name resolution. This is because when the request rate is low, the AN strategy forwards resolution requests to all neighbors to effectively improve the resolution success rate, while the RN strategy only sends random requests without targeting, resulting in underutilizing the resolution capacity of neighbors. ACNR and DP take advantage of the connectivity of neighbors, thus effectively improving the name resolution success rate. As the speed of user requests increases, the number of name resolution requests and cooperative name resolution requests received by each name resolution node increases, and some hot name resolution nodes will gradually become overloaded due to the limitation of the nodes’ computation, storage, or bandwidth resources, and cannot complete the higher concurrent volume of name resolution requests. So, the name resolution success rate will decrease. As shown in Figure 5, when the request rate reaches 50 K, the name resolution success rates of all strategies are at 27–31% with a small difference. Among the different strategies, the AN strategy will overload more name resolution nodes faster, thus its success rate decreases the fastest. The RN strategy, since it does not take into account any factors, makes the most balanced load on the name resolution nodes, so it has the slowest success rate decrease. Even when the request rate reaches a certain value, RN becomes the strategy with the highest success rate. Finally, we can see that ACNR has the most stable name resolution success rate regardless of the request rate variation, and it generally outperforms the DP strategy which only considers the node degree. The effectiveness of the ACNR method proposed in this paper is demonstrated.
5.3.2. Name Resolution Node Load
We notice that the name resolution success rate has a relationship with the distribution of request load by name resolution nodes in the NRS. With an inappropriate cooperative name resolution strategy, it can lead to an excessive load on some nodes, according to queuing theory and the long-tail effect. After exceeding the threshold value, the node will not be able to complete the local resolution in a limited time, and cannot complete the cooperative name resolution with other name resolution nodes. We measure the performance of each cooperative resolution strategy in terms of the total request load of the name resolution nodes and the standard deviation of the request load.
Due to the relatively small number of high-level name resolution nodes and their latency neighbors, the variability across policies is not obvious, so we choose the bottom level to explore the request load characteristics. Figure 6a shows the total number of name resolution requests received by the NRS from users’ name resolution requests and cooperative name resolution requests from other nodes under each strategy. It can be seen that the total number of name resolution requests increases as the user request rate increases for each strategy. The reason is that the increasing number of parsing nodes that reach full load, and some name resolution requests that could have been processed locally are forwarded by these nodes to latency neighbors. Among them, the AN strategy imposes the largest additional load, while several other strategies are closer. Figure 6b also shows the standard deviation of a load of each name resolution node in the NRS under each strategy. The AN strategy exacerbates the impact caused by the scale-free characteristic in terms of load and has the worst balance. The RN strategy has the best balance among the strategies that use latency neighbor cooperative name resolution. ACNR and DP are in between, with LNCR being relatively more advantageous. ACNR uses ILN to better quantify the structure of latency neighbors, reflecting a balance that is likely to be the reason for the superiority of the name resolution success rate over the DP strategy. It can be noticed that the LR strategy which does not use latency neighbors to cooperate has the best balance. The reason is that in scale-free networks, the distribution of the latency neighbors is affected by the power law property, so the strategies using latency neighbors have some negative impact in terms of load balancing more or less.
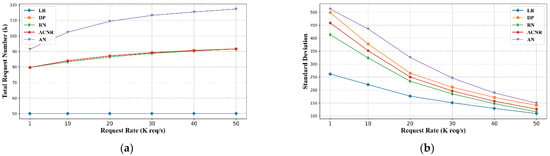
Figure 6.
Load metrics comparison for each strategy with different name resolution request rates. (a) Total request number with different name resolution request rates. (b) Standard deviation of the loads on name resolution nodes comparison with different name resolution request rates.
5.3.3. Parameter Discussion
In addition to the comparison with other strategies, we further explore the parameters in the ACNR approach. As shown in Figure 7a, the name resolution success rate has a positive correlation with the number of nodes selected at the latency neighbor cooperation, but as the value of k increases, the increase in the success rate of resolution becomes small. Figure 7b shows that the total number of name resolution requests in the network is positively correlated with the value of k. In practice, the value of k for ACNR does not need to be set too large, and the specific characteristics of the network should be fully considered, weighing the name resolution success rate and the overhead of cooperative name resolution requests.
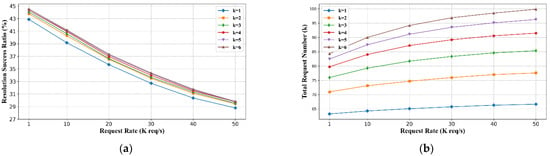
Figure 7.
Experiment result of parameter k in ACNR approach. (a) Name resolution success rate comparison for each k with different name resolution request rates. (b) Total request number comparison for each k with different name resolution request rates.
We conducted the same experiment to compare the name resolution success rate with different parameter k of the DP strategy, as shown in Figure 8a, and the RN strategy, as shown in Figure 8b. The experiment results present the positive correlation between success rate and parameter k as well.
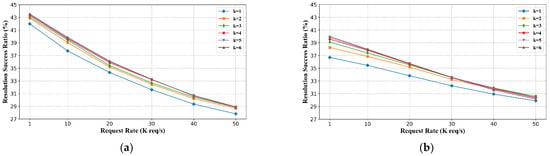
Figure 8.
Name resolution success rate with different parameter k. (a) Name resolution success rate of the DP strategy. (b) Name resolution success rate of the RN strategy.
Considering that the effect trend of a change in k is essentially the same for all algorithms and the benefit brought by a larger k value is too low, we finally selected as the parameter tuning result for each comparison algorithm for experiment in this paper.
6. Conclusions
The deterministic latency name resolution proposed in LNMRS is a very important feature to meet the demanding performance requirements of future networks. To achieve this feature, LNMRS imposes a strict constraint on the partition of the resolution domain based on the latency, and the name resolution success rate of users is not high enough to fully exploit the potential of the NRS. To address this problem, we propose the ACNR approach, which includes the discovery of latency neighbor and the cooperative name resolution based on it. ACNR uses the nested tree structure of LNMRS for latency neighbor initialization and dynamically updates them according to the transferability characteristic. Adjacency information entropy is used as an important metric in ACNR, to quantify the information of the neighbor structure more accurately. We conducted rich comparative experiments on ACNR, and the results show that the proposed approach can discover more latency neighbors with lower overhead and can perform latency neighbor cooperative name resolution in a balanced way, reaching a higher name resolution success rate. Future work will focus on the optimization problem of cooperative name resolution in dynamic networks, where name resolution nodes should dynamically maintain the state of latency neighbors to avoid frequent request processing overloads of name resolution nodes in the system, thus improving the overall resolution success rate and efficiency of the system.
Author Contributions
Conceptualization, J.L., J.Y. and H.D.; methodology, J.L. and J.Y.; software, J.L.; writing—original draft preparation, J.L.; writing—review and editing, J.L., J.Y. and H.D.; supervision, J.Y.; project administration, J.Y.; funding acquisition, H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Key R&D Program of China: Polymorphic Intelligent Network Environment (PINE) for Testing and Demonstrations (Project No. 2020YFB1806402).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable, the study does not report any data.
Acknowledgments
We would like to express our gratitude to Jinlin Wang and Yang Li for their meaningful support in this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, S.; Da Xu, L.; Zhao, S. 5G Internet of Things: A survey. J. Ind. Inf. Integr. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Agiwal, M.; Saxena, N.; Roy, A. Towards Connected Living: 5G Enabled Internet of Things (IoT). IETE Tech. Rev. 2019, 36, 190–202. [Google Scholar] [CrossRef]
- Anju, M.; Gawas, U. An Overview on Evolution of Mobile Wireless Communication Networks: 1G–6G. Int. J. Recent Innov. Trends Comput. Commun. 2015, 3, 3130–3133. [Google Scholar]
- Parvez, I.; Rahmati, A.; Guvenc, I.; Sarwat, A.I.; Dai, H. A survey on low latency towards 5G: RAN, core network and caching solutions. IEEE Commun. Surv. Tutor. 2018, 20, 3098–3130. [Google Scholar] [CrossRef]
- Chien, W.C.; Cho, H.H.; Lai, C.F.; Tseng, F.H.; Chao, H.C.; Hassan, M.M.; Alelaiwi, A. Intelligent architecture for mobile hetnet in b5g. IEEE Netw. 2019, 33, 34–41. [Google Scholar] [CrossRef]
- ITU Web Site. ITU FG-Net-2030 Network 2030 (A Blueprint of Technology, Applications and Market Drivers Towards the Year 2030 and Beyond Written). 2020. Available online: https://www.itu.int/en/ITU-T/focusgroups/net2030/Documents/White_Paper.pdf (accessed on 27 January 2022).
- Ohlman, B. From ID/locator split to ICN. In Proceedings of the 2015 12th Annual IEEE Consumer Communications and Networking Conference, CCNC 2015, Las Vegas, NV, USA, 9–12 January 2015; pp. 256–261. [Google Scholar] [CrossRef]
- Menth, M.; Hartmann, M.; Klein, D. Global locator, local locator, and identifier split (GLI-Split). Future Internet 2013, 5, 67–94. [Google Scholar] [CrossRef]
- Barakabitze, A.A.; Xiaoheng, T.; Tan, G. A Survey on Naming, Name Resolution and Data Routing in Information Centric Networking (ICN). Int. J. Adv. Res. Comput. Commun. Eng. 2014, 3, 8322–8330. [Google Scholar] [CrossRef]
- Xylomenos, G.; Ververidis, C.N.; Siris, V.A.; Fotiou, N.; Tsilopoulos, C.; Vasilakos, X.; Katsaros, K.V.; Polyzos, G.C. A survey of information-centric networking research. IEEE Commun. Surv. Tutor. 2014, 16, 1024–1049. [Google Scholar] [CrossRef]
- Wang, J.; Chen, G.; You, J.; Sun, P. SEANet: Architecture and Technologies of an On-site, Elastic, Autonomous Network. J. Netw. New Media 2020, 6, 1–8. [Google Scholar]
- Naeem, M.A.; Rehman, M.A.U.; Ullah, R.; Kim, B.S. A Comparative Performance Analysis of Popularity-Based Caching Strategies in Named Data Networking. IEEE Access 2020, 8, 50057–50077. [Google Scholar] [CrossRef]
- Jacobson, V.; Smetters, D.K.; Thornton, J.D.; Plass, M.F.; Briggs, N.H.; Braynard, R.L. Networking named content. In Proceedings of the CoNEXT’09—2009 ACM Conference on Emerging Networking Experiments and Technologies, Rome, Italy, 1–4 December 2009; pp. 1–12. [Google Scholar] [CrossRef]
- Zhang, L.; Afanasyev, A.; Burke, J.; Jacobson, V.; Claffy, K.; Crowley, P.; Papadopoulos, C.; Wang, L.; Zhang, B. Named data networking. ACM SIGCOMM Comput. Commun. Rev. 2014, 44, 66–73. [Google Scholar] [CrossRef]
- Koponen, T.; Chawla, M.; Chun, B.G.; Ermolinskiy, A.; Kim, K.H.; Shenker, S.; Stoica, I. A data-oriented (and Beyond) network architecture. Comput. Commun. Rev. 2007, 37, 181–192. [Google Scholar] [CrossRef]
- Raychaudhuri, D.; Nagaraja, K.; Venkataramani, A. MobilityFirst: A robust and trustworthy mobility-centric architecture for the future internet. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2012, 16, 2–13. [Google Scholar] [CrossRef]
- Dannewitz, C.; Kutscher, D.; Ohlman, B.; Farrell, S.; Ahlgren, B.; Karl, H. Network of information (NetInf)-An information-centric networking architecture. Comput. Commun. 2013, 36, 721–735. [Google Scholar] [CrossRef]
- Fotiou, N.; Nikander, P.; Trossen, D.; Polyzos, G.C. Developing information networking further: From PSIRP to PURSUIT. In Proceedings of the International Conference on Broadband Communications, Networks and Systems, Athens, Greece, 25–27 October 2010; pp. 11–13. [Google Scholar] [CrossRef]
- Fadahunsi, O.; Maheswaran, M. Locality sensitive request distribution for fog and cloud servers. Serv. Oriented Comput. Appl. 2019, 13, 127–140. [Google Scholar] [CrossRef]
- Mathy, L.; Iannone, L. LISP-DHT: Towards a DHT to map identifiers onto locators. In Proceedings of the 2008 ACM CoNEXT Conference—4th International Conference on Emerging Networking EXperiments and Technologies, Madrid, Spain, 9 December 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Luo, H.; Qin, Y.; Zhang, H. A DHT-based identifier-to-locator mapping approach for a scalable internet. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 1790–1802. [Google Scholar] [CrossRef]
- Stoica, I.; Morris, R.; Karger, D.; Kaashoek, M.F.; Balakrishnan, H. Chord: A scalable peer-to-peer lookup service for internet applications. Comput. Commun. Rev. 2001, 31, 149–160. [Google Scholar] [CrossRef]
- Ratnasamy, S.; Francis, P.; Handley, M.; Karp, R.; Schenker, S. A scalable content-addressable network. Comput. Commun. Rev. 2001, 31, 161–172. [Google Scholar] [CrossRef]
- Liao, Y.; Sheng, Y.; Wang, J. A temporally hierarchical deployment architecture for an enhanced name resolution system. Appl. Sci. 2019, 9, 2891. [Google Scholar] [CrossRef]
- D’Ambrosio, M.; Dannewitz, C.; Karl, H.; Vercellone, V. MDHT: A hierarchical name resolution service for information-centric networks. In Proceedings of the ACM SIGCOMM Workshop on Information-Centric Networking, Toronto, ON, Canada, 19 August 2011; pp. 7–12. [Google Scholar] [CrossRef]
- Katsaros, K.V.; Fotiou, N.; Vasilakos, X.; Ververidis, C.N.; Tsilopoulos, C.; Xylomenos, G.; Polyzos, G.C. On inter-domain name resolution for information-centric networks. Lect. Notes Comput. Sci. 2012, 7289, 13–26. [Google Scholar] [CrossRef]
- Liu, H.; Azhandeh, K.; de Foy, X.; Gazda, R. A comparative study of name resolution and routing mechanisms in information-centric networks. Digit. Commun. Netw. 2019, 5, 69–75. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Y.; Zhang, H.; Fang, B.; Du, X. Geometric routing on flat names for ICN. In Proceedings of the 2015 IEEE Global Communications Conference, San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Louati, W.; Ben-Ameur, W.; Zeghlache, D. A bottleneck-free tree-based name resolution system for Information-Centric Networking. Comput. Netw. 2015, 91, 341–355. [Google Scholar] [CrossRef]
- Hong, J.; Chun, W.; Jung, H. Demonstrating a scalable name resolution system for information-centric networking. In Proceedings of the ICN 2015—2nd International Conference on Information-Centric Networking, San Francisco, CA, USA, 30 September–2 October 2015; pp. 221–222. [Google Scholar] [CrossRef]
- Jung, H.; Lim, W.S.; Hong, J.; Hur, C.; Lee, J.C.; You, T.; Eun, J.; Kwak, B.; Kim, J.; Jeon, H.S.; et al. IDNet: Beyond ALL-IP network. ETRI J. 2015, 37, 833–844. [Google Scholar] [CrossRef][Green Version]
- Hassan, S.; Elbreiki, W.; Arlimatti, S.; Habbal, A. Named data object organization in distributed name resolution system for information centric network environment. J. Telecommun. Electron. Comput. Eng. 2017, 9, 119–122. [Google Scholar]
- RezaAbbasifard, M.; Ghahremani, B.; Naderi, H. A Survey on Nearest Neighbor Search Methods. Int. J. Comput. Appl. 2014, 95, 39–52. [Google Scholar] [CrossRef]
- Lv, Q.; Cno, P.; Cohen, E.; Li, K. Search and replication in unstructured peer-to-peer networks. In Proceedings of the 16th International Conference on Supercomputing, New York, NY, USA, 22–26 June 2012; 2002; Volume 2, pp. 84–95. [Google Scholar] [CrossRef]
- Li, J.; Zhang, T.; Wang, F.; Li, J.; Huang, D. Search algorithm based on peers division in unstructured P2P network. In Proceedings of the 2012 5th International Conference on Intelligent Computation Technology and Automation, ICICTA 2012, Zhangjiajie, China, 12–14 January 2012; pp. 471–473. [Google Scholar] [CrossRef]
- Lin, T.; Lin, P.; Wang, H.; Chen, C. Dynamic search algorithm in unstructured peer-to-peer networks. IEEE Trans. Parallel Distrib. Syst. 2008, 20, 654–666. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, Z. Non-backtracking centrality based random walk on networks. Comput. J. 2019, 62, 63–80. [Google Scholar] [CrossRef]
- Chan, Y.W.; Lai, C.H.; Chung, Y.C. A flexible locality-aware peer-to-peer streaming system. Int. J. Pervasive Comput. Commun. 2010, 6, 104–124. [Google Scholar] [CrossRef]
- Sun, W.; Lin, A.; Yu, H.; Liang, Q.; Wu, G. All-dimension neighborhood based particle swarm optimization with randomly selected neighbors. Inf. Sci. 2017, 405, 141–156. [Google Scholar] [CrossRef]
- Noghabi, H.B.; Ismail, A.S.; Ahmed, A.A.; Khodaei, M. Optimized query forwarding for resource discovery in unstructured peer-to-peer grids. Cybern. Syst. 2012, 43, 687–703. [Google Scholar] [CrossRef]
- Li, S.S. An Improved DBSCAN Algorithm Based on the Neighbor Similarity and Fast Nearest Neighbor Query. IEEE Access 2020, 8, 47468–47476. [Google Scholar] [CrossRef]
- Rogers, E.M.; Valente, T.W. A History of Information Theory in Communication Research. In Between Communication and Information; Routledge: London, UK, 2017; pp. 35–56. [Google Scholar]
- Zhang, Q.; Li, M.; Deng, Y. Measure the structure similarity of nodes in complex networks based on relative entropy. Phys. A Stat. Mech. Its Appl. 2018, 491, 749–763. [Google Scholar] [CrossRef]
- Zareie, A.; Sheikhahmadi, A.; Fatemi, A. Influential nodes ranking in complex networks: An entropy-based approach. Chaos Solitons Fractals 2017, 104, 485–494. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, C.; Wang, Q.; Zhu, X.; Zhou, Y. Identifying vital nodes in complex networks by adjacency information entropy. Sci. Rep. 2020, 10, 2691. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Yang, L.; Chen, X.; Chen, D.; Gao, H.; Ma, J. Influential nodes identification in complex networks via information entropy. Entropy 2020, 22, 242. [Google Scholar] [CrossRef]
- Sibo, C.; Zhiwei, L.; Hong, H. Wireless sensor network node localization algorithm based on adjacent node relationship. In Proceedings of the 2011 IEEE 3rd International Conference on Communication Software and Networks, ICCSN 2011, Xi’an, China, 27–29 May 2011; pp. 215–218. [Google Scholar] [CrossRef]
- Matloff, N. Introduction to Discrete-Event Simulation and the Simpy Language; Department of Computer Science, University of California at Davis: Davis, CA, USA, 2008; Volume 2, pp. 1–33. [Google Scholar]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Nasrallah, A.; Thyagaturu, A.; Alharbi, Z.; Wang, C.; Shao, X.; Reisslein, M.; ElBakoury, H. Ultra-Low Latency (ULL) Networks: A Comprehensive Survey Covering the IEEE TSN Standard and Related ULL Research. arXiv 2018, arXiv:1803.07673. [Google Scholar]
- Schulz, P.; Matthe, M.; Klessig, H.; Simsek, M.; Fettweis, G.; Ansari, J.; Ashraf, S.A.; Almeroth, B.; Voigt, J.; Riedel, I.; et al. Latency Critical IoT Applications in 5G: Perspective on the Design of Radio Interface and Network Architecture. IEEE Commun. Mag. 2017, 55, 70–78. [Google Scholar] [CrossRef]
- Breslau, L.; Cao, P.; Fan, L.; Phillips, G.; Shenker, S. Web caching and Zipf-like distributions: Evidence and implications. In Proceedings of the Eighteenth Annual Joint Conference of the IEEE Computer and Communications Societies, The Future is Now (Cat. No. 99CH36320), New York, NY, USA, 21–25 March 1999; IEEE: Piscataway, NJ, USA; Volume 1, pp. 126–134. [Google Scholar] [CrossRef]
- Fricker, C.; Robert, P.; Roberts, J. A versatile and accurate approximation for LRU cache performance. In Proceedings of the Final Program—2012 24th International Teletraffic Congress, ITC 24, Krakow, Poland, 4–7 September 2012; pp. 1–8. [Google Scholar]
- Somula, R.; Sasikala, R. A load and distance aware cloudlet selection strategy in multi-cloudlet environment. Int. J. Grid High Perform. Comput. 2019, 11, 85–102. [Google Scholar] [CrossRef]
- Orenshtein, T.; Shinkar, I. Greedy random walk. Comb. Probab. Comput. 2014, 23, 269–289. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).