ERGCN: Enhanced Relational Graph Convolution Network, an Optimization for Entity Prediction Tasks on Temporal Knowledge Graphs

Abstract

Reasoning on temporal knowledge graphs, which aims to infer new facts from existing knowledge, has attracted extensive attention and in-depth research recently. One of the important tasks of reasoning on temporal knowledge graphs is entity prediction, which focuses on predicting the missing objects in facts at current time step when relevant histories are known. The problem is that, for entity prediction task on temporal knowledge graphs, most previous studies pay attention to aggregating various semantic information from entities but ignore the impact of semantic information from relation types. We believe that relation types is a good supplement for our task and making full use of semantic information of facts can promote the results. Therefore, a framework of Enhanced Relational Graph Convolution Network (ERGCN) is put forward in this paper. Rather than only considering representations of entities, the context semantic information of both relations and entities is considered and merged together in this framework. Experimental results show that the proposed approach outperforms the state-of-the-art methods.

1. Introduction

Knowledge graphs (KGs), which stores a human’s knowledge and facts of the real world, are widely used in various applications [1,2,3]. However, knowledge graphs are often uncompleted, which limits its application in real world. As the incompleteness of facts may obstruct the reasoning procedure, it is necessary to complete knowledge graphs by predicting the missing facts. Several methods have been proposed for completing knowledge graphs, such as TransE [4], DistMult [5], ConvE [6]. The other issue that cannot be ignored is that facts often change over time. In order to depict the changing trend of facts over time, the relevant information can be organized into a series of knowledge graphs and each of them corresponds to a group of facts at different time stamps [1,3,7,8]. This series of knowledge graphs organized in chronological order is called temporal knowledge graphs (TKGs). There is concern regarding whether we can predict unseen facts through historical information. Therefore, learning the evolution of facts over time and then predicting unseen entities on TKGs has attracted the attention of researchers and has become a hot topic recently.

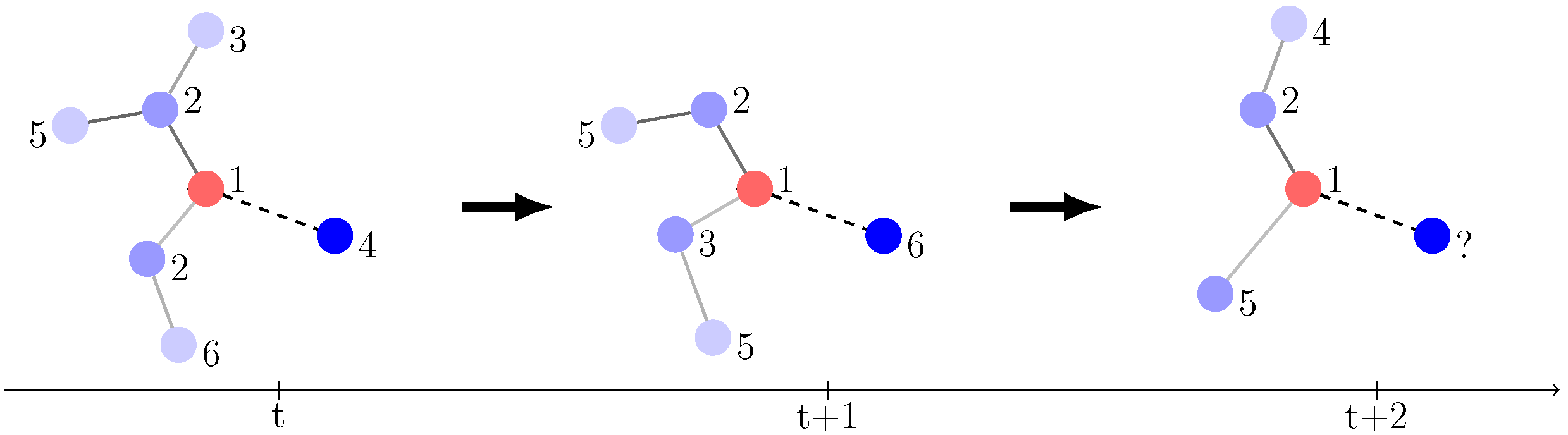
Prediction of facts over TKGs is classified into two categories: interpolation and extrapolation [9]. Interpolation, known as the completion problem, is mainly used for completing missing information during a given time interval [10,11,12]. A sample of the interpolation problem is to infer the president of America in 2016 when this fact is not seen between 1990 and 2020. Extrapolation, which is also known as entity prediction tasks, involves making a forecast of unknown facts at a future time. Extrapolation is a more difficult challenge than interpolation. An example of extrapolation is predicting who will win the next US presidential election. We prepare a example of entity prediction in Figure 1. Extrapolation research is not only of practical significance, but also theoretical value, because studying the evolution of facts can help us understand the informative relationship hidden behind the structural knowledge graphs. There have been many efforts focused on this problem but it is far from being solved.

The entity prediction tasks on knowledge graphs can be separated into two parts—static prediction methods and dynamic prediction models.

According to the optimization targets, static prediction methods can be further classified into three types: distance-based methods, semantic similarity-based methods and deep learning methods. Among the distance-based methods, TransE [4] is a classical approach to interpret relations on KGs. TransE regards the representation of entities and relations as transitional vectors, the goal is to minimize the distance of representation in the triple $(s,r,o)$, i.e., $min\left|\right|s+r-o\left|\right|$. Based on the idea, TransD [13], TransR [14] and TransH [14] were proposed with different weight matrices to transfer entities’ vectors before scoring the distance loss. The semantic similarity-based methods, e.g., DistMult [5], use a bi-linear function to calculate the plausibility in the triple. Some studies on knowledge graph completion follow this idea, such as HolE [15] and Ripplenet [3]. The scoring function is generally formed as $f(s,r,o)=s^T{W}_{r}o$ where $W_r$ is a parameter matrix to represent the relation types. A popular genre of deep learning methods for entity prediction in KGs is GCN-based approaches, such as GAT [16], SAGE [17]. A GCN-based block consists of multiple layers of neural network blocks to generate hidden representations of entities which include rich semantic information of context. A common GCN block is formed as $h_s^{(l+1)}=\sigma ({\sum }_{m\in M_s}{g}_m(h_s^l,h_j^l))$ Here, $h_s^l,h_j^l$ represent the hidden representations of entity s and its related entity j in the l-th layer. $M_s$ denotes the set of neighbors of entity s. $g_m$ is a specific neural network function for propagating messages. For instance, Kifp et al. [18] propose a linear parameter matrix to transform representations of entities and their neighbors. GAT [16] uses a local attention weight to distinguish the importance of the target entity’s neighbors. SAGE [17] concatenates the embedding of a target entity and its neighbors as a type of feature vector which is able to reserve more original features of the target. Different from models mentioned above for graphs where there is only one type of relations, RGCN [19] is a notable approach which introduces a relational specific transformation function to deal with multiple relation types.

As static methods ignore the influence of time, they cannot model the evolutionary trend of facts on knowledge graphs. In order to predict future facts based on histories, dynamic prediction models try to train time-varying representation of facts to reflect the evolution over time. Several works modified static methods to adapt to the temporal change of data. One aspect of efforts adds extra weights or features to entities’ representations, such as Time-Aware [12], TA-TransE [11], DE-TransE [20]. The comparative experiments show that dynamic methods which learn the evolution of facts perform better. Time-aware [12] is an early work to predict the changes of relations on TKGs. It uses an asymmetric matrix to translate the relation matrix of TransE and add integer programming as constraints to capture temporal features. TTransE [21] uses a series of weights to represent the relations on different time. TA-TransE [11] directly defines the representation of time as a series of vectors. DE-TransE [20] creates a diachronic method to represent evolution of entities. Know-Evolve [10] and its follow-up Dyrep [22] use RNN-based models to create dynamic representation of entities. The other aspect of efforts uses sequence-encoder modeling methods to create extra hidden vectors standing for chronological features of facts [9]. GCRN [23] is the first sequence modeling method on TKGs. RE-NET [1] follows GCRN’s structure but adds a global vector to represent global states of whole facts at each time. Evolve-GCN [24] merges GCN block into a GRU [25] unit to update GCN’s weights which allows the GCN block adapts to relations at a different time. REGCN [26] designs a static properties algorithm to reflect the evolutionary trend of TKGs.

However, most of the previous dynamic prediction methods pay attention to extracting semantic features on entities and their neighbors, but fail to consider the interactions between entities and pairwise relations. Therefore, in this research, we try to make up for the deficiencies of previous methods through learning semantic interactions between entities and relations, and then combining them into the prediction model. We believe that these semantic interactions contain informative clues about context dependencies. Capturing these factors for inferring on TKGs holds promise for making the results more reasonable.

Therefore, we propose a GCN-based model, Enhanced Relation Graph Convolution Network (ERGCN) (code is available at https://github.com/Uynixu/ERGCN (accessed on 22 November 2022)), to accomplish the entity prediction task. The model especially focuses on learning the full semantic information of facts between relations and entities. We try to evaluate the performance of the model, and try to prove the necessity of adding the full semantic interaction between relations and entities into the model. We will compare the proposed models in this paper with previous models on relevant data through several experiments designed for the task and then reach a conclusion. Overall, the contributions in this paper can be summarized as below:

1. We test a new GCN-based method, named ERGCN, which takes context dependencies between pairwise entities and relations into account during training, and achieves better performance than previous methods;

2. We design a new approach to predict unseen facts on TKGs and compare it with different models to demonstrate the necessity of using the full semantic information of facts in relevant reasoning tasks.

2. Methodology

2.1. Problem Definition

We firstly give the following definitions used in this paper.

Definition 1

(Temporal knowledge graphs). A temporal knowledge graph (TKG) is represented as a set of chronological knowledge graphs with discrete time stamps, $\{G_1,G_2,\cdots ,G_T\}$, where each graph at time t is $G_t=(V,R,E_t),t\in [1,T]$. Here, V is the set of entities, R is the set of relation types, and $E_t$ is the set of edges. Each edge represents a fact which includes two entities linked by a relation type. Therefore, $E_t\subset \left\{{(s,r,o)}_t\right|s\in V,o\in V,r\in R\}$, where the triple ${(s,r,o)}_t$ stands for an event or fact that the subject entity s has the relationship r with object entity o at time t.

Definition 2

(Entity prediction task). Given the query $(s,r,?,t)$, the entity prediction task is to model the conditional probability distributions of all object entities under the subjects s when relation r is given and historical graphs in a fixed length of observation windows m, $\{G_{(t-m+1)},\cdots ,G_{t-1}\}$, are also given. The conditional probability distribution is represented as function $f_1$ in Formula (1). Meanwhile, we add a sub-query $(s,?,t)$ to constrain the reasoning process. The sub-query is to model the conditional probability distribution of all relation types when s and historical graphs are given. This probability distribution is represented as function $f_2$ in Formula (2). Therefore, our task is to find appropriate trainable functions $f_1$ to fit the conditional probability distribution of entities on TKGs. The formulations are shown as:

$$\begin{array}{c}\hfill p\left(o\right|s,r,t)=f_1(s,r,G_{t-1:t-m+1})\end{array}$$

(1)

$$\begin{array}{c}\hfill p\left(r\right|s,t)=f_2(s,G_{t-1:t-m+1})\end{array}$$

(2)

Definition 3

(Neighbor set of an entity). Given a snapshot of the TKG at time t, the entity s with its neighbor entities and linked relations types make a sub-graph $Su{b}^t\left(s\right)$. In this sub-graph, all nodes from the neighbor entity set of s, which is denoted as $N_e^t\left(s\right)$. Its linked relations constitute the neighbor relation set of s, denoted as $N_r^t\left(s\right)$.

2.2. Framework of the Model

Following the study of RENET [1], the key idea of our approach is to learn the local context dependencies near the central facts by our ERGCN block as well as to learn the global semantic structure of the whole graph on TKGs. The reasoning logic is based on the following assumptions: (1) Reasoning future facts can be regarded as a sequential inference processing via past relevant histories at different timestamps. (2) Temporal adjacent of facts may contain necessary informative patterns which imply the evolutionary trend of facts.

To approach the problem, our model is divided into two parts, the local learning unit and the global unit. The local learning unit is made for aggregating features in the neighborhood to extract the local dependency around the specific entity which stands for the local temporal features. As the same time, the goal of the global unit is to generate a single vector to represent the informative structure of the current graph as a whole, referred to as the global representation.

Both the local learning unit and the global unit follow the encoder–decoder structure. Here, the encoder part consist of certain layers of the GCN block and one layer of the GRU block. The GCN block integrates the dependencies of edges in a knowledge graph at each timestamp, and then the informative sequential features learned in GCN and their pairwise time presentations are merged into single vectors to represent the evolution of facts at different timestamp via the GRU block. Based on these various vectors and the static representation of entities and relations, temporal reasoning results at the next timestamps can be evaluated by the decoder function. The structure of our model that reflects the above idea is illustrated in Figure 2.

2.3. Local Learning Unit

To represent the semantic features of entities and relations, we use internal initialized embedding vectors, $E_{(s,o)}\in R^{n\times d}$ and $E_r\in R^{r\times d}$, to stand for entities and relations, respectively. Here, n, r stand for the number of entities and relation types, respectively, and d is the dimension size of each embedding.

Since static embedding vectors are not able to reflect the evolution characteristics of facts over time, two types of representations, the local temporal feature and the global vector, are proposed to reflect the evolution of facts. The local temporal feature $h_s^t$ summarizes the local information around a central entity until timestamp t, reflecting the change of relationships between these linked facts in the past. The global vector $g_t$ focuses on leaning the trend of background information of entire facts on the current knowledge graph. The two types of dynamic representation capture different aspect of informative knowledge from TKGs, which allows us to verify the reasoning process in different ways.

To capture the local structural information around the fact, GCN blocks are proposed to aggregate neighbor information and transform them into a single representation standing for the main feature of the central entity. The problem is that previous GCN blocks used in knowledge graphs ignore the semantics of relations, and some recent models only regard relation types as a part of entities. However, classical knowledge graph embedding studies show that semantic features from entities and relations have different effects on the performance in the model. To illustrate this divergence, we introduce a new GCN algorithm, which uses the full semantic information of facts to create representations of facts, named ERGCN. The aggregator is formally defined as follows:

$$\begin{array}{c}\hfill h_{s,t}^{l+1}=W_0^l{h}_{s,t}^l+\frac{1}{n}\sum _{r\in N_r^t\left(s\right)}\sum _{o\in N_e^t\left(s\right)}(W_{r,1}^l{e}_o+W_{r,2}^l{e}_r)\end{array}$$

(3)

Here, $h_{s,t}^l$ stands for the neighborhood message of entity s at the l-th layer. $W_0^l$ and $W_{r,1}^l,W_{r,2}^l$ are trainable parameters for self-loop and aggregating features at the l-th layer. $e_o,e_r$ represent the embedding of entities and relations. n is the number of neighbor of entity s.

Therefore, the local historical representation of entity s at time t can be illustrated as a sequence of the neighborhood message in an observed length m:

$$\begin{array}{c}\hfill h(s,t)=\{h_{s,t-1},h_{s,t-2},\cdots ,h_{s,t-m+1}\}\end{array}$$

(4)

Then, we update the state of the local temporal feature for query and its sub-query via a GRU block:

$$\begin{array}{c}\hfill H_s^t=GR{U}_1\left([h_m(s,t):T_m\left(t\right)]\right)\end{array}$$

(5)

We use the final hidden state vector $H_s^t$ to represent the local temporal feature of entity s at time t. $T_m\left(t\right)$ is the sequential temporal features trained in the global unit and it will be discussed in the next part. The symbol: represents the concatenation operation.

2.4. Global Unit

Distribution of entities on certain knowledge graphs represents specific temporal information to imply the evolutionary trend of facts. Therefore, we try to represent these global evolutionary trends by modeling the entity distribution over time. We assume that the entity distributions depend on historical graph features at the last m steps. Therefore, the entity distribution is modeled by function $f_3$ in Formula (6), where the current graph embedding vector $T_t$ is inputs:

$$\begin{array}{c}\hfill p\left(s\right|t)=f_3\left(T_t\right)\end{array}$$

(6)

To learn the graph embedding, we propose the global unit to capture the global structural state of the entire current graph and record the evolutionary trend of the state. To capture the global structural state at each TKG, we use our ERGCN block to learn the semantic vectors of all entities $\left\{h_{s,t}\right\}$ and then propose an element-wise max-pooling operation $f_{max}$ to represent the current global state:

$$\begin{array}{c}\hfill g_t=f_{max}\left(\left\{h_{s,t}\right\}\right)\end{array}$$

(7)

Then, we use the graph historical sequence in the last timestamps m to represent the evolutionary trend:

$$\begin{array}{c}\hfill g_m\left(t\right)=\{g_{t-1},g_{t-2},\cdots ,g_{t-m+1}\}\end{array}$$

(8)

To reflect the evolutionary trend from $g_m\left(t\right)$, we use the hidden state trained from a GRU block:

$$\begin{array}{c}\hfill T_t=GR{U}_2\left(g_m\left(t\right)\right)\end{array}$$

(9)

$T_t$ summarizes the evolutionary trend of the whole graph with a global view. Obviously, a neighbor message aggregated from ERGCN only provides a local view around the facts. Therefore, many context dependencies and semantic interactions between distant facts lose if we only focus on the local views. To compensate for this drawback, we use the graph embedding as a complement of the local views to represent a global view of whole facts. Then, we define the historical sequences of global embedding $T_m\left(t\right)$ as the global temporal features in an observed windows with length m:

$$\begin{array}{c}\hfill T_m\left(t\right)=\{T_{t-1},T_{t-2},\cdots ,T_{t-m+1}\}\end{array}$$

(10)

2.5. Decoding Process

To answer the query and sub-query, the conditional distributions of predicted objects $p\left({\overline{o}}_t\right|s,r)$ and relations $p\left({\overline{r}}_t\right|s)$ are modeled by two linear functions. The formulas are presented as Formula (11) and (12)

$$\begin{array}{cc}\hfill p\left(\tilde{o}\right|s,r,t)& =[H_s^t;e_s;e_r]W_o^{\top }+b_o\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill p\left(\tilde{r}\right|s,t)& =[H_s^t;e_s]W_r^{\top }+b_r\hfill \end{array}$$

(12)

As the entities prediction task is considered as a multi-classification task, cross-entropy loss is selected as the loss function. For simplicity of expression, we omit the notations of prediction in Formula (13). The loss function is as follows:

$$\begin{array}{c}\hfill L=-\sum _{{(s,r,o)}_t\in G_t}logp\left(o\right|s,r,t)+\lambda logp\left(r\right|s,t)\end{array}$$

(13)

Here, $\lambda$ is a hyper-parameter to balance the importance between two parts. In entity prediction tasks, we aim to predict objects depending on relevant subjects and their linked relations.

We summarize the whole training process as shown in Algorithm 1. Our training approach is divided into two steps. In the first step, during the preset maximum number of iterations $epochs$, we generate the graph embedding from the global unit and save the optimal results for the next step. It is noticed that we choose 2-norm as the loss function in the global model to fit the temporal distribution of all subject entities $D_{s,t}$. In the second step, we use the local learning unit to estimate the conditional probability distribution of object entities $\widehat{p}\left(o\right|s,r,t)$ and answer the queries. It is worth noting that, at the preset maximum iteration number $epochs$, we regard the model with the best $MRR$ ratio as the best situation of our model.

Algorithm 1: Learning algorithm of ERGCN

3. Results

3.1. Datasets

To evaluate the performance of ERGCN, we selected six representative datasets widely used in previous works for the entity prediction task on TKGs. They are YAGO [27], WIKI [21], ICEWS14 [11], ICEWS15 [11], ICEWS18 [28] and GDELT [29]. YAGO and WIKI include temporal facts extracted from open-source datasets. The series of ICEWS are event-based datasets from the Integrated Crisis Early Warning System. GDELT is from the Global Database of Events, Language and Tone. The statistical details of all datasets are shown in

Table 1. Dataset statistics.

Dataset	N_Train	N_Valid	N_Test	Entities	Relations	Time Gap
YAGO	161,540	19,523	20,026	10,623	10	1 year
WIKI	539,286	67,538	63,110	12,554	24	1 year
GDELT	1,734,399	238,765	305,241	7,691	240	15 min
ICEWS14	74,845	8,514	7,371	6,869	230	24 h
ICEWS15	368,868	46,302	46,159	10,094	251	24 h
ICEWS18	373,018	45,995	45,995	23,033	256	24 h

.

3.2. Evaluation Metrics

In the experiments, MRR and Hits@1, 3, 10 are selected as the metrics for entity prediction. Because the Hit@1 in YAGO and WIKI are not reported in previous works [1,26], we only record Hit@3, 10. It is worth noting that some previous works use different filter settings to evaluate the performance of their works. Hence, in order to make the results comparable, we only report the original results (named $rawmetric$) of each model.

3.3. Benchmarks

Our ERGCN model is compared to two types of models: static KG models and dynamic TKG reasoning models. Here, Distmult [5], ConvE [6], RGCN [19], HyTE [30] are selected as static models. On the other hand, TTransE [21], TA-Distmult [11], R-GCRN [23], RENET [1], REGCN [26] are selected as dynamic methods released in recent years.

3.4. Implementation Settings

The embedding dimension d is 200 in both the local learning unit and the global unit. The number of ERGCN layers in the local learning unit is 1, but that in the global unit is 2. The dropout rate is 0.2 in both units. We test the length of history m from 1 to 10 and find that the optimal length is 5 in all datasets. The experiments include one-step inference in the validation and test. All experiments only report the results of reasoning the objects in test set with the raw metric. We obtain the results in five runs on each datasets and report the average of the results.

3.5. Result Analysis

The experimental results are illustrated in

Table 2. Experimental results of entity prediction on ICEWS14, 15 and 18 in raw metrics.

Model	ICEWS14				ICEWS15				ICEWS18
	MRR	hit1	hit3	hit10	MRR	hit1	hit3	hit10	MRR	hit1	hit3	hit10
Distmult	20.32	6.13	27.59	46.61	19.91	5.63	27.22	47.33	13.86	5.61	15.22	31.26
ConvE	30.30	21.30	34.42	47.89	31.40	21.56	35.70	50.96	22.81	13.63	25.83	41.43
RGCN	28.03	19.42	31.95	44.83	27.13	18.83	30.41	43.16	15.05	8.13	16.49	29.01
HyTE	16.78	2.13	24.84	43.94	16.05	6.53	20.2	34.72	7.41	3.11	7.33	16.01
TTransE	12.86	3.14	15.72	33.65	16.53	5.51	20.77	39.26	8.44	1.85	8.95	22.38
TA-Distmult	26.22	16.83	29.72	45.23	27.51	17.57	31.46	47.32	16.42	8.61	18.13	32.51
R-GCRN	33.31	24.08	36.55	51.54	35.93	26.23	40.02	54.63	23.46	14.24	26.62	41.96
RENET	35.77	25.99	40.10	54.87	36.86	26.24	41.85	57.60	26.17	16.43	29.89	44.37
REGCN	37.78	27.17	42.50	58.84	38.27	27.43	43.06	59.93	27.51	17.82	31.17	46.55
ERGCN (ours)	37.95	28.77	42.54	55.32	43.65	33.48	48.92	62.94	28.29	18.46	32.60	47.47

and

Table 3. Experimental results of entity prediction on WIKI, YAGO and GDELT in raw metrics.

Model	WIKI				YAGO				GDELT
	MRR	hit1	hit3	hit10	MRR	hit1	hit3	hit10	MRR	hit1	hit3	hit10
Distmult	27.96	-	32.45	39.51	44.05	-	49.70	59.94	8.61	3.91	8.27	17.04
ConvE	26.03	-	30.51	39.18	41.22	-	47.03	59.90	18.37	11.29	19.36	32.13
RGCN	13.96	-	15.75	22.05	20.25	-	24.01	37.30	12.17	7.40	12.37	20.63
HyTE	25.40	-	29.16	37.54	14.42	-	39.73	46.98	6.69	0.01	7.57	19.06
TTransE	20.66	-	23.88	33.04	26.10	-	36.28	47.73	5.53	0.46	4.97	15.37
TA-Distmult	26.44	-	31.36	38.97	44.98	-	50.64	61.11	10.34	4.44	10.44	21.63
R-GCRN	28.68	-	31.44	38.58	38.58	-	43.71	48.53	18.63	11.53	19.81	32.42
RENET	30.87	-	33.55	41.27	46.81	-	52.71	61.93	19.60	12.03	20.56	33.89
REGCN	39.84	-	44.43	53.88	58.27	-	65.62	72.97	19.15	11.92	20.41	33.19
ERGCN (ours)	51.28	-	55.78	62.28	55.25	-	64.22	70.69	18.96	11.65	20.24	33.14

. ERGCN outperforms the benchmarks on WIKI and ICEWS. Especially, the performances on WIKI rise significantly. The experimental results show that it is helpful to make full use of semantic information in entity prediction tasks. Obviously, ERGCN works better than static models because ERGCN captures the evolutionary pattern of facts. Thus, it can achieve higher performance when testing on unseen temporal knowledge graphs. Compared with recent dynamic models, such as REGCN and RENET, our ERGCN overtakes the others in most tasks. Although ERGCN does not have the best performance on YAGO and GDELT, its performance is very close to the best results. Therefore, ERGCN’s overall performance is better. The results verify the importance of differential treatment for various relation types, which contains much useful semantic information about the temporal dependencies of facts. As mentioned above, we only use a one-layer ERGCN block in the tasks. The reason is that the performance on the high-accuracy metrics, such as Hit@1 and Hit@3, drops significantly when the layers are more than one. This phenomenon may indicate that ERGCN focuses on 1-hop neighborhoods, while long-distance relationships may interfere with the entity reasoning process. However, ERGCN still outperforms the other dynamic models and these results suggest that information in the 1-hop neighborhood is underutilized in previous approaches, and that ERGCN can extract these information more effectively.

ERGCN is similar to RENET, but we pay more attention to applying full semantic information of facts. By capturing more precise temporal representation of sequential knowledge, ERGCN overtakes RENET in the majority of the datasets and our results are close to those of RENET on GDELT. Different from REGCN, which includes a new recurrent block to learn sequential histories of entities, the structure of ERGCN is simple, but the performance is good.

Compared with the previous best results on WIKI, ERGCN has improved 11.44% in MRR metric, 11.35% in Hit@3 metric and 8.40% in Hit@10 metric, respectively. In this dataset, temporal facts are widely collected from the open-source dataset, Wikipedia. The informative interactions between different entities are discrete, temporal dependencies around facts are often limited in small areas, and then 1-hop neighborhoods contain the most important structural information of dependencies. Different from concentrating attention on neighbors’ entities, ERGCN concerns the interaction between entities and their linked relation types, which provides more relevant structural dependencies between facts.

The results on ICEWS show that, compared with other methods, using more semantic information of facts provides more accurate temporal characteristics for the reasoning process. In terms of the MRR metric, the performance of ERGCN is 0.17/5.38/0.78% higher than the previous best on ICEWS14/ICEWS15/ICEWS18, respectively. Moreover, ERGCN improves Hit@1,3,10 in each dataset as well. The ICEWS series dataset is event-based and facts here often change frequently. Therefore, learning the relation type becomes a key point, which is able to provide basic information indicating the trend of the facts. Different from previous studies, ERGCN focuses on learning the interaction between entities and relation types, which reserves various temporal dependencies. If these complex structural dependencies are ignored, there will be a lot of loss in modeling sequential patterns. The results demonstrate that ERGCN is more capable of learning the complex temporal structures in TKG.

ERGCN’s performances on YAGO and GDELT are a little worse than the previous best. YAGO consists of lots of temporal facts with repetitive patterns. ERGCN does not handle this problem well, but this phenomenon does not appear in other datasets. GDELT includes massive concepts and definitions that follow specific rules. This situation makes entity reasoning difficult. The results of all models are similarly poor in GDELT.

It is noticed that the results of all methods on ICEWS18 and GDELT are still at a low level. For example, the $MRR$ is under 20% and 30% in GDELT and ICEWS18, respectively. This phenomenon shows that capturing the evolutionary trends of facts on TKGs is still a hard challenge and we need further studies to identify the complex dependent relationships between facts at different time.

3.6. Ablation Study

In this part, we discuss the effect of each part in ERGCN. To test the contribution of each part in ERGCN, we conduct the ablation studies in WIKI and ICEWS18. To test the importance of graph embedding, we remove the global unit in our approach, named as $ERGCNwtg$. To illustrate the essential context semantic information, we remove the learnable weight $W_{r,2}$ in ERGCN, named $ERGCNwtr$. To demonstrate the necessity of the semantic interaction, we remove the sub-query when training, named $ERGCNwtc$. The further discussion of the contributions of each part in ERGCN is reported in

Table 4. Ablation studies on WIKI.

Model	MRR	hit1	hit3	hit10
ERGCN	51.28	44.52	55.78	62.28
ERGCN wtg	40.87	31.21	48.71	54.36
ERGCN wtr	49.09	42.71	53.41	59.07
ERGCN wtc	49.12	42.67	53.55	59.22

and

Table 5. Ablation studies on ICEWS18.

Model	MRR	hit1	hit3	hit10
ERGCN	28.29	18.46	32.60	47.47
ERGCN wtg	26.97	17.31	31.94	46.71
ERGCN wtr	27.13	16.68	31.18	47.07
ERGCN wtc	26.88	16.59	30.98	46.77

.

To illustrate how the global embedding affects the results, we conduct experiments without the global model. The results are denoted as $ERGCNwtg$. It can be seen that removing the global embedding results in a significant decline in the performance on WIKI and ICEWS18. When we remove the global embedding, ERGCN will lose lots of temporal dependencies around the whole graphs and the model will only focus on learning the neighbor structural information.

After removing the independent weight on relation types from the model, the model becomes $ERGCNwtr$. Therefore, our ERGCN becomes similar to the other studies where entities and relations share the same transform weights in training process. Since the correlations between various entities and relations are usually different, after removing the weight on relation types from the model, we will lose specific features between certain combinations of facts. The results prove our prediction as the results decrease by about 1–2% in WIKI and ICEWS18.

The results are labeled as ERGCN wtc, where the relation constraint between entities and relations are removed. The relation constraint can be seen as interactions between entities and their linked relations, which helps the model obtains the combination features of facts.

4. Conclusions

After reviewing previous literature, we found that the interaction of semantic features between entities and relations are often omitted and many studies focus on designing methods to extract features on entities and their neighbors. We propose different approaches to model the interaction of semantic features between entities and relations and we propose the Enhanced Relational Graph Convolution Network (ERGCN), which is modified from previous GCN models to assemble relations and entities together. Although experiments show that relations themselves can provide less information for prediction tasks than entities, combining relations and entities together enhances the context information between entities and relations and benefits the tasks. The results of experiments show that the improvement is significant.

In future work, we are going to apply ERGCN in different datasets or applications to verify the effectiveness of this model and we will also try other possible methods to further extract information from the interaction between entities and relations. We notice that our method focuses on aggregating closed information around the source entity, but it is hard to utilize the information of long-distance relational paths. Finding ways to capture this information to promote the model’s performance is an important part of our further work.