1. Introduction and Related Work
This work is a comprehensive treatment of filesystem synchronization and conflict resolution on a simple but powerful theoretical model of filesystems. Synchronizing diverged copies of some data stored on a variety of devices and locations is an important and ubiquitous task. The last two decades have seen tremendous advancement, both theoretical and practical, in the closely related fields of distributed data storage [
1,
2] and group editors [
3,
4]. This progress has been based on, and has expanded significantly, two competing theoretical frameworks: Operational Transformation (OT) and Conflict-free Replicated Data Types (CRDT). OT appeared in the seminal work [
5] and was refined later in [
4]. The general idea is that operations are enriched with the context in which they were generated. Before applying them, they are transformed depending on the context of their origin and the context where they are to be applied. Main applications are collaborative editors, the most notable example being Google Docs [
6]. The core concept of CRDT is commutativity, see [
1,
2]. Basic data types with special operators are devised so that executing the operators in different orders yield the same results. Examples are counters or sets with add and delete operators. The basic types are used as building blocks in more complex applications such as collaborative editors [
7], the commercial product Riak [
8], and others.
Both OT and CRDT have been successfully applied in a variety of synchronization tasks [
9,
10]. Filesystem synchronization, however, fits very poorly into these frameworks, mainly because it works under a completely different modus operandi: constant, low latency communication in OT and CRDT versus a single data exchange in filesystem synchronization; frequent loose synchronization with eventual convergence requirement versus a single but complete synchronization; small number of differences versus significant structural differences accumulated during an extended time period; and so on. Consequently, for a theoretical investigation of filesystem synchronization, we follow a traditional framework instead, described in e.g., [
11] and depicted in
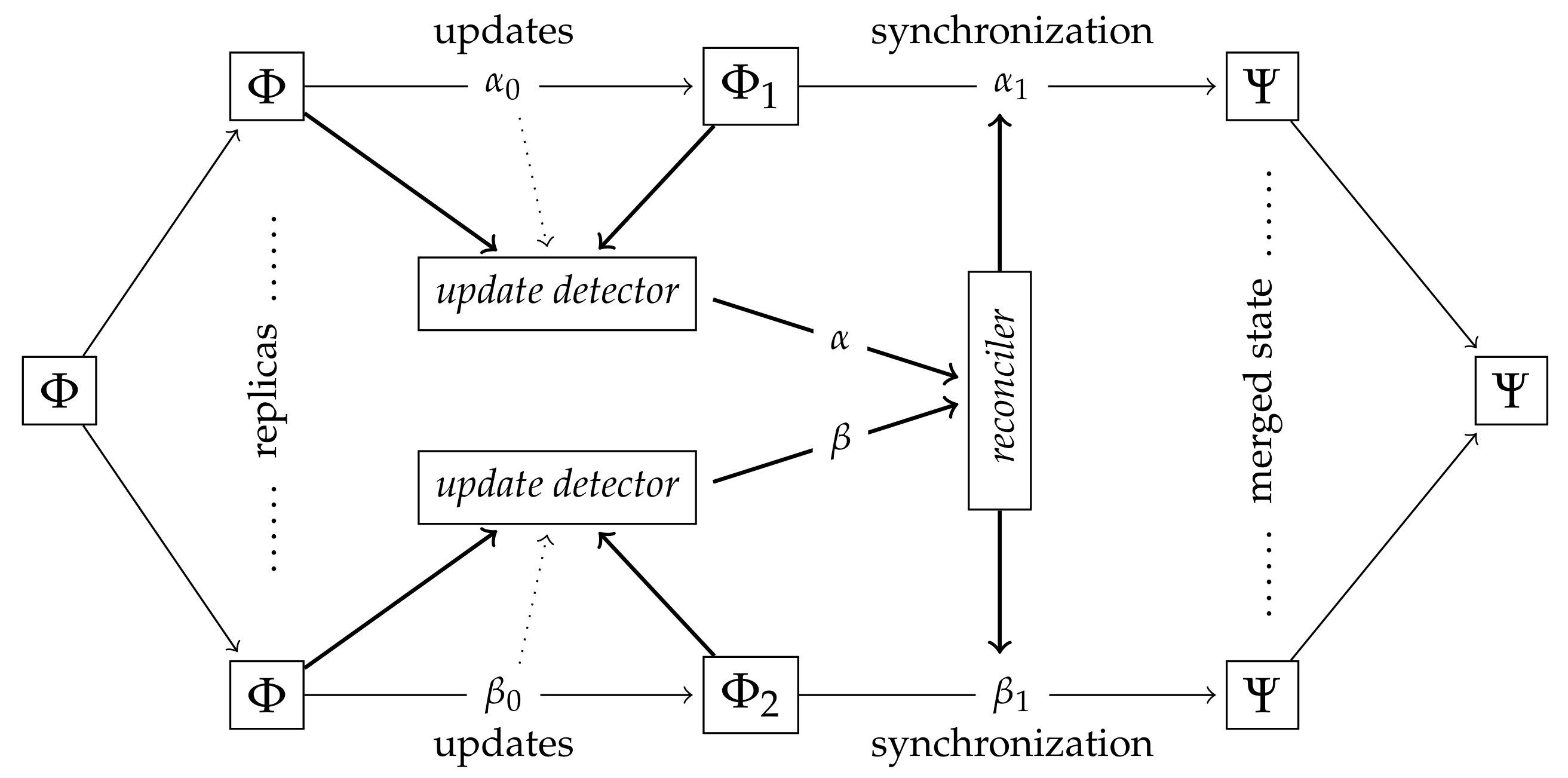
Figure 1 adapted from [
12].
Two identical replicas of the original filesystem are updated independently, yielding the divergent replicas and . In the state-based case the update detector receives the original () and the current ( or ) states, and generates the update information (or ) describing the differences between the original filesystem and the replica. In the operation-based case the update decoder has access to the performed operations () only. The reconciler receives the information provided by the update detectors and generates the synchronizing instructions and , respectively. These instructions, applied to the replicas and , create the identical merged state Ψ.
In order to reach such a common synchronized state, existing theoretical and practical filesystem synchronizers, such as [
10,
13,
14,
15,
16,
17], apply some conflict-resolution strategy. They identify all (or some) of the conflicts, then apply their strategy to the conflicts one at a time. These algorithms are typically fixed and defined by some rationale or heuristics, or dictated by the underlying technology. In contrast, we
define what comprises a synchronized state. Intuitively, it is a maximal consistent merger of the replicas, meaning that no further changes can be applied to the merged state from those that were applied to the replicas during the update phase. Then we proceed to prove that every such maximal state (and only these states) can be reached by resolving the conflicts in some order.
In the meticulous survey [
16] of existing theoretical and practical filesystem synchronizers it has been observed that “resolving conflicts is an open problem where [...] most academic works present arbitrary resolution methods that lack a rationale for their decisions” (page i), and that “a file system can be affected by more than one conflict at once, which has not been discussed in related academic works” (page 65). By presenting, for the first time, a complete analysis of the synchronization process for two replicas of a theoretical filesystem model, we fill these gaps.
Our Contribution
This paper is a complete analysis of the synchronization process of two replicas of a theoretical filesystem. Our filesystem model together with the commands considered—such as
create,
rmdir, or
edit—are discussed in Secion
Section 3. The changes between the original replica and the locally updated versions are captured by a special command set as defined in
Section 4, which also defines algorithms generating this update information.
The important question of which filesystems can, in general, be considered to be a synchronized state of two divergent replicas is tackled in
Section 5. Our definition captures this notion in its full generality without prescribing how the synchronized state can be reached. Providing such a declaration-based definition of the synchronized state is one of our main contributions.
Section 6 presents the generic synchronization algorithm based on conflict resolution. By using different strategies to resolve conflicts, any of the synchronized states allowed by our definition, and only those, can be the result of the algorithm. Finally,
Section 7 summarizes the results and lists open problems and directions for future research.
2. Methodology
Our filesystem model, defined in
Section 3, is arguably simple, but it retains all important structural properties of real filesystems. It is this simplicity that allows us to exploit a rich and intriguing algebraic structure [
12,
18] which eventually leads to the claimed theoretical results. In
Section 7 we discuss some possible extensions of the filesystem model.
Depending on the data communicated by the replicas, synchronizers are categorized as either
state-based or
operation-based [
1,
16]. In state-based synchronization replicas send their current versions of the filesystem, or merely the differences (called
diffs) between the current states and the last known synchronized state [
19]. Operation-based synchronizers transmit the complete log (or trace) of all operations performed by the user [
13]. The synchronization method of this paper is reminiscent of operation-based one, but can also be considered, with similar overhead, to be state-based. A set of virtual filesystem operations (commands) will be defined in
Section 3. Each of these commands have a clear and intuitive operational meaning, but are not necessarily available to the end-user. The current state of the filesystem is described by a special—called
canonical—sequence of virtual commands, which transforms the original filesystem to the actual replica. The
update detector can generate this canonical sequence from the operations performed by the user on the replica (operation-based) as well as from the differences between the original and final state (state-based). On
Figure 1 these sequences correspond to the information in
and
passed to the reconciler.
Filesystem synchronization must resolve all conflicts between the replicas. Conflict resolution, however, should be “intuitively correct,” i.e., discarding all changes made by both replicas is not a viable alternative. The majority of commercially or theoretically available synchronizers do not present a rationale to explain their concrete conflict resolution approach [
16]. Two notable exceptions are [
10] and [
9] which describe high-level consistency philosophies. In [
10] the main principles are (1)
no lost update: preserve all updates on all replicas because these updates are equally valid; and (2)
no side effects: such as a merge where objects unexpectedly disappear. While these principles intuitively make sense, it is easy to see that neither could possibly be upheld for every conflict; even the authors provide counterexamples. In [
9] the relevant consistency requirements are worded as follows:
- R1
intention-confined effect: operations applied to the replicas by the synchronizer must be based on operations generated by the end-user; and
- R2
aggressive effect preservation: the effect of compatible operations should be preserved fully; and the effect of conflicting operations should be preserved as much as possible.
These requirements are in fact variations of the OT consistency model, see for example the notion of intention preservation in [
4]. (We note that the other two OT principles—convergence and causality preservation—do not apply to filesystem synchronizers.)
In agreement with R1 and R2 we declare what a synchronized state is, rather than present an algorithm which generates it. Our declaration can be outlined as follows. Suppose that the two replicas and are represented by the canonical sequences and , respectively, that is, and , where is the result of applying the command sequence to . The synchronized or merged state Ψ is determined by the canonical sequence as such that
- C0
is applicable to the original filesystem ,
- C1
every command in can be found either in , in , or in both, and
- C2
is maximal, i.e., no canonical sequence adding more commands to can satisfy both C0 and C1.
Condition C0 is the obvious requirement that the synchronizer must not cause errors. Condition C1 ensures that the synchronization satisfies the intention-confined effect (no surprise changes in the merged filesystem) requirement R1 as should consist only of commands which were supplied by the replicas. The other consistency requirement R2 is guaranteed by C2 as is maximal, therefore it preserves as much of the intention of the users as possible. Note that this definition of a synchronized state is never vacuous. There are only finitely many sequences which satisfy C0 and C1 (as every command in comes from either or and no repetitions are allowed), and there are at least two, namely and . Because of this, the empty sequence (undoing all changes) will not satisfy C2 (assuming one of and is not empty), in line with our requirements.
The declaration-based synchronization is intuitively clear, easy to understand, and does not use any predetermined conflict-resolving policy. An operational characterization is proved in Theorem 2. The essence of this theorem is that any merged filesystem can be generated from the replica, say , by
- 1.
rolling back some of the commands in , followed by (*)
- 2.
applying some commands from the other sequence ,
and vice versa for the other replica. The commands rolled back represent a minimal set whose removal resolves all conflicts. These commands also give users a clear understanding of the changes the synchronizer wants to perform on their filesystem. They are also helpful when some of the rolled-back commands should be introduced again after the merging (doing a redo of the undo).
Turning to traditional conflict-based synchronization,
Section 6 proves that any declaration-based merged state, and only those states, can be the result of a conflict-based synchronization algorithm. For each pair of canonical sequences describing the replicas to be synchronized we define what the conflicting command pairs are. Their resolution uses the winner/loser paradigm: the winner command is accepted while the loser command is discarded. It turns out that resolving a conflict may automatically resolve some of the subsequent conflicts, but no new conflicts are created. Using this result the outcomes of different conflict resolving policies can be investigated easily. In particular, the
iterative approach [
16] always works, which applies all non-conflicting commands, resolves, in any way, the first conflict (which might automatically resolve other existing conflicts), and iterates.
3. Definitions
This section defines the basic notation which will be used throughout the rest of the paper. The exposition follows [
12,
18] with some substantial modifications. Some results from these papers are included without proof.
3.1. Namespace and Filesystems
Our filesystem model is arguably simplistic, nevertheless it captures all important aspects of real-word implementations. In spirit, it is a mixture of
identity- and
path-based models [
10,
16]. Objects are stored in nodes, which are uniquely identified by fixed and predetermined
paths. The set of available nodes is fixed in advance, and no path operations are considered. Filesystems are required to have the
tree-property at all times: in a given filesystem along any branch starting from any of the root nodes, there must be zero or more
directories, zero or one
file, followed by
empty nodes. Our model does not support
links (but see
Section 7.4), thus the namespace—the set of available nodes or paths—forms a collection of rooted trees. Filesystems are defined over and populate this fixed namespace.
Formally, the namespace is a set endowed with the partial function returning the parent of every non-root node (it is not defined on roots). If then n is the parent of m, and m is a child of n. For two nodes we say that n is above m, or n is an ancestor of m, and write if for some . As usual, means or . As the parent function induces a tree-like structure, ≼ is a partial order. Two nodes are comparable if either or , and they are uncomparable or independent otherwise.
A
filesystem Φ populates the nodes of the namespace with values. The value stored at node
is denoted by
. This value can be
indicating that the node is
empty (no content, not to be confused with the empty file); can be
indicating that the node is a
directory; otherwise it is a
file storing the complete content (which could happen to be “no content”). We use
,
and
to denote the
type of the content corresponding to these possibilities. While there is only one value of type
and one value of type
(see
Section 7.3 for a discussion on lifting this limitation), there are many different file values of type
representing different file contents.
3.2. Internal Filesystem Commands
The synchronizer operates using a specially designed and highly symmetrical set of
internal filesystem commands. They each modify the filesystem at a single node only, and contain additional information usually not thought of as part of a command which allows them to be inverted, and makes them amenable to algebraic manipulation. Inventing such a command set was one of the main contributions of [
18].
The commands basically implement creating and deleting files and directories. Modifying a part of a file only is not available as a command; whenever a file is modified, the new content must be supplied in its entirety. Still, commands issued by a real-life user or system can be easily transformed into the internal commands; for example, the move or rename operation can be modeled as a sequence of a delete and a create.
The set of the internal commands is denoted by , and each command has three components, written as , as follows:
is the node on which the command acts,
x is the content at node n before the command is executed (precondition), and
y is the content at node n after the command was executed.
Thus rmdir corresponds to the internal command , which replaces the directory value at n by the empty value. The command creates a directory at n, but only if the node n has no content, i.e., there is no directory or file at n (a usual requirement for mkdir). For files f1 and the command replaces f1 stored at node n by the new content f2. This latter command can be considered to be an equivalent of edit.
Applying to a filesystem is written as the left action . The command is applicable to if
contains x at the node n, that is, , and
after changing the content at n to y the filesystem still has the tree property.
If is not applicable to then we say that breaks the filesystem, and write . If does not break , then is the filesystem where every node has the same value as in except for the node n where the new content is y. Command sequences are applied from left to right, thus . The composition of sequences and is written as ; occasionally we write it as to emphasize that is to be executed after . A sequence breaks if one of its commands is not applicable. More formally, breaks if either breaks , or breaks .
Two additional commands will be used, which are denoted by and , respectively. In practice they do not occur, and cannot be elements of command sequences, but are useful in algebraic derivations. The command breaks every filesystem, while acts as identity: and for every filesystem .
The command sequences and are semantically equivalent, written as if they have the same effect on all filesystems: for all . We write to denote that β semantically extends α, that is, for all filesystems that does not break. Clearly, if and only if both and . The sequence is non-breaking if there is at least one filesystem which does not break. This is the same as requesting .
The inverse of is . For a command sequence its inverse is defined in the usual way: consists of the inverse of the commands in written in reverse order. This inverse has the expected property: if does not break , then . In particular, .
3.3. Command Types and Execution Order
A node value has type , , or depending on whether it is the empty value, a directory, or a file. For a command the type of x is its input type and the type of y is its output type. Depending on their input and output types commands can be partitioned into nine disjoint classes. To make their descriptions clearer, we use patterns. The command matches the pattern if the type of x is listed in and the type of y is listed in . In a pattern the symbol • matches any value. As an example, every command matches the pattern .
Structural commands change the type of the stored data, while transient commands retain it. In other words, commands matching , or are structural commands, while those matching , or are transient ones. Commands with identical input and output values are null commands. Every null command is transient, and transient commands which are not null match the pattern . If is a null command, then meaning that does not change the filesystem (but can break it), and if then is a null command.
Structural commands are further split into constructors and destructors. Constructor commands upgrade the type from to to , while destructors downgrade it. That is, constructors are commands matching or , while the destructors match or .
Some command pairs on parent–child nodes can only be executed in a certain order. This notion is captured by the binary relation with the meaning that must precede in the execution order.
Definition 1 (Execution order). For a command pair the binary relation holds if the pair matches either or . An ≪-chain is a sequence of commands such that . An ≪-chain connects its first and last element.
The first case in Definition 1 of the ≪ relation corresponds to the requirement that a directory cannot be deleted when its descendants are not empty. The second case requires that before creating a file or directory, the directory holding it should exist. Observe that
implies that both
and
are structural commands on parent–child nodes, and either both are constructors or both are destructors. It means that elements of an ≪-chain match either the pattern
where
is the parent of
(we move up along a branch), or they match
where
is the parent of
(we move down).
Figure 2 illustrates the structure of ≪-chains. The circles represent the nodes on which the commands act: the top, input type row denotes the types of their values before executing the commands, while the bottom, output type row shows the types of their values afterwards. The black arrows point towards the parent nodes, and the read arrows indicate the execution order.
4. Canonical Sequences and Sets
Our synchronizer, including the update detector, relies heavily on the algebraic structure of internal command sequences. The theory of this structure has been developed in [
12,
18]. We provide high-level overviews of the proofs whenever appropriate to make this paper self-contained and also available to non-experts. For full proofs the reader is referred to the original papers.
To understand the semantical properties of command sequences, the first step is to investigate command pairs and determine when they commute, and when they require a special execution order. Proposition 1 covers the case when the commands act on the same node, and Proposition 2 considers command pairs on different nodes.
Proposition 1 ([
12], Proposition 4).
Suppose are on the same node n. Then one of the following two possibilities hold:- (a)
for some also on the same node n,
- (b)
, that is, the pair breaks every filesystem.
Proof. Suppose and . If then (a) holds with . If then (b) holds: if does not break the filesystem, then it leaves at node n. Now requires there, but finds a different value, thus breaks the filesystem. □
For two commands we write to mean that the nodes they act on are uncomparable, i.e., the nodes are different and neither is an ancestor of the other.
Recall that is a null command if it has the same input and output value, that is, it is of the form .
Proposition 2 ([
12], Proposition 5).
Suppose σ and τ are non-null commands on different nodes. Then- (a)
if then , and
- (b)
if then if and only if .
Proof. By checking all possibilities. □
4.1. Canonical Sequences
Informally, canonical sequences are the “clean” versions of non-breaking command sequences. The initial definition is a mixture of syntactical and semantical properties. Proposition 3 defines an algorithm which converts any sequence into a canonical one purification, and Theorem 1 gives a complete syntactical characterization. An important consequence of this characterization is that the semantics of a canonical sequence is determined uniquely by the unordered set of commands it contains. It means that the order of the commands—up to semantical equivalence—can be recovered from their set only.
Definition 2 (Canonical sequences). A command sequence is canonical if
- (a)
it does not contain null commands, that is, a command of the form ,
- (b)
no two commands in the sequence are on the same node, and
- (c)
it is non-breaking.
Conditions (a) and (b) are clearly syntactical, and can be checked by looking at the commands in the sequence. In Theorem 1 below we give a purely syntactical characterization of canonical sequences. Before stating the theorem we show that canonical sequences are the “clean” versions of arbitrary command sequences.
Proposition 3 ([
18], Theorem 27).
For every non-breaking command sequence α there is a canonical sequence such that , that is, if α does not break Φ, then both α and have the same effect on Φ. Proof. Null commands can be deleted from as they do not change the filesystem (but may break it). Suppose has two commands on the same node. Choose two which are closest to each other; let these be and , both on node n. The output value of must be the same as the input value of (as is non-breaking and the value at node n does not change between and ). If and are not next to each other, then using Proposition 2, either can be moved forward by swapping it with the immediately following command (which, by assumption, is on a different node), or can be moved backward by swapping it with the immediately preceding command. If none of those swaps can be done, then would break every filesystem. Eventually and can be moved next to each other. In this case, however, Proposition 1 implies that can be replaced by a simgle command. □
This proof is constructive and specifies a quadratic algorithm which transforms any non-breaking sequence into a canonical one. To state the purely syntactical characterization of canonical sequences we need further definitions.
Definition 3. Let α be a command sequence.
- (a)
α honors ≪, if for commands , σ precedes τ whenever .
- (b)
α is≪-connected, if for any two commands , either , or σ and τ are connected by an ≪-chain (see Definition 1) whose elements are in α.
Theorem 1 (Syntactical characterization of canonical sequences). A command sequence is canonical if and only if
- (a)
it does not contain null commands,
- (b)
no two commands in the sequence are on the same node,
- (c1)
it honors ≪, and
- (c2)
it is ≪-connected.
Proof. Let be a canonical sequence according to Definition 2. To see that if either (c1) or (c2) fails then breaks every filesystem, use induction on the length of . This shows that if contains commands on nodes n and m which lie on the same branch, then must contain commands on every node between n and m in the right order.
For the reverse direction assume satisfies conditions (a), (b), (c1) and (c2). We create a filesystem which does not break. The values at nodes mentioned in the sequence are set to the input values of the commands. Values at nodes that are ancestors of the ones mentioned in the sequence are set to directories. Other nodes of the filesystem remain empty. This is a valid filesystem, and by property (c2) every command in has the correct input value. Using property (c1) one can prove that works on this filesystem. □
4.2. Canonical Sets
An important consequence of Theorem 1 is that the semantics of a canonical sequence is uniquely determined by the commands it contains. This is expressed formally in the following Proposition.
Proposition 4 ([
12], Theorem 14).
If the canonical sequences α and β contain the same commands, then they are semantically equivalent, that is, for every filesystem. Proof. In fact,
and
can be transformed into each other using the commutativity rules given in Proposition 2(a), see ([
12], Lemma 10). □
Definition 4 (Canonical set). The set A of internal commands is canonical if
- (a)
it does not contains null commands,
- (b)
no two commands in A are on the same node, and
- (c2)
the set A is ≪-connected, meaning that if two of its commands are on comparable nodes, then they are connected by an ≪-chain whose elements are in A.
Commands in a canonical sequence form a canonical set by Theorem 1. In the other direction, a canonical set can be ordered in many ways to become a canonical sequence—the only requirement is (c1) which requires that the order honors the relation ≪. This can be achieved by using, e.g., topological sort. Any two such orderings give semantically equivalent sequences, as was proved in Proposition 4. Consequently we can, and will, use canonical sets in places where command sequences are required with the implicit understanding that the commands in it are ordered in an appropriate fashion. For example, we write to mean where contains the elements of A in an order which honors ≪.
Canonical sets play an essential role in reconciliation (
Section 5) and conflict resolution (
Section 6). One of their crucial properties is, as we have seen, that their commands can be executed in different orders while preserving their semantics—a variant of the
commutativity principle of CRDT [
20]. Proposition 5 discusses the special case when a subset of the commands should be moved to the beginning of the execution line. Then we define and investigate
clusters in a canonical set, and observe that the clusters can be freely rearranged, and even intertwined.
Definition 5. For a canonical set A we write to indicate that B is not only a subset of A but can also be moved to the beginning while keeping the semantics, namely .
Proposition 5. Let A be a canonical set and . Then if and only if , and imply . If then both B and are canonical.
Proof. An ordering of
A does not break every filesystem if and only if it honors ≪, see ([
12], Lemma 10). Consequently, if
then this split must honor ≪, which is exactly the stated condition. If this condition holds, then
A has an ordering which honors ≪ and in which
B precedes
.
For the second part it suffices to check that both B and are ≪-connected. However, it is immediate from the condition and from the fact that A is ≪-connected. □
The ≪ relation connects commands in a canonical set
A. The
clusters of
A are the components of this connection graph. All commands in a cluster are constructors, or all commands are destructors, or the cluster has a single element matching
. Accordingly, we call the cluster
constructor,
destructor, or
editor, respectively. Nodes of the commands within a cluster form a connected subtree of the namespace
, and the topmost elements of the subtrees are pairwise incomparable. In a constructor cluster the “being the parent” and the ≪ relations coincide, while in a destructor cluster they are the reverse of each other, see
Figure 2. As feasible orders of the commands in
A must only honor the relation ≪, clusters can freely move around. In a constructor cluster a command can be executed only
after all commands on its ancestors have been executed. In a destructor cluster it is the other way around: a command can be executed only after all commands on its descendants have been executed. Editor commands form single-element clusters, thus they can be executed at any point.
4.3. The Update Detector
Algorithms creating the canonical sets required by the reconciler (see
Figure 1) are described in Propositions 6 and 7. The update detector is either
state-based, in which case it has access to the original and modified filesystems, or it is
command-based, in which case it has access to the exact sequence of commands used to modify the filesystem. Both update algorithms are highly effective; essentially their runtime is linear in the input size.
Proposition 6 (State-based update detector, ([
12], Theorem 19)).
Let Φ be the original filesystem and let be the replica. The command setis canonical, and . Proof. To show that
is canonical we need to check that it is ≪-connected. By ([
18], Lemma 23) if
and
and
differ at
n and at
m, then they must differ at every node between
n and
m. Moreover, the differences follow one of the the patterns on
Figure 2, thus these commands form the required ≪-chain. A consequence of this is that
does not break
, and since after executing the commands every node will have the output value from
, we know
. □
The set can be generated by performing simultaneous depth-first searches on the visible (non-empty) parts of the filesystems and . Such an algorithm runs in constant space, and the running time is linear in the total size of the visible parts of the filesystems.
Figure 3 provides two examples for the result of the state-based update detector. The namespace
consists of the nodes
to
. The original filesystem
contains directories at nodes
to
and the empty value at
to
. The first replica deletes all directories, setting the empty value everywhere. The second replica stores file contents in
and in the empty nodes. The canonical command set transforming
into
consists of the five commands
where
corresponding to the five differences between
and
. The second command set also has five commands
with
and
for
. The set
A has a single execution order honoring ≪, namely
,
,
,
,
. Any ordering of the commands in
B honors ≪, as no two commands in
B are ≪-related.
Proposition 7 (Command-based update detector). Let α be a command sequence that transforms the original filesystem Φ into the replica . The following procedure creates a canonical set for which . Let be empty initially, and iterate over the commands in α from left to right. Let the next command be σ. If there is no command in on the same node as σ, add σ to . If and σ are on the same node, then using Proposition 1(a) replace with the single command corresponding to the composition . Finally, when the iteration ends, delete the null-commands from .
Proof. It is clear that on each node of the filesystem the sequence and the set have the same effect. Consequently is equivalent to the command set created in Proposition 6, therefore it is canonical. □
If a hash value of the nodes is also stored, the algorithm can be implented so that its time and space complexity is linear in the length of sequence .
5. The Reconciler—Synchronizing Two Replicas
The update detector—either state-based or operation-based—passes the canonical sets
A and
B to the reconciler, see
Figure 1. These sets describe, in a straightforward and intuitive way, how the replicas
and
relate to the original filesystem
. As discussed in
Section 2, the merged filesystem is also specified by a canonical set
M (that of the sequence
) to be applied to the original
. The next definition, which is the formalization of the informal discussion in
Section 2 about synchronization,
declares when the command set
M represents an intuitively correct synchronization.
Definition 6 (Merger command set). The merger of the canonical sets A and B is a maximal canonical set , meaning that no proper superset of M within is canonical.
Note that the merger
M is not necessarily unique, and typically many different mergers exist (see the example below). This definition covers every permissible synchronization outcome which satisfies both the
intention-confined effect R1 (
M is a subset of
) and the
aggressive effect preservation R2 (
M is maximal) requirements as discussed in
Section 2. When performing the actual file synchronization, one of the mergers should be chosen, either by the system or the user.
Section 6 discusses how this choice can be made by successive conflict resolutions.
In this section we prove that every synchronized state defined by a merger
M has a clear operational characterization: both replicas can be transformed into the merged state by first rolling back some of the commands executed earlier on this replica, and then applying some commands executed on the other replica. Using the terminology of [
12], the canonical sets
A and
B are called
refluent if there is filesystem on which both of them work (neither of them breaks). This condition is clearly met when
A and
B describe two replicas, as both are applied to their common original filesystem.
Theorem 2. Let A and B be refluent canonical sets and be a merger. Then
- (a)
, where and ,
- (b)
where and ,
- (c)
if both A and B are applicable to a filesystem, then so are M, and .
In case of synchronizing the replicas
and
, let
be (one of) the merged filesystem(s). According to this theorem, we have
The first line says that the replica
can be transformed into the synchronized filesystem
first by applying
, that is, rolling back those commands in
A which are not in
M, and then applying some further commands
from
B. The similar statement for the other replica
follows from the second line. This justifies the informal statement (∗) in
Section 2.
Theorem 2 is illustrated on the filesystems in
Figure 3. The canonical sets transforming the original filesystem to the replicas are
(where
) and
(where
), respectively. The synchronized states shown on
Figure 4 correspond to the mergers
,
, and
, respectively. Altogether there are six mergers of
A and
B depending on how many levels of the directory erasures in
A are kept. To get
from the replica
we first roll back the commands
,
,
and
in this order (commands in the set
), which restores the four directories. Then we apply the commands
,
,
,
from the other command set
B to set the file values. Getting
from the second replica requires fewer commands. First roll back
(the only member of
) restoring the directory at
, then apply
to erase this directory.
The proof of Theorem 2 uses some intricate properties of canonical sets and mergers which we prove first.
Proposition 8. Let A and B be refluent canonical sets with , and . Then .
Proof. Let , be on nodes n and m, respectively, and be any filesystem on which both A and B work. The value is the input value of , and is the input value of . Now matches either the pattern or the pattern , see Definition 1. If A has no command on node n, then executing would break as still has its original value. Thus let be on node n. The input value of is the same as that of , moreover (as A is canonical and and are on parent–child nodes). Then the output values of and are also equal since they are either both or , thus . □
A similar statement holds for mergers, but the proof is more involved.
Proposition 9. Let A and B be refluent canonical sets, be a merger with , and . Then .
Proof. Let and be a lowest counterexample to the claim, and n and m be their respective nodes. By “lowest” we mean that there is no other counterexample pair where the node of would be below n.
The argument of the proof of Proposition 8 gives that if M has a command on n (the node of ), then . Thus cannot be added to M only if M already contains a command on a node such that and n are comparable and and cannot be connected by an ≪-chain. If m and are comparable, then there is an ≪-chain in M between and as both are in M. As no command in M is on n, the node n cannot be between m and , but then is an ≪-chain in M connecting and , a contradiction. (Note that the chain between and cannot be in the other direction.)
Therefore m and are uncomparable, which means that m and are both below n, consequently and are constructors. Let be any filesystem on which both A and B work. As matches , is either empty or is a file. It means that all nodes below n are empty, in particular , and changes this empty value to something else. Now suppose . As A does not break , it must change the non-directory value at n to a directory, consequently as well. Then there is an ≪-chain between and in A starting with and ending with . As was chosen to be the lowest counterexample, all elements of this chain are in M, which is a contradiction again. □
Recall from Proposition 5 that if and only if and there are no such that and .
Proposition 10. Let A, B be refluent canonical sets, and M be a merger. Then , and .
Proof. Both statements follow from the combination of Propositions 8 and 9. If and with , then . □
Claim (a) of Theorem 2 follows immediately from Proposition 10. Let
,
, and
. By Propositions 10 and 5 we have
, and
. Thus
and a similar reasoning gives claim (b).
Recall that the notation means that the nodes which the commands and are acting on are uncomparable (that is, independent). We write to mean that for every we have , and to mean that for every we have .
Proposition 11. Suppose that the canonical sets A and B are applicable to the filesystem Φ; moreover, . Then is canonical and is applicable to Φ.
Proof. First we show that
is canonical. This is so as
and
do not have commands on comparable or coinciding nodes, thus any two commands in
on comparable nodes are both in
A, or are both in
B. Second,
is applicable to
when
A and
B are disjoint as in this case, by assumption,
, see also ([
18], Lemma 36).
When A and B are not disjoint, let . By Proposition 8, , thus which means . Similarly, . Applying the first case of this proof to the disjoint sets , and the filesystem shows that is applicable to . Since also holds, we get that is applicable to . □
After these preparations claim (c) of Theorem 2 can be proved as follows. Let and . Then and . Now by Proposition 10, which means that is canonical and , and similarly . We claim that . This is because these sets are disjoint and if in the first set and in the second set are on comparable nodes, then they are ≪-connected (as both are in the canonical set M), thus in any ordering of M which honors ≪ they are in a fixed order, but in comes before , and in comes before , which is a contradiction.
Let be a filesystem to which both A and B can be applied. Again by Proposition 10, , thus is also applicable to , and similarly is applicable to . By Proposition 11, is also applicable to , which is the first claim in Theorem 2 (c). For the other two claims observe that and . We know , thus , which is applicable to and gives . Since and M is applicable to , is applicable to . All together, is applicable to , as claimed. Similar reasoning gives that is also applicable to .
6. Synchronization by Conflict Resolution
In the realm of file synchronization a
conflict is represented by two filesystem commands which can be executed individually, but not together. Resolving the conflict means choosing one of the following actions (see, among others, [
9,
16]):
discard both commands,
discard one command and keep the other (loser/winner paradigm), or
replace one or both commands by a new one.
Only the second alternative satisfies both the
intention-confined effect principle R1 (use only commands issued by the user), and the
aggressive effect preservation principle R2 (carry over as many operations as possible). Our synchronizer uses this loser/winner paradigm to solve all conflicts. Resolving a conflict might create new ones, or automatically solve—or make irrelevant—others. Thus after each step the set of conflicts has to be regenerated, or at least revalidated/reviewed. Termination of the synchronization process is not automatic and has to be proved, see [
16]. Fortunately, in our case no new conflicts are generated, and resolved and disappearing conflicts can be identified easily. As each step eliminates at least one conflict, the synchronizer clearly stops after finitely many steps.
6.1. Theoretical Foundation
In this subsection we fix the refluent canonical sets A and B and the merger M which the synchronization is supposed to reach, but is not necessarily known at the start. First we show that synchronization can be reduced to the case when A and B are disjoint (though they might contain different commands on the same node). Then we define when a command pair represents a conflict, and show that this notion has the expected properties: a merger M does not contain conflicting pairs, and if there are no conflicts, then M is the disjoint union of A and B. The main novelty of our conflict resolution algorithm is that instead using the winner to build up the merger, it only discards the losing command from future considerations. In other words, the algorithm thins out the sets A and B until only the merger M remains.
Proposition 12. Let be refluent canonical sets, and M be a merger. Then (a) and , (b) , and (c) .
Proof. Claim (a) follows from Proposition 8 since if , and , then . From this and from (b) claim (c) follows, too.
To prove (b) it suffices to check that is canonical. First, all commands in this union are on different nodes. Both M and are canonical, so if their union were not, then there are commands and on comparable nodes which are not connected by an ≪-chain in . Assume . There is a chain between and in A. Since , we know this chain has the direction . From this and because , we know all members of this chain are in M based on Proposition 9, which is a contradiction. □
Let and let be a filesystem which shows that A and B are refluent, that is, both A and B work on . Let , , and ; observe that the command sets and are disjoint. By Proposition 12C is canonical and can be moved to the front of A and B and M; moreover and and are also canonical. Now and are refluent (both are applicable to ), and is a merger for and . The converse of the last statement is also true: if is any merger of and , then is a merger of A and B. Consequently it suffices to find the merger of the disjoint command sets and , and then adding the intersection to . For this reason, from this point on we assume that A and B share no commands.
Definition 7. Let A and B be fixed disjoint, refluent canonical sets. The pair is a conflict if , and , that is, the nodes of σ and τ are comparable (including when they coincide).
The
conflict graph is the bipartite graph with the disjoint command sets
A and
B as the two classes, and an edge between
and
if they are in conflict.
Figure 5a shows the conflict graph of the synchronization problem depicted on
Figure 3. As an example, command
is connected to
only, as both
and
are on node
, while
is independent of the nodes
, …,
on which the other commands in
B are.
Proposition 13. It is impossible that both commands of the conflict are in M.
Proof. The meanings of the symbols are as in Definition 7. Suppose by contradiction that both are in M. As they are on comparable nodes, there is an ≪-chain in M between and . Consequently there are two consecutive commands in this chain so that one is in A and the other is in B, say , and . However, Proposition 8 says that in this case , contradicting that A and B are disjoint. □
Proposition 14. Suppose is a conflict, and . Then is also a conflict.
Proof. Let , be on nodes n and , respectively. If is the parent of n, then the node of is comparable to , thus we are done. Therefore n is the parent of , and are constructors, and matches . If the node of is not below n, then we are done. If it is, then the input type of is (as in the original filesystem , is not a directory, therefore every node below it is empty). For the same reason the command set B must contain a command on node n (otherwise when executing , still has the original content at n, and then breaks ). This command has the same input type as , must create a directory, thus it is equal to , contradicting that A and B are disjoint. □
By symmetry, the same claim holds when
A and
B are swapped. Fix
, and split
B into
and
as follows:
We know by Propositions 5 and 14, which means that if is a filesystem B does not break, then neither does . Moreover, if , then . In particular, if is empty, then so is . Next we show that if there are no conflicts, then the synchronization is done; however, we need a stronger statement which will be used to justify the correctness of the synchronization process.
Proposition 15. Suppose is empty, that is, no is in conflict with . Then .
Proof. It is enough to show that is canonical. Since , it has at most one command on every node. It can only be non-canonical if there is a on a related node that cannot be connected to using an ≪-chain from the commands in M. This must be in A, which has a chain between and . If this chain goes in the direction , then by Proposition 9. Otherwise we know , and based on the remark above, is empty for all members of this chain and so are independent of B. This means the chain can be added to M, which is a contradiction. □
Corollary 1 (Termination). If there are no conflicts, then the merger M is .
Proof. By Proposition 15 every command in A is in M, and similarly . As M is a subset of , they must be equal. □
6.2. The Synchronization Algorithm
The input of the synchronization algorithm is , , which is a pair of refluent canonical command sets. The goal is to find, using successive conflict resolution steps, a merger command set M that fits Definition 6. In addition, we aim to show that our algorithm can produce any of the mergers allowed by the definition, and only valid mergers. To achieve this, the algorithm accepts a pre-set merger as an optional argument. Whenever the algorithm needs to make an otherwise arbitrary choice, is used to choose one of the possibilities. While choosing any of the possibilities will generate a valid merger, guiding the choice will guarantee that will be generated.
According to the discussion in
Section 6.1, the synchronization algorithm has two main components. The first one, called Algorithm 1, reduces the general problem to the special case when the input command sets have no common elements. Properties of the merger set proved in Proposition 12 provide the foundation of the reduction. The second component, called Algorithm 2, assumes that its input command sets
and
are disjoint so that it can rely on the intrinsic properties of the conflict graph when generating the merger
M. The two algorithms are visalized in
Figure 6 and
Figure 7, respectively. The detailed description is followed by the proofs of the correctness and a short discussion on time and space complexity.
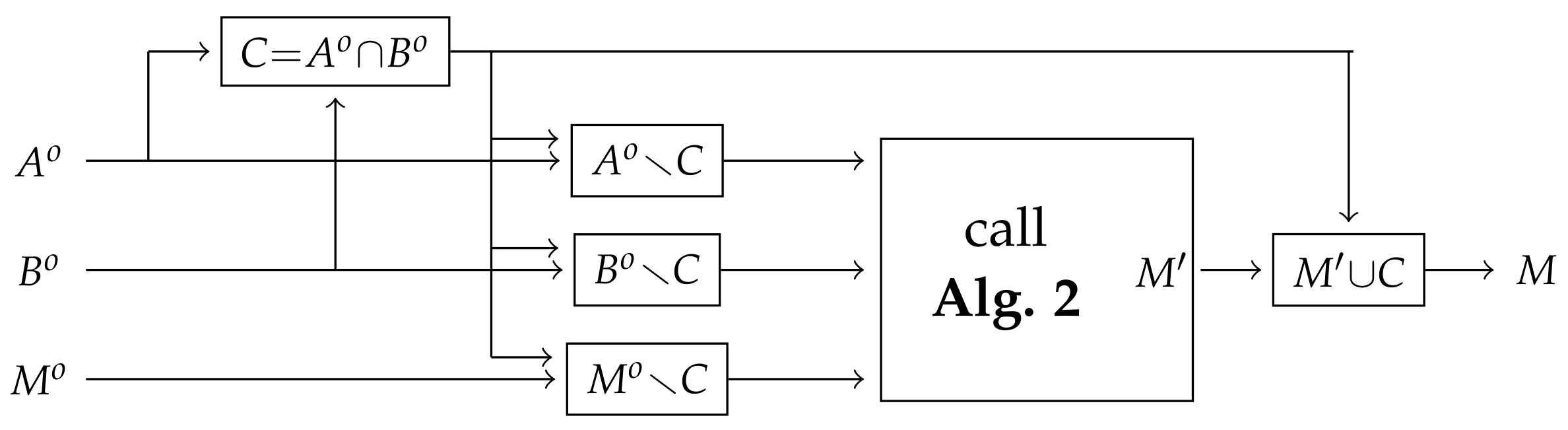
Algorithm 1 (Synchronization in the general case)
Let . Execute Algorithm 2 with the command sets and . If is specified, then it must satisfy ; in this case pass as the optional input to Algorithm 2. When Algorithm 2 returns , return .
Correctness of Algorithm 1. As discussed after the proof of Proposition 12, and are refluent canonical sets, and C is an initial segment of every merger of and . Moreover, if is a merger of and , then is a merger of and . From here the correctness of the algorithm follows easily. □
Complexity of Algorithm 1. Apart from the time and space requirements of Algorithm 2, the five operations here require computing the union, intersection and difference of sets. Using hashing techniques, these operations can be performed both in time and space linear in the input size. □
Inputs of the main Algorithm 2 are the disjoint refluent canonical sets and , and the optional target merger of and . The goal is to produce a merger M. If is given, then, at the end, M and must be equal.
The algorithm maintains two command sets A and B, initially set to and . During execution these sets satisfy the following invariants:
- 1.
, , consequently A and B are refluent canonical subsets of and ;
- 2.
all mergers of A and B are mergers of and ;
- 3.
if is specified, then is a merger of A and B.
In each iteration one or more commands are deleted either from A or from B until only the commands of the merger remain.
Algorithm 2 (Synchronization of disjunct sets).
Initialize: Set and .
- Iterate:
Choose and such that is a conflict. If no such pair exists, go to Finish. If is given, choose a conflict so that either or is in .
Conflict resolution: Out of and , choose the winner and the loser commands. If is given, let the winner be the one in . If is the winner, delete all commands from B which are in conflict with (including ). If is the winner, delete all commands from A which are in conflict with . Go back to Iterate.
- Finish:
Return as the merger.
Execution of Algorithm 2 is illustrated in
Figure 5. The initial command sets are
and
. In the first iteration
is the winner; therefore, commands in
A which are in conflict with
(
and
) are removed from
A. In the next iteration the winner is
, and
and
are removed from
B. In the last iteration
is removed from
A, thus the remaining sets are
and
. The returned merger is
.
Correctness of Algorithm 2. After the initialization step all three invariants hold. The algorithm terminates as in each iteration the total number of remaining conflicts strictly decreases. When it terminates, the returned set is a merger of the original command sets and . This is because at that point there are no conflicts between A and B, thus, by Corollary 1, M is a merger of A and B—in fact, the only one—, and then the second invariant guarantees that M is also a merger of and . If was submitted to the algorithm, then the third invariant ensures . Thus we only need to show that the iteration preserves all three invariants. Suppose there is a conflict between A and B, and the winner of the conflict is .
Invariant 1. Commands in conflict with
are deleted from
B, thus
B is replaced by the set
Proposition 14 (see the discussion following the proof) and the invariant imply . Consequently the invariant remains true.
Invariant 2. We know that if a merger of A and B contains , then it cannot contain any of the discarded elements of B (see Proposition 13). We also know that all mergers of A and contain by Proposition 15 as it is not in conflict with any other command. Consequently the set of mergers of A and consists of those mergers of A and B that contain , and the invariant continues to hold.
Invariant 3. If was specified for the algorithm, then we chose the winner accordingly, and so . A consequence of the discussion above is that remains part of the set of mergers of A and .
Finally we show that if is specified, then one of the conflicting commands can be chosen from . By Proposition 15 if is not in conflict with any command in B, then is in every merger of A and B; in particular, it is in by the third invariant. Thus, if no conflicting commands remain in , but there is a conflict, then would be a proper subset of the merger returned by the algorithm, which is absurd. □
Complexity of Algorithm 2. Both the Initialization and Finish steps can be done in time and space that is linear in the input size. Updating the sets A and B in the Iteration step discards some of their elements which will never be used again. It means the total time used by the updates is bounded by the number of elements in the original input set . Finding conflicting pairs in constant time, however, requires building a structure which stores the bipartite conflict graph. This requires time and space which is proportional to the number of nodes (commands in and ) plus the number of conflicting pairs. It means that Algorithm 2 can be implemented with both time and space complexity that is linear in the input size plus the total number of conflicts. While the latter number can be expected to be comparable to the input size, in the worst case it can be quadratic, meaning that this implementation guarantees at most quadratic time and space complexity. □
We conjecture that a more efficient implementation of Algorithm 2 can be created using the structural properties of the conflict graph. Some of those properties are discussed in the next Section.
6.3. Structural Properties of the Conflict Graph
We call a conflict between two commands structural if the out types of the commands are different, and a content conflict otherwise. An example for a content conflict is when both replicas replace the same directory with different file contents. The best resolution of a content conflict cannot necessarily be achieved by the above winner/loser paradigm, as it uses filesystem-level information only. Fortunately, content conflicts are represented in the conflict graph as isolated edges. It means that all of these conflicts must (and can) be resolved independently of all the other conflicts. We deem it good practice to resolve all content conflicts first.
If
is a conflicting pair and
is on a node which is above the node of
, then
is also a conflicting pair. Proposition 14 implies the same when
. Consequently all elements of a
constructor cluster (see
Section 4.2) of
A are in conflict with exactly the same elements of
B, and so the whole constructor cluster can be replaced by a single graph node, thus reducing the graph size.
Figure 5 shows the typical structure of conflict graphs. Elements of the destructor chain
are connected to more and more conflicting commands (this is so as the corresponding nodes go upwards). Choosing
as a winner automatically resolves all conflicts by wiping out all
.
Automatic conflict-based synchronizers typically give precedence to constructors in conflicts between a constructor and a destructor command [
10,
16], arguing that it is easier to remove some content again than recreating it. While this is good guidance most of the time, one has to be aware that in the current framework, replacing a directory node with some file content is a
destructor. Confronted with the conflicting constructor command that creates a file under the same directory, marking this latter command as the winner is not self-evident.
7. Conclusions
We have presented a complete theoretical investigation of filesystem synchronization. Our definition of a filesystem is arguably simplistic, but it captures the important features of real-word implementations. The changes between the original and the updated filesystems are encoded using a sequence of virtual filesystem commands. The synchronizer receives two sequences corresponding to the two replicas to be synchronized, and produces a third sequence which describes the synchronized, or merged state. Definition 6 gives an intuitively correct and convincing description of when the resulting sequence leads to a meaningful merged filesystem. In
Section 5 we proved an operational characterization of the possible merged filesystems. The main result of
Section 6 is a conflict-based non-deterministic synchronization algorithm which creates exactly those merger sequences which are allowed by Definition 6. The simplicity of this algorithm and the complexity of proving its correctness was a surprise to us. Its success underlines the power of the algebraic framework of file synchronization developed in [
18].
Multiple questions and possible extensions of the current work remain which are the subject of future research. Some of them are discussed in the next subsections.
7.1. Synchronizing More Than Two Replicas
The first natural question is to extend the synchronization algorithm from two to three or more replicas. An encouraging observation is that if several canonical sets are pairwise refluent (for any pair there is a filesystem on which both of them work), then they are jointly refluent, meaning that there is a single filesystem on which all of them work. The natural extension of Definition 6 for three canonical sets A, B and C is to define their merger as a maximal canonical set . This definition has the additional advantage that it is symmetric in the filesystems, and does not give precedence to any of them over the others. We can prove that such a merger also satisfies an operational characterization similar to the one stated in Theorem 2. It seems that such a three-way merger can be generated first by merging A and B to M, and then merging M and C. Is this claim true?
Another question is whether the general task of finding a three-way merger can be reduced to the case when A, B and C are pairwise disjoint. Finally, at least in the case when the sets A, B, C are pairwise disjoint, whether the following variant of the Iteration step of Algorithm 2 generates a 3-way merger, and if yes, whether it generates all possibilities:
Iterate: Pick a winner command from , and discard those commands from the other two sets which are in conflict with .
7.2. Efficiency of the Algorithms
Algorithm 1 can be implemented with a runtime that increases linearly with the size of its input, so it is efficient. The trivial running time estimation of Algorithm 2 is proportional to the product of the sizes of the command sets
A and
B—assuming that the “above” relation in the node structure
can be checked in constant time, as generating the conflict graph takes that much time.
Section 6.3 discusses some possible improvements by exploiting the structure of the conflict graph. As to whether the running time of the algorithm can be improved significantly, or it is substantially quadratic, our conjecture is that the algorithm can be made sub-quadratic.
7.3. Attributes
Attributes typically store metainformation about a node, such as different timestamps (e.g., creation date, last modification or last access) and permissions (e.g., read and write access), and whether the metainformation refers to the node only or to the whole subtree below it. Attributes are set and modified either automatically, or by special filesystem commands. In our filesystem model attributes can be best modeled by storing them as node content. For file nodes it means that the attributes are added to the actual file content, which means that any change to the attributes can be handled as a change in content. Therefore, file attributes pose no special problems and can be integrated seamlessly into our model. Handling directory attributes, however, is a challenging open problem. A general algebraic framework of filesystems allowing content in directory (and even in empty) nodes was developed in [
12] at the expense of more complicated notions and theorems. Unfortunately, with this extension many of the Propositions in
Section 5 and
Section 6 on which the correctness of our method relies do not remain true. To illustrate the problem, suppose
A changes some attribute from “private” to “public” at some directory node
n, and creates a file under
n; while
B, under the impression that the directory is still private, creates another file under it. Then the file creation command from
B cannot be unconditionally moved to the merging sequence.
One possible solution is to consider and resolve all attribute conflicts (including when A and B modify attributes at the same node differently) as the first stage of the synchronization process, and then proceed according to the algorithms described in this paper. This approach, however, is not necessarily compatible with our declarative Definition 6 of what a synchronized state is. It is not even clear whether all possible mergers satisfying this definition are intuitively correct or not if directory attributes are taken into account.
7.4. Links
From the user’s perspective, a link between the nodes n and is a promise, or a commitment, that the filesystem at and below n is exactly the same as at and below . Executing a command below n automatically executes the same command on the corresponding node below . A link system must be loopless meaning that any node has only finitely many other nodes equivalent to it. In particular, n and must be uncomparable nodes.
If the original filesystem contains links, but the users do not have tools or permissions to manipulate them, the following synchronization method works. The update detector, knowing the link structure, unfolds it, and replaces each user command by the collection of all “hidden” or “implicit” commands on the equivalent nodes. After creating the canonical command set A, it marks the commands which are on equivalent nodes. For the merger M to be applicable to it must also contain, with each command in M, all of its equivalents. This can be achieved by the following modification to the Iterate part of Algorithm 2: if is chosen as a winner, then all commands equivalent to it will be winners as well.
It is an open problem to introduce filesystem commands which manipulate the link structure and can be incorporated into our synchronization process.