Abstract
The significant advancements in intelligent transportation systems (ITS) have contributed to the increased development in traffic modeling. These advancements include prediction and simulation models that are used to simulate and predict traffic behaviors on highway roads and urban networks. These models are capable of precise modeling of the current traffic status and accurate predictions of the future status based on varying traffic conditions. However, selecting the appropriate traffic model for a specific environmental setting is challenging and expensive due to the different requirements that need to be considered, such as accuracy, performance, and efficiency. In this research, we present a comprehensive literature review of the research related to traffic prediction and simulation models. We start by highlighting the challenges in the long-term and short-term prediction of traffic modeling. Then, we review the most common nonparametric prediction models. Lastly, we look into the existing literature on traffic simulation tools and traffic simulation algorithms. We summarize the available traffic models, define the required parameters, and discuss the limitations of each model. We hope that this survey serves as a useful resource for traffic management engineers, researchers, and practitioners in this domain.
1. Introduction
Traffic modeling is beneficial in controlling the high volume of vehicular traffic on major roadways and optimizing the level of complexity of the road networks’ infrastructure. It has been used quite extensively in recent years to analyze, simulate, and predict traffic behavior at different levels of complexity, from congested urban settings to rural modeling at the macro and micro scales [1]. Traffic behavior is defined as the volume, speed, and density of traffic flow as estimated by given data, whether historical or real-time. Furthermore, with the tremendous growth in the number of intelligent transportation services, traffic monitoring applications, and the emergence of the Internet of Things (IoT), traffic modeling has received substantial attention from the research community [2]. The majority of traffic modeling research focuses on proposing models to analyze and predict traffic congestion problems as well as simulate the traffic flow in different road environments, such as freeways, junctions, and intersections [3]. The availability of these models plays an essential role in traffic engineering and in assessing the performance of road traffic facilities. These models study the spatial and temporal interactions within the traffic status to capture their significant effect on traffic behavior. The temporal factor in traffic models is used to identify a directional movement in a time series format, while the spatial factor will take into account the geographical space to build the prediction outcome. By combining the temporal and spatial factors in traffic prediction models, an improvement in the prediction results is noticeable [4]. Numerous studies have proven that machine learning models are capable of modeling the spatiotemporal correlations in continuous spatiotemporal traffic data [5]. On the other hand, traffic simulation models are used to simulate vehicle movements and describe the traffic flow realistically [6]. Traffic simulation models are used to optimize road design and assess the effects of road network design on vehicle movements. These models provide a geographical environment to plan scenarios of driver behavior in a wide variety of road types, such as urban and freeway networks. Traffic simulation uses mathematical models to demonstrate how vehicles would move in real time using car-following theories. The difference between traffic prediction and traffic simulation models is that in prediction, we estimate the traffic value (volume, speed, density, etc.) at a future time point using historical data under given conditions. In traffic simulation, models estimate the traffic value (volume, speed, density, etc.) under given conditions.
In this paper, we examine the implementations of the most common spatiotemporal machine learning models, focusing on nonparametric models that are widely used to estimate and predict traffic status. In addition, we provide a comprehensive comparison of the existing traffic simulators used in smart cities and intelligent transportation applications, specifically for traffic flow modeling. This study aims to explore spatiotemporal nonparametric traffic models and microscopic simulation models. Although there has been a considerable amount of survey papers introduced in traffic modeling, none has been found focusing on nonparametric modeling techniques for traffic prediction or methods for traffic data analysis and the prediction of different time intervals. A number of advanced models will be critically examined and compared in this survey. This paper seeks to address the following questions: What are the suitable models for long-term and short-term predictions in traffic modeling? What are the performance metrics used to evaluate the efficiency of each model? What are the drawbacks of each model, and how can these issues be overcome? In which ways does the nonparametric predictive method differ from the parametric predictive method? What is the required data structure that is suitable to implement the predictive model? The findings of this paper will make an important contribution to the field of spatiotemporal prediction of traffic flows. In addition, it will highlight a number of common nonparametric statistical methods. By demonstrating the challenges in the long-term and short-term prediction of traffic modeling in this survey, abundant room for further development in traffic modeling will be considered.
In addition to the above-mentioned questions on nonparametric modeling techniques, we provide a comparative study on the most used simulation models in the traffic modeling literature, where we explore the state of the art of these simulation tools and discuss their functionalities and characteristics. A number of criteria, such as the nature of the tool (e.g., free, open source, or commercial) and functional capabilities of the simulator, are addressed in this section [7]. Figure 1 shows a high-level overview of the papers discussed in this survey, categorized into techniques that are applied to achieve traffic prediction.
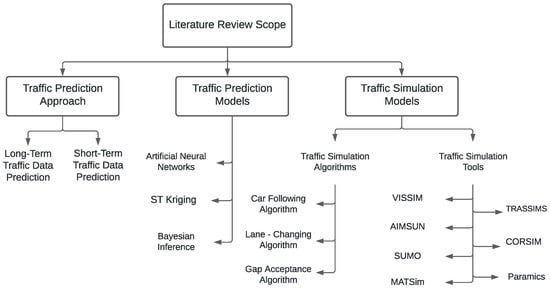
Figure 1.
Structure of the survey.
The remainder of the paper is structured as follows. Section 2 presents the motivation for traffic modeling and identifies its significant impact on smart city systems and intelligent transportation applications. Section 3 gives a brief overview of the different types of spatiotemporal models and real-world applications that benefit from them. In Section 4, we discuss the challenges of traffic modeling for long-term prediction. Section 5 provides a comprehensive review of the traffic modeling approaches for long-term prediction. In Section 6, we discuss the challenges of each approach and how they could be further explored. Lastly, the Conclusions section gives a brief summary of the implications of the findings on future research directions in this area.
2. Motivations
The need for traffic modeling can be seen in its reliability in predicting the changes in traffic behavior and demonstrating the traffic status under different road network conditions. For example, modeling the characteristics of some traffic-related problems, such as traffic congestion, travel delays, and traffic accidents, will provide a description of the traffic status to help traffic management to control these traffic problems.
Furthermore, when constructing a new urban plan, traffic management will employ the findings of the traffic modeling study to test and assess a set of transportation road systems offline. According to a number of research studies on the topic of road networks and transportation planning, urban areas that are poorly designed, such as Mumbai, New Delhi, and Mexico City, experience increased traffic congestion problems. As claimed in a statement by TomTom, a well-known GPS company, driving in cities that are poorly designed will require between to extra time for travel due to traffic congestion [8]. The use of traffic simulation models can aid in determining the level of improvement required in road networks designed to alleviate traffic congestion.
Another significant motivation for traffic modeling studies is to improve road safety and reduce accident severity. As heavy traffic slows down on highways, drivers can begin cutting in front of others or engaging in distracting behaviors such as texting or making phone calls before the congestion eases. This type of behavior may result in accidents and raise the likelihood of traffic collisions. The Canadian Motor Vehicle Traffic Collision Statistics [9] show that traffic collisions led to more than 1900 premature deaths and 9000 serious injuries in Canada in 2018. Using traffic modeling to predict traffic collisions raises public awareness of the causes of these collisions in order to avoid them.
Recognizing the importance of traffic modeling studies in assessing urban transportation systems has led to numerous research studies in traffic modeling. The following section of the survey begins with a brief comparison of the time intervals used in spatiotemporal traffic prediction and demonstrates the challenges in long-term and short-term traffic modeling prediction.
3. Traffic Status Prediction
A number of traffic modeling studies have been proposed to predict traffic conditions according to the length of the prediction period, such as short-term prediction and long-term prediction. The characteristics of each prediction require a different modeling process to suit the temporal components and the targeted prediction period. Defining the length of the prediction period will help to decide the best technique to adopt for the traffic modeling study. Short-term and long-term predictions are used to define the time intervals in traffic flow prediction. Short-term prediction involves a short range of time periods such as seconds, minutes, hours, days, or weeks, while long-term prediction involves a long range of time periods such as several months or several years [10].
3.1. Short-Term Traffic Prediction
Research on traffic prediction has been mostly restricted to short-term prediction. According to a definition provided by Vlahogianni et al. [11], short-term traffic predictions are made to predict a period of time in the future that can range between a few seconds and a few days. The authors listed two reasons why short-term traffic prediction has become so dominant in the traffic prediction models field. The first reason is the availability of traffic data that represents a short period of time. The second reason is the availability of many traffic data analytical models that can be used to explore the data. However, traffic data that are collected every 10 s or less is meaningless and not useful for short-term traffic prediction [12]. A number of studies claimed that collecting traffic conditions every 15–30 min would be more effective for prediction results [13,14]. A study by Song et al. [15] on short-term traffic speed prediction provided a comparison between four prediction methods under different data collected in time windows that ranged from 1 min up to 30 min [15]. The study proposed a seasonal discrete grey model (SDGM) and compared the prediction accuracy with the seasonal autoregressive integrated moving average (SARIMA) model, artificial neural network (ANN) model, and support vector regression (SVR) model. The findings of this study show that the prediction accuracy increases when the targeted time window is more than 10 min, while the prediction of a time window that is less than 10 min suffers from instability. Additionally, the study shows that the SARIMA model’s performance had the highest error indicator in the prediction results. A probable explanation regarding these results is that SARIMA cannot capture the variation characteristics of the traffic data in a small time window.
3.2. Long-Term Traffic Data Prediction
Regardless of the importance of long-term traffic prediction in enhancing the city roads infrastructure, most of the literature in traffic modeling is focused on short-term prediction. The time intervals of the long-term traffic prediction study the time window that ranges from several months to several years. Although studies claimed that long-term traffic prediction is not beneficial to obtain an accurate prediction, other studies that apply traffic modeling for long-term prediction highlighted the importance of long-term prediction to improve traffic management systems [16]. Because of the large time window in the long-term prediction, seasonal patterns and cycle patterns will be detected in the traffic data, therefore, models that are able to identify these patterns are strongly recommended such as the SARIMA model, and seasonal autoregressive fractionally integrated moving average (SARFIMA) model [17]. Another study indicates that exponential smoothing models are powerful in capturing seasonality in the traffic data as well as handling trends and white noise satisfactorily [18].
3.3. Challenges in Traffic Prediction
There are a number of challenges in the field of traffic prediction modeling concerning time intervals. Employing the traffic prediction modeling for long-term time intervals faces several issues [19]. First, the uncertainties of the prediction increase due to the lack of data associated with short time intervals. Second, aggregating traffic data will lead to a high rate of errors in the prediction outcome. On the other hand, modeling short-term traffic prediction requires high computations and is highly sensitive to outliers. Therefore, using data analysis in traffic modeling plays an important role in reducing the drawbacks of predicting short-term or long-term traffic status, where it provides tools and functions that help in cleansing and transforming data into useful information before applying prediction models [20].
4. Spatiotemporal Traffic Prediction Models
Spatiotemporal traffic prediction techniques are statistical methods that model given traffic data to study the patterns of traffic flow and construct knowledge to predict the future traffic status [5]. Figure 2 shows the schematic diagram of the most common spatiotemporal models that are used in predicting different real-world applications, such as environment and healthcare. Among these spatiotemporal models are Bayesian inference, ST-Kriging, and artificial neural networks (ANNs). ANNs are considered one of the most widely used models in the traffic domain. The following section provides a comprehensive review of three state-of-the-art spatiotemporal methods and investigates the research gap in these existing models.
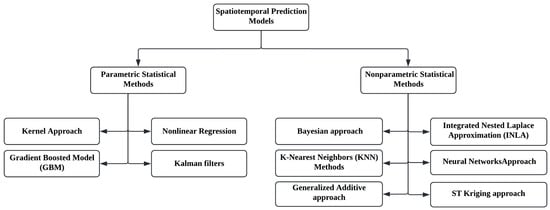
Figure 2.
A schematic diagram of spatiotemporal models.
4.1. The ST-Kriging Approach
The Kriging method [21] was first developed by George Matheron in 1960 and is mainly used for spatial interpolation prediction. Kriging techniques are well known for optimal spatial prediction and Gaussian process regression. Kriging is a common statistical prediction method that is used by geologists. Subsequently, Kriging became widely used in numerous research works and studies, which made Kriging an essential tool in statistical studies of geographical data. Kriging was later generalized for spatiotemporal prediction and given the name ST-Kriging. The main idea in ST-Kriging is that spatial variability can be characterized by two major components. The first one deals with large-scale variation, exploring the data distribution and capturing trends and outliers. The second component deals with small-scale spatial variation to calculate the spatial autocorrelation and fitting semivariogram to obtain the prediction [22]. Spatial autocorrelation will take into account two functions—the distance and the degree of variation between known data points—when estimating values in unknown areas. Formally, the ST-Kriging equation can be derived from the following:
In Equation (1), the random variable Z is the value at location s at time t, and is a vector of spatial coordinates , where :
In Equation (2), Z is a function of random variables at location s at time t, and is the conditional mean of large-scale variability. The second component that defines the spatial variability of the Kriging architecture is the small-scale variability that is represented as , or it can be defined as the noise that captures the large-scale variation. The mean in Equation (3) refers to a function of the observed variables through the parameter .
A major step in fitting the ST-Kriging model is to estimate the space–time covariance model, which will be estimated by cross-validation (CV) methods. The covariance function shown in Equation (4) estimates the covariance of the observation of random variables at two spatial points. ST-Kriging is governed by a prior covariance matrix based on the data distribution:
The ST-Kriging method yields the mean square error (MSE) of the variance () and a number of linear predictors. It develops its prediction by selecting the minimum variance linear unbiased predictors. A study conducted by Brent and Kara [23] provided a comparison between Kriging methods and geographically weighted regression (GWR) to predict the annual average daily traffic (AADT) counts when the temporal component was excluded. The findings observed in this study have shown that the prediction accuracy of AADT that was provided by Kriging achieved more confidence than GWR. Kriging can control the spatial attributes at unsampled locations by calculating the distance using the spatial autocorrelation function. This function reduces the error in the AADT prediction, with their results indicating that the average absolute error was reduced by up to 63% and the mean square error was reduced by 50%. However, this study highlights a number of challenges when using Kriging for prediction. First, Kriging’s prediction lies on a covariance matrix and an inverse covariance matrix, and with large-scale data, matrix inversion is difficult. Therefore, Kriging prediction is implemented on data with a limited size. Another challenge is optimizing the semivariogram estimation and selecting the optimal lag size and number of lags.
Another piece of research by Kennedy et al. [24] studies the problem of modeling the missing values in traffic data that are collected by road sensors. One of the more significant aspects of this study is modeling traffic data that have a high ratio of missing values collected from 1000 road networks. To identify the most information-rich segments, the authors used a method called reduced measurement space [25]. The study indicates the ability of ST-Kriging methods in handling missing observations, where they recommend modeling the road networks as one connected spatial component. This approach helps in reducing the impact of the missing observation on the prediction accuracy, but it does increase the computational overhead. In contrast, the prediction accuracy was reduced when each road network was considered separately. Therefore, the authors suggested using a distributed approach with a central control unit in future work.
Another study by Son et al. [26] applied ST-Kriging methods to handle road segments that take into consideration spatial characteristics and spatial homogeneity. Unlike other approaches, point-based Kriging considers the road segments as a single point and ignores these two factors, despite their importance in building more accurate traffic prediction. Their study proposes a segment-based regression Kriging (SRK) method to predict the traffic volume with a comparison between heavy vehicles, such as trucks, and light vehicles. There was a slight improvement in the prediction accuracy compared with point-based Kriging prediction. In the case of heavy vehicles, the prediction accuracy improved by 0.67%, whereas the uncertainty estimation showed significant results and improved by 53.63% compared with point-based Kriging. On the other hand, there was no increase in the prediction accuracy of the light vehicle, where the prediction accuracy results were less than the prediction accuracy in the point-based ST-Kriging approach.
Much of the usage of the ST-Kriging approach in traffic modeling research to date has been for improving the traffic system by modeling traffic conditions, such as by analyzing traffic congestion [27] or predicting traffic speed and travel time [28,29].
4.2. Bayesian Inference Approach
There are several similarities between the ST-Kriging approach and the Bayesian approach in terms of employing the covariance matrix in estimating the minimum variance and mean. However, the Bayesian approach yields a posterior and probability density function (PDF) of the conditional distribution which defines the probability distribution of a random variable. In addition, the Bayesian approach does not depend on assumptions in the model settings, unlike ST-Kriging. It computes the prediction probability by sampling the data using the Markov chain Monte Carlo (MCMC) algorithm. Bayesian inference approaches use Bayes theory to produce statistical inference. To simplify the concept of Bayesian inference, three main terminologies need to be defined: prior, likelihood, and posterior. The prior refers to a prior probability of knowledge that is modeled by a probability distribution. This prior will be updated on a continuous basis as new data are acquired, as will the so-called likelihood probability. Incorporating the prior probability and the likelihood probability gives the posterior probability [10].
Equation (5) refers to the Bayes theorem that is used in the Bayesian inference process, where is the initial prior probability distribution of the parameter from the current observation, also known as the initial hypothesis, and is the likelihood probability distribution of the observed data given a parameter value. The product of the likelihood and the prior gives , which is the posterior probability of the parameter given the observed data [30]:
In the literature, tends to be used to refer to the marginal likelihood or the evidence, but Bayesian inference treats the evidence as a normalizing constant [31].
DAZIAN et al. [32] employed Bayesian methods in a study on analyzing road safety and modeling travel behavior. Additionally, a Gibbs sampler was used in MCMC computation, which is considered one of the common sampling methods used in Bayesian approaches. In their study, they modeled data into samples that were different in size, consisting of 30, 50, and 100 sites. Furthermore, they applied the experiment to data with missing observations. A comparison was introduced to evaluate two different Bayesian approaches: the empirical Bayesian (EB) approach and the hierarchical Bayesian (HB) approach, which estimates the posterior within multiple levels. The results of this study show that in both approaches, modeling different sizes of samples is effective. However, the EB approach has a drawback in that other studies [33] have criticized the need for a repeated process, in which in the first run, the process uses the data to determine the model parameters, and in the second run, the process uses the data again to identify the posterior. In comparison, the HB approach can overcome this problem and provide a more flexible framework to determine the model hyperparameters and the posterior through its hierarchy. On the other hand, both the EB and HB approaches handle missing observations and multidimensional attributes appropriately.
In 2019, Zheng and Sayed [34] proposed a study that applied to traffic safety, where they used the HB approach in predicting traffic accidents, particularly rear-end accidents that occur at intersections. The traffic data followed a generalized Pareto distribution, which is described as a probability distribution that is used to model the tails of another distribution. Additionally, a comparison was conducted between Bayesian hierarchical generalized Pareto distribution models (BHM-GPD) and the hierarchical generalized extreme value model (BHM-GEV), which models a distribution that has very rare or extreme behaviors [35]. The traffic data included a few traffic conflict (e.g., accident) observations that represented extreme events at a specific intersection. The results show that the BHM-GEV approach performs better when the traffic conflict observations are distributed over different intersections. However, the BHM-GEV approach may provide inefficient performance when there is a limited number of traffic conflict observations. A number of limitations are discussed in the study, where there are still some challenges in predicting traffic accidents at intersections, such as having short traffic observations at intersections, which are not preferable for modeling. However, the authors recommended collecting data over a longer period of time, with temporal dimensions such as days, weeks, and months. The limited number of traffic observations that are collected at intersections restricts other researchers from tackling this important topic in traffic modeling.
4.3. The Artificial Neural Network Approach
In the 1990s, artificial neural networks (ANNs) became a popular approach for binary and numerical data prediction. ANNs are data-driven machine learning algorithms that work similarly to smoothing algorithms in terms of learning the patterns from the data. It also works similarly to regression algorithms, in that, they are designed to capture a relationship between the input and output using cross-sectional data. In the literature, the ANN approach has mixed results regarding the performance of neural networks compared with other prediction methods, where neural networks work best with high-frequency data [36]. As we can see from Figure 3, a basic ANN model has an input layer and an output layer [37]. All the layers in between the input and output layers are denoted as hidden layers. The neurons between different layers are connected via an edge associated with a certain weight. The ANN computes the values of these neurons in association with their weights and forwards the values to an activation function. An activation function maps the aggregated values from the input layer to the output layer.
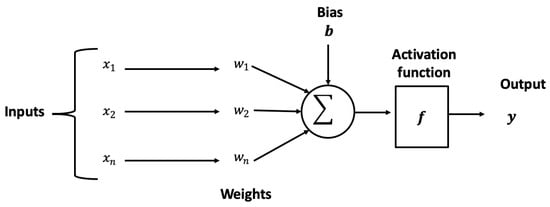
Figure 3.
The basic components of an ANN.
One of the earliest studies on traffic modeling using ANNs was proposed by Ledoux in 1997 [38], where she designed a traffic modeling system based on ANNs. The system has the capability to simulate the traffic flow for connected junctions and then model the traffic flow over a wide range of intersections. The study confirms the potential of using ANNs in traffic prediction modeling and recommends further investigation.
A predictive model based on the ANN approach was introduced by Li et al. [39] to predict traffic accidents and improve traffic safety. They discussed integrating backpropagation neural networks with genetic algorithms to identify potential jamming spots that were likely to cause traffic accidents. The model analyzes the traffic conditions and then produces samples of the possible road accident spots. Additionally, they applied the model on real-time data to predict traffic accident spots. Their conclusion was that integrating ANNs and genetic algorithms as a hybrid genetic algorithm backpropagation (GA-BP) model helped in optimizing the network. The computational overhead of this process produces the local minimum problem, which means that the ANN will continue training the data and updating the network’s weights until it reaches the lowest point of the error function. The model has the ability to classify the static factors and the dynamic factors within the road traffic conditions to achieve a high prediction accuracy.
Çetine et al. [40] proposed a study to model historical traffic data using the ANN approach. The study focused on predicting the traffic flow at each main intersection in the city of Istanbul. The model predicted the traffic based on a specific scenario, such as during holidays and school hours. One of the model’s features is informing the drivers of the traffic status for the next hour. This study proposed testing the feasibility of applying the ANN approach in the traffic modeling domain. The findings of this study show that ANNs successfully provide accurate predictions in different scenarios. However, the lack of long-term data might enhance the results, as was recommended by the authors.
4.4. Summary of Spatiotemporal Traffic Prediction Models
Having discussed the concepts of the previous models and how they were used in various traffic modeling studies, constructing a comparison to evaluate different aspects of each model will help to decide which one is more suitable for our research. The comparison was restricted to evaluating the predictive accuracy, computational complexity, and evaluation criteria (see Table 1).

Table 1.
Comparison between ST-Kriging, Bayesian inference, and ANNs.
In terms of prediction accuracy, ST-Kriging prediction accuracy relies on the covariance matrix to produce data samples that are highly correlated. Therefore, defining the correct correlation function in the correlation matrix is important for obtaining an accurate prediction. The Gaussian correlation function and Matérn correlation function are two of the most commonly used correlation functions in the correlation matrix in the ST-Kriging method. To identify the best correlation function, estimation tools are required to estimate the correlation function parameters, such as maximum likelihood estimation (MLE) and semivariogram estimation [44]. However, these tools suffer from a number of challenges. In the case of using semivariogram estimation, a plotted semivariogram will be given to determine the appropriate function parameter. Yet, the process of optimizing semivariogram estimation requires deep knowledge of the ST-Kriging approach.
On the other hand, maximum likelihood estimation requires a large sample size to identify the correct function parameters. Additionally, the distance between the spatial points in each sample needs to be small [45]. These factors affect the prediction accuracy and need to be taken into consideration when applying the ST-Kriging approach in traffic prediction. Another point to consider is the computational cost of the model, where in ST-Kriging, the computational complexity will be estimated based on the number of data spatial points N. When having a large number of spatial points, the covariance matrix becomes more complex, and thus detecting correlation in space and time becomes more complex as well [46]. In addition, ST-Kriging methods require high training times with a computational complexity of [47]. This leads to the conclusion that the overhead cost of the ST-Kriging methods is represented in the high complexity when computing traffic data that are large in size. In contrast, large traffic data produce samples that help to improve the prediction accuracy [47].
From the perspective of evaluating the model performance, ST-Kriging methods can be evaluated using cross-validation techniques and fundamental statistical parameters such as the variance of errors. Additionally, examining the model residuals helps assess the minimum variance of linear unbiased predictors [48]. Turning now to the data structure, ST-Kriging methods were implemented to model data with a Gaussian distribution. ST-Kriging does not perform the best when the value we want to predict indicates that there is a non-normal distribution, where the values either are higher or lower than the real values [49]. Cooper et al. [41] showed that probabilistic inference by using Bayesian belief networks is NP-hard. As a result, it is unlikely that a generalized algorithm will be designed in order to perform probabilistic inference efficiently in Bayesian belief networks over all possible classes. Therefore, for each of the special case, average case, and approximation algorithms, specific domain-centric Bayesian inference needs to be applied.
In Bayesian inferences, the prediction accuracy depends on reducing the uncertainty of the posterior distribution, where the Bayesian inference generates samples from the posterior distribution. These generated samples will be updated using the Markov chain Monte Carlo (MCMC) algorithm until reaching the accurate posterior predictive distribution, which can be represented by the maximum likelihood [46]. Informative priors increase the accuracy of the Bayesian inference since they provide prior knowledge to help build the likelihood function. However, using informative priors requires more data to update the posterior since the posterior will be very much driven by the prior information. Computing more data can dominate the posterior distribution and cause an overfitting problem.
The computational complexity in a Bayesian inference manifests in the MCMC algorithm’s intensive computation required to compute the maximum likelihood estimation. Furthermore, when modeling traffic data that have a short temporal component using Bayesian inference, the MCMC algorithm’s computational cost increases dramatically due to the high dimension of the temporal component [47]. In addition, improper priors can maximize the variance in the posterior samples, and hence more computational time is needed to identify the proper prior in order to reduce the variance in each sample [50]. Overall, estimating priors is a computationally intensive process, and this is considered one of the drawbacks of the Bayesian inference approach. Despite this, Bayesian inference has the capability to handle large traffic data with missing values and assign priors to these missing values [48]. It can also model data that are small in size, such as one observation, and be able to compute the prior of one observation. This process can be performed iteratively in real time [49]. Another advantage of Bayesian inference is that it can handle multilevel models and compute its hyperparameters [34]. In terms of evaluating the model performance, it is recommended to use coefficient estimates and standard deviation errors to measure the uncertainty of the model performance.
When comparing the neural network approach to the previous approaches, specifying the proper network structure can affect the prediction accuracy, while optimizing the network structure can be achieved through experience [40]. Moreover, training ANNs can lead to an overfitting problem. Therefore, it is important to ensure that the validation accuracy is higher than the training accuracy [51].
Various ANN architectures, such as the multilayer perceptron (MLP) and fuzzy neural network (FNN), can be combined to predict the values of MPEG and JPEG video, Ethernet, and Internet traffic data one step ahead. The output of the individual ANN predictors is combined to enhance the prediction accuracy using an adaptive updating scheme that allows the predictors to be dynamic. Moreover, this type of combined model can capture the non-stationary traffic characteristics, as it considers prediction at different time scales so that the predicted values can be applied to the congestion control schemes. This approach outperformed the parametric autoregressive (AR) model, as the combination of ANN predictors enhanced the prediction accuracy [52]. The use of ANNs overcomes many failings related to traditional methods for the prediction of a congested freeway’s traffic status, as most data prediction techniques highly depend on the accuracy of the stochastic processes governing the freeway [42]. The freeway modeling process is not mandatory for ANNs because the multilayer perceptron (MLP) type of ANN requires only an input training set along with appropriate outputs for prediction. As a result, this ANN architecture can be applied generally since it is not dependent on the particular geometry of a freeway section. Artificial neural networks are relatively insensitive to missing data for predicting traffic conditions and faulty data. In addition, ANNs can deal with nonlinear systems to handle highly dynamic traffic data. However, for traffic speed prediction problems, ANN models are time-consuming to train with high-dimensional data. Therefore, dimension reduction through proper feature selection would help to improve the modeling accuracy [53].
5. Traffic Simulation Models
In spite of the fact that traffic analytical models are helpful in giving insights into traffic status, traffic simulation systems play a significant role in representing and evaluating traffic behavior under a number of circumstances [54]. Traffic simulators are also considered a key enabler in the effective implementation of smart mobility services. Extensive simulation to evaluate and test the impact of such services will be essential prior to real-world testing. Hence, traffic analysis and modeling of ‘what if’ scenarios assist policymakers and traffic planners with making informed decisions regarding infrastructure planning and investments. The ability of these traffic simulators to model various levels of traffic complexity and city-wide scales ranging from a single detailed intersection to a specific region will provide valuable insights into traffic modeling and analysis [55]. This provides different levels of granularity among commercial and open-source traffic simulators which can vary extensively. Hence, these traffic simulators can be classified into three categories based on their level of representation, which are macroscopic, microscopic, and mesoscopic [7]. Macroscopic models formulate the relationships between traffic flow, traffic speed, and traffic density. These models adopt an abstracted level of traffic details, and the simulation occurs on a segment basis approach rather than individual vehicle tracking [56]. The travel demand models associated with the macroscopic-based simulators have a prime focus on the traffic flow of vehicles and the vehicles’ routing choices that are selected based on algorithms that optimize the vehicles’ travel time. While microscopic models capture traffic, dynamic factors are processed in more detail [54]. Therefore, microscopic models are suitable when simulating traffic in large network areas. In these simulators, vehicles’ movements are simulated according to car-following and lane-changing algorithms. Due to the high level of traffic details, these simulators are considered efficient in modeling and evaluating complex scenarios such as rush hour traffic congestion cases, complicated geometric traffic configurations, and many others [57]. Even with the aforementioned benefits offered by these simulators, microscopic models are considered time-consuming and expensive, and they suffer from calibration challenges [56]. The third model that represents some of the features of both microscopic and macroscopic models is the mesoscopic model [6]. All three of these different types of traffic simulation models are used to simulate the driving experiments and utilize their results in order to enhance the facilities and intelligent transportation systems (ITS). However, these traffic simulation systems are limited to specific scenarios, where they simulate the traffic status and interaction of vehicles under specific conditions [58].
To simulate the traffic status, simulation models primarily focus on the number of input and output parameters. The trip description is an input used to specify the destination and departure time. The second input is the network geometry layout, which describes the network’s length, the number of lanes, etc. The third input is traffic flow, which indicates the number of vehicles on the network [59]. In terms of the simulation model output parameters, the outputs can be defined as the travel cost of the simulated scenario and the updated traffic flow value when the network layout has been changed. For instance, it simulates the traffic flow behavior when vehicles travel from location A to location B. The simulation’s output will show the road capacity as well as how traffic congestion breaks down or spreads across different networks [60]. Therefore, traffic simulation models may have various adjustable parameters that can detail underlying traffic behavior such as vehicles’ routing choices, the selection of a shorter planned path, and driving behavior. Calibration, prediction, and validation of the inputs and parameters are considered data-demanding and require efficient computation tools [55]. These simulation models also use a number of algorithms, such as the car following algorithm, the lane changing algorithm, and the gap acceptance algorithm. These algorithms are used to view the traffic status dynamically when increasing the speed of the vehicle or driving within multiple lanes. We describe these different algorithms in the traffic simulation models to comprehend how these models work realistically. Figure 4 shows a typical illustration of the car following, lane change, and gap acceptance algorithms used in traffic simulation models.
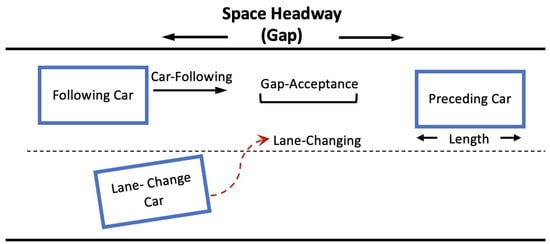
Figure 4.
Illustration for the car-following, lane-change, and gap-acceptance algorithms.
Traffic simulation models are implemented in different traffic and transport planning software to show the traffic behavior in a graphical user interface, where the user can define the input parameters and view the output parameters [61]. According to Ejercito et al. [7], the seven most widely known traffic simulation tools are SUMO, MATSim, AIMSUN, CORSIM, Paramics, VISSIM, and TRANSIMS. We can consider traffic simulators to be dynamic visualization models that use statistical methods to examine traffic behavior and provide statistical reports for the simulated scenario.
There are also some useful traffic simulators such as FreeSim [62], Traffsim [63], SUMMIT [64], and SifTraffic [65] that are designed for either microscopic or macroscopic traffic simulation. FreeSim traffic simulator is designed to conduct traffic simulations of freeways in real-time [62]. Traffsim simulator is widely known for modeling isolated traffic control strategies in different complex traffic environments [63]. In large traffic scenarios with massive and mixed traffic, SUMMIT traffic simulator provides useful features and functionalities to simulate vehicle driving, especially in urban scenarios [64]. SifTraffic is a traffic simulation tool that provides practical implications for different types of traffic applications [65].
5.1. Traffic Simulation Algorithms
The car-following algorithm, the lane-changing algorithm, and the gap-acceptance algorithm are used in microscopic traffic simulation models. However, they can be implemented differently in terms of the vehicle’s process of speed deceleration increasing, the gap size, and the accepted and rejected procedures for determining the safe distance between floating vehicles [66]:
- Car following models: A car-following algorithm is intended to describe how the simulated vehicles interact with the preceding vehicle in the same lane. For any car-following algorithm, the basic parameters used to define the speed–spacing relations are the capacity of a lane, the speed, and the average spacing between the preceding vehicle and the following vehicle [67]. Let n be the preceding vehicle, and be the following vehicle with a speed s and vehicle position x at time t. Therefore, the speed and position of the preceding vehicle are denoted by and , respectively. Similarly, the speed and position of the following vehicle are given by and , respectively [66,68]. The acceleration in speed is denoted by at time t, and the difference in speed between the preceding and the following vehicle is denoted by . Let t+ be the time period when the vehicle accelerates, where is the time required for the driver to respond to a changing scenario. As a result, the safe distance between the preceding and the following vehicle is computed as , which we refer to as the space headway . Let be the sensitivity coefficient parameter that is estimated by modeling the sensitivity of the relative distance between the following and preceding vehicles as well as the sensitivity of the relative speed for the subject vehicle [67,69]. The notations used to describe the car-following algorithm are shown in Figure 5, and the basic equation of the car-following algorithm can be represented as follows:Let be the sensitivity coefficient parameter that is estimated by modeling the sensitivity of the relative distance between the following and preceding vehicles, as well as the sensitivity of the relative speed for the subject vehicle.
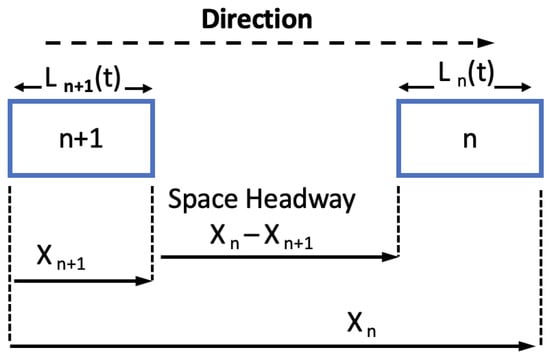 Figure 5. Basic car-following model.In traffic simulators, car-following algorithms adopt exact replicas of the car-following maneuvers which are carried out by drivers or automated vehicles in real driving conditions. The essential concept of the car following algorithms is to control the longitudinal motion of vehicles [70]. In real-world settings, autonomous vehicles such as Google cars or Apple cars integrate the data-driven machine learning car by following the model’s approach. This approach extracts the patterns or associated rules of drivers’ car following strategies and behaviors, in addition to capturing the relationships among variables that can have an impact on the car’s following behaviors. This approach yields high accuracy in replicating drivers’ car following behaviors for automated vehicles. Another car following model is the kinematics-based approach, which relies on kinematics processes such as the GM, intelligent driver, and safe distance approaches. These approaches adopt an explicit mathematical form, where most of the model parameters have physical meanings and the model outputs can be controlled through refined adjustments of the model parameters [71].
Figure 5. Basic car-following model.In traffic simulators, car-following algorithms adopt exact replicas of the car-following maneuvers which are carried out by drivers or automated vehicles in real driving conditions. The essential concept of the car following algorithms is to control the longitudinal motion of vehicles [70]. In real-world settings, autonomous vehicles such as Google cars or Apple cars integrate the data-driven machine learning car by following the model’s approach. This approach extracts the patterns or associated rules of drivers’ car following strategies and behaviors, in addition to capturing the relationships among variables that can have an impact on the car’s following behaviors. This approach yields high accuracy in replicating drivers’ car following behaviors for automated vehicles. Another car following model is the kinematics-based approach, which relies on kinematics processes such as the GM, intelligent driver, and safe distance approaches. These approaches adopt an explicit mathematical form, where most of the model parameters have physical meanings and the model outputs can be controlled through refined adjustments of the model parameters [71]. - Lane Changing Models: Lane-changing algorithms are used to simulate the impact of vehicles on adjacent lanes as they change lanes. These algorithms take into account the speed and position of the preceding vehicle as well as the time when this action takes place [72]. The concept of the lane-changing algorithm can be simply described as follows. When the vehicle intends to change lanes, the model assesses the existing headway space to determine whether changing lanes is achievable. If it is, then the process happens. If not, then the vehicle remains in the current lane [73]. A simple illustration of the lane-changing decision of a vehicle is depicted in Figure 6. The model must meet certain criteria such that for a given adjacent lane, both the space headway for the following and preceding cars must be more than the unsafe distance, which can be computed as follows:Let and denote the following and preceding vehicle speeds, respectively, and b be the vehicle’s maximum deceleration. We refer to the actual vehicle following distance if the vehicle moved into the adjacent lane by d. Equation (9) is derived from Equations (7) and (8), which compute the smallest acceptable headway gap between each vehicle C and the minimum safe distance between the subject vehicle and the following vehicle [66,74].
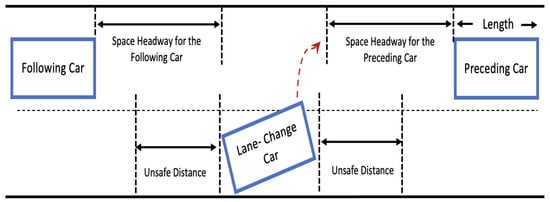 Figure 6. Basic lane-change model.
Figure 6. Basic lane-change model. - Gap acceptance models: Gap-acceptance models are mainly used to determine the traffic conditions in adjacent lanes prior to a vehicle accessing the available space. They are used to estimate the amount of space and time required to cross a junction, enter a roundabout, or change lanes [75]. These two factors are dependent on the traffic conditions, such as the road characteristics, the speed, and the lengths of the following and preceding vehicles as well as the passive vehicle. The minimum safe distance between the subject vehicle and the following vehicle, which is also known as the critical gap, is a significant parameter affecting gap acceptance behavior. An important assumption that has to be addressed in the gap acceptance models is the headway distribution in the circulating flow to measure the road capacity [66,76]:where Y denotes the vehicle’s decision of whether or not to overtake the adjacent lane at a given time , is the available headway gap, and is the critical gap. The vehicle forces entry when the gap size is equally likely to be accepted ; otherwise, the vehicle rejects the observed gap and stays in the same lane [75].
5.2. Traffic Simulation Tools
In this section, we limit the focus to the most used simulation tools in the traffic modeling literature, where we explore the state of the art of these simulation tools and discuss their functionalities and characteristics. A number of criteria, such as the nature of the tool (e.g., free, open source, or commercial) and functional capabilities of the simulator, are addressed in this section [7].
- The Verkehr In Städten - SIMulationsmodell (VISSIM) is a commercial microscopic traffic simulation tool developed by Planning Transport Verkehr in Karlsruhe, Germany [77]. VISSIM is one of the common simulation tools used to simulate and evaluate traffic status and transportation control systems. It can simulate different elements such as buses, trucks, pedestrians, and bicycles. VISSIM uses the component object model (COM) interface, which enables users to create and deploy a custom tool in VISSIM using C++, Visual Basic, or Python [54]. The latest versions of VISSIM incorporate additional autonomous vehicle-related features (communication and cooperation among vehicles) and detailed behavior specifications. The aforementioned features will utilize cooperation in lane changing and advanced merging algorithms for enhanced traffic network scaling. In this simulator, smaller headways have been chosen to model the cooperation among vehicles. Other add-on features are the new means of mobility that have also been introduced within the VISSIM simulator, which include cooperative autonomous vehicles (CAVs) and mobility as a service (MAAS) [78]. VISSIM is a microscopic traffic simulator for behavior-based multi-purpose traffic flow simulation [79].
- Advanced Interactive Microscopic Simulator for Urban and Non-Urban Networks (AIMSUN) is a new simulation tool that was developed by J. Barcelo and J.L. Ferrer in 2005 [80]. It is a commercial simulation tool that is capable of simulating real-world traffic situations in an urban network in order to build and validate traffic structures, public transportation networks, and new transportation infrastructure [54]. AIMSUN is integrated with GETRAM, a simulation environment that includes different components: a traffic network editor (TEDI), a network database, a simulation module, and an application programming interface [81]. AIMSUN has developed AIMSUN LIVE, which integrates predictive-based systems that can provide real-time traffic prediction and management. In this aspect, AIMSUN LIVE can provide accurate real-time predictions of future traffic flow patterns that can be the outcome of a specific traffic management strategy. This is because AIMSUN LIVE leverages the combination of historical and real-time streaming data along with traffic congestion mitigation policies to provide accurate traffic forecasting. Subsequently, this can assist traffic control centers in utilizing the aforementioned traffic data to make real-time decisions about road network management [55].
- Multi-Agent Transport Simulation (MATSim) is another open-source simulation tool developed by the Polytechnic of Zurich that offers a range of tools for implementing very large simulation-based agents. In MATSIM, agents hold a list that simulates the daily routine of traffic in a large area. MATSIM adopts activity-based methods that are used to model travel demand. Since MATSIM is an agent-based simulator, these agents hold a list of actionable plans and choices which includes traditional traffic properties (e.g., travel routes and modes) and time schedules. In the MATSIM simulator, agents make their decisions according to the utilization of the integrated discrete choice models [82]. MATSIM mainly focuses on modeling individual vehicle behavior, which can be considered a drawback if we are interested in traffic behavior in general [54,83].
- Simulation of Urban MObility (SUMO) is an open-source simulation tool that was developed in 2001 by the Institute of Transportation Systems at the German Aerospace Centre. It is capable of simulating traffic at the microscopic level and simulates moving vehicles and accidents [84]. In this simulator, the vehicle width is fixed, and it does not take into account the different types of vehicles such as buses, light rail, heavy rail, and trucks [54,77]. SUMO is designed as an intermodal traffic-based simulator that includes public transportation, traffic road networks, and users such as pedestrians. SUMO simulators encompass a number of built-in features which include C2X communication among vehicles that are achieved through the integration of SUMO simulators with network simulators (such as OMNeT++ or ns-3), multi-modal traffic, and automated driving. Traffic management is also an additional add-on feature that can model vehicle detection loops and video detectors to manage and control traffic through traffic lights, monitoring vehicles’ behaviors and adjusting traffic parameters such as vehicles’ speed limits [58,85].
- CORridor SIMulation (CORSIM) [86] is known as one of the most widely used microscopic traffic simulator software programs worldwide. CORSIM is used in thousands of applications as a standard traffic simulation tool. CORSIM is equipped with reliable validation, continuous logic enhancement, solid verification, and calibration efforts. It can produce real-world traffic flow realistically and with high accuracy. All types of geometric conditions including complicated traffic scenarios can be handled virtually by CORSIM. Some of these conditions include the surfaces of streets that have different combinations of turning pockets and lanes, different types of on and off-ramps, and multi-lane freeway segments.
- Paramics addresses road networks with drivers and simulates the decisions, intentions, and subsequent actions of drivers when they move toward their destinations [87]. Depending on the characteristics of the basic network and the probability of encountering traffic congestion, drivers are considered to choose the possible route in the simulator. A set of decisions is prioritized by each driver throughout the network. These decisions include traffic speed and specific moments to change, cross, or merge into different traffic lanes. In the Paramics simulator, the network topology and travel demand drive the calibration. Flows of saturation and the proportion of lane usage are generated as outputs from the simulator to examine the road network’s performance. However, these parameters cannot be provided as input for calibration assistance. Although Paramics does not prescribe the effect of a traffic model, it can simulate and model the cause of action. This way, the simulator preserves the predictive power of the simulation process in subsequent changes in the model and tests the change in the traffic road network.
- The TRansportation ANalysis and SIMulation System (TRANSIMS) creates an integrated regional transportation system environment by employing advanced computational and analytical techniques [88]. The simulation environment includes a regional population of individual travelers. TRANSIMS simulates the activities and individual interactions of travelers and their plans for the transportation system. It also simulates and determines the environmental impact of these activities. TRANSIMS contains an interim operational capability (IOC) with numerous features, applicability, and readiness for each major module to complete different types of specific traffic case studies.
5.3. Summary of the Traffic Simulation Tools
Several articles have focused on the comparison of urban road traffic simulators and provided comprehensive assessments of the existing simulation tools. Table 2 provides a comparison between these traffic simulators based on seven features along with their strengths and weaknesses points. We also list several key challenges in these traffic simulators that conflict with our research goal.
- A major drawback of the exciting simulation tools is the inability to implement or integrate advanced Bayesian-based models or algorithms. They use the objective optimization algorithm to simulate traffic behavior based on different traffic parameters such as route choice and vehicle movement.
- Another issue that has gained the attention of the traffic simulation community is the CPU and memory performance. Adding a number of parameters to represent different aspects of the traffic simulation model such as traffic speed, the number of lanes, route length, and the width of the lane requires high usage of memory and the CPU, thus increasing the computation time.
- These traffic simulators embed sample events that we examine for their impact on the traffic status. These events are implemented as modules to represent limited events. These traffic simulators share similar events such as traffic acceleration events, traffic deceleration events, and traffic red signal events.

Table 2.
Different traffic simulation tools and their main features and capabilities.
Table 2.
Different traffic simulation tools and their main features and capabilities.
| Feature Simulator | MATSim | AIMSUN | VISSIM | SUMO | CORSIM | Paramics | TRANSIMS |
|---|---|---|---|---|---|---|---|
| Open Source | Yes | No | No | Yes | No | No | Yes |
| Visualization | 2D | 2D, 3D | 2D, 3D | 2D, 3D | 2D, 3D | 2D, 3D | 2D, 3D |
| Output | Text | Graphs | XML | XML | Text | Graphs | XML |
| Import Map | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Programming Language | C++, Java | Python, C++ | C++, VB, Matlab, Python | C++, VB, Matlab, Python | Python, C++ | C++, VB, Matlab, Python | C++, VB, Matlab, Python |
| Flexibility in infrastructure Development | Limited | Flexible | Flexible | Flexible | Flexible | Flexible | Flexible |
| Coding | Easy | Difficult | Easy | Difficult | Difficult | Easy | Difficult |
| Objectives | Simulate traffic congestion level | Simulate vehicle counts, road occupancy, and traffic speed | Simulate and analyze traffic flow | Evaluate the traffic light system | Simulate traffic flow and traffic light system | Simulate traffic congestion level | Simulate and analyze traffic flow |
6. Conclusions
Our study revealed that no particular non-parametric model outperforms all other methodologies in general. Rather, all these models have some pros and cons over each other. Above all, they are designed to work for specific problems in the traffic domain, such as the prediction of speed, congestion flow, accidents, freeway traffic volume, and multi-scale high-speed traffic. Moreover, the design process of these models largely depends on the data structure and other associated factors such as data dimension reduction, feature extraction, and handling the missing values. All these models can be used for both short-term and long-term prediction by considering the spatiotemporal correlations based on the time interval of each observation in the dataset. We found that in some scenarios, hybrid models that combine different models together provide better prediction accuracy. That combination could be in between parametric and non-parametric models such as ST-Kriging and ANNs, in between different versions of ANNs, or even in between the MCMC and Bayesian approaches. These findings emphasize the need for more hybrid non-parametric spatiotemporal models to predict traffic-related outcomes.
In the second part of this survey, numerous state-of-the-art simulation models for traffic have been conducted to outline the differences between different traffic simulation tools. In the literature, most microscopic traffic simulation tools use three main simulation algorithms: car following, gap acceptance, and lane changing. These algorithms were developed to mimic human driving capabilities and were discussed to show how they use real-world driving strategies. Finally, a comparison between different traffic simulator tools was conducted in Table 2 to study SUMO, MATSim, AIMSUN, CORSIM, Paramics, VISSIM, and TRANSIMS. We evaluated these different simulation tools based on their capabilities, availability, features, and implementation flexibility. The user can specify the suitable tool for practice based on the intended outcome, whether simulating traffic flow, analyzing traffic light systems, or simulating vehicle counts, road occupancy, or traffic speed. Defining the purpose of the simulator’s usage is an important step in selecting the appropriate simulator.
Author Contributions
Conceptualization, T.A., S.M. and G.A.; methodology, T.A., S.M. and G.A.; validation, T.A. and K.E.; investigation, T.A., S.M. and G.A.; writing—original draft preparation, T.A., S.M. and G.A.; writing—review and editing, T.A., S.M. and G.A.; visualization, T.A.; supervision, K.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC), grant number: CRC-2017-00170.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chao, W.; Quddus, M.; Ison, S. A spatio-temporal analysis of the impact of congestion on traffic safety on major roads in the UK. Transp. A Transp. Sci. 2013, 9, 124–148. [Google Scholar]
- Bachechi, C.; Po, L. Traffic analysis in a smart city. In Proceedings of the WI ’19: IEEE/WIC/ACM International Conference on Web Intelligence-Companion, Thessaloniki, Greece, 14–17 October 2019. [Google Scholar]
- Antonella, F.; Sacone, S.; Siri, S. Freeway Traffic Modeling and Control; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Xiaokun, W.; Kockelman, K.M. Forecasting network data: Spatial interpolation of traffic counts from Texas data. Transp. Res. Rec. 2015, 2105, 100–108. [Google Scholar]
- Nectaria, T.; Jensen, C.S. Conceptual data modeling for spatiotemporal applications. GeoInformatica 1999, 3, 245–268. [Google Scholar]
- Algers, S.; Bernauer, E.; Boero, M.; Breheret, L.; Taranto, C.; Fox, K. A Review of Micro-Simulation Models, SMARTEST: Simulation Modeling Applied to Transport European Scheme Tests; Institute for Transport Studies, University of Leeds: Leeds, UK, 1996; pp. 100–108. [Google Scholar]
- Ejercito Paolo, M.; Kristine Gayle, E.; Nebrija, R.P.F.; Lara-Figueroa, L.L. Traffic simulation software review. In Proceedings of the 2017 8th International Conference on Information, Intelligence, Systems & Applications (IISA), Larnaca, Cyprus, 28–30 August 2017. [Google Scholar]
- TomTom. Traffic Congestion Ranking|TomTom Traffic Index. Available online: https://tomtom.com/en-gb/traffic-index/ranking/ (accessed on 2 March 2022).
- Government of Canada. Canadian Motor Vehicle Traffic Collision Statistics: 2018. Available online: https://tc.canada.ca/en/road-transportation/statistics-data/canadian-motor-vehicle-traffic-collision-statistics-2018 (accessed on 1 March 2022).
- Box George, E.P.; Tiao George, C. Bayesian Inference in Statistical Analysis; John Wiley and Sons: Hoboken, NJ, USA, 2011; Volume 40. [Google Scholar]
- Eleni, V.; Karlaftis, M.G.; Golias, J.C. Short-term traffic forecasting: Where we are and where we’re going. Transp. Res. Part C Emerg. Technol. 2014, 43, 3–19. [Google Scholar]
- Xiaolei, M.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction. Sensors 2017, 17, 818. [Google Scholar]
- Afshin, A.; Rajabioun, T.; Ioannou, P. Traffic flow prediction for road transportation networks with limited traffic data. IEEE Trans. Intell. Transp. Syst. 2014, 16, 653–662. [Google Scholar]
- Yisheng, L.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.-Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar]
- Zhanguo, S.; Guo, Y.; Wu, Y.; Ma, J. Short-term traffic speed prediction under different data collection time intervals using a SARIMA-SDGM hybrid prediction model. PloS ONE 2019, 14, e0218626. [Google Scholar]
- Ibai, L.; Ser, J.D.; Velez, M.; Vlahogianni, E. Road traffic forecasting: Recent advances and new challenges. IEEE Intell. Transp. Syst. Mag. 2018, 10, 93–109. [Google Scholar]
- Reisen Valdério, A.; Zamprogno, B.; Palma, W.; Arteche, J. A semiparametric approach to estimate two seasonal fractional parameters in the SARFIMA model. Math. Comput. Simul. 2014, 98, 1–17. [Google Scholar] [CrossRef]
- Raikwar Aditya, R.; Sadawarte, R.R.; More, R.G.; Gunjal, R.S.; Mahalle, P.N.; Railkar, P.N. Long-term and short-term traffic forecasting using holt-winters method: A comparability approach with comparable data in multiple seasons. Int. J. Synth. Emot. (IJSE) 2017, 8, 38–50. [Google Scholar] [CrossRef]
- Antti, S.; Hao, J.; Reyhani, N.; Ji, Y.; Lendasse, A. Methodology for long-term prediction of time series. Neurocomputing 2007, 70, 2861–2869. [Google Scholar]
- Gregorio, G.; Rossi, R.; Gastaldi, M.; Caprini, A. Data mining methods for traffic monitoring data analysis: A case study. Procedia-Soc. Behav. Sci. 2011, 20, 455–464. [Google Scholar]
- Yi, Y.; Shang, P. Forecasting traffic time series with multivariate predicting method. Applied Math. Comput. 2016, 3, 266–278. [Google Scholar]
- Qianlong, W.; Guo, Y.; Yu, L.; Li, P. Earthquake prediction based on spatio-temporal data mining: An LSTM network approach. IEEE Trans. Emerg. Top. Comput. 2017, 8, 148–158. [Google Scholar]
- Brent, S.; Kockelman Kara, M. Spatial prediction of traffic levels in unmeasured locations: Applications of universal Kriging and geographically weighted regression. J. Transp. Geogr. 2013, 29, 24–32. [Google Scholar]
- John, O.K.; Vaci, L.; Mihaylova, L.S. Traffic estimation for large urban road network with high missing data ratio. Sensors 2019, 19, 2813. [Google Scholar]
- Matthew, H.; Amer, H.M.; Mihaylova, L. Traffic state estimation via a particle filter over a reduced measurement space. In Proceedings of the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017; pp. 1–8. [Google Scholar]
- Matthew, H.; Amer, H.M.; Mihaylova, L. Traffic volume prediction with segment-based regression Kriging and its implementation in assessing the impact of heavy vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 20, 232–243. [Google Scholar]
- Haixiang, Z.; Yang, Y.; Qingquan, L.; Go, Y.A. An improved distance metric for the interpolation of link-based traffic data using Kriging: A case study of a large-scale urban road network. Int. J. Geogr. Inf. Sci. 2012, 26, 667–689. [Google Scholar]
- Hackney Jeremy, K.; Michael, B.; Sumit, B.; Axhausen Kay, W. Predicting road system speeds using spatial structure variables and network characteristics. J. Geogr. Syst. 2007, 9, 397–417. [Google Scholar] [CrossRef]
- Hidetoshi, M. A Study of Travel Time Prediction Using Universal Kriging; Springer: Berlin/Heidelberg, Germany, 2010; pp. 257–270. [Google Scholar]
- John, S. Nested sampling for general Bayesian computation. Bayesian Anal. 2006, 1, 2833–2859. [Google Scholar]
- Lee Peter, M. Bayesian Statistics; Oxford University Press: London, UK, 1989. [Google Scholar]
- Daziano Ricardo, A.; Luis, M.-M.; Shahram, H. Computational Bayesian statistics in transportation modeling: From road safety analysis to discrete choice. Transp. Rev. 2013, 33, 570–592. [Google Scholar] [CrossRef]
- Subhadeep, M.; Fletcher, D. Generalized empirical Bayes modeling via frequentist goodness of fit. Sci. Rep. 2018, 8, 1–15. [Google Scholar]
- Lai, Z.; Tarek, S. Bayesian hierarchical modeling of traffic conflict extremes for crash estimation: A non-stationary peak over threshold approach. Anal. Methods Accid. Res. 2019, 24, 100–106. [Google Scholar]
- Faustino, P.; Gómez-Déniz, E.; Sarabia, J.M. Modeling road accident blackspots data with the discrete generalized Pareto distribution. Accid. Anal. Prev. 2014, 71, 38–49. [Google Scholar]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R. Artificial neural networks approach in evapotranspiration modeling: A review. Irrig. Sci. 2011, 29, 11–25. [Google Scholar] [CrossRef]
- Mohamed Zahraa, E. Using the artificial neural networks for prediction and validating solar radiation. J. Egypt. Math. Soc. 2019, 27, 1–13. [Google Scholar] [CrossRef]
- Gregorio, G.; Riccardo, R.; Massimiliano, G.; Armando, C. Data mining methods for traffic monitoring data analysis: A case study. Procedia-Soc. Behav. Sci. 2011, 29, 455–464. [Google Scholar]
- Chen, W.; Guo, F.; Wang, F.-Y. A survey of traffic data visualization. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2970–2984. [Google Scholar] [CrossRef]
- Gültekin, Ç.B.; Sari, M.; Borat, O. A neural network based traffic-flow prediction model. Math. Comput. Appl. 2010, 15, 269–278. [Google Scholar]
- Romi, S.; Jonathan, A.; Maria, C. Spatial analysis of road crash frequency using Bayesian models with Integrated Nested Laplace Approximation (INLA). J. Transp. Saf. Secur. 2021, 13, 1240–1262. [Google Scholar]
- Cynthia, T.; Deirdre, M.; Jonathan, A. Freeway traffic data prediction using neural networks. In Proceedings of the Pacific Rim TransTech Conference, 1995 Vehicle Navigation and Information Systems Conference Proceedings, 6th International VNIS. A Ride into the Future, Seattle, WA, USA, 30 July–2 August 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 225–230. [Google Scholar]
- Cheng, C.A.; Boots, B. Variational inference for Gaussian process models with linear complexity. arXiv 2017, arXiv:1711.10127. [Google Scholar]
- Somnath, C. Spatio-Temporal Modeling of Traffic Risk Mapping on Urban Road Networks. Master’s Thesis, Jaume I University, Castelló, Spain, February 2020. [Google Scholar]
- Dawkins, L.C.; Williamson, D.B.; Mengersen, K.L.; Morawska, L.; Jayaratne, R.; Shaddick, G. Where is the clean Air? A bayesian decision framework for personalised cyclist route selection using R-INLA. Bayesian Anal. 2021, 16, 61–91. [Google Scholar] [CrossRef]
- Broemeling Lyle, D. Bayesian methods for medical test accuracy. Diagnostics 2011, 1, 1. [Google Scholar] [CrossRef] [PubMed]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Daniels Michael, J.; Hogan Joseph, W. Missing Data in Longitudinal Studies: Strategies for Bayesian Modeling and Sensitivity Analysis; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Van De Schoot, R.; Broere, J.J.; Perryck, K.H.; Zondervan-Zwijnenburg, M.; Van Loey, N.E. Analyzing small data sets using Bayesian estimation: The case of posttraumatic stress symptoms following mechanical ventilation in burn survivors. Eur. J. Psychotraumatology 2015, 6, 25216. [Google Scholar] [CrossRef]
- Gary, C.; Dan, L. When optimal choices feel wrong: A laboratory study of Bayesian updating, complexity, and affect. Am. Econ. Rev. 2005, 95, 1300–1309. [Google Scholar]
- Khaz’ali, A.R.; Emamjomeh, A.; Andayesh, M. An accuracy comparison between artificial neural network and some conventional empirical relationships in estimation of relative permeability. Pet. Sci. Technol. 2011, 29, 1603–1614. [Google Scholar] [CrossRef]
- Alireza, K.; Nayyara, S. Multi-scale high-speed network traffic prediction using combination of neural networks. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; pp. 1071–1075. [Google Scholar]
- Alfréd, C.; Viharos, Z.J.; Kis, K.B.; Tettamanti, T.; Varga, I. Traffic speed prediction method for urban networks—An ANN approach. In Proceedings of the 2015 International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Budapest, Hungary, 3–5 June 2015. [Google Scholar]
- Nesrine, G.; Sabeur, E.; Saber, D.; Ben, S.L. A survey of simulation platforms for the assessment of public transport control systems. In Proceedings of the 2014 International Conference on Advanced Logistics and Transport (ICALT), Tunis, Tunisia, 1–3 May 2014. [Google Scholar]
- Djukic, T.; van Lint, H.; Casas, J. An open, sustainable, ubiquitous data and service ecosystem for efficient, effective, safe, resilient mobility in metropolitan areas. H2020-ICT 2015. [Google Scholar] [CrossRef]
- US Department of Transportation. Types of Traffic Analysis Tools. Available online: https://ops.fhwa.dot.gov/trafficanalysistools/typetools.htm (accessed on 11 March 2022).
- David, W.; Sewall, J.; Li, W.; Lin, M.C. Virtualized traffic at metropolitan scales. Front. Robot. AI 2015, 2, 11. [Google Scholar]
- Saidallah, M.; Fergougui, A.E.; Elalaoui, A.E. A comparative study of urban road traffic simulators. MATEC Web Conf. 2016, 81, 05002. [Google Scholar] [CrossRef]
- Sohel, M.S.M.; Ferreira, L.; Hoque, M.S.; Tavassoli, A. Micro-simulation modeling for traffic safety: A review and potential application to heterogeneous traffic environment. IATSS Res. 2019, 43, 27–36. [Google Scholar]
- Sokolowski John, A.; Banks Catherine, M. Principles of Modeling and Simulation: A Multidisciplinary Approach; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zhang, Y.; Owen Larry, E.; Clark James, E. Multiregime approach for microscopic traffic simulation. Transp. Res. Rec. 1998, 1644, 103–114. [Google Scholar] [CrossRef]
- Miller, J.; Horowitz, E. FreeSim—A free real time freeway traffic simulator. In Proceedings of the 2007 IEEE Intelligent Transportation Systems Conference, Seattle, WA, USA, 30 September–3 October 2007; pp. 18–23. [Google Scholar]
- Lindorfer, M.; Backfrieder, C.; Mecklenbräuker, C.F.; Ostermayer, G. Modeling Isolated Traffic Control Strategies in TraffSim. In Proceedings of the UKSim-AMSS 19th International Conference on Computer modeling & Simulation (UKSim), Cambridge, UK, 5–7 April 2017; pp. 143–148. [Google Scholar]
- Cai, P.; Lee, Y.; Luo, Y.; Hsu, D. SUMMIT: A Simulator for Urban Driving in Massive Mixed Traffic. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Virtually, 31 May–31 August 2020; pp. 4023–4029. [Google Scholar]
- Sorenson, D.K.; Collins, J. Practical Applications Of Traffic Simulation Using SifTraffic. Presented at the Compendium of Papers, Institute of Transportation Engineers 2000, District 6 Annual Meeting, San Diego, CA, USA, 24–28 June 2000; Available online: https://trid.trb.org/view/671329 (accessed on 30 July 2021).
- Usman, A.H.; Huang, Y.; Lu, P. A review of car-following models and modeling tools for human and autonomous-ready driving behaviors in micro-simulation. Smart Cities 2021, 4, 314–335. [Google Scholar]
- Rothery, R.W. Car Following Models. 1992. Available online: https://ocw.mit.edu/courses/1-225j-transportation-flow-systems-fall-2002/a884475721d0645b8ce2ee8640976caf_carfollowinga.pdf (accessed on 11 March 2022).
- Janson, O.J.; Tapani, A. Comparison of Car-Following Models; Swedish National Road and Transport Research Institute: Linkö ping, Sweden, 2004; Volume 960. [Google Scholar]
- Aycin, M.F.; Benekohal, R.F. Comparison of car-following models for simulation. Transp. Res. Rec. 1999, 1678, 1116–1127. [Google Scholar] [CrossRef]
- Haiyang, Y.; Jiang, R.; He, Z.; Zheng, Z.; Li, L.; Liu, R.; Chen, X. Automated vehicle-involved traffic flow studies: A survey of assumptions, models, speculations, and perspectives. Transp. Res. Part C Emerg. Technol. 2021, 127, 1–127. [Google Scholar]
- Yang, D.; Zhu, L.; Liu, Y.; Wu, D.; Ran, B. A novel car-following control model combining machine learning and kinematics models for automated vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1991–2000. [Google Scholar]
- Sara, M.; Sarvi, M.; Rose, G. Lane changing models: A critical review. Transp. Lett. 2010, 2, 157–173. [Google Scholar]
- Gipps Peter, G. A model for the structure of lane-changing decisions. Transp. Res. Part Methodol. 1986, 20, 403–414. [Google Scholar] [CrossRef]
- Mizanur, R.; Chowdhury, M.; Xie, Y.; He, Y. Review of microscopic lane-changing models and future research opportunities. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1942–1956. [Google Scholar]
- Rahmi, A. A Review Of Gap-Acceptance Capacity Models. In Proceedings of the Conference of Australian Institutes of Transport Research (Caitr), Adelaide, Australia, 5–7 December 2017. [Google Scholar]
- Ahmed, K.; Ben-Akiva, M.; Koutsopoulos, H.; Mishalani, R. Models of freeway lane changing and gap acceptance behavior. Transp. Traffic Theory 1996, 13, 501–515. [Google Scholar]
- Kotusevski, G.; Hawick, K.A. A review of traffic simulation software. Res. Lett. Inf. Math. Sci. 2009, 13, 35–54. [Google Scholar]
- PTV Group. PTV Vissim is the World’s Most Advanced and Flexible Traffic Simulation Software. Available online: https://www.ptvgroup.com/en/solutions/products/ptv-vissim/ (accessed on 11 March 2022).
- Fellendorf, M.; Vortisch, P. Microscopic traffic flow simulator VISSIM. In Fundamentals of Traffic Simulation; Barceló, J., Ed.; Springer: New York, NY, USA, 2010; pp. 63–93. [Google Scholar]
- Jordi, C.; L, F.J.; David, G.; Josep, P.; Alex, T. Traffic Simulation with Aimsun; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Rehmat, U.M.; Shehzad, K.K.; Hussain, K.Z.; Ahmad, K.M.; Nasru, M.; Nawaz, K.A. Vehicular Traffic Simulation Software: A Systematic Comparative Analysis. Pak. J. Eng. Technol. 2021, 4, 103–114. [Google Scholar]
- Johannes, N.; Powers, S.T.; Urquhart, N.; Farrenkopf, T.; Guckert, M. An overview of agent-based traffic simulators. Transp. Res. Interdiscip. Perspect. 2021, 12, 100486. [Google Scholar]
- Andreas, H.; Kai, N.; Axhausen Kay, W. The Multi-Agent Transport Simulation MATSim; Ubiquity Press: London, UK, 2016. [Google Scholar]
- Alvarez, L.P.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wießner, E. Microscopic Traffic Simulation Using sumo. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2575–2582. [Google Scholar]
- SUMO. Simulation of Urban Mobility. Available online: https://www.eclipse.org/sumo/ (accessed on 11 March 2022).
- Owen, L.E.; Zhang, Y.; Rao, L.; McHale, G. Traffic flow simulation using CORSIM. In Proceedings of the 2000 Winter Simulation Conference Proceedings (Cat. No.00CH37165), Orlando, FL, USA, 10–13 December 2000; Volume 2, pp. 1143–1147. [Google Scholar]
- Sykes, P. Traffic Simulation with Paramics. In Fundamentals of Traffic Simulation; Barceló, J., Ed.; Springer: New York, NY, USA, 2010; pp. 131–171. [Google Scholar]
- Smith, L.; Beckman, R.; Baggerly, K. TRANSIMS: Transportation Analysis and Simulation System; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 1995. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).