Minimization of nth Order Rate Matching in Satellite Networks with One to Many Pairings

Abstract

This paper studies the minimization of nth (positive integer) order rate matching in high-throughput multi-beam satellite systems, based on one-to-many capacity allocation pairings, for the first time in the literature. The offered and requested capacities of gateways and users’ beams are exploited, respectively. Due to the high complexity of the binary optimization problem, its solution is approached with a two-step heuristic scheme. Firstly, the corresponding continuous, in [0, 1], pairing problem is solved applying the difference of convex optimization theory, and then, a transformation from continuous to binary feasible allocation is provided to extract the pairings among gateways and users’ beams. Comparing with the exponential-time optimal exhaustive mechanism that investigates all possible pairs to extract the best matching for minimizing the rate matching, extended simulations show that the presented approximation for the solution of the non-convex optimization problem has fast convergence and achieves a generally low relative error for lower value of n. Finally, the simulation results show the importance of n in the examined problem. Specifically, pairings originated by the minimization of rate matching with larger n result in more fair rate matching among users’ beams, which is a valuable result for satellite and generally wireless systems operators.

1. Introduction

The data-hungry Internet-based services make of utmost importance the synergy between the 5G and satellite networks [1,2,3]. Specifically, Cisco’s report stated that the monthly global mobile data traffic will be 77 exabytes by 2022, and annual traffic will reach almost one zettabyte [4]. Satellites can also be useful in the domain of Internet of Things (IoT) for the connection of multiple devices, particularly for emergency scenarios and industrial applications [5]. Hence, the satellite operators are directed toward the employment of high-throughput satellite (HTS) multi-beam systems [6,7,8] that can offer up to Tbps capacities.

The configuration of HTS systems includes the links of satellite–user equipment (UE) beams and the gateways (GWs)–satellite links that operate at Ka Band and Q/V, W bands, respectively. The tropospheric phenomena cause severe signal degradations in these bands that can be mitigated by the Smart Gateway Diversity (SGD) concept [6,9,10], similarly in this paper, exploiting the different geographical locations of GWs.

1.1. Motivation and Related Literature

The challenging wireless networks’ ecosystem, with strict demands for higher data rates, not only requires their performance evaluation through new channel model frameworks [11] but also makes the investigation in the resource management field an important ally toward the users’ quality of service (QoS) satisfaction. Specifically, in terms of satellite communication (SatComs) systems [12,13], there are many scientific works presenting methods based on optimization, game theory and recently artificial intelligence (AI) techniques, targeting the appropriate allocation of resources including power, time, bandwidth and user pairing.

Especially, in [14], a terrestrial-satellite network (TSN) with hot air balloons at different heights and elevation angles that relay the signals between satellites and ground stations is presented. The maximization of network energy efficiency is assumed subject to the optimization of the transmission power, the serving period of satellites and the required number of lasers per satellites at the relays. The resource allocation problem is modeled and solved by geometric programming with Taylor series approximation. Moreover, in [15], a broadband GEO multi-beam SatCom system is presented, and the goal of resource management is to satisfy the beam traffic demand by making use of the minimum transmit power and utilized bandwidth. The scope is the maximization of spectrum utilization based on the spectrum reuse considering tolerable interference. Due to the non-convexity of joint power and carrier assignment optimization problem, the authors propose the solution of two sub-problems, i.e., carrier and power assignment, respectively. These are solved using successive convex approximation (SCA). The same mathematical technique is applied in [16] to a satellite and aerial-integrated network to support IoT devices. Especially, the maximization of the sum rate is depicted, and the use of first-order Taylor expansion is made.

Finally, another use of SCA is shown in [17], where a secure beamforming scheme for rate-splitting multiple access cognitive TSN is investigated in the presence of multiple eavesdroppers. The intention is the maximization of the secrecy-energy efficiency of the earth station (ES) with respect to the constraints on the ES secrecy rate, the cellular users’ rate requirements and transmit power budgets of the satellite and base station. The objective and constraints are non-convex and are solved iteratively using convex conversions.

Regarding the application of game theory, in [18], the cooperative transmission and resource allocation in a cloud-based integrated TSN is studied as a game-based resource allocation problem. The operator offers two levels of services of different QoS and price and the maximization of the utility of the operator, which is composed by the Stackelberg game between the operator and users, the evolutionary game between all users, and the energy minimization problem is implemented.

Furthermore, in terms of AI, techniques such as convolutional networks [19], long-short-term memory (LSTM) networks [20] and deep reinforcement learning (DRL) [21,22,23] have already been used. In [19], a convolutional neural networks’ approach is presented for flexible payload management in very high-throughput satellite systems. The authors use a realistic traffic model and suggest a cost function aiming to minimize both the error between the offered capacity and the required capacity and the amount of resources used in the satellite. Additionally, in [20], a LSTM prediction-based resource-matching scheme for low earth orbit (LEO) SatComs is presented. The traffic is predicted, and a resource allocation method is proposed to efficiently match power and spectrum resources.

The DRL framework is considered in [21] for dynamic resource allocation in a multi-beam satellite system, where image-like tensors are exploited to extract traffic spatial and temporal features. Moreover, the SatCom networks are a promising architecture for supporting the Internet of Remote Things (IoRT). Thus, in [22], the model-free reinforcement learning is exploited for the joint resource-scheduling and IoRT data-scheduling problem subject to the maximization of the amount of the IoRT data of the overall satellite IoRT network. Finally, in [23], the authors apply a multiobjective reinforcement learning for cognitive SatComs, where the uncertainty in the thousands of possible radio parameter combinations and the dynamic variation of the radio channel over time result in a continuous multidimensional state-action space. This requires a fixed-size memory continuous state-action mapping and not the traditional discrete mapping. The authors give trade-off analyses considering the execution time, the performance accuracy and the computational cost of the proposed scheme.

1.2. Our Contribution

Generally, the recent literature has expressed interest in the concept of appropriate GW–UE pairings in HTS systems to optimize different performance metrics [6,9,10]. Particularly, suboptimal one-to-many pairings are provided for the minimization of both losses and rate matching (RM) in [9], in which a special case with $n=1$ for the latter is provided, while here, the nth order rate matching is examined. The one-to-many pairings, in the previous paper and the current paper, are investigated to model the important scenario where less GWs have to serve more UEs in realistic scenarios of HTS systems. The rate matching is a widely known performance metric in satellite networks [6,9,24]; however, to the best of our knowledge, the influence of the nth power in the pairings originated by the minimization of the rate-matching function has not yet been investigated. In the current work, this case is studied, and useful conclusions are extracted.

Suboptimal one-to-many GW-UE matching, based on the gateways’ offered and users’ requested capacities, namely OCs and RCs, similarly to this work, is investigated in [10] where the maximization of both the minimum and total system’s satisfaction ratio and minimization of both the maximum and total system’s dissatisfaction ratio are studied. Due to the difficulty of the aforementioned binary optimization problems, in all cases, a two-step heuristic approach is shown. Firstly, the optimization problem from the binary case is “relaxed”, and a continuous pairing solution in [0,1] is extracted. Hence, an iterative algorithm is implemented, and then, a continuous to binary feasible transformation of this solution is applied. Specifically, in the related literature, [9,10], in metrics of losses, rate matching and dissatisfaction ratio, that include quadratic functions, the continuous pairings are extracted by the convex–concave procedure (CCP) [25]. This is a known method for the solution of difference of convex (DC) optimization problems. The CCP algorithm theoretically converges to a stationary point of the optimization problem. The aforementioned two-step approach is also implemented here for the minimization of the nth order rate matching. The main contributions of the current work, based on GWs’ OCs and UEs’ RCs, are summarized below:

• The problem of optimal one-to-many (O2M) pairs extracted by minimization of the nth order rate matching is a difficult non-convex problem, and the optimal solution has exponential-time complexity. Thus, a fast convergence mechanism is presented to address this problem for the first time to the best of our knowledge. To do that, the initial problem is “relaxed” and after appropriate transformations, quadratic forms appear. Then, by using the binomial expansion (BE) and considering positive integer n, to guarantee the BE convergence ([26], Equation (5.12)), we prove that BE includes convex and concave terms. Afterwards, the CCP method is directly applied to solve the problem, and an iterative scheme with low complexity is presented. The proposed two-step approach can be used as a benchmark compared to other algorithms for facing similar problems in the future.
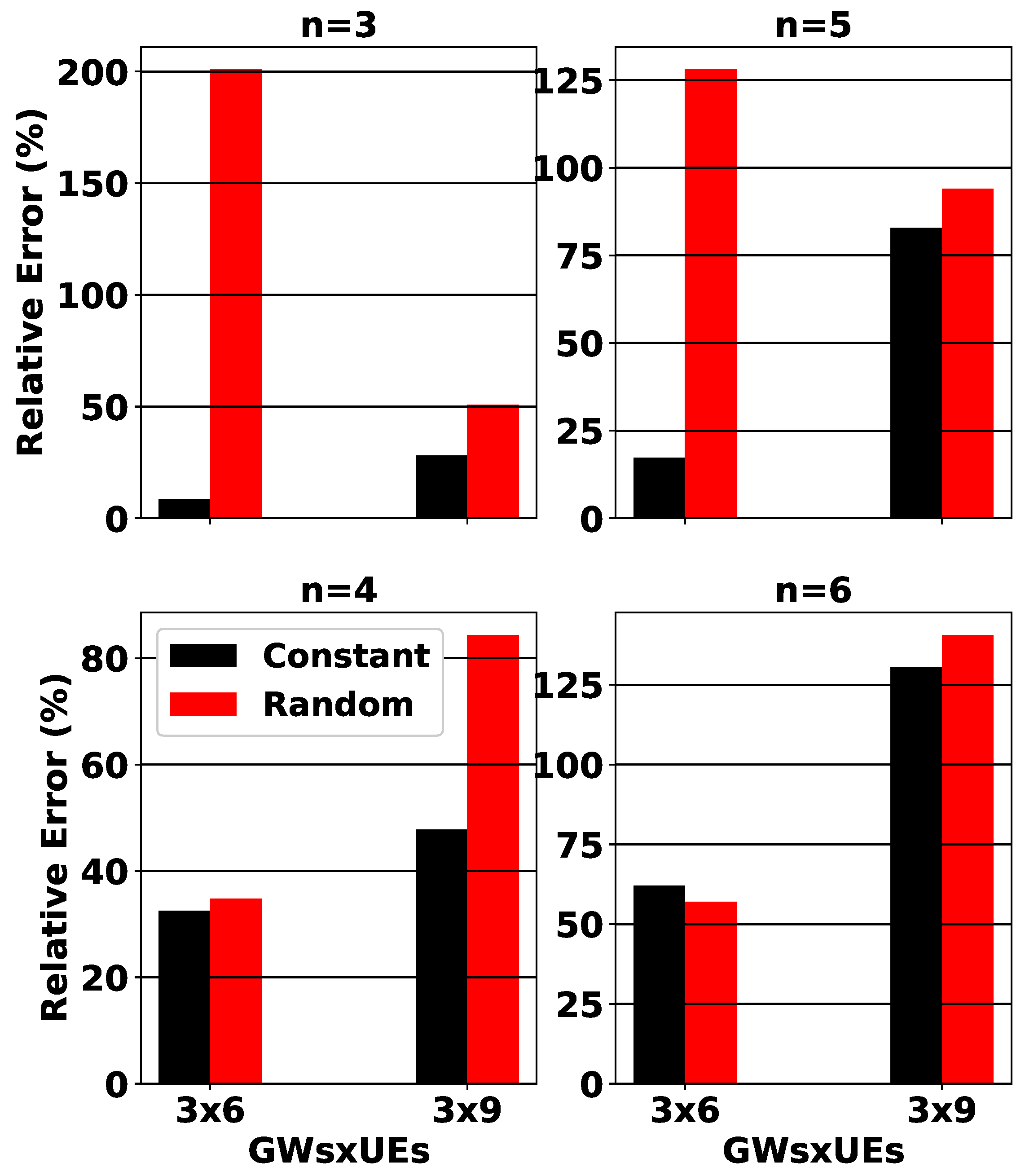
• Assuming even or odd n, two different problems are solved. The solution of both is based on the CCP algorithm whose outcome depends on the initial feasible points [9,10], because non-convex functions, as in our case, have multiple stationary points. The relative error among the rate matching originated by the proposed scheme and the corresponding from exhaustive mechanism, exploring all the feasible pairs, becomes generally greater as n increases. This can be explained by the fact that in larger n, the binomial expansion includes more factors, resulting in more linear approximations by the CCP approach, ending up with lower performance. However, for smaller n, the performance is ameliorated.
• Simulations have also depicted that pairings originated by greater than $n=1$ order RM lead to generally more UEs’ fairness, assuming the rate matchings between the UEs. Particularly, as we observe in Figure 1 and Figure 2, even a slight increase from $n=1$ to $n=2$ leads to much more fair UE pairings, and in this case, our practical approach can be fast implemented, resulting in a small relative error compared to the time-consuming exhaustive mechanism, as discussed in Section 3. The increment of fairness with increment in n is explained by the focus to the minimization of larger absolute differences of OCs and RCs in the minimization of rate matching as n becomes larger. This observation, based on the simulations, is of utmost importance for the satellite and generally wireless systems’ operators, because n can be used as a fairness controller for the rate-matching problem that has been used widely in the literature.

For the rest of the article, Section 2 presents the system model, the allocation problem and the proposed pairing mechanisms for the nth order RM. In Section 3, simulation results of the performance of the proposed allocation schemes are presented, while Section 4 concludes the work.

2. Dynamic Capacity Allocation

2.1. System Model

A practical and realistic scenario where fewer M GWs serve more N UEs $(\mathrm{M}\le \mathrm{N})$ under O2M pairings in an HTS system, including a non-generative GEO satellite, is studied. Especially, in each time-slot of time multiplexing SGD concept, similar to [9,10], each GWi, with $\mathrm{i}\in \mathbf{M}$ where $\mathbf{M}=\{1,2,\cdots ,\mathrm{M}\}$, serves $k_i>0$ UEs and ${\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}}}{\mathrm{k}}_{\mathrm{i}}=\mathrm{N}$. Moreover, each UEj, with $\mathrm{j}\in \mathbf{N}$ where $\mathbf{N}=\{1,2,\cdots ,\mathrm{N}\}$, has requested capacity RCj and the offered capacity, ${\mathrm{OC}}_{\mathrm{ij}}$, between GWi and UEj, is expressed by the Shannon formula ${\mathrm{OC}}_{\mathrm{ij}}={\mathrm{B}}_{\mathrm{C}}{\log }_2(1+{\gamma }_{\mathrm{ij}})$ where $B_C$ is the bandwidth and ${\gamma }_{\mathrm{ij}}^{-1}{=\mathrm{CNIR}}_{\mathrm{up},\mathrm{i}}^{-1}{+\mathrm{CNIR}}_{\mathrm{dn},\mathrm{j}}^{-1}$. The RCs and OCs are in bps, and the total carrier to interference plus noise ratio CNIRij, named as ${\gamma }_{\mathrm{ij}}^{}$, includes the CNIRs of feeder link i and downlink j. Afterwards, the ${\mathrm{CNIR}}_{\mathrm{up},\mathrm{i}}^{}{=\mathrm{CNIR}}_{\mathrm{CS},\mathrm{i}}^{}10^{-\mathrm{At}{\mathrm{t}}_{\mathrm{i}}/10}$, where $CNI{R}_{CS,i}$ is the clear sky CNIR for the feeder link i and $At{t}_i$, expressing the total atmospheric attenuation originated by the rain, clouds, scintillation and atmospheric gases, is the same as that in [9,10]. Finally, each GWi offers ${\mathrm{OC}}_{\mathrm{ij}}^{{}^{″}}={\mathrm{OC}}_{\mathrm{ij}}/\phantom{{\mathrm{OC}}_{\mathrm{ij}}^{{}^{\prime \prime }}{\mathrm{k}}_{\mathrm{i}}}{\mathrm{k}}_{\mathrm{i}}$, because its bandwidth is shared among its $k_i$ simultaneously served UEs under the O2M scenario.

2.2. Capacity Allocation Problem and Proposed Mechanism

We focus on finding GWs–UEs pairing matrices $\mathbf{X}\in \{0{,1\}}^{\mathrm{M}\times \mathrm{N}}$ for approaching the minimization of the system’s nth order rate matching and formulate separately the cases of even and odd n. Setting $b_{ij}={\left(R{C}_j-O{C}_{ij}^{}/\phantom{O{C}_{ij}^{}{\displaystyle \sum _{o=1}^N}{x}_{io}}{\displaystyle \sum _{o=1}^N}{x}_{io}\right)}^n$, where ${\mathrm{k}}_{\mathrm{i}}^{}={\displaystyle \sum _{\mathrm{o}=1}^{\mathrm{N}}}{\mathrm{x}}_{\mathrm{io}}^{},\forall \mathrm{i}$, describes the O2M case, and applying the BE, we conclude in (1) where n has to be a positive integer to guarantee the convergence of right-hand side (RHS) ([26], Equation (5.12) and $\left(\begin{array}{c}n\hfill \\ m\hfill \end{array}\right)$ is the binomial coefficient. Moreover, considering the identity $|c^{\alpha }|=|c{|}^{\alpha }$ for every real c and a (c must be nonzero for negative a), the initial problem becomes as in (2).

$${\mathrm{b}}_{\mathrm{ij}}=\sum _{\mathrm{m}=0}^{\mathrm{n}}\left[{\left(-1\right)}^{\mathrm{m}}\left(\begin{array}{c}\mathrm{n}\hfill \\ \mathrm{m}\hfill \end{array}\right)R{C_j}^{n-m}O{C}_{ij}^m{\left(\sum _{o=1}^N{x}_{io}\right)}^{-m}\right],$$

(1)

$$\begin{array}{c}\underset{\mathbf{X}\in \mathrm{S}}{\min }{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}}}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}}{\mathrm{x}}_{\mathrm{ij}}{\left|\mathrm{R}{\mathrm{C}}_{\mathrm{j}}-\frac{{\mathrm{OC}}_{\mathrm{ij}}^{}}{{\displaystyle \sum _{\mathrm{o}=1}^{\mathrm{N}}}{\mathrm{x}}_{\mathrm{io}}}\right|}^{\mathrm{n}}=\underset{\mathbf{X}\in \mathrm{S}}{\min }{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}}}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}}{\mathrm{x}}_{\mathrm{ij}}\left|{\mathrm{b}}_{\mathrm{ij}}^{}\right|=\hfill \\ \underset{(\mathbf{X},\mathrm{T})\in {\mathrm{S}}_1^{\mu }}{\min }{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}}}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}}{\mathrm{x}}_{\mathrm{ij}}{\mathrm{t}}_{\mathrm{ij}}^{}.\hfill \end{array}$$

(2)

The minimization of the initial problem on the left-hand side (LHS) of (2) has the feasible set S, where the inequality constraint guarantees that each GW serves at least one UE and the equality constraint guarantees that each UE is served by one GW, $\mathrm{S}=\left\{1\le {\displaystyle \sum _{\mathrm{o}=1}^{\mathrm{N}}}{\mathrm{x}}_{\mathrm{io}}^{},\forall \mathrm{i},{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}}}{\mathrm{x}}_{\mathrm{ij}}^{}=1,\forall \mathrm{j},\mathbf{X}\in {\{0,1\}}^{\mathrm{M}\times \mathrm{N}}\right\}$. The initial problem on the LHS of (2) is transformed appropriately in last relation of (2) with feasible set ${\mathrm{S}}_1^{\mu }$, where $\mu$ is even or odd, considering the problem with even and odd n, respectively, and auxiliary variables $\mathbf{T}\in {\mathrm{R}}^{\mathrm{M}\times \mathrm{N}}$ are added. Specifically, by setting $\mathrm{u}=\left(\begin{array}{c}n\hfill \\ m\hfill \end{array}\right)R{C_j}^{n-m}O{C}_{ij}^m{\left({\displaystyle \sum _{o=1}^N}{x}_{io}\right)}^{1-m}$ and assuming that ${\mathrm{t}}_{\mathrm{ij}}^{}\ge \left|{\mathrm{b}}_{\mathrm{ij}}\right|$, since the objective on the right-hand side (RHS) of the first line in (2) is an increasing function of auxiliary ${\mathrm{t}}_{\mathrm{ij}}^{}$ ($\partial \mathrm{obj}/\phantom{\partial \mathrm{obj}\partial {\mathrm{t}}_{\mathrm{ij}}^{}}\partial {\mathrm{t}}_{\mathrm{ij}}^{}{=\mathrm{x}}_{ij}^{}\ge 0$), we have for the even nth RM that ${\mathrm{t}}_{\mathrm{ij}}^{}\ge \left|{\mathrm{b}}_{\mathrm{ij}}\right|={\mathrm{b}}_{\mathrm{ij}}$ and for the odd one ${\mathrm{t}}_{\mathrm{ij}}^{}\ge \left|{\mathrm{b}}_{\mathrm{ij}}\right|\iff {-\mathrm{t}}_{\mathrm{ij}}^{}\le {\mathrm{b}}_{\mathrm{ij}}\le {\mathrm{t}}_{\mathrm{ij}}^{}$. Thus, the sets of corresponding problems become ${\mathrm{S}}_1^{\mathrm{even}}=\left\{\mathbf{X}\in \mathrm{S},{\displaystyle \sum _{o=1}^N}{x}_{io}{t}_{ij}\ge {\displaystyle \sum _{m=0}^n}\left[{\left(-1\right)}^m\mathrm{u}\right],\forall \mathrm{i},\mathrm{j}\right\}$ and ${\mathrm{S}}_1^{\mathrm{odd}}=\left\{\mathbf{X}\in {\mathrm{S}}_1^{\mathrm{even}},{\displaystyle \sum _{o=1}^N}{x}_{io}{t}_{ij}\ge {\displaystyle \sum _{m=0}^n}\left[{\left(-1\right)}^{m+1}\mathrm{u}\right],\forall \mathrm{i},\mathrm{j}\right\}$, respectively.

Continuing the retransformation of problem (2), we assume the matrix $\mathbf{Y}\in {\mathrm{R}}^{\mathrm{M}\times 2\mathrm{N}}$ where ${\mathrm{y}}_{\mathrm{i}}^{}{=[\mathrm{x}}_{\mathrm{i}1}^{}{,\mathrm{x}}_{\mathrm{i}2}^{},\cdots ,{\mathrm{x}}_{\mathrm{iN}}^{}{,\mathrm{t}}_{\mathrm{i}1}^{}{,\mathrm{t}}_{\mathrm{i}2}^{},\cdots ,{\mathrm{t}}_{\mathrm{iN}}^{}{]}^{\mathrm{T}}$ is a 2N × 1 vector related with the ith GW. Furthermore, we set $\mathbf{D}=\left[\begin{array}{cc}{\mathbf{0}}_{\mathrm{N}\times \mathrm{N}}& {\mathbf{0}}_{\mathrm{N}\times \mathrm{N}}\\ {\mathbf{I}}_{\mathrm{N}\times \mathrm{N}}& {\mathbf{0}}_{\mathrm{N}\times \mathrm{N}}\end{array}\right]$, where ${\mathbf{0}}_{\mathrm{N}\times \mathrm{N}}$ is the zero matrix and $\mathbf{I}$ is the identity matrix both of shape N × N, and $\mathbf{Aj}$ is a zero 2N × 2N matrix with 1 in row N+j until the first N columns. Hence, the objective in (2) and the LHS of inequalities in ${\mathrm{S}}_1^{\mathrm{even}}$ and ${\mathrm{S}}_1^{\mathrm{odd}}$ take the quadratic forms ${\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}}}{\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}\mathbf{D}{\mathrm{y}}_{\mathrm{i}}^{}$ and ${\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}{\mathbf{A}}_{\mathrm{j}}{\mathrm{y}}_{\mathrm{i}}^{}$, respectively. Moreover, we set the $\mathrm{e}={[1_{1:\mathrm{N}},0_{\mathrm{N}+1:2\mathrm{N}}^{}]}^{\mathrm{T}}$ as a 2N × 1 vector, with 1 in the first N positions and 0 in the rest, resulting in ${\displaystyle \sum _{o=1}^N}{x}_{io}=e^T{y}_i$. This is assumed inside u for the analysis below ((5) and (6)). Taking, also, into consideration that the problem belongs to binary optimization, having generally no polynomial time complexity, a heuristic two-step approach is applied.

Firstly, the constraint $\mathbf{X}\in {\{0,1\}}^{\mathrm{M}\times \mathrm{N}}$ is relaxed to $\mathbf{X}\in {[0,1]}^{\mathrm{M}\times \mathrm{N}}$, a widely applied relaxation method, and $S_2$ is the convex counterpart of feasible set S. Based on this relaxation and the aforementioned transformations, the continuous problem that is solved in the first step, called relaxed, is presented in (3).

$$\underset{\mathbf{Y}\in {\mathrm{S}}_3^{\mu }\subset {\mathrm{R}}^{\mathrm{M}\times 2\mathrm{N}}}{min}{\displaystyle \sum _{i=1}^M}{\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}{\mathbf{D}}^{\ast }{\mathrm{y}}_{\mathrm{i}}^{}-{\displaystyle \sum _{i=1}^M}{\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}\mathbf{P}{\mathrm{y}}_{\mathrm{i}}^{},$$

(3)

where

$$\begin{array}{c}{\mathrm{S}}_2=\left\{1\le {\mathrm{e}}^T{y}_i,\forall \mathrm{i}\in \mathbf{M},{\displaystyle \sum _{i=1}^M}{y}_{ij}=1,\forall \mathrm{j}\in \mathbf{N},\right.\hfill \\ \left.0\le {\mathrm{y}}_{ij}\le 1,\forall \mathrm{i}\in \mathbf{M},\forall \mathrm{j}\in \mathbf{N}\right\},\hfill \end{array}$$

(4)

$$\begin{array}{c}{\mathrm{S}}_3^{\mathrm{even}}=\left\{\mathbf{Y}\in {\mathrm{S}}_2,\right.{\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}{\mathbf{P}}_{\mathrm{j}}^{}{\mathrm{y}}_{\mathrm{i}}^{}{-\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}{\mathbf{A}}_{\mathrm{j}}^{\ast }{\mathrm{y}}_{\mathrm{i}}^{}+\mathrm{R}{{\mathrm{C}}_{\mathrm{j}}}^{\mathrm{n}}\left({\mathrm{e}}^{\mathrm{T}}{\mathrm{y}}_{\mathrm{i}}\right)\hfill \\ -\mathrm{nR}{{\mathrm{C}}_{\mathrm{j}}}^{\mathrm{n}-1}{\mathrm{OC}}_{\mathrm{ij}}^{}+{\displaystyle \sum _{\mathrm{m}=2}^{\mathrm{n}}}\left[{\left(-1\right)}^{\mathrm{m}}\mathrm{u}\right]\le 0,\left.\forall \mathrm{i}\in \mathbf{M},\forall \mathrm{j}\in \mathbf{N}\right\},\hfill \end{array}$$

(5)

$$\begin{array}{c}{\mathrm{S}}_3^{\mathrm{odd}}=\left\{\mathbf{Y}\in {\mathrm{S}}_3^{\mathrm{even}},\right.{\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}{\mathbf{P}}_{\mathrm{j}}^{}{\mathrm{y}}_{\mathrm{i}}^{}{-\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}{\mathbf{A}}_{\mathrm{j}}^{\ast }{\mathrm{y}}_{\mathrm{i}}^{}-\mathrm{R}{{\mathrm{C}}_{\mathrm{j}}}^{\mathrm{n}}\left({\mathrm{e}}^{\mathrm{T}}{\mathrm{y}}_{\mathrm{i}}\right)\hfill \\ +\mathrm{nR}{{\mathrm{C}}_{\mathrm{j}}}^{\mathrm{n}-1}{\mathrm{OC}}_{\mathrm{ij}}^{}+{\displaystyle \sum _{\mathrm{m}=2}^{\mathrm{n}}}\left[{\left(-1\right)}^{\mathrm{m}+1}\mathrm{u}\right]\le 0,\left.\forall \mathrm{i}\in \mathbf{M},\forall \mathrm{j}\in \mathbf{N}\right\}.\hfill \end{array}$$

(6)

Especially, Proposition 1 in [10] about the transformation of quadratic forms to the difference of convex functions is exploited in (3), (5) and (6). This proposition proves that every quadratic form ${\mathbf{x}}^{\mathrm{T}}\mathbf{Qx}$ can be converted to a difference of convex functions by the addition and subtraction from Q’s main diagonal of a number larger than the absolute value of a minimum eigenvalue of Q. Hence, considering the analysis of Proposition 1, we have that ${\mathbf{D}}_{}^{\mathrm{sym}}=0.5\left(\mathbf{D}+{\mathbf{D}}^{\mathrm{T}}\right)$, ${\mathbf{A}}_{\mathrm{j}}^{\mathrm{sym}}=0.5({\mathbf{A}}_j+{\mathbf{A}}_j^T)$, ${\mathbf{D}}^{\ast }={\mathbf{D}}_{}^{\mathrm{sym}}+\mathrm{r}\mathbf{I}$, ${\mathbf{A}}_{\mathrm{j}}^{\ast }={\mathbf{A}}_{\mathrm{j}}^{\mathrm{sym}}+{\mathrm{r}}_{\mathrm{j}}\mathbf{I}$, $\mathbf{P}=r\mathbf{I}$ and ${\mathbf{P}}_j=r_j\mathbf{I}$ with I representing the 2N × 2N identity matrix and $r\ge \left|{\lambda }_{min}^{{\mathbf{D}}^{\mathrm{sym}}}\right|$, $r_j\ge \left|{\lambda }_{min}^{{\mathbf{A}}_{\mathrm{j}}^{\mathrm{sym}}}\right|$, where ${\lambda }_{min}^o$ is the minimum eigenvalue of o = ${\mathbf{D}}_{}^{\mathrm{sym}}$, ${\mathbf{A}}_{\mathrm{j}}^{\mathrm{sym}}$, respectively. Furthermore, it is easy to prove, given in Appendix A, that the term ${\left({\mathrm{e}}^{\mathrm{T}}{y}_i\right)}^{1-m}$ inside u of (5), (6) is convex. This is originated by the rule about the composition with an affine mapping [27]. Hence, each $m$ term’s convexity depends on the sign of term ${(-1)}^m$ (${(-1)}^{m+1}$) in (5) and (6), respectively. Thus, in (5), the terms of even/odd m are convex/concave, respectively, and the opposite happens in (6). Afterwards, the convex (concave) parts from quadratic forms are grouped together with the convex (concave) terms in the summations appearing in (5) and (6), and the relaxed problem in (3) is solved by the iterative CCP heuristic approach [25], as presented in Algorithm 1, that converges to a stationary point of the problem.

Algorithm 1 CCP Iterative Mechanism for Problems in (3).

1: Select a tolerance $\epsilon >0$ and ${\mathbf{Y}}^0$ as a feasible point for relaxed problem with $0\le {\mathrm{y}}_{{}_{\mathrm{ij}}}^0\le 1,\forall \mathrm{i}\in \mathbf{M},$ $\forall \mathrm{j}\in \mathbf{N}\left(C1\right)$ and ${\mathrm{y}}_{{}_{\mathrm{ij}}}^0=\left|{\mathrm{b}}_{\mathrm{ij}}\right|$, $\forall \mathrm{i}\in \mathbf{M},\mathrm{N}<\mathrm{j}\le 2\mathrm{N}$, where $b_{ij}$ in (1) is computed from the values of (C1).

2: Repeat

2a: Set as $g_1$, $g_2$ and $g_3$ the convexified parts of objective in (3) and in inequalities of (5) and (6), respectively, and $f_1$, $f_2$ the convex parts in (5) and (6), respectively. $g_3$ is the same as $g_2$ having the even terms in the summation. $f_2$ is the same with $f_1$ having the odd terms in the summation and the constant and linear terms with opposite signs compared with $f_1$.

${\mathrm{g}}_1={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}}}{\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)\mathrm{T}}\mathbf{P}{\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)}+2{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}}}\left[{\left(\mathbf{P}{\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)}\right)}^{\mathrm{T}}\left({\mathrm{y}}_{\mathrm{i}}^{}{-\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)}\right)\right],$

$\begin{array}{c}{\mathrm{g}}_2={\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)\mathrm{T}}{\mathbf{A}}_{\mathrm{j}}^{\ast }{\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)}+{\displaystyle \sum _{\mathrm{m}=3,5,7,\dots }^{\mathrm{n}}}\left[\left(\begin{array}{c}\mathrm{n}\hfill \\ \mathrm{m}\hfill \end{array}\right){\mathrm{RC}}_{\mathrm{j}}^{{}^{\mathrm{n}-\mathrm{m}}}{\mathrm{OC}}_{\mathrm{ij}}^{\mathrm{m}}{\left({\mathrm{e}}^{\mathrm{T}}{\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)}\right)}^{1-\mathrm{m}}\right]+\hfill \\ \left[2{\left({\mathbf{A}}_{\mathrm{j}}^{\ast }{\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)}\right)}^{\mathrm{T}}\right.+\left.\left({\displaystyle \sum _{\mathrm{m}=3,5,7,\dots }^{\mathrm{n}}}\left[\left(\begin{array}{c}\mathrm{n}\hfill \\ \mathrm{m}\hfill \end{array}\right){\mathrm{RC}}_{\mathrm{j}}^{\mathrm{n}-\mathrm{m}}{\mathrm{OC}}_{\mathrm{ij}}^{\mathrm{m}}(1-\mathrm{m}){\left({\mathrm{e}}^{\mathrm{T}}{\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)}\right)}^{-\mathrm{m}}\right]\right){\mathrm{e}}^{\mathrm{T}}\right]\ast \left({\mathrm{y}}_{\mathrm{i}}^{}{-\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)}\right),\hfill \end{array}$

$\begin{array}{c}{{\mathrm{f}}_1=\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}{\mathbf{P}}_{\mathrm{j}}{\mathrm{y}}_{\mathrm{i}}^{}{+\mathrm{RC}}_{\mathrm{j}}^{\mathrm{n}}\left({\mathrm{e}}^{\mathrm{T}}{\mathrm{y}}_{\mathrm{i}}\right)+{\displaystyle \sum _{\mathrm{m}=2,4,6,\dots }^{\mathrm{n}}}\left[\left(\begin{array}{c}\mathrm{n}\hfill \\ \mathrm{m}\hfill \end{array}\right){\mathrm{RC}}_{\mathrm{j}}^{{}^{\mathrm{n}-\mathrm{m}}}{\mathrm{OC}}_{\mathrm{ij}}^{\mathrm{m}}{\left({\mathrm{e}}^{\mathrm{T}}{\mathrm{y}}_{\mathrm{i}}\right)}^{1-\mathrm{m}}\right]-{\mathrm{nRC}}_{\mathrm{j}}^{\mathrm{n}-1}{\mathrm{OC}}_{\mathrm{ij}}^{}.\hfill \end{array}$

2b: Solve $\underset{\mathbf{Y}\in {\mathrm{S}}_4^{\mu }\subset {\mathrm{R}}^{\mathrm{M}\times 2\mathrm{N}}}{min}{\displaystyle \sum _{i=1}^M}{\mathrm{y}}_{\mathrm{i}}^{\mathrm{T}}{\mathbf{D}}^{\ast }{\mathrm{y}}_{\mathrm{i}}^{}-{\mathrm{g}}_1$ for even and odd n with sets

${\mathrm{S}}_4^{\mathrm{even}}=\left\{\mathbf{Y}\in {\mathrm{S}}_2,{\mathrm{f}}_1-{\mathrm{g}}_2\le 0,\forall \mathrm{i}\in \mathbf{M},\forall \mathrm{j}\in \mathbf{N}\right\}$ and

${\mathrm{S}}_4^{\mathrm{odd}}=\left\{\mathbf{Y}\in {\mathrm{S}}_4^{\mathrm{even}},{\mathrm{f}}_2-{\mathrm{g}}_3\le 0,\forall \mathrm{i}\in \mathbf{M},\forall \mathrm{j}\in \mathbf{N}\right\}$, respectively.

2c: Update iteration q: = q + 1.

2d: Set as ${\mathrm{y}}_{\mathrm{i}}^{\left(\mathrm{q}\right)}$ the solution of problem in (2b).

3: Until the values of the objective in two sequential steps have relative error $\le \epsilon$.

In terms of the two-step procedure’s time complexity, we have that in the first step, Algorithm 1, due to the sequential solution of convex optimization problems, has complexity $O\left(IxG\right(M,N\left)\right)$, where I is the number of iterations and $G(M,N)$ is the complexity of solving a convex problem which is known to be polynomial in M and N. In the second step, the continuous matching solution of (3) is converted, applying Algorithm 2 in [9] to a binary feasible solution of the X allocation matrix. Thus, it has complexity $O\left(MNlog\right(MN\left)\right)$ due to the sorting of elements of the M × N X matrix. Afterwards, the overall complexity is $O\left(IxG\right(M,N)+MNlog(MN\left)\right)$. According to the simulation results in Section 3, the number of iterations I is small, so the total complexity of the proposed approach is lower than the exponential complexity of the exhaustive mechanism.

3. Simulation Results and Discussion

A GEO HTS network is simulated with 3, 4 GWs and 6–9 UEs under the same assumptions and values of the parameters as in [9]. The only differences here are: (a) the GWs’ locations in Nemea in Greece, Sintra in Portugal, Harwell in the UK and the City of Luxembourg and (b) the CNIRs of downlinks that are uniformly distributed in (5, 30) dB. In terms of the users’ number, we have to say that the SGD-based HTS networks are usually employed with the maximum of gateways and users that have been simulated [28,29]. There are not the multi-beam satellite systems with many beams. Moreover, another reason for keeping these numbers for UEs is the prohibitive time complexity of finding the pairs in exhaustive research in order to find the corresponding relative error among the proposed and exhaustive approach. However, the literature regarding the iterative solution of convex/concave problems, that is the basis of our Algorithm 1, shows that generally, the convergence iterations are kept in low order. To evaluate the performance of the proposed CCP scheme, the CVXPY library in PYTHON is used, and statistical averages for 1000 independent simulation scenarios are studied.

Due to the dependence of the $\mathbf{Proposed}$ method’s outcome on the initial feasible points, the comparison of a $\mathbf{Constant}$ feasible point and a $\mathbf{Random}$ procedure is made. In the Constant case, the (1/M)${\mathbf{1}}_{M\times N}$ point is used, where ${\mathbf{1}}_{M\times N}$ is the all-ones M × N matrix, while in the Random process, the point, among 200 random feasible points, resulting in the minimum objective in LHS of (2) is selected. Moreover, the tolerance of the Proposed iterative algorithm is $\epsilon ={10}^{-3}$ and r, $r_j$ are the ceiling numbers of the corresponding absolute minimum eigenvalues, as described in Section 2.

Due to the fact that the proposed scheme consists of the first effort to approximate the solution of the nth order rate-matching minimization and no other known techniques exist in the literature, its performance is examined by the comparison with the corresponding optimal $\mathbf{Exhaustive}$ scheme. The latter explores all the feasible pairs to arrive at the best result. Specifically, the values of rate-matching objectives based on the pairs of Exhaustive (${\mathrm{obj}}_{\mathrm{Exh}}$) and Proposed (${\mathrm{obj}}_{\mathrm{Prop}}$) schemes are used for the relative error expressed as $\left|{\mathrm{obj}}_{\mathrm{Exh}}^{}{-\mathrm{obj}}_{\mathrm{Prop}}^{}\right|/\phantom{\left|{\mathrm{obj}}_{\mathrm{Exh}}^{}{-\mathrm{obj}}_{\mathrm{Prop}}^{}\right|{\mathrm{obj}}_{\mathrm{Exh}}^{}}{\mathrm{obj}}_{\mathrm{Exh}}^{}$. This error is computed in each simulation scenario and then is averaged.

For the average relative error, a useful performance indicator is the maximum among the minimum relative errors through the different GWs–UEs configurations. Considering the 1st and 2nd order RM in Figure 1, this is about 14% for the 3 × 9 and 28.4% for the 4 × 6 GWsxUEs configurations, respectively, while the iterative proposed process has fast convergence, as shown from the average iterations of Algorithm 1 that are low. In case of HTS systems, with a larger number of GWs/UEs where a pairing allocation decision has to be completed in short time, it is practical to use an additional termination criterion with the maximum number of iterations in Algorithm 1.

Moreover, in Figure 3, without any loss of generality for 3 × 6 and 3 × 9 systems, we depict that for both odd (first line subplots) and even (second line subplots) values of n, an increase of the latter, from 3 to 5 and 4 to 6, respectively, results in an increase of the best (minimum) relative error for each separate system, which has also been observed for all the rest of the systems. Indicatively, for the $3\times 9$ system, the best relative error is about 28% and 82% for $n=3$ and $n=5$, respectively, and 48% and 130% for $n=4$ and $n=6$, respectively. A possible reason is that more concave terms appear in BE as n increases, which are approximated by linearizations in the convexified step of the CCP method; hence, more approximations are made, leading to worse performance compared with the optimal Exhaustive scheme.

Finally, in Figure 2, the average value of Jain’s fairness index [30] is shown, which is defined in each simulation scenario as ${\left({\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}}{\mathrm{w}}_{\mathrm{j}}\right)}^2/\phantom{{\left({\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}}{\mathrm{w}}_{\mathrm{j}}\right)}^2\left(\mathrm{N}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}}{\mathrm{w}}_{\mathrm{j}}^2\right)}\left(\mathrm{N}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}}{\mathrm{w}}_{\mathrm{j}}^2\right)$, where $w_j$ is computed for each UE based on the absolute difference presented on the LHS of the first line in (2). In each separate GWs–UEs system (i.e., in each of the four subplots), observing the performance of the optimal Exhaustive scheme, represented by the blue lines, the minimization of higher than $n=1$ order RM leads to higher fairness among UEs. The UEs’ fairness is denoted as the absolute difference between their requested capacities and the offered capacities of gateways that are matched with them. For practical systems, even the increase from $n=1$ to $n=2$ results in a solution with much more fairness, and our fast convergent approach achieves a relative error less than $30\%$. This effect can be explained by the fact that a higher n focuses on the minimization of the higher absolute differences in the minimization process of the initial problem, resulting in more similar absolute differences among the UEs. Moreover, this trend is also observed in most cases of the Proposed schemes (black and red lines), which confirms the robustness of this important remark. In conclusion, in an optimization problem that does not contain the ‘fairness’, because of its minimization structure, the increase of n can indirectly assist the increase of UEs’ fairness. This is a valuable observation for the network’s operators, because this factor can be exploited as a fairness controller in terms of rate matching not only in investigated satellite but also in other wireless systems.

4. Conclusions

In this paper, considering realistic scenarios with fewer gateways than the users’ beams in the HTS system, we present one-to-many capacity allocation schemes for the minimization of the nth order rate matching for positive and integer n. Due to the high complexity of the optimization problem, a fast convergent two-step heuristic approach is proposed for the first time in the literature. This pairing scheme includes the relaxation of the initial problem and the application of the difference of convex programming theory in the first step, while the continuous to discrete conversion of the pairing solution is made in the second step. Moreover, the existence of multiple stationary points in non-convex functions, as in our case, makes the presented solution approach to depend on the starting feasible point. Thus, different initial points, constant and random, are investigated. Extended simulations show the fast convergence and a generally smaller relative error of the proposed schemes for smaller n and the very good performance of our approach for small values of n, such as $n=1$ and $n=2$ cases. Our algorithm can be used as a benchmark compared to other algorithms for facing similar problems in the future. Finally, even though the rate matching is a widely applied performance metric in the literature, the role of n has not been investigated. The factor n can be used as a fairness controller. Greater fairness among UEs’ rate matchings, in terms of their absolute differences between the requested and offered capacities, has been depicted as n increases compared to the $n=1$ case. The key functionality of n in UEs’ fairness is an important point for operators not only of satellites but also in the rest of the wireless systems.