Towards Practical Applications in Modeling Blockchain System
Abstract
1. Introduction
- Network discovery. The first time a node is connected to the network, it is booted and connected to the initial boot node to get a list of neighbor’s nodes, synchronize and get the current version of the blockchain, subsequently disconnected;
- Transaction creation and verification. All nodes in the network can initiate transactions to transfer digital assets to available peers in the network. The creation of a new transaction implies that certain conditions are fulfilled by the exchange participants, so the transaction specifies the amount and the addressee and may additionally specify the terms of the transaction. Once the transaction has been created, the sender signs it with their electronic key and sends it to the network. The transaction will be rejected if it is incorrectly generated, invalid or does not contain all the information required for execution, or if the user does not have sufficient funds to complete the transaction;
- Mining. When a new transaction is received, the node initializes its addition to the block. The block is generated based on information about the past block received and the information collected. The miners try to find a solution; the block is checked, added to the registry and sent to the network to other nodes. If a solution is found by the second node, it is discarded to avoid branching;
- Checking the block for correctness. Checking the block before adding it to the register implies that the previous block exists, that the data structure is intact, that the sender has sufficient funds, that the signature is correct, that the syntax is correct, that the inputs and outputs are within acceptable values, that the transaction size is not higher than the maximum, that the transaction has not yet been processed. If confirmed, the chain is updated in the general ledger, and the transaction and user status are validated.
- We aim to create a simulation model of a communication network with a blockchain system awaiting the results of network delay simulation;
- We are dedicated to providing analysis solutions for simulation and analytical modeling;
- We include a comparison of simulation results with analytical solution results.
2. Related Works
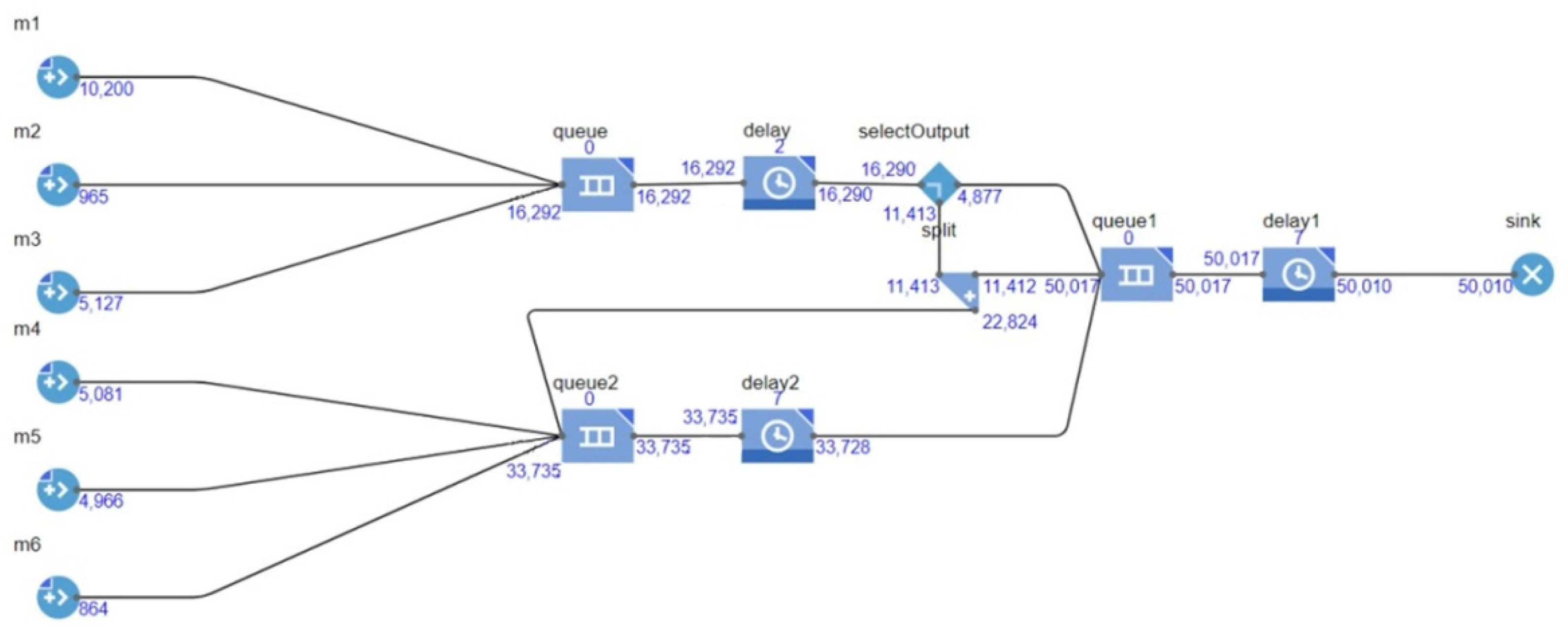
3. Modeling Blockchain Systems on a Communication Network
- M is the scale parameter;
- a is the shape parameter.
- Rn (k) is the correlation function for the aggregated time series;
- H is the Hurst parameter;
- k is the time shift;
- σ2 is the sampling variance of the sequence.
- ρ is the system utilization factor;
- CB2 is the normalized variance of the service time.
- λ is the average rate of receipt of an application
- 𝜑2 is the second-order momentum of a random variable.
- k—the number of nodes initiating creating the transactions needed to form the block (depends on the number of transactions in the Memory Pool), varies with the number of connected active nodes;
- tproc i—the time taken for node i to send a transaction to the network, depends on the network card and network configuration;
- m—the number of network devices the packet passes through during transmission, depends on network configuration;
- tdelay m—the network latency introduced by devices when transmitting a packet—a problem that can create greater potential for forks and vulnerability to hostile attacks;
- tMP—dwell time of unconfirmed transactions in Memory Pool before being added to the block;
- tm—time to check the block and solve the computational problem by the miners, depends on the consensus algorithm;
- tver—time taken to check the block and add it to the common chain (approximately a few milliseconds), depends on network configuration.
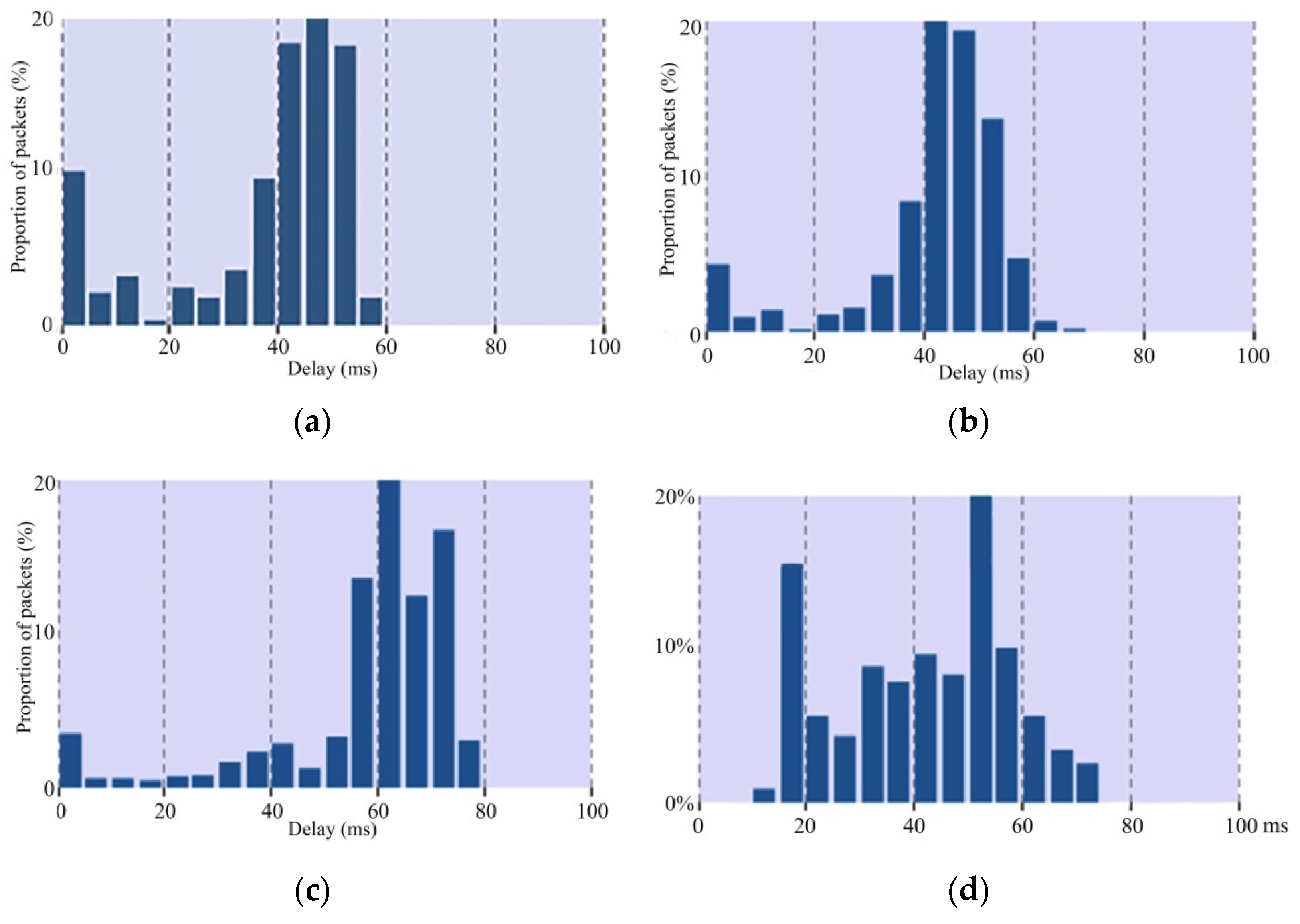
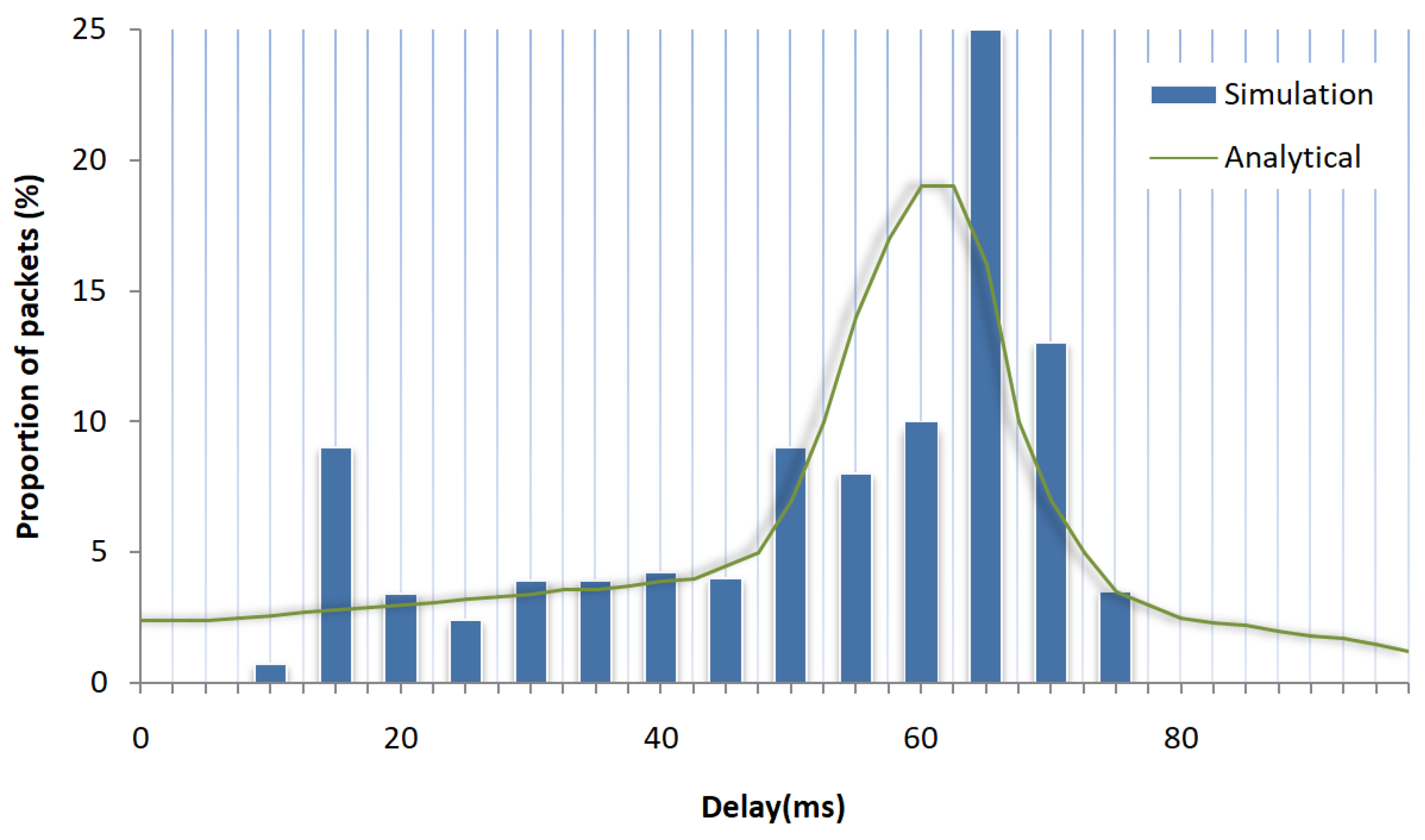
4. Comparative Analysis of the Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Pautasso, C.; Zhu, L.; Gramoli, V.; Ponomarev, A.; Tran, A.B.; Chen, S. The blockchain as a software connector. In Proceedings of the 2016 13th Working IEEE/IFIP Conference on Software Architecture, Venice, Italy, 5–8 April 2016; pp. 182–191. [Google Scholar]
- Palmara, P. Tracing and Tracking with the Blockchain. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2018. [Google Scholar]
- Elagin, V.; Spirkina, A.; Levakov, A.; Belozertsev, I. Blockchain Behavioral Traffic Model as a Tool to Influence Service IT Security. Future Internet 2020, 12, 68. [Google Scholar] [CrossRef]
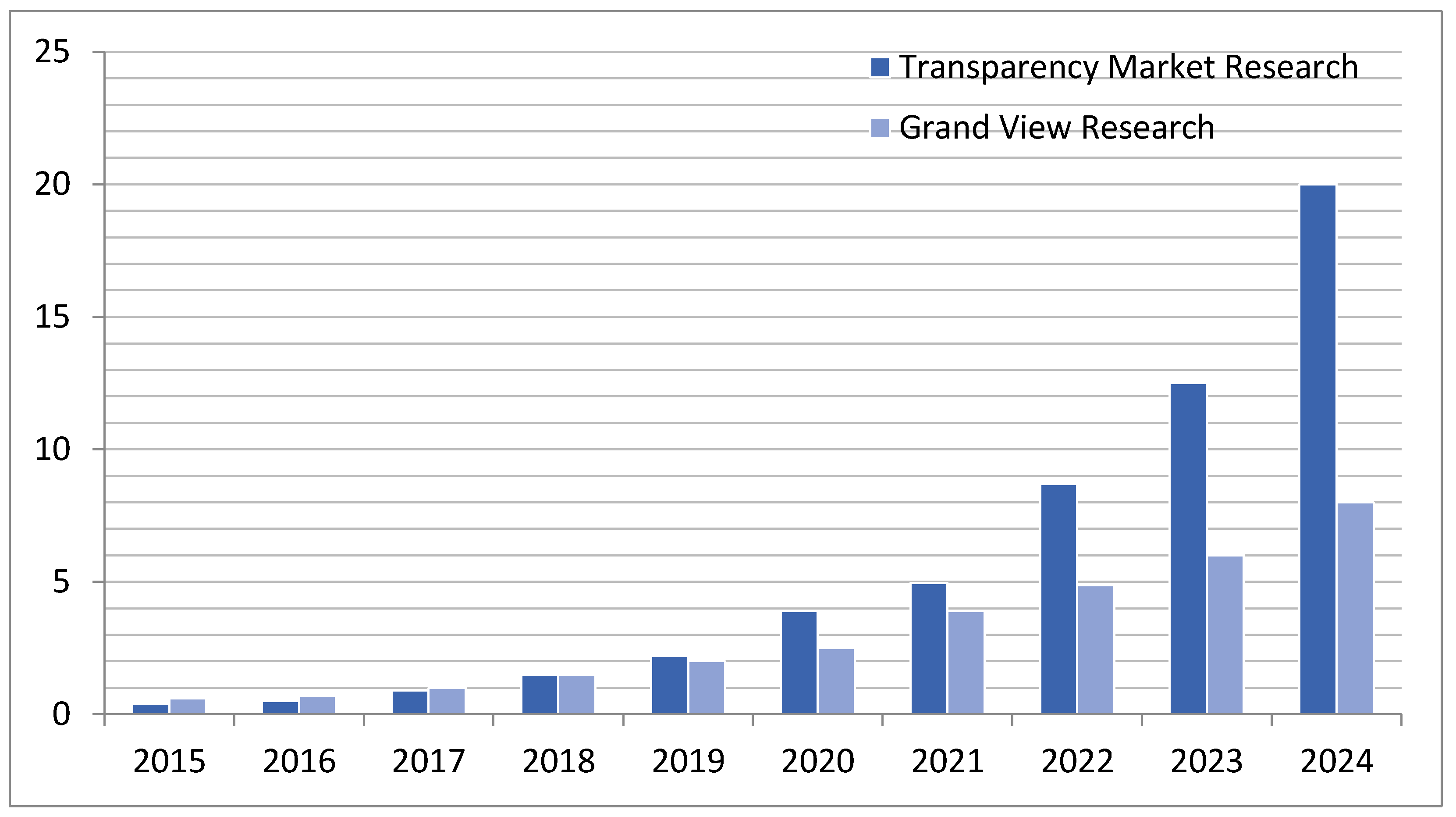
- Blockchain Technology Market (Type-Public Blockchain, Private Blockchain, and Consortium Blockchain; Application-Financial Services and Non-financial Sector)-Global Industry Analysis, Size, Share, Growth, Trends, and Forecast 2016–2024. Available online: https://www.transparencymarketresearch.com/blockchain-technology-market.html (accessed on 9 May 2021).
- C-RAN Market Size, Share & Trends Analysis Report by Architecture Type (Centralized-RAN, Virtual/Cloud-RAN), by Component, By Network Type, By Deployment Model, And Segment Forecasts, 2020–2027. Available online: https://www.grandviewresearch.com/industry-analysis/cloud-ran-market (accessed on 7 May 2021).
- Vladyko, A.G.; Spirkina, A.V.; Elagin, V.S.; Belozertsev, I.A.; Aptrieva, E.A. Blockchain Models to Improve the Service Security on Board Communications. In Proceedings of the 2020 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 19–20 March 2020; pp. 1–5. [Google Scholar]
- Lao, L.; Li, Z.; Hou, S.; Xiao, B.; Guo, S.; Yang, Y. A survey of IoT applications in blockchain systems: Architecture, consensus, and traffic modeling. ACM Comput. Surv. 2020, 53, 1–32. [Google Scholar] [CrossRef]
- Spirkina, A.V. Scientific aspects of structural and parametric simulation of blockchain systems. Proc. Telecommun. Univ. 2021, 7, 45–59. [Google Scholar]
- Smetanin, S.; Ometov, A.; Komarov, M.; Masek, P.; Koucheryavy, Y. Blockchain Evaluation Approaches: State-of-the-Art and Future Perspective. Sensors 2020, 20, 3358. [Google Scholar] [CrossRef]
- Ling, X.; Le, Y.; Wang, J.; Ding, Z.; Gao, X. Practical Modeling and Analysis of Blockchain Radio Access Network. IEEE Trans. Commun. 2020, 1. [Google Scholar] [CrossRef]
- Memon, R.A.; Li, J.; Ahmed, J.; Khan, A.; Nazir, M.I.; Mangrio, M.I. Modeling of blockchain based systems using queuing theory simulation. In Proceedings of the 2018 15th International Computer Conference on Wavelet Active Media Technology and Information Processing, Chengdu, China, 14–16 December 2018; pp. 107–111. [Google Scholar]
- Memon, R.A.; Li, J.P.; Ahmed, J. Simulation model for blockchain systems using queuing theory. Electronics 2019, 2, 234. [Google Scholar] [CrossRef]
- Kawase, Y.; Kasahara, S. Transaction-Confirmation Time for Bitcoin: A Queueing Analytical Approach to Blockchain Mechanism; Springer: Cham, Switzerland, 2017; pp. 75–88. [Google Scholar]
- Mišić, J.; Mišić, V.B.; Chang, X.; Motlagh, S.G.; Ali, M.Z. Modeling of bitcoin’s blockchain delivery network. IEEE Trans. Netw. Sci. Eng. 2019, 3, 1368–1381. [Google Scholar]
- Papadis, N.; Borst, S.; Walid, A.; Grissa, M.; Tassiulas, L. Stochastic models and wide-area network measurements for blockchain design and analysis. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications, Honolulu, HI, USA, 16–19 April 2018; pp. 2546–2554. [Google Scholar]
- Liu, Z.; Luong, N.C.; Wang, W.; Niyato, D.; Wang, P.; Liang, Y.C.; Kim, D.I. A survey on applications of game theory in blockchain. arXiv 2019, arXiv:1902.10865. [Google Scholar]
- Frolkova, M.; Mandjes, M.A. Bitcoin-inspired infinite-server model with a random fluid limit. Stoch. Models 2019, 1, 1–32. [Google Scholar] [CrossRef]
- Li, Q.L.; Ma, J.Y.; Chang, Y.X. Blockchain Queue Theory; Springer: Cham, Switzerland, 2018; pp. 25–40. [Google Scholar]
- Bitcoin Testnet Explorer. Available online: https://blockstream.info/testnet/ (accessed on 10 January 2021).
- BlockCypher. Available online: https://www.blockcypher.com/ (accessed on 13 January 2021).
- Bitcoin Testnet Faucet. Available online: https://testnet-faucet.mempool.co/ (accessed on 15 January 2021).
- Rinkeby Network. Available online: https://www.rinkeby.io/#stats (accessed on 25 January 2021).
- GitHub. Ganache-cli. 2021. Available online: https://github.com/trufflesuite/ganache-cli (accessed on 3 February 2021).
- GitHub. Eth-tester. 2021. Available online: https://github.com/ethereum/eth-tester (accessed on 3 February 2021).
- GitHub. Truffle. 2021. Available online: https://github.com/trufflesuite/truffle (accessed on 5 February 2021).
- GitHub. Remix-ide. 2021. Available online: https://github.com/ethereum/remix-ide (accessed on 11 February 2021).
- Microsoft. Available online: https://marketplace.visualstudio.com/items?itemName=IBMBlockchain.ibm-blockchain-platform (accessed on 12 February 2021).
- Remme. Available online: https://remme.io/ (accessed on 15 February 2021).
- Cryptospaniards. Available online: https://cryptospaniards.com/ (accessed on 25 February 2021).
- Blockchain Demo. Available online: https://blockchaindemo.io/ (accessed on 5 March 2021).
- GitHub. Vibes. 2020. Available online: https://github.com/i13-msrg/vibes (accessed on 12 March 2021).
- GitHub. Simblock. 2021. Available online: https://github.com/dsg-titech/simblock (accessed on 15 March 2021).
- GitHub. BlockSim. 2020. Available online: https://github.com/maher243/BlockSim (accessed on 15 March 2021).
- GitHub. Blocklite. 2019. Available online: https://github.com/hpdic/blocklite (accessed on 15 March 2021).
- Bitcoin Simulator. Available online: https://www.bitcoinsimulator.tk/blockchain?chain=public (accessed on 16 March 2021).
- Blockbench. Available online: https://blockbench.net/ (accessed on 16 March 2021).
- Hyperledger. Available online: https://github.com/hyperledger/caliper (accessed on 28 April 2021).
- The AnyLogic Company. Available online: https://www.anylogic.ru/ (accessed on 17 March 2021).
- The MathWorks. Available online: https://www.mathworks.com/products/matlab.html (accessed on 17 March 2021).
- Nsnam. Available online: https://www.nsnam.org/ (accessed on 17 March 2021).
- Minuteman Software. Available online: http://www.minutemansoftware.com/ (accessed on 17 March 2021).
- Sheluhin, O. Multifractals, Infocommunicational Application; Hot Line-Telecom: Moscow, Russia, 2014; p. 579. [Google Scholar]
- Livshits, B.S.; Pshenichnikov, A.P.; Kharkevich, A.D. Teoriya Teletrafika; Svyaz’: Moscow, Russia, 1979; p. 224. [Google Scholar]
- Koucheryavy, A.; Lokhmotko, V.; Revelova, Z.; Paramonov, A. Application of network planning tools for information content allocation. In Proceedings of the International Teletraffic Congress-18, International Telecommunication Union and International Teletraffic Congress Workshop, Berlin, Germany, 31 August–5 September 2003; pp. 2.4/1–2.4/12. [Google Scholar]
- Nazarov, A.; Sychev, K. Models and research methods the functioning of switching nodes ngn networks with arbitrary distributions of income and service applications of different classes of quality. T-Comm Telecommun. Transp. 2012, 15, 4–10. [Google Scholar]
- Klejnrock, L. Vychislitel'nye Seti s Ocheredyami; Mir: Moscow, Russia, 1979; p. 600. [Google Scholar]
- Mazzini, G.; Rovatti, R.; Setti, G. On the Aggregation of Self-Similar Processes. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2005, E88-A, 2656–2663. [Google Scholar] [CrossRef]
- Kirichek, R.; Paramonov, A.; Vladyko, A.; Borisov, E. Implementation of the Communication Network for the Multi-Agent Robotic Systems. Int. J. Embed. Real Time Commun. Syst. 2016, 7, 48–63. [Google Scholar] [CrossRef]
- Spirkina, A.V.; Aptrieva, E.A.; Elagin, V.S.; Shvidkiy, A.A.; Savelieva, A.A. Approaches to Modeling Blockchain Systems. In Proceedings of the 2020 12th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops, Brno, Czech Republic, 5–7 October 2020; pp. 242–247. [Google Scholar]
- Raikwar, M.; Gligoroski, D.; Kralevska, K. SoK of Used Cryptography in Blockchain. IEEE Access 2019, 7, 148550–148575. [Google Scholar] [CrossRef]
| Research | Presented Solution | Tool/Technology | Parameters to be Considered and Characteristics to be Modeled |
|---|---|---|---|
| [10] | Modeling the process using multiple queues based on four phases (waiting for inclusion in the block; waiting for confirmation; waiting for service; servicing) | A state transition graph; Mass service theory; Markov processes | Simulation of block generation; State transition probabilities; Access delays |
| [11] | The mining organization model is defined by M/M/n/L. The queue capacity is set as TxB, the queue policy is first-come, first-served, and the discard rule is block after service, which means that only transactions of block size TxB remain in the dynamic memory of the mining nodes, while other transactions, even if they are processed, are in the memory pool | Mass service theory | Average number of transactions per block; Total mining capacity; Number of transactions per second |
| [12] | The M/M/1 model is used to model the blockchain memory pool, and the mining pool is modeled by the M/M/n model. There can only be one block in a mining pool at any one time. However, within a mining pool, processes can be divided into multiple tasks or threads for parallel processing by multiple mining nodes in the network. | Mass service theory | Average number of transactions per block; The speed at which transactions arrive; Average mining time per block; system/transaction throughput; waiting time in memory pool; The number of unconfirmed transactions in the entire system; Total number of transactions |
| [13] | The mining process is modeled using a queuing system, analyzing transaction confirmation times. The authors consider the M/G/1 model with batch service, in which a newly arrived transaction cannot reach the service facility even if the number of transactions in the service facility does not reach the maximum batch size. In this model, the dwell time of a transaction corresponds to its confirmation time. | Mass service theory | Average block generation time; Average number of transactions in the system |
| [14] | The system is considered using the M/G/1 model as an example. Data arrivals to nodes are modeled as a heterogeneous Poisson process, where the distribution of arrival rate to nodes is derived from an analytical model of the data delivery protocol. | Mass service theory | Block and transaction allocation time probabilities; Node response time; The likelihood of a branching chain; Duration of the period of the inconsistency of the register |
| [15] | Stochastic network models are proposed to capture the evolution and dynamics of the blockchain. A combination of analytical calculations and simulation experiments is used to investigate both steady-state and transient performance characteristics | Stochastic models | The effect of a block’s propagation delay; Hashing power of nodes |
| [16] | Game theories are proposed for modeling to address common problems in the blockchain network, such as security, problems related to mining management, and issues related to the economics of the blockchain. | Game theory | Economic aspects |
| [17] | The system is examined using the M/G/∞ model as an example. Equivalence between two specific service disciplines is used to obtain the stationary distribution of the model. | Mass service theory | Distribution of busy periods; service delays |
| [18] | The theory of mass service in blockchain systems is developed, and system performance is evaluated. For this purpose, a Markov queuing system of packet service is developed with two different stages, which are suitable for explicitly expressing the process of mining in a pool of miners and constructing a new blockchain. | Mass service theory; Markov processes | Average number of transactions per queue, Average number of transactions per block; Average transaction confirmation time. |
| The Solution | Description | Software Packages |
|---|---|---|
| Test networks | A test network of a particular system is used to test the performance or relevance of an application. Coin analyses that have no real value are used | Bitcoin Testnet Explorer [19]; Blockcypher [20]; Bitcoin Testnet Faucet [21]; Rinkeby network [22]; Ganachecli [23]; Ethereum Tester [24]; Truffle framework [25]; Remix ide [26]; IBM Blockchain platform [27]; Remme [28]; Cryptospaniards [29] |
| Demonstration of how the technology works | These solutions show how basic blockchain operations work, such as hashing, mining and distribution. It also provides information about the result of the procedure when certain parameters are changed | Blockchain demo [30]; |
| Simulators for event management | With these solutions, users can explore the underlying characteristics and performance of the network, investigate interactions between nodes and compare different simulation scenarios. They serve as a fair comparison across platforms and provide a deeper understanding of different system design options. Applied to pretest to evaluate overall performance and with workloads to evaluate individual tier performance | Vibes [31]; Simblock [32]; Blocksim [33]; BlockLite [34]; Bitcoin simulator [35]; Blockbench [36]; Hyperledger Caliper [37] |
| Network section simulator | The solutions combine mathematical and logical aspects and reproduce the real behavior of the system using computer software | AnyLogic [38]; MATLAB [39]; NS3 [40]; GPSS World [41] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladyko, A.; Spirkina, A.; Elagin, V. Towards Practical Applications in Modeling Blockchain System. Future Internet 2021, 13, 125. https://doi.org/10.3390/fi13050125
Vladyko A, Spirkina A, Elagin V. Towards Practical Applications in Modeling Blockchain System. Future Internet. 2021; 13(5):125. https://doi.org/10.3390/fi13050125
Chicago/Turabian StyleVladyko, Andrei, Anastasia Spirkina, and Vasiliy Elagin. 2021. "Towards Practical Applications in Modeling Blockchain System" Future Internet 13, no. 5: 125. https://doi.org/10.3390/fi13050125
APA StyleVladyko, A., Spirkina, A., & Elagin, V. (2021). Towards Practical Applications in Modeling Blockchain System. Future Internet, 13(5), 125. https://doi.org/10.3390/fi13050125








