Exploiting Machine Learning for Improving In-Memory Execution of Data-Intensive Workflows on Parallel Machines
Abstract
1. Introduction
- Workflow structure, in terms of tasks and data dependencies.
- Input format, such as the number of rows, dimensionality, and all other features required to describe the complexity of input data.
- The types of tasks, i.e., the computation performed by a given node of the workflow. For example, in the case of data analysis workflows, we can distinguish among supervised learning, unsupervised learning, and association rule discovery tasks, as well as between learning and prediction tasks.
Problem Statement
2. Related Work
2.1. Analytical-Based
- Dynamically adapting resources to data storage, using a feedback-based mechanism with real-time monitoring of the memory usage of the application [17].
2.2. Machine Learning-Based
- It focuses on data-intensive workflows, while in [10], general workloads were addressed.
- It uses high-level information for describing an application (e.g., task and dataset features), while in [10], low-level system features were exploited, such as the cache miss rate and the number of blocks sent, collected by running the application on a small portion (100 MB) of the input data.
- It proposes a more general approach, since the approach proposed in [10] is only appliable to applications whose memory usage is a function of the input size.
3. Materials and Methods
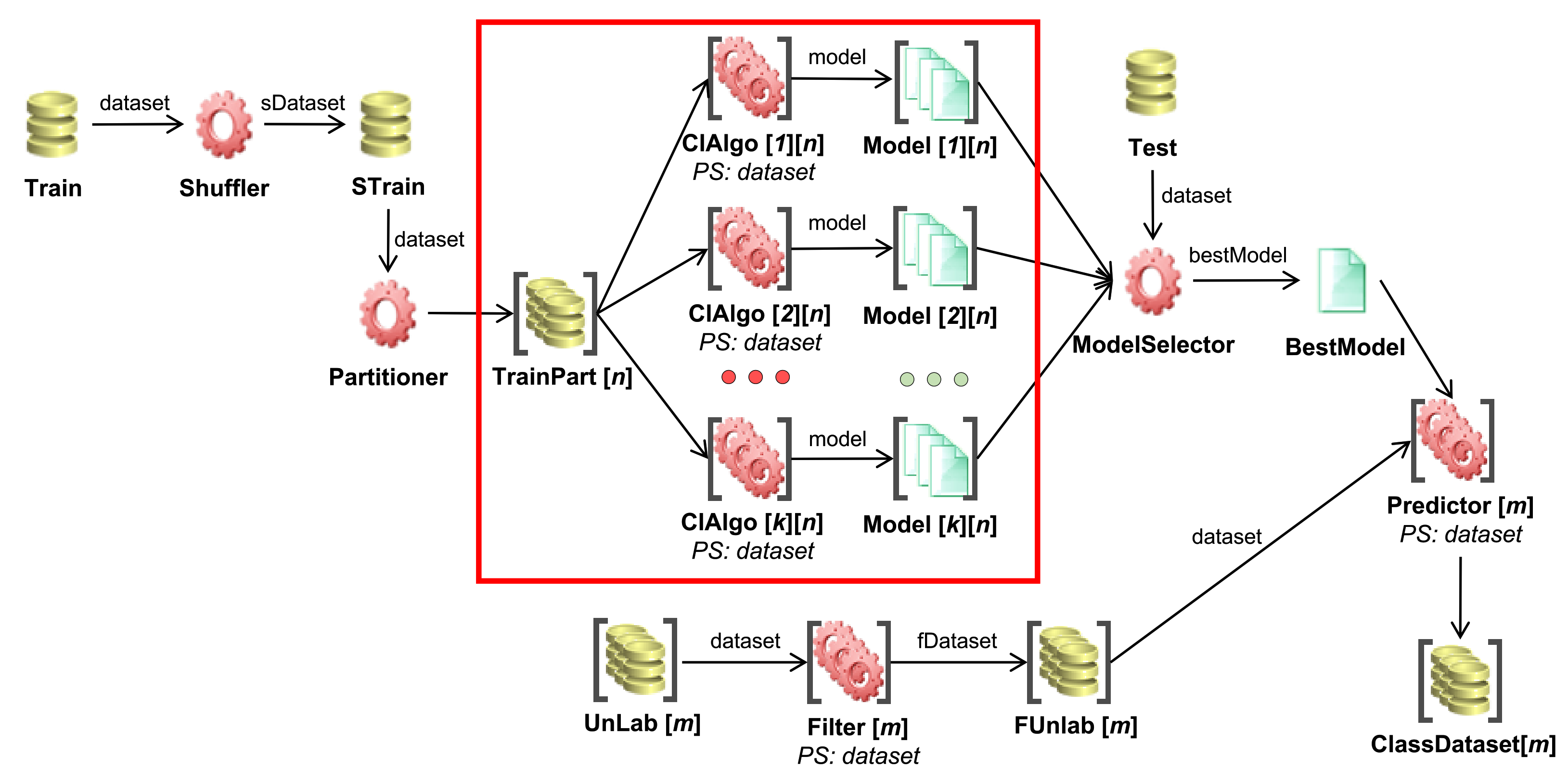
- Execution monitoring and dataset creation: starting from a given set of workflows, a transactional dataset is generated by monitoring the memory usage and execution time of each task, specifying how it is designed and giving concise information about the input.
- Prediction model training: from the transactional dataset of executions, a regression model is trained in order to fit the distribution of memory occupancy and execution time, according to the features that represent the different tasks of a workflow.
- Workflow scheduling: taking into account the predicted memory occupancy, and execution time of each task, provided by the trained model, and the available memory of the computing node, tasks are scheduled using an informed strategy. In this way, a controlled degree of parallelism can be ensured, while minimizing the risk of memory saturation.
3.1. Execution Monitoring and Dataset Creation
3.1.1. Execution Monitoring within the Spark Unified Memory Model
3.1.2. Dataset Creation
- The description of the task, such as its class (e.g., classification, clustering, etc.), type (fitting or predicting task), and algorithm (e.g., SVM, K-means, etc.).
- The description of the input dataset in terms of the number of rows, columns, categorical columns, and overall dataset size.
- Peak memory usage (both execution and storage) and execution time, which represent the three target variables to be predicted by the regressor. In order to obtain more significant data, the metrics were aggregated on median values by performing ten executions per task.
- For datasets used in classification or regression tasks, we considered only the k highest scoring features based on:
- –
- the analysis of variance (F-value) for integer labels (classification problems);
- –
- the correlation-based univariate linear regression test for real labels (regression problems).
- For clustering datasets, we used a correlation-based test to maintain the k features with the smallest probability to be correlated with the others.
- For association rule discovery datasets, no feature selection is required, as the number of columns refers to the average number of items in the different transactions.
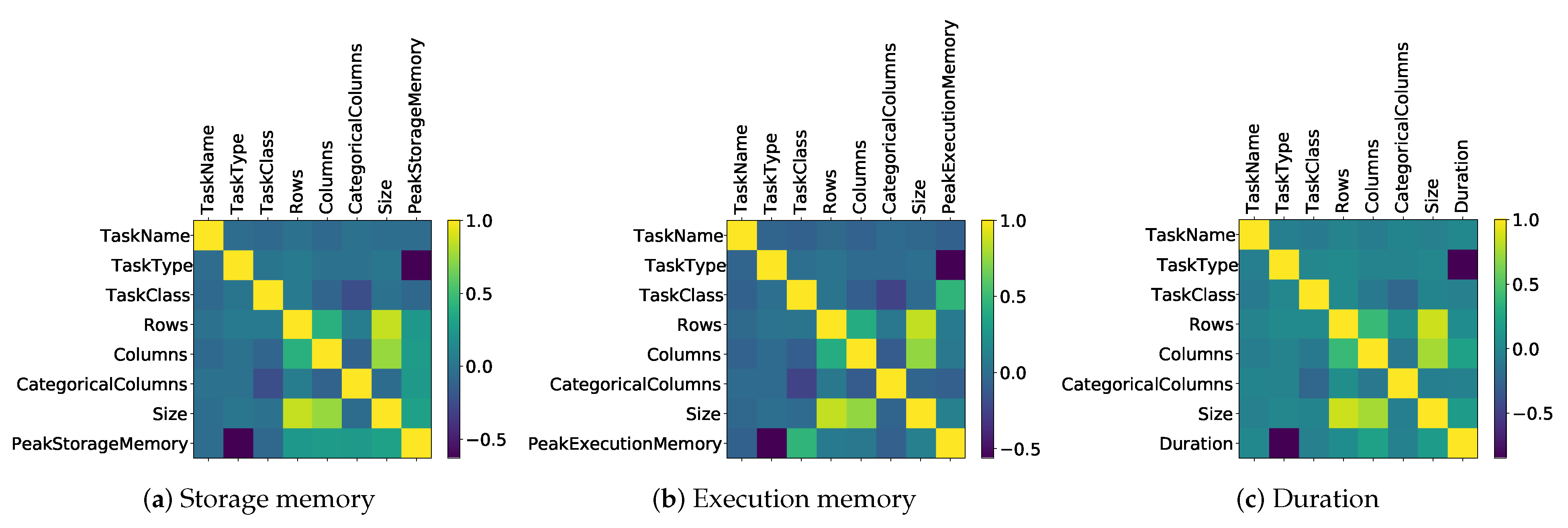
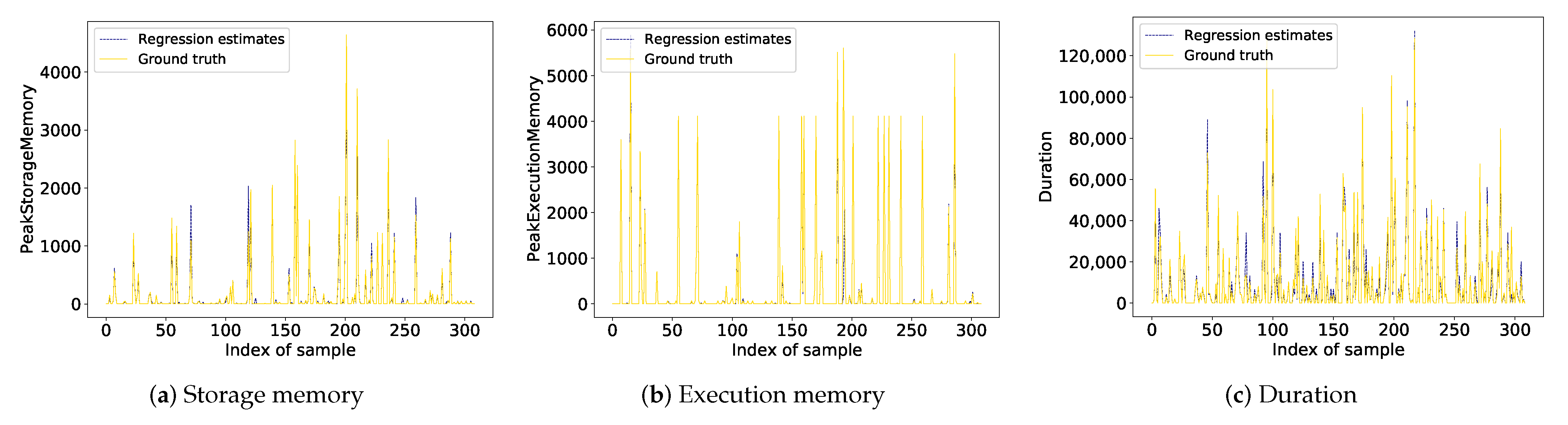
3.2. Prediction Model Training
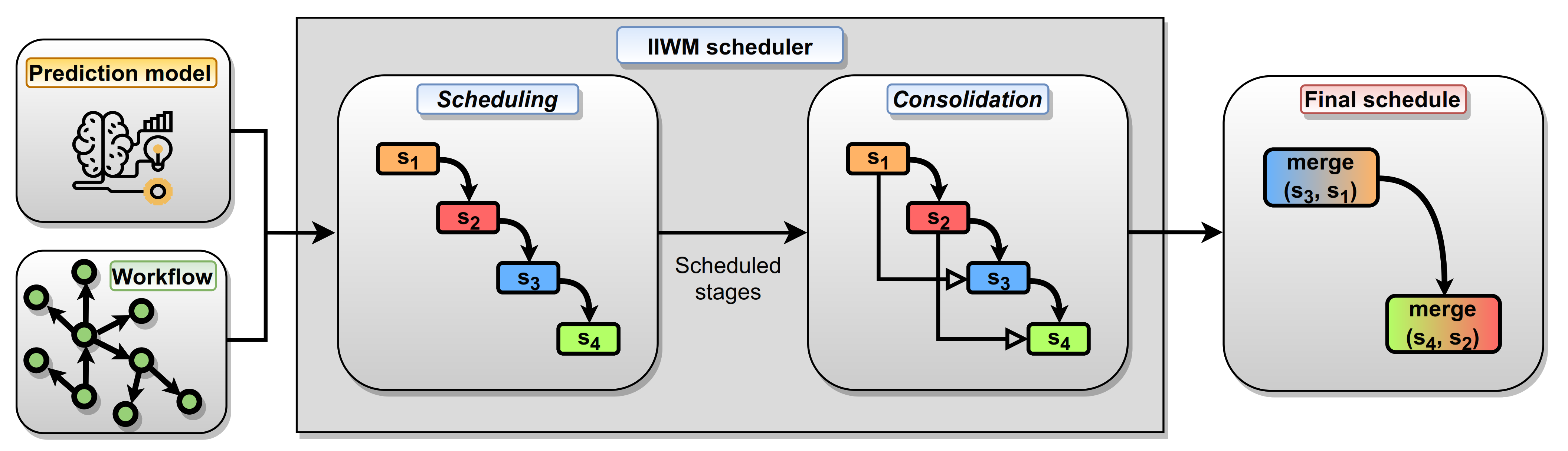
3.3. Workflow Scheduling
- An item is a task to be executed.
- A bin identifies a stage, i.e., a set of tasks that can be run in parallel.
- The capacity of a bin is the maximum amount C of available memory in a computing node. When assigning a task to a stage , its residual available memory is indicated with .
- The weight of an item is the memory occupancy estimated by the prediction model. In the case of the Spark testbed, it is the maximum of the execution and storage memory, in order to model a peak in the unified memory. As concerns the estimated execution time, it is used for selecting the stage to be assigned when memory constraints hold for multiple stages.
- All workflow tasks have to be executed, so the capacity of a stage may still be exceeded if a task takes up more memory than the available one.
- The assignment of a task t to a stage s is subject to dependency constraints. Hence, if a dependency exists between and , then the stage of has to be executed before the one of .
- The residual capacity of the selected stage is not exceeded by the addition of the task t.
- There does not exist a dependency between t and any task belonging to and every subsequent stage (), where a dependency is identified by a path of length .
| Algorithm 1: The IIWM scheduler. |
 |
4. Results and Discussion
- Execution time: Let and be the makespan for two different executions. If , we can compute the improvement on makespan () and application performance () as follows:
- Disk usage: We used the on-disk usage metric, which measures the amount of disk usage, jointly considering the volume and the duration of disk writes. Formally, given a sequence of disk writes , let , be the start and end time of the write, respectively. Let also be a function representing the amount of megabytes written to disk over time . We define on-disk usage as:
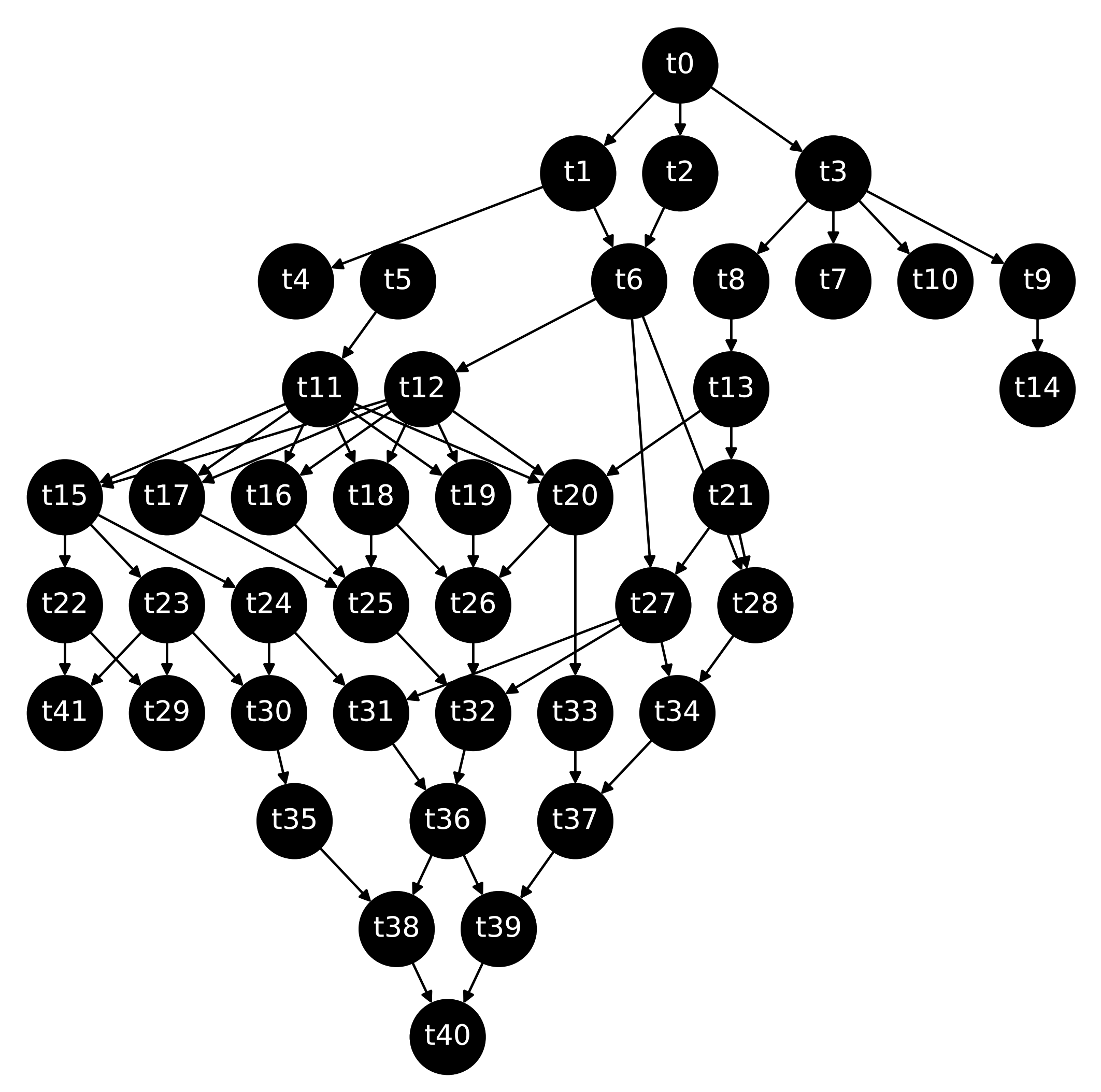
4.1. Synthetic Workflows
4.2. Real Case Study
5. Conclusions and Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Talia, D.; Trunfio, P.; Marozzo, F. Data Analysis in the Cloud; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 978-0-12-802881-0. [Google Scholar]
- Da Costa, G.; Fahringer, T.; Rico-Gallego, J.A.; Grasso, I.; Hristov, A.; Karatza, H.D.; Lastovetsky, A.; Marozzo, F.; Petcu, D.; Stavrinides, G.L.; et al. Exascale machines require new programming paradigms and runtimes. Supercomput. Front. Innov. 2015, 2, 6–27. [Google Scholar]
- Li, M.; Tan, J.; Wang, Y.; Zhang, L.; Salapura, V. SparkBench: A Comprehensive Benchmarking Suite for in Memory Data Analytic Platform Spark. In Proceedings of the 12th ACM International Conference on Computing Frontiers, Ischia, Italy, 18–21 May 2015; Association for Computing Machinery: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- De Oliveira, D.C.; Liu, J.; Pacitti, E. Data-intensive workflow management: For clouds and data-intensive and scalable computing environments. Synth. Lect. Data Manag. 2019, 14, 1–179. [Google Scholar] [CrossRef]
- Verma, A.; Mansuri, A.H.; Jain, N. Big data management processing with Hadoop MapReduce and spark technology: A comparison. In Proceedings of the 2016 Symposium on Colossal Data Analysis and Networking (CDAN), Indore, India, 18–19 March 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Zaharia, M.; Chowdhury, M.; Das, T.; Dave, A.; Ma, J.; McCauly, M.; Franklin, M.J.; Shenker, S.; Stoica, I. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing. In Proceedings of the 9th USENIX Symposium on Networked Systems Design and Implementation (NSDI 12), San Jose, CA, USA, 25–27 April 2012; pp. 15–28. [Google Scholar]
- Samadi, Y.; Zbakh, M.; Tadonki, C. Performance comparison between Hadoop and Spark frameworks using HiBench benchmarks. Concurr. Comput. Pract. Exp. 2018, 30, e4367. [Google Scholar] [CrossRef]
- Delimitrou, C.; Kozyrakis, C. Quasar: Resource-Efficient and QoS-Aware Cluster Management. In Proceedings of the 19th International Conference on Architectural Support for Programming Languages and Operating Systems, Salt Lake City, UT, USA, 1–5 March 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 127–144. [Google Scholar] [CrossRef]
- Llull, Q.; Fan, S.; Zahedi, S.M.; Lee, B.C. Cooper: Task Colocation with Cooperative Games. In Proceedings of the 2017 IEEE International Symposium on High Performance Computer Architecture (HPCA), Austin, TX, USA, 4–8 February 2017; pp. 421–432. [Google Scholar] [CrossRef]
- Marco, V.S.; Taylor, B.; Porter, B.; Wang, Z. Improving Spark Application Throughput via Memory Aware Task Co-Location: A Mixture of Experts Approach. In Proceedings of the 18th ACM/IFIP/USENIX Middleware Conference, Las Vegas, NV, USA, 11–15 December 2017; Association for Computing Machinery: New York, NY, USA, 2017. Middleware’17. pp. 95–108. [Google Scholar] [CrossRef]
- Maros, A.; Murai, F.; Couto da Silva, A.P.; Almeida, J.M.; Lattuada, M.; Gianniti, E.; Hosseini, M.; Ardagna, D. Machine Learning for Performance Prediction of Spark Cloud Applications. In Proceedings of the 2019 IEEE 12th International Conference on Cloud Computing (CLOUD), Milan, Italy, 8–13 July 2019; pp. 99–106. [Google Scholar] [CrossRef]
- Talia, D. Workflow Systems for Science: Concepts and Tools. Int. Sch. Res. Not. 2013, 2013, 404525. [Google Scholar] [CrossRef]
- Smanchat, S.; Viriyapant, K. Taxonomies of workflow scheduling problem and techniques in the cloud. Future Gener. Comput. Syst. 2015, 52, 1–12. [Google Scholar] [CrossRef]
- Bittencourt, L.F.; Madeira, E.R.M.; Da Fonseca, N.L.S. Scheduling in hybrid clouds. IEEE Commun. Mag. 2012, 50, 42–47. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, F.; Chen, H. An adaptive tuning strategy on spark based on in-memory computation characteristics. In Proceedings of the 2016 18th International Conference on Advanced Communication Technology (ICACT), Pyeongchang, Korea, 31 January–3 February 2016; pp. 484–488. [Google Scholar] [CrossRef]
- Chen, D.; Chen, H.; Jiang, Z.; Zhao, Y. An adaptive memory tuning strategy with high performance for Spark. Int. J. Big Data Intell. 2017, 4, 276–286. [Google Scholar] [CrossRef]
- Xuan, P.; Luo, F.; Ge, R.; Srimani, P.K. Dynamic Management of In-Memory Storage for Efficiently Integrating Compute-and Data-Intensive Computing on HPC Systems. In Proceedings of the 2017 17th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGRID), Madrid, Spain, 14–17 May 2017; pp. 549–558. [Google Scholar] [CrossRef]
- Tang, Z.; Zeng, A.; Zhang, X.; Yang, L.; Li, K. Dynamic memory-aware scheduling in spark computing environment. J. Parallel Distrib. Comput. 2020, 141, 10–22. [Google Scholar] [CrossRef]
- Bae, J.; Jang, H.; Jin, W.; Heo, J.; Jang, J.; Hwang, J.; Cho, S.; Lee, J.W. Jointly optimizing task granularity and concurrency for in-memory mapreduce frameworks. In Proceedings of the 2017 IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017; pp. 130–140. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Liu, J.; Pacitti, E.; Valduriez, P.; Mattoso, M. A Survey of Data-Intensive Scientific Workflow Management. J. Grid Comput. 2015, 13, 457–493. [Google Scholar] [CrossRef]
- Raj, P.H.; Kumar, P.R.; Jelciana, P. Load Balancing in Mobile Cloud Computing using Bin Packing’s First Fit Decreasing Method. In Proceedings of the International Conference on Computational Intelligence in Information System, Brunei, 16–18 November 2018; Springer: Berlin, Germany, 2018; pp. 97–106. [Google Scholar]
- Baker, T.; Aldawsari, B.; Asim, M.; Tawfik, H.; Maamar, Z.; Buyya, R. Cloud-SEnergy: A bin-packing based multi-cloud service broker for energy efficient composition and execution of data-intensive applications. Sustain. Comput. Informatics Syst. 2018, 19, 242–252. [Google Scholar] [CrossRef]
- Stavrinides, G.L.; Karatza, H.D. Scheduling real-time DAGs in heterogeneous clusters by combining imprecise computations and bin packing techniques for the exploitation of schedule holes. Future Gener. Comput. Syst. 2012, 28, 977–988. [Google Scholar] [CrossRef]
- Coffman, E.G., Jr.; Garey, M.R.; Johnson, D.S. An application of bin-packing to multiprocessor scheduling. SIAM J. Comput. 1978, 7, 1–17. [Google Scholar] [CrossRef]
- Darapuneni, Y.J. A Survey of Classical and Recent Results in Bin Packing Problem. UNLV Theses, Dissertations, Professional Papers, and Capstones. 2012. Available online: https://digitalscholarship.unlv.edu/cgi/viewcontent.cgi?article=2664&context=thesesdissertations (accessed on 29 April 2021).
- Marozzo, F.; Rodrigo Duro, F.; Garcia Blas, J.; Carretero, J.; Talia, D.; Trunfio, P. A data-aware scheduling strategy for workflow execution in clouds. Concurr. Comput. Pract. Exp. 2017, 29, e4229. [Google Scholar] [CrossRef]
- Marozzo, F.; Talia, D.; Trunfio, P. A Workflow Management System for Scalable Data Mining on Clouds. IEEE Trans. Serv. Comput. 2018, 11, 480–492. [Google Scholar] [CrossRef]
- Aseeri, A.O.; Zhuang, Y.; Alkatheiri, M.S. A Machine Learning-Based Security Vulnerability Study on XOR PUFs for Resource-Constraint Internet of Things. In Proceedings of the 2018 IEEE International Congress on Internet of Things (ICIOT), San Francisco, CA, USA, 2–7 July 2018; pp. 49–56. [Google Scholar] [CrossRef]


| Symbol | Meaning |
|---|---|
| Set of tasks. | |
| Dependencies. . | |
| Description of the dataset processed by task t. | |
| Workflow. | |
| In-neighborhood of task t. | |
| Out-neighborhood of task t. | |
| Regression prediction model. | |
| List of stages. . | |
| C | Maximum amount of memory available for a computing node. |
| Residual capacity of a stage s. |
| MLlib Algorithm | Persist Call |
|---|---|
| K-Means | //Compute squared norms and cache them norms.cache() |
| Decision Tree | //Cache input RDD for speedup during multiple passes BaggedPoint.convertToBaggedRDD(treeInput,…).cache() |
| GMM | instances.cache() … data.map(_.asBreeze).cache() |
| FPGrowth | items.cache() |
| SVM | IstanceBlock.blokifyWithMaxMemUsage(…).cache() |
| Task Name | Task Type | Task Class | Dataset Rows | Dataset Columns | Categorical Columns | Dataset Size (MB) | Peak Storage Memory (MB) | Peak Execution Memory (MB) | Duration (ms) |
|---|---|---|---|---|---|---|---|---|---|
| GMM | Estimator | Clustering | 1,474,971 | 28 | 0 | 87.00 | 433.37 | 1413.50 | 108,204.00 |
| K-Means | Estimator | Clustering | 5,000,000 | 104 | 0 | 1239.78 | 4624.52 | 4112.00 | 56,233.50 |
| Decision Tree | Estimator | Classification | 9606 | 1921 | 0 | 84.91 | 730.09 | 297.90 | 39,292.00 |
| Naive Bayes | Estimator | Classification | 260,924 | 4 | 0 | 13.50 | 340.92 | 6982.80 | 16,531.50 |
| SVM | Estimator | Classification | 5,000,000 | 129 | 0 | 1542.58 | 6199.11 | 106.60 | 238,594.50 |
| FPGrowth | Estimator | Association Rules | 823,593 | 180 | 180 | 697.00 | 9493.85 | 1371.03 | 96,071.50 |
| GMM | Transformer | Clustering | 165,474 | 14 | 1 | 6.37 | 2.34 | 1 × 10 | 62.50 |
| K-Means | Transformer | Clustering | 4,898,431 | 42 | 3 | 648.89 | 3.23 | 1 × 10 | 35.00 |
| Decision Tree | Transformer | Classification | 1,959,372 | 42 | 4 | 257.69 | 3.68 | 1 × 10 | 65.50 |
| Naive Bayes | Transformer | Classification | 347,899 | 4 | 0 | 17.99 | 4.26 | 1 × 10 | 92.50 |
| SVM | Transformer | Classification | 5,000,000 | 129 | 0 | 1542.58 | 2.36 | 1 × 10 | 55.50 |
| FPGrowth | Transformer | Association Rules | 136,073 | 34 | 34 | 13.55 | 1229.95 | 633.50 | 52,429.00 |
| … | … | … | … | … | … | … | … | … | … |
| Hyperparameter | Value |
|---|---|
| n_estimators | 500 |
| learning_rate | 0.01 |
| max_depth | 7 |
| loss | least squares |
| RMSE | MAE | Adjusted | Pearson Correlation | |
|---|---|---|---|---|
| Storage Memory | ||||
| Execution Memory | ||||
| Duration | 4443.17 | 2003.70 |
| Node | Task Name | Task Type | Task Class | Rows | Columns | Categorical Columns | Dataset Size (MB) |
|---|---|---|---|---|---|---|---|
| Naive Bayes | Estimator | Classification | 2,939,059 | 18 | 4 | 198.94 | |
| FPGrowth | Estimator | Association Rules | 494,156 | 180 | 180 | 417.01 | |
| Naive Bayes | Estimator | Classification | 5,000,000 | 27 | 0 | 321.86 | |
| K-Means | Estimator | Clustering | 1,000,000 | 104 | 0 | 247.96 | |
| Decision Tree | Estimator | Classification | 4,000,000 | 53 | 0 | 505.45 | |
| Decision Tree | Estimator | Classification | 4,000,000 | 27 | 0 | 257.49 | |
| Decision Tree | Estimator | Classification | 5,000,000 | 129 | 0 | 1542.58 | |
| K-Means | Estimator | Clustering | 2,000,000 | 53 | 0 | 252.73 | |
| Naive Bayes | Estimator | Classification | 2,000,000 | 104 | 0 | 495.90 | |
| Naive Bayes | Estimator | Classification | 1,000,000 | 129 | 0 | 307.57 | |
| SVM | Estimator | Classification | 2,000,000 | 53 | 0 | 252.72 | |
| K-Means | Estimator | Clustering | 2,049,280 | 9 | 2 | 122.03 | |
| GMM | Estimator | Clustering | 2,458,285 | 28 | 0 | 145.01 | |
| K-Means | Estimator | Clustering | 9169 | 5812 | 1 | 101.89 | |
| SVM | Estimator | Classification | 2,000,000 | 27 | 0 | 128.75 | |
| K-Means | Estimator | Clustering | 3,000,000 | 104 | 0 | 743.87 | |
| SVM | Estimator | Classification | 3,000,000 | 53 | 0 | 379.09 | |
| SVM | Estimator | Classification | 14,410 | 1921 | 0 | 127.38 | |
| K-Means | Estimator | Clustering | 5,000,000 | 53 | 0 | 631.81 | |
| K-Means | Estimator | Clustering | 5,000,000 | 104 | 0 | 1239.78 | |
| K-Means | Estimator | Clustering | 2,000,000 | 78 | 0 | 371.93 | |
| SVM | Estimator | Classification | 3,000,000 | 104 | 0 | 743.87 | |
| K-Means | Estimator | Clustering | 2,939,059 | 18 | 4 | 198.94 | |
| SVM | Estimator | Classification | 19,213 | 1442 | 0 | 123.28 | |
| Decision Tree | Estimator | Classification | 3,000,000 | 129 | 0 | 922.69 | |
| K-Means | Estimator | Clustering | 1,959,372 | 26 | 4 | 189.55 | |
| Decision Tree | Estimator | Classification | 4,898,431 | 18 | 4 | 331.57 | |
| Naive Bayes | Estimator | Classification | 4,898,431 | 18 | 4 | 331.57 | |
| K-Means | Estimator | Clustering | 2,939,059 | 34 | 4 | 334.91 | |
| K-Means | Estimator | Clustering | 4,898,431 | 18 | 4 | 331.57 | |
| K-Means | Estimator | Clustering | 1,966,628 | 42 | 0 | 170.49 | |
| Naive Bayes | Estimator | Classification | 1,959,372 | 18 | 4 | 132.62 | |
| K-Means | Estimator | Clustering | 3,000,000 | 78 | 0 | 557.91 | |
| Decision Tree | Estimator | Classification | 3,000,000 | 53 | 0 | 379.09 | |
| Decision Tree | Estimator | Classification | 14,410 | 2401 | 0 | 159.71 | |
| K-Means | Estimator | Clustering | 2,939,059 | 42 | 4 | 386.53 | |
| Decision Tree | Estimator | Classification | 2,939,059 | 34 | 4 | 334.91 | |
| Decision Tree | Estimator | Classification | 4,000,000 | 129 | 0 | 1230.24 | |
| Naive Bayes | Estimator | Classification | 1,000,000 | 53 | 0 | 126.36 | |
| GMM | Estimator | Clustering | 1,000,000 | 53 | 0 | 126.36 | |
| Decision Tree | Estimator | Classification | 2,939,059 | 18 | 4 | 198.94 | |
| K-Means | Estimator | Clustering | 4,898,431 | 18 | 4 | 331.57 |
| RMSE | MAE | Adjusted | Pearson Correlation | |
|---|---|---|---|---|
| Storage Memory | ||||
| Execution Memory | ||||
| Duration | 20,354.38 | 7,877.72 |
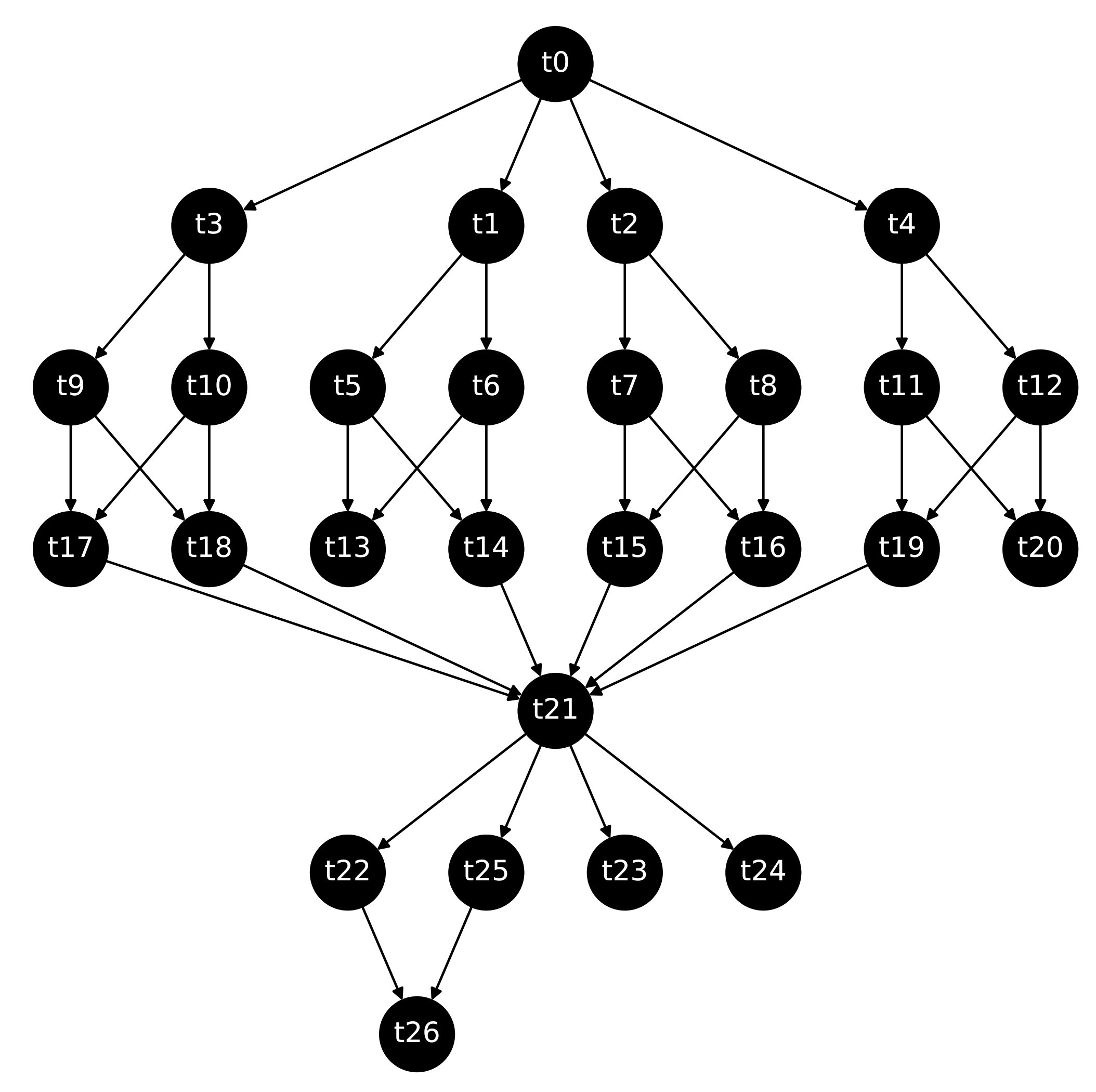
| Iteration | State | Stages |
|---|---|---|
| It. 0 | Create and assign Unlock {} | |
| It. 1 | Create and assign Unlock {} | , |
| It. 2 | Create and assign Unlock {} | , , |
| It. 3 | Create and assign | , , , |
| It. 4 | Assign to | , , , |
| ⋯ | ⋯ | ⋯ |
| It. 17 | Assign to Unlock {} | , , , , , , , |
| ⋯ | ⋯ | ⋯ |
| Strategy | Task-Scheduling Plan | Number of Stages | Time (min) | Peak Disk Usage (MB) | Writes Duration (min) | On-Disk Usage (MB) |
|---|---|---|---|---|---|---|
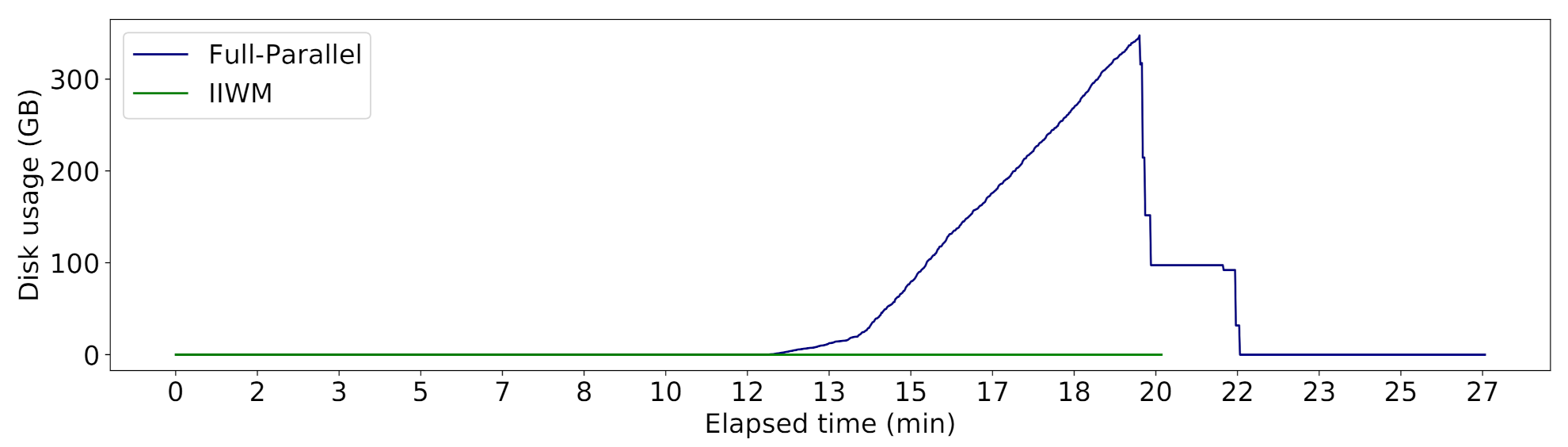
| Full-Parallel | (), ( ‖ ‖ ), ( ‖ ‖ ‖ ‖ ‖ ‖ ), ( ‖ ‖ ‖ ), ( ‖ ‖ ‖ ‖ ‖ ‖ ), ( ‖ ‖ ‖ ‖ ‖ ‖ ), ( ‖ ‖ ‖ ‖ ‖ ‖ ), ( ‖ ‖ ), ( ‖ ), () | 10 | 356,106.60 | 126,867.06 | ||
| IIWM | (), ( ‖ ), ( ‖ ‖ ), ( ‖ ‖ ‖ ‖ ), ( ‖ ‖ ), ( ‖ ), ( ‖ ‖ ), ( ‖ ‖ ‖ ), ( ‖ ), ( ‖ ), ( ‖ ‖ ), ( ‖ ‖ ), ( ‖ ‖ ‖ ), ( ‖ ), ( ‖ ), () | 16 | 0 | 0 | 0 |
| Node | Task Name | Task Type | Task Class | Rows | Columns | Categorical Columns | Dataset Size (MB) |
|---|---|---|---|---|---|---|---|
| K-Means | Estimator | Clustering | 3,918,745 | 34 | 4 | 446.55 | |
| Decision Tree | Estimator | Classification | 4,000,000 | 27 | 0 | 257.49 | |
| GMM | Estimator | Clustering | 2,458,285 | 28 | 0 | 145.01 | |
| Decision Tree | Estimator | Classification | 3,000,000 | 53 | 0 | 379.09 | |
| Decision Tree | Estimator | Classification | 4,000,000 | 129 | 0 | 1230.24 | |
| Decision Tree | Estimator | Classification | 3,918,745 | 18 | 4 | 265.25 | |
| Decision Tree | Estimator | Classification | 4,898,431 | 42 | 3 | 648.89 | |
| Decision Tree | Estimator | Classification | 2,939,059 | 42 | 4 | 386.53 | |
| K-Means | Estimator | Clustering | 2,458,285 | 56 | 0 | 278.75 | |
| GMM | Estimator | Clustering | 3,000,000 | 53 | 0 | 379.09 | |
| SVM | Estimator | Classification | 4,000,000 | 53 | 0 | 505.45 | |
| K-Means | Estimator | Clustering | 2,939,059 | 42 | 4 | 386.53 | |
| SVM | Estimator | Classification | 2,000,000 | 53 | 0 | 252.72 | |
| K-Means | Estimator | Clustering | 1,639,424 | 9 | 2 | 93.70 | |
| Naive Bayes | Estimator | Classification | 260,924 | 3 | 0 | 10.33 | |
| K-Means | Estimator | Clustering | 2,000,000 | 78 | 0 | 371.93 | |
| Decision Tree | Estimator | Classification | 3,918,745 | 26 | 4 | 379.11 | |
| Decision Tree | Estimator | Classification | 3,918,745 | 34 | 4 | 446.55 | |
| FPGrowth | Estimator | Association Rules | 823,593 | 180 | 180 | 697.00 | |
| Decision Tree | Estimator | Classification | 2,939,059 | 26 | 4 | 284.33 | |
| SVM | Estimator | Classification | 5,000,000 | 27 | 0 | 321.86 | |
| FPGrowth | Estimator | Association Rules | 164,719 | 180 | 180 | 139.87 | |
| GMM | Estimator | Clustering | 3,000,000 | 27 | 0 | 193.12 | |
| K-Means | Estimator | Clustering | 4,898,431 | 26 | 4 | 473.88 | |
| Decision Tree | Estimator | Classification | 2,000,000 | 104 | 0 | 495.90 | |
| K-Means | Estimator | Clustering | 2,458,285 | 69 | 0 | 344.60 | |
| FPGrowth | Estimator | Association Rules | 494,156 | 180 | 180 | 417.01 |
| RMSE | MAE | Adjusted | Pearson Correlation | |
|---|---|---|---|---|
| Storage Memory | ||||
| Execution Memory | ||||
| Duration | 20,086.80 | 9925.13 |
| Strategy | Task-Scheduling Plan | Number of Stages | Time (min) | Peak Disk Usage (MB) | Writes Duration (min) | On-Disk Usage (MB) |
|---|---|---|---|---|---|---|
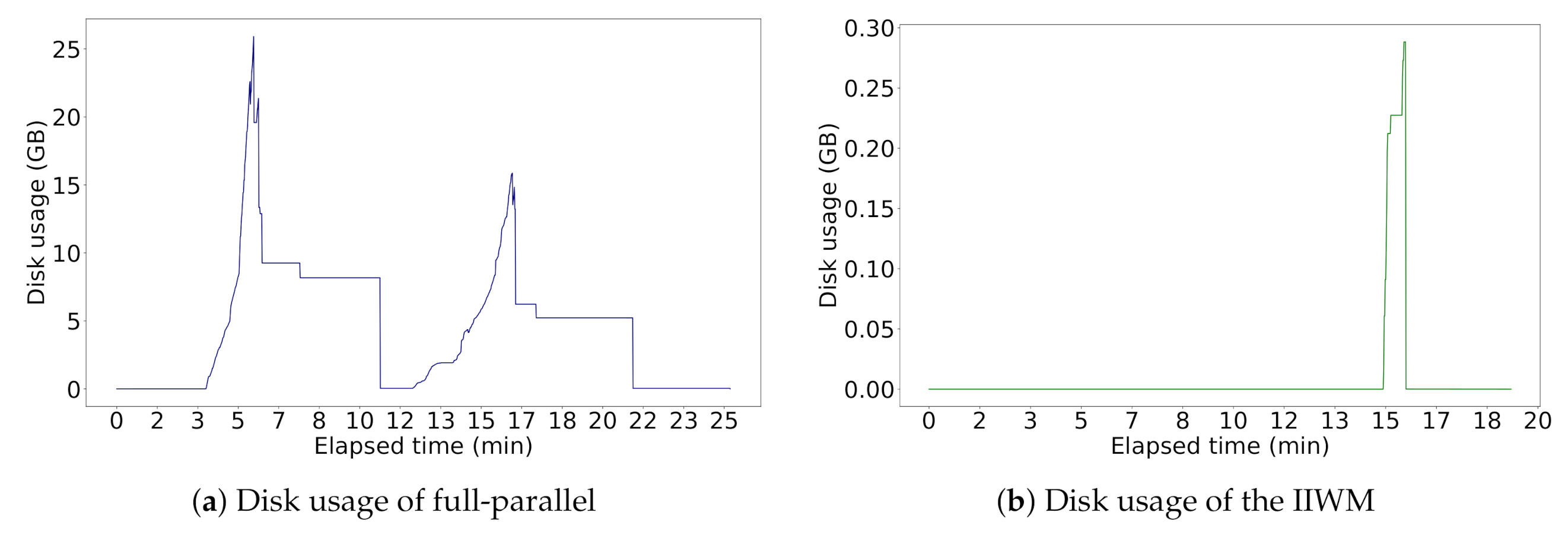
| Full-Parallel | (), ( ‖ ‖ ‖ ), ( ‖ ‖ ‖ ‖ ‖ ‖ ‖ ), ( ‖ ‖ ‖ ‖ ‖ ‖ ‖ ), (), ( ‖ ‖ ‖ ), () | 7 | 27,095.84 | 10,593.79 | ||
| IIWM | (), ( ‖ ), ( ‖ ), ( ‖ ), ( ‖ ‖ ‖ ), (), ( ‖ ‖ ), ( ‖ ), (), ( ‖ ‖ ), (), ( ‖ ), (), (), () | 15 |
| Strategy | Task-Scheduling Plan | Number of Stages | Time (min) | Peak Disk Usage (MB) | Writes Duration (min) | On-Disk Usage (MB) |
|---|---|---|---|---|---|---|
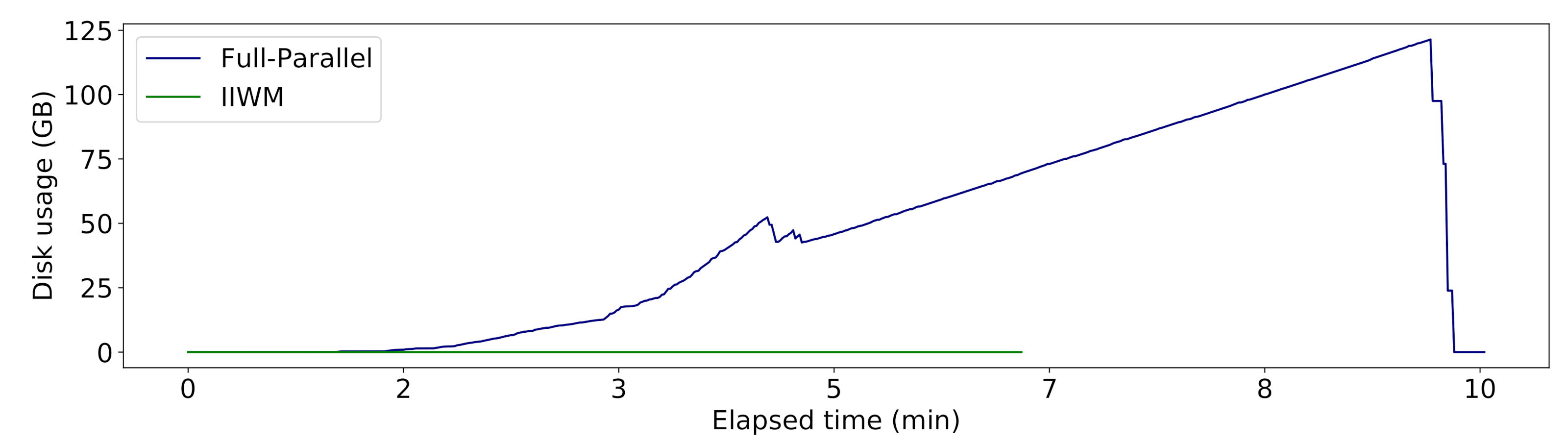
| Full-Parallel | ( ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ), ( ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ) | 2 | 124,730.87 | 54,443.19 | ||
| IIWM | ( ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ), ( ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ), ( ‖ ‖ ‖ ‖ ‖ ) | 3 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cantini, R.; Marozzo, F.; Orsino, A.; Talia, D.; Trunfio, P. Exploiting Machine Learning for Improving In-Memory Execution of Data-Intensive Workflows on Parallel Machines. Future Internet 2021, 13, 121. https://doi.org/10.3390/fi13050121
Cantini R, Marozzo F, Orsino A, Talia D, Trunfio P. Exploiting Machine Learning for Improving In-Memory Execution of Data-Intensive Workflows on Parallel Machines. Future Internet. 2021; 13(5):121. https://doi.org/10.3390/fi13050121
Chicago/Turabian StyleCantini, Riccardo, Fabrizio Marozzo, Alessio Orsino, Domenico Talia, and Paolo Trunfio. 2021. "Exploiting Machine Learning for Improving In-Memory Execution of Data-Intensive Workflows on Parallel Machines" Future Internet 13, no. 5: 121. https://doi.org/10.3390/fi13050121
APA StyleCantini, R., Marozzo, F., Orsino, A., Talia, D., & Trunfio, P. (2021). Exploiting Machine Learning for Improving In-Memory Execution of Data-Intensive Workflows on Parallel Machines. Future Internet, 13(5), 121. https://doi.org/10.3390/fi13050121










