Abstract
Community detection plays an essential role in understanding network topology and mining underlying information. A bipartite network is a complex network with more important authenticity and applicability than a one-mode network in the real world. There are many communities in the network that present natural overlapping structures in the real world. However, most of the research focuses on detecting non-overlapping community structures in the bipartite network, and the resolution of the existing evaluation function for the community structure’s merits are limited. So, we propose a novel function for community detection and evaluation of the bipartite network, called community density D. And based on community density, a bipartite network community detection algorithm DSNE (Density Sub-community Node-pair Extraction) is proposed, which is effective for overlapping community detection from a micro point of view. The experiments based on artificially-generated networks and real-world networks show that the DSNE algorithm is superior to some existing excellent algorithms; in comparison, the community density (D) is better than the bipartite network’s modularity.
1. Introduction
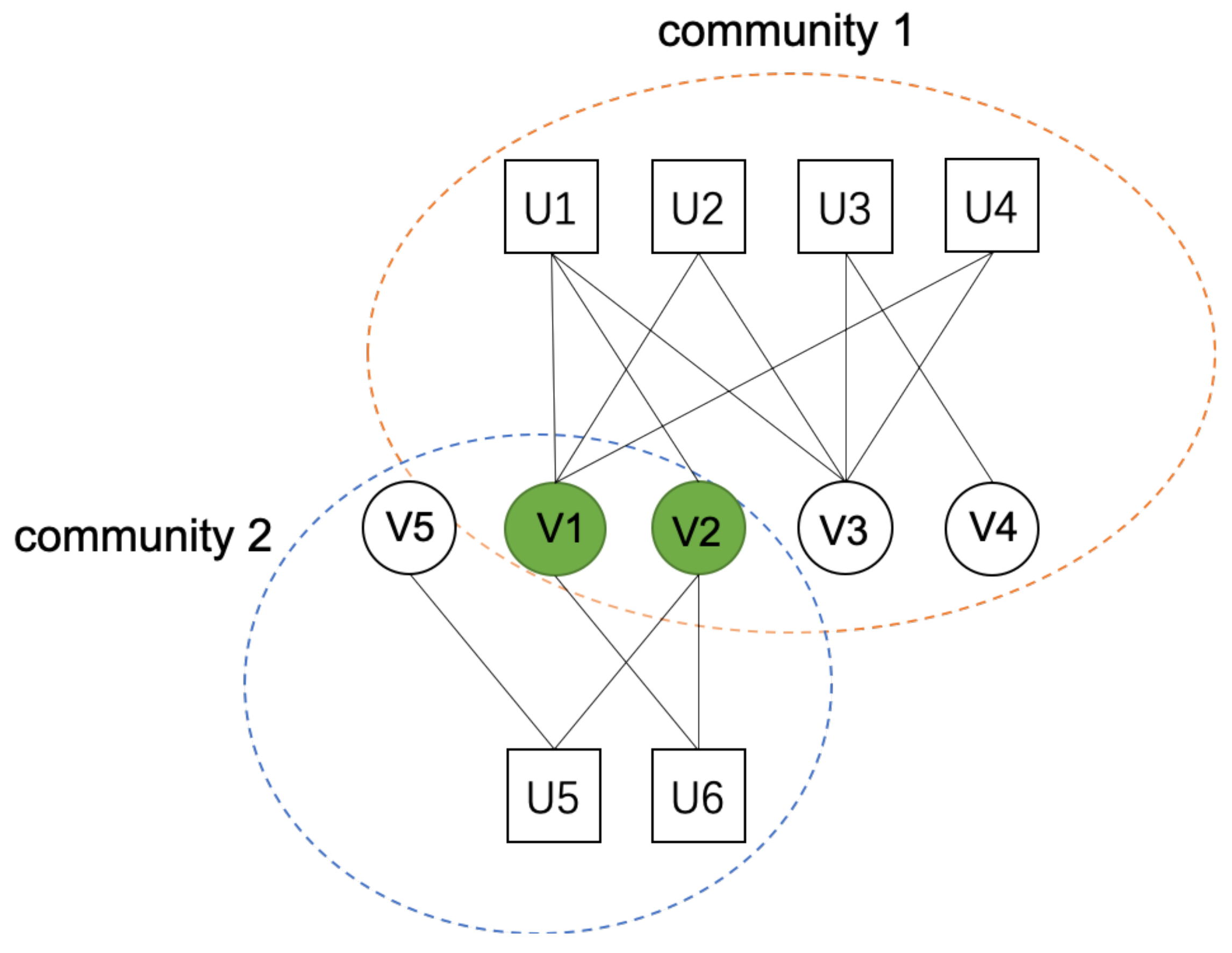
A complex network is the network with a high degree of complexity, and its complexity is mainly reflected in the large scale of the system, diverse structures, and complex types of nodes. According to the number of node types, the complex network can be classified as the one-mode network and multi-mode network. The network that contains only one type of node is called the one-mode network, such as financial networks [1], social networks [2], and the Internet [3]. The network containing more than two types of nodes in the network is called the multi-mode network. The bipartite network is one of the multi-mode networks defined as containing two types of nodes. There is no internal connection of the same type of node, but there are edges that exist only between different types of nodes. In the real world, there are various types of bipartite networks, such as protein networks [4] and scientific collaboration networks [5]. The community of a complex network is a set composed of vertices in the complex network. The vertices in the same community are closely connected, while the vertices in different communities are sparsely connected. Such as various associations generally tend to communicate with people in the same association rather than with people outside the association. Figure 1 shows a community example of a South African Companies bipartite network [6]. The areas framed by blue and yellow dotted lines represent community 1 and community 2, respectively, and the green nodes represent the overlapping nodes in the community. Because of its wide applicability and universality, the bipartite network is the hotspot of current researchers. There are various perspectives and methods around complex network research. As an important feature, we can obtain deeper topology, hidden meaning, and network information through community structure detection. In the real world, a bipartite network community has been found to solve many practical problems. For example, the study of bipartite network mining provides a new research basis and method for the epidemic model [7]. In the field of recommendation, the research on the community structure detection of the bipartite network can provide a new method for the recommendation technology of bipartite network systems. For example, in the bipartite network recommendation system of e-commerce users and commodities, if users are divided according to their characteristics, users with different characteristics are divided into different communities, and products are recommended for users according to the relationship between users in the communities, then the recommended products will be more in line with the needs of users.
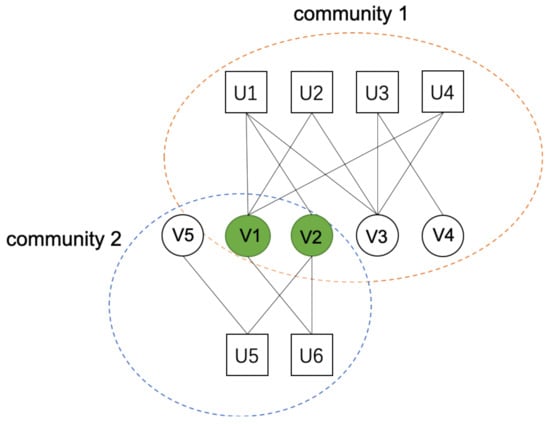
Figure 1.
Bipartite network example—South Africa companies bipartite network.
According to the subordinate relationship of nodes, community structure can be divided into overlapping community structure and non-overlapping community structure. Traditional community detection algorithms mostly focus on the non-overlapping communities in the bipartite network, while few studies focus on the overlapping communities in the bipartite network. But in the real world, a node usually has more than one attribute. A node can belong to more than one community. For example, in the scientific collaboration network [5], various authors can write a paper, and an author can sign various papers. Therefore, it has more crucial practical value and scientific research value to study the detection of bipartite network overlapping communities.
Recently, with more and more researchers going deep into the field of bipartite network community detection, quite a few algorithms have emerged in the field of community detection [7,8,9,10,11]. In general, these algorithms can be divided into two categories. One is to project the bipartite network to the one-mode network [12,13,14]; the advantages of this approach can be based on the current research results of the one-mode network, which is easier to operate. However, in projecting to the one-mode network, the bipartite network would lose some original information and increase the noise. The other is to directly detect the community on the bipartite network [15]. Compared with the projection of the bipartite network, it is more challenging to operate. Still, the original network structure information can be protected to the greatest extent not to be destroyed in the projection process. However, this kind of approach mainly starts from the network’s topology structure and carries out community detection from the macro perspective. It takes little consideration of the relationship between nodes and fails to discover some microscopic structural features of the bipartite network.
How to measure the merits of community detection algorithm results is another crucial problem. So, far, there has not been a recognized universal evaluation index for detecting bipartite network communities. The existing evaluation indexes are mostly based on the modularity of bipartite network [11,16,17] and make some improvements to it. However, due to the modularity resolution limitation [18], modularity cannot judge the merits and demerits of community detection results in some particular cases.
In this article, our main contribution is:
- A new evaluation index (Community Density D) is proposed, which alleviates the problem of modularity resolution limitation and evaluates the bipartite network’s merits and demerits from a new point.
- A new community detection algorithm (Density Sub-community Node-pair Extraction (DSNE)) is proposed. It has the advantages of a micro-network model, adopts a new merging strategy for community merging, and can detect the bipartite network’s overlapping community structure.
- The experimental results show that the proposed algorithm is superior to other algorithms’ accuracy and effectiveness.
2. Related Work
Compared with the one-mode network, the bipartite network’s topology is more complex, and it has stronger universality and practicability. Therefore, the research on the problem detection of the bipartite network community is more valuable. There are two main problems in the bipartite network community detection: finding the community structure more effectively, and another is how to evaluate the merits and demerits of the community detection results. In conclusion, there are mainly two kinds of research on the bipartite network’s community detection algorithm, and the evaluation index of the bipartite network is mainly aimed at the improvement of the modularity of the bipartite network.
2.1. Based on the Projecting of the Bipartite Network Community Detection Algorithm
The methods of projecting bipartite networks to one-mode networks are mainly divided into unweighted one-mode projecting and weighted one-mode projecting. Unweighted one-mode projecting is simply projecting bipartite networks to one-mode networks. Newman et al. [19] converted a bipartite network (scientific collaboration network) into two one-mode networks by using a single-mode right projection. Horvat et al. [20] proposed a statistical method that extends the bipartite network projection algorithm containing a single relationship and solves multiple types of relationship projection in large datasets. Valejo et al. [21] applied the traditional layered method to the projection process of bipartite network, proposes a multi-layered method based on projection. Comar et al. [22] proposed a framework that could simultaneously detect the network structures of different communities and their communication, with advantages, such as strong adaptability and fast convergence. However, in the process of unweighted one-mode projection, network structure information, such as edge frequency, may be lost, leading to a significant decrease in the accuracy of community detection by this method. Due to the apparent defects of unweighted modular projecting, researchers turned their attention to weighted modular projecting.
The weighted one-mode projecting converts the frequency of edges in a bipartite network to the weight of edges in a one-mode network during the projection process. Liu et al. [23] presented a novel fast nonnegative matrix (F-NMTF) method for clustering two kinds of nodes in a bipartite network. Zhang et al. [12] used a structure that can describe the relationship between two kinds of nodes, the Weighted Symmetric Bipartite Matrix Factorization (WSBMF), to detect the overlapping communities in the bipartite network. Wang et al. [13] presented a new way to find and extend the second part of the network’s core community. Define two parameters to represent the relationship between nodes of the same type and heterogeneous nodes, respectively. In Zhou et al. [14], based on the Louvain algorithm, the Bi-Louvain algorithm suitable for the bipartite network is proposed, and a two-stage algorithm with partial modularization and quantification of partition strength is applied to bipartite network community detection. Pesantez-Cabrera et al. [24] proposed an efficient algorithm, called Bilouvann, which implements a set of heuristics for fast and accurate community detection in bipartite networks. Compared with non-weighted modular projecting, the weighted modular projecting method can reduce structural information loss to a large extent. Still, its disadvantage is that the accuracy of the community detection results depends on the calculation of weights, which has substantial uncertainty, affecting the use of such methods.
2.2. Processed Directly on the Bipartite Network
The advantage of direct processing of bipartite network community detection algorithm is that it can not only effectively avoid the loss of structural information in the process of unweighted projection, keep the original network structural information to the maximum extent, but also avoid the problem of increasing noise in the process of weighted projection. Liu et al. [25] proposed a new algorithm, LP&BRIM, based on label propagation (LP) algorithm and BRIM algorithm, which is suitable for large-scale bipartite network detection. Beckett et al. [26] proposed two new algorithms, LPAWB + DirtLAPWB. It can find the largest community in the network by maximizing the bipartite network’s weighted modularity and searching the partition with the largest modularity. Sun et al. [27] proposed a new bipartite community Attractor algorithm, BiAttractor, to extend the distance dynamic model Attractor into the bipartite network. Wang et al. [28] proposed a bipartite network overlapping community detection algorithm (MACD-BNS). This algorithm realizes overlapping community detection by optimizing the four existing methods for calculating similar nodes’ similarity. Che et al. [29] proposed a new meme algorithm, MATMCD-BN, which approximates the optimal global solution by local search through a new population initialization method and a new crossover operator. Chang et al. [30] proposed a new community detection algorithm, CBG&BEN, which is based on the complete bipartite graph (CBG) and micro-network model (Bi-EgoNet). Gmati et al. [31] proposed a new algorithm called Bi-Comdet, the main thrust of the introduced approach is that it stresses the importance of grouping two types of nodes in communities having a full connection between its node. Taguchi et al. [32] proposed a new multi-label propagation algorithm BIMLPA, which overcomes the limitations of previous propagation algorithms and has good speed and stability. Yen et al. [33] extended the stochastic block model (SBM) model to bipartite networks and proposed biSBM; the biSBM improves community detection results over general SBM when data are noisy and improves the model resolution limit by a factor of two.
2.3. Community Detection Evaluation Criteria
If there is no scientific evaluation index of community detection results, then the community detection algorithm is at a loss, so how to evaluate the merits of community detection results is another important topic in community detection research. Especially for overlapping communities, the criteria for evaluation of community structure are very complex. It is difficult to give a unified and recognized evaluation index. Barber [16] extended the modularity of the traditional one-mode network to the bipartite network. Murata et al. [17] proposed another kind of modularity of bipartite networks, which can be represented by a pair of two numerical groups in two directions, allowing one-to-many correspondence of communities of different vertex types. Suzuki et al. [34] proposed a new modularity measurement method based on M.E.J Newman, which applies to bipartite networks and non-uniform networks. Chang et al. [30] proposed a new modularity evaluation method, which extended the modularity to overlapping community detection based on M.E.J Newman’s method. This evaluation criterion can evaluate the findings of overlapping communities in bipartite networks. All evaluation criteria described above are limited by modularity resolution [18]. The problem of resolution limit was first proposed by Fortunato et al. [35] in 2007. Fortunato et al. [36] find that multi-resolution modularity may not be able to prepare to identify a large number of network community structures with scale-free characteristics in reality. Specifically, multi-resolution modularity may merge some small communities into large communities and may split large communities into small communities. Li et al. [37] proposed a mass function of community partition community density to measure the quality of community structure in a bipartite network. Still, this mass function is only applicable to the flying overlapping community structure in the bipartite network.
3. Community Density
This section is divided into two parts: the definition of community density D, reasoning D solves the modularity resolution limitation to a certain extent. We want to define community density D to measure the quality of community division is mainly due to the problems left by the history of modularity. Take the latest methods as examples. Chang et al. [30] proposed modularity suitable for bipartite network overlapping community structure, but it is still limited by modularity resolution. Li [37] proposed Bipartite Partition Density, which can effectively alleviate the modularity resolution limitation and considers the community as a whole and cannot be used for overlapping communities. Although these methods can detect community structure, they lack to consider community structure from a micro perspective, such as the relationship between node pairs within the community. Based on this, from the micro point of view, this paper considers the relationship between the node pairs within the community and puts forward an evaluation standard suitable for the bipartite network overlapping community structure, which can effectively alleviate the modularity resolution limitation.
3.1. Key Definitions
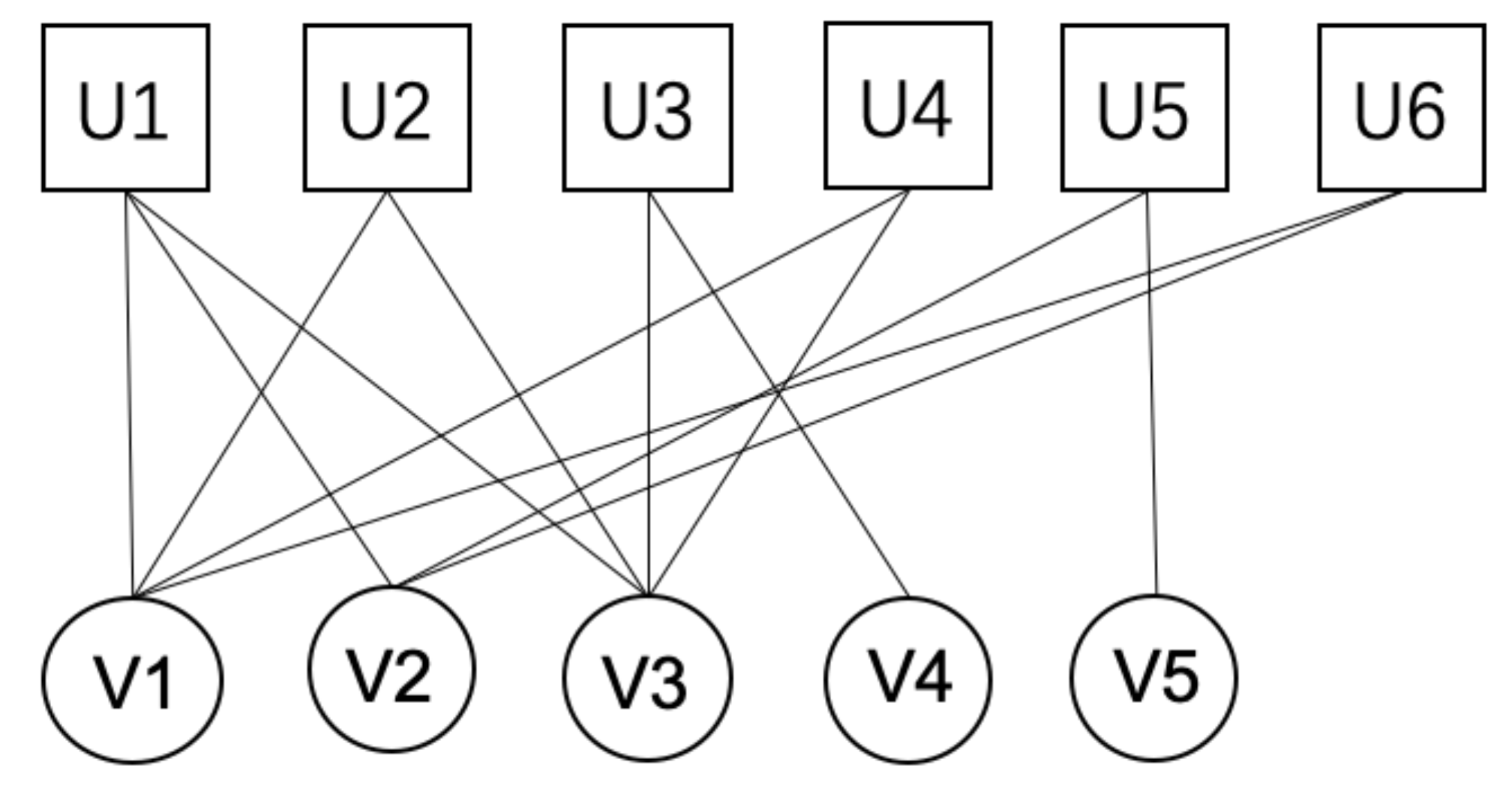
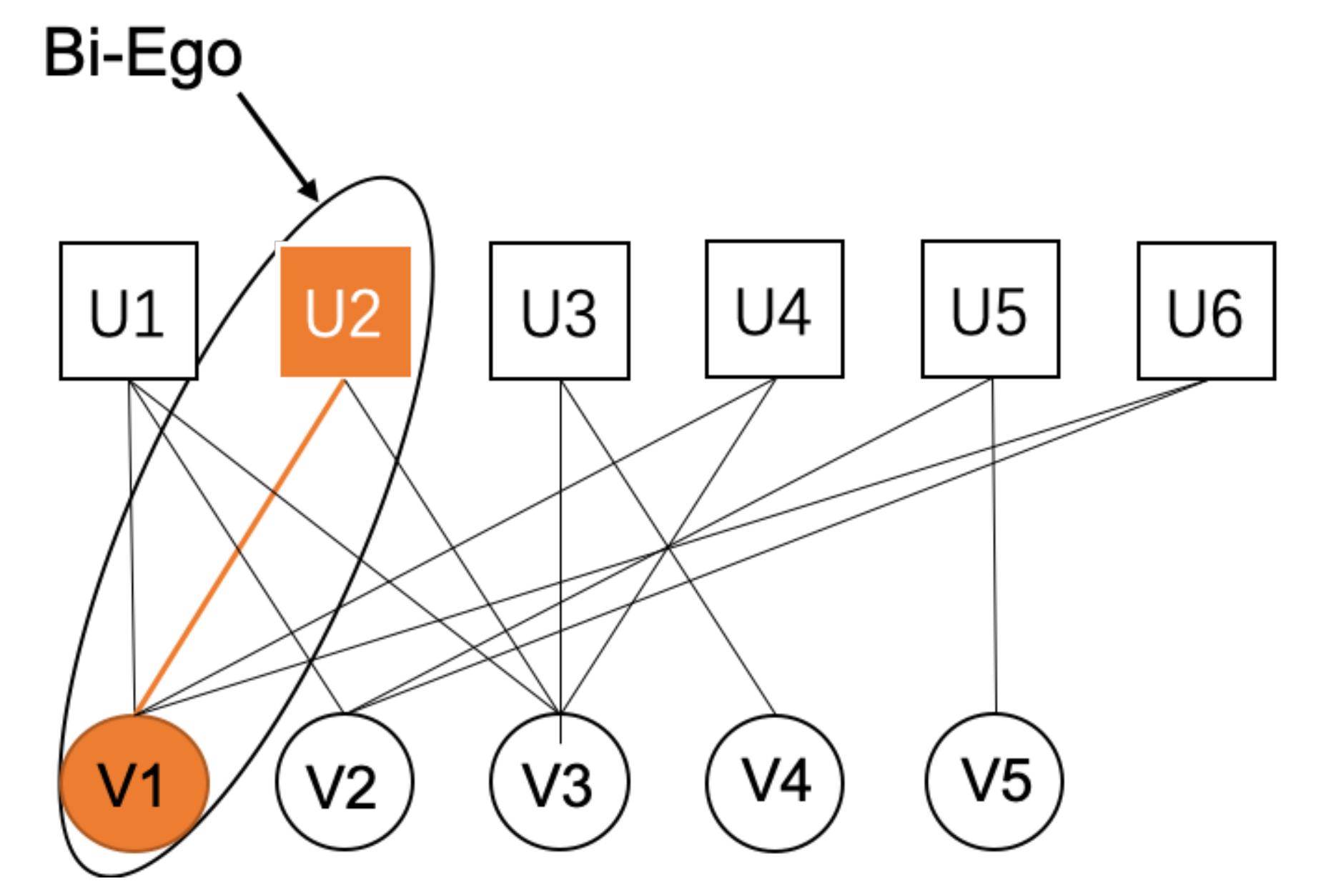
Given a bipartite network with no weight, no direction and the edges exist only between nodes of different types. : U is a one node typeset, : V is a another node typeset. a represents the number of nodes of type U, and b represents the number of nodes of type V. E represents the set of edges connected by two types of nodes, and represents a pair of nodes connected by edge . An example diagram of a bipartite network is shown in Figure 2. There are five U nodes and six V nodes, with a total of thirteen edges.
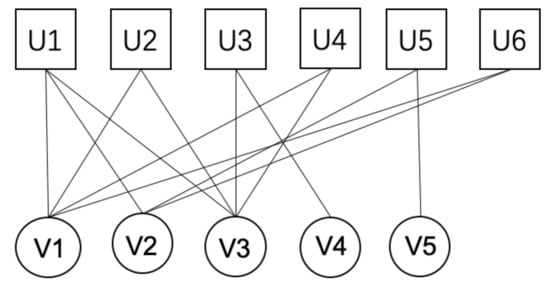
Figure 2.
Bipartite network example.
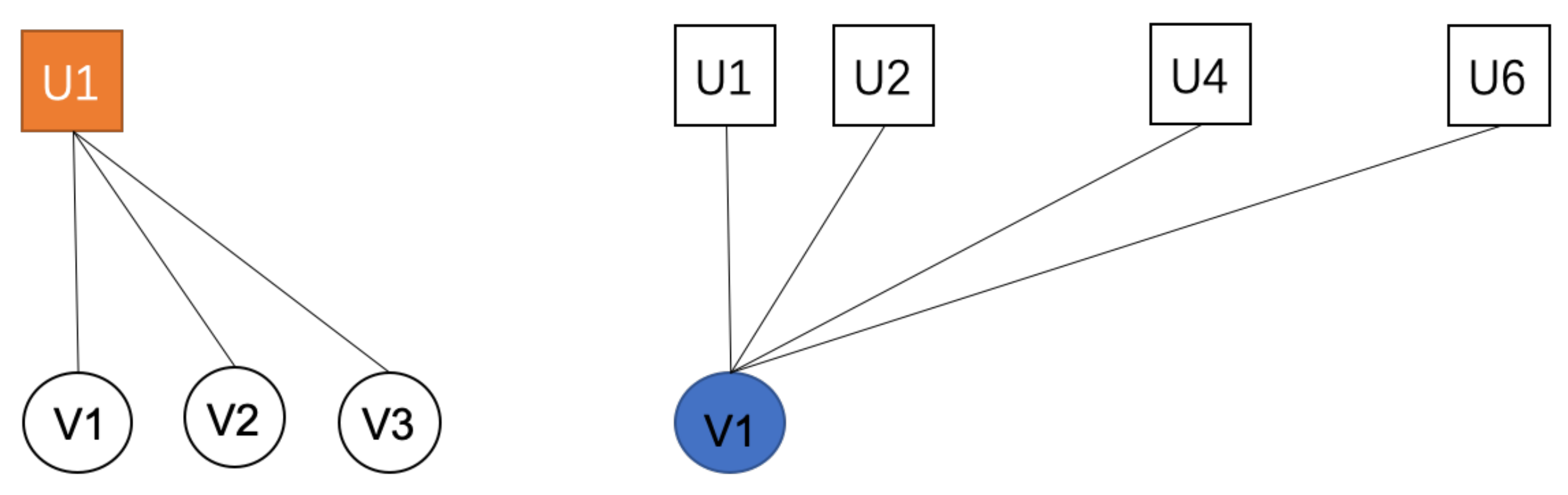
In a bipartite network , represents the set of all node pairs containing node u, represents the number of node pairs u in U, and then is the total number of node pairs in the set. Likewise, represents the set of all node pairs containing node v, we let be the number of node pairs v in V, and then is the total number of node pairs in the set. As shown in Figure 3: For node , ; for node , . We express these as:
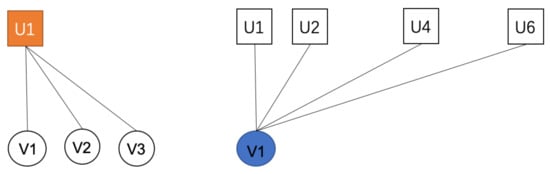
Figure 3.
All node pairs containing nodes and .
In a bipartite network , represents a set of neighbor node pairs of node pairs (u,v).
In Figure 2, select a node pair , and then its neighbor node pairs set is . Figure 4 shows a set of neighbor node pairs of node pair .
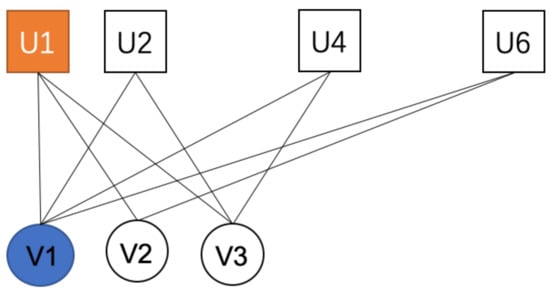
Figure 4.
A set of neighbor node pairs of node pairs .
In a bipartite network , assume that the bipartite network G is divided into X communities, where the t-th community is expressed as , and represents whether the node pair is a node pair within the community. represents the node pair density of node pairs in community ; in , represents the total number of all V nodes connected to m, k represents the serial number of node connected to m, and, when k = 1, it means that m is connected to V node . For node pair , if they are edges within the t-th community, then . We express these as:
Suppose we use the bipartite network shown in Figure 2 for community detection, and the results are shown in Figure 1. There are two communities in Figure 2. In community 1, select node pair to calculate . For node pair , , , , . The calculation formula of is shown in Formula (9).
In the t-th community , by adding and averaging the node pair density of node pairs , the density of the t-th community can be shown as Formula (10). Among them, represents the sum of all U nodes in the t-th community, represents the sum of all V nodes in the t-th community, represents the sum of node pair density of all node pairs in the t-th community, represents the sum of all node pairs in the t-th community.
In community 1, , , the calculation formula of is shown in Formula (11).
Likewise, we can obtain . After obtaining the density of a certain community , the density of the whole bipartite network community D is the average density of all communities. X represents the number of communities in the bipartite network .
For the community detection shown in Figure 1, .
When we use community density D as an evaluation criterion of community detection, the higher the community density is, the closer the node pairs within the community are, and the sparser the node pairs between the communities are. This trend is very consistent with the community structure required by community detection. Therefore, community density can be used to determine whether community detection results are good or bad.
3.2. Reasoning Community Density Alleviates the Modularity Resolution Limitation
The root cause of the problem of modularity resolution limitation [18] is that modularity cannot effectively identify the results of community division. This problem has existed for quite a long time, but there has been no suitable method to completely solve this problem. The community density proposed in this paper can effectively solve the modularity resolution limitation in some cases. Now, let us look at an example.
There is a bipartite network G(U,V,E). This bipartite network is a complete graph, in which there are nodes of type u, and nodes of type v, , , . Then, this bipartite network has vertices and edges. This type of picture is called SCBG (Special Complete Bipartite Graph).
The community detection of this graph yielded the following two results:
R1: Divide the result into a community G.
R2: Evenly divided into two communities . , , , . For community , , , the total number of edges in community is . Among them, the number of edges in the community accounts for half of the total number of edges in the community , and the number of edges outside the community accounts for the other half. Likewise, for community , , , owns half of node U and node V, and owns the other half of node U and V, and the total number of edges in community is . Among them, the number of edges in the community accounts for half of the total number of edges in the community , and the number of edges outside the community accounts for the other half.
An example of the above situation is given in Figure 5, where and . Figure 5a is divided according to R1, and Figure 5b is divided according to R2.
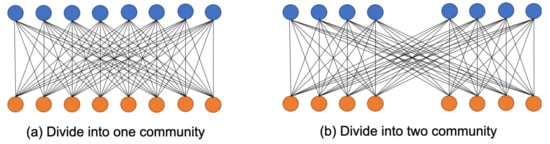
Figure 5.
When u = 4 and V = 4, the complete bipartite graph (CBG) is divided according to R1 and R2.
Barber [16] proposed the modularity suitable for bipartite networks. Assuming that a bipartite network can be expressed as , the formula for the modularity of the bipartite network is as Formula (15):
where M represents the number of edges in the bipartite network, C represents the set of community in the bipartite network, c means the c-th community , and m and n represent the number of two types of nodes in the bipartite network, respectively. represents the membership degree of node i to community c, and if node i belongs to community c, then c is 1, otherwise c is 0. represents the degree of node i. represents the adjacency matrix of bipartite network, if there is an edge between i and j, , else .
For the two kinds of community partition results, and , the modularity is calculated, respectively. For the community structure in Figure 5a, the calculation of modularity is shown in Formula (16). For the community structure in Figure 5b, the calculation of modularity is shown in Formula (17).
As Equations (16) and (17) show, the modularity of the two community detection results calculated by Barber’s modularity is 0. However, and have different community detection but . In , divide the network into a community. Logically, the best partition is the one where all the nodes are put in a single cluster. So, there are no cuts, no edges between clusters. So, the modularity proposed by Barber cannot effectively judge the merits and demerits of the results.
Let us use the community density proposed in this paper to calculate the two partition results. represents the community density divided according to R1, and represents the community density divided according to R2.
For R1, any node pair in community G, all node pairs containing G are within the community, so the calculation formula of node pair density is as follows (18).
For R2, in community , for any node pair , half of any node pair containing is in the community, and the other half is outside the community. Similarly, the situation in community is exactly the same as in .
After calculation, . Therefore, community density can be used to evaluate the merits and demarcations of such results. Effectively alleviate the resolution limit of modularity.
4. DSNE Algorithm
4.1. Definition of Community Similarity and Bi-EgoNet
Given two communities and , and represents the similarity of the two communities, as shown in Formula (24):
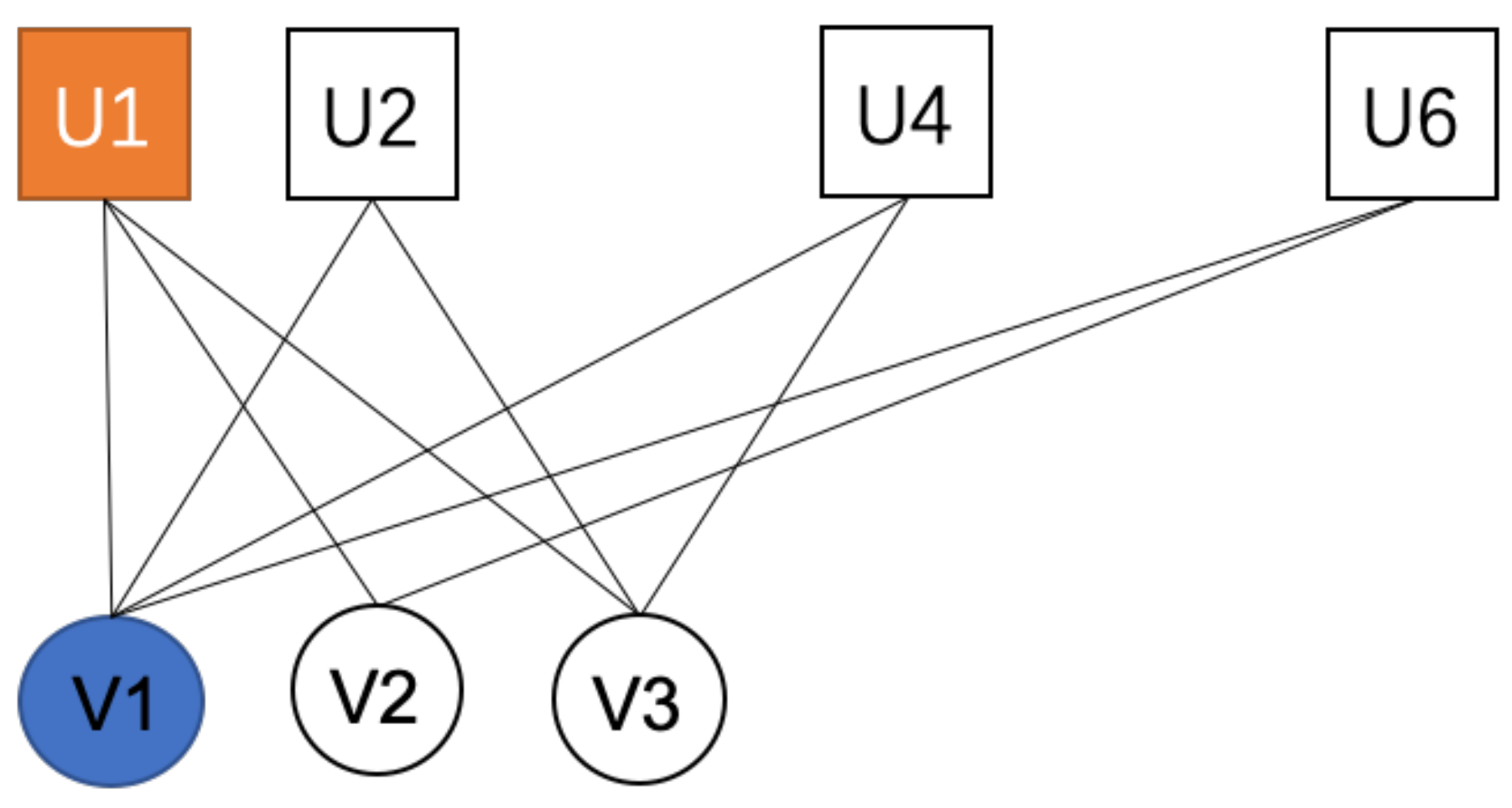
In the DSNE (Density Sub_community and Node-pair Extraction) algorithm, we use the Bi-EgoNet [11] network model proposed by Chang et al., which can detect the overlapping communities of the bipartite network from a microscopic point of view. Figure 6 shows an example of this model. As shown in Figure 6, in a bipartite network , the microscopic bipartite network model Bi-EgoNet of node pair is composed of a central node pair , its neighbor node pair set , and the edges between these node pairs. is the Bi-Ego, which is the center node pair; is the Bi-Alter, which is the each neighbor node pair.
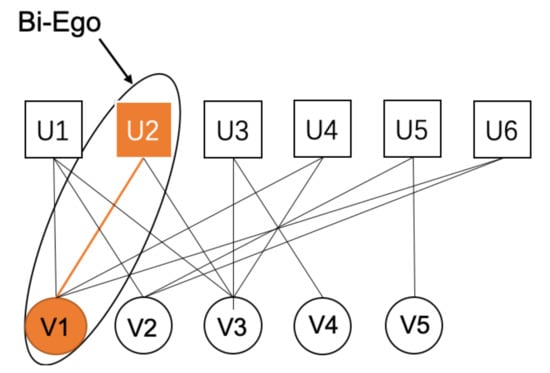
Figure 6.
Bi-EgoNet microscopic network model of node pairs .
The algorithm is divided into two stages: the first stage is to construct a sub-community for each node pair centered on each node pair; the second stage is to combine all node pair sub-communities to get the global community structure.
4.2. Construct Sub-Communities for Each Node Pair
In this stage, it is important to calculate node pairs’ density (Equation (8)). The flow of the first stage is shown in Algorithm 1.
| Algorithm 1 Construct Sub-communities For Node Pair. |
| Input: A bipartite network ; |
| Output: Sub-communities set: ; |
|
4.3. A New Strategy to Merge The Sub-Communities
For two communities to be merged, and , the usual practice is to merge the node pairs and edges directly. However, this will increase the noise, such as adding some node pairs that are not very closely connected to the newly merged community. In this regard, we provide a new merging idea: starting from the perspective of node pairs, we extract the central node pairs and from two communities and to be merged, and form a new community from the two type of node pairs. We define an identifier for each sub-community : , which indicates whether the central node pair in the sub-community has participated in the merge.
The flow of the first stage is shown in Algorithm 2.
| Algorithm 2 Use New Strategy To Merge Sub-communities. |
| Input: Sub-communities set ; |
| Output: The merged community set NC; |
|
In the DSNE algorithm, parameter is used to judge whether the neighbor node pair can join the sub-community . We believe that, if half of all the neighbor node pairs of a node pair are in the community, then the node pair should be in the community, so parameter is set to . The parameter is defined as the ratio of all identical node pairs in both communities and to the total node pairs, parameter is set to .
Complexity Analysis
Algorithm DSNE is divided into two stages to complete, so we analyze the complexity in turn according to the stage. Assume that there are m nodes of type U and n nodes of type V in the bipartite network. In constructing sub-communities for each node pair, the time complexity required for constructing sub-communities for each central node pair is , and, in merging sub-communities, the time complexity required is . Therefore, is the time complexity of the algorithm. Since the algorithm does not use unknown storage space during execution, the space complexity is .
5. Experimental Evaluation
In this section, we choose two methods, LOCD [9] and CBG&BEN [30], as the comparison algorithm, community density (D), NMI [38], and [11] as the evaluation indexes, and we use manually generated network [37] and the network in the real world as the dataset to evaluate DSNE algorithm. The LOCD algorithm and CBG&BEN algorithm are written in the Java programming language, while the DSNE algorithm is written in the C ++ programming language and runs on a 2.3 GHz processor, 8 GB of memory, and the macOS Big Sur operating system. Finally, the superiority of the proposed evaluation index, community density (D), is verified in evaluating community detection results compared with modularity.
5.1. Contrast Algorithm
The DSNE algorithm proposed in this paper uses community density to detect the overlapping community structure in the bipartite network starting from node pairs. LOCD algorithm uses the similarity of nodes to detect the overlapping community structure in the bipartite network from the graph’s topology. CBG&BEN algorithm uses the Bi-EgoNet, a micro-network model to detect the bipartite network’s overlapping community structure based on the complete dichotomous graph. These three methods have certain similarities, and the LOCD algorithm and CBG&BEN algorithm are relatively novel and excellent in community detection results. Therefore, comparing the DSNE algorithm with these two algorithms can better illustrate the DSNE algorithm’s superiority. We briefly describe the two algorithms below.
Wang et al. [9] proposed LOCD algorithm for selecting the right partitions in bipartite networks in 2017. This method contains two parameters; one parameter is used to represent the similarity between nodes of the same types, and the other parameter is used to represent the similarity between nodes of different types. The two types of nodes are processed separately. Firstly, extend the sub-community with the first parameter, which is the similarity between nodes of the same type. The similarity between nodes of different types is used to merge different types of nodes with the sub-community, and many sub-communities are obtained. Then, the sub-communities are merged according to some specific merge rules to obtain the global community structure.
In 2019, Chang et al. [30] proposed a community detection algorithm, CBG&BEN, which is based on the micro-network model (Bi-EgoNet) and complete bipartite graph (CBG). First, the algorithm constructed the micro bipartite network model Bi-EgoNet for each node pair. Second, it used the complete binary graph to extract the basic complete binary graph from each Bi-EgoNet, and the set of local communities was obtained by merging rules. Third, according to specific merging rules, the global bipartite network community structure is obtained. Finally, the network’s divergent nodes are collected and allocated to the corresponding global community, and the final global community structure is finally obtained.
5.2. Evaluation Criteria
5.2.1. Extended Modularity of Bipartite Networks
Chang et al. [30] extended the modularity of bipartite network proposed by Baber [16] and proposed , which is suitable for the evaluation of detection results in the overlapping communities of the bipartite network. The formula of is shown in (26).
We introduced Barber’s modularity in Formula (16), Except for , the meanings of other attributes in are consistent with the modularity proposed by Barber. The membership coefficient represents the proportion of node i belonging to community c. The membership coefficient should meet the normalized characteristics, such as and . For example, there are a total of edges connected to node i, among which m edges belong to community c, and n edges do not belong to community c; then, .
5.2.2. NMI
Andrea et al. [39] proposed a standardized mutual information index NMI (Normalized Mutual Information Index) for community detection in complex networks. When we want to measure the difference between the community structure obtained by the algorithm and the known real community structure, NMI is generally used as the evaluation index. NMI applies to many types of complex networks and is also applicable to evaluating the bipartite network’s detection results overlapping communities. The value of NMI is between 0 and 1. The larger the NMI value is, the closer the algorithm’s community structure is to the real community. The calculation formula of NMI is shown in (31).
represents the mutual information between X and Y, represents entropy information, and represents and entropy information under certain conditions. When , , then NMI reaches the maximum value of 1; otherwise, when X and Y are completely different, , then NMI is the minimum value of 0.
5.3. Experiments on Artificially Generated Networks
We refer to the artificially-generated network model proposed by Li [37]. The artificially-generated network model consists of three parameters: the number of network nodes N, the number of network edges , and the noise parameter . In Li’s artificially-generated network, each network has four communities with the same number of nodes. There are two different types of nodes, U and V in the community, and each community contains the same number of U and V nodes. The number of sides , that is, each U node is associated with 4 V nodes. is the network’s noise, that is, the number of sides between different communities in the network. The size of ranges from 0 to 1. When is 0, it means that the network is full of noise. When is 1, it means that there is no noise in the network.
In this experiment, an artificially-generated network with 256 nodes is selected. There are 128 U nodes and 128 V nodes in the network. There are four communities in the network. Each community contains 32 U nodes and 32 V nodes. There are 128 edges in each community. The initial value of is 0.1, increasing by 0.1 every time, increasing by nine times until the maximum value is 1. The DSNE algorithm, LOCD algorithm, and CBG&BEN algorithm are applied to the designed network, and the community detection is obtained. Table 1 shows the results of NMI evaluation.

Table 1.
Normalized Mutual Information Index (NMI) evaluation of the experimental results of three methods in artificially-generated network with different indexes .
As Table 1 shows, the NMI index of the DSNE algorithm is better than the other two algorithms in most cases, which indicates that the community structure found by the DSNE algorithm is closer to the real community structure than the other two algorithms. Compared with the CBG&BEN algorithm, the average NMI of the DSNE algorithm is improved by 2.6%, compared with the LOCD algorithm, 12.5% improves the average NMI of the DSNE algorithm. In the decreasing from 0.6 to 0.4, the value of the NMI index showed a cliff-like downward trend. As Table 1 shows, when fluctuates around 0.5, the impact on the algorithm’s accuracy is huge. When , the value of NMI does not exceed 0.1, which indicates that only less than 10% of the nodes in the community found by the algorithm correspond to the real network. Therefore, when , the community structures found by the three algorithms are invalid.
The decreasing speed of the algorithm represents the anti-noise ability of the algorithm. We consider setting and comparing the decreasing speed of the three algorithms under different . The results are shown in Table 2. The average decreasing speed of the DSNE algorithm was 2.7% less than that of CBG&BEN and 7.3% less than that of LOCD. Therefore, the anti-noise ability of LOCD algorithm is superior to the other two algorithms.

Table 2.
When , NMI decreasing speed with noise increasing ( decreasing) under different algorithms.
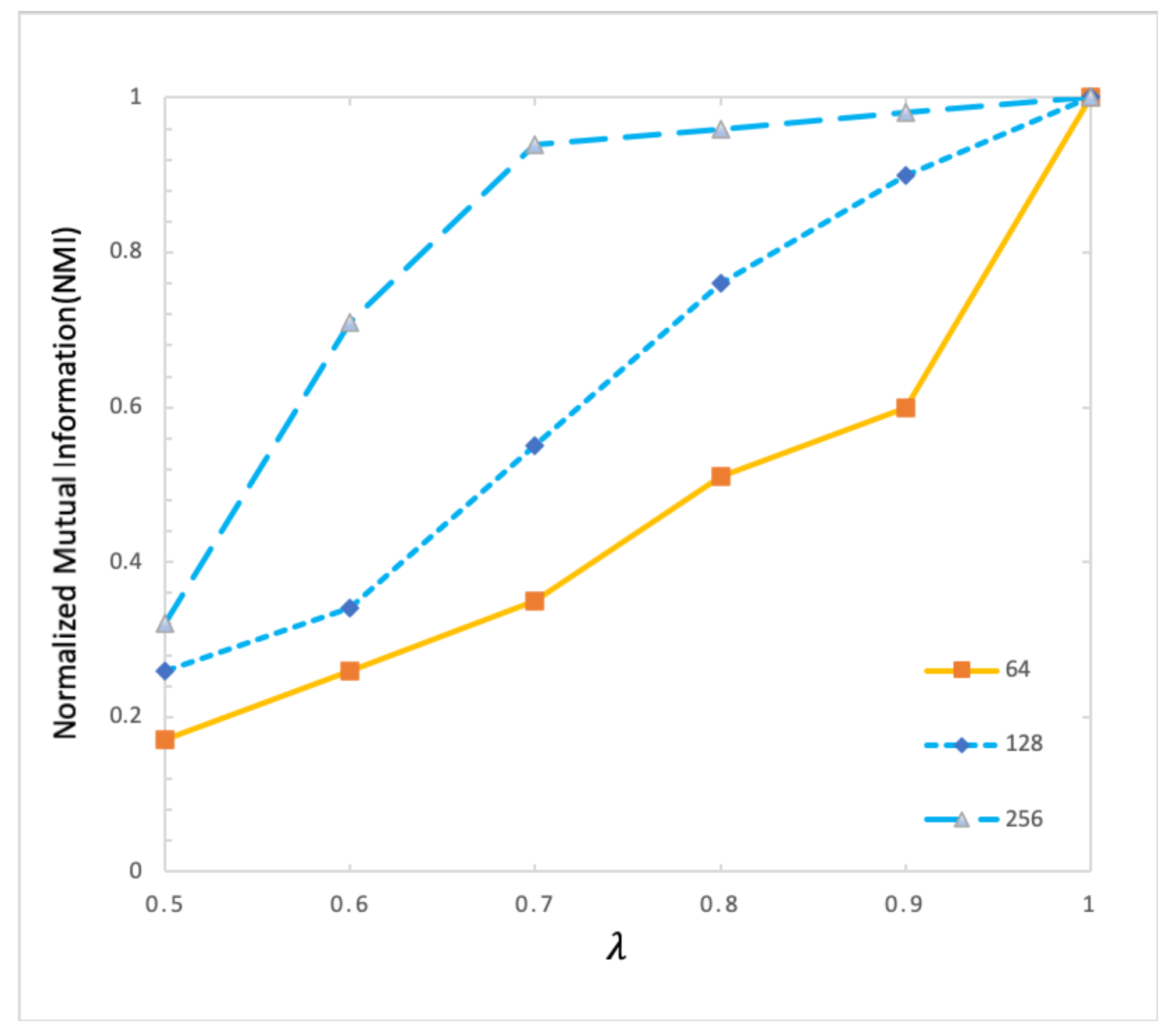
In artificially-generated networks, the number of nodes directly affects network structure information. Therefore, we consider setting and implementing the DSNE algorithm on artificially-generated networks with 64, 128, and 256 nodes. The results are shown in Figure 7.
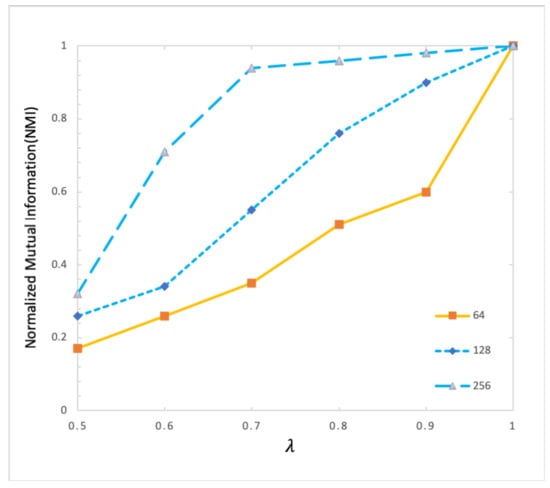
Figure 7.
Density Sub-community Node-pair Extraction (DSNE) algorithm uses NMI to evaluate experimental results under different N conditions.
Obviously, under different N, with the increase of noise, that is, during the process of decreasing from 1 to 0, the decrease rate of NMI is different. Table 3 shows the decrease rate of NMI under different N.

Table 3.
NMI decreasing speed with noise increasing ( decreasing) under different N.
According to Table 3 and Figure 7, when , with the increase of noise, i.e., the decrease of , NMI decreases more slowly. When , and decreases rapidly when a hovers around 0.5. When , NMI’s value showed a strong downward trend when hovered around 0.6. When , NMI showed a strong downward trend when hovered around 0.9. Therefore, we find that the increase of the number of network edges N is negatively related to NMI and ; that is to say, more noise is needed to make the algorithm imprecise. When the value of N is 64, 128 and 256, the corresponding average decline rates of NMI are 29.6%, 22.6%, and 17.%, which indicates that with the increasing value of N, the decline rate of NMI is getting slower and slower, that is, the stability of the algorithm is getting better. Besides, with the increase of N, there is more and more structural information in the network, and the average value of NMI is also increasing. In other words, the matching degree between the community detected by the algorithm and the real community is higher.
5.4. Experiments on Real-World Bipartite Network
In this section, we will verify the performance of the DSNE algorithm in the real world network, the CBG&BEN algorithm, and LOCD algorithm is used as the comparison algorithm, and eleven real bipartite network datasets from different domains are used as the dataset to evaluate the DSNE algorithm. The detailed information of these networks is shown in Table 4, where m and n represent the number of different types of nodes in the bipartite network, represents the number of edges between nodes, and represents the average degree of the network. Taking the SAC dataset in Figure 2 as an example, there are six U nodes and five V nodes, and the network has a total of thirteen edges, so , , , and .

Table 4.
Details of 11 real-world networks.
In order to explain the better understand the dataset we used in Table 4, the South African Companies Bipartite Network (SAC) is taken as an example to illustrate. Figure 2 shows the SAC dataset. Among them, the square nodes (U1 to U6) represent different leaders, the round nodes (V1 to V5) represent different companies, and the edges between nodes represent the leadership relationship between leaders and companies. The community detection results after DSNE algorithm is run are given in Figure 1. The merged community set NC contains two communities, which are, respectively, and . In , , , . In , , , .
Table 5 shows the number of communities found in the 11 datasets by the three methods. Table 5 shows that the DSNE algorithm and CBG&BEN algorithm can effectively get the number of communities, while the LOCD algorithm cannot effectively get the community structure in some datasets. LOCD algorithm cannot effectively obtain the number of SAC communities; the main reason is that the SAC dataset contains too little network information than the LOCD algorithm, so the number of communities obtained in the SAC dataset using the LOCD algorithm is 1. In the COL dataset, the LOCD algorithm is considered ineffective because it still fails to obtain sufficient community numbers after a long time (6 h) of operation. In most datasets, the number of communities is not always the more, the better. The more the number of communities, the more the noise interference in the merger process, the less the communities involved in the merger, the lower the merger rate, and the final number of communities is too many. DSNE algorithm is superior to CBG&BEN algorithm and LOCD algorithm in the number of communities in most datasets.

Table 5.
Number of communities obtained by the three algorithms in the eleven datasets.
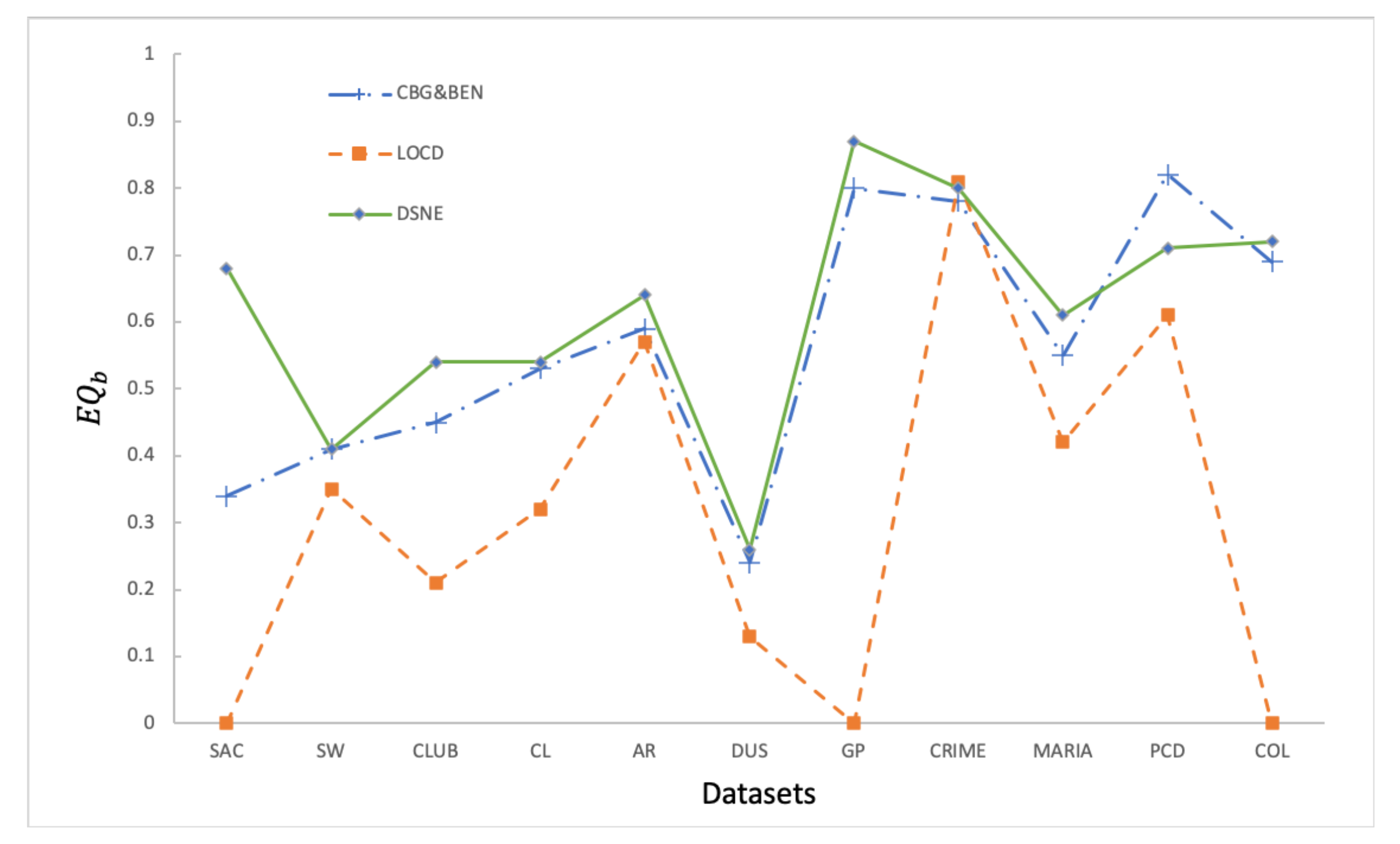
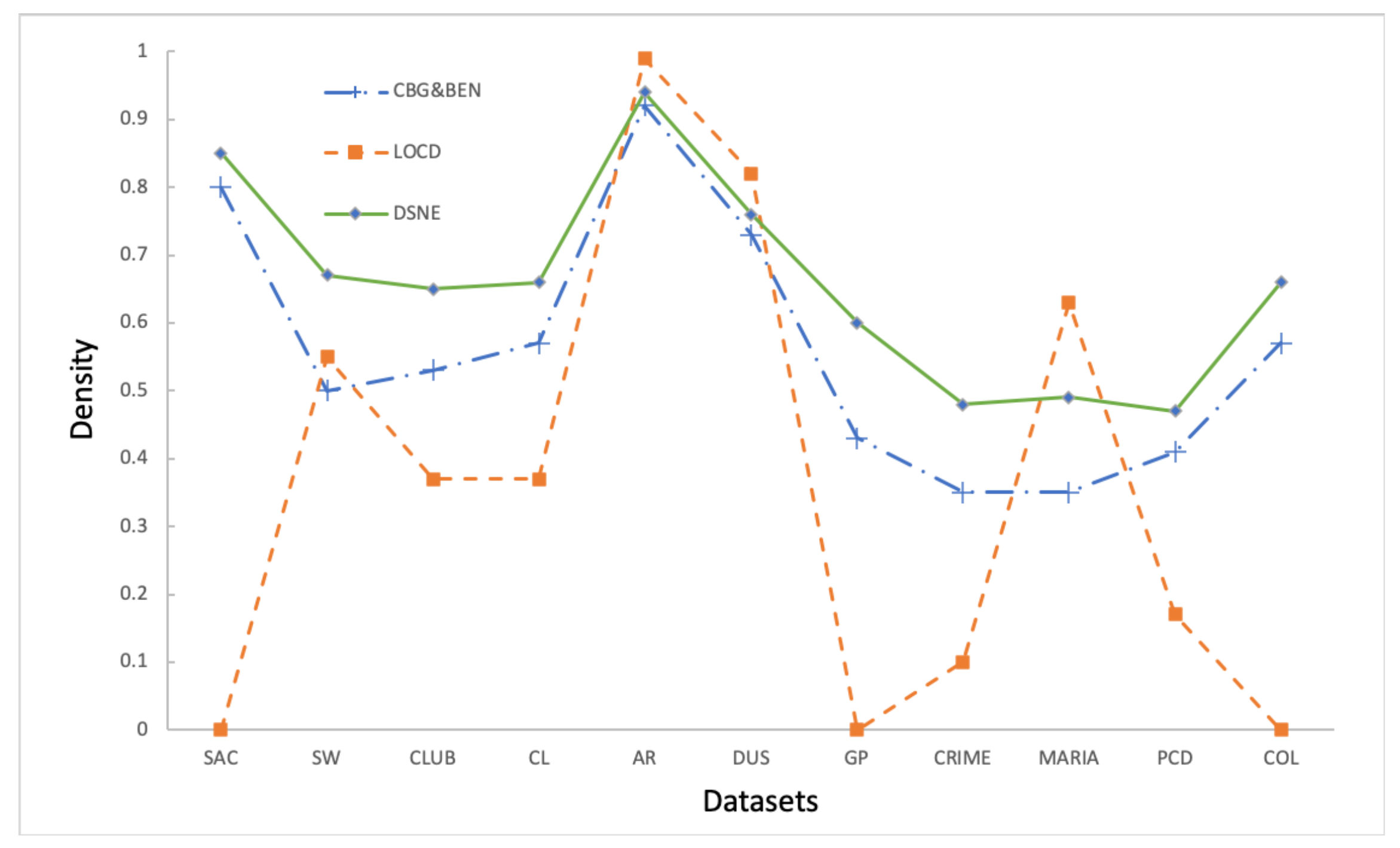
Figure 8 shows the experimental results of 3 algorithms evaluated by in 11 datasets. From Figure 8, we can get a conclusion: the of the DSNE algorithm is better than the other two algorithms. Because the LOCD algorithm cannot effectively detect the community structure in SAC and COL datasets, LOCD modularity in these two datasets is 0. Except for CL, PCD, and CRIM datasets, the DSNE algorithm’s performance is better than the other two algorithms. In the CL dataset, DSNE is slightly 0.02 less than the CBG&BEN algorithm. In the PCD dataset, DSNE is 0.11 less than the CBG&BEN algorithm, and in the CRIME dataset, DSNE is 0.01 less than the LOCD algorithm. In conclusion, the average of the DSNE algorithm is 5.5% higher than that of the CBG&BEN algorithm and 33.3% higher than that of LOCD algorithm.
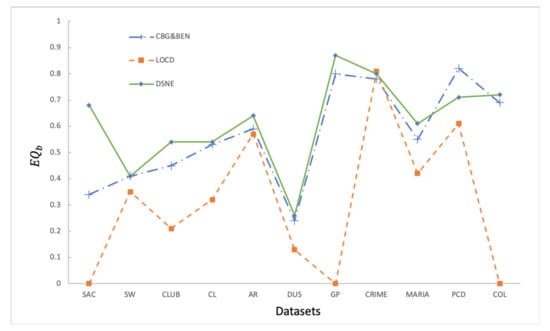
Figure 8.
Experimental results of three algorithms evaluated by in 11 datasets.
Figure 9 shows the experimental results of 3 algorithms evaluated by D in 11 datasets. Compared with the LOCD algorithm, except for Maria, AR, and DUS datasets, the D of the DCIM algorithm is better than the LOCD algorithm. In the Maria dataset, the D of the DSNE algorithm is 14% less than the LOCD algorithm, and in the AR dataset, the D of the DSNE algorithm is 5% less than the LOCD algorithm. In the DUS dataset, the DSNE algorithm is compared with LOCD 6% less. In SAC and GP datasets, because the LOCD algorithm could not effectively divide the community, the D of the LOCD algorithm on these two datasets is 0. Compared with the CBG&BEN algorithm, the D of DSNE is better than the CBG&BEN algorithm in all datasets. In the SW, GP, and CRIME datasets, the D of DSNE algorithm is 17%, 17%, and 12% higher than that of the CBG&BEN algorithm, respectively. In general, the DSNE algorithm’s performance on D is better than that of LOCD room rate and CBG&BEN algorithm. Using D as the evaluation criterion, the average D of the DSNE algorithm is 8.6% higher than the CBG&BEN algorithm and 30.6% higher than the LOCD algorithm.
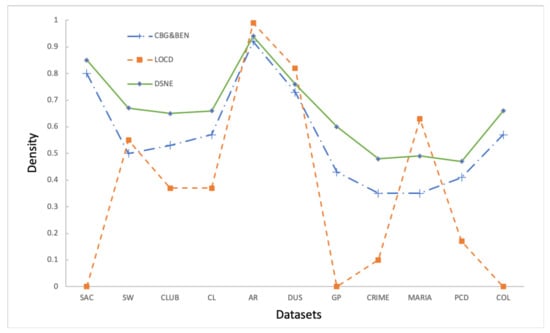
Figure 9.
Experimental results of three algorithms evaluated by D in 11 datasets.
Table 6 show the results of the comparison between D and under different datasets using the DSNE algorithm and CBG&BEN algorithm for community detection. Since can’t evaluate the detected community structure properly, Both algorithms are 0 in SCBG using evaluation, the D value of CBG&BEN is 0.5 more than that of DSNE because DSNE adopts a more strict strategy when conducting sub-community merger. In SW, CL, and DUS datasets, the CBG&BEN algorithm, and DSNE algorithm use as the evaluation index, and the values are relatively close. Within the range of effective data accuracy, the values of the two algorithms are the same. We can see from Table 6 that, when the two algorithms use D as the evaluation index, their performance is different in the above three datasets; so, when as the evaluation standard appears, the same value in the dataset, we can use D to measure the merits and demerits of community detection. In DUS and Maria datasets, is used as the evaluation standard, and CBG&BEN algorithm and DSNE algorithm are used for community detection. The results show that the value of the MARIA dataset is better than that of the DUS dataset. Still, the MARIA dataset’s D value is lower than that of the DUS dataset when D is used as the evaluation standard, which indicates that there are more edges between communities, but the community division is relatively broken. It is not very complete.

Table 6.
DSNE algorithm and CBG&BEN algorithm are compared to use and D as evaluation index on different datasets.
6. Conclusions
In this paper, we propose a new evaluation index: community density D, which can effectively solve the modularity resolution limitation to a certain extent. Besides, a novel algorithm, DSNE, is proposed, which combines the advantages of the proposed community density D to obtain the community. Among them, in the second stage of the DSNE algorithm: merging communities, we put forward a new merging idea to reduce the increase of noise during merging.
The DSNE algorithm is evaluated in the artificial and real-world networks and compared with the CBG&BEN algorithm and LOCD algorithm. Experimental results show that the DSNE algorithm can detect meaningful community structures in artificial and real-world networks, and its accuracy and effectiveness are better than LOCD and CBG&BEN algorithms. The average of the DSNE algorithm is 5.5% higher than that of the CBG&BEN algorithm and 33.3% higher than that of the LOCD algorithm. The average D of the DSNE algorithm is 8.6% higher than the CBG&BEN algorithm and 30.6% higher than the LOCD algorithm. In the future, we will carry out further research on the following aspects: to find the optimal global solution based on the optimal local solution in the first stage of the algorithm and to find a more effective bipartite network community detection algorithm based on community density D.
Author Contributions
Conceptualization, Y.P.; Data curation, Y.P.; Formal analysis, Y.P.; Investigation, Y.P.; Methodology, Y.P.; Project administration, Y.P.; Supervision, B.Z.; Validation, Y.P.; Visualization, Y.P.; Writing—original draft, Y.P.; Writing—review & editing, B.Z. and F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Key R&D Program of China under Grant 2017YFC0907505.
Data Availability Statement
Not Applicable, the study does not report any data.
Acknowledgments
The authors would like to thank anonymous reviewers for their fruitful feedback and comments that have helped them improve the quality of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bollmer, G.D. Community as a Financial Network: Mortgages, Citizenship, and Connectivity. Democr. Commun. 2011, 24, 39. [Google Scholar]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, H.; Zhang, P.; Li, M.; Di, Z.; Fan, Y. A New Comparative Definition of Community and Corresponding Identifying Algorithm. arXiv 2008, arXiv:0802.0242. [Google Scholar]
- Jeong, H.; Mason, S.; Barabasi, A. Oltvai ZN: Lethality and centrality in protein networks. Nature 2001, 411, 41–42. [Google Scholar] [CrossRef]
- Everett, M.G.; Borgatti, S.P. The dual-projection approach for two-mode networks. Soc. Netw. 2013, 35, 204–210. [Google Scholar] [CrossRef]
- South African Companies Network Dataset—KONECT. Available online: http://konect.cc/networks/brunson_south-africa/ (accessed on 29 March 2021).
- Wu, G.; Gu, C.; Qiu, L.; Yang, H. A uniform framework of projection and community detection for one-mode network in bipartite networks. Chin. Phys. B. 2017, 26, 128901. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, X. Uncovering Overlapping Community Structures by the Key Bi-Community and Intimate Degree in Bipartite Networks. Phys. A Stat. Mech. Its Appl. 2014, 407, 7–14. [Google Scholar] [CrossRef]
- Wang, X.; Liu, G.; Li, J. Overlapping Community Detection Based on Structural Centrality in Complex Networks. IEEE Access 2017, 5, 25258–25269. [Google Scholar] [CrossRef]
- Feng, L.; Zhou, C.; Zhao, Q. A spectral method to find communities in bipartite networks. Phys. A Stat. Mech. Its Appl. 2019, 513, 424–437. [Google Scholar] [CrossRef]
- Chang, F.; Zhang, B.; Zhao, Y.; Wu, S.; Niu, S. Overlapping Community Detection in Bipartite Networks using a Micro-bipartite Network Model: Bi-EgoNet. J. Intell. Fuzzy Syst. 2019, 37, 7965–7976. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Ahn, Y.Y. Community Detection in Bipartite Networks Using Weighted Symmetric Binary Matrix Factorization. Int. J. Mod. Phys. C 2015, 26, 1550096. [Google Scholar] [CrossRef]
- Wang, X.; Qin, X. Asymmetric Intimacy and Algorithm for Detecting Communities in Bipartite Networks. Phys. A Stat. Mech. Its Appl. 2016, 462, 569–578. [Google Scholar] [CrossRef]
- Zhou, C.; Feng, L.; Zhao, Q. A Novel Community Detection Method in Bipartite Networks. Phys. A Stat. Mech. Its Appl. 2018, 492, 1679–1693. [Google Scholar] [CrossRef]
- Yang, J.; McAuley, J.; Leskovec, J. Detecting Cohesive and 2-Mode Communities Indirected and Undirected Networks. In Proceedings of the 7th ACM International Conference on Web Search and Data Mining, New York, NY, USA, 24–28 February 2014; pp. 323–332. [Google Scholar] [CrossRef]
- Barber, M.J. Modularity and community detection in bipartite networks. Phys. Rev. E. 2007, 76, 066102. [Google Scholar] [CrossRef] [PubMed]
- Tsuyoshi Murata, T.I. A new modularity for detecting one-to-many correspondence of communities in bipartite networks. Adv. Complex Syst. 2010, 13, 19–31. [Google Scholar] [CrossRef]
- Guimerà, R.; Sales-Pardo, M.; Amaral, L.A.N. Module identification in bipartite and directed networks. Phys. Rev. E. 2007, 76, 036102. [Google Scholar] [CrossRef]
- Newman, M.E.J. The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. USA 2001, 98, 404–409. [Google Scholar] [CrossRef]
- Horvat, E.A.; Zweig, K.A. One-mode Projection of Multiplex Bipartite Graphs. In Proceedings of the IEEE/ACM International Conference on Advances in Social Networks Analysis & Mining, Istanbul, Turkey, 26–29 August 2013. [Google Scholar]
- Valejo, A.; Ferreira, V.; Filho, G.P.R.; de Oliveira, M.C.F.; de Andrade Lopes, A. One-Mode Projection-Based Multilevel Approach for Community Detection in Bipartite Networks. Available online: http://ceur-ws.org/Vol-2029/paper8.pdf (accessed on 29 March 2021).
- Comar, P.M.; Tan, P.N.; Jain, A.K. A Framework for Joint Community Detection across Multiple Related Networks. Neurocomputing 2012, 76, 93–104. [Google Scholar] [CrossRef]
- Yang, L.; Tao, W.; Xin-Sheng, J.; Caixia, L.; Mingyan, X. Detecting Communities in 2-Mode Networks via Fast Nonnegative Matrix Trifactorization. Available online: https://www.hindawi.com/journals/mpe/2015/937090/ (accessed on 29 March 2021).
- Pesantez-Cabrera, P.; Kalyanaraman, A. Efficient Detection of Communities in Biological Bipartite Networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 16, 258–271. [Google Scholar] [CrossRef]
- Liu, X.; Murata, T. Community Detection in Large-scale Bipartite Networks. In Proceedings of the 2009 IEEE/WIC/ACM International Joint Conference on Web Intelligence and Intelligent Agent Technology, Milan, Italy, 15–18 September 2009. [Google Scholar]
- Beckett, S.J. Improved community detection in weighted bipartite networks. R. Soc. Open Sci. 2016, 3, 140536. [Google Scholar] [CrossRef]
- Sun, H.L.; Ch’ng, E.; Yong, X.; Garibaldi, J.M.; See, S.; Chen, D.B. A Fast Community Detection Method in Bipartite Networks by Distance Dynamics. Phys. A Stat. Mech. Its Appl. 2018, 496, 108–120. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J. A Comparative Study of the Measures for Evaluating Community Structure in Bipartite Networks. Inf. Sci. 2018, 448, 249–262. [Google Scholar] [CrossRef]
- Che, S.; Yang, W.; Wang, W. A Memetic Algorithm for Community Detection in Bipartite Networks. IEEE Access 2019, 7, 126897–126912. [Google Scholar] [CrossRef]
- Chang, F.; Zhang, B.; Zhao, Y.; Wu, S.; Yoshigoe, K. Overlapping Community Detecting Based on Complete Bipartite Graphs in Micro-Bipartite Network Bi-Egonet. IEEE Access 2019, 7, 91488–91498. [Google Scholar] [CrossRef]
- Gmati, H.; Mouakher, A.; Hilali-Jaghdam, I. Bi-ComDet: Community Detection in Bipartite Networks. Procedia Comput. Sci. 2019, 159, 313–322. [Google Scholar] [CrossRef]
- Taguchi, H.; Murata, T.; Liu, X. BiMLPA: Community Detection in Bipartite Networks by Multi-Label Propagation. In Proceedings of NetSci-X 2020: Sixth International Winter School and Conference on Network Science; Masuda, N., Goh, K.I., Jia, T., Yamanoi, J., Sayama, H., Eds.; Springer: Cham, Switzerland, 2020; pp. 17–31. [Google Scholar]
- Yen, T.C.; Larremore, D.B. Community Detection in Bipartite Networks with Stochastic Blockmodels. Phys. Rev. E. 2020, 102, 032309. [Google Scholar] [CrossRef]
- Suzuki, K.; Wakita, K. Extracting Multi-facet Community Structure from Bipartite Networks. In Proceedings of the 2009 International Conference on Computational Science and Engineering, Vancouver, BC, Canada, 29–31 August 2009. [Google Scholar]
- Fortunato, S.; Barthélemy, M. Resolution Limit in Community Detection. Available online: https://www.pnas.org/content/pnas/104/1/36.full.pdf (accessed on 29 March 2021).
- Lancichinetti, A.; Fortunato, S. Limits of modularity maximization in community detection. Phys. Rev. E 2011, 84, 066122. [Google Scholar] [CrossRef]
- Li, Z.; Wang, R.S.; Zhang, S.; Zhang, X.S. Quantitative function and algorithm for community detection in bipartite networks. Inf. Sci. 2016, 367, 874–889. [Google Scholar] [CrossRef]
- Mcdaid, A.F.; Greene, D.; Hurley, N. Normalized Mutual Information to evaluate overlapping community finding algorithms. arXiv 2011, arXiv:1110.2515. [Google Scholar]
- Lancichinetti, A.; Fortunato, S.; Kertész, J. Detecting the overlapping and hierarchical community structure in complex networks. New J. Phys. 2009, 11, 033015. [Google Scholar] [CrossRef]
- Davis, A.; Gardner, B.B.; Gardner, M.R.; Pierson, D. Deep South: A Social Anthropological Study of Caste and Class; University of South Carolina Press: Columbia, SC, USA, 1941; Volume 2, pp. 117–118. [Google Scholar]
- Club Membership Network Dataset–KONECT. Available online: http://www.konect.cc/networks/brunson_club-membership/ (accessed on 29 March 2021).
- Barnes, R.; Burkett, T. Structural redundancy and multiplicity in corporate networks. Int. Netw. Soc. Netw. Anal. 2010, 30, 4–20. [Google Scholar]
- American Revolution Network Dataset. Available online: http://konect.cc/networks/brunson_revolution/ (accessed on 29 March 2021).
- Divorce in US. Available online: http://vlado.fmf.uni-lj.si/pub/networks/data/2mode/divorce.net (accessed on 29 March 2021).
- Imrich, W.; Klavžar, S.; Hammack, R.H. Product Graphs: Structure and Recognition; JohnWiley & Sons: Hoboken, NJ, USA, 2000; Available online: http://2017drama-st.tvbs.com.tw/4rcw/15-dr-christophe-schumm/read-product-graphs-structure-and-recognition-0471370398.pdf (accessed on 29 March 2021).
- Crime Network Dataset—KONECT. Available online: http://konect.cc/networks/moreno_crime/ (accessed on 29 March 2021).
- Li, H.J.; Xiang, J. Explore of the fuzzy community structure integrating the directed line graph and likelihood optimization. J. Intell. Fuzzy Syst. 2017, 32, 4503–4511. [Google Scholar] [CrossRef]
- Nacher, J.C.; Jean-Marc, S.; John, P. Modularity in Protein Complex and Drug Interactions Reveals New Polypharmacological Properties. PLoS ONE 2012, 7, e30028. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. The Structure of Scientific Collaboration Networks; Princeton University Press: Princeton, NJ, USA, 2011; pp. 221–226. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).