Cooperation in Social Dilemmas: A Group Game Model with Double-Layer Networks
Abstract
1. Introduction
- We merge an improved group game with double-layer networks and demonstrate the evolution of cooperation in the double-layer networks based on small-world and scale-free networks. By comparing the evolution behavior of single- and double-layer networks, it is proven that double-layer networks can promote cooperation in multiplayer games. Subsequently, we further discuss the reasons for this phenomenon and the roles of the important parameters in the network.
- We propose a model called PGG-SP to overcome the problem of previous strategy learning methods not considering individual characteristics, in which an individual’s preferred characteristics represent the probability that an individual tends to cooperate in the game. This attribute is the result of individual accumulation through the long-term game. Thus, this assumption better conforms with the process of making decisions in a practical scenario.
- To imitate dynamic social interaction between individuals, a dynamic double-layer network is designed which realizes the co-evolution behavior of game strategy and network topology. It is proven that the adaptive adjustment of the strategy and structure can credibly enhance cooperation and maintain stability by comparing the cooperation performance between dynamic, static, single-layer, and double-layer networks. In addition, we construct a dynamic heterogeneous double-layer network to depict a practical scenario.
2. Related Work
2.1. Related Definition
2.1.1. Complex Networks
- In a regular network [14], nodes are connected according to specific rules. For example, any nodes may be connected in pairs to form a fully connected network. The structure of a regular network is simple and has certain limitations for describing real-world networks.
- Random networks [15] were proposed in 1959. Assuming that the network size is N, there will be at most edges between nodes, and the probability p is used to determine whether these edges can be connected, thereby generating a random network. There are edges in the network, where .
- A small-world network [16] defines the total number of network nodes as N, where all nodes are connected to the left and right nodes and then randomly reconnected with an edge with a fixed probability.
- In a scale-free network [17], first, there are M isolated nodes in the network. Second, a new node with edges is added at each time step t. Finally, the new node is connected to existing nodes .
2.1.2. Public Goods Games
2.2. Recent Research
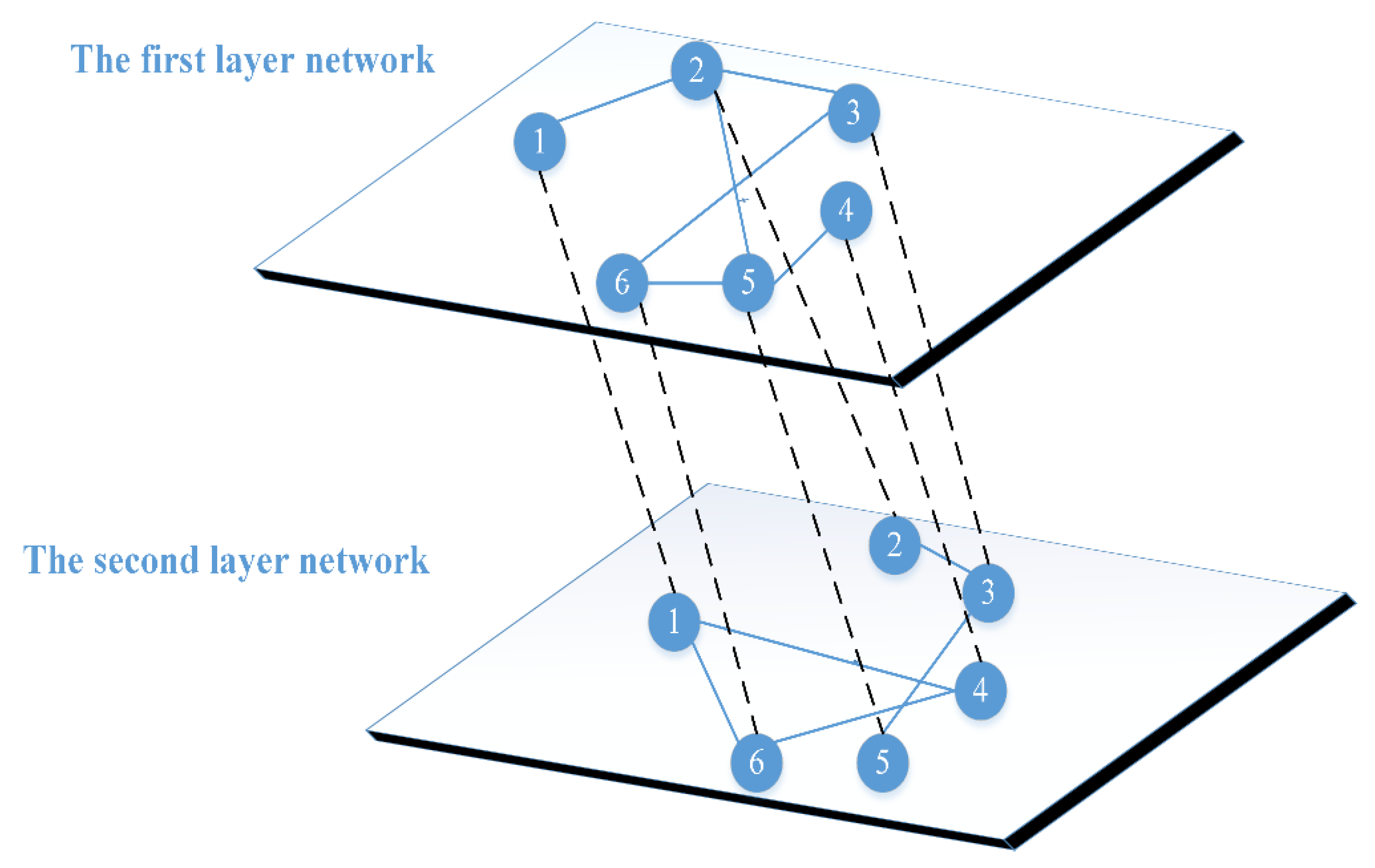
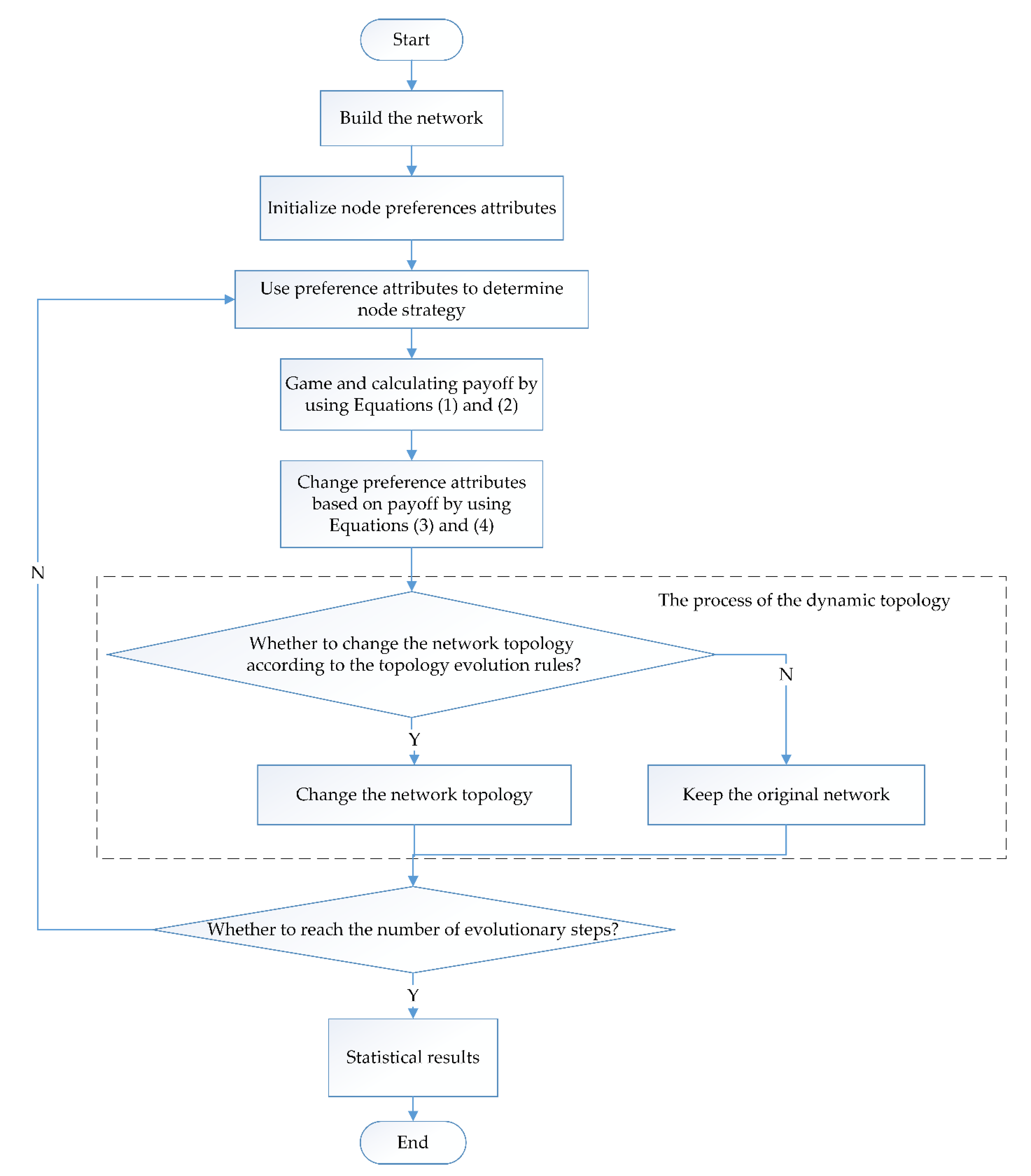
3. Model
3.1. Calculation of Payoff
3.2. Strategy Learning
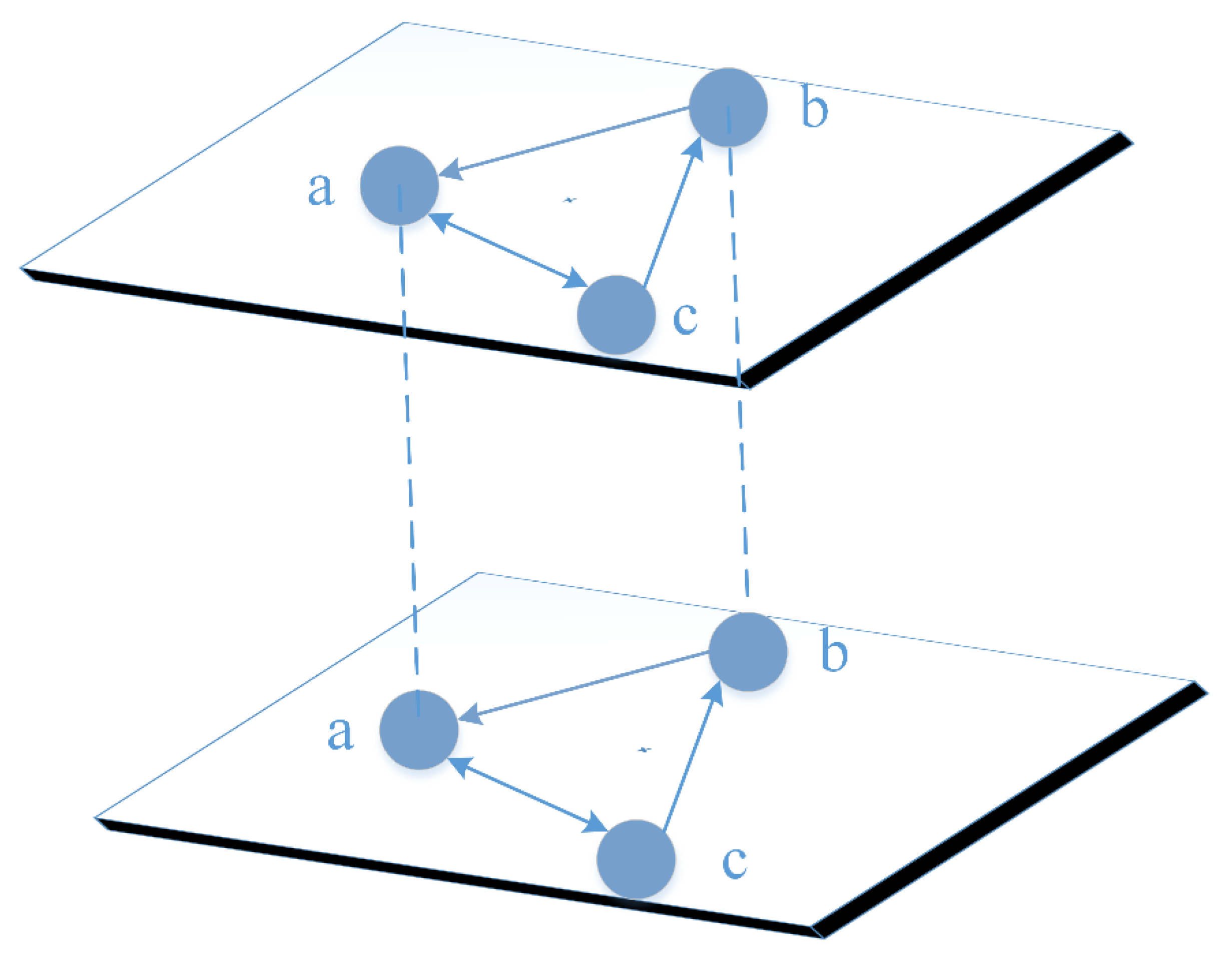
3.3. Network Adjustment
| Algorithm 1: The process of the game | |
| 1. | Define and initialize the related parameters: game rounds Ngame, number of individuals N, preference attributes bi of each individual, strategy Si of each individual, fraction of cooperators fc, etc.; |
| 2. | fort = 1 to Ngame do |
| 3. | for i = 1 to N do |
| 4. | If random() ≤ bi then |
| 5. | Si = 1; |
| 6. | end if |
| 7. | else |
| 8. | Si = 0; |
| 9. | end |
| 10. | end |
| 11. | Calculate the payoff of all nodes by using Equations (1) and (2); |
| 12. | Calculate fraction of cooperators fc; |
| 13. | for i = 1 to N do |
| 14. | Find the appropriate node j, where j is the neighbor node with the largest payoff in the same layer of the network, or the corresponding node in a different layer |
| 15. | if Sj = 1 then |
| 16. | Update bi of the node i by using Equation (3); |
| 17. | end if |
| 18. | else |
| 19. | Update bi of the node i by using Equation (4); |
| 20. | end |
| 21. | end |
| 22. | end |
| 23. | Return fc; |
| Algorithm 2: Updating process of the dynamic network | |
| 1. | Define and initialize the related parameters: game rounds Ngame, number of individuals N, the probability of reconnection edge T, etc.; |
| 2. | fort = 1 to Ngame do |
| 3. | if random() ≤ T then |
| 4. | for i = 1 to N do |
| 5. | Find the neighbor node A with the smallest payoff of node i; |
| 6. | Randomly obtain a non-neighbor node B of the individual i, which is a neighbor of i’s neighbor; |
| 7. | Calculate q by using Equation (5); |
| 8. | if then |
| 9. | Update the network: disconnect from the individual A and reconnect with the individual B; |
| 10. | end if |
| 11. | else |
| 12. | Keep the network unchanged; |
| 13. | end |
| 14. | end |
| 15. | end if |
| 16. | end |
3.4. The Process of the PGG-SP Model in the Network
4. Experiment and Analysis
4.1. PGG-SP on the Static Network
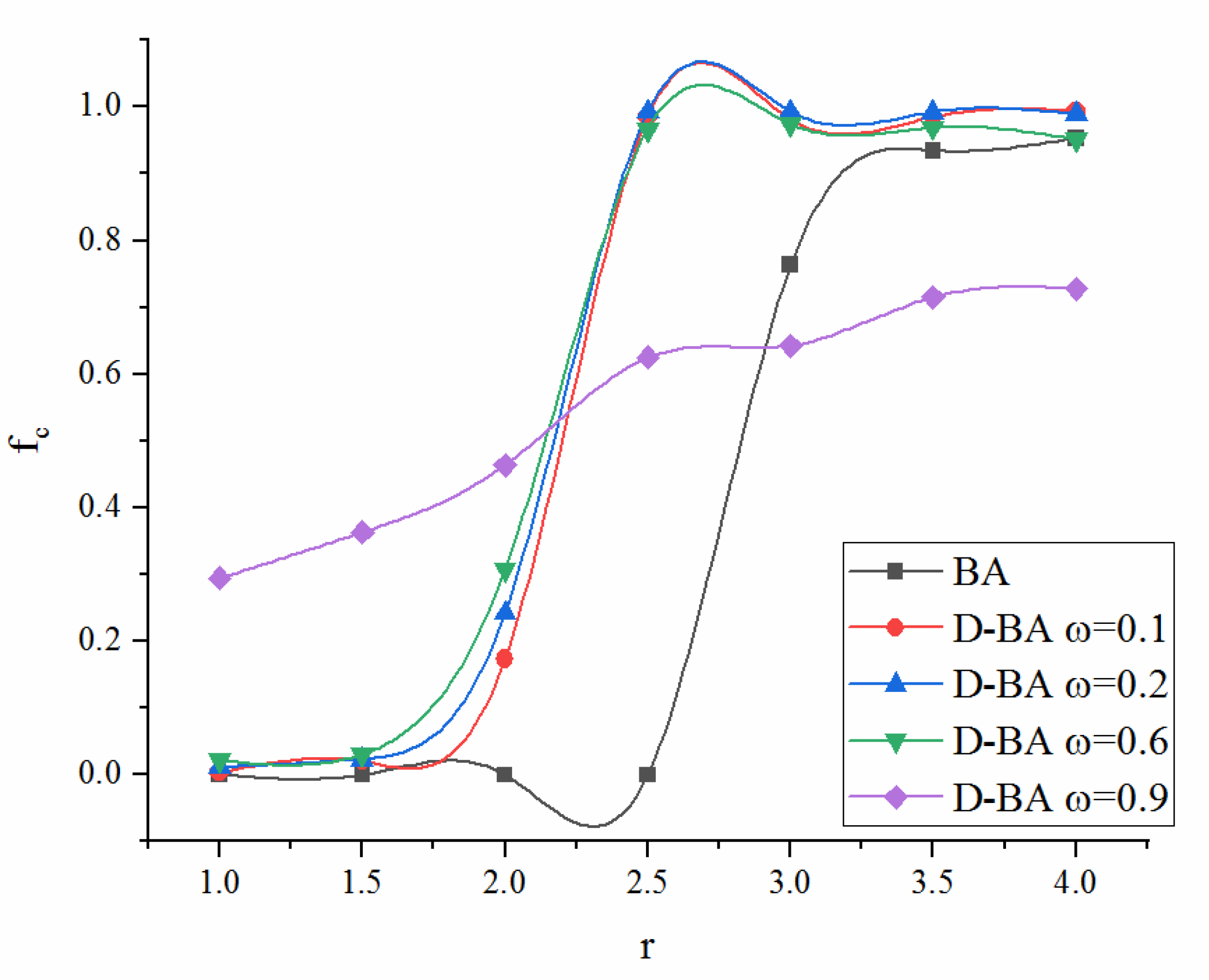
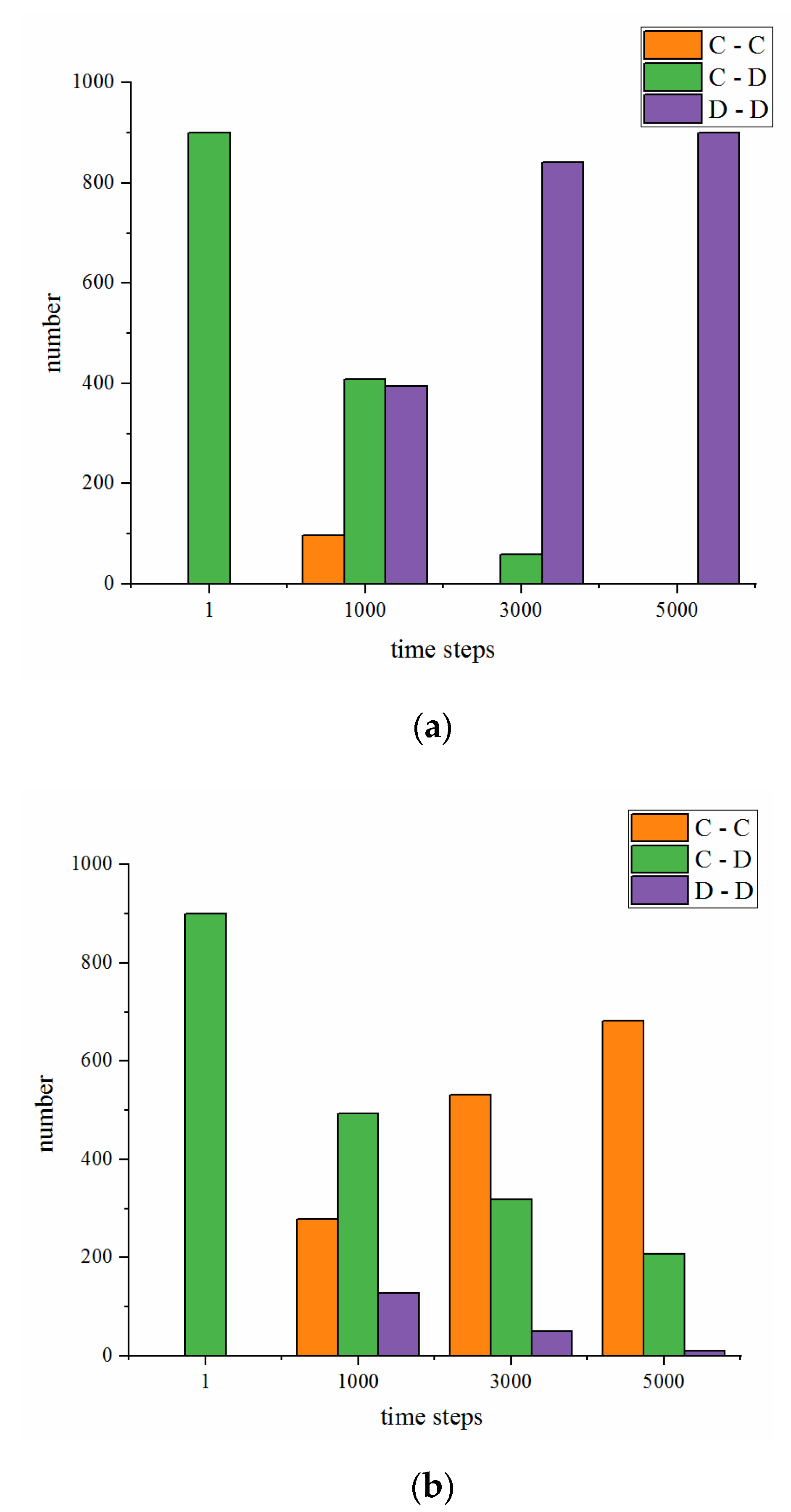
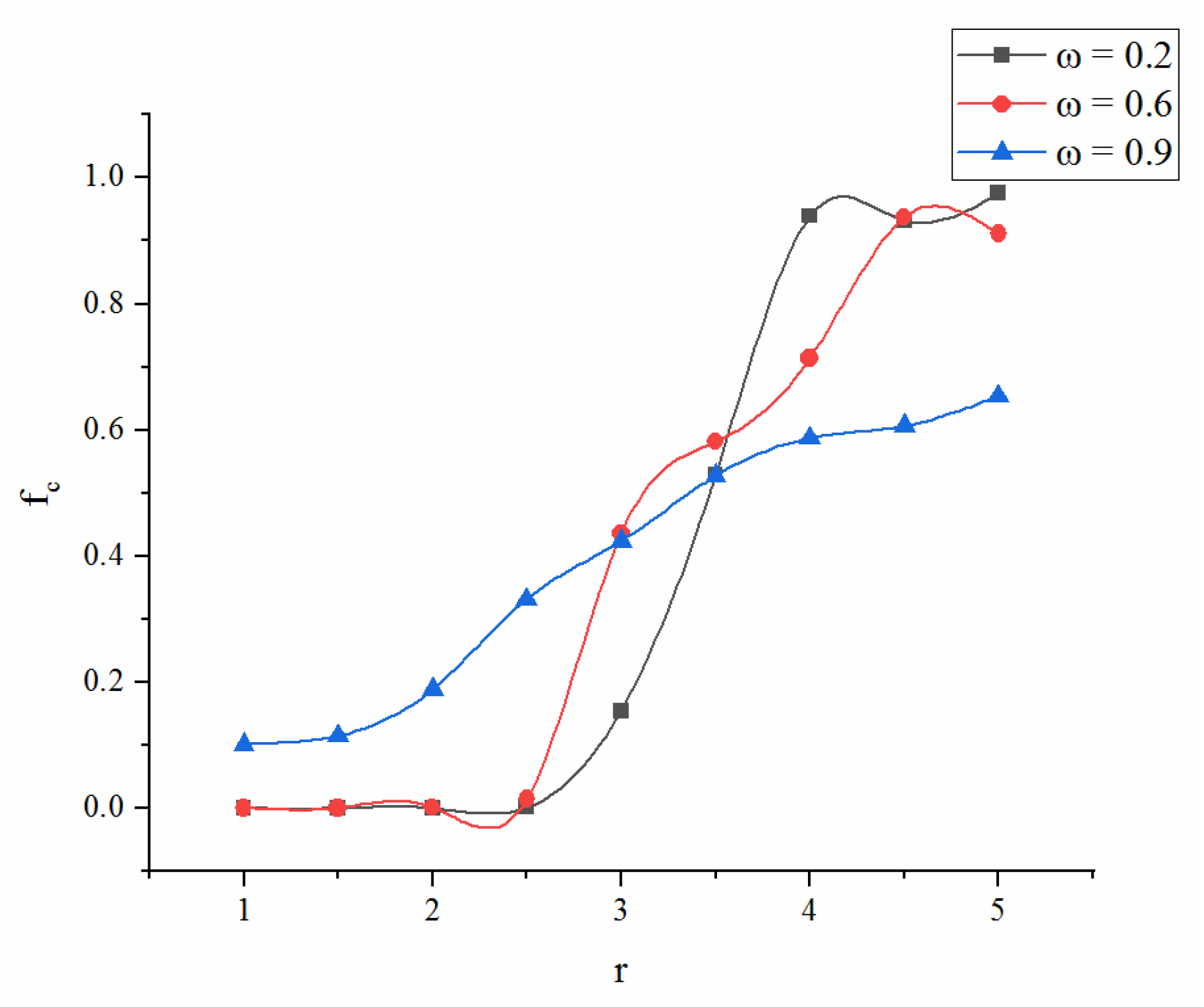
4.1.1. Comparison of the Single-layer and Double-layer Networks
4.1.2. Exploring Cooperation in Double-layer Network
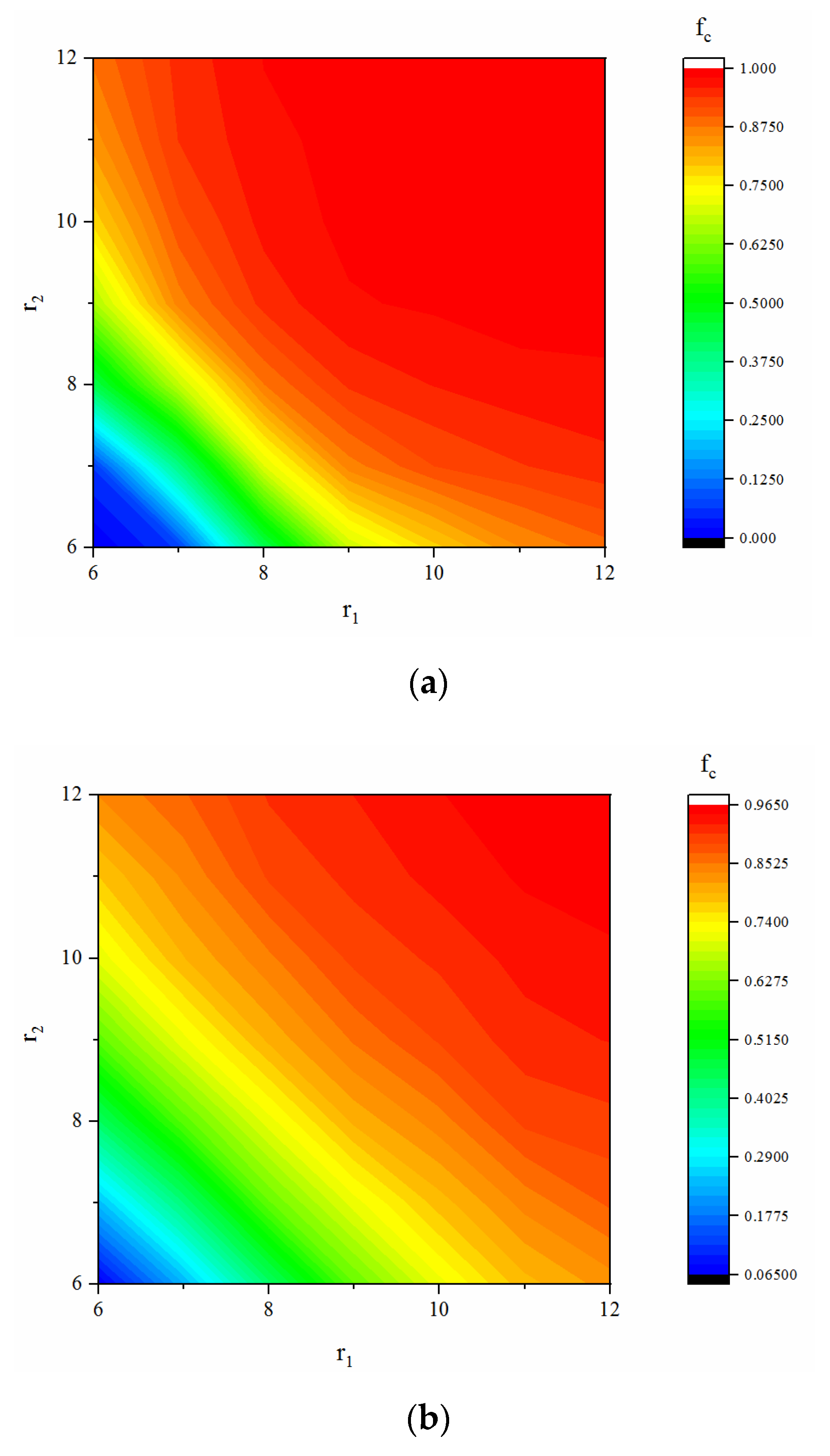
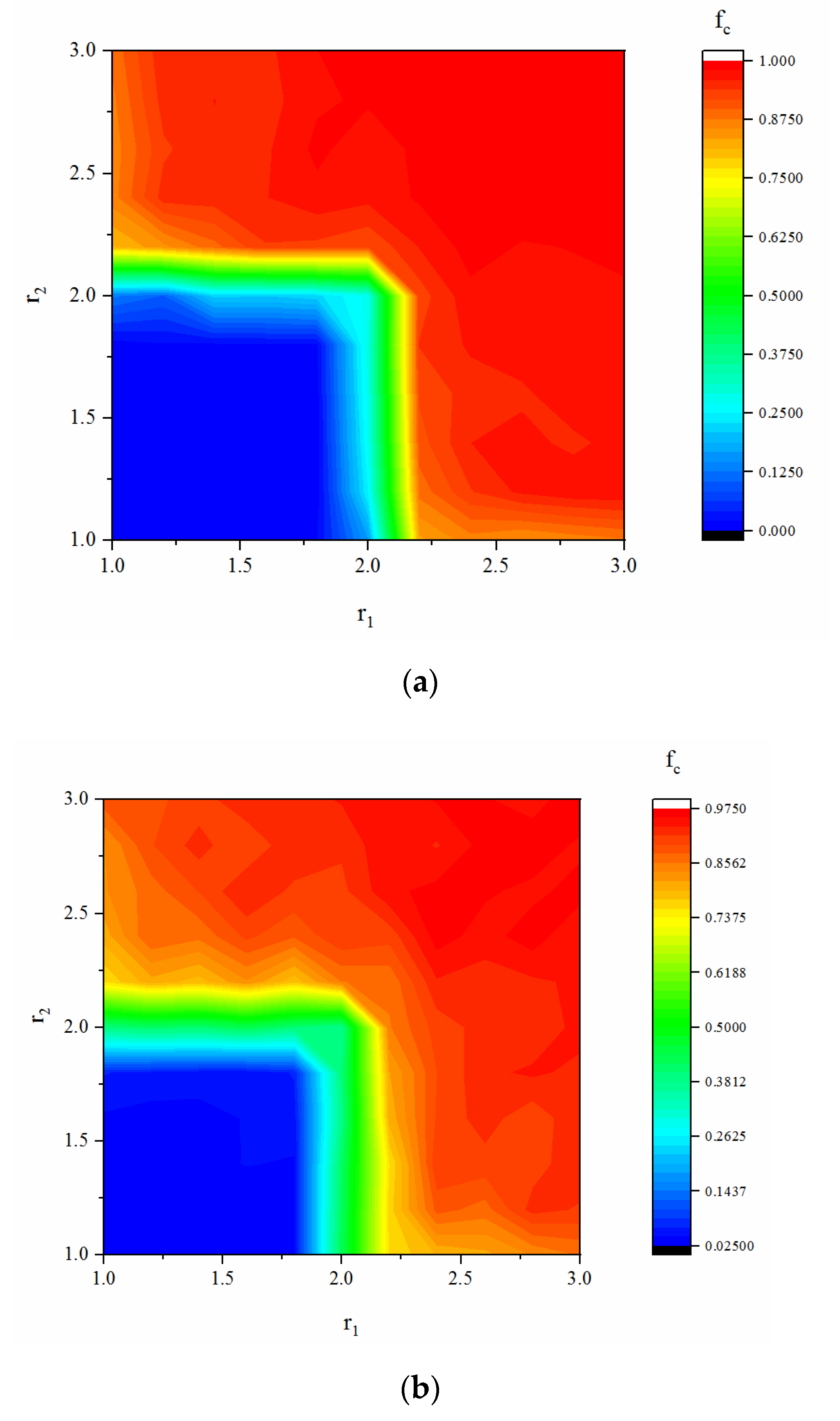
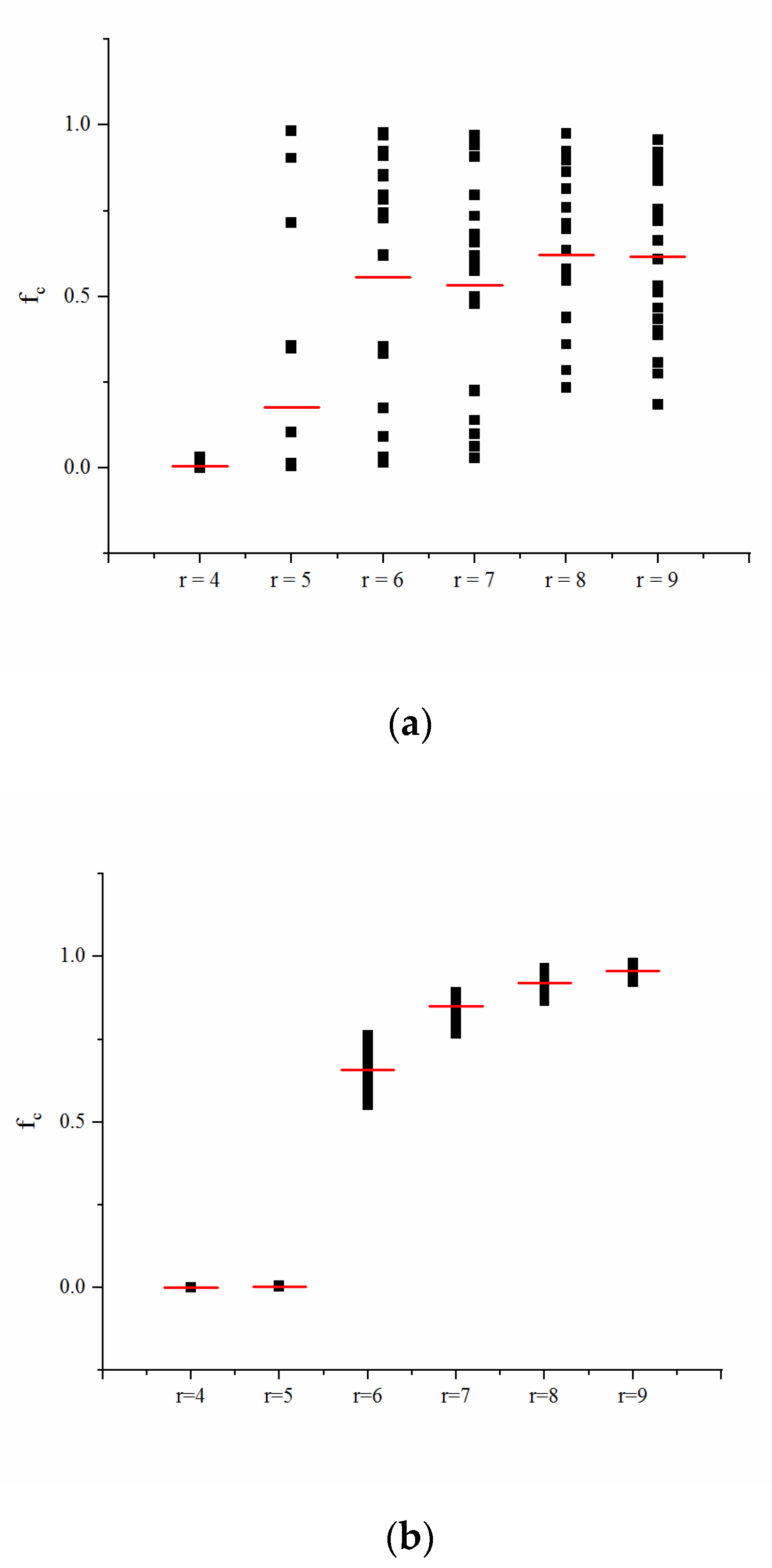
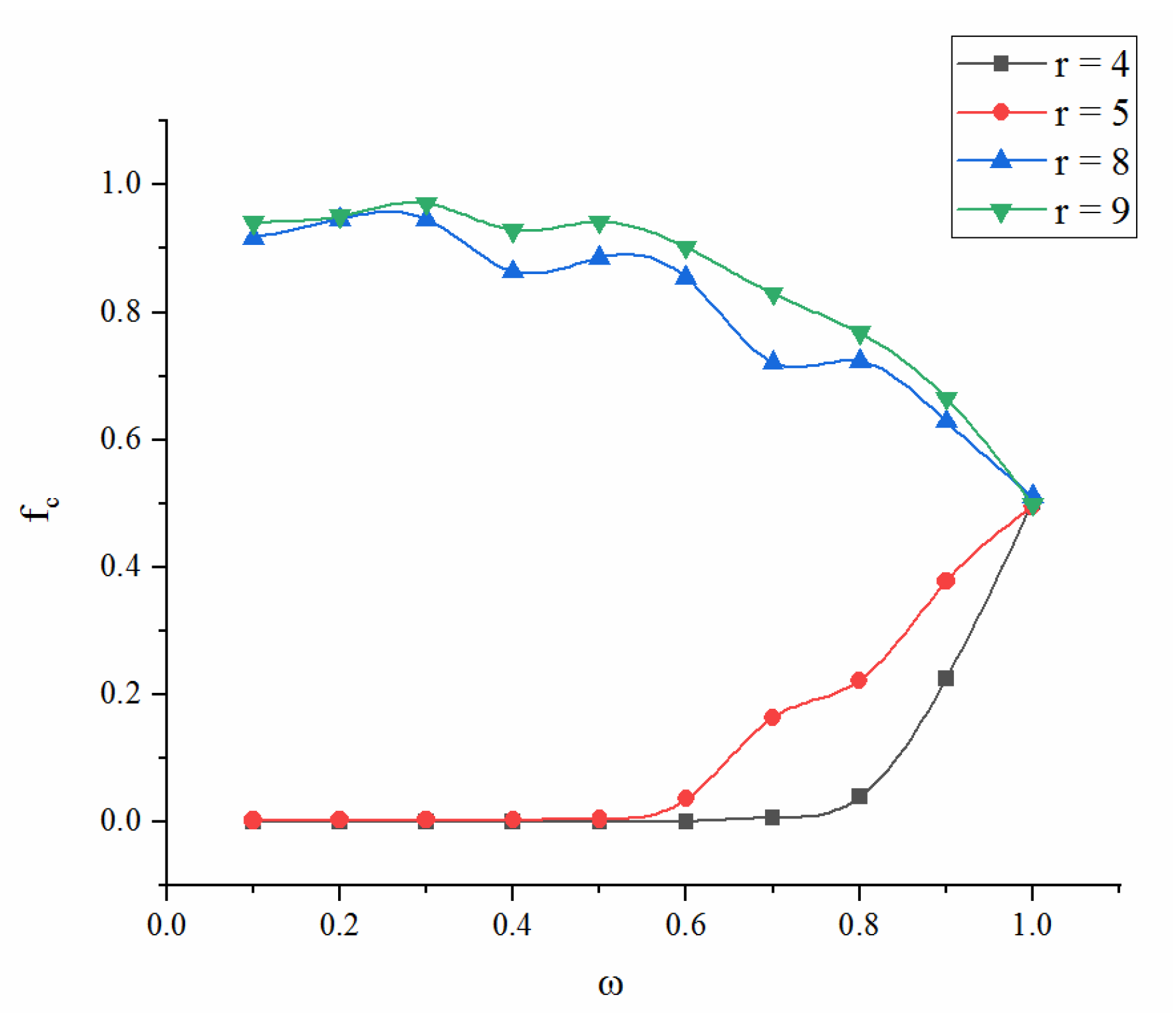
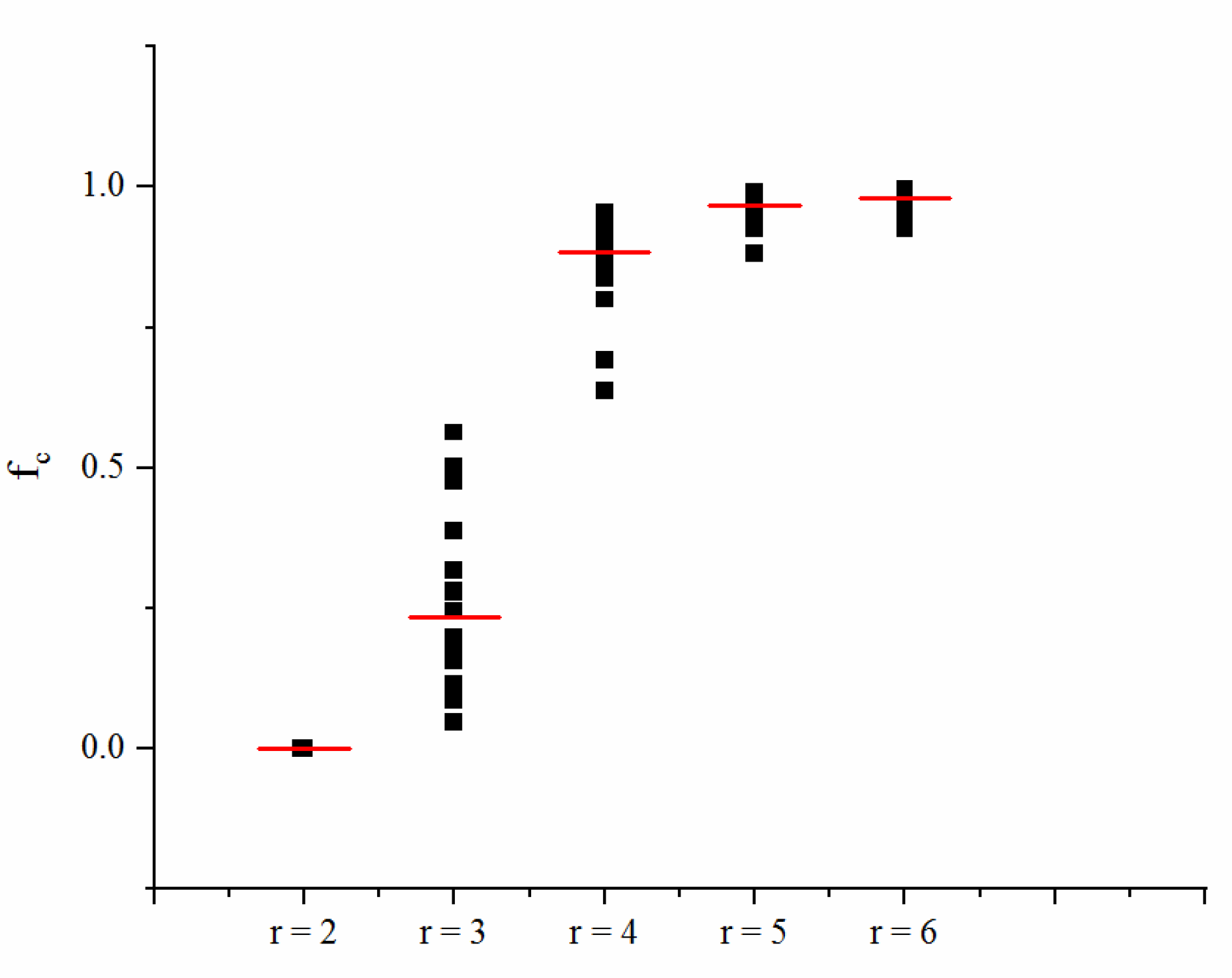
4.1.3. Influence of the other Network Parameters on Cooperation
4.1.4. Exploration of Coordinated Development of the Double-layer Network
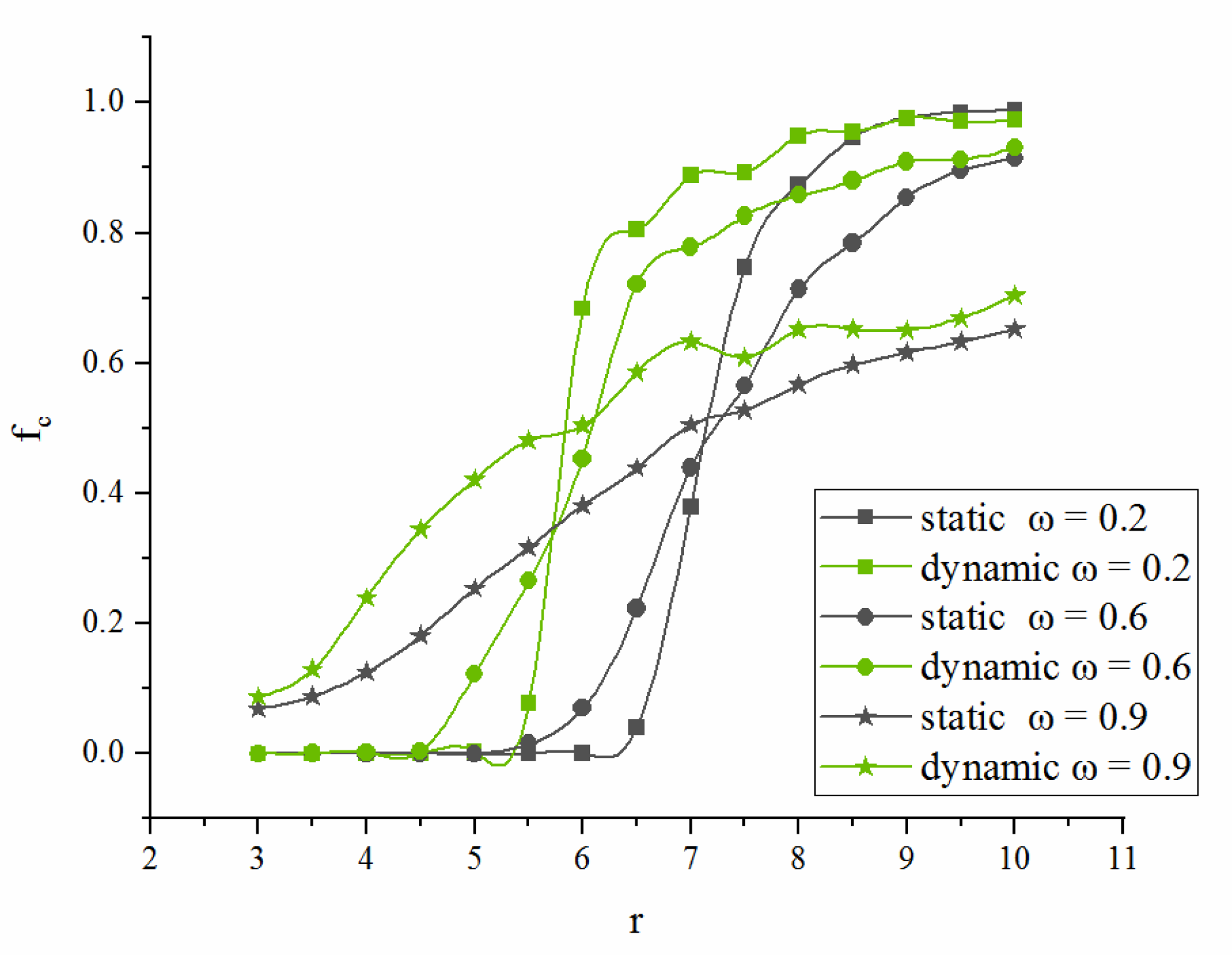
4.2. PGG-SP on the Dynamic Network
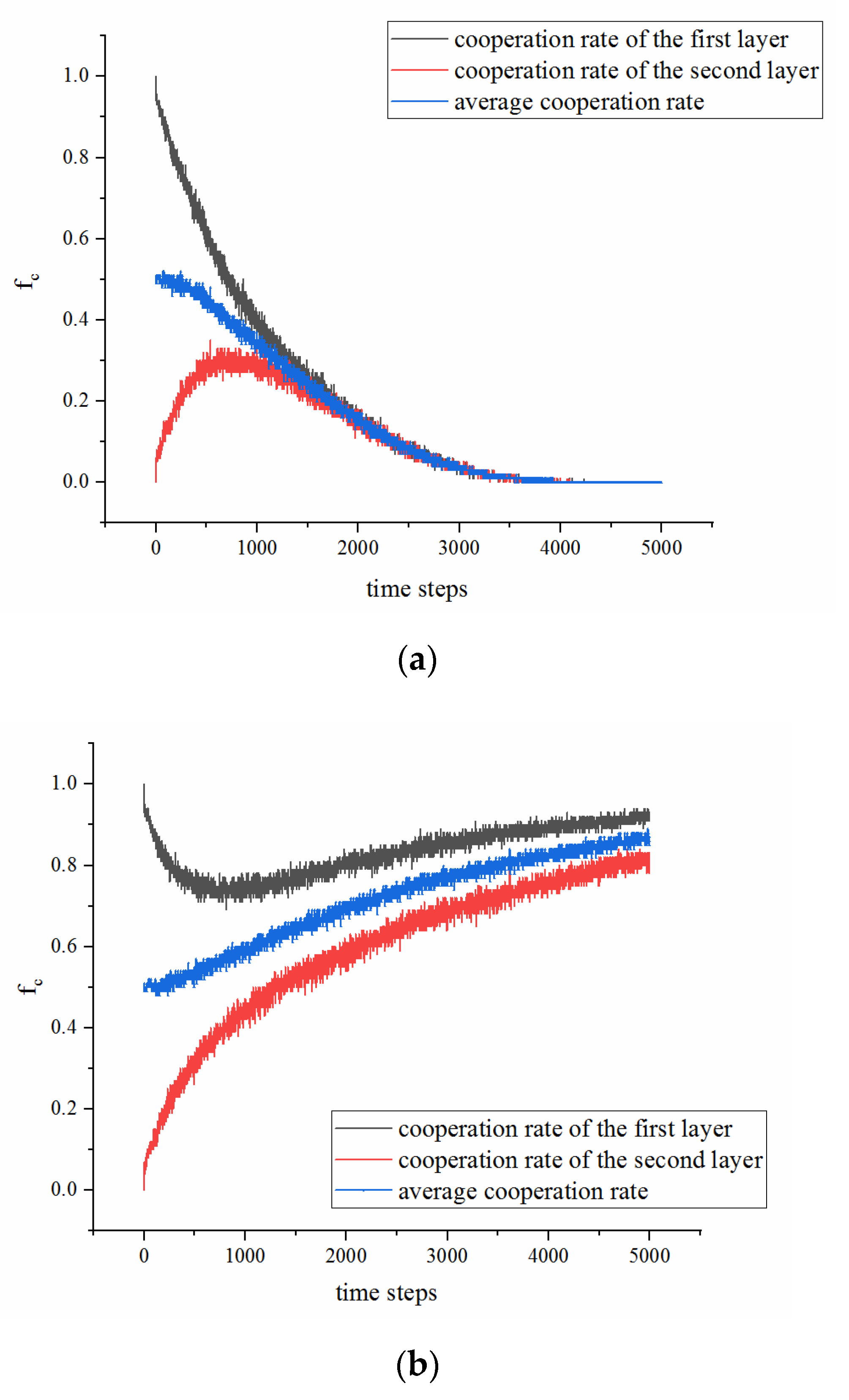
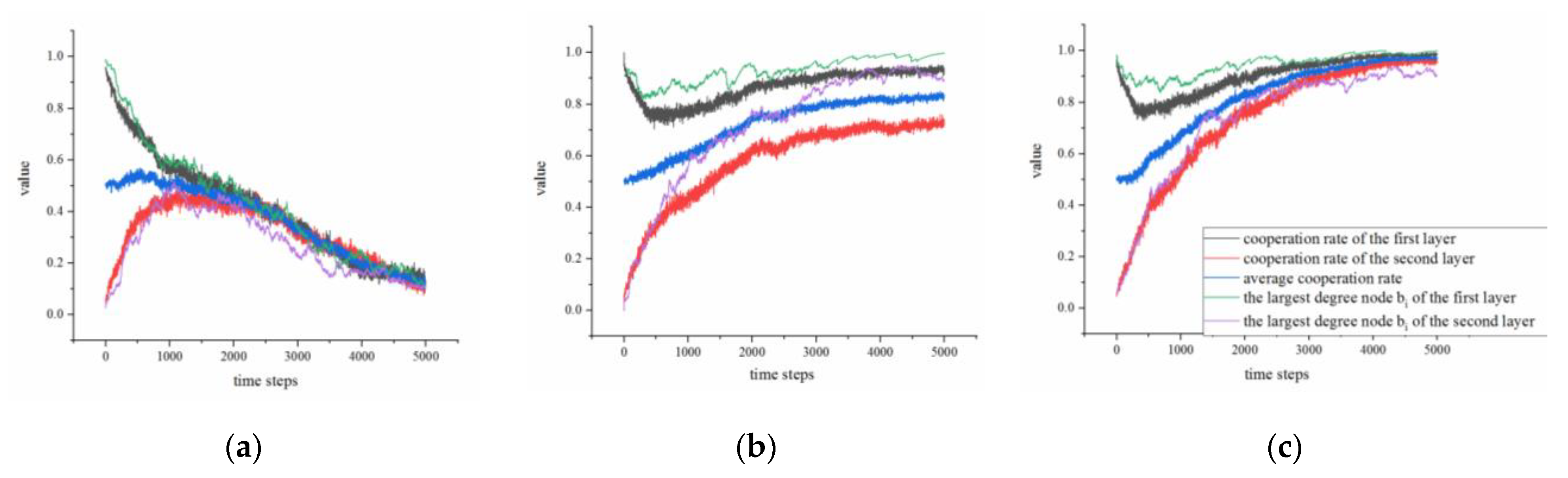
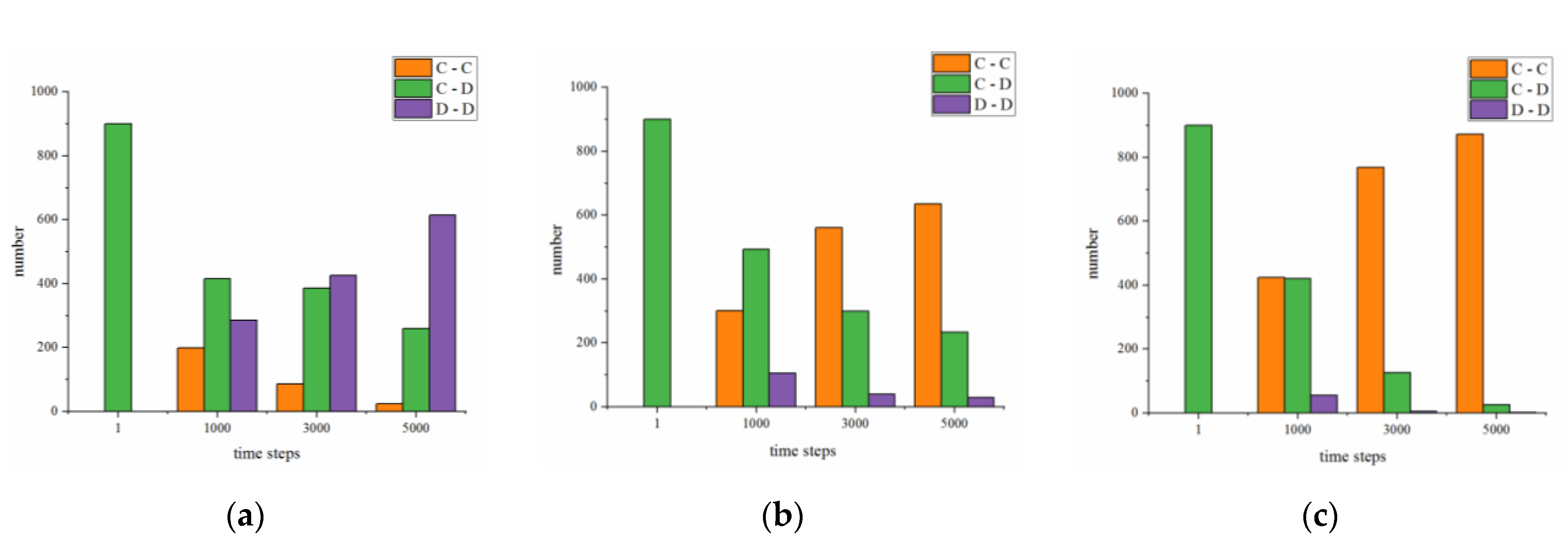
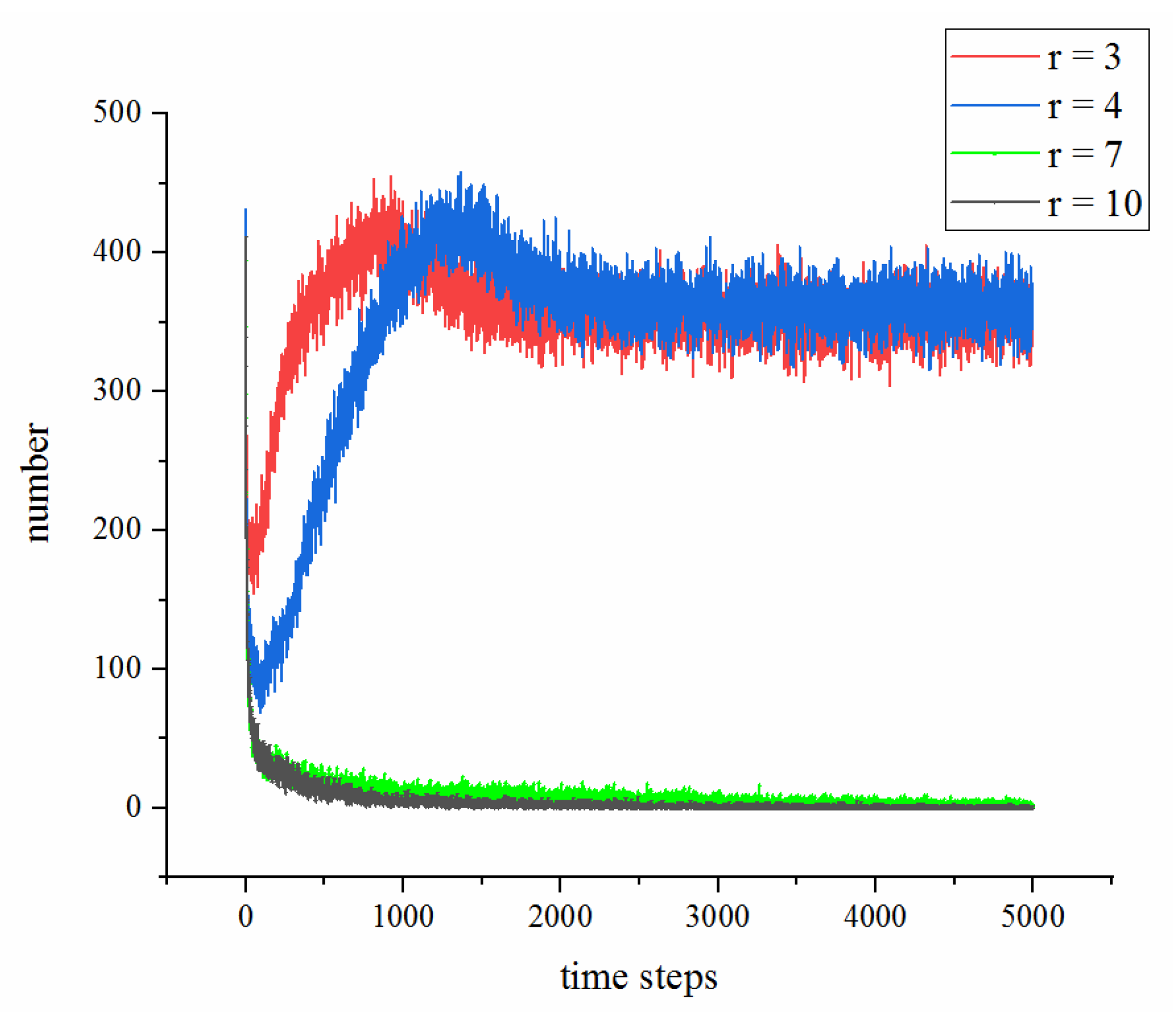
4.2.1. Comparison of the Static and Dynamic Double-layer Networks
4.2.2. Comparison of the Dynamic Single-layer and Double-layer NW Networks
4.2.3. Performance of the Dynamic Double-layer NW Network
4.2.4. Simulating Real-world Dynamic Double-layer Networks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2001, 74, 47–97. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Chen, Y.; Niu, X. A Privacy Measurement Framework for Multiple Online Social Networks against Social Identity Linkage. Appl. Sci. 2018, 8, 1790. [Google Scholar] [CrossRef]
- Pilosof, S.; Porter, M.A.; Pascual, M.; Kefi, S. The multilayer nature of ecological networks. Nat. Ecol. Evol. 2017, 1, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Rao, X.; Zhao, J.; Chen, Z.; Lin, F. Substitute Seed Nodes Mining Algorithms for Influence Maximization in Multi-Social Networks. Future Internet 2019, 11, 112. [Google Scholar] [CrossRef]
- Wang, C.; Wang, G.; Luo, X.; Li, H. Modeling rumor propagation and mitigation across multiple social networks. Phys. Stat. Mech. Appl. 2019, 535, 122240. [Google Scholar] [CrossRef]
- Jiang, C.; Zhu, X. Reinforcement Learning Based Capacity Management in Multi-Layer Satellite Networks. IEEE Trans. Wirel. Commun. 2020, 19, 4685–4699. [Google Scholar] [CrossRef]
- Guazzini, A.; Duradoni, M.; Lazzeri, A.; Gronchi, G. Simulating the Cost of Cooperation: A Recipe for Collaborative Problem-Solving. Future Internet 2018, 10, 55. [Google Scholar] [CrossRef]
- Fehr, E.; Fischbacher, U. The nature of human altruism. Nature 2003, 425, 785–791. [Google Scholar] [CrossRef]
- Moore, A.D.; Martin, S. Privacy, transparency, and the prisoner’s dilemma. Ethics Inf. Technol. 2020, 22, 211–222. [Google Scholar] [CrossRef]
- Ramazi, P.; Cao, M. Global Convergence for Replicator Dynamics of Repeated Snowdrift Games. IEEE Trans. Autom. Control. 2021, 66, 291–298. [Google Scholar] [CrossRef]
- Buyukboyaci, M. Risk attitudes and the stag-hunt game. Econ. Lett. 2014, 124, 323–325. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Xu, Z.; Zhang, C. Evolutionary Dynamics of Strategies without Complete Information on Complex Networks. Asian J. Control 2018, 22, 362–372. [Google Scholar] [CrossRef]
- Lu, R.; Yu, W.; Lü, J.; Xue, A. Synchronization on Complex Networks of Networks. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 2110–2118. [Google Scholar] [CrossRef] [PubMed]
- Kibangou, A.Y.; Commault, C. Observability in Connected Strongly Regular Graphs and Distance Regular Graphs. IEEE Trans. Control. Netw. Syst. 2014, 1, 360–369. [Google Scholar] [CrossRef]
- Erdos, P.; Renyi, A. On the evolution of random graphs. Bull. Int. Stat. Inst. 1960, 38, 343–347. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- BArabási, A.L.; Albert, R. Emergence of Scaling in Random Network. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Watts, D.J. Renormalization group analysis of the small-world network model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
- Galbiati, R.; Vertova, P. Obligations and cooperative behaviour in public good games. Games Econ. Behav. 2008, 64, 146–170. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Szolnoki, A.; Perc, M. Evolutionary games on multilayer networks: A colloquium. Eur. Phys. J. B 2015, 88, 124. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R.; del Genio, C.I.; Gómez-Gardeñes, J.; Romance, M.; Sendiña-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef] [PubMed]
- Gulati, R.; Sytch, M.; Tatarynowicz, A. The rise and fall of small worlds: Exploring the dynamics of social structure. Organ. Sci. 2012, 23, 449–471. [Google Scholar] [CrossRef]
- Shen, C.; Chu, C.; Guo, H.; Shi, L.; Duan, J. Coevolution of Vertex Weights Resolves Social Dilemma in Spatial Networks. Sci. Rep. 2017, 7, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Xia, C.; Wang, J. Coevolution of network structure and cooperation in the public goods game. Phys. Scr. 2013, 87, 055001. [Google Scholar] [CrossRef]
- Li, Y.; Shen, B. The coevolution of partner switching and strategy updating in non-excludable public goods game. Phys. A 2013, 392, 4956–4965. [Google Scholar] [CrossRef]
- Liu, X.; Wang, S.; Ji, H. Double-layer P2P networks supporting semantic search and keeping scalability. Int. J. Commun. Syst. 2015, 27, 3956–3970. [Google Scholar] [CrossRef]
- Duh, M.; Gosak, M.; Slavinec, M.; Perc, M. Assortativity provides a narrow margin for enhanced cooperation on multilayer networks. New J. Phys. 2019, 21, 123016. [Google Scholar] [CrossRef]
- Nowak, M.A. Five Rules for the Evolution of Cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef]
- Hardin, G. The Tragedy of the Commons. Science 1969, 162, 1243–1248. [Google Scholar]
- Sinha, A.; Anastasopoulos, A. Distributed Mechanism Design with Learning Guarantees for Private and Public Goods Problems. IEEE Trans. Autom. Control 2020, 65, 4106–4121. [Google Scholar] [CrossRef]
- Fang, Y.; Benko, T.P.; Perc, M.; Xu, H.; Tan, Q. Synergistic third-party rewarding and punishment in the public goods game. Proc. R. Soc. A. 2019, 475, 20190349. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Cui, Z.; Yue, X. Cluster evolution in public goods game with fairness mechanism. Phys. A 2019, 532, 121796. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Z.; Wu, Y.; Yan, M.; Xie, Y. Tolerance-based punishment and cooperation in spatial public goods game. Chaos Soliton Fract. 2018, 110, 267–272. [Google Scholar] [CrossRef]
- Quan, J.; Yang, W.; Li, X.; Wang, X.; Yang, J. Social exclusion with dynamic cost on the evolution of cooperation in spatial public goods games. Appl. Math. Comput. 2020, 372, 124994. [Google Scholar] [CrossRef]
- Li, K.; Cong, R.; Wu, T.; Wang, L. Social exclusion in finite populations. Phys. Rev. E 2015, 91, 042810. [Google Scholar] [CrossRef]
- Szolnoki, A.; Chen, X. Alliance formation with exclusion in the spatial public goods game. Phys. Rev. E 2017, 95, 052316. [Google Scholar] [CrossRef]
- İriş, D.; Lee, J.; Tavoni, A. Delegation and Public Pressure in a Threshold Public Goods Game. Environ. Resour. Econ. 2019, 74, 1331–1353. [Google Scholar] [CrossRef]
- Li, P.P.; Ke, J.; Lin, Z.; Hui, P.M. Cooperative behavior in evolutionary snowdrift games with the unconditional imitation rule on regular lattices. Phys. Rev. E 2012, 85, 021111. [Google Scholar] [CrossRef]
- Santos, F.C.; Pacheco, J.M. Scale-Free Networks Provide a Unifying Framework for the Emergence of Cooperation. Phys. Rev. Lett. 2005, 95, 098104. [Google Scholar] [CrossRef]
- Gyorgy, S.; Toke, C. Evolutionary prisoner’s dilemma game on a square lattice. Phys. Rev. E 1998, 58, 69–73. [Google Scholar]
- Sarkar, B. Moran-evolution of cooperation: From well-mixed to heterogeneous complex networks. Phys. A 2018, 497, 319–334. [Google Scholar] [CrossRef]
- Wang, Z.; Szolnoki, A.; Perc, M. Interdependent network reciprocity in evolutionary games. Sci. Rep. 2013, 3, 1183. [Google Scholar] [CrossRef] [PubMed]
- Nag Chowdhury, S.; Kundu, S.; Duh, M.; Perc, M.; Ghosh, D. Cooperation on Interdependent Networks by Means of Migration and Stochastic Imitation. Entropy 2020, 22, 485. [Google Scholar] [CrossRef] [PubMed]
- Szolnoki, A.; Perc, M. Reward and cooperation in the spatial public goods game. Europhys. Lett. EPL 2010, 92, 38003. [Google Scholar] [CrossRef]
- Szabó, G.; Fáth, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Strogatz, S. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Milgram, S. The small world problem. Psychol. Today 1967, 2, 60–67. [Google Scholar]







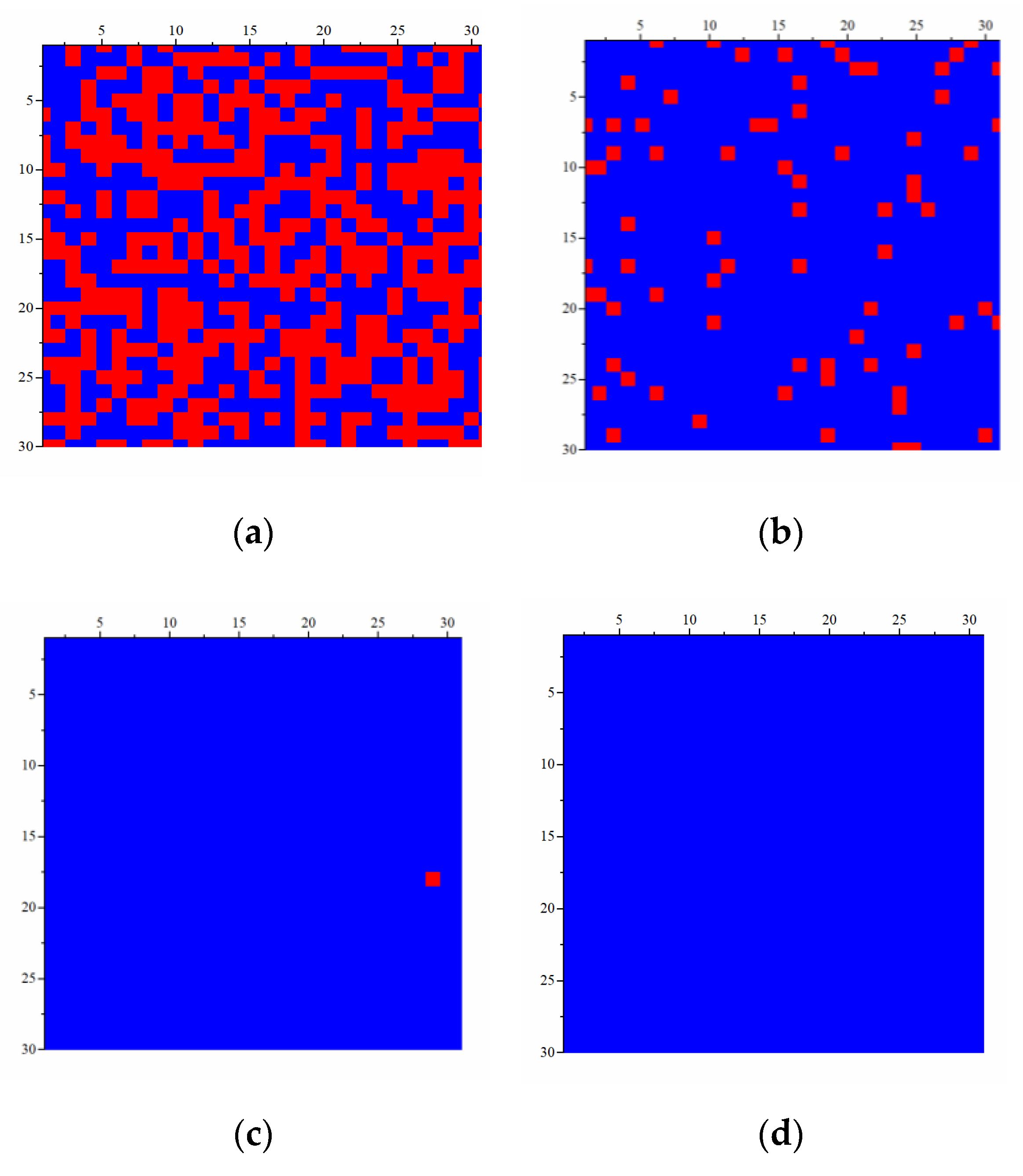

| Parameter | Meaning | Default Value |
|---|---|---|
| Influence factor | 0.01 | |
| k | Influence factor | 0.1 |
| T | The probability of reconnection edge | 0.5 |
| N | Network size | 900 |
| p | The edge addition probability in the NW network | |
| The number of edges added per time step in the BA network | ||
| Learning probability for different layers | ||
| r | Average enhancement factor | |
| Enhancement factor of the first layer network | ||
| Enhancement factor of the second layer network | ||
| Fraction of cooperators |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Fu, M.; Li, H. Cooperation in Social Dilemmas: A Group Game Model with Double-Layer Networks. Future Internet 2021, 13, 33. https://doi.org/10.3390/fi13020033
Guo D, Fu M, Li H. Cooperation in Social Dilemmas: A Group Game Model with Double-Layer Networks. Future Internet. 2021; 13(2):33. https://doi.org/10.3390/fi13020033
Chicago/Turabian StyleGuo, Dongwei, Mengmeng Fu, and Hai Li. 2021. "Cooperation in Social Dilemmas: A Group Game Model with Double-Layer Networks" Future Internet 13, no. 2: 33. https://doi.org/10.3390/fi13020033
APA StyleGuo, D., Fu, M., & Li, H. (2021). Cooperation in Social Dilemmas: A Group Game Model with Double-Layer Networks. Future Internet, 13(2), 33. https://doi.org/10.3390/fi13020033






