Underwater Target Recognition Based on Multi-Decision LOFAR Spectrum Enhancement: A Deep-Learning Approach
Abstract
:1. Introduction
1.1. Contributions
- (1)
- In contrast to the traditional algorithm, we use the decomposition algorithm based on resonance signal to preprocess the signal. Based on the multi-step decision algorithm with the line spectrum characteristic cost function [4], this paper proposes the specific calculation method of double threshold. In the purpose, this algorithm not only retains the continuous spectrum information in the original LOFAR spectrum, but also merges the extracted line spectrum with the original LOFAR spectrum. Finally, the breakpoint completion of the LOFAR spectrum is realized.
- (2)
- To further improve the recognition rate of underwater targets, we adopt the enhanced LOFAR spectrum as the input of CNN and develop a LOFAR-based CNN (LOFAR-CNN) for online recognition. Taking advantage of the powerful capability of CNN in feature extraction, the proposed LOFAR-CNN can further improve the recognition accuracy.
- (3)
- Simulation results demonstrate that when testing on the ShipsEar database [5], our proposed LOFAR-CNN method can achieve a recognition accuracy of 95.22% which outperforms the state-of-the-art methods.
1.2. Related Works
1.3. Organization
2. System Model
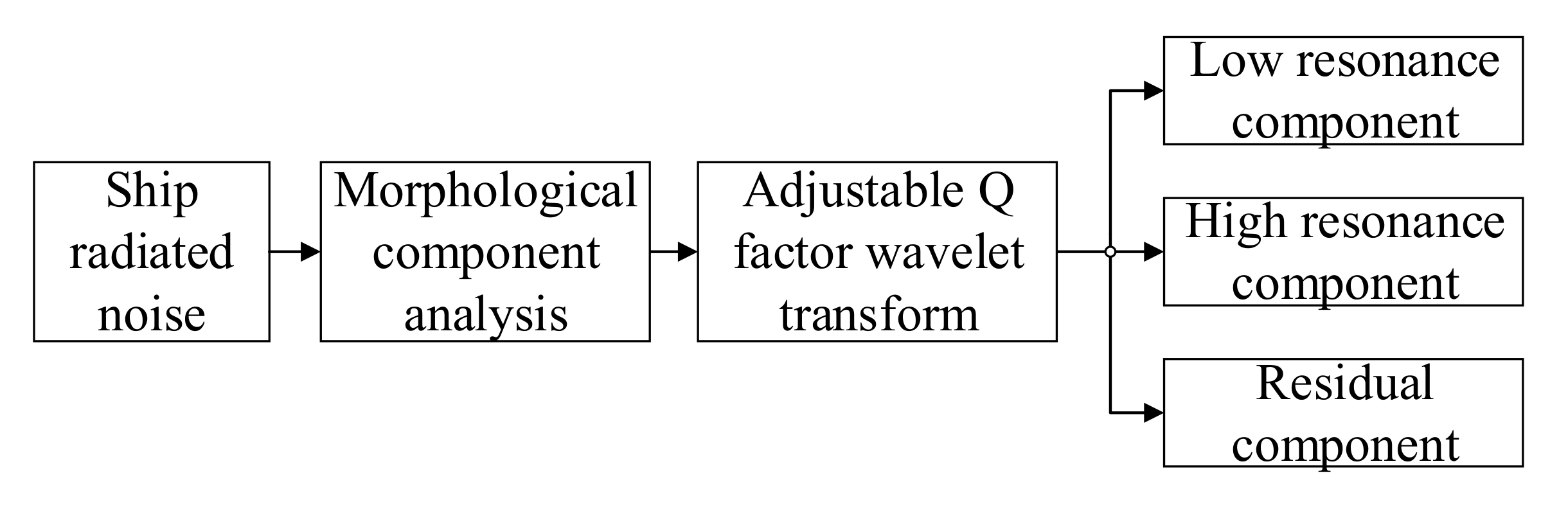
2.1. Signal Decomposition Algorithm Based on Resonance
2.1.1. Morphological Component Analysis
- (1)
- Select the appropriate filter scaling factor , according to the waveform characteristics of the signal. Then calculate the parameters , , corresponding to the high-resonance component, and the parameters , , corresponding to the low-resonance component. At last, construct the corresponding wavelet basis function , .
- (2)
- Reasonably set the weighting coefficient , of the L1 norm of the wavelet coefficients of each layer. Obtain the optimal wavelet coefficient , by minimizing the objective function through the SALSA algorithm.
- (3)
- Reconstruct the optimal sparse representation , of high-resonance components and low-resonance components.
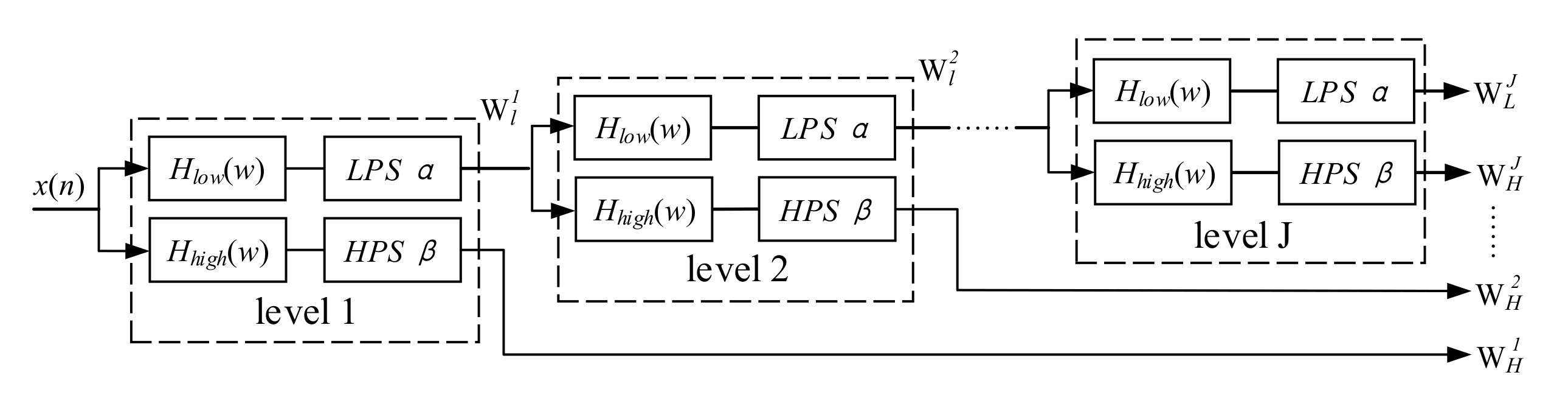
2.1.2. Adjustable Q-Factor Wavelet Transform
3. LOFAR Spectral Line Enhancement Based on Multi-Step Decision
3.1. Structure LOFAR Spectrum
- (1)
- Framing and windowing. The sound signal is unstable globally, but can be regarded as stable locally. In the subsequent speech processing, a stable signal needs to be input. Therefore, it is necessary to frame the entire speech signal, i.e., to divide it into multiple segments. We divide the sampling sequence of the signal into K frames and each frame contains N sampling points. The larger the N and K, the larger the amount of data, and the closer the final result is to the true value. Due to the correlation between the frames, there are usually some points overlap between the two frames. Framing is equivalent to truncating the signal, which will cause distortion of its spectrum and leakage of its spectral energy. To reduce spectral energy leakage, different truncation functions which are called window function can be used to truncate the signal. The practical application window functions include Hamming window, rectangular window and Hanning window, etc.
- (2)
- Normalization and decentralization. The signal of each frame needs to be normalized and decentralized, which can be calculated by the following formula:Here, is the normalization of , which makes the power of the signal uniform in time. is the decentralization of , which makes the mean of the samples zero.
- (3)
- Perform Fourier transform on each frame signal and arrange the transformed spectrum in the time domain to obtain the LOFAR spectrum.
3.2. Analysis and Construction of Line Spectrum Cost Function
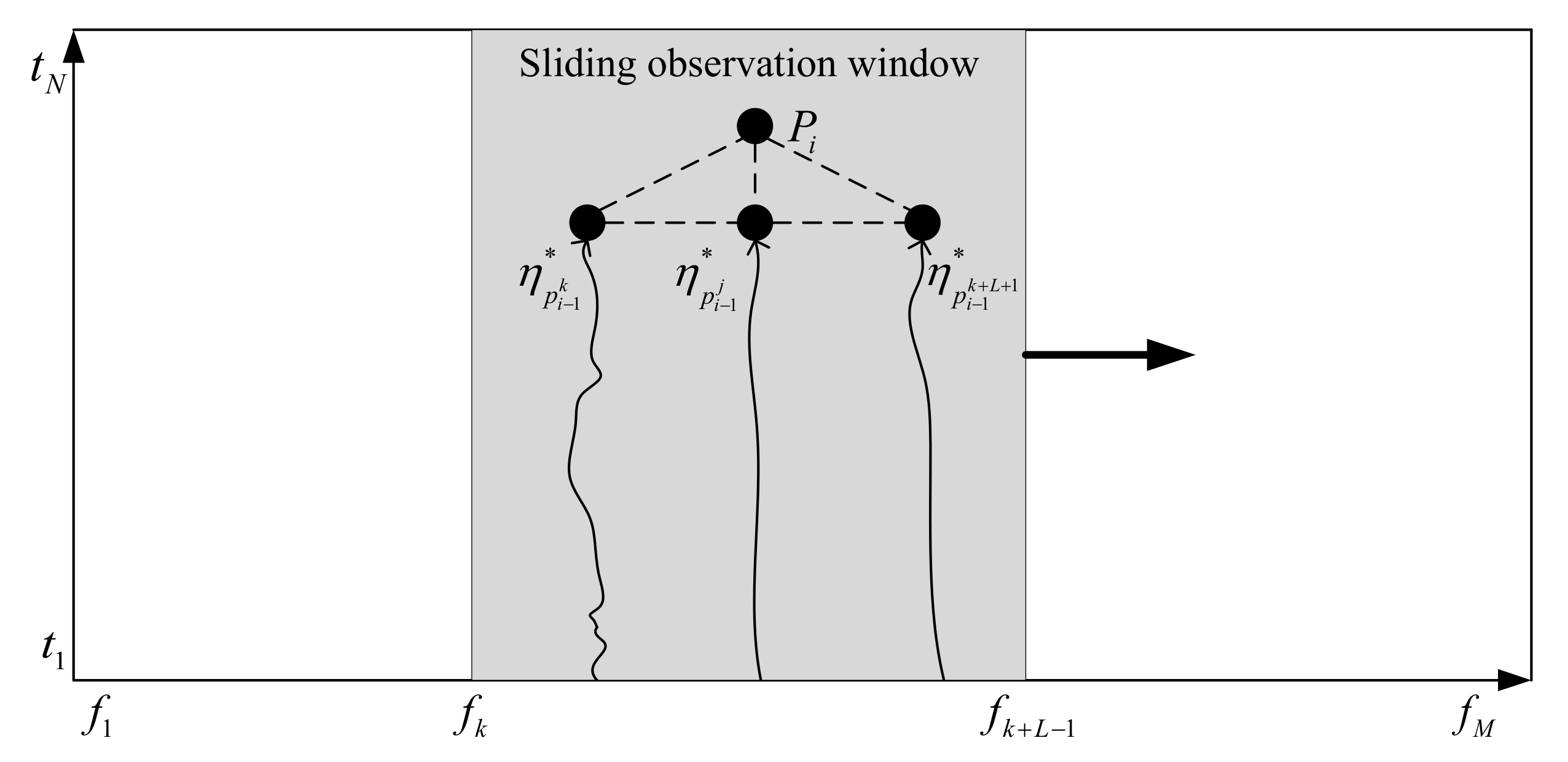
3.3. Sliding Window Line Spectrum Extraction Algorithm Based on Multi-Step Decision
- (1)
- The length of the frequency axis in the LOFAR spectrums M. The start point is , and the end point is . The length of the time axis is N. The start point is , and the end points . The search window size is defined as L.
- (2)
- Each point in the figure is defined as , representing the time-frequency pixel on the jth column on the frequency axis and the ith row on the time axis, where , . represents the optimal path from to in the observation window, defines as a set of ternary vectors for points , and the triplet of each point at is initialized to .
- (3)
- From to , find the optimal path with length from 2 to N in the search window line by line. In the figure, is set to any point in , the start position of the observation window is , and the corresponding end position is . At , the neighboring L points of form a set as follows, , the optimal path to the length i of the point is obtained from the optimal path of , i.e., , where satisfies:where represents the set of points .
- (4)
- At , the optimal path of the k points in the search window is , where , then the optimal path of length N in the search window is:
- (5)
- Set a counter for each time-frequency point in the LOFAR spectrum, and the counter value is initialized to 0. If the value of the objective function corresponding to the optimal path in the search window is greater than the threshold , we would consider that there is a line spectrum on the optimal path, and the counter values corresponding to the N points on the optimal path are increased by 1 respectively. The specific steps of threshold calculation are as follows:First, the input of the algorithm is changed from the LOFAR spectrum of ship radiation noise to the LOFAR spectrum of marine environmental noise. The corresponding cost function of the optimal path in the observation window is obtained, where then the threshold is:
- (6)
- Slide the search window with a step size of 1. Repeat the above steps until the observation window slides to the end. The output count value graph is the traced line spectrum.
4. Underwater Target-Recognition Framework Based on CNN
5. Numerical Results
5.1. Source of Experimental Data
5.2. Experimental Software and Hardware Platform
5.3. Multi-Step Decision LOFAR Line Spectrum Enhancement Algorithm Validity Test
5.4. Experimental Verification of Underwater Target Recognition Based on Convolutional Neural Network (CNN)
5.4.1. CNN Network Offline Training Process
- (1)
- Read the high-resonance component signals in sequence, then windowing and framing the signal. We choose Hanning window (Hanning), and the window size is 2048 (i.e., FFT points are 2048). The overlap between frames is 75%.
- (2)
- The signal of each frame is normalized and decentralized. The power of the signal is uniform in time and the average value of the sample is 0. It means the data are limited to a certain range, which can eliminate singular sample data. At the same time, it can also avoid the saturation of neurons and accelerate the convergence rate of the network.
- (3)
- First, perform Fourier transform on each frame signal. Second, take the logarithmic amplitude spectrum of the transformed spectrum and arrange it in the time domain. Last, take 64 points on the time axis as a sample, which means obtaining a size of LOFAR spectrum sample. The sampling frequency of audio is 52,734 Hz, and the duration of each sample is about s. The numbers of training and testing sets of various samples are shown in Table 6. The ID in the table is the label of the audio in the ShipsEar database. The corresponding type of ship for each segment can be obtained according to the ID. The type of ship corresponding to audio is used as a label for supervised learning of deep neural networks.
- (4)
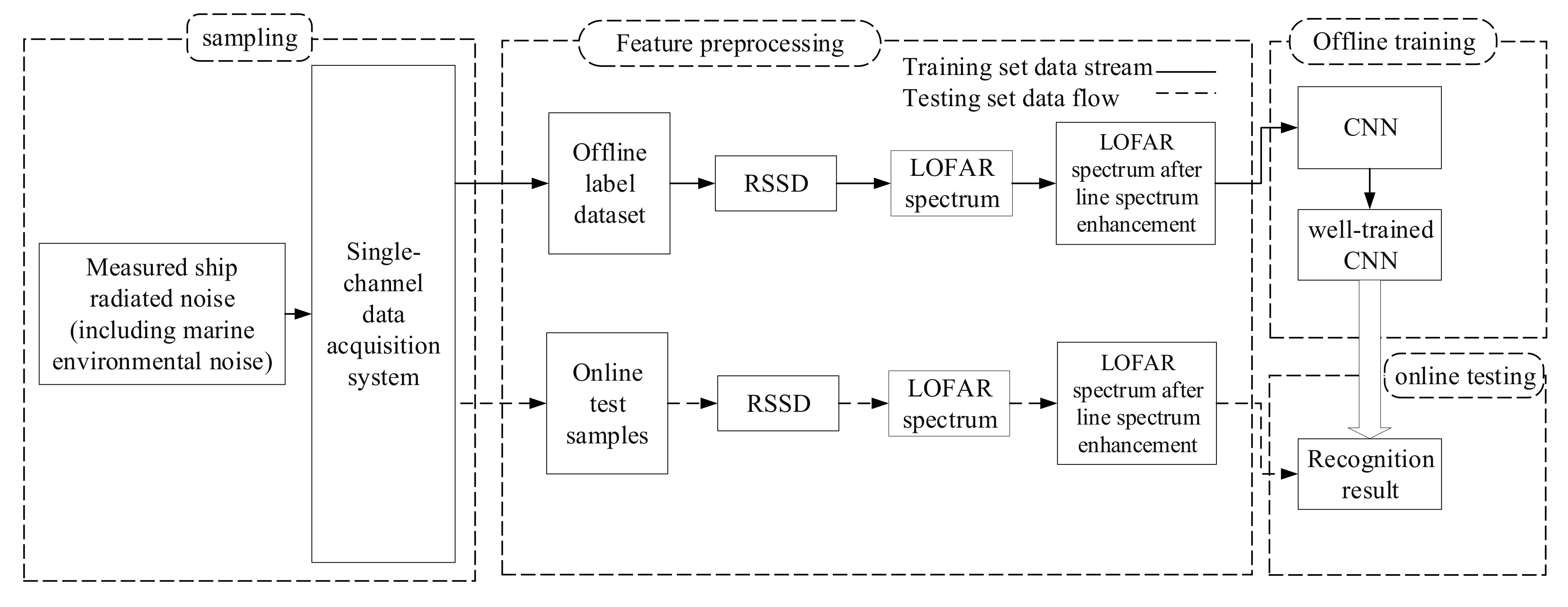
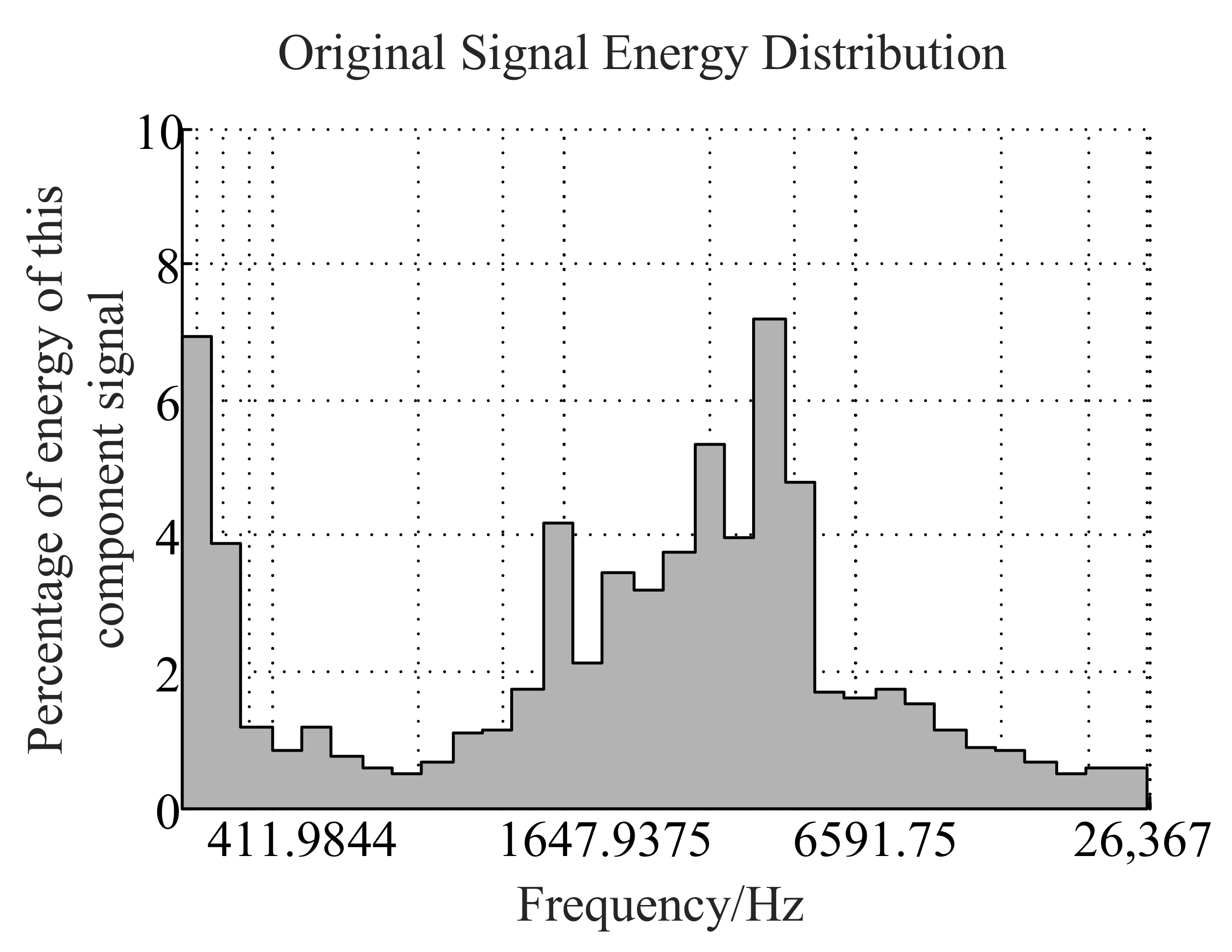
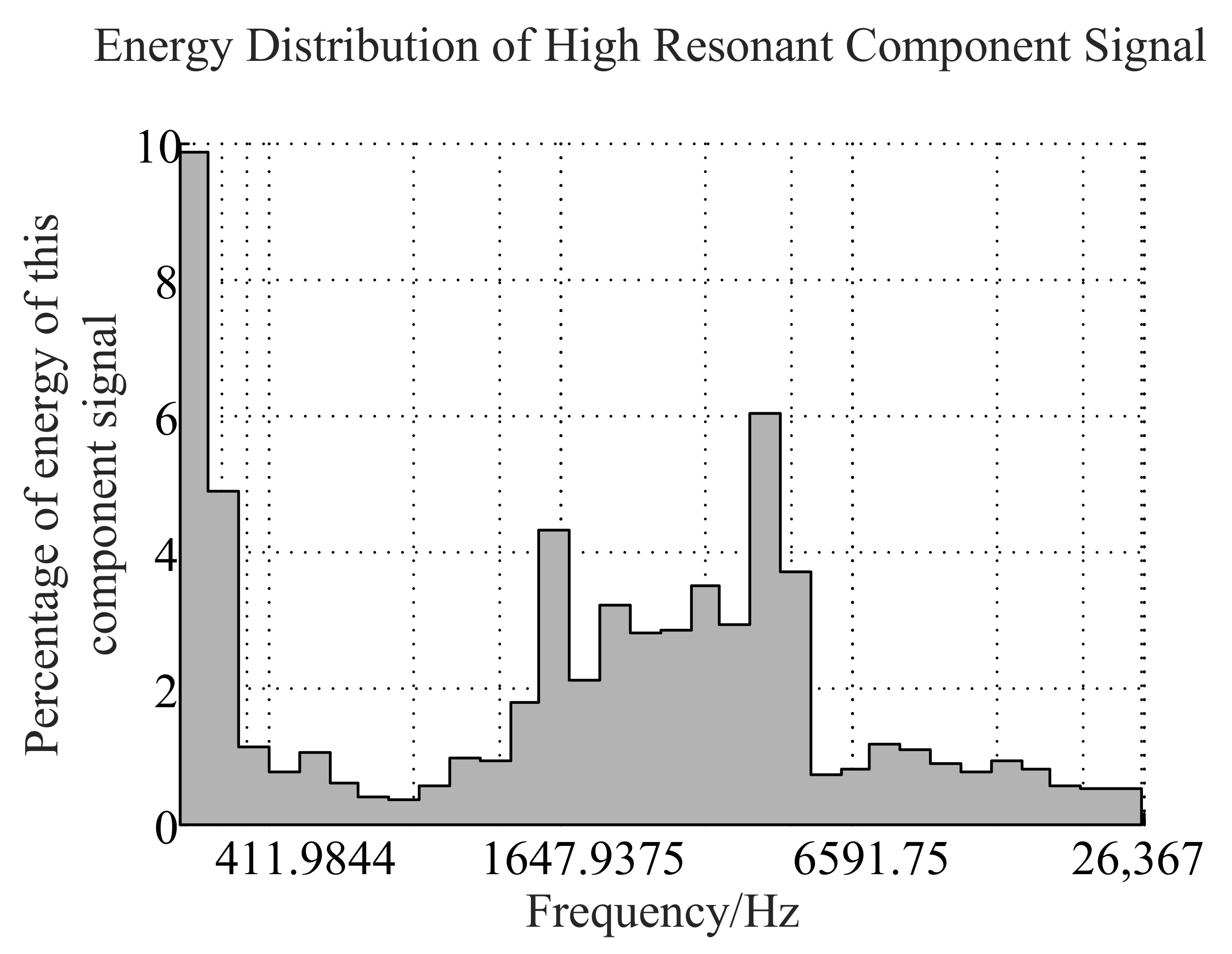
- The sample obtained in step (3) is treated with LOFAR spectrum enhancement. The specific sample processing process and calculation process are in Section 3.3. Then the LOFAR spectrum with enhanced line spectrum characteristics is obtained. The LOFAR spectrum is a two-dimensional matrix, which can be regarded as a single-channel image. After that as shown in Figure 1, the data enhanced by the multi-step decision LOFAR spectrum is input into the CNN network for subsequent identification.
5.4.2. Identification of Measured Ship Radiated Noise
6. Conclusions
7. Future Works
- (1)
- Most studies on underwater target recognition do not disclose data sources for reasons such as confidentiality. There is also a lack of unified and standardized data sets in the industry. The actual measured ship radiated noise data set used in this article is already one of the few publicly available underwater acoustic data sets. However, the data set itself is seriously disturbed by marine environmental noise. The number of samples of various types of ships is unevenly distributed, and the total number of samples is also insufficient. Therefore, how to combine underwater target recognition with deep learning under limited conditions is a big problem.
- (2)
- Because the data set is seriously disturbed, this paper adopts a series of feature-enhancing preprocessing methods to improve the recognition rate, and has achieved excellent results. In fact, further reducing the impact of ocean noise and evaluating the impact of various neural networks on the recognition effect can be considered in the future work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, J.; Fang, J.; Liu, C.; Li, X. Deep learning-based spectrum sensing in cognitive radio: A CNN-LSTM approach. IEEE Commun. Lett. 2020, 24, 2196–2200. [Google Scholar] [CrossRef]
- Liu, C.; Yuan, W.; Li, S.; Liu, X.; Ng, D.W.K.; Li, Y. Learning-based Predictive Beamforming for Integrated Sensing and Communication in Vehicular Networks. arXiv 2021, arXiv:2108.11540. [Google Scholar]
- Xie, J.; Fang, J.; Liu, C.; Yang, L. Unsupervised deep spectrum sensing: A variational auto-encoder based approach. IEEE Trans. Veh. Technol. 2020, 69, 5307–5319. [Google Scholar] [CrossRef]
- Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Phy. 1962, 160, 106–154. [Google Scholar] [CrossRef]
- Santos-Domínguez, D.; Torres-Guijarro, S.; Cardenal-López, A.; Pena-Gimenez, A. ShipsEar: An underwater vessel noise database. Appl. Acoust. 2016, 113, 64–69. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G. Improving Smart Cities Safety Using Sound Events Detection Based on Deep Neural Network Algorithms. Informatics 2020, 7, 23. [Google Scholar] [CrossRef]
- Liu, C.; Wei, Z.; Ng, D.W.K.; Yuan, J.; Liang, Y.C. Deep transfer learning for signal detection in ambient backscatter communications. IEEE Trans. Wirel. Commun. 2020, 20, 1624–1638. [Google Scholar] [CrossRef]
- Ciaburro, G. Sound Event Detection in Underground Parking Garage Using Convolutional Neural Network. Big Data Cogn. Comput. 2020, 4, 20. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016. [Google Scholar]
- Liu, C.; Wang, J.; Liu, X.; Liang, Y.C. Deep CM-CNN for spectrum sensing in cognitive radio. IEEE J. Sel. Areas Commun. 2019, 37, 2306–2321. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.E.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.E.; Jackel, L.D. Handwritten digit recognition with a back-propagation network. In Proceedings of the Handwritten Digit Recognition with a Back-Propagation Network. Advances in Neural Information Processing Systems, Denver, CO, USA, 27–30 November 1989; pp. 396–404. Available online: https://proceedings.neurips.cc/paper/1989/file/53c3bce66e43be4f209556518c2fcb54-Paper.pdf (accessed on 4 October 2021).
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the Thirty-first AAAI conference on artificial intelligence (AAAI), San Francisco, CA, USA, 4–9 February 2017; pp. 4278–4284. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), Las Vegas, NV, USA, 17–19 June 2016; pp. 770–778. [Google Scholar]
- Jin, G.; Liu, F.; Wu, H.; Song, Q. Deep learning-based framework for expansion, recognition and classification of underwater acoustic signal. J. Exp. Theor. Artif. Intell. 2019, 32, 205–218. [Google Scholar] [CrossRef]
- Liu, F.; Song, Q.; Jin, G. Expansion of restricted sample for underwater acoustic signal based on generative adversarial networks. May 2019. In Proceedings of the Tenth International Conference on Graphics and Image Processing (ICGIP), Chengdu, China, 12–14 December 2018; Volume 11069, pp. 1106948–1106957. [Google Scholar]
- Yang, H.; Shen, S.; Yao, X.; Sheng, M.; Wang, C. Competitive deep-belief networks for underwater acoustic target recognition. Sensors 2018, 18, 952–965. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.; Yang, H.; Sheng, M. Compression of a deep competitive network based on mutual information for underwater acoustic targets recognition. Entropy 2018, 20, 243–256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, J.; Sun, H.; Chen, H.; Junejo, N.U.R.; Cheng, E. Resonance-based time-frequency manifold for feature extraction of ship-radiated noise. Sensors 2018, 18, 936–957. [Google Scholar] [CrossRef] [Green Version]
- Ke, X.; Yuan, F.; Cheng, E. Underwater Acoustic Target Recognition Based on Supervised Feature-Separation Algorithm. Sensors 2018, 18, 4318–4342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, P.; Isaacs, J.; Fu, B.; Ferrari, S. Deep learning feature extraction for target recognition and classification in underwater sonar images. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control CDC), Melbourne, Australia, 12–15 December 2017; pp. 2724–2731. [Google Scholar]
- McQuay, C.; Sattar, F.; Driessen, P.F. Deep learning for hydrophone big data. In Proceedings of the 2017 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing (PACRIM), Victoria, QC, Canada, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Hu, G.; Wang, K.; Peng, Y.; Qiu, M.; Shi, J.; Liu, L. Deep learning methods for underwater target feature extraction and recognition. Comput. Intell. Neurosci. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Kubáčková, L.; Burda, M. Mathematical model of the spectral decomposition of periodic and non-periodic geophysical stationary random signals. Stud. Geophys. Geod. 1977, 21, 1–10. [Google Scholar] [CrossRef]
- Huang, W.; Sun, H.; Liu, Y.; Wang, W. Feature extraction for rolling element bearing faults using resonance sparse signal decomposition. Exp. Tech. 2017, 41, 251–265. [Google Scholar] [CrossRef]
- Selesnick, I.W. Wavelet transform with tunable Q-factor. IEEE Trans. Signal Process. 2011, 59, 3560–3575. [Google Scholar] [CrossRef]
- Starck, J.L.; Elad, M.; Donoho, D.L. Image decomposition via the combination of sparse representations and a variational approach. IEEE Trans. Image Process. 2005, 14, 1570–1582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Raheem, K.F.; Roy, A.; Ramachandran, K.; Harrison, D.K.; Grainger, S. Rolling element bearing faults diagnosis based on autocorrelation of optimized: Wavelet de-noising technique. Int. J. Adv. Manuf. Technol. 2009, 40, 393–402. [Google Scholar] [CrossRef]
- Shensa, M.J. The discrete wavelet transform: Wedding the a trous and Mallat algorithms. IEEE Trans. Signal Process. 1992, 40, 2464–2482. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Chen, J.; Dong, G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Proc. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Di Martino, J.C.; Haton, J.P.; Laporte, A. Lofargram line tracking by multistage decision process. In Proceedings of the 1993 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Minneapolis, MN, USA, 27–30 April 1993; Volume 1, pp. 317–320. [Google Scholar]
- Liu, C.; Liu, X.; Ng, D.W.K.; Yuan, J. Deep Residual Learning for Channel Estimation in Intelligent Reflecting Surface-Assisted Multi-User Communications. IEEE Trans. Wirel. Commun. 2021, 1. [Google Scholar] [CrossRef]
- Liu, X.; Liu, C.; Li, Y.; Vucetic, B.; Ng, D.W.K. Deep residual learning-assisted channel estimation in ambient backscatter communications. IEEE Wirel. Commun. Lett. 2020, 10, 339–343. [Google Scholar] [CrossRef]
- Liu, C.; Yuan, W.; Wei, Z.; Liu, X.; Ng, D.W.K. Location-aware predictive beamforming for UAV communications: A deep learning approach. IEEE Wirel. Commun. Lett. 2020, 10, 668–672. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Chen, Z.; Li, Y.; Cao, R.; Ali, W.; Yu, J.; Liang, H. A New Feature Extraction Method for Ship-Radiated Noise Based on Improved CEEMDAN, Normalized Mutual Information and Multiscale Improved Permutation Entropy. Entropy 2019, 21, 624–640. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.; Ke, X.; Cheng, E. Joint Representation and Recognition for Ship-Radiated Noise Based on Multimodal Deep Learning. J. Mar. Sci. Technol. Eng. 2019, 7, 380–397. [Google Scholar] [CrossRef] [Green Version]
- Ke, X.; Yuan, F.; Cheng, E. Integrated optimization of underwater acoustic ship-radiated noise recognition based on two-dimensional feature fusion. Appl. Acoust. 2020, 159, 107057–107070. [Google Scholar] [CrossRef]
- Hou, W. Spectrum autocorrelation. Acta Acust 1988, 2, 46–49. [Google Scholar]




| Input Layer (1024) × 64 × 1 | ||||
|---|---|---|---|---|
| Conv+ ReLU (7 × 7) × 16 stride = 2 × 1 | Conv+ ReLU (7 × 5) × 16 stride = 2 × 1 | Conv+ ReLU (5 × 5) × 16 stride = 2 × 1 | Conv+ ReLU (3 × 3) × 16 stride = 2 × 1 | MaxPool (3 × 3) Conv+ReLU (1 × 1) × 16 stride = 1 × 1 |
| Fileter concatenation | ||||
| ReLU+MaxPool (3 × 3) | ||||
| Conv+ReLU(5 × 5) × 16 stride = 2 × 1 | ||||
| MaxPool (3 × 3) | ||||
| Conv+ReLU(5 × 5) × 16 stride = 2 × 1 | ||||
| MaxPool (3 × 3) | ||||
| Conv+ReLU (3 × 3) × 32 stride = 2 × 2 | ||||
| MaxPool (3 × 3) | ||||
| Flattern | ||||
| Dense (4) | ||||
| Item | Value |
|---|---|
| Optimizer | adam |
| Learning rate | 0.01 |
| Number of samples | 200 |
| Training round | 30 |
| Loss function | Cross entropy loss function |
| Item | Value |
|---|---|
| W | Fishing boat, trawler, mussel harvester, tugboat, dredge |
| X | Motorboat, pilot boat, sailboat |
| Y | Passenger ferry |
| Z | Ocean liner, ro-ro ship |
| Lab Environment | Configuration |
|---|---|
| Operating system | Ubuntu 16.04 |
| Graphics card | GTX 1080ti |
| Programming language and software | Pycharm 2019.1 + Python 3.6 |
| Matlab R2016b | |
| Deep-learning library and software toolbox | Keras 2.3 (tensorflow backed) |
| Librosa Audio processing library (python) | |
| TQWT Toolbox (Matlab language) |
| Signal | , | , |
|---|---|---|
| 0.7161 | 0.7074 |
| ID | Training Set | Testing Set | |
|---|---|---|---|
| Number of Samples | Number of Samples | ||
| W | 46, 48, 66, 73, 74, 75, 80, 93, 94, 95, 96 | 836 | 531 |
| X | 21, 26, 29, 30, 50, 52, 57, 70, 72, 77, 79 | 837 | 516 |
| Y | 6, 7, 8, 10, 11, 13, 14 | 1016 | 526 |
| Z | 18, 19, 20 | 1149 | 603 |
| Total | 3838 | 2176 |
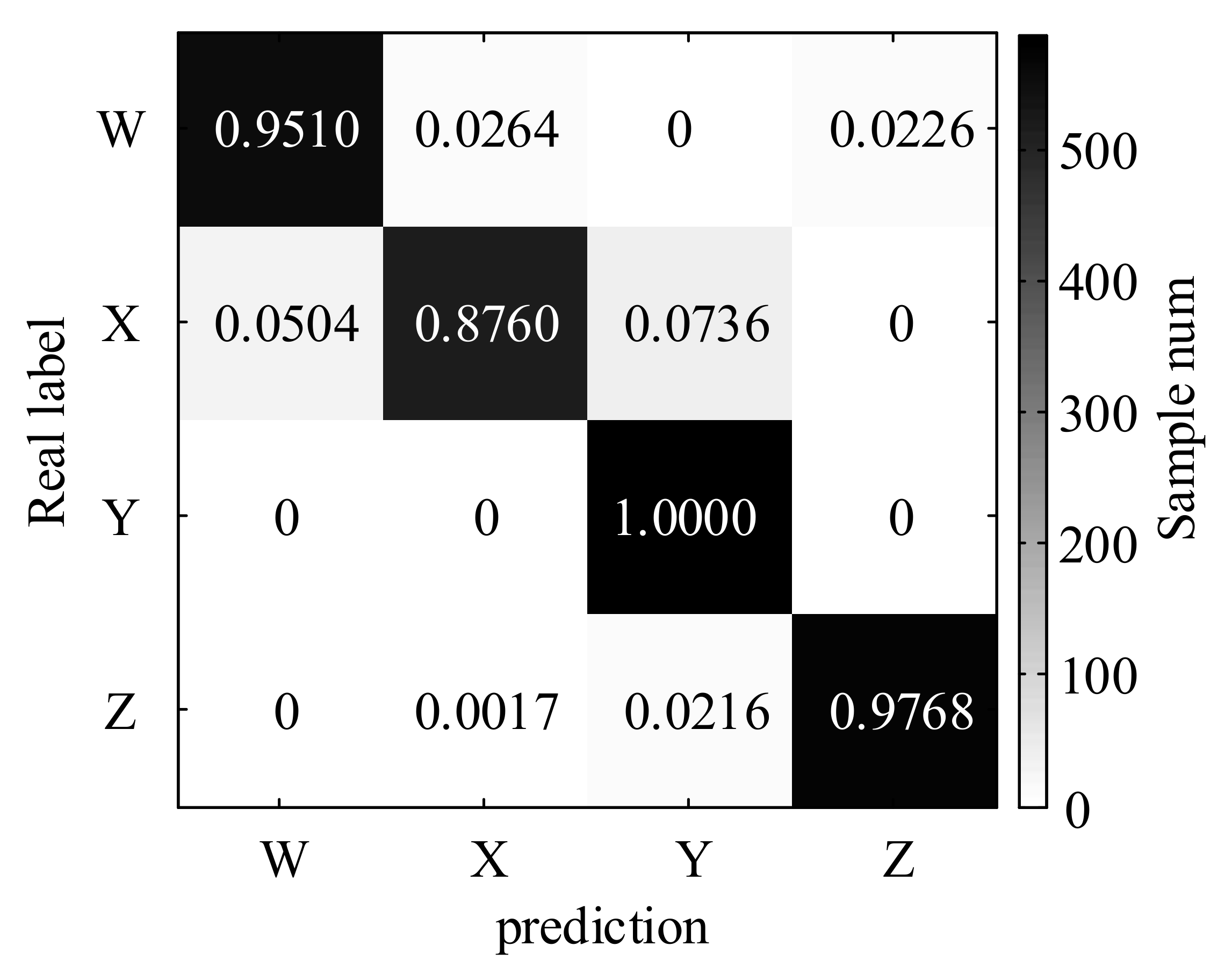
| Recognition Rate | Class W | Class X | Class Y | Class Z | Average |
|---|---|---|---|---|---|
| CNN | 95.10% | 87.60% | 100.0% | 97.78% | 95.22% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Han, B.; Ma, X.; Zhang, J. Underwater Target Recognition Based on Multi-Decision LOFAR Spectrum Enhancement: A Deep-Learning Approach. Future Internet 2021, 13, 265. https://doi.org/10.3390/fi13100265
Chen J, Han B, Ma X, Zhang J. Underwater Target Recognition Based on Multi-Decision LOFAR Spectrum Enhancement: A Deep-Learning Approach. Future Internet. 2021; 13(10):265. https://doi.org/10.3390/fi13100265
Chicago/Turabian StyleChen, Jie, Bing Han, Xufeng Ma, and Jian Zhang. 2021. "Underwater Target Recognition Based on Multi-Decision LOFAR Spectrum Enhancement: A Deep-Learning Approach" Future Internet 13, no. 10: 265. https://doi.org/10.3390/fi13100265
APA StyleChen, J., Han, B., Ma, X., & Zhang, J. (2021). Underwater Target Recognition Based on Multi-Decision LOFAR Spectrum Enhancement: A Deep-Learning Approach. Future Internet, 13(10), 265. https://doi.org/10.3390/fi13100265







