Generic Tasks for Algorithms
Abstract
1. Introduction
2. Materials and Methods
2.1. The Concept of Generic Tasks
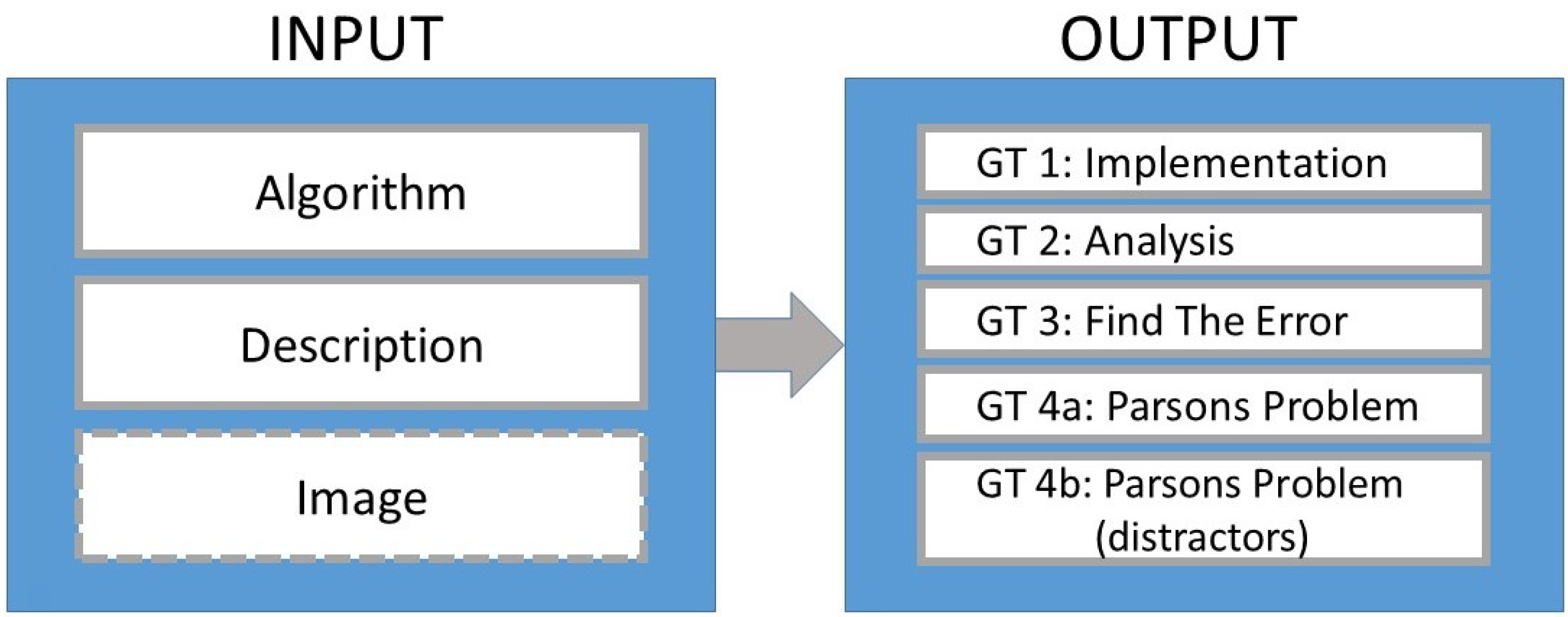
Definition of the Generic Tasks for Algorithms
- GT 1 Implementation: Create a program for the following description:
- <description>
- Optional: The result should look like this:
- <image>
- GT 2 Analysis: What happens when the following program is executed? Describe!
- <code>
- GT 3 Find the Error: Given is the following program:
- <erroneous code>
- Originally, the program is supposed to work like this:
- <description>
- Find and correct the errors so that the program does what it is supposed to do.
- GT 4a Parsons Problem: Create a program for the following description:
- <description>
- Use the following blocks/lines:
- <code puzzle>
- GT 4b Parsons Problem (Distractor): Create a program for the following description:
- <description>
- Use some of the following blocks/lines:
- <code puzzle redundant>
- RQ1:
- Which core skills of CT (according to [8]) can be fostered using one of the defined Generic Tasks for algorithms?
- RQ2:
- To which degree are the corresponding skills addressed by the Generic Tasks for algorithms?
2.2. Methodology
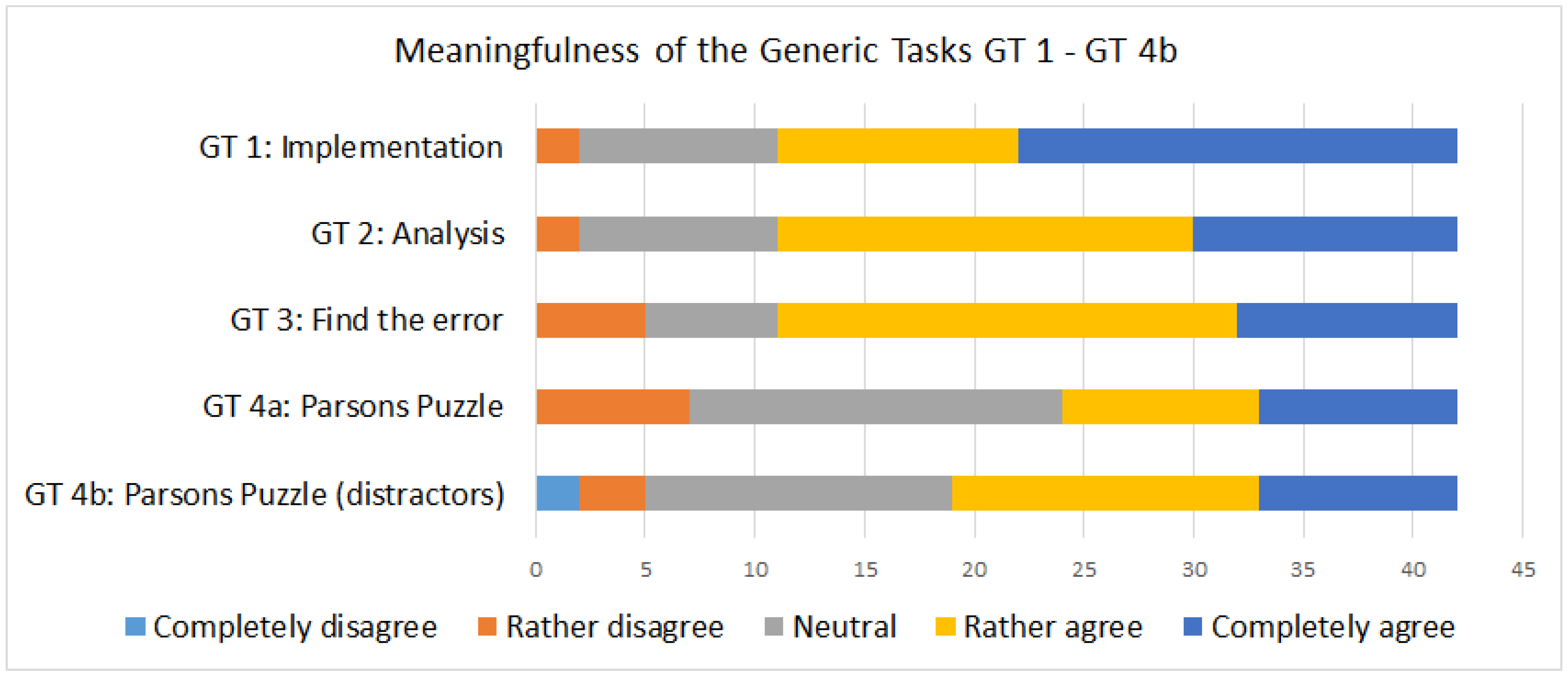
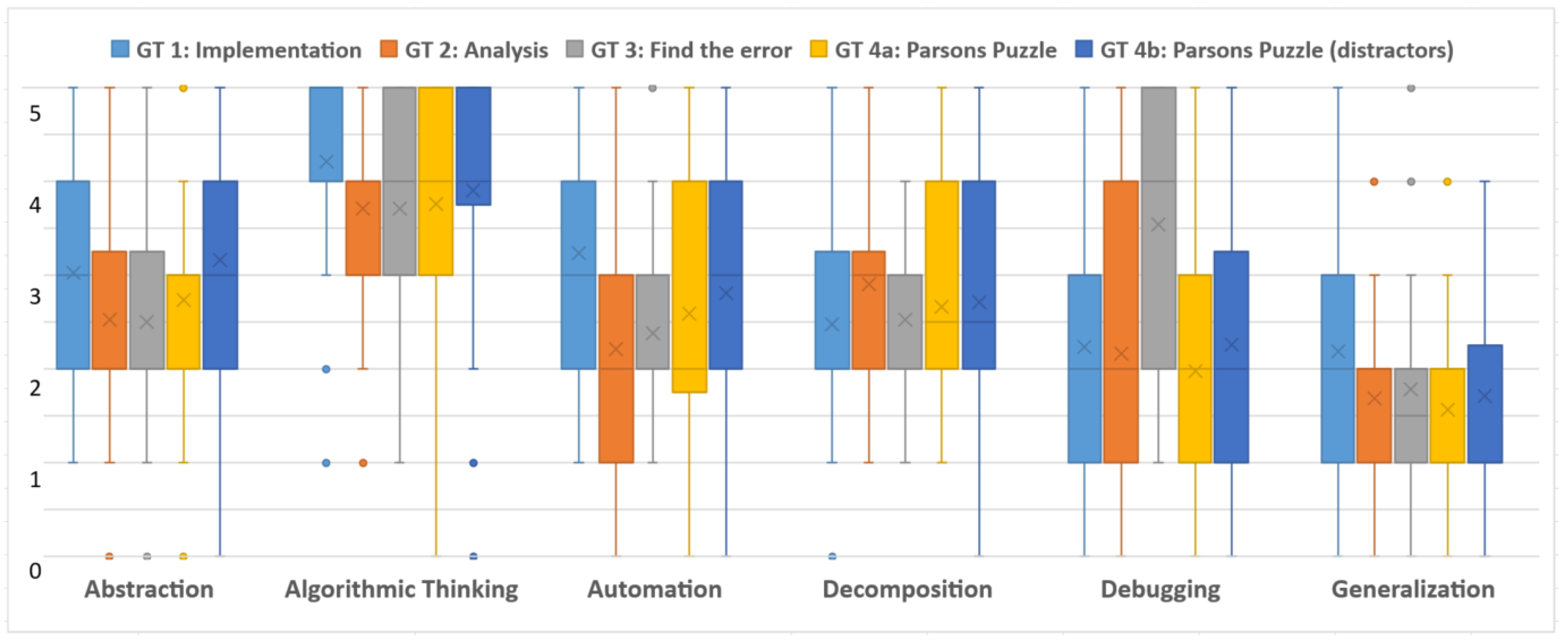
3. Results and Discussion
Limitations of the Study
4. Conclusions
4.1. Responses to Research Questions
4.2. Implications and Suggestions for Future Studies
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CT | Computational Thinking |
| CS | Computer Science |
| GT | Generic Task |
| STEM | Science, Technology, Engineering, and Mathematics |
Appendix A. Given Original Examples
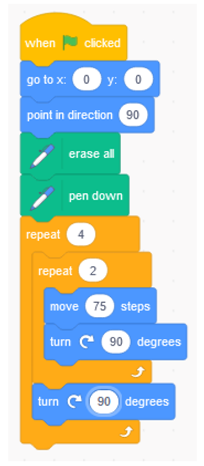
Appendix A.1. Plus

Appendix A.2. Odd–Even
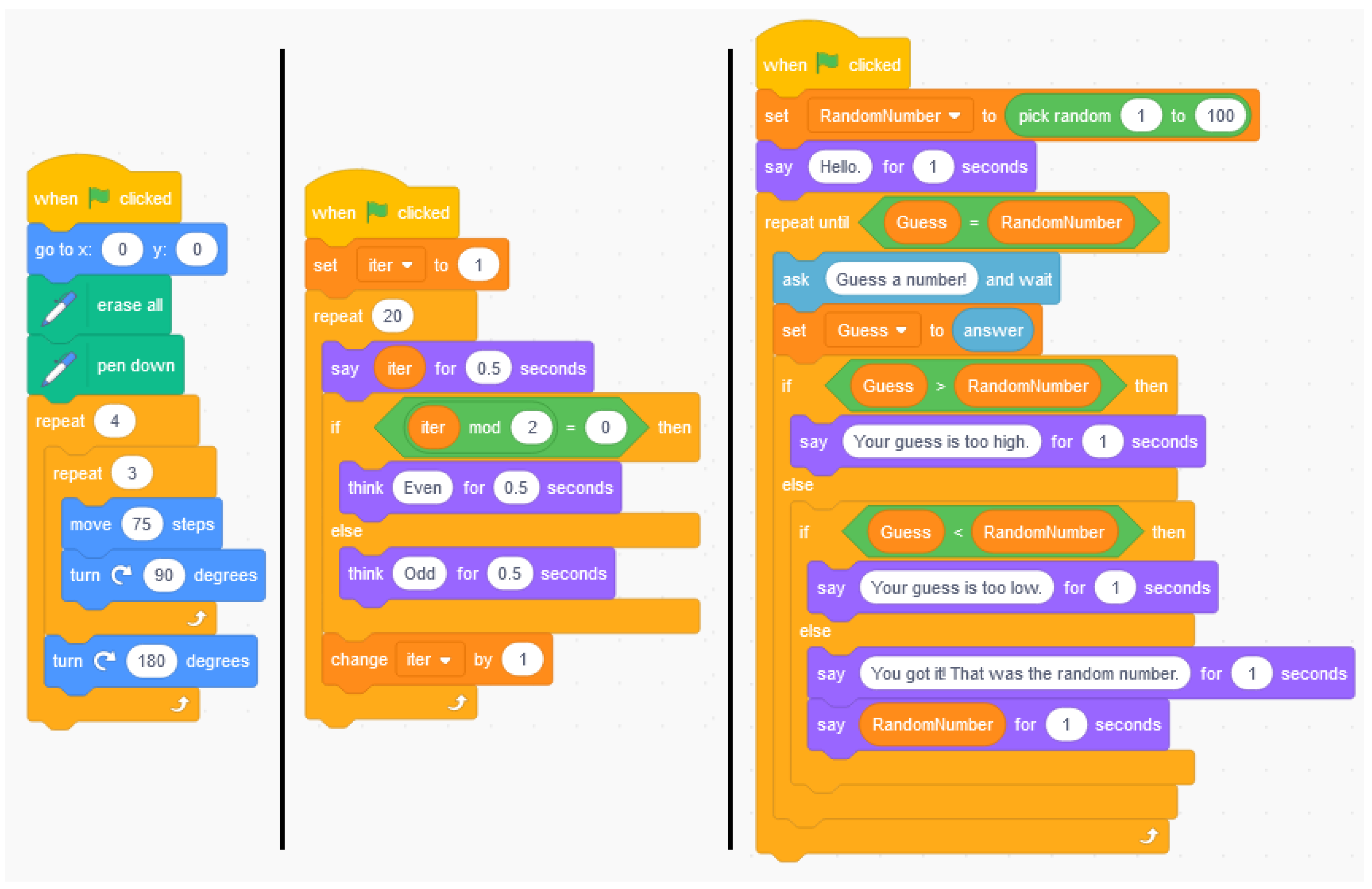
- <description> The sprite goes through the numbers from 1 to 20 and thinks about whether the number is odd or even for each number.
- <code>Figure A1 middle
Appendix A.3. Guess A Number
- <description> A random number between 1 and 100 is generated. The user should guess the number. After each input, the program tells the user whether his guess was too high or too low until the random number is guessed correctly.
- <code>Figure A1 right
Appendix B. Generic Tasks Based on the Task “Plus”
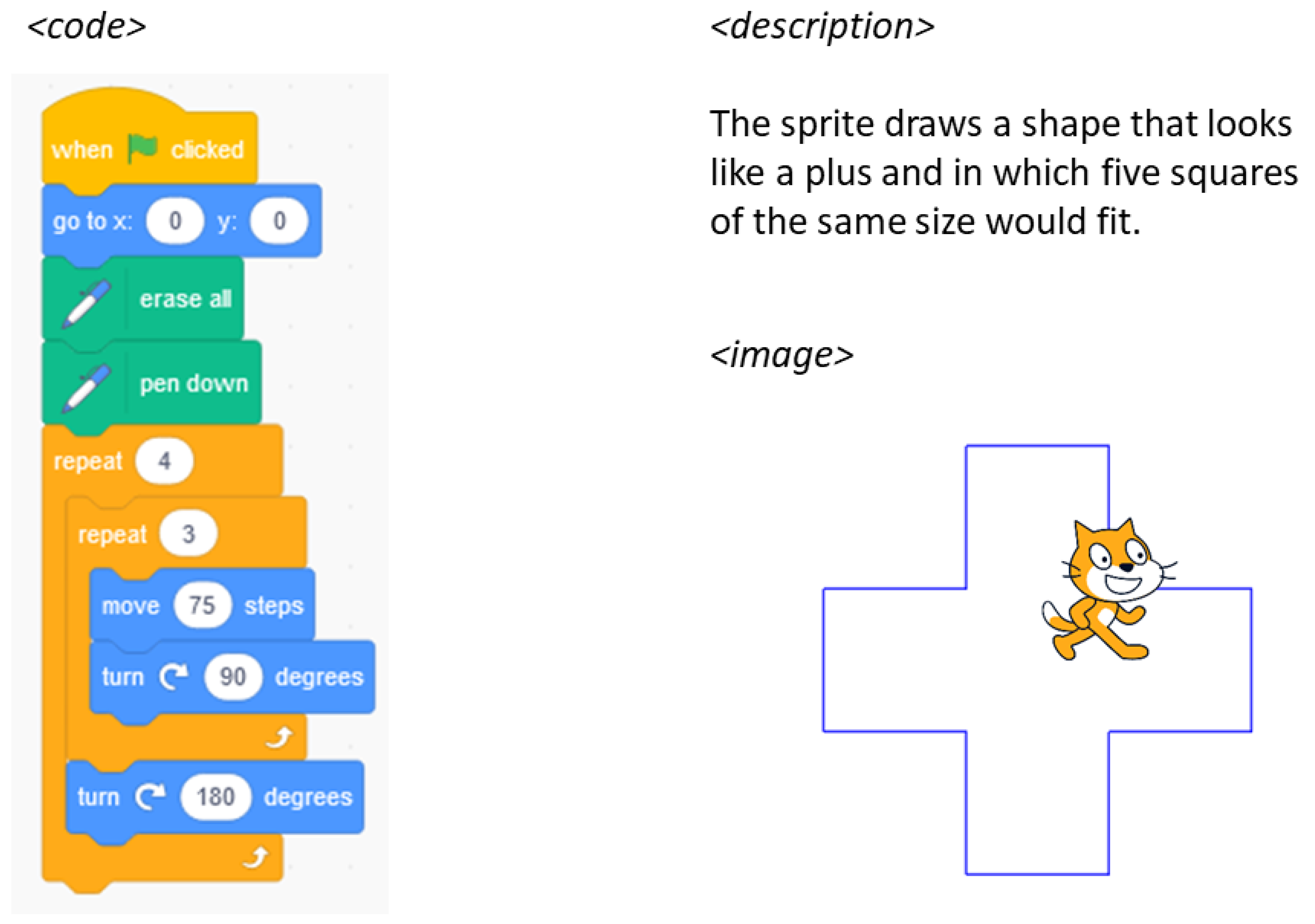
- GT 1 Implementation: Create a program for the following description:
- The sprite draws a shape that looks like a plus and that consists of five squares of the same size.
- The result of should look like this:
- GT 2 Analysis: What happens when the following program is executed? Describe!
- GT 3 Find the Error: Given is the following program:
- Originally, the program is supposed to work like this:
- The sprite draws a shape that looks like a plus and that consists of five squares of the same size.
- Find and correct the errors so that the program does what it is supposed to do.
- GT 4a Parsons problem: Create a program for the following description:
- The sprite draws a shape that looks like a plus and that consists of five squares of the same size.
- Use the following blocks/lines:
- GT 4b Parsons problem (Distractor): Create a program for the following description:
- The sprite draws a shape that looks like a plus and that consists of five squares of the same size.
- Use some of the following blocks/lines:
References
- Fraillon, J.; Ainley, J.; Schulz, W.; Friedman, T.; Duckworth, D. Preparing for Life in a Digital World: IEA International Computer and Information Literacy Study 2018; IEA: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Pollak, M.; Ebner, M. The Missing Link to Computational Thinking. Future Internet 2019, 11, 263. [Google Scholar] [CrossRef]
- Wing, J. Computational thinking’s influence on research and education for all. Ital. J. Educ. Technol. 2017, 25, 7–14. [Google Scholar]
- Wing, J. Computational thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Voogt, J.; Fisser, P.; Good, J.; Mishra, P.; Yadav, A. Computational thinking in compulsory education: Towards an agenda for research and practice. Educ. Inf. Technol. 2011, 20, 715–728. [Google Scholar] [CrossRef]
- Hu, C. Computational thinking: What it might mean and what we might do about it. In Proceedings of the 16th Annual Joint Conference on Innovation and Technology in Computer Science Education, Darmstadt, Germany, 27–29 June 2011; pp. 223–227. [Google Scholar]
- Lu, J.; Fletcher, G.H. Thinking about computational thinking. In Proceedings of the 40th ACM Technical Symposium on Computer Science Education, Chattanooga, TN, USA, 4–7 March 2009; pp. 260–264. [Google Scholar]
- Bocconi, S.; Chioccariello, A.; Dettori, G.; Ferrari, A.; Engelhardt, K. Developing Computational Thinking in Compulsory Education; JRC Science Hub: Seville, Spain, 2016. [Google Scholar]
- Zapata-Cáceres, M.; Martín-Barroso, E.; Román-González, M. Computational Thinking Test for Beginners: Design and Content Validation. In Proceedings of the IEEE Global Engineering Education Conference (EDUCON), Porto, Portugal, 27–30 April 2020; pp. 1905–1914. [Google Scholar] [CrossRef]
- Román-González, M. Computational Thinking Test: Design Guidelines and Content Validation. In Proceedings of the EDULEARN15, Barcelona, Spain, 6–8 July 2015; pp. 2436–2444. [Google Scholar] [CrossRef]
- Wetzel, S.; Milicic, G.; Ludwig, M. Gifted Students’ Use of Computational Thinking Skills Approaching A Graph Problem: A Case Study. In Proceedings of the EduLearn20, Palma de Mallorca, Spain, 6–7 July 2020; pp. 6936–6944. [Google Scholar]
- Ludwig, M.; Jablonski, S. MathCityMap-Mit mobilen Mathtrails Mathe draußen entdecken [MathCityMap-Discovering Mathematics Outside with Mobile Mathtrails]. Mnu J. 2020, 1, 29–36. [Google Scholar]
- Barlovits, S.; Baumann-Wehner, M.; Ludwig, M. Curricular Learning with MathCityMap: Creating Theme-Based Math Trails. In Proceedings of the Mathematics Education in the Digital Age, Linz, Austria, 16–18 September 2020. [Google Scholar]
- Helfrich-Schkarbanenko, A.; Rapedius, K.; Rutka, V.; Sommer, A. Mathematische Aufgaben und Lösungen Automatisch Generieren: Effizientes Lehren und Lernen mit MATLAB [Generate Mathematical Tasks and Solutions Automatically: Efficient Teaching and Learning with MATLAB]; Springer: Berlin, Germany, 2018. [Google Scholar]
- Hattie, J.; Timperley, H. The Power of Feedback. Rev. Educ. Res. 2007, 77, 81–112. [Google Scholar] [CrossRef]
- Keuning, H.; Jeuring, J.; Heeren, B. Towards a Systematic Review of Automated Feedback Generation for Programming Exercises. In Proceedings of the 2016 ACM Conference on Innovation and Technology in Computer Science Education (ITiCSE ’16), Arequipa, Peru, 9–13 July 2016; pp. 41–46. [Google Scholar] [CrossRef]
- Romagosa i Carrasquer, B. The Snap! Programming System. In Encyclopedia of Education and Information Technologies; Tatnall, A., Ed.; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Resnick, M.; Maloney, J.; Monroy-Hernández, A.; Rusk, N.; Eastmond, E.; Brennan, K.; Millner, A.; Rosenbaum, E.; Silver, J.; Silverman, B.; et al. Scratch: Programming for all. Commun. ACM 2009, 52, 60–67. [Google Scholar] [CrossRef]
- Price, T.W.; Dong, Y.; Lipovac, D. ISnap: Towards Intelligent Tutoring in Novice Programming Environments. In Proceedings of the 2017 ACM SIGCSE Technical Symposium on Computer Science Education (SIGCSE ’17), Seattle, WA, USA, 8–11 March 2017; pp. 483–488. [Google Scholar] [CrossRef]
- Moreno-León, J.; Robles, G. Dr. Scratch: A Web Tool to Automatically Evaluate Scratch Projects. In Proceedings of the Workshop in Primary and Secondary Computing Education (WiPSCE ’15), London, UK, 9–11 November 2015; pp. 132–133. [Google Scholar] [CrossRef]
- Venables, A.; Tan, G.; Lister, R. A Closer Look at Tracing, Explaining and Code Writing Skills in the Novice Programmer. In Proceedings of the Fifth International Workshop on Computing Education Research Workshop, Berkeley CA, USA, 10–11 August 2009; pp. 117–128. [Google Scholar]
- Lopez, M.; Whalley, J.; Robbins, P.; Lister, R. Relationships Between Reading, Tracing and Writing Skills in Introductory Programming. In Proceedings of the Fourth International Workshop on Computing Education Research, Sydney, Australia, 6–7 September 2008; pp. 101–111. [Google Scholar]
- Izu, C.; Schulte, C.; Aggarwal, A.; Cutts, Q.; Duran, R.; Gutica, M.; Heinemann, B.; Kraemer, E.; Lonati, V.; Mirolo, C.; et al. Fostering Program Comprehension in Novice Programmers-Learning Activities and Learning Trajectories. In Proceedings of the Working Group Reports on Innovation and Technology in Computer Science Education (ITiCSE-WGR ’19), Aberdeen, UK, 15–17 July 2019; pp. 27–52. [Google Scholar] [CrossRef]
- Ericson, B.J.; Margulieux, L.E.; Rick, J. Solving parsons problems versus fixing and writing code. In Proceedings of the 17th Koli Calling International Conference on Computing Education Research (Koli Calling ’17), Koli, Finland, 16–19 November 2017; pp. 20–29. [Google Scholar] [CrossRef]
- Moreno-León, J.; Robles, G.; Román-González, M.; Rodríguez, J. Not the same: A text network analysis on computational thinking definitions to study its relationship with computer programming. Rev. Interuniv. Investig. Technol. Educ. 2019, 7, 26–35. [Google Scholar] [CrossRef]
- Hromkovic, J.; Kohn, T.; Komm, D.; Serafini, G. Examples of Algorithmic Thinking in Programming Education. Olymp. Inform. 2016, 10, 111–124. [Google Scholar] [CrossRef]
- Parsons, D.; Haden, P. Parsons programming puzzles: A fun and effective learning tool for first programming courses. In Proceedings of the 8th Australasian Conference on Computing Education-Volume 52 (ACE ’06), Hobart, Australia, 16–19 January 2006; pp. 157–163. [Google Scholar]
- Zhi, R.; Chi, M.; Barnes, T.; Price, T.W. Evaluating the Effectiveness of Parsons Problems for Block-based Programming. In Proceedings of the 2019 ACM Conference on International Computing Education Research (ICER ’19), Toronto, ON, Canada, 12–14 August 2019; pp. 51–59. [Google Scholar] [CrossRef]
- Kumar, A.N. Epplets: A Tool for Solving Parsons Puzzles. In Proceedings of the 49th ACM Technical Symposium on Computer Science Education (SIGCSE ’18), Baltimore, MD, USA, 21–24 February 2018; pp. 527–532. [Google Scholar] [CrossRef]
- Ihantola, P.; Helminen, J.; Karavirta, V. How to study programming on mobile touch devices: Interactive Python code exercises. In Proceedings of the 13th Koli Calling International Conference on Computing Education Research (Koli Calling ’13), Koli, Finland, 14–17 November 2013; pp. 51–58. [Google Scholar] [CrossRef]
- Ericson, B.J.; Foley, J.D.; Rick, J. Evaluating the Efficiency and Effectiveness of Adaptive Parsons Problems. In Proceedings of the 2018 ACM Conference on International Computing Education Research (ICER ’18), Espoo, Finland, 13–15 August 2018; pp. 60–68. [Google Scholar] [CrossRef]
- Ericson, B.J.; Miller, B.N. Runestone: A Platform for Free, On-line, and Interactive Ebooks. In Proceedings of the 51st ACM Technical Symposium on Computer Science Education (SIGCSE ’20), Portland, OR, USA, 11–14 March 2020; pp. 1012–1018. [Google Scholar] [CrossRef]
- Schulte, C. Block Model: An educational model of program comprehension as a tool for a scholarly approach to teaching. In Proceedings of the Fourth international Workshop on Computing Education Research (ICER ’08), Sydney, Australia, 6–7 September 2008; pp. 149–160. [Google Scholar] [CrossRef]
- Rich, K.M.; Binkowski, T.A.; Strickland, C.; Franklin, D. Decomposition: A K-8 Computational Thinking Learning Trajectory. In Proceedings of the 2018 ACM Conference on International Computing Education Research (ICER ’18), Espoo, Finland, 13–15 August 2018; pp. 124–132. [Google Scholar] [CrossRef]
- National Research Council. Report of a Workshop on the Scope and Nature of Computational Thinking; The National Academies Press: Washington, DC, USA, 2010. [Google Scholar] [CrossRef]
- Kafai, Y.; Proctor, C.; Lui, D. From Theory Bias to Theory Dialogue: Embracing Cognitive, Situated, and Critical Framings of Computational Thinking in K-12 CS Education. In Proceedings of the 2019 ACM Conference on International Computing Education Research (ICER ’19), Toronto, ON, Canada, 12–14 August 2019; pp. 101–109. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milicic, G.; Wetzel, S.; Ludwig, M. Generic Tasks for Algorithms. Future Internet 2020, 12, 152. https://doi.org/10.3390/fi12090152
Milicic G, Wetzel S, Ludwig M. Generic Tasks for Algorithms. Future Internet. 2020; 12(9):152. https://doi.org/10.3390/fi12090152
Chicago/Turabian StyleMilicic, Gregor, Sina Wetzel, and Matthias Ludwig. 2020. "Generic Tasks for Algorithms" Future Internet 12, no. 9: 152. https://doi.org/10.3390/fi12090152
APA StyleMilicic, G., Wetzel, S., & Ludwig, M. (2020). Generic Tasks for Algorithms. Future Internet, 12(9), 152. https://doi.org/10.3390/fi12090152