Abstract
Video playback on mobile consumer electronic (CE) devices is plagued by fluctuations in the network bandwidth and by limitations in processing and energy availability at the individual devices. Seen as a potential solution, the state-of-the-art adaptive streaming mechanisms address the first aspect, yet the efficient control of the decoding-complexity and the energy use when decoding the video remain unaddressed. The quality of experience (QoE) of the end-users’ experiences, however, depends on the capability to adapt the bit streams to both these constraints (i.e., network bandwidth and device’s energy availability). As a solution, this paper proposes an encoding framework that is capable of generating video bit streams with arbitrary bit rates and decoding-complexity levels using a decoding-complexity–rate–distortion model. The proposed algorithm allocates rate and decoding-complexity levels across frames and coding tree units (CTUs) and adaptively derives the CTU-level coding parameters to achieve their imposed targets with minimal distortion. The experimental results reveal that the proposed algorithm can achieve the target bit rate and the decoding-complexity with 0.4% and 1.78% average errors, respectively, for multiple bit rate and decoding-complexity levels. The proposed algorithm also demonstrates a stable frame-wise rate and decoding-complexity control capability when achieving a decoding-complexity reduction of 10.11 (%/dB). The resultant decoding-complexity reduction translates into an overall energy-consumption reduction of up to 10.52 (%/dB) for a 1 dB peak signal-to-noise ratio (PSNR) quality loss compared to the HM 16.0 encoded bit streams.
1. Introduction
Increasingly mobile consumption of video content, advancements in consumer electronics, and the popularity of video on-demand services, have immensely contributed towards the dramatic increase in video data traffic (expected to exceed 75% of the overall data traffic [1]) in the Internet. However, fluctuations in the network bandwidth, together with the limited processing and energy resources in mobile hand-held devices affect the quality of the video streams and the viewing experiences of the end users. As such, jointly adapting the video content to meet the network bandwidth and the device’s energy supply becomes a crucial element to enhance the quality of experience (QoE) of video streaming services and applications.
The fluctuations in the network bandwidth during video streaming are currently addressed through HTTP adaptive streaming [2]. However, it currently lacks the necessary awareness to alter the video content based on its decoding-complexity to reduce the energy demand on the end user’s device. (The term decoding-complexity in this manuscript refers to the number of CPU instructions consumed by the processor to decode an encoded bit stream.) This will become more pronounced with time, especially due to the complexity of modern standards such as High Efficiency Video Coding (HEVC) and the upcoming Versatile Video Coding (VVC), and the increasing demand for high definition (HD) content on hand-held devices [3,4]. As a solution, simultaneous control of both bit rate and decoding-complexity of an encoded video sequence could potentially address both these constraints. For instance, such an algorithm could generate bit streams with arbitrary bit rates and decoding-complexity levels that could be used with HTTP adaptive streaming where the requested bit stream segments are adapted based on both network bandwidth and the device’s remaining energy constraints. Yet, thus far, this has not been considered in the literature.
Broadly, the state-of-the-art attempts to reduce decoding-complexity include efficient decoder implementations [5,6,7,8], dynamic alterations to the decoding process [9], dynamic voltage and frequency scaling (DVFS) methods [10,11,12,13], content adaptation based on scalable coding architectures [14,15,16], and media transcoding [17] approaches. Out of these, the latter two are encoder-side operations, and operate together with HTTP adaptive streaming solutions such as MPEG-DASH [2,18] to fetch videos of different decoding-complexities based on a device’s remaining energy level. However, existing content adaptation algorithms simply manipulate the bit rate, quantization parameter (QP), spatial resolution, etc., in an attempt to reduce the decoding-complexity and the device’s energy consumption [19,20,21,22,23], which eventually results in poor visual quality and minimal decoding-complexity reductions. In contrast to these approaches, the authors’ previous work in [24] proposes a decoding-complexity–rate–distortion model within the encoder to determine the coding modes that minimize the joint rate, decoding-complexity, and distortion cost for a given QP. However, the deficiencies of the basic concept in [24] could be traced back to the lack of simultaneous allocation and control of the bit rate and the decoding-complexity levels (e.g., being able achieve multiple arbitrary decoding-complexities at the same bit rate) for rate and decoding-complexity-controlled video coding—an aspect that is also overlooked in the literature and that is developed in this work [3].
In this context, this paper proposes a novel joint coding tree unit (CTU)-level decoding-complexity and rate-controlled encoding algorithm for HEVC. This includes, (i) a decoding-complexity–rate–distortion model along with a mode selection cost function that incorporate both bit rate and decoding-complexity as constraints. Furthermore, a (ii) mean square error (MSE)-based algorithm that utilizes the proposed decoding-complexity–rate–distortion model is proposed to allocate bits and decoding-complexity levels across frames and CTUs. Finally, (iii) a content-adaptive, CTU-level, decoding-complexity-controlled video coding algorithm that derives the appropriate coding parameters and trade-offs for bit rate and decoding-complexity, is proposed to meet the constraints imposed on the bit rate and decoding-complexity with minimal distortion.
The remainder of the paper is organized as follows. An overview of state-of-the-art is presented in Section 2, followed up by a detailed description of the decoding-complexity, rate, and distortion model in Section 3. Section 4 describes the proposed joint decoding-complexity and rate control algorithm. Finally, Section 5 and Section 6 present the experimental results and the concluding remarks together with the potential future work, respectively.
2. Background and Related Work
Video streaming on mobile devices consumes energy at all layers of the TCP/IP stack [25]. Solutions to this problem in the recent literature can be categorized into two types: the link-layer solutions that focus on managing the wireless network interface with energy-aware scheduling [26,27,28,29], and application-layer solutions that alter the video decoding and processing functions. This manuscript focuses on a content-adaptive video-encoding solution for HEVC; thus the following section briefly elaborates on the state-of-the-art with respect to the application layer class of solutions.
Certain application-layer approaches propose alterations to the decoder implementations (both software and hardware decoders) such as data and task-level parallelization techniques [30,31]. The more advanced of variants of this concept, such as Green-MPEG, use metadata to specify the decoding-complexity requirements to the decoder [32,33], which can then skip certain decoding operations in order to reduce the decoding energy consumption. The approach by Nogues et al. [34] is one such technique where two of the most complex decoding operations in the HEVC decoder (the in-loop filtering and the interpolation filters) are altered during the decoding process. However, such alterations in the interpolation filter at the decoder during motion compensation severely compromise the video quality. This is due to the use of a modified filter at the decoder on prediction unit (PU) residuals that are computed at an encoder which is unaware of the changes in the decoding process [3,24].
The use of DVFS algorithms is seen as another common approach to reduce the energy consumption of a video decoder. In this case, the video quality and energy usage are balanced [11,35,36,37], by controlling the idle-time of the video decoder in real-time by adjusting the CPU frequency and operational voltage [12]. However, this has been shown to have drawbacks such as frame drops and impact on the overall system performance which adversely affect the user’s QoE, especially in the case of high frame rate, high quality video content [36]. The poor estimation of the complexity of subsequent frame/video segment is largely to blame in many cases, which leads to the sub-optimal selection of CPU frequencies and voltages. A recent Green-MPEG specification suggests the inclusion of codec-dynamic voltage frequency scaling (C-DVFS) metadata into the bit stream [13] to aid the frequency selection process in DVFS. However, estimating frame complexity in order to predict the operational CPU frequency still remains a challenging task. Such operations can greatly benefit from using an encoder (such as that proposed in this manuscript) which is capable of generating HEVC bit streams for given decoding-complexity and bit rate constraints.
The encoder-side content adaptation offers another alternative to reduce the decoding energy consumption during video playback. For example, scalable video coding (SVC) using proxy servers, media transcoding solutions [27], and dynamic adaptive streaming technologies such as MPEG-DASH [20] facilitate dynamic video content adaptation in order to meet the constraints of video playback devices. However, in general, these and other similar solutions, such as device-oriented [23], battery-aware [19], adaptive multimedia delivery and rate adaptation [38] schemes, are limited to manipulating basic video coding parameters such as the quantization parameter (QP), spatial resolution, and frame rate to adapt the video content and achieve energy savings.
Following a similar concept, decoder-friendly bit stream generation at the encoder has been attempted for H.264/AVC in [39,40,41]. For instance, the algorithm proposed in [39] constrains the encoder to select sub-pel motion vectors to control the decoding-complexity. A power consumption model for the deblocking filter is proposed in [40] to support the encoder in preparing decoder friendly H.264/AVC bit streams. A complexity analysis of H.264/AVC entropy decoder is presented in [41] to facilitate the encoder to effectively trade off bit rate, distortion, and decoding-complexity during the encoding process. However, mechanisms to dynamically allocate and control the decoding-complexity levels across video frames and macroblock units have been overlooked in these state-of-the-art algorithms.
The MPEG-DASH-based energy-aware HEVC streaming solutions [20] that exist in the literature only consider the decoding energy in PU mode decision and motion vector selection (i.e., integer-pel vs. fractional-pel). Hence, the reduction in energy consumption is marginal with respect to the similar approaches. In addition, the encoding techniques targeting energy-efficient HEVC decoding proposed in [42] consider the inverse transform and inverse quantization operations to reduce the decoding energy consumption. In this regard, our previous work in [24] takes a step ahead by introducing a decoding-complexity–rate–distortion model which is capable of determining the optimal combination of Langrangian multipliers that minimizes a cost function that constitutes all three parameters (i.e., rate, distortion, and decoding-complexity). The solution presented in [24] is capable of determining the coding modes for given content that minimize the decoding-complexity, and by extension the decoding energy, have minimal impact to the coding efficiency in a fixed QP encoding scenario. However, this solution lacks the capability to arbitrarily allocate rate and decoding-complexity levels to frames or CTUs, and control them in order to generate bit streams with multiple bit rate decoding-complexity levels, which is crucial for video streaming applications that target resource-constrained video decoding devices with high quality HD/UHD video contents.
Furthermore, the network-aware and receiver-aware adaptation algorithms and the complexity-rate-distortion models [14,15,16] which have been introduced based on the previous coding standards typically focus on creating spatial, temporal, and quality scalable video bit streams. These approaches lack a comprehensive analysis of the decoding-complexity, rate, and distortion trade-offs with respect to the features available to the modern coding standards such as HEVC.
Finally, it has been shown that the increasingly popular HTTP-based video streaming solutions are sufficiently flexible to incorporate decoding-energy in their content prefetch logic [20]. This is typically achieved by utilizing an algorithm that monitors the device’s remaining energy level to determine the next most appropriate video segment to meet that energy level. However, as discussed above, the content creation algorithms used in these solutions consider bit rate, QP, and spatial resolution changes as means for generating bit streams at different energy levels [19,21,22,23]. This is primarily due to the lack of a direct approach to generate rate-controlled bit streams at specified decoding-complexities—a crucial missing element in the state-of-the-art. Therefore, it is clear that a need exists for a mechanism to generate decoding-complexity and rate-controlled bit streams at the encoder to fully realize the energy efficiency goals of standards such as Green-MPEG [32,33] that can also co-exist with current streaming solutions and decoder-side energy efficiency initiatives such as DVFS.
3. The Decoding-Complexity, Rate, and Distortion Relationship
In order to develop an algorithm to control the bit rate and decoding-complexity of a video sequence, it is necessary to first determine the relationship between these two parameters and the distortion produced when a particular coding parameter combination is selected by the encoder for a given content. As such, a content-adaptive decoding-complexity–rate–distortion model is necessary, where the decoding-complexity can be determined for various decoding operations based on the coding modes and features selected by the encoder. To achieve this, the decoding-complexity estimation models developed in [24,43,44,45] for both inter-predicted and intra-predicted coding units (CU) are used as a basis for this work, which will equip the encoder to compute the relative complexity of each decoding operation. This section describes the approach used to analyze the behavior of these three parameters and a content-dependent model that can be generated for the decoding-complexity–rate–distortion space.
3.1. The Decoding-Complexity, Rate, and Distortion Space
In HEVC, the optimum coding parameter combination of a CU is derived by using a Lagrangian optimization approach with the rate-distortion (RD) cost function
where is the empirically determined Lagrangian multiplier, p is a coding structure in the set of combinations , and and represent the distortion (squared error per pixel) and bit rate (bits per pixel), respectively. Each p in (1) results in different decoding-complexities at the decoder [24,44,45,46] that remain unknown to the encoder. In order to assess the impact of each p on the decoding-complexity, we first redefine the optimization function in (1) as
where is the relative decoding-complexity (cycles per pixel) of p obtained from [43,44,45]. Here, and are bit rate and decoding-complexity trade-off parameters analogous to in (1), respectively. The ranges of and define the decoding-complexity–rate–distortion space spanned by the coding parameter combinations in . Next, we analyze this relationship and derive a model of these parameters for use in a joint decoding-complexity and rate-controlled encoding algorithm.
3.2. The Decoding-Complexity, Rate and Distortion Behaviour
In order to determine the behavior of decoding-complexity, rate, and distortion, the parameter space created by (2) must first be determined. To achieve this, an experimental sweep of the space created by and was performed on six different test sequences (with representative and varying spatial and temporal characteristics). Empirical data were collected from both inter- and intra-predicted frames of these test sequences for QPs ranging from 0–51 [24]. The resulting decoding-complexity, rate, and distortion can thereafter be expressed for further analysis in terms of cycles per pixel (), bits per pixel (), and the mean squared error (), respectively, as follows.
where and correspond to the ith original and reconstructed pixel, respectively, q is the QP, and N is the number of pixels in the frame. Similarly, the and are defined as,
and
where and correspond to the frame width and frame height, respectively. Further, R and C represent the total number of bits required to encode the frame and the estimated decoding-complexity of that frame once encoded. In the model used in this work, the relative decoding-complexity is expressed in terms of the number of CPU cycles used by the HM 16.0 reference decoder for each operation when executed on an Intel x86 CPU architecture platform.
Figure 1 graphically illustrates the behaviors of decoding-complexity, rate, and distortion in the parameter space spanned by p, and for the “kimono 1080p” sequence, including the discrete operating points that can be achieved by the encoder (i.e., each data point in Figure 1 represents the resultant bit rate, decoding-complexity and distortion for a particular combination of and ). (The behaviors of decoding-complexity, rate, and distortion remain similar across QPs and sequences, albeit with different model parameters). It was observed that this general behavior can be modeled in a content-dependent manner using a 2-dimensional nth-power model given by
where , , , and are QP and content-dependent model parameters. Naturally, this implies that a content-adaptive approach is necessary to compute the appropriate model parameters dynamically, in order to determine the optimum coding structure p for particular content. The next section describes an approach to build upon the model in (6) and to adaptively compute its model parameters (as described in Section 4.3), which leads to the novel joint decoding-complexity and rate-controlled encoding algorithm proposed in this manuscript.
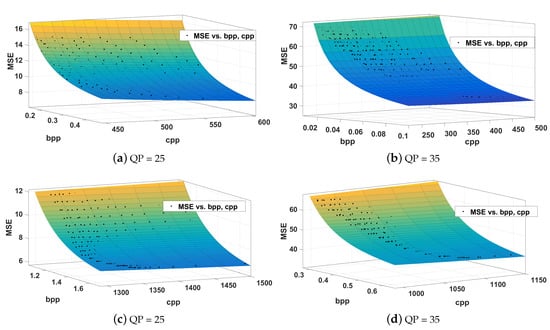
Figure 1.
The decoding-complexity (), rate () and distortion () behavior of inter-predicted (top row) and intra-predicted (bottom row) frames.
4. Joint Decoding-Complexity and Rate Control
As with any rate control algorithm, the joint control of both decoding-complexity and rate also requires target decoding-complexities and bit rates to be defined. In this context, this section first describes how these can be allocated at the CTU-level. This is followed by the derivation of an appropriate QP and content-adaptive decoding-complexity and rate trade-off factors in (6), and finally by an update algorithm to dynamically adapt the model parameters in (6).
4.1. CTU-Level Rate and Decoding-Complexity Allocation
Adopting a similar approach to the rate controller in the HM reference encoder [47,48], the group of picture (GOP)-level and frame-level bit rate and decoding-complexity targets can be used to derive their CTU-level allocations. In this case, the target number of bits for the GOP can be expressed as
where , , , , and W are the GOP size, bits remaining, average bits per frame, frames remaining, and window size, respectively [48]. (In this case, it is assumed that the bit rate and the number of frames to be encoded in the sequence is known ahead of the encoding process. E.g., an on-demand video streaming scenario.) The average bits per frame is given by where is the total number of bits assigned to the sequence and M is the total number of frames in the sequence. Similarly, the target decoding-complexity for the GOP becomes
where and are the total decoding-complexity budget left over and the average complexity per frame, which is given by Here, represents the total decoding-complexity assigned to the sequence. (The available decoding-complexity budget in this case is defined as the total number of CPU cycles that can be spent for the purpose of decoding a particular sequence with a known number of frames. This can be determined based on the remaining energy capacity of the battery powered decoding device, and is considered outside the scope of this work.) Throughout the remainder of the manuscript, as in the default configuration used in the HM 16.0 [49] encoder implementation.
Next, the bits and decoding-complexities allocated for the GOP in (7) and (8), respectively, must be distributed across the individual frames in the GOP. In this case, a similar approach is adopted for both quantities (i.e., bits and decoding-complexity) leading to a weighted distribution of the GOP-level allocation to each frame as shown in (9). For the jth frame in the GOP, the bit and decoding-complexity allocations are given by
where and the weights are defined as
Here, is the default weighting factor defined in HM16.0 reference encoder implementation [48,50] for the jth frame in the GOP. The weighting factor is experimentally determined based on the ratio of bits and decoding-complexities consumed by intra-predicted and inter-predicted frames in a typical video sequence. In this case, the numbers of bits and the decoding-complexities utilized within intra-predicted and inter-predicted frames were averaged across 50 frames for the six test sequences (Section 3.2) to determine , which is defined as
Finally, bit rates and decoding-complexity targets are allocated to the individual CTUs based on the MSE of the previous co-located CTU, as is often done in traditional rate control [51,52]. The decoding-complexity–rate–distortion model in (6) is used to these ends, and as the model parameters therein are functions of QP and content, the MSE of the kth CTU in the jth frame of the GOP is first predicted for each QP q which can be expressed as
where , , , and are the appropriate model parameters for that CTU. Here, and are the bpp and cpp calculated as the averages of the minimum and maximum of each respective parameter observed so far within the encoded sequence for the kth QP for a given frame type. Next, the actual MSE of the co-located CTU, , is then compared with for all QPs to obtain a QP such that
The and for QP are then used as the weights for both the bit rate and decoding-complexity to the CTU, respectively. Thus, the final target bit rate and decoding-complexity of the kth CTU in the jth frame in the GOP can be expressed as
where is the remaining bits or decoding-complexity available to the remaining CTUs in the frame, is the total number of CTUs in the frame, and is the bit or decoding-complexity weight for the CTU. Note that these bit rates and decoding-complexities can be expressed in terms of or by simply dividing by the number of pixels in the CTU.
4.2. Determining the Model Parameters and Trade-Off Factors
Having established the target bit rates and decoding-complexities at the CTU-level, the remaining modeling parameters in (6), QP and the trade-off factors for the bit rate and decoding-complexity must be determined at the CTU-level in order to apply the optimization function in (2) to determine the most appropriate coding structure for that CTU.
4.2.1. Determining QP
Once the CTU-level decoding-complexity and bit allocations are made, the QP selection is first performed using a similar MSE based approach. In this case, MSE of the co-located CTU, , is now compared with for all QPs to obtain a QP such that
In this case, MSE of the kth CTU in the jth frame of the GOP is estimated for each QP q using
where, N is the total number of pixels in the CTU and , and are the bit and decoding-complexity levels allocated for the CTU, respectively.
4.2.2. Determining and
Equations (16) and (17) imply that the CTU-level model parameters, together with the CTU-level bit rate and decoding-complexity allocations described in the previous subsection, completely define the optimization function in (2) needed to determine the optimum coding structure. Thus, from (14)–(17) for the kth CTU in the jth frame the bit rate and decoding-complexity trade-off parameters can be expressed as
and
respectively, where N is the number of pixels in the CTU.
It now becomes apparent that the two trade-off parameters are both content and QP-dependent via the four modeling parameters in (6), (16), and (17). However, a content-independent generic set of parameters can also be obtained (to be used as initial values in the adaptive model parameter computation process described in the following subsection (Section 4.3) from the data collected in Section 3 and [24]. In this case, MSE, bpp, and cpp values from 50 inter-coded and intra-coded frames of six different test sequences (three HD, and three CIF) [24] have been considered to derive these generic model parameters, which can be expressed as
and
for the two frame types. Naturally, the bit rate and decoding-complexity achieved using (20) and (21) will be inaccurate and not adaptive to the content. Hence, a mechanism to dynamically update the model parameters is necessary for joint decoding-complexity and rate-controlled encoding.
4.3. Dynamic Model Parameter Adaptation
In order to derive content-dependent model parameters, the generic parameter set in (20) and (21) can be adapted using a least mean square (LMS)-based approach [3,53]. To that end, the error between the assigned and achieved bit rate and decoding-complexity must be minimized. To do so in this case, a joint error function for the two quantities is first defined. Note that the following derivations will omit the k, j, and subscripts for notational simplicity, but the adaptation process must be applied independently to each CTU to compute their unique model parameters.
Now, let the difference between the assigned and achieved bit rate and decoding-complexity per pixel be and , respectively. Similarly, let the difference between the predicted distortion and actual distortion in terms of be . The total derivative of distortion in terms of can be expressed as the sum of partial derivatives of the dependent variables in the model in (6) and the definitions in (16) and (17) as
Obtaining the squared term of (23) and rearranging the terms
and dividing both sides by
The right hand side of (25) can be simplified further as
The objective of minimizing and simultaneously is now made possible by multiplying (26) and therefore (25) by . Hence, by combining (25) and (26), the joint error function to be minimized can be defined as
Thus, using (27) and a LMS adaptive filter, the updated model parameters can be expressed as
where , , , , , , , and are the newly computed and previous model parameters for the QP being considered. Further, , , , and are the LMS filter’s step size controlling the adaption speed and are empirically determined as , , , and respectively. Finally, the partial derivatives of in (28) with respect to the model parameters are
and
where , are the target bit rate and decoding-complexities, respectively. Once the model parameters are updated as per (28) in this manner, the new parameters can be used to determine the and trade-off factors for the mode selection in the cost function in (2).
5. Experimental Results and Discussion
This section presents the performance of the proposed CTU-level decoding-complexity and rate control algorithm. In this case, the rate and complexity-controlling capabilities of the proposed algorithm are first compared with two state-of-the-art decoding-complexity-aware encoding algorithms in the literature. Thereafter, experimental results for the power consumption characteristics of the decoder during a video streaming session are compared for two different CPU frequency governing methods. Finally, the experimental results and observations are discussed in detail for different use cases.
5.1. Simulation Environment
The proposed encoding algorithm is implemented in the HM 16.0 reference encoder. The decoding-complexity estimation models presented in [24,43,44,45], the Lagrangian cost function that determines the coding modes and the proposed decoding-complexity, and rate-controlling algorithm, are integrated into the HEVC encoding tool chain. The resultant bit streams are decoded using the openHEVC [54] software decoder. The decoding was performed on an Intel x86 Core i7-6500U system running Ubuntu 16.04 to measure the decoding-complexity performance of the bit streams. The proposed algorithm’s performance is compared with three state-of-the-art approaches: the power-aware encoding algorithm proposed by He et al. [20]; the rate, distortion, and decoder energy optimized encoding algorithm proposed by Herglotz et al. [46]; and the tunable HEVC decoder proposed by Nogues et al. [34]. The video sequences used in the experiments reported in this section are of HD (1920 × 1080) resolution. In this case, “Kimono” and “Parkscene” sequences are defined in the HEVC common test configurations [55] and the rest are a collection of proprietary sequences. Their sequence categories (i.e., motion and texture complexity levels) are defined in the Table 1. Each video sequence is encoded at 900 kbps, 1 Mbps, 2 Mbps, and 4 Mbps video bit rates using the random access configuration with rate control enabled. Moreover, the bit streams corresponding to the proposed algorithm were generated with two decoding-complexity levels, which are referred to as L1 and L2. The bit streams corresponding to these two levels are encoded such that decoding-complexities are 30% and 40% less (in terms of CPU cycles) as compared to HM encoded bit streams, respectively. The complexity of the decoding process was measured using the instruction level analysis tools callgrind/valgrind [56]. The numbers of CPU cycles identified were assigned as the available decoding-complexity budget for the sequence, when performing the decoding-complexity allocation calculations described in Section 4.1.

Table 1.
Rate controlling performances of the encoding algorithms.
Finally, the decoder’s energy consumption was determined by measuring the energy dissipated by the system during the video playback. In this context, a test bed that implements an online video streaming scenario where the openHEVC decoder is used as the playback client was used for this assessment. The encoded bit streams were streamed for a duration of 15 min and the energy capacity reduction of the playback device’s battery was measured using the Linux power measurement tools [57]. It should be noted that the measured battery capacity reduction corresponds to the overall energy consumption by the device that includes the energy consumed for the wireless transmission, video decoding, and video presentation. Furthermore, the relative energy consumption performances when using an application-specific DVFS algorithm [10] and the Linux ondemand frequency governor were also analyzed and are compared in the experimental results.
5.2. Evaluation Metrics
The performance of the proposed algorithm is evaluated in multiple stages. The evaluation metrics are described below.
5.2.1. Decoding-Complexity and Rate Control Performance
First, the decoding-complexity and rate-controlling capabilities of the proposed algorithm are evaluated by measuring the percentage error in achieving the target decoding-complexity and rate. In this case, the percentage error in bit rate is calculated using
where and are the achieved and target bit rate, respectively. Similarly, the overall decoding-complexity controlling performance of the proposed algorithm is measured using
where and are the target and achieved decoding-complexity levels in terms of the CPU cycles, for a particular number of frames. Moreover, the frame-wise rate and decoding-complexity control performances are measured using the percentage error between the allocated and actual number of bits and decoding-complexity per frame, respectively. (The decoding-complexity controlling performance is presented only for the proposed algorithm as the state-of-the-art algorithms do not support a mechanism to achieve a specified decoding-complexity).
5.2.2. Decoding-Complexity, Energy Reduction Performance, and Video Quality Impact
Next, the impact on video quality, decoding-complexity, and the respective energy reduction achieved at a particular decoding-complexity by the proposed algorithm (e.g., complexity level L2 is considered in this case), are compared against the state-of-the-art algorithms while keeping HM 16.0 as the reference. The impact on video quality for a given bit rate is assessed using the impact on PSNR given by
where and are the resultant average PSNRs for the reconstructed video sequences when using HM 16.0 and proposed and other state-of-the-art algorithms, respectively. Similarly, the reduction in decoding-complexity and the corresponding energy reduction are assessed using
and
respectively. Finally, for normalized comparison purposes, the proposed and state-of-the-art algorithms are assessed on the decoding-complexity and energy reduction achieved for a 1 dB PSNR loss in the video quality. In this case, per is given by
5.3. Performance Evaluation and Analysis
This section presents and analyzes the experimental results. In this context, the decoding-complexity and rate-controlling performances are analyzed first. Thereafter, the decoding-complexity reductions achieved by the proposed as well as state-of-the-art algorithms and their quality impacts are discussed with respect to the experimental setup discussed in Section 5.1. Here, the proposed algorithm considers generating bit streams with a 40% decoding-complexity reduction target over HM 16.0 (i.e., complexity level L2).
5.3.1. Rate Controlling Performance
The percentage deviations of the final bit rate achieved after encoding using the proposed (with joint rate and decoding-complexity controlling) and state-of-the-art algorithms (with rate controlling enabled) are presented in the Table 1. Here, the video sequences are encoded at four different bit rates (described in Section 5.1) and the averaged percentage error is presented for comparison.
It can be observed that the rate-controlling algorithm implemented in the HM 16.0 reference encoder shows 1.75% average error, which is less than the 3.08% deviation from the target bit rate experienced by He et al. [20]. This is mainly due to the content and QP-agnostic nature of the algorithm, despite its use of PU level prediction modes, integer-pel vs. fractional-pel motion vectors, and in-loop filtering decisions. However, ref. [46] uses QP-dependent trade-off factors for both rate and decoding-complexity; thus the impact on the rate controller is significantly improved compared to He et al. [20].
In contrast, the proposed algorithm uses a content-adaptive, decoding-complexity, rate, and distortion model to derive the QP as well as rate and decoding-complexity trade-off factors to determine the set of coding modes and structures that minimize the distortion while achieving a given bit and decoding-complexity budget. Therefore, as illustrated in the Table 1, the proposed algorithm achieves the allocated bit rate targets with <1% error indicating that both CTU-level bit allocation as well as coding parameter selection are more accurate and content-adaptive compared to the state-of-the-art approaches.
In addition, the frame-wise rate-controlling performances of the encoding algorithms were analyzed using the percentages of error between the allocated bits and actual bits per frame. A graphical illustration of this frame-wise percentage error is presented in the Figure 2. It can be observed that the rate-controlling algorithms implemented in HM 16.0 and other state-of-the-art encoding algorithms suffer from large percentage errors throughout the video sequence. The incorporation of a third parameter within the mode selection cost function in He et al. [20] and Herglotz et al. [46] crucially affect the rate controller in achieving the allocated number of bits for a given block. For example, both these algorithms use an RD-optimization-based bit allocation, QP, and Lagrangian parameter determination approach [48] for the rate control while utilizing three parameters in the cost function (rate, distortion, and decoding-complexity) for the coding mode selection. The correlation that exists between the three parameters is, however, ignored when performing the rate control, which results in large average rate-controlling errors, as illustrated in the Table 1. The rate-controlling algorithm in HM 16.0 which follows a R--based bit allocation and coding parameter selection approach also shows some deficiency in achieving the allocated bit budget for each frame. However, as illustrated in the Table 1, the HM 16.0 encoder still demonstrated a 1.75% error in its rate-controlling function.
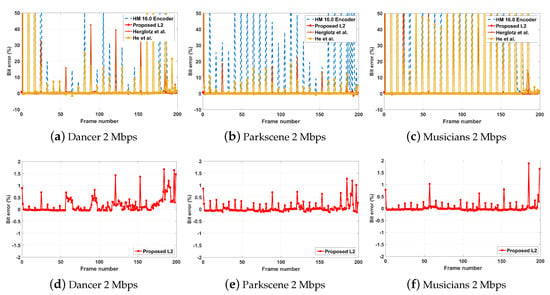
Figure 2.
(Top row): An illustration of the frame-wise percentage error between the allocated bits and actual bits for the HM 16.0, proposed, and other state-of-the-art algorithms for three HD test sequences. (Bottom row): A further illustration of the percentage frame-wise rate control performance of the proposed algorithm.
In contrast, the proposed algorithm enables the encoder to effectively utilize the correlation between the three parameters to perform rate and decoding-complexity allocation, and appropriate coding mode selection, resulting in a smaller percentage bit error (illustrated in the bottom row of Figure 2 and Table 1). Moreover, the parameter update process in Section 4.3 keeps the algorithm content-adaptive, further minimizing the rate control error.
5.3.2. Decoding-Complexity Controlling Performance
The experimental results summarized in Table 2 show the percentage error in the decoding-complexity controlling function of the proposed encoding algorithm (achieving a specified decoding-complexity is not possible for any of the state-of-the-art algorithms). The proposed algorithm shows on average an ≈1.78% decoding-complexity controlling error for both complexity levels considered (30% and 40% reductions over HM 16.0). The results suggest that the proposed algorithm is capable of generating a bit stream that adheres to a given bit rate and a decoding-complexity level. Furthermore, the frame-wise decoding-complexity error illustrated in the Figure 3 also reveals that the proposed encoding algorithm is capable of maintaining a very low error despite the dynamic nature of the video content. In summary, numerical and graphical results for the simultaneous rate and decoding-complexity control capability of the proposed method indicate that the proposed method is content-adaptive and capable of achieving specified bit and decoding-complexity targets.

Table 2.
Decoding-complexity-controlling performance of the proposed encoding algorithm.
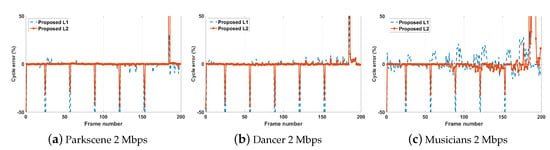
Figure 3.
An illustration of the frame-wise percentage error between the target decoding-complexity and the achieved decoding-complexity for the proposed algorithm at two complexity levels for a given bit rate (2 Mbps) for (a) Parkscene, (b) Dancer and (c) Musicians test sequences.
5.3.3. Decoding-Complexity Reduction and the Impact on Video Quality
The Table 3 demonstrates the average decoding-complexity reductions and the corresponding quality impact, in PSNR, for the proposed and state-of-the-art algorithms.

Table 3.
Decoding-complexity-reduction performance.
The algorithms proposed by He et al. [20] and Herglotz et al. [46] both achieved decoding-complexity reductions in the range of 10% and 20%, respectively. However, it was observed that those were achieved at the expense of a significant reduction in PSNR for a given bit rate. For example, although Herglotz et al. [46] uses a decoding-complexity estimation model [58,59,60], the bit rate, decoding-complexity trade-off factors are selected independently; thus, the impact on each other is overlooked during the coding mode selection. Furthermore, only the bit rate trade-off factor [47,49] is content-adaptive, and the decoding-complexity trade-off factor remains agnostic to the dynamics of the video sequence, which ultimately results in a higher quality loss. Similarly, the method proposed in [20] uses predefined trade-off factors and decoding-complexity-aware coding mode selection only at the PU level. Thus, the sacrifice made in video quality to maintain the bit rate requirement is greater, and performance is inferior to Herglotz et al. [46]. These results are illustrated graphically in the vs. decoding-complexity graphs presented in the Figure 4. Here, it can be observed that both these algorithms would experience a higher quality impact in a rate-controlled scenario if they were to achieve a particular decoding-complexity. However, it should be noted that the encoding algorithm proposed by Herglotz et al. has shown improvements in very low-in-complexity video sequences, such as “band,” “cafe,” “poznan st.,” etc.
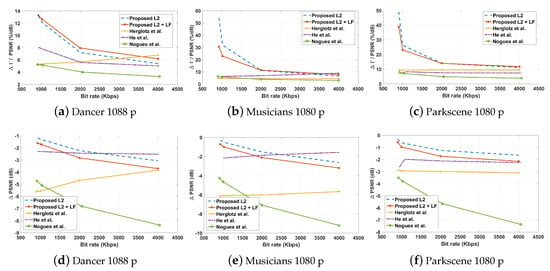
Figure 4.
An illustration of the variation of the , ratio (top row), i.e., , and (bottom row), with respect to the bit rate.
The approach by Nogues et al. [11] modifies the decoding operations to reduce the decoding-complexity. For example, the skipping of in-loop filtering and simplifying the motion compensation operations within the decoder results in a significant complexity reduction. (It should be noted that the presented results correspond to the highest complexity reduction that can be achieved by applying the decoder modifications proposed in [11] to all frames in the bit stream). However, changing the motion compensation filters and thereby applying the decoded residuals on a predicted PU which is different from that of the encoder’s, causes more distortions in the reconstructed block. Although the intra-frames that appear within the given intervals avoid the propagation of these errors, the algorithm results in a much larger PSNR reduction (cf. Figure 4).
In contrast, the proposed algorithm uses a more comprehensive and dynamic approach to simultaneously control both decoding-complexity and bit rate. First, the use of more accurate and detailed decoding-complexity estimation models enables the encoder to estimate the decoding-complexity requirements for a given coding mode. Next, the proposed decoding-complexity–rate–distortion model allows the encoder to determine the impact of a coding mode on all three parameters. Finally, the continuous update of the decoding-complexity–rate–distortion model allows the encoder to pick the most content-relevant trade-off factors when selecting the coding modes that minimize the distortion while achieving the given rate and decoding-complexity constraints. As observed from Figure 4, the proposed algorithm allows the encoder to generate bit streams that provide the least quality impacts on a given decoding-complexity. Moreover, the proposed algorithm is highly scalable and provides the capability to generate bit streams with multiple bit rate and decoding-complexity levels—a crucial benefit for adaptive video streaming services that target streaming videos to mobile devices. For instance, in this case, the decoding-complexity level L2 (i.e., 40% decoding-complexity reduction with respect to HM16.0) results in on average −12.71% decoding-complexity reduction when using the openHEVC decoder. Finally, if the bit streams generated by the proposed algorithms are decoded with a decoder that skips the in-loop filter operations (e.g., openHEVC), it can be observed that decoding-complexity can be further reduced by , with only a minor impact on the video quality. Thus, it is evident that the bit streams generated by the proposed algorithm can be subjected to decoder modifications such as [34] to attain further complexity reductions.
Figure 4 also demonstrates the decoding-complexity reduction that can be achieved for a 1 dB quality loss in PSNR. It can be observed that the proposed algorithm on average achieves a greater across all bit rates. This is much larger for the proposed algorithm at lower bit rates, due to the reduced quality impact with respect to the HM encoded bit stream. Thus, it is apparent that the proposed algorithm can produce more decoding-complexity reduction than state-of-the-art algorithms for each 1 dB quality loss. Finally, Figure 5 illustrates the visual quality impact of the video sequences reconstructed from the bit streams encoded by HM16.0, the proposed algorithm, and other state-of-the-art methods. It can be observed that despite the PSNR drops listed in the Table 3, the bit streams generated by the proposed algorithm retain a visual quality level similar to that of the bit streams prepared by the HM 16.0 encoder.

Figure 5.
An illustration on the visual quality impact of the reconstructed video sequences of bit streams prepared by the (a) HM 16.0 encoder, (b) proposed algorithm, and other state-of-the-art algorithms proposed by (c) He et al. [20], (d) Herglotz et al. [46], and (e) Nogues et al. [34]. The figures correspond to the frame number 36 of the “Kimono HD” sequence encoded at 2 Mbps.
5.3.4. Decoding Energy Reduction Performance
Next, the actual energy consumption performance for the bit streams generated by the proposed and state-of-the-art algorithms is compared for a video streaming use case. First, the generated bit streams are decoded using the openHEVC video decoder with Linux ondemand as the frequency scaling governor [61]. It can be observed in the Table 4 that the proposed and state-of-the-art algorithms demonstrate an energy-consumption reduction in the range of ≈4% compared to HM 16.0 encoded video bit streams. Moreover, forcing the decoder to skip in-loop filters enables the proposed algorithm to increase the energy-consumption reduction up to 5.65%.

Table 4.
Energy reduction performance during video streaming.
Changing the Linux ondemand governor to a more application-specific DVFS algorithm [10] that alters the CPU’s operational frequency based on the estimated complexity of the next video frame improves the energy-consumption reduction of all the algorithm. In this case, the proposed algorithm has achieved 7.77% and 9.10% decoding energy-consumption reductions compared to the HM encoded bit streams—a non-trivial performance with only −1.44 dB and −2.03 dB quality impacts for with and without in-loop filter operations, respectively. The decoding energy reduction achieved per 1 dB PSNR video quality loss for the proposed and state-of-the-art algorithms is presented in the Table 5, and the achieved for a 1 dB quality loss is graphically demonstrated for three different test sequences in Figure 6. These results further corroborate that the energy reductions achieved by the bit streams generated with the proposed algorithm result in smaller impacts on quality compared to the state-of-the-art approaches. Thus, the decoding energy consumption reduction achieved for each 1 dB PSNR loss is also relatively large for the proposed encoding algorithm.

Table 5.
Decoding-complexity and energy reduction per 1 dB quality loss for the proposed and state-of-the-art algorithms.
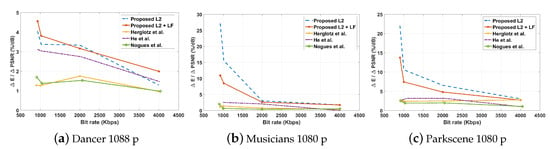
Figure 6.
An illustration of the variation of the , ratio, i.e., , with respect to the bit rate for (a) Dancer, (b) Musicians and (c) Parkscene HD test sequences.
5.3.5. Impact of the Proposed Encoding Framework on Different Decoders and CPU Architectures
The proposed encoding algorithm presented in this manuscript is based on the HM 16.0 reference encoder and decoder implementations on an Intel x86 CPU architecture. For instance, the bpp and MSE parameters defined in Section 3 are based on the corresponding values generated by the HM 16.0 encoder. Furthermore, cpp values utilized throughout the modeling phase in Section 3 correspond to the decoding-complexity levels profiled for HM 16.0 decoder implementation.
The decoding-complexity level is tightly coupled with the implementation details, CPU architecture, and hardware level optimization. Therefore, it is important that complete decoder profiling is carried out for each decoder implementation on each CPU architecture to achieve an optimal decoding-complexity/energy reduction. However, the focus of this work is to present a framework which can be used to achieve decoding-complexity/energy reduction by generating joint decoding-complexity and rate-controlled bit streams. Therefore, decoder profiling for individual implementation and architecture is considered outside the scope of this work.
However, the experimental results presented in Table 3, Table 4 and Table 5 correspond to the decoding-complexity and associated energy reductions when decoding bit streams use openHEVC decoder implementation on an Intel x86 CPU. These results correspond to the decoding-complexity/energy reductions achieved when bit streams are encoded with 40% less decoding-complexity to that of HM 16.0 decoder. Similarly, the experimental results in Table 6 present the decoding energy reduction achieved when decoding the bit streams using MXplayer [62] running on a Samsung Galaxy Tab A device that consists of an Exynos 8890 processor with ARMv8 Instruction Set Architecture [63]. It can be observed that the percentage energy reduction level is different to that in the Intel x86 results. However, overall, the bit streams generated by the proposed algorithm outperform the energy reduction per 1 dB PSNR quality loss compared to the state-of-the-art methods. Thus, the resultant energy reductions with the proposed encoding framework with different CPU architectures and decoder implementations (even though they are sub-optimal) are still significant, despite being optimized for a different encoding and decoding architecture.

Table 6.
Decoder energy reduction performance on a RISC-based ARM CPU architecture.
6. Conclusions
Fluctuations in network bandwidth and the limited availability of processing and energy resources of consumer electronic devices demand video streaming solutions that adapt to changing network and device constraints. In this context, although solutions such as HTTP adaptive streaming consider the network bandwidth problem, adapting the transmitted video contents by considering both the network bandwidth and an individual device’s energy constraints remains a compelling challenge.
To this end, this paper presents an encoding algorithm that can generate HEVC-compliant bit streams with multiple arbitrary bit rate and decoding-complexity levels. The experimental results with respect to the simultaneous bit rate and decoding-complexity control suggest that the proposed algorithm achieves a target bit rate and a decoding-complexity level with 0.47% and 1.78% average errors, respectively. Furthermore, the proposed algorithm demonstrates an average 10.11 (%/dB) decoding-complexity reduction and up to 10.52 (%/dB) decoding energy reduction for 1 dB PSNR quality loss compared to HM 16.0 encoded bit streams in an Intel x86 CPU architecture—a significant improvement compared to the state-of-the-art techniques. In addition, the bit streams generated by the proposed algorithm demonstrate 20.36 (%/dB) average energy reduction per 1 dB quality loss for a RISC-based ARM CPU architecture. Finally, the future work will focus on developing the proposed model into an adaptive video streaming solution that considers the end-to-end network and device resource availability to determine coding parameters used to encode the streaming video.
Author Contributions
Conceptualization, T.M.; methodology, T.M.; software, T.M.; validation, T.M., D.T., and H.K.A.; formal analysis, D.T. and H.K.A.; investigation, T.M. and D.T.; resources, A.F. and C.H.; data curation, T.M.; writing—original draft preparation, T.M.; writing—review and editing, D.T., H.K.A., C.H., and A.F.; visualization, D.T. and H.K.A.; supervision, D.T., H.K.A., and A.F.; project administration, A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cisco. Cisco Annual Internet Report (2018–2023) White Paper; Cisco: San Jose, CA, USA, 2020. [Google Scholar]
- Stockhammer, T.; Sodagar, I. MPEG DASH: The Enabler Standard for Video Delivery over the Internet. SMPTE Motion Imaging J. 2012, 121, 40–46. [Google Scholar] [CrossRef]
- Mallikarachchi, T. HEVC Encoder Optimization and Decoding-Complexity-Aware Video Encoding; University of Surrey: Guildford, UK, 2017. [Google Scholar]
- Erabadda, B.; Mallikarachchi, T.; Hewage, C.; Fernando, A. Quality of Experience (QoE)-Aware Fast Coding Unit Size Selection for HEVC Intra-Prediction. Future Internet 2019, 11, 175. [Google Scholar] [CrossRef]
- Ren, R.; Juarez, E.; Sanz, C.; Raulet, M.; Pescador, F. On-line energy estimation model of an RVC-CAL HEVC decoder. In Proceedings of the 2014 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 10–13 January 2014. [Google Scholar]
- Meng, S.; Duan, Y.; Sun, J.; Guo, Z. Highly optimized implementation of HEVC decoder for general processors. In Proceedings of the 2014 IEEE 16th International Workshop on Multimedia Signal Processing (MMSP), Jakarta, Indonesia, 22–24 September 2014. [Google Scholar]
- Magoulianitis, V.; Katsavounidis, I. HEVC decoder optimization in low power configurable architecture for wireless devices. In Proceedings of the 2015 IEEE 16th International Symposium on A World of Wireless, Mobile and Multimedia Networks (WoWMoM), Boston, MA, USA, 14–17 June 2015. [Google Scholar]
- Ren, R.; Juárez, E.; Sanz, C.; Raulet, M.; Pescador, F. Energy-aware decoders: A case study based on an RVC-CAL specification. In Proceedings of the IEEE International Conference Design and Architectures for Signal and Image Processing (DASIP), Madrid, Spain, 8–10 October 2014. [Google Scholar]
- Erwan Nogues, D.M.; Pelcat, M. Algorithmic-level Approximate Computing Applied to Energy Efficient HEVC Decoding. IEEE Trans. Emerg. Top. Comput. 2016, 7, 5–17. [Google Scholar] [CrossRef]
- Raffin, E.; Nogues, E.; Hamidouche, W.; Tomperi, S.; Pelcat, M.; Menard, D. Low power HEVC software decoder for mobile devices. J. Real Time Image Process. 2016, 12, 495–507. [Google Scholar] [CrossRef]
- Nogues, E.; Berrada, R.; Pelcat, M.; Menard, D.; Raffin, E. A DVFS based HEVC decoder for energy-efficient software implementation on embedded processors. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), Turin, Italy, 29 June–3 July 2015; pp. 1–6. [Google Scholar]
- Kim, W.; Shin, D.; Yun, H.S.; Kim, J.; Min, S.L. Performance comparison of dynamic voltage scaling algorithms for hard real-time systems. In Proceedings of the IEEE Real-Time and Embedded Technology and Applications Symposium, San Jose, CA, USA, 27 September 2002. [Google Scholar]
- Benmoussa, Y.; Senn, E.; Derouineau, N.; Tizon, N.; Boukhobza, J. Green metadata based adaptive DVFS for energy efficient video decoding. In Proceedings of the IEEE Workshop on Power and Timing Modeling, Optimization and Simulation (PATMOS), Bremen, Germany, 21–23 September 2016. [Google Scholar]
- Van der Schaar, M.; Andreopoulos, Y. Rate-distortion-complexity modeling for network and receiver aware adaptation. IEEE Trans. Multimed. 2005, 7, 1520–9210. [Google Scholar] [CrossRef]
- Van der Schaar, M.; Andreopoulos, Y.; Li, Q. Real-time ubiquitous multimedia streaming using rate-distortion-complexity models. In Proceedings of the IEEE International Conference on Global Telecommunications, Dallas, TX, USA, 29 November–3 December 2004; pp. 639–643. [Google Scholar]
- Andreopoulos, Y.; der Schaar, M.V. Complexity-Constrained Video Bitstream Shaping. IEEE Trans. Signal Process. 2007, 55, 1967–1974. [Google Scholar] [CrossRef]
- Shenoy, P.; Radkov, P. Proxy-assisted power-friendly streaming to mobile devices. In Proceedings of the Multimedia Computing and Networking Conference, Santa Clara, CA, USA, 20–24 January 2003; pp. 177–191. [Google Scholar]
- Sodagar, I. The MPEG-DASH Standard for Multimedia Streaming Over the Internet. IEEE Multimed. 2011, 18, 62–67. [Google Scholar] [CrossRef]
- Kennedy, M.; Venkataraman, H.; Muntean, G. Battery and Stream-Aware Adaptive Multimedia Delivery for wireless devices. In Proceedings of the IEEE Conference on Local Computer Networks (LCN), Denver, CO, USA, 10–14 October 2010; pp. 843–846. [Google Scholar]
- He, Y.; Kunstner, M.; Gudumasu, S.; Ryu, E.S.; Ye, Y.; Xiu, X. Power aware HEVC streaming for mobile. In Proceedings of the IEEE International Conference on Visual Communications and Image Processing, Kuching, Malaysia, 17–20 November 2013; pp. 2–6. [Google Scholar]
- Moldovan, A.N.; Muntean, C.H. Subjective Assessment of BitDetect—A Mechanism for Energy-Aware Multimedia Content Adaptation. IEEE Trans. Broadcast. 2012, 58, 480–492. [Google Scholar] [CrossRef]
- Lee, H.; Lee, Y.; Lee, J.; Lee, D.; Shin, H. Design of a mobile video streaming system using adaptive spatial resolution control. IEEE Trans. Consum. Electron. 2009, 55, 1682–1689. [Google Scholar] [CrossRef]
- Longhao, Z.; Trestian, R.; Muntean, G.M. eDOAS: Energy-aware device-oriented adaptive multimedia scheme for Wi-Fi offload. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 2916–2921. [Google Scholar]
- Mallikarachchi, T.; Talagala, D.S.; Arachchi, H.K.; Fernando, A. Decoding-Complexity-Aware HEVC Encoding Using a Complexity–Rate–Distortion Model. IEEE Trans. Consum. Electron. 2018, 64, 35–43. [Google Scholar] [CrossRef]
- Hoque, M.A.; Siekkinen, M.; Nurminen, J.K. Energy efficient multimedia streaming to mobile devices—A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 579–597. [Google Scholar] [CrossRef]
- Almowuena, S.; Rahman, M.M.; Hsu, C.H.; Hassan, A.A.; Hefeeda, M. Energy-Aware and Bandwidth-Efficient Hybrid Video Streaming Over Mobile Networks. IEEE Trans. Multimed. 2016, 18, 102–115. [Google Scholar] [CrossRef]
- Sharangi, S.; Krishnamurti, R.; Hefeeda, M. Energy-Efficient Multicasting of Scalable Video Streams over WiMAX Networks. IEEE Trans. Multimed. 2011, 13, 102–115. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Dong, M.; Ma, Z.; Fernandes, F.C. GreenTube: Power Optimization for Mobile Videostreaming via Dynamic Cache Management. In Proceedings of the ACM International Conference on Multimedia, MM’12, Nara, Japan, 29 October–2 November 2012; ACM: New York, NY, USA, 2012; pp. 279–288. [Google Scholar]
- Wang, L.; Ukhanova, A.; Belyaev, E. Power consumption analysis of constant bit rate data transmission over 3G mobile wireless networks. In Proceedings of the in International Conference on ITS Telecommunications (ITST), St. Petersburg, Russia, 23–25 August 2011; pp. 23–25. [Google Scholar]
- Duan, Y.; Sun, J.; Yan, L.; Chen, K.; Guo, Z. Novel Efficient HEVC Decoding Solution on General-Purpose Processors. IEEE Trans. Multimed. 2014, 16, 1915–1928. [Google Scholar] [CrossRef]
- Pescador, F.; Chavarrias, M.; Garrido, M.J.; Juarez, E.; Sanz, C. Complexity analysis of an HEVC decoder based on a digital signal processor. IEEE Trans. Consum. Electron. 2013, 59, 391–399. [Google Scholar] [CrossRef]
- Moving Picture Experts Group (MPEG). Call for Proposals on Green MPEG; Joint Collaborative Team on Video Coding (JCT-VC): Incheon, Korea, 2013. [Google Scholar]
- Fernandes, F.C.; Ducloux, X.; Ma, Z.; Faramarzi, E.; Gendron, P.; Wen, J. The Green Metadata Standard for Energy-Efficient Video Consumption. Math. Comp. 2015, 22, 80–87. [Google Scholar] [CrossRef]
- Nogues, E.; Holmbacka, S.; Pelcat, M.; Menard, D.; Lilius, J. Power-aware HEVC decoding with tunable image quality. In Proceedings of the IEEE Workshop on Signal Processing Systems, Belfast, UK, 20–22 October 2014; pp. 1–6. [Google Scholar]
- Kim, E.; Jeong, H.; Yang, J.; Song, M. Balancing energy use against video quality in mobile devices. IEEE Trans. Consum. Electron. 2014, 60, 517–524. [Google Scholar] [CrossRef]
- Liang, W.Y.; Chang, M.F.; Chen, Y.L.; Lai, C.F. Energy efficient video decoding for the Android operating system. In Proceedings of the IEEE International Conference on Consumer Electronics, Las Vegas, NV, USA, 11–14 January 2013; pp. 344–345. [Google Scholar]
- Chen, Y.L.; Chang, M.F.; Liang, W.Y. Energy-efficient video decoding schemes for embedded handheld devices. Multimed. Tools Appl. 2015, 1–20. [Google Scholar] [CrossRef]
- Ahmad, H.; Saxena, N.; Roy, A.; De, P. Battery-aware rate adaptation for extending video streaming playback time. Multimed. Tools Appl. 2018, 77, 23877–23908. [Google Scholar] [CrossRef]
- Zhang, Q.; Dai, Y.; Ma, S.; Kuo, C.C.J. Decoder-Friendly Subpel MV Selection for H.264/AVC Video Encoding. In Proceedings of the IEEE International Conference on Intelligent Information Hiding and Multimedia, Pasadena, CA, USA, 18–20 December 2006. [Google Scholar]
- Hu, Y.; Li, Q.; Ma, S.; Kuo, C.C.J. Decoder-Friendly Adaptive Deblocking Filter (DF-ADF) Mode Decision in H.264/AVC. In Proceedings of the IEEE Symposium on Circuits and Systems, New Orleans, LA, USA, 27–30 May 2007. [Google Scholar]
- Lee, S.W.; Kuo, C.C.J. H.264/AVC entropy decoder complexity analysis and its applications. J. Vis. Commun. Image Represent. 2011, 22, 61–72. [Google Scholar] [CrossRef]
- Corrêa, D.; Correa, G.; Palomino, D.; Zatt, B. OTED: Encoding Optimization Technique Targeting Energy-Efficient HEVC Decoding. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018. [Google Scholar]
- Mallikarachchi, T.; Arachchi, H.K.; Talagala, D.; Fernando, A. CTU Level Decoder Energy Consumption Modelling for Decoder Energy-Aware HEVC Encoding. In Proceedings of the IEEE International Conference on Consumer Electronics, Las Vegas, NV, USA, 7–11 January 2016. [Google Scholar]
- Mallikarachchi, T.; Talagala, D.; Arachchi, H.K.; Fernando, A. A feature based complexity model for decoder complexity optimized HEVC video encoding. In Proceedings of the IEEE International Conference on Consumer Electronics, Las Vegas, NV, USA, 8–10 January 2017. [Google Scholar]
- Mallikarachchi, T.; Arachchi, H.K.; Talagala, D.; Fernando, A. Decoder energy-aware intra-coded HEVC bit stream generation. In Proceedings of the IEEE International Conference on Multimedia and Expo, Seattle, WA, USA, 11–15 July 2016. [Google Scholar]
- Herglotz, C.; Kaup, A. Joint optimization of rate, distortion, and decoding energy for HEVC intraframe coding. In Proceedings of the IEEE International Conference on Image Processing, Phoenix, AZ, USA, 25–28 September 2016. [Google Scholar]
- Li, B.; Li, H.; Li, L.; Zhang, J. Lambda-Domain Rate Control Algorithm for High Efficiency Video Coding. IEEE Trans. Image Process. 2014, 23, 3841–3854. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Li, H.; Li, L.; Zhang, J. Rate Control by R-Lambda Model for HEVC. In Joint Collaborative Team on Video Coding (JCT-VC); ITU-T: Shanghai, China, 2012. [Google Scholar]
- JCT-VC. HEVC Reference Software—HM-16.0. Available online: https://hevc.hhi.fraunhofer.de/svn/svn_HEVCSoftware/tags/HM-16.0/ (accessed on 15 July 2020).
- McCann, K.; Rosewarne, C.; Bross, B.; Naccari, M.; Sharman, K.; Sullivan, G. High Efficiency Video Coding (HEVC) Test Model 16 (HM16) Encoder Description; Joint Collaborative Team on Video Coding (JCT-VC): Torino, Italy, 2014. [Google Scholar]
- Sun, H.; Zhang, C.; Gao, S. LCU-Level bit allocation for rate control in High Efficiency Video Coding. In Proceedings of the IEEE China Summit and Inter. Conference Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014. [Google Scholar]
- Choi, H.; Yoo, J.; Nam, J.; Sim, D.; Bajic, I.V. Pixel-Wise Unified Rate-Quantization Model for Multi-Level Rate Control. IEEE J. Sel. Top. Signal Process. 2013, 7, 1112–1123. [Google Scholar] [CrossRef]
- Haykin, S.; Widrow, B. Least-Mean-Square Adaptive Filters; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; pp. 175–240. [Google Scholar] [CrossRef]
- OpenHEVC. Open-Source HEVC Decoder. Available online: https://github.com/OpenHEVC/openHEVC (accessed on 15 July 2020).
- Bossen, F. Common Test Conditions and Software Reference Configurations; Joint Collaborative Team on Video Coding (JCT-VC): Torino, Italy, 2013. [Google Scholar]
- Valgrind. The Valgrind Quick Start Guide. Available online: http://valgrind.org/docs/manual/quick-start.html (accessed on 15 July 2020).
- UPower. Middleware for Power Management on Linux Systems. Available online: https://upower.freedesktop.org/ (accessed on 15 July 2020).
- Herglotz, C.; Springer, D.; Eichenseer, A.; Kaup, A. Modeling the energy consumption of HEVC intra decoding. In Proceedings of the IEEE International Conference on Systems, Signals, and Image Processing, Bucharest, Romania, 7–9 July 2013; pp. 91–94. [Google Scholar]
- Herglotz, C.; Springer, D.; Kaup, A. Modeling the energy consumption of HEVC P- and B-frame decoding. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 3661–3665. [Google Scholar]
- Herglotz, C.; Walencik, E.; Kaup, A. Estimating the HEVC decoding energy using the decoder processing time. In Proceedings of the IEEE Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 513–516. [Google Scholar]
- Brodowski, D.; Golde, N. CPU Frequency and Voltage Scaling Code in the Linux(TM) Kernel. Available online: https://www.kernel.org/doc/Documentation/cpu-freq/governors.txt (accessed on 15 July 2020).
- MXplayer. Video Player with Hardware Acceleration. Available online: https://play.google.com/store/apps/details?id=com.mxtech.videoplayer.ad&hl=en_GB (accessed on 15 July 2020).
- Exynos 8 Octa (8890). Available online: https://en.wikichip.org/wiki/samsung/exynos/8890 (accessed on 15 July 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).