Input Selection Methods for Soft Sensor Design: A Survey
Abstract
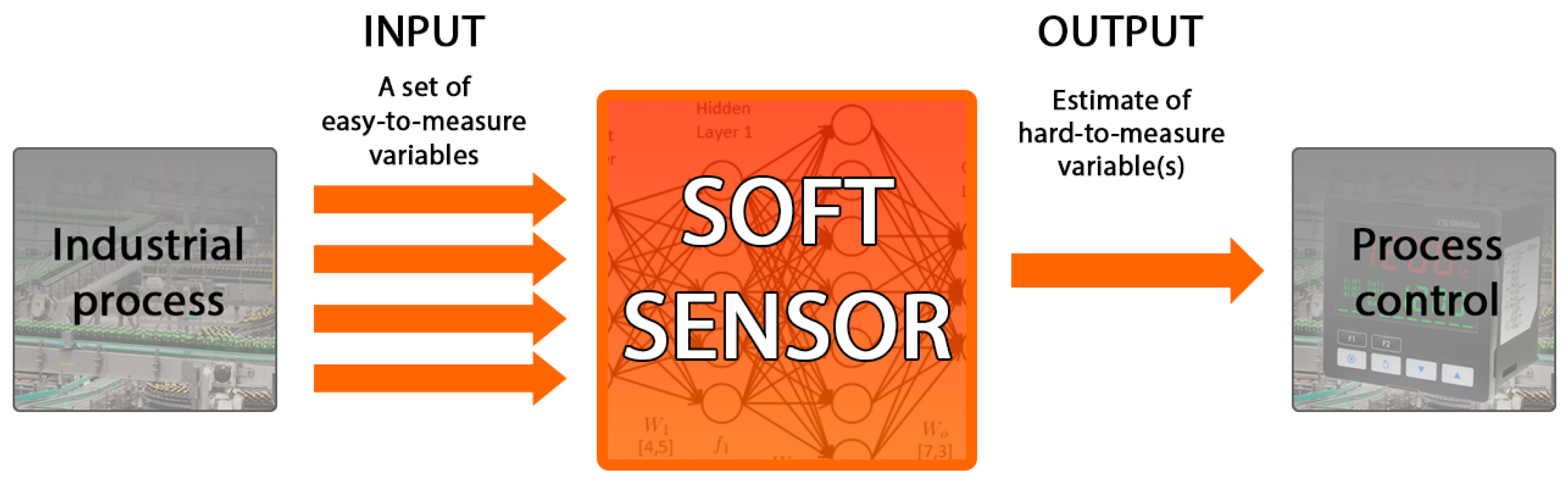
1. Introduction
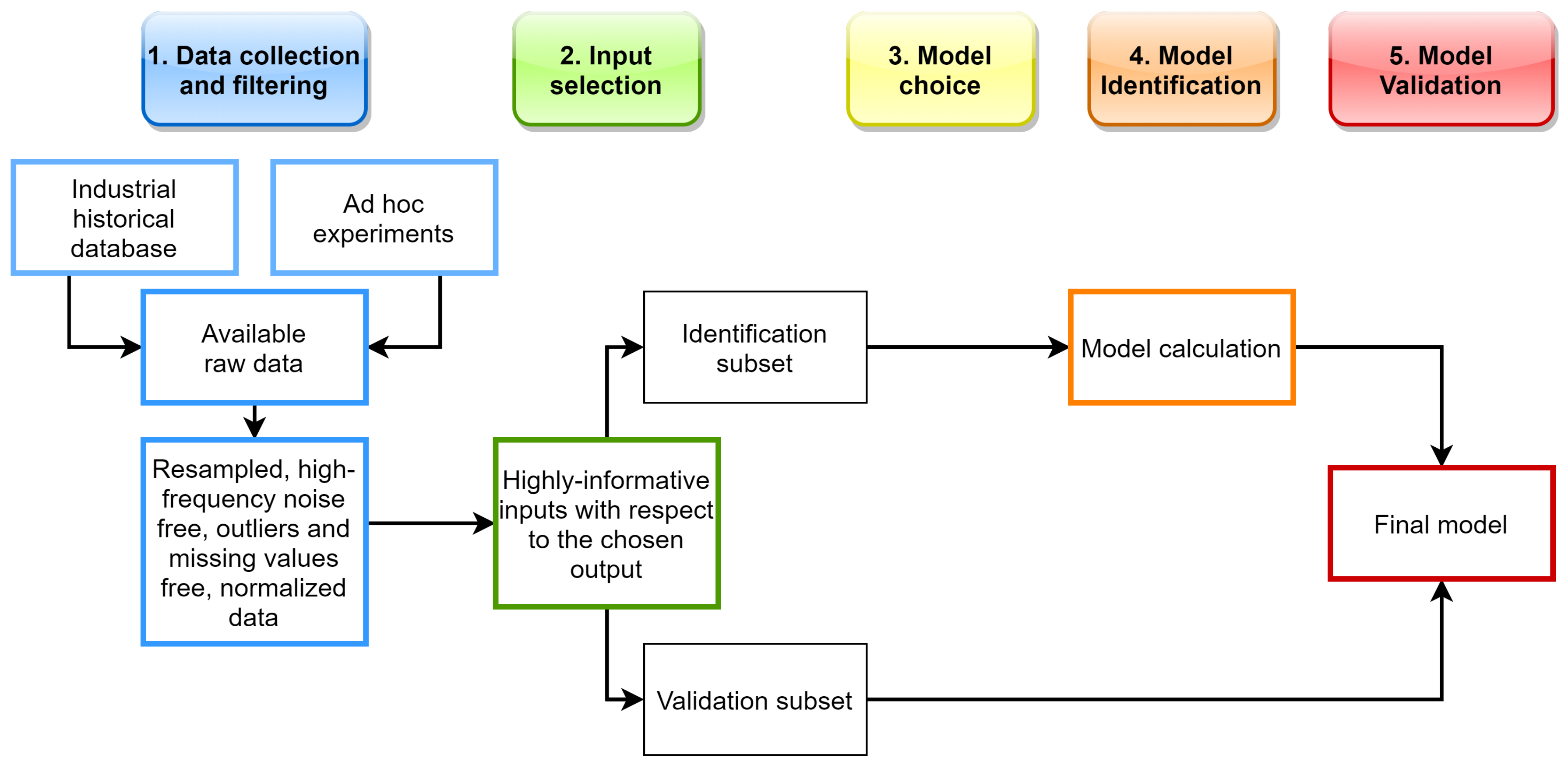
2. SS Design Stages
- Data collection and filtering;
- Input variables selection;
- Model structure choice;
- Model identification;
- Model validation.
- Identification data
- Validation data
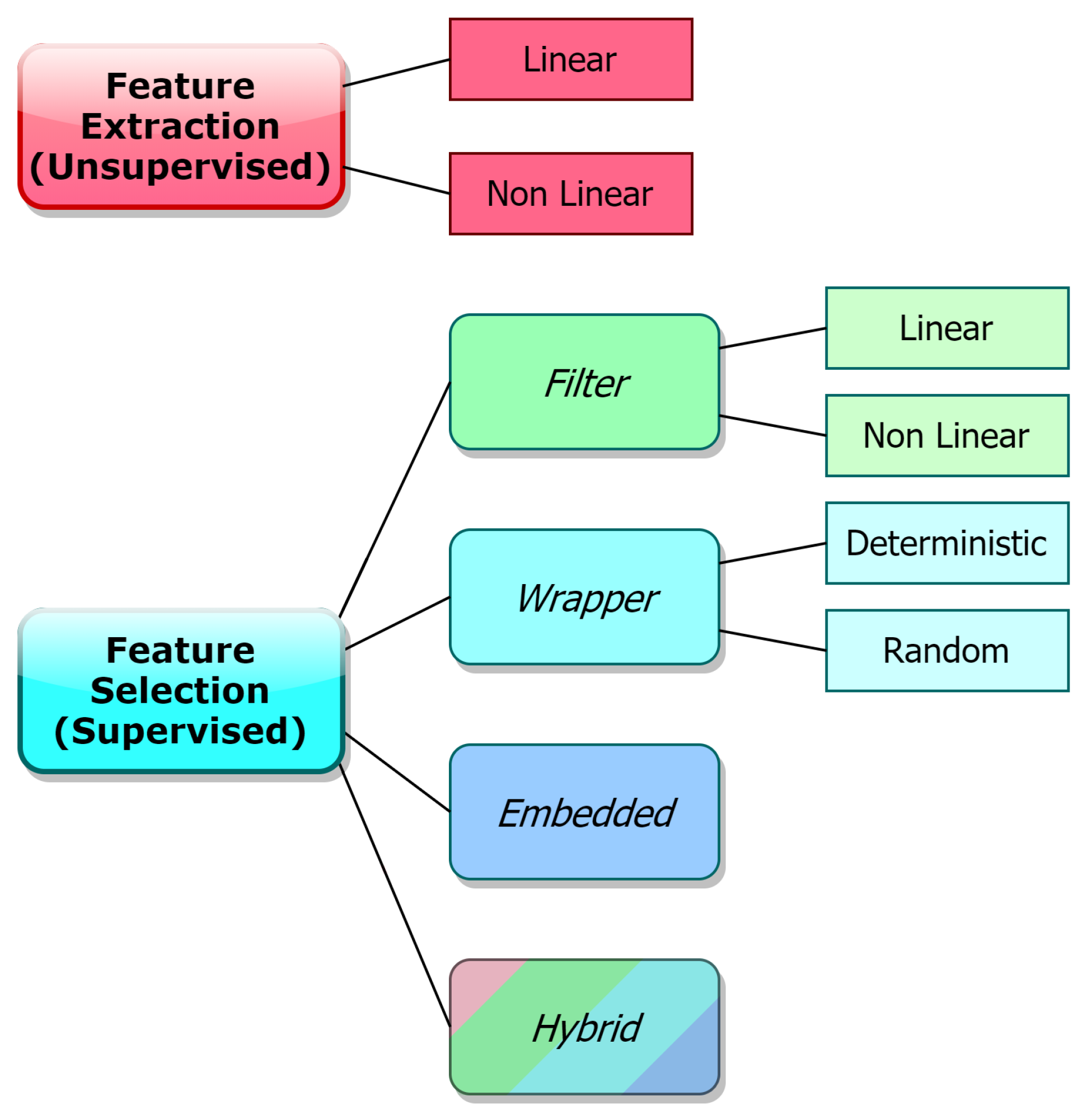
3. The Input Selection Problem in SS Design
- Feature Extraction (FE, Unsupervised)
- Feature Selection (FS, Supervised)
4. Feature Extraction
5. Feature Selection
- Filters
- Wrappers
- Embedded (model-based)
- Hybrid approaches
5.1. Filter Methods
5.2. Wrapper Methods
5.3. Embedded Methods
5.4. Hybrid Methods
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fortuna, L.; Graziani, S.; Rizzo, A.; Xibilia, M.G. Soft Sensors for Monitoring and Control of Industrial Processes, 1st ed.; Springer: London, UK, 2007. [Google Scholar]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven soft sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]
- Wold, S. Chemometrics; what do we mean with it, and what do we want from it? Chem. Intell. Lab. Syst. 1995, 30, 109–115. [Google Scholar] [CrossRef]
- Otto, M. Chemometrics: Statistics and Computer Application in Analytical Chemistry, 3rd ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Souza, F.A.A.; Araújo, R.; Mendes, J. Review of Soft Sensors Methods for Regression Applications. Chem. Intell. Lab. Syst. 2016, 152, 69–79. [Google Scholar] [CrossRef]
- Fortuna, L.; Giannone, P.; Graziani, S.; Xibilia, M.G. Virtual Instruments Based on Stacked Neural Networks to Improve Product Quality Monitoring in a Refinery. IEEE Trans. Instrum. Meas. 2007, 56, 95–101. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Xibilia, M.G. Virtual instruments in refineries. IEEE Instrum. Meas. Mag. 2005, 8, 26–34. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Xibilia, M.G. Soft sensors for product quality monitoring in debutanizer distillation columns. Control Eng. Pract. 2005, 13, 499–508. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Xibilia, M.G.; Barbalace, N. Fuzzy activated neural models for product quality monitoring in refineries. IFAC Proc. Vol. 2005, 38, 159–164. [Google Scholar] [CrossRef]
- Graziani, S.; Xibilia, M.G. Design of a Soft Sensor for an Industrial Plant with Unknown Delay by Using Deep Learning. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Pani, A.K.; Amin, K.G.; Mohanta, H.K. Soft sensing of product quality in the debutanizer column with principal component analysis and feed-forward artificial neural network. Alex. Eng. J. 2016, 55, 1667–1674. [Google Scholar] [CrossRef]
- Graziani, S.; Xibilia, M.G. Deep Structures for a Reformer Unit Soft Sensor. In Proceedings of the 2018 IEEE 16th International Conference on Industrial Informatics (INDIN), Porto, Portugal, 18–20 July 2018; pp. 927–932. [Google Scholar] [CrossRef]
- Stanišić, D.; Jorgovanović, N.; Popov, N.; Čongradac, V. Soft sensor for real-time cement fineness estimation. ISA Trans. 2015, 55, 250–259. [Google Scholar] [CrossRef]
- Seraj, M.; Aliyari Shoorehdeli, M. Data-driven predictor and soft-sensor models of a cement grate cooler based on neural network and effective dynamics. In Proceedings of the 2017 Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017. [Google Scholar] [CrossRef]
- Bhavani, N.P.G.; Sujatha, K.; Kumaresan, M.; Ponmagal, R.S.; Reddy, S.B. Soft sensor for temperature measurement in gas turbine power plant. Int. J. App. Eng. Res. 2014, 9, 21305–21316. [Google Scholar]
- Sujatha, K.; Bhavani, N.P.G.; Cao, S.-Q.; Kumar, K.S.R. Soft Sensor for Flame Temperature Measurement and IoT based Monitoring in Power Plants. Mater. Proc. 2018, 5, 10755–10762. [Google Scholar] [CrossRef]
- Amazouz, M.; Champagne, M.; Platon, R. Soft sensor application in the pulp and paper industry: Assessment study. Available online: https://www.researchgate.net/publication/280256929 (accessed on 3 June 2020). [CrossRef]
- Runkler, T.; Gerstorfer, E.; Schlang, M.; Jj, E.; Villforth, K. Data Compression and Soft Sensors in the Pulp and Paper Industry. 2015. Available online: https://www.researchgate.net/publication/266507240_Data_compression_and_soft_sensors_in_the_pulp_and_paper_industry (accessed on 3 June 2020).
- Osorio, D.; Pérez-Correa, J.; Agosin, E.; Cabrera, M. Soft-sensor for on-line estimation of ethanol concentrations in wine stills. J. Food Eng. 2008, 87, 571–577. [Google Scholar] [CrossRef]
- Rizzo, A. Soft sensors and artificial intelligence for nuclear fusion experiments. In Proceedings of the 15th IEEE Mediterranean Electrotechnical Conference, Valletta, Malta, 26–28 April 2010; pp. 1068–1072. [Google Scholar] [CrossRef]
- Fortuna, L.; Fradkov, A.; Frasca, M. From Physics to Control Through an Emergent View; From World Scientific Series on Nonlinear Science Series B, Volume 15; World Scientific: London, UK, 2010. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Xibilia, M.G.; Napoli, G. Virtual Instruments for the what-if analysis of a process for pollution minimization in an industrial application. In Proceedings of the 14th Mediterranean Conference on Control and Automation, Ancona, Italy, 28–30 June 2006; pp. 1–4. [Google Scholar] [CrossRef]
- Gonzaga, J.C.B.; Meleiro, L.A.C.; Kiang, C.; Filho, R.M. Ann-based soft-sensor for real-time process monitoring and control of an industrial polymerization process. Comput. Chem. Eng. 2009, 33, 43–49. [Google Scholar] [CrossRef]
- Frauendorfer, E.; Hergeth, W.-D. Soft Sensor Applications in Industrial Vinylacetate-ethylene (VAE) Polymerization Processes. Macromol. React. Eng. 2017, 11. [Google Scholar] [CrossRef]
- Zhu, C.-H.; Zhang, J. Developing Soft Sensors for Polymer Melt Index in an Industrial Polymerization Process Using Deep Belief Networks. Int. J. Aut. Comput. 2020, 117, 44–54. [Google Scholar] [CrossRef]
- Graziani, S.; Xibilia, M.G. A deep learning based soft sensor for a sour water stripping plant. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Pisa, I.; Santin, I.; Vicario, J.L.; Morell, A.; Vilanova, R. ANN-Based Soft Sensor to Predict Effluent Violations in Wastewater Treatment Plants. Sensors 2019, 19, 1280. [Google Scholar] [CrossRef]
- Choi, D.J.; Park, H. A hybrid artificial neural network as a software sensor for optimal control of a wastewater treatment process. Wat. Res. 2001, 35, 3959–3967. [Google Scholar] [CrossRef]
- Bowden, G.J.; Dandy, G.C.; Maier, H.R. Input determination for neural network models in water resources applications. Part 1—Background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- Andò, B.; Graziani, S.; Xibilia, M.G. Low-order Nonlinear Finite-Impulse Response Soft Sensors for Ionic Electroactive Actuators based on Deep Learning. IEEE Trans. Instrum. Meas. 2019, 68, 1637–1646. [Google Scholar] [CrossRef]
- Bao, Y.; Zhu, Y.; Du, W.; Zhong, W.; Quian, F. A distributed PCA-TSS based soft sensor for raw meal finesses in VRM system. Control Eng. Pract. 2019, 90, 38–49. [Google Scholar] [CrossRef]
- He, K.; Quian, F.; Cheng, H.; Du, W. A novel adaptive algorithm with near-infrared spectroscopy and its applications in online gasoline blending processes. Chem. Intell. Lab. Syst. 2015, 140, 117–125. [Google Scholar] [CrossRef]
- Kang, J.; Shao, Z.; Chen, X.; Gu, X.; Feng, L. Fast and reliable computational strategy for developing a rigorous model-driven soft sensor of dynamic molecular weight distribution. J. Process Control 2017, 56, 79–99. [Google Scholar] [CrossRef]
- Mandal, S.; Santhi, B.; Sridar, S.; Vinolia, K.; Swaminathan, P. Sensor fault detection in nuclear power plant using statistical methods. Nucl. Eng. Des. 2017, 324, 103–110. [Google Scholar] [CrossRef]
- Marinkovic, Z.; Atanaskovic, A.; Xibilia, M.G.; Pace, C.; Latino, M.; Donato, N. A neural network approach for safety monitoring applications. In Proceedings of the 2016 IEEE Sensors Applications Symposium (SAS), Catania, Italy, 20–22 April 2016; pp. 297–301. [Google Scholar] [CrossRef]
- Zamprogna, E.; Barolo, M.; Seborg, D.E. Optimal selection of soft sensor inputs for batch distillation columns using principal component analysis. J. Process Control 2005, 15, 39–52. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, D.; Li, Y.; Zhu, X. Development of a novel self-validation soft sensor. Korean J. Chem. Eng. 2012, 29, 1135–1143. [Google Scholar] [CrossRef]
- Yao, L.; Ge, Z. Moving window adaptive soft sensor for state shifting process based on weighted supervised latent factor analysis. Control Eng. Pract. 2017, 61, 72–80. [Google Scholar] [CrossRef]
- Nassour, J.; Ghadiya, V.; Hugel, V.; Hamker, F.H. Design of new Sensory Soft Hand: Combining air-pump actuation with superimposed curvature and pressure sensors. In Proceedings of the IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 164–169. [Google Scholar] [CrossRef]
- Vogt, D.; Park, Y.; Wood, R.J. A soft multi-axis force sensor. In Proceedings of the 2012 IEEE, Taipei, Taiwan, 28–31 October 2012; pp. 1–4. [Google Scholar] [CrossRef][Green Version]
- Xu, S.; Vogt, D.M.; Hsu, W.-H.; Osborne, J.; Walsh, T.; Foster, J.R.; Sullivan, S.K.; Smith, V.C.; Rousing, A.W.; Goldfield, E.C.; et al. Biocompatible Soft Fluidic Strain and Force Sensors for Wearable Devices. Adv. Funct. Mater. 2019, 29. [Google Scholar] [CrossRef]
- May, R.J.; Dandy, G.C.; Mayer, H.R. Review of Input Variable Selection Methods for Artificial Neural Networks. In Artificial Neural Networks—Methodological Advances and Biomedical Applications; Suzuki, K., Ed.; InTechOpen: London, UK, 2011; pp. 19–44. [Google Scholar] [CrossRef]
- Hira, Z.; Gillies, D. A Review of Feature Selection and Feature Extraction Methods Applied on Microarray Data. Adv. Bioinf. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Vergara, J.R.; Estévez, P.A. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2014, 24, 175–186. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Sheikhpour, R.; Sarram, M.A.; Gharaghani, S.; Chahooki, M.A.Z. A Survey on semi-supervised feature selection methods. Patton Rec. 2017, 64, 141–158. [Google Scholar] [CrossRef]
- ABB, Human in the Loop. Abb Review 2007, January 2007. Available online: https://library.e.abb.com/public/b9f582f7087d8a27c125728b0047ce18/Review_1_2007_72dpi.pdf (accessed on 3 June 2020).
- Cimini, C.; Pirola, F.; Pinto, R.; Cavalieri, S. A human-in-the-loop manufacturing control architecture for the next generation of production systems. J. Manuf. Syst. 2020, 54, 258–271. [Google Scholar] [CrossRef]
- Curreri, F.; Graziani, S.; Xibilia, M.G. Input selection methods for data-driven Soft Sensors design: Application to an industrial process. Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Boyer, S.A. SCADA: Supervisory Control and Data Acquisition, 4th ed.; ISA—Internation Society of Automation: Pittsburgh, PA, USA, 2010. [Google Scholar]
- D’Andrea, R.; Dullerud, G.E. Distributed control design for spatially interconnected systems. IEEE Trans. Autom. Control 2003, 48, 1478–1495. [Google Scholar] [CrossRef]
- Di Bella, A.; Fortuna, L.; Graziani, S.; Napoli, G.; Xibilia, M.G. A comparative analysis of the influence of methods for outliers detection on the performance of data driven models. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Warsaw, Poland, 1–3 May 2007. [Google Scholar] [CrossRef]
- Ge, Z. Active probabilistic sample selection for intelligent soft sensing of industrial processes. Chem. Intell. Lab. Syst. 2016, 152, 181–189. [Google Scholar] [CrossRef]
- Lin, B.; Knudsen, J.K.H.; Jorgensen, S.B. A systematic approach for soft sensor development. Comput. Chem. Eng. 2007, 31, 419–425. [Google Scholar] [CrossRef]
- Xie, L.; Yang, H.; Huang, B. Fir model identification of multirate processes with random delays using em algorithm. AIChE J. 2013, 59, 4124–4132. [Google Scholar] [CrossRef]
- Kadlec, P.; Gabrys, B. Local learning-based adaptive soft sensor for catalyst activation prediction. AIChE J. 2011, 57, 1288–1301. [Google Scholar] [CrossRef]
- Lu, L.; Yang, Y.; Gao, F.; Wang, F. Multirate dynamic inferential modeling for multivariable processes. Chem. Eng. Sci. 2004, 59, 855–864. [Google Scholar] [CrossRef]
- Wu, Y.; Luo, X. A novel calibration approach of soft sensor based on multirate data fusion technology. J. Proc Control 2010, 20, 1252–1260. [Google Scholar] [CrossRef]
- Pearson, R.K. Outliers in process modeling and identification. IEEE Trans. Control Syst. Tech. 2002, 10, 55–63. [Google Scholar] [CrossRef]
- Piltan, F.; TayebiHaghighi, S.; Sulaiman, N.B. Comparative study between ARX and ARMAX system identification. Int. J. Intell. Control Appl. 2017, 9, 25–34. [Google Scholar] [CrossRef]
- Sjöberg, J.; Zhang, Q.; Ljung, L.; Benveniste, A.; Delyon, B.; Glorennec, P.-Y.; Hjalmarsson, H.; Juditsky, A. Nonlinear Black-Box Modeling in System Identification: A Unified Overview; Linköping University: Linköping, Sweden, 1995; Volume 31, pp. 1691–1724. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Xibilia, M.G. Comparison of soft-sensor design methods for industrial plants using small data sets. IEEE Trans. Instrum. Meas. 2009, 58, 2444–2451. [Google Scholar] [CrossRef]
- Wei, J.; Guo, L.; Xu, X.; Yan, G. Soft sensor modeling of mill level based on convolutional neural network. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015. [Google Scholar] [CrossRef]
- Wang, K.; Shang, C.; Liu, L.; Jiang, Y.; Huang, D.; Yang, F. Dynamic Soft Sensor Development Based on Convolutional Neural Networks. Ind. Eng. Chem. Res. 2019, 58, 11521–11531. [Google Scholar] [CrossRef]
- Wang, X. Data Preprocessing for Soft Sensor Using Generative Adversarial Networks. In Proceedings of the International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, 18–21 November 2018. [Google Scholar] [CrossRef]
- Hong, Y.; Hwang, U.; Yoo, J.; Yoon, S. How Generative Adversarial Networks and Their Variants Work: An Overview. arXiv 2019, arXiv:1711.05914. [Google Scholar] [CrossRef]
- Wang, J.-S.; Han, S.; Yang, Y. RBF Neural Network Soft-Sensor Model of Electroslag Remelting Process Optimized by Artificial Fish Swarm Optimization Algorithm. Adv. Mech. Eng. 2015, 6. [Google Scholar] [CrossRef]
- Gao, M.-J.; Tian, J.-W.; Li, K. The study of soft sensor modeling method based on wavelet neural network for sewage treatment. In Proceedings of the 2007 International Conference on Wavelet Analysis and Pattern Recognition, Beijing, China, 2–4 November 2007; pp. 721–726. [Google Scholar] [CrossRef]
- Wei, Y.; Jiang, Y.; Yang, F.; Huang, D. Three-Stage Decomposition Modeling for Quality of Gas-Phase Polyethylene Process Based on Adaptive Hinging Hyperplanes and Impulse Response Template. Ind. Eng. Chem. Res. 2013, 52, 5747–5756. [Google Scholar] [CrossRef]
- Lu, M.; Kang, Y.; Han, X.; Yan, G. Soft sensor modeling of mill level based on Deep Belief Network. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 189–193. [Google Scholar] [CrossRef]
- Liu, R.; Rong, Z.; Jiang, B.; Pang, Z.; Tang, C. Soft Sensor of 4-CBA Concentration Using Deep Belief Networks with Continuous Restricted Boltzmann Machine. In Proceedings of the 5th IEEE International Conference on Cloud Computing and Intelligence Systems (CCIS), Nanjing, China, 23–25 November 2018; pp. 421–424. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H. Soft sensor based on stacked auto-encoder deep neural network for air preheater rotor deformation prediction. Adv. Eng. Inf. 2018, 36, 112–119. [Google Scholar] [CrossRef]
- Li, D.; Li, Z.; Sun, K. Development of a Novel Soft Sensor with Long Short-Term Memory Network and Normalized Mutual Information Feature Selection. Math. Probl. Eng. 2020. [Google Scholar] [CrossRef]
- Chitralekha, S.B.; Shah, S. Support Vector Regression for soft sensor design of nonlinear processes. In Proceedings of the 18th Mediterranean Conference on Control and Automation, Marrakech, Morocco, 23–25 June 2010; pp. 569–574. [Google Scholar] [CrossRef]
- Grbić, R.; Sliskovic, D.; Kadlec, P. Adaptive soft sensor for online prediction and process monitoring based on mixture of Gaussian process models. Comput. Chem. Eng. 2013, 58, 84–97. [Google Scholar] [CrossRef]
- Shao, W.; Ge, Z.; Song, Z.; Wang, K. Nonlinear Industrial soft sensor development based on semi-supervised probabilistic mixture of extreme learning machines. Control Eng. Pract. 2019, 91. [Google Scholar] [CrossRef]
- Mendes, J.; Souza, F.; Araújo, R.; Gonçalves, N. Genetic fuzzy system for data-driven soft sensors. Appl. Soft Comput. 2012, 12, 3237–3245. [Google Scholar] [CrossRef]
- Mendes, J.; Pinto, S.; Araújo, R.; Souza, F. Evolutionary fuzzy models for nonlinear identification. In Proceedings of the IEEE 17th International Conference on Emerging Technologies & Factory Automation (ETFA 2012), Krakow, Poland, 17–21 September 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Sjöberg, J.; Hjalmarsson, H.; Ljung, L. Neural networks in system identification. IFAC Proc. Vol. 1994, 27, 359–382. [Google Scholar] [CrossRef]
- Juditsky, A.; Hjalmarsson, H.; Benveniste, A.; Delyon, B.; Ljung, L.; Sjoberg, J.; Zhang, Q. Nonlinear black-box models in system identification: Mathematical foundations. Automatica 1995, 31, 1725–1750. [Google Scholar] [CrossRef]
- Han, M.; Zhang, R.; Xu, M. Multivariate chaotic time series prediction based on ELM-PLSR and hybrid variable selection algorithm. Neural Proc. Lett. 2017, 46, 705–717. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, Y.; Huang, D. Development of a novel adaptive soft sensor using variational Bayesian PLS with accounting for online identification of key variables. Ind. Eng. Chem. Res. 2015, 54, 338–350. [Google Scholar] [CrossRef]
- Liu, Z.; Ge, Z.; Chen, G.; Song, Z. Adaptive soft sensors for quality prediction under the framework of Bayesian network. Control Eng. Pract. 2018, 72, 19–29. [Google Scholar] [CrossRef]
- Graziani, S.; Xibilia, M.G. Deep Learning for Soft Sensor Design, in Development and Analysis of Deep Learning Architectures; Springer: Basel, Switzerland, 2020. [Google Scholar] [CrossRef]
- Shoorehdeli, M.A.; Teshnehlab, M.; Sedigh, A.K. Training ANFIS as an identifier with intelligent hybrid stable learning algorithm based on particle swarm optimization and extended Kalman filter. Fuzzy Sets Syst. 2009, 160, 922–948. [Google Scholar] [CrossRef]
- Soares, S.; Araújio, R.; Sousa, P.; Souza, F. Design and application of soft sensors using ensemble methods. In Proceedings of the IEEE International Conference on Emerging Technologies & Factory Automation, ETFA2011, Toulouse, France, 5–9 September 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Shakil, M.; Elshafei, M.; Habib, M.A.; Maleki, F.A. Soft sensor for NOx and O2 using dynamic neural networks. Comput. Elect. Eng. 2009, 35, 578–586. [Google Scholar] [CrossRef]
- Ludwig, O.; Nunes, U.; Araújo, R.; Schnitman, L.; Lepikson, H.A. Applications of information theory, genetic algorithms, and neural models to predict oil flow. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2870–2885. [Google Scholar] [CrossRef]
- Souza, F.; Araújo, R. Variable and time-lag selection using empirical data. In Proceedings of the IEEE International Conference on Emerging Technologies & Factory Automation, ETFA2011, Toulouse, France, 5–9 September 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Souza, F.; Santos, P.; Araújio, R. Variable and delay selection using neural networks and mutual information for data-driven soft sensors. In Proceedings of the IEEE Conference on Emerging Technologies and Factory Automation (ETFA), Bilbao, Spain, 13–16 September 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Lou, H.; Su, H.; Xie, L.; Gu, Y.; Rong, G. Inferential Model for Industrial Polypropylene Melt Index Prediction with Embedded Priori Knowledge and Delay Estimation. Ind. Eng. Chem. Res. 2012, 51, 8510–8525. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1974, 14, 465–658. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Mallows, C.L. Some Comments on CP. Technometrics 1973, 15, 661–675. [Google Scholar] [CrossRef]
- Gabriel, D.; Matias, T.; Pereira, J.C.; Araújo, R. Predicting gas emissions in a cement kiln plant using hard and soft modeling strategies. In Proceedings of the IEEE 18th Conference on Emerging Technologies & Factory Automation (ETFA), Cagliari, Italy, 10–13 September 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Judd, J.S. Neural Network Design and the Complexity of Learning; The MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural Networks and the Bias/Variance Dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Bellman, R. Adaptive Control Processes: A Guided Tour; Princeton University Press: New Jersey, NJ, USA, 1961. [Google Scholar]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice and Visualisation; John Wiley and Sons: New York, NY, USA, 1992. [Google Scholar]
- Jain, A.K.; Duin, R.P.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Patton Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Joliffe, I.T. Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 1991, 37, 233–243. [Google Scholar] [CrossRef]
- Schölkopf, B. Nonlinear Component Analysis as a Kernel Eigenvalue Problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Bair, E.; Hastie, T.; Paul, D.; Tibshirani, R. Prediction by Supervised Principal Components. J. Am. Stat. Assess. 2006, 101, 119–137. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, A new concept? Signal Proc. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Tipping, M.E.; Bishop, C.M. Probabilistic Principal Component Analysis. J. R. Stat. Soc. Ser. B 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Eshghi, P. Dimensionality choice in principal components analysis via cross-validatory methods. Chem. Intell. Lab. Syst. 2014, 130, 6–13. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Eisen, M.B.; Alizadeh, A.; Levy, R.; Staudt, L.; Chan, W.C.; Botstein, D.; Brown, P. ‘Gene shaving’ as a method for identifying distinct sets of genes with similar expression patterns. Genome Biol. 2000, 1, 1–21. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, D.; Bensmail, H. Gene expression data classification with kernel principal component analysis. BioMed Res. Int. 2005, 37, 155–159. [Google Scholar] [CrossRef]
- Reverter, F.; Vegas, E.; Oller, J.M. Kernel-PCA data integration with enhanced interpretability. BMC Syst. Biol. 2014, 8. [Google Scholar] [CrossRef][Green Version]
- Yao, M.; Wang, H. On-line monitoring of batch processes using generalized additive kernel principal component analysis. J. Proc. Control 2015, 28, 56–72. [Google Scholar] [CrossRef]
- Cao, L.J.; Chua, K.S.; Chong, W.K.; Lee, H.P.; Gu, Q.M. A comparison of PCA, KPCA and ICA for dimensionality reduction in support vector machine. IEEE Trans. Patton Anal. Mach. Intell. 2003, 55, 321–336. [Google Scholar] [CrossRef]
- Li, T.; Su, Y.; Yi, J.; Yao, L.; Xu, M. Original feature selection in soft-sensor modeling process based on ICA_FNN. Chin. J. Sci. Instrum. 2013, 4, 736–742. [Google Scholar]
- Torgerson, W.S. Multidimensional scaling: I. Theory and method. Psychometrika 1952, 17, 401–419. [Google Scholar] [CrossRef]
- Borg, I.; Groenen, P.J.F. Modern Multidimensional Scaling: Theory and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Gower, J.C. Principal Coordinates Analysis. Encycl. Biostat. 2005. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, M.; Schwartz, E.L. The isomap algorithm and topological stability. Science 2002, 295, 7. [Google Scholar] [CrossRef] [PubMed]
- Orsenigo, C.; Vercellis, C. An effective double-bounded tree-connected Isomap algorithm for microarray data classification. Patton Rec. Lett. 2012, 33, 9–13. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Shi, C.; Chen, L. Feature dimension reduction for microarray data analysis using locally linear embedding. In Proceedings of the 3rd Asia-Pacific Bioinformatics Conference, APBC ’05, Singapore, 17–21 January 2005; pp. 211–217. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 56–69. [Google Scholar] [CrossRef]
- Reitermanová, Z. Information Theory Methods for Feature Selection, 2010. Available online: https://pdfs.semanticscholar.org/ad7c/9cbb5411a4ff10cec3c9ac5ddc18f1f60979.pdf (accessed on 3 June 2020).
- Guyon, I. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Aha, D.W.; Bankert, R.L. A Comparative Evaluation of Sequential Feature Selection Algorithms. In Learning from Data; Lecture Notes in Statistics; Springer: New York, NY, USA, 1996; Volume 112, pp. 199–206. [Google Scholar] [CrossRef]
- Somol, P.; Novovicova, J.; Pudil, P. Efficient Feature Subset Selection and Subset Size Optimization. Patton Rec. Recent Adv. 2010, 56. [Google Scholar] [CrossRef][Green Version]
- Izrailev, S.; Agrafiotis, D.K. Variable selection for QSAR by artificial ant colony systems. SAR QSAR Environ. Res. 2002, 13, 417–423. [Google Scholar] [CrossRef]
- Marcoulides, G.A.; Drezner, Z. Model specification searches using ant colony optimization algorithms. Struct. Eq. Model. 2003, 10, 154–164. [Google Scholar] [CrossRef]
- Shen, Q.; Jiang, J.-H.; Tao, J.-C.; Shen, G.-L.; Yu, R.-Q. Modified ant colony optimization algorithm for variable selection in QSAR modeling: QSAR studies of cyclooxygenase inhibitors. J. Chem. Inf. Model. 2005, 45, 1024–1029. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. Data Class. Algorithms Appl. 2014, 37–64. [Google Scholar] [CrossRef]
- Chen, P.Y.; Popovich, P.M. Correlation: Parametric and Nonparametric Measures; Sage Publications: Thousand Oaks, CA, USA, 2002. [Google Scholar]
- Delgado, M.R.; Nagai, E.Y.; Arruda, L.V.R. A neuro-coevolutionary genetic fuzzy system to design soft sensors. Soft Comput. 2009, 13, 481–495. [Google Scholar] [CrossRef]
- Deebani, W.; Kachouie, N.N. Ensemble Correlation Coefficient. In Proceedings of the International Symposium on Artificial Intelligence and Mathematics, ISAIM 2018, Fort Lauderdale, FL, USA, 3–5 January 2018; Available online: https://dblp.org/rec/conf/isaim/DeebaniK18 (accessed on 3 June 2020).
- Székely, G.J.; Rizzo, M.L.; Bakirov, N.K. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H. Estimating Optimal Transformations for Multiple Regression and Correlation. J. Am. Stat. Assess. 1985, 80, 580–598. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Mitzenmacher, M.M.; Sabeti, P.C. Equitability Analysis of the Maximal Information Coefficient, with Comparisons. arXiv 2013, arXiv:1301.6314. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Wang, X.; Han, M.; Wang, J. Applying input variables selection technique on input weighted support vector machine modeling for BOF endpoint prediction. Eng. Appl. Artif. Intell. 2010, 23, 1012–1018. [Google Scholar] [CrossRef]
- Rossi, F.; Lendasse, A.; François, D.; Wertz, V.; Verleysen, M. Mutual information for the selection of relevant variables in spectrometric nonlinear modelling. Chem. Intell. Lab. Syst. 2006, 80, 215–226. [Google Scholar] [CrossRef]
- François, D.; Rossi, F.; Wertz, V.; Verleysen, M. Resampling methods for parameter-free and robust feature selection with mutual information. Neurocomputing 2007, 70, 1276–1288. [Google Scholar] [CrossRef]
- Xing, H.-J.; Hu, B.-G. Two-phase construction of multilayer perceptrons using information theory. IEEE Trans. Neural Netw. 2009, 20, 715–721. [Google Scholar] [CrossRef] [PubMed]
- Doquire, G.; Verleysen, M. A comparison of multivariate mutual information estimators for feature selection. In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, Algarve, Portugal, 6–8 February 2012; pp. 176–185. [Google Scholar] [CrossRef]
- Frénay, B.; Doquire, G.; Verleysen, M. Is mutual information adequate for feature selection in regression? Neural Netw. 2013, 48, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Battiti, R. Using Mutual Information for Selecting Features in Supervised Neural Net Learning. IEEE Trans. Neual Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef] [PubMed]
- Kwak, N.; Choi, C.H. Input Feature Selection for Classification Problems. IEEE Trans. Neural Netw. 2002, 13, 143–159. [Google Scholar] [CrossRef]
- Balagani, K.S.; Phoha, V.V. On the feature selection criterion based on an approximation of multidimensional mutual information. IEEE Trans. Patton Anal. Mach. Intell. 2010, 32, 1342–1343. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Patton Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Che, J.; Yang, Y.; Li, L.; Bai, X.; Zhang, S.; Deng, C. Maximum relevance minimum common redundancy feature selection for nonlinear data. Inf. Sci. 2017, 409–410, 68–86. [Google Scholar] [CrossRef]
- Estévez, P.A.; Tesmer, M.; Perez, C.A.; Zurada, J.M. Normalized Mutual Information Feature Selection. IEEE Trans. Neual Netw. 2009, 20, 189–201. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J.; Liu, L.; Zhang, H. Feature selection with dynamic mutual information. Patton Rec. 2009, 42, 1330–1339. [Google Scholar] [CrossRef]
- Sharma, A. Seasonal to interannual rainfall probabilistic forecasts for improved water supply management: Part 1—A strategy for system predictor identification. J. Hydrol. 2000, 239, 232–239. [Google Scholar] [CrossRef]
- May, R.J.; Maier, H.R.; Dandy, G.C.; Fernando, T.M.K.G. Non-linear variable selection for artificial neural networks using partial mutual information. Environ. Model. Softw 2008, 23, 1312–1326. [Google Scholar] [CrossRef]
- Fernando, T.M.K.G.; Maier, H.R.; Dandy, G.C. Selection of input variables for data driven models: An average shifted histogram partial mutual information estimator approach. J. Hydrol. 2009, 367, 165–176. [Google Scholar] [CrossRef]
- Liu, H.; Ditzler, G. A semi-parallel framework for greedy information-theoretic feature selection. Inf. Sci. 2019, 492, 13–28. [Google Scholar] [CrossRef]
- Sridhar, D.V.; Bartlett, E.B.; Seagrave, R.C. Information theoretic subset selection for neural network models. Comput. Chem. Eng. 1998, 22, 613–626. [Google Scholar] [CrossRef]
- He, X.; Asada, H. A new method for identifying orders of input-output models for nonlinear dynamic systems. In Proceedings of the American Control Conference, San Francisco, CA, USA, 2–4 June 1993. [Google Scholar] [CrossRef]
- Xibilia, M.G.; Gemelli, N.; Consolo, G. Input variables selection criteria for data-driven Soft Sensors design. In Proceedings of the IEEE International Conference on Networking, Sensing and Control, Calabria, Italy, 16–18 May 2017. [Google Scholar] [CrossRef]
- Krakovska, O.; Christie, G.; Sixsmith, A.; Ester, M.; Moreno, S. Performance comparison of linear and non-linear feature selection methods for the analysis of large survey datasets. PLoS ONE 2019, 14. [Google Scholar] [CrossRef]
- Chu, Y.-H.; Lee, Y.-H.; Han, C. Improved Quality Estimation and Knowledge Extraction in a Batch Process by Bootstrapping-Based Generalized Variable Selection. Ind. Eng. Chem. Res. 2004, 43, 2680–2690. [Google Scholar] [CrossRef]
- Kaneko, H.; Funatsu, K. A new process variable and dynamics selection method based on a genetic algorithm-based wavelength selection method. AIChE J. 2012, 58, 1829–1840. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bhattacherjee, A. Genetic algorithms for feature selection of image analysis-based quality monitoring model: An application to an iron mine. Eng. Appl. Artif. Intell. 2011, 24, 786–795. [Google Scholar] [CrossRef]
- Arakawa, M.; Yamashita, Y.; Funatsu, K. Genetic algorithmbased wavelength selection method for spectral calibration. J. Chem. 2011, 25, 10–19. [Google Scholar] [CrossRef]
- Kaneko, H.; Funatsu, K. Nonlinear regression method with variable region selection and application to soft sensors. Chem. Intell. Lab. Syst. 2013, 121, 26–32. [Google Scholar] [CrossRef]
- Pierna, J.A.F.; Abbas, O.; Baeten, V.; Dardenne, P. A backward variable selection method for PLS regression (BVSPLS). Anal. Chim. Acta 2009, 642, 89–93. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Zhou, D.; Xu, H.; Mei, C. Model optimization of SVM for a fermentation soft sensor. Exp. Syst. Appl. 2010, 37, 2708–2713. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chem. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Centner, V.; Massart, D.L.; De Noord, O.; De Jong, S.; Vandeginste, B.G.M.; Sterna, C. Elimination of uninformative variables for multivariate calibration. Anal. Chem. 1996, 68, 3851–3858. [Google Scholar] [CrossRef]
- Li, H.-D.; Zeng, M.-M.; Tan, B.-B.; Liang, Y.-Z.; Xu, Q.-S.; Cao, D.-S. Recipe for revealing informative metabolites based on model population analysis. Metabolomics 2010, 6, 353–361. [Google Scholar] [CrossRef]
- Mehmood, T.; Martens, H.; Sæbø, S.; Warringer, J.; Snipen, L. A Partial least squares-based algorithm for parsimonious variable selection. Algorithms Mol. Biol. 2011, 6. [Google Scholar] [CrossRef]
- Cai, W.; Li, Y.; Shao, X. A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra. Chem. Intell. Lab. Syst. 2008, 90, 188–194. [Google Scholar] [CrossRef]
- Hasegawa, K.; Miyashita, Y.; Funatsu, K. GA strategy for variable selection in QSAR studies: GA-based PLS analysis of calcium channel antagonists. J. Chem. Inf. Comput. Sci. 1997, 37, 306–310. [Google Scholar] [CrossRef]
- Liu, Q.; Sung, A.H.; Chen, Z.; Liu, J.; Huang, X.; Deng, Y. Feature selection and classification of MAQC-II breast cancer and multiple myeloma microarray gene expression data. PLoS ONE 2019, 4. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Y.-Q.; Huang, Z. Development of two-stage SVM-RFE gene selection strategy for microarray expression data analysis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2007, 4, 365–381. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.-W.; Jeong, J.C. Enhanced recursive feature elimination. In Proceedings of the Sixth International Conference on Machine Learning and Applications (ICMLA 2007), Cincinnati, OH, USA, 13–15 December 2007; pp. 429–435. [Google Scholar] [CrossRef]
- Escanilla, N.S.; Hellerstein, L.; Kleiman, R.; Kuang, Z.; Shull, J.; Page, D. Recursive Feature Elimination by Sensitivity Testing. In Proceedings of the 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 40–47. [Google Scholar] [CrossRef]
- Yeh, I.-C.; Cheng, W.-L. First and second order sensitivity analysis of MLP. Neurocomp. 2010, 73, 2225–2233. [Google Scholar] [CrossRef]
- Garson, G.D. Interpreting neural-network connection weights. AI Exp. 1991, 6, 46–51. [Google Scholar]
- Dimopoulos, Y.; Bourret, P.; Lek, S. Use of some sensitivity criteria for choosing networks with good generalization ability. Neural Proc. Lett. 1995, 2, 1–4. [Google Scholar] [CrossRef]
- Dimopoulos, I.; Chronopoulos, J.; Chronopoulou-Sereli, A.; Lek, S. Neural network models to study relationships between lead concentration in grasses and permanent urban descriptors in Athens city (Greece). Ecol. Model. 1999, 120, 157–165. [Google Scholar] [CrossRef]
- Lemaire, V.; Féraud, R. Driven forward features selection: A comparative study on neural networks. In Proceedings of the 13th International Conference, ICONIP 2006, Hong Kong, China, 3–6 October 2006; pp. 693–702. [Google Scholar] [CrossRef]
- Ding, S.; Li, H.; Su, C.; Yu, J.; Jin, F. Evolutionary artificial neural networks: A review. Artif. Intell. Rev. 2013, 39, 251–260. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Radchenko, P.; James, G.M. Improved variable selection with forward-LASSO adaptive shrinkage. Ann. Appl. Stat. 2011, 5, 427–448. [Google Scholar] [CrossRef][Green Version]
- Tikhonov, A.N.; Goncharsky, A.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Sun, K.; Huang, S.-H.; Wong, D.S.-H.; Jang, S.-S. Design and Application of a Variable Selection Method for Multilayer perceptron Neural Network with LASSO. IEEE Trans. Neual Netw. Learn. Syst. 2017, 28, 1386–1396. [Google Scholar] [CrossRef]
- Souza, F.A.A.; Araújo, R.; Matias, T.; Mendes, J. A multilayer-perceptron based method for variable selection in soft sensor design. J. Proc. Control 2013, 23, 1371–1378. [Google Scholar] [CrossRef]
- Fujiwara, K.; Kano, M. Efficient input variable selection for soft-sensor design based on nearest correlation spectral clustering and group Lasso. ISA Trans. 2015, 58, 367–379. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, K.; Kano, M. Nearest Correlation-Based Input Variable Weighting for Soft-Sensor Design. Front. Chem. 2018, 6. [Google Scholar] [CrossRef] [PubMed]
- Tang, E.K.; Suganthan, P.N.; Yao, X. Gene selection algorithms for microarray data based on least squares support vector machine. BMC Bioinf. 2006, 7. [Google Scholar] [CrossRef]
- Cui, C.; Wang, D. High dimensional data regression using Lasso model and neural networks with random weights. Inf. Sci. 2016, 372, 505–517. [Google Scholar] [CrossRef]
| Class | Type | Pros | Cons | |
|---|---|---|---|---|
| FE | ||||
| Linear | Nonlinear | |||
| PCA, SPCA, PPCA. | NLPCA, KPCA, ICA, MDS, PCoA, Isomap, LLE, LE, SOM. | Reduced computational demand. | Unsupervised. Final projections do not have any physical meaning and all measurement sensors are still needed. | |
| FS | ||||
| Linear | NonLinear | |||
| Filter | CC analysis. (Pearson, Spearman) | Ensemble CC an. or MI an. (MIFS, MIFS-U, NMIFS, DMIFS, ITSS), Lipschitz coeff. | Simplest, fastest, model-independent. Good when n < p. | Inputs are considered individually. Dependencies and interactions are disregarded. |
| Deterministic | Random | |||
| Wrapper | FS, SFFS, BE, SBFS. | Heuristic search (GA, ACO, SA). | Evaluation on the final model gives very good results. | Model-dependent. Most computationally and time expensive. Models obtained can suffer overfitting. |
| Embedded | RFE, RFEST, EnRFE, Sensitivity analysis, Evolutionary ANNs, LASSO, LASSO-MLP, Elastic net. | Best methods when n > p. | Model-dependent. Computationally expensive. High overfitting when n < p. | |
| Hybrid | Every possible combination of methods from different classes. | Merge best results from the most performing methods for the case in exam. | Different tests have to be done, methods have to be combined with a criterion. This can make them time consuming. | |
| Methods References Table | |||
|---|---|---|---|
| FE | PCA | [105,106,107,108,109,110,117] | |
| MDS | [118,119] | ||
| PCoA | [120] | ||
| Isomap | [121,122,123] | ||
| LLE | [124,125] | ||
| LE | [126] | ||
| SOM | [127] | ||
| FS | Filter | CC | [1,136,138,139,140,141] |
| Univariate MI | [129] | ||
| Multivariate MI | [149,150,152,153,154,155,156,159] | ||
| ITSS | [160] | ||
| Lipschitz quot. | [161] | ||
| Wrapper | [45] | ||
| FS, BE | [130] | ||
| SFFS, SFBS | [131] | ||
| Random | [173,174,175] | ||
| ACO based | [132,133,134] | ||
| Embedded | RFE | [129,180,181] | |
| Sensitivity analysis | [182,183,184] | ||
| EANN | [187] | ||
| LASSO | [188,189,192] | ||
| Semi-supervised | [46] | ||
| Real Case Applications References Table | |||
|---|---|---|---|
| Plant experts’ knowledge | [7,8,9,10,22,26,64] | ||
| FE | PCA | [11,19,28,34,36,37,56,58,89,111,112] | |
| Distributed PCA | [31] | ||
| Kernel PCA | [113,114,115] | ||
| PLS | [32,84] | ||
| Discriminant anal. | [16] | ||
| FS | Filter | CC | [6,12,23,30,49,137] |
| Univariate MI | [143] | ||
| Multivariate MI | [75,77,90,91,92,144,145,146,156,157,158] | ||
| ITSS | [13,49] | ||
| Lipschitz quot. | [49,162] | ||
| Wrapper | FS, BE | [14,99,165] | |
| SFFS, SFBS | [164] | ||
| Random | [166,167,168,170,176,177] | ||
| Embedded | RFE | [178,179] | |
| Sensitivity analysis | [185] | ||
| LASSO | [49,162] | ||
| Hybrid | [29,49,83,193,194,195,196,197] | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curreri, F.; Fiumara, G.; Xibilia, M.G. Input Selection Methods for Soft Sensor Design: A Survey. Future Internet 2020, 12, 97. https://doi.org/10.3390/fi12060097
Curreri F, Fiumara G, Xibilia MG. Input Selection Methods for Soft Sensor Design: A Survey. Future Internet. 2020; 12(6):97. https://doi.org/10.3390/fi12060097
Chicago/Turabian StyleCurreri, Francesco, Giacomo Fiumara, and Maria Gabriella Xibilia. 2020. "Input Selection Methods for Soft Sensor Design: A Survey" Future Internet 12, no. 6: 97. https://doi.org/10.3390/fi12060097
APA StyleCurreri, F., Fiumara, G., & Xibilia, M. G. (2020). Input Selection Methods for Soft Sensor Design: A Survey. Future Internet, 12(6), 97. https://doi.org/10.3390/fi12060097







