Adolescent’s Collective Intelligence: Empirical Evidence in Real and Online Classmates Groups
Abstract
1. Introduction
The Group Problem-Solving
2. Hypothesis
3. Materials and Methods
3.1. Sample
3.1.1. The Psycho-Social Survey
- Personality traits: the I-TIPI inventory test () [42] is based on the Big Five factors Personality model purposed by Costa and McCrae (1992) [43]. According to this model, personality is composed of five different dimensions, namely extroversion, agreeableness, conscientiousness, neuroticism, and openness. Therefore, the I-TIPI test is composed of five sub-scales useful to assess the factors included in the Big Five Model. Therefore, the personality test adopted was composed of ten items through a seven-point Likert scale (1 = strongly disagree, 7 = strongly agree). Each of the five dimensions assessed through the I-TIPI inventory test was measured by means the combination of two items.
- Group members sense of community (Group cohesion): the sense of community (SOC) was measured using the Classroom and School Community Inventory (CSCI) () [44], which assigns two separate scores to participants: one for the Learning Community () and one for the Social community (). The scale was composed of 10 items, 5 for each sub-scale, on a five-point scale (1 = strongly agree, 5 = strongly disagree). Therefore, high scores on this scale denote a low level of perceived SOC, while low scores indicate a high level of it. The literature defined the generalized sense of community as the group members feeling of belonging to a group [40]. Therefore, the sense of community can be considered as a proxy for the study of groups’ cohesion.
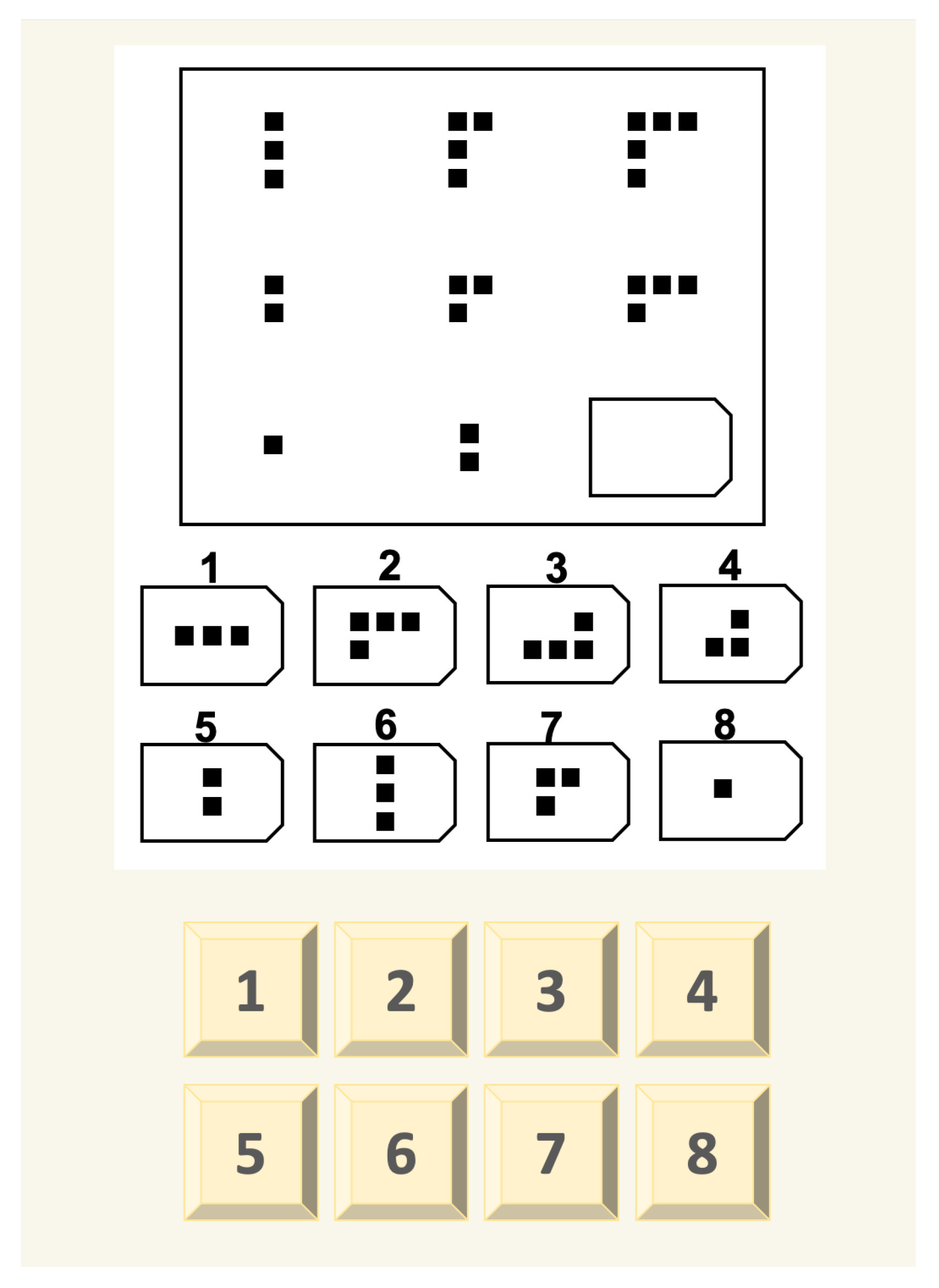
- Social abilities: the Italian version of the Reading the Mind in the Eyes test (RME) () [45] has been administered to measure participants’ social abilities. RME is a widely used test for the assessment of the theory of mind, namely the ability of a person to understand what another individual thinks and feels. Here, we adopted this test for the evaluation of students’ social abilities because it was included in the pioneering empirical study on CI [4] and in its more recent replication [7]. The RME test was composed of 36 images displaying the eyes of different people that present a variety of emotions, and the participants were asked to select which emotion was shown, with a choice of four different options.
3.1.2. Stimuli
3.1.3. Procedures
3.2. Analysis
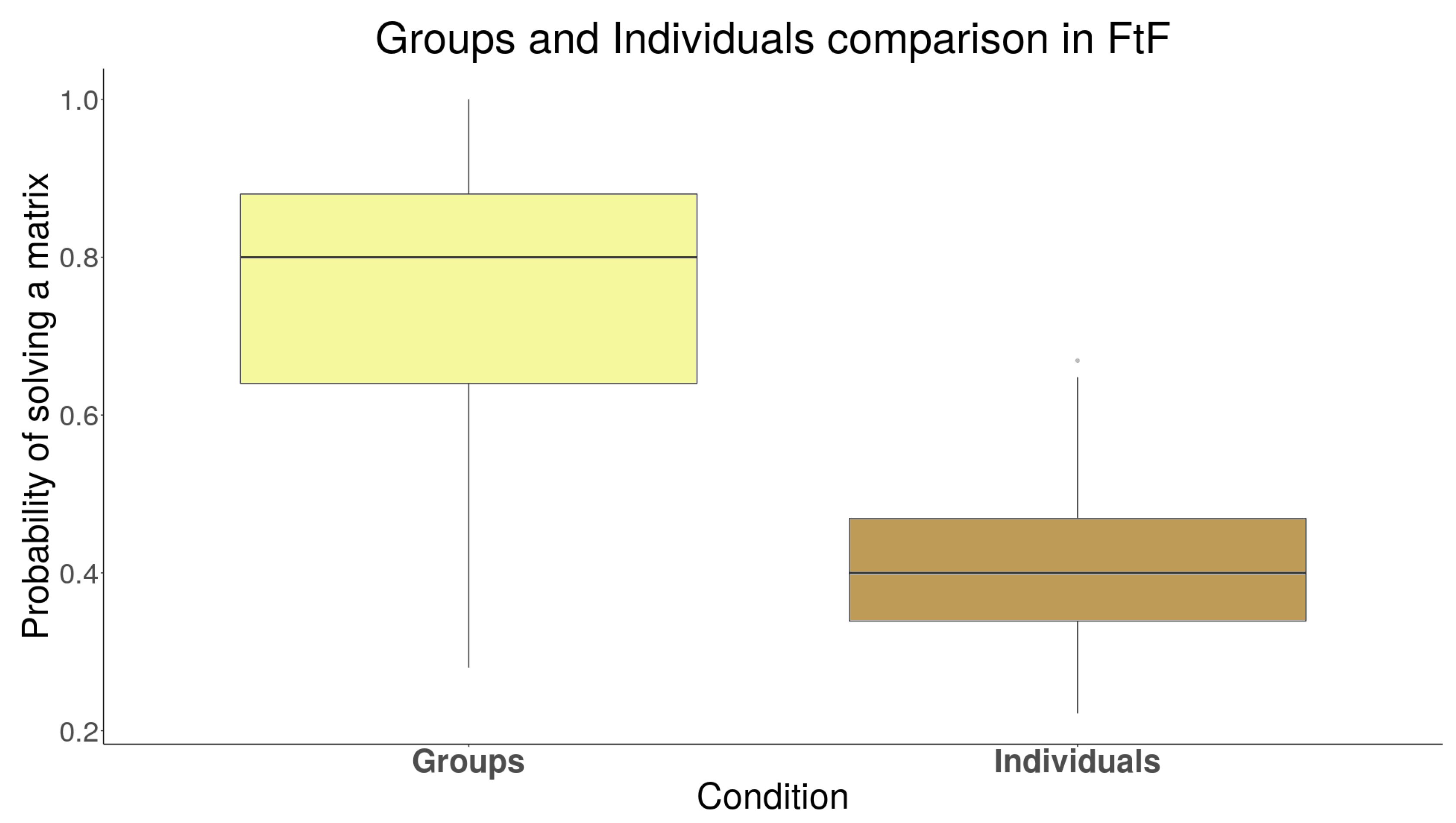
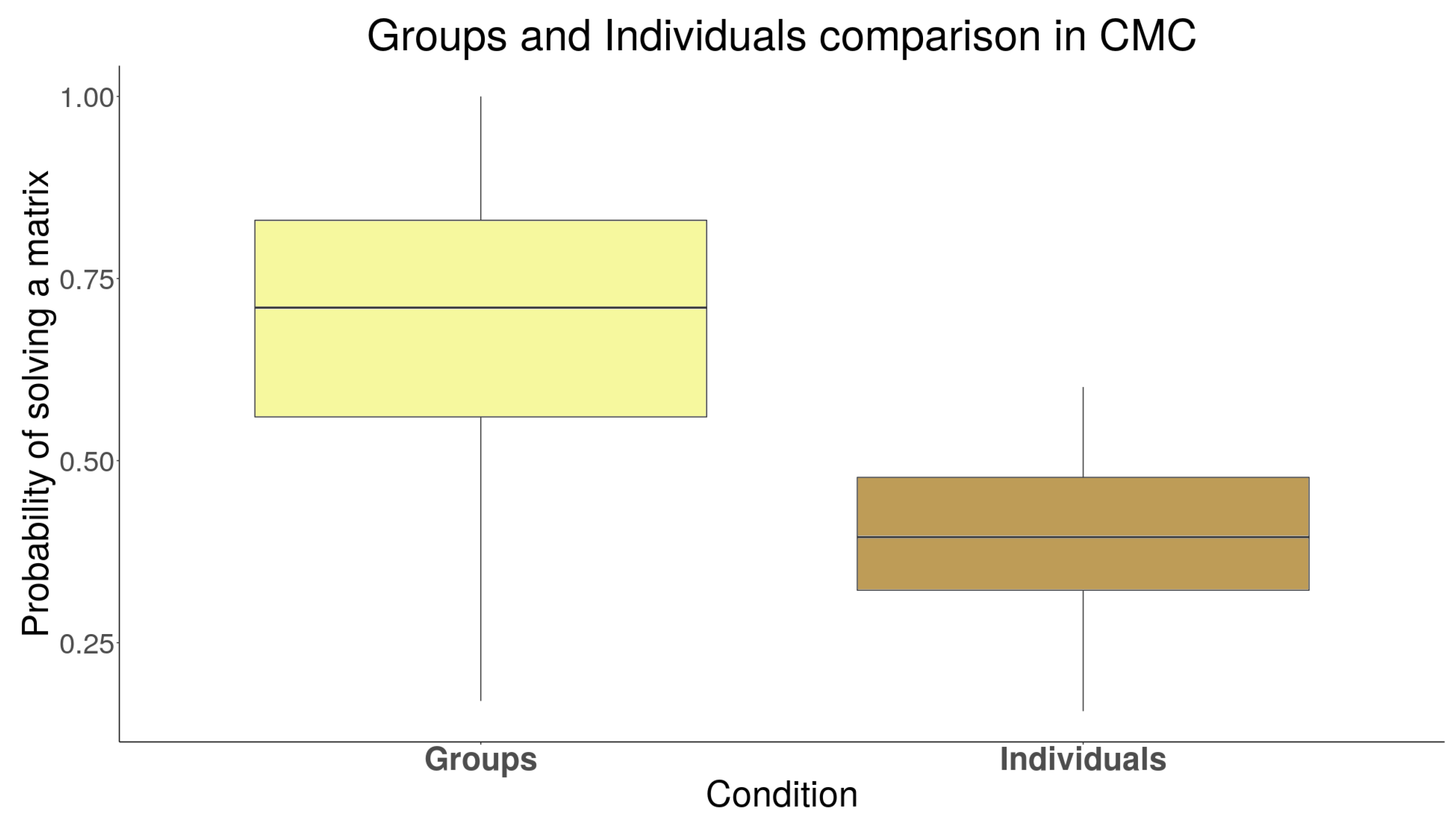
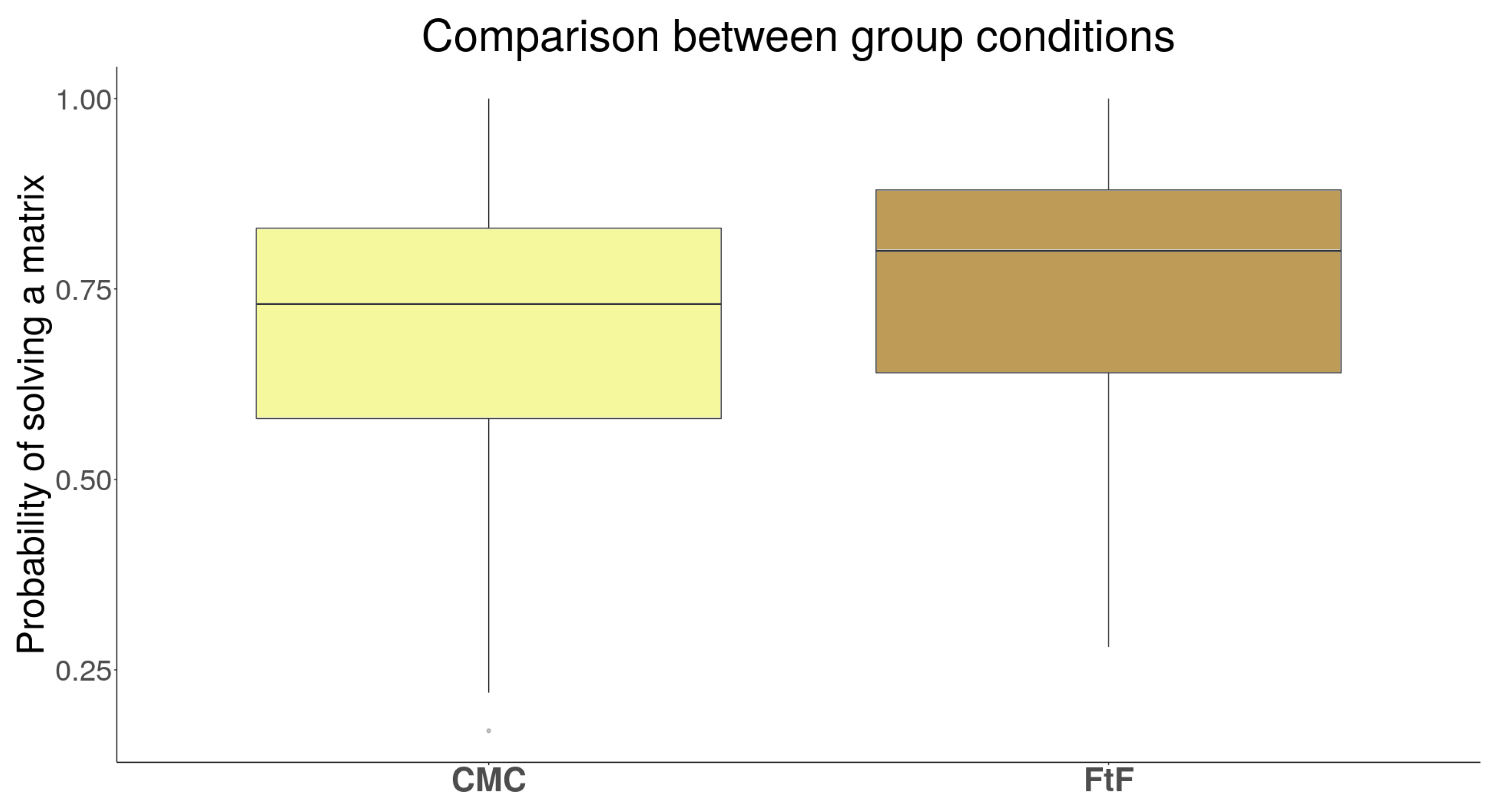
3.3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Heylighen, F. Collective Intelligence and its Implementation on the Web: Algorithms to develop a collective mental map. Comput. Math. Organ. Theory 1999, 5, 253–280. [Google Scholar] [CrossRef]
- Forsyth, D.R. Group Dynamics, 5th ed.; Wadsworth, Cengage Learning: Belmont, CA, USA, 2006. [Google Scholar]
- Gardner, H. Frames of Mind: The Theory of Multiple Intelligences; Basic Books: New York, NY, USA, 1983; p. 438. [Google Scholar]
- Woolley, A.W.; Chabris, C.F.; Pentland, A.; Hashmi, N.; Malone, T.W. Evidence for a collective intelligence factor in the performance of human groups. Science 2010, 330, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Graf, V.; Barlow, J.B. Clarifying the Structure of Collective Intelligence in Teams: A Meta-Analysis. In Proceedings of the Collective Intelligence, Pittsburgh, PA, USA, 12–14 June 2019. [Google Scholar]
- Woolley, A.W.; Aggarwal, I.; Malone, T.W. Collective Intelligence and Group Performance. Curr. Dir. Psychol. Sci. 2015, 24, 420–424. [Google Scholar] [CrossRef]
- Bates, T.C.; Gupta, S. Smart groups of smart people: Evidence for IQ as the origin of collective intelligence in the performance of human groups. Intelligence 2017, 60, 46–56. [Google Scholar] [CrossRef]
- Credé, M.; Howardson, G. The structure of group task performance—A second look at “collective intelligence”: Comment on Woolley et al. (2010). J. Appl. Psychol. 2017, 102, 1483–1492. [Google Scholar] [CrossRef] [PubMed]
- Barlow, J.B.; Dennis, A.R. Not as smart as we think: A study of collective intelligence in virtual groups. J. Manag. Inf. Syst. 2016, 33, 684–712. [Google Scholar] [CrossRef]
- Engel, D.; Woolley, A.W.; Aggarwal, I.; Chabris, C.F.; Takahashi, M.; Nemoto, K.; Kaiser, C.; Kim, Y.J.; Malone, T.W. Collective Intelligence in Computer-Mediated Collaboration Emerges in Different Contexts and Cultures. In Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems, Seoul, Korea, 18–23 April 2015. [Google Scholar] [CrossRef]
- Engel, D.; Woolley, A.W.; Jing, L.X.; Chabris, C.F.; Malone, T.W. Reading the mind in the eyes or reading between the lines? Theory of mind predicts collective intelligence equally well online and face-to-face. PLoS ONE 2014, 9, e115212. [Google Scholar] [CrossRef]
- Wildman, J.L.; Thayer, A.L.; Rosen, M.A.; Salas, E.; Mathieu, J.E.; Rayne, S.R. Task types and team-level attributes: Synthesis of team classification literature. Hum. Resour. Dev. Rev. 2012, 11, 97–129. [Google Scholar] [CrossRef]
- Lam, S.S.K. The effects of group decision support systems and task structures on group communication and decision quality. J. Manag. Inf. Syst. 1997, 13, 193–215. [Google Scholar] [CrossRef]
- Steiner, I.D. Group Process and Productivity; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Zaccaro, S.J.; Lowe, C.A. Cohesiveness and performance on an additive task: Evidence for multidimensionality. J. Soc. Psychol. 1988, 128, 547–558. [Google Scholar] [CrossRef]
- Littlepage, G.E. Effects of group size and task characteristics on group performance: A test of Steiner’s model. Personal. Soc. Psychol. Bull. 1991, 17, 449–456. [Google Scholar] [CrossRef]
- Laughlin, P.R. Social combination processes of cooperative problem-solving groups on verbal intellective tasks. In Progress in Social Psychology; Hillsdale: Erlbaum, NJ, USA, 1980; Volume 1, pp. 127–155. [Google Scholar]
- Laughlin, P.R.; Ellis, A.L. Demonstrability and social combination processes on mathematical intellective tasks. J. Exp. Soc. Psychol. 1986, 22, 177–189. [Google Scholar] [CrossRef]
- Guazzini, A.; Stefanelli, F.; Imbimbo, E.; Vilone, D.; Bagnoli, F.; Levnajić, Z. Humans best judge how much to cooperate when facing hard problems in large groups. Sci. Rep. 2019, 9, 5497. [Google Scholar] [CrossRef] [PubMed]
- D’Zurilla, T.J.; Goldfried, M.R. Problem solving and behavior modification. J. Abnorm. Psychol. 1971, 78, 107–126. [Google Scholar] [CrossRef] [PubMed]
- Hayes, J.R. The Complete Problem Solver, 2nd ed.; Routledge: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Laughlin, P.R. Group Problem Solving; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Ingham, A.G.; Levinger, G.; Graves, J.; Peckham, V. The Ringelmann effect: Studies of group size and group performance. J. Exp. Soc. Psychol. 1974, 10, 371–384. [Google Scholar] [CrossRef]
- Kerr, N.L.; MacCoun, R.J.; Kramer, G.P. Bias in judgment: Comparing individuals and groups. Psychol. Rev. 1996, 103, 687. [Google Scholar] [CrossRef]
- Latané, B.; Williams, K.; Harkins, S. Many hands make light the work: The causes and consequences of social loafing. J. Personal. Soc. Psychol. 1979, 37, 822. [Google Scholar] [CrossRef]
- Aggarwal, I.; Woolley, A.W.; Chabris, C.F.; Malone, T.W. The impact of cognitive style diversity on implicit learning in teams. Front. Psychol. 2019, 10, 112. [Google Scholar] [CrossRef]
- Moede, W. Die Richtlinien der Leistungs-psychologie. Ind. Psychotech. 1927, 4, 193–209. [Google Scholar]
- Shaw, M.E. A Comparison of Individuals and Small Groups in the Rational Solution of Complex Problems. Am. J. Psychol. 1932, 44, 491–504. [Google Scholar] [CrossRef]
- Lorge, I.; Solomon, H. Two models of group behavior in the solution of eureka-type problems. Psychometrika 1955, 20, 139–148. [Google Scholar] [CrossRef]
- McGrath, J.E. Groups: Interaction and Performance; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984; Volume 14. [Google Scholar]
- Laughlin, P.R. Collective Induction: Twelve Postulates. Organ. Behav. Hum. Decis. Process. 1999, 80, 50–69. [Google Scholar] [CrossRef] [PubMed]
- Mesmer-Magnus, J. Information Sharing and Team Performance: A Meta-Analysis CREWS: Crew Recommender for Effective Work in Space View project. Artic. J. Appl. Psychol. 2009, 94, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Laughlin, P.R.; Bonner, B.L. Collective induction: Effects of multiple hypotheses and multiple evidence in two problem domains. J. Personal. Soc. Psychol. 1999, 77, 1163–1172. [Google Scholar] [CrossRef]
- Straus, S.G.; Olivera, F. Knowledge acquisition in virtual teams. In Research on Managing Groups and Teams; Griffith, T., Ed.; JAI Press: Stamford, CT, USA, 2000; pp. 257–282. [Google Scholar]
- Miller, S.A.; Brownell, C.A. Peers, Persuasion, and Piaget: Dyadic Interaction between Conservers and Nonconservers. Child Dev. 1975, 46, 992. [Google Scholar] [CrossRef]
- Perret-Clermont, A.N. Social Interaction and Cognitive Development in Children; Academic Press: London, UK, 1980. [Google Scholar]
- Doise, W.; Mugny, G. The Social Development of the Intellect; Pergamon Press: Oxford, UK, 1984. [Google Scholar]
- Gadeceau, J.F.; Training, I. Collective intelligence as an efficient tool for learning. Eur. Police Sci. Res. Bull. 2015, 12, 43–50. [Google Scholar]
- Kim, Y.J.; Engel, D.; Woolley, A.W.; Lin, J.Y.T.; McArthur, N.; Malone, T.W. What Makes a Strong Team?: Using Collective Intelligence to Predict Team Performance in League of Legends. In Proceedings of the 2017 ACM Conference on Computer Supported Cooperative Work and Social Computing, Portland, OR, USA, 25 February–1 March 2017; pp. 2316–2329. [Google Scholar]
- McMillan, D.W.; Chavis, D.M. Sense of community: A definition and theory. J. Community Psychol. 1986, 14, 6–23. [Google Scholar] [CrossRef]
- Wittenbaum, G.M.; Hollingshead, A.B.; Paulus, P.B.; Hirokawa, R.Y.; Ancona, D.G.; Peterson, R.S.; Jehn, K.A.; Yoon, K. The functional perspective as a lens for understanding groups. Small Group Res. 2004, 35, 17–43. [Google Scholar] [CrossRef]
- Chiorri, C.; Bracco, F.; Piccinno, T.; Modafferi, C.; Battini, V. Psychometric Properties of a Revised Version of the Ten Item Personality Inventory. Eur. J. Psychol. Assess. 2015, 31, 109–119. [Google Scholar] [CrossRef]
- Costa, P.T.; McCrae, R.R. Normal personality assessment in clinical practice: The NEO Personality Inventory. Psychol. Assess. 1992, 4, 5–13. [Google Scholar] [CrossRef]
- Rovai, A.P.; Wighting, M.J.; Lucking, R. The classroom and school community inventory: Development, refinement, and validation of a self-report measure for educational research. Internet High. Educ. 2004, 7, 263–280. [Google Scholar] [CrossRef]
- Vellante, M.; Baron-Cohen, S.; Melis, M.; Marrone, M.; Petretto, D.R.; Masala, C.; Preti, A. The “reading the Mind in the Eyes” test: Systematic review of psychometric properties and a validation study in Italy. Cogn. Neuropsychiatry 2013, 18, 326–354. [Google Scholar] [CrossRef] [PubMed]
- Raven, J. The Raven’s Progressive Matrices: Change and Stability over Culture and Time. Cogn. Psychol. 2000, 41, 1–48. [Google Scholar] [CrossRef] [PubMed]
- Rushton, J.P.; Skuy, M.; Bons, T.A. Construct validity of Raven’s Advanced Progressive Matrices for African and non-African engineering students in South Africa. Int. J. Sel. Assess. 2004, 12, 220–229. [Google Scholar] [CrossRef]
- Brouwers, S.A.; Van de Vijver, F.J.; Van Hemert, D.A. Variation in Raven’s Progressive Matrices scores across time and place. Learn. Individ. Differ. 2009, 19, 330–338. [Google Scholar] [CrossRef]
- Arce-Ferrer, A.J.; Guzmán, E.M. Studying the equivalence of computer-delivered and paper-based administrations of the raven standard progressive matrices test. Educ. Psychol. Meas. 2009, 69, 855–867. [Google Scholar] [CrossRef]
- Szuba, T. A formal definition of the phenomenon of collective intelligence and its IQ measure. Future Gener. Comput. Syst. 2001, 17, 489–500. [Google Scholar] [CrossRef]
- Perc, M.; Jordan, J.J.; Rand, D.G.; Wang, Z.; Boccaletti, S.; Szolnoki, A. Statistical physics of human cooperation. Phys. Rep. 2017, 687, 1–51. [Google Scholar] [CrossRef]
| Akaike | F | Df-1(2) | Model Precision | |
|---|---|---|---|---|
| Best Model | 17,453.795 | 100.412 *** | 7(3662) | 76.4% |
| Fixed Effects | ||||
| Factors | F | Df-1(2) | Coefficient () | Student t |
| Teammates’ Variability in RME Score | 26.761 | 1(3662) | 0.206 | 5.173 *** |
| Conversational Turnover | 8.639 | 1(3662) | −0.003 | −2.939 ** |
| Teammates’ Average Neuroticism Score | 19.356 | 1(3662) | 0.175 | 4.400 *** |
| Teammates’ Average CSCI Score (SOC) | 19.656 | 1(3662) | 0.091 | 4.434 *** |
| Teammates’ Average RAPM Score | 103.351 | 1(3662) | 4.942 | 10.166 *** |
| Difficulty of the Task | 262.929 | 2(3662) | −2.838 | −22.697 *** |
| 2(3662) | −1.220 | −13.252 *** | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imbimbo, E.; Stefanelli, F.; Guazzini, A. Adolescent’s Collective Intelligence: Empirical Evidence in Real and Online Classmates Groups. Future Internet 2020, 12, 81. https://doi.org/10.3390/fi12050081
Imbimbo E, Stefanelli F, Guazzini A. Adolescent’s Collective Intelligence: Empirical Evidence in Real and Online Classmates Groups. Future Internet. 2020; 12(5):81. https://doi.org/10.3390/fi12050081
Chicago/Turabian StyleImbimbo, Enrico, Federica Stefanelli, and Andrea Guazzini. 2020. "Adolescent’s Collective Intelligence: Empirical Evidence in Real and Online Classmates Groups" Future Internet 12, no. 5: 81. https://doi.org/10.3390/fi12050081
APA StyleImbimbo, E., Stefanelli, F., & Guazzini, A. (2020). Adolescent’s Collective Intelligence: Empirical Evidence in Real and Online Classmates Groups. Future Internet, 12(5), 81. https://doi.org/10.3390/fi12050081







