Consensus Crash Testing: Exploring Ripple’s Decentralization Degree in Adversarial Environments

Abstract

The inception of Bitcoin as a peer-to-peer payment system, and its underlying blockchain data-structure and protocol, has led to an increased interest in deploying scalable and reliable distributed-ledger systems that build on robust consensus protocols. A critical requirement of such systems is to provide enough fault tolerance in the presence of adversarial attacks or network faults. This is essential to guarantee liveness when the network does not behave as expected and ensure that the underlying nodes agree on a unique order of transactions over a shared state. In comparison with traditional distributed systems, the deployment of a distributed-ledger system should take into account the hidden game theoretical aspects of such protocols, where actors are competing with each other in an environment which is likely to experience various well-motivated malicious and adversarial attacks. Firstly, this paper discusses the fundamental principles of existing consensus protocols in the context of both permissioned and permissionless distributed-ledger systems. The main contribution of this work deals with observations from experimenting with Ripple’s consensus protocol as it is embodied in the XRP Ledger. The main experimental finding suggests that, when a low percentage of malicious nodes is present, the centralization degree of the network can be significantly relaxed ensuring low convergence times. Those findings are of particular importance when engineering a consensus algorithm that would like to balance security with decentralization.

1. Introduction

A distributed system provides an abstraction of a coherent system, whereas in reality it consists of a collection of many distributed, autonomous computational entities (referred to as nodes/peers), which communicate and coordinate their actions through the exchange of messages (i.e., message passing) over a network layer [1]. The implementation of a message passing system allows nodes to operate concurrently, even with a partial view of the information, usually operating under a shared state to achieve a common goal (e.g., a computational task). The ultimate goal of such systems is to provide increased performance and enhanced reliability of a service when compared to a centralized system [2]. A fundamental challenge of such systems is how to provide a level of guarantee in collaboration and exchange of information in a highly dynamic, untrusted, and heterogeneous environment.

Especially for distributed system applications that build on an open-participation environment (e.g., peer-to-peer), the federation of nodes must be able to provide the conditions under which the nodes will collaborate and mechanisms to achieve reliability of the services even in the presence of unreliable participants or components—more specifically, in settings where the federation of nodes communicates over a network layer different faults are likely to be exhibited. The network layer may fail to deliver messages to other nodes, messages are likely to have different delays or duplicated; due to some hardware or software failure. In addition, nodes may behave arbitrarily (either on purpose or due to a malicious attack) and not conform to the rules of the protocol, e.g., either by sending malicious messages and/or not responding to other messages. These malicious attacks and software/hardware faults are common in distributed settings, especially in open participation systems that consist of independent actors in a highly scalable and dynamic environment. In the literature, such faults are referred to as Byzantine [3,4] with a significant body of work on algorithms that enable Byzantine fault-tolerance on such systems (e.g., [5,6,7]), despite the failure of a limited number of their components [8].

To enable collaboration between a set of federated nodes, a fundamental challenge is for the nodes to agree with finality on some data upon which some other computational process will be executed. Similar challenge exists in unreliable distributed databases where the system needs to decide on whether to commit a data transaction to the state of the database or to abort it [2,8]. This problem is realized as the agreement problem where the challenge is not what the processes will be agreeing on but how all processes reach the same conclusion (i.e., consensus (the state in which nodes in a distributed system reach final agreement)), in the presence of faults where distinct nodes are likely to receive conflicting conclusions [8].

1.1. The Blockchain Consensus Paradigm

Bitcoin’s data-structure (i.e., blockchain) builds on top of an open-participation, decentralized, and distributed group of nodes that collaborate under a federation. Their ultimate goal is to agree upon a global state which is made redundant to each peer. To put this into context, the decentralized property is implied from the disintermediation of the global state (i.e., the ledger) from any single entity, whereas the distributed nature of the protocol needs to guarantee that the ledger is persistent. In doing so, it is required that the protocol reaches consensus deciding on which data to append on the ledger—i.e., as blocks to the blockchain. In addition, several cryptographic functions are utilized for hashing and digital signatures to support the distributed transaction that are recorded securely to the network. Furthermore, the so-called Nakamoto consensus (i.e., Proof-of-Work (PoW) [9]) adds another dimension to classical consensus protocols used in distributed systems. That is the incentivization dimension embedded to the protocol which also adds a self-governance layer to the system. This relates to the hidden game-theoretical aspects of blockchains where actors are insentivized (by a reward model) to participate to a computational race for validating a block of transactions by finding the solution to a hash puzzle [10]. This dimension implies a game among competing actors (in this context peers) that can either be honest, by following the protocol rules and remain active throughout the execution of the protocol, or malicious, by attempting to alter the state of the ledger and attempt to stretch the protocol to its limits, for maximizing their payoffs in the game.

Considering the aforementioned characteristics of the blockchain consensus paradigm, we expose the following set of key properties that consensus protocols tailored for blockchains should exhibit: (i) liveness/utility: requests to the services (e.g., execution of a smart contract or the distributed payment system using the native cryptocurrency) are accommodated for non-malicious actors (within a reasonable time delay), i.e., assumptions that guarantee forward progress of the network need to be in place; (ii) agreement/consistency: maintain a global truth of the final ledger that is resilient to faults caused by the potentially adversarial environment; and (iii) termination: all processes decide and define a total order of the blocks to be appended on the ledger, no two correct processes agree on different blocks at any given index, and thus preventing double-spending attacks (this prevention mechanism is utilizing cryptographic signatures and time-stamping techniques) [9].

1.2. Contribution

In this work, we analyze the robustness of consensus algorithms proposed in private distributed ledgers specifically focusing in the context of the Ripple protocol. Following from a simulation analysis of Ripple’s protocol consensus algorithm proposed by Schwartz et al. [11], we conduct a first step regarding the identification of the optimal decentralization degree with respect to the consensus time minimization in the presence of malicious nodes in the underlying network. Specifically, this is experimentally investigated by studying those network configuration parameters that characterize the decentralization character of the network.

The rest of this paper is organized as follows. In Section 2, an overview of the blockchain consensus paradigm is provided along with a series of key properties. The role of consensus protocols as safe-guarding mechanisms is explained in Section 3 with reference to both permissioned and permissionless blockchains. The experimental part of this work focusing on a semi-permissioned network (Ripple) is described in Section 4, while the respective evaluation results are reported in Section 5. Section 6 concludes the present work.

2. Blockchains an Encapsulation of a Distributed System

A new class of distributed systems is encapsulated in various blockchain protocol implementations (such as, Blockchain-based or DAG (Direct Acyclic Graph)-based systems). Since the parameterization and components of such systems may differ, we refer to them with the more general term as Distributed Ledger Systems (DLS).

Compared to the performance of classical distributed systems, Bitcoin’s consensus algorithm offers a high latency (10 min) for a transaction to be confirmed and appended to a block with a low throughput—in the order of ∼10 tx/s as the maximum time required for the protocol to confirm transactions. In general, this performance is far from optimal if compared with implementations of traditional distributed systems. However, this low performance of the Bitcoin protocol is exchanged with high robustness. We note that this robustness in public DLS is considered as a first-class citizen since the open-participation dimension is expected to motivate malicious actors thus stretching the protocol to its limits is expected. The proof-of-work algorithm safe-guards the protocol by maintaining an incentivized level of robustness (preventing double spending, etc.), which is theoretically difficult to scale [12]. In addition, we note that the challenge of robustness offered by consensus algorithms is closely related with the challenge of decentralization since consensus algorithms are offering a governance model to the system, which will eventually offer a safe reliable system.

Since the backbone of distributed-ledger systems is the consensus algorithm utilized, the design and deployment of such fault tolerant protocols should also consider ways for maintaining low-latency and high-throughput while at the same time guaranteeing enough security. This is an important factor especially for distributed payment systems, such as Ripple [11] or other financial settlement networks. An effective strategy to deal with arbitrary component failures and malicious (adversarial actors) is state machine replication [13,14,15], e.g., variations of Paxos [16] and Practical Byzantine Fault Tolerance (pBFT) [5]. We note that, for Byzantine fault tolerant (BFT) blockchain protocols and especially for open-participation, i.e., permissionless settings, such algorithms need to be adapted for the masses [7] and beyond the challenges of block size and block intervals (e.g., [11,17,18]).

In subsequent sections, we discuss the robustness of XRP’s consensus protocol in the presence of malicious peers and how the UNL overlapping between peers influences the behavior of the network. We argue that this is critical for the XRP ledger since the current assumption of imposing a static UNL list, where validators are assumed to be incentivized enough to play honest, could challenge the reliability of the network (and possibly cause a network halt). Furthermore, we note that the robustness of the network in such a case is highly related with the demand of increasing the decentralization of the network as much as possible.

Despite the low performance of PoW and power consumption concerns, this implementation shared useful insights and led to a significant body of research work on combining PoW with other innovative ideas for BFT consensus protocols for the masses [7]. In principle, engineering consensus algorithms for DLSs are expected to consider the following: How decentralized a DLS system should be? What is the role of the consensus algorithm to maintain an equilibrium among performance, robustness, and decentralization? How much should throughput be favored over latency?

3. Byzantine Fault Tolerance for Distributed-Ledger Systems

We describe above how consensus is the backbone of many distributed systems and position its fundamental role in distributed-ledger systems. Despite the importance of such algorithms to enable reliable distributed services, most research in the field has been studied in the context of controlled environments (where participants are static and known) with a limited body of work in the context of open networks, where the set of participants is dynamic and unknown (e.g., [19]). This section positions consensus protocols in the context of safe-guarding distributed-ledger systems where reliability and resilience of such systems needs to be preserved even with sporadic participation. More specifically, for blockchain-based systems, the properties of reliability, resilience, and security are enhanced by replicating data from the ledger (for blockchain protocols, we consider that nodes need to reach agreement on a linearly ordered set of transactions) in many nodes [20].

This section provides a discussion on the fundamental principles of the various consensus algorithms (or protocols) proposed in the literature. We first describe the two main categories of DLS based on access-control and consensus participation policy; the general categories are: (i) permissionless; and (ii) permissioned. The remainder of this section discusses Nakamoto consensus along with a discussion on the principles introduced by BFT variants.

3.1. Permissionless

Permissionless DLS (also known as public) focuses on a more democratic, decentralized policy for network participation that is not controlled by a central authority (or a governing body) to overlook the network authorization process. All participants are treated equally, and are free to join the network either as a client, reading or writing on the share state by invoking transactions, or participating in the consensus protocol, according to the rules implemented by the network. Usually, such open networks (e.g., Bitcoin and Ethereum) build on consensus protocols that assume some kind of voting power which is proportional to the resources dedicated to the network. More specifically, variations of such consensus protocols (e.g., implementing some Proof-of-X scheme [20,21]) are typically based on the possession of some commonly accessible resource (e.g., storage space or computational cycles, network token staking, etc.).

Such networks use a fair incentivization policy, embodied in the protocol, to encourage honest participation of entities. Typically, such policies offer some financial responsibility and reward. This is important to ensure the reliable operation of the network by encouraging honest actors to continuously participate. Especially for large scale, dynamic (in the sense that participants may join or leave the network at any point in time), and decentralized DLS, a well defined incentivization mechanism is considered critical to mitigate Sybil attacks, where some adversarial entity attempts to manipulate protocol rules (i.e., the consensus mechanism) with the use of many identities [22] in creating a disproportionate control of the network. Bitcoin employs the idea of moderately hard puzzles [9] as a mechanism to prevent such attacks where the identity of participants is highly prized respective to their computational power.

Nakamoto Consensus

One of the main challenges solved by the Bitcoin paper [9] is the double spending problem, where users are prevented from spending the same virtual currency twice. Since there is no central authority to overlook the spending process, some form of agreement between the participants of a p2p network is required to agree on the ordering of transactions and their state. However, Nakamoto does not explicitly refer to the state replication paradigm this is implied since the ledger is commonly shared and replicated within all network participants. According to Xiao et al. [20], Nakamoto consensus is comprised on the following rules: (1) block generation, which relates to the use of PoW to generate a hash result that satisfies a certain target; (2) Broadcasting, which relates to the gossiping rule of the protocol; (3) validation, which relates to the various validity checks for double spending and for validating the form of each transaction or block; (4) longest-chain rule, which relates to resolving any conflicting states of the shared ledger to achieve network consensus; and (5) incentives, which relates to the block rewards or transaction fees that are attached to the process. Overall, incentivization is used to enforce security in Bitcoin’s PoW. We also note that in PoW a single leader is elected to propose a new block to be added on the chain, and that leader is selected probabilistically. Defining more leaders to propose blocks causes a fork to the state of the blockchain and thus a mechanism is required for its resolution (this is solved by the longest-chain rule). For this consensus proposal, an adversarial entity is required to poses computational power equal to $51\%$ of the computational power of the network in order to control the network.

Although Nakamoto consensus (and in principle its variations) enable pseudonymous or anonymous entities to participate concurrently to the consensus process, the network suffers from scalability bounds that do not relate to the available computational power of the entire network. It has been argued that increasing the block size, to accommodate more transactions and thus more throughput, or attempting to decrease latency the network runs the risk into becoming more vulnerable to $51\%$ attacks [21].

3.2. Permissioned

In a permissioned DLS, a governing body is authorizing access to the operations of the network only to known participants who are trusted (or semi-trusted). These participants are often controlled by a single entity or a consortium of entities [23]. The initiator of the network controls this close ecosystem and assigns privileges to entities for validating transactions, participating to the consensus process, writing on the ledger’s data structure, and deploying smart contracts. Deployments of permissioned DLS are becoming a favorable solution for many protocols due to the fact that the set of nodes participating to the consensus body of the network can be restricted to a small set of trusted entities that can reach agreement in less time, thus providing an increased transaction throughput [24]. Compared to permissionless DLS, the additional security layer for access control, assignment of privileges to nodes, the requirement for revealing the identity of nodes, and the different model of governance makes this category suitable for private or internal business networks. A notable example of such a DLS is the Hyperledger Fabric [25] that permits several roles to be assigned to nodes. In Fabric, there is a separation between linearly ordering transactions and execution of transactions that execute embedded code for smart contracts. This partitioning helps the network to avoid conflicts in atomic broadcast operations and ensure consistency. In the spectrum of permissioned DLS, there is also the subcategory of semi-permissioned systems where anyone can join the network and act as a validator towards maintaining their own world-state of the ledger.

3.2.1. Ripple Consensus Protocol

A notable example of a semi-permissioned network is Ripple [11] and the consensus protocol that it is embodied in the XRP Ledger. The consensus mechanism implemented by Ripple (known as the Ripple Consensus Algorithm (RPCA)) is influenced by the idea of a Byzantine quorum system [26] where a minimum set of nodes (i.e., a quorum) collaborates to attain the agreement process. Specifically, for Ripple, the quorum is defined as a list of trusted nodes called the UNL. Each node that is trusted as a validating server to the XRP Ledger maintains its own UNL list and votes on transactions they support. Validating servers collaborate under a binding relationship and only trust the votes cast by other servers included in their UNL. Transactions that are broadcasted to the network are collected by the validating servers that are the ones that participate in the consensus. These transactions are then exchanged with the other validating servers for the creation of a candidate set of transactions. In brief, the process for advancing the ledger is done periodically in rounds and with voting from the nodes that are part of each validating server’s UNL list [27]. For RPCA, each node defines a minimum number of agreeing nodes, denoted by q, in the UNL list before committing to a decision. This is set to $q_i=0.8$, which means that $80\%$ of the UNL list must agree. According to Chase et al. [27], the network can tolerate $f<n/5$, where, n is the number of nodes and f is the number of byzantine (faulty) nodes. Typically, a classical BFT protocol can tolerate $f<(n-1)/3$. It is argued that Ripple is trading fault tolerance capabilities of the network in an attempt to increase performance. In addition, the high level of synchrony assumed by the nodes participating in Ripple’s UNL list might be restrictive in environments of low trust [20,24]. In addition, this impacts on the decentralization of the Ripple’s network.

In terms of network participation, anyone can deploy an instance of the Ripple network (https://github.com/ripple/rippled), as well as act as a validator, contributing on that private instance. For example, the XRP Ledger is the ledger maintained by Ripple Labs, Inc. (https://ripple.com/).

On another note, Stellar [28], which is a protocol initially forked from Ripple, further expands on the idea of a quorum by introducing quorum slices and federated byzantine fault tolerance. Thus, the Stellar Consensus Protocol (SCP) allows for a loose synchrony of participants and achieves a bound of $1/3$ Byzantine fault tolerance compared to the $1/5$ fault tolerant bound achieved by Ripple. Stellar allows more flexibility in terms of which participants to trust and thus for more decentralization when compared to RPCA, but it is less decentralized than the classical PoW [29]. For Stellar, safety is compromised when a user node trusts a quorum slice that is inefficient [28].

3.2.2. Classical Consensus

The need for consensus has been studied extensively in the research area of distributed systems [3,4,8]. As mentioned above, the reliability of services and coordination of multiple individual processes are major challenges for such systems. Thus, distributed systems employ different types of failure models in an attempt to provide resilience against different types of failures: (i) crash failures, where nodes can fail at any time mostly by stop responding or disconnected; and (ii) byzantine failures, where nodes can act arbitrarily (i.e., maliciously) with an ultimate aim to interfere and eventually defeat the original purpose of the consensus protocol, e.g., by sending contradicting or even injecting malware messages, etc. [2,6,8]. In the context of DLS consensus, and especially in a public (or permissionless) environment—where participation to the network is dynamic and open to unknown participants—the Byzantine setting is of relevance [19]. Therefore, the consideration of classical consensus proposals, such as Paxos [16] or Raft [30], are not sufficient. DLS suggests the definition of improved versions of such protocols based on the classical consensus paradigm, suitable for dynamic and highly adversarial environments. BFT consensus protocols are algorithms that provide resilience to one or many byzantine failures while at the same time ensuring that the system is functioning as intended. The implementation of such algorithms originates from the paradigm of state machine replication [7], where consistency of data is ensured by consulting a set of replicas of databases [7,15]. Often, the boundary condition that is satisfied for the operation of such algorithms in the presence of faulty processes f in a systems of N nodes is, $f=\lfloor {\displaystyle \frac{N-1}{3}}\rfloor$ (the reader is referred to the work of [31] for a formal proof).

3.2.3. Discussion

Practically, variations of BFT protocols assume the existence of some fixed set of known and static entities that participate to the consensus protocol. The adaptation of such algorithms in dynamic membership settings with sporadic participation is challenging, although proposals exist on solving some of the challenges based on several assumptions (e.g., [19])—which are sometimes unrealistic in large scale open environments [32]. The message complexity, which is expected to be quadratic $O\left(n^2\right)$ in many classical BFT systems has been a bottleneck in scaling such network deployments. This remains an active research area with proposals on sub-linear or polygon communication costs (the reader is referred to [33,34] for some examples). On the other hand, Nakamoto consensus trades off bandwidth with computation, where consensus requires the election of a random leader to propose the next block (where everyone adopts) and thus a single broadcast is required to reach agreement (eventually if there is no disagreement on the block proposal). From that respect, Nakamoto consensus can scale on a large scale of participants where participation in the consensus agreement protocol is concurrent. We note that Nakamoto consensus does not utilize the computational power to achieve high transaction throughput, which remains 10 min on average irrespective to the network’s overall computational power. It remains that for large scale environments variations of BFT algorithms must comprised on $n\ge 3f+1$ [32].

In subsequent sections, we discuss our results from experimenting with the XRP ledger and its UNL list, which is critical for the liveness of the network. It remains a challenge on how Byzantine consensus protocols can become more decentralized or even adapted in permisionless networks. For RPCA, each node individually defines a static UNL list, and it is the intersection of that list (between pairs of honest nodes) that determines the correct network state. To keep a high level of robustness, the UNL list comprises of validators owned by reputable entities that are incentivized to respond to failures and downtime. However, this limits the degree of decentralization of the entire network. The current implementation of the RPCA consensus algorithm assumes that the UNL list is a trusted subset of the network which defines the minimum overlapping condition.

There is no mechanism in place for detecting which nodes are not behaving according to the protocol and then act upon any potential adversarial action, e.g., by dynamically replacing nodes from the UNL list in order to maintain the minimum overlapping bound of agreeing nodes. One proposal is to maintain the UNL list along with a second list that reports unreliable validator nodes. Under certain conditions, the unreliable list of validators will not influence the minimum overlapping bound of the $80\%$ or even not affect the advancing of the ledger (e.g., voting from adversarial nodes is ignored). Alternatively, it is suggested that the XRP ledger consensus protocol can benefit from a dynamic adaptation of the UNL list (in cases of any failures) or even a reconfiguration of the UNL list members who participate in the consensus protocol. Similar works in the literature suggest the use of wedging as a reconfiguration mechanism [33]. ByzCoin [35] and PeerCensus [36] elaborate on mechanisms for updating the committee members that participate in consensus using a practical approach to BFT for permissioned settings.

Specifically, in Section 4 and Section 5, we experimentally investigate the configuration of the UNL list and its effect on the network performance with respect to varying numbers of malicious nodes. Since the UNL list constitutes an indicator regarding the network’s decentralization degree, this investigation helps us better understand the near-to-optimal UNL setup, targeting increased decentralization, as a function of the malicious nodes that are present in the network.

4. Experimental Setup

In this section, the experimental setup is described, which consists of two scenarios. The purpose of both scenarios is to help us gain deeper understanding of the performance of the underlying consensus mechanisms with respect to the security of the network in terms of malicious nodes. Regarding the latter, the underlying hypothesis is that a subset of the network nodes is malicious i.e., the respective nodes propagate falsified messages to the entire network. Specifically, the experimental parameters are as follows:

• percentage of malicious nodes in the network;
• percentage of UNL overlap; and
• performance-related metrics.

For both scenarios, the first two experimental parameters are identical. The first parameter aims to simulate the conditions under which varying numbers of malicious nodes participate in the network. These numbers are relative to the total number of network nodes. Specifically, 0–$35\%$ malicious nodes were used in the experiments conducted in the present work. This particular range (0–$35\%$) followed the analysis reported in [11,27]. The second experimental parameter was used for incorporating various degrees of decentralization regarding the underlying consensus. In particular, the percentage of UNL overlap can be considered being inversely proportional to the decentralization degree of the consensus process. For example, a network configuration that utilizes $10\%$ UNL overlap is more decentralized compared to the case of $90\%$ UNL overlap. In the next paragraphs, a number of scenario-specific parameters are briefly described.

Scenario 1: Convergence Time. The experiments conducted in this scenario were based on the simulator implementation that is publicly available via the following link: https://github.com/ripple/simulator. This is described in [11]. The convergence time (i.e., the time required for reaching consensus between the network nodes) was used as a performance metric. The performance of the consensus mechanism (and, in general, the network as a whole) is inversely proportional to the convergence time.

Scenario 2: Network Health Indicator. In this scenario, a more recent version of the simulator was applied, which is also publicly available at: https://github.com/ripple/rippled/tree/develop/src/test/csf. This simulator is described in [27]. This newer implementation enabled the computation of a new performance metric, which is more insightful compared to the convergence time used in the first scenario. Specifically, we define the Network Health Indicator ($NHI$) as follows:

$$NHI=\frac{L_C-L_V}{L_C}, \mathrm{for}{L}_C>0\mathrm{and}{L}_V>0,$$

(1)

where $L_C$ and $L_V$ denote the number of candidate ledgers and the number of fully validated ledgers, respectively. By definition, $L_C\ge L_V$, i.e., some candidate ledgers may not be validated. According to the above definition, there are two extreme cases. The worst case takes place when none of the candidate ledgers is validated (i.e., $L_V=0$) resulting in $NHI=1$. The best case happens when $L_C=L_V$, which yields $NHI=0$. Thus, the performance is inversely proportional to $NHI$.

5. Evaluation Results

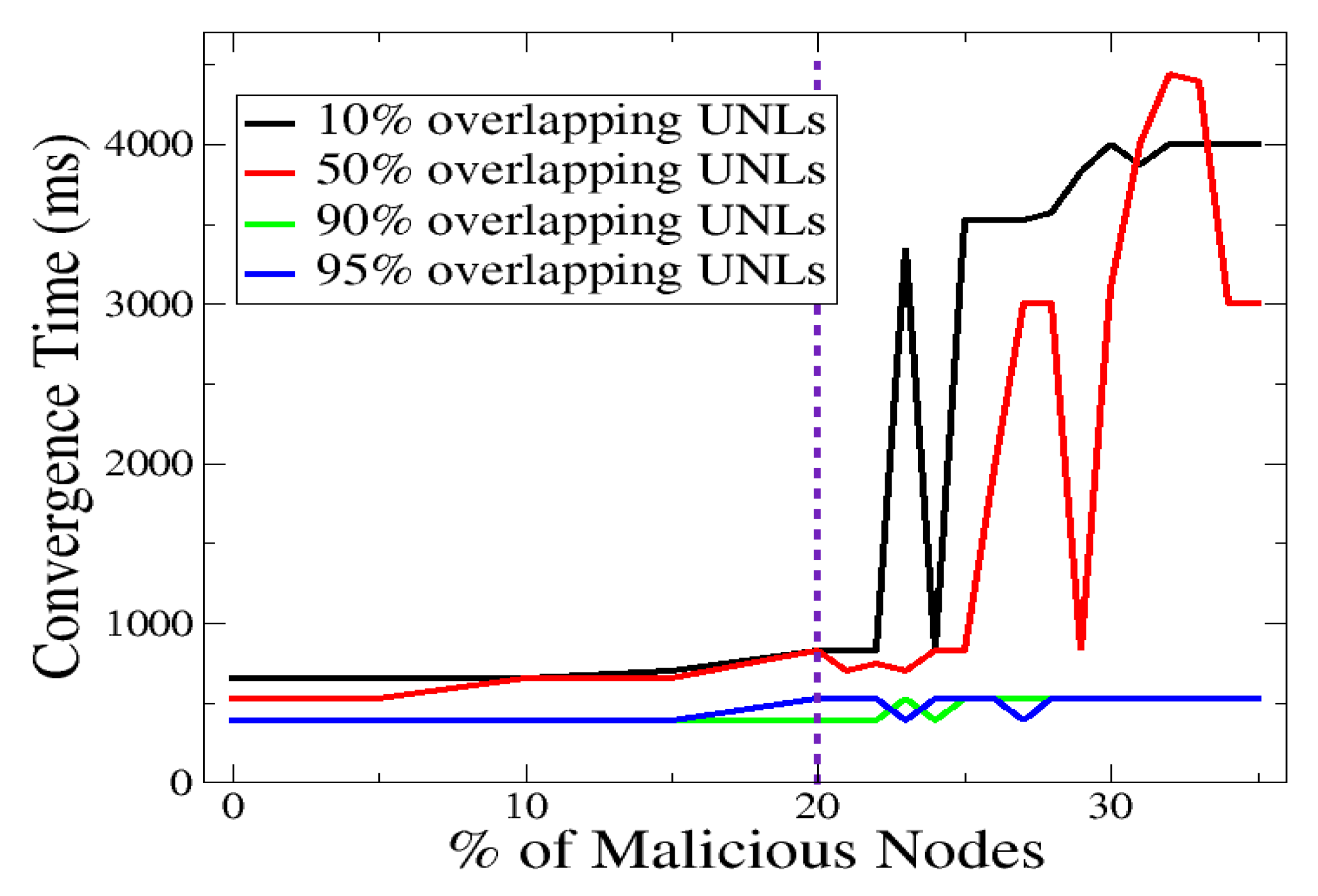
In this section, we present the evaluation results for the two scenarios described in Section 4. Regarding the first scenario, the convergence time is plotted in Figure 1 as a function of the malicious nodes percentage. The latter spans from $0\%$ to $35\%$.

This is shown for various percentages of the UNL overlap, namely, $10\%$, $50\%$, $90\%$, and $95\%$. (These values are representative and adequately cover the parameter’s space. That is, in-between UNL overlap percentages consistently yielded analogous performance scores. They are not depicted for the sake of plot’s readability.) Overall, we observe that low convergence times (less than 1000 ms) are achieved when $90\%$ and $95\%$ UNL overlap is applied. A key observation deals with the broad separation of the considered operational space, in terms of UNL overlap, into two regions, $[0\%,20\%]$ and $(20\%,35\%]$, denoted as $R_1^1$ and $R_2^1$, respectively. Regarding $R_1^1$, all convergence times lie below 1000 ms, while the utilization of $90\%$ and $95\%$ UNL overlaps exhibits better performance compared to the case of $10\%$ and $50\%$ UNL overlaps. Within the $R_2^1$ region, the use of $10\%$ and $50\%$ UNL overlaps exhibits a non-robust behavior yielding convergence times that reach, and occasionally exceed, 4000 ms. These observations suggest that high UNL overlaps are needed only when the percentage of malicious nodes increases beyond a certain threshold. This threshold is (empirically) shown to be approximately equal to $20\%$.

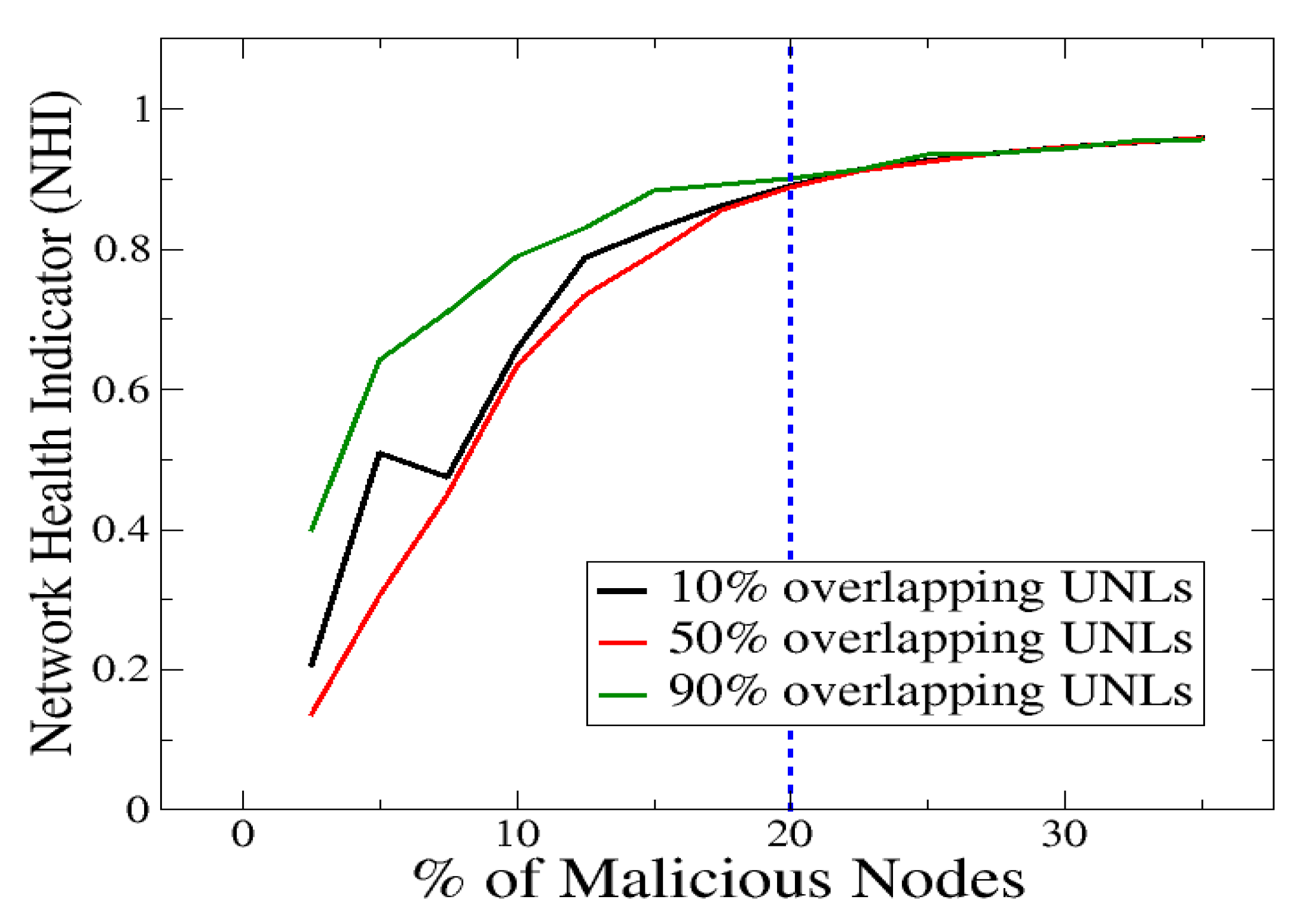
The evaluation results for the second scenario are reported in Figure 2. In this figure, NHI (defined in Section 4) is plotted as a function of the percentage of malicious nodes. As in the case of the first scenario, the percentage of malicious nodes ranges from $0\%$ to $35\%$. NHI scores are shown for three percentages of UNL overlap, namely, $10\%$, $50\%$, and $90\%$ (i.e., weak, mild, and strong UNL overlap). Overall, it is observed that, for all three UNL overlaps, higher NHI scores are reached (i.e., the performance drops) as the percentage of malicious nodes increases. The two operational regions identified in the first scenario, are also evident here, i.e., $[0\%,20\%]$ and $(20\%,35\%]$ (denoted as $R_1^2$ and $R_2^2$, respectively). Interestingly, in the entire $R_1^2$ region, the lowest NHI scores (corresponding to better performance) are consistently achieved for the case of $50\%$ UNL overlap. In $R_2^2$, almost identical NHI scores are yielded by all three UNL overlaps. The top performance of $50\%$ UNL overlap within $R_1^2$, agrees with the main finding of the first scenario, which indicates that a strict (i.e., high) UNL overlap is not required when a low percentage of malicious nodes is present in the network. As before, the respective threshold is empirically found to be approximately equal to $20\%$.

Overall, the aforementioned finding aligns with the theoretical foundations and analysis of Chase et al. [27]. On this basis, the 90% threshold reported was not only justified in our work, but also it was further investigated. Specifically, a wide range of such thresholds (10–99%) are experimentally studied in combination with a range of malicious nodes percentages (0–35%) within the bounds of strong and weak correctness [11].

6. Conclusions

This work complements the analysis presented in [27] where a minimum bound on the percentage of UNL overlapping is suggested. More specifically, we report results from our empirical experimentation with different percentages of UNL overlaps in conjunction with varying numbers of malicious nodes, measuring their respective effect in terms of network performance. The main experimental finding suggests that, when a low percentage (0–20%) of malicious nodes is present, the centralization degree of the network—as implemented by the UNL’s percent overlap—can be significantly relaxed ensuring convergence times being shorter than 1000 ms. A strong UNL overlap, for example 90–99%, is needed only when the percentage of malicious nodes exceeds a critical threshold, which equals to 20%. This threshold can be considered as an empirical boundary between two broad operational regions. When the percentage of malicious nodes is less than 20%, the convergence time is upper-bounded at 1000 ms—this holds for all (10–99%) UNL overlaps applied in this work. If the 20% is exceeded, a “burst” effect occurs making the consensus less robust, in terms of time, as the percentage of UNL overlap decreases. The above observations clearly indicate the opportunity for engineering an adaptive scheme for dynamically (i.e., as the networks operates) determining an optimal (or nearly-optimal) UNL overlap. The optimization problem deals with the identification of the lowest possible UNL overlap (thus enhancing the decentralization degree of the network) while constraining the consensus time under a desirable threshold. This is fully aligned with one of the main points reported in [37] according to which the enhancement of the network decentralization is of greater importance compared to the protocol efficiency. For this purpose, an additional computational element is required, namely a malicious nodes estimator (or, ideally, identifier/tracker). In this framework, one may configure networks that combine the high reliability of private networks (e.g., Ripple) with the decentralized spirit of open blockchains (e.g., Bitcoin).