A Novel Resource Allocation Scheme in NOMA-Based Cellular Network with D2D Communications
Abstract
1. Introduction
- (1)
- The proposed algorithm can jointly solve the user scheduling, power allocation and link selection problems for the D2D underlaying cellular network with the NOMA technology, which is a candidate technology for future networks. The D2D communication is introduced to offload traffic from the base station (BS) and increase network capacity.
- (2)
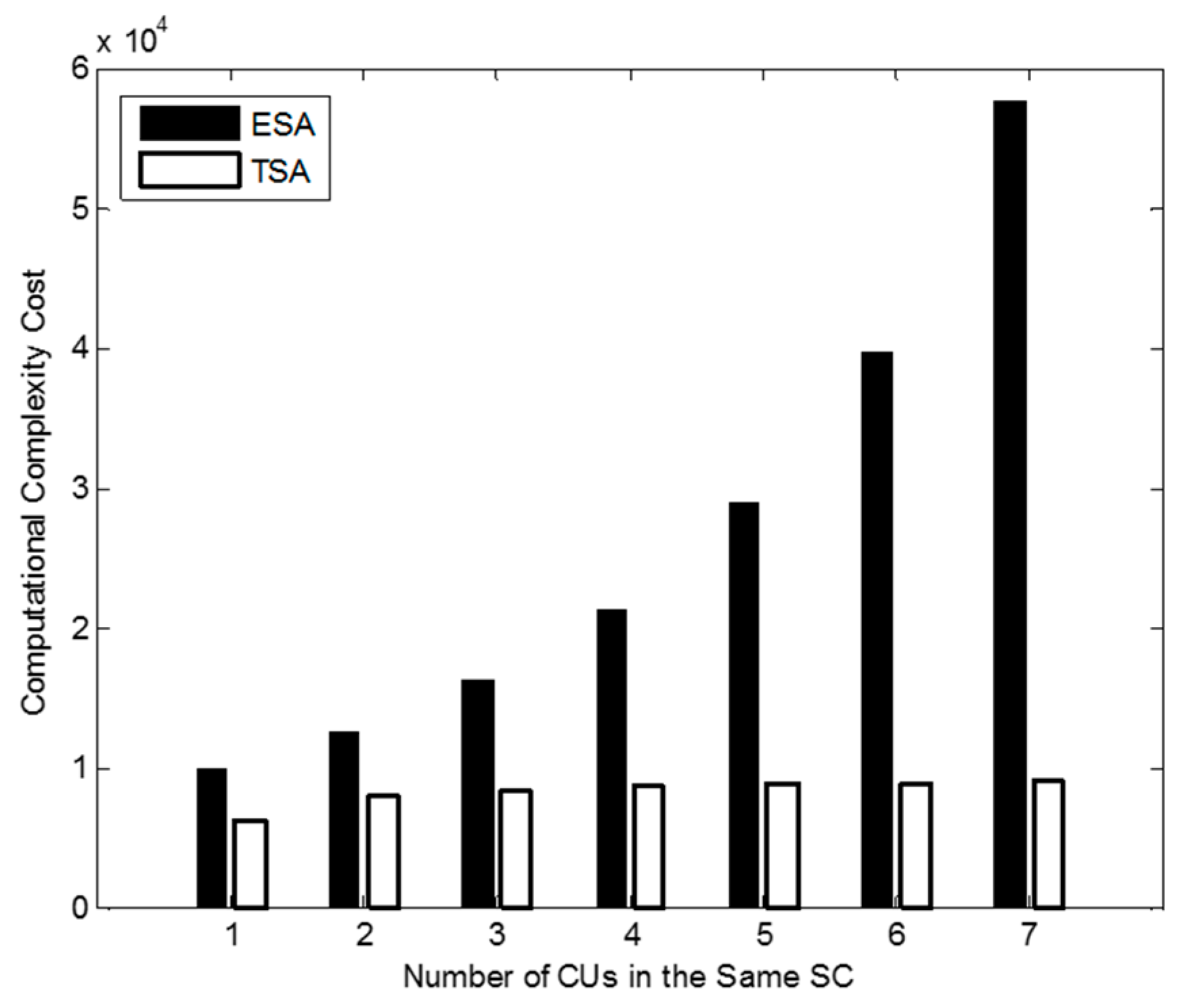
- A low computational complexity cost search algorithm has been given. Compared with the ESA, it reduces the number of searches by considering the SIC decoding order and thus improves the search rate. It is analytically proved that compared with ESA in OMA, the proposed method can reduce the computational complexity cost. Because of the way of searching for solutions without derivation, it becomes easy for the algorithm to give an optimal solution.
- (3)
- We use the geometric mean value and the arithmetic mean value of the data rates as two objective functions of the tree-based search algorithm, respectively. The former considers the impact of the mean value when extremely high or low power signals exist, while the latter reflects the real mean value of the sum rate.
- (4)
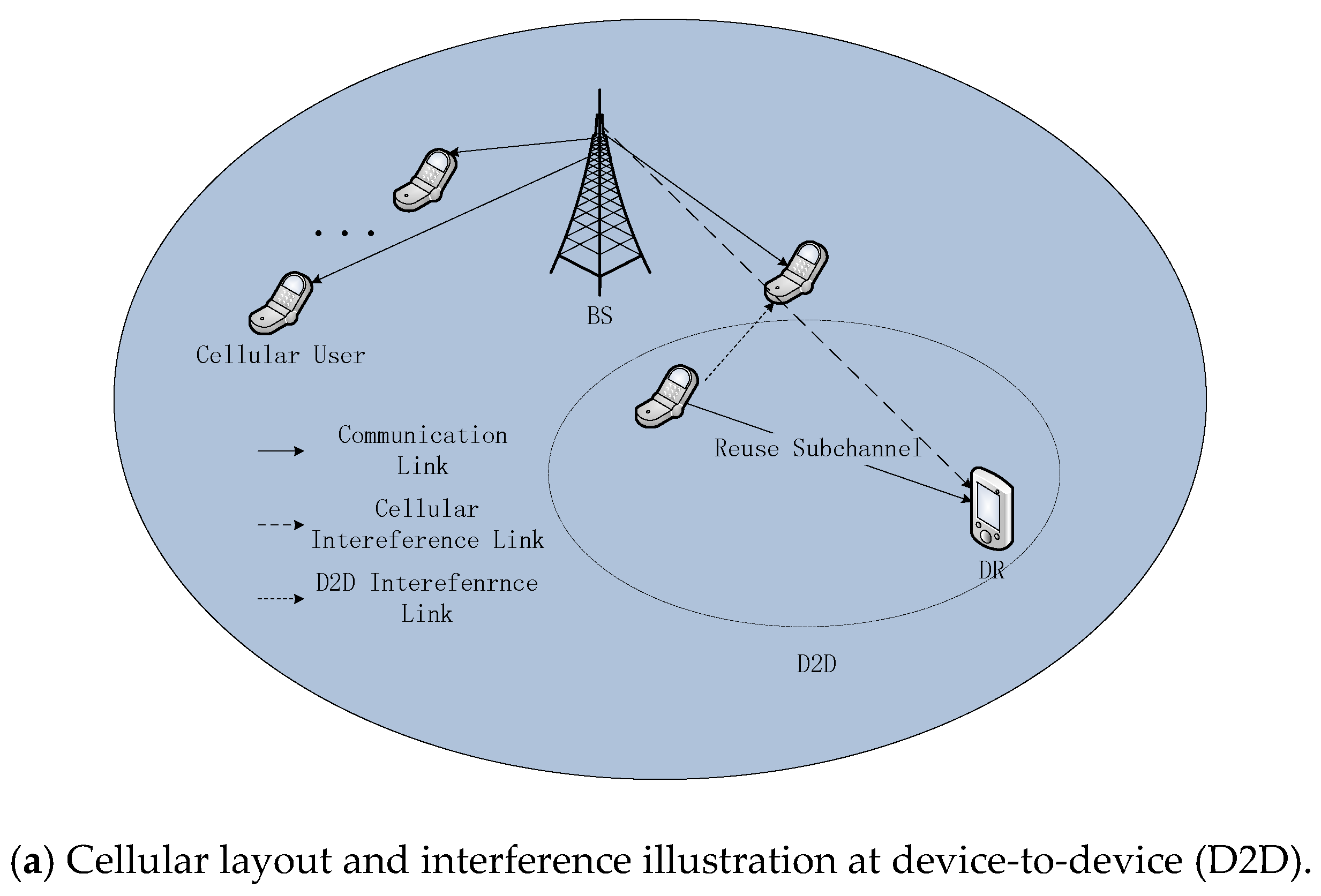
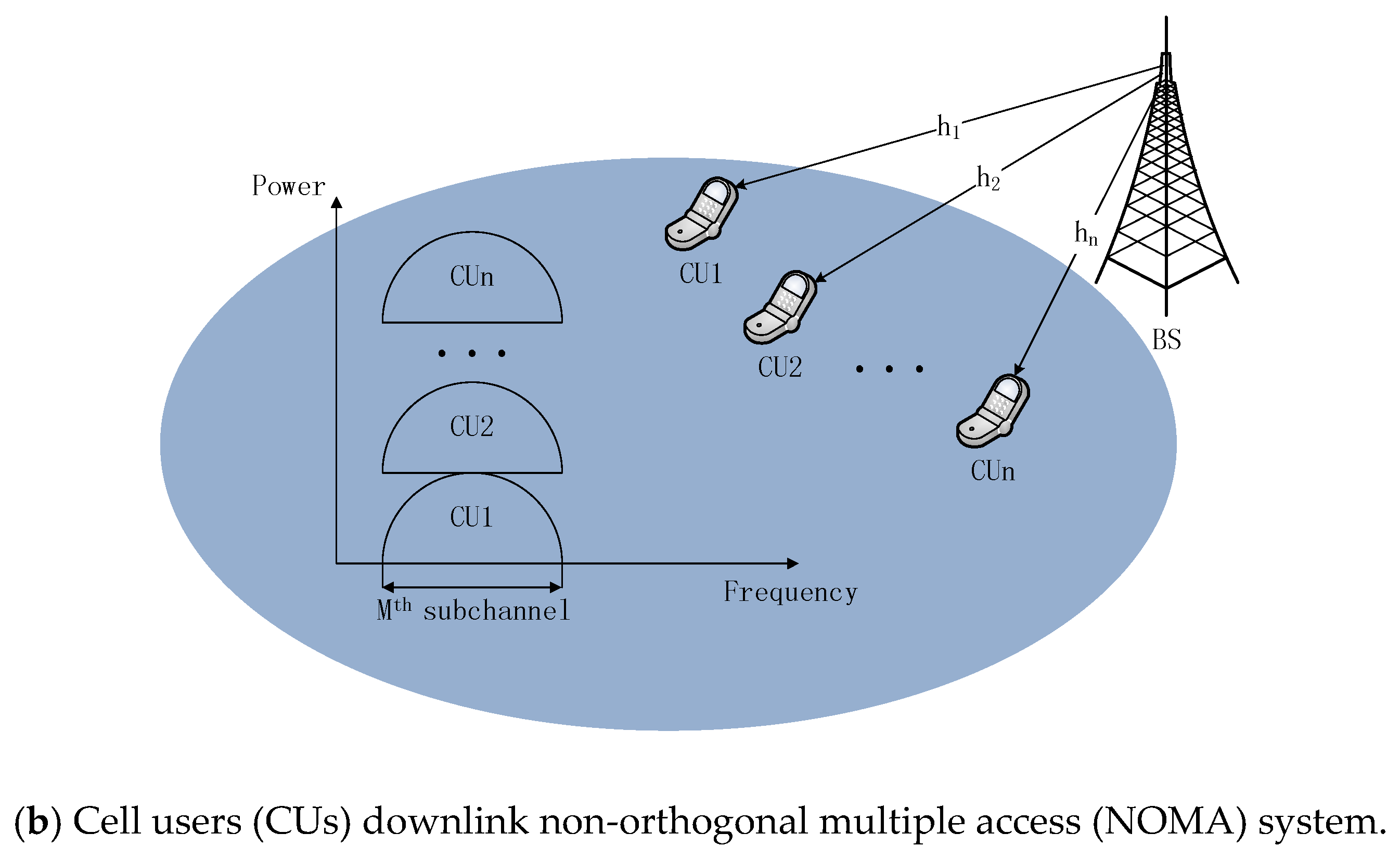
2. Network Model
2.1. Channel Model
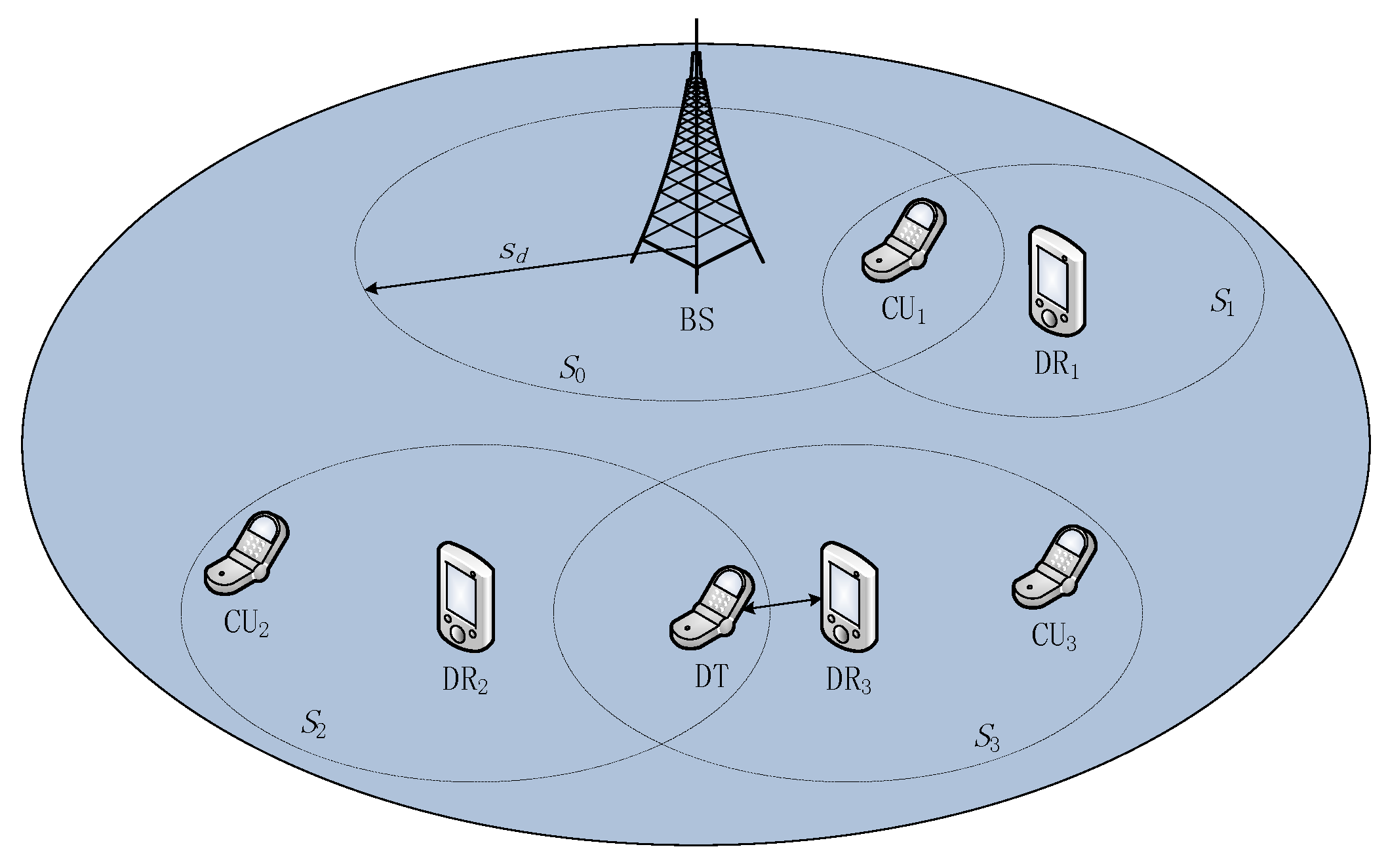
2.2. System Description
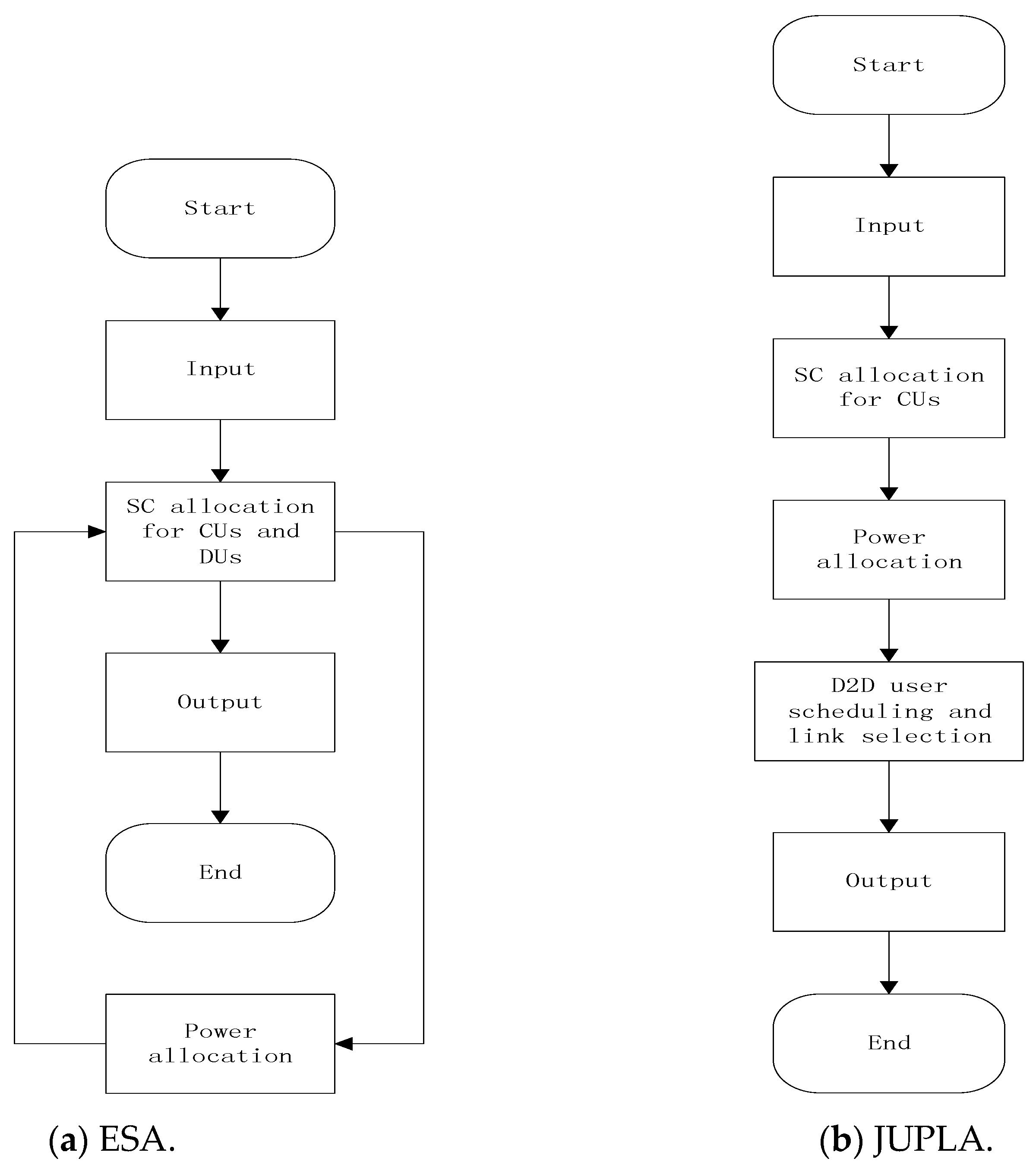
3. Proposed Joint User Scheduling, Tree-Based Search Power Allocation and Link Selection Algorithm
3.1. System Formulation
3.2. User Scheduling Algorithm of the Network
| Algorithm 1 A User Scheduling Algorithm |
| 1: Initialize the power allocation for each CU 2: Construct the channel gains 3: Initial the sets to record the unallocated CUs in the system. 4: Initial the sets to record the candidate CUs in the SC. 5: Initial the sets to record the unallocated DUs in the system. 6: Initial the sets to record the candidate DUs in the SC. 7: while do 8: Find the maximum value in using 9: if the number of multiplexed CUs on this SC is less than then 10: (a) Schedule the CU onto the SC 11: (b) = \ 12: end if 13: if the number of multiplexed CUs on this SC equals then 14: (a) Assume CU is allocated on the SC and the CU set is 15: (b) Calculate the data rate of the CUs from and get a set of 16: (c) and 17: (d) = \ 18: Let the and row’s elements in be zeros. 19: Let the column’s elements in be zeros. 20: end if 21: end while 22: Allocate power to the CUs (Algorithm 2). 23: Construct the channel gains 24: Initialize the power allocation for each DU. 25: while do 26: Find the maximum value in using 27: if the number of multiplexed DUs on this SC is less than then 28: (a) Schedule the DU onto the SC 29: (b) = \ 30: end if 31: if the number of multiplexed DUs on this SC equals then 32: (a) Assume DU is allocated on the SC and the DU set is 33: (b) Calculate the data rate of the DUs from and get a set of 34: (c) and 35: (d) = \ 36: Let the and row’s elements in be zeros. 37: Let the column’s elements in be zeros. 38: end if 39: end while |
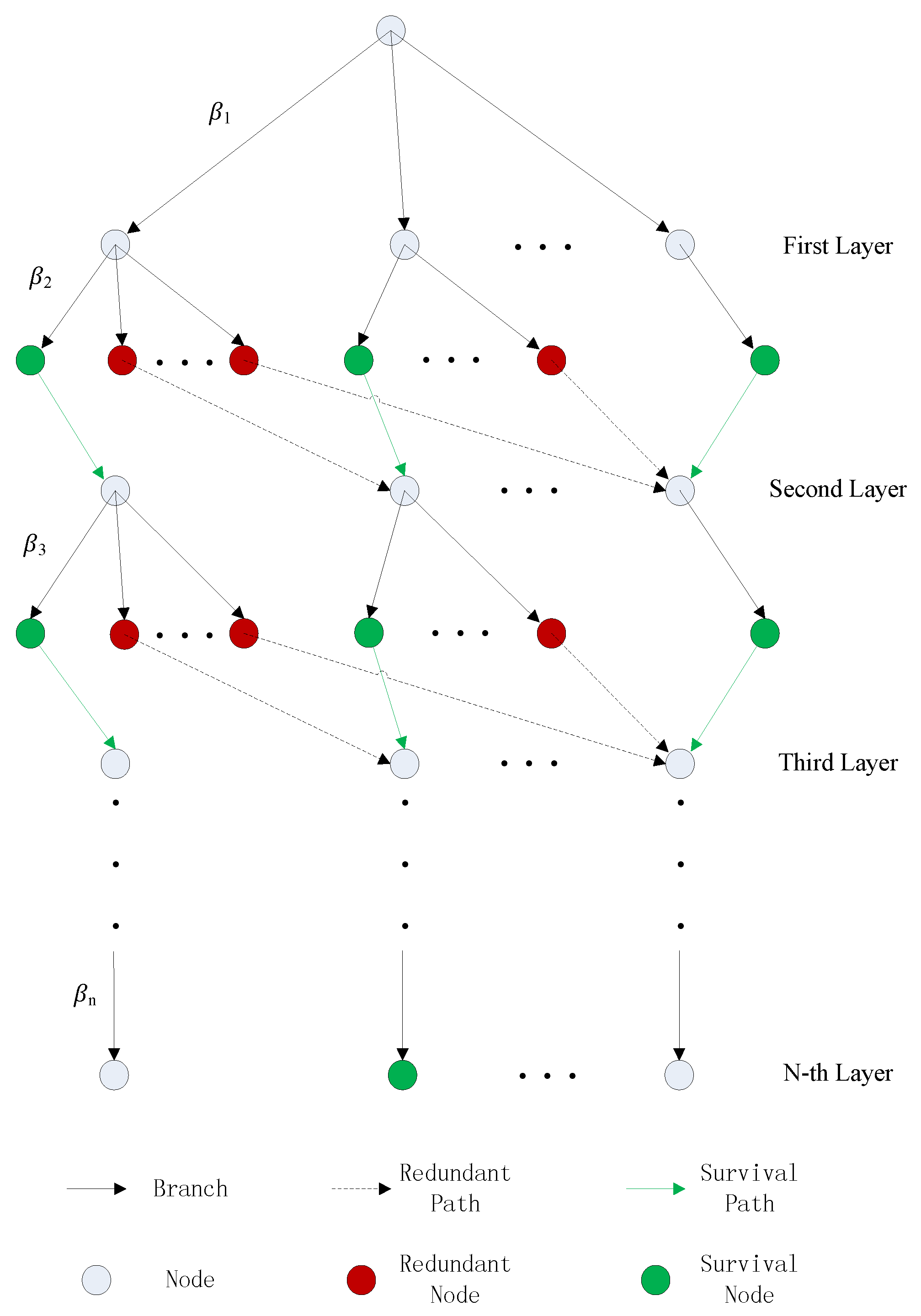
3.3. Principles of Tree-Based Search Power Allocation Algorithm
3.4. Proposed Tree-Based Search Algorithm (TSA) for Power Allocation
- (1)
- Initialization: First, we initialize the standards (28) and (29) mentioned above and the channel gain of each CU on the same SC.
- (2)
- Calculate the values of the power allocation coefficients: Calculate the matrix of candidate power allocation coefficients in the layer, according to (26) and (27), determined by the number of survival nodes of the previous layer and the minimum interval of the power allocation coefficients.
- (3)
- Delete the redundant nodes: We first divide the nodes into several groups. In each group, through (26), we calculate and find out the nodes belong to the layer which has the same to be classified to the same group. Then through the formulation derived from (26), we get the results of in each group and pick out the maximum nodes. Finally, we select the survival nodes and delete the redundant paths.
- (4)
- Select the final survival path: Repeat step (2) and step (3) until the last layer where and the number of the branches equals to the number of the survival nodes in the previous layer. Satisfying the unique value of we pick out the group of survival nodes with the maximum and get the final survival path.
- (5)
- Output: From final survival path we can get the suboptimal set of power allocation coefficients
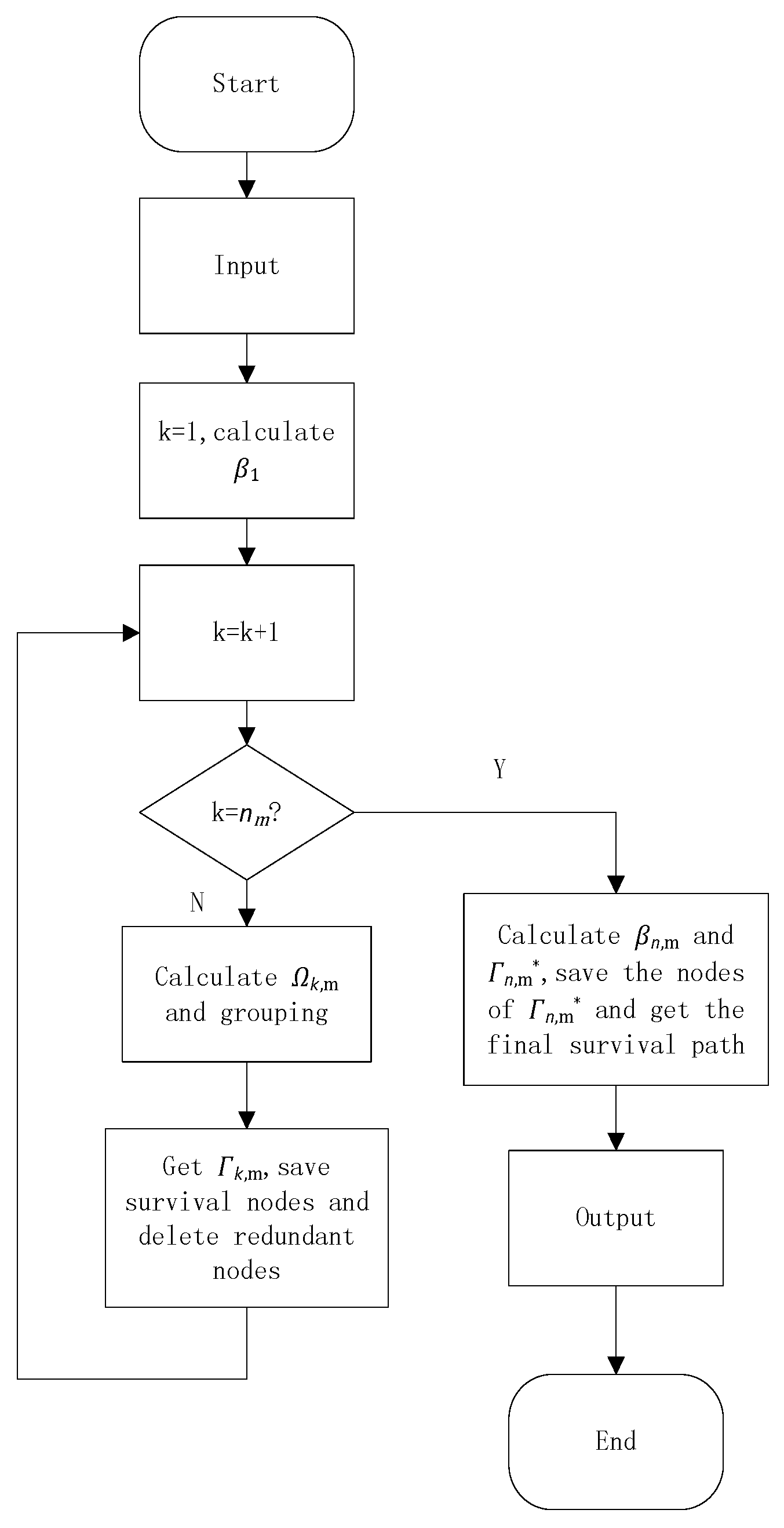
| Algorithm 2 Tree-based Search Power Allocation Algorithm (TSA) |
| 1: Input: |
| ⦁ Initial the judgement criteria: Ω0 = 0 and Γ0 = 0. |
| ⦁ Initial list of the channel states of the CUs in the same SC {h1,m, …, hn,m}. |
| 2: Tree-based search: |
| for k ∈ {1, …, nm} do |
| repeat |
| Calculate βk,m according to survival nodes of the previous layer and the minimum interval of the power allocation coefficients which satisfies the condition (26) and (27). |
| Calculate Ωk and find out the nodes of the same Ωk to put them into z groups. |
| for r ∈ {1, …, z} do |
| Calculate the set of Γr and Γr* = max { } and make the new set of Γk. Save the nodes of Γr* and delete the others. |
| end for |
| until k = nm. |
| If k = nm then |
| Calculate and g = 1. Γn,m* = max {Γn,m}. Save the nodes of Γn,m* and delete the others. Finally get the final survival path. |
| end if |
| end for |
| 3: Output: |
| Final set of power allocation coefficients |
3.5. Distance-Aware Link Selection Algorithm
- (1)
- CU1 cannot be chosen as a DT by DR1, because it is inside the limited area
- (2)
- In area DR2 has two CUs to be selected to build a D2D link. But one of the CUs has already been chosen by DR3 because the distance between the D2D pair is shorter. Thus, DR2 can choose CU2 to be the DT, in the same area
- (3)
- When two areas have a communal area (e.g., and ), the DRs may choose the same CU as the DT. In this case, we allocate them in different SCs to limit the co-spectrum interference.
3.6. Joint User Scheduling, Power Allocation and Link Selection Algorithm
4. Numerical Results and Discussions
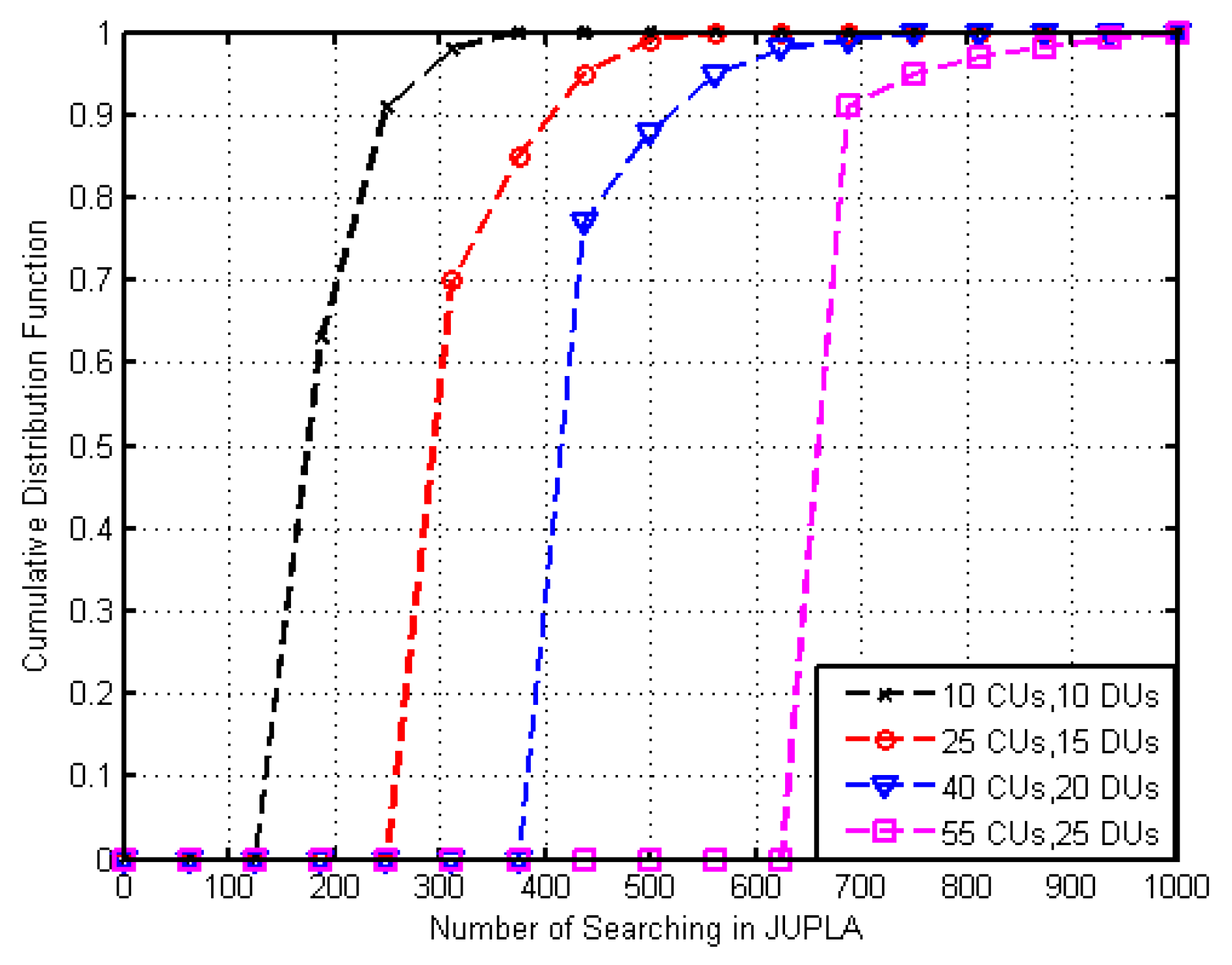
4.1. Convergence of the Proposed Algorithm
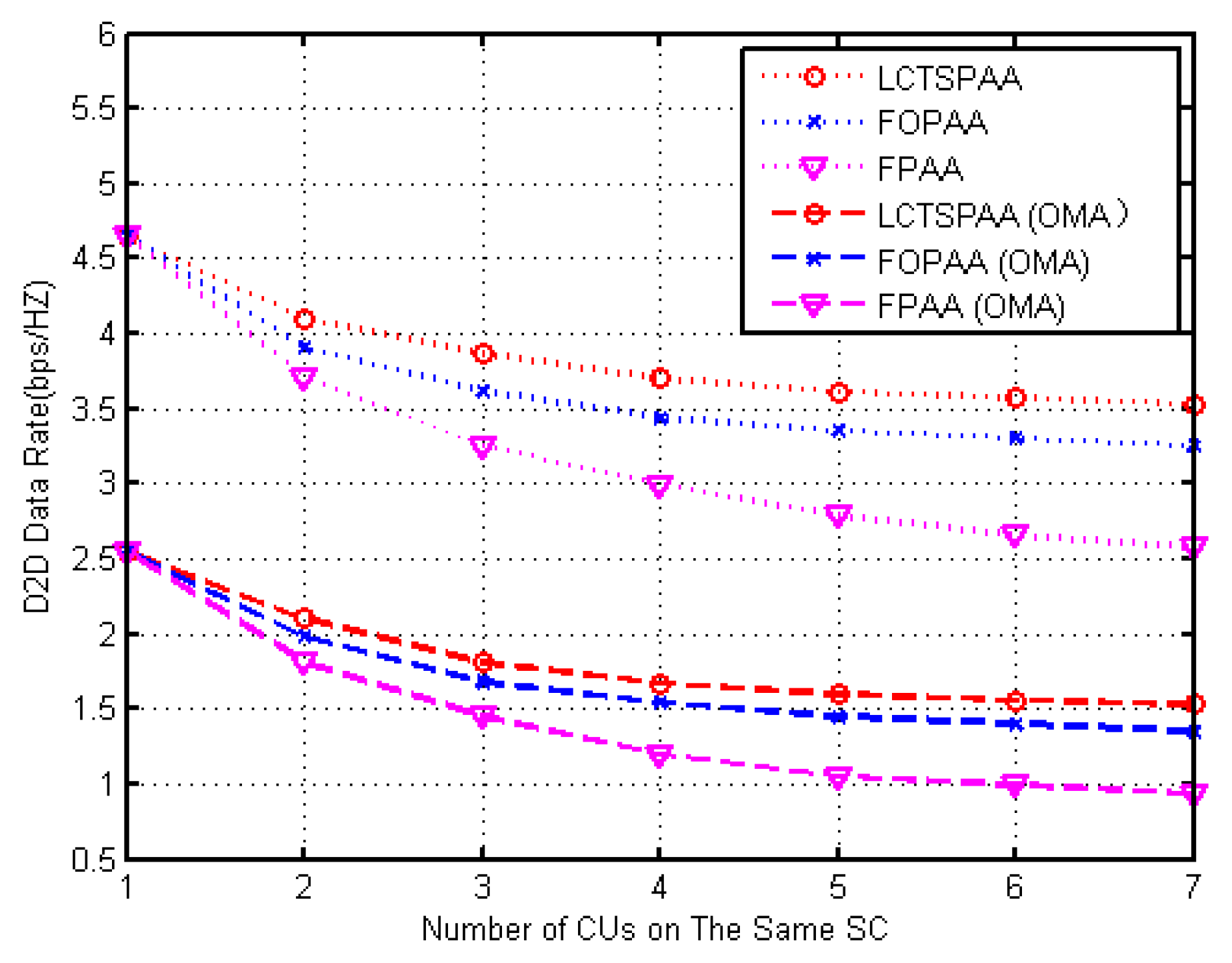
4.2. NOMA-Enhanced Versus OMA-Based D2D Communication
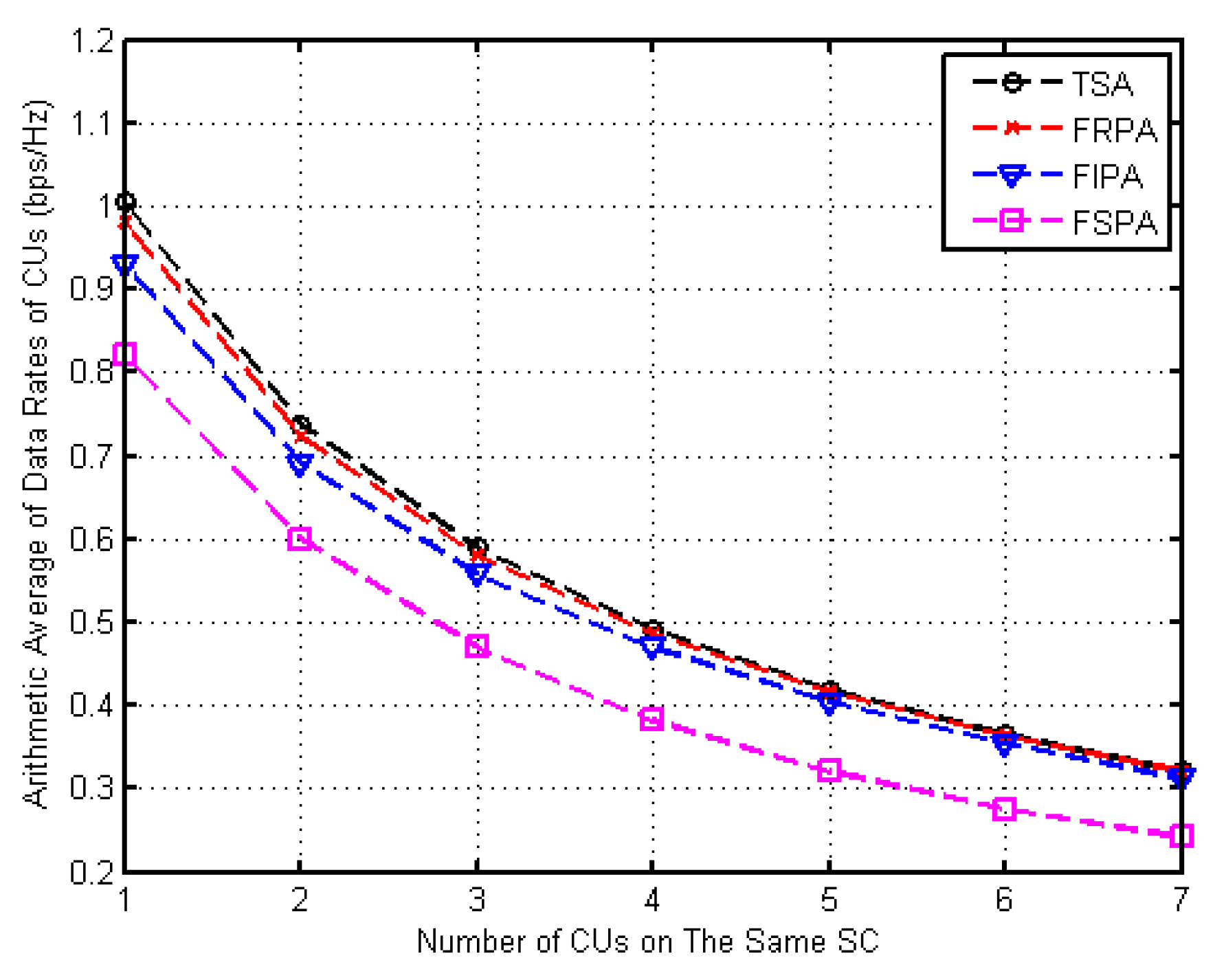
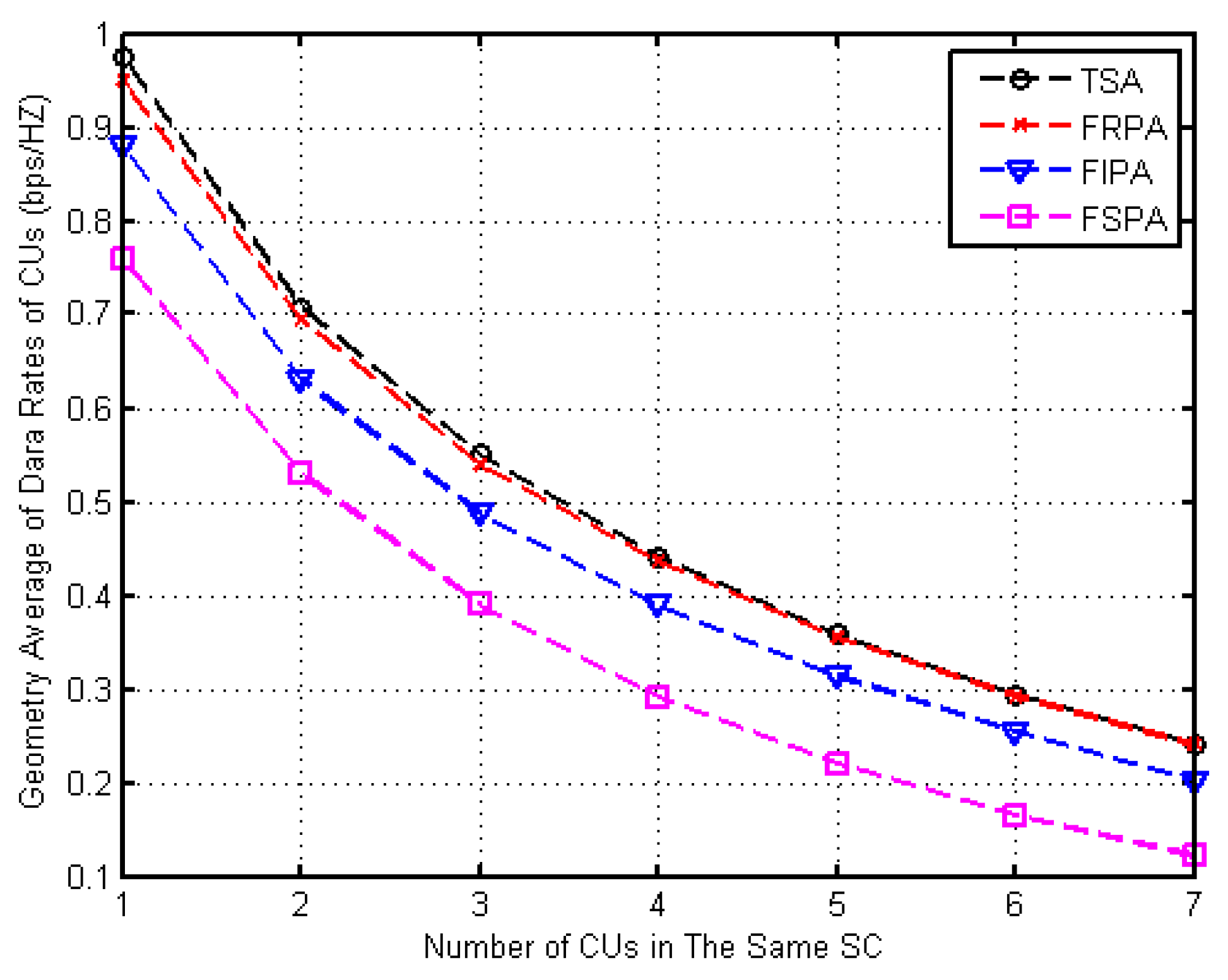
4.3. Data Transmission Rates of CUs in the Same SC in the Network
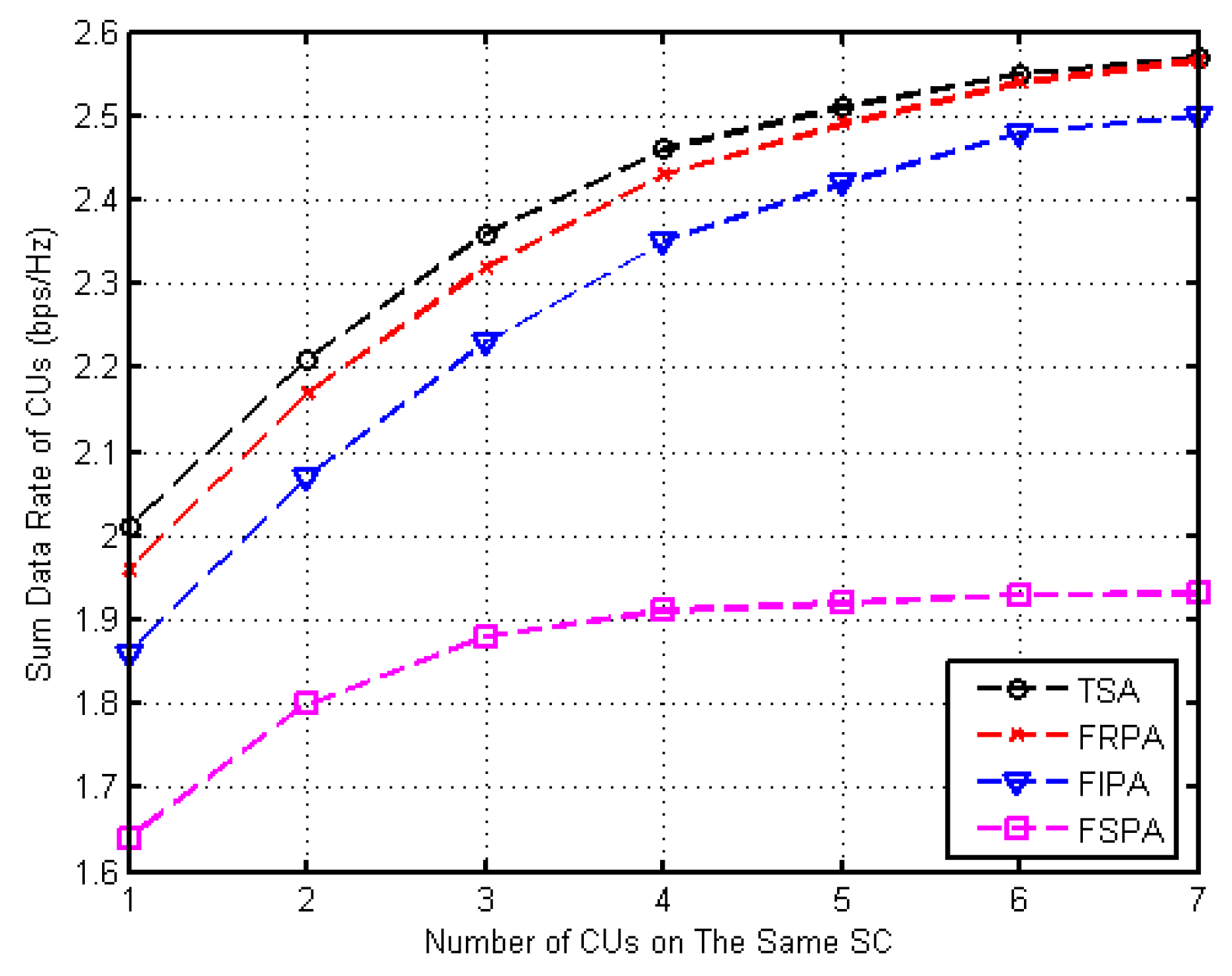
4.4. Sum Data Rate of CUs in the Same SC in the Network
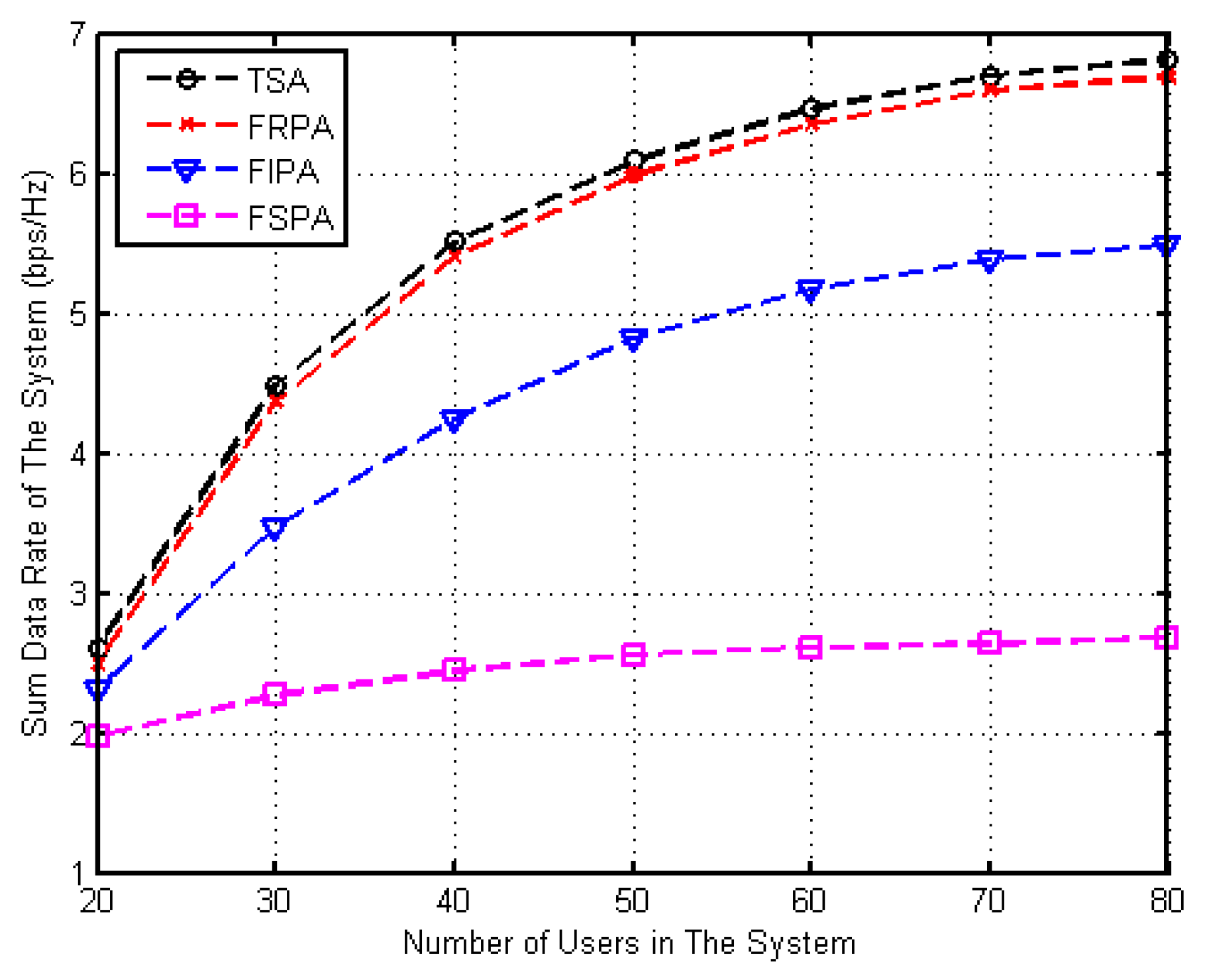
4.5. Sum Data Rate of the System
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haci, H.; Zhu, H.; Wang, J. Performance of Non-orthogonal Multiple Access With a Novel Asynchronous Interference Cancellation Technique. IEEE Trans. Commun. 2017, 65, 1319–1335. [Google Scholar] [CrossRef]
- Qian, L.P.; Wu, Y.; Zhou, H.; Shen, X. Non-Orthogonal Multiple Access Vehicular Small Cell Networks: Architecture and Solution. IEEE Netw. 2017, 31, 15–21. [Google Scholar] [CrossRef]
- Vamvakas, P.; Tsiropoulou, E.E.; Papavassiliou, S.; Baras, J.S. Optimization and Resource Management in NOMA Wireless Networks Supporting Real and Non-Real Time Service Bundling. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 697–703. [Google Scholar]
- Zeng, J.; Lv, T.; Liu, R.P.; Su, X.; Peng, M.; Wang, C.; Mei, J. Investigation on Evolving Single-Carrier NOMA Into Multi-Carrier NOMA in 5G. IEEE Access 2018, 6, 48268–48288. [Google Scholar] [CrossRef]
- Ali, M.S.; Hossain, E.; Kim, D.I. Coordinated Multipoint Transmission in Downlink Multi-Cell NOMA Systems: Models and Spectral Efficiency Performance. IEEE Wirel. Commun. 2018, 25, 24–31. [Google Scholar] [CrossRef]
- Wang, Q.; Ge, J.; Li, Q.; Bu, Q. Performance Analysis of NOMA for Multiple-Antenna Relaying Networks with Energy Harvesting over Nakagami-M Fading Channels. In Proceedings of the 2017 IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, China, 22–24 October 2017; pp. 1–5. [Google Scholar]
- Huang, Y.; Zhang, C.; Wang, J.; Jing, Y.; Yang, L.; You, X. Signal Processing for MIMO-NOMA: Present and Future Challenges. IEEE Wirel. Commun. 2018, 25, 32–38. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y.; Zhou, F.; Chu, Z.; Wu, Y.; Yuan, F. Multi-Objective Resource Allocation in a NOMA Cognitive Radio Network With a Practical Non-Linear Energy Harvesting Model. IEEE Access 2018, 6, 12973–12982. [Google Scholar] [CrossRef]
- Moltafet, M.; Azmi, P.; Mokari, N.; Javan, M.R.; Mokdad, A. Optimal and Fair Energy Efficient Resource Allocation for Energy Harvesting-Enabled-PD-NOMA-Based HetNets. IEEE Trans. Wirel. Commun. 2018, 17, 2054–2067. [Google Scholar] [CrossRef]
- Zeng, M.; Yadav, A.; Dobre, O.A.; Poor, H.V. Energy-Efficient Power Allocation for MIMO-NOMA With Multiple Users in a Cluster. IEEE Access 2018, 6, 5170–5181. [Google Scholar] [CrossRef]
- Jiang, K.; Jing, T.; Huo, Y.; Zhang, F.; Li, Z. SIC-Based Secrecy Performance in Uplink NOMA Multi-Eavesdropper Wiretap Channels. IEEE Access 2018, 6, 19664–19680. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Zeng, M.; Dobre, O.A.; Kwak, K.S. Resource Allocation for Downlink NOMA Systems: Key Techniques and Open Issues. IEEE Wirel. Commun. 2018, 25, 40–47. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, Y.; Hu, R.Q.; Wang, Y.; Wong, K.K. Energy-Efficient NOMA Enabled Heterogeneous Cloud Radio Access Networks. IEEE Netw. 2018, 32, 152–160. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.H. Performance Analysis and Resource Allocation for Cooperative D2D Communication in Cellular Networks with Multiple D2D Pairs. IEEE Commun. Lett. 2019, 23, 909–912. [Google Scholar] [CrossRef]
- Zeng, S.; Wang, C.; Qin, C.; Wang, W. Interference Alignment Assisted by D2D Communication for the Downlink of MIMO Heterogeneous Networks. IEEE Access 2018, 6, 24757–24766. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Agnihotri, S. Energy- and Spectral-Efficiency Trade-Off for D2D-Multicasts in Underlay Cellular Networks. IEEE Wirel. Commun. Lett. 2018, 7, 546–549. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Choi, K.W.; Song, L.; Han, Z. ROOMMATES: An Unsupervised Indoor Peer Discovery Approach for LTE D2D Communications. IEEE Trans. Veh. Technol. 2018, 67, 5069–5083. [Google Scholar] [CrossRef]
- Dang, S.; Chen, G.; Coon, J.P. Multicarrier Relay Selection for Full-Duplex Relay-Assisted OFDM D2D Systems. IEEE Trans. Veh. Technol. 2018, 67, 7204–7218. [Google Scholar] [CrossRef]
- Ma, B.; Shah-Mansouri, H.; Wong, V.W.S. Full-Duplex Relaying for D2D Communication in Millimeter Wave-based 5G Networks. IEEE Trans. Wirel. Commun. 2018, 17, 4417–4431. [Google Scholar] [CrossRef]
- Zulkifli, A.A.; Kuroda, K.; Hasegawa, M. Game Theory-Based Power Allocation and Channel Selection of Multi-channel D2D. In Proceedings of the 2017 Fifth International Symposium on Computing and Networking (CANDAR), Aomori, Japan, 19–22 November 2017; pp. 256–262. [Google Scholar]
- Lv, S.; Wang, X.; Meng, X.; Zhang, Z.; Long, K. Energy-Efficient Joint Power Control and Resource Allocation for D2d-Aided Heterogeneous Networks. In Proceedings of the 2017 IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, China, 22–24 October 2017; pp. 1–6. [Google Scholar]
- Ni, Y.; Zhao, J.; Wang, Y.; Zhu, H. Beamforming and interference cancellation for D2D communication assisted by two-way decode-and-forward relay node. China Commun. 2018, 15, 100–111. [Google Scholar] [CrossRef]
- Kim, J.B.; Lee, I.H.; Lee, J. Capacity Scaling for D2D Aided Cooperative Relaying Systems Using NOMA. IEEE Wirel. Commun. Lett. 2018, 7, 42–45. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, Z.; Xiao, M.; Ding, Z.; Fan, P. Full-Duplex Device-to-Device-Aided Cooperative Nonorthogonal Multiple Access. IEEE Trans. Veh. Technol. 2017, 66, 4467–4471. [Google Scholar]
- Pei, L.; Yang, Z.; Pan, C.; Huang, W.; Chen, M.; Elkashlan, M. Energy-Efficient D2D Communications Underlaying NOMA-Based Networks with Energy Harvesting. IEEE Commun. Lett. 2018, 22, 914–917. [Google Scholar] [CrossRef]
- Ahmad, A.; Rehmani, M.H.; Tembine, H.; Mohammed, O.A.; Jamalipour, A. IEEE Access Special Section Editorial: Optimization for Emerging Wireless Networks: IoT, 5G, and Smart Grid Communication Networks. IEEE Access 2017, 5, 2096–2100. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Chai, K.K.; Chen, Y.; Elkashlan, M. Joint Subchannel and Power Allocation for NOMA Enhanced D2D Communications. IEEE Trans. Commun. 2017, 65, 5081–5094. [Google Scholar] [CrossRef]
- Pan, Y.; Pan, C.; Yang, Z.; Chen, M. Resource Allocation for D2D Communications Underlaying a NOMA-Based Cellular Network. IEEE Wirel. Commun. Lett. 2018, 7, 130–133. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Nonlinear Programming; Athena Scientific: Belmont, MA, USA, 1999. [Google Scholar]
- Li, A.; Harada, A.; Kayama, H. A novel low computational complexity power assignment method for non-orthogonal multiple access systems. In IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences; The Institute of Electronics, Information and Communication Engineers: Tokyo, Japan, 2014; Volume 97, pp. 57–68. [Google Scholar]
- Gao, X.; Tan, X.; Wu, G.; Xiao, J. Tree-based search algorithm for power allocation in non-orthogonal multiple access systems. J. Chongqing Univ. Posts Telecommun. 2017, 29, 665–671. [Google Scholar]
- Otao, N.; Kishiyama, Y.; Higuchi, K. Performance of Non-Orthogonal Access with Sic in Cellular Downlink Using Proportional Fair-Based Resource Allocation. In Proceedings of the 2012 International Symposium on Wireless Communication Systems (ISWCS), Paris, France, 28–31 August 2012; pp. 476–480. [Google Scholar]
- Chu, P.; Wang, X.; Wang, D.; Yu, L. A D2d Mode Selection Scheme with Energy Consumption Minimization Underlaying Two-Tier Heterogeneous Cellular Networks. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–5. [Google Scholar]
- Joshi, S.; Mallik, R.K. Cooperative NOMA with AF Relaying over Nakagami-m Fading in a D2D Network. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–6. [Google Scholar]
- Budhiraja, I.; Tyagi, S.; Tanwar, S.; Kumar, N.; Rodrigues, J.J. DIYA: Tactile Internet Driven Delay Assessment NOMA-based Scheme for D2D Communication. IEEE Trans. Ind. Inf. 2019, 15, 6354–6366. [Google Scholar] [CrossRef]
- Li, N.; Xiao, M.; Rasmussen, L.K. Diverse Communication Modes in Cooperative Downlink Non-Orthogonal Multiple Access—Invited Paper. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–5. [Google Scholar]
- Zhang, Y.; Liu, F. A Novel Cooperative Full Duplex Device to Device Communication Underlaying Cellular Networks. In Proceedings of the 2019 IEEE International Conference on Energy Internet (ICEI), Nanjing, China, 27–31 May 2019; pp. 548–553. [Google Scholar]
- Saito, Y.; Kishiyama, Y.; Benjebbour, A.; Nakamura, T.; Li, A.; Higuchi, K. Non-Orthogonal Multiple Access (NOMA) for Cellular Future Radio Access. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar]
- Balevi, E.; Gitlin, R.D. Pareto Optimization for Uplink NOMA Power Control. In Proceedings of the 2018 Wireless Telecommunications Symposium (WTS), Phoenix, AZ, USA, 17–20 April 2018; pp. 1–5. [Google Scholar]
- Reddy, M.H.; Rebekka, B. Power Allocation Policies for QoS Satisfaction in IoT Using NOMA. In Proceedings of the 2018 2nd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 11–12 May 2018; pp. 576–581. [Google Scholar]
- Chen, Y.; Bayesteh, A.; Wu, Y.; Ren, B.; Kang, S.; Sun, S.; Xiong, Q.; Qian, C.; Yu, B.; Ding, Z.; et al. Toward the Standardization of Non-Orthogonal Multiple Access for Next Generation Wireless Networks. IEEE Commun. Mag. 2018, 56, 19–27. [Google Scholar] [CrossRef]
- Fang, F.; Zhang, H.; Cheng, J.; Roy, S.; Leung, V.C.M. Joint User Scheduling and Power Allocation Optimization for Energy-Efficient NOMA Systems with Imperfect CSI. IEEE J. Sel. Areas Commun. 2017, 35, 2874–2885. [Google Scholar] [CrossRef]
- Wu, C.S.; Khoury, I. Tree-based Search Algorithm for Web Service Composition in SaaS. In Proceedings of the 2012 Ninth International Conference on Information Technology—New Generations, Las Vegas, NV, USA, 16–18 April 2012; pp. 132–138. [Google Scholar]
- Khatiri, A.; Mirjalily, G.; Khademzadeh, A. Energy-Efficient Shortcut Tree Routing in ZigBee Networks. In Proceedings of the 2012 Fourth International Conference on Computational Intelligence, Communication Systems and Networks, Phuket, Thailand, 24–26 July 2012; pp. 117–122. [Google Scholar]
- Yousefvand, M.; Ansari, N.; Khorsandi, S. Maximizing Network Capacity of Cognitive Radio Networks by Capacity-Aware Spectrum Allocation. IEEE Trans. Wirel. Commun. 2015, 14, 5058–5067. [Google Scholar] [CrossRef]
- Chinnadurai, S.; Yoon, D. Energy Efficient MIMO-NOMA HCN with IoT for Wireless Communication Systems. In Proceedings of the 2018 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea, 17–19 October 2018; pp. 856–859. [Google Scholar]
- Tang, F.; Fadlullah, Z.M.; Kato, N.; Ono, F.; Miura, R. AC-POCA: Anticoordination Game Based Partially Overlapping Channels Assignment in Combined UAV and D2D-Based Networks. IEEE Trans. Veh. Technol. 2018, 67, 1672–1683. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Cellular radius | 450 m |
| Maximum distance between D2D pairs | 75 m |
| Total bandwidth | 2.0 MHz |
| Carrier frequency | 2.6 GHz |
| Maximum Transmission power of CU | 21 dBm |
| Maximum transmission power of D2D | 21 dBm |
| Maximum transmission power of BS | 26 dBm |
| Number of CU | 10 |
| Number of D2D pairs | 10 |
| Number of users on each subchannel | 3 |
| SINR threshold of D2D | 1.8 dB |
| SINR threshold of CU | 1.3 dB |
| Noise Spectral density | −173 dBm |
| Path loss constant | 0.01 |
| Path-loss exponent | 3.76 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Song, X.; Ma, Y. A Novel Resource Allocation Scheme in NOMA-Based Cellular Network with D2D Communications. Future Internet 2020, 12, 8. https://doi.org/10.3390/fi12010008
Wang J, Song X, Ma Y. A Novel Resource Allocation Scheme in NOMA-Based Cellular Network with D2D Communications. Future Internet. 2020; 12(1):8. https://doi.org/10.3390/fi12010008
Chicago/Turabian StyleWang, Jingpu, Xin Song, and Yatao Ma. 2020. "A Novel Resource Allocation Scheme in NOMA-Based Cellular Network with D2D Communications" Future Internet 12, no. 1: 8. https://doi.org/10.3390/fi12010008
APA StyleWang, J., Song, X., & Ma, Y. (2020). A Novel Resource Allocation Scheme in NOMA-Based Cellular Network with D2D Communications. Future Internet, 12(1), 8. https://doi.org/10.3390/fi12010008





