Sustainable Communication Systems: A Graph-Labeling Approach for Cellular Frequency Allocation in Densely-Populated Areas
Abstract
1. Introduction
2. Related Works
2.1. The L(2,1) Algorithm
2.2. The L(2,1,1) Algorithm
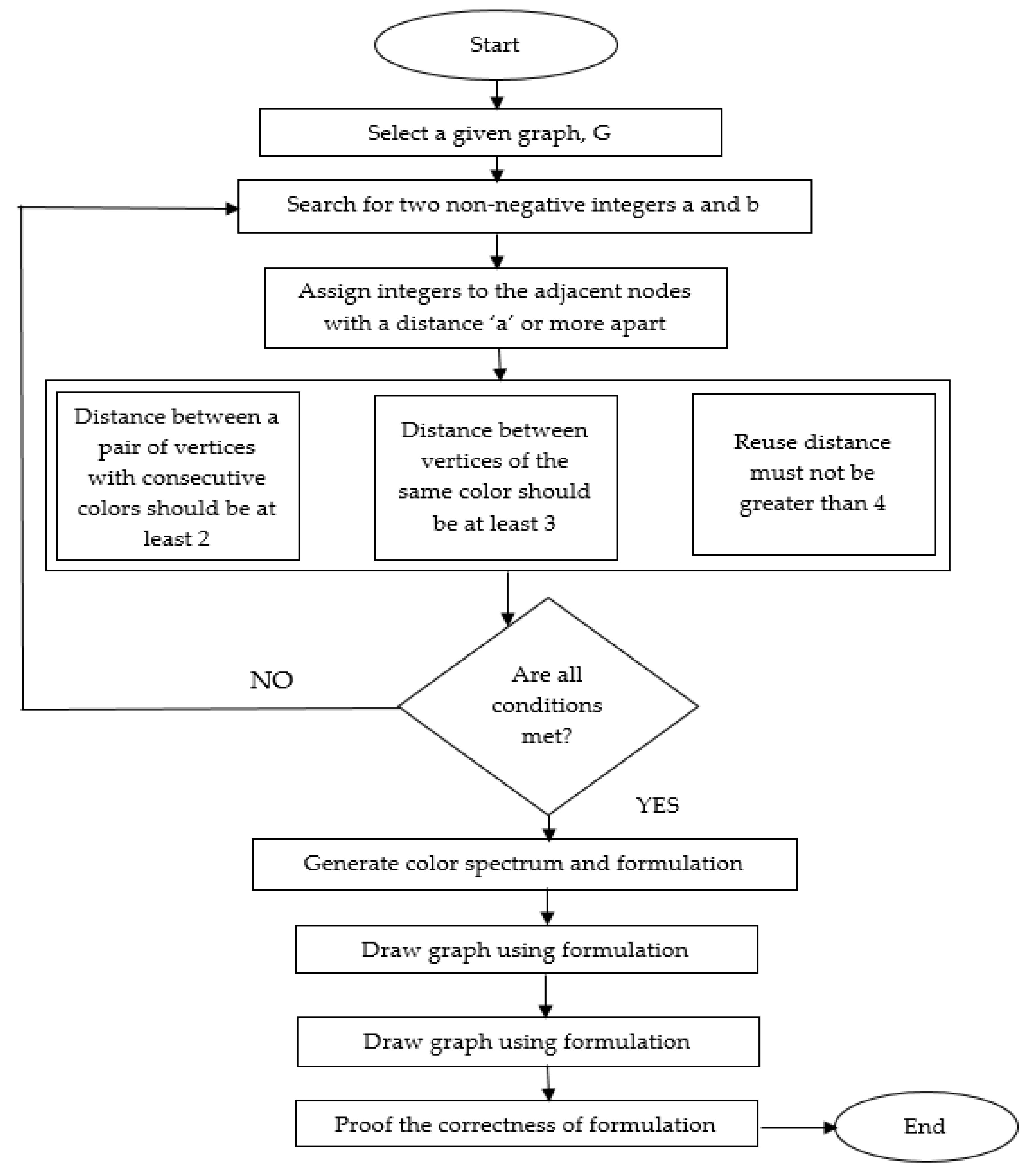
3. Method
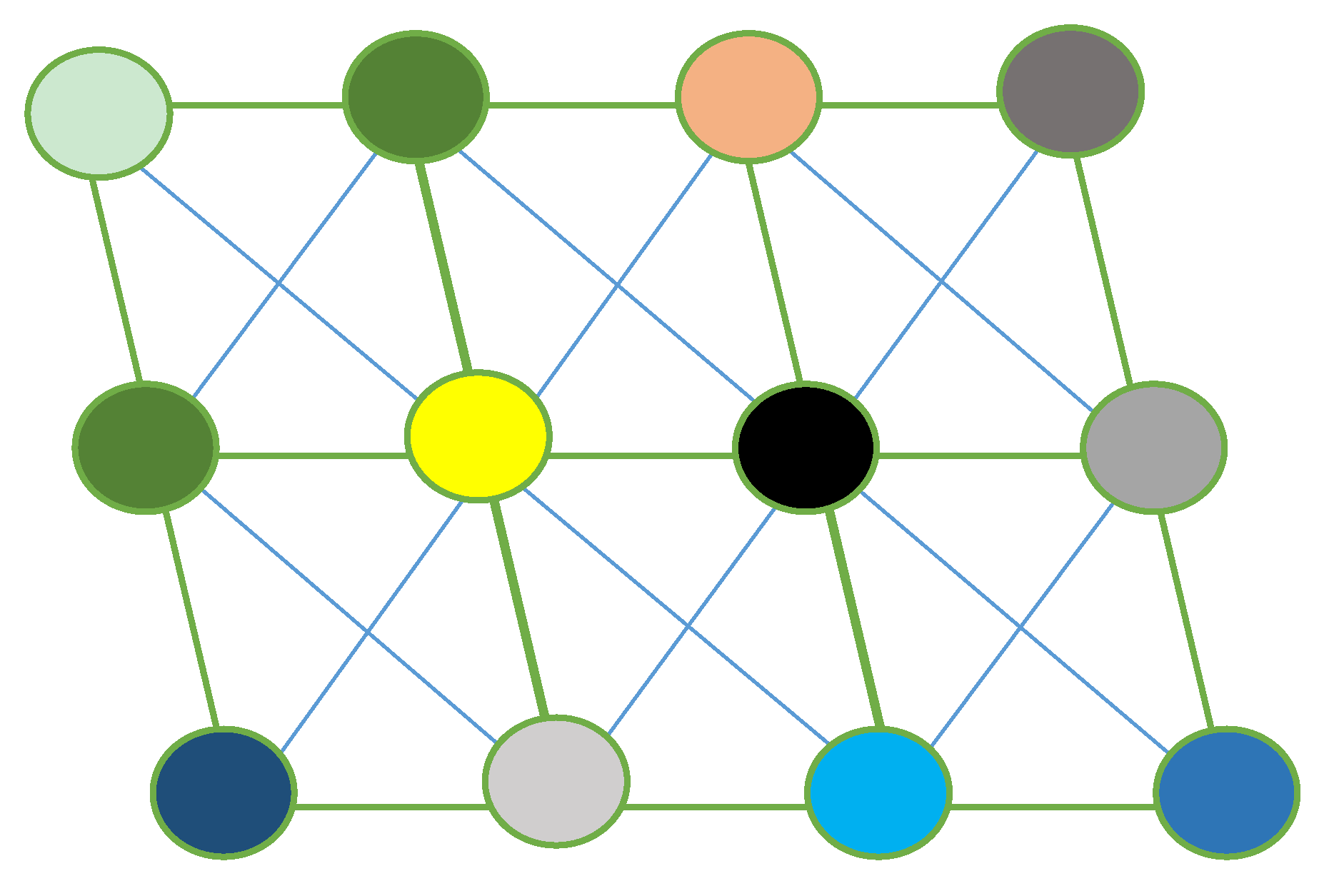
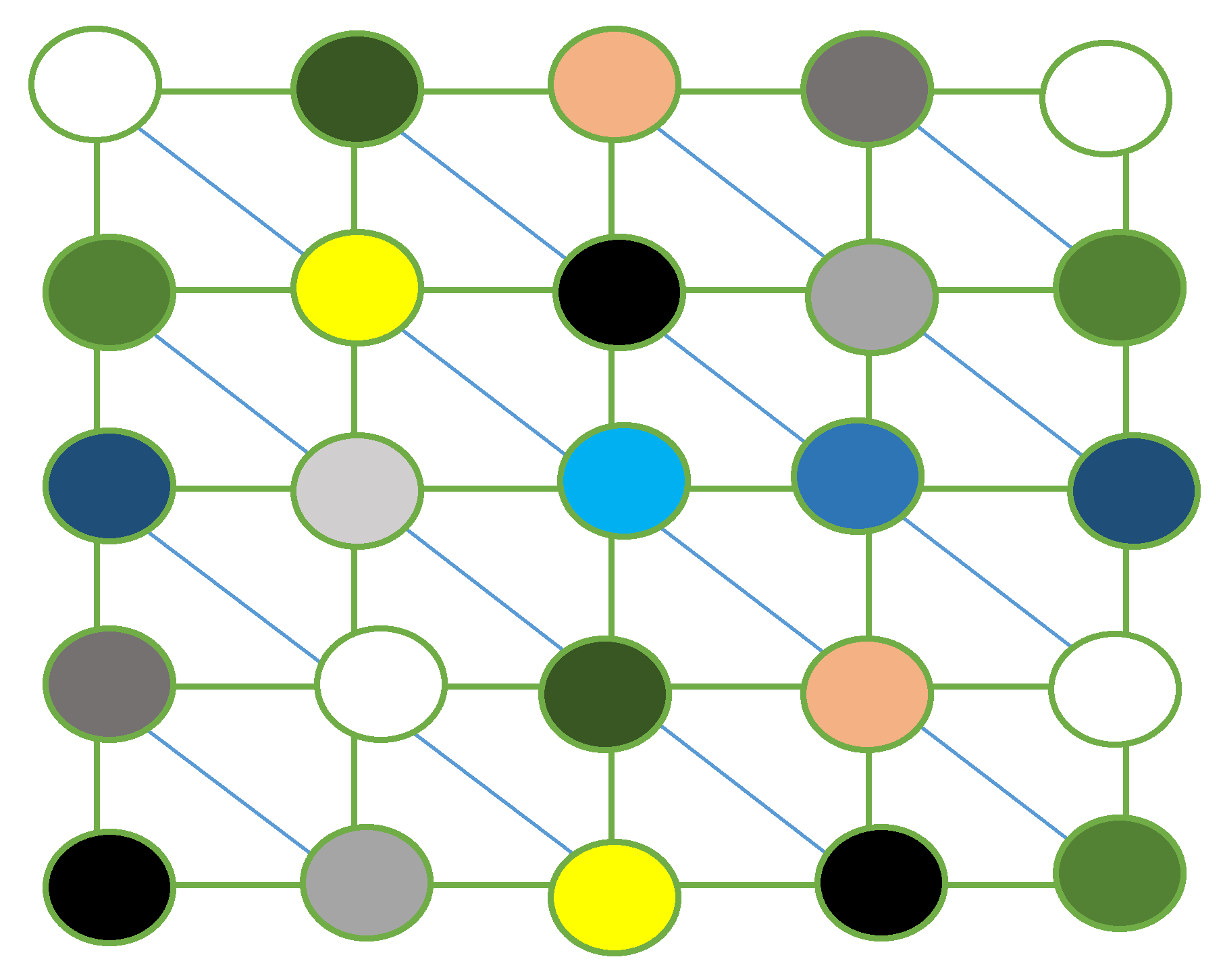
4. Results and Discussion
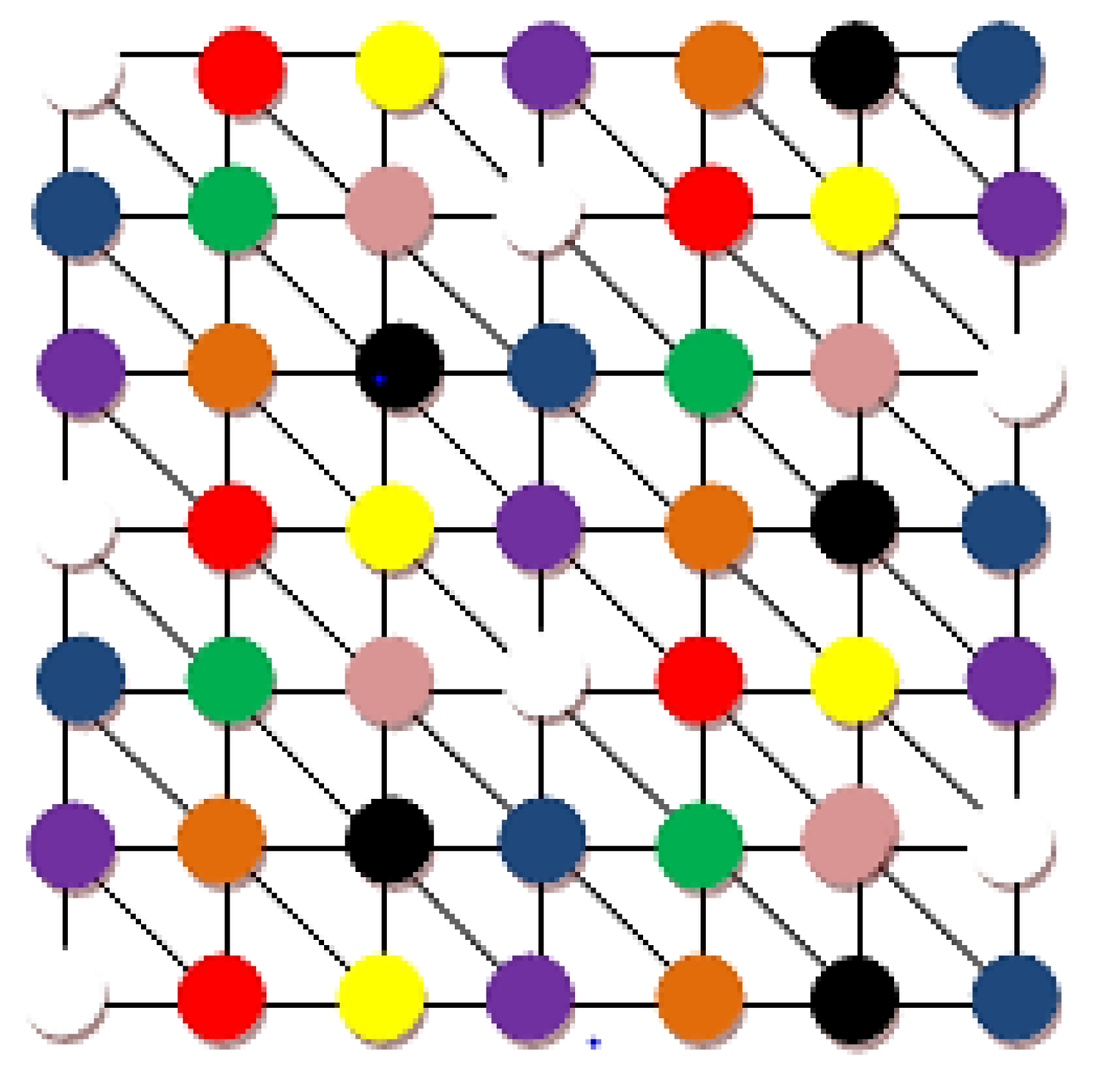
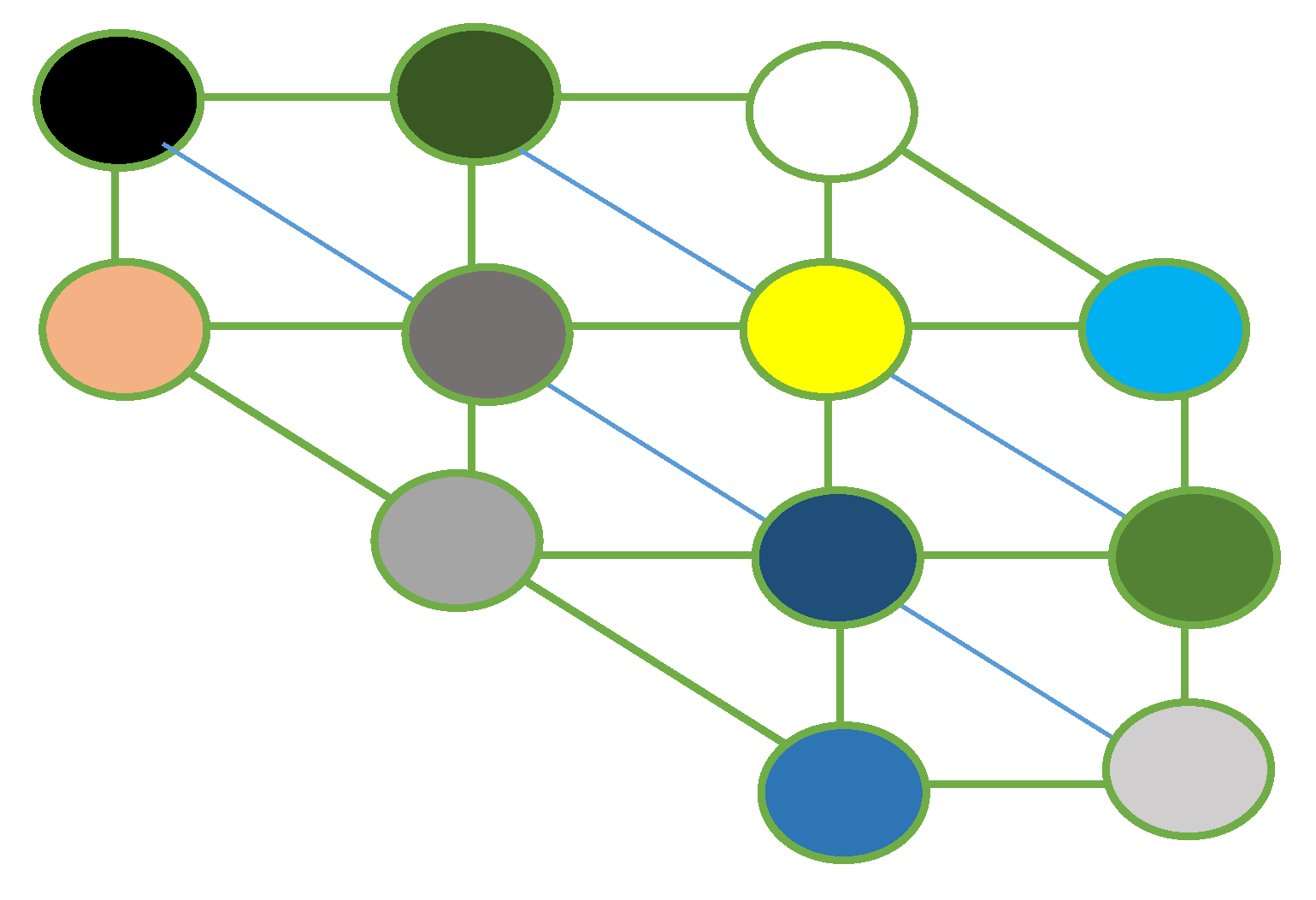
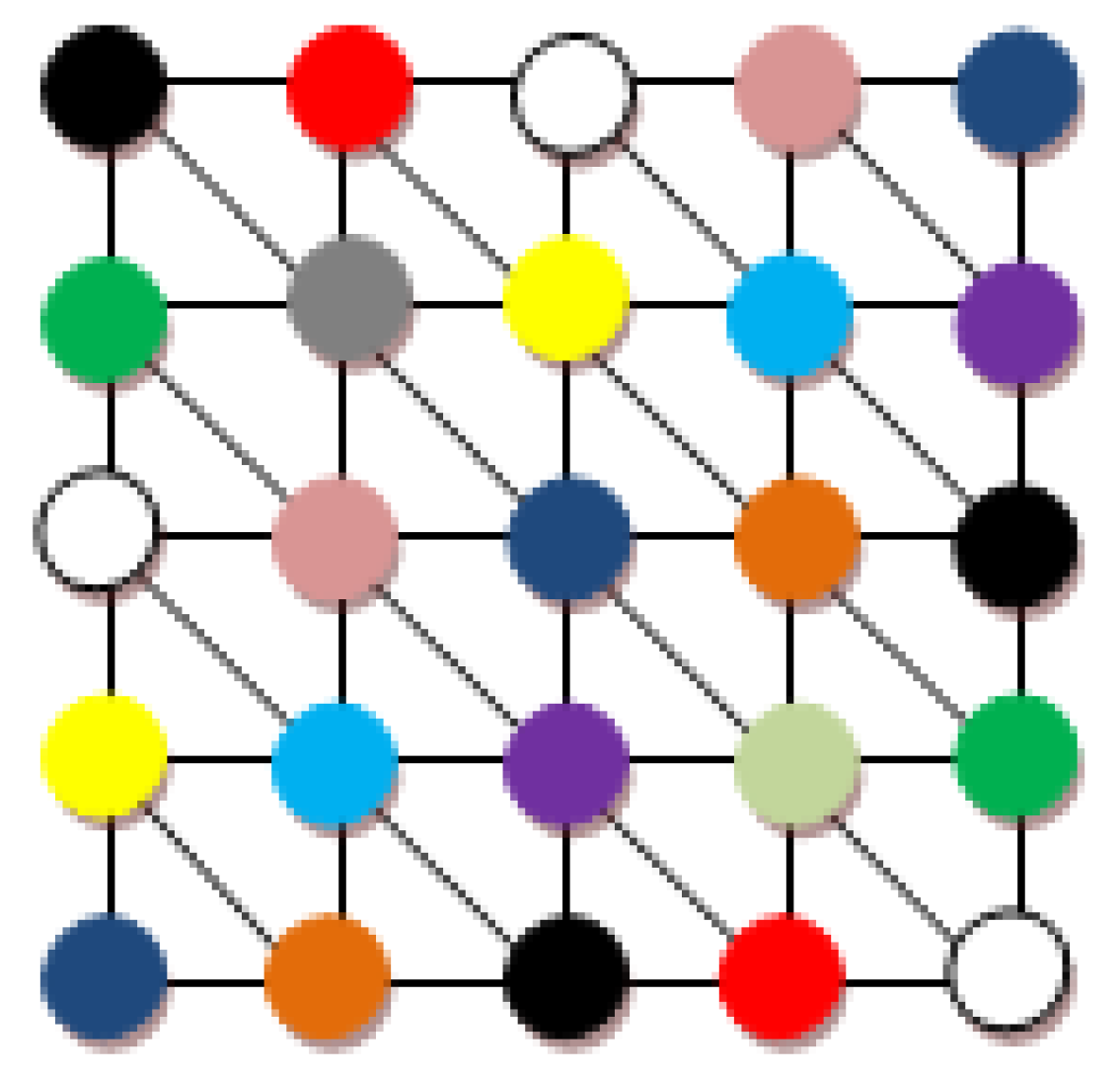
4.1. Checking the Correctness of the L(3,1) Coloring Algorithm
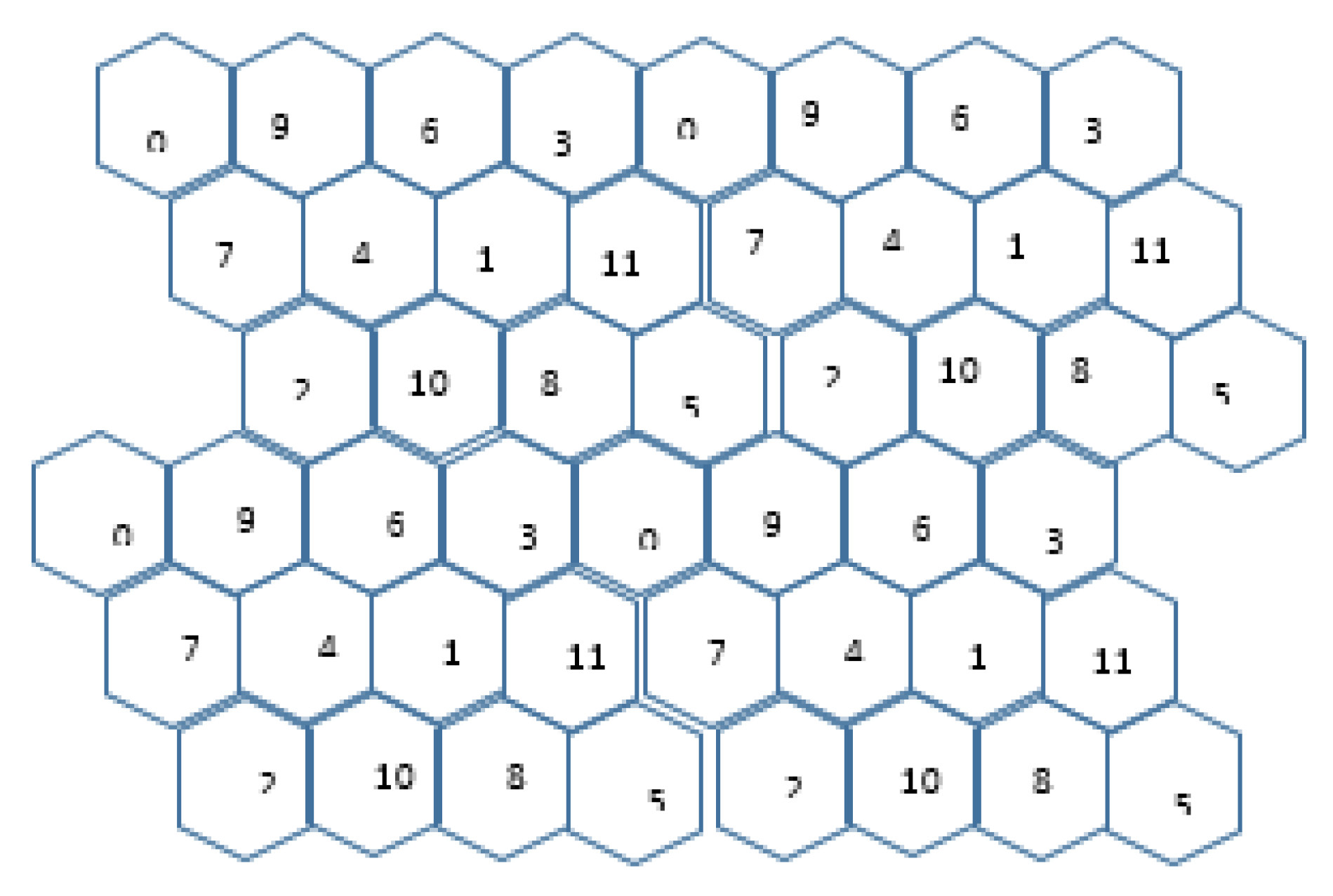
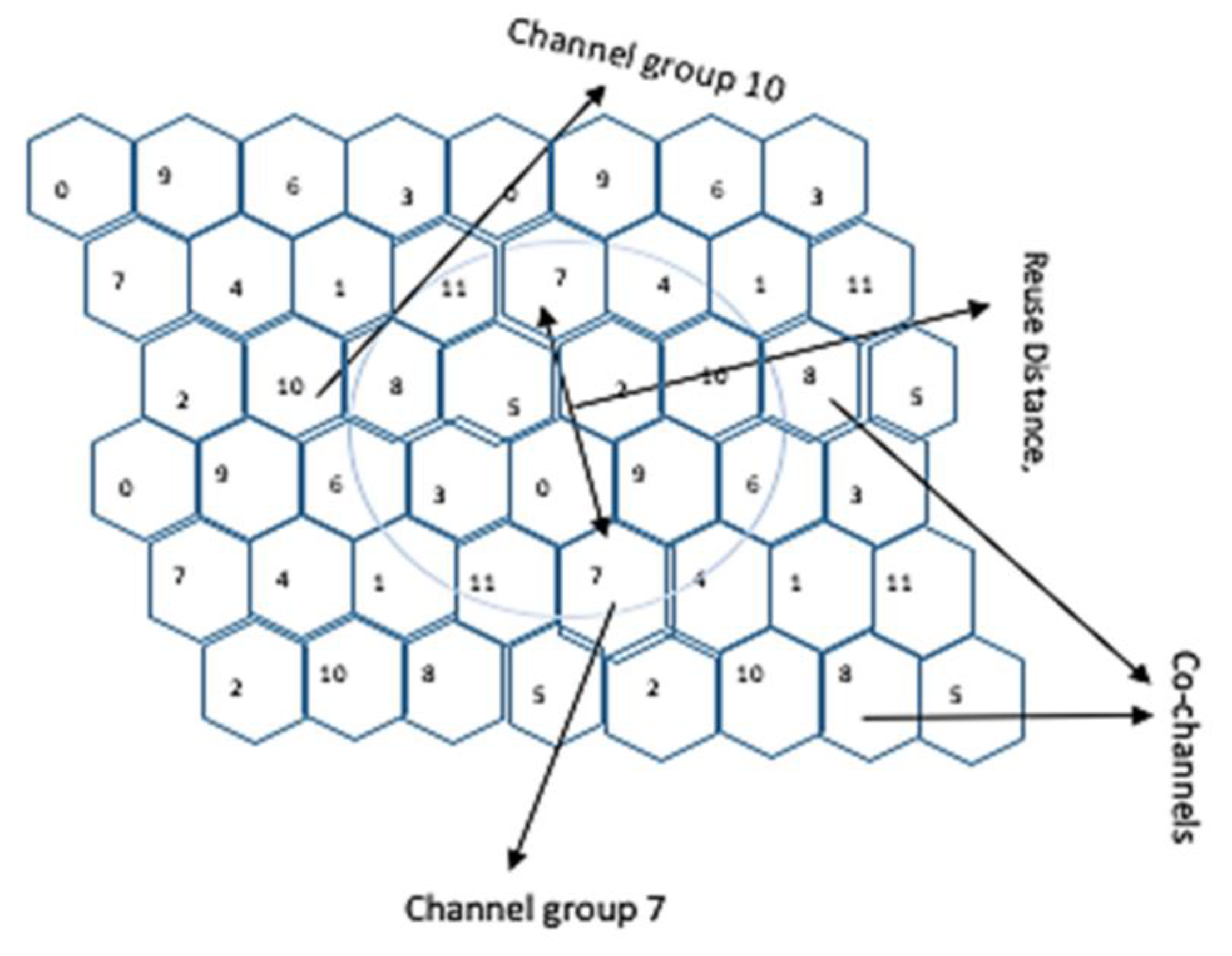
4.2. Design of Channel Group Allocation
4.3. Method for Calculating the Reuse Distance
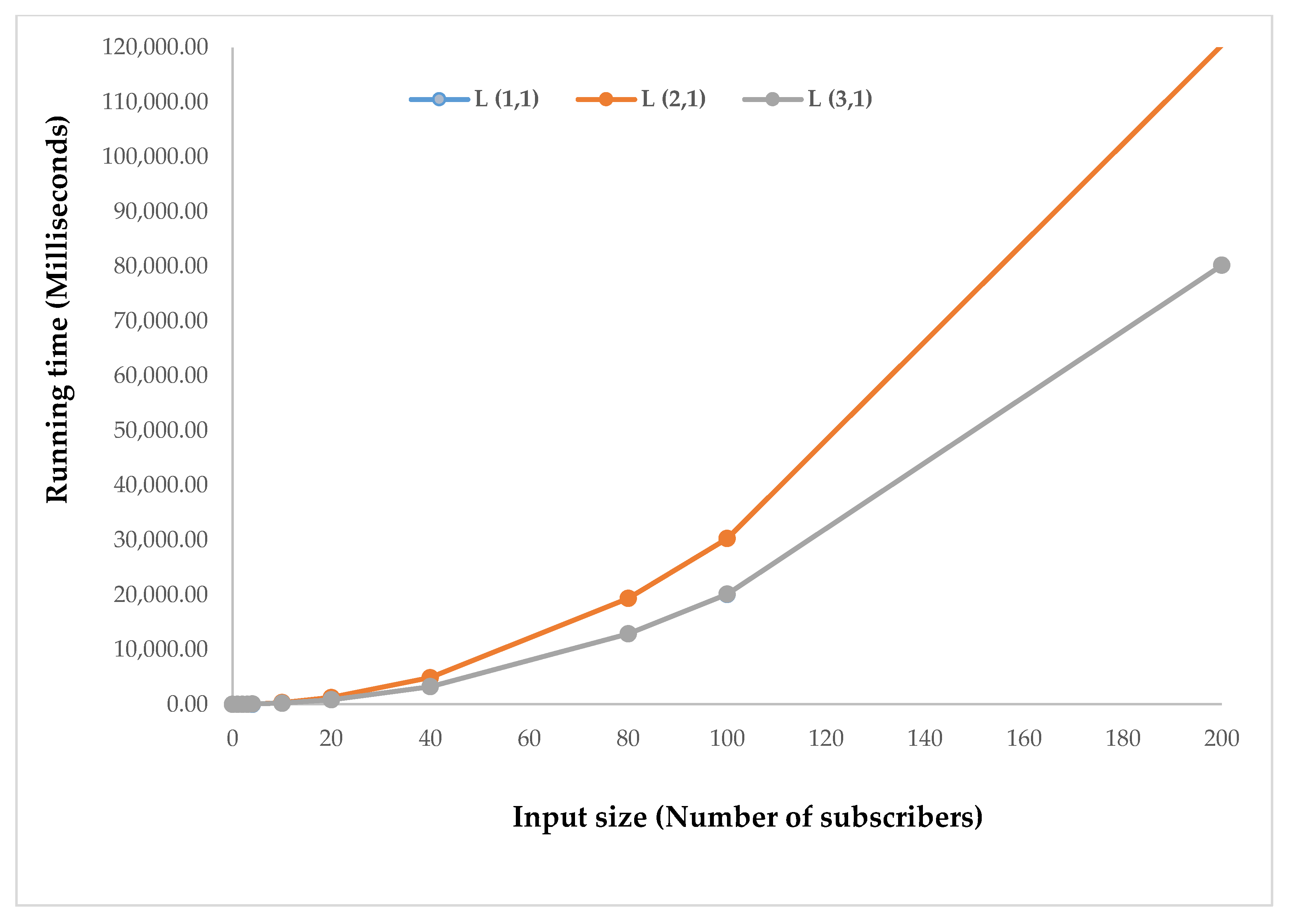
4.4. Time Complexity for Selected Algorithms
5. Conclusions
6. Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kuboye, B.M.; Alese, B.K.; Fajuiyigbe, O.; Adewale, S.O. Development of Models for Managing Network Congestion on Global System for Mobile Communication (GSM) in Nigeria. J. Wirel. Netw. Commun. 2011, 1, 8–15. [Google Scholar]
- Haider, B.; Zafrullah, M.; Islam, M.K. Radio Frequency Optimization & QoS Evaluation in Operational GSM Network. In Proceedings of the world Congress on Engineering and Computer Science, San Francisco, CA, USA, 20–22 October 2009; pp. 1–6. [Google Scholar]
- Józefowicz, R.; Poźniak-Koszałka, I.; Koszałka, I.L.; Kasprzak, A. Algorithms for Solving Frequency Assignment Problem in Wireless Networks. In Recent Developments in Computational Collective Intelligence; Badica, A., Trawinski, B., Nguyen, N., Eds.; Springer: Cham, Switzerland, 2014; Volume 513, pp. 135–144. [Google Scholar]
- Biral, A.; Centenaro, M.; Zanella, A.; Vangelista, L.; Zorzi, M. The challenges of M2M massive access in wireless cellular networks. Digit. Commun. Netw. 2015, 1, 1–19. [Google Scholar] [CrossRef]
- Landström, S.; Bergström, J.; Westerberg, E.; Hammarwall, D. NB-IoT: A sustainable technology for connecting billions of devices. Ericsson Technol. Rev. 2016, 4, 2–11. [Google Scholar]
- Garcia, A.J.; Buenestado, V.; Toril, M.; Luna-Ramírez, S.; Ruiz, J.M. A Geometric Method for Estimating the Nominal Cell Range in Cellular Networks. Mob. Inf. Syst. 2018, 2018, 3479246. [Google Scholar]
- Mouly, M.; Pautet, M.B. The GSM System for Mobile Communications. Available online: https://dl.acm.org/citation.cfm?id=573838 (accessed on 21 August 2019).
- Hamad-Ameen, J.J. Frequency Planning in GSM Mobile. In Proceedings of the TELE-INFO’08 Proceedings of the 7th WSEAS International Conference on Telecommunications and Informatics, Istanbul, Turkey, 27–30 May 2008. [Google Scholar]
- Xu, Y.; Sakho, I. Frequencies Assignment in Cellular Networks. In Intelligent Information and Database Systems; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Rughooputh, S.; Coomar, H.; Cheeneebash, J. A Comprehensive Review of Methods for the Channel Allocation Problem; African Minds: Cape Town, South Africa, 2014. [Google Scholar]
- Nurelmadina, N.; Nafea, I.; Younas, M. Evaluation of a channel assignment scheme in mobile network systems. Hum.Centric Comput Inf. Sci. 2016, 6, 1–15. [Google Scholar] [CrossRef]
- Idoumghar, L.; Debreux, P. New modeling approach to the frequency assignment problem in broadcasting. IEEE Trans. Broadcast. 2002, 48, 293–298. [Google Scholar] [CrossRef]
- Gozupek, D.; Genc, G.; Ersoy, C. Channel assignment problem in cellular networks: A reactive tabu search approach. In Proceedings of the 2009 24th International Symposium on Computer and Information Sciences, Guzelyurt, Cyprus, 23 October 2009. [Google Scholar]
- Katzela, I.; Naghshineh, M. Channel assignment schemes for cellular mobile telecommunication systems: A comprehensive survey. IEEE Commun. Surv. Tutor. 1996, 3, 10–31. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, L.; Soong, B.H. Optimal channel assignment in cellular systems using tabu search. In Proceedings of the 14th IEEE Proceedings on Personal, Indoor and Mobile Radio Communications, Beijing, China, 7–10 September 2003. [Google Scholar]
- Bertossi, A.A.; Pinotti, C.M.; Tan, R.B. Efficient Use of Radio Spectrum in Wireless Networks with Channel Separation Between Close Stations. In Proceedings of the 4th International Workshop on Discrete Algorithms and Methods for Mobile Computing and Communication, Boston, MA, USA, 11 August 2000. [Google Scholar]
- Tech Republic, Hybrid Channel Allocation in Wireless Cellular Networks. Available online: https://www.techrepublic.com/resource-library/whitepapers/hybrid-channel-allocation-in-wireless-cellular-networks (accessed on 21 August 2019).
- Davis, J.S. Channel Allocation. Available online: http://www.wirelesscommunication.nl/reference/chaptr04/cellplan/dca.htm (accessed on 21 August 2019).
- Li, J.; Shroff, N.B.; Chong, E.K.P. A new localized channel sharing scheme for cellular networks. Wirel. Netw. 1999, 5, 503–517. [Google Scholar] [CrossRef]
- Kim, J.-S.; Park, S.; Dowd, P.; Nasrabadi, N. Channel assignment in cellular radio using genetic algorithms. Wirel. Pers. Commun. 1996, 3, 273–286. [Google Scholar] [CrossRef]
- Duran, M. How to Unlock Your Phone’s Trusty Call-Blocking Powers. Available online: https://www.wired.com/2016/07/unlock-phones-trusty-call-blocking-powers/ (accessed on 21 August 2019).
- Acampora, A.S. An Introduction to Broadband Networks: LANs, MANs, ATM, B-ISDN, and Optical Networks for Integrated Multimedia Telecommunications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ali, N.A.; El-Dakroury, M.A.; El-Soudani, M.; ElSayed, H.M.; Daoud, R.M.; Amer, H.H. New hybrid frequency reuse method for packet loss minimization in LTE network. J. Adv. Res. 2015, 6, 949–955. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jiang, F.; Wang, H.; Ren, H.; Xu, S. Energy-efficient resource and power allocation for underlay multicast device-to-device transmission. Future Internet 2017, 9, 84. [Google Scholar] [CrossRef]
- Chu, Ta.; Rappaport, S.S. Generalized fixed channel assignment in microcellular communication systems. IEEE Trans. Veh. Technol. 1994, 43, 713–721. [Google Scholar]
- Idris, I.; Selamat, A.; Nguyen, N.T.; Omatu, S.; Krejcar, O.; Kuča, K.; Penhaker, M. A combined negative selection algorithm-particle swarm optimization for an email spam detection system. Eng. Appl. Artif. Intell. 2015, 39, 33–44. [Google Scholar] [CrossRef]
- Yin, L.; Li, X.; Lu, C.; Gao, L. Energy-efficient scheduling problem using an effective hybrid multi-objective evolutionary algorithm. Sustainability 2016, 8, 1268. [Google Scholar] [CrossRef]
- Salehi, S.; Selamat, A.; Krejcar, O.; Kuca, K. Fuzzy granular classifier approach for spam detection. J. Intell. Fuzzy Syst. 2017, 32, 1355–1363. [Google Scholar] [CrossRef]
- Lim, K.C.; Selamat, A.; Zabil, M.H.M.; Selamat, M.H.; Alias, R.A.; Puteh, F.; Mohamed, F.; Krejcar, O.; Herrera-Viedma, E.; Fujita, H. Feasibility comparison of HAC algorithm on usability performance and self-reported metric features for MAR learning. In Proceedings of the 17th International Conference on New Trends in Intelligent Software Methodology Tools and Techniques (SoMeT 2018), Granada, Spain, 26–28 September 2018; pp. 896–910. [Google Scholar]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Bäck, T.; Hoffmeister, F. Extended Selection Mechanisms in Genetic Algorithms. In Proceedings of the Fourth International Conference on Genetic Algorithms, San Diego, CA, USA, 13–16 July 1991. [Google Scholar]
- Shao, Z. The Research on the L(2,1)-labeling problem from Graph theoretic and Graph Algorithmic Approaches. 2012. Available online: https://ir.lib.uwo.ca/cgi/viewcontent.cgi?article=1604&context=etd (accessed on 21 August 2019).
- Tsang, V.; Stevenson, S. A Graph-theoretic Framework for Semantic Distance. Comput. Linguist. 2010, 36, 31–69. [Google Scholar] [CrossRef]
- Klavzar, S.; Vesel, A. Computing graph invariants on rotagraphs using dynamic algorithm approach: the case of (2,1)-colorings and independence numbers. Discrete Appl. Math. 2003, 129, 449–460. [Google Scholar] [CrossRef]
- Matula, D.W.; Marble, G.; Isaacson, J.D. Graph Coloring Algorithm. In Graph Theory and Computing; Read, R.C., Ed.; Academic Press: Cambridge, MA, USA, 1972; pp. 109–122. [Google Scholar]
- Wigderson, A. A New Approximate Graph Coloring Algorithm. In Proceedings of the Fourteenth Annual ACM Symposium on Theory of Computing, San Francisco, CA, USA, 5–7 May 1982. [Google Scholar]
- Lee, W.C.Y. Chapter 46: Cellular Telecommunications Systems. In Reference Data for Engineers, 9th ed.; Middleton, W.M., Van Valkenburg, M.E., Eds.; Newnes: Woburn, MA, USA, 2002; p. 1. [Google Scholar]
- Adediran, Y.A.; Lasisi, H.; Okedere, O.B. Interference management techniques in cellular networks: A review. Cogent Eng. 2017, 4, 1294133. [Google Scholar] [CrossRef]
- Horalek, J.; Sobeslav, V.; Krejcar, O.; Balik, L. Communications and security aspects of smart grid networks design. In Proceedings of the International Conference on Information and Software Technologies; Springer: Cham, Switzerland, 2014; pp. 35–46. [Google Scholar]
- Klimova, B.; Maresova, P. Social network sites and their use in education. In Emerging Technologies for Education; Wu, T.T., Gennari, R., Huang, Y.M., Xie, H., Cao, Y., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Hruska, J.; Maresova, P. Design of business canvas model for social media. In Emerging Technologies in Data Mining and Information Security; Springer: Singapore, 2019. [Google Scholar]
- Deen, M.J. Information and communications technologies for elderly ubiquitous healthcare in a smart home. Pers. Ubiquitous Comput. 2015, 19, 573–599. [Google Scholar] [CrossRef]
- Rezny, L.; White, J.B.; Maresova, P. The knowledge economy: Key to sustainable development? Available online: https://www.sciencedirect.com/science/article/abs/pii/S0954349X18302200 (accessed on 21 August 2019).
- Guan, X.; Zhang, S.; Li, R.; Chen, L.; Yang, W. Anti-k-labeling of graphs. Appl. Math. Comput. 2019, 363, 124549. [Google Scholar] [CrossRef]
- Pan, X.; Gao, L.; Zhang, B.; Yang, F.; Liao, W. High-Resolution Aerial Imagery Semantic Labeling with Dense Pyramid Network. Sensors 2018, 18, 3774. [Google Scholar] [CrossRef]
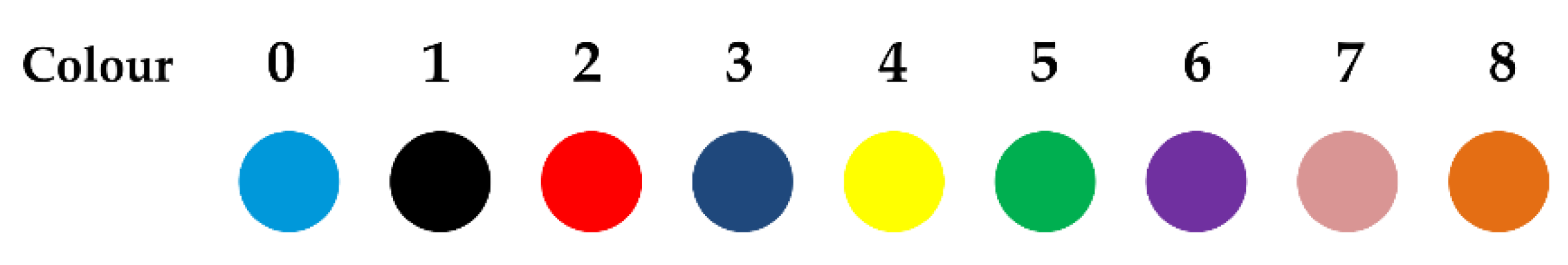





| (n+0), (m+0) | (n+1), (m+0) | (n+2), (m+0) | (n+3), (m+0) | (n+4), (m+0) | (n+5), (m+0) | (n+6), (m+0) | (n+7), (m+0) | (n+8), (m+0) | (n+9), (m+0) |
|---|---|---|---|---|---|---|---|---|---|
| (n+0), (m+3) | (n+1), (m+3) | (n+2), (m+3) | (n+3), (m+3) | (n+4), (m+3) | (n+5), (m+3) | (n+6), (m+3) | (n+7), (m+3) | (n+8), (m+3) | (n+9), (m+3) |
| (n+0), (m+2) | (n+1), (m+2) | (n+2), (m+2) | (n+3), (m+2) | (n+4), (m+2) | (n+5), (m+2) | (n+6), (m+2) | (n+7), (m+2) | (n+8), (m+2) | (n+9), (m+2) |
| (n+0), (m+1) | (n+1), (m+1) | (n+2), (m+1) | (n+3), (m+1) | (n+4), (m+1) | (n+5), (m+1) | (n+6), (m+1) | (n+7), (m+1) | (n+8), (m+1) | (n+9), (m+1) |
| (n+0), (m+4) | (n+1), (m+4) | (n+2), (m+4) | (n+3), (m+4) | (n+4), (m+4) | (n+5), (m+4) | (n+6), (m+4) | (n+7), (m+4) | (n+8), (m+4) | (n+9), (m+4) |
| (n+0), (m+7) | (n+1), (m+7) | (n+2), (m+7) | (n+3), (m+7) | (n+4), (m+7) | (n+5), (m+7) | (n+6), (m+7) | (n+7), (m+7) | (n+8), (m+7) | (n+9), (m+7) |
| (n+0), (m+6) | (n+1), (m+6) | (n+2), (m+6) | (n+3), (m+6) | (n+4), (m+6) | (n+5), (m+6) | (n+6), (m+6) | (n+7), (m+6) | (n+8), (m+6) | (n+9), (m+6) |
| (n+0), (m+5) | (n+1), (m+5) | (n+2), (m+5) | (n+3), (m+5) | (n+4), (m+5) | (n+5), (m+5) | (n+6), (m+5) | (n+7), (m+5) | (n+8), (m+5) | (n+9), (m+5) |
| (n+0), (m+8) | (n+1), (m+8) | (n+2), (m+8) | (n+3), (m+8) | (n+4), (m+8) | (n+5), (m+8) | (n+6), (m+8) | (n+7), (m+8) | (n+8), (j+8) | (n+9), (m+8) |
| (n+0), (m+11) | (n+1), (m+1) | (n+2), (m+11) | (n+3), (m+11) | (n+4), (m+11) | (n+5), (m+11) | (n+6), (m+11) | (n+7), (m+11) | (n+8), (j+11) | (n+9), (m+11) |
| Consecutive Colors | Manhattan Distance | i Parity | j Parity |
|---|---|---|---|
| (0,1) | ≥3 | even, odd | even, even |
| (1,2) | ≥3 | odd, even | even, even |
| (2,3) | ≥3 | even, even | even, odd |
| (3,4) | ≥3 | even, odd | odd, odd |
| (4,5) | ≥3 | odd, even | odd, odd |
| (5,6) | ≥3 | even, even | odd, even |
| (6,7) | ≥3 | even, odd | even, even |
| (7,8) | ≥3 | odd, even | even, even |
| (8,9) | ≥3 | even, odd | even, even |
| (9,10) | ≥3 | odd, odd | even, odd |
| (10,11) | ≥3 | odd, even | odd, odd |
| Algorithm/Input Size | L (1,1) | L (2,1) | L (3,1) |
|---|---|---|---|
| 0 | 2 | 3 | 5 |
| 1 | 5 | 8 | 8 |
| 2 | 12 | 19 | 15 |
| 3 | 23 | 36 | 26 |
| 4 | 38 | 59 | 41 |
| 10 | 212 | 323 | 215 |
| 20 | 822 | 1243 | 825 |
| 40 | 3242 | 4883 | 3245 |
| 80 | 12,882 | 19,363 | 12,885 |
| 100 | 20,108 | 30,303 | 20,111 |
| 200 | 80,202 | 120,403 | 80,205 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orogun, A.; Fadeyi, O.; Krejcar, O. Sustainable Communication Systems: A Graph-Labeling Approach for Cellular Frequency Allocation in Densely-Populated Areas. Future Internet 2019, 11, 186. https://doi.org/10.3390/fi11090186
Orogun A, Fadeyi O, Krejcar O. Sustainable Communication Systems: A Graph-Labeling Approach for Cellular Frequency Allocation in Densely-Populated Areas. Future Internet. 2019; 11(9):186. https://doi.org/10.3390/fi11090186
Chicago/Turabian StyleOrogun, Adebola, Oluwaseun Fadeyi, and Ondrej Krejcar. 2019. "Sustainable Communication Systems: A Graph-Labeling Approach for Cellular Frequency Allocation in Densely-Populated Areas" Future Internet 11, no. 9: 186. https://doi.org/10.3390/fi11090186
APA StyleOrogun, A., Fadeyi, O., & Krejcar, O. (2019). Sustainable Communication Systems: A Graph-Labeling Approach for Cellular Frequency Allocation in Densely-Populated Areas. Future Internet, 11(9), 186. https://doi.org/10.3390/fi11090186






