Mobility-Enabled Edge Server Selection for Multi-User Composite Services
Abstract
1. Introduction
- We formally model the problem of selecting edge servers for multiple users in mobile environments and establish a computation model of total user time consumption.
- We analyze the resource contention among mobile users and design the MESP algorithm to select edge servers in advance for each mobile user in order to minimize all users’ total waiting time. We conduct extensive simulation to verify the effectiveness of the proposed algorithm comparing baseline approaches.
2. Motivation Scenarios
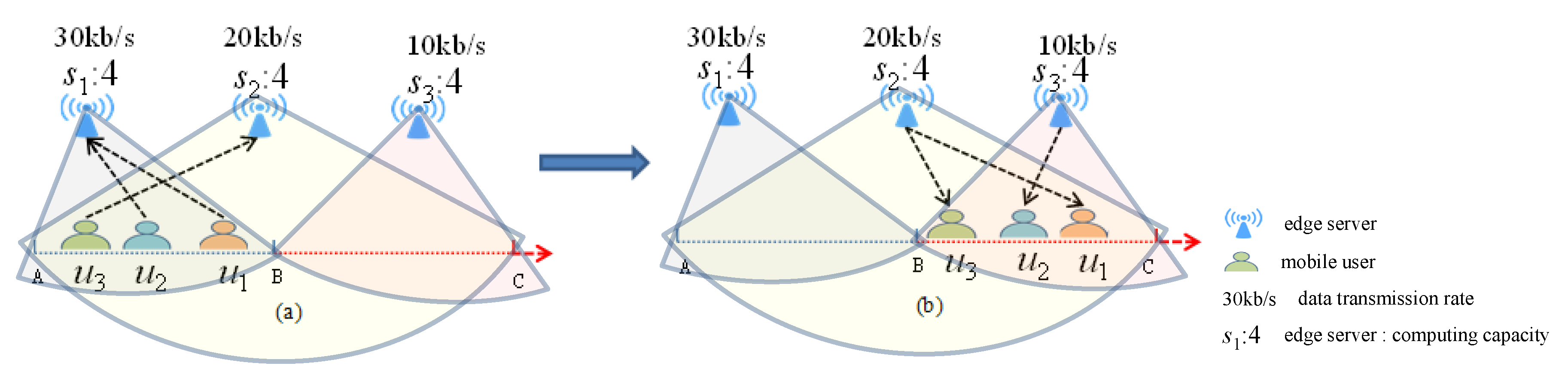
2.1. Multi-User Edge Server Selection with a Single Service
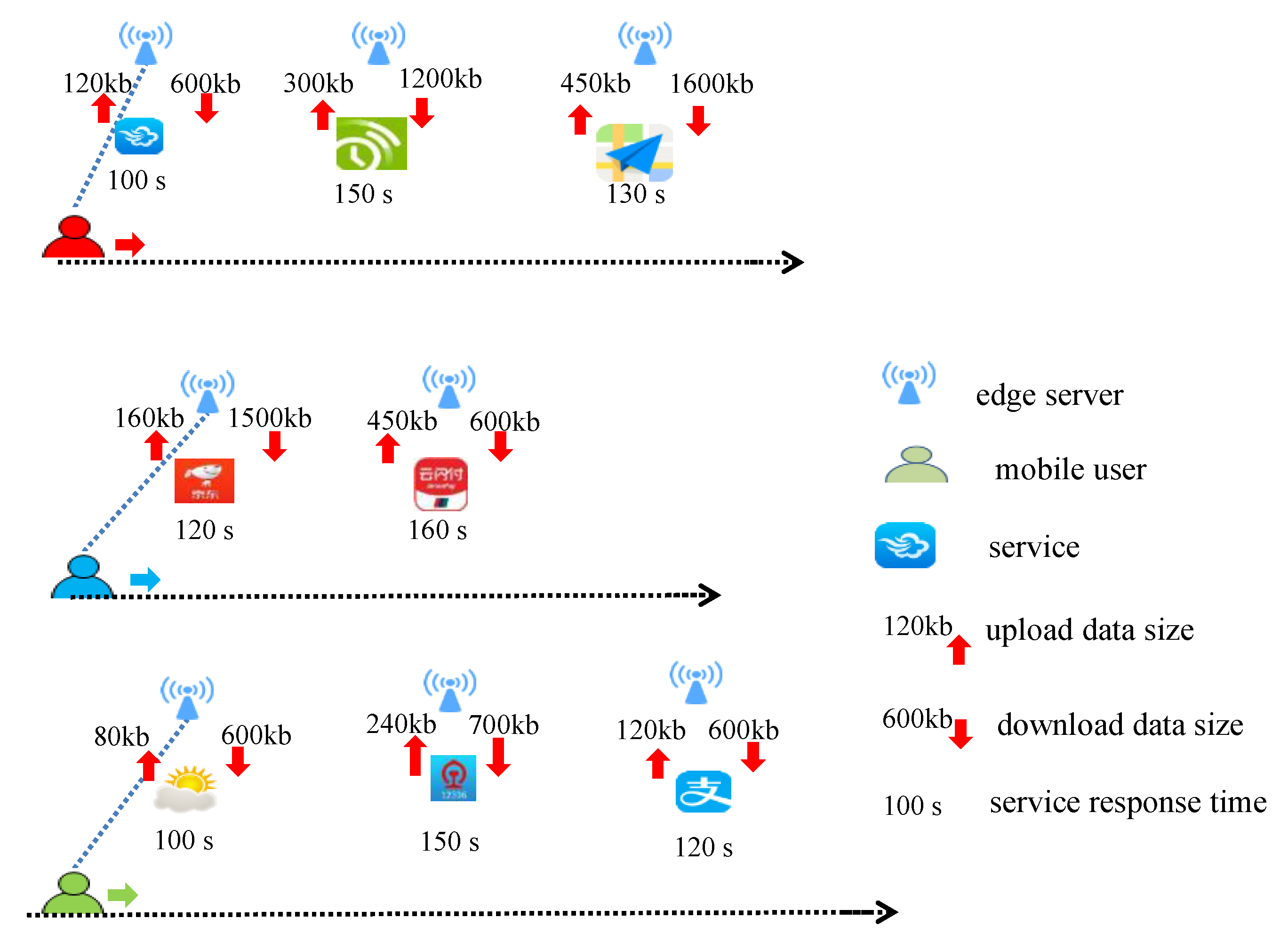
2.2. Multi-User Edge Server Selection with Composite Services
3. System Model
3.1. Prerequisite Definitions
- (1)
- I is the input parameters;
- (2)
- O is the output parameters;
- (3)
- C represents the resources required by the service, which is an n-tuple , where each is the resource type, including CPU, RAM, VRAM, etc.;
- (4)
- QoS is an n-tuple , where each denotes a QoS property of a service, including execution cost, response time, throughput, reputation, etc.
- (1)
- is the longitude and latitude of the edge server;
- (2)
- is coverage radius of the edge server;
- (3)
- C represents the capacity of an edge server and is an n-tuple , where each is the resource type of an edge server, including CPU, RAM, VRAM, etc.;
- (4)
- r is the average data transmission rate between the user and the edge server.
- (1)
- is the set of discrete location points (the mobile path is composed of lines between two adjacent points);
- (2)
- is a set of discrete path segments of the mobile path (the mobile path is composed of all path segments);
- (3)
- F is a mapping function between the set of location points and path segments:
- (1)
- denotes the initial location of the user in the mobile path;
- (2)
- is a set of discrete time points, with as the start time and as the stop time;
- (3)
- L is a set of discrete location points of the user;
- (4)
- F is a mapping function between time and location: .
3.2. Multi-User Mobility-Aware Time Latency Computation
- (1)
- is the time latency of uploading input data, which is given by:where is the data size of I and is the data transmission rate between the server and the user u.
- (2)
- is the response time of service ;
- (3)
- is time latency of downloading output data, which is given by:where is the data size of O and is the data transmission rate between the edge server and the user u;
- (4)
- denotes the round-trip latency, and is an indicator function, which is expressed as:
- (5)
- denotes the downtime generated by service migration, and is an indicator function, which is expressed as:
4. Edge Server Selection Method
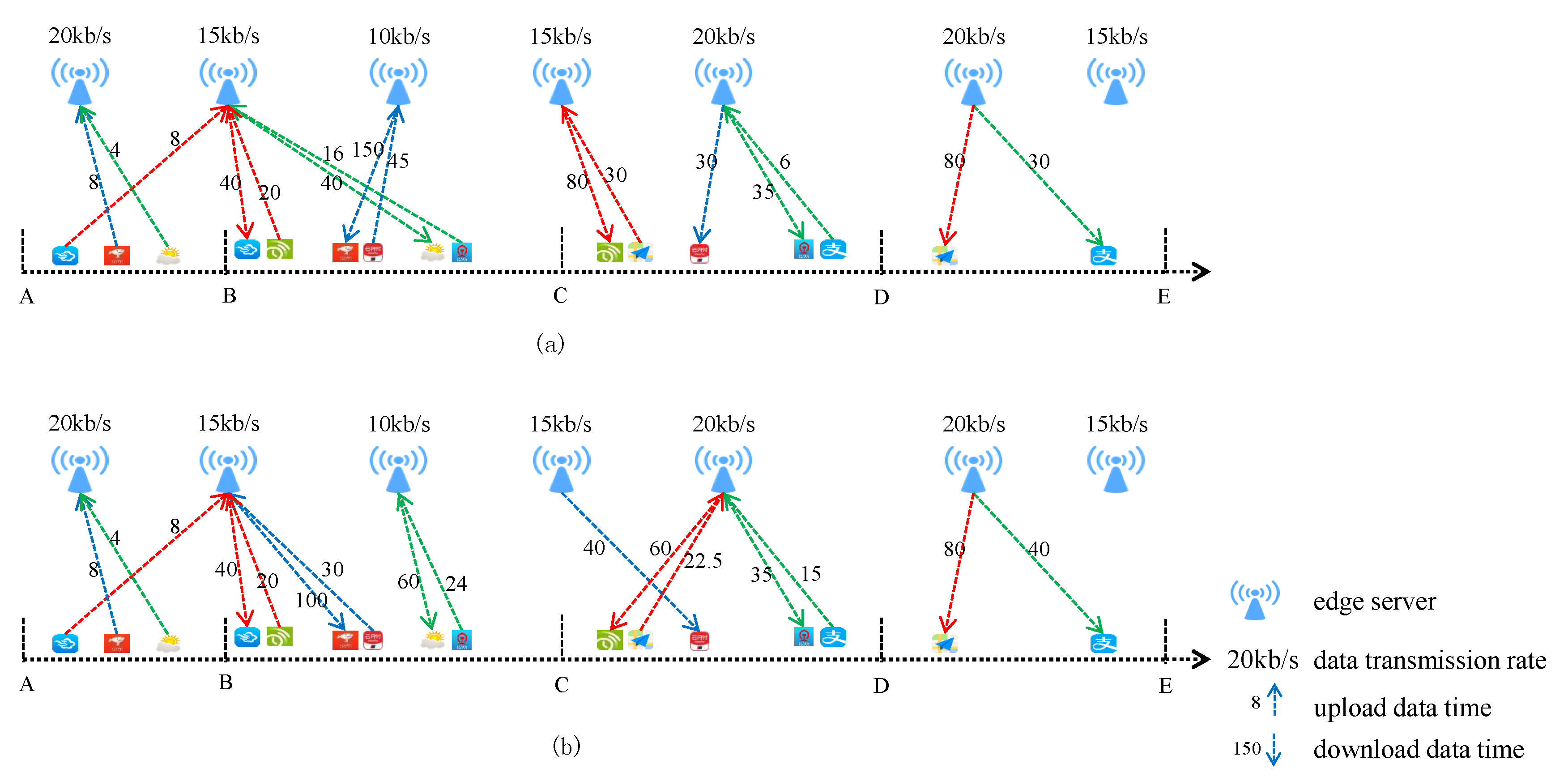
4.1. Resource Contention among Mobile Users
4.2. Multi-User Edge Server Selection Method Based on PSO
| Algorithm 1: Renewal algorithm. |
| Input: original decision solution Output: renewal decision solution while all services are not finished do for each user u do u selects edge severs S according to |
| for each selected server s in S, do |
| if s cannot meet the requirement from u |
| It randomly selects another server that has sufficient remaining capacity |
| end if |
| end for |
| end for |
| end while |
| return |
| Algorithm 2: MESP algorithm. |
| Input: iteration times , constant inertia weight w, cognitive and social parameters , quantity of particle , initial random particle position and velocity Output: best swarm position and minimizing total waiting time while not stopping |
| for each particle , do |
| compute response time of each particle , and set best individual particle position |
| end for |
| best swarm position, |
| for each particle i do |
| update particle velocity |
| update particle position |
| if is not feasible |
| is modified by Algorithm 1 |
| end if |
| end for |
| end while |
| return |
5. Simulated Experiments and Analysis
5.1. Baseline Approaches
- : Each user will randomly select an edge server as long as the server has sufficient remaining resources to accommodate the invoking service and has the users within its coverage.
- : Each user will select an edge server with the least data transmission time as long as the server has sufficient remaining resources to accommodate the invoking service and has the user within its coverage.
5.2. Experiment Settings
5.3. Experiment Results and Analysis
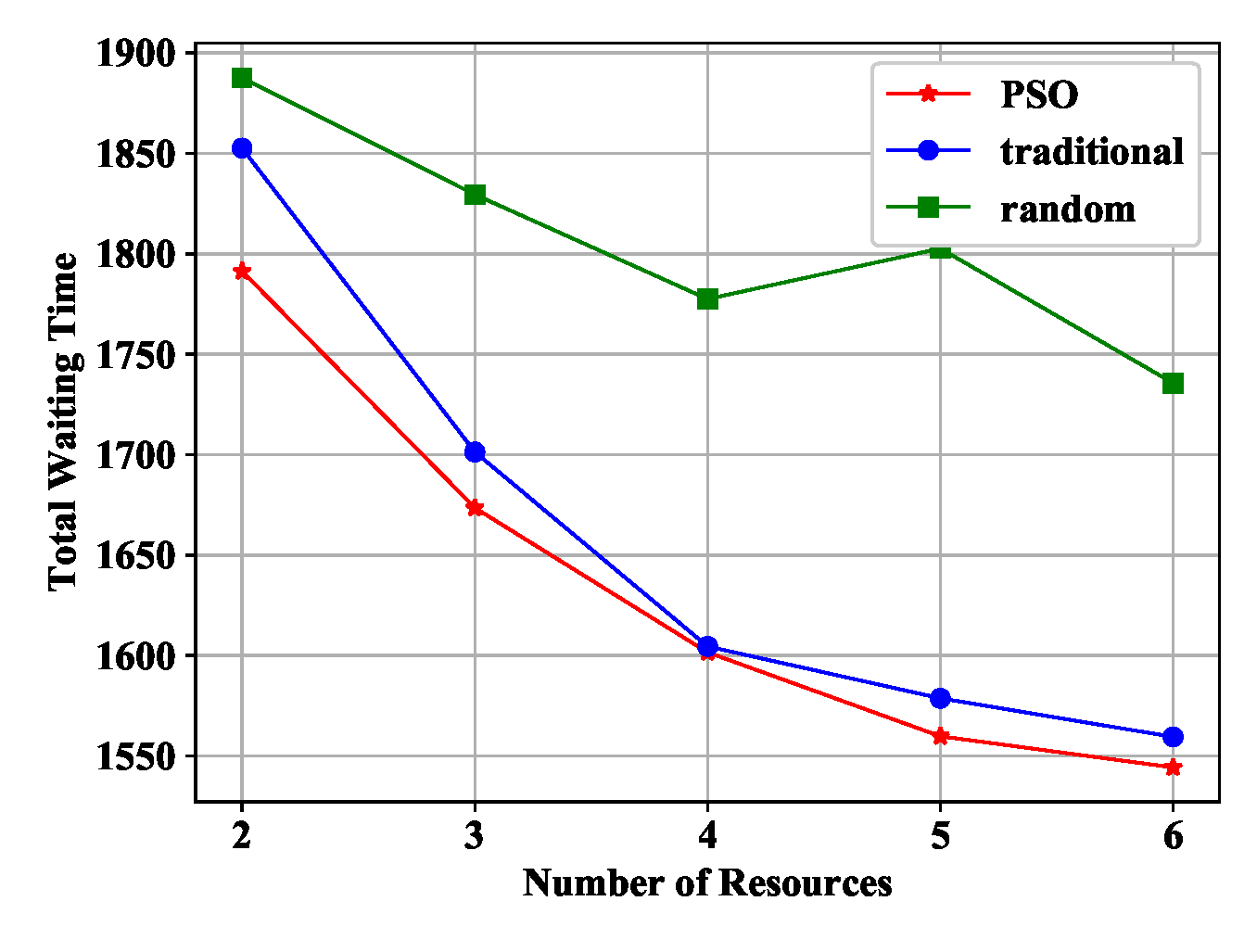
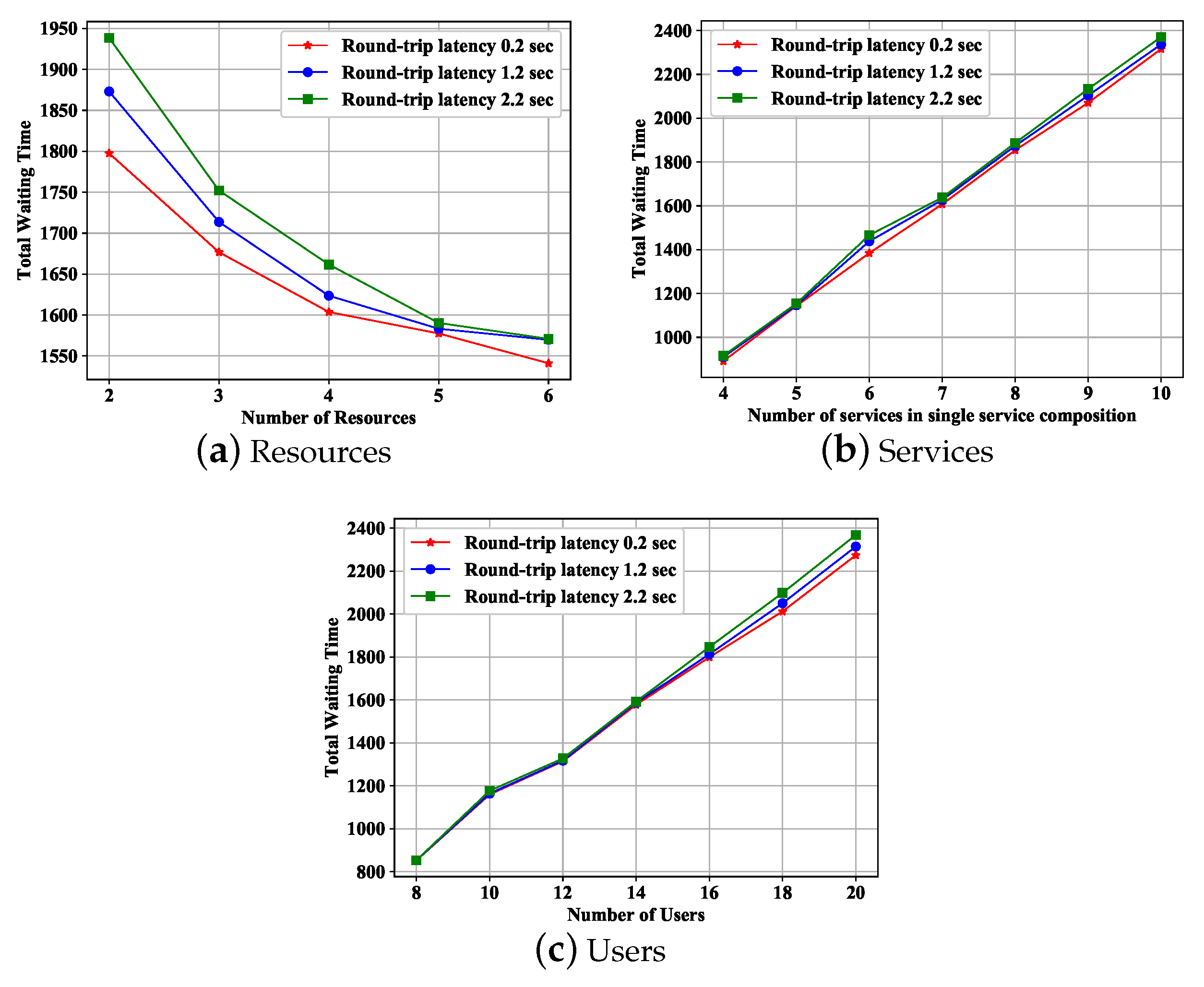
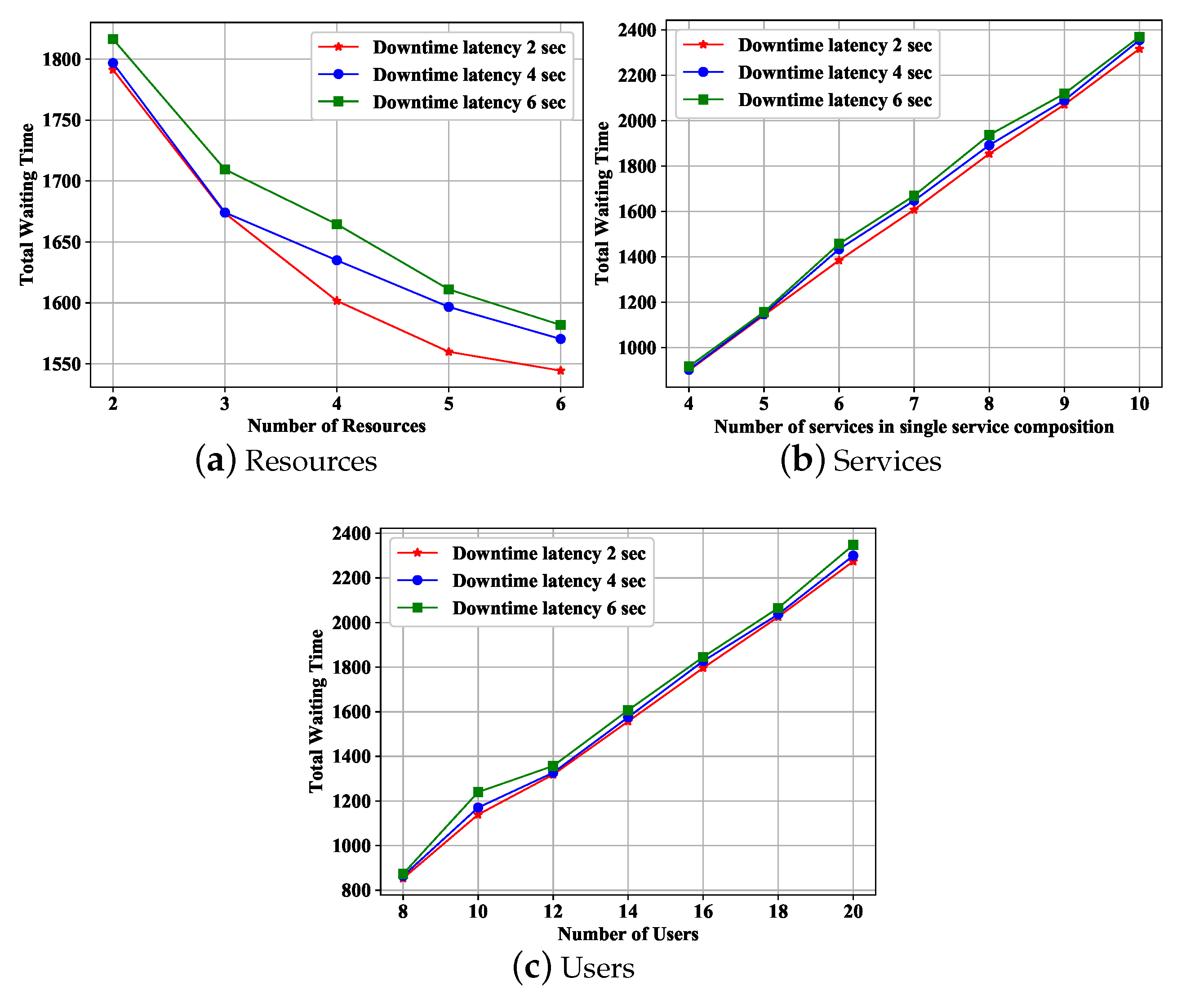
5.3.1. The Impact of Resources
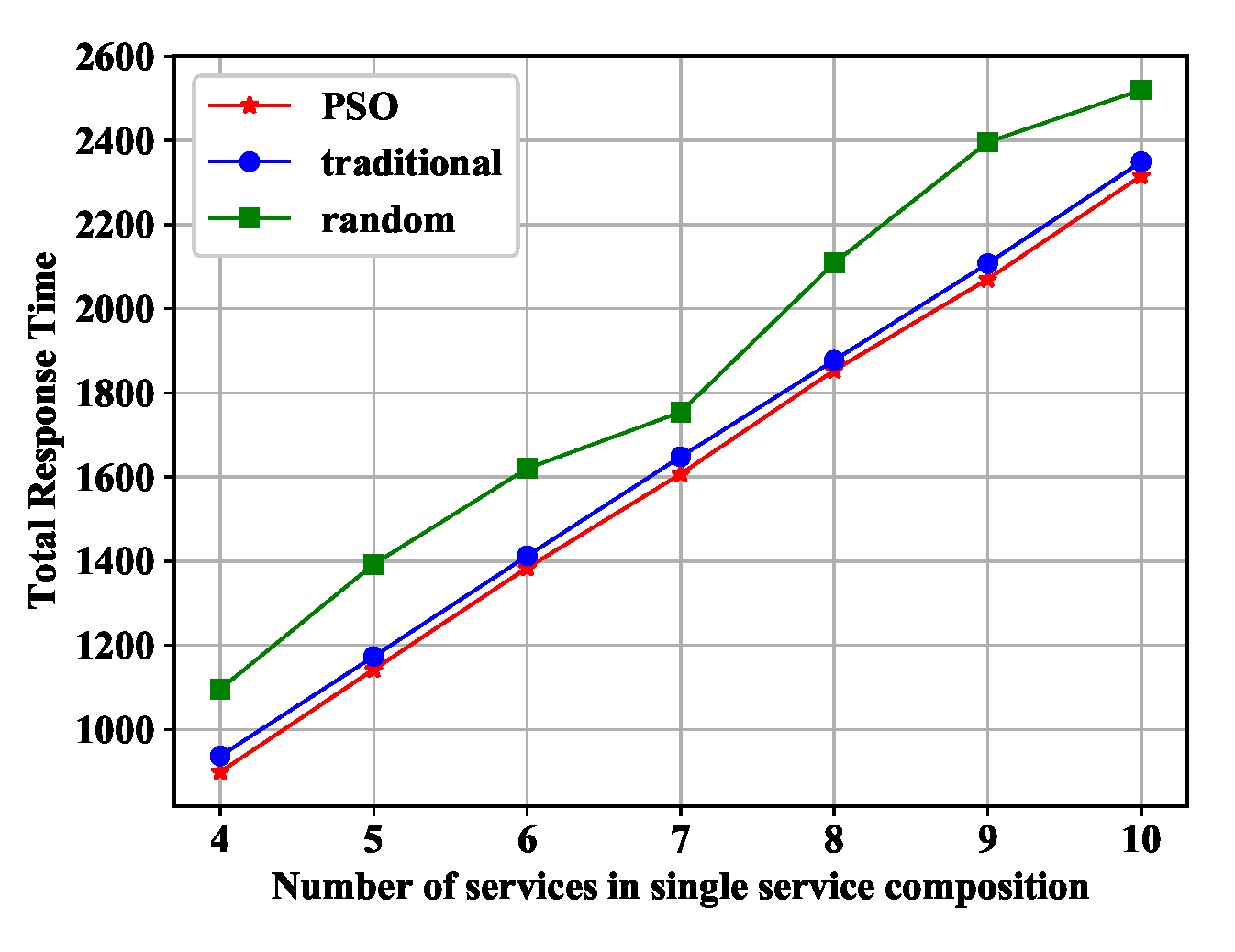
5.3.2. The Impact of the Number of Services
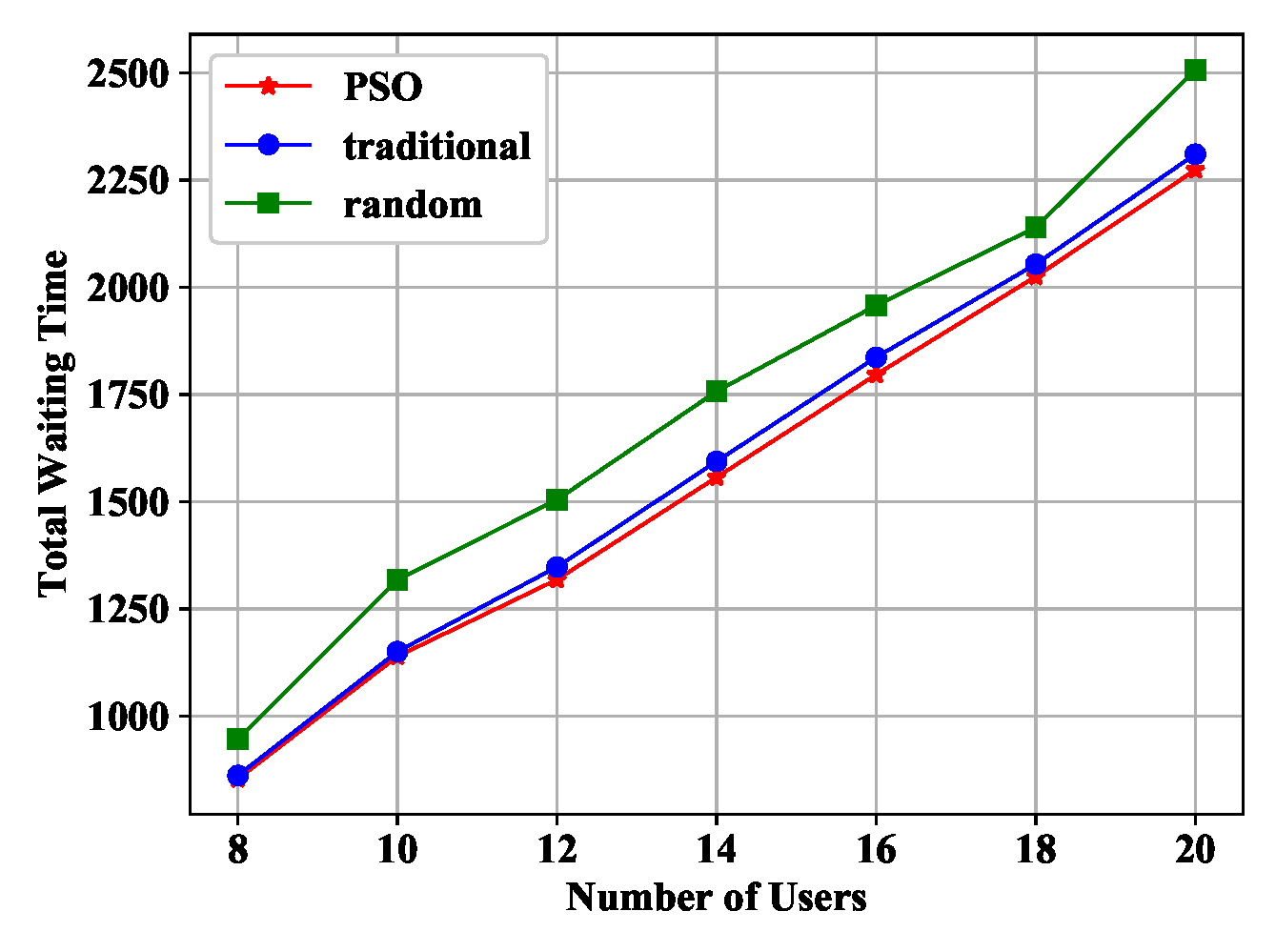
5.3.3. The Impact of Users
5.3.4. The Impact of the Round-Trip
5.3.5. The Impact of Downtime
6. Related Work
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hoang, D.T.; Lee, C.; Niyato, D.; Wang, P. A survey of mobile cloud computing: architecture, applications, and approaches. Wirel. Commun. Mob. Comput. 2013, 13, 1587–1611. [Google Scholar] [CrossRef]
- Shah-Mansouri, H.; Wong, V.W.S. Hierarchical Fog-Cloud Computing for IoT Systems: A Computation Offloading Game. IEEE Internet Things J. 2018, 5, 3246–3257. [Google Scholar] [CrossRef]
- Peng, K.; Leung, V.C.M.; Xu, X.; Zheng, L.; Wang, J.; Huang, Q. A Survey on Mobile Edge Computing: Focusing on Service Adoption and Provision. Wirel. Commun. Mob. Comput. 2018, 2018, 8267838:1–8267838:16. [Google Scholar] [CrossRef]
- Xu, X.; Li, Y.; Huang, T.; Xue, Y.; Peng, K.; Qi, L.; Dou, W. An energy-aware computation offloading method for smart edge computing in wireless metropolitan area networks. J. Netw. Comput. Appl. 2019, 133, 75–85. [Google Scholar] [CrossRef]
- Wang, S.; Xu, J.; Zhang, N.; Liu, Y. A Survey on Service Migration in Mobile Edge Computing. IEEE Access 2018, 6, 23511–23528. [Google Scholar] [CrossRef]
- Drolia, U.; Martins, R.; Tan, J.; Chheda, A.; Sanghavi, M.; Gandhi, R.; Narasimhan, P. The Case for Mobile Edge-Clouds. In Proceedings of the 2013 IEEE 10th International Conference on Ubiquitous Intelligence and Computing UIC/ATC 2013, Vietri sul Mare, Sorrento Peninsula, Italy, 18–21 December 2013. [Google Scholar]
- Lai, P.; He, Q.; Abdelrazek, M.; Chen, F.; Hosking, J.G.; Grundy, J.C.; Yang, Y. Optimal Edge User Allocation in Edge Computing with Variable Sized Vector Bin Packing. In Proceedings of the Service-Oriented Computing—16th International Conference, ICSOC 2018, Hangzhou, China, 12–15 November 2018. [Google Scholar]
- Zhang, Y.; Zhou, Y.; Wang, F.; Sun, Z.; He, Q. Service recommendation based on quotient space granularity analysis and covering algorithm on Spark. Knowl. Based Syst. 2018, 147, 25–35. [Google Scholar] [CrossRef]
- Tan, H.; Han, Z.; Li, X.; Lau, F.C.M. Online job dispatching and scheduling in edge-clouds. In Proceedings of the 2017 IEEE Conference on Computer Communications, INFOCOM 2017, Atlanta, GA, USA, 1–4 May 2017. [Google Scholar]
- Hou, I.; Zhao, T.; Wang, S.; Chan, K. Asymptotically optimal algorithm for online reconfiguration of edge-clouds. In Proceedings of the 17th ACM International Symposium on Mobile Ad Hoc Networking and Computing, MobiHoc 2016, Paderborn, Germany, 4–8 July 2016. [Google Scholar]
- Deng, S.; Wu, H.; Tan, W.; Xiang, Z.; Wu, Z. Mobile Service Selection for Composition: An Energy Consumption Perspective. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1478–1490. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, K.; He, Q.; Chen, F.; Deng, S.; Zheng, Z.; Yang, Y. Covering-based Web Service Quality Prediction via Neighborhood-aware Matrix Factorization. IEEE Trans. Serv. Comput. 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, G.; Deng, S.; Chen, F.; Wang, Y.; He, Q. Efficient Query of Quality Correlation for Service Composition. IEEE Trans. Serv. Comput. 2018. [Google Scholar] [CrossRef]
- Ascigil, O.; Phan, T.K.; Tasiopoulos, A.G.; Sourlas, V.; Psaras, I.; Pavlou, G. On Uncoordinated Service Placement in Edge-Clouds. In Proceedings of the IEEE International Conference on Cloud Computing Technology and Science, CloudCom 2017, Hong Kong, China, 11–14 December 2017. [Google Scholar]
- Machen, A.; Wang, S.; Leung, K.K.; Ko, B.; Salonidis, T. Migrating running applications across mobile edge clouds: poster. In Proceedings of the 22nd Annual International Conference on Mobile Computing and Networking, MobiCom 2016, New York City, NY, USA, 3–7 October 2016. [Google Scholar]
- Deng, S.; Huang, L.; Hu, D.; Zhao, J.L.; Wu, Z. Mobility-Enabled Service Selection for Composite Services. IEEE Trans. Serv. Comput. 2016, 9, 394–407. [Google Scholar] [CrossRef]
- Yi, S.; Li, C.; Li, Q. A Survey of Fog Computing: Concepts, Applications and Issues. In Proceedings of the 2015 Workshop on Mobile Big Data, Mobidata@MobiHoc 2015, Hangzhou, China, 21 June 2015. [Google Scholar]
- Taherizadeh, S.; Stankovski, V.; Grobelnik, M. A Capillary Computing Architecture for Dynamic Internet of Things: Orchestration of Microservices from Edge Devices to Fog and Cloud Providers. Sensors 2018, 18, 2938. [Google Scholar] [CrossRef] [PubMed]
- Poularakis, K.; Llorca, J.; Tulino, A.M.; Taylor, I.; Tassiulas, L. Joint Service Placement and Request Routing in Multi-cell Mobile Edge Computing Networks. In Proceedings of the 2019 IEEE Conference on Computer Communications, INFOCOM 2019, Paris, France, 29 April–2 May 2019; pp. 10–18. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization (PSO). In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997. [Google Scholar]
- Zhu, H.; Wang, Y.; Wang, K.; Chen, Y. Particle Swarm Optimization (PSO) for the constrained portfolio optimization problem. Expert Syst. Appl. 2011, 38, 10161–10169. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y.; Huang, L.; Xu, J.; Hsu, C. QoS prediction for service recommendations in mobile edge computing. J. Parallel Distrib. Comput. 2019, 127, 134–144. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y.; Xu, J.; Yuan, J.; Hsu, C. Edge server placement in mobile edge computing. J. Parallel Distrib. Comput. 2019, 127, 160–168. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, L.; Li, W.; Fu, X. Efficient Multi-User Computation Offloading for Mobile-Edge Cloud Computing. IEEE/ACM Trans. Netw. 2016, 24, 2795–2808. [Google Scholar] [CrossRef]
- Li, T.; Wu, M.; Zhao, M.; Liao, W. An Overhead-Optimizing Task Scheduling Strategy for Ad-hoc Based Mobile Edge Computing. IEEE Access 2017, 5, 5609–5622. [Google Scholar] [CrossRef]
- Tong, L.; Li, Y.; Gao, W. A hierarchical edge cloud architecture for mobile computing. In Proceedings of the 35th Annual IEEE International Conference on Computer Communications, INFOCOM 2016, San Francisco, CA, USA, 10–14 April 2016. [Google Scholar]
- Wang, S.; Urgaonkar, R.; He, T.; Chan, K.; Zafer, M.; Leung, K.K. Dynamic Service Placement for Mobile Micro-Clouds with Predicted Future Costs. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 1002–1016. [Google Scholar] [CrossRef]
- Ksentini, A.; Taleb, T.; Chen, M. A Markov Decision Process-based service migration procedure for follow me cloud. In Proceedings of the IEEE International Conference on Communications, ICC 2014, Sydney, Australia, 10–14 June 2014. [Google Scholar]
- Wang, S.; Urgaonkar, R.; Zafer, M.; He, T.; Chan, K.S.; Leung, K.K. Dynamic service migration in mobile edge-clouds. In Proceedings of the 14th IFIP Networking Conference, Networking 2015, Toulouse, France, 20–22 May 2015. [Google Scholar]
- Taleb, T.; Ksentini, A. An analytical model for Follow Me Cloud. In Proceedings of the 2013 IEEE Global Communications Conference, GLOBECOM 2013, Atlanta, GA, USA, 9–13 December 2013. [Google Scholar]
- Wang, S.; Urgaonkar, R.; He, T.; Zafer, M.; Chan, K.S.; Leung, K.K. Mobility-Induced Service Migration in Mobile Micro-Clouds. CoRR 2015, abs/1503.05141. [Google Scholar] [CrossRef]
- Taleb, T.; Ksentini, A. Follow me cloud: interworking federated clouds and distributed mobile networks. IEEE Netw. 2013, 27, 12–19. [Google Scholar] [CrossRef]
- Pack, S.; Shen, X.; Mark, J.W.; Pan, J. Mobility Management in Mobile Hotspots with Heterogeneous Multihop Wireless Links. IEEE Commun. Mag. 2007, 45, 106–112. [Google Scholar] [CrossRef]
- Bao, W.; Liang, B. Stochastic geometric analysis of handoffs in user-centric cooperative wireless networks. In Proceedings of the 35th Annual IEEE International Conference on Computer Communications, INFOCOM 2016, San Francisco, CA, USA, 10–14 April 2016. [Google Scholar]
| Service | RR | UDS (kb) | DDS (kb) | RT (s) | SD (s) |
|---|---|---|---|---|---|
| T1 | 2 | 120 | 300 | 10 | 2 |
| T2 | 2 | 120 | 800 | 10 | 2 |
| T3 | 2 | 40 | 300 | 10 | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhang, Y.; Wu, Q.; Peng, K. Mobility-Enabled Edge Server Selection for Multi-User Composite Services. Future Internet 2019, 11, 184. https://doi.org/10.3390/fi11090184
Zhang W, Zhang Y, Wu Q, Peng K. Mobility-Enabled Edge Server Selection for Multi-User Composite Services. Future Internet. 2019; 11(9):184. https://doi.org/10.3390/fi11090184
Chicago/Turabian StyleZhang, Wenming, Yiwen Zhang, Qilin Wu, and Kai Peng. 2019. "Mobility-Enabled Edge Server Selection for Multi-User Composite Services" Future Internet 11, no. 9: 184. https://doi.org/10.3390/fi11090184
APA StyleZhang, W., Zhang, Y., Wu, Q., & Peng, K. (2019). Mobility-Enabled Edge Server Selection for Multi-User Composite Services. Future Internet, 11(9), 184. https://doi.org/10.3390/fi11090184





