1. Introduction
A single-channel full duplex (SCFD or in short FD) transmission scheme is considered as one of the promising technologies in the next generation networks. It is a recent method that significantly increases the transmission spectral efficiency. In SCFD, any wireless device is permitted to simultaneously transmit and receive data over the same frequency channel. Conventionally, upload and download bit streams are transmitted either at different instants or over different frequencies [
1].
Self interference, which is a major obstacle facing FD implementation, may damage the whole system if it is not well suppressed. Self interference is the interference caused by the terminal on itself due to simultaneous in-band transmission and reception. In other words, self interference manifests when a high power transmitted signal interferes a weak received signal on the same terminal.
There are different techniques for self interference mitigation such as antenna directionality and polarization [
2,
3,
4,
5,
6]. Even more sophisticated adaptive methods in both analog and digital domains [
7,
8,
9,
10,
11,
12,
13] are used in case of multipath and scattered self interference channels. It is noteworthy that digital baseband interference cancellation methods [
14] mitigate the self interference. However, they are not enough due to the high level of distortion introduced by the analog circuits in the front end of the transceiver and the limited dynamic range of the analogue-to-digital convertors (ADC). Therefore, despite the reported progress in the cancellation techniques [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
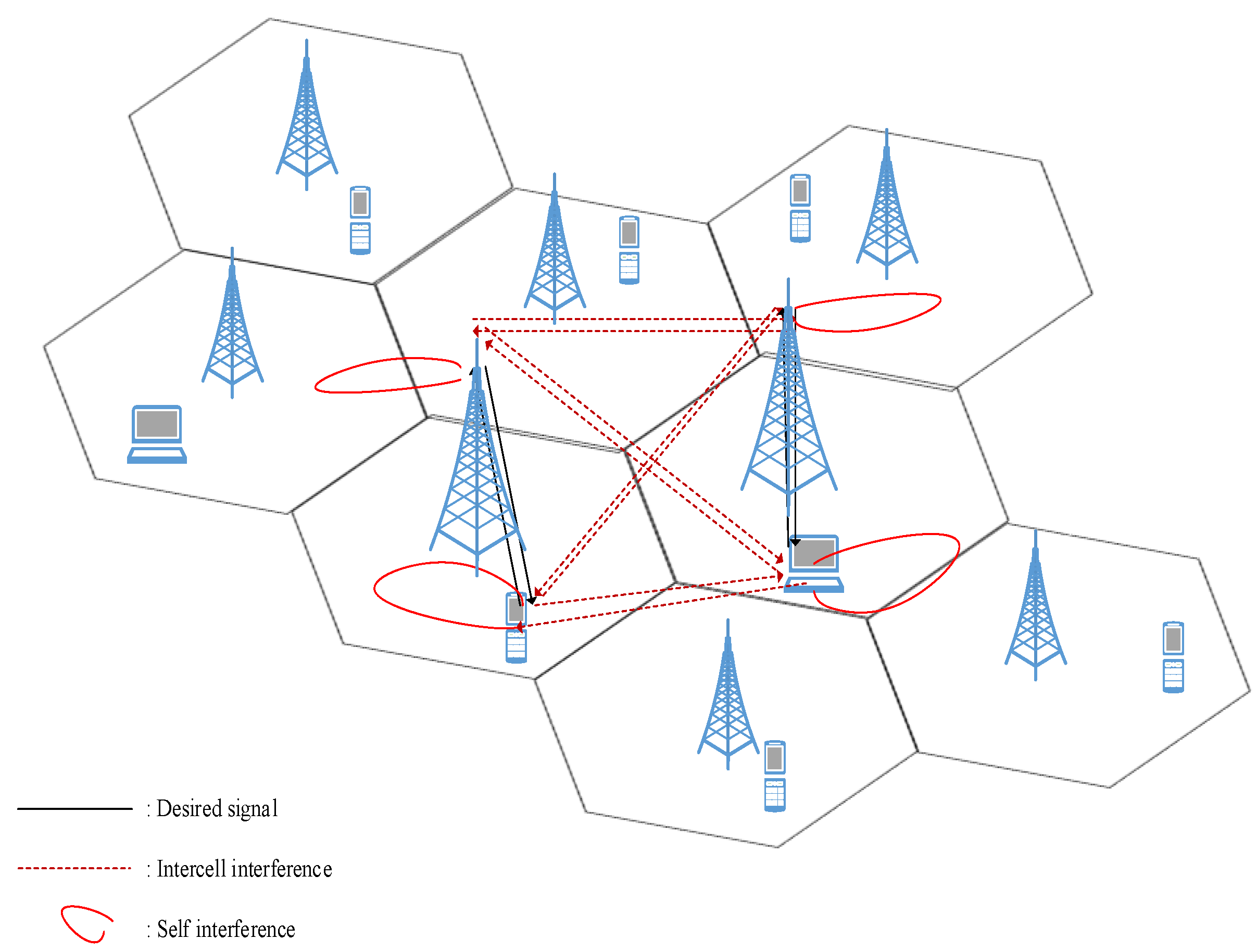
13], the interference problem is far from being over, and it becomes worse when FD is implemented in multi-cell networks. In multi-cell networks, and in the half duplex downlink case, there is only one type of intercell interference (i.e., downlink-to-downlink interference), and so is the case for the half duplex uplink (i.e., uplink-to-uplink interference). On the other hand, there are two types of intercell interference in the case of a full duplex downlink; they are downlink-to-downlink interference and uplink-to-downlink interference. The uplink stream in full duplex case is likewise affected by two types of intercell interference (i.e., downlink-to-uplink interference and uplink-to-uplink interference). This double amount of interference limits the performance of the full duplex schemes in multi-cell networks to the extent that it may destroy the merit of the full duplex.
Although a large amount of research work has been reported in the area of SCFD-based wireless networks, few papers consider large SCFD-based cellular networks with imperfect self interference cancellation. A simple decode-and-forward full duplex relaying aided with multiple-input-multiple-output (MIMO) was considered in [
15]. The dynamic range limitations in both transmitter and receiver sides were modelled. More importantly, a tight upper and lower bounds on the end-to-end achievable rate were derived. In addition, a transmission policy that maximizes the lower bound was proposed. The authors also found a theoretical approximation for the achievable rate which helps to gain insights in the trade-offs of the system design. In an FD-MIMO system, a transceiver filter design was considered in [
16], which aimed at maximizing the weighted sum rate (WSR) subject to the system or individual power constraints. The design was based on the relationship between the WSR and weighted minimum-mean-squared-error. In [
17], the authors addressed two optimization problems in FD-MIMO cognitive radio networks. The first problem is related with minimizing the sum of mean-squared errors (MSE) of all estimated symbols while the second problem deals with minimization of the maximum MSE per-secondary user (SU) of estimated symbols. Both problems are subject to power constraints at SUs and interference constraints projected to each primary user. Authors in [
18] analyzed the effects of adopting SCFD enabled base stations (BSs) in an OFDM multicell network with the legacy user equipments (UEs). However, they assumed perfect self-interference cancellation, which is currently unrealistic assumption. In [
19], the end-to-end capacity of SCFD relaying with two modes: amplify-and-forward and decode-and-forward was investigated. The authors characterized threshold of the self interference below which the full duplex transmission performs better than the half duplex transmission. In their research, they considered an isolated system of three nodes only (i.e., one link of two hops (source-relay-destination)). Authors in [
20] developed an optimal dynamic power allocation schemes for different scenarios with an objective of maximizing the sum rate of an SCFD bidirectional link. However, they did not consider the intercell interference. In [
21], a single cell full duplex MIMO system was studied. A large number of antennas at the BS were exploited for self interference cancellation.
In cellular networks, there are two kinds of wireless full duplex communications: symmetric and asymmetric. In the symmetric full duplex communication, the full duplex transmission takes place between two nodes; they are usually the BS and one UE, and hence it is sometimes called bidirectional FD. On the other hand, the asymmetric full duplex transmission involves three nodes. They are usually BS, downloader UE and uploader UE.
In the present research, the problem of intercell interference in multi-cell SCFD wireless systems under the assumption of imperfect cancellation of self interference is investigated. Accordingly, intercell interference control schemes are designed to best satisfy the users, even when their quality of service (QoS) requirements are infeasible. The proposed designs are general in that they are applicable to both kinds of FD: symmetric and asymmetric.
The rest of this paper is organized as follows. In
Section 2, the model of the full duplex cellular system is developed. In
Section 3, we present our proposed game theoretic approach for the best effort service in full duplex cellular system under an infeasible set of target signal-to-interference plus noise ratios (SINRs). Then, the proposed game is analyzed in
Section 4. Afterwards, the simulation results are shown and discussed in
Section 5. Finally, this work is concluded, and possible future directions are presented in
Section 6.
2. Full Duplex System Model
We consider
N simultaneous, co-channel full duplex links each of which is located in a separate cell as shown in
Figure 1. Focusing on a typical link, the receiver receives a desired signal
from its associated transmitter, and some other interfering signals as shown in
Figure 2. In fact, the desired signal
will be initially distorted by the radio frequency (RF) analog circuits in the transmitter front end. After passing though the channel and corrupted by different interfering signals, the signal
entering the receiver RF front end will be distorted again by the RF analog circuits.
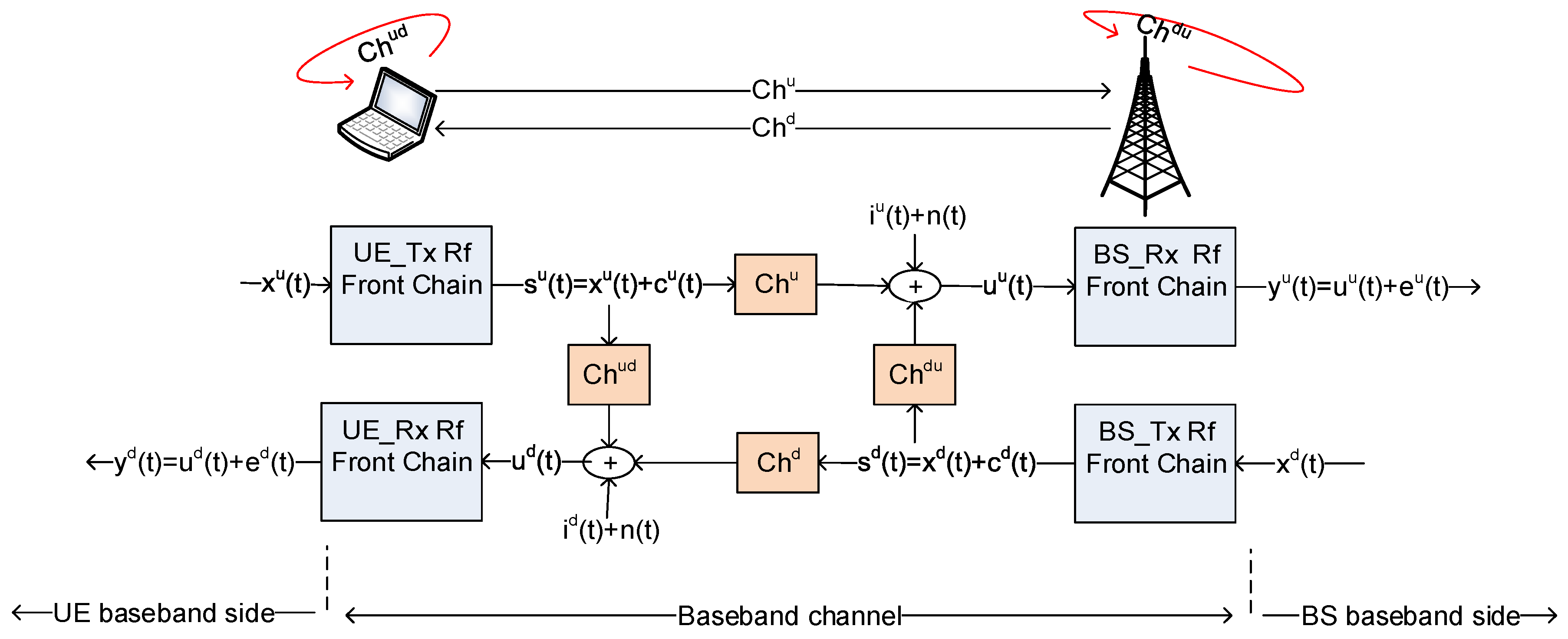
Figure 2 shows the discrete-time baseband-equivalent model for full duplex (FD) link, and captures the effects of analog circuits and the limited dynamic range in both sides of the link.
An independent zero-mean Gaussian noise
whose variance equals
times the energy of the intended signal
is injected in the model to capture the effect of the transmitter distortion created by the RF front end. This noise closely approximates the combined effects of additive power-amp harmonics, nonlinearities in the DAC and power-amp, as well as oscillator phase noise [
15]. Therefore, the equivalent baseband signal in the air
would be:
Furthermore, an independent zero-mean Gaussian noise
whose variance equals
times the energy collected at the receiving antenna is injected in the model to to capture the effects of the receiving RF front end and the DAC. Therefore, the received baseband signal after DAC would be:
Note that and are system parameters.
After careful manipulation presented in [
22], the SINR at both ends can be written as:
where
is the SINR of the downlink signal at the UE while
is the SINR of the uplink signal at the BS (Throughout this paper, the superscript
d and
u indicate downlink and uplink, respectively).
and
are the total amount of intercell interference at UE and BS, respectively. Moreover, the
and
are the downlink and uplink transmit power, respectively.
and
are the desired downlink and uplink channel gains.
is the channel gain of the uplink to downlink self interference (i.e., self interference at UE), whereas
is the channel gain of the downlink to uplink self interference (i.e., self interference at BS). Finally,
is an indicator parameter that equals 0 in case of symmetric communication and 1 for asymmetric communication.
is the power of the additive white Gaussian noise.
In each cell
n, the required QoS (i.e., the minimum required data rate and the maximum bit error rate (BER) in both downlink and uplink) can be mapped into a pair of target SINRs
and
. Therefore, the following two inequalities present two conditions that should be satisfied in every cell
:
where the first two terms in the denominators account for intercell interference.
3. Infeasible Target SINRs and the Best Effort Service
When the set of target SINRs is feasible, the best response of cell
n to a given intercell interference can be found to be rearranging (
4) as follows [
22]:
If all nodes simultaneously iterate the above equations, they will converge to a fixed point which achieves the set of target SINRs
[
22]. However, in case of infeasibility, the iteration will diverge and thus a solution is needed for such a case. In this section, we propose a game based solution that guarantees QoS achievement in case of feasible target SINRs and provides the best effort service otherwise.
In case of infeasibility, it is obviously more desirable to reach an equilibrium point that minimizes the gap between the right-hand side (RHS) and the left-hand side (LHS) of both equations in (
5), in all cells (If the target SINRs are feasible, the gap would be zero in all cells). Therefore, we define
as a column vector whose rows are the difference between RHS and LHS of the first and second equations in (
5). Thus,
For a given amount of interference (), each player should be able to find the best response () such that the norm of is minimized. According to the power constraints, the problem of intercell interference in full duplex wireless system can be formulated in two different ways as follows:
P1: Least difference with separate power constraints P2: Least difference with joint power constraints
Theorem 1. The problemsP1andP2are convex onand.
Proof. First, the constraint inequalities in each problem constitute polyhedron set, which is a convex set [
23]. Second, the objective function can be written as a least square objective function that is
, where
and
It is worth mentioning that
is a full rank matrix, and, hence, it is nonsingular. Therefore, the Hessian of the objective function (i.e.,
) is positive definite which means that the objective function is a strictly convex function in
[
23]. Thus, the convexity of the problems
P1 and
P2 follows directly. □
As a result, the above two problems can be casted as least-square optimization problems with inequality constraints [
24,
25].
Now, the non-cooperative game for interference management is formally introduced. The proposed game is , where
is the set of the players. Players are the cells each of which consisting of BS and its associated user/s. BS is assumed to take decisions and dictates its user/s to act accordingly.
is a convex set of transmit power that represents the space of actions available to the nth player. Two instances of the action set are examined:
- -
(separated power constraint),
- -
(Joint power constraint),
where and are the maximum transmit power allowable for BS and UE, respectively.
: is the nth player’s utility function. To comply with the game theory literature in which players are traditionally set to maximize their utility functions, the utility function here is chosen to be the negative of a convex objective function; that is, .
Each player in this game seeks to maximize its utility function.
4. Game Analysis
This section is dedicated for the analysis of the proposed game . We first demonstrate the existence of the Nash equilibrium.
Theorem 2. The gamepossesses a Nash equilibrium.
Proof. For each player , notice the following:
In both proposed instances, the actions set of every player is closed and bounded, and hence it is compact. Moreover, both actions’ sets are convex.
Theorem 1 shows that is a strictly convex function on , which implies that the utility function of the nth player is strictly concave on its own actions.
The utility function is a continuous function on the power vector .
As a result, using Theorem (1) in [
26], it follows in a straightforward manner that
has a Nash equilibrium point. □
Due to the fact that each player’s utility function is strictly concave in the player’s own action , there is only one strategy that maximizes the utility of that player (given a particular strategy profile of the rest of the players). Thus, if every player plays its best response (iteratively), they would achieve a unique Nash equilibrium.
For a typical cell n, let the experienced intercell interference at the user equipment (UE) be and the intercell interference at the base station (BS) be . The best response and of cell n against the actions of the other cells is a crucial quantity for finding the Nash equilibrium. Obviously, the best response should maximize the utility function subject to , where
For computational efficiency reasons, it is beneficial to transform to a triangular matrix using QR factorization; , where is an orthogonal matrix and is an upper triangular matrix (Since is nonsingular, the diagonal elements of are nonzero). Since is orthogonal, the objective function can equivalently be written as: , where .
Now, let
, which implies
. Thus, the above problem can equivalently be written as:
where
,
and
. This problem is called the least distance problem (LDP). The constraint in (
11) can also be written as
, or equivalently in short
.
For solving the problem in (
11), we restate a useful theorem in ([
24], Chap. 23) that transforms LDP into a nonnegative constrained least-square problem (NNLS) using a dual method. The NNLS problem can then be easily solved using any software package such as MATLAB.
Theorem 3. Consider the least distance problem with lower boundswhereand. Letbe the solution to the nonnegativity constrained problemwhere.
Let the residual corresponding to the solution beand put.
if; then, the constraintsare inconsistent and (12) has no solution. If, then the vectordefined by, whereis the unique solution to (12). For proof of the theorem, the reader is encouraged to refer to ([
24], Chap. 23).
Algorithm (1) summarizes the steps for calculating the best response of each cell (i.e., player). This algorithm is applied iteratively in each cell until they all converge to the Nash equilibrium.
| Algorithm 1 Equilibrium Achieving Algorithm |
- 1:
Given: - 2:
initial value of , assuming intercell interference is zero. - 3:
; Start iteration: - 4:
whiledo - 5:
- 6:
▹ Using QR factorization - 7:
- 8:
- 9:
- 10:
- 11:
- 12:
- 13:
Apply Theorem 3 to find - 14:
▹ This is the best response of cell n. - 15:
Measure the amount of interference and find to be used for next iteration. - 16:
if then ▹ If this condition is satisfied then NE is achieved, where is sufficiently small. - 17:
end if - 18:
end while
|
It is worth mentioning that the proposed algorithm is completely distributed. Thus, each player will act upon local information collected at the BS and its associated UE. Each UE has to send the gain of the desired channel as well as the measured interference to its home BS since all computation should be performed at the BS for powerful computing capability and large memory capacity.
5. Simulation Results and Discussion
This section shows and discusses the results of extensive computer simulations which are conducted in accordance with the system setup explained in
Section 2. The simulation parameters are shown in
Table 1.
Obviously, as the half duplex systems suffer less interference, and hence requires less transmit power for achieving certain SINR, the full duplex; on the other hand, it requires less bandwidth to achieve the same SINR. Therefore, a general metric that measures the overall performance is required for a fair comparison between full duplex based system and half duplex based system. The energy efficiency (EE) in terms of bits per Hz per joule (bits/Hz/J) measures the overall performance of a given system as it simultaneously takes into account both the effect of the bandwidth and the effect of the transmit power.
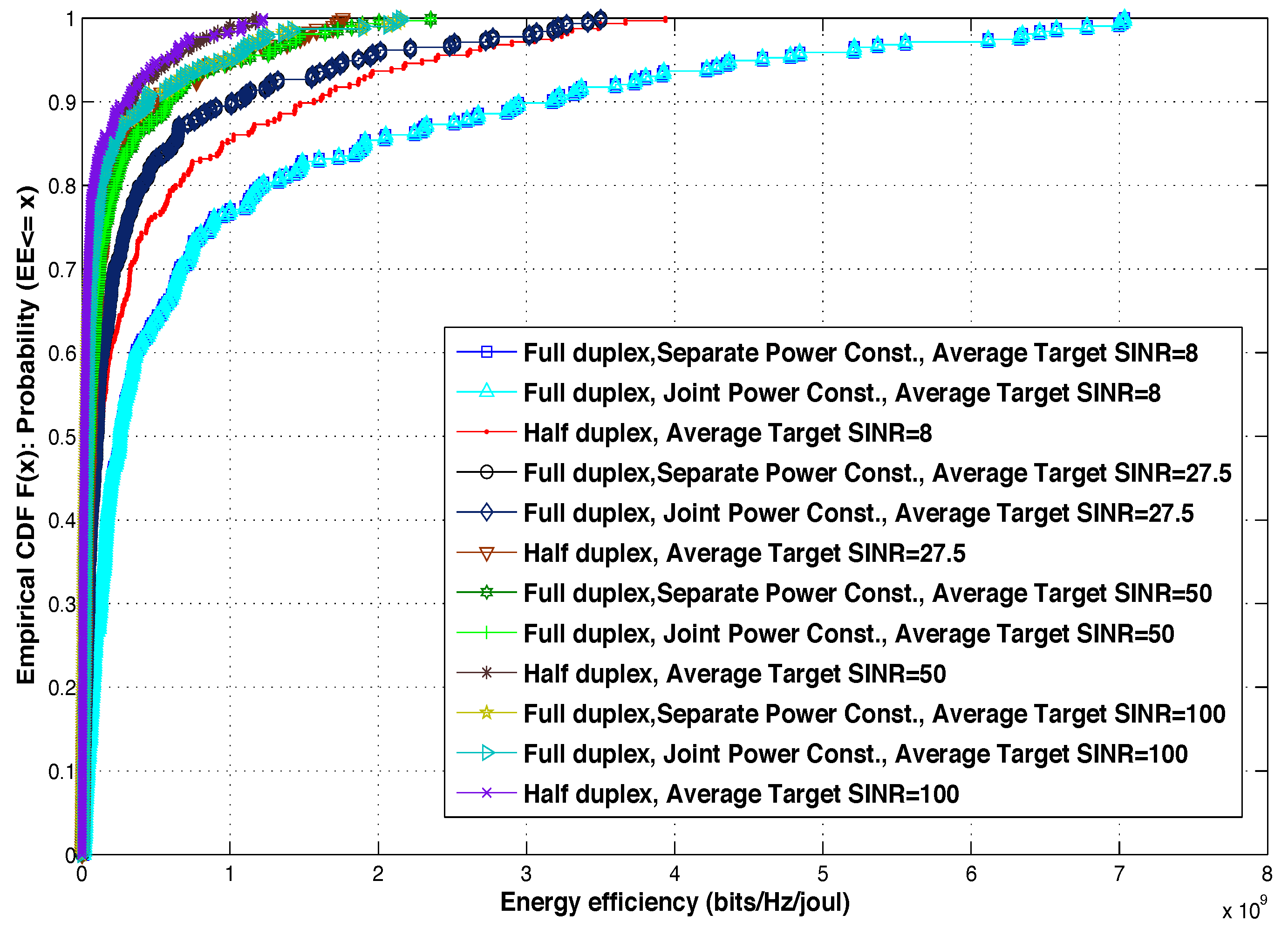
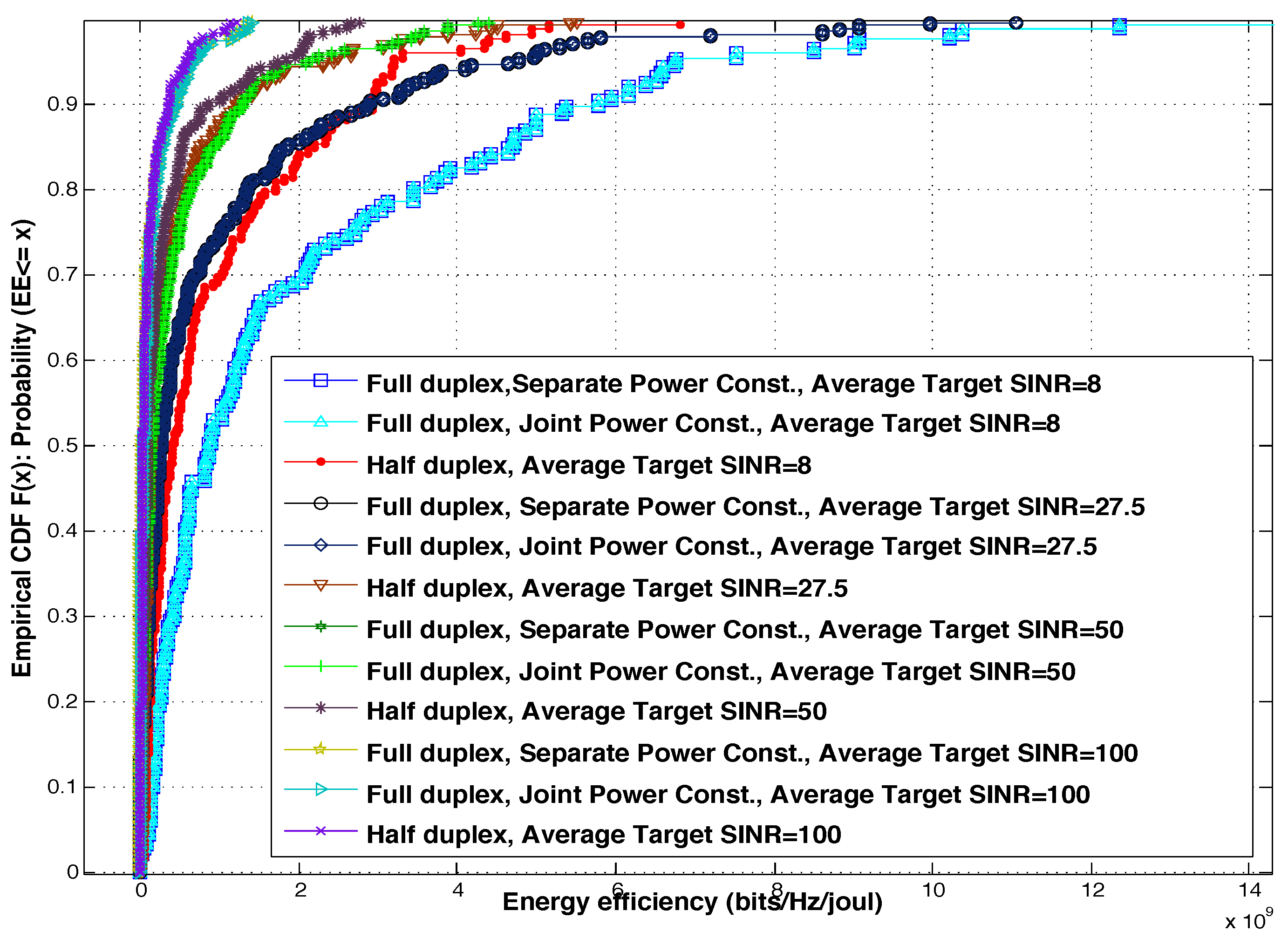
Figure 3 and
Figure 4 show the cumulative density function (CDF) of EE for half duplex based system and full duplex based system with the two schemes introduced in this paper, FD system with separate power constraint and FD system with joint power constraint. All systems have been tested under different target SINR averages in two network sizes; 12-cell network and 36-cell network. Looking carefully at the figures, the following are remarkable:
In all cases, the EE of the full duplex schemes outperforms that of the half duplex scheme. In fact, the 97% confidence interval of the EE average in (bits/Hz/J) for all tested schemes are (when the target SINR is 100 in a 12-cell network.):
- -
FD scheme with separate power constraint:
- -
FD scheme with joint power constraint:
- -
hald duplex scheme: .
There is no significant difference between the two kinds of full duplex schemes introduced in this paper due to the fact that they both operate in intense interference dominant regime.
As the average target SINR increases, the gap between the full duplex EE and half duplex EE diminishes. This is because each transmitter is likely to radiate more power to be able to achieve higher SINR, and hence decreasing the EE.
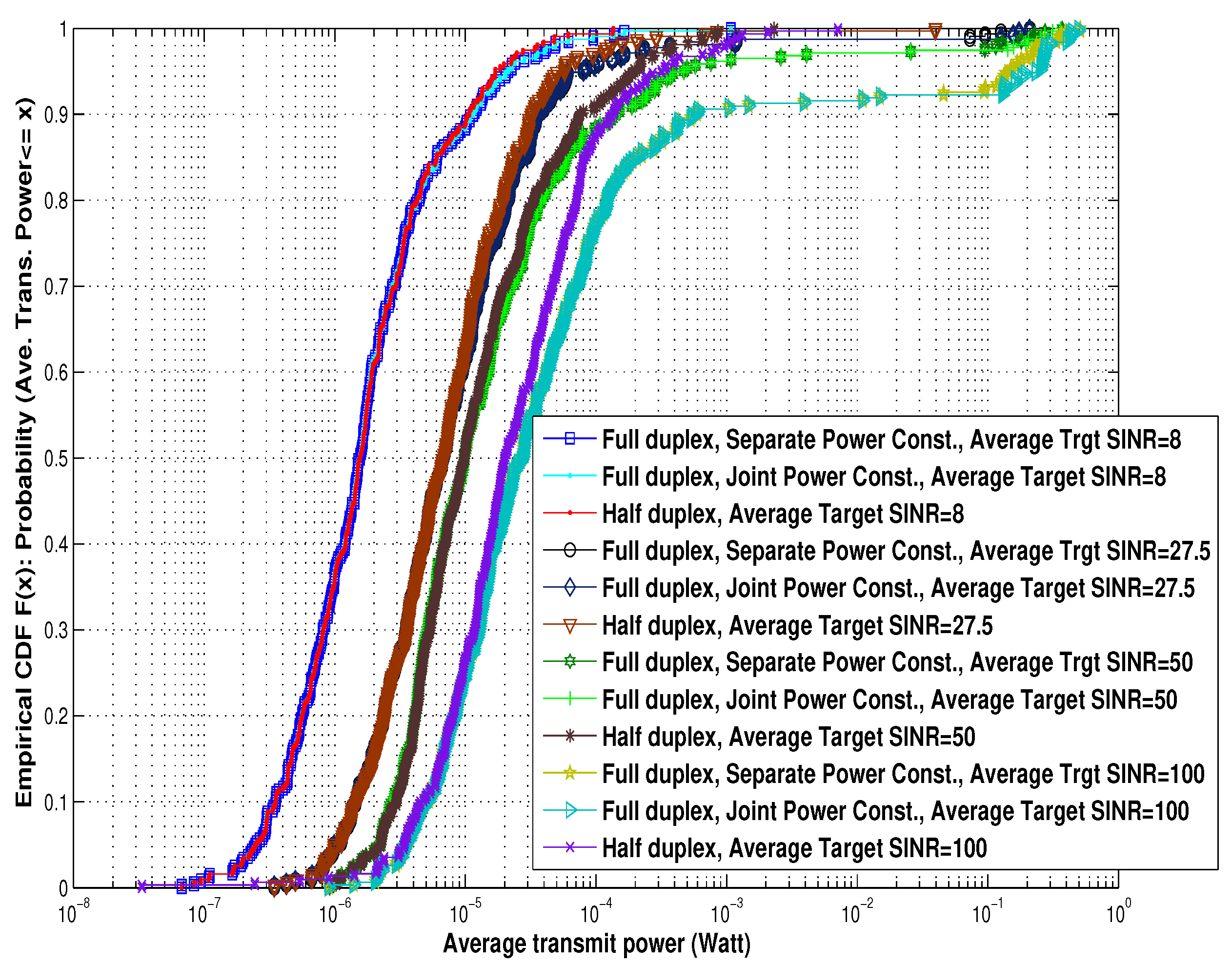
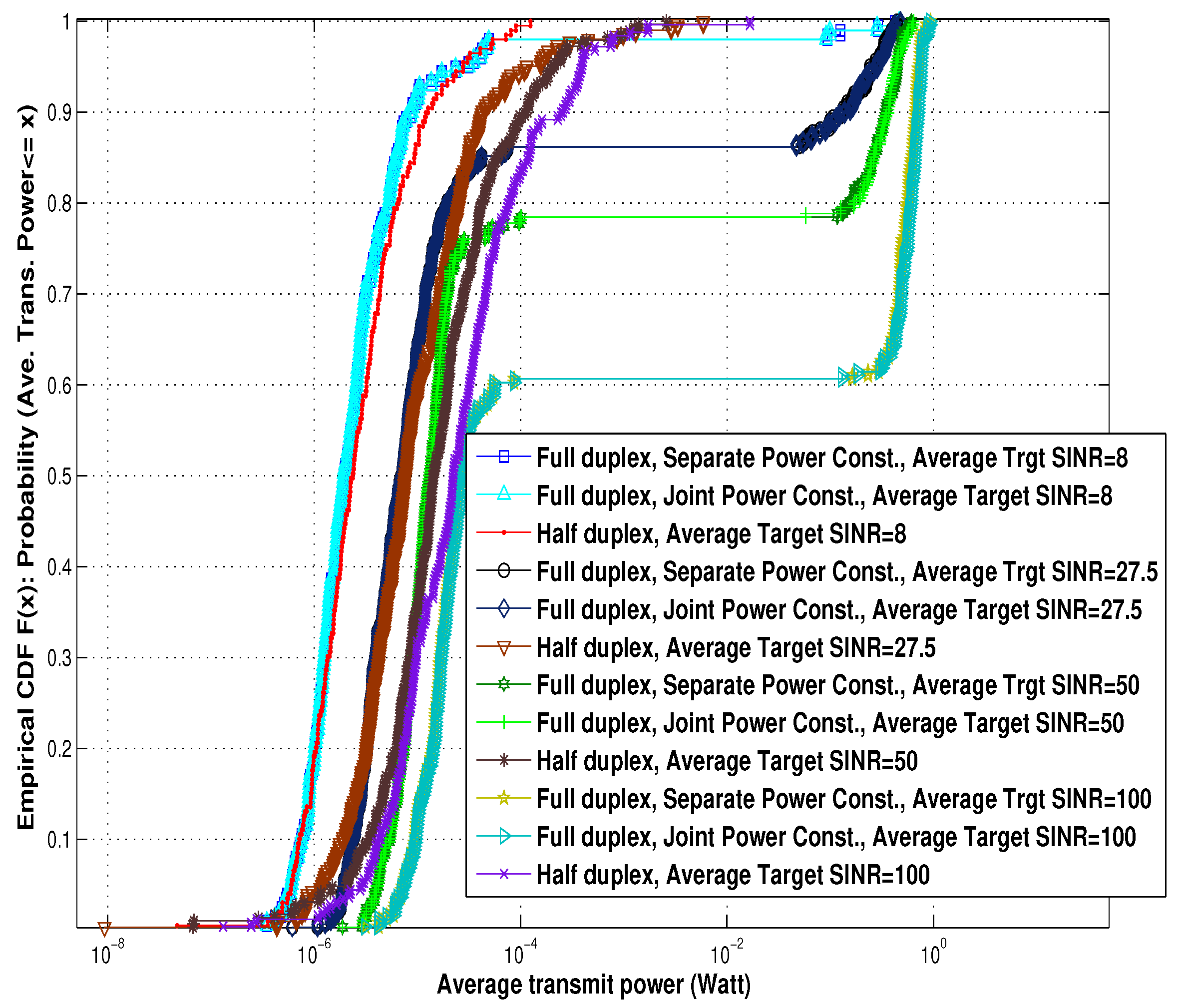
Figure 5 and
Figure 6 show the CDF of the average transmit power under different average target SINRs in a 12-cell network and a 36-cell network, respectively. In
Figure 6, for example, the average transmitted power exceeds 0.1 Watt %40 of the time when the average target SINR is 100. On the other hand, when the average target SINR is 8, the average transmitted power exceeds 0.1 Watt only %3 of the time.
Therefore, the phenomenon of diminishing EE can be further justified as follows. As illustrated in
Figure 5 and
Figure 6, when the system tries to achieve a set of higher SINRs, the transmit power of all transmitters tend to increase. This will increase the amount of interference in the whole netwrok, which in turn causes the actual SINR growth to diminish.
Comparing
Figure 5 and
Figure 6, it is observable that, as the network size increases, the average transmit power increases as well. This can be interpreted as follows. The intercell interference amount increases with the number of cells, which in turn shifts the equilibrium point (the best vector of the transmit powers) into a higher profile.
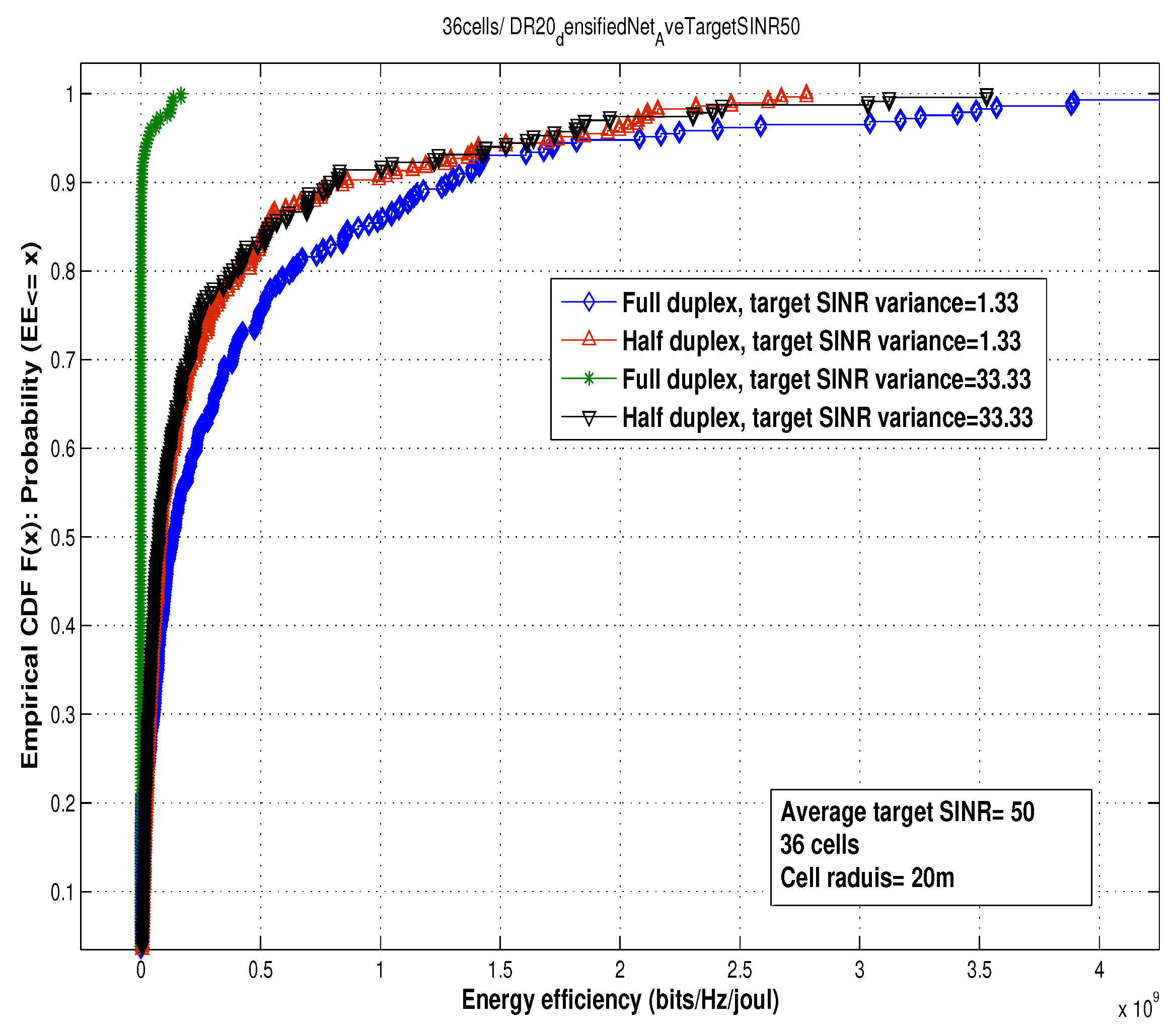
Effect of the target SINR variance among users (i.e., when the running applications among users are entirely different):
Not only do the average of users’ target SINRs affect the EE of the full duplex schemes, but also the variance of these target SINRs affects the EE. Contrary to the half duplex scheme, the EE of the full duplex schemes decreases as the variance of the target SINRs among the users increases (see
Figure 7). This phenomenon occurs because of the increase in the average of the required transmitted power as the spread of the interference distribution increases.
Figure 8 shows that, in case the average target SINR among users is 50, the average transmit power exceeds 100 mW 90% of the time when the target SINR variance is 33.3. On the other hand, the average transmit power exceeds 100 mW only 20% of the time in low target SINR variance among the users.
6. Conclusions
Unlike half duplex-based systems, the amount of intercell interference in a full duplex-based system is almost double. In fact, there are two types of intercell interference in the case of full duplex downlink; they are downlink-to-downlink interference and uplink-to-downlink interference, and this is also the case for the full duplex uplink (i.e., downlink-to-uplink interference and uplink-to-uplink interference). This double amount of interference limits the performance of the full duplex schemes in large networks to the extent that it may destroy the merit of the full duplex. In this paper, we proposed a game theoretic solution which guarantees QoS achievement in the case of feasible target SINRs, and provides best effort service otherwise. The game was formulated to perfectly reflect the system, the existence of the Nash equilibrium was proven, and an enabling distributed algorithm was developed. Finally, the simulation results were presented to show the effectiveness of the proposed solution.
In order to further improve the performance of full duplex schemes in large networks, future research effort should be given to the area of multi-objective optimal solutions (i.e., goal attainment and multi-objective genetic algorithm). Moreover, our game based solution will be generalized to include massive MU-MIMO systems [
27,
28].