Time Series Irradiance Synthesizer for Optical GEO Satellite Downlinks in 5G Networks
Abstract
:1. Introduction
- Downlink Propagation
- GEO satellite-to-ground optical link
- Rytov’s theory is considered and Kolmogorov’s spatial spectrum of refractive index is applied
- Optical links with elevation angle greater than 20 deg are assumed
- A single collimated Gaussian beam is transmitted
- Perfect link pointing and tracking
2. ARTEMIS Optical Satellite Program
3. Proposed Time Series Synthesizer
3.1. Important Metrics
3.2. Time Series Generator
4. Validation and Numerical Results
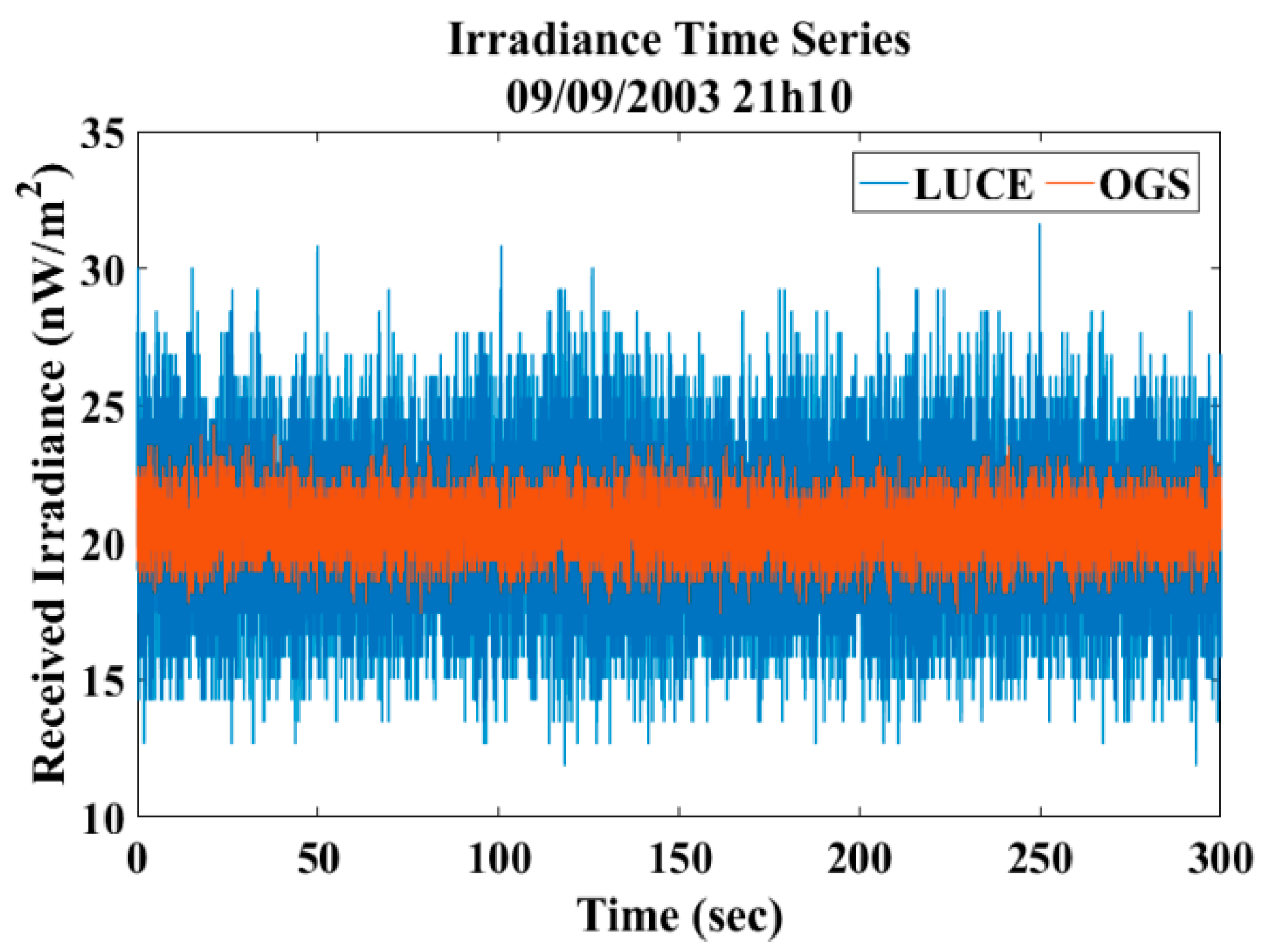
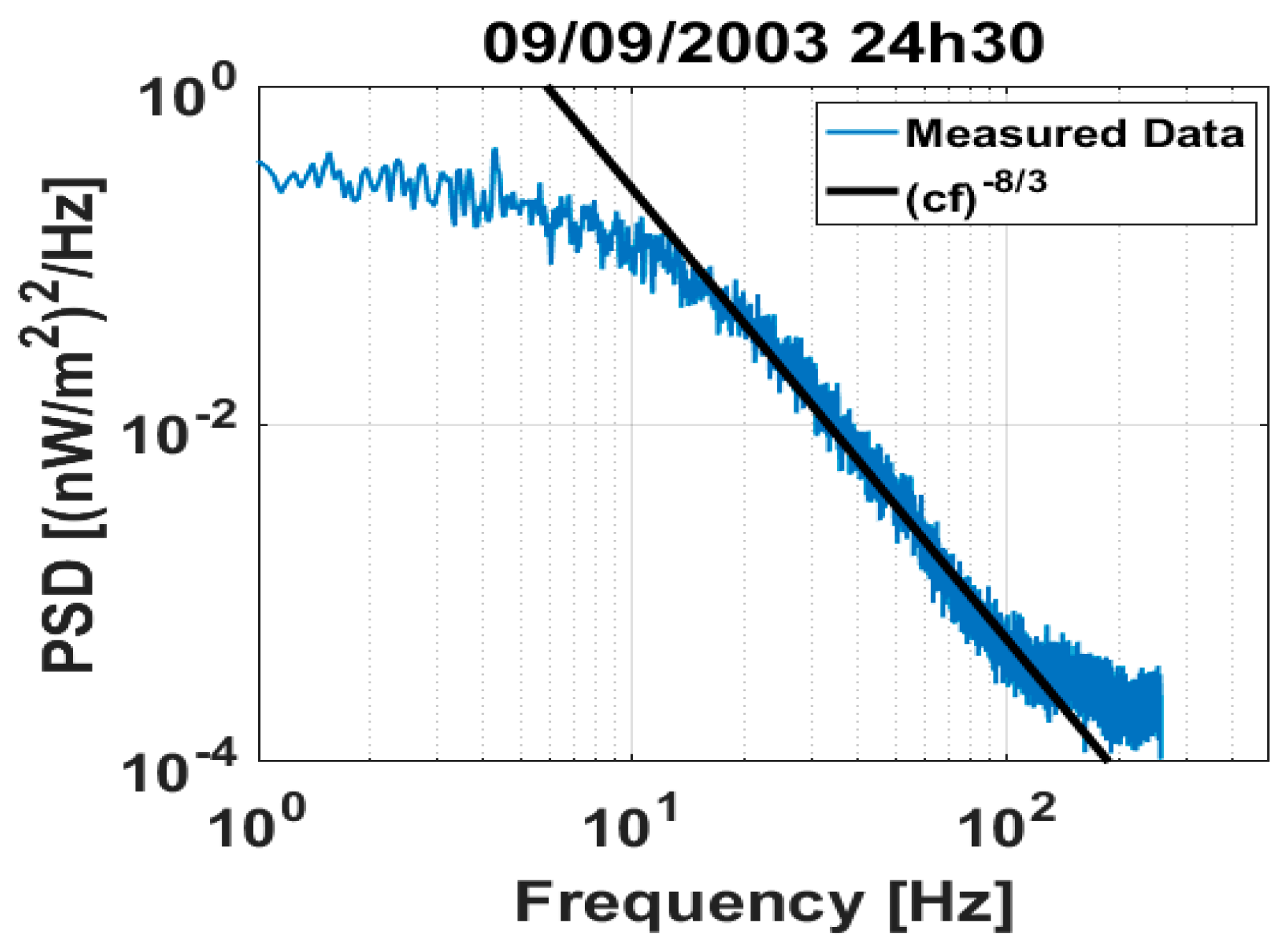
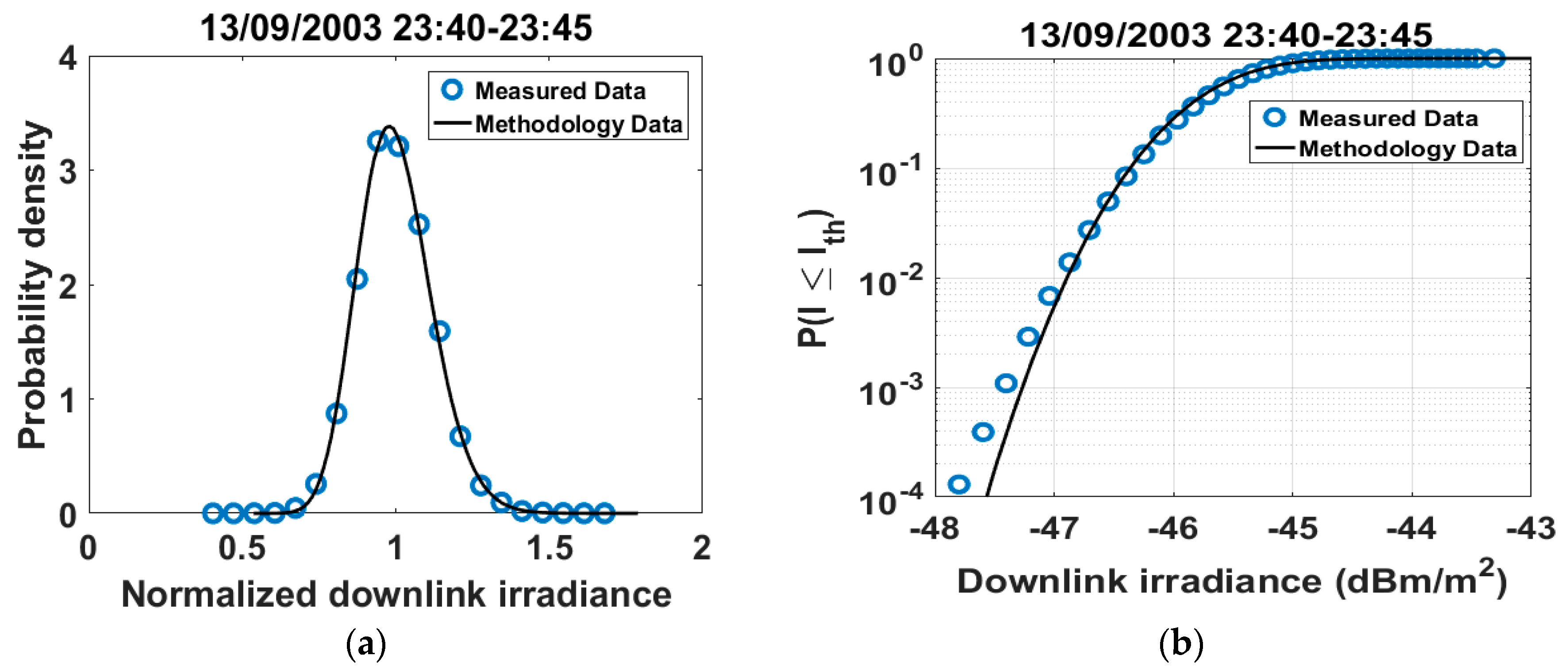
4.1. Validation with Experimental Data
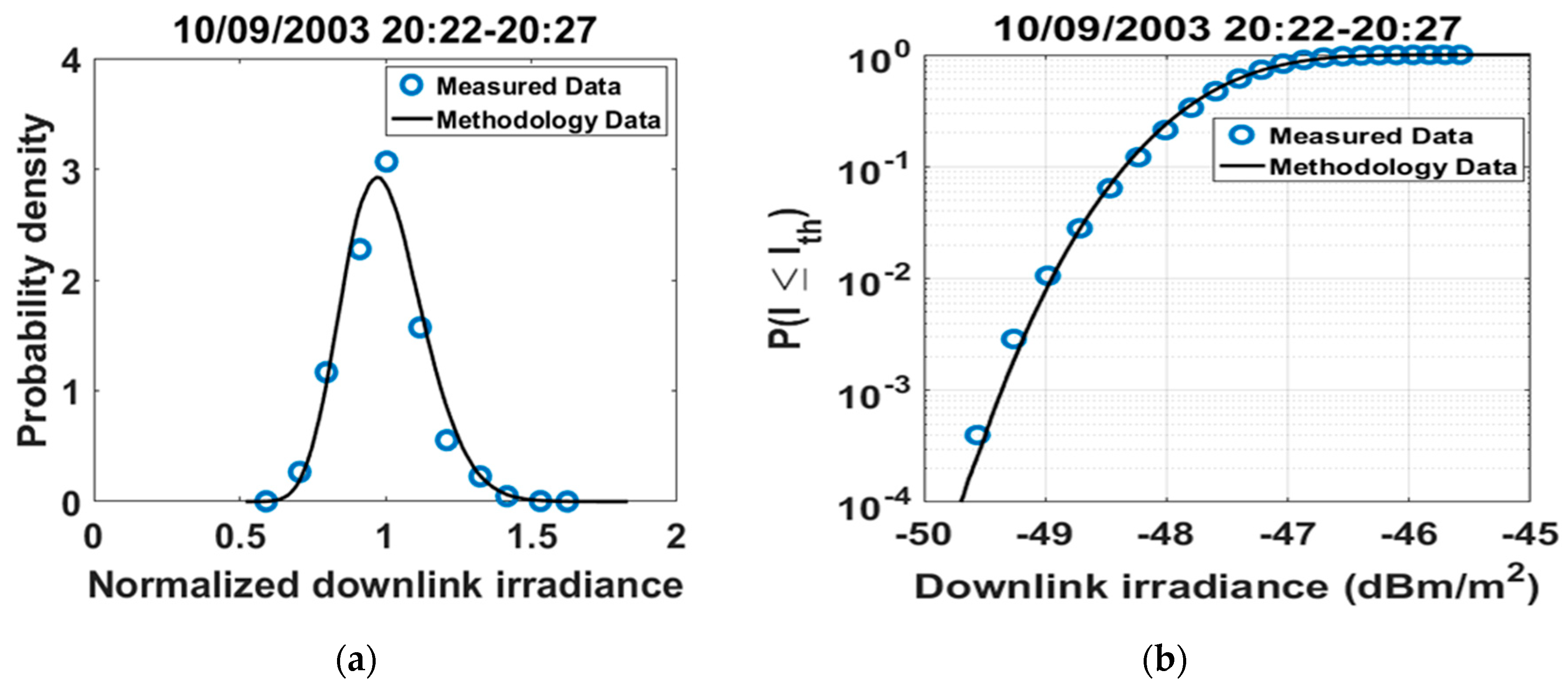
- Computation of the first order statistics, that is, normalized probability density function (PDF), cumulative distribution function (CDF) of the available data from ARTEMIS optical experiments. For every session the SI is also calculated.
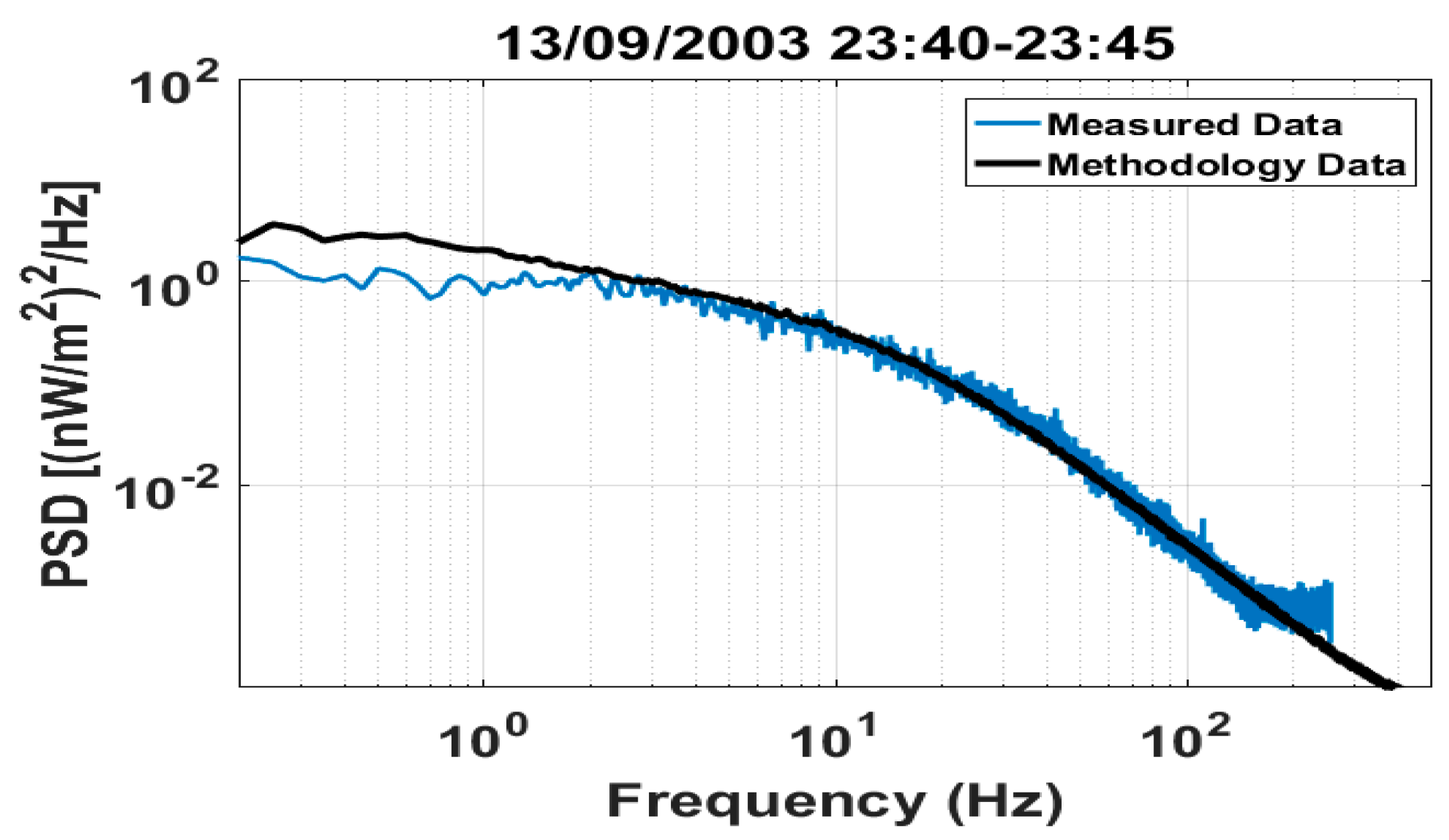
- Computation of the second order statistics, that is, power spectral density (PSD) of the available experimental data.
- Generation of received irradiance time-series using the proposed methodology. The model inputs are the ARTEMIS coordinates and transmitting settings given by Table 1 and Table 2, the refractive index structure parameter at ground level A0 which was kept fixed at a value of due to the fact that the sessions took place at night, the session’s ground wind speed which was provided by the nearby installed weather station and the aperture averaging factor where is the LUCE’s diameter. The is estimated close to 0.1 using (9).
- Computation of normalized PDF, CDF and PSD of the synthesized data and the corresponding SIs.
- Comparison of the derived numerical results with the respective experimental results and examination of possible discrepancies.
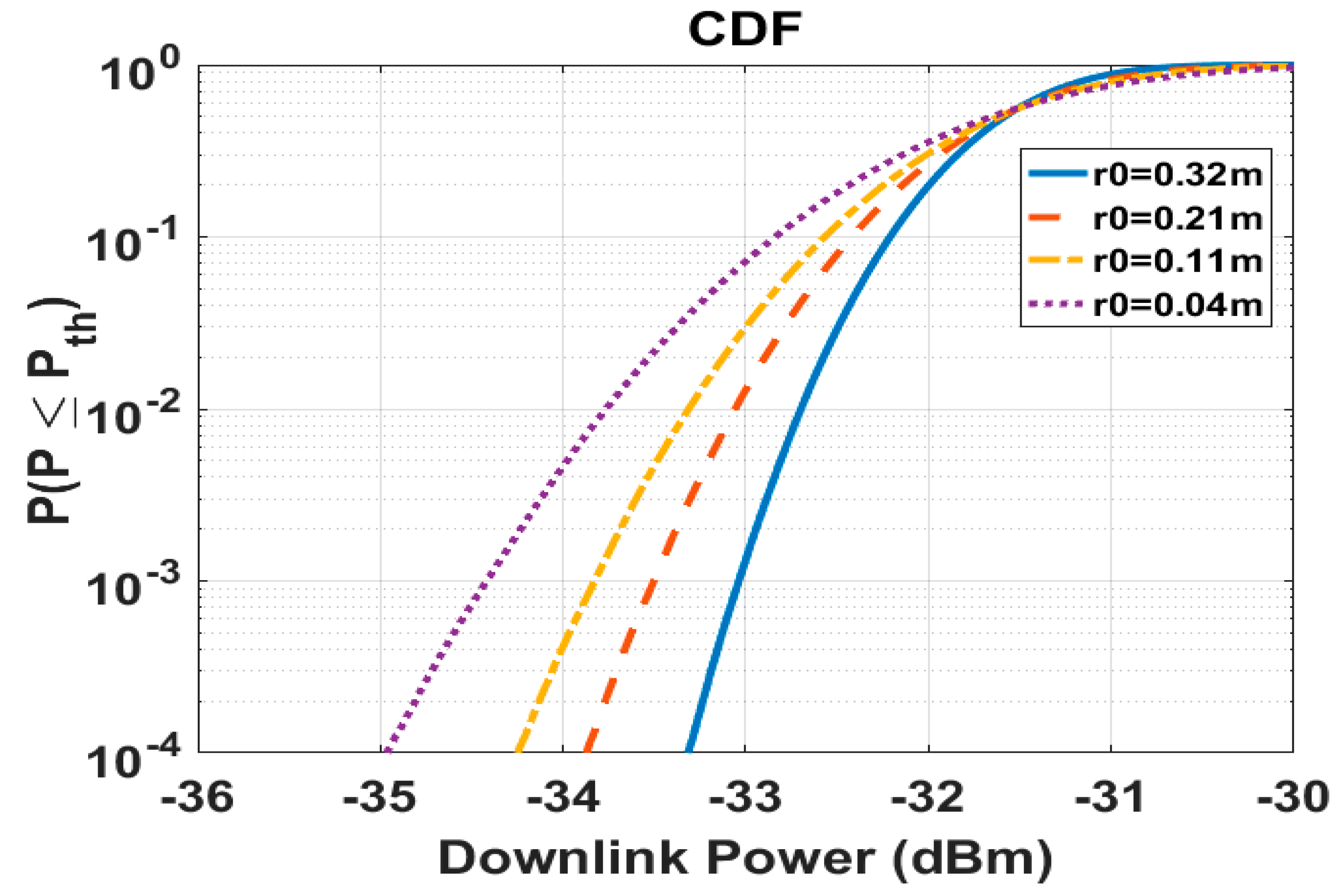
4.2. Long-term Received Power
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Illi, E.; El Bouanani, F.; Ayoub, F. A Performance Study of a Hybrid 5G RF/FSO Transmission System. In Proceedings of the 2017 International Conference on Wireless Networks and Mobile Communications (WINCOM), Rabat, Morocco, 1–4 November 2017. [Google Scholar]
- Leitgeb, E. Future Applications of Optical Wireless and Combination Scenarios with RF Technology. In Proceedings of the 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 22–26 May 2017. [Google Scholar]
- Jou, B.T.; Vidal, O.; Cahill, J.; Arnal, F.; Honssin, L.M.; Boutin, M.; Chau, D.K. Architecture Options for Satellite Integration into 5G Networks. In Proceedings of the 2018 European Conference on Networks and Communications (EuCNC), Ljubljana, Slovenia, 18–21 June 2018. [Google Scholar]
- Sharma, S.K.; Chatzinotas, S.; Arapoglou, P.D. Satellite Communications in the 5G Era, 1st ed.; The Institution of Engineering and Technology: London, UK, 2018. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Comm. Surv. Tutor. 2016, 19, 57–96. [Google Scholar] [CrossRef]
- Hemmati, H. Near-Earth Laser Communications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Lyras, N.K.; Kourogiorgas, C.I.; Panagopoulos, A.D. Cloud Attenuation Statistics Prediction From Ka-Band to Optical Frequencies: Integrated Liquid Water Content Field Synthesizer. IEEE Trans. Antennas Propag. 2017, 65, 319–328. [Google Scholar] [CrossRef]
- Lyras, Ν.Κ.; Kourogiorgas, C.I.; Panagopoulos, A.D. Cloud Free Line of Sight Prediction Modelling for Optical Satellite Communication Network. IEEE Commun. Lett. 2017, 21, 1537–1540. [Google Scholar] [CrossRef]
- Kourogiorgas, C.I.; Lyras, N.; Panagopoulos, A.D.; Tarchi, D.; Vanelli-Coralli, A.; Ugolini, A.; Colavolpe, G.; Arapoglou, P.D. Capacity Statistics Evaluation for Next Generation Broadband MEO Satellite Systems. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2344–2358. [Google Scholar] [CrossRef]
- Lyras, N.K.; Efrem, C.N.; Kourogiorgas, C.I.; Panagopoulos, A.D. Optimum Monthly-Based Selection of Ground Stations for Optical Satellite Networks. IEEE Commun. Lett. 2018, 22, 1192–1195. [Google Scholar] [CrossRef]
- Andrews, L.; Phillips, R. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Kolev, D.R.; Toyoshima, M. Received-Power Fluctuation Analysis for LEO Satellite-to-Ground Laser Links. J. Lightwave Technol. 2017, 35, 103–112. [Google Scholar] [CrossRef]
- Alonso, A.; Reyes, M.; Sodnik, Z. Performance of satellite-to-ground communications link between ARTEMIS and the Optical Ground Station. Proc. SPIE Opt. Atmos. Propag. Adapt. Syst. VII 2004, 5572, 372–384. [Google Scholar]
- Toyoshima, M.; Yamakawa, S.; Yamawaki, T.; Arai, K.; García-Talavera, M.R.; Alonso, A.; Sodnik, Z.; Demelenne, B. Long-term statistics of laser beam propagation in an optical ground-to-geostationary satellite communications link. IEEE Trans. Antennas Propag. 2005, 53, 842–850. [Google Scholar] [CrossRef]
- Kapsis, T.T.; Lyras, N.K.; Panagopoulos, A.D. Long Term Irradiance Statistics for Optical GEO Downlinks: Validation with ARTEMIS Experimental Measurements. Prog. Electromagn. Res. 2019, 82, 89–94. [Google Scholar] [CrossRef]
- Calvo, R.M.; Becker, P.; Giggenbach, D.; Moll, F.; Schwarzer, M.; Hinz, M.; Sodni, Z. Transmitter diversity verification on ARTEMIS geostationary satellite. Proc. SPIE Free-Space Laser Commun. Atmos. Propag. 2014, 8971, 897104. [Google Scholar]
- Yura, H.T.; McKinley, W.G. Aperture averaging of scintillation for space-to-ground optical communications. Appl. Opt. 1983, 22, 1608–1609. [Google Scholar] [CrossRef] [PubMed]
- Kolev, D.R.; Toyoshima, M. Satellite-to-ground optical communications using small optical transponder (SOTA)–received-power fluctuations. Opt. Express 2017, 25, 28319–28329. [Google Scholar] [CrossRef]
- Reyes, M.; Comeron, A.; Alonso, A.; Rodriguez, A.; Rubio, J.A.; Dios, V.F.; Chueca, S.; Sodnik, Z. Ground-to-satellite bidirectional laser links for validation of atmospheric turbulence model. Proc. SPIE Free Space Laser Commun. Act. Laser Illum. III 2003, 5160, 44–55. [Google Scholar]
- Shao, Y. The Fractional Ornstein-Uhlenbeck Process as a Representation of Homogeneous Eulerian Velocity Turbulence. Physica D 1995, 83, 461–477. [Google Scholar] [CrossRef]
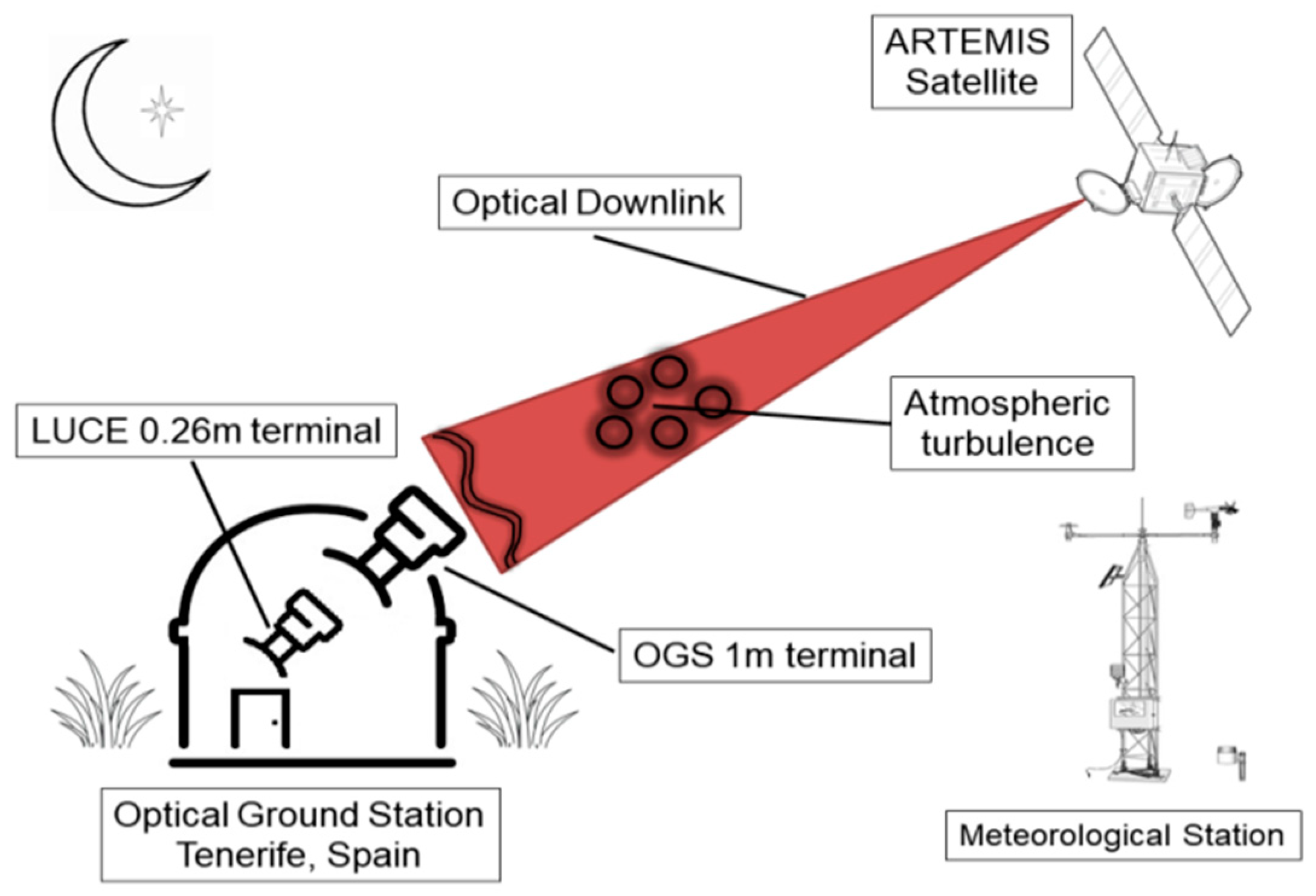



| Longitude | Latitude | Altitude | Elevation Angle |
|---|---|---|---|
| 21.5° East | 0.0° ± 2.81° North | 35,787 km | 37° |
| Wavelength | Beam Diameter (1/e2) | Transmitted Power |
|---|---|---|
| 819 nm | 125 mm | 10 mW |
| Session Date | Wind Speed on Ground (m/s) | Methodology Scintillation Index | Measured Scintillation Index |
|---|---|---|---|
| 13/09/2003 23h30 | 0.3 | 0.0142 | 0.0140 |
| 16/09/2003 21h10 | 2.8 | 0.0170 | 0.0164 |
| 10/09/2003 20h10 | 4.3 | 0.0190 | 0.0183 |
| Vg (m/s) | A0 | r0 (m) | SIpoint |
|---|---|---|---|
| 0 | 0.32 | 0.126 | |
| 8 | 0.21 | 0.215 | |
| 12 | 0.11 | 0.302 | |
| 12 | 0.04 | 0.459 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapsis, T.T.; Lyras, N.K.; Kourogiorgas, C.I.; Panagopoulos, A.D. Time Series Irradiance Synthesizer for Optical GEO Satellite Downlinks in 5G Networks. Future Internet 2019, 11, 131. https://doi.org/10.3390/fi11060131
Kapsis TT, Lyras NK, Kourogiorgas CI, Panagopoulos AD. Time Series Irradiance Synthesizer for Optical GEO Satellite Downlinks in 5G Networks. Future Internet. 2019; 11(6):131. https://doi.org/10.3390/fi11060131
Chicago/Turabian StyleKapsis, Theodore T., Nikolaos K. Lyras, Charilaos I. Kourogiorgas, and Athanasios D. Panagopoulos. 2019. "Time Series Irradiance Synthesizer for Optical GEO Satellite Downlinks in 5G Networks" Future Internet 11, no. 6: 131. https://doi.org/10.3390/fi11060131
APA StyleKapsis, T. T., Lyras, N. K., Kourogiorgas, C. I., & Panagopoulos, A. D. (2019). Time Series Irradiance Synthesizer for Optical GEO Satellite Downlinks in 5G Networks. Future Internet, 11(6), 131. https://doi.org/10.3390/fi11060131






