1. Introduction
In recent years, volunteer computing (VC) [
1] has supported diverse large-scale scientific research applications using idle resources from a large number of heterogeneous volunteer computers. VC provides not only almost free unlimited computing resources for scientific research projects, such as SETI@home [
2], Folding@home [
3], and ATLAS@Home [
4], but also opportunities for volunteers to participate in scientific research. At the same time, increasingly more researchers have extended the unlimited computing resources provided by VC to cloud computing [
5] and big data fields [
6]. The network structure of VC is a master-slave distributed network computing model [
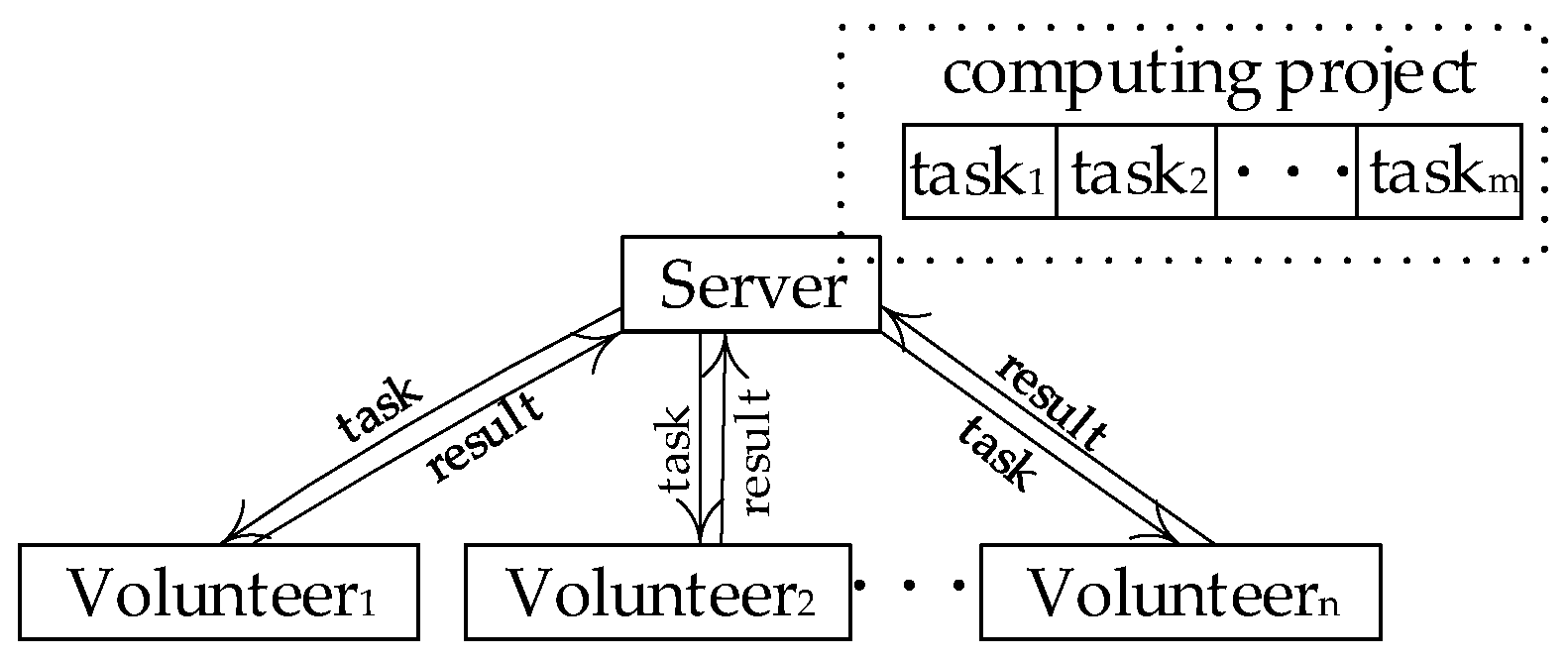
7], as shown in
Figure 1. The computers that provide resources are called volunteer nodes (VN), and the server is responsible for assigning tasks and collecting results.
In volunteer computing platforms, the computing power of VN is different. One of the challenges is to the algorithm of scheduling parallel tasks in such heterogeneous and dynamic platforms. At the same time, although studies have shown that assigning parallel tasks to multiple processors are NP-hard, because of its importance, many researchers have done lots of work for this problem [
8,
9,
10,
11]. However, these scheduling algorithms can’t be fully applied to volunteer computing, because VN may quit at any time without any responsibility.
Generally speaking, volunteer computing applications are so complex that they are divided into many tasks and assigned to volunteer nodes with a hard deadline constraint [
12]. If a task misses its deadline, the completion time of the whole project will be affected. For example, during the production of a chemical product, the delay of a certain ingredient will not only cause the waste of raw materials, but also postpone the delivery time. Therefore, the research on task scheduling with the deadline has great significance.
In addition, since there are not enough resources to complete all tasks in volunteer computing platforms, we mainly focus on the algorithm of completing as many tasks as possible before the deadline for each task. Similarly, Salehi et al. proposed a maximum on-time completions (MOC) [
13] algorithm for task scheduling with deadline constraint for heterogeneous distributed platforms. In the MOC algorithm, a stochastic robustness measure is defined to assign tasks, and the algorithm discards tasks that miss their deadlines to maximize the number of the completed tasks. However, the MOC algorithm cannot be fully applied to the volunteer computing platform, because it does not consider suddenly offline nodes. Therefore, it is indispensable to study the dynamic task scheduling for VC platforms.
To tackle the aforementioned problems, this paper proposes two novel dynamic task scheduling algorithms with deadline constraint in heterogeneous VC platforms. To the best of our knowledge, it is the first attempt to study dynamic task scheduling with deadline constraint in the volunteer computing platform. The main contributions of this paper are summarized as follows:
- (1)
A formal definition of the task assignment problem with deadline constraint in heterogeneous VC platforms for the first time.
- (2)
A basic deadline preference dispatch scheduling algorithm (DPDS) that can guarantee the task with minimum deadline constraint will be computed first, a match function to select the most suitable VN in task assignment, and an improved dispatch constraint scheduling algorithm (IDCS) that selects tasks according to their priorities and utilizes a risk prediction model to improve the execution efficiency of the application.
- (3)
A comprehensive evaluation of the proposed algorithms and a comparison with existing algorithms.
The remainder of this paper is organized as follows: The next section presents the related work.
Section 3 introduces the definition of the problems.
Section 4 illustrates our task scheduling algorithms.
Section 5 gives the experimental results and analysis of the proposed task scheduling algorithms.
Section 6 concludes this paper.
3. Problem Description
This paper studies the dynamic task allocation method with deadline constraint in the volunteer computing platforms. The notations used in the paper are summarized in
Table 1.
Given a number of tasks in VC platforms, denoted by the set T = {t1, t2, …, tm}. Suppose that each task ti can be completed by any node nj or several other nodes in the VC platforms. For easy expression, two unified concepts are first introduced in the VC platforms. The server hour means the unit time of the server. One unit means the number of tasks completed within one server hour.
The concepts of task and node are given as follows:
Definition 1 (task).Task ti is a double dimension array that is denoted by (ti.cost,ti.deadline). The unit of ti.cost is called server hour, meaning that ti can be finished on the server for ti.cost hours; ti.deadline means the constraint of task ti, whose unit is hours. If the task ti begins at time l1, the deadline constraint of task ti means that task ti must be completed before l1 + ti.deadline.
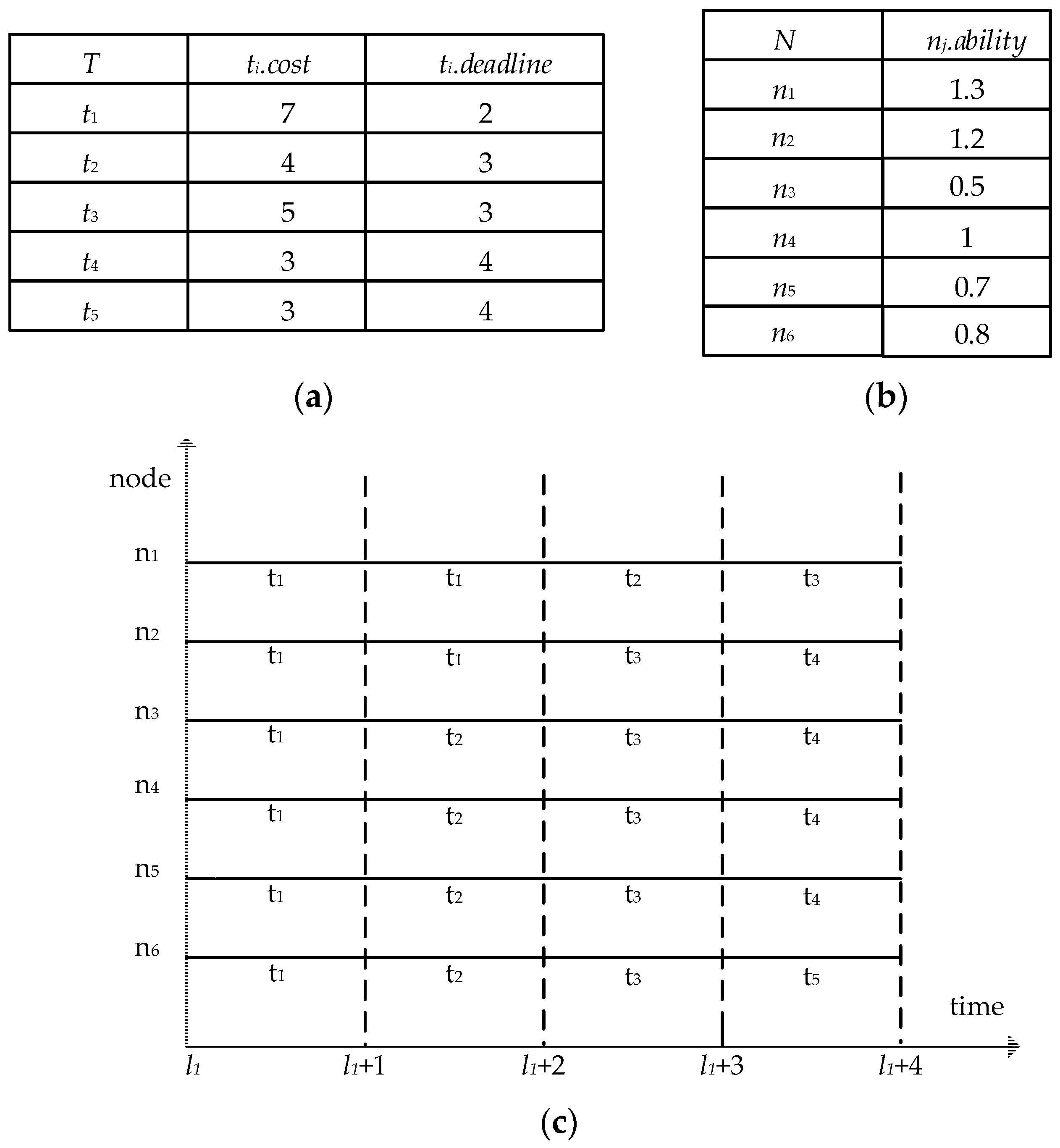
For example, as shown in
Figure 2a,
t3.cost = 5, which means that it will take five server hours to complete the task
t3. If the deadline constraint of task
t3 is three hours and begins at time
l1, it means that task
t3 must be finished before
l1 + 3.
Definition 2 (node).Given a volunteer node set, denoted by the set N = {n1, n, …, nj}, the computing power of each volunteer node nj is denoted by nj.ablitlity, it means that the number of tasks the node nj can complete in an hour is nj. ability units.
For example, as shown in
Figure 2b,
n1. ability = 1.3, which means that the volunteer node
n1 can complete the number of tasks in an hour is 1.3 times unit.
A dynamic task scheduling with deadline constraint at l1 moment can be denoted by ti. assign = {(n1, t1, l1), (n2, t1, l1), … (ns, t1, l1)}.
List of tasks at time
l1 is shown in
Figure 2a, List of volunteer nodes at time
l1 is shown in
Figure 2b and the task allocation process is shown in
Figure 2c. Task
t1 is taken as an example: The server starts to allocate computing resource to the task
t1 at the initial time
l1 and the task
t1’s allocation is denoted by
t1.assign = {(
n1,
t1,
l1), (
n2,
t1,
l1), (
n3,
t1,
l1), (
n4,
t1,
l1), (
n5,
t1,
l1), (
n6,
t1,
l1), (
n1,
t1,
l1 + 1), (
n2,
t1,
l1 + 1)}.
The calculation cost of
t1 is seven units and
n1 is scheduled to complete two-hour task
t1 by the server. It is known that the number of tasks
n1 can complete in an hour is 1.3 times unit. So,
n1 can complete 2.6 units in two hours. By analogy, the total computing resources allocated to
t1 can complete a total of eight units, which are more than seven units of
t1. Furthermore, because the deadline constraint of
t1 is two hours, so,
t1 can be completed. Similarly, the computing resources allocated to
t2 is
t2.assign = {(
n3,
t2,
l1 + 1), (
n4,
t2,
l1 + 1), (
n5,
t2,
l1 + 1), (
n6,
t2,
l1 + 1), (
n1,
t2,
l1 + 2)}. The calculation cost of
t2 is four units, and the deadline constraint of
t2 is three hours, so
t2 can be completed. The computing resources allocated to
t3 is
t3.
assign = {(
n2,
t3,
l1 + 2), (
n3,
t3,
l1 + 2), (
n4,
t3,
l1 + 2), (
n5,
t3,
l1 + 2), (
n6,
t3,
l1 + 2), (
n1,
t3,
l1 + 3)}. The calculation cost of
t3 is five units and the deadline constraint of
t3 is three hours. The deadline constraint of
t3 cannot be satisfied, therefore
t3 cannot be completed. By analogy, it can be concluded that
t4 can be completed and
t5 cannot be completed. Finally, according to the task allocation of
Figure 2c, the tasks that can be completed before deadline constraint are
t1,
t2 and
t4.
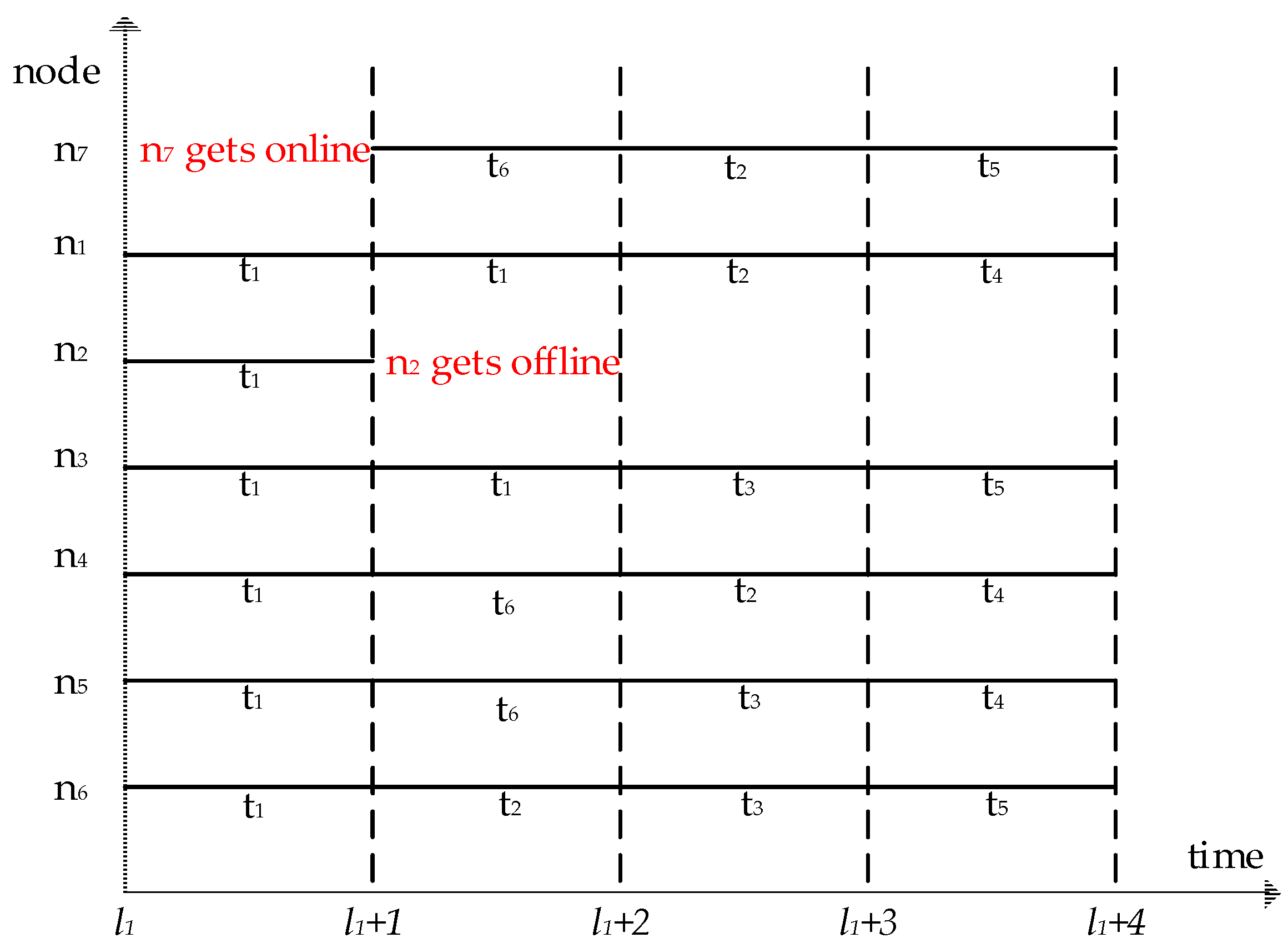
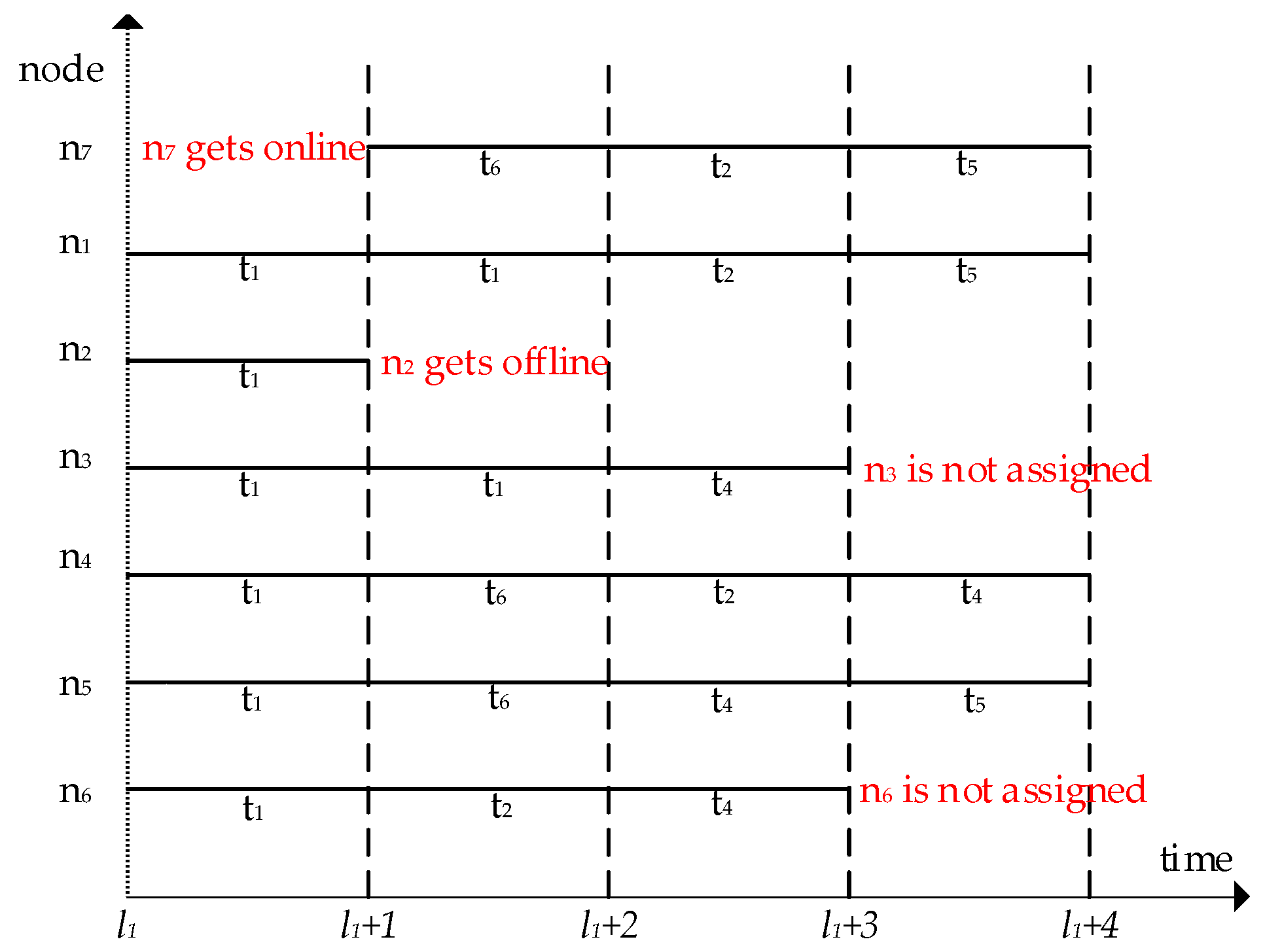
In a dynamic network environment, the volunteer nodes are updated hourly. List of tasks at time
l1 + 1 is shown in
Figure 3a, and the list of volunteer nodes at time
l1 + 1 is shown in
Figure 3b. At time
l1 + 1, the node
n2 goes offline, the node
n7 goes online. Obviously, the task assignment process in
Figure 2c cannot meet the requirements of dynamics, so it is necessary to design a corresponding dynamic task assignment algorithm. The task scheduling algorithm of this paper will be described in the following section.
In VC platforms, the set of volunteer nodes and task sets are updated dynamically over time. In this paper, the objective of the task allocation is to solve the dynamic task scheduling problem and maximize the number of completed tasks before deadline constraint.
4. Algorithm Description
In this section, we introduce the DPDS algorithm and the IDCS algorithm in detail.
4.1. The Deadline Preference Dispatch Scheduling (DPDS) Algorithm
The DPDS algorithm is a dynamic task scheduling algorithm based on deadline constraint priority. Firstly, the DPDS algorithm sorts the tasks in ascending order according to their deadline and sorts the VN in descending order according to their computing power. Secondly, the DPDS algorithm adopts a matching function to select the most suitable volunteer node to assign a task, which make the computing resource will be freed in the least possible amount of time. Consequently, the DPDS algorithm can ensure that the task with nearest deadline constraint is completed first, and free computing resource in the least possible amount of time. The DPDS algorithm is described in detail in Algorithm 1.
Significantly, in the DPDS algorithm, we use a monitoring mechanism, which is triggered to meet the following two conditions simultaneously.
| Algorithm 1. The DPDS Algorithm Taskassign(Tl,Nl,l) |
| Input: task set Tl, volunteer nod set Nl, the current time l |
| Output: final task assignment set T.assign. |
Wait until the monitoring mechanism is trigged T.assign = ∅ Sort Tl in ascending order according to the task’s deadline at time l Sort Nl in descending order according to the node’s computing power at time l WhileTl ≠ ∅ do Take the first task from Tl to t’ Call the match(t’, Nl, l) // select the most suitable volunteer node to t’ Delete t’ from Tl T.assign = T.assign + t’.assign End While ReturnT.assign
|
If the monitoring mechanism is triggered, to make full use of the computing resources provided by the idle VN, we adopt the match function to select the suitable VN that wastes the least amount of computing resources in the DPDS algorithm. The match function is described in detail in Algorithm 2.
For example, the list of tasks at time l
1 is shown in
Figure 2a and list of volunteer nodes at time l
1 is shown in
Figure 2b. According to the first to fourth lines of Algorithm 1, at time
l1, T
l = {
t1,
t2,
t3,
t4,
t5}, N
l = {
n1,
n2,
n4,
n6,
n5,
n3}. Take
t1 as an example, according to the sixth line of Algorithm 1, it can be seen that t
1 is allocated first. According to Algorithm 2, at time
l1,
t1.assign = {(
n1, t1, l1), (
n2, t1, l1), (
n3, t1, l1), (
n4, t1, l1), (
n5, t1, l1), (
n6, t1, l1)}. As can be seen from the task assignment above, there is still 1.5 units left in task
t1, which needs to be allocated at time
l1 + 1. At time
l1 + 1, both the task list and the node list are updated, which are shown in
Figure 3a and
Figure 3b, so the monitoring mechanism is triggered. According to the first to fourth lines of Algorithm 1, at time
l1 + 1, T
l = {
t1, t6, t2, t3, t4, t5}, N
l = {
n1, n4, n7, n6, n5, n3}. According to the sixth line of Algorithm 1, it can be seen that
t1 is allocated first. According to Algorithm 2, at time
l1 + 1,
t1.assign = {(
n1, t1, l1 + 1), (
n3, t1, l1 + 1) }. By analogy, we assume that tasks and nodes are updated only at time
l1 + 1, so the rest of the task assignments are shown in
Figure 4.
Figure 4 shows
t3 and
t5 cannot be completed within the deadline.
| Algorithm 2. The Match(t’, Nl, l) |
| Input: the task t’, volunteer node set Nl, the current time l |
| Output: task assignment set t’.assign |
Initialize t’.assign = ∅; t’.remain = t’.cost; t’.hasassign = 0 total_ability = the total computing power of the set Nl at time l Whilet’.remain>0&&t’.deadline<ldo // t’.remain indicates the remaining unallocated workload of t’ If t’.remain >= total_ability For each node n’ in Nl do add < n’, t’, l > to t’.assign Delete n’ from Nl End For t’.remain = t’.remain- total_ability L = l + 1 // all nodes have been assigned to calculate t’ at time l Reset Nl // node set at time l + 1 Else j = 1 While the jth node n’ in Nl is not null do If n’.ability <= t’.remain add < n’, t’, l > to t’. assign Delete n’ from Nl t’.remain = t’.remain-n’.ability; ElseIf t’.remain == 0 t’.cost = 0 Return t’.assign Else While n’.ability >= t’.remain&&n’ is not null do j = j + 1 n’ = the jth node in Nl Endwhile n’ = the (j − 1)th node in Nl add < n’, t’, l > to t’.assign Delete n’ from Nl t’.cost = t’.remain = 0; EndIf EndWhile EndIf EndWhile Returnt’.assign
|
4.2. The Improved Dispatch Constrain Scheduling (IDCS) Algorithm
The DPDS algorithm is a deadline priority allocation method, which can ensure that the most urgent tasks are given the highest priority in dynamic allocation. However, it cannot guarantee the largest number of tasks to be completed. And we find that the task cannot be completed within deadline constraint is still assigned, which causes a waste of computing resources. On this basis, this paper proposes an improved IDCS algorithm. The IDCS algorithm uses a risk prediction model to reduce the waste of computing resources. Before introducing the IDCS algorithm, we introduce the risk prediction model firstly.
4.2.1. The Risk Prediction Model
In this paper, we propose a risk prediction model that can predict the completion risk of each task, which is described in Algorithm 3. In VC platforms, VN is constantly updated at every moment. Although, it is impossible to accurately determine the number of updated nodes and their computing power, the range of the number of possible online nodes at each time can be estimated based on historical data. For easy calculation, we assume that the computing power of all predicted online VN is 1 unit, and the probability of the number of possible VN at each time is the same. On this basis, we calculate the completion risk of each task by completion probability. We will introduce the definition of the completion probability below.
Definition 3 (Completion probability).Given a possible world [30] set W and a task t’ at time l, the completion probability of t’ at time l is defined as follows:where w represents a possible world in a possible world set W, W’ is a possible world set which is composed of a possible world that can complete t’ within the deadline, and Pr(w) represents the possible probability of w. | Algorithm 3. The Risk Prediction Model Risk(t,W,l) |
| Input: the task t, possible world set W, the current time l |
| Output: the completion risk R of the task t |
l’ = t.deadline W = possible world set from time l to time l′ Prl(t) = 0 For each w ∈ W do If t can be completed by w Prl(t) = Prl(t) + Pr(w) EndIf EndFor R = 1 − Prl(t) Return completion riskR of the task t
|
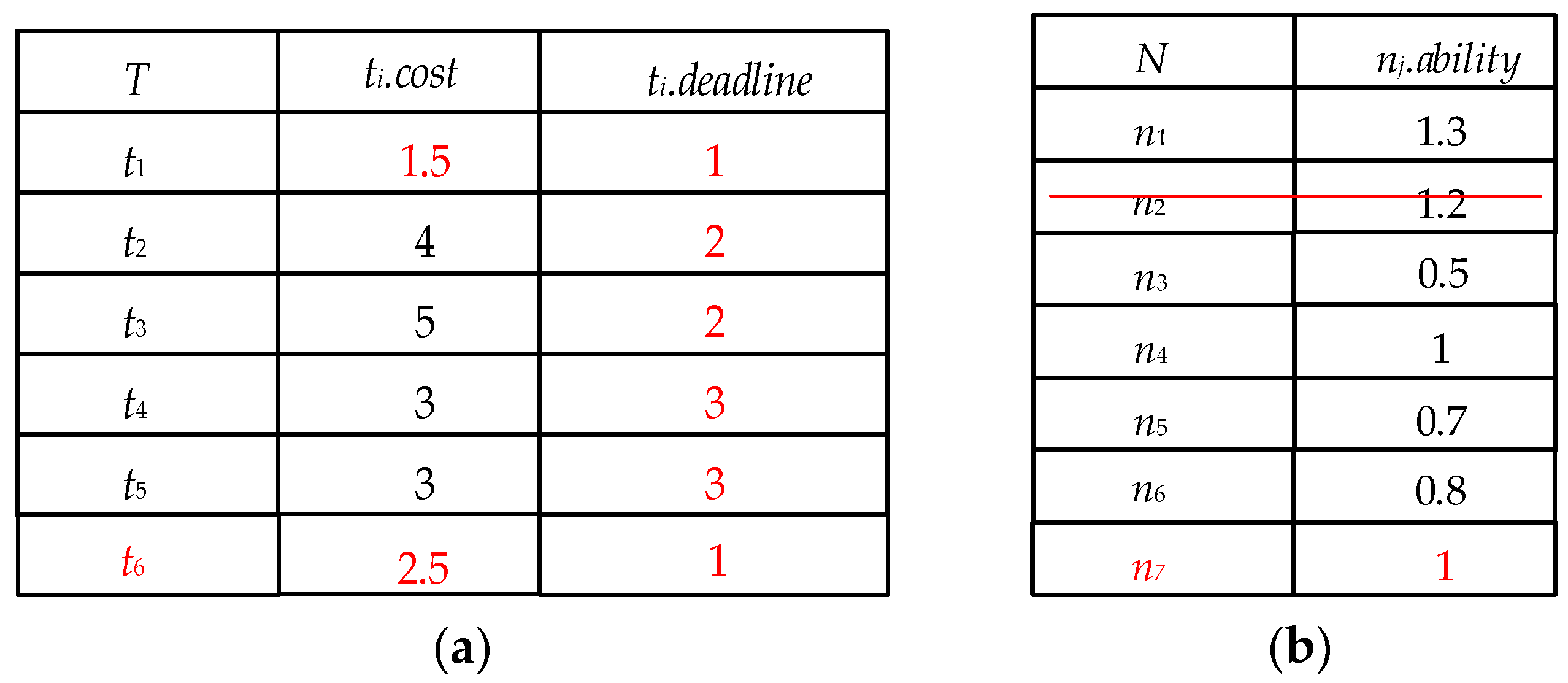
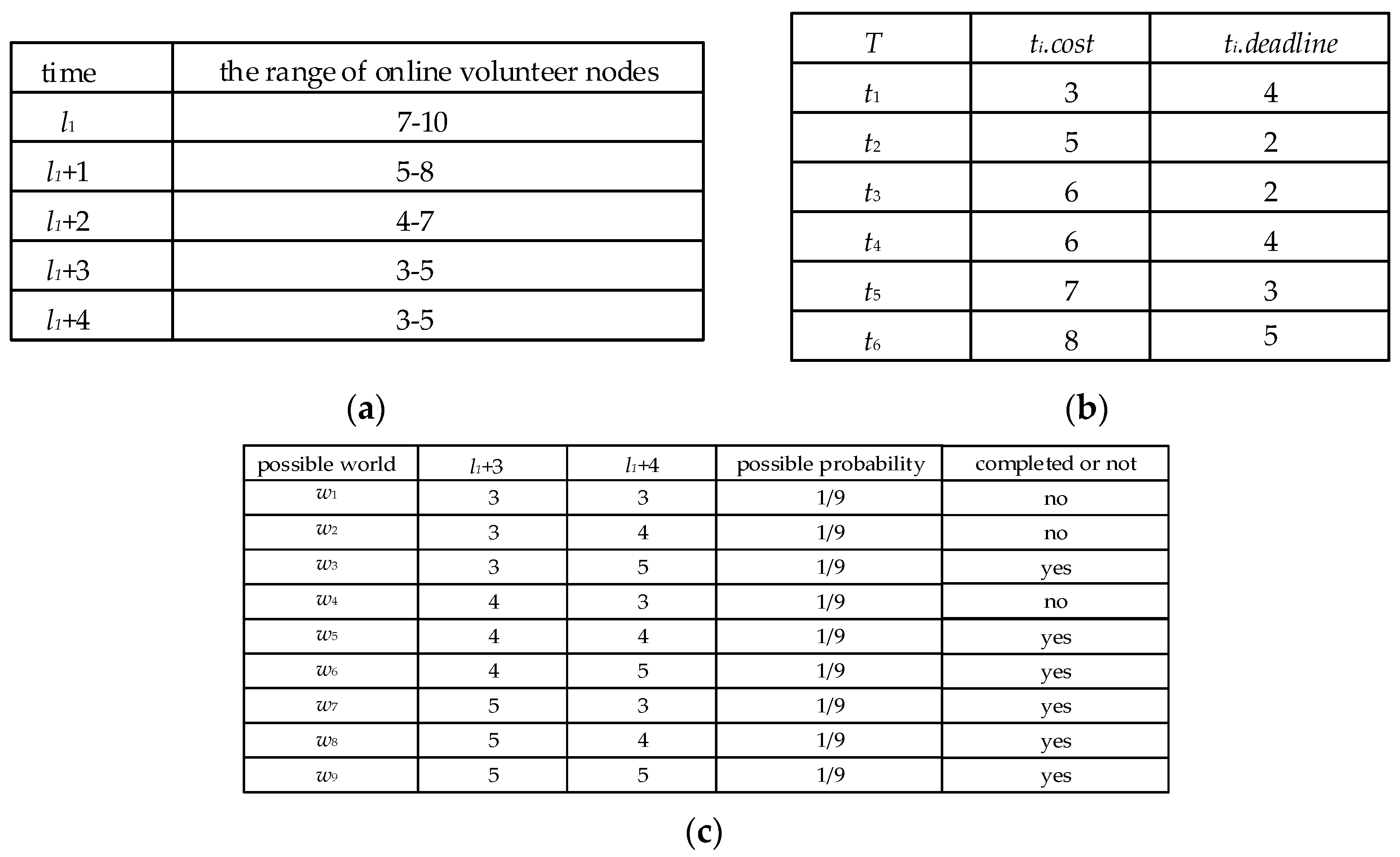
For example, at time
l1, the task
t6 is allocated at time
l1 + 3, and the deadline of
t6 is
l1 + 4.
Figure 5a shows that the number of possible VN at time
l1 + 3 is 3, 4, and 5, and the number of possible VN at time
l1 + 4 is 3, 4, and 5. The possible world set
W of
t6 is shown in
Figure 5c. The
completion probability Pr
l1(
t6) of
t6 is 66.7%, which is calculated by Equation (1), so the
completion risk of the task
t6 is 33.3%.
4.2.2. The Description of the IDCS Algorithm
The IDCS algorithm is a dynamic allocation method based on the objective of maximizing the number of tasks completed. To achieve the objective of completing the maximum number of tasks with limited computing resources, the IDCS algorithm chooses the task to assign based on task priority and completion risk of the task.
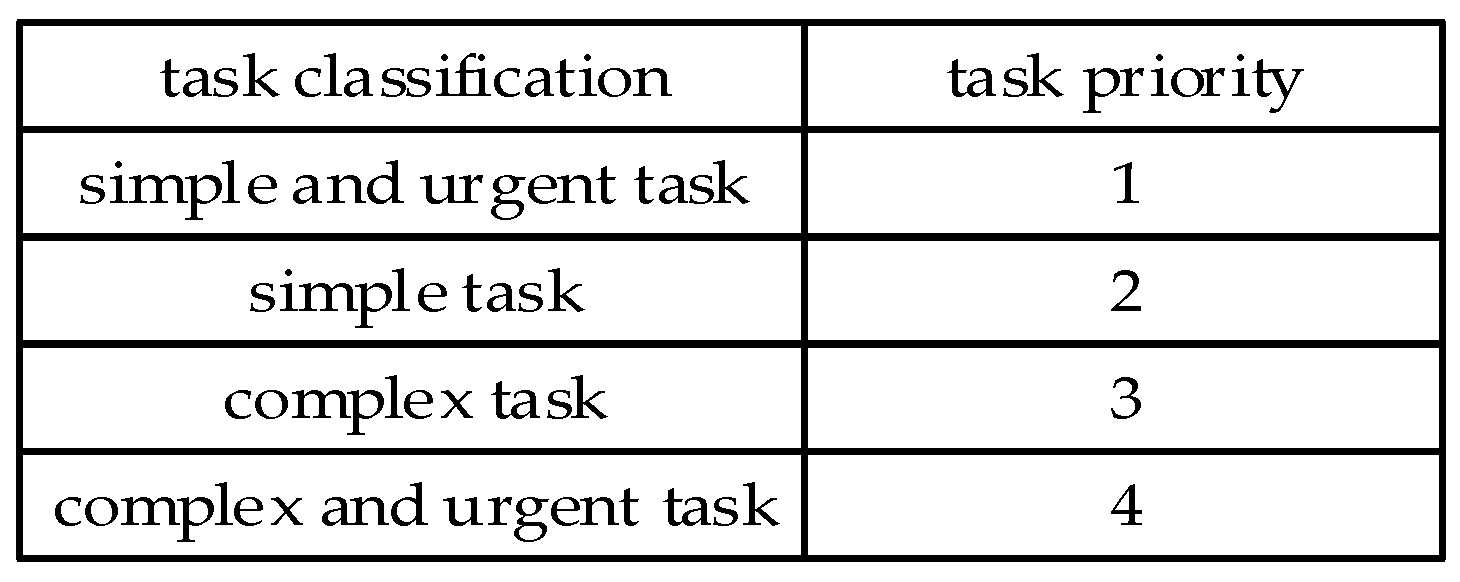
Task partitioning is divided into simple and urgent tasks, simple tasks, complex tasks and complex and urgent tasks according to their computational cost and the size of deadline constraints, which correspond to different
task priority, as shown in
Figure 6.
The specific ways of division are as follows:
If the computational cost of task t is less than the average computational cost of all tasks in the task list, and t. deadline is less than the middle time of the whole computing time, it is considered that the task t is simple and urgent, and the task priority corresponding to t is 1. If the computational cost of the task t is less than the average computational cost of all tasks in the task list, and t. deadline is greater than the middle time of the whole computing time, it is considered that task t is a simple task, and the task priority corresponding to t is 2. If the computational cost of task t is greater than the average computational cost of all tasks in the task list and t. deadline is greater than the middle time of the whole computing time, it is considered that t is a complex task, and the task priority corresponding to t is 3. If the computational cost of task t is greater than the average computational cost of all tasks in the task list, and t. deadline is less than the middle time of the whole computing time, it is considered that task t is complex and urgent, and the task priority corresponding to t is 4.
For example, as shown in
Figure 5b, the average computational cost of all tasks is 5.8 and the middle time of the whole computing time is 2.5. Therefore, according to the division criteria mentioned above, the task
t1 is a simple task and the
task priority of
t1 is 2. The task
t2 is a simple and urgent task, and the
task priority of
t2 is 1. The task
t3 is a complex and urgent task, and the
task priority of
t3 is 4. The task
t4,
t5,
t6 are complex tasks, and their
task priority is 3.
In the IDCS algorithm, firstly, the task priority and the completion risk are calculated as described above. Secondly, the IDCS algorithm deletes tasks that cannot be completed based on task priority and completion risk. Finally, Algorithm 1 is called to allocate tasks. The IDCS algorithm is described in detail in Algorithm 4.
| Algorithm 4. The IDCS Algorithm |
| Input: task set Tl, volunteer node set Nl, threshold θ, the current time l, possible world W |
| Output: task assignment set T.assign. |
Calculate the task priority and the completion risk of each task in Tl For each t’ ∈ Tl do If Risk(t’,W,l)> θ&& (task priority of t’ = 4 or task priority of t’ = 3 ) Delete the task t’ from Tl EndIf End For Call taskassign(Tl, Nl, l)// call Algorithm 1 ReturnT.assign
|
For example, the list of tasks at time
l1 is shown in
Figure 2a, and the list of volunteer nodes at time
l1 is shown in
Figure 2b. List of tasks at time
l1 + 1 is shown in
Figure 3a, and the list of volunteer nodes at time
l1 + 1 is shown in
Figure 3b. For the easy calculation, we assume that the nodes and tasks are not updated at other times, and the value of
θ is 0.5. The
completion risk of
t3 is 0.67 according to Algorithm 3, which is assigned at time
l1 + 3. According to Algorithm 4,
t3 is deleted from the task set
Tl. According to Algorithm 1, the assignment of the remaining tasks is shown in
Figure 7. According to the task allocation of
Figure 7, the tasks can be completed within deadline constraint are
t1,
t2,
t4 and
t5.
Figure 7 shows that the IDCS algorithm can maximize the number of the completed tasks within deadline constraint.
5. Experimental Evaluation
In this section, we first implement the DPDS algorithm and the IDCS algorithm, and use static task set and dynamic task set to compare the performance between the MOC algorithm and our proposed algorithms. The volunteer computing used in the experiment consists of one master node and fifty volunteer nodes. All nodes are configured with Intel Core i7 4790 CPU@3.4GHZ, 8GB DDR3 memory, 1TB hard disk and Windows 10 operating system. To be closer to the real volunteer computing environment and meet the heterogeneity of volunteer computing, 10–20 threads are opened on each host to simulate volunteer nodes, thus, whose number will be between 500 and 1000. Task data fragmentation size is 64 MB, and the parameter nj.ability is tested by the server sending the applet to the node before assigning tasks.
Specifically, to achieve the heterogeneity of nodes, we use a program to specify different CPU cores for some specific threads. In this way, scheduling delays can be reduced by specifying the CPU core for some specific threads. Thus, the performance of some specific threads will be improved.
5.1. Experimental Results and Analysis of the Static Task Sets
In the experiment of the static task set, three common tasks are used: Word frequency statistics, inverted index and distributed Grep. The input files are the data and dump files provided by Wikipedia (the main contents are entries, templates, picture descriptions and basic meta-pages, etc.). We mainly consider the influence of three main parameters as follows:
The task set scale which is the number of tasks included in the task set T.
The average size of tasks in task set T is measured by the number of task input file fragments.
The average completion time of tasks in T.
We assume that the size of a task set fragment is 64 MB, the threshold
θ is 0.5 and the completion time of each task fragment is 70 s. The task amount of word frequency statistics for a fragment (unit) is 40 s, the task amount of inverted index for a fragment (unit) is 80 s, and the task amount of distributed Grep for a fragment (unit) is 120 s. The average completion time of the tasks in
T is 80 s, denoted by
L. For any task in
T,
t. deadline is a random value in the interval [0.5
L, 1.5
L].
Table 2 shows the default values and ranges of the main parameters.
Table 2 shows the default values and ranges of the main parameters.
In this paper, the number of the completed tasks is the primary performance index. In addition, this paper also uses the completion rate to measure the performance of the algorithm more comprehensively. The completion rate is defined as follows:
5.1.1. The Impact of Average Size of Tasks
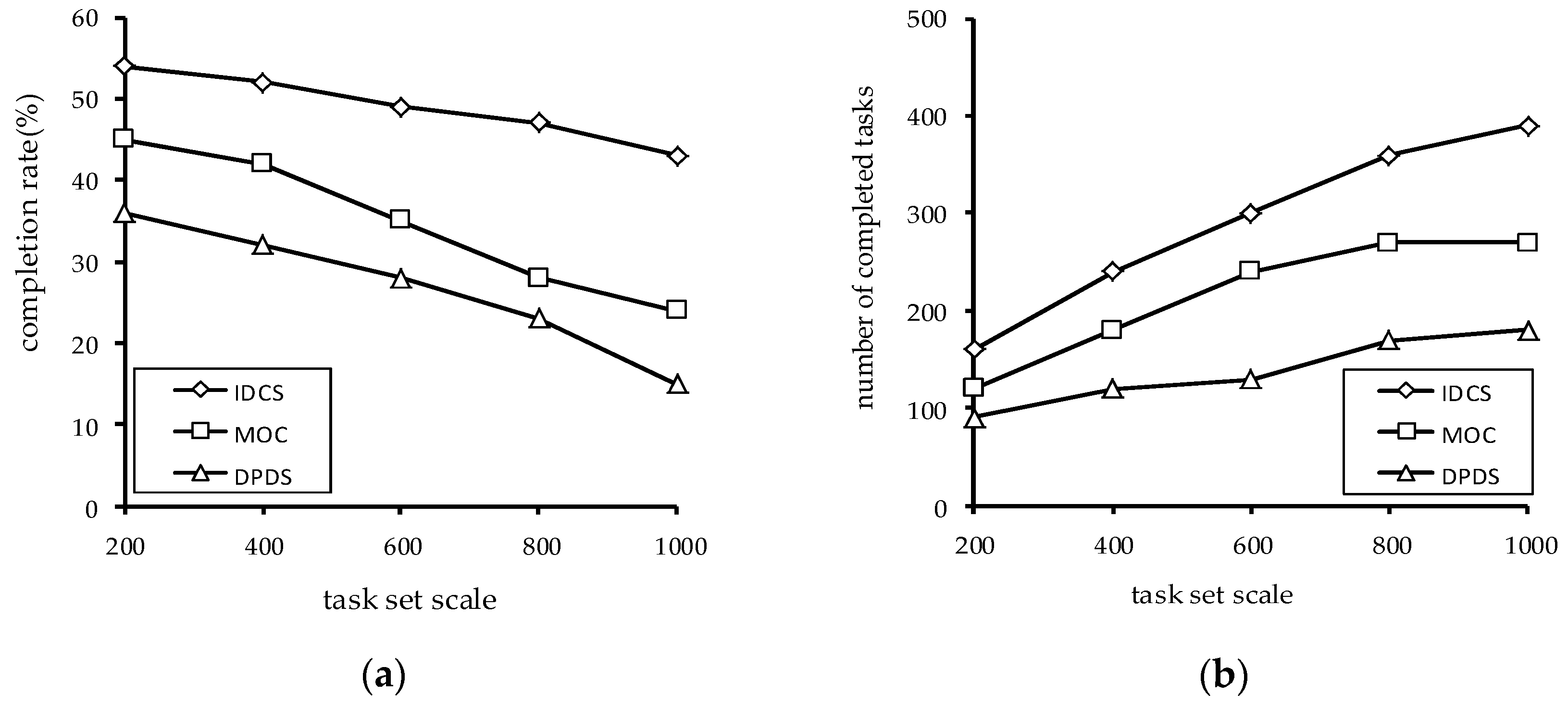
As shown in
Figure 8, we test the impact of the different average size of tasks on the performance of the algorithms. It can be seen that IDCS perform the best among the three algorithms in both the number of the completed tasks and completion rate, and the MOC algorithm is slightly worse than the IDCS algorithm. The DPDS algorithm is much less efficient. This is because the IDCS algorithm divides the task priority, which can ensure that the IDCS algorithm completes the less expensive task first, and discards the risky task. In contrast, the DPDS algorithm can’t fully utilize the computing power of the volunteer computing system. Even if it encounters the task that is expensive, the DPDS algorithm will also calculate it, which causes a waste of computing resources. Since the objective of MOC is complete each task before its deadline, it is less efficient than the IDCS algorithm. Moreover, since the computing power of the system is fixed in a certain period of time, the performance of three algorithms decreases as the average size of tasks increases.
5.1.2. The Impact of Task Set Scale
In
Figure 9, we analyze the impact of task set scale. It can be seen that with the increase of the task set scale, the number of the completed task of the three algorithms finally tends to be stable. This is because the number of nodes does not increase, but the number of tasks increases. Therefore, the number of the completed tasks by VN is changeless.
At the same time, it can be seen from
Figure 9b that the larger the size of the task set scale is, the more the number of tasks completed by the IDCS algorithm is. This is mainly because IDCS can make full use of computing resources to discards the tasks with high risks, which improves the number of tasks completed.
The task completion rate of the three algorithms decreases with the task set scale increase. This is because the number of tasks has increased, but there has been no relative increase in computing resources. In
Figure 9a, it is obvious that the increase of task set scale has the least impact on IDCS algorithm.
5.1.3. The Impact of the Number of Volunteer Nodes
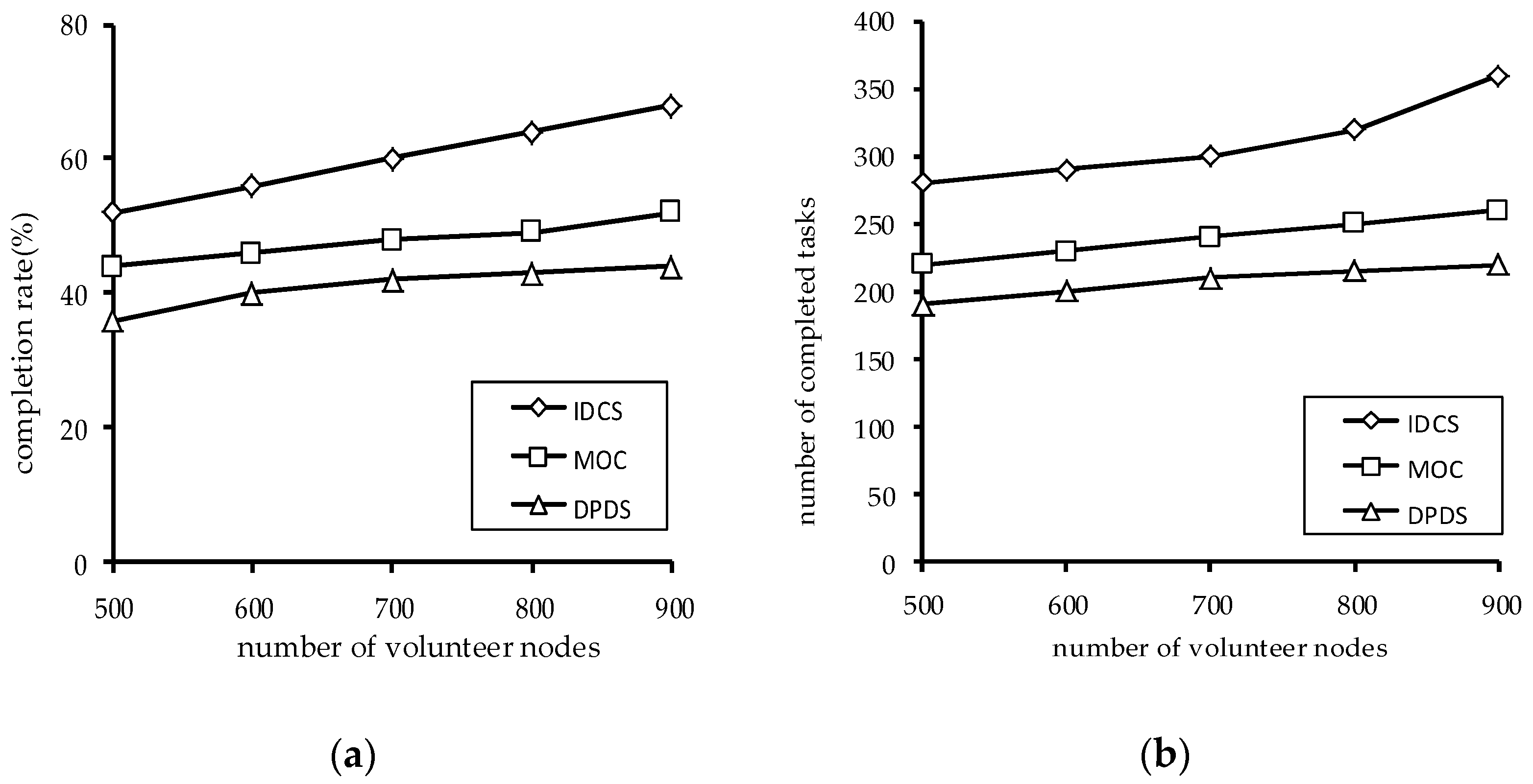
Figure 10 shows the impact of the number of volunteer nodes on the performance of the algorithms. It can be seen that the task completion rate increases when the number of volunteer nodes increases, and the number of the completed tasks also increases. This is because the more nodes there are, the more computing power there is. At the same time, the IDCS algorithm is superior to the MOC algorithm and DPBS algorithm in both task completion rate and the number of the completed tasks.
5.2. Experimental Results and Analysis of Dynamic Task Sets
In order to be closer to the real application scenario, this section uses a dynamic set of application tasks. The experiment generated five task sets, and each task set has an average of 100 tasks. The average size of each task is four units. The deadline for each task is set to a random value within 200–400 s after the task arrives. Other parameters settings are the same as the
Section 5.1. In the experiment, we assume a task request was submitted to the server every two minutes and the task completion status is tested every 100 min.
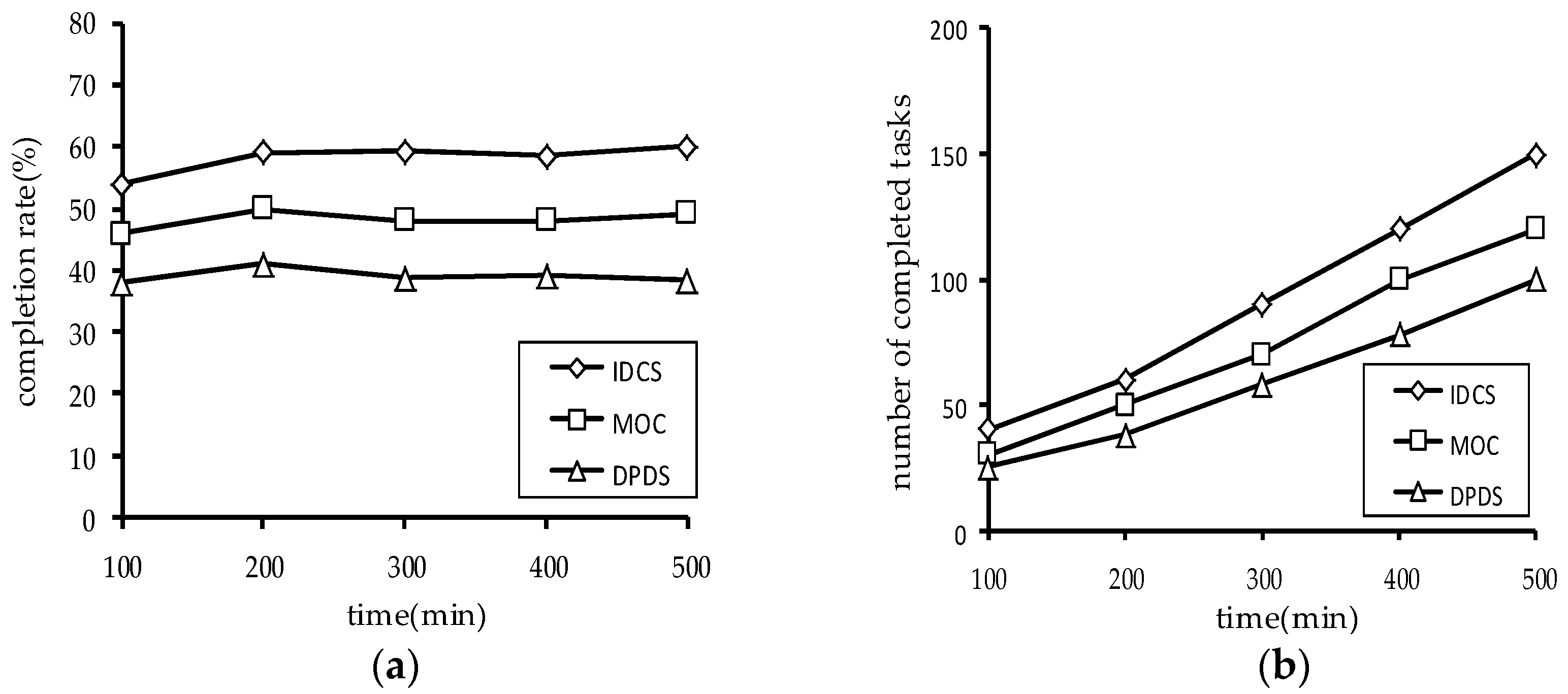
Figure 11 shows the number of the completed tasks and the task completion rate of the three algorithms.
Figure 11 shows the experimental results. It can be seen that the IDCS algorithm has obvious advantages on dynamic task sets, regardless of the number of the completed tasks or the task completion rate. Through the above experimental results, the validity of the IDCS algorithm proposed in this paper is further proved.