Dynamic Lognormal Shadowing Framework for the Performance Evaluation of Next Generation Cellular Systems
Abstract
:1. Introduction
2. Dynamic Lognormal Shadowing Framework
2.1. Random Field of Shadowing
2.2. Dynamic Model
2.3. Transition Probabilities
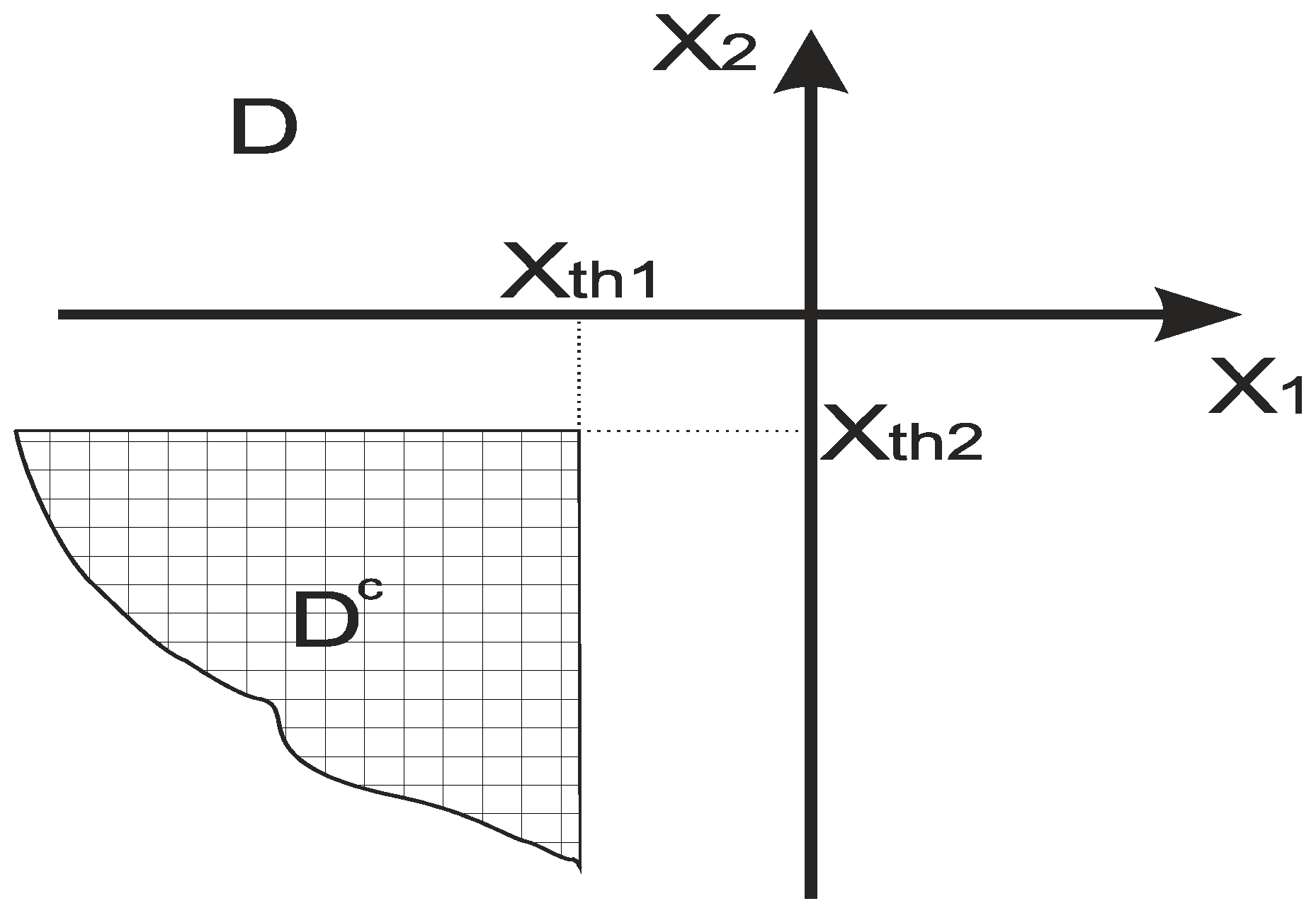
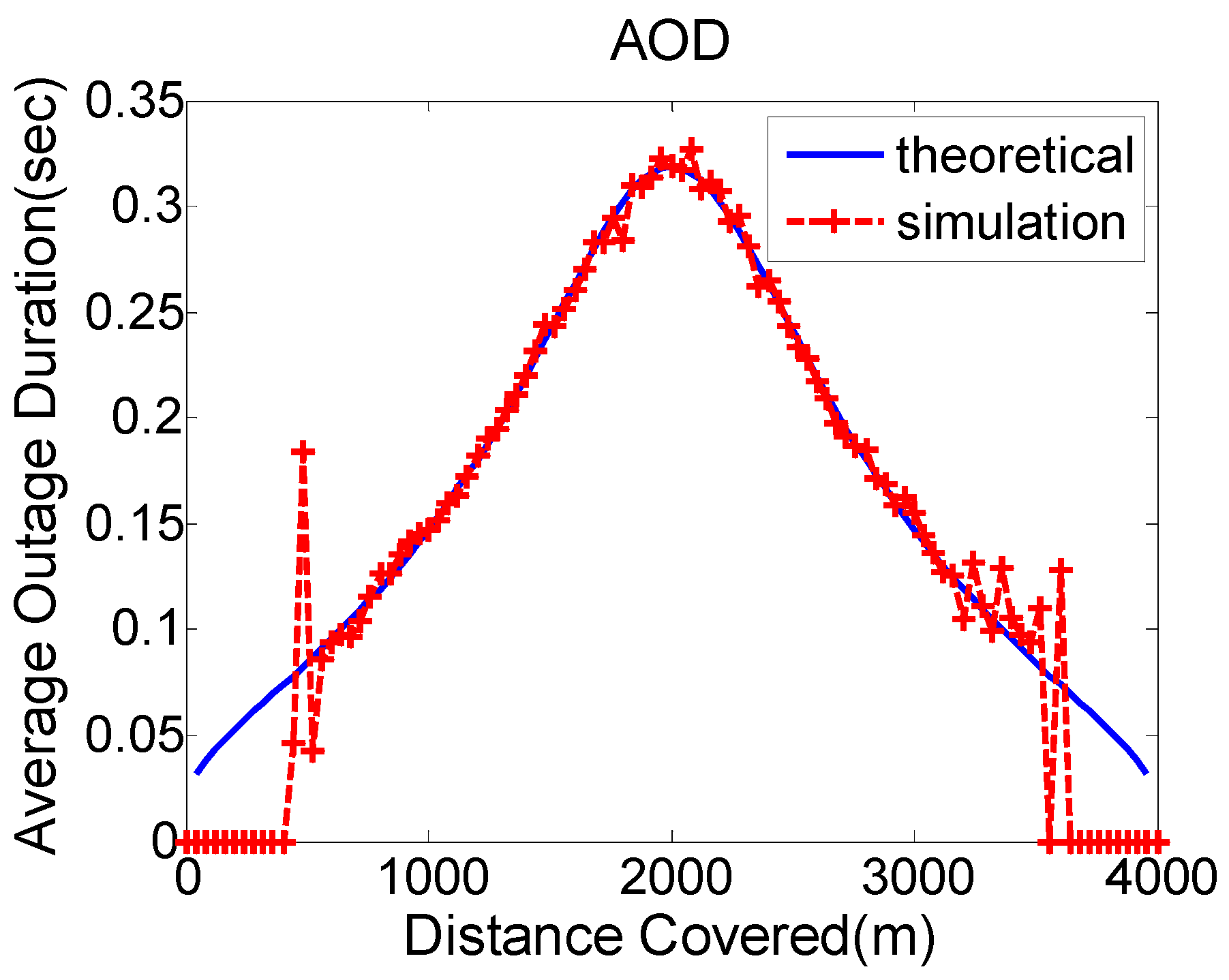
2.4. Fade Durations and Level Crossings
3. Numerical Results and Discussion
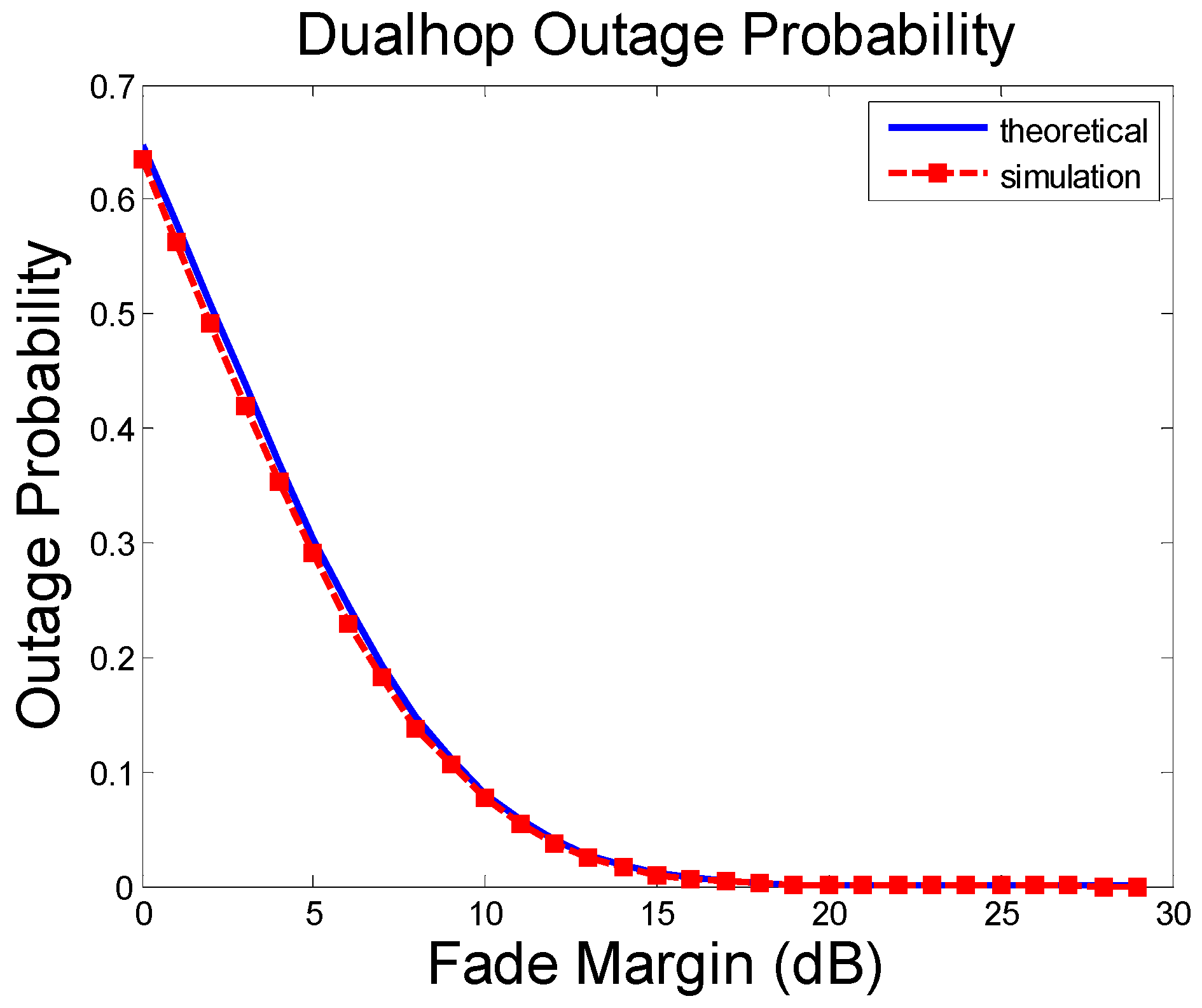
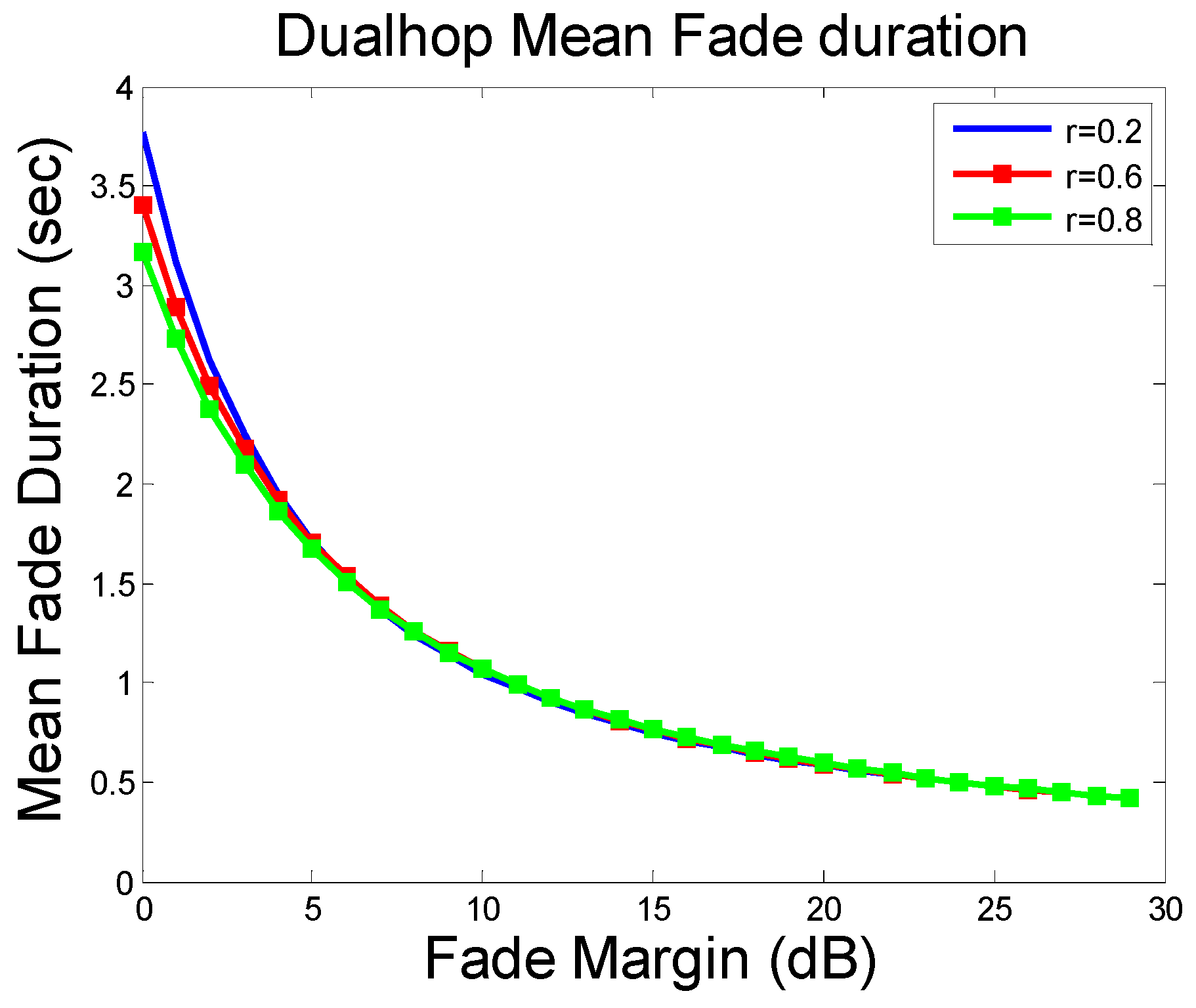
3.1. Dual-Hop
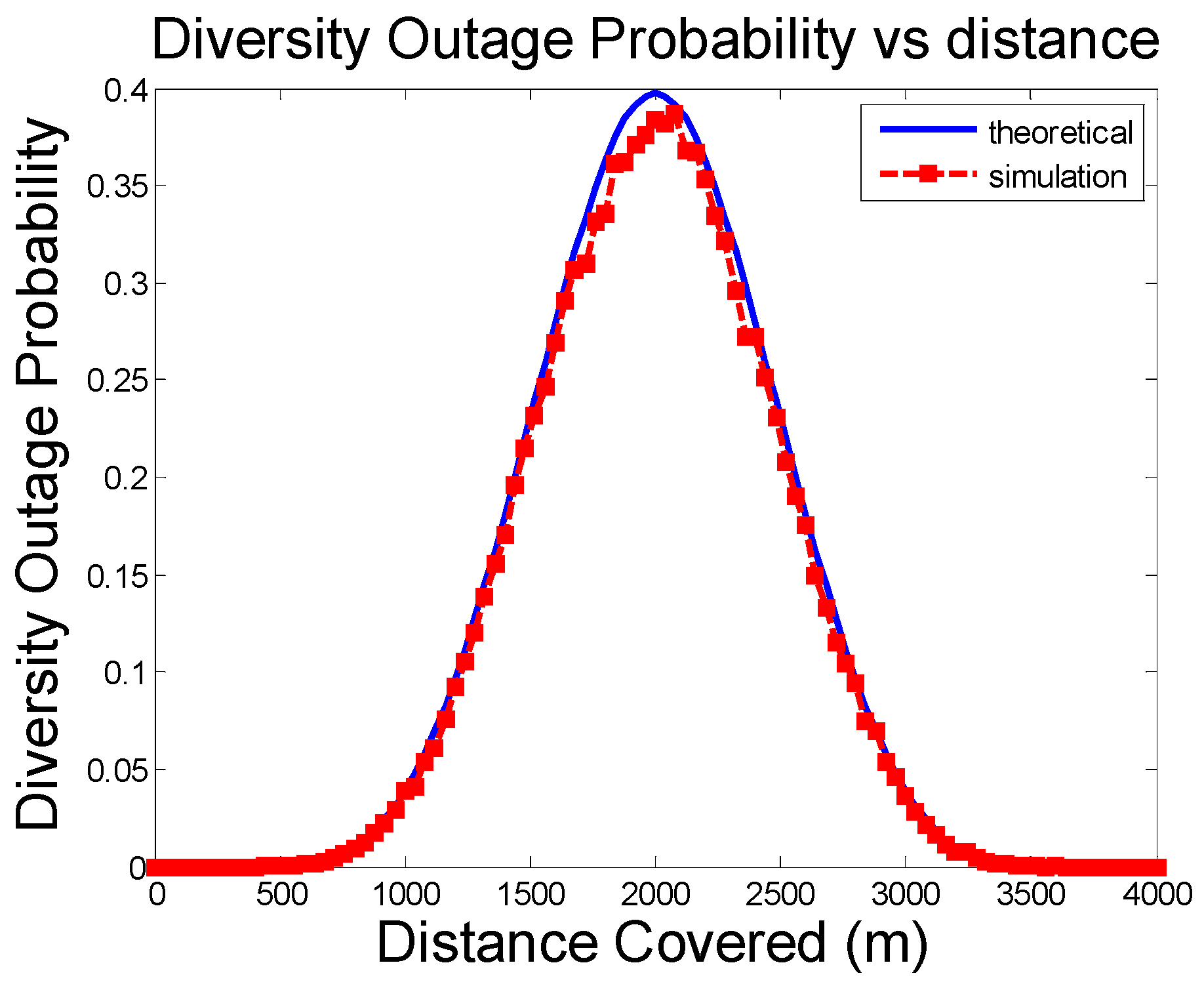
3.2. Cellular Network
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rappaport, T.S.; Sun, S.; Mayuz, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierez, F. Millimeter wave mobile communications for 5G cellular: It will work! IEEE Access J. 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Gutierez, F.; Dor, B.E.; Murdokc, J.N.; Qiao, Y.; Tamir, J.I. Broadband millimeter wave propagation measurements and models using adaptive-beam antennas for outdoor urban cellular communications. IEEE Trans. Antennas Propag. 2013, 61, 1850–1859. [Google Scholar] [CrossRef]
- Ghosh, A.; Thomas, T.A.; Cudak, M.C.; Ratasuk, R.; Moorut, P.; Vook, F.W.; Rappaport, T.S.; Sun, S.; Nie, S. Millimeter wave enhanced local area systems: A high data-rate approach for future wireless networks. IEEE J. Sel. Areas Commun. 2014, 32, 1152–1163. [Google Scholar] [CrossRef]
- Thompson, J.; Ge, X.; Wu, H.C.; Irmer, R.; Jiang, H.; Fettweis, G.; Alamouti, S. 5G wireless communication systems: Prospects and challenges. Commun. Mag. 2014, 52, 62–64. [Google Scholar] [CrossRef]
- Sun, S.; Rappaport, T.S.; Shafi, M.; Tang, P.; Zhang, J.; Smith, P.J. Propagation models and performance evaluation for 5G millimeter-wave bands. IEEE Trans. Veh. Technol. 2018, 67, 8422–8439. [Google Scholar] [CrossRef]
- Iyanda Sulyman, A.; Alwarafy, A.; MacCartney, G.R.; Rappaport, T.S.; Alsanie, A. Directional radio propagation path loss models for millimeter-wave wireless networks in the 28-, 60 and 73-GHz Bands. IEEE Trans Wirel. Commun. 2016, 35, 6939–6947. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications; Prentice Hall PTR: Upper Saddle River, NJ, USA; London, UK, 2001. [Google Scholar]
- Liberti, J.C.; Rappaport, T.S. Statistics of shadowing in indoor radio channels at 900 and 1900 MHz. In Proceedings of the 1992 IEEE Military Communications Conference, MILCOM 92 Conference Record, Communications—Fusing Command, Control and Intelligence, San Diego, CA, USA, 11–14 October 1992; pp. 1066–1070. [Google Scholar]
- Szyszkowicz, S.S.; Yanikomeroglu, H.; Thompson, J.S. On the Feasibility of wireless shadowing correlation models. IEEE Trans. Veh. Technol. 2010, 59, 4222–4236. [Google Scholar] [CrossRef]
- Catrein, D.; Mathar, R. Gaussian random fields as a model for spatially correlated log-normal fading. In Proceedings of the Telecommunication Networks and Applications Conference, Adelaide, Australia, 7–10 December 2008; pp. 153–157. [Google Scholar]
- Cai, X.; Giannakis, G.B. A two-dimensional channel simulation model for shadowing processes. IEEE Trans. Veh. Technol. 2003, 52, 1558–1567. [Google Scholar]
- Fraile, R.; Monserrat, J.F.; Gozálvez, J.; Cardona, N. Mobile radio bi-dimensional large-scale fading modelling with site-to-site cross-correlation. Eur. Trans. Telecommun. 2008, 19, 101–106. [Google Scholar] [CrossRef]
- Patwari, N.; Agrawal, P. NeSh: A joint shadowing model for links in a multi-hop network. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 31 March–4 April 2008; pp. 2873–2876. [Google Scholar]
- Forkel, I.; Schinnenburg, M.; Ang, M. Generation of Two-dimensional correlated shadowing for mobile radio network simulation. In Proceedings of the 7th International Symposium on Wireless Personal Multimedia Communications (WPMC), Abano Terme, Italy, 12–15 September 2004. [Google Scholar]
- Seetharam, A.; Kurose, J.; Goeckel, D.; Bhanage, G. A Markov chain model for coarse timescale channel variation in an 802.16e wireless network. In Proceedings of the IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 1800–1807. [Google Scholar]
- Mukherjee, S.; Avidor, D. Dynamics of path losses between a mobile terminal and multiple base stations in a cellular environment. IEEE Trans. Veh. Technol. 2001, 50, 1590–1603. [Google Scholar] [CrossRef]
- Hashemi, H. The indoor radio propagation channel. Proc. IEEE 1993, 81, 943–968. [Google Scholar] [CrossRef]
- Kashiwagi, I.; Taga, T.; Imai, T. Time-Varying path-shadowing model for indoor populated environments. IEEE Trans. Veh. Technol. 2010, 59, 16–28. [Google Scholar] [CrossRef]
- Zhang, R.; Cai, L. A Markov model for indoor ultra-wideband channel with people shadowing. Mob. Netw. Appl. 2007, 12, 438–449. [Google Scholar] [CrossRef]
- Klingenbrunn, T.; Mogensen, P. Modelling cross-correlated shadowing in network simulations. In Proceedings of the IEEE VTS 50th Vehicular Technology Conference, VTC 1999—Fall, Amsterdam, The Netherlands, 19–22 September 1999; pp. 1407–1411. [Google Scholar]
- Butterworth, K.S.; Sowerby, K.W.; Williamson, A.G. Base station placement for in-building mobile communication systems to yield high capacity and efficiency. IEEE Trans. Commun. 2000, 48, 658–669. [Google Scholar] [CrossRef]
- Jalden, N.; Zetterberg, P.; Ottersten, B.; Hong, A.; Thoma, R. Correlation Properties of large scale fading based on indoor measurements. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Kowloon, China, 11–15 March 2007; pp. 1894–1899. [Google Scholar]
- Patwari, N.; Wang, Y.; O’Dea, R.J. The importance of the multipoint-to-multipoint indoor radio channel in ad hoc networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC2002), Orlando, FL, USA, 17–21 March 2002; pp. 608–612. [Google Scholar]
- Agrawal, P.; Patwari, N. Correlated link shadow fading in multi-hop wireless networks. IEEE Trans. Wirel. Commun. 2009, 8, 4024–4036. [Google Scholar] [CrossRef]
- Charalambous, C.D.; Menemenlis, N. Dynamical Spatial log-normal shadowing models for mobile communications. In Proceedings of the XXVIIth Triennial General Assembly of the International Union of Radio Science (URSI), Maastricht, The Netherlands, 17–24 August 2002; pp. 1–4. [Google Scholar]
- Skraparlis, D.; Sakarellos, V.K.; Panagopoulos, A.D.; Kanellopoulos, J.D. Outage performance analysis of cooperative diversity with MRC and SC in Correlated lognormal channels. EURASIP J. Wirel. Commun. Netw. 2009, 2009, 707839. [Google Scholar] [CrossRef]
- Skraparlis, D.; Sakarellos, V.; Panagopoulos, A.D.; Kanellopoulos, J.D. Performance of N-branch receive diversity combining in correlated lognormal channels. IEEE Commun. Lett. 2009, 13, 489–491. [Google Scholar] [CrossRef]
- Skraparlis, D.; Sakarellos, V.; Sandell, M.; Panagopoulos, A.D.; Kanellopoulos, J.D. On the effect of correlation on the performance of dual diversity receivers in lognormal fading. IEEE Commun. Lett. 2010, 14, 1038–1040. [Google Scholar] [CrossRef]
- Sakarellos, V.; Skraparlis, D.; Panagopoulos, A.D.; Kanellopoulos, J.D. Cooperative Diversity Performance of Selection Relaying over Correlated Shadowing; Elsevier Physical Communication: Amsterdam, The Netherlands, 2011; pp. 182–189. [Google Scholar]
- Skraparlis, D.; Sakarellos, V.K.; Panagopoulos, A.D.; Kanellopoulos, J.D. New results on the statistics and the capacity of dual-branch MRC and EGC Diversity in correlated lognormal channels. IEEE Commun. Lett. 2011, 15, 617–619. [Google Scholar] [CrossRef]
- Sakarellos, V.K.; Skraparlis, D.; Panagopoulos, A.D.; Kanellopoulos, J.D. Cooperative Diversity performance in millimeter wave radio systems. IEEE Trans. Commun. 2012, 60, 3641–3649. [Google Scholar] [CrossRef]
- Karagiannis, G.; Panagopoulos, A.D.; Kanellopoulos, J.D. Multi-Dimensional rain attenuation stochastic dynamic modeling: Application to earth-space diversity systems. IEEE Trans. Antennas Propag. 2012, 60, 5400–5411. [Google Scholar] [CrossRef]
- Karagiannis, G.; Panagopoulos, A.D.; Kanellopoulos, J.D. Short-term rain attenuation frequency scaling for satellite up-link power control applications. IEEE Trans. Antennas Propag. 2013, 61, 2829–2837. [Google Scholar] [CrossRef]
- Gudmundson, M. Correlation model for shadow fading in mobile radio systems. Electron. Lett. 1991, 27, 2145–2146. [Google Scholar] [CrossRef]
- Graziosi, F.; Santucci, F. A general correlation model for shadow fading in mobile radio systems. IEEE Commun. Lett. 2002, 6, 102–104. [Google Scholar] [CrossRef]
- Avidor, D.; Mukherjee, S. Hidden issues in the simulation of fixed wireless systems. Wirel. Netw. 2001, 7, 187–200. [Google Scholar] [CrossRef]
- Karatzas, I.; Shreve, S.E. Brownian Motion and Stochastic Calculus; Springer: New York, NY, USA, 1991; Volume 113, p. 470. [Google Scholar]
- Graziosi, F.; Santucci, F. Distribution of outage intervals in macrodiversity cellular systems. IEEE J. Sel. Areas Commun. 1999, 17, 2011–2021. [Google Scholar] [CrossRef]
- Rice, S.O. Distribution of the duration of fades in radio transmission: Gaussian noise model. Bell Syst. Tech. J. 1958, 37, 581–635. [Google Scholar] [CrossRef]
- Stratonovich, R.L.; Silverman, R.A. Topics in the Theory of Random Noise; Revis Engl; Gordon and Breach: New York, NY, USA, 1967. [Google Scholar]
- Giancristofaro, D. Correlation model for shadow fading in mobile radio channels. Electron. Lett. 1996, 32, 958–959. [Google Scholar] [CrossRef]
- Stüber, G.L. Principles of Mobile Communication; Kluwer Academic: Boston, MA, USA, 2001; Volume 2, p. 752. [Google Scholar]
- Jeon, N.-R.; Kim, K.-H.; Choi, J.-H.; Kim, S. A Spatial correlation model for shadow fading in indoor multipath propagation. In Proceedings of the Vehicular Technology Conference Fall (VTC 2010-Fall), Ottawa, ON, Canada, 6–9 September 2010; pp. 1–6. [Google Scholar]
- Belyaev, Y. On the number of exits across the boundary of a region by a vector stochastic process. Theory Probab. Appl. 1968, 13, 320–324. [Google Scholar] [CrossRef]
- Lindgren, G. Stationary stochastic processes. In Theory and Applications; Texts in Statistical Science Series; CRC Press: Boca Raton, FL, USA, 2013; p. 347. [Google Scholar]
- Adler, R.J.; Taylor, J. Random Fields and Geometry; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karagiannis, G.A.; Panagopoulos, A.D. Dynamic Lognormal Shadowing Framework for the Performance Evaluation of Next Generation Cellular Systems. Future Internet 2019, 11, 106. https://doi.org/10.3390/fi11050106
Karagiannis GA, Panagopoulos AD. Dynamic Lognormal Shadowing Framework for the Performance Evaluation of Next Generation Cellular Systems. Future Internet. 2019; 11(5):106. https://doi.org/10.3390/fi11050106
Chicago/Turabian StyleKaragiannis, Georgios A., and Athanasios D. Panagopoulos. 2019. "Dynamic Lognormal Shadowing Framework for the Performance Evaluation of Next Generation Cellular Systems" Future Internet 11, no. 5: 106. https://doi.org/10.3390/fi11050106
APA StyleKaragiannis, G. A., & Panagopoulos, A. D. (2019). Dynamic Lognormal Shadowing Framework for the Performance Evaluation of Next Generation Cellular Systems. Future Internet, 11(5), 106. https://doi.org/10.3390/fi11050106





