1. Introduction
Mobile opportunistic networks (MONs) utilize node mobility to form communication opportunities to overcome challenging scenarios. This approach naturally makes it possible to achieve the goals of ubiquitous interconnection and a thorough perception for the Internet of Things, and can be applied to many fields such as device-to-device communication, data offloading, and intelligent transportation [
1].
The collaboration behavior of nodes plays an important role in MONs because nodes need to store/forward packets from/to others. However, considering the limited storage space and the consumption of battery power, nodes show a certain degree of selfishness in MONs. They tend to maintain their own interests sometimes and refuse to serve others. Therefore, it is highly important to encourage additional nodes to participate in the data forwarding process.
Many incentive models have been proposed to improve the cooperative behavior of nodes, such as the reputation system [
2], the virtual money mechanism [
3], and the tit-for-tat method [
4]. All of these models are based on a passive scheme, that is, nodes have to forward/receive packets as much as possible to enable them to gain a higher reputation, or earn more money, or send a larger number of packets. In fact, the nodes in MONs show strong self-similarities as they are carried by people. Based on the social learning and psychological theories, they always imitate others’ behavior, especially those of high social importance. Recent studies verified the existence of imitating behavior in ethics [
5], consumption [
6] and cooperation [
7]. Taking this into account, in this paper, we propose FollowMe, an evolutionary game-based solution to motivate nodes participating in MONs. FollowMe introduces the sociality of nodes into the signal game model, in which the signal indicates the social importance of nodes and will be sent to the other nodes in each round. A node designated as a social node in an MON sends the signal reference
with high social importance; otherwise, it sends the signal
with low social importance. Our main contributions are summarized as follows:
We establish the signaling game model between nodes by introducing the social importance, which is deemed to be a signal.
We calculate the income of a node based on the prisoner’s dilemma model and combine the income with the forwarding probability of nodes, rather than merely considering the cumulative incomes for all rounds.
Compared with the random update strategy, FollowMe achieves more effective network performance in terms of routing.
The remainder of this paper is organized as follows.
Section 2 reviews related work. In
Section 3, we introduce the preliminaries.
Section 4 describes the FollowMe solution. In
Section 5, we apply FollowMe to the classical opportunity routing algorithm PRoPHET and SimBet.
Section 6 presents the experimental results and analysis.
Section 7 concludes the paper.
2. Related Works
The incentive model used in MONs can be classified into three types: the reputation system, the virtual money mechanism, and the tit-for-tat method. In the reputation system, packets are forwarded to nodes with a more favorable reputation. The value of the reputation is calculated from the historical behavior of nodes [
2]. The authors of [
8] use the number of forwarding times and success rate to estimate the reputation of nodes. A node aiming to enhance its reputation score has to receive/forward packets from/to other nodes; otherwise, it would be excluded from the network if its reputation is below a threshold. The reputation system is effective in situations in which the difference among nodes’ reputation scores is large. In contrast, the improvement in collaborative behavior among nodes with similar scores is not obvious.
The virtual currency mechanism enables nodes to gain a certain amount of income if they assist others to forward packets, and the income is paid by the node-sending packets [
3]. Other researchers proposed Nuglet [
9], which installs anti-modified hardware on nodes as a security measure to protect the currency swapping process. The virtual currency mechanism generally requires a central control node in networks and the realization of this mechanism is also extremely complex. Both of these features limit the applicability and scalability of this solution.
The tit-for-tat method is based on the principle of equivalent exchange and uses game theory to construct the knowledge model. In each round, the participants in the game initially adopt a cooperation strategy, after which they imitate their opponent’s recent behavior. If the game player in the latest round adopts the cooperation strategy, then the node chooses the cooperation strategy; otherwise, it chooses the betrayal strategy [
4]. From the perspective of a non-cooperative game, the authors of [
10] present a cooperation model with asymmetric information. This model reduces the cheating behavior of rational nodes, which use forged feedback information to increase their income. Although the tit-for-tat method seems to be fair, it may in fact weaken the forwarding efficiency. Imagine a situation in which a node attempts to send additional packets to the receiver, but the node is unable to do this if it only obtains a few packets from the receiver.
Apart from the above mechanisms, some researchers use evolutionary game theory to study the cooperative behavior of bounded rational nodes in different systems and networks [
11].
In an evolutionary game, nodes decide their own strategy by observing others’ behavior; therefore, designing the game strategy is of key importance. A cautious idea was put forward [
12], and properly introduced into the prisoner’s dilemma model, and then the random Fermi update rule was used to describe the way in which the prudent idea affects the evolution of cooperative behavior. Martinez et al. [
13] proposed a repeated game model to search the services in complex networks, and they used the random walk strategy to forward messages to neighbors. Luo et al. [
14] investigated the evolution of cooperation in a memory-based prisoner’s dilemma game (PDG) on interdependent networks. Similarly, Meng et al. [
15] studied the influence of the neighborhood size and individual density on two interdependent lattices with the PDG model.
Note that none of these researchers considered the influence of the sociality of a node on the collaborative behavior (Many routing algorithms such as Bubble and Hotent [
16] employ the social property of nodes; however, to the best of our knowledge, currently incentive works do not evaluate the influence of social importance on the incentive process.), i.e., in each updating round, nodes select strategies randomly from their neighbors to use in the game. In fact, nodes in MONs are always carried by people or installed in vehicles and show strong sociality. They tend to approach other nodes with higher importance in the virtual space similar to human beings in the physical world. Motivated by the aforementioned challenges other researchers encountered, this paper proposes FollowMe, a mechanism for the promotion of cooperative behavior among nodes based on the signal game. We next introduce the details thereof.
3. Preliminaries
3.1. Prisoner’s Dilemma Model
Generally, the packet forwarding process of MONs may achieve improved forwarding efficiency by way of the vigorous cooperation among nodes. However, because of the limitations imposed by cache space and energy power, nodes are usually confronted by a dilemma. On the one hand, nodes hope to receive help from others; on the other hand, given individuals’ selfishness in society, they are unwilling to help others to forward packets. In this study, we use the prisoner’s dilemma model to reflect this conflict.
Suppose that there are two nodes
x,
y and both of them enter each other’s communication range, in which case they face the dilemma of deciding whether to forward packets to the other. Based on the prisoner’s dilemma model, the two nodes will obtain different profits by using different combinations of strategies, as shown in the following matrix
A. If both of them take the cooperative strategy, the reward is
R. If one of them takes the cooperative strategy, its bonus is
S, whereas that of the opponent is
T; otherwise, if neither of them is cooperative, they attract a publishment
P. The positive feedback for rewarding the non-selfish behavior in this model maintains a high cooperation efficiency:
3.2. Signal Game Model Based on Social Importance
In an MON composed of portable devices, the behavior of nodes reflects certain social attributes due to the sociality of carriers. In addition, nodes are more willing to imitate those of high social importance. Therefore, we reflect the sociality of nodes by introducing the social importance of nodes into game procedure.
Social Importance: We employ the Degree Centrality (DC) [
17] to measure the social importance of nodes. The DC of a node is the number of neighbors it has. In general, higher DC signifies higher social importance. Mathematically, let
denote the DC of node
x; thus, we have
, where
denotes the number of neighbors of node
x and
N is the number of nodes in the network. This enables us to evaluate the social importance of nodes. Suppose node
y is one of the neighbors of
x, with its social importance
being
, where
is the set of neighbors of
x. Subsequently, the average social importance of the neighbors of
x is
. Finally, we denote
x as a node with high social importance if
.
Signal Game Model: In game theory, a signal game is a dynamic game with incomplete information between two participants: a signal sender S and a receiver R. The game process can be summarized as follows:
- (a)
The sender is assumed to be one type from a set ; for all of the types, the probability and their sum equals 1.
- (b)
The sender observes the type and selects a signal from the signal set .
- (c)
After viewing the signal (but the receiver cannot see the type ), it selects an action from the action set .
- (d)
The sender has a bonus
and that of the receiver is
. In this study, we assume there are two types of nodes: cooperative and non-cooperative, and set
=
and
=
. If one of the nodes belongs to
, it participates in the forwarding process with a probability
; otherwise,
. In addition, based on the social attributes of nodes, they can select signals
or
to send, where
and
indicate nodes of high and low social importance, respectively. Furthermore, if the sender or receiver is a highly social node, the receiver will receive and forward the packet, mainly because social nodes help to improve the network performance [
18]. We here use
to denote the forwarding action; otherwise,
is dependent on the participant status of the receiver. The type of receiver tends to be
only if the receiver/sender is a node with low sociality, i.e., when one of these nodes is not social, the receiver is not willing to participate in the data forwarding process.
4. FollowMe
4.1. The Construction of the Game Tree
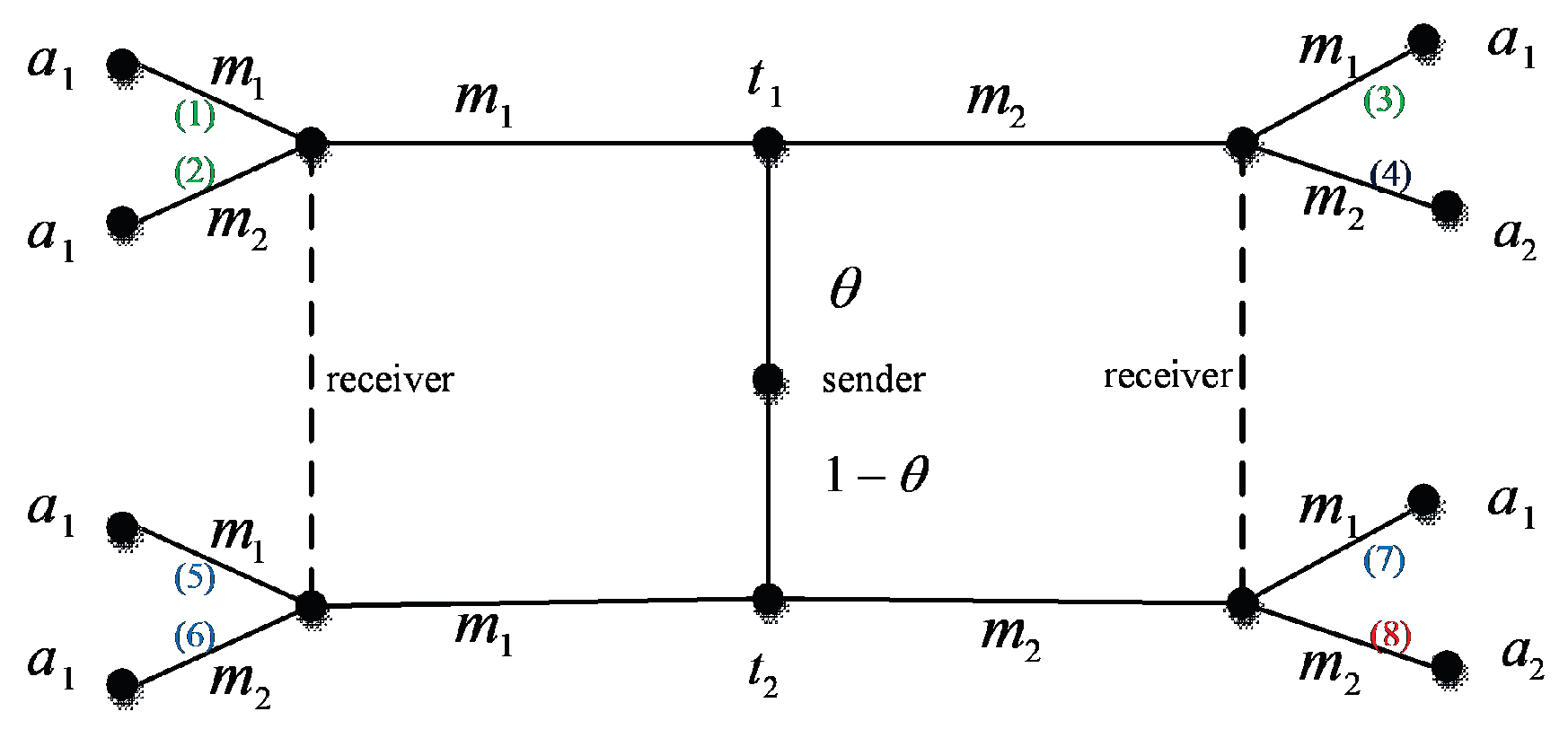
First, the social importance degree of a node is regarded as the game signal, and any two nodes of the game are defined as the sender and receiver of the signal. Eight paths are shown in
Figure 1:
- (1)
If the sender belongs to the type and sends the signal , and the receiver itself is a node of high social importance , the receiver forwards the packet;
- (2)
If the sender belongs to the type and sends the signal , and the receiver itself belongs to , it still forwards the packet;
- (3)
If the sender belongs to the type and sends the signal , and the receiver itself is a node of high social importance, it chooses the action ;
- (4)
If the sender belongs to the type and sends the signal , and the receiver itself is a node of low social importance , it refuses to receive the packet and selects the action ;
- (5)
If the sender belongs to the type and sends the signal , and the receiver itself is a node of high social importance , it forwards the packet;
- (6)
If the sender belongs to the type and sends the signal , and the receiver itself is a node of low sociality, it forwards the packet;
- (7)
If the sender belongs to the type and sends the signal , and the receiver itself is a highly social node, it still forwards the packet;
- (8)
If the sender belongs to the type and sends the signal , and the receiver itself is a node of low social importance, it selects the action . According to the signal game process provided above, the packet is collected and spread by the node with high social importance. Because these nodes have more opportunities to contact other nodes, the packet is quickly delivered. On the other hand, considering the fact that the proposed method tends to propagate the cooperative forwarding behavior between social nodes and others, the method encourages additional nodes to participate in the forwarding process.
4.2. Game Strategy Update
Income of a node in a round: Based on the prisoner’s dilemma game and the aforementioned game tree, nodes have the following four possibilities to earn income. Here, we use two nodes x and y to illustrate these possibilities and suppose x is a signal sender and y is a receiver.
- (1)
Both of them are willing to forward packets, thus each of them has an income
R. Let
and
denote the forwarding probability, we have:
Proof. From the game tree, we know that there exist three paths (step 1, 2, and 3) in which both nodes take the forwarding strategy.
In step 1, node x belongs to the cooperative type with a probability . In addition, both of them are social nodes with a signal , hence the receiver is also cooperative and forwards the packet with a probability . The probability of the path thus is .
In step 2, the node y is non-cooperative with a probability ; this is mainly because node y itself is a non-social node. The probability of this path is .
In step 3, the node y remains non-cooperative, but this time the reason is that node x is a social node. The probability of this path is .
The combination of these steps concludes the proof. □
- (2)
Node
x forwards packets with an income
S, but
y is declined with an income
T. This situation happens along path 4. Similarly, we obtain the probability:
where
denotes the probability of rejection.
- (3)
Node
x is declined with an income
T, but
y forwards packets with an income
S. This situation happens along paths 5, 6, and 7 since the sender belongs to
. The probability is
where
denotes the probability of rejection of node
x. The proof process is similar to that of (1), and we omit it here for a concise presentation.
- (4)
Both of the nodes refuse to forward the packet and each of them has an income
P. The probability is
Updates of the game strategy: After a round of game with all neighboring nodes, the cumulative gain of node
x, i.e.,
can be calculated as follows:
where
,
,
, and
are the number of times that
x gains
R,
T,
S, and
P in a round, and
. Simultaneously, node
y can obtain its gains by using a similar method. After calculating the accumulated income of each node, the Fermi function is deployed to determine whether node
x follows the opponent’s game strategy:
where
and
represent the strategy adopted by nodes
x and node
y for the current round, respectively;
and
are the corresponding cumulative earnings in the current round, and
is the noise factor. If
(
is a random number homogeneously distributed within the interval [0, 1]), node
x follows the strategy of node
y; otherwise, the current strategy is retained. Algorithm 1 expresses the aforementioned process.
| Algorithm 1: FollowMe. |
| 1: if it is time to start the game then |
| 2: for each node pair () do |
| 3: if x and y enter each other’s communication range then |
| 4: if both of them are willing to forward packets then |
| 5: ++ |
| 6: else if x will forward packets but y is declined then |
| 7: ++ |
| 8: else if x refuses to forward packets but y is friendly then |
| 9: ++ |
| 10: else if both of them are not friendly then |
| 11: ++ |
| 12: end if |
| 13: end if |
| 14: Calculate the benefits of x |
| 15: end for |
| 16: end if |
| 17: if it is time to update the game strategy then |
| 18: for each node pair (x, y) do |
| 19: Calculate W |
| 20: if then |
| 21: x follows the game strategy of y |
| 22: end if |
| 23: end for |
| 24: end if |
4.3. Theory Analysis
Theorem 1. Every finite game has at least one Nash Equilibrium.
Proof. We first prove that there exists a fixed point. Let
(
) denote the two players, where
. We have
. Similarly, let
and
denote the signal and action of the node pairs, respectively, we have
and
. Now, for
, we can define the following function [
19]:
Next, let
f be a map from
to
and
, where
The function f and C are continuous and the signal set is concave and compact. Therefore, the function f must exit one fixed point based on the fixed point theorem.
Now, we prove that the fixed point is in the Nash Equilibrium. Suppose
s is in the Nash Equilibrium, i.e.,
, we obtain
. Using the aforementioned two equations, we obtain
, which implies
s is a fixed point of function
f. Conversely, let
s be any arbitrary fixed point, we have
, which implies
must satisfy
s, i.e.,
. Using Equation (
5), we have
Since
support
players, the denominator of Equation (
6) must be 1, i.e.,
. Note that
, we have
, i.e., no pairs can improve their expected income by deviating from their current action. Thus, there exists a Nash equilibrium. □
5. Application
In this section, we integrate FollowMe with the classical opportunity routing algorithms PRoPHET [
20] and SimBet [
21]. Here, we continue using node
as examples. Suppose node
x encounters node
y, node
x sends its signal to node
y, and the latter then runs FollowMe to determine its action. If both of them are cooperative, then node
x runs the corresponding protocol to determine whether it forwards packets to node
y. The specific process is shown in Algorithm 2.
| Algorithm 2: Process of applying FollowMe to opportunity routing algorithm. |
| 1: for each node ∈V do |
| 2: if x and y are within the communication range and x is the sender of the packet then |
| 3: run FollowMe |
| 4: if both of them want to receive and forward packets then |
| 5: for any packets to be sent to y do |
| 6: if y is the destination node of the packet then |
| 7: y receives and stores the packet in the buffer |
| 8: else if y is the more appropriate carrier for the packet than x then |
| 9: y receives the packet and stores it in the buffer |
| 10: end if |
| 11: end for |
| 12: end if |
| 13: end if |
| 14: end for |
6. Experimental Results and Analysis
In this paper, we integrate FollowME into the classical routing algorithms PRoPHET and SimBet, and implement it in a custom routing simulation platform based on the Visual C++ 6.0. We evaluate its performance metrics by comparing it with the performance of the random update strategy, which is widely used in recent works [
13,
14,
15]. We used two real data sets, KAIST and NCSU [
22], and one mobility model SLAW, to test the performance of FollowMe under different network conditions. KAIST is obtained from the Korea Institute of Science and Technology (KAIST) and records the daily activities of the population on campus. A total of 34 people participated in the data collection process, each with a handheld GPS device to collect 92 days movement trajectory. NCSU records the moving traces of 20 students in the campus dormitory area from North Carolina University. The detailed information of the datasets are shown in
Table 1.
This paper uses three metrics to evaluate the performance of routing algorithms: (1) Cooperation Rate (CR): the ratio of the total number of cooperating nodes to the total number of nodes in the network. The higher the cooperation rate, the more nodes in the network are willing to forward messages to other nodes; (2) Packet Delivery Ratio (PDR): the number of data packets to the destination over the total number of packets generated. The higher the PDR, the larger the number of data packets in the network that are successfully delivered to the destination node; (3) Packet Delivery Hops (PDH): the average number of hops required for the data packet to arrive at the destination node from the birth node. The lower the number of hops, the fewer the number of intermediate nodes needed to forward the message, i.e., the lower the demand for network resources.
The simulation parameters are as follows: in the prisoner’s dilemma game payoff matrix, R = 1, S = −1, T = 1.5, and P = 0. In the Fermi function, the noise coefficient = 0.5 and the initial cooperation rate of all nodes in the network .
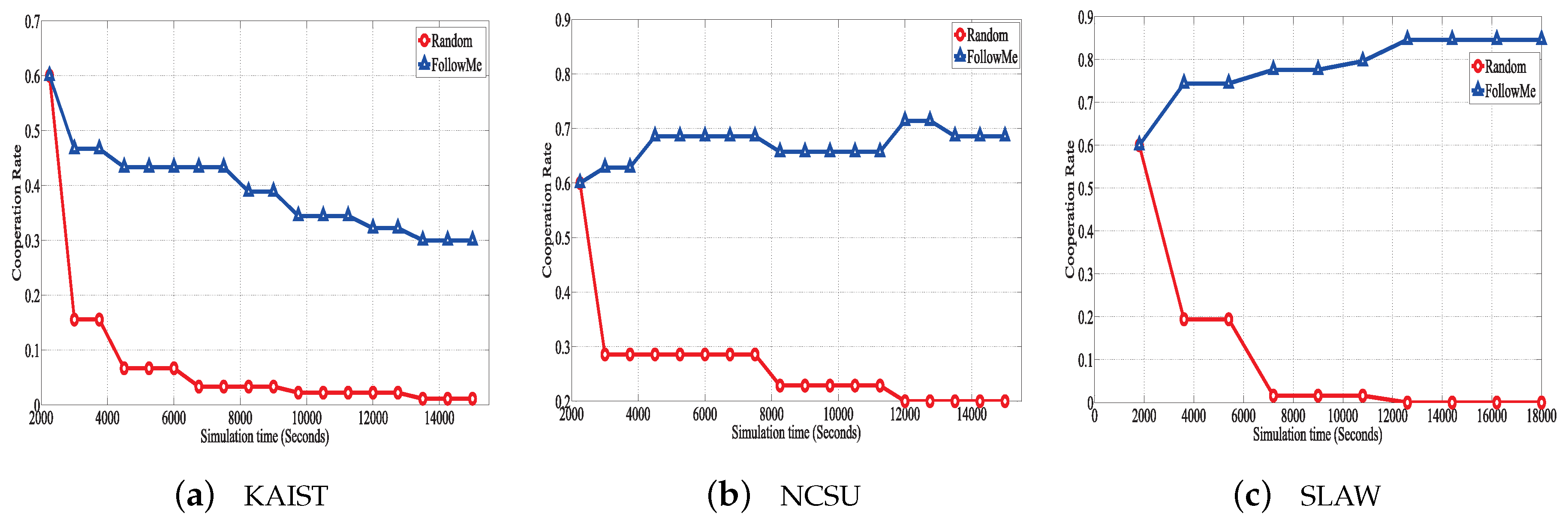
Figure 2 shows the results of CR between FollowMe and Random. We can observe that the cooperation rate is initially similar; however, FollowMe obviously has a higher CR than Random with the simulation process. Moreover, as the time increases, FollowMe still maintains a high CR while the Random strategy fails to drive nodes. This is mainly because FollowME takes the social importance of nodes into account and use it as a signal to motivate nodes to cooperate. On the contrary, the Random solution just takes the action from one of neighbors as a reference, and the selected neighbors maybe a node with lowly social importance, which has little help to forward packets. The cliff point in the initial stage of the random algorithm is because the random update strategy does not consider the imitation behavior between nodes, and all nodes tend not to forward data (the most benefit when not forwarding). Therefore, in order to maximize the benefits of each node, each node achieves a stable state in a short period of time, but the cooperation rate is low.
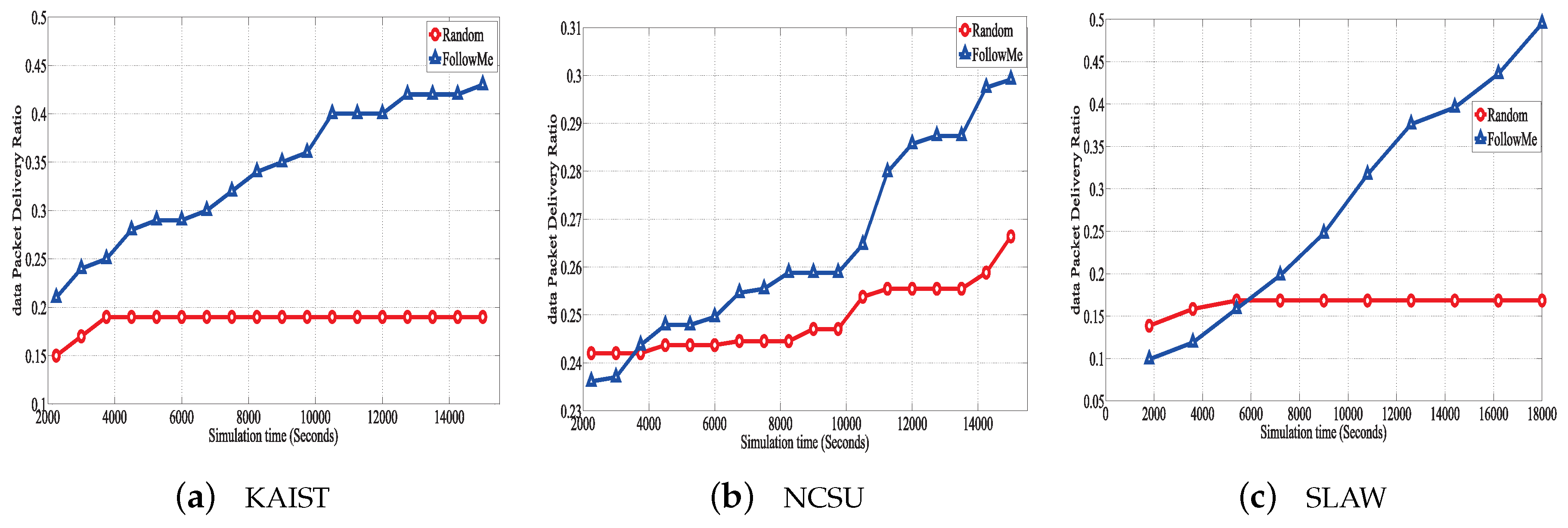
Figure 3 and
Figure 4 evaluate the PDR performance of FollowMe in PRoPHET and SimBet, respectively. Clearly, the PDR of FollowMe is almost twice as high than that of Random during the entire simulation. This is mainly because the CR of FollowMe is higher than that of Random, which means more nodes are willing to assist other nodes to relay data packets. Hence, additional data packets can be relayed, increasing the probability of contact with the destination and improving the PDR slightly. On the other hand, FollowMe introduces the social-related signal game strategy, which allows data packets to be relayed mainly by nodes of high social importance that could contact a greater number of other nodes. This helps to increase the probability of data packets reaching their destination.
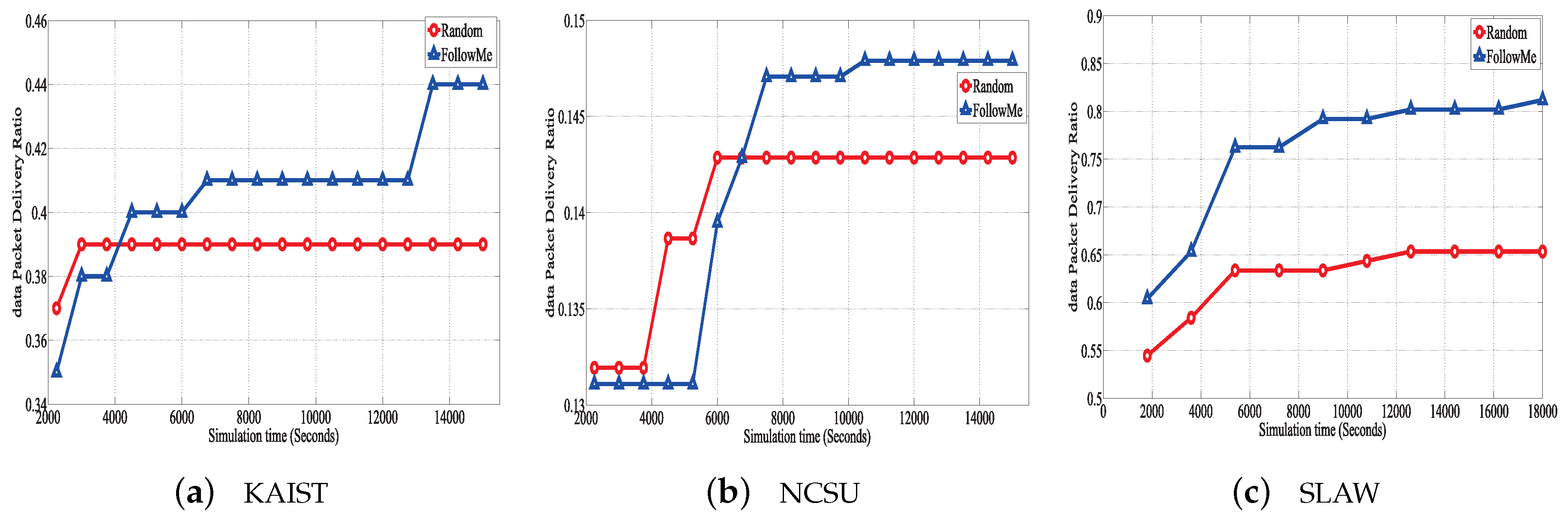
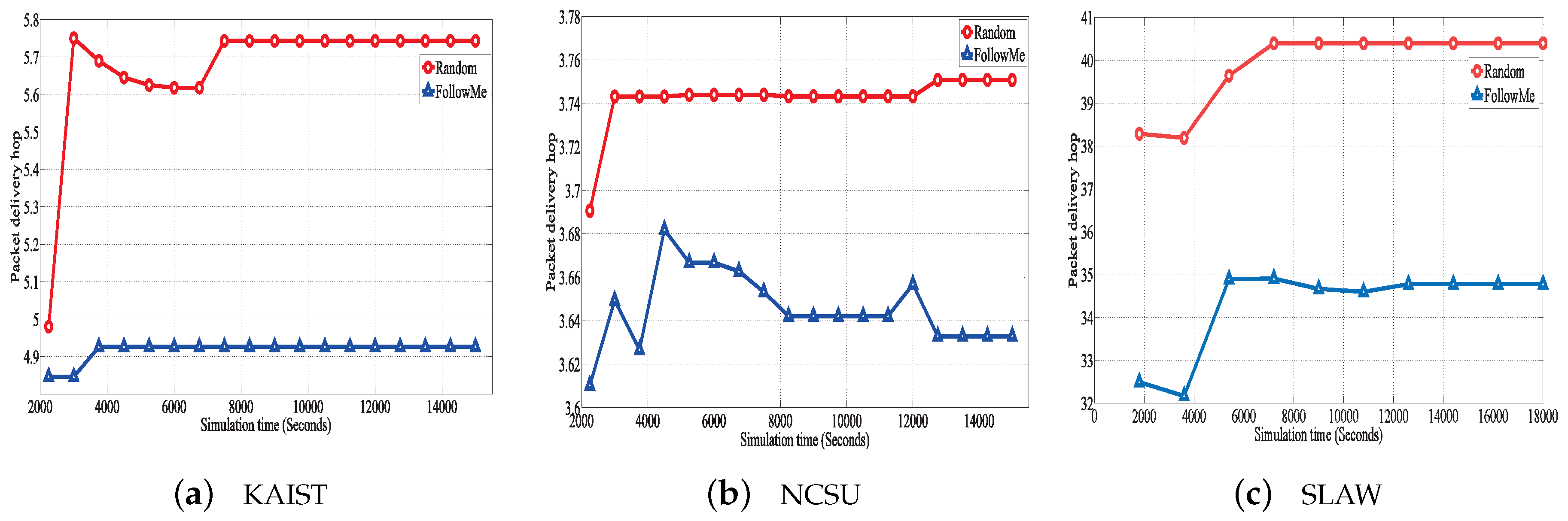
Figure 5 shows the number of hops of the two incentive mechanisms with ProPHET. It is obvious to see that FollowMe generally has a smaller hop than Random. For example, in the SLAW scenario, the length of forwarding path generated by FollowME within ProPHET tends to an average of 4.9, while that of Random within ProPHET is about 5.7 and higher as shown in
Figure 5c. The reason is similar as those of PDR. Recall that FollowME employs social nodes to forward packets, which naturally reduces the number of hops.
7. Conclusions
In this paper, we introduce the signal reference in the game process of the node, and combine the social attribute, i.e., the degree of social importance, with the packet forwarding mechanism of the node to simulate the dynamic behavior of the node in a real network. Then, the experimental results are compared with the random update rule. The simulation results showed that, for the same real data set, the model greatly improves the cooperation rate among nodes and the packet delivery rate for promoting the node cooperative behavior, and the number of hops is also lower.
These indicators show that the proposed strategy to promote cooperative behavior has greatly progressed toward improving the overall performance of the network, by actively promoting the cooperative behavior of the nodes in the network.
Author Contributions
Conceptualization, P.Y.; Formal Analysis, P.L.; Investigation, E.Z.; Methodology, X.P.
Funding
This research was funded in part by the National Natural Science Foundation of China under Grant Nos. U1804164. U1404602, and U1604156, in part by the Young Scholar Program of Henan Province under Grant No. 2015GGJS-086, in part by the Science and Technology Foundation of Henan Educational Committee under Grant No. 19A510015, in part by the Science and Technology Foundation of Henan Province under Grant Nos. 172102210341, 162102310442, in part by the Startup Project of Henan Normal University under Grant No. qd14136, and in part by the Young Scholar Program of Henan Normal University with No. 15018.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ma, H.; Zhao, D.; Yuan, P. Opportunities in mobile crowd sensing. IEEE Commun. Mag. 2014, 52, 29–35. [Google Scholar] [CrossRef]
- Rezvani, M.; Ignjatović, A.; Bertino, E.; Jha, S. Secure data aggregation technique for wireless sensor networks in the presence of collusion attacks. IEEE Trans. Dependable Secur. Comput. 2015, 12, 98–110. [Google Scholar] [CrossRef]
- Sharma, A. A credit based routing mechanism to contrast selfish nodes in Delay tolerant networks. In Proceedings of the International Conference on Parallel, Distributed and Grid Computing, Solan, India, 11–13 December 2015; pp. 295–300. [Google Scholar]
- Shevade, U.; Song, H.H.; Qiu, V.; Zhang, Y. Incentive-aware routing in DTNs. In Proceedings of the IEEE International Conference on Network Protocols, Orlando, FL, USA, 19–22 October 2008; pp. 238–247. [Google Scholar]
- Bauman, C.W.; Tost, L.P.; Ong, M. Blame the shepherd not the sheep: Imitating higher-ranking transgressors mitigates punishment for unethical behavior. Organ. Behav. Hum. Decis. Process. 2016, 137, 123–141. [Google Scholar] [CrossRef]
- Shen, X.L.; Zhang, K.Z.K.; Zhao, S.J. Herd Behavior in Consumers’ Adoption of Online Reviews; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Lu, P. Imitating winner or sympathizing loser? Quadratic effects on cooperative behavior in prisoners’ dilemma games. Phys. A Stat. Mech. Appl. 2015, 436, 327–337. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; An, C.J.; Tang, C.J. A reputation-based incentive scheme for delay tolerant networks. Acta Electron. Sin. 2014, 42, 1738–1743. [Google Scholar]
- Hubaux, J.P. Stimulating Cooperation in Self-Organizing Mobile Ad Hoc Networks; Springer: New York, NY, USA, 2003; pp. 579–592. [Google Scholar]
- Long, T.; Chen, Z.G.; Zhao, M.; Yang-Hui, L.I. Game analysis of incentive-cooperative mechanism in opportunistic routing. Comput. Eng. 2010, 36, 126–128. [Google Scholar]
- Vincent, T.L. An Evolutionary Game Theory for Differential Equation Models with Reference to Ecosystem Management; Springer: Boston, MA, USA, 1994. [Google Scholar]
- Liu, Y.; Zhang, L.; Chen, X.; Ren, L.; Wang, L. Cautious strategy update promotes cooperation in spatial prisoner’s dilemma game. Phys. A Stat. Mech. Appl. 2013, 392, 3640–3647. [Google Scholar] [CrossRef][Green Version]
- Martinez-Canovas, G.; Val, E.D.; Botti, V.; Hernandez, P.; Rebollo, M. A formal model based on Game Theory for the analysis of cooperation in distributed service discovery. Inf. Sci. Int. J. 2016, 326, 59–70. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, X.; Liu, H.; Shao, R. Cooperation in memory-based prisoner’s dilemma game on interdependent networks. Phys. A Stat. Mech. Appl. 2016, 450, 560–569. [Google Scholar] [CrossRef]
- Meng, X.K.; Xia, C.Y.; Gao, Z.K.; Wang, L.; Sun, S.W. Spatial prisoner’s dilemma games with increasing neighborhood size and individual diversity on two interdependent lattices. Phys. Lett. A 2015, 379, 767–773. [Google Scholar] [CrossRef]
- Yuan, P.; Fan, L.; Liu, P.; Tang, S. Recent progress in routing protocols of mobile opportunistic networks. J. Netw. Comput. Appl. 2016, 62, 163–170. [Google Scholar] [CrossRef]
- Callaway, D.S.; Newman, M.E.J.; Strogatz, S.H.; Watts, D.J. Network robustness and fragility: Percolation on random graphs. Phys. Rev. Lett. 2000, 85, 5468. [Google Scholar] [CrossRef] [PubMed]
- Yuan, P.; Ma, H.; Fu, H. Hotspot-Entropy Based Data Forwarding in Opportunistic Social Networks; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 2015; pp. 136–154. [Google Scholar]
- Jiang, A.X.; Leyton-Brown, K. A Tutorial on the Proof of the Existence of Nash Equilibria; University of British Columbia: Vancouver, BC, Canada, 2008. [Google Scholar]
- Lindgren, A.; Doria, A. Probabilistic routing in intermittently connected networks. In Proceedings of the ACM International Symposium on Mobilde Ad Hoc Networking and Computing, Annapolis, MD, USA, 1–3 June 2003; pp. 19–20. [Google Scholar]
- Daly, E.M.; Haahr, M. Social network analysis for routing in disconnected delay-tolerant MANETs. In Proceedings of the ACM Interational Symposium on Mobile Ad Hoc Networking and Computing, Montreal, QC, Canada, 9–14 September 2007; pp. 32–40. [Google Scholar]
- Rhee, I.; Shin, M.; Hong, S.; Lee, K.; Kim, S.J.; Chong, S. On the levy-walk nature of human mobility. IEEE/ACM Trans. Netw. 2011, 19, 630–643. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).