Partial Pre-Emphasis for Pluggable 400 G Short-Reach Coherent Systems
Abstract
1. Introduction
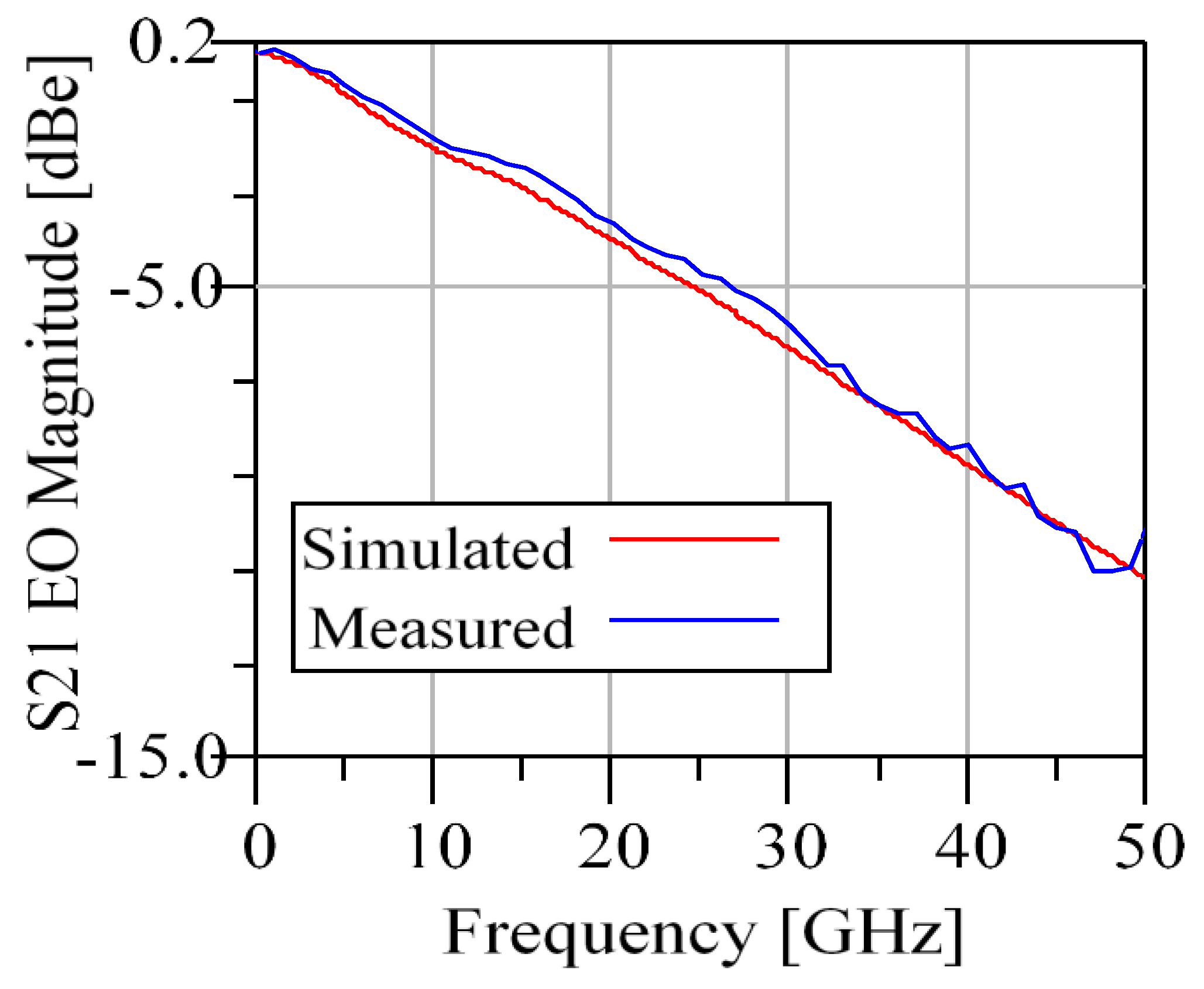
2. Silicon Photonics Modulators
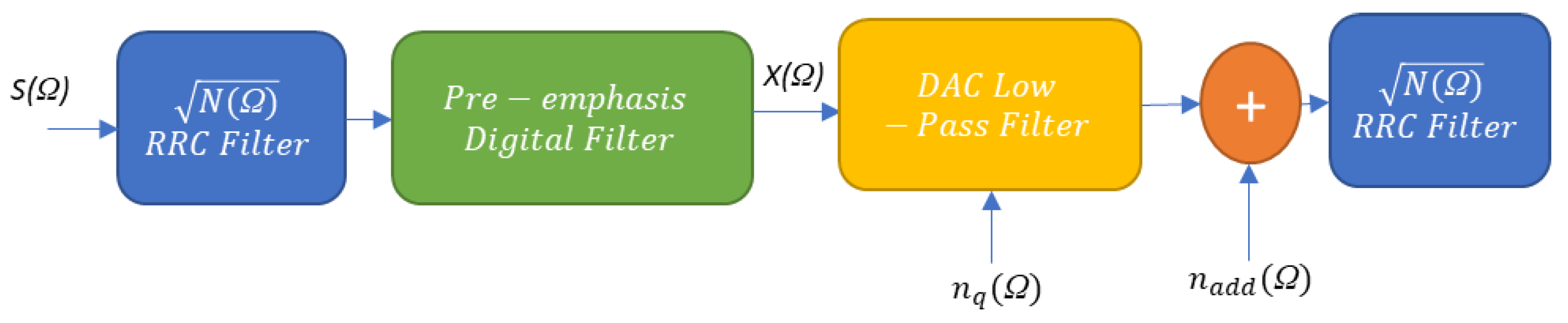
3. Pre-Emphasis in Layer-0 Optical Systems
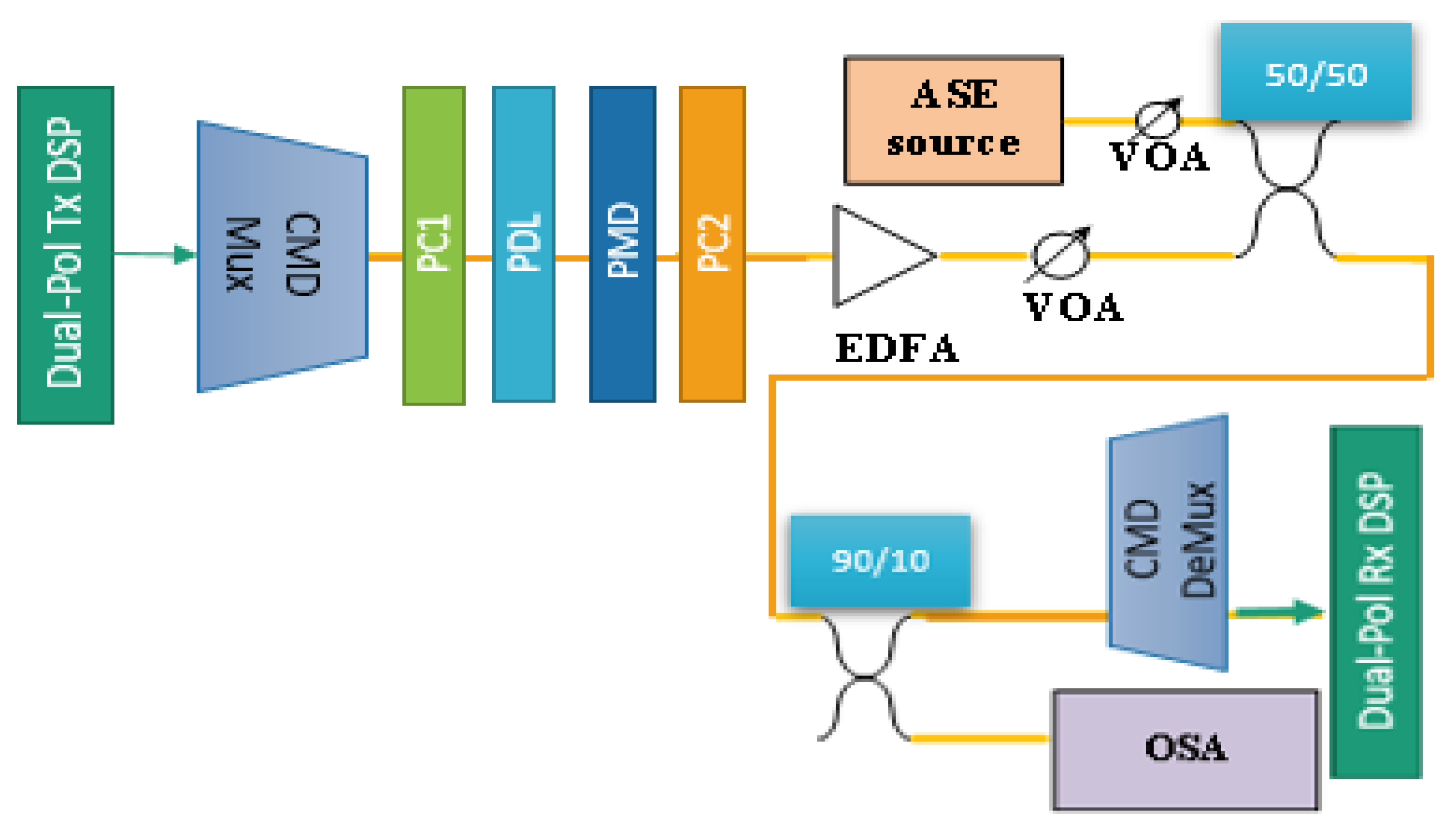
4. Experimental Setup and DSP
4.1. Results and Discussion
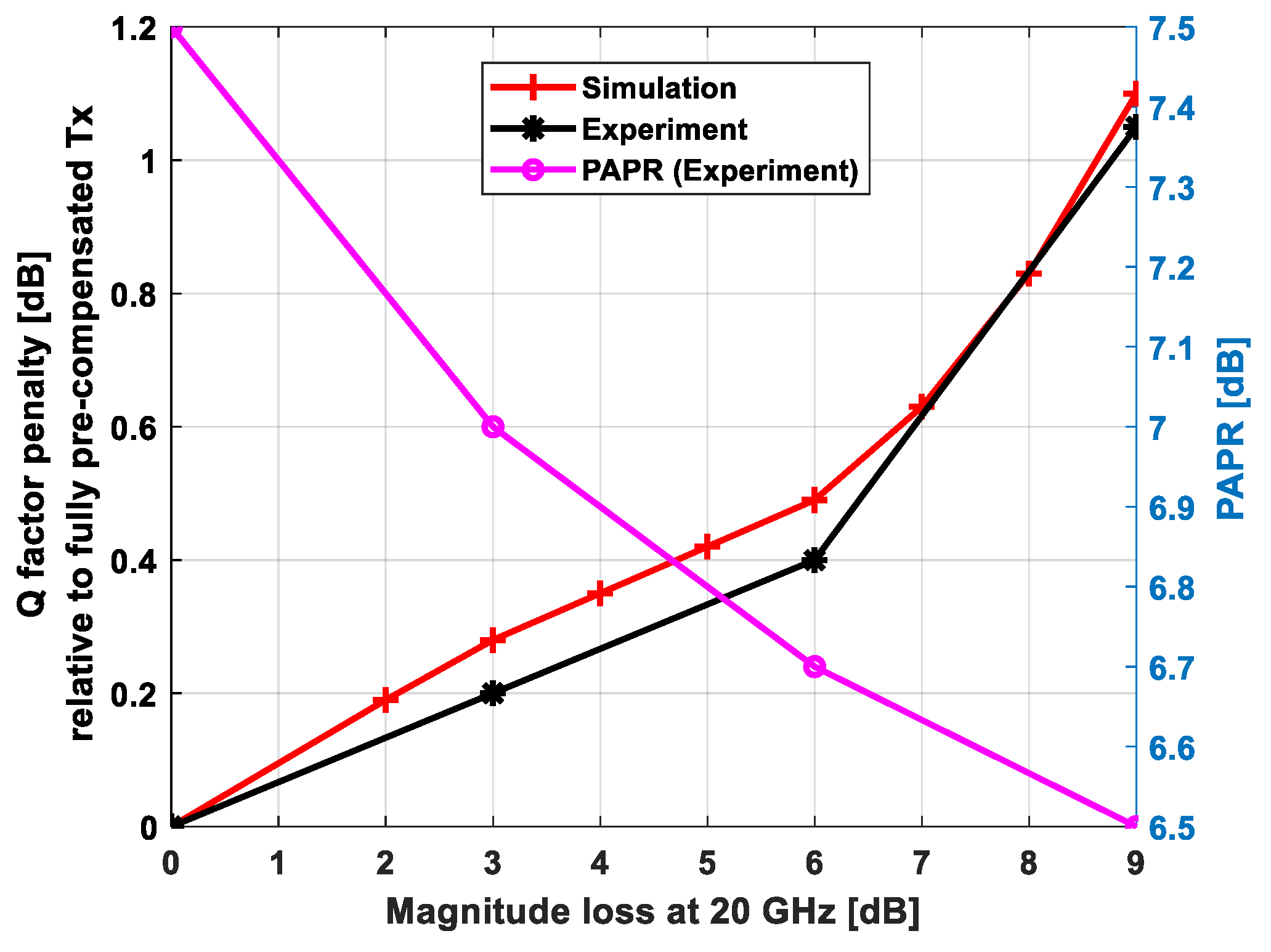
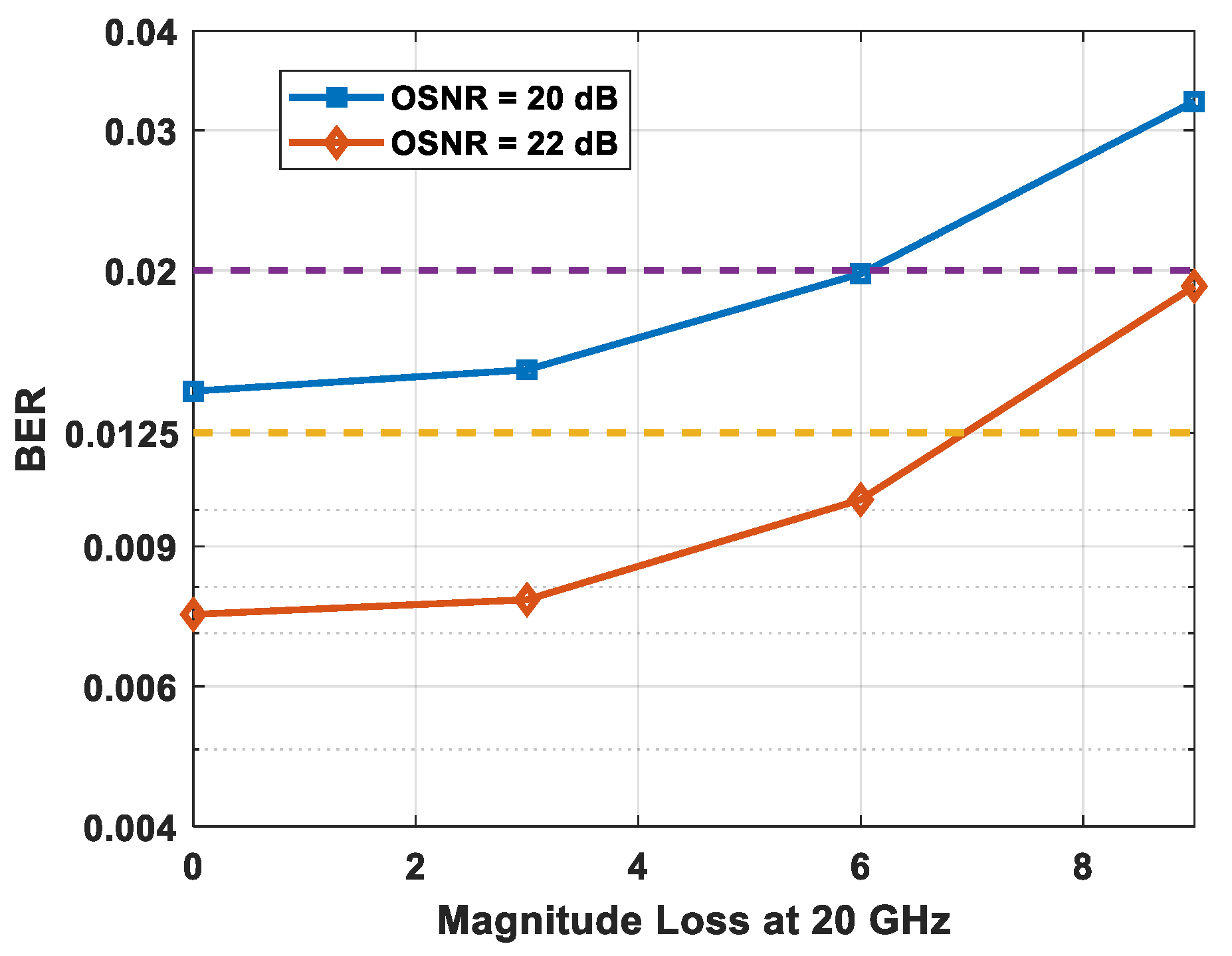
4.1.1. Impact of Partial Pre-Compensation on Q-Factor in a Single-Polarization Coherent System
4.1.2. Impact of Partial Pre-Compensation on Q-Factor in a Dual-Polarization Coherent System with PDL and PMD
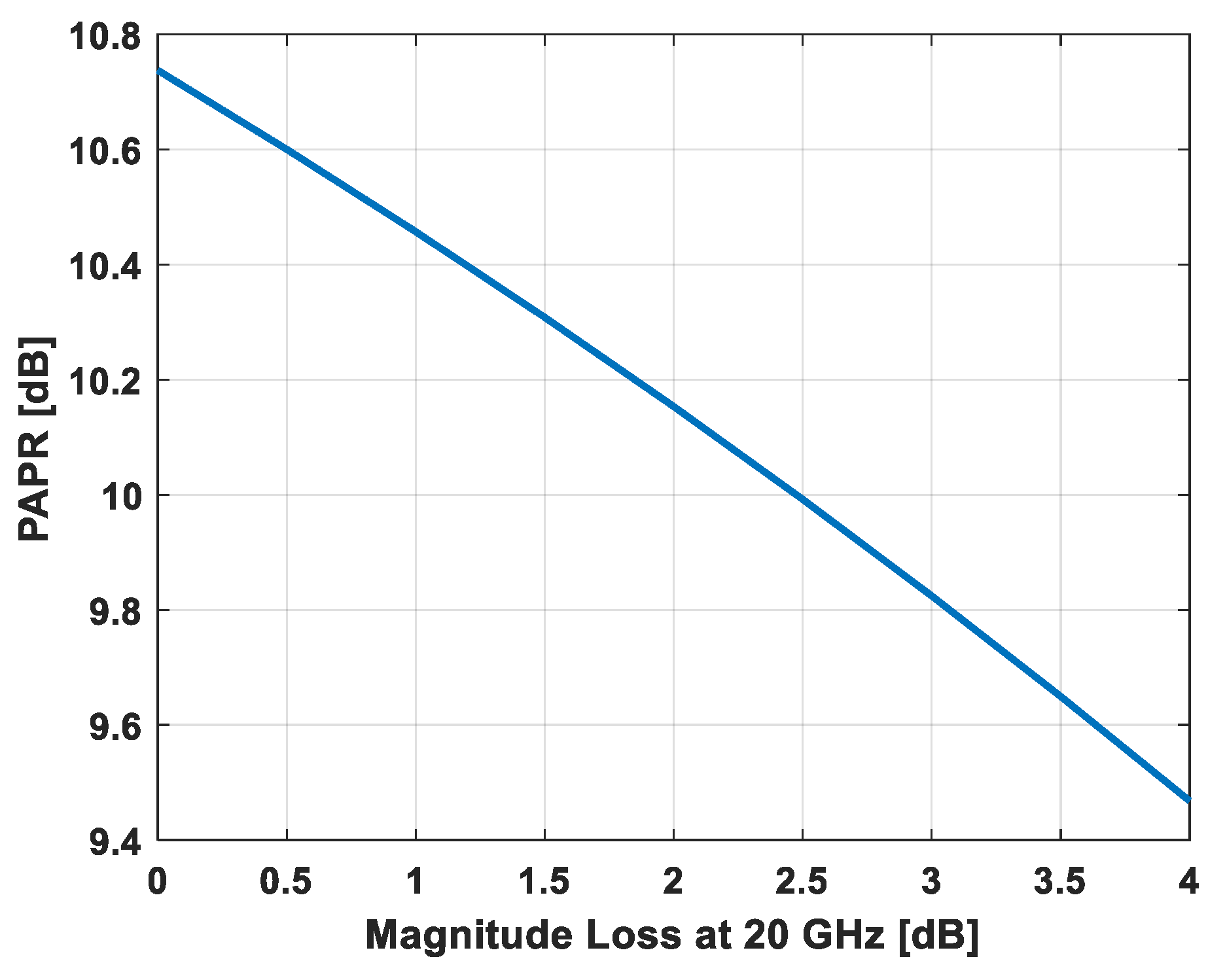
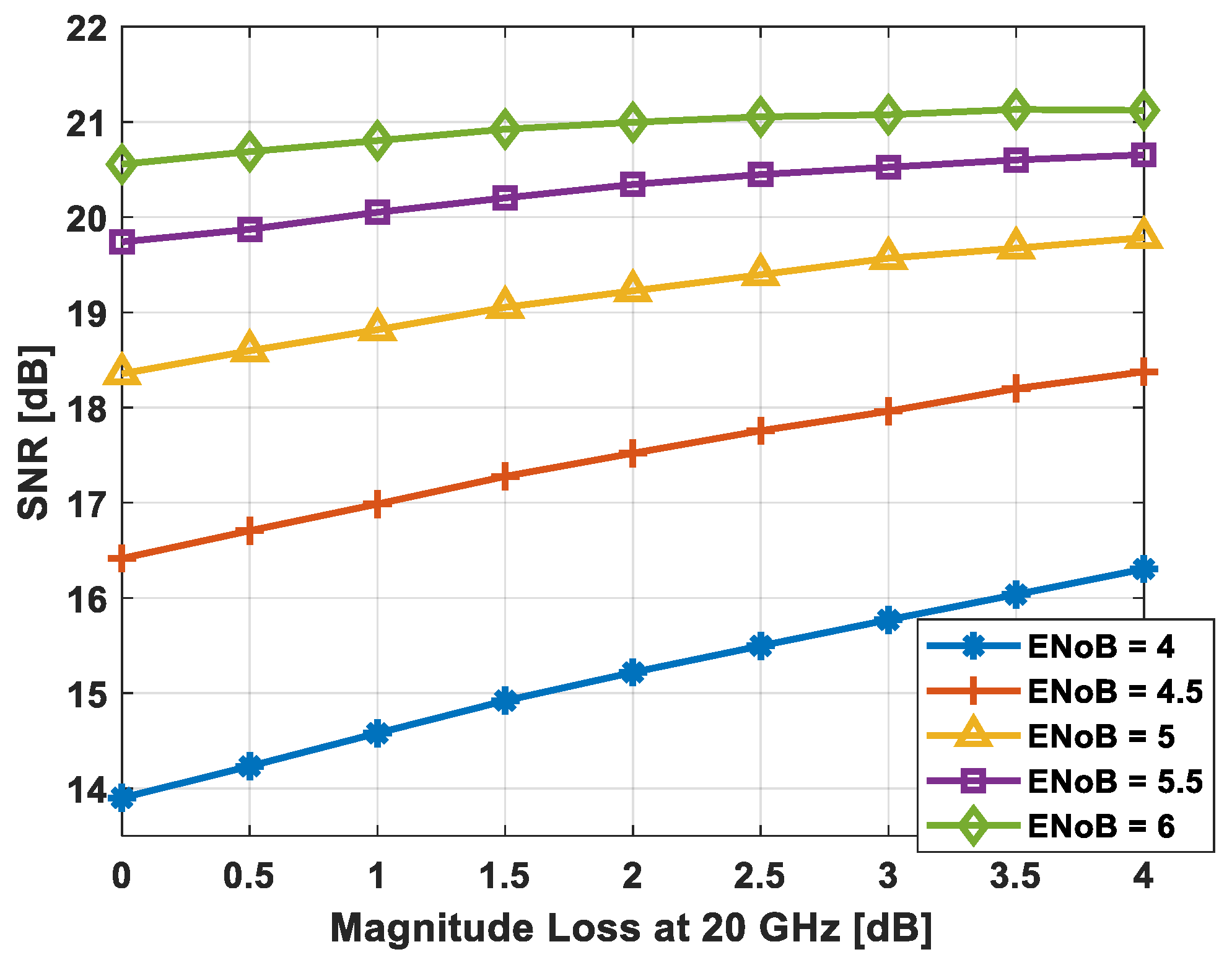
5. Design Trade-Offs
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- OIF. Implementation Agreement 400ZR, IA # OIF-400ZR 0.10-Draft, oif2017.245.10.pdf. Available online: https://www.oiforum.com/technical-work/hot-topics/400zr-2/ (accessed on 10 December 2019).
- Patel, D.; Ghosh, S.; Chagnon, M.; Samani, A.; Veerasubramanian, V.; Osman, M.; Plant, D.V. Design, analysis, and transmission system performance of a 41 GHz silicon photonic modulator. Opt. Exp. 2015, 23, 14263–14287. [Google Scholar] [CrossRef] [PubMed]
- Samani, A.; Chagnon, M.; Patel, D.; Veerasubramanian, V.; Ghosh, S.; Osman, M.; Zhong, Q.; Plant, D.V. A Low-Voltage 35-GHz Silicon Photonic Modulator-Enabled 112-Gb/s Transmission System. IEEE Photon. J. 2015, 7, 1–13. [Google Scholar] [CrossRef]
- Dong, P.; Xie, C.; Chen, L.; Buhl, L.L.; Chen, Y.K. 112-Gb/s monolithic PDM-QPSK modulator in silicon. Opt. Exp. 2012, 20, B624–B629. [Google Scholar] [CrossRef] [PubMed]
- Verbist, J.; Zhang, J.; Moeneclaey, B.; Soenen, W.; Van Weerdenburg, J.; Van Uden, R.; Okonkwo, C.; Bauwelinck, J.; Roelkens, G.; Yin, X. A 40-GBd QPSK/16-QAM integrated silicon coherent receiver. IEEE Photon. Technol. Lett. 2016, 28, 2070–2073. [Google Scholar] [CrossRef]
- Shi, W.; Lin, J.; Sepehrian, H.; Zhalehpour, S.; Zhang, Z.; Rusch, L.A. Silicon photonic modulators for high-capacity coherent transmissions. In Proceedings of the Optical Fiber Communication Conference 2019, San Diego, CA, USA, 3–7 March 2019. [Google Scholar]
- Doerr, C.; Chen, L.; Vermeulen, D.; Nielsen, T.; Azemati, S.; Stulz, S.; McBrien, G.; Xu, X.-M.; Mikkelsen, B.; Givehchi, M.; et al. Single-chip silicon photonics 100-Gb/s coherent transceiver. In Proceedings of the Optical Fiber Communication Conference 2014, San Francisco, CA, USA, 9–13 March 2014. [Google Scholar]
- Petousi, D.; Zimmermann, L.; Gajda, A.; Kroh, M.; Voigt, K.; Winzer, G.; Tillack, B.; Petermann, K. Analysis of optical and electrical tradeoffs of traveling-wave depletion-type Si Mach–Zehnder modulators for high-speed operation. IEEE J. Sel. Topics Quantum Electron. 2014, 21, 199–206. [Google Scholar] [CrossRef]
- Patel, D.; Parvizi, M.; Ben-Hamida, N.; Rolland, C.; Plant, D.V. Frequency response of dual-drive silicon photonic modulators with coupling between electrodes. Opt. Express 2018, 26, 8904–8915. [Google Scholar] [CrossRef]
- Wettlin, T.; Ohlendorf, S.; Rahman, T.; Wei, J.; Calabrò, S.; Stojanovic, N.; Pachnicke, S. Beyond 200 Gb/s PAM4 transmission using Tomlinson-Harashima precoding. In Proceedings of the 2019 European Conference on Optical Communication (ECOC), Dublin, Ireland, 22–26 September 2019. [Google Scholar]
- Hu, Q.; Schuh, K.; Chagnon, M.; Buchali, F.; Bülow, H. 84 GBd Faster-Than-Nyquist PAM-4 Transmission Using Only Linear Equalizer at Receiver. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019. [Google Scholar]
- Wei, J.; Zhang, L.; Prodaniuc, C.; Stojanović, N.; Xie, C. Linear Pre-Equalization Techniques for Short Reach Single Lambda 225 Gb/s PAM IMDD Systems. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Wei, J.; Stojanovic, N.; Zhang, L.; Calabrò, S.; Rahman, T.; Xie, C.; Charlet, G. Experimental comparison of modulation formats for 200 G/λ IMDD data center networks. In Proceedings of the 2019 European Conference on Optical Communication (ECOC), Dublin, Ireland, 22–26 September 2019. [Google Scholar]
- Napoli, A.; Mezghanni, M.M.; Rafique, D.; Sleiffer, V.A.; Rahman, T.; Spinnler, B.; Calabrò, S.; Bohn, M. Novel DAC digital pre-emphasis algorithm for next generation flexible optical transponders. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 22–26 March 2015. [Google Scholar]
- Rafique, D.; Napoli, A.; Calabro, S.; Spinnler, B. Digital preemphasis in optical communication systems: On the DAC requirements for terabit transmission applications. J. Lightw. Technol. 2014, 32, 3247–3256. [Google Scholar] [CrossRef]
- Khanna, G.; Spinnler, B.; Calabrò, S.; De Man, E.; Hanik, N. A Robust Adaptive Pre-Distortion Method for Optical Communication Transmitter. IEEE Photon. Technol. Lett. 2015, 28, 752–755. [Google Scholar] [CrossRef]
- Rafique, D. Interplay of Pulse Shaping and Pre-Emphasis for High Symbol Rate Coherent Transmission Systems. In Proceedings of the 2018 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018. [Google Scholar]
- Napoli, A.; Mezghanni, M.M.; Rahman, T.; Rafique, D.; Palmer, R.; Spinnler, B.; Calabrò, S.; Castro, C.; Kuschnerov, M.; Bohn, M. Digital compensation of bandwidth limitations for high-speed DAC and ADCs. J. Lightw. Technol. 2016, 34, 3053–3064. [Google Scholar] [CrossRef]
- Park, M.; Jun, H.; Cho, J.; Cho, N.; Hong, D.; Kang, C. PAPR Reduction in OFDM Transmission Using Hadamard Transform. In Proceedings of the 2000 IEEE International Conference on Communications. ICC 2000. Global Convergence Through Communications. Conference Record, New Orleans, LA, USA, 18–22 June 2000. [Google Scholar]
- Azeredo-Leme, C. Clock Jitter Effects on Sampling: A Tutorial. IEEE Circuits Syst. Mag. 2011, 11, 26–37. [Google Scholar] [CrossRef]
- Gardner, F. A BPSK/QPSK timing-error detector for sampled receivers. IEEE Trans. Commun. 1986, 34, 423–429. [Google Scholar] [CrossRef]
- Godard, D. Passband Timing Recovery in an All-Digital Modem Receiver. IEEE Trans. Commun. 1978, 26, 517–523. [Google Scholar] [CrossRef]
- Abdo, A.; Aouini, S.; Riaz, B.; Ben-Hamida, N.; D’Amours, C. Adaptive Coherent Receiver Settings for Optimum Channel Spacing in Gridless Optical Networks. Future Internet 2019, 11, 206. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdo, A.; Li, X.; Alam, M.S.; Parvizi, M.; Ben-Hamida, N.; D’Amours, C.; Plant, D. Partial Pre-Emphasis for Pluggable 400 G Short-Reach Coherent Systems. Future Internet 2019, 11, 256. https://doi.org/10.3390/fi11120256
Abdo A, Li X, Alam MS, Parvizi M, Ben-Hamida N, D’Amours C, Plant D. Partial Pre-Emphasis for Pluggable 400 G Short-Reach Coherent Systems. Future Internet. 2019; 11(12):256. https://doi.org/10.3390/fi11120256
Chicago/Turabian StyleAbdo, Ahmad, Xueyang Li, Md Samiul Alam, Mahdi Parvizi, Naim Ben-Hamida, Claude D’Amours, and David Plant. 2019. "Partial Pre-Emphasis for Pluggable 400 G Short-Reach Coherent Systems" Future Internet 11, no. 12: 256. https://doi.org/10.3390/fi11120256
APA StyleAbdo, A., Li, X., Alam, M. S., Parvizi, M., Ben-Hamida, N., D’Amours, C., & Plant, D. (2019). Partial Pre-Emphasis for Pluggable 400 G Short-Reach Coherent Systems. Future Internet, 11(12), 256. https://doi.org/10.3390/fi11120256



