Reinforcement Learning Based Query Routing Approach for P2P Systems
Abstract
1. Introduction
- We introduce a fully distributed query routing approach for pure unstructured P2P systems, in which each peer learns only from its local gathered data.
- We introduce a new formulation for the K-Neighbors-Selection (K-NS) problem different from that of the existing approaches. Indeed, we consider that the natural model for this issue are formalizations from reinforcement learning, in which an agent learns by taking actions that produce rewards. The goal of the agent is to find a selection policy of actions that maximizes the cumulative reward. In the query routing setting, the forwarder peer could run a learning algorithm (e.g., agent) that selects k neighbors (e.g., actions) for each search query. Each selected neighbor yields a binomial reward which expresses its ability to produce pertinent documents to the query. Indeed, the agent must learn a K-NS policy to maximize the cumulative rewards leading to higher user satisfaction.
- We address the cold-start issue during training, which is considered as the main hindrance of query routing approaches based on supervised machine learning or data-mining methods. Indeed, a cold start happens when a new peer joins the network. Existing query-oriented methods assume that each peer has submitted certain number of queries and received replies from relevant peers. Hence, the gathered data from previous queries are stored in the sender log file then used as training data. However, this assumption is not fulfilled in the case of a newly joined peer. Therefore, existing methods [7,9,15,16] required to randomly flood a certain number of queries to gather training data, which undoubtedly leads to achieving low performances during the training phase. To tackle this problem, we introduce here reinforcement learning into the neighbors selection algorithm. Indeed, our approach RLQR balances between exploration (pulling different neighbors to learn new information) and exploitation (i.e., pulling the neighbor with the highest estimated reward based on previous queries). Doing so, RLQR improves the routing performance continuously and therefore goes quickly through the cold-start phase [7,17,18,19].
2. Related Work
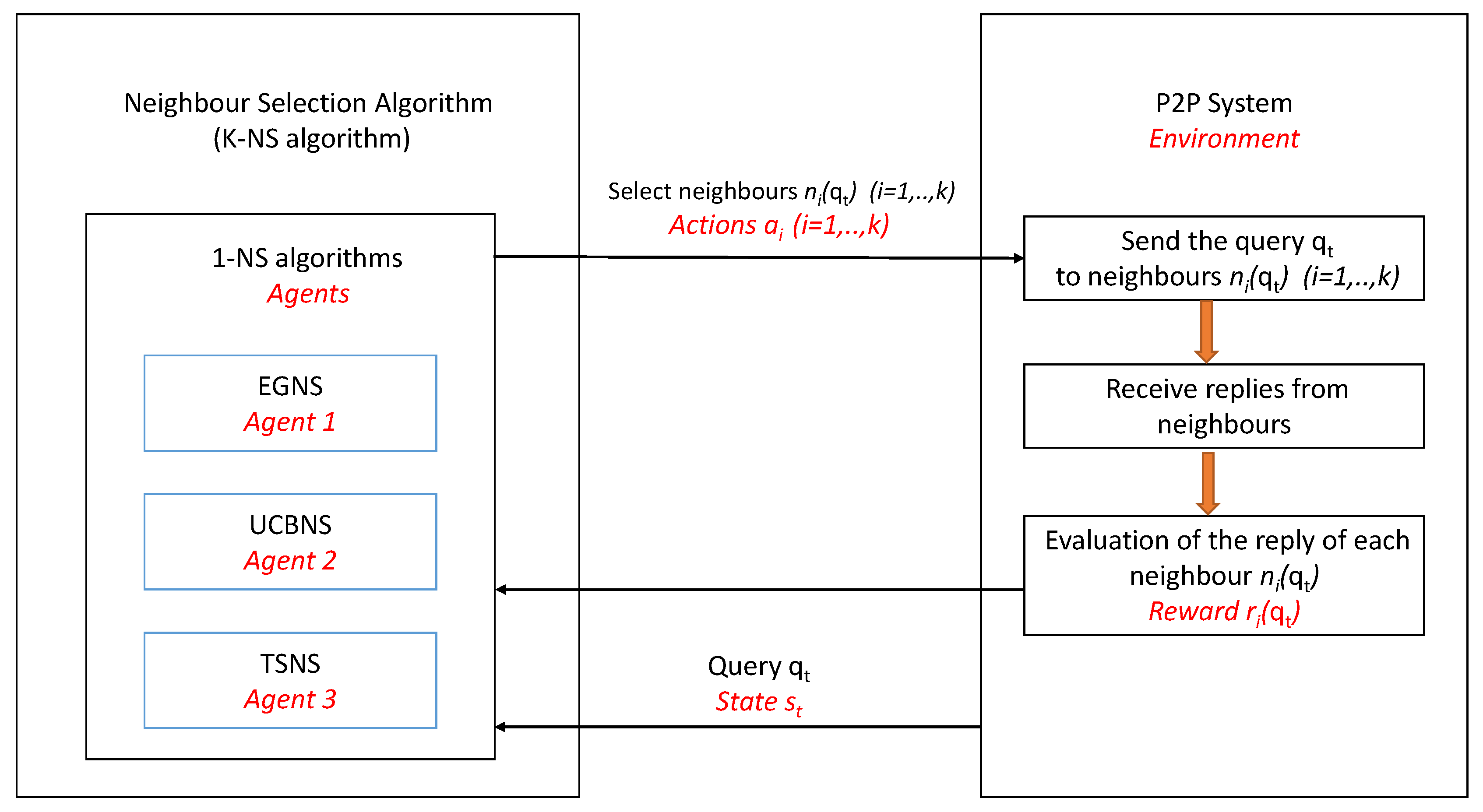
3. RLQR Approach
3.1. Problem Formulation
3.2. 1-Neighbor-Selection Algorithms
3.2.1. EGNS: Epsilon-Greedy Based 1-NS Algorithm
| Algorithm 1 EGNS: Epsilon-greedy-based 1-NS algorithm |
| Parameters: : search query at trial t. : set of all neighbors : average rewards of the m neighbors : specified value of epsilon : the neighbor to be selected for
|
3.2.2. UCBNS: UBC-Based 1-NS Algorithm
| Algorithm 2 UCBNS: UBC-based 1-NS algorithm |
| Parameters: : search query at trial t. : set of neighbors : average rewards of the K neighbors : vector storing the number of times we have selected each of the K neighbors : the neighbor to be selected for
|
3.2.3. TSNS: Thompson Sampling-Based 1-NS Algorithm
| Algorithm 3 TSNS: Thompson sampling-based 1-NS algorithm |
| Parameters: : search query at trial t. : set of neighbors : alpha parameters of the m neighbors : beta parameters of the m neighbors : the neighbor to be selected for Initialisation:
|
3.3. K-NS Algorithm
| Algorithm 4 K-NS algorithm |
| Input: : search query at trial t. : set of all neighbors k: number of neighbors to be selected for Output: S: set of neighbors to be selected Initialization: :
|
4. Performance Evaluation
4.1. Evaluation Measures
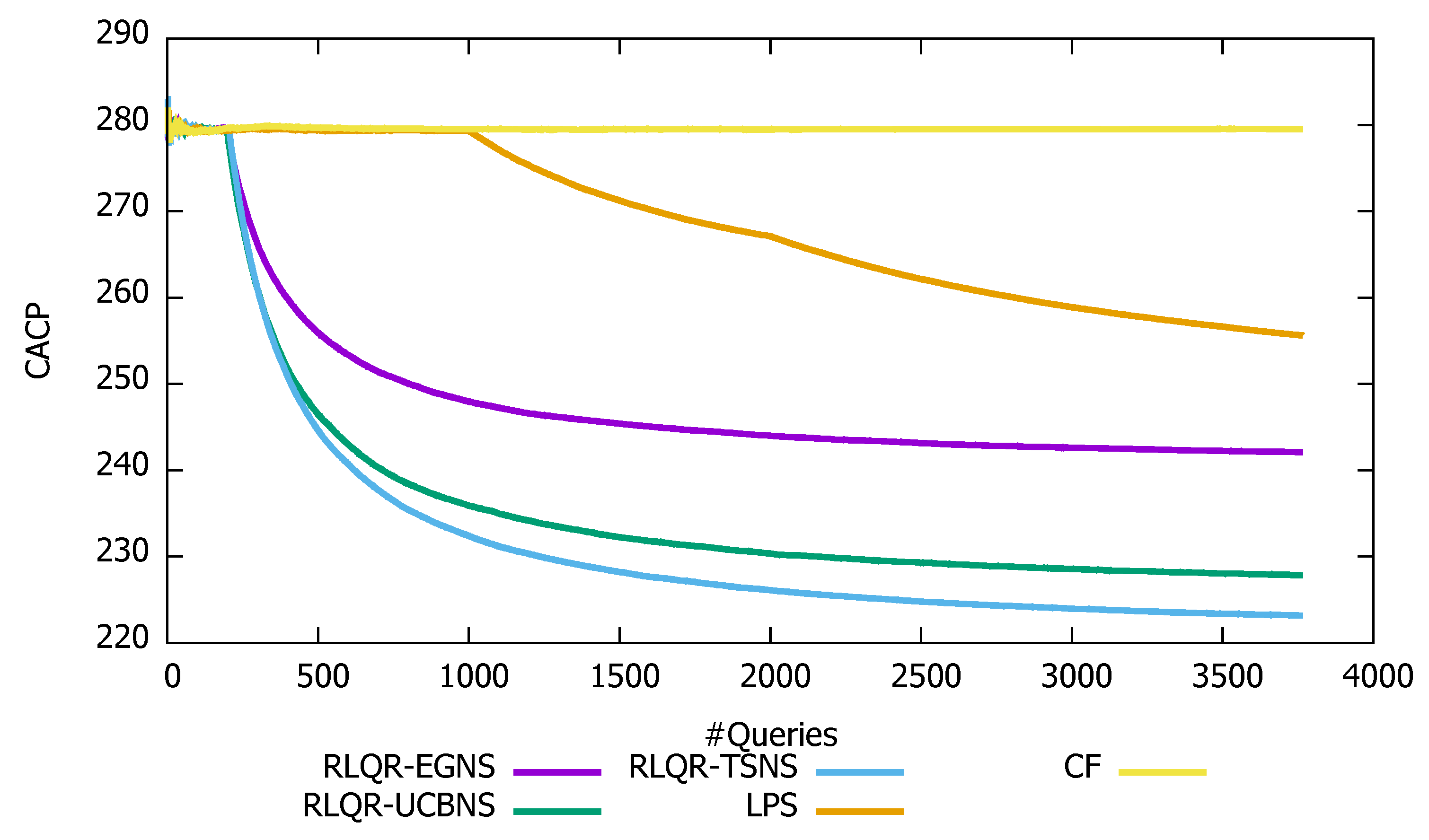
- CP(): it refers to the number of contacted peers for the query . The Cumulative Average of the number of Contacted Peers up to n sent queries () is defined as follows:
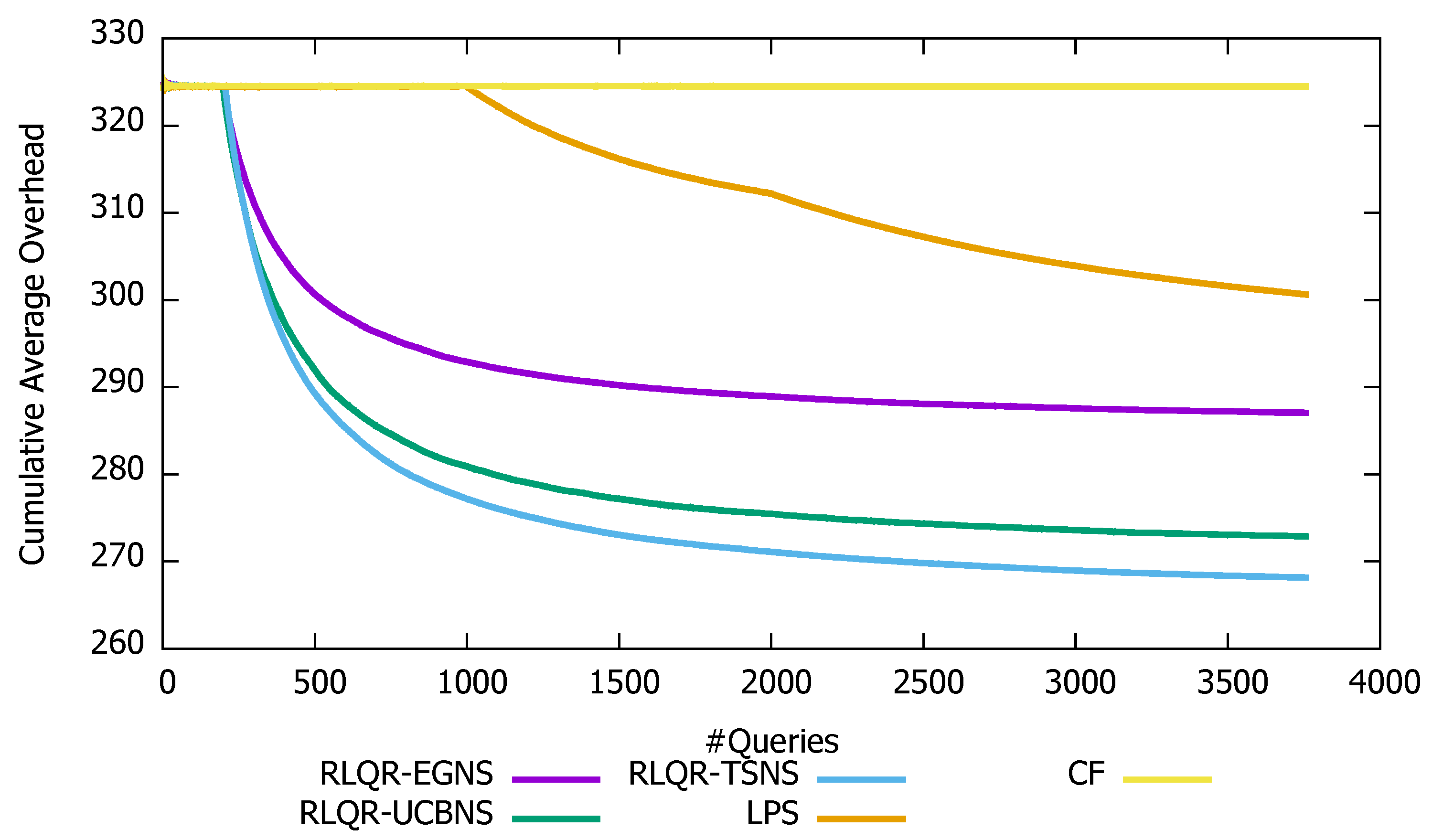
- Overhead(): it refers to the number of exchanged messages for the query . The Cumulative Average Overhead up to n sent queries () is defined as follows:
4.1.1. Retrieval Effectiveness of the Routing Algorithms
4.1.2. Search Cost of the Routing Algorithms
5. Conclusions
- Studying the impact of the churn problem on the introduced neighbor selection strategies. Indeed, in P2P systems peers could join and leave the network at any time leading to frequent changes of neighbors links. This latter may have an impact on the performance of the neighbor selection algorithm.
- Introducing a reinforcement learning model that includes the context in the neighbor selection strategy to make the forwarding decision conditional on the state of the environment.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chernov, S.; Serdyukov, P.; Bender, M.; Michel, S.; Weikum, G.; Zimmer, C. Database selection and result merging in P2P web search. In Proceedings of the 3rd International Workshop on Databases, Information Systems, and Peer-to-Peer Computing (DBISP2P 2005), Trondheim, Norway, 28–29 August 2005; Lecture Notes in Computer Science. Springer: Heidelberg, Germany, 2005; Volume 4125. [Google Scholar]
- Chawathe, Y.; Ratnasamy, S.; Breslau, L. Making gnutella-like P2P systems scalable. In Proceedings of the 2003 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Karlsruhe, Germany, 25–29 August 2003; pp. 407–418. [Google Scholar]
- Stoica, I.; Morris, R.; Liben-Nowell, D.; Karger, D.R.; Kaashoek, M.F.; Dabek, F.; Balakrishnan, H. Chord: A Scalable Peer-to-Peer Lookup Protocol for Internet Applications. IEEE/ACM Trans. Netw. 2003, 11, 17–32. [Google Scholar] [CrossRef]
- Rowstron, A.; Druschel, P. Pastry: Scalable, decentralized object location, and routing for large-scale peer-to-peer systems. In Proceedings of the IFIP/ACM International Conference on Distributed Systems Platforms, Heidelberg, Germany, 12–16 November 2001; Volume 2218, pp. 329–350. [Google Scholar]
- Taoufik, Y.; Sofian, H.; Yahia, S.B. Query Learning-Based Scheme for Pertinent Resource Lookup in Mobile P2P Networks. IEEE Access 2019, 7, 49059–49068. [Google Scholar]
- Deshpande, M.; Venkatasubramanian, N. The Different Dimensions of Dynamicity. In Proceedings of the 4th International Conference on Peer-to-Peer Computing (P2P’04), Zurich, Switzerland, 25–27 August 2004; pp. 244–251. [Google Scholar]
- Yeferny, T.; Arour, K. Efficient routing method in p2p systems based upon training knowledge. In Proceedings of the 26th International Conference on Advanced Information Networking and Applications Workshops, Fukuoka, Japan, 26–29 March 2012; pp. 300–305. [Google Scholar]
- Yeferny, T.; Arour, K.; Bouzeghoub, A. An efficient peer-to-peer semantic overlay network for learning query routing. In Proceedings of the 27th IEEE International Conference on Advanced Information Networking and Applications (AINA), Barcelona, Spain, 25–28 March 2013; pp. 1025–1032. [Google Scholar]
- Arour, K.; Yeferny, T. Learning model for efficient query routing in P2P information retrieval systems. Peer-to-Peer Netw. Appl. 2015, 8, 741–757. [Google Scholar] [CrossRef]
- Yeferny, T.; Hamad, S.; Belhaj, S. CDP: A Content Discovery Protocol for Mobile P2P Systems. Int. J. Comput. Sci. Netw. Secur. 2018, 18, 28. [Google Scholar]
- Lv, Q.; Cao, P.; Cohen, E.; Li, K.; Shenker, S. Search and replication in unstructured peer-to-peer networks. In Proceedings of the 16th International Conference on Supercomputing, New York, NY, USA, 22–26 June 2002; ACM: New York, NY, USA, 2002; pp. 84–95. [Google Scholar] [CrossRef]
- Jia, Z.; You, J.; Rao, R.; Li, M. Random walk search in unstructured P2P. J. Syst. Eng. Electron. 2006, 17, 648–653. [Google Scholar]
- Kalogeraki, V.; Gunopulos, D.; Zeinalipour-Yazti, D. A local search mechanism for peer-to-peer networks. In Proceedings of the Eleventh International Conference on Information and Knowledge Management, McLean, VA, USA, 4–9 November 2002; pp. 300–307. [Google Scholar]
- Dietzfelbinger, M. Gossiping and broadcasting versus computing functions in networks. Discret. Appl. Math. 2004, 137, 127–153. [Google Scholar] [CrossRef][Green Version]
- da Hora, D.N.; Macedo, D.F.; Oliveira, L.B.; Siqueira, I.G.; Loureiro, A.A.F.; Nogueira, J.M.; Pujolle, G. Enhancing peer-to-peer content discovery techniques over mobile ad hoc networks. Comput. Commun. 2009, 32, 1445–1459. [Google Scholar] [CrossRef]
- Ciraci, S.; Korpeoglu, I.; Ulusoy, Z. Reducing query overhead through route learning in unstructured peer-to-peer network. J. Netw. Comput. Appl. 2009, 32, 550–567. [Google Scholar] [CrossRef]
- Li, L.; Chu, W.; Langford, J.; Schapire, R.E. A Contextual-bandit Approach to Personalized News Article Recommendation. In Proceedings of the 19th International Conference on World Wide Web WWW ’10, Raleigh, NC, USA, 26–30 April 2010; pp. 661–670. [Google Scholar]
- Wang, L.; Wang, C.; Wang, K.; He, X. BiUCB: A Contextual Bandit Algorithm for Cold-Start and Diversified Recommendation. In Proceedings of the 2017 IEEE International Conference on Big Knowledge (ICBK), Hefei, China, 9–10 August 2017; pp. 248–253. [Google Scholar]
- Qiao, R.; Yan, S.; Shen, B. A Reinforcement Learning Solution to Cold-Start Problem in Software Crowdsourcing Recommendations. In Proceedings of the 2018 IEEE International Conference on Progress in Informatics and Computing (PIC), Suzhou, China, 14–16 December 2018; pp. 8–14. [Google Scholar]
- Lu, J.; Callan, J. Content-based retrieval in hybrid peer-to-peer networks. In Proceedings of the Twelfth International Conference on Information and Knowledge Management, CIKM ’03, New Orleans, LA, USA, 3–8 November 2003. [Google Scholar]
- Kurid, H.A.; Alnusairi, T.S.; Almujahed, H.S. OBAME: Optimized Bio-inspired Algorithm to Maximize Search Efficiency in P2P Databases. Procedia Comput. Sci. 2013, 21, 60–67. [Google Scholar] [CrossRef][Green Version]
- Shen, W.W.; Su, S.; Shuang, K.; Yang, F.C. SKIP: An efficient search mechanism in unstructured P2P networks. J. China Univ. Posts Telecommun. 2011, 17, 64–71. [Google Scholar] [CrossRef]
- Christoph, T.; Steffen, S.; Adrian, W. Semantic Query Routing in Peer-to-Peer Networks based on Social Metaphors. In Proceedings of the 13th International World Wide Web Conference, New York, NY, USA, 17–20 May 2004; pp. 55–68. [Google Scholar]
- Ganter, B.; Wille, R. Formal Concept Analysis: Mathematical Foundations; Springer: New York, NY, USA, 1997. [Google Scholar]
- Berry, D.A.; Fristedt, B. Bandit Problems. Sequential Allocation of Experiments. Monographs on Statistics and Applied Probability. Biom. J. 1987, 29, 20. [Google Scholar]
- Agrawal, R. Sample Mean Based Index Policies with O(log n) Regret for the Multi-Armed Bandit Problem. Adv. Appl. Probab. 1995, 27, 1054–1078. [Google Scholar] [CrossRef]
- Thompson, W.R. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika 1933, 25, 285–294. [Google Scholar] [CrossRef]
- Jelasity, M.; Montresor, A.; Jesi, G.P.; Voulgaris, S. The Peersim Simulator. March 2010. Available online: http://peersim.sf.net (accessed on 7 December 2019).
- Zammali, S.; Arour, K. P2PIRB: Benchmarking framework for P2PIR. In Proceedings of the Third International Conference on Data Management in Grid and Peer-to-Peer Systems (Globe), Bilbao, Spain, 1–2 September 2010; pp. 100–111. [Google Scholar]
- Makhoul, J.; Kubala, F.; Schwartz, R.; Weischedel, R. Performance Measures For Information Extraction. In Proceedings of the DARPA Broadcast News Workshop, Herndon, VA, USA, 28 February–3 March 1999; pp. 249–252. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alanazi, F.; Yeferny, T. Reinforcement Learning Based Query Routing Approach for P2P Systems. Future Internet 2019, 11, 253. https://doi.org/10.3390/fi11120253
Alanazi F, Yeferny T. Reinforcement Learning Based Query Routing Approach for P2P Systems. Future Internet. 2019; 11(12):253. https://doi.org/10.3390/fi11120253
Chicago/Turabian StyleAlanazi, Fawaz, and Taoufik Yeferny. 2019. "Reinforcement Learning Based Query Routing Approach for P2P Systems" Future Internet 11, no. 12: 253. https://doi.org/10.3390/fi11120253
APA StyleAlanazi, F., & Yeferny, T. (2019). Reinforcement Learning Based Query Routing Approach for P2P Systems. Future Internet, 11(12), 253. https://doi.org/10.3390/fi11120253




