Abstract
Static multi-controller deployment architecture cannot adapt to the drastic changes of network traffic, which will lead to a load imbalance between controllers, resulting in a high packet loss rate, high latency, and other network performance degradation problems. In this paper, an efficient dynamic load balancing scheme based on Nash bargaining is proposed for a distributed software-defined network. Firstly, considering the connectivity of network nodes, the switch migration problem is transformed into a network mapping relationship reconstruction problem. Then, we establish the Nash bargaining game model to fairly optimize the two contradictory goals of migration cost and load balance. Finally, the model is solved by an improved firefly algorithm, and the optimal network mapping state is obtained. The experimental results show that this scheme can optimize the migration cost and load balance at the same time. Compared with the existing research schemes, the migration process of the switch is optimized, and, while effectively balancing the load of the control plane, the migration cost is reduced by 14.5%.
1. Introduction
The Software-Definition Network (SDN) [1] is an innovative network architecture. Its core technology, OpenFlow, separates the network control plane from the data plane, enabling flexible centralized control of distributed forwarding devices and providing an excellent platform for the creation of core networks and applications. With the increasing demand of the network, a large amount of data traffic is sent from a forwarding device, such as a switch, to the control plane. Traditional single-controller architecture is constrained by its own performance and capacity. It faces significant challenges in network security, reliability, and robustness [2,3]. Therefore, industry proposes to establish a multi-controller architecture with logically centralized physical distribution based on the original single-controller architecture [4]. This architecture requires multiple controllers to be deployed on the control plane and divide the appropriate subdomain for each controller. Each controller is responsible for centrally managing switches in its domain. Multiple controllers cooperate with each other to achieve efficient network management [5,6,7,8,9]. However, multi-controller deployment is a static network architecture. Switches and controller nodes form a fixed network topology, which cannot adapt to the dynamic changes of network traffic. If the switching traffic in the domain increases or decreases sharply in a specific period of time, the load difference between controllers will be huge, which will cause a load imbalance of the multi-controller network architecture, resulting in a high packet loss rate, high latency, low throughput, and other network performance degradation problems.
Load imbalance issues severely impact the performance of an entire network. Therefore, in recent years, the load balancing problem of the SDN multi-controller has become a research hotspot. Fu et al. [7] proposed a multi-controller sleep model for software-defined networks, allowing some controllers to enter a sleep state under light load conditions to save system costs. Following the introduction of OpenFlow 1.3 [10], Dixit et al. [11] proposed an elastic distributed network architecture for the first time, changing the mapping relationship between the controllers and switches through switch migration to implement controller load transfer of the OpenFlow standard. As an elastic flow control solution, switch migration can effectively balance the load imbalance network. Based on this idea, Yao et al. [12] proposed to migrate the switch to the controller with the lowest resource utilization to achieve load balancing. Zhang et al. [13] proposed an online load balancing method, which describes the load balancing problem as an optimization problem that minimizes the control plane’s response time. Because the migration process depends on the actual response time, the scheme can be implemented online.
The above studies are all based on choosing a suitable switch from the overload controller to migrate to the light-load controller to achieve load balancing. Although this method reduces the number of migrations, it easily causes load oscillations. Zhou et al. [14] proposed a switch group-based SDN multi-controller load balancing mechanism. This mechanism chooses a group of switches to reduce the load of the overload controller to an average level and then considers the load and delay factors of the light-load controller and transfers multiple switches to the appropriate controllers. This method not only balances the load between controllers but also solves the problem of load oscillation. Mohanasundaram et al. [15] proposed game theoretic switch-controller mapping with traffic variations in software-defined networks, describing the problem as a Markov decision process, reducing frequent migration between controllers and obtaining a stable mapping relationship. Wang et al. [16] proposed a switch migration-based decision-making scheme, which considered the load balancing degree and migration cost and achieved a compromise between the two performance indicators. Since the dimensions of the two performance indicators are not consistent, it is impossible to obtain the same degree of optimization. The authors in [17] proposed a heuristic approach considering the benefits of the immigration and outmigration controllers. Liu et al. [18] proposed a load balancing scheme based on multi-objective optimization for a software-defined network. Using a multi-objective genetic algorithm based on NSGA-II, two conflicting objectives (i.e., the load balancing degree of the control plane and the communication overhead caused by switch migration) were optimized simultaneously to obtain a high-quality and wide Pareto frontier. However, the genetic algorithm has weak convergence and can only obtain a set of non-inferior solutions. This previous article does not suggest how to choose the optimal solution.
According to the current research, switch migration as an elastic control scheme can effectively solve the problem of the unbalanced load distribution of controllers in a network. By moving the switch managed by the overload controller to the light-load controller, the dynamic load adjustment of the controllers can be realized. However, in the research on switch migration, most of the schemes still have the following problems:
- Although the existing switch migration schemes can dynamically adjust the controller load, in the process of switch migration, network performance and migration cost are not fully considered, resulting in low migration efficiency and easily leading to the rigidity of the selection of the target controller. At the same time, the high complexity migration algorithm and multi-switch migration conflict also reduce the resource utilization of the controller.
- The migration strategy is too idealized to consider the connectivity between the network’s topological nodes, and the influence of isolated nodes on network performance is neglected.
- Based on the above multi-objective optimization problem, it is impossible to weigh the contradictory goals fairly, and the multi-objective intelligent optimization algorithm cannot obtain the optimal solution.
This paper proposes an efficient load balancing scheme based on Nash bargaining (LBSNB). Firstly, the switch migration problem is equivalent to the network remapping problem. Based on the Nash bargaining game model, two contradictory indicators, load balance degree and migration cost, are modeled and the connectivity between network devices is considered to build the policy set, which prevents an idealized reconstruction state. Then, an improved firefly algorithm is proposed to solve the model. Finally, experiments are carried out based on simulated scenarios and compared with other optimization algorithms. The experimental results show that the proposed algorithm can fairly balance the load balancing degree and migration costs and can quickly obtain a Pareto optimal solution, which verifies the effectiveness of the proposed strategy.
The rest of the paper is organized as follows: Section 2 presents the model and the problem formulation of switch migration. The LBSNB schemes proposed in this paper are explained in Section 3. In Section 4, the optimization algorithm for solving the model is proposed. In Section 5, multiple scenarios, experiments, and analyses are carried out. Finally, we conclude the paper and suggest future work in Section 6.
2. Analysis and Modeling
In this section, we illustrate the problem of controller load imbalance in the process of multi-controller deployment in a distributed network and demonstrate that node connectivity is an essential factor that cannot be ignored in switch migration. Then, based on the connectivity of the network nodes, the load balance degree and migration cost of the network reconstruction are analyzed and modeled, and the parameter definitions and related calculations are given.
2.1. Problem Analysis
SDN is a new network architecture with programmable functions and a separate forwarding plane and control plane. It is mainly divided into three layers: the data layer, the control layer, and the application layer. Based on the three-tier architecture of the SDN, the controller can control and manage the SDN switch through the South interface (such as the OpenFlow protocol [19]) and provide programmable support to the application layer through the north interface.
The OpenFlow protocol provides more solutions for controller load imbalance. The OpenFlow protocol is a standard protocol used for the interaction information between the controller and the SDN switch. The general OpenFlow 1.3 protocol presently supports three message types: controller-switch message (such as Role-Request), asynchronous message (such as Packet-In), and symmetric message (such as Echo request). At the same time, OpenFlow requires that the controller has three roles for each switch: equal, master, and slave [20]. The default role of the controller is equal. Controllers in the equal role can receive all asynchronous messages from the switch. The controller can request to be a slave through Role-Request. The slave controller can only read the connected switch (i.e., read-only). The controller can also request to assume the master role of the switch. The controller with the master role is similar to the equal role controller and can fully access the switch. However, the switch guarantees that only one controller in the master role can be connected.
The definition of the three roles of the controller in OpenFlow ensures the security of the network. Once the master controller fails or overloads, the managed switch can be migrated to the slave controller to avoid controller outages. As shown in Figure 1, the traffic in control domain 2 surges, causing controller to be the overload controller. Based on the idea of switch migration, switch in control domain 2 can be migrated to the slave controller (i.e., , , and ). However, is not connected to all intra-domain switches in control domain 4. In fact, the migration of to is only the ideal situation, as it is impossible to achieve migration in a real network. Therefore, considering the connectivity between the actual network topology nodes, switch can only be migrated to slave controller or .
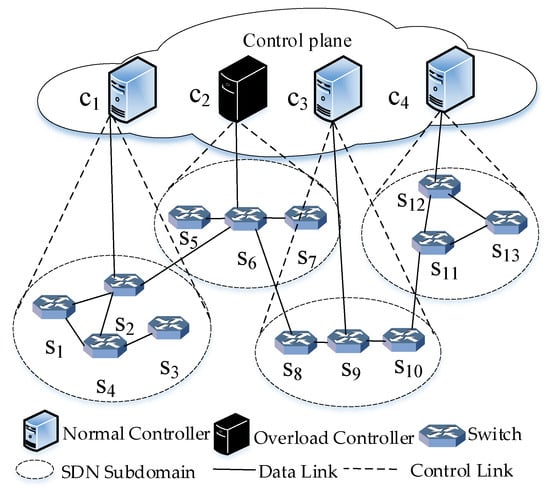
Figure 1.
Multi-controller network architecture.
How to choose the optimal network remapping state based on the connectivity of nodes is the critical problem to be solved in this paper. It is assumed that after the two performance indicators of load balancing and migration cost are optimized according to the algorithm in this paper, the overload controller chooses to migrate to controller to relieve its load pressure. Controller first installs flow rules to , and then forwards migration requests to controller through . Finally, accepts the migration request, changes the slave role to master, and the main controller of is converted from to to complete the migration operation.
2.2. Model Construction
The multi-controller network generally adopts the in-band communication mode [21]—that is, the switch and the controller are deployed at the same node, and the control flow and the data flow are transmitted using the same channel. According to the relevant knowledge of graph theory, SDN is modeled as an undirected graph . In network , represents the set of controllers and switch nodes, and represents the set of links between the nodes. Suppose there are controllers in the network; the controller set is represented as , and the capacity is . There are switches, and the switch set is represented as . Each controller and its managed switches form a subdomain, and controllers between different domains communicate with each other and share the same network view. Moreover, each switch in the network has only one master controller and any slave controller. In order to clearly describe the network model, the network topology corresponding to Figure 1 is given below, as shown in Figure 2.
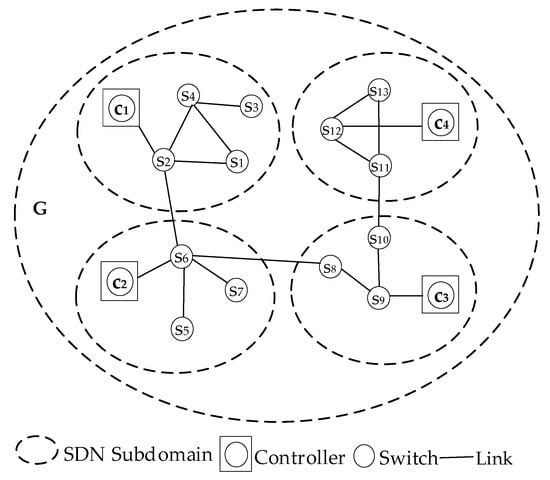
Figure 2.
Network topological structure.
Detailed descriptions of the main parameters are shown in Table 1.

Table 1.
Network parameters and description.
In order to explain the migration process of the switch in detail, the related parameters in the network are defined as follows.
Definition 1.
Mapping matrix. The connection relationship between the controller and the switch in the domain is defined as the mapping matrix—i.e.,, wheremeans that switchis managed by the controller,means that it is not managed by; moreover, a switch can only be managed by one controller, so it satisfies
Definition 2.
Node connectivity. The connection between two nodes is denoted as, wheremeans that there is a connection relationship between nodesand. If, the two nodes do not have a connection relationship.
The purpose of switch migration is to balance the load on the control plane effectively. However, switch migration can also produce high migration costs. Therefore, this paper focuses on load balancing and migration cost issues after network remapping. Next, the two performance indicators are described in detail.
2.2.1. Load Balancing Degree
When an unknown flow enters the switch, it needs to send PACKET-IN messages to the controller to query the forwarding policy. The controller responds to the switch request, delivers the flow table items, and installs a new routing rule to the switch. The controller load is mainly composed of maintenance management domain information, flow table installation, and inter-domain controller synchronization overhead.
Maintaining management domain information overhead
In SDN network architecture, distributed controllers manage switches centrally. In order to maintain global network information, controllers need to communicate with switches periodically to collect information such as traffic and the hops of switches in their management domain. As shown in Equation (1), the traffic required to maintain the management domain is related to the polling switch speed, the connection relationship between switches and controllers, and the number of hops between devices.
Among them, denotes the traffic required by controller to maintain the management domain, denotes the average rate of the controller polling switch in the control domain, denotes the connection relationship between switch and controller , and denotes the hops between device and .
Flow table installation overhead
When a new flow arrives at the switch, the switch sends a flow request to the controller. The controller formulates the flow table rule according to the flow request and delivers the rule to the corresponding switch. The generated flow table installation overhead is shown in Equation (2),
where represents the flow table installation cost generated by controller , and represents the flow request rate of switch .
Inter-domain controller synchronization overhead
When the data flows through different control domains, the controllers need to perform state synchronization to maintain the consistency of the SDN global network view. The inter-domain controller synchronization overhead generated by this process is shown in Equation (3),
where represents the inter-domain controller synchronization cost of controller , and represents the average rate of polling the controller, because the controller does not synchronize all the information of the switch, so it satisfies .
The load of controller is a linear addition of the above three parts, as shown in Equation (4).
The average load of the controller is shown in Equation (5).
In statistics, the coefficient of variation is usually used to characterize the degree of dispersion between data, expressed as the ratio of the standard deviation of the data to the mean, which is a normalized measure of the degree of the dispersion of the probability distribution. Therefore, the coefficient of variation is used in SDN to measure the load balancing degree of the controller, as shown in Equations (6) and (7),
where is the standard deviation and is the load balancing degree. The larger the value, the more balanced the load.
2.2.2. Migration Cost
Although switch migration can effectively balance the load, it inevitably produces an additional migration overhead. The overload controller issues a migration command to the intra-domain switch and installs the migration rule to the switch to be migrated. Then the switch forwards the rule to the target controller through the devices of other management domains to issue a migration request. The switch migration cost generated by this process is mainly composed of the switch communication cost and the migration request cost.
1. Switch communication cost
The communication cost of the switch mainly refers to the normal communication cost generated by the data to be migrated by the switch through the devices in different domains reaching the target controller. The communication cost of the switch can be expressed as:
where represents the average transmission rate of the switch communication, represents the hop count between the switch to be migrated and the overload controller , and represents the hop count between the switch to be migrated and the target controller .
2. Migration request cost
The cost of sending migration requests through the shortest path to the radial target controller is mainly related to the minimum hops, data transmission rate between the switch to be migrated and the target controller, as shown in Equation (9),
where represents the minimum hop count between the switch to be migrated and the target controller .
The switch migration cost is a linear sum of the switch communication cost and the migration request cost and is represented as
The migration cost of the SDN control plane may be composed of the migration cost of multiple switches, which is expressed as the cost of changing the mapping state between the switch and the controller to a better network topology state. If the adjusted network mapping relationship is , then the total cost of the network from state to is
where denotes whether the switch has migrated and satisfies
To change the network mapping relationship through switch migration and promote the scalability of the control plane, we need to optimize the performance of two aspects: on the one hand, to improve the controller load balance; on the other hand, to reduce the switch’s migration cost. Since these are two conflicting goals, optimizing one of these goals will inevitably impair the performance of the other. Based on this, a multi-objective model can be expressed as
where indicates the threshold factor of controller . The constraint condition (14) indicates that the load of each controller must not exceed the threshold after the switch is migrated; constraint condition (15) indicates the mapping relationship after the switch is migrated; constraint (16) indicates that a switch can only have one master controller.
3. Multi-Objective Decision Making Based on Nash Bargaining
There are two commonly used methods for solving multi-objective optimization problems. The first is to set weights for each sub-goal, converting the problem into an aggregate function by a specific mathematical approach, and the second is to transform a multi-objective problem into a single-objective problem [22,23]. However, the dimensions and magnitudes of the various objectives may not be the same. It is difficult to set reasonable weights for each goal based on experience. That is, a fair compromise between the two contradictory goals cannot be achieved. The second is to use an intelligent optimization algorithm to determine the optimal solution [24]. This method obtains an approximate optimal non-inferior solution set and cannot acquire an accurate optimal solution. Therefore, the Nash bargaining game method was introduced. The Nash bargaining game is a classic cooperative game. It no longer needs to set weights for each goal. Each goal has equal importance. The Nash bargaining game focuses on collective rationality and fairness and can determine the Pareto optimal value. It is a useful mathematical tool for studying competitive or conflicting problems and provides a new solution for multi-objective optimization problems.
3.1. Nash Bargaining Model
Nash proposed to use the Nash bargaining model to solve the cooperative game problem [25]. Firstly, different targets are regarded as different players, and the initial strategy and the income functions are set. Each player party continuously negotiates and negotiates in the policy space and finally obtains a Nash equilibrium solution. This solution has Pareto validity, equivalent income invariance, and irrelevant selection independence [26]. Nash uses the Nash product to represent global benefits and proves that the largest solution of the Nash product is the Nash equilibrium solution, which falls on the Pareto frontier and can achieve fairness and global optimization for multiple targets.
The mathematical expression of game is as follows: Suppose has game players, i.e., , and all the alternative strategies of each game player in the strategy space are called the strategy set, i.e., . The gain function obtained by the player according to the selected strategy is expressed as . Then, the game can be expressed as .
Switch migration can be viewed as a remapping of the connection between the switch and the controller in the network. In an actual network, the switch does not form a mapping relationship with all controllers. If the connectivity between the node devices is not considered, the new mapping relationship obtained can only be an ideal state. Based on the above considerations, the remapping of the switch (that is, the policy set) needs to satisfy the connectivity constraint, as shown in Equation (17),
where is the original mapping relationship between switch and controller , and is the mapping relationship after network remapping. If switch in the management domain of controller has connectivity with any switch in the management domain of controller , then switch can form a new connection relationship with controller (that is, ) or maintain the original mapping relationship (i.e., ). If there is no connectivity, switch migration cannot be achieved (that is, can only be taken as 0).
In this paper, the load balancing degree and migration cost are regarded as two players. and are the gain functions of these two players, respectively. The possible mapping relationship between the switch and controller is used as the strategy space of both sides of the game, and the Nash bargaining game model is established, as shown in Formulas (18)–(23),
where and are the bargaining breakdown points for the load balance and the migration cost, respectively, i.e., the worst possible return for both sides of the game. The goal of the game is to achieve a game agreement at least at this breakpoint.
In the game process, each game player will tend to change their own breakpoint to improve their own income. If there is no restriction on this selfish behavior, each player will continuously change the breakpoint value, causing the bargaining to fail. In order to avoid bargaining failure, it is necessary to establish a bargaining agreement for the players to make the game fair and orderly. Under the premise of following the agreement, the game players find the optimal breakpoint of the negotiation through multiple games, and then obtain the maximum benefit from both sides of the game, namely the optimal value of the load balancing degree and migration cost.
3.2. Fair Bargaining Agreement
The fair bargaining agreement is mainly used to impose regular constraints on the initial breakpoint of the bargaining and the update of the bargaining point.
3.2.1. Initial bargaining breakpoint
At the beginning of the game, the initial bargaining breakpoint needs to be set for the game player, and the breakpoint can also be considered the minimum performance threshold for load balancing and migration costs. The optimal and worst load balance degree is easily obtained according to Formula (4), and the optimal and worst migration cost is obtained according to Formula (10). Therefore, the worst target of load balancing and migration cost is taken as the bargaining point , and the bargaining game is performed based on the minimum performance threshold.
3.2.2. Update of the bargaining breakpoint
In order to prevent the game players from unrestrictedly changing their own bargaining breakpoints to obtain the maximum benefit of selfish behavior, an updated agreement must be followed for each game player. That is to say, when the players renew their breakdown point, the change of the breakdown point is, at most, half of the difference between the current revenue and the previous breakdown point. The updated rules for the bargaining point are as follows:
Among them, and are the bargaining breakpoints of the load balance degree and migration cost in the kth iteration process.
4. Model Solving
The multi-objective decision-making method based on Nash bargaining proposed in this paper belongs to the non-convex nonlinear optimization problem with multiple constraints. It is complicated to solve with traditional mathematical methods and is not suitable for large-scale SDN networks. Emerging intelligent optimization algorithms, such as the genetic algorithm, simulated annealing algorithm, and particle swarm optimization algorithm, have shown good optimization computing power and have been widely used in the computer field. In this paper, the firefly algorithm is used to solve the model. The firefly algorithm [27] is a stochastic nonlinear global search algorithm with strong global search ability and high precision. Compared to the heuristic algorithm described above, the firefly algorithm has a simple structure and fewer parameters. Moreover, its parameters have less influence on the algorithm, and the algorithm is easy to implement.
Considering that, in a large-scale network structure, the application of the genetic algorithm, particle swarm optimization, and other heuristic algorithms requires a very long running time and a large storage space, it is necessary to find a simple and easy to implement algorithm to solve the nonlinear optimization problem with multiple constraints. The firefly algorithm has a fast global search ability and does not depend on parameter settings, so it is easy to implement on a computer. Therefore, it is suitable for solving the model in this paper.
4.1. The Basic Firefly Optimization Algorithm
The firefly algorithm is a bionic optimization algorithm. Its principle is to simulate firefly individuals with points in the search space. Each individual has brightness and attractiveness. Because of the phototaxis characteristics of fireflies, fireflies move towards brighter individuals. The core is used to keep fireflies close to brighter individuals by continually updating their positions. Combined with the SDN load balancing problem, the mapping relationship between the switch and controller in the strategy space is considered to be the location of a firefly, and the objective function of the Nash bargaining game is regarded as the brightness of the firefly. Individuals with low brightness will move to individuals with high brightness, and the process of firefly movement is the process of target optimization. The brightness of each firefly is expressed as follows: , is the brightness of the i-th firefly, is the position of the i-th firefly, and is the dimension of the problem.
If the brightness of firefly is greater than the brightness of firefly , firefly is attracted by . The formula for calculating the attractiveness of to is as follows:
where is the maximum attractive force, is the light absorption coefficient, and is the Cartesian distance between firefly and firefly —i.e., .
Firefly is attracted by and moves to . The position update formula is as follows:
where is the position of firefly during the kth iteration, is a random disturbance term, is a constant, and is a random number obtained by uniform distribution.
4.2. Improved Algorithm
Although the firefly algorithm shows good performance advantages in global optimization, it also has some shortcomings; for example, it is premature and can easily fall into the local optimum. In this paper, chaos theory and the elite retention strategy are introduced to improve the traditional firefly algorithm.
4.2.1. Chaos Theory
Chaos is a kind of non-linear phenomenon in nature, which has the characteristics of randomness and non-periodicity. Logistic mapping is a classic model for studying chaotic systems. This model can traverse all states without repeating within a certain range. Therefore, this paper introduces the Logistic map in chaos theory into the firefly optimization algorithm and optimizes the random disturbance parameter . This method can improve the premature phenomenon and improve the global optimization ability. The mathematical expression of the Logistic iterative process is as follows:
The improvement of is as follows:
Set the chaos parameter ,and . Logistic mapping generates a random function during each iteration. This process implements dynamic control of the parameters and improves the global search capability of the firefly algorithm.
4.2.2. Elite Strategy
In order to prevent the Pareto optimal solution from being lost, the elite retention strategy in the genetic algorithm is used to retain the optimal solution during each iteration, and then the firefly individual in the next iteration is replaced by the optimal solution to ensure that the optimal solution is not lost and speeds up the convergence. The specific steps are as follows:
- Initialize the parameters;
- Initialize the firefly position on the premise of satisfying the constraint;
- Initialize the corresponding brightness according to the objective function;
- Save the optimal solution that maximizes brightness;
- Update the firefly position, increasing the number of iterations by one;
- Replace the worst individual with ;
- Calculate the corresponding brightness according to the objective function;
- Check whether the maximum number of iterations is reached. If the maximum number of iterations is reached, the search ends; otherwise, go to step 4.
4.3. SDN Network Reconstruction Algorithm
By balancing the control plane load through switch migration, the mapping between the switch and the controller is inevitably reconstructed. In order to optimize network performance, a new mapping relationship needs to be found to optimize the load balancing and migration costs. According to this idea, the Nash bargaining model is established. Combining the Nash bargaining game process and the optimization mechanism of the firefly algorithm, the optimal strategy for the game players is solved, and the Pareto optimal solution is obtained. The specific optimization process is shown in Algorithm 1.
| Algorithm 1 LBSNB |
| Input: The network topology ; The original network mapping matrix ; The flow request rate of the switch ; The number of hops between devices ; The controller capacity ; The maximum number of iterations . Output: The new network mapping matrix 1: Initialize the number of the firefly populations, the maximum number of iterations, and the associated parameters and . 2: Randomly generate an initial feasible strategy in the game strategy set to initialize the firefly position . 3: Initialize the bargaining breakpoints and . 4: The corresponding firefly brightness is determined according to the objective function of the game model, and the individual with the highest brightness is saved. 5: The firefly position is updated according to chaos theory and Formula (27). 6: Calculate the brightness of each firefly after the location update and replace the worst-case individual with . 7: Determine whether the difference between the highest and worst brightness is less than the constant and, if so, update the bargaining breakpoint according to Equations (24) and (25); otherwise, perform Steps 4–7. 8: The termination condition is judged. If the maximum number of iterations is reached, the loop is ended, and the optimal firefly position is output; otherwise, Step 4 is continued. |
5. Simulation Experiment
5.1. Simulation Environment Settings
5.1.1. Experiment platform
In order to verify the adaptability of this method to different scales of networks, the experiment is carried out on a PC with an Intel Core i7 CPU at 3.4 GHz with 8 GB of RAM, using the North American Internet 2 OS3E [28] and Columbus [29] network topologies. OS3E has 34 nodes and 42 links, while Columbus has 70 nodes and 85 links. This experiment uses OpenDaylight as the controller, performs simulation experiments on the Mininet, and uses the Cbench [30] tool to measure the maximum rate at which the controller processes the stream request.
5.1.2. Parameter settings
According to the traffic characteristics, the traffic generator is used to simulate real network traffic. The average flow generation rate is 250 KB/s, the polling switch rate , the average communication rate , the polling controller rate , and the threshold factor is set to 0.8. The parameters of the firefly algorithm are set as follows: the value of the maximum attraction is 1, the light absorption coefficient meets , and the range of step factor is . The higher the step factor, the stronger the global search ability, which will, however, reduce the convergence accuracy. The step factor is generally set to 0.4, and is a random number obeying uniform distribution on . The maximum number of iterations is , and the constant is set to 0.01.
5.2. Simulation Environment Settings
In order to verify the effectiveness of the Nash bargaining based load balancing scheme (LBSNB), this scheme is compared with the under-utilization migration strategy (UMS) [12] and the multi-objective optimization scheme based on multi-objective optimization (MOS) [18]. Among these models, UMS migrates the switches managed by the overload controller to the light-load controller with the lowest resource utilization. MOS uses the genetic algorithm to optimize the load balancing degree and migration cost and obtains a better mapping relationship. Moreover, the comparative performance indicators include the load balancing degree, controller response time, and migration cost.
5.2.1. Load Balancing Degree
MOS, UMS, and LBSNB are run in the two network topologies, and their load conditions are compared and analyzed. The comparison results of the load balancing degree are obtained from Formula (7), as shown in Figure 3 and Figure 4.
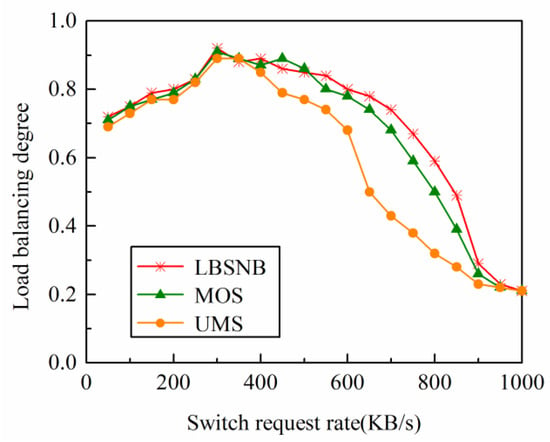
Figure 3.
Load balancing degree in the OS3E network.
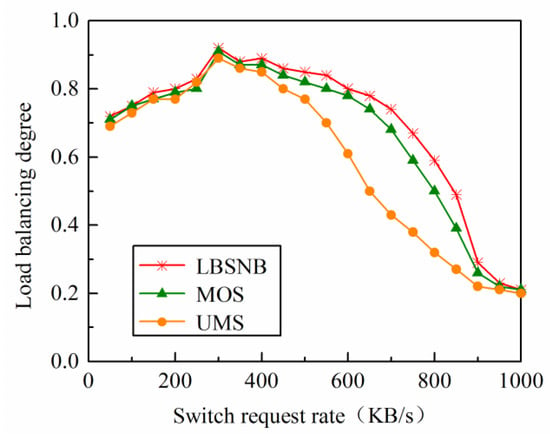
Figure 4.
Load balancing degree in the Columbus network.
From the results of the load balancing of the controllers in both networks, it can be seen that when the switch request rate is low, the load balancing degree of the three algorithms is basically the same, indicating that the controller in the network does not overload. When the request rate continues to increase (300 KB/s–800 KB/s), the load balancing degree of the three algorithms shows a downward trend, indicating that the network controller begins to overload. It can be seen from Figure 3 and Figure 4 that UMS performance is the worst, MOS is second, and the algorithm is optimal. Because UMS does not quantify the migrated switch, it is easy to make the target controller’s load too high. MOS is solved based on the genetic algorithm and obtains the approximate optimal solution. The proposed algorithm can obtain a fair Pareto optimal solution based on the Nash bargaining model. When the switch request rate reaches its maximum, the load balance is the lowest, indicating that all controllers are overloaded. At this time, all three algorithms are invalid, and the controller needs to be added to relieve the load pressure.
5.2.2. Controller Response Time
The response time of the controller is an essential factor in measuring the performance of the network. Therefore, the experiment is repeated 30 times, and the average response time of the controllers of the three strategies is compared. The results are shown in Figure 5 and Figure 6.
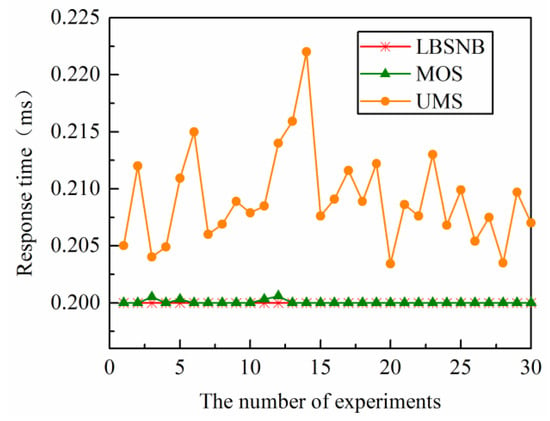
Figure 5.
Average response time of the controller in the OS3E network.
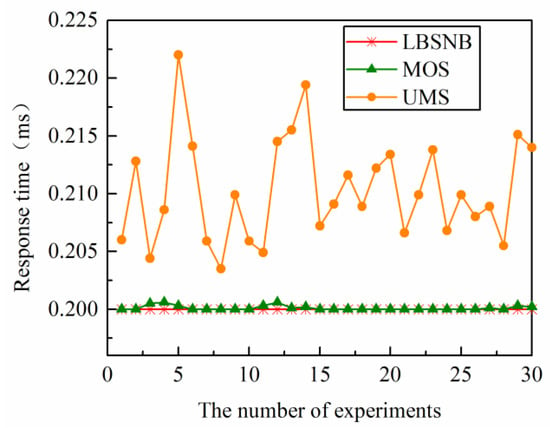
Figure 6.
Average response time of the controller in the Columbus network.
As can be seen from Figure 5 and Figure 6, the average response time of the UMS is the largest, and its distribution is the most uneven because the migration of the switch to the controller with the lowest resource utilization does not accurately balance the control plane load. The load is unrestricted, and the target controller may be overloaded again, resulting in an extended response time for the controller. The response time of MOS and UMS is generally consistent because both strategies can effectively balance the controller load, and the balanced network does not experience controller overload.
5.2.3. Migration Cost
The cost of switch migration was compared, and the results are shown in Figure 7 and Figure 8. The migration cost of UMS is higher than that of MOS and LBSNB because it only considers resource utilization as a single factor in selecting the target controller and does not consider the migration cost. Both MOS and LBSNB strategies can maintain a short migration time and migration cost. The experimental results show that LBSNB is slightly better than MOS in terms of migration time, indicating that the firefly algorithm in this strategy is superior to the MOS genetic algorithm in optimization time. This paper’s strategy thus performs better in multi-objective optimization.
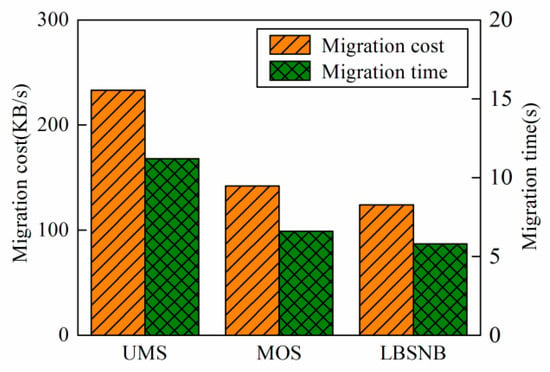
Figure 7.
Comparison of the migration costs in the OS3E network.
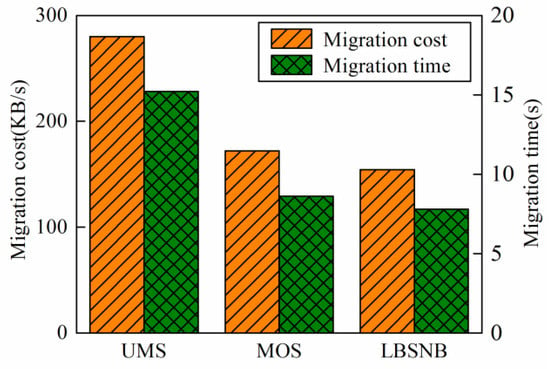
Figure 8.
Comparison of the migration costs in the Columbus network.
6. Conclusions
Aiming at the problem of load imbalance in distributed multi-controller architecture, a multi-objective optimization model considering load balance and migration cost is proposed using a Nash bargaining mechanism and firefly algorithm to solve the model quickly. The experimental results show that this scheme can effectively balance the controller load with less migration time, reduce the additional migration cost introduced by switch migration, shorten the controller response time, and adapt to different scales of network structures. The proposed scheme has resulted in an ideal network environment. The next study will take into account the particular situation of equipment failure in the network and offer a safer and more efficient load balancing scheme.
Author Contributions
The authors contributed equally to the preparation of the manuscript and the concept of the research. The writing of the draft was by G.L. and K.L.; the review and editing of the draft were done by Y.L. and Y.P.
Funding
This research was funded by the Natural Science Foundation of Tianjin, grant number 17JCQNJC00500, the Tianjin Educational Science Project Planning for 13th Five-year, grant number HE3045, and the Fund for Development of Science and Technology of Tianjin Education Committee, grant number 2018KJ174.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feamster, N.; Rexford, J.; Zegura, E. The road to SDN: An intellectual history of programmable networks. ACM SIGCOMM Comput. Commun. Rev. 2014, 44, 87–98. [Google Scholar] [CrossRef]
- Bhaumik, P.; Zhang, S.; Chowdhury, P.; Lee, S.-S.; Lee, J.H.; Mukherjee, B. Software-defined optical networks (SDONs): A survey. Photonic Netw. Commun. 2014, 28, 4–18. [Google Scholar] [CrossRef]
- Xue, H.; Kim, K.T.; Youn, H.Y. Dynamic Load Balancing of Software-Defined Networking Based on Genetic-Ant Colony Optimization. Sensors 2019, 19, 311. [Google Scholar] [CrossRef] [PubMed]
- Muthanna, A.; Ateya, A.A.; Makolkina, M.; Vybornova, A.; Markova, E.; Gogol, A.; Koucheryavy, A. SDN multi-controller networks with load balanced. In Proceedings of the 2th International Conference on Future Networks and Distributed Systems (IC-FNDS), New York, NY, USA, 26–27 June 2018. [Google Scholar]
- Zhao, Y.; Liu, C.; Wang, H.; Fu, X.; Shao, Q.; Zhang, J. Load balancing-based multi-controller coordinated deployment strategy in software defined optical networks. Opt. Fiber Technol. 2018, 46, 198–204. [Google Scholar] [CrossRef]
- Hu, T.; Yi, P.; Guo, Z.; Lan, J.; Hu, Y. Dynamic slave controller assignment for enhancing control plane robustness in software-defined networks. Future Gener. Comput. Syst. 2019, 95, 681–693. [Google Scholar] [CrossRef]
- Fu, Y.H.; Bi, J.; Wu, J.P.; Chen, Z.; Wang, K.; Luo, M. A dormant multi-controller model for software defined networking. China Commun. 2014, 11, 45–55. [Google Scholar]
- Li, G.; Wang, X.; Zhang, Z.; Chen, Y.; Liu, S. A Scalable Load Balancing Scheme for Software-Defined Datacenter Networks based on Fuzzy Logic. Int. J. Perform. Eng. 2019, 15, 2217–2227. [Google Scholar]
- Ros, F.J.; Ruiz, P.M. On reliable controller placements in software-defined networks. Comput. Commun. 2016, 77, 41–51. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Nag, A. Quantum-Key-Distribution (QKD) Networks Enabled by Software-Defined Networks (SDN). Appl. Sci. 2019, 9, 2081. [Google Scholar] [CrossRef]
- Dixit, A.; Hao, F.; Mukherjee, S.; Lakshman, T.; Kompella, R.R. ElastiCon; an elastic distributed SDN controller. In Proceedings of the 2014 ACM/IEEE Symposium on Architectures for Networking and Communications Systems (ANCS), Marina del Rey, CA, USA, 20–21 October 2014; pp. 17–27. [Google Scholar]
- Yao, G.; Bi, J.; Li, Y. On the capacitated controller placement problem in software defined networks. IEEE Commun. Lett. 2014, 18, 1339–1342. [Google Scholar] [CrossRef]
- Zhang, S.; Lan, J.; Sun, P.; Jiang, Y. Online load balancing for distributed control plane in software-defined data center network. IEEE Access 2018, 6, 18184–18191. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Y.; Yu, J.; Ba, J.; Zhang, S. Load balancing for multiple controllers in SDN Based on switches group. In Proceedings of the 2017 19th Asia-Pacific Network Operations and Management Symposium (APNOMS), Seoul, Korea, 27–29 September 2017; pp. 227–230. [Google Scholar]
- Mohanasundaram, J.G.; Truong-Huu, T.; Gurusamy, M. Game Theoretic Switch-controller Mapping with Traffic Variations in Software Defined Networks. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Wang, C.A.; Hu, B.; Chen, S.; Li, D.; Liu, B. A switch migration-based decision-making scheme for balancing load in SDN. IEEE Access 2017, 5, 4537–4544. [Google Scholar] [CrossRef]
- Al-Tam, F.; Correia, N. On Load Balancing via Switch Migration in Software-Defined Networking. IEEE Access 2019, 7, 95998–96010. [Google Scholar] [CrossRef]
- Liu, B.G.; Shu, Y.A.; Fu, Y.H. Load balancing scheme based on multi-objective optimization for software defined network. Comput. Appl. 2017, 37, 1555–1559, 1573. [Google Scholar]
- OpenFlow Switch Specification Version 1.4.0. Available online: https://www.opennetworking.org/ (accessed on 23 March 2018).
- Ren, T.; Xu, Y. Analysis of the New Features of OpenFlow 1.4. In Proceedings of the 2nd International Conference on Information, Electronics and Computer (ICIEAC), Wuhan, China, 7–9 March 2014. [Google Scholar]
- Akyildiz, I.F.; Wang, P.; Lin, S.-C. SoftAir: A software defined networking architecture for 5G wireless systems. Comput. Netw. 2015, 85, 1–18. [Google Scholar] [CrossRef]
- Liu, H.-L.; Gu, F.; Zhang, Q. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Trans. Evol. Comput. 2013, 18, 450–455. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.; Zhang, Z. SDN-Based Load Balancing Scheme for Multi-Controller Deployment. IEEE Access 2019, 7, 39612–39622. [Google Scholar] [CrossRef]
- Akbar Neghabi, A.; Jafari Navimipour, N.; Hosseinzadeh, M.; Rezaee, A. Nature-inspired meta-heuristic algorithms for solving the load balancing problem in the software-defined network. Int. J. Commun. Syst. 2019, 32, e3875. [Google Scholar] [CrossRef]
- Binmore, K.; Rubinstein, A.; Wolinsky, A. The Nash bargaining solution in economic modelling. Rand J. Econ. 1986, 17, 176–188. [Google Scholar] [CrossRef]
- Ksentini, A.; Bagaa, M.; Taleb, T.; Balasingham, I. On using bargaining game for optimal placement of SDN controllers. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Wang, H.; Wang, W.; Zhou, X.; Sun, H.; Zhao, J.; Yu, X.; Cui, Z. Firefly algorithm with neighborhood attraction. Inf. Sci. 2017, 382, 374–387. [Google Scholar] [CrossRef]
- Internet 2 Open Science, Scholarship and Services Exchange. Available online: http://www.internet2.edu/network/ose/ (accessed on 5 March 2019).
- The Internet Topology Zoo. Available online: http://www.topology-zoo.org/ (accessed on 5 March 2019).
- Cbench. Available online: http://sourceforge.net/projects/cbench/ (accessed on 10 March 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).