Research on Cooperative Communication Strategy and Intelligent Agent Directional Source Grouping Algorithms for Internet of Things
Abstract
:1. Introduction
- (1)
- In the aspect of cooperative communication technology, a new cooperative communication algorithm KCN (k-cooperative node) is proposed. K cooperative nodes for transmission are used in each hop. Moreover, the reliability of transmission in dynamic network is improved.
- (2)
- Intelligent mobile agent has a view of the whole network. Sink node centralizes the planning of proxy routing. The proxy routing can be controlled by programming. In fact, the idea of software defining network has been applied in the realization of an intelligent agent. In this paper, the multi-agent routing planning algorithm is studied, and a directional source grouping based multi-agent itinerary planning (D-MIP) is proposed.
2. Related Research
3. Cooperative Communication Algorithms
3.1. Cooperative Communication
3.1.1. Beaconless Routing Protocol
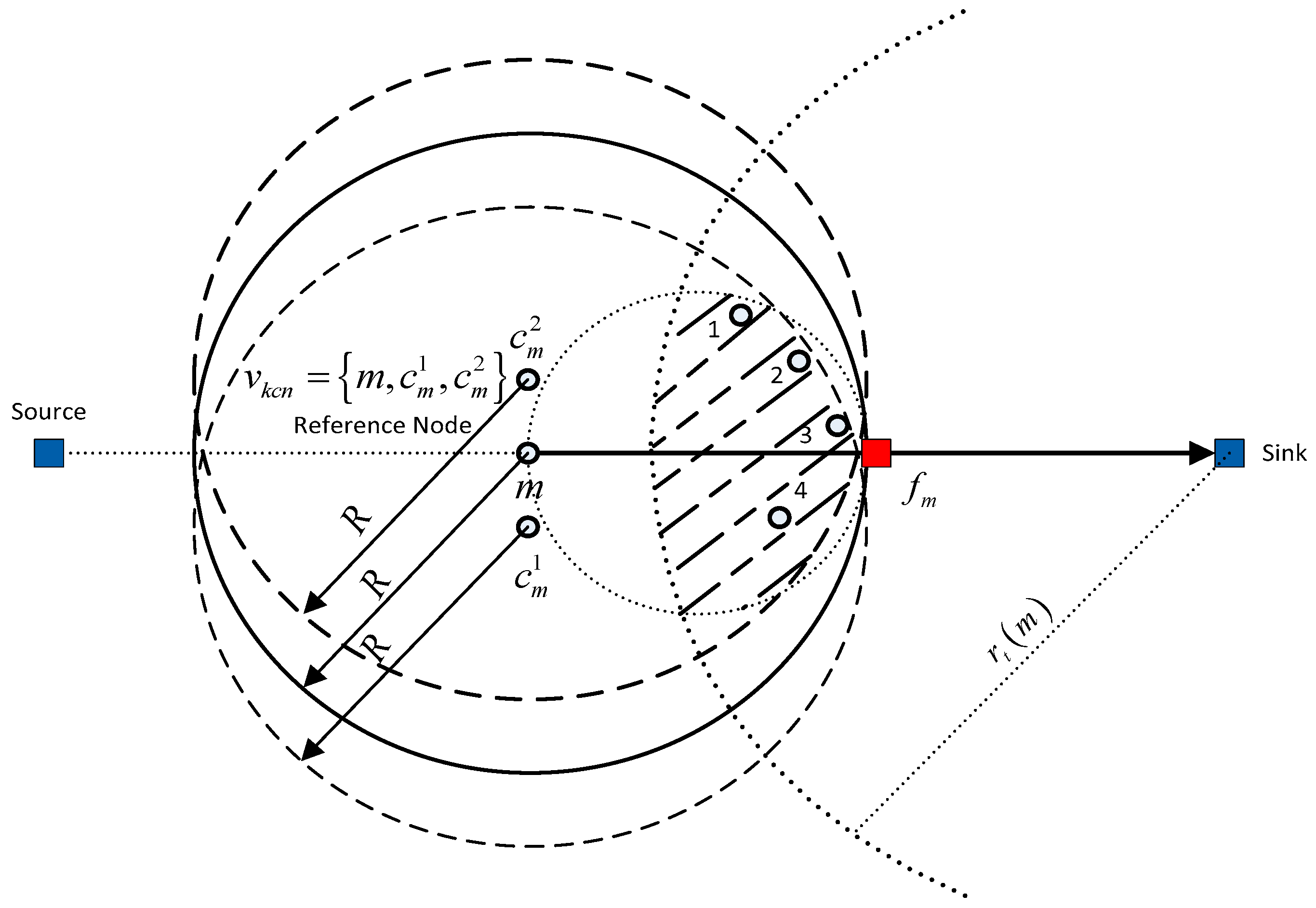
3.1.2. KCN Algorithm
3.2. End-to-End Reliability Model
3.3. Model Validation
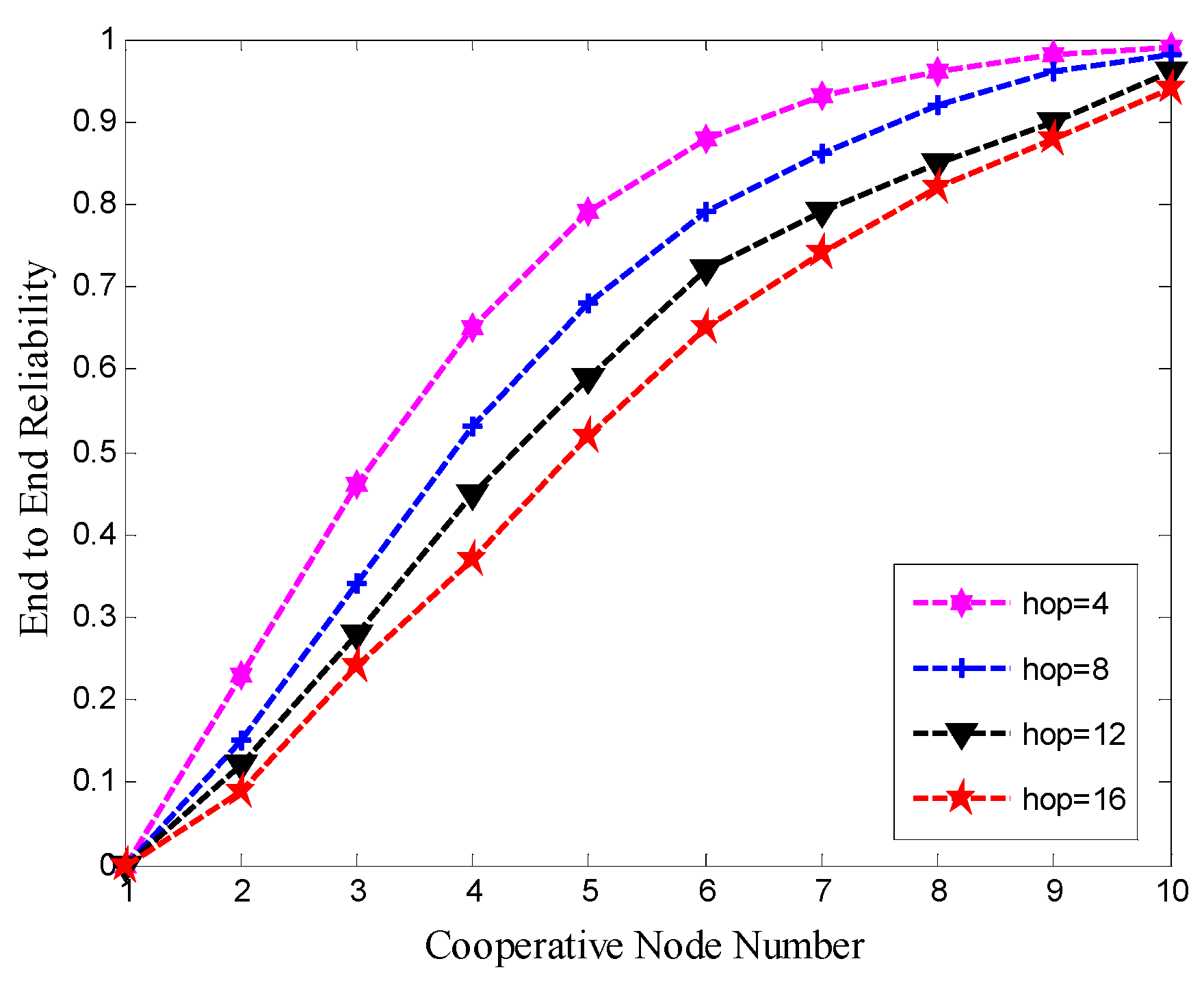
3.3.1. The Effect of Hops and Number of Cooperative Nodes on End-to-End Reliability
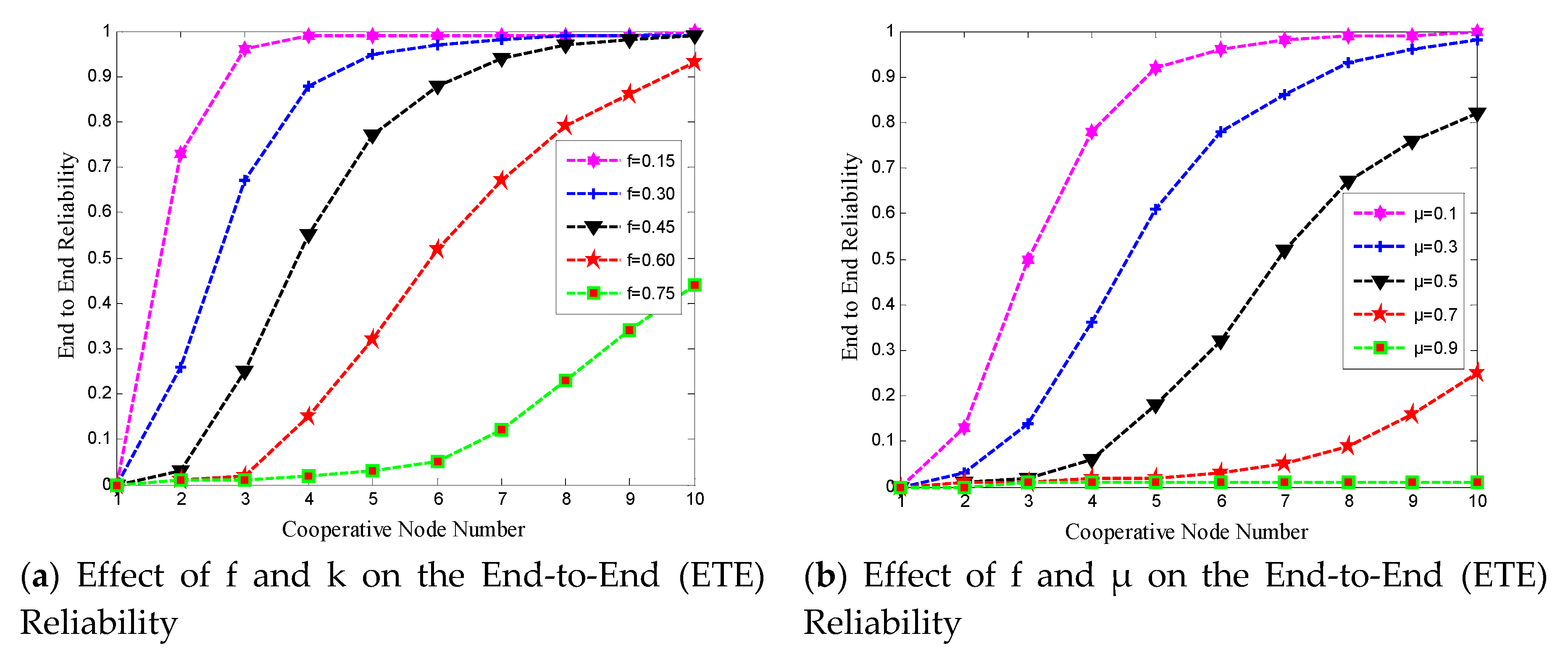
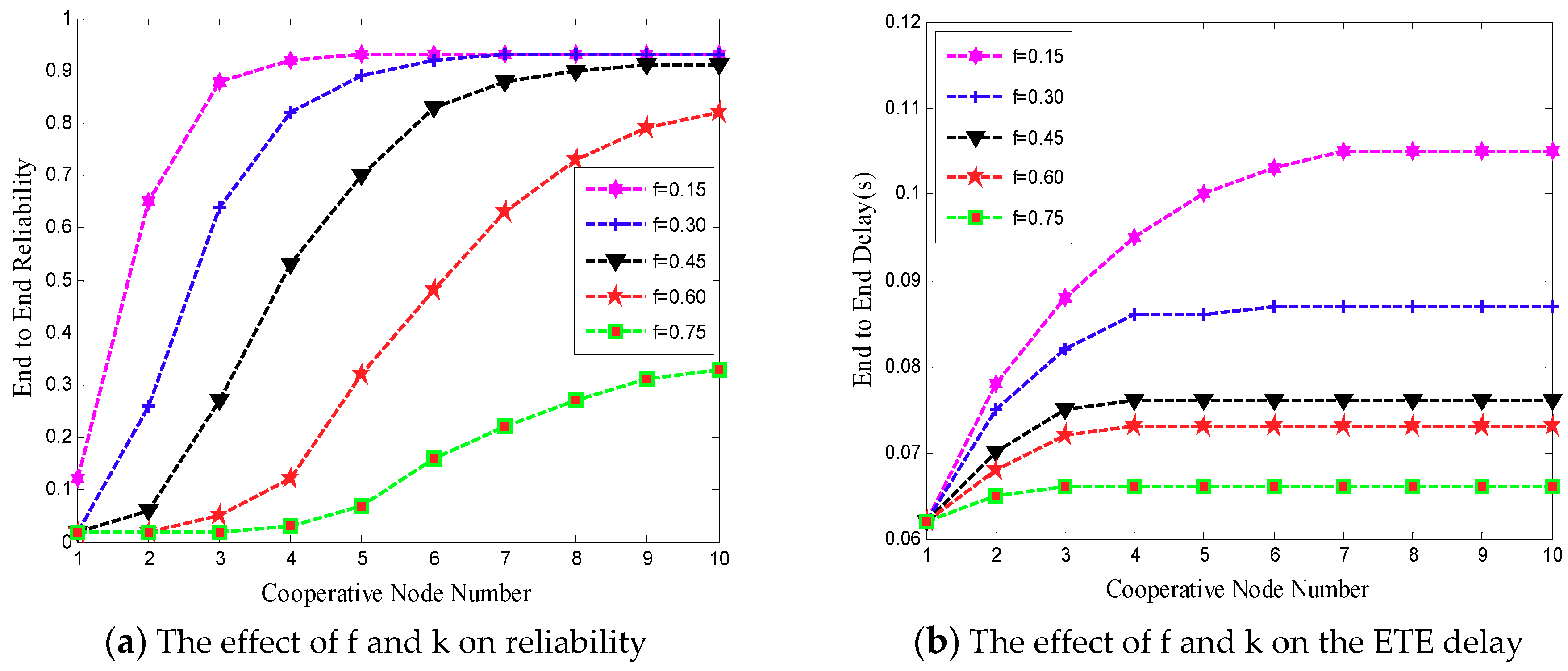
3.3.2. The Effect of and k on End-to-End Reliability
3.3.3. The Effect of and on End-to-End Reliability
3.4. Algorithm Design
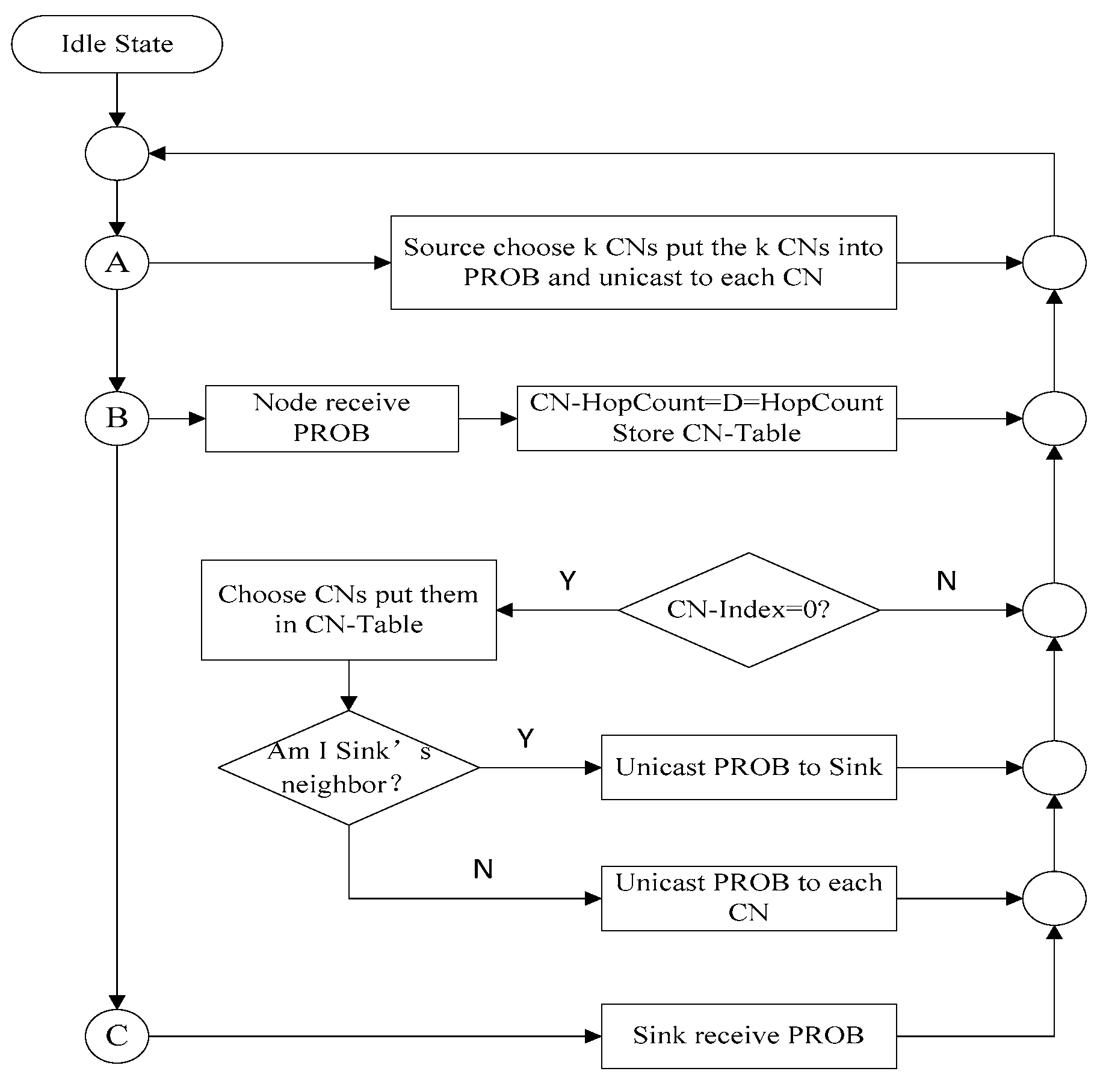
3.5. Implementation of KCN Algorithm
| Algorithm 1. Choose CN (,,,,). |
| Input: denotes the total number of neighbor nodes of ; denotes the array of neighbor nodes of ; t is the Sink node; denotes the cooperative nodes search region of ; is array of priority for every neighbor node of m; |
| Output:Cm (Cm is array of cooperative nodes of ;) |
| 1. For i = 0 to K-1 do 2. ; 3. ; 4. for j = 1 to nm do 5. if is t then 6. break; 7. end if 8. if ( in ) or ( not in ) then 9. continue; 10. end if 11. if then 12. ; 13. ; 14. end if 15. end for 16. ; 17. if is t then 18. break; 19. end if 20. return |
3.6. OPNET Simulation
4. Intelligent Agent Algorithms
4.1. Multiple Intelligent Agent Route Planning (MIP)
4.2. Directional Source Packets for Multi-Agent Routing Planning
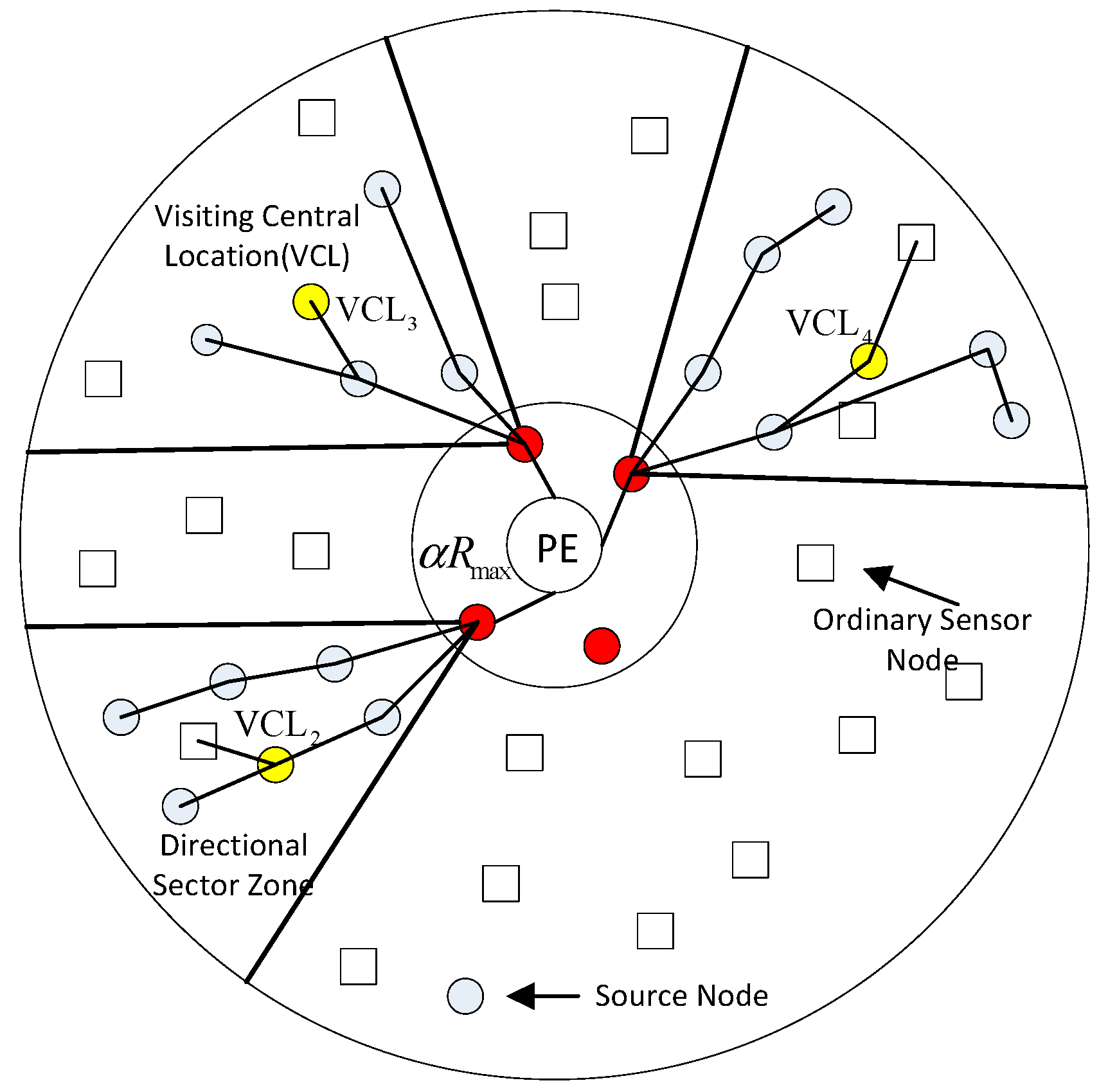
4.2.1. Directional Source Grouping Algorithms
| Algorithm 2. Directional source-grouping(V,CL). |
| Input: V is the set of source nodes, CL is the central location of source nodes |
| Output: T denotes the set of source nodes to be grouped, SN represents sensor node j within Zpe |
| Notation: V′ is the set of remaining sources, part of which will be allocated to an MA. n is the total number of sources. α is a constant, which is set to 70% in this paper. RMax is the maximum transmission range of the sensor node. is the PE-zone which includes the sink node and its one hop neighbors within a radius of αRMax. SNj represents sensor node j within . K is the maximum number of the starting points for MA itineraries, . . is the set of remaining starting points, one of which will be allocated to an MA. Zj is the j-th directional sector zone for source-grouping. θ is the selection angle of a directional sector zone. |
|
4.2.2. Iterative Algorithm
| Algorithm 3. MIP(V) |
| Input: V is the set of original sources to be visited |
| Output: Iterations of MAs 1,2,…k). |
| Notation: V′ denotes the set of remaining source nodes, currently. T denotes the set of grouped sources at each iteration. k denotes the index of MAs. |
| 1. ;
2. ; 3. loop; 4. if then 5. ; 6. CL-CL-selection(V′); 7. source-grouping(V′, CL); 8. ; 9. determine (Itinerary of MA k) to visit sources T with SN as starting point by some SIP algorithm; 10. end if 11. end loop 12. return (Itineraries of MAs 1,2,...,k); |
4.2.3. Sector Angle Designation
5. Simulation Verification
5.1. Simulation Settings
5.2. Evaluation Criterion
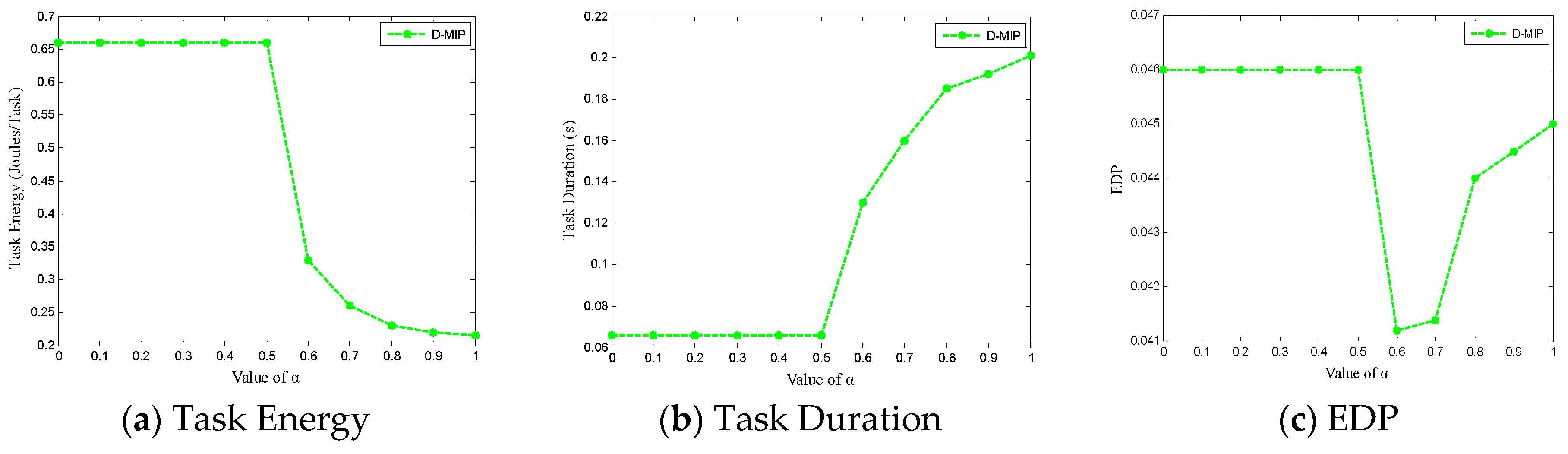
5.3. Measurement and Selection of Control Parameter α
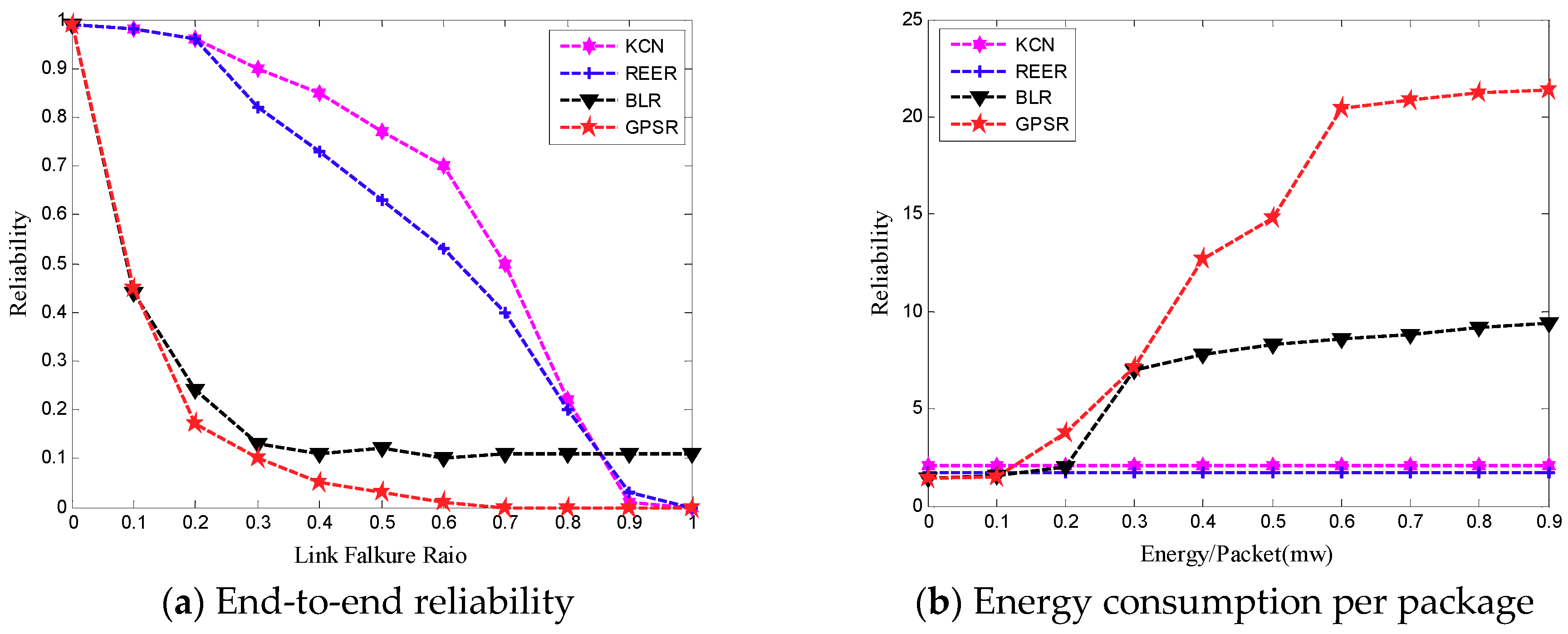
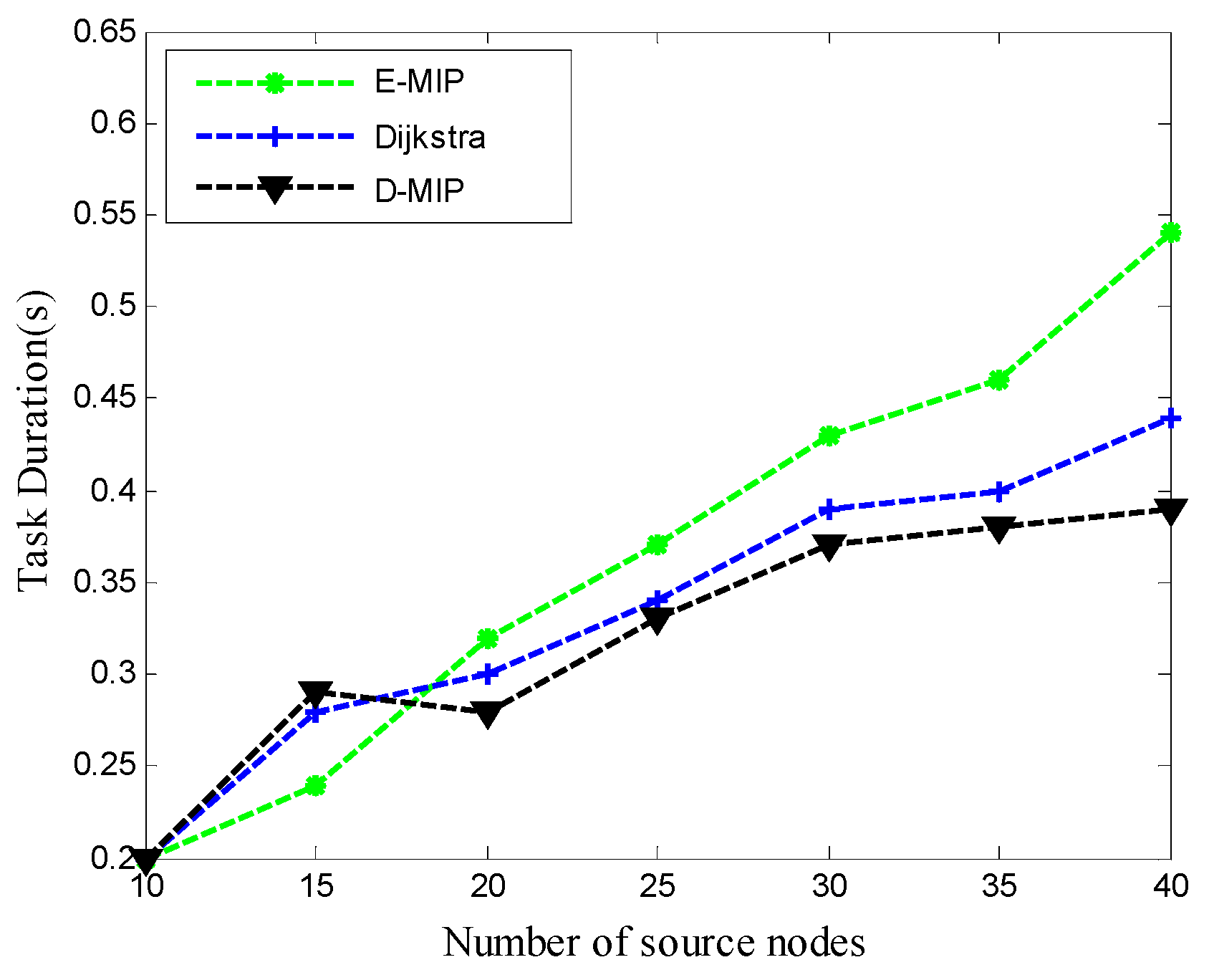
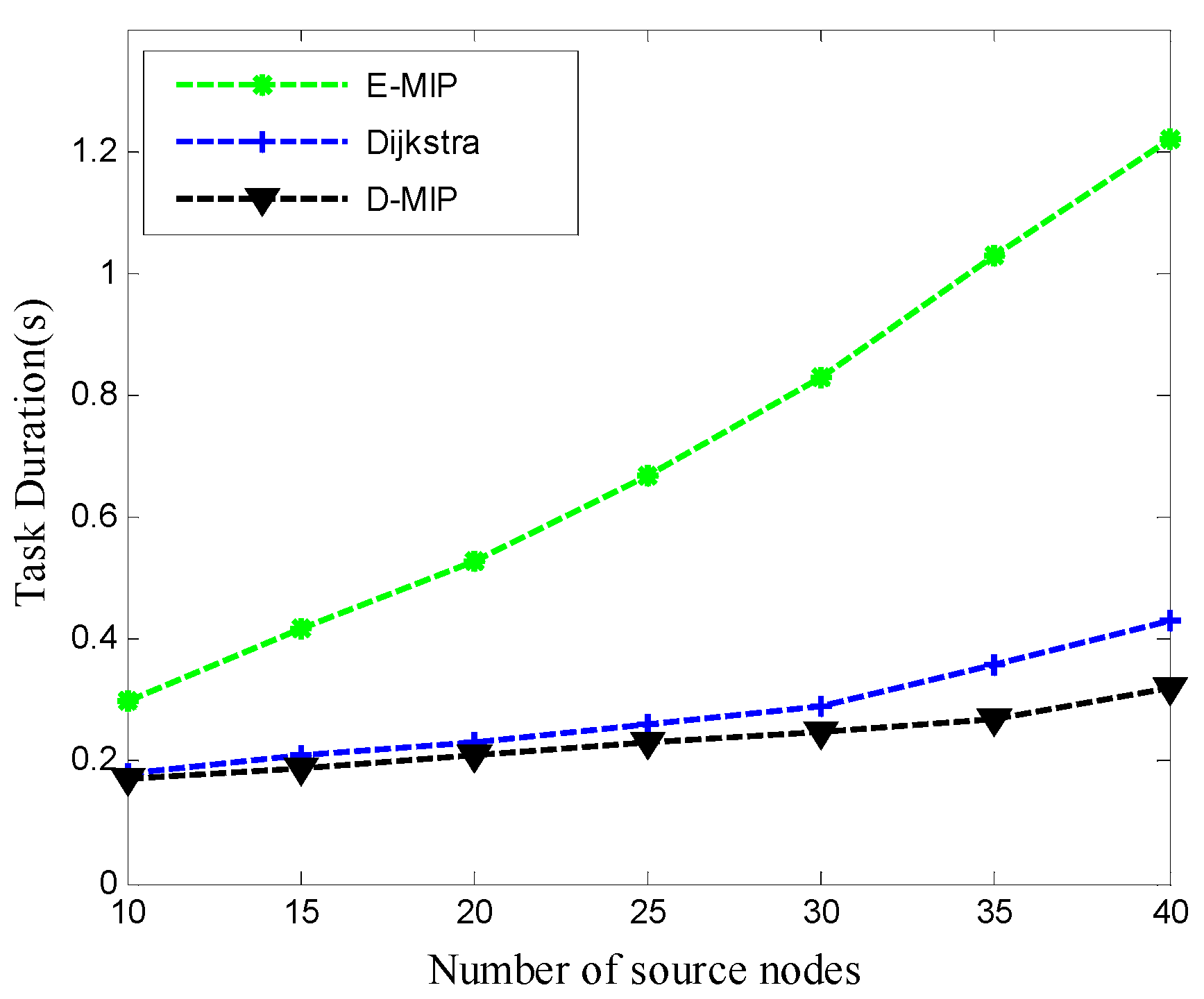
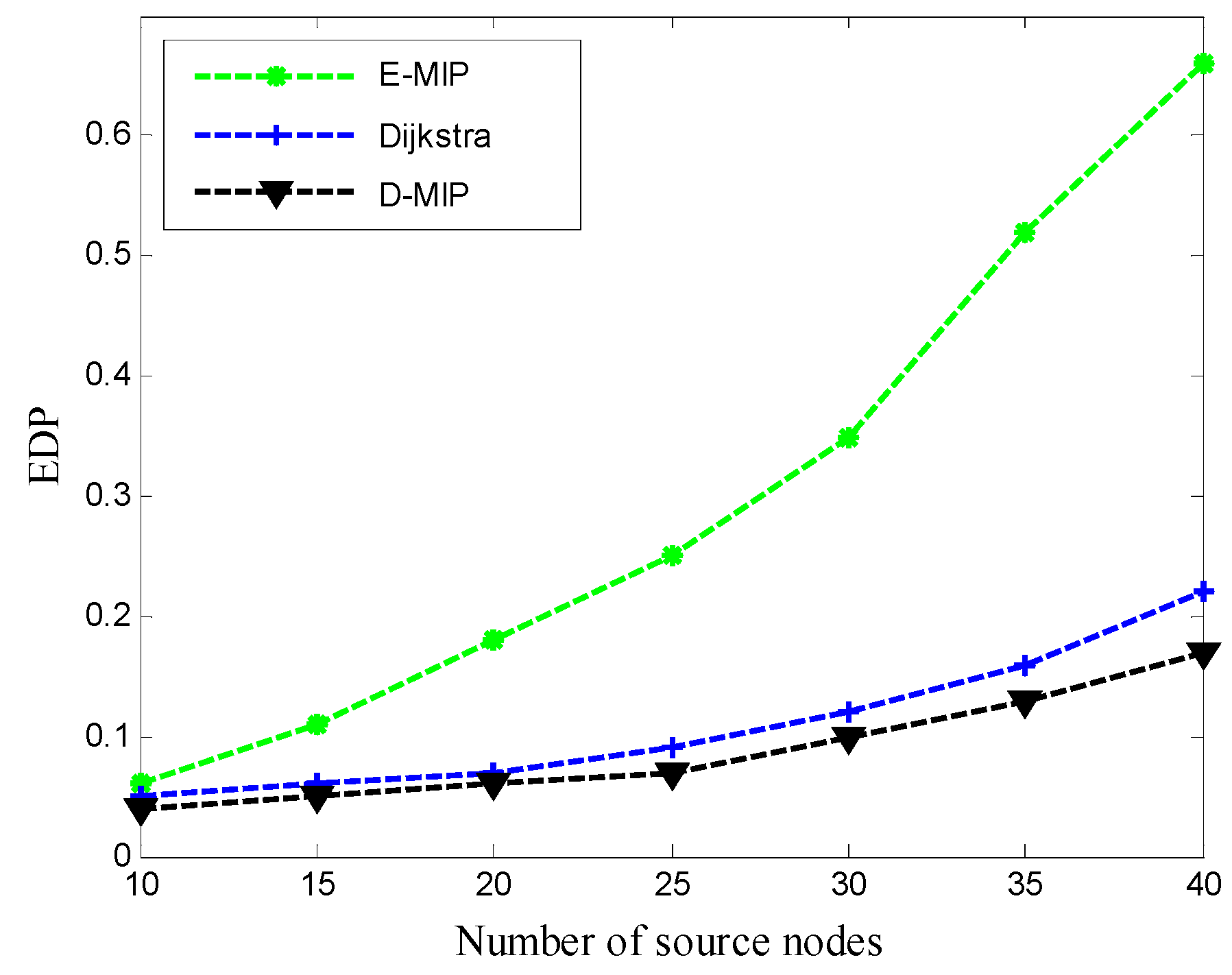
5.4. Performance Comparison and Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nundloll, V.; Porter, B.; Blair, G.S.; Emmett, B.; Cosby, J.; Jones, D.L.; Chadwick, D.; Winterbourn, B.; Beattie, P.; Dean, G.; et al. The Design and Deployment of an End-To-End IoT Infrastructure for the Natural Environment. Future Internet 2019, 11, 129. [Google Scholar] [CrossRef]
- Akila, I.S.; Venkatesan, R. A Fuzzy Based Energy-aware Clustering Architecture for Cooperative Communication in WSN. Comput. J. 2018, 59, 1551–1562. [Google Scholar] [CrossRef]
- Porambage, P.; Braeken, A.; Kumar, P.; Gurtov, A.; Ylianttila, M. CHIP: Collaborative Host Identity Protocol with Efficient Key Establishment for Constrained Devices in Internet of Things. Wirel. Pers. Commun. 2017, 96, 421–440. [Google Scholar] [CrossRef]
- Tan, R.; Li, Z.; Bai, P.; Shi, K.; Ren, B.; Wang, X. Directional AF Cooperative Communication System Based on Outage Probability. Int. J. Bus. Data Commun. Netw. 2017, 13, 55–68. [Google Scholar] [CrossRef] [Green Version]
- Qadori, H.Q.; A Zulkarnain, Z.; Hanapi, Z.M.; Subramaniam, S. Multi-mobile agent itinerary planning algorithms for data gathering in wireless sensor networks: A review paper. Int. J. Distrib. Sens. Netw. 2017, 13. [Google Scholar] [CrossRef]
- Savaglio, C.; Ganzha, M.; Paprzycki, M.; Bădică, C.; Ivanović, M.; Fortino, G. Agent-based Internet of Things: State-of-the-art and research challenges. Future Gener. Comput. Syst. 2020, 102, 1038–1053. [Google Scholar] [CrossRef]
- Chen, M.; Gonzalez, S.; Zhang, Y.; Leung, V.C. Multi-Agent Itinerary Planning for Wireless Sensor Networks. In Proceedings of the International Conference on Heterogeneous Networking for Quality, Reliability, Security and Robustness, QShine 2009: Quality of Service in Heterogeneous Networks, Las Palmas, Spain, 23–25 November 2009. [Google Scholar]
- Gupta, J.K.; Egorov, M.; Kochenderfer, M. Cooperative Multi-agent Control Using Deep Reinforcement Learning. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, AAMAS 2017: Autonomous Agents and Multiagent Systems, Sao Paolo, Brazil, 8–12 May 2017; pp. 66–83. [Google Scholar]
- Lloret, J.; Garcia, M.; Tomas, J.; Boronat, F. GBP-WAHSN: A Group-Based Protocol for Large Wireless Ad Hoc and Sensor Networks. J. Comput. Sci. Technol. 2008, 23, 461–480. [Google Scholar] [CrossRef]
- Lloret, J.; Canovas, A.; Catalá, A.; Garcia, M. Group-based protocol and mobility model for VANETs to offer internet access. J. Netw. Comput. Appl. 2013, 36, 1027–1038. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.; Cheng, Z.; Qin, J. On wireless sensor network mobile agent multi-objective optimization route planning algorithm. In Proceedings of the 2017 IEEE International Conference on Agents (ICA), Beijing, China, 6–9 July 2017. [Google Scholar]
- Guan, Q.; Yu, F.R.; Jiang, S.; Leung, V.C.; Mehrvar, H. Topology control in mobile Ad Hoc networks with cooperative communications. IEEE Wirel. Commun. 2012, 19, 74–79. [Google Scholar] [CrossRef]
- Li, Q.; Hu, R.Q.; Qian, Y.; Wu, G. Cooperative communications for wireless networks: Techniques and applications in LTE-advanced systems. IEEE Wirel. Commun. 2012, 19, 22–29. [Google Scholar]
- Pita, R.; Utrilla, R.; Rodriguez-Zurrunero, R.; Araujo, A. Experimental Evaluation of an RSSI-Based Localization Algorithm on IoT End-Devices. Future Internet Sens. 2019, 19, 3931. [Google Scholar] [CrossRef] [PubMed]
- Calvert, S.C.; Wageningen-Kessels, F.L.M.V.; Hoogendoorn, S.P. Capacity drop through reaction times in heterogeneous traffic. J. Traffic Transp. Eng. 2018, 5, 20–28. [Google Scholar] [CrossRef]
- Zeroual, A.; Harrou, F.; Sun, Y.; Messai, N. Integrating Model-Based Observer and Kullback–Leibler Metric for Estimating and Detecting Road Traffic Congestion. IEEE Sens. J. 2018, 18, 8605–8616. [Google Scholar] [CrossRef]
- Heissenbüttel, M.; Braun, T.; Bernoulli, T.; Wälchli, M. BLR: Beacon-less routing algorithm for mobile ad hoc networks. Comput. Commun. 2004, 27, 1076–1086. [Google Scholar] [CrossRef]
- Chen, M.; Kwon, T.; Mao, S.; Yuan, Y.; Leung, V.C. Reliable and energy-efficient routing protocol in dense wireless sensor networks. Int. J. Sens. Netw. 2008, 4, 104. [Google Scholar] [CrossRef]
- Alharbi, A.; Al-Dhalaan, A.; Al-Rodhaan, M. A Mobile Ad hoc Network Q-Routing Algorithm: Self-Aware Approach. Int. J. Comput. Appl. 2015, 127, 1–6. [Google Scholar] [CrossRef]
- Zhao, G.; Huang, L.; Li, Z.; Xu, H. Hybrid routing by joint optimization of per-flow routing and tag-based routing in software-defined networks. Tsinghua Sci. Technol. 2018, 23, 440–452. [Google Scholar] [CrossRef]
- Saravanan, P.; Kalpana, P. Novel Reversible Design of Advanced Encryption Standard Cryptographic Algorithm for Wireless Sensor Networks. Wirel. Pers. Commun. 2018, 100, 1427–1458. [Google Scholar] [CrossRef]
- Montazerolghaem, A.; Moghaddam, M.H.Y.; Tashtarian, F. Overload Control in SIP Networks: A Heuristic Approach Based on Mathematical Optimization. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2017. [Google Scholar]
- Gong, D.-W.; Sun, J.; Miao, Z. A Set-Based Genetic Algorithm for Interval Many-Objective Optimization Problems. IEEE Trans. Evol. Comput. 2018, 22, 47–60. [Google Scholar] [CrossRef]
- Patra, M.; Thakur, R.; Murthy, C.S.R. Improving Delay and Energy Efficiency of Vehicular Networks Using Mobile Femto Access Points. IEEE Trans. Veh. Technol. 2017, 66, 1496–1505. [Google Scholar] [CrossRef]
- Li, Y.; Chai, K.K.; Chen, Y.; Loo, J. Duty cycle control with joint optimization of delay and energy efficiency for capillary machine-to-machine networks in 5G communication system. Trans. Emerg. Telecommun. Technol. 2015, 26, 56–69. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Cheng, Z.; Zhu, X. EMIP: Energy-efficient itinerary planning for multiple mobile agents in wireless sensor network. Telecommun. Syst. 2016, 62, 93–100. [Google Scholar] [CrossRef]
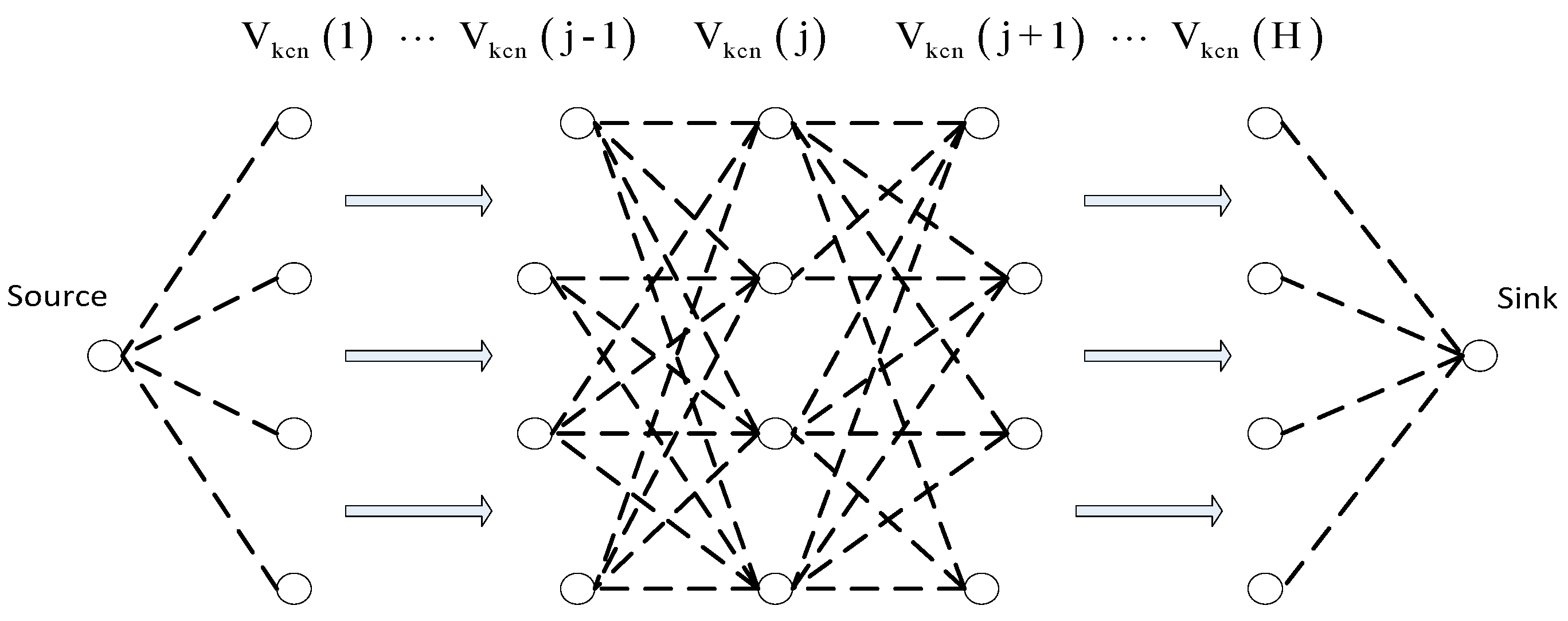


| Beaconless Geographic Routing | KCN | |
|---|---|---|
| Number of potential forwarding nodes per hop | The number is uncertain and the reliability cannot be guaranteed | The quantity is k, and the reliability can be predicted. |
| Delay of forwarding data | Three-time handshake is required, and the time is extended and uncertain. | Reference nodes are selected centrally, allocated slots are set, and the delay is smaller. |
| Remaining Energy of Forwarding Node | Not considered | Will consider |
| Regular redistribution | No | Yes |
| Node dormancy | No | Yes |
| Symbol | Explain | Symbol | Explain |
|---|---|---|---|
| Source node | Probability of k awakening at K nodes per hop | ||
| Sink node | Reference node of node m of hop i | ||
| Number of hops from source to target | Search area of collaboration node | ||
| Link Failure Rate | Rmt | With sink node t as the center of the circle with radius , the radius meets formula | |
| Node density | The diameter of the circle is connected between the ideal position of the next hop of node m. | ||
| Transmission radius | Number of all neighbors of node m | ||
| Distance between nodes u and v | All the cooperative nodes of the i-hop | ||
| Total number of cooperative nodes per hop design | Residual energy of the node | ||
| Number of active nodes per hop | The success rate of the i-hop k available collaboration nodes | ||
| Construction cycle of KCN | End-to-end reliability | ||
| Node duty cycle |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Raw data size | 2048 bits | Network size | 1000 × 500 m |
| MA code size | 1024 bits | Radio transmission range | 60 m |
| MA accessing delay | 10 ms | Number of sensor node | 800 |
| Data processing rate | 100 Mbps | Media Access Control (MAC) layer standard | 802.11b |
| Aggregation ratio | 0.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Zhang, Y.; Yi, X. Research on Cooperative Communication Strategy and Intelligent Agent Directional Source Grouping Algorithms for Internet of Things. Future Internet 2019, 11, 233. https://doi.org/10.3390/fi11110233
Zou Y, Zhang Y, Yi X. Research on Cooperative Communication Strategy and Intelligent Agent Directional Source Grouping Algorithms for Internet of Things. Future Internet. 2019; 11(11):233. https://doi.org/10.3390/fi11110233
Chicago/Turabian StyleZou, Yongyan, Yanzhi Zhang, and Xin Yi. 2019. "Research on Cooperative Communication Strategy and Intelligent Agent Directional Source Grouping Algorithms for Internet of Things" Future Internet 11, no. 11: 233. https://doi.org/10.3390/fi11110233




